Multimodal Mapping of the Face Connectome

Abstract

Face processing supports our ability to recognize friend from foe, form tribes, and understand the emotional implications of changes in facial musculature. This skill relies on a distributed network of brain regions but how these regions interact is poorly understood. Here, we integrate anatomical and functional connectivity measurements with behavioral assays to create a global model of the face connectome. We dissect key features such as the network topology and fiber composition. We propose a neurocognitive model with three core streams, and face processing along these streams occurs in a parallel and reciprocal fashion. While long-range fiber paths are important, face network is dominated by short-range fibers. Last, we provide some evidence that the well-known right lateralization of face processing arises from imbalanced intra/interhemispheric connections. In sum, the face network relies on dynamic communication across highly structured fiber tracts, which enables coherent face processing that underpins behavior and cognition.

Introduction

Face perception is a highly developed skill in humans due to its unique evolutionary and social significance. From a brief glance at a face, we are able to effortlessly glean information about a person’s age, gender, identity, social group, emotional state, attentional focus, and several other characteristics such as trustworthiness ¹.

Early work on individuals with focal brain lesions revealed that portions of the inferior temporal cortex in the right hemisphere might be critical for face processing since damage to this region often resulted in the clinical syndrome of prosopagnosia ¹. Lesion work gave way to single-unit recording and fMRI studies that documented a distributed set of specialized face patches ^2–4. Many of these patches run along the ventral visual stream to the temporal pole, with more posterior regions processing fundamental aspects of faces (e.g. the occipital face area (OFA) analyzes facial parts and the fusiform face area (FFA) engages in more holistic processing of the face) ^1,5–7, while more anterior regions such as the anterior temporal lobe (ATL) and amygdala (AMG) link faces to conceptual knowledge and affective states ^8–11. Other regions that appear to play a role in face processing include the posterior superior temporal sulcus (STS), involved in processing facial movements ^5,12, the posterior cingulate cortex (PCC), potentially involved in episodic memory related to faces ⁶, the inferior frontal gyrus (IFG) which mediates emotion and gaze perception ^13,14, and the orbitofrontal cortex (OFC) which is thought to evaluate socially rewarding aspects of faces such as their attractiveness and trustworthiness ^15–19.

How these regions are interconnected and how they functionally interact to give rise to the detailed perceptual, social, affective, and mnemonic abilities that constitute face processing is poorly understood. One highly influential model of face processing – the Haxby model ^5,6,20 – postulates a serial-hierarchical structure in which information flows from face patch to face patch in an orderly manner, from posterior brain regions to anterior regions (e.g. the OFA → FFA; OFA → STS). In addition, this model claims that there is a unique face processing “core” system – the OFA, FFA and STS – that does the most important aspects of face processing while the extended system – the ATL, AMG, and PCC – gleans other information from faces. More recent models have extended the Haxby model by suggesting that there are two face processing streams – a dorsal stream and a ventral stream – and that there is some reciprocal processing within each stream ^1,7,21.

Initial forays into understanding how face-sensitive regions are interconnected have primarily implicated portions of a large white matter tract that runs along the ventral visual stream, the inferior longitudinal fasciculus (ILF) in face processing ²². However these studies are limited because they relied on small sample sizes, they examined partial connectomes, links to behavioral performance are often lacking, and they did not look at structural and functional/effective connectivity together ^23–26. It remains unclear how the full set of face-sensitive regions is anatomically interconnected, how they functionally interact with each other across tasks and contexts, and how network-level characteristics relate to behavior.

In the present study we tested predictions of prominent neurocognitive models of face processing ^1,5,6,20, in addition to asking several new questions derived from anatomy studies about the role of short-range vs. long-range white matter, in addition testing an older idea about the possible genesis of hemispheric asymmetries in face processing. We used the human connectome project (HCP) ²⁷ dataset because it provides a large population of subjects and high quality of multimodal neuroimaging data. We functionally defined nine face-sensitive regions in each subject, then used tractography to delineate local, long-range, and cross-hemisphere white matter connections. We also investigated functional and dynamical properties of this network using paired resting-state and task-state functional datasets, and we explored the anatomy-function relation by interrogating the correspondence between anatomical and functional connectomes. Finally, we employed HCP behavioral tests to examine whether individual differences of certain face skills (e.g. facial emotion recognition) can be explained by any connectome characteristics.

Results

Anatomical connectome

Diffusion MRI (dMRI) combined with tractography is currently the only in vivo method to delineate the fiber tracts between brain regions. Tractography takes diffusion measurements as input and produces the connectome, a collection of white matter fascicles, as output ²⁸. Tractography is not without its limitations ^29,30 but there are now several instances in which it has been demonstrated that the results of tractography correlate well with the results from histology ^31–33. By employing five independent but complementary tractography analyses, we obtained a detailed and comprehensive picture of the face network structural connectome.

First, we mapped the global connectivity pattern for each face ROI. Axonal projections determine where a region receives information from and where it can exert effects. Although each face ROI’s major cortical projections were its neighboring areas, they exhibited idiosyncratic distant projections (see Supplementary Figure 1). Posterior areas (OFA and FFA) had large projections to the temporal pole along the ventral temporal cortex. In contrast, the STS had prominent projections in and around the IFG, and vice versa. Medial ROIs (AMG, OFC and PCC) only had projections to medial structures. In addition, most face ROIs seemed to have direct fiber projections from early visual cortex (EVC).

The global connectivity patterns also implied that each region might have differential cross-hemispheric projections to its counterpart in the other hemisphere (see different corpus callosum projections from each face ROI in Supplementary Figure 1). To further explore this, we reconstructed interhemispheric connections for each pair of bilateral ROIs (e.g. Left FFA with right FFA). Results confirmed our speculation by showing that bilateral face ROIs were mainly connected through four different midline structures (see Extended Data Figure 1): the rostrum (OFC), the genu (IFG), and the splenium (OFA, FFA, STS, PCC and ATL) of the corpus callosum, and the anterior commissure (AMG and ATL).

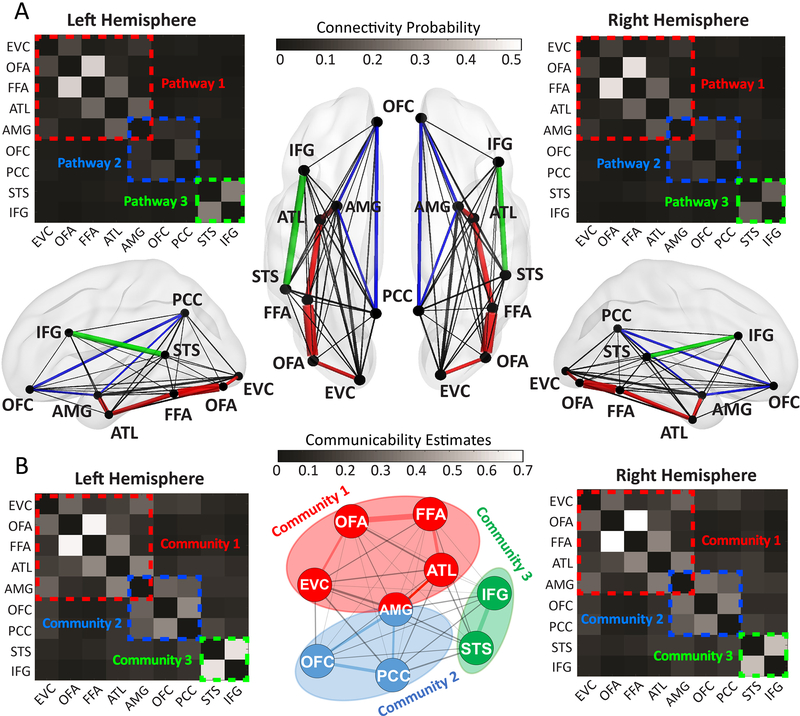
Thirdly, we delineated inter-regional connections between face areas within the same hemisphere. Anatomical connection strength is often interpreted as a measure of capacity for information flow and provides insights about key pathways through which neural signals propagate within the network ³⁴. Here, we reconstructed 36 pairwise connections between 9 face ROIs in each hemisphere and extracted their microstructural properties (e.g. connectivity probability, streamline counts) to estimate structural connectivity. The landscape of the connectivity probability map (Fig 1A) indicated three core pathways in the face network: a ventral pathway (EVC-OFA-FFA-ATL-AMG), a medial pathway (AMG-OFC-PCC) and a dorsal pathway (STS-IFG). A similar pattern can also found in the streamline count map (see Supplementary Figure 2). To further validate this partition of three core pathways, we examined another established graph theoretic measure, the ‘communicability’, between each ROI pair ³⁵. Different from the connection weight between a pair of regions (which only measures the direct path), communicability quantifies the “ease of communication” via all possible paths between regions by taking into consideration both direct and indirect connections. Hence, communicability encodes additional useful information about the global organization of a network mediating interregional communication and has been widely used to determine anatomical communities ³⁶. Here, the community detection analysis on the communicability graph confirmed the existence of three separate communities in the face network and they corresponded well with the partitions of three core pathways (Fig 1B).

Figure 1. The Anatomical Connectome of the Face Network.

(A) The structural connectivity map for each hemisphere. The pairwise connection strength (i.e. connectivity probability) between nine face ROIs were plotted in weighted matrices and wiring diagrams. The width of each line in wiring diagrams proportionally reflects their mean connectivity probability across all subjects. Three colored dashed rectangles indicate three core pathways: EVC-OFA-FFA-ATL-AMG (pathway 1, red), AMG-OFC-PCC (pathway 2, blue) and STS-IFG (pathway3, green). (B) The communicability map for each hemisphere. Based on graph theory, we derived the communicability map from individuals’ structural connectivity matrix (see methods). Subsequent community detection analysis (the middle panel) indicated three communities within the face network: EVC-OFA-FFA-ATL-AMG (community 1, red), AMG-OFC-PCC (community 2, blue), and STS-IFG (community 3, green). AMG was found to be shared by Community 1 and 2. The three communities found in the communicability graph resonated well with the partition of three core pathways on structural connectivity graphs.

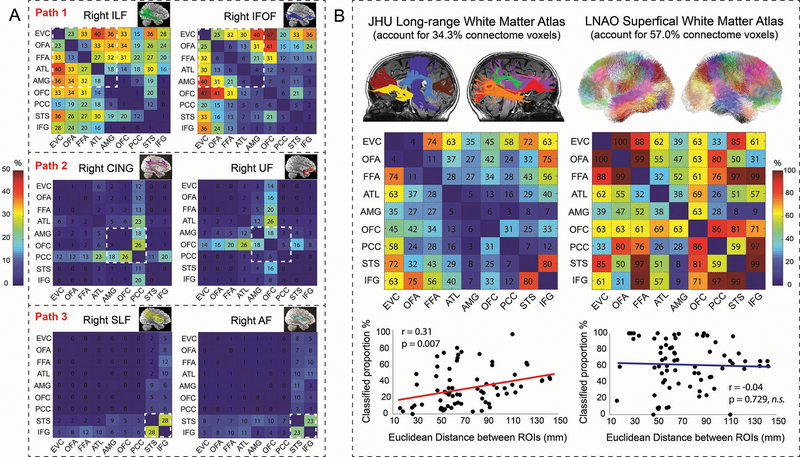
But how are these core pathways formed? One possibility is that they are constructed of large white matter bundles such as major fasciculi. Indeed, a small number of long-range tracts has been repeatedly reported in the face perception literature and disruption of these tracts can lead to prosopagnosia ²². Here we used an automatic fiber reconstruction technique ³⁷ to delineate ten major fasciculi for each subject and compared them with the ROI-ROI tracts at the individual level. By calculating the degree of their overlapped trajectories, we can estimate the involvement of major fasciculi in the face connectome. Results revealed the three core pathways were mainly supported by six major fasciculi, but to a much lesser degree than we expected (Fig 2). Specifically, less than 30% of the ventral pathway was mediated by the inferior longitudinal fasciculus (ILF, 28.79 ± 8.11% (mean ± SD)) and inferior fronto-occipital fasciculus (IFOF, 20.76 ± 12.27%); only ~12% of the medial pathway overlapped with the cingulum (CING, 15.03 ± 10.24%) and uncinate fasciculus (UF, 8.96 ± 6.58%); less than 30% of the dorsal pathway was found to be merged with the arcuate fasciculus (AF, 29.05 ± 9.15%) and superior longitudinal fasciculus (SLF, 25.01 ± 7.46%).

Figure 2. The Relative Contribution of Large-range and Short-range Fibers to the Face Connectome.

(A) The overlap between six major white matter bundles ³⁷ and the face connectome in the right hemisphere. Each percentage number in the matrices represents the mean overlapped volumes between an ROI-ROI connection and a major fasciculi across all subjects. Taking the FFA-ATL connection as an example, 27% voxels of the tract overlapped with the ILF and 6% overlapped with the IFOF; the tract did not overlap with the SLF (0%) and had minimal portion with the CING (2%), UF (2%), and AF (1%). After reviewing all overlap maps with 10 major fasciculi in the right hemisphere, we found the ventral pathway (EVC-OFA-FFA-ATL-AMG) was primarily contributed by the ILF and IFOF; the medial pathway (AMG-OFC-PCC) was mainly constructed with the UF and CING; the dorsal pathway (STS-IFG) was mostly supported by the SLF and AF. Similar results were found in the left hemisphere (see Supplementary Figure 3). (B) After overlaying all 72 ROI-ROI connections (across two hemispheres) onto two standard white matter atlases, we found ~57% of the face connectome can be classified as short-range fibers whereas only ~34.3% can be labelled as long-range fibers. For each ROI-ROI connection, the numbers in the matrices represent how well it can be explained by the tracts in each atlas. Take the OFA-FFA connection as an example, 11% voxels in bilateral OFA-FFA connections were overlapped with long-range tracts in the JHU atlas ⁴¹, whereas 99% voxels in bilateral OFA-FFA connections were overlapped with superficial tracts in the LNAO atlas ⁴³. For each hemisphere’s results, see Supplementary Figure 4. In addition, we found an important relationship between the face connectome and the long-range fibers: the more two face ROIs were spatially separated from each other (e.g. EVC-OFA vs EVC-OFC), the more contributions long-range fibers would make for their connections (e.g. 4% vs 45%). No credible evidence of such linear relationship was found for short-range fibers (r =−0.042, p = 0.729, BF₁₀ =0.098).

Since only a small proportion of the anatomical connectome was contributed by major fasciculi, we directed our attention to another important class of white matter—short-range or U-shaped fibers. Tracer studies have demonstrated that long-range fasciculi comprise only a minority of the whole brain connectome with the majority consisting of short association fibers that lie immediately beneath the gray matter, connecting adjacent gyri ^38–40. By projecting all 72 ROI-ROI connections over two standard white matter atlases of long-range ⁴¹ and short-range fibers ^42,43, we interrogated the relative contribution of the two white matter systems for the face connectome (Fig 2). While more than 57.0% of the ROI-ROI connections can be classified as short-range fibers, only 34.3% of the connectome can be labelled by the tracts in the long-range white matter atlas. In addition, we found a positive relationship between two ROIs’ spatial distance and the contribution of long-range fibers (r(72) =0.314, p=0.007, 95% CI: 0.088, 0.540), suggesting that the further two face ROIs are separated from each other (e.g. EVC-OFA vs EVC-OFC), the more long-range fibers would get involved in constructing their connections (e.g. 4% vs. 45%).

Functional connectome

The anatomical connectome strictly allows some neuronal populations to directly interact while excluding most others. In contrast, the functional connectome is inherently dynamic and context-dependent ⁴⁴. We mapped three different classes of functional brain connectivity to reveal the way face ROIs interact: co-activation patterns were identified during rest (resting-state functional connectivity, rsFC) or during the face localizer task (task-state functional connectivity, taskFC), and effective connectivity (EC) was modelled by psychophysiological interaction (PPI) and dynamic causal modelling (DCM) to reveal directional information flow driven by the face stimuli ^45–47.

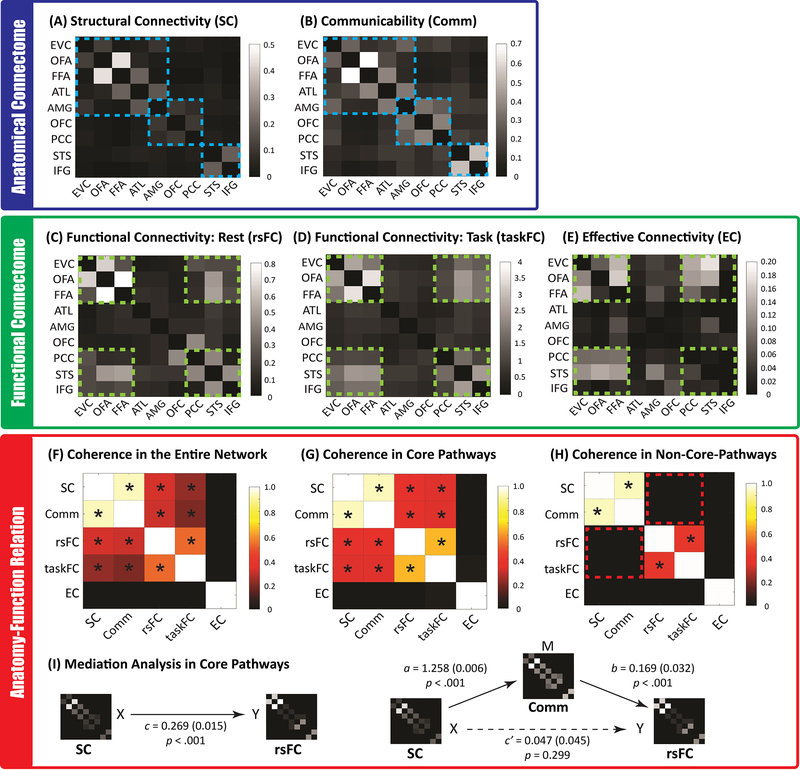
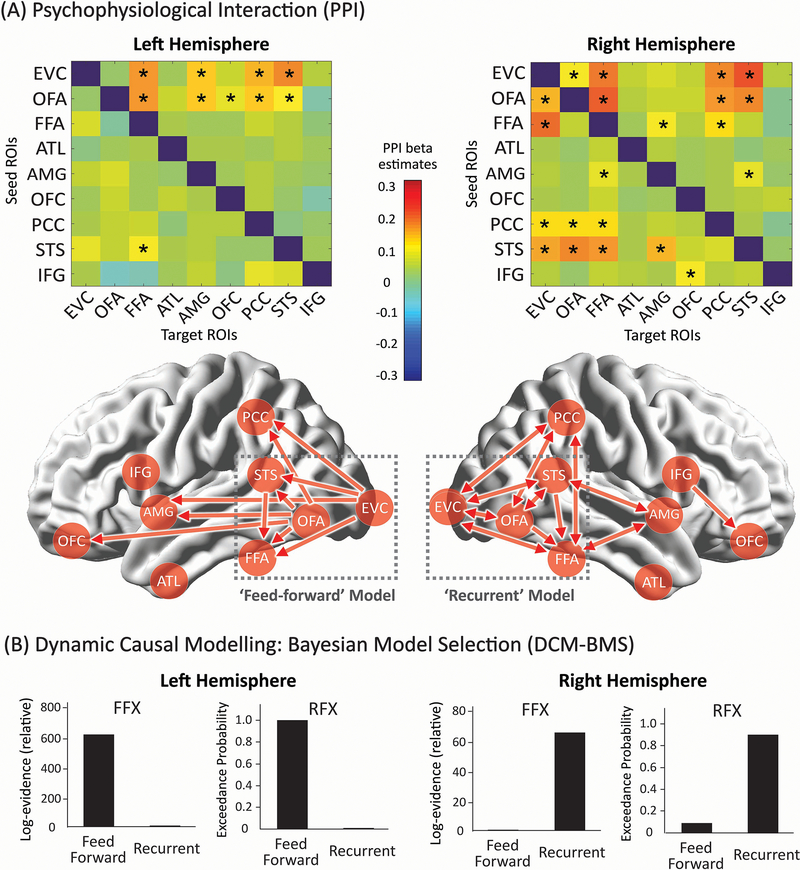
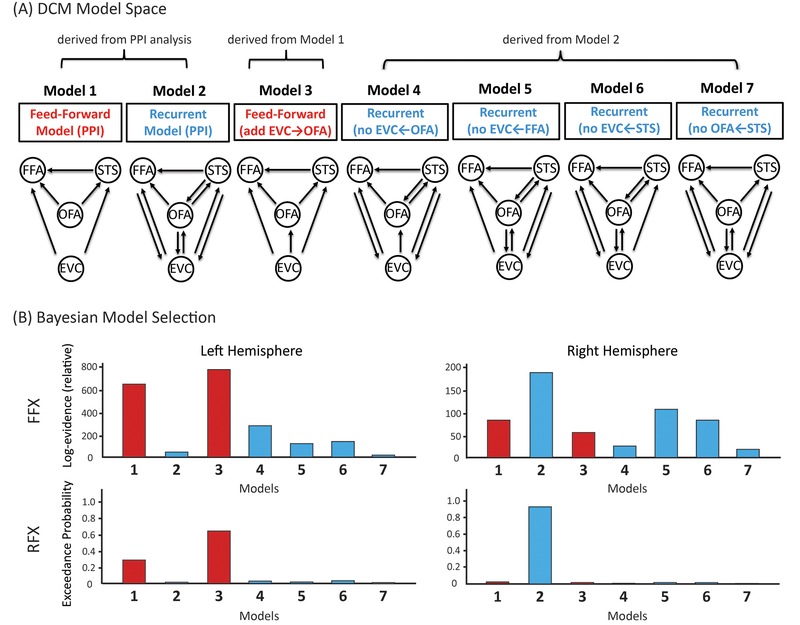
We found the results from the rsFC and taskFC analysis to be highly correlated (mean r=0.518, t(666)=80.97, p<0.001, Cohen’s d=4.43, 95% CI: 0.505, 0.531)(Fig. 3F), consistent with recent findings from the connectome at large ^48,49. Both showed strong co-activations among six face ROIs (EVC, OFA, FFA, STS, IFG and PCC) (Fig. 3C and 3D). This suggests the existence of an ‘intrinsic’ functional subnetwork within the face system that is constantly active and synchronized across contexts ^44,48,50. However, functional connectivity only expresses statistical dependencies (correlations) among time courses that do not generally represent direct neuronal signaling ³⁴. In contrast, effective connectivity has been proposed as a more powerful way to capture stimulus-driven patterns of directional influence among neural areas ⁵¹. Here we implemented PPI to explore network-level dynamics evoked by face stimuli and then used DCM for confirmatory analyses. PPI analyses build simple static models of coupling between one or more brain regions and allow researchers to explore directed changes in connectivity by establishing a significant interaction between the seed region and the psychological context ^51–53, whereas DCM is a framework for testing alternative hypotheses/models of neural dynamics, fitting them to data and comparing their evidence using Bayesian model comparison ^47,54. Our PPI analyses revealed that face-sensitive brain dynamics primarily occurred to the same functional subnetwork (Fig. 3E) but with entirely different patterns between the two hemispheres (Fig. 4). While information processing within the left hemisphere was organized in a purely feed-forward fashion (i.e. the information cascade unfolded from posterior to anterior ROIs), the right hemisphere exhibited a predominantly recurrent architecture (i.e. reciprocal connections). For example, multiple bidirectional effective connections were observed among right core face areas (EVC, OFA, FFA, and STS; see Fig 4), suggesting the coexistence of bottom-up and top-down interactions and computations during face viewing. Critically, this differential pattern across two hemispheres was supported by subsequent DCM analyses (Fig 4B). Results from Bayesian model comparison suggest the feed-forward processing model fits best with the data observed in the left hemisphere whereas the recurrent processing model fits best for data in the right hemisphere. For Bayesian model selection fixed-effects and random-effects analysis, the feed-forward model exhibited higher group log-evidence (619.04 vs 1.12) and exceedance probability (99.83% vs 0.17%) than the recurrent model in the left hemisphere, whereas the recurrent model exhibited higher group log-evidence (65.39 vs 0.84) and exceedance probability (91.21% vs 8.79%) than the feed-forward model in the right hemisphere. An analysis of absolute model fit suggests the feed-forward model can explain 16 ± 8% (mean ± std) of the observed variance in the left hemisphere and the recurrent model accounts for 18 ± 9% of the observed variance in the right hemisphere. An additional DCM analysis with larger model space was also performed to re-validate this differential pattern of face-evoked information processing across two hemispheres (see Extended Data Figure 2).

Figure 3. All Brain Connectivity Maps of the Face Network and Their Correspondence.

The top level blue box (A & B) depicts the anatomical connectome consisting of three core pathways/communities (highlighted in blue dashed lines). The middle level green box displays the functional brain connectivity patterns during rest or during the face localizer task. Most co-activations (C and D) and task-modulated brain dynamics (E was from PPI analyses) were observed among six face areas (i.e. EVC, OFA, FFA, PCC, STS, and IFG, which were highlighted in green dashed lines). The lower level red box shows the correspondence between different types of brain connectivity, either across the entire network or only within the three core pathways. Asterisks in (F), (G), and (H) denote significant positive correlations between two connectivity types. The results in (F) showed that the structural connectivity (SC) and communicability map (Comm) across the entire face network were highly correlated with functional connectivity maps (rsFC and taskFC), but the effective connectivity (EC) map was dissimilar with any of them, owing to its nature of reflecting asymmetrical and directional information processing during face perception. We further demonstrated that the tight anatomy-function relationship across the entire network was mainly driven by core pathways (G) because little evidence of such anatomy-function association was found outside of the core pathways (H) (the red dashed boxes represent the null anatomy-function correspondence). For simplicity, all maps from (A) to (H) were results from the right hemisphere. The left hemisphere yielded a very similar pattern of correspondence and can be found in Supplementary Figure 5. Finally, mediation analyses revealed (I) the network communicability functions as mediator for the association between anatomical and functional connectivity. This mediator role was only found in the core pathways (but no evidence for the entire face network). Numbers in the bracket indicate the standard error of the coefficient in each mediation model.

Figure 4. The Brain Dynamics within the Face Network during the Face Localizer Task.

(A) PPI results. The upper row shows the effective connectivity matrices for each hemisphere. Asterisks indicate statistically significant effective connectivity. The lower row is an illustration of all directional information flow summarized from the two effective connectivity matrices. Qualitatively, the two hemispheres exhibited entirely different patterns of brain dynamics. Only feed-forward information cascades were identified in the left hemisphere while both feed-forward and feed-back processing were found in the right hemisphere. To further validate these PPI findings, we built two DCM models (i.e. feedforward vs recurrent) and tested their respective fitness to the observed data in each hemisphere. As the most powerful applications of DCM have used networks with relatively small number of nodes and relatively simple model space motivated by priori knowledge, the two DCM models were constructed with four core face areas interacting the same way as they exhibited in PPI results (i.e. two dash-line grey boxes). For more details of model specifications as well as additional exploratory analysis on larger model space, please check Extended Data Figure 2. (B) DCM Bayesian model selection results. The fixed-effects (FFX) and random-effects (RFX) group analyses consistently indicated that the ‘Feedforward’ model was optimal for the left hemisphere whereas the ‘Recurrent model’ was optimal for the right hemisphere. Overall, the effective connectivity analyses by PPI and DCM both suggested a differential pattern of face-evoked information processing across two hemispheres.

Spatial specificity of the face connectome

It is important to consider whether the brain connectivity patterns we observed demonstrate spatial specificity (Fig 5). Based on subject-specific ROIs defined by the face localizer, we discovered three distinct pathways in the anatomical connectome and six synchronized areas in the functional connectome (Fig 3). To further explore how these connectivity organizations are spread and changed in space, we performed analogous tractography and connectivity analyses while using two other ways to select ROIs’ locations. When we shuffled subject-specific ROIs across subjects (so that subject A’s OFA coordinates now became subject B’s OFA coordinates), we found the shuffled maps remained almost the same as the original ones for structural connectivity (SC) (r(36)=0.995, p<0.001, 95% CI: 0.961, 1.029), rsFC (r(36)=0.991, p<0.001, 95% CI: 0.944, 1.038) and taskFC (r(36)=0.987, p<0.001, 95% CI: 0.930, 1.043), but the effective connectivity (EC) pattern was substantially altered after this permutation manipulation (i.e. the shuffled and original EC maps were no longer correlated, r(72)=−0.091, p=0.445, 95% CI: −0.329, 0.146; BF₁₀=0.124) (Fig 5 middle row). When we moved each ROI farther away from its putative range (e.g. 20mm apart from its original coordinates), we found the topologies of all brain connectivity were completely changed (i.e. the 20mm shifting maps were no longer correlated with original ones. For SC: r(36)=0.231, p=0.175, 95% CI: −0.108, 0.570; BF10=0.323; for rsFC: r(36)=0.241, p=0.156, 95% CI: −0.097, 0.579; BF10=0.351; for taskFC, r(36)=0.113, p=0.510, 95% CI: −0.233, 0.460; BF10=0.161; for EC: r(72)=−0.191, p=0.109, 95% CI: −0.425, 0.043; BF10=0.334) (Fig 5 bottom row). These findings suggest the ‘intrinsic’ architectures of the face network (i.e. SC, rsFC, taskFC) might follow a more global pattern that is configured as relatively stable across small spatial extent (e.g. <15mm) and face-sensitive voxels and nearby non-face sensitive voxels share similar fiber tracts and hence exhibit resembled neural signal propagations. In contrast, the dynamic features of the face connectome (i.e. effective connectivity pattern) seem to be highly determined by the voxel-level face-selectivity.

Figure 5. The Spatial Specificity of Face Connectome Organizations in the Right Hemisphere.

Brain connectivity patterns were measured and compared across three different ways of ROI definition. We first (Top Row) defined each ROI by using subject-specific coordinates from the functional face localizer. The major findings in this article came from this method, such as three distinct pathways founded in the structural connectivity (blue dash line) and six synchronized areas exhibited in the functional and effective connectivity (Green dash line). We then (Middle Row) permuted subject-specific coordinates across subjects (e.g. subject A’s FFA coordinates now became subject B’s; subject C’s ATL coordinates now became subject D’s). Since the individual variations of each ROI’s coordinates can be typically circumscribed by a 10–15mm radius sphere (see group coordinate ranges listed in Table S1), these new shuffled coordinates were in relatively close proximity to the original subject-specific ones. We found the patterns of structural connectivity and functional connectivity during rest and task remained the same after this permutation manipulation but the effectivity connectivity was changed significantly. Lastly (Bottom Row), we chose each ROI even farther away in space—with new coordinates just outside the putative range (i.e. 20 mm apart from its original coordinates, so that subject A’s FFA coordinates could now fall into inferior temporal gyrus). After this 20mm shifting manipulation, these out-of-range coordinates drastically altered all four brain connectivity patterns, thus showing spatial specificity of our findings. Similar results of spatial specificity were found in the left hemisphere.

Individual variance of the face connectome

It is also important to consider how similarly the face network is organized across subjects. Since Fig 3 only showed group-averaged brain connectivity maps, we would like to validate how representative these group-averaged maps were. To reveal the distribution of group-to-individual similarity across all subjects, we conducted correlation analyses between group-averaged maps and subject-specific maps for each type of brain connectivity measure (see histograms in Supplementary Figure 6A). Results suggested that group-averaged matrices were strongly correlated with subject-specific matrices for SC, rsFC and taskFC (see stats details in Supplementary Figure 6A) and most subjects (>75%) exhibited highly similar maps (r > 0.5) as the group-averaged ones. The group-averaged EC matrices, however, showed moderate correlation with subject-specific EC matrices and most subjects (>67%) exhibited small-to-medium correlation (0.1<r<0.5) with the group-averaged ones.

Next, we used two cross-validation schemes to further probe group-to-group and group-to-individual similarity, that is, the split-half cross-validation (using 50% subjects’ matrices to predict the other 50% subjects’ matrices) and the leave-one-out cross-validation (using N-1 subjects’ matrices to predict a new subject’s matrices) (see Supplementary Figure 6B). Again, both methods revealed very high train-test correlation for SC, rsFC and taskFC and relative moderate train-test correlation for the EC (see stats details in Supplementary Figure 6B). In sum, we found the organization of face connectome is highly homogeneous across subjects and in particular for SC, rsFC and taskFC. Thus, our reported group-averaged matrices indeed reflect most individuals’ connectivity patterns.

Structural-functional connectivity relationships

To further explore the anatomy-function relationship within the face network, we examined the correspondence between anatomical and functional connectome. Across the entire network, functional connectivity patterns (rsFC and taskFC) appeared to correlate highly with structural connectivity (SC) and communicability (Comm) patterns (see Fig. 3F; rsFC & SC: mean r=0.321, t(666)=43.72, p<0.001, d=1.69, 95% CI: 0.306, 0.335; rsFC & Comm: mean r=0.304, t(666)=47.42, p<0.001, d=1.84, 95% CI: 0.291, 0.316; taskFC & SC: mean r=0.234, t(666)=33.73, p<0.001, d=1.31, 95% CI: 0.221, 0.248; taskFC & Comm: mean r=0.199, t(666)=32.50, p<0.001, d=1.26, 95% CI: 0.187, 0.211). This supports the idea that functional connectivity is dictated by the underlying white matter architecture and network communicability ^34,55. However, when we scrutinized the anatomy-function similarity inside or outside the core pathways, we found the tight relationship was only observed in the core pathways (rsFC & SC: mean r=0.358, t(666)=26.46, p<0.001, d=1.02, 95% CI: 0.331, 0.384; rsFC & Comm: mean r=0.367, t(666)=30.21, p<0.001, d=1.17, 95% CI: 0.343, 0.391; taskFC & SC: mean r=0.343, t(666)=25.92, p<0.001, d=1.00, 95% CI: 0.317, 0.369; taskFC & Comm: mean r=0.335, t(666)=27.56, p<0.001, d=1.07, 95% CI: 0.312, 0.359)(see Fig. 3G) but no statistically significant association in the non-core-pathways (rsFC & SC: mean r=0.005, t(666)=0.72, p=0.473, d=0.03, 95% CI: −0.009, 0.020, BF₁₀=0.040; rsFC & Comm: mean r=0.007, t(666)=0.72, p=0.472, d=0.03, 95% CI: −0.012, 0.025, BF₁₀=0.040; taskFC & SC: mean r=0.003, t(666)=0.36, p=0.722, d=0.01, 95% CI: −0.012, 0.018, BF₁₀=0.033; taskFC & Comm: mean r=0.004, t(666)=0.44, p=0.659, d=0.02, 95% CI: −0.015, 0.023, BF₁₀=0.034)(see Fig. 3H). This suggested that the high anatomical-function coherence across the entire face network was mainly driven by the core pathways. Furthermore, even though the general pattern of structural and functional connectivity were highly correlated inside the core pathways, strong disagreement can still be observed in multiple connections (Fig 3A & 3C). For example, we found the FFA and ATL are structurally interconnected but not functionally interconnected (the same applies to ATL-AMG). In contrast, the OFA/FFA and STS were functionally interconnected but showed weak structural connectivity. All of these observations suggest that rsFC is an imperfect representation of the underlying structural connectivity ^56,57.

Previous research reported that communicability might be a useful analytic measure to link structural and functional connectivity ^58,59. To test this hypothesis, we applied multilevel mediation analyses to our data, assessing whether communicability mediated the relationship between structural connectivity and rsFC. For the core pathways (Fig 3I), the results showed that structural connectivity significantly predicted rsFC (path c: B=0.269, SE=0.015 p<0.001), which was consistent with our correlation analysis in Fig 3G; however, after adding communicability into the model, there was no statistically significant association between structural connectivity and rsFC (path c’: B=0.047, SE=0.045, p=0.299). Moreover, as assessed by Akaike’s information criterion (AIC) and Bayesian information criterion (BIC), model fit was greater with communicability added in as the mediator (AIC = 1211.84; BIC = 1271.08) than with the model in which structural connectivity independently predicted rsFC (AIC = 1230.10; BIC = 1289.33), indicating communicability fully mediated the relationship between structural connectivity and rsFC. In contrast, no credible evidence suggests communicability as a mediator between structural connectivity and rsFC for the entire face network (path c: B=0.220, SE=0.008, p<0.001, AIC=−15981.75, BIC=−15340.85; path c’: B=0.279, SE=0.022, p<0.001, AIC=−15982.39, BIC=−15341.50). In summary, we found communicability mediated the anatomy-function relationship only in core face pathways and it outperformed the standard structural connectivity as a predictor of rsFC.

Brain-behavior associations

The simplest and most popular method for establishing brain-behavior relationships is correlation. We first computed simple Pearson correlations between individual’s facial emotion recognition performance and all types of brain measurements (e.g. BOLD signals from each face area, white matter characteristics, functional connectivity, and effective connectivity). There was no statistically significant univariate correlation in this whole-connectome search (all rs<0.065, ps>0.092, all BF₁₀<0.119).

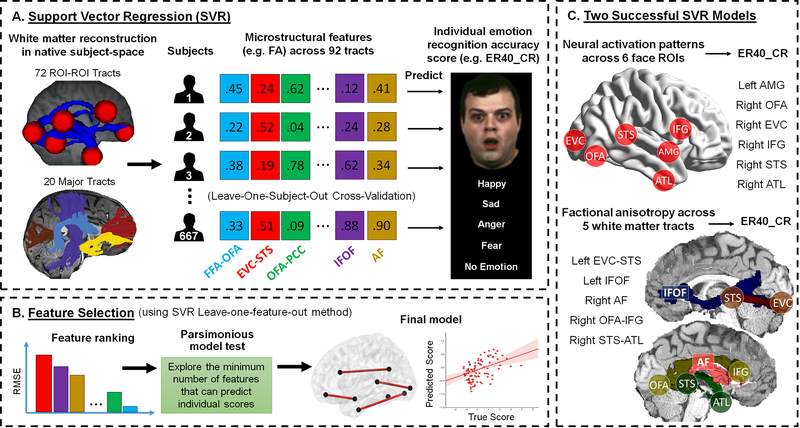
Since the simple correlation method is not robust when studying a complex brain-behavior association ⁶⁰ and can typically incur serious problems of multiple comparison when searching the whole connectome, we subsequently employed a machine learning regression algorithm. Individualized behavioral prediction using machine learning regression is becoming increasingly popular in neuroimaging and this approach has been deemed as multivariate pattern analysis for exploring complex relationship between behavior and distributed patterns of brain features ^61,62. Here we used support vector regression to examine whether the global pattern of any groups of brain metrics can predict individual face processing skills (Fig 6).

Figure 6. Schematic Overview of the Methods and Results Used in the Brain-Behavior Association.

(A) For each group of brain metrics (e.g. neural activity, white matter characteristics, functional connectivity, or effectivity connectivity), we built up a separate model for support vector regression (SVR). Take the white matter factional anisotropy (FA) as an example, we extracted FA values from 92 white matter tracts (72 ROI-ROI connections + 20 major fasciculi) across all subjects and set them as independent features in the model. We adopted the leave-one-subject-out cross-validation (LOOCV) scheme to train and test data and examined if the SVR model of a particular brain metric (e.g. FA) can predict a performance score (e.g. emotion recognition accuracy, ER40_CR ¹⁰¹). If the predicted score was significantly associated with the true score, we proceeded to the feature selection step. (B) We used a leave-one-feature-out method for feature selection (with a five-fold cross-validation scheme) and ranked each feature’s importance based on the incurred root-mean-square error (RMSE) in the absence of that feature. After that, we performed the parsimonious model test by sequentially testing a series of SVR models with combination of top n important features (e.g. top 10 at first, then top 9, 8, 7 …) until a model with n-1 feature that were no longer able to predict individual’s performance. Again, we adopted the LOOCV scheme to train and test data in the parsimonious model test. (C) Among all groups of brain metrics, we found only the SVM model with neural activity of all face ROIs and the model with FA value of all tracts can successfully predict individual’s emotion recognition accuracy. The parsimonious model tests further revealed a subset of 6 face ROIs and a subset of 5 white matter tracts that were the most predictive features for the two successful SVM models. It’s important to note that these two subsets of face ROIs and white matter tracts corresponded well with each other, suggesting that critical tracts were also connecting critical ROIs.

The support vector regression analyses revealed two groups of brain metrics that can successfully predict individual differences in facial emotion recognition accuracy: the neural activity features from all face ROIs (adjusted R²=0.014, F(1,665)=10.271, p=0.001, 95% CI: 0.048, 0.199) and the fractional anisotropy profile of all white matter tracts (adjusted R²=0.016, F(1,665)=12.136, p=0.001, 95% CI: 0.058, 0.209). To find which subsets of ROIs or white matter tracts were essential for prediction, we did feature selection to rank each feature’s contribution to the support vector regression model and implemented the parsimonious model test to reveal the minimal subsets that can successfully predict the behavior. The results revealed a subset of 6 face ROIs (left AMG, right OFA, right EVC, right IFG, right STS, right ATL) and a subgroup of white matter fiberpaths (left EVC-STS, left IFOF, right AF, right OFA-IFG, and right STS-ATL) as the most predictive and essential features for the two successful support vector regression models (Fig 6C). Surprisingly, the white matter parsimonious model (RMSE: 0.982) predicted behavior better than the neural activity parsimonious model (RMSE: 1.035). To further rule out these neural correlates’ function for general performance (e.g. task accuracy and reaction times), we used them to predict other HCP non-face behavioral performance. We found no credible evidence that these features are predictive for the working memory 2-back task accuracy and speed (i.e. neural activity model for accuracy: adjusted R²<0.001, F=0.57, p=0.450, 95% CI for B: −0.047, 0.105, BF₁₀=0.041; neural activity model for speed: adjusted R²=0.002, F=2.23, p=0.135, 95% CI for B: −0.018, 0.134, BF₁₀=0.093; white matter model for accuracy: adjusted R²<0.001, F=0.09, p=0.770, 95% CI for B: −0.065, 0.087, BF₁₀=0.032; white matter model for speed: adjusted R²<0.001, F=0.03, p=0.859, 95% CI for B: −0.083, 0.069, BF₁₀=0.031), theory of mind judgment speed (i.e. “neural activity model”: adjusted R²=0.001, F=1.89, p=0.169, 95% CI for B: −0.023, 0.129, BF₁₀=0.079; “white matter model”: adjusted R²<0.001, F=0.01, p=0.911, 95% CI for B: −0.072, 0.080, BF₁₀=0.031), and delay-discounting ability (“neural activity model”: adjusted R²=0.001, F=1.80, p=0.180, 95% CI for B: −0.024, 0.128, BF₁₀=0.076; “white matter model”: adjusted R²=0.003, F=3.17, p=0.080, 95% CI for B: −0.145, 0.007, BF₁₀=0.149). This confirms that our predictive brain features are specific to face processing. Note that little credible evidence suggests any functional or effective connectivity measures that were able to predict accuracy on the facial emotion recognition task (e.g. rsFC performance: adjusted R²=0.002, F=2.24, p=0.135, 95% CI for B: −0.018, 0.135, BF₁₀=0.094; EC performance: adjusted R²<0.001, F=0.01, p=0.931, 95% CI for B: −0.079, 0.073, BF₁₀=0.031).

Hemisphere lateralization

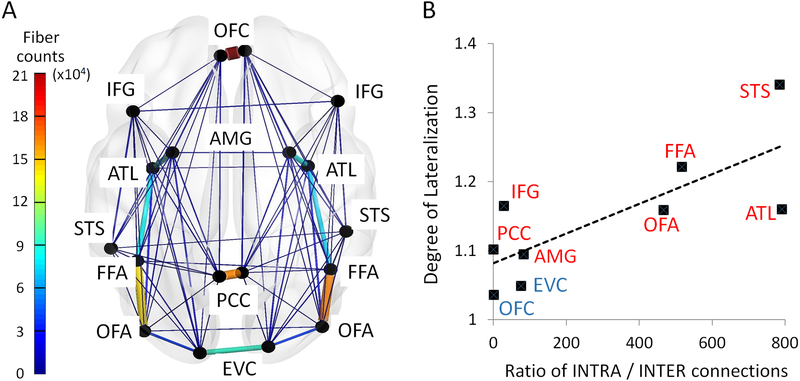
Face processing has been consistently linked to activity in the right hemisphere and unilateral right hemisphere damage can result in prosopagnosia while the same is not true of left hemisphere damage ¹. Here we asked whether such lateralization exists at the connectome level. Repeated-measure ANOVA revealed significant hemispheric asymmetry in face ROIs’ neural responses (F(1,666) = 238.64, p<0.001, η² = 0.264; mean difference: 0.617, 90% CI: 0.551, 0.683), white matter connectivity probability (F(1,666) = 9.25, p=0.002, η² = 0.014; mean difference: 0.002, 90% CI: 0.001, 0.002), functional connectivity during rest (F(1,666) = 17.63, p<0.001, η² = 0.026; mean difference: 0.008, 90% CI: 0.005, 0.011), and effective connectivity during the face localizer task (F(1,666) = 9.17, p=0.003, η² = 0.014; mean difference: 0.023, 90% CI: 0.011, 0.036). Post hoc t-tests further indicated the direction of lateralization for each condition (Supplementary Table 2). 7 out of 9 face areas showed stronger responses in the right hemisphere, except the EVC and OFC with no credible evidence of hemispheric difference (EVC: t=−0.36, p=0.716, d=0.01, 95% CI: −0.164, 0.113, BF₁₀ =0.033; OFC: t=−0.71, p=0.477, d=0.03, 95% CI: −0.183, 0.086, BF₁₀ =0.028). Turning to the diffusion imaging data, mixed results were found in the anatomical connectome, with 9 connections lateralized to the right hemisphere (e.g. STS, AMG and OFC fibers) and 7 connections lateralized to the left hemisphere (e.g. IFG and PCC fibers). Eighteen connections in the functional connectome exhibited right-hemispheric predominance (9 connections in rsFC and 11 connections in EC) whereas only 2 connections had left-hemispheric predominance (2 connections in rsFC). More importantly, we found a positive correlation between face area’s intra/interhemispheric connection ratio and the degree of lateralization of its neural activation (Fig 7): those face areas with high ratio of intra- over interhemispheric connections (e.g. STS, OFA, FFA, ATL) exhibited more prominent right hemispheric lateralization in their neural responses to face stimuli (r(9)=0.769, p=0.015, 95% CI: 0.197, 1.340). In sum, we found strong evidence of hemispheric asymmetry at all levels of the face network and face areas in the right hemisphere generally exhibited enhanced neural responses and stronger structural and functional connectivity.

Figure 7. The Association between the Degree of Lateralization and Intra-/inter-hemispheric Connection Ratio across All Face Areas.

(A) The wiring diagram illustrates the interhemispheric and intrahemispheric connection strength for each face ROI. The width and the color of each line in the diagram proportionally reflect their mean streamline counts across all subjects. (B) Across all nine face areas, we found a positive correlation between an area’s degree of lateralization to face stimuli (the y-axis: the ratio of BOLD signal magnitude in the right hemisphere node over the left hemisphere node) and its intrahemispheric/interhemispheric connection ratio (the x-axis: INTRA/INTER). Those areas with low ratio of INTRA/INTER connection (e.g. EVC and OFC) exhibited no degree of lateralization in their neural responses to face stimuli, whereas the areas with high ratio of INTRA/INTER connection (e.g. STS and FFA) exhibited strong right hemisphere predominance.

Discussion

The present study systematically investigated the anatomical and functional connectome of a well-defined domain-specific system: face processing. Nodes in the face processing network have been rigorously investigated in cognitive neuroscience and neuropsychology for more than 40 years ^1–5. This literature provides a strong foundation for our network-based analyses that were both hypothesis-driven and data-driven, allowing us to unravel the underlying mechanisms of face processing at the connectome level.

Our large-scale multi-modal study revealed several interesting findings. First, prior diffusion imaging studies focused on a subset of face-sensitive regions ^23,24 and proposed the existence of two face processing streams, a ventral pathway for identity processing and a dorsal pathway for processing dynamic aspects of faces ^1,5. Our study looked at nine functionally and individually defined face-sensitive regions in each hemisphere, stretching from the occipital lobe to the frontal lobe, and encompassing both core and extended face processing ^1,5,20. This allowed us to describe segregated pathways of a precise and comprehensive face connectome. The network communicability analysis indicated that the face network can be anatomically divided into three separate pathways: (1) the OFA, FFA and ATL constitute a ventral pathway, possibly extracting static features from faces; (2) the STS and IFG comprise a dorsal pathway, which is specialized for processing dynamic information from faces; and (3) the PCC-AMG-OFC form a medial pathway, which might be responsible for processing the social, motivational, and emotional significance of faces. Multiple medial areas for value and reward processing have been associated with judgments of facial attractiveness and trustworthiness ^10,19,63. Last, the ROI to ROI tractography patterns showed very weak connection strengths between OFA/FFA and the STS, suggesting that they belong to different face processing subsystems, a finding that is consistent with prior diffusion imaging work ^23,24.

Second, our results shed light on a disagreement in the literature about the serial and hierarchical nature of the face processing system. An early and prominent model by Haxby and colleagues ⁵ postulated a serial-hierarchical structure, with the “core” regions having a strict serial ordering: OFA feeding into the FFA and STS. More recent human imaging work has modified this scheme by proposing an additional processing node, the ATL, and by suggested that the system is somewhat recursive ⁶⁴. While some of our data indeed suggest that the OFA, FFA, and STS are the most active parts of the face network since they had the largest neural responses to face stimuli and were constantly synchronized during rest and tasks, our overall results challenge these frameworks. The global connectivity patterns demonstrated that early visual cortex sends projections to most of the face sensitive areas, suggesting no gateway (or solo entry point) for FFA and STS. This is consistent with prior research in patients ^65–67. Moreover, the dynamic patterns of effective connectivity suggest that face processing does not proceed strictly in sequence but rather in a parallel and reciprocal fashion. Our results are more consistent with work in macaques showing that face patches are densely and bidirectionally interconnected, inconsistent with a serial hierarchy ^3,21. Importantly, and potentially unique to humans, the two hemispheres appear to carry out distinct schemes of computations and interactions during the face localizer task (left hemisphere = feedforward vs. right hemisphere = recurrent). Similar functional asymmetries have been reported in face MEG studies ^68,69.

Our third interesting finding is that local white matter plays a disproportionate role in the anatomical connectome supporting face processing. Based on a recent literature review ²², two long-range fiber pathways—the ILF and IFOF—are the most frequently reported tracts associated with face processing (11 out of 16 studies) whereas the local white matter was rarely mentioned (2 out of 16 studies). In addition, since most face ROIs are spatially far apart (e.g. 75% connections had Euclidian distance > 50mm, see Fig 2b), long-range fibers would be expected to play the primary role in the structural connectome. Indeed, our results have shown the incremental proportion of long-range fibers as the distance of two face ROIs increases (Fig 2b) and there is solid spatial overlap between major fasciculi and three face pathways (i.e. the ventral pathway maps onto the ILF and IFOF; the medial pathway was constructed of the UF and CING; and the dorsal pathway consisted of the SLF and AF) (Fig 2a). However, this description of fiber pathways is incomplete because these long-range fiber bundles only account for around 30% of the face connectome. Instead, most face nodes are interconnected by short-range fibers. Our observation is consistent with older histology studies reporting that the human cerebral white matter is dominated by short-range fibers that connect adjacent gyri ³⁸ and complies well with the ‘small-world’ characteristic of brain networks ⁷⁰. It is believed that abundant short-range fibers serve to adaptively minimize global wiring costs whereas sparse long-range connections contribute to functional integration ^71,72. Here, we found most ROI-ROI connections were redundantly constructed by both types of fibers (see Fig. 2B), e.g. the STS and IFG can be directly linked via major fasciculi (80%) or be connected indirectly by superficial fibers via multiple-hop-relays (99%). This redundant architecture may provide the face network with resiliency in the case of brain injury and disease, which may explain why prosopagnosia is so rare ^64,73. Future research needs to explore whether these features (i.e. disproportionate local connectivity, distance effect on long-range fibers, and redundant connections) are specific to the face network, or exist in other domain-specific systems, or can be generalizable to the entire cortical ‘neighborhoods’.

Fourth, we provide empirical evidence of the face processing lateralization at the connectome level. The functional asymmetry of face processing is often referred to as a fundamental lateralization of the human brain ⁷⁴. Right hemispheric predominance has been repeatedly found in behavioral performance ⁷⁵, neural activation ⁷⁶, electrophysiological responses ⁷⁷, intracranial stimulation effects ⁷⁸ and prosopagnosia cases ¹. Compared with the left hemisphere, face areas in the right hemisphere were more anatomically connected, more synchronized during rest, and more actively communicating with each other during face perception. In addition, we found a critical association between the ratio of intra/interhemispheric connection and the degree of lateralization, which lends support to an older theory claiming that hemispheric asymmetry arises from interhemispheric conduction delay ⁷⁹. According to the theory, brain size expansion during evolution led to the emergence of functional lateralization to avoid excessive conduction delays between the hemispheres. This theory predicts that to function efficiently, functionally lateralized brain regions will have relatively weak callosal connectivity as compared to non-lateralized regions ⁸⁰. Our data support this prediction by showing that face areas with stronger functional lateralization exhibited less interhemispheric (but more intrahemispheric) connections. It is plausible that the connectome-level origin of face network lateralization arises from extremely imbalanced intra/interhemispheric connections, which causes neural signals to spread more easily among face areas within the same hemisphere than across hemispheres.

We also examined the anatomy-function relationship of the face network by systematically examining relationships between different types of brain connectivity. We found the topological organization of the anatomical connectome (i.e. three core pathways) was consistent across measures (e.g. connection probability, communicability, and streamline count maps) and the functional connectivity patterns were highly similar across resting and task states. This within-modality coherence is in line with reports on other neural networks ^36,48. We also explored the spatial specificity of all brain connectivity patterns and found those intrinsic network architectures (i.e. SC, rsFC, taskFC) followed a more global pattern that was relatively stable across small spatial scales whereas the effective connectivity pattern seemed to be specific to the face-sensitive sub-regions. The relationship between structural connectivity and functional connectivity, however, is not straightforward. Although the structural connectivity and rsFC were globally correlated across the entire network, this effect was mainly driven by high anatomy-function coherence from the core pathways (Fig 3G), whereas other parts of the network showed no such correspondence (Fig 3H). Interestingly, we found a similar ‘global vs. local’ discordant pattern in the subsequent mediation analyses where the communicability fully mediated the prediction from the structural connectivity to rsFC in core pathways (Fig 3I) but not across the entire network. Together, these findings add to a growing literature on the complex nature of the anatomy–function relation ^55,81–87 and shed light on why rsFC is an imperfect representation of the underlying neural architecture. Our results demonstrated that even for a domain-specific system like the face network, the anatomy-function relationship is heterogeneous across different connections and depends highly on local degree of communicability. In addition, our data clearly showed that the communicability metric is superior to the structural connectivity measure when predicting functional connectivity. This is because conventional structural connectivity is based on direct connectivity weight but this is too simplistic to model distributed neural communications. The communicability metric takes into consideration all direct and indirect relationships between two nodes and thus provides additional information about the global dynamics of the network ^36,59.

Finally, to explore the brain-behavior association for individual face skills, we investigated how emotion recognition proficiency emerges from patterns of neural activity and connectivity among face-sensitive regions. Using multiple support vector regression analyses, we found that the most predictive brain features for individual performance were distributed across six face-sensitive brain regions and five white matter connections. The HCP emotion recognition test is a complex task that taps into multiple mental constructs and operations (e.g. perceptual, cognitive, affective, and semantic processes). The most predictive brain features corresponded well with the neural bases of these operations—facial identification (EVC, OFA, IFOF), embodied simulation (STS, IFG, arcuate fasciculus), affective processing (AMG), and the retrieval of emotion concepts and labels (ATL, STS-ATL) ^22,73,88. Both hemispheres were likely involved because the task requires face recognition as well as lexical retrieval. Our results only accounted for a small amount of the behavioral variance, potentially due to the fact that the behavioral task is very easy for non-clinical samples thereby limiting behavioral variance. However, white matter characteristics outperformed other brain features in individualized behavioral prediction, which signifies that the anatomical connectome is a useful biomarker for individual variation in high-level cognition ⁶² and social skills ⁷³.

Limitations

This study has some methodological limitations. First, like other large-scale publicly available dataset, the HCP has certain inherent problems. For instance, the psychometric and neuroimaging data may be sub-optimally designed for studying ‘pure’ face processing (e.g. the face localizer is embedded in a working memory task and there is only one face-related behavioral test, which is to name emotional faces) so that they may contain substantial noise and confounding factors that could partly drive the observed effect ^89,90. Second, some behavioral tasks (e.g. Penn Emotion Recognition Test) were too easy for healthy subjects since they were originally designed for clinical populations, thus lead to ceiling effects for brain-behavior correlation. In addition, there are extremely unbalanced number of right-handed and left-handed subjects in the HCP dataset (680 vs 70), which prohibits us from comparing the face connectome between two handedness groups (especially for the genesis of hemispheric asymmetries in face processing).

Second, resting state functional connectivity is prone to methodological and conceptual problems ^91,92, thereby interpretations should be cautious with regard to their cognitive and causality meanings ^56,81,93. In addition, dMRI tractography has recently been criticized for high false positives and there is an urgent need for methodological innovation in tractography algorithms to address this issue ^29,30,94. Notwithstanding, these tools provide considerable insights on the structural and functional architecture of brain networks. As both techniques develop, we hope other researchers replicate and extend our findings.

Third, the notion of “directionality” in PPI is an important topic that often causes confusion. The “unidirectional” or “asymmetric” patterns are not uncommon in the PPI literature ^52,53,95 and they were clearly observed in the present work (e.g. the left hemisphere had only feed-forward directions). In a very strict sense, PPI analyses should be interpreted as a (simple) test for effective connectivity because they are based on an explicit (and often linear) model of coupling between one or more brain regions ^45,51. However, we note that the post hoc interpretation of PPI results can be ambiguous as significant increase in coupling from one region to another region may be significant when testing for a PPI in the opposite direction ⁵². More work is needed to determine if the hemispheric differences of information processing observed here is true or an inflated artifact ⁹⁶ or caused by other experimental confounds (e.g. button press by right hand during the task). In addition, as DCM is computationally expensive for big data, we only tested few simplistic models with four nodes in the present study. Future investigation is needed to examine larger model space with other datasets or use other effective connectivity approaches ^97–100 to confirm our findings.

Conclusions

Face processing has been investigated in neuroscience research for more than 40 years. While much work has addressed the functional specialization of single face-selective regions, the connectome-level organization and brain-wide mechanisms for functional integration of face processing remains poorly understood. New trends in connectomics suggest that the function of any face areas should be considered within an integrative approach, including not only patterns revealed by local properties, but also interactions with other face areas ⁹⁰. For that, the present study used large-scale multimodal neuroimaging data to investigate the anatomical and functional connectome of the face network. Functionally-defined white matter tracts, using probabilistic tractography, delineated a well-organized anatomical architecture with three core pathways for different types of information processing. Fiber composition analyses revealed that the anatomical connectome is primarily constructed by short-range fibers, not major white matter bundles. Functional and effective connectivity analyses discovered a subnetwork of face areas that are constantly synchronized across contexts and they exhibit differential neural dynamics across hemispheres during face perception (feed-forward vs recurrent interactions). In addition, we found the structural and functional connectivity are highly associated in the face network and network communicability mediates this close correspondence in core pathways. Furthermore, individual differences in face skills can be predicted by a distributed pattern of connectome characteristics, in particular the white matter integrity. Finally, we demonstrate that an imbalanced pattern of intra- and interhemispheric connections might be the connectome-level basis for the hemispheric asymmetry of the face network. Collectively, we discovered a wide range of important features of the face connectome that go beyond the classic as well as more recent models of face processing. These connectome-level characteristics provide new constraints for face perception theories and offer valuable empirical evidence for a fine-grained organization and interactive mechanisms of face processing.

Methods

Participants

All data used in the present study came from the WU-Minn HCP Consortium S900 Release. Subjects were included if they had completed all brain scans (T1/T2, tfMRI, rsfMRI, and dMRI) as well as the behavioral Penn Emotion Recognition Test ¹⁰¹. To reduce variance in the human connectome ¹⁰², we restricted our population to only to right-handed subjects, resulting in 680 healthy young adults in the final sample (381 females, 22–36 year-old). It’s worth mentioning that only 667 out of 680 subjects were detected with enough robust signals in all 9 bilateral face ROIs in the face localizer task (see Supplementary Table 1), thus most connectome-level findings were based on 667 subjects. No statistical methods were used to pre-determine this sample size but it is much larger than those reported in previous publications ^23–26. The study was reviewed and approved by Temple University’s Institutional Review Board.

Data Acquisition, Preprocessing and Analysis

Due to the complexity of the HCP data acquisition and preprocessing pipeline, listing all scanning protocols and data analysis procedures are beyond the scope of this paper; instead, they can be checked in full detail elsewhere ^27,103–106. Basically, we adopted the ‘minimally pre-processed’ images of tfMRI, rsfMRI and dMRI that were provided by the HCP S900 release. The dMRI data had gone through EPI distortion, eddy current, and motion correction, gradient nonlinearity correction, and registration of the mean b0 volume to a native T1 volume. The fMRI data had undergone spatial artifact/distortion correction, cross-modal registration, and spatial normalization to MNI space. In addition, we further processed the dMRI data with FSL’s BEDPOSTX ¹⁰⁷ to model white matter fiber orientations and crossing fibers, and denoised the rsfMRI data with ICA-FIX and tfMRI data with ICA-AROMA ¹⁰⁸ to remove motion artifacts. All fMRI data were spatially smoothed at 4mm. In addition, to precisely localize each face ROI ^109,110, the face localizer task was processed on the ‘grayordinate-based’ space (i.e. cortical surface vertices + subcortical voxels) with MSM-All registration ¹¹¹.

We used the HCP Penn Emotion Recognition Test as a behavioral measure of individual face skill ¹⁰¹. Subjects were presented with 40 faces, one at a time. They were asked to choose what emotion the face depicted: Happy, Sad, Angry, Scared, or No Feeling. Half of the faces were males and half were females. The task overall accuracy (ER40_CR) and median reaction time (ER40_CRT) were used in the brain-behavior association analyses.

To ensure sensitivity to the connectome within each subject, we not only defined subject-specific ROIs based on the face localizer, but also performed all analyses firstly at the single subject level and then combined them into an aggregate statistic for group-level inference and significance tests. Unless otherwise stated, all significant results reported in this study were two-tailed tests and corrected for multiple comparisons using false discovery rate (FDR). Data distribution was assumed to be normal but this was not formally tested. In addition, all null results were further evaluated with Bayesian statistics (i.e. JZS Bayes factor (BF₁₀) as support for H1 over H0) in SPSS 25.

Functional Face Localizer and Selection of Face ROIs

The working memory task in the HCP tfMRI data can be effectively used as a functional face localizer ¹⁰⁵. Subjects were presented with alternating blocks of four categories of stimuli (i.e. faces, places, tools and body parts) and were instructed to respond in a manner of 2-back and 0-back task. Since the HCP S900 release had already provided the individual-level (within-subject) tfMRI analysis data that were fully processed on grayordinate space, we used the connectome workbench software to manually extract the vertices (later transformed to MNI coordinates) of the peak activation of bilateral nine predefined face ROIs (as well as its magnitude) from the contrast ‘Faces > Other categories’ for each subject separately (see Supplementary Table 1). This task paradigm and contrast has been widely used to define human face-sensitive areas ^112,113 and the processing for face and working memory are orthogonal to each other in this contrast (i.e. face conditions were collapsed across both 0-back and 2-back trials). To ensure the selection of face-sensitive voxels, we also inspected another conjunction contrast (‘faces > places’ ∩ ‘faces > tools’ ∩ ‘faces >body parts’) and got very similar peak coordinates. These subject-specific cluster peak coordinates were used as input (6mm-radius spheres) to subsequent seed-based brain connectivity analyses at the individual level (probabilistic tractography, resting-state analysis, psychophysiological interaction, dynamic causal modelling), and the cluster peak magnitudes were adopted as the index of neural activity for face ROIs in brain-behavior association and hemispheric asymmetry analysis.

Since we are interested in the broader face network, we selected areas not only for basic face perception (OFA, FFA, STS), but also for social, emotional and mnemonic processing of faces (ATL, OFC, AMG, IFG, PCC). A similar set of areas was included in the Haxby model ^5,6,20 and they were widely used in previous face network studies ^23–26,112. In addition, for face areas with multiple clusters (e.g. OFA, FFA, STS) we simply chose the strongest one to avoid excessive inter-subject variability ²⁴. We note that some regions recently identified in a study of non-human primates that showed strong connectivity with face patches (e.g. the pulvinar and claustrum; Grimaldi et al., 2016) were not selected in our study because they were not consistently activated by our face localizer task and the relevant human literature on these regions is scant.

Probabilistic Tractography

Tractography analyses were performed in subjects’ native space and all results were transformed to Montreal Neurological Institute (MNI) standard space. We used both a single-ROI and an ROI-to-ROI approach. In the single-ROI approach, each ROI was used as a seed with tractography running in the whole brain to obtain a global connectivity pattern. In the ROI-to-ROI approach, tractography was implemented between each pair of ROIs for either intra-hemispherical (e.g. left AMG to left ATL) or inter-hemispherical connections (e.g. left AMG to right AMG). Fiber tracking was initiated in both directions (from seed to target and vice versa) and 25000 streamlines were drawn from each voxel in the ROI. A binarized cerebellum mask was set as an exclusion mask for all analyses. The resulting 3D image files containing the output connectivity distribution were standardized using the maximum voxel intensity of each image resulting to a standardized 3D image with voxel values spanning from 0 to 1. This standardized paths images were then thresholded at the 0.1 level to reduce false-positive fiber tracks. Binary connectivity maps were further generated for each subject and added across subjects. For global connectivity pattern and cross-hemisphere projection analyses, fiber projections existed in more than 10% of the subjects were retained and rendered for visualization (e.g. Supplementary Figure 1 and Extended Data Figure 1).

FSL’s dtifit was used to fit a diffusion tensor model at each voxel. For each subject, the fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (AD), and axial diffusivity (RD) maps were created and their mean values for each ROI-ROI connection were extracted. The number of streamline for each path was calculated by averaging two waytotal numbers produced by tractography. The connectivity probability for an ROI-ROI connection (e.g. FFA-OFA) was defined as the streamline count of that connection divided by the sum of streamline counts of all connections passing either ROIs (e.g. there were totally 15 paths connecting either FFA or OFA) ²³.

Communicability Measure and Community Detection Analysis

Communicability was quantified as the weighted sum of direct and indirect structural connectivity, where shorter paths (i.e. those with fewer steps) are weighted exponentially more heavily ³⁵. For each subject (and each hemisphere), we derived a communicability map from their connectivity probability matrix. This communicability map was subsequently compared with other brain connectivity maps at the individual level to reveal the anatomy-function relationship.

At the group level, we prepared an averaged communicability map for each hemisphere for community detection analysis. Modular partitions of this averaged communicability map were obtained using Louvain community detection method (https://python-louvain.readthedocs.io/en/latest/). The algorithm computes the partition of the graph nodes that maximizes the modularity using the Louvain heuristics. Potential shared nodes between communities were also checked by using the k-clique percolation method ¹¹⁴ in the NetworkX toolbox (https://networkx.github.io/).

Analyses on Major White Matter Bundles and Superficial White Matter System

For each hemisphere, ten major white matter bundles were identified for each subject using the Automated Fiber Quantification (AFQ) software package (https://github.com/jyeatman/AFQ) ³⁷. We focused our analysis on six major fiber tracts that were found to be critical for face processing in a recent meta-analysis ²² : the inferior longitudinal fasciculus (ILF), inferior fronto-occipital fasciculus (IFOF), cingulum (CING), uncinate fasciculus (UF), superior longitudinal fasciculus (SLF), and arcuate fasciculus (AF). We also analyzed four additional fasciculi provided by the AFQ algorithm (i.e. thalamic radiations, corticospinal tracts, anterior and posterior corpus callosum) and found no overlap between them and all ROI-ROI connections (hence we did not report here).

We used FSL’s atlasquery tool to evaluate the relative contribution of major fasciculi and superficial white matter to the face network ²². A binarized image for each ROI-ROI connection was created for each subject and then added together across all subjects. We also combined all 72 bilateral connections together into one binarized image for each subject and added together across subjects to obtain the entire connectome image. Only voxels that existed in more than 50% of the subjects were retained (i.e. the skeleton image) and projected on two white matter atlases: the JHU white-matter tractography atlas with 48 long-range tract labels ⁴¹ and the LNAO superficial white matter atlas with 79 U-shaped bundles ⁴². Voxelwise analyses were then implemented to calculate the probability of the skeleton image being a member of any labelled tracts within each atlas. Note that human white matter is somewhat idiosyncratic across individuals and the two atlases we used only represent the skeleton of the most common white matter bundles in standard MNI space; since they were created by different research groups and different methods, the two atlases are not mutually exclusive and their combination does not explain all face connectome voxels (i.e. the sum is 92%).

Psychophysiological Interaction (PPI) and Functional Connectivity Analysis on HCP Task Data

The statistical model employed in estimating effective connectivity (EC) and task-state functional connectivity (taskFC) is a simple general linear regression model (GLM). We used two ways to build the ‘generalized PPI’ ¹¹⁵ model (with non-deconvolution method ¹¹⁶) for each seed ROI. A simple ‘partial’ model had 17 separate regressors: 8 psychological regressors of task events (e.g., face/body/place/tool stimuli in either 2-back or 1-back mode), 1 physiological regressor of the seed ROI’s timeseries, and 8 corresponding interaction regressors (task events x seed ROI’s timeseries). A more complex ‘full’ model had 25 regressors, including the identical 17 regressors in the partial model plus 8 extra physiological regressors of non-seed-ROIs’ timeseries. Compared to the partial model, the full model was designed to aggressively control for neural responses in non-seed regions.

To estimate the taskFC between the seed ROI and other ROIs, we used the contrast between regressors of task events (faces > other categories). To estimate the EC, we used the contrast between interaction regressors (faces PPI > other categories’ PPI). Z-scored beta-weights were extracted for each pair of ROIs, which resulted in one 9×9 matrix for each connectivity type (taskFC or EC), each model (full or partial), each hemisphere and each subject. While the taskFC matrices were further symmetrized, no symmetrization was applied to EC matrices due to its directional character (i.e. PPI effects indicate some information on directional neural interactions) ^45,52,53. At the group level of the EC, one sample t-test across subjects was performed at each pair of ROIs to detect any significant effectivity connectivity. Non-parametric permutation tests (10,000 times) were also implemented to re-validate all significant results.

It’s important to note that all significant findings reported in this paper were based on the ‘partial’ PPI model, as null results were found in the ‘full’ model. Although a PPI model would approximate EC better as more controlled ROIs are added to the model, this approach is rarely done in practice due to multicollinearity and the relative paucity of observations compared to potential regions (i.e., degrees of freedom) ⁵². Here the null results in the full model reflect that two region’s effective connectivity identified in the partial model might be contaminated by a third region’s influence. This methodological issue requires further exploration.

Dynamic Causal Modelling (DCM) on HCP Task Data

To validate our PPI findings, we performed DCM analyses using DCM10 in SPM8 ⁴⁷. As it is common practice in DCM to restrict the analysis to a small number of nodes ^54,117, we only applied DCM to four core face areas (EVC, OFA, FFA, STS). Motivated by our testing hypotheses (i.e. ‘left hemisphere = feedforward’ vs. ‘right hemisphere = recurrent’), we defined two simple models based on PPI connectivity patterns (Fig 4A) and tested their fitness to the observed data in each hemisphere separately. The ‘Feedforward Model’ was derived from PPI left-hemisphere connectivity pattern (i.e. face stimuli only drive feedforward processing) whereas the ‘Recurrent Model’ was adapted from PPI right hemisphere patterns (i.e. face stimuli mainly drive recurrent processing). For each model, sensory inputs started from EVC and all four ROIs were intrinsically set to be bidirectionally connected and self-connected, and their time-courses (i.e. first eigenvariate) were extracted for each subject individually. To examine the modulatory effects by extrinsic face stimuli, we built DCM GLM design matrix with six regressors (face, place, tool, body, 2-back, and 0-back) and tested the two models with the face condition. To determine the optimal model, fixed-effects (FFX) and random-effects (RFX) group analyses were implemented by Bayesian models selection (BMS) ¹¹⁸. FFX BMS assumes that the optimal model is identical across the population and uses the group Bayes factor (log-evidence) to quantify the relative goodness of models. In contrast, RFX BMS accounts for heterogeneity of model structure across subjects and yields posterior model probabilities and exceedance probabilities.

Functional Connectivity Analysis on HCP Resting-State Data

Resting-state functional connectivity between 9 face ROIs was estimated by building nine general linear regression models. Each model defined one ROI’s time series as the dependent variable and the rest eight ROIs’ time series as independent variables. For each hemisphere, Fisher-transformed correlation coefficients (z-scored beta-weights) were extracted for each pair of 9×9 ROIs, symmetrized, and then averaged across two separate resting-state scans.

Comparison Between Different Brain Connectivity Maps

At the individual subject level, we did pairwise correlations among five brain connectivity matrices by taking all elements of each matrix except the diagonal ones (self-connections), applying a Fisher’s Z-transform, and then computing a Pearson correlation. Conventional one sample t-tests (against 0) were used at the group level to determine the statistical significance after controlling for multiple comparisons. Non-parametric permutation tests (10,000 times) were also implemented to re-validate all results.

Two different scales were examined when comparing different brain connectivity graphs: 1) at the entire face network level (72 connections in each hemisphere); or 2) only at the level of three core pathways. The core pathways were defined to include 16 ‘core connections’ in each hemisphere: EVC-OFA, OFA-FFA, FFA-ATL, ATL-AMG, AMG-PCC, AMG-OFC, PCC-OFC, STS-IFG, given that they had the highest connection probability in Fig 1A (top 25%).

We conducted multilevel mediation analyses to test whether communicability mediated the relationship between structural connectivity and functional connectivity (rsFC). Multilevel mediation analyses were implemented via the ‘Mixed linear model’ function in SPSS 25 and the models included random intercepts at the subject level. To examine the mediation at the entire face network level, we firstly set 72 bilateral rsFC (across all subjects) as the dependent variable “Y”, 72 corresponding communicability measures as the mediator variable “M”, and 72 corresponding fiber connection probability as the independent variable “X”. After that, we built another model only for core pathways, with rsFC of 16 bilateral core connections as the dependent variable “Y”, 16 corresponding communicability measures as the mediator variable “M”, and 16 corresponding fiber connection probabilities as the independent variable “X”.

Brain-behavior Associations

Two different statistical analyses were used to examine the brain-behavior association: simple Pearson correlation, and support vector regression (SVR). The first was conducted using SPSS 25.0 and the SVR was implemented using Matlab Statistics and Machine Learning Toolbox.

On the brain side, there were four independent sets of metrics: 1) neural activity profiles from 18 bilateral ROIs (the magnitude of BOLD responses to face stimuli); 2) white matter characteristics from 72 bilateral ROI-ROI connections and 20 major fasciculi; 3) 72 bilateral functional connectivity during rest, and 4) 144 bilateral directional effective connectivity during the face localizer task. On the behavior side, we had two metrics from the HCP Penn Emotion Recognition Test: task overall accuracy (ER40_CR) and median reaction time (ER40_CRT). For the SVR analyses, each time we only built one model to test the association between one particular set of brain metric (as independent variables) and one behavioral measure (as the dependent variable). For the richness of white matter properties, we tested seven microstructural measures separately (i.e. factional anisotropy, mean diffusivity, axial diffusivity, radial diffusivity, streamline counts, connectivity probability, and tract volume size). More details about the SVR procedure is described in the caption of Fig 6.

To further validate that the final two parsimonious models were specific to face processing but not predictive for general performance (e.g. task accuracy and reaction times), we used them to predict other HCP non-face behavioral performance, such as the working memory 2-back task accuracy and speed (i.e. “WM_Task_2bk_Acc”, “WM_Task_2bk_RT”), theory of mind judgment speed (i.e. “Social_Task_TOM_Median_RT_TOM”), and delay-discounting ability (i.e. “DDisc_AUC_200”).

Hemisphere Lateralization

We used a 2-way repeated-measure ANOVA to examine hemisphere lateralization at each level of measurements. At the neural activation level, we set the ANOVA with factors of ‘hemisphere’ and ‘9 Face ROIs’. At the structural connectivity (i.e. connectivity probability) or resting-state functional connectivity level, we set the ANOVA with factors of ‘hemisphere’ and ‘36 ROI-ROI connections’. At the effective connectivity level, we set the ANOVA with factors of ‘hemisphere’ and ‘72 directional ROI-ROI connections’. If a main effect of hemisphere was found in the ANOVA analysis, pairwise t-tests were further implemented to determine which hemisphere was dominant.

To prepare for the association analysis, we computed the streamline counts ratio between intrahemispheric connections and interhemispheric connections for each face area and then averaged the ratio across two hemispheres and across all subjects. To define the degree of lateralization of each face area, we computed the BOLD signal ratio between the right and left area during the face localizer and averaged the ratio across subjects.

Data Availability

All data used in the present study came from the WU-Minn HCP Consortium S900 Release. They are publicly available, accessible at https://www.humanconnectome.org.

Code Availability

Most analyses were conducted by common software (FSL, SPM), or open source toolbox that can be downloaded from GitHub (Louvain community detection algorithm, NetworkX, or AFQ toolbox). Custom codes can be accessed at https://github.com/mirrorneuronwang/HCP_face_connectome, or are available from the corresponding author upon request.

Extended Data

Extended Data Figure 1. The Interhemispheric Fibers Connecting Bilateral Face ROIs.

Probabilistic tractography indicated that bilateral posterior ROIs (EVC, OFA, FFA, STS and PCC) are connected through the splenium of the corpus callosum whereas bilateral frontal ROIs are connected through the genu (IFG) or rostrum (OFC) of the corpus callosum. Bilateral ATLs have two separate interhemispheric connections, either via the splenium of the corpus callosum (by climbing up posteriorly along the temploral lobe) or the anterior commissure. Each amygdala is connected to the other by the anterior commissure. These findings accord well with previous work on the callosal fiber organization 118, AMG/ATL interhemispheric connections 119, and EVC interhemispheric connections which begin at the boundary of V1 and V2 120–122. Upper row: medial views; Lower row: axial views.

Extended Data Figure 2. Additional DCM Analysis With Larger Model Space.

For simplicity, we only compared two DCM models in Fig 4. These two models, however, have limitations, given that they were merely built from preceding PPI results. For instance, the EVC→OFA connectivity is theoretically important but was not significant in the left hemisphere (LH) of PPI results (that’s why we did not included it in the original feed-forward model). In addition, one might also be interested in exploring the relative contribution of each recurrent connection to the right hemisphere (RH) face processing. To address these questions, we built larger model space with seven competing models (feedforward models in red colour and recurrent ones in blue colour). (A) The first two models were the ones we used in Fig 4. Model 1 was feedforward (based on PPI results in LH) and Model 2 was recurrent (based on PPI results in RH). Since Model 1 had no direct feedforward connectivity from EVC to OFA, we next built Model 3 with additional EVC→OFA. Model 4 to 7 were recurrent models modified from Model 2. As there were four recurrent connections in Model 2, we removed one feedback connection each time to examine their respective importance to the recurrent model (i.e. how much the model performance would suffer in the absence of a particular recurrent connection). Model 4 removed EVC←OFA; Model 5 removed EVC←FFA; Model 6 removed EVC←STS; and Model 7 removed OFA←STS. (B) Bayesian model selection (both FFX and RFX) indicates the EVC→OFA connection is important for the feedforward model, as Model 3 performs better than Model 1 in LH. This is consistent with the Haxby model suggesting the critical role of the OFA receiving information from EVC to initiate the face processing. In addition, both feedforward models perform better than any recurrent models in LH, whereas the PPI-derived recurrent model (Model 2) performed the best in RH. These results accord well with our results in Fig 4. Moreover, among all four recurrent connections, two feedback connections (EVC←OFA, OFA←STS) seem to be particularly important for RH recurrent processing, since removal of either one can lead to enormous drop of model performance (i.e. Model 4 and 7). In sum, this additional DCM analysis supports our claims in Fig 4: the LH is dominant with feedforward face processing whereas the RH is dominant with recurrent processing.