A multi-resolution air temperature model for France from MODIS and Landsat thermal data

Abstract

Understanding and managing the health effects of ambient temperature (T_a) in a warming, urbanizing world requires spatially- and temporally-resolved T_a at high resolutions. This is challenging in a large area like France which includes highly variable topography, rural areas with few weather stations, and heterogeneous urban areas where T_a can vary at fine spatial scales. We have modeled daily T_a from 2000 – 2016 at a base resolution of 1 km² across continental France and at a 200 × 200 m² resolution over large urban areas. For each day we predict three T_a measures: minimum (T_min), mean (T_mean), and maximum (T_max). We start by using linear mixed models to calibrate daily T_a observations from weather stations with remotely sensed MODIS land surface temperature (LST) and other spatial predictors (e.g. NDVI, elevation) on a 1 km² grid. We fill gaps where LST is missing (e.g. due to cloud cover) with additional mixed models that capture the relationship between predicted T_a at each location and observed T_a at nearby weather stations. The resulting 1 km T_a models perform very well, with ten-fold cross-validated R² of 0.92, 0.97, and 0.95, mean absolute error (MAE) of 1.4 °C, 0.9 °C, and 1.4 °C, and root mean square error (RMSE) of 1.9 °C, 1.3 °C, and 1.8 °C (T_min, T_mean, and T_max, respectively) for the initial calibration stage. To increase the spatial resolution over large urban areas, we train random forest and extreme gradient boosting models to predict the residuals (R) of the 1 km T_a predictions on a 200 × 200 m² grid. In this stage we replace MODIS LST and NDVI with composited top-of-atmosphere brightness temperature and NDVI from the Landsat 5, 7, and 8 satellites. We use a generalized additive model to ensemble the random forest and extreme gradient boosting predictions with weights that vary spatially and by the magnitude of the predicted residual. The 200 m models also perform well, with ten-fold cross-validated R² of 0.79, 0.79, and 0.85, MAE of 0.4, 0.3, and 0.3, and RMSE of 0.6, 0.4, and 0.5 (R_min, R_mean, and R_max, respectively). Our model will reduce bias in epidemiological studies in France by improving T_a exposure assessment in both urban and rural areas, and our methodology demonstrates that MODIS and Landsat thermal data can be used to generate gap-free timeseries of daily minimum, maximum, and mean T_a at a 200 × 200 m² spatial resolution.

1. Introduction

Ambient or near-surface air temperature (T_a) is increasingly recognized as an important health risk. High or low T_a is associated with increased morbidity and mortality across regions and climates (Gasparrini et al., 2015; Guo et al., 2014; Song et al., 2017), and recent work suggests that high T_a may exacerbate the effect of exposure to particulate matter (PM), another major health hazard (Li et al., 2017). T_a exposure is a growing concern in cities, which are often warmer than the surrounding countryside due to increased heat accumulation and slower heat diffusion (Arnfield, 2003). Urban areas are now home to more than half the world’s population, and this share is projected to increase to almost 70% by 2050 (United Nations, 2018). Health effects of T_a are also seen in rural populations (Lee et al., 2016), although fewer studies have examined these due to the difficulty of estimating T_a exposure. Meanwhile climate change is increasing T_a and the frequency of extreme events such as heat waves in both urban and rural areas (IPCC, 2013). The health burden of T_a exposure is expected to grow as climate change and urbanization continue (Gasparrini et al., 2017; Wang et al., 2018).

Understanding, monitoring, and managing T_a health effects requires spatiotemporally-resolved T_a at high resolutions. Weather station networks measure T_a at high temporal resolution, but rarely capture spatial variation at the scales needed for epidemiological studies (e.g. across a region, within a city). Failure to account for spatial variation in T_a can introduce error in exposure assessment, which tends to bias health effect estimates towards the null (Zeger et al., 2000). Some recent epidemiological studies have addressed this issue by using spatiotemporally-resolved T_a estimates from numerical weather prediction models such as WRF (Ha et al., 2017b, 2017a), but computational limitations currently restrict these models to medium spatial resolutions (e.g. 4 km) or small geographic areas (e.g. a single city). In urban areas, studies have used weather model T_a estimates or indicators such as sky view factor, vegetation abundance, and land surface temperature to create indexes that identify warmer and cooler areas within a city (Goggins et al., 2012; Ho et al., 2017; Laaidi et al., 2012; Milojevic et al., 2016; Smargiassi et al., 2009). Studies to date have focused on the typical spatial distribution of T_a during a specific time period (e.g. a single heat wave, the hot season) as the limited temporal variability of the indicator variables and cost of numerical weather prediction have precluded consideration of changes in the pattern of warmer and cooler areas over time.

Other recent studies have used T_a estimates from hybrid land use regression models that predict T_a based on remotely sensed 1 km land surface temperature (LST) and spatial and spatiotemporal variables such as elevation and normalized difference vegetation index (NDVI) (Kloog et al., 2015; Shi et al., 2016b, 2015). This approach takes advantage of the growing body of satellite earth observation data and the fact that LST is a good indicator of spatiotemporal variation in T_a (Oyler et al., 2016). In particular, a technique that uses linear mixed models to calibrate the relationship between daily 1 km LST from the Moderate Resolution Imaging Spectroradiometer (MODIS) instrument and T_a has been shown to perform well over large, heterogeneous areas including the northeastern USA (root mean square error [RMSE] 2.2 °C) (Kloog et al., 2014), the southeastern USA (RMSE 1.4 °C) (Shi et al., 2016a), France (RMSE 1.7 °C) (Kloog et al., 2017), and Israel (RMSE 1.2 °C) (Rosenfeld et al., 2017). These models are parsimonious compared to numerical weather prediction, which allows them to capture both spatial and temporal variation in T_a over large areas and long time periods. Their spatial resolution suffices for areas where T_a varies little at scales of less than 1 km and for studies where subjects’ locations are only approximately known. But finer spatial resolution estimates are needed for studies with address-level location data, particularly in urban areas where T_a can vary markedly within a square kilometer. Very high spatiotemporal resolutions would also benefit studies that have time-location data (e.g. GPS tracks).

In this study we extend the mixed modeling approach to predict daily minimum, mean, and maximum T_a (T_min, T_mean, T_max, respectively) at a 1 km resolution across continental France and at a 200 m resolution across 103 urban areas in continental France. We improve performance at the 1 km resolution by allowing the daily T_a ~ LST relationship to vary between climatic regions, and we consider both daytime and nighttime MODIS LST, which allows us to predict diurnal (T_max) and nocturnal (T_min) temperature in addition to T_mean. This is useful both for studies of urban heat islands, which exhibit different spatial patterns and intensities during day vs. night (Arnfield, 2003), and for studies of T_a variability, which recent work suggests may independently affect health (Guo et al., 2016; Molina and Saldarriaga, 2017; Shi et al., 2015). We also add a local stage that uses an ensemble of machine learning algorithms to predict the residuals of the 1 km model in urban areas based on higher spatial resolution predictors including thermal data from the Landsat 5, 7, and 8 satellites. This allows us to predict daily T_a over 17 years at a 200 m spatial resolution which better captures intra-urban T_a variation across 103 urban areas.

2. Data and methods

2.1. Study area and period

Our study area is continental France, comprising all French territory in Europe except Corsica. It covers 542,973 km² of topographically and climatically diverse terrain with elevations that range from −10 to 4,809 m. Joly et al. (2010) classify France into eight climatic regions based on the magnitude, variability, and seasonality of temperature and precipitation (Fig. 1). The north and west coasts have a wet, temperate oceanic climate, which transitions to a drier, cooler modified oceanic climate in the north center. The mountainous east, south center, and southwest have variable montane and semi-continental climates with cold winters. In the southeast, the Mediterranean coast has hot, dry summers with mild wet winters; the inland southeast and isolated segments of the west coast are similar but cooler. The southwest basin resembles the inland southeast but with drier winters.

Fig. 1.

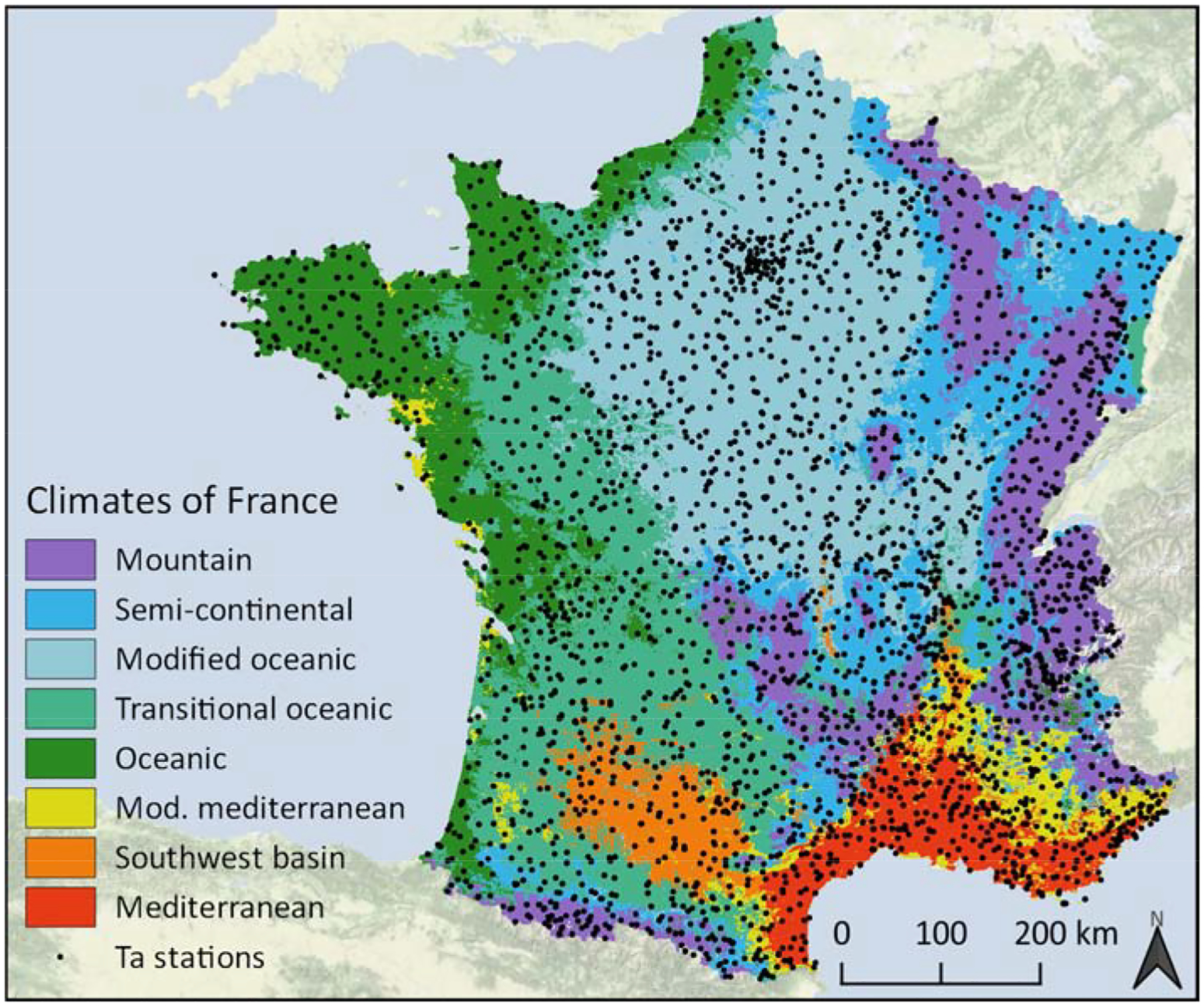
Climatic regions of France according to Joly et al. (2010) and METEO-FRANCE stations used in the current study

The estimated population on January 1, 2018 was 64,388,583 (INSEE, 2018). About 80% of the population is urban, and this share is projected to grow to 88% by 2050 (United Nations, 2018). The largest urban area, Paris, has a population of 12.5 million (20% of the total) and the six next largest urban areas have a population of one to 2.3 million (combined 14% of total). A further 10% of the population lives in cities of one half to one million, and 37% live in urban areas with fewer than half a million residents (Fig. S1). Our study period is January 1, 2000 through December 31, 2016.

2.2. Meteorological observations

We use daily weather station observations from Météo France, the French national meteorological service. About 64% of the observations come from stations managed by Météo France; the remaining stations are managed by other entities. All observations are quality controlled by Météo France. We exclude stations with no metadata or that do not record hourly T_a, and for each month during the study period we exclude stations that were active for fewer than 21 days in the month. This leaves 1710 to 2314 stations on each day. The stations are distributed over the entire study region, but are denser in populous areas (e.g. Paris, the southeast) and the Alps (which has many ski resorts, hydroelectric dams, and avalanche monitors) (Fig. 1). Just 3% of the stations are located within large urban areas (as defined in section 2.7), 7% are in peri-urban areas (within 5 km of an urban area), and the remaining 90% are rural.

The stations calculate daily T_min as the lowest T_a observed from 18 UTC the previous day until 18 UTC on the day; daily T_max is the highest T_a observed from 6:00 UTC on the day until 6:00 UTC the following day. Most stations calculate Tmean as the mean of all (at least 24) T_a observations from 0 UTC on the day until 0 UTC the following day. However, about 40% of the T_mean observations were calculated as the average of T_min and T_max. We exclude these observations, meaning our final dataset has fewer observations for T_mean than for T_min or T_max. Daily T_a at the included stations during the study period ranged from T_min of −31.2 °C to T_max of 44.1 °C; mean T_mean was 11.3 °C with a standard deviation of 7.1 °C (Table S1).

2.3. Land surface temperature and emissivity

We use version 6 of the widely-used MODIS daily 1 km land surface temperature and emissivity product from the Terra and Aqua satellites (MOD11A1 and MYD11A1, respectively) (Table 1). These products include daytime and nighttime LST derived using a split-window algorithm and land use classification-based emissivity and have been masked for clouds and validated to ± 2 K in clear-sky conditions across 47 sites on all seven continents (Wan, 2014). We use the quality assessment band to exclude pixels with LST error > 2 K. As LST retrieval error increases over snow and water, we also exclude pixels with NDVI < 0 or where the corresponding 1 km grid cell has land cover of > 33% water.

Table 1.

Satellite instruments used in this study

Instrument	Satellite	Resolution	Revisit time	Overpass*	Time period
MODIS	Terra	1 km	12 hours	10:00	2000-02-02 – present
				22:00
MODIS	Aqua	1 km	12 hours	13:00	2002-07-04 – present
				01:00
TM	Landsat 5	120 m†	16 days	10:00	1984-03-01 – 2011-11-18
ETM+	Landsat 7	60 m†	16 days	10:00	1999-04-15 – present
TIRS	Landsat 8	100 m†	16 days	10:00	2013-02-11 – present

^*Approximate local solar time;

^†Resampled to 30 m

2.4. Top-of-atmosphere brightness temperature

For large urban areas, we composite 30 m top-of-atmosphere brightness temperature (T_b) from the Landsat 5, 7, and 8 satellites (Table 1). T_b is the kinetic temperature a perfect blackbody would have if it emitted the quantity of thermal radiation measured by the satellite instrument. Converting T_b to LST requires correcting for atmospheric effects and accounting for the emissivity of the earth’s surface. This is difficult in the case of the Landsat satellites because Landsat 5 and 7 have only a single thermal band and the USGS Landsat 8’s second thermal band is contaminated by stray light, precluding the use of the split-window algorithm (Li et al., 2013). A global Landsat LST product is under development but not yet available (Malakar et al., 2018), so for this study we use T_b from the USGS Landsat Collection 1 Level-2 surface reflectance products (USGS, 2018a, 2018b).

The 16-day revisit time of the Landsat satellites means that T_b is unavailable for many locations on many days. Cloud cover and sensor malfunctions also contribute to these data gaps and can increase error in T_b retrieval. To reduce error, we discard all scenes with cloud cover > 75%. We also discard all scenes captured during periods of instrument malfunction, which we identified by checking summary statistics of each scene for unrealistic values (e.g. mean T_b > 100 °C). We then trim the edges of Landsat 5 scenes by 2.5 km to remove abnormalities (Robinson et al., 2017) and mask pixels identified as high- or medium-confidence cloud in the pixel quality assessment band. We mask any remaining pixels where T_b ≤ −25 °C or T_b ≥ 50 °C. Finally, for each calendar month we composite all T_b retrievals during the entire study period (e.g. every January in 2000 – 2016). This yields 12 gap-free T_b datasets representing the 17-year mean T_b of each pixel in each calendar month.

2.5. NDVI

We use version 6 of the MODIS monthly composite 1 km NDVI product from the Terra and Aqua satellites (MOD13A3 and MYD13A3, respectively). For large urban areas we also composite 30 m NDVI from the Landsat 5, 7, and 8 Collection 1 Level-2 surface reflectance products. We use a similar quality assurance and compositing procedure as for T_b, first discarding all scenes with greater than 75% cloud cover or during periods of thermal sensor malfunction (as this results in unreliable cloud confidence scores in the pixel quality assessment band). We then trim the edges of Landsat 5 scenes by 2.5 km and adjust NDVI from Landsat 5 and Landsat 7 to match Landsat 8 using equation Eq. 1 (Robinson et al., 2017).

$${\text{NDVI}}_{\text{L}8}=0.0235+0.9723\times {\text{NDVI}}_{L5,L7}$$ Eq. 1

Similar to Robinson et al. (2017), for each calendar month we create two 17-year mean composites, one using pixels marked as clear in the pixel quality assurance band (i.e. not cloud, cloud shadow, snow, or water) and a second using pixels marked as snow or water. Finally, we mosaic the two composites preferring the clear pixels composite.

2.6. Elevation, Population, Land Cover, and Climatic Regions

We use version 1.1 of the European Digital Elevation Model (EU-DEM) from the Copernicus Land Monitoring Service. These data have a 25 m spatial resolution and vertical RMSE of ±7 m (Tøttrup, 2014). We also use 200 m gridded 2010 population from INSEE, the French national statistics agency (INSEE, 2017). We use the 100 m Corine Land Cover (CLC) inventory for 2000, 2006, and 2012. The 2000 edition has been validated to better than 85% thematic accuracy (Bossard et al., 2000). We aggregate the land cover classes into four groups: artificial, vegetation, bare, and water (Table S2). Finally, we use the eight climatic regions of Joly et al. (2010), which are based on temperature and precipitation patterns (Fig. 1).

2.7. Model grids

For the 1 km model, we create a grid covering continental France by making a 1 km square buffer around the centroid of each MODIS 1 km LST pixel in the ETRS89-LAEA Europe (EPSG:3035) equal-area projection. We associate each 1 km grid cell with the MODIS LST and NDVI pixel having the same centroid and calculate the mean elevation, total population, percent area of each land cover group, and climate region with greatest spatial overlap.

For the 200 m model, we create a grid covering large urban areas. Starting from a 200 m grid in the ETRS89-LAEA Europe (EPSG:3035) equal-area projection, we select all cells in continental France containing “Urban fabric” or “Industrial or commercial units” in the 2012 CLC inventory. We associate each cell with the corresponding INSEE gridded population and select cells with 50 or more inhabitants as well as the eight surrounding cells (i.e. including diagonal neighbors). We define urban areas as four-wise contiguous (i.e. excluding diagonal neighbors) groups of cells and sum the population of all cells in each urban area. Finally, we eliminate urban areas with population < 50,000. This leaves 103 large urban areas ranging from greater Paris (9.4 million inhabitants) to Armentières (50,260 inhabitants). For each 200 m grid cell in a large urban area or that contains a weather station we calculate the mean 17-year composite Landsat T_b and NDVI for each calendar month, mean elevation, and percent area of each land cover group.

2.8. Statistical methods

We use a four-stage approach to predict T_a: stages 1 and 2 predict daily 1 km T_a across continental France and stages 3 and 4 predict daily 200 m T_a within large urban areas. We consider each year during the study period (2000 – 2016) and each T_a measure (T_min, T_max, and T_mean) separately. Stages 1 and 2 are an extension of the method used in (Kloog et al., 2017) and are detailed in Appendix A. Sections 2.8.1 to 2.8.2 detail stages 3 and 4; the following is a brief overview of all stages.

In stage 1 we calibrate T_a at each station as a function of daily 1 km LST and emissivity, monthly 1 km NDVI, and 1 km elevation, population, and land cover. We use a linear mixed model to allow the T_a ~ LST relationship to vary by day within each climatic region. We use this calibrated relationship to predict 1 km T_a (T_{ap_s1}) for all cell-days where LST is available.

In stage 2, we fill gaps in T_{ap_s1} where 1 km LST was not available by calibrating T_{ap_s1} as a function of daily 1 km inverse distance weighting interpolated observed T_a (T_IDW). We use a linear mixed model to allow the T_{ap_s1} ~ T_IDW relationship to vary by location. We use this calibrated relationship to fill gaps in T_{ap_s1}, producing gap-free daily 1 km predicted T_a (T_{ap_1km}). This is the 1 km T_a model.

In stage 3, we calculate the daily 200 m residuals of the 1 km T_a model (R) and train random forest (RF) and extreme gradient boosting (GB) models to predict R based on latitude, longitude, Julian day, climatic region, 200 m composite T_b and NDVI, and 200 m elevation, population, and land cover. We use each of these models predict the residual for all 200 m cell-days (R_{p_rf} and R_{p_gb}, respectively).

In stage 4, we calibrate a generalized additive model that ensembles R_{p_rf} and R_{p_gb}. We use a tensor product smooth with interaction to allow the relative performance of the RF and GB models to vary by location and with the magnitude of the predicted residual. Finally, we add the ensemble predictions to T_{ap_1km} to get daily 200 m predicted T_a for large urban areas (T_{ap_200m}). This is the 200 m T_a model.

2.8.1. Stage 3: increasing spatial resolution to 200 m across large urban areas

In stage 3 we increase the spatial resolution of our predictions over large urban areas. We start by associating each 200 m grid cell with T_{ap_1km} (T_a predicted in stage 2 by the final 1 km model) from the 1 km grid cell that contains the 200 m grid cell. Next, we calculate the residuals (R) for all 200 m grid cell-days with a weather station T_a observation by subtracting observed T_a from T_{ap_1km}. The number of cell-days with a weather station observation varies by year; on average there are about 462 thousand for T_mean and 789 thousand for each of T_min and T_max. We use these cell-days to train a random forest and an extreme gradient boosting (XGBoost) model with the equation:

$${\text{R}}_{ij}=f\left(\begin{array}{c}{\text{T}}_{\text{ap\_1km}ij},{\text{T}}_{\text{b}im},{\text{NDVI}}_{im},{\text{Land Cover}}_{ily},\\ {\text{ Climate}}_i,{\text{Elevation}}_i,{\text{Population}}_i,{\text{x}}_i,{\text{y}}_i,\text{j}\end{array}\right)+{\epsilon }_{ij}$$ Eq. 2

where R_ij is the residual of the 1 km T_a model associated with 200 m grid cell i on day j; f designates the random forest or extreme gradient boosting function; T_{ap_1kmij} is the 1 km T_a model prediction associated with 200 m grid cell i on day j; T_bim is the Landsat top-of-atmosphere brightness temperature of cell i for the calendar month m in which day j falls; NDVI_im is the Landsat NDVI of cell i for the calendar month m in which day j falls; Land Cover_ily is the fraction of cell i occupied by each land cover group l in the CLC inventory year y closest to day j; Climate_i is the climatic region of cell i; Elevation_i is the elevation of cell i; Population_i is the population of cell i; x_i and y_i are the geographical coordinates of cell i; j is the Julian day; and ε_ij is the error for cell i on day j.

We use the R packages ranger (Wright and Ziegler, 2017), XGBoost (Chen and Guestrin, 2016), and mlr (Bischl et al., 2016) to train the random forest and XGBoost models. We tune the models using the sequential model-based optimization of package mlrMBO (Bischl et al., 2017). Briefly, mlrMBO estimates optimal hyperparameter values by iteratively training and evaluating a model using hyperparameter values that are chosen based on the performance of previous iterations. We use a fixed number of iterations and evaluate performance as the mean RMSE of two random 80% holdouts (i.e. we train the model on a 20% random sample of the data, predict and calculate RMSE for the held-out 80%, repeat, and take the mean of the two RMSEs). Initial exploration showed that this resampling approach produced stable estimates of RMSE at a lower computational cost than cross-validation.

For the random forest, we use 400 trees and a minimum of 5 observations per node, and tune mtry (the number of variables to consider for each split) from 3 to 12 (25% to 100% of the explanatory variables) using 6 mlrMBO iterations. Initial exploration showed that using more than 400 trees only marginally increased performance and had a high computational cost. For the XGBoost model, we use the gbtree booster with 100 rounds and set gamma (the minimum loss reduction for a split) to 5. We use 24 mlrMBO iterations to tune eta (the learning rate) from 0.1 to 0.3, the maximum tree depth from 5 to 20, the minimum number of observations per node from 3 to 30, and the fraction of features used in each tree from 0.75 to 1.

We evaluate the performance of the stage 3 models using 5-fold cross-validation with nested tuning. We use the final stage 3 random forest and XGBoost models to predict the residual of the 1 km T_a model (R_{p_rf} and R_{p_xgb}, respectively) for all 200 m cell-days.

2.8.2. Stage 4: improving 200 m predictions

In stage 4 we improve the stage 3 predictions by ensembling. We use all 200 m grid cell-days with a weather station T_a observation to calibrate a generalized additive model (GAM) with the formula:

$${\text{R}}_{ij}=t\left({\text{x}}_i,{\text{y}}_i,\right)\times {\text{R}}_{\text{p\_rf}ij}+t\left({\text{x}}_i,{\text{y}}_i\right)\times {\text{R}}_{\text{p\_gb}ij}+{\epsilon }_{ij}$$ Eq. 3

where R_ij is the residual of the 1 km T_a model associated with 200 m grid cell i on day j; t(x_i, y_i) is a tensor product smooth of the x and y coordinates of cell i; R_{p_rfij} and R_{p_gbij} are the predicted residuals of the 1 km T_a model from the stage 3 random forest and XGBoost model, respectively, for cell i on day j; and ε_ij is the error for cell i on day j. The GAM averages the random forest and XGBoost predicted residuals using weights that vary both by location and with the magnitude of each model’s predicted residual. Finally, we add the ensemble-predicted residuals for all 200 m grid cells to T_{ap_1km} (T_a predicted in stage 2 by the final 1 km model) to obtain daily 200 m predicted T_a (T_{ap_200m}) across large urban areas.

2.8.3. Performance assessment

We use 10-fold out-of-sample cross-validation to assess the overall performance of the models. For the random forest and XGBoost model we use nested tuning (i.e. within each cross-validation fold we tune the model as described in section 2.8.1). To evaluate the models’ ability to capture both spatial and temporal patterns in T_a, we also calculate the spatial and temporal components of the errors. The spatial component is the difference at each station between the annual mean of daily observed ${\text{T}}_{\text{a}}(\overline{{\text{T}}_{\text{a}}})$, and the annual mean of daily predicted ${\text{T}}_{\text{a}}(\overline{{\text{T}}_{\text{ap}}})$. The temporal component is the difference at each station between ΔT_a and ΔT_ap where ΔT_a is the difference between daily observed T_a and $\overline{{\text{T}}_{\text{a}}}$ and ΔT_ap is the difference between daily predicted T_a and $\overline{{\text{T}}_{\text{ap}}}$.

We use Google Earth Engine (Gorelick et al., 2017) to quality assure and composite Landsat T_b and NDVI and aggregate them to the 200 m grid cells. For all other data processing and analyses we use R version 3.4.4 (R Core Team, 2018).

3. Results

Table 2 presents the mean 10-fold cross-validated performance of the stage 1 models (predicting daily 1 km T_a from LST) across all years. The models perform very well, with R² of 0.92 or higher, RMSE of less than 2 °C, and mean absolute error (MAE) of less than 1.5 °C. All models have very low bias: the slope of observed vs. predicted T_a is 1.00 while the intercept ranges from 0.01 to 0.02. The T_mean models perform best overall (MAE 0.94), followed by the T_max (MAE 1.35) and T_min (MAE 1.43) models. The models capture both spatial and temporal variation in T_a and show little variation in performance between years, although overall T_mean performance decreases slightly after 2010, possibly reflecting degradation of the Terra MODIS instrument (Table S4). Consistent with previous studies, nighttime LST is the best predictor of T_min and T_mean while daytime LST is the best predictor of T_max (Oyler et al., 2016; Rosenfeld et al., 2017; Yoo et al., 2018). Aqua LST is a better predictor of T_min and T_max while Terra LST is a better predictor of T_mean. This is expected as the Aqua overpasses (approximately 1:30 and 13:30 local solar time) are closer to the time at which T_min and T_max typically occur in France. However, Aqua LST is only available since July 2002, so we use Terra LST for all models prior to 2003.

Table 2.

Stage 1 model (predicting daily 1 km T_a from LST): 10-fold cross-validated performance across all years (2000 – 2016), overall, spatial, and temporal components.

		Overall			Spatial			Temporal
	N*	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE
Tmin	354	0.92	1.89	1.43	0.89	1.10	0.80	0.94	1.61	1.19
Tmean	205	0.97	1.29	0.94	0.95	0.83	0.57	0.97	1.15	0.84
Tmax	324	0.95	1.81	1.35	0.88	1.23	0.89	0.96	1.52	1.12

^*N = mean thousands of observations used to fit each annual model

Table 3 presents the 10-fold cross-validated performance of the stage 1 models across all years by calendar month and season and Table 4 presents the performance by climatic region and urban vs. rural locations. The T_min and T_mean models perform slightly less well in winter months, possibly due to higher LST missingness from more frequent cloud cover. The T_max model performs best in late winter, early spring, and fall. The models perform less well in the mountain, semi-continental, and modified Mediterranean climates. These climates occur in mountainous areas where large contrasts in topography and land cover make modelling particularly challenging; other factors not included in the model may also reduce performance in these areas. The models perform slightly better in peri-urban areas than in urban and rural areas, possibly due to the higher density of weather stations (peri-urban areas have the most stations per km²).

Table 3.

Stage 1 model performance (predicting daily 1 km T_a from LST): 10-fold cross-validated performance across all years (2000 – 2016), by month and season.

	Tmin			Tmean			Tmax
	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE
Jan	0.83	2.16	1.60	0.89	1.54	1.11	0.86	1.87	1.37
Feb	0.84	2.03	1.51	0.91	1.37	0.99	0.89	1.74	1.28
Mar	0.80	1.92	1.46	0.91	1.22	0.91	0.89	1.72	1.28
Apr	0.77	1.82	1.39	0.91	1.17	0.85	0.87	1.75	1.32
May	0.80	1.75	1.33	0.92	1.20	0.86	0.85	1.85	1.39
Jun	0.81	1.74	1.32	0.92	1.23	0.90	0.84	1.94	1.46
Jul	0.79	1.71	1.30	0.92	1.19	0.88	0.84	1.90	1.44
Aug	0.78	1.77	1.35	0.92	1.18	0.88	0.87	1.89	1.43
Sep	0.79	1.83	1.40	0.92	1.12	0.84	0.87	1.70	1.29
Oct	0.83	1.94	1.47	0.91	1.26	0.93	0.88	1.67	1.25
Nov	0.82	2.02	1.52	0.89	1.42	1.03	0.88	1.69	1.25
Dec	0.82	2.17	1.61	0.86	1.69	1.21	0.84	1.94	1.39
Winter	0.83	2.12	1.57	0.89	1.55	1.11	0.86	1.86	1.35
Spring	0.86	1.83	1.40	0.94	1.20	0.87	0.91	1.77	1.33
Summer	0.80	1.74	1.32	0.92	1.20	0.89	0.86	1.91	1.44
Fall	0.87	1.92	1.46	0.95	1.26	0.92	0.93	1.69	1.27

Table 4.

Stage 1 model performance (predicting daily 1 km T_a from LST): 10-fold cross-validated performance across all years (2000 – 2016), by climatic region and urban vs. rural locations.

	Tmin			Tmean			Tmax
	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE
Mountain	0.90	2.22	1.71	0.95	1.69	1.25	0.93	2.26	1.73
Semi-continental	0.91	2.11	1.61	0.96	1.44	1.07	0.95	2.00	1.52
Modified oceanic	0.94	1.53	1.16	0.98	0.98	0.73	0.98	1.33	1.01
Transitional oceanic	0.92	1.81	1.37	0.97	1.20	0.88	0.95	1.74	1.31
Oceanic	0.90	1.79	1.33	0.96	1.20	0.88	0.94	1.83	1.36
Mod. Mediterranean	0.90	2.22	1.71	0.96	1.43	1.07	0.94	2.03	1.55
Southwest basin	0.94	1.60	1.22	0.98	1.04	0.76	0.97	1.40	1.04
Mediterranean	0.93	1.81	1.40	0.98	1.11	0.84	0.96	1.62	1.25
Urban	0.93	1.85	1.35	0.97	1.32	0.96	0.95	1.79	1.35
Peri-urban*	0.93	1.71	1.29	0.97	1.18	0.87	0.96	1.71	1.27
Rural	0.92	1.90	1.44	0.97	1.30	0.94	0.95	1.82	1.36

^*non-urban locations within 5 km of a large urban area

Fig. 2 shows the spatial pattern of the daily 1 km T_a predictions of the stage 2 model on selected winter and summer days. On the cold winter day of Feb 18, 2003, predictions range from T_min of −17 °C in parts of the Alps, the Massif Central, and the Pyrenees to T_max of 11 °C on the Mediterranean coast. The urban heat island of Paris is faintly visible in the north center of the T_min and T_mean maps but disappears on the T_max map. Spatial contrasts corresponding to terrain features are well resolved, and the spatial pattern of T_min vs. T_mean vs. T_max varies most in the north, northeast, and southwest.

Fig. 2.

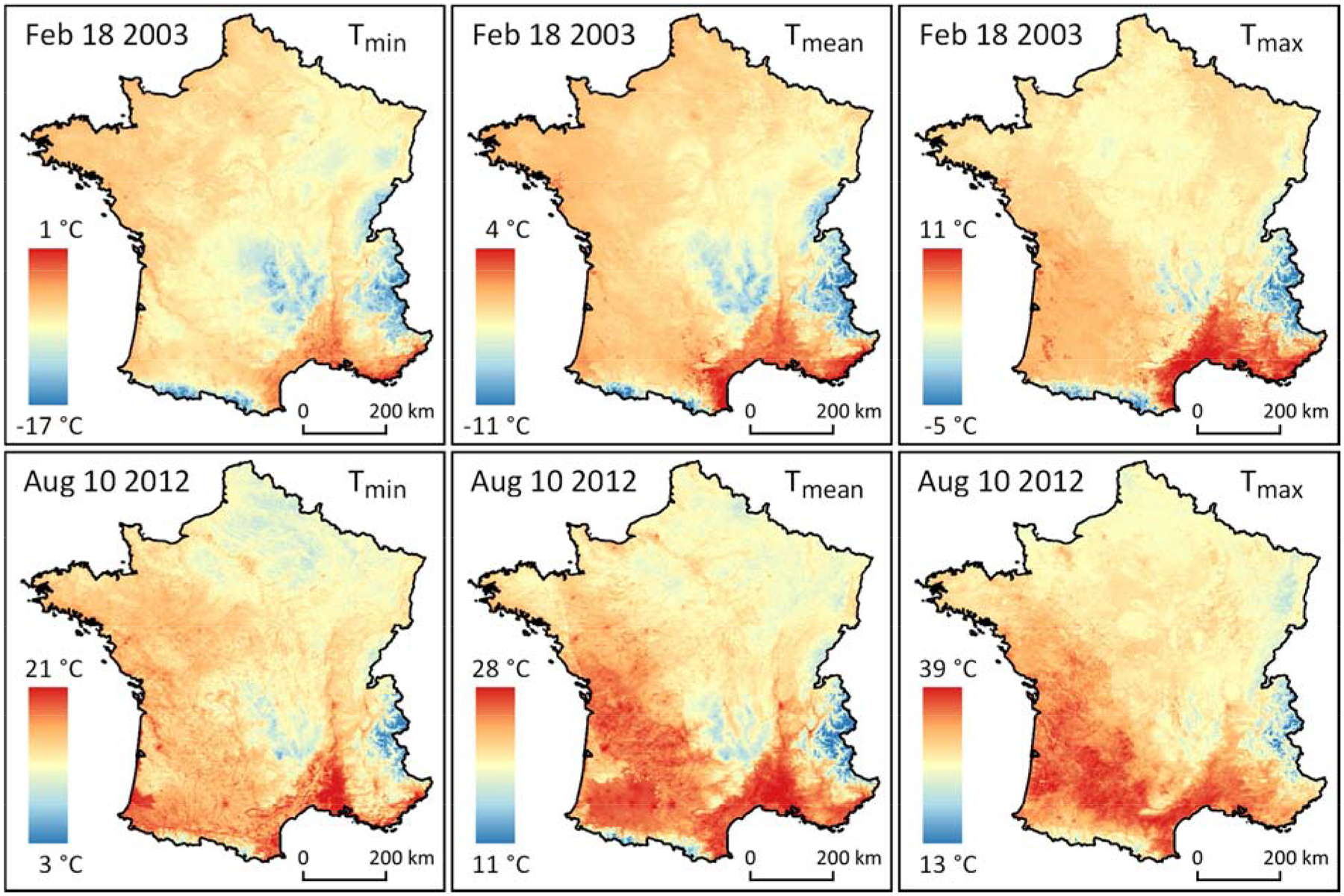
Predicted 1 km T_a from the stage 2 model on selected days: Feb 18, 2003 (top row) and Aug 10, 2012 (bottom row).

On the hot summer day of Aug 10, 2012, predictions ranged from a T_min of 3 °C in parts of the Alps to a T_max of 39 °C in the southeast and southwest. On the T_min map, the southwestern cities of Toulouse and Bordeaux stand out as hotspots, while Paris and Rouen are faintly visible as warm spots in the north. The north is colder than the Vosges mountains in the northeast and the Pyrenees in the southwest are warmer than the alps. The warmest areas are the southern Rhone river valley in the southeast and a patch of the southwestern Atlantic coast. On the T_mean map, Paris and Rouen are still visible, Lyon stands out in the east, and a few northwestern cities appear. Much of the southwest is as warm as the southeast, and the southwestern cities are harder to distinguish from the countryside. On the T_max map, Lyon, Rouen, and some northwestern cities remain faintly visible, Pau and Tarbes appear in the southwest, and the north is warmer than the Vosges.

Table 5 presents the 10-fold cross-validated performance of the stage 4 models (predicting daily 200 m residuals of the 1 km model using an ensemble) across all years and by month and season; Table 6 presents the performance by climatic region and urban vs. rural locations. These models also perform well, with overall R² of 0.79 to 0.85, RMSE of 0.41 to 0.63, and MAE of 0.26 to 0.39 (residual scale). As with the stage 1 models, the R_Tmean predictions are slightly better than the R_Tmin or R_Tmax predictions and the models perform least well in the mountain, semi-continental, and modified Mediterranean climates. The R_Tmin model performs slightly worse in late summer; otherwise performance is quite consistent across months and seasons. The models have low bias, with a slope of observed vs. predicted of 1.00 and intercept of zero for every year. Performance is consistent across years except for the R_Tmin model, which performs slightly better in 2000 – 2002, and the R_Tmean model, which performs best in 2004 (Table S6).

Table 5.

Stage 4 model performance (predicting daily 200 m residuals with an ensemble): 10-fold cross-validated performance across all years (2000 – 2016), overall and by month and season (residual scale).

	RTmin			RTmean			RTmax
	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE
Overall	0.79	0.63	0.39	0.79	0.41	0.26	0.85	0.51	0.31
Jan	0.84	0.56	0.34	0.82	0.40	0.24	0.85	0.48	0.27
Feb	0.82	0.59	0.36	0.81	0.39	0.24	0.84	0.49	0.28
Mar	0.80	0.63	0.39	0.79	0.40	0.26	0.83	0.50	0.30
Apr	0.77	0.63	0.40	0.76	0.39	0.25	0.83	0.51	0.31
May	0.77	0.60	0.37	0.76	0.38	0.24	0.84	0.51	0.31
Jun	0.77	0.62	0.40	0.79	0.39	0.25	0.87	0.52	0.33
Jul	0.76	0.66	0.43	0.77	0.42	0.28	0.86	0.55	0.35
Aug	0.77	0.67	0.44	0.78	0.41	0.28	0.87	0.54	0.34
Sep	0.77	0.69	0.46	0.75	0.42	0.29	0.84	0.54	0.34
Oct	0.78	0.65	0.41	0.76	0.42	0.27	0.82	0.52	0.32
Nov	0.80	0.61	0.37	0.79	0.41	0.25	0.81	0.50	0.29
Dec	0.83	0.60	0.37	0.84	0.43	0.27	0.84	0.52	0.31
Winter	0.83	0.58	0.36	0.83	0.41	0.25	0.84	0.50	0.28
Spring	0.78	0.62	0.39	0.77	0.39	0.25	0.84	0.51	0.31
Summer	0.76	0.65	0.42	0.78	0.41	0.27	0.86	0.54	0.34
Fall	0.78	0.65	0.41	0.77	0.42	0.27	0.82	0.52	0.32

Table 6.

Stage 4 model performance (predicting daily 200 m residuals with an ensemble): 10-fold cross-validated performance across all years (2000 – 2016), by climatic region and urban vs. rural locations (residual scale).

	RTmin			RTmean			RTmax
	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE
Mountain	0.83	0.67	0.42	0.83	0.46	0.30	0.88	0.58	0.36
Semi-continental	0.81	0.66	0.42	0.79	0.43	0.28	0.86	0.55	0.34
Modified oceanic	0.75	0.54	0.33	0.76	0.33	0.21	0.81	0.40	0.23
Transitional oceanic	0.77	0.62	0.39	0.78	0.39	0.25	0.84	0.50	0.30
Oceanic	0.75	0.62	0.40	0.77	0.39	0.26	0.83	0.50	0.30
Mod. Mediterranean	0.82	0.73	0.47	0.78	0.47	0.31	0.84	0.62	0.41
Southwest basin	0.75	0.59	0.36	0.69	0.38	0.24	0.78	0.48	0.29
Mediterranean	0.77	0.67	0.44	0.73	0.42	0.28	0.80	0.57	0.39
Urban	0.79	0.53	0.32	0.82	0.37	0.23	0.84	0.46	0.27
Peri-urban*	0.76	0.58	0.36	0.78	0.37	0.24	0.83	0.47	0.28
Rural	0.79	0.63	0.40	0.79	0.41	0.26	0.85	0.52	0.32

^*non-urban locations within 5 km of a large urban area

Spatial location and elevation are generally the most important features in the random forest and XGBoost models (Fig. S2 – S3). Day of year and predicted 1 km T_a were equally or even more important in some models but less important in others. Landsat T_b and NDVI and population also contributed to the models, particularly for R_Tmean. The land cover and climatic region variables were the least important.

Fig. 3 shows the spatial pattern of predicted 1 km T_min from the stage 2 model and predicted 200 m T_min from the stage 4 model for the Paris metropolitan area (northern France, population 12.5 million), the Toulouse metropolitan area (southwestern France, Population 1.3 million), and the Nancy metropolitan area (northeastern France, population 250,000) on the cold winter day of Feb 18, 2003. In the large city of Paris, an urban heat island is clearly visible centered over the large urban core where T_min is about 5 °C warmer than the rural surroundings. The 200 m predictions are slightly higher than the 1 km predictions in the peripheral built-up areas and capture fine details such as the warmer Seine river and cooler parks. In the midsize city of Toulouse, the 1 km predictions capture an urban heat island over the dense city center and the suburbs to the northwest and southeast, with T_min about 3 °C warmer than the rural surroundings. The 200 m predictions show warm T_min in the southwestern suburbs where 1 km T_min was cool and capture the Garonne river in the center. The northwestern and northeastern suburbs have greater contrast with some areas slightly cooler than in the 1 km predictions and others slightly warmer. In the small city of Nancy, at 1 km both the city center and an area of ponds to the southeast have T_min about 2 °C warmer than the surroundings. The 200 m predictions show warmer T_min throughout most of the built-up area with sharp contrasts between built and open areas: compared to the 1 km predictions, T_min is up to 2 °C higher in the center, north, and west of the built-up area and up to 2 °C lower over parks and over fields abutting the eastern edges of the city.

Fig. 3.

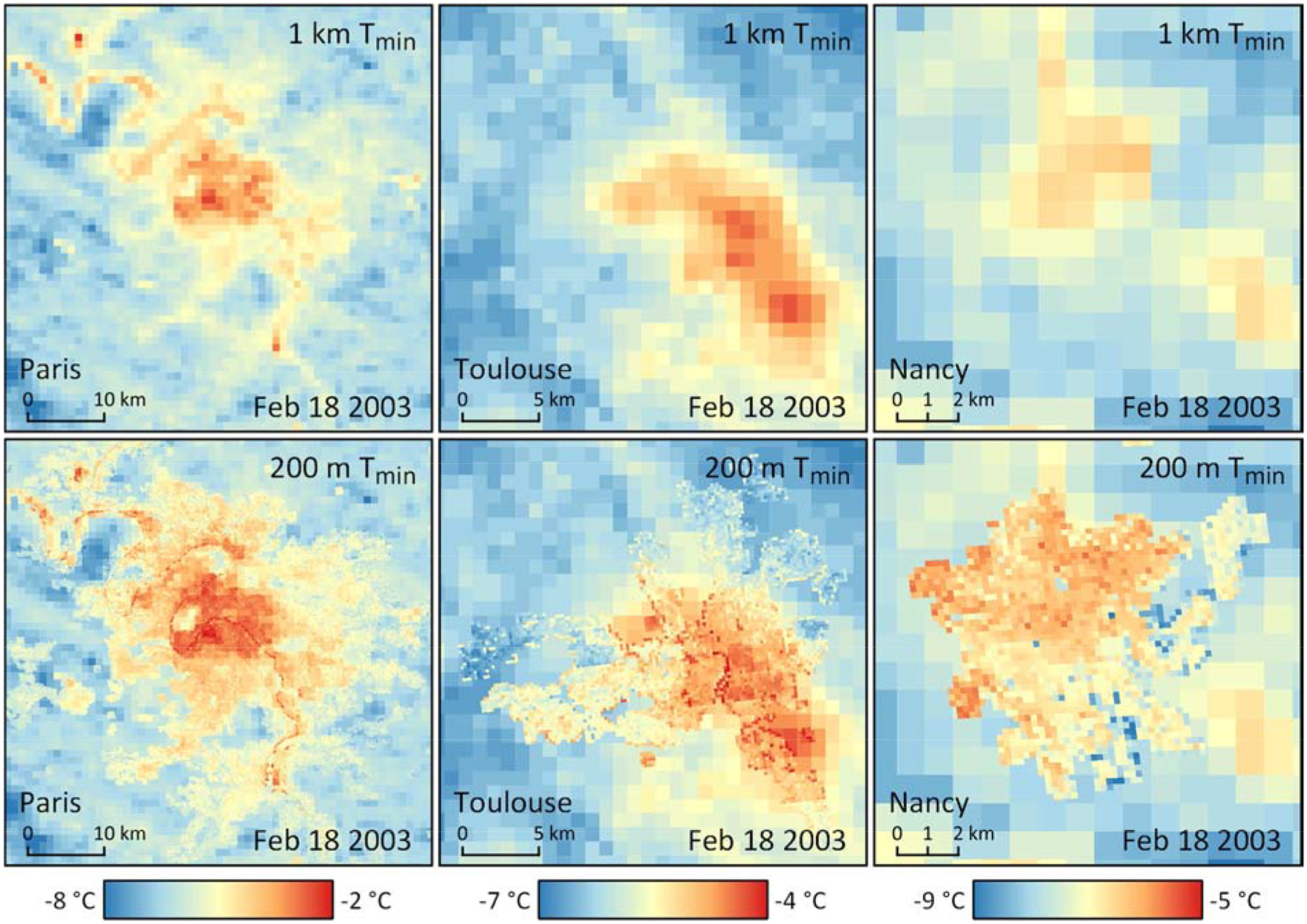
Predicted 1 km T_min from the stage 2 model alone (top row) and with predicted 200 m T_min from the stage 4 model overlaid (bottom row) on Feb 18, 2003 over the Paris, Toulouse, and Nancy metropolitan areas.

4. Discussion

Spatiotemporally-resolved T_a at high resolutions is essential to understanding, monitoring, and managing the health effects of T_a, a pressing issue in a warming, urbanizing world. We have developed the longest (2000 – 2016), highest spatial resolution (1 km) model of daily T_a available for continental France aimed at public health research. Furthermore, our model provides an unprecedented spatial resolution of 200 m over large urban areas.

A key feature of our model is its ability to capture spatial variation in T_a. Previous epidemiological research in France linked geographical variation in mortality risk to both typical (Laaidi et al., 2006) and extreme T_a (Le Tertre et al., 2006) using weather stations. Recent studies in the USA showed that a daily 1 km T_a dataset similar to ours was needed to detect associations with low birth weight (Kloog et al., 2015) and mortality (Shi et al., 2015). Our model will allow future studies in France to include participants in rural areas far from weather stations and will also improve exposure estimates in urban areas.

Another key feature is our model’s 200 m spatial resolution over urban areas. Estimating T_a exposure in cities is particularly challenging due to complex built environments and the scarcity of representative T_a measurements, as weather stations tend to be located outside cities (e.g. at airports) or in large parks. Consequently, few epidemiological studies have examined intra-urban variation in T_a. In Milan, Italy, de’Donato et al. (2008) found that on hot summer days temperature measured at a nearby airport tended to be higher and more strongly associated with mortality than temperature measured in the city center, but in Turin and Rome there was little difference in temperature or its association with mortality between the city center and a nearby airport. In Paris, France, Laaidi et al. (2012) used 1 km LST as a proxy for T_a and found an association between minimum LST and mortality during the August 2003 heatwave. In Brisbane, Australia, Guo et al. (2013) found no significant difference in the mortality ~ T_a relationship when estimating T_a exposure using a central weather station vs. kriging, but noted that there was little spatial variation in temperature across the city. In Seattle, USA, Ho et al. (2017) found a significant association between spatial variation in mortality on extremely hot days and modeled humidex (a measure of both T_a and humidity). Our model will help future studies clarify the health effects of intra-urban T_a variation.

Our model’s unique combination of lower spatial resolution (1 km) predictions over a large geographical extent and higher spatial resolution (200 m) predictions over more densely populated areas will be particularly helpful for epidemiological studies. Broad geographical coverage is essential to including rural residents which have often been excluded from epidemiological studies, especially in France where the 103 largest urban areas covered by our 200 m T_a model contain less than half of the population. At the same time, high spatial resolution is important in dense urban areas where T_a can vary at fine spatial scales and the effect of spatial T_a variation is less well understood. Limiting the 200 m resolution predictions to large urban areas reduces computational effort while still covering a large portion of the population.

A fourth feature of our model is its ability to predict daily T_min, T_mean, and T_max. While T_mean suffices for many health studies (Barnett et al., 2010), certain research questions may benefit from having T_min and T_max. For example, heatwave studies may wish to use heatwave definitions that refer to T_min or T_max (Xu et al., 2016) or explore whether certain populations are sensitive to T_min or nighttime T_a (Laaidi et al., 2012; Murage et al., 2017). T_max might also be of interest because it tends to occur in the afternoon when people are more likely to be outside and active (Guo et al., 2017). T_min and T_max also allow calculating diurnal T_a range for studies of T_a variability and delineating diurnal and nocturnal urban heat islands for urban climate studies.

We demonstrate that allowing the relationship between 1 km LST and T_a to vary by climatic region as well as by day slightly improves performance: our stage 1 T_mean model achieves overall R² of 0.97 with RMSE of 1.29 whereas an initial version achieved R² of 0.96 with RMSE of 1.52 (Kloog et al., 2017). We also demonstrate that a GAM ensemble of machine learning models can use higher spatial resolution predictors including Landsat thermal data to account for some of the residual error in our daily 1 km T_a predictions. Adding this local stage both increases the spatial resolution of our model and improves performance.

One limitation of our method is its reliance on historical satellite thermal data. Our model is restricted to the MODIS period of record, which starts in 2000. Older thermal data is available from other satellites (e.g. Landsat), but not with a twice-daily revisit time. In the USA, Oyler et al. (2015) showed that an anomaly-climatology approach could model daily T_min and T_max since 1948 from 8-day composite MODIS LST, although their approach may have smoothed spatiotemporal T_a trends.

Our model can estimate past T_a but, unlike numerical weather prediction models, cannot forecast future T_a. However, our model is much simpler, which allows us to run it at relatively high spatial resolutions (1 km and 200 m). In comparison, Météo France’s weather prediction model has run at a spatial resolution of 1.3 km only since 2015, and the ECMWF’s most recent ERA5 reanalysis has a spatial resolution of just 30 km. And recent studies suggest that incorporating LST from geostationary satellites might allow us to estimate close to real-time T_a (Bechtel et al., 2017; Keramitsoglou et al., 2016), or possibly forecast next-day T_a from present-day MODIS LST (Yoo et al., 2018).

Another limitation of our approach is the temporal misalignment between observations of LST and T_a in the stage 1 model: the satellite overpass does not always coincide with the time that T_min or T_max occurs. Our model’s low MAE (typically less than 1.5 °C) suggests that it produces good T_a estimates despite this; incorporating high temporal-resolution (e.g. hourly) LST from geostationary satellites might improve performance.

A fourth limitation of our model is the need to fill gaps in satellite thermal data. This can introduce error and may make modelling impossible in some areas or time periods. Landsat data is particularly challenging due to the satellites’ 16-day revisit time; parts of France have no usable Landsat observations during some winters. The few previous studies that used Landsat thermal data to model T_a limited their analysis to days and locations where Landsat data was available (Pelta and Chudnovsky, 2017) or used a few scenes that were deemed typical of hot summer days (Ho et al., 2016, 2014; Wicki et al., 2018). We fill gaps in Landsat T_b by compositing all scenes for each calendar month across 17 years. This smooths spatial patterns and means we rely entirely on MODIS to capture short-term temporal variation in LST. Combining data from Landsat 5, 7, and 8 may also introduce error as the sensors operate at different wavelengths and spatial resolutions (Table 1). Future studies may benefit from the forthcoming Landsat Surface Temperature product (Malakar et al., 2018) which might be more consistent, and would allow using LST as a predictor rather than brightness temperature.

Future studies could also make use of high spatial-resolution LST from forthcoming satellites. Landsat 9 will have a spatial resolution and revisit time similar to the previous Landsat satellites, but should offer better LST retrieval thanks to the correction of the stray light contamination that affects Landsat 8 (Hair et al., 2018). HyspIRI aims to provide a 60 m spatial resolution with a revisit time of 5 days (Lee et al., 2015), while MISTIGRI aims for 50 m spatial resolution with a daily revisit, but with coverage only within 15 ground tracks (Lagouarde et al., 2013). If these satellites improve LST retrieval and reduce missingness then they could improve our method’s ability to capture T_a over urban areas.

MODIS LST also contains gaps, which we do not fill. Rather, we predict daily 1 km T_a only where MODIS LST is available and fill gaps in the predictions based on nearby T_a observations. Li et al. (2018) achieved similar performance (RMSE 2.1 °C T_min, 1.9 °C T_max) for urban and surrounding areas in the USA by first filling gaps in MODIS LST using spatiotemporally nearby LST observations and then predicting daily T_a using geographically weighted regression. These approaches both assume that the spatial distribution of T_a or LST is similar on clear and cloudy days. Zhu et al. (2017) used the MODIS atmospheric profile and cloud cover products to estimate instantaneous T_a in parts of China and the USA. Their approach had the additional advantage of not requiring any weather station T_a observations to calibrate the model, but it produced larger errors (RMSE 3.4 °C China, 2.9, USA).

Despite these limitations, our model provides very good predictions of historical daily T_a for continental France at a 1 km or finer spatial resolution. These predictions may help compare rural and urban populations, identify and monitor urban heat islands, and better understand health effects. More broadly, our methodology and predictions may be useful in other geographical areas and for any application where T_a is a key variable.

• We model daily min, max, and mean air temperature in France 2000 – 2016

• Linear mixed models using MODIS LST predict daily 1 km Ta

• Machine learning ensemble using Landsat data increases resolution to 200 m

• MODIS and Landsat data can predict daily T_a at up to 200 m resolution