Using Serology to Anticipate Measles Post-honeymoon Period Outbreaks

Abstract

Measles vaccination is a public health ‘best buy’, with the highest cost of illness averted of any vaccine-preventable disease (Ozawa et al., Bull. WHO 2017;95:629). In recent decades, substantial reductions have been made in the number of measles cases, with an estimated 20 million deaths averted from 2000 to 2017 (Dabbagh et al., MMWR 2018;67:1323). Yet, an important feature of epidemic dynamics is that large outbreaks can occur following years of apparently successful control (Mclean et al., Epidemiol. Infect. 1988;100:419–442). Such ‘post-honeymoon period’ outbreaks are a result of the nonlinear dynamics of epidemics (Mclean et al., Epidemiol. Infect. 1988;100:419–442). Anticipating post-honeymoon outbreaks could lead to substantial gains in public health, helping to guide the timing, age-range, and location of catch-up vaccination campaigns (Grais et al., J. Roy. Soc. Interface 2008003B6:67–74). Theoretical conditions for such outbreaks are well understood for measles, yet the information required to make these calculations policy-relevant is largely lacking. We propose that a major extension of serological studies to directly characterize measles susceptibility is a high priority.

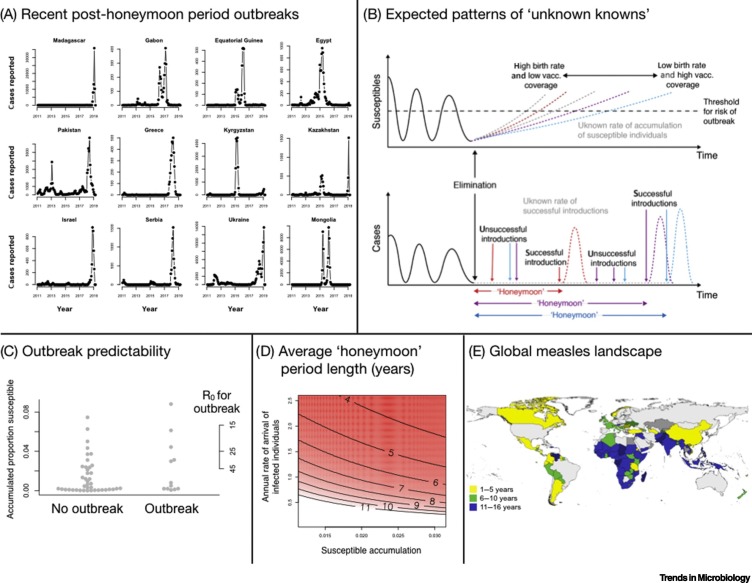
‘Post-honeymoon outbreaks’ have recently affected multiple countries around the world, including Madagascar, the Philippines, and Egypt (Figure 1A). The ‘honeymoon’ consists of the period following vaccine introduction or a mass vaccination campaign where cases are low, resulting in reduced immunization by natural infection of individuals born into the population (or already in the population) who remain unvaccinated and susceptible. Once the size of the susceptible pool exceeds a threshold, a new outbreak can occur if an infectious individual enters the population (Figure 1B).

Figure 1.

(A) Time-series of Exemplar Countries Having Experienced a Measles Post-honeymoon Outbreak Showing Numbers of Cases Each Month.

(B) Schematic indicating that, following extinction, when cases are reduced to zero (lower panel), which occurs when there are too few susceptible individuals for the infection to keep spreading, the duration of a honeymoon is shaped by two ‘known unknowns’: (i) effective vaccination coverage, which, in combination with birth rates, determines the time until susceptible individuals exceed the threshold for an outbreak (upper panel, blue lines); and (ii) the arrival of an infected individual. (C) For non-outbreak (left) and outbreak (right) years in the countries from Figure 1A during the honeymoon period, the proportion susceptible in each year (y axis, left) is established by accumulating the unvaccinated fraction of the birth cohort for each year without an outbreak. Outbreak years do not have significantly more susceptibles, and furthermore the span of R₀ values inferred to be required to result in an outbreak under these conditions (defined by the fact that R_E = SR₀ must be >1, where S is the proportion susceptible) suggests unrealistically large magnitudes of R₀ (y axis, right), noting that this framing makes the simplifying assumption that populations are well mixed. (D) Predicted average waiting times to a new outbreak (contours indicate years, also shown by the colors) over the span of turnover of human populations (x axis) that emerges as a result of birth rates and vaccination coverage; and rates of introduction of infected individuals (y axis); assuming that, following local extinction, the starting proportion susceptible S_t=0 = 1/R₀, that is, the proportion susceptible expected in an endemic setting. (E) Map of countries having experienced a post-honeymoon outbreak between 2010 and 2020 (hashed lines) where all countries are colored by the number of years that they experienced vaccination coverage <90% (yellow indicates 1–5 years, green 6–10 years, and blue 11–16 years).

Measles is an exceptionally well understood infection epidemiologically [1], and the theoretical conditions necessary for an outbreak to occur are clearly defined. Following extinction, the shortest possible waiting time until a post-honeymoon outbreak is determined by the growth of the susceptible population, that is, the cumulative number of births subsequently unimmunized by vaccination and susceptible individuals who enter the population (Figure 1B). Outbreaks can only occur if the size of the susceptible pool is above the threshold for herd immunity, most simply defined as 1/R₀ (the basic reproduction number, R₀, or expected number of new infections per one infectious individual in a completely susceptible population, which, for measles, typically ranges from 15 to 20). The other key requirement for a post-honeymoon outbreak is the arrival of an infectious individual who sparks a new outbreak (Figure 1B).

However, deploying this rich mechanistic understanding of measles requires core processes to be adequately observed. In general, they are not. For example, when the size of the susceptible pool is calculated for each of the outbreaks illustrated (Figure 1A), using data on vaccination coverage, births, and estimates of extinction time, this quantity cannot predict epidemic occurrence (Figure 1C). Outbreaks occur at a wide range of sizes of the susceptible pool, including values so small as to suggest (if susceptibles are evenly distributed in the population) an R₀ >45, which is at the larger end of values reported (Figure 1C, right hand axis). While birth rates are reasonably characterized globally, vaccination coverage remains surprisingly uncertain [2], making it a critical ‘known unknown’ for predicting the timing of post-honeymoon outbreaks (Figure 1B).

The other ‘known unknown’ concerns introduction rates. Formally, the hazard of a reintroduction sparking a measles epidemic can be expressed as [3]:

$$h\left(t\right)=\frac{R_0{S}_t\left(1-exp\left(-c{S}_t\right)\right)}{1+R_0{S}_t}$$ [1]

where S _t is the proportion of susceptible individuals at time t and the term 1 −  exp (−cS _t) represents the probability that, during a time step, a contact occurs between a susceptible from the community and an infected individual that arrives from the outside, R ₀ S _t/[1 + R ₀ S _t] represents the probability that that contact initiates an outbreak, that is, that at least one person will be infected by the arrived infectious individual. S _t grows according to S _t+1 = S _t + (1 − v)B, where the interval separating t and t + 1 is the approximate generation time of the infection (approximately 2 weeks for measles), B is the number of births expected to occur during this time period, v is the effective vaccination coverage (proportion immune after vaccination), and c is the rate of arrival of infected individuals.

The waiting time to reintroduction is defined by a waiting time distribution which is defined by W(T) = h(T)∏_t=1 ^T−1(1 − h(t)). Around the globe, annual birth rates range from ~12 to 45 per 1000 people per year; and immunization via routine vaccination coverage is generally >70%, and can exceed 95%. From this, we can bound the range of growth of susceptible individuals (Figure 1D, x axis) and establish the average waiting time to an outbreak (Figure 1D, surface) for a range of rates of introduction of infectious individuals (Figure 1D, y axis).

High rates of introduction correspond to short delays and this is amplified at greater susceptible accumulation (Figure 1D). Yet, estimating stochastic introduction rates is not straightforward, requiring both nuanced travel data and information on infection status. Furthermore, successful introduction may take longer than the rates of travel by infectious individuals might suggest, as populations are not well mixed, such that an infectious individual may not come into contact with the susceptible population (e.g., contact between individuals of different ages may be limited [4]). Seasonality in transmission [1] reflecting periods of the year, when contact between susceptibles is low, will also make introductions at certain times of year ineffectual.

These threads of uncertainty indicate a need to reframe the prediction question more conservatively, to focus on the more tractable ‘known unknown’ of population susceptibility. Every community is likely to be at risk of reintroduction of measles given current travel patterns and measles incidence (Figure 1E). We argue that the key issue is therefore to know how far the population is from the threshold for herd immunity: once the size of the susceptible population exceeds this threshold, longer delays allow a larger pool of susceptibles, and bigger eventual outbreaks. Theoretically, knowledge of vaccination history and incidence are sufficient to project population immunity and characterize the risk and urgency of interventions to prevent a post-honeymoon outbreak. In reality, heterogeneity in vaccination coverage [5] combined with uncertainty in vaccination data [2], and under-reporting of disease incidence (also a source of immunity) makes this indirect calculation intractable [6].

Instead, population immunity can be directly measured by serology. Crucially, this has proven successful in predicting the risk of measles outbreaks in a few settings. A cross-sectional population serological survey was harnessed to launch a vaccination campaign and thus avert a post-honeymoon outbreak in England and Wales [7]. More recently, analysis of a serological convenience sample, taken from fever/rash surveillance, estimated a large susceptible population in Madagascar, suggesting that the country had been experiencing a ‘honeymoon period’ and was at considerable risk of a measles outbreak [8]. This subsequently occurred (Figure 1A).

In practice, serological data necessary for such predictions are rare. We can approach this problem via two immediately available sources of samples, allowing increasing granularity of prediction; there is also potential for a much more comprehensive approach. First, samples that could be leveraged for serological analysis are often available, collected as part of efforts for routine surveillance (such as fever and rash surveillance [8]), and stored at national reference laboratories in countries around the world. Second, large cross-sectional surveys [7] that include blood samples taken to test for other health outcomes (e.g., HIV prevalence studies) are widespread, often multinational (e.g., the Demographic Health Surveys) and may be repeated across years, providing the important perspective of changes across time. However, these existing sources of data and samples are not sufficient to provide a systematic assessment of susceptibility in all key contexts. A Global Immunological Observatory [9], that unified and significantly extended current samples, would allow much more systematic prediction of risk, severity, and, importantly, the likely age ranges of measles cases following outbreaks in many settings. Inevitably, no sampling scheme for serological data (whether opportunistic or systematic) will be without uncertainties in terms of range and characteristics of individuals reached, or in our ability to delineate heterogeneities in space and time. Additionally, the measles serological assay has its own challenges, including a small but existing probability of false negatives and the necessity for both a laboratory and laboratory expertise to conduct the assay with quality control and assurance. Nevertheless, these threads are likely to bring another key angle on the data already available, and would prove a powerful asset for targeting vaccination campaigns to those communities, age groups, or subpopulations at highest risk, ultimately improving the efficiency of campaigns. Furthermore, expanding research in this area could lead to important innovations [9], such as the ability to distinguish natural and vaccine-induced immunity, which will improve our understanding of vaccination coverage, arguably the critical known unknown. Such advances will yield dividends both in low- and middle-income countries, where low vaccination coverage is generally driven by logistical barriers; but also in countries where vaccine hesitancy is the main barrier to achieving population immunity, yet vaccination rates are often uncertain in key settings [10]. With the potential for the current COVID-19 pandemic to disrupt vaccination programs, evaluating population measles immunity will become increasingly important to understand the impact on outbreak risk.