Structure based computational assessment of channel properties of assembled ORF‐8a from SARS‐CoV

ABSTRACT

ORF 8a is a short 39 amino acid bitopic membrane protein encoded by severe acute respiratory syndrome causing corona virus (SARS‐CoV). It has been identified to increase permeability of the lipid membrane for cations. Permeability is suggested to occur due to the assembly of helical bundles. Computational models of a pentameric assembly of 8a peptides are generated using the first 22 amino acids, which include the transmembrane domain. Low energy structures reveal a hydrophilic pore mantled by residues Thr‐8, and −18, Ser‐11, Cys‐13, and Arg‐22. Potential of mean force (PMF) profiles for mono (Na⁺, K⁺, Cl⁻) and divalent (Ca²⁺) ions along the pore are calculated. The data support experimental findings of a weak cation selectivity of the channel. Calculations on 8a are compared to data derived for a pentameric bundle consisting of the M2 helices of the bacterial pentameric ligand gated ion channel GLIC (3EHZ). PMF curves of both, bundles 8a and M2, show sigmoidal shaped profiles. In comparison to the data for the M2‐GLIC model, data of the 8a bundle show lower amplitude of the PMF values between maximum and minimum and less discrimination amongst ions. Proteins 2015; 83:300–308. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Structure based computational modeling plays an important role in predicting the properties of biological macromolecules such as dynamics and mechanism of function. Focusing on proteins, especially small membrane proteins, structures of these molecules have already been built ‘ab initio’ using a combination of bioinformatics and assembly protocols1, 2; see Ref. 3 and references therein. Implementation of experimentally derived information from structural biology further improves the quality of the prediction. Investigations of channel proteins,4, 5, 6, 7, 8, 9 the assembly of short membrane proteins in lipid bilayers,10 and bending of bilayers11, 12 are just a few examples of how computational methods enable insights into the mechanics of the proteins on a molecular level.

A major challenge in structure based computation is to simulate ion flux and deliver information about the conductivity and selectivity of an ion channel. On the basis of classical molecular dynamics (MD) simulations, umbrella sampling (US) techniques in combination with steered MD is a tool to calculate the potential of mean force (PMF) of an ion permeating through the lumen of a protein pore.13, 14, 15 The energy profile allows qualitative assessment of the selectivity of the pore, with respect to particular ions.

ORF8a of the severe acute respiratory syndrome causing corona virus (SARS‐CoV) has been recently identified to induce channel activity.16 Experiments have been done with synthetic peptides reconstituted into artificial lipid bilayers. 8a protein is with its 39 amino acids the shortest member of the class of viral channel proteins (VCPs),17 also named viroporins.18 Its role in the infectivity cycle of SARS‐CoV is to enhance particle release and induce apoptosis in a mitochondria‐dependent pathway.19 Structural information is not yet available and thus, application of computational modeling is a reliable tool suggesting plausible structures. VCPs are found in many enveloped and naked human viruses as well as in plant viruses.20, 21, 22 Generally they are about 100 amino acids in length, with the exception of 3a from SARS‐CoV, which is found to be made of 274 amino acids. In many cases, the role of the VCPs in the infectivity cycle of the virus is not univocally established. Up to now, structural investigations of individual VCPs reveal, that they adopt a helical motif to span the bilayer, which is also supported by secondary structure prediction programs. On the basis of the latter, 8a has been simulated using a helical motif for its transmembrane domain (TMD).16 Furthermore, it has been suggested, that a pentameric assembly forms the most plausible bundle model. Bilayer recording studies reveal weak cation selectivity of the protein.

In this study, a pentameric assembly of the TMD of 8a is generated using established protocols.2, 23 1D PMF calculations are applied to investigate structural features causing selectivity of the putative bundle model. The data are correlated with earlier experimental findings.16

MATERIALS AND METHODS

An ideal helix of the first 22 amino acids of ORF8a from SARS‐CoV (LLIVLTCI10 SLCSCICTVV20 QR, 8a_1–22), including the putative TMD has been created with backbone dihedrals of ϕ = −65° and φ = −39° using the program MOE (Molecular Operation Environment, http://www.chemcomp.com) and its integrated protein builder.16 The sequence of the M2 helices (EANVTLVVST³⁰⁰ LIAHIAFNIL³¹⁰ VET) was taken from the proton‐activated pentameric ligand gated ion channel (pLGIC) of the cyanobacterium Gloebacter violaceus (GLIC, 3EHZ).24

Assembly of the bundle

The peptide structures from the last 10 ns of a MD simulation were averaged over their backbone atoms. The peptide structure of each frame was mapped onto the starting structure to remove rotational and translational motions. The program g_covar from GROMACS package was used for these calculations.23 The pentameric bundle of 8a was generated by copying the original single TMD around a central (C5) axis with an inter‐helical separation angle of 72°.16 Each of the following degrees of freedom were independently varied stepwise to sample the entire conformation space of the bundle: (i) interhelical distance in steps of 0.25° Å covering 9–15 Å; (ii) rotational angles around the helical axis in steps of 5° covering 360°; (iii) tilt in steps of 2° covering −36 to +36°. In each step, the backbone was moved and the side chains consequently added according to the most probable orientation according to the integrated rotamer library of the MOE suit. Short minimization steps of steepest descent and conjugated gradient were used to avoid steric clashes. The potential energy of each conformation was evaluated according to the AMBER94 force field in an implicit lipid environment characterized by a dielectric constant of ε = 2.

MD simulations

The single TMD and the respective bundles were embedded into a fully hydrated POPC (16:0−18:1 diester PC, 1‐palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phospho‐chloine) bilayer system for which the lipid parameters according to Chandrasekhar et al.25 were used. Prior to the insertion of the proteins the lipid system was equilibrated for 70 ns¹. When inserting the proteins, lipid molecules overlapping with the proteins were removed using the MOE suite. Equilibration of the protein–lipid system was done by gradually increasing the temperature of the system from 100 to 200 K and 310 K. At each of the temperatures the system was run for 750 ps. At this stage, the peptide was kept fully restraint using k = 1000 kJ mol⁻¹ nm⁻². Holding the system at 310 K, the restraints on the peptide were gradually released in 4 steps (k = 500, 250, 100, and 25 kJ mol⁻¹ nm⁻²), running each of the steps for 2.0 ns. The unconstrained systems were then submitted to production runs of 50 ns.

In total, 48 Na⁺ and 58 Cl⁻ ions were added to neutralize the bundle system and to generate a 150 mM NaCl solution. The whole system consisted of the bundle (1035 atoms), 112 POPC lipids, and 3681 SPC‐water molecules (18,008 atoms in total).

GROMACS‐4.5 with the Gromos96 (ffG45a3) force field was used for simulations. The simulations were conducted in the NPT ensemble employing the velocity‐rescaling thermostat at constant temperature 310 K, and 1 bar. The temperature of the protein, lipid, and the solvent were separately coupled with a coupling time of 0.1 ps. Semi‐isotropic pressure coupling was applied with a coupling time of 0.1 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹ for the x‐y‐plane as well as for the z‐direction. Long‐range electrostatics were calculated using the particle‐mesh Ewald (PME) summation algorithm with grid dimensions of 0.12 nm. Lennard‐Jones and short‐range Coulomb interactions were cut off at 1.4 and 1.0 nm, respectively.

Calculations of the potential of mean force

PMF was calculated based on the umbrella sampling (US) technique.14, 26 The starting configurations for the US simulations were generated by steering an ion through the bundle along the central pore axis (here the z‐axis) at a rate of 0.5 nm/ns. At this stage, the ion was attached to a virtual spring with a force constant of 2000 kJ/mol/nm². Frames in steps of 0.5 Å were chosen as starting configurations for US. A harmonic restraint of 4000 kJ/mol was applied on the ion position along the central pore axis. The subsequent simulations were carried out for 1.2 ns each. The PMFs were constructed with the WHAM procedure (g_wham in GROMACS). Bootstrap analysis (n = 50) was conducted to estimate the statistical error. The first 200 ps were omitted and a cyclic correction for the periodic system was applied, using α = 1.75.

The simulations were run on a DELL T7500 workstation, 28 core Opteron based computer cluster with Infiniband interconnects and the ALPS‐Acer AR585 F1 Cluster in National Center for High‐Performance Computing (NCHC).

Plot and pictures were made with VMD‐1.8.6 and 1.9, MOE 2008.10, and 2011.10.

RESULTS

Single TMD and bundles

The TMD of 8a remains intact during a 50 ns MD simulation [Fig. 1(A)]. Residues Thr‐8, Ser‐11, and −14 do not lead to any unwinding of the helix. The RMSD levels at around 0.1 nm [Fig. 2(A), left]. The RMSF values show a typical w‐shape with dynamic residues in the central part of the helix, here Cys‐9 to Cys‐15, with a maximum of 0.1 nm (Leu‐12), and similar values at either end [Fig. 2(A), right]. A lipid thickness of (35.5 ± 1.3) Å and a lipid area of (73.3 ± 0.0) Ų is calculated.

Figure 1.

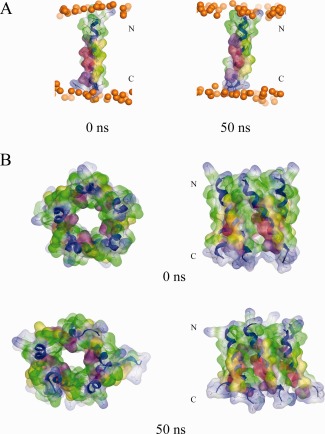
The single transmembrane domain (TMD) 8a_1–22 is shown at the beginning (0 ns) and end of a 50 ns MD simulation (A). Top view (left) and side view (right) of a pentameric bundle of 8a_1–22 at the beginning (upper) and end of 50 ns MD simulation (lower) (B). The protein backbones are drawn in blue with the side chains shown in stick modus and van der Waals surface representation (MOE). Residues Thr‐8, Ser‐11, and −14 are shown in pink and light red, respectively. All cysteine residues, Cys‐9, −13, and −17, are shown in yellow. Phosphorous atoms of the lipids are shown in orange spheres. Lipid and water molecules are omitted for clarity. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 2.

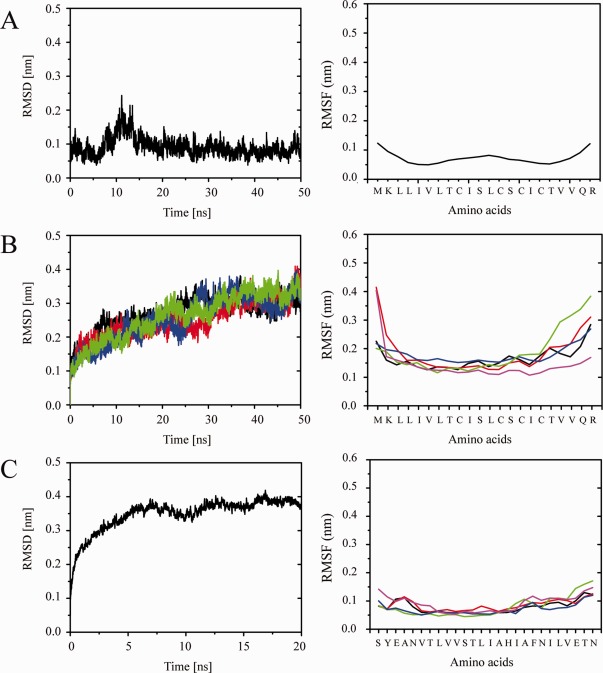
RMSD (left) and RMSF (right) values from simulations of the single TMD of 8a (A) as well as in a pentameric state forming a bundle (B), and the bundle of the M2 TMDs of GLIC (C). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Assembling an averaged structure (backbone averaged) of the monomer leads to a minimum energy structure with an inter‐helical distance of 10.7 Å and −1825.3 kcal/mol interaction energy (Fig. S1, Supporting Information). A bundle with the rank 20 (−1741.3 kcal/mol) shows the best poses of the hydrophilic residues (Thr‐8, Ser‐11, and −14, pink and red spheres, respectively, in Fig. 1) pointing into the lumen of the pore and is therefore taken for further analysis [Fig. 1(B)]. In this bundle configuration, the cysteine residues (Cys‐9, −15, −17) face the outside of the bundle. After a 50 ns MD simulation in the presence of Na‐ and Cl‐ions (mimicking a 150 mM solution, at 0 mV) the bundle remains open [Fig. 1(B)]. The RMSD values for the simulation level off after 40 ns [Fig. 2(B), left, black line]. The RMSF values of all the 5 helices reveal the loss of the dynamic (w‐shape) center of the TMDs [Fig. 2(B), right]. Averaged kink and tilt angles from the data of the individual TMDs of the bundle are calculated as (11.9 ± 2.7)° and (30.6 ± 1.9)°, respectively (Table 1, 0 mV).

Table 1.

Averaged Kink and Tilt Over All TMDs and the entire MD Simulations (50 ns)

	TMD1	TMD2	TMD3	TMD4	TMD5	Avg. t‐value
0 mV
Kink	14.6 ± 6.6	14.5 ± 7.1	8.3 ± 4.0	14.1 ± 6.6	11.2 ± 5.3	11.9 ± 2.7 0.1
Tilt	28.8 ± 4.3	31.5 ± 4.9	35.8 ± 4.4	33.0 ± 4.4	26.5 ± 3.4	30.6 ± 1.9 5.2
15 mV
Kink	11.5 ± 5.8	10.7 ± 6.5	12.1 ± 6.0	14.7 ± 6.4	11.7 ± 5.2	12.1 ± 2.6 0.35
Tilt	36.0 ± 4.5	34.4 ± 3.9	39.5 ± 3.1	35.8 ± 4.5	34.8 ± 6.1	36.7 ± 1.8 0.4
30 mV
Kink	13.3 ± 6.0	9.6 ± 5.4	14.2 ± 6.5	15.3 ± 6.3	12.3 ± 6.5	12.7 ± 2.7 0.5
Tilt	35.0 ± 5.3	35.1 ± 4.7	42.3 ± 4.8	37.7 ± 2.9	33.8 ± 6.0	37.2 ± 1.9 2.4
45 mV
Kink	13.7 ± 7.6	9.7 ± 5.2	10.8 ± 5.7	15.9 ± 6.8	12.0 ± 6.8	11.9 ± 2.8 0.0
Tilt	31.9 ± 5.6	29.3 ± 4.3	36.4 ± 5.4	39.5 ± 4.4	33.2 ± 4.4	34.1 ± 2.1 2.8

The t‐values for independent samples are given and refer to the respective sample below. The t‐values calculated from the data at 45 mV refer to the same data at 0 mV. The respective value on the p = 0.05 level for 8 degrees of freedom is 2.31. Null hypothesis is that the values are similar.

Short equilibration of the GLIC bundle over 20 ns leads to a stable structure after 5 ns, shown by a leveling‐off of the RMSD values beyond this time [Fig. 2(C), left]. The RMSF values for almost all residues remain at or below 0.1 nm [Fig. 2(C), right].

The bundle under applied voltage

Application of voltage [15 mV (blue lines), 30 mV (green lines), 45 mV (pink lines)] during the simulation of the bundle‐lipid system embedded into a 150 mM solution leads to equilibrated structures [see RMSD values in Fig. 2(B), left] after around 30 ns. Lipid thickness is calculated to be around 35 Å [e.g., (35.2 ± 1.2) Å at 15 mV and (35.1 ± 1.5) Å at 45 mV] and the area per lipid is calculated to be of 74–75 Ų [e.g., (75.5 ± 0.0) Ų at 15 mV and (74.4 ± 0.0) Ų at 45 mV]. The RMSF values of the residues do not show a w‐shape pattern when voltage is applied (data not shown). The kink angles [e.g. (11.9 ± 2.8)° (45 mV) and (12.7 ± 2.7)° (30 mV)] remain unaffected by the values as shown by small t‐values [0.1 (0 mV), 0.35 (15 mV), 0.5 (30 mV)] for independent samples. Upon voltage the tilt angle significantly increases from (30.6 ± 1.9)° at 0 mV to about 37° at 15 mV (36.7 ± 1.8)° and (37.2 ± 1.9)° at 30 mV (Table 1) to fall slightly back to (34.1 ± 2.1)° at 45 mV. Thus, the voltage has an effect on the pore architecture. In an earlier study on p7 of HCV it is found that the RMSD of a bundle under large voltage continuously increases over the duration of the simulation.27 Data from such simulations had not been considered for data evaluation.

Calculating the pore radius for the structures obtained after 50 ns under the applied voltages reveals the widest pore at 45 mV [pink line, Fig. 3(A)]. The shape is uniformly wide over the entire length of the pore. During the MD simulation at zero voltage, the minimum radius of the lumen of the pore is found to be at the N terminal side (radius 0.28 nm at position 1.3 nm at 50 ns) [red lines, respectively, in Fig. 3(A)]. A similar feature, widening at the C‐terminal side and narrowing at the N terminal side at around z = 13 Å, is also observed for the bundles simulated under applied voltage at 15 mV (blue line), 30 mV (green line) [Fig. 3(A)].

Figure 3.

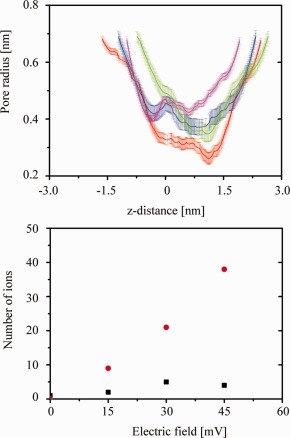
Upper panel: Calculations of the pore radii of the bundles at different voltages: 0 mV (red (from structure at 50 ns) lines), 15 mV (blue line), 30 mV (green line), and 45 mV (pink line). The error bars derive from calculations of the pore radii from three different time frames within the first and the respective last nanosecond of the simulations. Lower panel: Calculated numbers of ions passing through the pore at various voltages. Black squares represent the Na‐ions, red circles represent the Cl‐ions. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Application of voltage leads to a movement of the Na‐ and Cl‐ions, through the pore of the 8a bundle in the respective directions [Fig. 3(B)]. The number of Cl‐ions passing through the bundle increases from below 9 Cl‐ions at 15 mV to 39 Cl‐ions at 45 mV. Under the same conditions, the number of Na‐ions passing through the bundle hardly changes (3 Na‐ions at 15 mV, 5 Na‐ions at 30 mV, 4 Na‐ions at 45 mV). As a result, the bundle conducts Cl‐ions over Na‐ions.

Potential of mean force calculations

8a bundle

The PMF for all ions passes through a maximum at the N terminal side of around 2.0 kcal/mol, and a minimum at the C‐terminal side of around −0.4 kcal/mol [Fig. 4(A)]. While the values of Na‐ion (black), K‐(red), and Ca‐ion (blue) remain below 2.0 kcal/mol, values for Cl‐ion (pink) are calculated to be slightly larger than 2.0 kcal/mol. PMF‐values remain high for a stretch of 0.5 nm for the cations and of 1 nm for the anion before falling sharply off to −0.4 kcal/mol. The energy barrier for all ions at the N‐terminal side is correlated with the position of the hydrophilic residues Thr‐8, Thr‐18, and Ser‐11. The minimum is found at the wider C‐terminal side at the level around Arg‐22. At the current computational conditions, the bundle allows for Cl‐ion flux. In the light of almost identical PMFs the discrimination of Na/K‐ions over Ca‐ions is marginal. Conductivity of Cl‐ions should be lower than for the cations.

Figure 4.

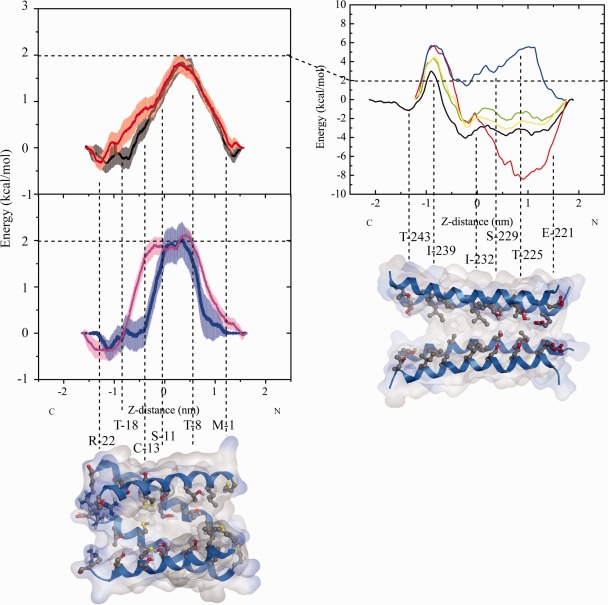
Calculation of the potential of mean force (PMF) for ions passing through the bundle of 8a (left graph) and a bundle model of the M2 helices (right graph) taken from the (GLIC, PDB entry code: 3EHZ). The estimated error calculated for each of the data points is based on a bootstrap analysis (n = 50) and shown as error bars. The color code for the ions passing through the 8a‐bundle is as following: Na‐ions (black, upper graph), K‐ion (red, upper graph), Ca‐ion (blue, lower graph), and Cl‐ion (pink, lower graph). The color code for ions passing through the M2 helices is: Cl‐ion (blue), Ca‐ion (red), two simulations for Na‐ion (yellow and green), and K‐ion (black). The color code for the structure motif and the atoms in the bundles is as following: helices in blue, oxygen in red, nitrogen in blue, sulfur in yellow, all other types of atoms in gray.

GLIC

Calculated maximal and minimal PMF values [Fig. 3(B)] are larger than those for the 8a bundle. Pulling from the N‐terminal side, a stretch of negative PMF values of −2.0 to −4.0 kcal/mol is calculated for the cations followed by a sharp increase to 2.5 kcal/mol (K‐ion, black), 4.0 kcal (both Na‐ions, yellow and green), and 6.0 kcal/mol (Ca‐ion, red) over a short stretch around Ile‐239 towards the C‐terminal side. The region of negative PMF values corresponds to a region including rings of Ile‐232, Ser‐229, and Thr‐225. The PMF of Ca‐ion is of −8.0 kcal/mol around Thr‐225. The Cl‐ion experiences positive PMF values over the entire stretch of the pore. On the basis of the PMF calculations GLIC‐M2 bundle should allow cations to enter the pore and repell anions. Ca‐ions may be trapped within the pore preventing a current. Repeated PMF calculations in the case of Na‐ions lead to matching data, promoting the quality of the calculations.

DISCUSSION

Reliability of the model

In this study, a bundle is chosen, which matches the conformation of a bundle which has been reported earlier.16 The idea is to deliver a functional analysis of the bundle embedded in a lipid environment and to evaluate its reliability as a proper structural representation of the “real bundle.” The study is in line with the idea to derive in silico protocols to build and assess channel forming proteins.2, 23, 28 Also the lipid environment is in line with previous simulations1 as well as experimental results of 38 Å found for lipid thickness29 and 68.3 Ų for area per lipid of POPC30 as well as 70–72 Ų calculated for area per lipid in the presence of membrane proteins in agreement with values derived from simulations.31 Structural features for a ‘proper’ channel are that the lumen of the pore should be mantled by hydrophilic amino acids.32 In this respect, the proposed 8a channel satisfies the request by having residues such as glutamic acids, threonines, and serines pointing into the pore.

Several techniques have been used to address ion selectivity: (i) application of voltage across the lipid membrane as reported in the literature for example, other channel proteins,8, 33 and (ii) calculation of PMF for ions crossing the channels. The latter calculations are a common practice to derive energy profiles of ions and solute along the lumen of a membrane embedded pore.13, 14 They are especially interesting in as much as they allow structural flexibility of the channels, which is an important criterion in ion conductance through narrow protein pore geometries, to be included.5 The outcome of the calculations provides proposals for ion selectivity and kinetics.

PMF calculations can also be used in more complex arrangements of ions within ion channels.15 PMF calculations are also used in evaluating free energy profiles of gating mechanisms of ion channels.9 The calculations complement similar calculations using continuum methods on rigid structures.34, 35 PMF calculations have been used to address the selectivity of various potassium channels,15, 36 porins,37 or gramicidin.38 Regarding viral channels, in earlier attempts the energy profiles of monovalent ions across the lumen of a circular pentameric bundle of peptides representing the TMD of Vpu of HIV‐1 has been done on the bases of potential energy calculations39 and PMF calculations.40 The calculations supported the low selectivity of the channel formed by Vpu.

The PMF calculated by others indicate that the energy barriers for a permeating K‐ion are up to 10 kcal/mol for permeating through gramicidine5 and through the selectivity filter of a potassium channel,15 as well as about 10–50 kcal/mol for permeation through a pentameric Vpu channel model.40 The values presented in this study of about 2.5 kcal/mol for 8a bundle and 10–14 kcal/mol for the GLIC model, fall within the mentioned range for both the pemtameric 8a bundle and the M2 model bundle of GLIC.

Qualitative analysis and interpretation of the data on ion selectivity

8a allows more Cl‐ions to pass when a voltage is applied. This would turn the bundle into a chloride channel, based on this rather qualitative analysis. Taking the PMF curve as the basis, only slightly larger energy barrier is calculated for Ca‐ and Cl‐ions than by Na‐ and K‐ions, with the latter two having indistinguishable values. The energy differences, especially between the monovalent Cl‐ and Na/K‐ions, are small (∼0.4 kcal/mol) in preference of the cations. Experimentally the pore has been identified to adopt a weak cation preference.16 During the simulations with applied voltage, the pore is widening during the sampling period of 50 ns. The individual PMF simulations are covering 1.2 ns for each frame, reflecting data of a comparatively ‘static’ conformation. Thus, the PMF calculations reflect the event of an ion passing through a narrow pore. The data from the applied voltage simulation include larger conformational changes, which lead to a widening of the pore, which in turn, comes with the loss of cation selectivity.

An energy barrier is found for all ions around the hydrophilic stretch (Thr‐8, Ser‐11). A possible interpretation of the data is that the ions have to strip off their hydration shell and that the two hydrophilic residues, with their hydroxyl groups together with Cys‐13, do not provide the adequate environment for compensation of the dehydration.

Since the entry energy‐rise for Cl‐ions from the N terminal side is lower for a longer stretch, it could be anticipated that the Cl‐ion could readily enter the pore whilst cations, for example Na/K‐ions, are still at the C‐terminal side. This could eventually lead to a counterion flux within the channel. This has been reported for Vpu based on experimental data.41

The GLIC channel is more permeable for Na‐ and K‐ions than Cl‐ions. The difference between the maximum and minimum PMF is the largest for the Cl‐ion. On the basis of current calculations, the PMF of the Ca‐ion increases the most when entering the channel. The PMF maxima and minima values for each of the ions are larger than for the calculations of the ions in the 8a bundle. On a qualitative level, this channel is permeable for monovalent ions and, possibly to a much larger extent, impermeable for Cl‐ions than the 8a channel. The current channel model may be the closed form.

The large PMF values at the C‐terminal side of GLIC‐M2 bundle arise from a hydrophobic stretch whilst negative PMF values at the N‐terminal side are due to the ring of glutamic acids (Glu‐221), threonins (Thr‐225), and serines (Ser‐229). Within the negative values for Na‐ and K‐ions, two weak maxima match with the sites for serines (Ser‐229) and threonines (Thr‐225), supporting the idea that serines and threonines could impose a barrier by inducing a stripping‐off hydrated water molecules.

The overall difference in energy levels between 8a and GLIC allows for the suggestion that distribution of hydrophilic residues within short stretches of the lumen of the pore generates channels with lower energy barriers for ions to pass, but their distribution over a larger stretch results in more pore like characteristics of the respective channel. Clearly separated stretches of hydrophobic and hydrophilic stretches induce selectivity. On the other hand, fully hydrophobic pores allow water molecules to flow, and eventually also ions, if the pore just gets large enough.42, 43 Larger pores are then gradually missing out on selectivity.

Another aspect still to debate is, how much flexibility of the bundle and especially the lumen affects the energy profile of passing ions and with this also the selectivity.5 On the basis of the low PMF values found for 8a in this study, besides the specific architecture and amino acid composition of the lumen, 8a could also possess a more flexible luminal structure than the pore model of M2‐GLIC. This is an aspect, which could generally hold for the selectivity of viral channel forming proteins.

CONCLUSION

PMF calculations are used to assess the functional features of a computational derived model of a bundle assembly of the 8a protein. The calculated data support the experimental findings of 8a channel forming protein being weakly cation selective. Having compared two channel models, it is concluded that selectivity occurs due to the interplay between clearly separated stretches of hydrophilic and hydrophobic residues in the lumen of the pore. Selectivity declines with increasing number of hydrophilic residues.

Supporting information

Supplementary Information Figure 1.