Critical Review and Uncertainty Analysis of Factors Influencing Influenza Transmission

Abstract

Influenza remains a significant threat to public health, yet there is significant uncertainty about the routes of influenza transmission from an infectious source through the environment to a receptor, and their relative risks. Herein, data pertaining to factors that influence the environmental mediation of influenza transmission are critically reviewed, including: frequency, magnitude and size distribution and virus expiration, inactivation rates, environmental and self‐contact rates, and viral transfer efficiencies during contacts. Where appropriate, two‐stage Monte Carlo uncertainty analysis is used to characterize variability and uncertainty in the reported data. Significant uncertainties are present in most factors, due to: limitations in instrumentation or study realism; lack of documentation of data variability; or lack of study. These analyses, and future experimental work, will improve parameterization of influenza transmission and risk models, facilitating more robust characterization of the magnitude and uncertainty in infection risk.

1. INTRODUCTION

Pandemics of influenza are significant threats to the public’s health.^{( 1} , ² , ^{3 )} Though vaccines offer the surest protection against influenza infection, it is expected, and has been the experience with 2009 H1N1, that the development and distribution of vaccines against novel strains may be delayed.^{( 4} , ⁵ , ^{6 )} Additionally, the stock of antiviral medications may be inadequate or ineffective.^{( 7} , ^{8 )} As a result, nonpharmaceutical interventions—for example, frequent hand washing, surface disinfection, the use of respiratory protection, and increased social distancing—are important tools for influenza mitigation.^{( 1} , ^{2 )} The selection of effective nonpharmaceutical interventions, however, requires understanding the routes by which influenza is transmitted, and the relative risk from each route. Hand washing, for example, will only interrupt transmission mediated by hand contact and only be an effective intervention if hand contact poses a high infection risk, relative to the other routes.

Influenza transmission is an environmentally mediated process: virus emitted by an infectious source moves through the environment—in the air and on surfaces—to the susceptible tissues of a receptor. Virus is emitted in droplets during breathing, talking, coughing, and sneezing, and in respiratory secretions discharged onto surfaces.^{( 9} , ^{10 )} Given an emission event, the transport of virus through the environment depends upon: the size distribution of virus‐laden expiratory particles; environmental conditions that influence the survival of infectious virus (temperature, relative humidity [RH], and surface types); physical forces that direct the movement of virus in air and onto surfaces (advective and turbulent airflow and gravitational settling); and human behaviors that transport virus and facilitate exposure (contact with surfaces and proximity to the source).

There are four possible routes for influenza exposure: (1) contact, (2) inhalation, (3) inspiration, and (4) direct spray. The contact route involves the deposition of virus on the eyes, nostrils, and/or lips by touching virus‐contaminated objects, that is, the fingertip, to those tissues, followed by transport of virus to the appropriate receptors.^{( 11} , ^{12 )} The inhalation route involves the inhalation of virus‐containing respirable particles (aerodynamic diameters, d_a ≤ 10  μm), which deposit throughout the respiratory tract, including the lung. The inspiration route involves the inhalation of inspirable particles (10 < d_a ≤ 100  μm), which deposit in the mouth and naso‐pharynx region. The inhalation and inspiration routes are distinguished because respirable and inspirable particles deposit in different regions of the respiratory tract;^{( 13 )} and influenza receptor localization and temperature gradients in respiratory tract differentially influence the likelihood of infection in each region.^{( 14} , ¹⁵ , ¹⁶ , ^{17 )}  In vivo studies demonstrate that the location of virus deposition differentially impacts infection risk.^{( 18} , ¹⁹ , ²⁰ , ^{21 )} The direct spray route involves the direct projection of virus carried in cough and sneeze particles (generally d_a > 100  μm) onto the eyes, nostrils, and lips.

The mechanics of influenza transmission from person to person and infection risk in a closed environment has been described mathematically by Nicas and Jones^{( 20 )} and Atkinson and Wein^{( 22 )} using two approaches, but with similar representations of the exposure routes. While Nicas and Jones,^{( 20 )} using point estimates for all model parameters, found that all four routes may contribute significantly to influenza infection risk, Atkinson and Wein^{( 22 )} concluded that inhalation was the predominate route of transmission. One reason for the different results is the parameterization of the contact route. Atkinson and Wein^{( 22 )} used a composite parameter to represent the transfer of virus from the surface to the facial membranes via hand contact (5 × 10⁻⁶ m²/h in the infectors bedroom), that is, two orders of magnitude lower than the equivalent rate estimated by Nicas and Jones^{( 20 )} (8.8 × 10⁻⁴ m²/h). This divergence reflects the latitude in interpretation of the sparse data of influenza transport and persistence in the environment.

Herein, data pertaining to the mechanics of influenza transmission through the environment are presented and critically reviewed. When possible, an uncertainty analysis quantifies uncertainty and variability in the data. Beyond facilitating the selection of influenza transmission model parameters, this work highlights what is known and unknown about factors influencing influenza transmission. The article follows the transmission pathway, beginning with the emission of virus, through survival and contact transport in the environment, and concluding with rates of self‐contact. Three aspects of influenza transmission modeling that may be of interest to readers are beyond the scope of this review: the likelihood and specific contexts that bring a receptor into contact with a source;^{( 23} , ²⁴ , ²⁵ , ^{26 )} the fluid mechanics of the transport and fate of virus‐laden particles in air;^{( 13} , ²⁷ , ²⁸ , ²⁹ , ^{30 )} and route‐specific dose‐response functions.^{( 20 )}

2. METHODS

2.1. Uncertainty Analysis

Uncertainty refers to the lack of completeness of information, while variability refers to true differences due to heterogeneity.^{( 31 )} Uncertainty analyses, which summarize the influence of both variability and uncertainty, were conducted using a two‐dimensional Monte Carlo simulation.^{( 32 )} Briefly, in the first dimension samples are drawn from parametric distributions fit to each data set by the method of maximum likelihood. The total sample size, N, equals the sum of replicate samples in each data set, n, to be integrated. Sampling is unweighted. To this sample population, a parametric (ψ) distribution is fit by the method of maximum likelihood. The first dimension is repeated B = 10⁴ times yielding a set of distribution parameters, Ψ={ψ₁, ψ₂, … , ψ_B}. The second dimension of the simulation is repeated B times. In each trial, samples of size N are drawn from the parametric (Ψ) distributions. Using the ordered sample populations, the median (50th percentile), 90%, and 99% ranges of the cumulative distribution are determined by percentile. The overall mean and its standard error, s_e, are equated with the mean value and standard deviation of the B sample population means, respectively. All analyses were conducted using R.^{( 33 )} An example is presented in the online supplement.

Given discontinuity in the data on the inactivation of influenza in air, which limited convergence of maximum likelihood estimates for fitting the parametric (ψ) distributions, a one‐dimensional Monte Carlo simulation was used. This method collapses the two‐dimensional Monte Carlo method into one step, omitting the fitting of the parametric (ψ) distribution. Briefly, samples of size n were sampled from the parametric distributions fit to each data set: this process was repeated B = 10⁴ times, and the ordered sample populations were used to determine the median, 90%, and 99% ranges of the cumulative distribution by percentile.

2.2. Inactivation Rate Calculation

The inactivation rate is the rate at which infectious virus becomes noninfectious. In inactivation studies, investigators measure virus persistence and report the concentration of infectious virus present over time, or the percentage of inoculated infectious virus present at subsequent times. I assumed that inactivation is a first‐order exponential process, and fit

(1)

to data using least squares regression, where C(t) is the virus concentration or percentage recovery at time t (h), β₁ is the slope, and β_o is the fitted intercept. The inactivation rate is defined: k =−β₁ (h⁻¹), where k > 0. More rapid inactivation is indicated by larger values of k.

When infectious virus was reported as being present or absent over time, I used a parametric bootstrap procedure to estimate the inactivation rate, and its variability.^{( 34 )} Briefly, for each time point studied, I generated a random sample of presence/absence results using the binomial (p, n) distribution, where p equaled the observed proportion of positive samples and n was the number of samples. I computed the proportion of positive random samples at each time point, and equated these proportions with C(t) to fit Equation (1). This process was repeated 10⁴ times to generate a probability distribution for the inactivation rate.

2.3. Statistical Tests and Terms

The coefficient of variation (CV) is defined as the ratio of the standard deviation to the mean value, times 100%. Correlations were tested using Pearson’s correlation coefficient, ρ. Pearson’s χ² test for independence was implemented using Monte Carlo estimation of the p‐value.^{( 35 )}

3. EMISSION FROM A SOURCE

3.1. Expiratory Event Frequency

Though cough has been observed in the majority of patients with 2009 H1N1,^{( 36} , ^{37 )} cough and sneeze frequency has not been reported in influenza patients. However, Kuhn et al. ^{( 38 )} reported cough rates during 6‐h intervals for 42 persons aged 18–30 years with acute respiratory illness of duration <48 h: to the data from the first 6‐h period studied, I fit the lognormal (GM = 51.4 cough per hour, GSD = 2.10) distribution. Over shorter durations (15–30 minutes), Paul et al. ^{( 39 )} reported cough frequency in six persons aged 6–49 years with acute respiratory infection: to these data I fit the lognormal (GM = 116 cough per hour, GSD = 2.50) distribution. Among 48 patients with pneumonia, Loudon and Brown^{( 40 )} reported nighttime cough rates in geometrically spaced frequency bins: over the range [<1.5, >48 coughs per hour]: to these data I fit a lognormal (GM = 9.5 coughs per hour, GSD = 3.2) distribution.

The three studies included a total of 96 persons (N = 96). Lognormal (ψ=(GM, GSD)) distributions were fit in the first dimension of the simulation. The ψ parameter pairs are slightly, but significantly, correlated (ρ=−0.228, p < 0.001, Fig. S2). The cumulative probability distribution of cough frequency is plotted against the logarithm of cough frequency (Fig. 1). The overall mean ± s_e cough frequency is 105 ± 34 coughs per hour. The 50th percentile of the distribution had median 38.5 coughs per hour, with 90% range [27.4, 53.6 coughs per hour] and 99% range [22.9, 64.3 coughs per hour]. An upper bound for cough frequency can be defined by the 95th percentile of the distribution, which has median 345 coughs per hour, and 90% and 99% ranges [207,615 coughs per hour] and [160, 876 coughs per hour], respectively.

Figure 1.

Uncertainty in cough frequency (coughs per hour) among persons with acute respiratory infection with cough^{( 38} , ^{39 )} and pneumonia.^{( 40 )}

3.2. Particle Size Distribution

Particle size distributions during exhalation and expiratory events vary between persons and expiratory activity type.^{( 41} , ⁴² , ⁴³ , ^{44 )} Exhaled particles are formed by the breaking of fluid films or bubbles during the opening of terminal airways during inhalation, and the particle number emission increases with tidal volume.^{( 44} , ^{45 )} During talking, coughing, and sneezing, expiratory droplets are formed by the passage of air across the surface of a liquid (wind shear), drawing tongues of liquid from the surface that thin and break into droplets.^{( 46} , ^{47 )} For this mechanism, factors that impact the surface tension or viscosity of respiratory secretions (such as putting sugar in the mouth^{( 42 )}) impact droplet formation.

The distribution of influenza virus among particles of different sizes has not yet been reported. The simplest assumption is that the virus concentration is uniform throughout the particle size distribution, such that larger particles contain more virus. While Gram‐negative bacteria and Mycobacterium tuberculosis bacilli have been found most frequently in cough particles with d_a < 3.3  μm,^{( 48} , ^{49 )} confidence in these findings is limited due to the high possibility of particle impaction and deposition in the 47.8 cm tube between the coughing participant and the sampling chamber. Morawska^{( 47 )} provides a more compelling reasons for nonuniform concentrations in the context of cough and sneeze particles: for wind shear particle formation, the magnitude and location of high air speeds that generate the particle size distribution vary with expiratory activity, and may or may not correspond to the location of peak pathogen concentrations in the respiratory tract. Thus, the number of pathogens in the particle will depend upon where the particle was formed and the site of infection.

Nicas et al. ^{( 50 )} reviewed the count and size distribution of particles emitted during coughs and sneezes, and judged the data from Loudon and Roberts^{( 51 )} to be the most relevant cough particle size distribution, noting that these data underestimate the number of small particles (d_a < 1  μm) relative to Papenini and Rosenthal,^{( 52 )} who measured respirable particles during exhalation with an optical particle counter. Nicas et al. ^{( 50 )} favored the results of Loudon and Roberts ^{( 51 )} due to lack of information to support calculation of equilibrium diameters measured by Duguid,^{( 53 )} and consistency of the Loudon and Roberts^{( 51 )} distribution with observed streptococci emission^{( 54 )} and photographically enumerated particle counts.^{( 55 )} More recent experimental work has been similar in methods and scope, with the exception of Chao et al.,^{( 56 )} who used a light scattering method.

Yang et al. ^{( 41 )} had participants cough into a bag with high RH and measured the concentration of particles with an aerodynamic particle sizer to be 0.62–15.9 μm: larger particles in the instrument detection range (0.6‐30 μm) may have been lost due to impaction on the bag walls. Overall, the average diameter was 8.35 μm (GSD = 2.05), though the distributions were multimodal with peaks around 1 μm, 2 μm, and 8 μm. Similarly, Morawska et al. ^{( 57 )} used an aerodynamic particle sizer to measure 0.3–20 μm particles during breathing and speaking, and found a multimodal distribution with peaks around 0.80 μm, 1.8 μm, 3.5 μm, and 5.5 μm, where the latter two modes were associated with speaking.

In contrast, Xie et al. ^{( 42 )} replicated the experiments of Loudon and Roberts:^{( 51 )} participants talked (count 1–100) or coughed (20 times) into a box, and particle residues on chamber surfaces were used to determine equilibrium diameters. Only particles with initial d_a > 47  μm could be identified. The particle size distribution was similar during talking with and without dye (no sugar), so combined results are presented in Fig. 2(a). No dye was used in the cough studies.

Figure 2.

Empirical distributions equilibrium particle size (μm) emitted during talking (counting 1–100) and coughing measured from diameter of particle residues by Xie et al. ^{( 42 )} and a light‐scattering system by Chao et al. ^{( 56 )} compared to that measured by Loudon and Roberts^{( 51 )} and Duguid^{( 53 )} using particle residues.

Chao et al. ^{( 56 )} measured the size distribution of droplets expelled during talking (count 1–100) and coughing (50 times) at 10 mm and 60 mm from the mouth using an interferometric imaging method, in which coherent optical radiation illuminates the droplets and the reflection and refraction patterns are used to determine droplet size. The size range and performance of the method was not described. The mean size distributions measured at 60 mm are presented in Fig. 2.

The range of particle sizes measured by Xie et al. ^{( 42 )} and Chao et al. ^{( 56 )} are similar to each other, and to the results of Loudon and Roberts^{( 51 )} and Duguid,^{( 53 )} ranging 2.5–1500 μm (Fig. 2). In studies of talking, Chao et al. ^{( 56 )} measured particles with diameters <50 μm more frequently than other investigators (Fig. 2a): the distributions measured by Xie et al. ^{( 42 )} and Loudon and Roberts^{( 51 )} are similar to each other, and shifted toward larger particles diameters relative to Duguid.^{( 53 )} In studies of coughing, again the distribution measured by Chao et al. ^{( 56 )} has more particles with diameters <50 μm than the other investigators (Fig. 2b), but the frequency of particles with diameters <5 μm is similar to that measured by Loudon and Roberts.^{( 51 )} The distribution measured by Xie et al. ^{( 42 )} includes particles with diameter >50 μm more frequently than the other investigators.

Given the size‐specificity of experimental methods, and variation in size distribution with expiratory activity, the particle size distribution is best defined with careful consideration for the research question, rather than through a generalized uncertainty analysis. In general, due to the size range characterized, the results of Yang et al.,^{( 41 )} Chao et al.,^{( 56 )} and Morawska et al. ^{( 57 )} may be the most relevant for modeling transmission by inhalation during conversation. However, the results of Loudon and Roberts^{( 51 )} or Xie et al. ^{( 42 )} may be the most relevant for modeling transmission by inspiration and direct spray, and from coughing and sneezing. Morawska et al. ^{( 57 )} have described a new experimental apparatus that can accommodate different types of instrumentation, which may provide more robust characterization of the entire size range of expiratory particles, and the distribution of respiratory pathogens therein.

3.3. Expiratory Event Magnitude

The magnitude of an expiratory event can be characterized in numerous ways, including: the number of particles, total particle volume, and total particle mass. The metric of expired particle concentration may be useful, but the magnitude of particle dilution at the time of measurement must be understood for application of these data in other contexts.^{( 41} , ^{57 )}

Total particle number can be determined for three studies.^{( 42} , ⁵¹ , ^{56 )} The total number of particles emitted during talking (count 1–100) varies two orders of magnitude, from an average of 43.7 particles measured by Chao et al.,^{( 56 )} to GM = 3,660 particles (GSD = 3.53) measured by Loudon and Roberts.^{( 51 )} The results of Xie et al. ^{( 42 )} fall in between with GM = 515 particles (GSD = 4.06). Total particle emission per cough is more similar, ranging from an average of 38.1 particles,^{( 56 )} to GM = 244 particles^{( 51 )} (GSD = 3.53). Again, the results of Xie et al. ^{( 42 )} fall in between, with GM = 34.4 particles (GSD = 1.99).

The total volume of expiratory particles can be calculated from the particle size distribution, total particle number, and density of respiratory secretions. Nicas et al.,^{( 50 )} for example, estimated that a total of 0.044 mL of fluid is emitted during a cough, with 6 × 10⁻⁸ mL of the volume in respirable particles. And, based on the particle size distribution and counts measured by Chao et al. ^{( 56 )} at 10 mm from the mouth, I estimated a total emission volume of 1.7 × 10⁻⁴ mL and 4.0 × 10⁻⁴ mL during talking and a cough, respectively.

Xie et al. ^{( 42 )} measured the total particle mass by having participants talk or cough into an airtight bag with a damp cloth, or a surgical mask. The emitted mass was determined by the change in weight. The bag method led to visible condensation, likely inflating the emitted mass: an average of 87.1 mg was emitted during talking, compared to 3.83 mg by a cough. Using the mask method, an average of 18.7 mg was emitted during talking, compared to 1.20 mg by a cough. Also using a mask, Zhu et al. ^{( 58 )} reported an average of 6.7 mg (6–8 mg) per cough.

The choice of parameter for characterization of expiratory event magnitude is highly dependent upon the context and modeling techniques used, so an uncertainty analysis is not conducted.

3.4. Viral Concentrations

The concentration of viable influenza virus in respiratory secretions in vivo or in expired aerosols has not been measured directly, but must be inferred from virus measured in the respiratory tract by nasal wash or swab. In nasal washes, a small volume (1 mL) of saline solution is used to wash the nares and nasal passages. In swab samples, a sterile cotton swab is rubbed on tissues of the nose and/or throat, and virus extracted using a small volume of fluid. Influenza virus concentrations are reported as median tissue culture infectious dose (TCID₅₀) or RNA copies per mL of nasal wash or extraction fluid.

The concentrations of influenza in the respiratory tract during naturally occurring infection decline precipitously in frequency and magnitude after 4 days of symptoms,^{( 59} , ^{60 )} so only data from symptom days 1–4 are considered to capture peak viral concentrations. Briefly, I represented the distribution of infectious influenza in respiratory secretions measured by Treanor et al. ^{( 59 )} using nose/throat swabs to be: normal (μ= 3.98, σ= 1.77  log₁₀TCID₅₀/mL) at baseline, and normal (μ= 2.78, σ= 1.69  log₁₀TCID₅₀/mL) 1 day after presentation. And I represented the distribution of infectious influenza virus in respiratory secretions measured by Lee et al. ^{( 60 )} using nasal wash to be: normal (μ= 4.30, σ= 0.93  log₁₀TCID₅₀/mL), normal (μ= 3.84, σ= 0.74  log₁₀TCID₅₀/mL), normal (μ= 2.50, σ= 1.03  log₁₀TCID₅₀/mL), and normal (μ= 2.54, σ= 1.17  log₁₀TCID₅₀/mL) at symptom days 1‐4, respectively, for hospitalized patients; and normal (μ= 2.51, σ= 1.93  log₁₀TCID₅₀/mL) for outpatients. Derivation of these distributions are described in the online supplement.

In the uncertainty analyses, a normal (ψ= (μ, σ)) distribution and N = 146 were used. The ψ parameter pairs are not significantly correlated (ρ= 0.006, p = 0.557, Fig. S3). The curvature in Fig. 3 indicates that the log₁₀ concentration of influenza virus in respiratory secretions is approximately normally distributed. The uncertainty ranges are largely symmetric around the median. The overall mean ± s_e viral concentration is 3.21 ± 0.16  log₁₀TCID₅₀/mL. The median cumulative distribution function spans six orders of magnitude. The 50th percentile of the distribution has median 3.21 log₁₀TCID₅₀/mL, with 90% range [2.91, 3.51 log₁₀TCID₅₀/mL] and 99% range [2.74, 3.67 log₁₀TCID₅₀/mL]. The 95th percentile of the cumulative distribution has median 5.45 log₁₀TCID₅₀/mL, with 90% range [4.98, 5.96 log₁₀TCID₅₀/mL] and 99% range [4.74, 6.25 log₁₀TCID₅₀/mL].

Figure 3.

Uncertainty in infectious influenza virus concentrations in respiratory secretions (log₁₀TCID₅₀/mL) on symptom days 1–4.^{( 59} , ^{60 )}

4. INACTIVATION IN THE ENVIRONMENT

4.1. In Air

Harper^{( 61 )} explored the effect of temperature on influenza inactivation, and found the inactivation rate to increase with temperature at all humidity levels (Table I). For example, at high RH (81–82%), the inactivation rate of influenza at 7–8 °C is 0.152 per hour, compared to 2.52 per hour at 30 °C. And, at low RH (20–51%), the inactivation rate of influenza at 7–8 °C is 0.033 per hour, compared to 0.285 per hour at 30 °C. At both humidity levels, these inactivation rates bound those measured at room temperature (20–24 °C). Both Harper^{( 61 )} and Hemmes et al. ^{( 62 )} measured inactivation in air at room temperature, though rates differ by an order of magnitude (Table I).

Table I.

Inactivation Rate of Influenza A (PR₈ Strain) in Air Measured in a Rotating^{( 61 )} or Static^{( 62 )} Aerosol System

RH(%)	Inactivation Rate (h−1)			Reference
		GM	GSD
Room temperatures (20–24 °C)
50–90	5.46	5.49	1.60	62
50–81	0.445	0.443	1.11	61
15–40	0.438	0.555	2.06	62
20–36	0.062	0.061	1.20	61
Cold temperatures (7–8 °C)
l82	0.152			61
23–51	0.033	0.027	2.52	61
Hot temperatures (32 °C)
81	2.52			61
20–50	0.285	0.261	1.81	61

The inactivation of influenza A PR₈ strain in air has been found to be an order of magnitude greater when the RH is in excess of 50%, compared to less than 40%, within each temperature range and study system (Table I). Inactivation rates graphically presented as a function of RH by Hemmes et al. ^{( 62 )} are approximately lognormally distributed. Based on eight studies at 50–90% RH (n = 3), the inactivation rate k ∼ lognormal (GM = 5.49 per hour, GSD = 1.60), with  per hour, compared to eight studies at 15–40% RH (n = 3), for which the inactivation rate k ∼ lognormal (GM = 0.555 hour, GSD = 2.06), with  per hour. Rates measured at room temperature by Harper^{( 61 )} are an order of magnitude lower. The sparseness of Harper’s data prevents assessment of the fit of probability distributions, so the lognormal distribution has been assumed in light of data from Hemmes et al. ^{( 62 )} Based on studies at three RH levels in the range 50–81% RH (n ={3, 4}), the inactivation rate k ∼ lognormal (GM = 0.443 per hour, GSD = 1.11), with  per hour. Based on studies at two RH levels in the range 20–36% RH (n ={3, 5}), the inactivation rate k ∼ lognormal (GM = 0.0614 per hour, GSD = 1.20), with  per hour. Reasons for this large disparity are unclear, though Hemmes et al. ^{( 62 )} used a static system, while Harper^{( 61 )} used a rotating drum for the aerosol studies.

Given that the rate measured by Hemmes et al. ^{( 62 )} at low RH is very similar to that measured by Harper^{( 61 )} at high RH ( per hour vs.  per hour), and the lack of obvious methodological limitations in either study, all data are combined for the uncertainty analysis (N = 66). The discontinuity in the data is strongly indicated in the cumulative distribution estimated by the one‐dimensional Monte Carlo simulation (Fig. 4). The uncertainty range is symmetric around the median cumulative distribution function. The overall mean ± s_e inactivation rate is 1.84 ± 0.198 per hour. The 50th percentile of the cumulative probability distribution has a median inactivation rate 0.455 per hour, with 90% range [0.427, 0.488 per hour] and 99% range [0.412, 0.509 per hour].

Figure 4.

Uncertainty in influenza A virus inactivation in air at room temperature,^{( 61} , ^{62 )} using one‐stage Monte Carlo simulation.

For reference, separate analyses for inactivation in air at low and high RH are reported in the online supplment.

4.2. On Porous Substrates

Porous substrates are matrices with voids that can be filled by fluids. The persistence of influenza virus has been measured on the porous substrates: paper, fabric, and wood (Table II).

Table II.

Mean () Influenza Virus A and B Inactivation Rates Measured on Substrates; Standard Deviation (s_k) Is Computed Using CV = 33% for Porous Surfaces, and CV = 47% for Nonporous Substrates

Substrate	Inactivation Rate (h−1)				Reference
	Influenza A		Influenza B
		sk		sk
Porous substrates
Pajamas	0.117	0.039	0.332	0.110	63
Magazine	0.451	0.149	0.522	0.172	63
Tissue	1.02	0.336	0.334	0.110	63
Handkerchief	>1.06	0.350	0.373	0.123	63
Bank notes	0.313	0.103	1.15	0.380	64
Nonporous substrates
Steel	0.112	0.053	0.265	0.125	63
Plastic	0.102	0.048	0.178	0.084	63
Glass	1.57a	0.738			68
Glass	1.29b	0.606			68
Glass	3.22c	1.51			68
Glass	2.40d	1.13			68
Skin
Skin	71.9	23.4			63

^aWS strain, 20% RH.

^bSwine strain, 20% RH.

^cWS strain, 84% RH.

^dSwine strain, 84% RH.

Bean et al. ^{( 63 )} measured the virus titer of influenza A (A/Brazil/11/78‐like [H1N1]) at 35–40% RH on four porous surfaces, and of influenza B at 55–65% RH (n = 6), and graphically reported the mean titer at each time point studied. From these data, I computed the inactivation rates for each substrate—pajamas, magazine paper, tissue paper, and handkerchief (, Table II).

Thomas et al. ^{( 64 )} measured the presence or absence of infectious influenza A virus (A/Moscow/10/99 [H3N2]) on bank notes in the absence of mucus (n = 12 allocated across four initial concentrations, 10^5.04–10^5.95). Given that the variation in initial concentration was less than one order of magnitude, I combined the data. At the time of inoculation, 100% (12/12) of the samples were positive for infectious influenza, declining to 50% (6/12), 33% (4/12), and 17% (2/12) at 2 h, 4 h, and 6 h postinoculation, respectively. Using the bootstrapping procedure, I estimated k ∼ normal ( per hour, s = 0.102 per hour), which has CV = 33%. Analogous studies with influenza B (B/Hong Kong/335/2001) on bank notes (n = 3) found that in the absence of mucus, at the time of inoculation 100% (3/3) of the samples were positive, declining to 33% (1/3) and 0% (0/3) at 1 h and 2 h postinoculation, respectively. Due to the small sample size and 0 < p < 1 at only one time, the bootstrapping procedure yielded a point estimate for the inactivation rate, k = 1.151 per hour.

Variability in inactivation rates on surfaces is uncertain. Only from the bootstrapping procedure applied to the influenza A results of Thomas et al. ^{( 64 )} was a variability estimate obtained, CV = 33%. Studies of the inactivation rates of similar viruses on porous substrates—avian influenza A,^{( 65 )} human coronaviruses,^{( 66 )} and human parainfluenza virus 2^{( 67 )}—are not informative because they also report only point estimates. Without information on variability, it is not possible to determine if the computed inactivation rates (; Table II) differ across the substrates or virus type (A or B) by chance alone. If inactivation rates are assumed to be normally distributed with CV = 33%, standard deviations can be computed for each rate: 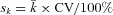 (Table II).

Given that sparsity of data, I used a bootstrap test to determine the likelihood that the observed variation by virus type, and across substrate type, could be explained by chance. Details are described in the online supplment. These bootstrap analyses provide evidence that if the true variability in inactivation rates is characterized by CV = 50%, then the data of Bean et al. ^{( 63 )} and Thomas et al. ^{( 64 )} likely come from the same distribution; however, for CV = 33%, inactivation is likely similar only for influenza A and B on pajamas and magazines (p ≥ 0.05). Given the uncertainty in inactivation rate variability, all data for the inactivation of influenza A and B on porous substrates were integrated in the uncertainty analysis, using the normal (k, s_k) distribution parameters specified in Table II for each virus type and substrate, and N = 63. Inspection of the sample populations indicated that the lognormal (ψ= (GM, GSD)) distribution was appropriate.

The ψ parameter pairs are significantly negatively correlated (ρ=−0.496, p < 0.001, Fig. S4). The cumulative distribution function is approximately lognormal (Fig. 5). The uncertainty ranges are symmetric around the median cumulative distribution. The overall mean ± s_e inactivation rate of influenza virus at room temperature, and 40–65% RH, on porous substrates is 0.590 ± 0.079 per hour. The 50th percentile of the cumulative distribution has median inactivation rate 0.432 per hour, with 90% range [0.343, 0.536 per hour] and 99% range [0.299, 0.637 per hour]. At the 5th percentile, the median inactivation rate is 0.113 per hour, with 90% range [0.067, 0.164 per hour] and 99% range [0.043, 0.216 per hour].

Figure 5.

Uncertainty in influenza A and B virus inactivation rate on porous substrates (absent respiratory secretions) at room temperature and 45–60% RH.^{( 63} , ^{64 )}

4.3. On Nonporous Substrates

Nonporous substrates have been separated from porous substrates based on the convention of the microbiology literature, but also from the expectation that virus survival may differ if substrate facilitates dispersion, and therefore evaporation, of virus inoculum. Inactivation of influenza viruses has been measured on steel, plastic, and glass.

Bean et al. ^{( 63 )} measured persistence of influenza A (A/Brazil/11/78‐like [H1N1]) under 35–45% RH and B (B/Illinois/1/79‐like) under 55–60% RH on stainless steel and plastic (n = 6). Based on graphically presented mean persistence over 24 h, I computed the inactivation rates for each virus strain on each substrate (; Table II). On glass at room temperature, Buckland and Tyrell^{( 68 )} observed two strains of influenza A virus to inactivate more slowly at 20% RH than at 84% RH over 2.5 hours on glass (n ={2, 3}). Based on the reported mean log reduction in virus titer over 2.5 hours, I computed the inactivation rate for the WS and swine strains at both humidity levels (Table II).

Neither of these authors reported variability across replicate samples, but it is described for related viruses. From graphically presented percentage survival ( and s, n = 3) of human parainfluenza virus 3 at 10–60 minutes postinoculation on stainless steel disks under 50% RH at 22 °C,^{( 70 )} I used a parametric bootstrapping procedure, characterizing persistence with a normal (,s) distribution at each time point, and estimated k ∼ normal(, s = 0.377 per hour), for which CV = 22%. To reported presence or absence of human parainfluenza virus 2 in six replicates on stainless steel and formica,^{( 67 )} I applied the parametric binomial (n, p) bootstrapping procedure: the predicted distributions were highly skewed. Inactivation rates in moist and dry droplets on steel are  per hour (CV = 21%) and  per hour (CV = 13%), respectively; and in moist and dry droplets on formica are  per hour (CV = 47%) and  per hour (CV = 31%), respectively. This analysis suggests that virus inactivates more rapidly in dry than moist conditions, but the inactivation rates on steel estimated from the presence/absence data () are much lower than that estimated from quantitative virus persistence data ( per hour). To provide the most conservative estimates of variability, CV = 47% is used to estimate the s_k in Table II.

As with inactivation rates on porous substrates, I used a bootstrap procedure to test if the inactivation rate varied by substrate and/or virus type. Details are available in the online supplement. The analysis provides no evidence to reject the hypothesis that the inactivation rates for the swine and WS strains of influenza A are from the specified distribution, characterized by CV = 47%. In addition, the analysis indicates that the inactivation rates of influenza A and B on steel and plastic are from the same distribution, and different from the distribution of influenza A inactivation rates on glass, given CV ≥ 47%. As a result, uncertainty analyses for steel and plastic, using lognormal (ψ = (GM, GSD)) distributions and N = 24, were conducted separately from analyses for glass. For glass, lognormal (ψ = (GM, GSD)) distributions were used, and the total sample size doubled to N = 16 for stability in the distribution tails.

For influenza A and B on steel and plastic, the fitted ψ parameter pairs are significantly negatively correlated (ρ=−0.686, p < 0.001; Fig. S5). The cumulative distribution is steep and linear on the log‐scale (Fig. 6): the median distribution spans one order of magnitude. Uncertainty ranges increase in magnitude and skewness at the distribution tails. The overall mean ± s_e inactivation rate is 0.178 ± 0.045 per hour. The 50th percentile of the cumulative probability distribution has median inactivation rate 0.133 per hour, with 90% range [0.084, 0.187 per hour] and 99% range [0.060, 0.251 per hour]. At the 5th percentile of the distribution, the median is 0.032 per hour, with 90% range [0.009, 0.068 per hour] and 99% range [0.003, 0.099 per hour].

Figure 6.

Uncertainty in influenza A and B virus inactivation on plastic and steel at room temperature and 45–60% RH.^{( 63 )}

For influenza A, WS and swine strains on glass, the fitted ψ parameter pairs are significantly negatively correlated (ρ=−0.824, p < 0.001), and show some discontinuity (Fig. S6). The median cumulative distribution function is linear on the log‐scale, indicating that it is approximately lognormal, and spans one order of magnitude (Fig. 7). Uncertainty ranges increase in skewness and magnitude at the distribution tails. The overall mean ± s_e inactivation rate on glass is 2.68 ± 2.01 per hour. The 50th percentile of the cumulative probability distribution has median inactivation rate 1.74 per hour, with 90% range [0.806, 2.64 per hour] and 99% range [0.438, 4.53 per hour]. Due to the small sample size, the values at the 10th percentile are reported: the median inactivation rate is 0.488 per hour, with 90% range [0.044, 1.10 per hour] and 99% range [0.008, 1.63 per hour].

Figure 7.

Uncertainty in influenza A (WS and swine strains) inactivation on glass at room temperature and 20% or 84% RH.^{( 68 )}

4.4. On Skin

Bean et al. ^{( 63 )} measured the transfer of influenza A virus from stainless steel and tissues to the hands, and subsequent survival of virus on the hands. In the text, Bean et al. ^{( 63 )} reported that 10^4.5 TCID₅₀ of virus per 0.1 mL could be transferred from stainless steel to the hands, which fell to 10^1.3 TCID₅₀ of virus per 0.1 mL within 5 minutes: the inactivation rate is k = 88.4 per hour. Similarly, 10^3.0 TCID₅₀ of virus per 0.1 mL was transferred to the hands from paper tissue, which fell to 10^1.0 TCID₅₀ of virus per 0.1 mL within 5 minutes: the inactivation rate is k = 55.3 per hour. Assuming that the inactivation rate of influenza A on skin is the same, regardless of the source of contamination, these data have  per hour and s_k = 23.4 per hour, giving CV = 33%.

5. ENVIRONMENTAL CONTACTS

Environmental contact refers to frequency and magnitude of touches between a person and other persons or objects in her environment, and not to the event that a source and receptor enter into spatial proximity. The later contact rate is critically important to the epidemiology of influenza transmission because it determines how many persons an infectious source will come into contact with, but is beyond this scope of this work.

5.1. Environmental Contact Rates and Duration

Hayden et al. ^{( 69 )} observed 131 health care workers (HCW) attending 22 unique hospitalized patients over 27 monitoring periods. A total of 1,072 physical contacts between an HCW and a patient or the environment were observed, such that on average, a worker made 8.2 contacts per episode. Less than half, 44% (58/131), of HCWs touched only the environment during a patient care episode, and made an average of 5.1 contacts per care episode, while 56% (73/131) touched both the patient and the patient’s environment, and made an average of 8.5 contacts per care episode. From more detailed data provided by Dr. Hayden (personal communication), I determined that of the 860 environmental contacts, 39 (5%) were to sites in contact with the patients, such as bedding and bed pans; 477 (55%) were to sites near the patients, typically medical equipment; and 344 (40%) were to sites away from the patients, typically room furnishings.

The duration of care episodes were not reported, so it is not possible to estimate the contact rates per unit time. However, Dr. Hayden (personal communication) shared the duration of contacts, categorized as: (1) 1–10 seconds, (2) 11 seconds to 1 minute, (3) 1–3 minutes, (4) 3–5 minutes, and (5) >5 minutes. Only 20 contacts fell into categories 4 and 5, so these categories were consolidated in the χ² test, where the null hypothesis is that the maximum likelihood estimates of the proportions of contacts in each duration category—, , , and —are the same for all contact types. The χ² test of the contingency table provides no evidence to reject the null hypothesis that the duration of contact and contact type are independent (χ²= 259, p < 0.001). This means that most contacts with patients and the patient’s environment (65%) are brief, less than 10 seconds.

Given the lack of additional studies, it is not possible to judge if these results are generalizable to other settings, but they provide insight into contact behaviors during patient care.

5.2. Transfer Efficiency: Surface to Skin

The transfer of influenza A (A/Brazil/11/78‐like [H1N1]) virus from stainless steel and paper tissues to the skin was described by Bean et al.,^{( 63 )} who had volunteers rub inoculated substrates with two fingers at moderate pressure for 3 seconds. Immediately after the inoculation of 10^5.6 TCID₅₀ virus per 0.1 mL onto stainless steel, 10^4.5 TCID₅₀/0.1 mL was recovered, indicating a transfer efficiency of 7.9% to the fingers. And, immediately after inoculation of 10^3.0, TCID₅₀/0.1 mL was recovered, indicating a transfer efficiency of 0.25%. Combining these results gives a mean transfer efficiency of 4.1%, with s = 5.4%. Transfer was also measured at different time points after inoculation onto steel and tissue, but these results are difficult to interpret due to inactivation of virus on the inoculated surface prior to contact. For reference, the transfer efficiency 2 and 8 hours subsequent to inoculation on steel was 0.5% and 0.02%, respectively; and 15 minutes subsequent to inoculation on paper tissues was 7.9 × 10⁻⁴%.

The transfer of influenza virus from contaminated skin to surfaces has not been studied, but studies of other respiratory viruses suggest that the transfer efficiency equals that from surfaces to skin. For example, the mean efficiency of rhinovirus 14 transfer from skin to stainless steel 20 minutes subsequent to inoculation was 0.92% (s = 0.3%), compared to the mean steel‐to‐skin efficiency of 0.67% (s = 0.1%).^{( 70)} And though skin‐to‐steel transfer of human parainfluenza virus 3 was not observed 20 minutes after inoculation, the mean transfer from steel to skin was only 1.5% (s = 0.98%). ^{( 70 )} Reciprocal transfer has also been measured with enteric virus^{( 71} , ^{72 )} and bacteriophage MS2.^{( 73 )}

Important limitations in the study of influenza virus from surface to skin transfer by Bean et al. ^{( 63 )} arise from the unrealistic nature of contact, and virus media studied. For comparison, Pancic et al. ^{( 74 )} found that rhinovirus HH suspended in normal nasal mucus had transfer efficiencies of 1.6–10% during the handling of doorknobs and faucets immediately after inoculation. Studies of bacteriophage transfer during the handling of household objects have conflicting results. Handling of faucet handles and telephones inoculated with PRD‐1 yielded, on average, transfer of 33.5% and 65.8% of the phage to the hands,^{( 75 )} while only 0.4% of ΦX174 bacteriophage transferred from a doorknob to a hand on the first contact.^{( 76 )}

5.3. Transfer Efficiency: Skin to Skin

Transfer of influenza between skin surfaces has not been reported, though this transfer efficiency is important to the quantification of exposure and risk via the contact route. Skin‐to‐skin transfer of rhinovirus, parainfluenza virus, and bacteriophage have been studied.

The most relevant study is that of Pancic et al.,^{( 74 )} which found the transfer of rhinovirus HH in normal nasal mucus from the inoculated fingertips of one person to the fingertips of another person immediately after inoculation ranged from 1.4 to 10.4%, with mean 5.49%: I found the transfer efficiency data to be approximately lognormal (GM = 4.58%, GSD = 1.90). Due to the 20‐minute delay between inoculation and contact, the observation of 0.71% (s = 0.02%) efficiency of rhinovirus 14 transfered between fingerpads is less useful.^{( 70 )}

Very high transfer efficiency—mean 33.9%—has been observed for bacteriophage PRD‐1 from an inoculated fingertip to the lip during a 10‐second contact.^{( 75 )} The efficiency is much greater than the 0.02% observed between fingertips immediately after inoculation with bacteriophage ΦX174,^{( 76 )} and is more similar to efficiencies observed for hepatitis A.^{( 72 )} This similarity is not necessarily surprising since PRD‐1 is frequently used as a surrogate for enteric virus in water, not respiratory viruses.^{( 77 )}

6. RECEPTOR EXPOSURES

6.1. Self‐Contact Rates

Self‐contact is defined as one person contacting her own susceptible tissues—the eyes, nostrils, and/or mouth—with fomites, for example, her own body part or an object. Self‐contact may transmit influenza virus if fomites contacting susceptible tissues is contaminated with infectious virus.

Few studies have examined self‐contact rates in adults. Observing 10 adults working alone in an office for 3 hours, Nicas and Best^{( 78 )} found the mean hand‐to‐face contact rate to be 15.7 (s = 11.7) touches per hour: the lip was the most frequently touched location on the face, with mean rate 8 (s = 8) touches per hour, followed by the nostril and eye with 5.3 (s = 3.7) touches per hour and 2.5 (s = 1.9) touches per hour, respectively. I fit Weibull distributions to the contact rate per hour by maximum likelihood estimation, due to successful representation of contact rates in similar contexts by this distribution.^{( 80} , ^{81 )} With parameter standard errors, the fitted distributions are: Weibull (1.28 ± 0.343, 16.8 ± 4.33) for all contacts, Weibull (0.760 ± 0.206, 7.07 ± 3.07) for lip contacts, Weibull (1.08 ± 0.295, 2.46 ± 0.780) for eye contacts, and Weibull (1.31 ± 0.357, 5.59 ± 1.41) for nose contacts. In contrast, the combined rate of nose‐picking and eye‐rubbing was observed to be only 0.70 touches per hour in a public auditorium.^{( 79 )}

More frequently, self‐contact rates have been investigated among children.^{( 73} , ⁸⁰ , ^{81 )} Meta‐analysis of hand‐to‐mouth and object‐to‐mouth activity studies found the frequency of contacts to decrease with age.^{( 80} , ^{81 )} Among the oldest age group studied, children 6 to <11 years, hand‐to‐mouth and object‐to‐mouth contact rates were observed to have mean 6.7 (s = 5.5) contacts per hour and 1.12 (s = 1.05) contacts per hour, respectively, in indoor environments. The mean rate of hand‐to‐mouth contacts is quite similar to the mean rate of hand‐to‐lip contact observed by Nicas and Best^{( 78 )} (6.7 per hout vs. 8 per hour). Probability distributions fit to these data were Weibull (1.36, 7.34) for hand‐to‐mouth contacts, and Weibull (0.85, 1.04) for object‐to‐mouth contacts.

Due to the dependence in self‐contact rates on activity, visibility, and age, it is more appropriate to select the distribution of contact rates for the specific exposure context, rather to to use a distribution based on an uncertainty analysis of combined studies.

6.2. Inspiration and Direct Spray Frequency

Influenza virus transmitted through the inspiration and direct spray routes is carried in relatively large droplets, which settle in close proximity to the emission point, ^{( 13 )} such that the receptor must be in close spatial proximity to the source, and in the trajectory of the expired virus‐laden droplets. There are many methods by which to model the physics of the particle trajectories, though this is beyond of the scope of this work. What remains unknown is the frequency with which a receptor is in this trajectory: that is, how often does a person with influenza cough or sneeze into the face of a susceptible person?

7. DISCUSSION

The transmission of influenza from person to person is a complex, environmentally mediated process that must be understood quantitatively to select effective nonpharmaceutical interventions. The effectiveness of nonpharmaceutical interventions is difficult to measure in epidemiological studies due to high cost, variation in influenza prevalence, lack of intervention adherence, and the challenge of generalization; ^{( 3} , ⁸² , ⁸³ , ⁸⁴ , ^{85 )} and the infection risks arising from each of the four transmission routes are more difficult to quantify because they may occur simultaneously. Mathematical modeling, however, can begin to explore these questions by quantitatively describing the mechanisms by which influenza virus moves from an infectious source through the environment to a susceptible person. Modeling of influenza transmission mechanisms and infection risk has been undertaken by several investigators,^{( 20} , ²² , ⁸⁶ , ^{87 )} but the representativeness of results is limited by the quality and quantity of data for parameterization of influenza transmission models.

Influenza virus has been found in air exhaled during breathing and talking,^{( 9} , ^{10 )} and in the air in a hospital emergency room.^{( 88 )} Influenza virus is also expected to be expelled during coughs and sneezes due to the high numbers of virus in the nose and throat.^{( 59} , ^{60 )} However, the complete size distribution of particles emitted by persons infected with influenza, and the concentration of virus in those particles, has not been determined experimentally. The respirable portion of the distribution has been characterized during breathing, talking, coughing, and sneezing using optical particle counting,^{( 41} , ⁴³ , ⁵² , ^{57 )} while the distribution of inspirable and larger particles has been characterized during talking, coughing, and sneezing by measuring the diameter of deposited droplet residues.^{( 42} , ⁵¹ , ^{53 )} The light scattering technique used by Chao et al. ^{( 56 )} may characterize a wide range of sizes, but the vast majority of particles measured had diameters <50 μm, though photographic evidence and our personal experiences assure us larger particles are present.^{( 55 )} Simultaneous characterization of the full range of the size distribution would be a useful result, and the new experimental apparatus described by Morawska et al. ^{( 57 )} may enable its determination.

An uncertainty associated with the emission of influenza is the distribution of influenza virus (and other respiratory pathogens) across the particle size distribution. Previous work has assumed that virus is uniformly distributed by volume, with the volumetric concentration defined by the concentration in nasal wash specimens, such that the number of virus per particle is a function of particle volume.^{( 20 )} Morawska,^{( 47 )} however, has suggested that the distribution of virus in particles may depend more upon the location of particle formation (type of expiratory event), and the site of viral shedding. The concentration of influenza virus in the respiratory tract during natural infections has been reasonably well characterized,^{( 59} , ^{60 )} though the relationship between the viral concentration in swab specimens and respiratory secretions is uncertain.

The inactivation of influenza virus has been characterized in air, on porous substrates, on nonporous substrates, and on skin:^{( 61} , ⁶² , ⁶³ , ⁶⁴ , ^{68 )} a significant limitation of this work has been the absence of information about variability in virus inactivation. Variation in experimental designs has led to inactivation rates that vary by an order of magnitude, such as influenza A PR₈ inactivation in air as studied by Hemmes et al. ^{( 62 )} and Harper^{( 61 )} ( per hour vs.  per hour at 15–40% RH and room temperature) and influenza A on glass versus steel and formica as studied by Buckland and Tyrell^{( 68 )} and Bean et al. ^{( 63 )} ( per hour vs.  per hour at room temperature). Even for less striking differences, absent variability data, it is difficult to assess if inactivation rates truly vary by virus type (A or B) or substrate. In uncertainty analyses presented here, variability in influenza virus inactivation on substrates has been based on the CV observed for related viruses. Due to uncertainty in variability, the viruses have been grouped for analysis: in air at room temperature, on porous substrates, on steel and formica, and on glass.

A consistent finding is that influenza inactivation rates increase with RH (Tables I and II): in general increasing the RH above 50% increased the inactivation rate by a factor of 2–10, within each experimental system. The effect was evident at room temperatures and at more extreme temperatures. For example, the inactivation rate of the WS strain on glass at room temperature increased from 1.57 per hour at 20% RH to 3.22 per hour at 84% RH.^{( 68 )} In cold air (7‐8 °C), the inactivation of influenza A PR₈ increased from  per hour at 23–51% RH to  per hour at 82%.^{( 61 )} In hot air (32 °C), the inactivation of influenza A PR₈ increased from  per hour at 20–50% RH to  per hour at 81%.^{( 61 )} The effect of RH (and temperature) in the inactivation studies are consistent with studies of influenza A infectivity in mice^{( 89 )} and guinea pigs,^{( 90} , ^{91 )} which have observed lower rates of transmission under conditions of higher RH (and temperature).

Of interest is the similarity in influenza inactivation rates in air, with rates on porous and nonporous substrates (Tables I and II). In studies at room temperature, the inactivation rate of influenza A and B in air ranged 0.06–5.5 per hour, compared to 0.1–3.2 per hour on porous and nonporous substrates. The inactivation rate measured on skin is an order of magnitude larger,  per hour.^{( 63 )} A significant uncertainty, which limits confidence in both the absolute and relative magnitudes of these inactivation rates, is the suspension of virus in laboratory media, rather than biological matrices such as human mucus or saliva. Thomas et al. ^{( 64 )} measured the presence or absence of influenza A and B over time on bank notes when suspended in laboratory media and human mucus: the presence of mucus increased persistence from a few hours to 1–17 days. Research into the influence of biological matrices on influenza inactivation, as has been conducted with enteric viruses in dilute feces suspensions,^{( 71} , ^{72 )} would be an important contribution to understanding transmission of influenza. Based on the results of Thomas et al.,^{( 64 )} use of inactivation rates for influenza virus in laboratory media will underestimate persistence, and therefore underestimate exposure and infection risk.

Our understanding of the transfer of influenza virus between substrates would also benefit from studies utilizing influenza suspended in biological matrices, and characterization of skin‐to‐skin influenza transfer. The transfer of influenza A has been measured once from steel to skin (7.9% transfer) and once from paper tissues to the skin (0.25% transfer):^{( 63 )} these transfer rates are similar to that seen for rhinovirus HH suspended in human mucus on doorknobs and faucets and handled immediately (1.6–10%), which suggests that skin‐to‐skin transfer of rhinovirus HH (1.4–10.4%, mean 5.49%) may be representative of influenza transfer during skin‐to‐skin contact.^{( 74 )} The influenza A and rhinovirus HH transfer efficiencies, however, are much smaller than transfer efficiencies of enteric viruses^{( 71} , ^{72 )} and some bacteriophages.^{( 73} , ^{75 )} Rusin et al.,^{( 75 )} for example, found 33.9% of bacteriophage PRD‐1 transfered from the finger to lip in 10 seconds.

Rates of self‐contact and environmental contacts have been little studied, even though they strongly influence infection risk through the contact route. Nicas and Best^{( 78 )} observed a mean hand‐to‐face contact rate of 15.7 contacts per hour, which is similar to hand‐to‐mouth and object‐to‐mouth contact rates for children aged 6 to <11 years in indoor environments.^{( 80} , ^{81 )} Hayden et al. ^{( 69 )} observed that HCW who touched only the environment during a patient care episode made an average of seven contacts, while workers who touched both the environment and the patient made an average of 8.5 contacts per care episode. I was unable to find additional data on the rate of environmental contacts, so it is not possible to determine if these rates are generalizable. Similarly, it is not known how often persons in close contact receive direct spray of expired particles, which facilitate inspirable and direct spray transmission.

From this review and analysis it seems that limitations and uncertainties in the understanding and characterization of factors influencing transmission fall into four categories: (1) instrumentation, (2) realism, (3) documentation of variability, and (4) rarely/never studied. Issues relating to instrumentation have largely impacted our understanding of the size and count distribution of emitted influenza‐laden particles. Understanding of influenza inactivation and transfer has been limited by a lack of realism and documentation of variability: increasing the realism in contact scenarios and virus matrix, and documenting study replicate results would contribute significantly to the knowledge about how the environment, virus strain, and human activity affects the transport of virus through the environment. Factors that have been rarely or never studied include: the transfer of influenza A between skin, including during self‐contact, environmental contact rates, and frequency of direct spray events. All of these factors directly affect the likelihood of exposure through contact, inspiration, and direct spray. None of the limitations are insurmountable.

In this work I have presented data about factors that influence the transmission of influenza from person to person through the environment, with the objectives of critically reviewing the quality and relevance of the data, and quantitatively describing uncertainty and variability in the data, where appropriate. This analysis will facilitate the selection of model parameter values in quantitative studies of influenza transmission mechanisms and infection risk, and stimulate targeted experimental research to inform our understanding of influenza transmission mechanisms and infection risk. Future work will integrate these results with an influenza transmission model to determine how the magnitude and uncertainty in the factors identified herein influence the magnitude of infection risk and the contributions from each of the four transmission routes.

Supporting information

Fig. 1. Distribution of influenza A virus inactivation rate in air at room temperature at low relative humidity (<50%) and high relative humidity (≥ 50%).^{(9, 10)} The uncertainty analysis used a one‐dimensional Monte Carlo simulation and N = 32 or N = 34 for low and high relative humidity, respectively.

Fig. 2. Lognormal (ψ = (GM, GSD)) distribution pairs in uncertainty analysis of cough frequency (coughs h^‐1) among persons with acute respiratory infection with cough^{(1, 2)} and pneumonia.⁽³⁾

Fig. 3. Normal (&xmacr;,s) distribution parameter pairs in uncertainty analysis of infectious influenza virus concentrations in respiratory secretions (log₁₀TCID₅₀/mL) on symptom days 1‐‐4.^{(4, 5)}

Fig. 4. Lognormal (ψ = (GM, GSD)) distribution parameter pairs in uncertainty analysis of influenza A and B virus inactivation rate on porous substrates (absent respiratory secretions) at room temperature and 45‐‐60% RH.^{(63, 64)}

Fig. 5. Lognormal (ψ = (GM, GSD)) distribution parameter pairs in uncertainty analysis of influenza A and B virus inactivation on plastic and steel at room temperature and 45‐‐60% RH.⁽¹¹⁾

Fig. 6. Lognormal (ψ = (GM, GSD)) distribution parameter pairs in uncertainty analysis of influenza A strains on glass at room temperature and 20% or 84&percnt ;RH.⁽¹³⁾

Supporting info item