Prediction for the spread of COVID-19 in India and effectiveness of preventive measures

Abstract

The spread of COVID-19 in the whole world has put the humanity at risk. The resources of some of the largest economies are stressed out due to the large infectivity and transmissibility of this disease. Due to the growing magnitude of number of cases and its subsequent stress on the administration and health professionals, some prediction methods would be required to predict the number of cases in future. In this paper, we have used data-driven estimation methods like long short-term memory (LSTM) and curve fitting for prediction of the number of COVID-19 cases in India 30 days ahead and effect of preventive measures like social isolation and lockdown on the spread of COVID-19. The prediction of various parameters (number of positive cases, number of recovered cases, etc.) obtained by the proposed method is accurate within a certain range and will be a beneficial tool for administrators and health officials.

Graphical abstract

1. Introduction

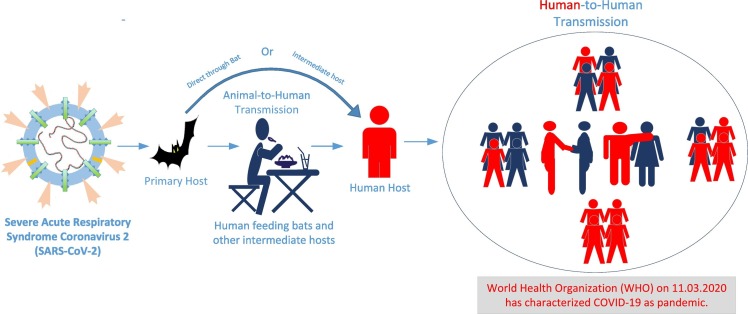
World is moving through a very distressing stage by the spread of novel coronavirus (SARS-CoV-2). It is a highly contagious disease and the World Health Organization (WHO) has declared it as a global public health emergency (L.-s. Wang et al., 2020). It is originated in Wuhan, Hubei Province, People's Republic of China (PRC) in late December 2019, when a case of unidentified pneumonia was reported (Huang et al., 2020). PRC Centers for Disease Control (CDC) experts declared that pneumonia as novel coronavirus pneumonia (NCP) as caused by a novel coronavirus and WHO officially named the disease COVID-19 (Huang et al., 2020). However, the International Committee on Taxonomy of Viruses (ICTV) named the virus as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). This is a class of β-coronavirus and has many potential natural hosts, intermediate hosts and final hosts as shown in Fig. 1 . Due to these characteristics, there is a great challenge for prevention and treatment of the virus infection (Vellingiri et al., 2020). Despite of the large number of cases worldwide (as shown in Fig. 2 (Statista, 2020)) and low mortality rate (Liu et al., 2020) compared to SARS and the middle east respiratory syndrome (MERS) (as shown in Fig. 3 (Statista, 2020)), this virus has high infectivity and transmissibility. Preventive measures for COVID-19 include maintaining social distancing, washing hands frequently, avoiding touching the mouth, nose, and face (WHO, 2020).

Fig. 1.

Transmission of COVID-19.

Fig. 2.

No of cases of COVID-19 worldwide (Statista, 2020).

Fig. 3.

Fatality rate of major virus outbreaks (Statista, 2020).

The first case of COVID-19 was reported in India on 30th January 2020 with origin from China (PIB, 2020). It spreads to the maximum of districts of the country. As on 9th April 2020 the total cases reported in India are 5734 with 472 recoveries and 166 deaths (Covid-19.in, 2020). However, the rate of infection is lower as compared to other countries.

There is a lot of stress on the part of administration and health officials for accommodating patients with possible symptoms of COVID-19. So, for that some prediction tools must be used to know about the number of cases in coming days for making preparations at the administrative level (Tobías, 2020; L. Wang et al., 2020; L.-s. Wang et al., 2020).

In this paper, we propose the data-driven LSTM method and the classical curve fitting method for the prediction of number of patients to be accommodated in the subsequent days based to the data available. The proposed model can approximately predict the number of new COVID-19 cases so, the administration can make preparations accordingly to accommodate them.

This paper has been organized as follows. In Section 2, LSTM technique for the prediction of COVID-19 has been explained in detail. In 3, 4, the results and conclusions of the work have been presented, respectively.

2. LSTM based technique for prediction of COVID-19

Deep learning methods like recurrent neural networks (RNN) proved to be effective for prediction (Jiang and Schotten, 2020) due to automatically extracting relevant features from the training samples, feeding the activation from the previous time step as input for the current time step and networks self-connections. RNN is good at processing data and exhibiting great potential in time-series prediction (Connor et al., 1994) through storing large historical information in its internal state. However, it has drawback of vanishing and gradient exploding problems which leads to the large training time or training does not work at all. To remove that shortcomings, Hochreiter and Schmidhuber designed long short-term memory RNN structure in 1997 (Hochreiter and Schmidhuber, 1997) to deal with a long-term dependency with the multiplicative gates that regulate the information flow and memory cells in the recurrent hidden layer.

The structure of LSTM consists of four gates i.e. input gate, forget gate, control gate, and output gate which is shown in Fig. 4 (Sun et al., n.d.).

Fig. 4.

Basic structure of LSTM.

The input gate is defined as

$$i_t=\sigma \left(W_i\times \left[h_{t-1},x_t\right]+b_i\right)$$ (1)

It decides which information can be transferred to the cell. The information from the input of previous memory which is to be neglected is decided by the forget gate and is defined as:

$$f_t=\sigma \left(W_f\times \left[h_{t-1},x_t\right]+b_f\right)$$ (2)

The update of the cell is controlled by the control gate and is given by the following equations:

$$\begin{array}{l}\widetilde{C_t}=tanh\left(W_c\times \left[h_{t-1},x_t\right]+b_c\right)\\ C_t=f_t\ast C_{t-1}+i_t\ast \widetilde{C_t}\end{array}$$ (3)

The hidden layer (h _t−1) is updated by output layer which is also responsible for updating the output as is given by:

$$\begin{array}{l}{o}_t=\sigma \left(W_o\times \left[h_{t-1},x_t\right]+b_o\right)\\ h_t=o_t\ast tanh\left(C_t\right)\end{array}$$ (4)

In the above equations, tanh is used to scale the values into range −1 to 1, σ is the activation function which is taken as sigmoid and W are the corresponding weight matrices.

3. Results

In this section, we study the spread of COVID-19 in India as there are hundreds of cases reported each day. For validation and analysis of the proposed model, data pertaining to India from (Covid-19.in, 2020) has been used with the Matlab environment.

3.1. Data-driven methods to predict COVID-19

The data has been used from 30th January 2020 (when the first case of COVID-19 was reported in India) to 4th April 2020 with 80% data is used for training and rest 20% for forecasting and validation purposes. The resulting plot showing the total number of confirmed cases is shown in Fig. 5(a). In this figure, the observed data (blue color) is the data used for training purposes (80% of the total data), official data (green line) indicates the official data available (Covid-19.in, 2020) and forecasted data (red line) indicates the forecast of a total number of confirmed cases. From this graph, it is observed that the forecasted number of total confirmed positive cases closely matches with the available official data.

Fig. 5.

(a) Total number of confirmed cases prediction using LSTM. (b) Daily total number of positive cases prediction using LSTM. (c) Total number of recovered cases prediction using LSTM. (d) Total number of deceased cases prediction using LSTM. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

Similar observations have also been made for daily reported positive cases, total recovered cases and total deceased cases, as shown in Fig. 5(b), (c) and (d) respectively.

The classical curve fitting technique also has been applied, considering two objectives: First, is to verify the above method and second is to analyze the impact of lockdown and social distance considering the various spread ratios. From this method it is observed that the data follows a power law (f(x) = ax ^b) and resulting estimation for total confirmed cases, daily positive cases, total recovered cases and total deceased cases are shown in Fig. 6(a), (b), (c) and (d) respectively. In these figures, official data is the data available for prediction (data of 66 days), estimated is the estimation/prediction curve and pred bnds represents the confidence of prediction, which is resulted as ±5% in the proposed work.

Fig. 6.

(a) Total number of confirmed cases prediction by curve fitting. (b) Daily number of positive cases prediction by curve fitting. (c) Total number of recovered cases prediction by curve fitting. (d) Total number of deceased cases prediction by curve fitting.

The recovery rate of confirmed cases is also high in case of COVID-19, however, the time taken for the patients to recover is also large. With a large number of patients, the stress on the medical resource increases, so estimation/prediction of time taken for recovery is also required for proper arrangement and utilization of available resources. Towards this goal estimation of the number of patients recovered has also been made, which is shown in Fig. 7(a).

Fig. 7.

(a) Estimation of number of days required for recovery (b) Effect of the transmission rate r on number of cases (c) Effect of r on number of cases with 6th April as initial point.

From this figure, it is observed that for the total number of confirmed cases up to 90 days from the starting point of the first case, 120 days are required for total recovery.

For these data-driven estimations, the data has been taken up to 4th of April. The comparison has also been made for the total positive reported cases and daily reported cases with estimated cases (by data-driven model) from 5th to 9th April 2020 as shown in Table. 1 .

Table 1.

Comparison of reported and estimated cases.

Day	Date	Official data	Estimation	Error percentage (%)
Comparison for total positive confirmed cases
67th	5th April 2020	4289	4012	−6.44
68th	6th April 2020	4778	4676	2.12
69th	7th April 2020	5351	5438	1.64
70th	8th April 2020	5916	6311	6.6
71st	9th April 2020	6725	7308	8
Comparison for daily reported positive cases
67th	5th April 2020	605	455	−24
68th	6th April 2020	489	522	6.7
69th	7th April 2020	573	598	4.4
70th	8th April 2020	565	683	20.8
71st	9th April 2020	809	779	−3.7

From the above tables and Fig. 7(a), it is observed that number of cases under different heads can be estimated by using the above two techniques with the available data. However, the limitation is only that limited data is available and initial data is nearly a flat curve and much cannot be deciphered from that.

3.2. Effect of measures adopted to prevent the spread of COVID-19

With the outbreak of the COVID-19 pandemic, various measures are has been adopted by the Govt. of India to prevent its spread (Covid-19.in, 2020). One of the measures is social isolation and lockdown. Social isolation is the complete lack of contact between an individual and society, while, lockdown is an emergency protocol that usually prevents people from leaving an area. These two measures prevent the spread of COVID-19 from effected person to healthy individual to a great extent.

Analysis of the adopted preventive measures has been done with different transmission rate (r) (Zhou et al., 2020) i.e. from r = 0.001 to r = 2.3. The transmission rate is the quantitative measure of spread of the virus from an effected individual to healthy individuals and low value of transmission rate can be obtained by strict social isolation and lockdown measures (Worldometers, 2020).

Let us consider a scenario that in case of India, the value of r before lockdown was 2.3 (i.e. an infected individual can infect the 2.3 persons) and after lockdown it reduced to 0.15. The estimated total positive cases have been compared with actual cases using different values of transmission rate and are shown in Fig. 7(b).

From this figure, it is observed that preventive measures (social isolation and lockdown) have worked well in containing this contagious virus in India.

Now, let us consider a scenario with 6th April 2020 having 4289 number of positive cases as the initial start and strict lockdown and social isolation measured adopted rigorously, the number of positive cases with variation in transmission rate is shown in Fig. 7(c).

From Fig. 7(c), it is observed that preventive measures of social isolation and lockdown will work perfectly in reducing the number of cases and making the curve flat. So preventive measure must be strictly adopted after 6th April.

4. Conclusion

In this paper, a data-driven forecasting/estimation method has been used to estimate the possible number of positive cases of COVID-19 in India for the next 30 days. The number of recovered cases, daily positive cases, deceased cases has also been estimated by using LSTM and curve fitting. The effect of preventing measures like social isolation and lockdown has also been observed which shows that by these preventive measures, spread of the virus can be reduced significantly.

CRediT authorship contribution statement

Anuradha Tomar: Conceptualization, Investigation, Methodology, Software, Validation, Writing - review & editing. Neeraj Gupta: Conceptualization, Data curation, Writing - original draft, Visualization, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.