Stable representations of decision variables for flexible behavior

Abstract

Decisions occur in dynamic environments. In the framework of reinforcement learning, the probability of performing an action is influenced by decision variables. Discrepancies between predicted and obtained rewards (reward prediction errors) update these variables, but they are otherwise stable between decisions. Whereas reward prediction errors have been mapped to midbrain dopamine neurons, it is unclear how the brain represents decision variables themselves. We trained mice on a dynamic foraging task, in which they chose between alternatives that delivered reward with changing probabilities. Neurons in medial prefrontal cortex, including projections to dorsomedial striatum, maintained persistent firing rate changes over long timescales. These changes stably represented relative action values (to bias choices) and represented total action values (to bias response times) with slow decay. In contrast, decision variables were mostly absent in anterolateral motor cortex, a region necessary for generating choices. Thus, we define a stable neural mechanism to drive flexible behavior.

eTOC

Flexible behavior requires a memory of previous interactions with the environment. Medial prefrontal cortex persistently represents value-based decision variables, bridging the time between choices. These decision variables are sent to the dorsomedial striatum to bias action selection.

INTRODUCTION

To maximize reward, the nervous system makes choices and receives feedback from the environment. Models of this process (Bertsekas and Tsitsiklis, 1996; Sutton and Barto, 1998) contain two components: brief feedback variables and sustained decision variables. Feedback, in the form of prediction errors (the discrepancy between predicted and obtained rewards; Schultz et al., 1997; Bayer and Glimcher, 2005; Cohen et al., 2012), is used to update the decision variables. Decision variables, in turn, prescribe what choices to make and how quickly to make them. These variables change in value upon feedback (for example, when a reward is or is not received), but are otherwise stable in the time between choices. How are these decision variables stably represented in the nervous system?

Previous studies have found neuronal correlates of decision variables in the form of brief firing rate changes that decay in the time between actions (Samejima et al., 2005; Lau and Glimcher, 2008; Cai et al., 2011; Wang et al., 2013; Tsutsui et al., 2016). These observations appear to suggest that these variables are maintained as stored synaptic weights, which are transformed into brief changes in firing rates at the time of decision (Barak and Tsodyks, 2007; Mongillo et al., 2008). However, the firing rates of individual neurons themselves could show persistent changes that directly and stably represent the decision variables. Recent computational work has proposed this as a viable mechanism for flexible control of behavior in changing environments (Wang et al., 2018).

To test the hypothesis that persistent changes in firing rates encode decision variables, we adapted a primate behavioral task (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016), and trained mice to forage dynamically at two possible reward sites. We studied the activity of neurons in the medial prefrontal cortex (mPFC), a region known to have persistent, working-memory-like correlates, to determine how decision variables are maintained in the nervous system over long timescales. There, we found persistent representations of decision variables. We then asked how this information may inform action selection. First, we measured activity in premotor cortex (anterolateral motor cortex, or ALM), a downstream structure necessary for actual choices, and saw that it did not inherit persistent activity from mPFC. Then, we measured outputs from mPFC to dorsomedial striatum, a structure thought to be critical for action selection. We found that decision variables were sent directly to dorsomedial striatum.

RESULTS

Reward History Informs Choices and Response Times

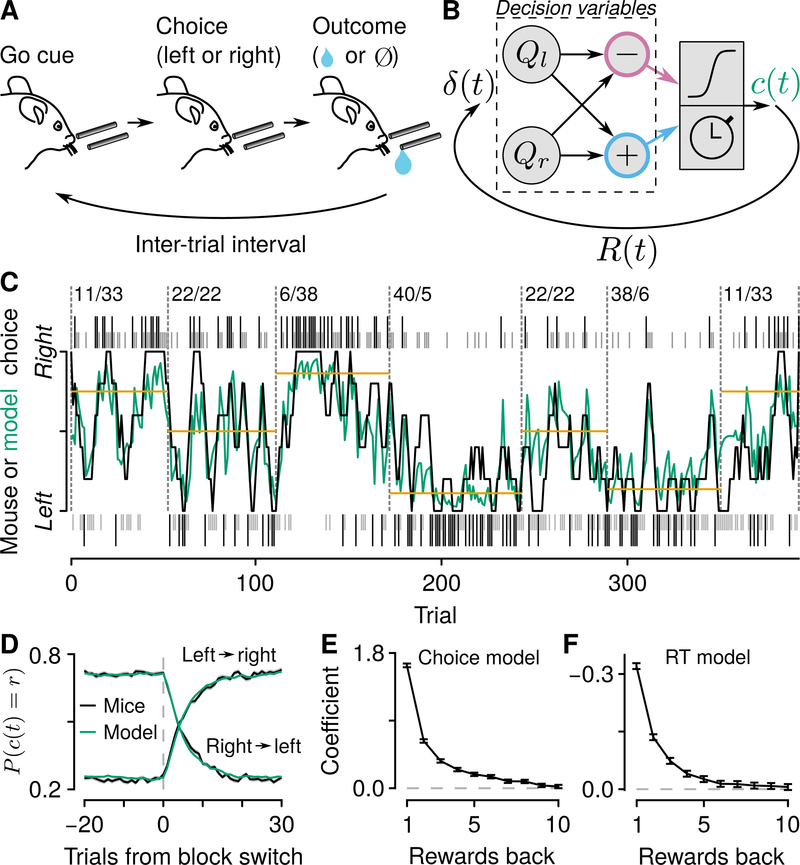
We adapted a primate behavioral task (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016), in which thirsty, head-restrained mice chose freely between two alternatives that delivered reward with nonstationary probabilities (Figures 1 and S1). On each trial, an olfactory “go” cue (or, on 5% of trials, a “no-go” cue) was delivered for 0.5 s. Mice licked toward a tube to their left or their right. Critically, the go cue did not instruct mice to make a particular choice. Depending on their choice, a drop of water was delivered with a probability that changed randomly after 40–100 trials. This outcome (reward or no reward) was followed by a random, exponentially-distributed inter-trial interval (ITI), which was followed by the next cue. This task isolates the decision problem to one of adapting choices to the ongoing reward dynamics of the environment. Indeed, mice rapidly adjusted their choice patterns as the probabilities of reward changed (Figures 1C and 1D).

Figure 1: Mice use reward history to drive flexible decisions.

(A) Dynamic foraging task in which mice chose freely between a leftward and rightward lick, followed by a drop of water with a probability that varied. (B) Reinforcement-learning model illustrating the distinction between decision variables (relative value, Q_r – Q_l, in pink, and total value, Q_r + Q_l, in blue), and feedback variables δ (t), the error between expected and received reward). Left and right action values (Q_l, Q_r ) are used to compute choice direction (c (t)) and response time (RT), and are followed by reward on a given trial ( R (t)). (C) Example mouse behavior in the “multiple-probability” task. Black (rewarded) and gray (unrewarded) ticks correspond to left (below) and right (above) choices. Black curve: mouse (smoothed over 5 trials) choices. Green curve: generative model probability of making a rightward choice. Gold lines correspond to matching behavior. Numbers indicate left/right reward probabilities. (D) Probability of rightward mouse and generative model choices around block changes (changes in reward probabilities) for both task variants. Blocks with 1:1 reward probabilities were excluded from this analysis. (E) Logistic regression coefficients for choice as a function of reward history (“choice model”). Error bars: 95% CI. (F) Linear regression coefficients for RT as a function of reward history (“RT model”). Error bars: 95% CI. See also Figure S1.

In this task, mice showed approximate matching behavior (Sugrue et al., 2004; Lau and Glimcher, 2005; Fonseca et al., 2015; Tsutsui et al., 2016), in which the fraction of choices was similar to the fraction of rewards obtained from each option (Figures S1A, S1B, and S1D). Under the conditions used here, matching is a policy that can maximize reward (Baum, 1981; Sakai and Fukai, 2008). We calculated logistic regressions to determine the statistical dependence of choices on reward history. This analysis showed a similar pattern as previously found in monkeys: recent outcomes were weighted more than those further in the past (Figures 1E and S1E). Response times, a second measure of behavioral performance, depended on reward history in a quantitatively similar way (τ = 1.38±0.25 for the choice model, τ = 1.35±0.22 for the response time model, 95% CI; Figures 1F and S1E). We used two variants of the task, one in which there were two, and another in which there were several reward probabilities. Mouse behavior was consistent across both variants of the task (Figure S1E).

Based on the observation that choices and response times depended on reward history, we adapted a generative model from control theory and reinforcement learning, called Q-learning (Bertsekas and Tsitsiklis, 1996; Sutton and Barto, 1998; Figures 1B–1D, S1C, S1F, and S1G). The model maintains estimates of the value of making a leftward or a rightward action. The chosen option is updated by learning from the outcome (presence or absence of reward), and the unchosen option is updated by a forgetting parameter. Here, the decision variables are these action values and their arithmetic combinations (Figure 1B). The latter comprise relative value, which biases choices toward one alternative (Samejima et al., 2005; Seo and Lee, 2007; Ito and Doya, 2009; Sul et al., 2010; Cai et al., 2011; Wang et al., 2013; Murakami et al., 2017), and total value, which modulates the vigor of choice (how fast to make an action; Figure S1H–J; Niv et al., 2007; Wang et al., 2013; Reppert et al., 2015; Hamid et al., 2016; Tsutsui et al., 2016).

mPFC is Specifically Required for Foraging

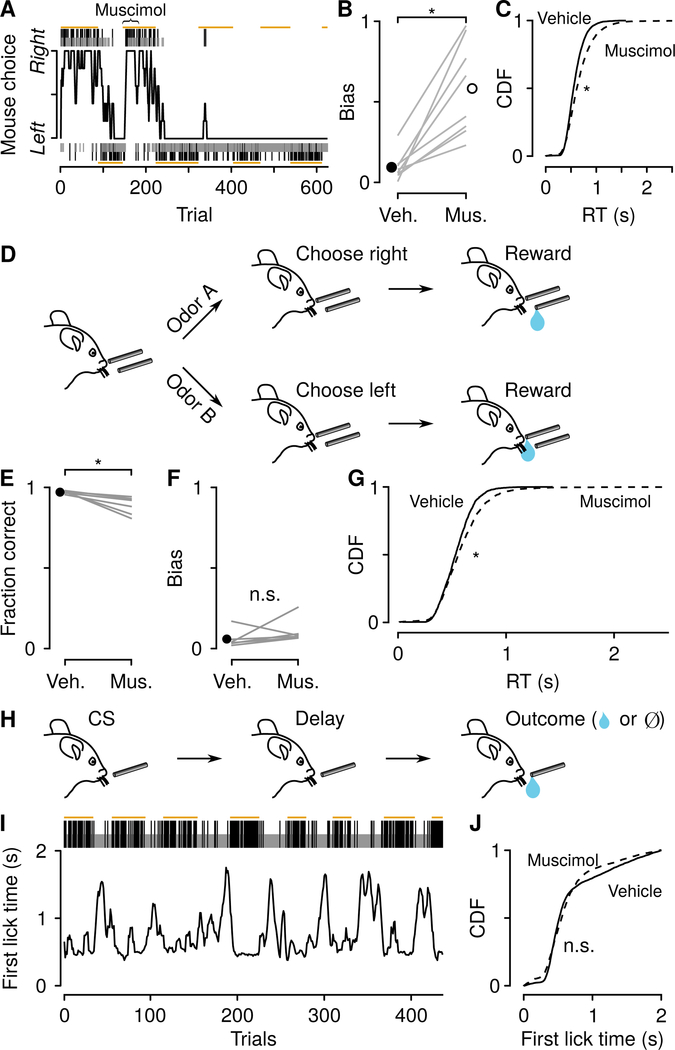
To determine where these long-lasting decision variables are represented, we reversibly inactivated the mPFC—an area implicated in action-outcome feedback (Kennerley et al., 2006; Matsumoto et al., 2007; Sul et al., 2010; Hyman et al., 2013; Iwata et al., 2013; Simon et al., 2015; Del Arco et al., 2017; Fiuzat et al., 2017; Ueda et al., 2017; Ebitz et al., 2018; Nakayama et al., 2018)—using bilateral injections of muscimol, a GABA_A receptor agonist. Following mPFC inactivation, mice showed both a strong choice bias and slowed response times (Figures 2A–2C). The direction of bias was idiosyncratic across mice (Figure S2). To test whether these effects were specific to the dynamic foraging task, we developed two other behavioral tasks to rule out general motor disruptions. In the first, we trained mice on a two-alternative forced choice task, in which they licked leftward to receive a reward following one olfactory stimulus, and rightward to receive a reward following a different olfactory stimulus. Inactivating mPFC in this task produced no comparable change in choice bias (Figures 2D–2G). However, there was a slowing of response times, consistent with a decrease in overall vigor (Wang et al., 2013). In the second task, we trained mice on a classical conditioning paradigm, in which an olfactory stimulus predicted a delayed reward. Importantly, unlike in the tasks described above, the time of reward delivery was independent of the mouse’s response time, so faster movements did not result in earlier receipt of reward. We varied the probability of reward over time, so that mice would show a large range of latencies to first lick (Figures 2H and 2I). Inactivating mPFC did not produce a significant increase in latency to first lick in this task (Figure 2J). Thus, the results across all three tasks indicate that computations in mPFC are specific for behavioral tasks that require the mouse to select actions using a local estimate of reward history. Moreover, they suggest the existence of a relative-value signal that biases choices and a total-value signal that biases response times.

Figure 2: mPFC drives choice bias and response time.

(A) Example mPFC inactivation (muscimol injected during trials under curly brace). (B) Choice bias after vehicle and muscimol injections within and across mice (Wilcoxon signed rank test, P< 0.01). (C) Cumulative distributions of response times (RT) after vehicle (solid) and muscimol (dashed) injections (vehicle mean, 581±2 ms, median, 553 ms, muscimol mean, 672±4 ms, median, 618 ms, Wilcoxon rank sum test, P < 0.0001 ). (D) Two-alternative forced choice (2AFC) task, in which two odors signaled leftward or rightward choice. (E) Mean fraction correct in the 2AFC task, with vehicle or muscimol injections, within and across mice. Inactivation produced a small reduction in fraction of correct choices (Wilcoxon signed rank test, P < 0.05). (F) Inactivation did not bias choices in this task (Wilcoxon signed rank test, P > 0.3). (G) Inactivation increased RT (vehicle mean, 542±3 ms, median, 533 ms, muscimol mean, 586±5 ms, median, 556 ms, Wilcoxon rank sum, P< 0.0001). (H) Dynamic classical conditioning task, in which a single odor was followed by a delayed reward with a nonstationary probability. (I) Example session, in which latency to first lick following the odor varied with the probability of reward. Gold lines correspond to high-probability blocks. (J) Inactivation did not slow the latency to first lick (4 mice; vehicle mean, 691±6 ms, median, 517 ms, muscimol mean, 647±7 ms, median, 550 ms, Wilcoxon rank sum, P > 0.7 ). See also Figure S2.

mPFC Represents Decision Variables Over Long Timescales

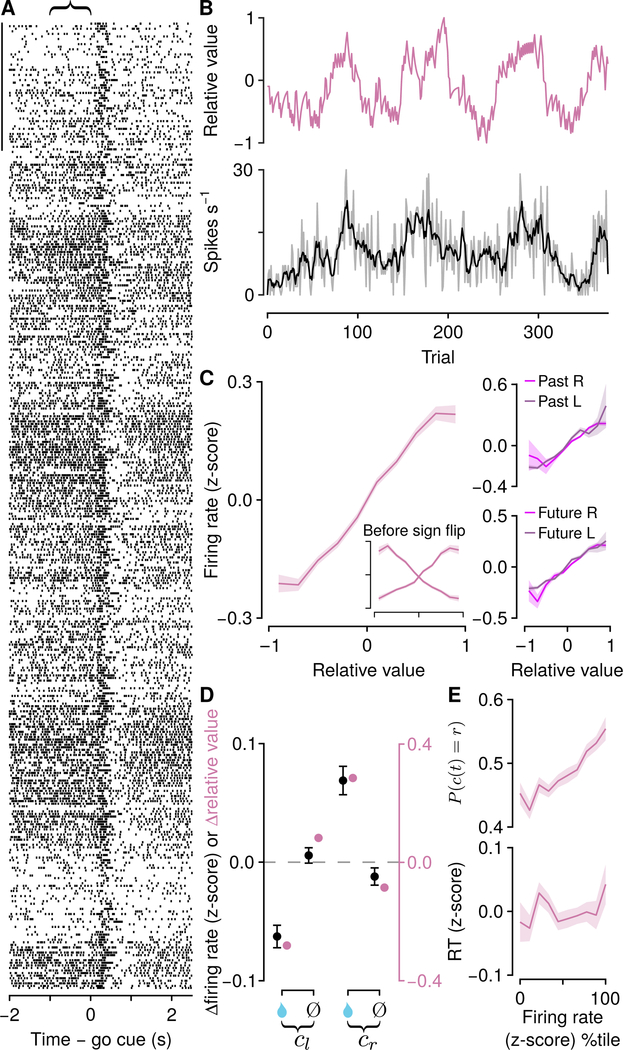
To determine how persistent decision variables are represented in mPFC, we recorded action potentials from 3,073 mPFC neurons in 14 mice, using 8–16 tetrodes per mouse (Figures 3 and S3). We observed changes in firing rates during the ITIs, lasting for many trials, as well as changes in firing rates occurring around the times of choices and outcomes (Figure 3). We focused on the slower (across tens of seconds to minutes) changes in firing rates and compared them to the decision variables extracted from the models.

Figure 3: Background, persistent activity in mPFC correlates with relative value.

(A) Example neuronal activity relative to go cues (each tick is an action potential). Trials proceed downward. Scale bar: 50 trials. Curly brace indicates analysis window. (B) Relative value (Q_l −Q_r ) and firing rate (gray; smoothed in black) in the 1 s before go cues for the same neuron. (C) Left: firing rate (z-score) for pure relative-value neurons (inset shows firing rates split by neurons that increase or decrease activity; neurons that decreased activity were sign-flipped and combined with those that increased activity). Right: the same neurons split by the direction of the previous (top) or next (bottom) choice (left, dark shading, right, light shading). (D) Comparison of changes in firing rate (black, in which neurons with increasing or decreasing activity are combined, mean ± SEM) and model relative value (pink) following rewards (water drop) or no rewards (Ø), for left choices (c_l ) and right choices (c_r ). (E) Relative-value neurons predict choice (top) but not RT (bottom). See also Figure S3 and S4.

We calculated generalized linear models (Poisson regressions) to predict spike counts at the end of ITIs (the 1 s before the next go cue). We used three regressors: relative value, total value, and future action. Relative value was defined as the difference between right and left action values (Q_r − Q_l ).

Total value was defined as the sum of right and left action values (Q_r + Q_l). We found that a large fraction of mPFC neurons (2,401 of 3,073, 78% ) had persistent activity in the ITIs that tracked these two evolving decision variables. Of these, some (770 of 2,400, 32%) had significant regression coefficients only for one decision variable (“pure” neurons). We found similar results in neurons recorded during both task variants (Figure S3J). We next analyzed these pure populations in more detail.

One population of neurons (252 with significant regression coefficients only for relative value) persistently and monotonically represented relative value, with roughly equal numbers preferring Q_r − Q_l and Q_l – Q_r (exact binomial test, 0.50±0.03, 95% CI, P > 0.9; Figures 3A–3C), distributed equally across hemispheres (proportion test, ${\chi }_1^2=1.85,P>0.16;$ Figure S3F). To analyze these neurons together, we sign-flipped those preferring Q_l – Q_r, thereby treating them as preferring Q_r − Q_l. Importantly, relative-value coding did not arise due to premotor activity, because tuning curves were similar regardless of future action (t_84,776 =−1.60,P > 0.1; Figure 3C). Similarly, the activity was not a long-lasting consequence of past actions, because tuning curves were similar regardless of previous action (t_84,776 = −0.43,P > 0.6; Figure 3C). An important prediction of the Q-learning model is that firing rates should be updated in a quantitative way following action-outcome pairs. Remarkably, relative-value neurons matched quantitative predictions from the model (Figure 3D). Also as predicted from the model, relative-value neuron firing rates scaled with choice, but not response time ( P (c (t) = r) over z-scored firing rate logistic slope, 0.13±0.014, 95% CI; RT over z-scored firing rate linear slope, 0.0053±0.0066, 95% CI; Figure 3E). Importantly, this reflects choice bias, rather than premotor activity, similar to the bias underlying a weighted coin.

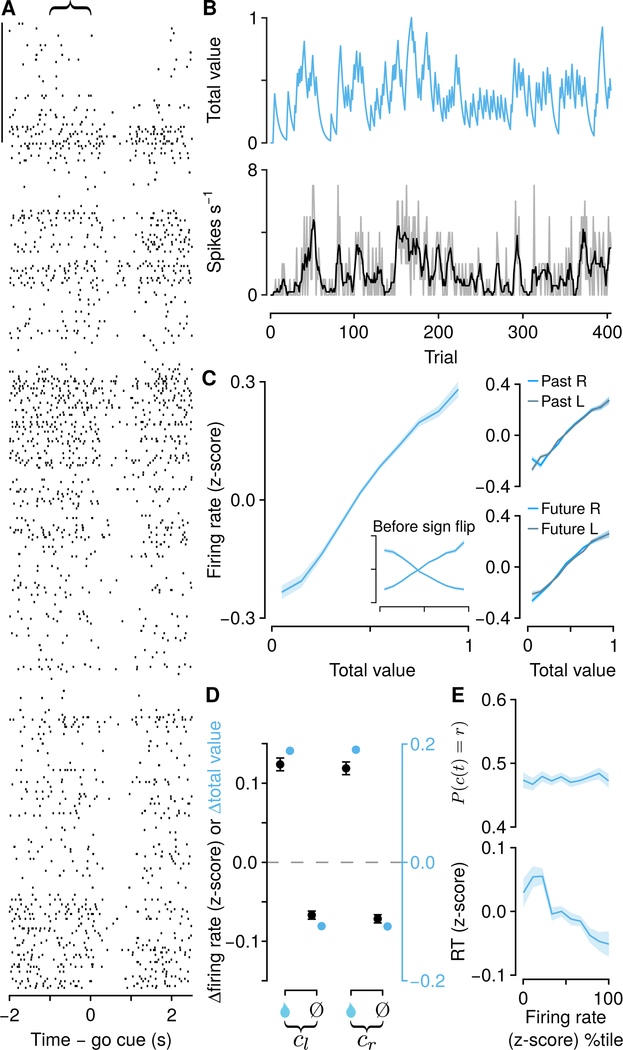
A second population of neurons (518 with significant regression coefficients only for total value) persistently and monotonically represented total value, with roughly equal numbers preferring Q_r + Q_l. and Q_r − Q_l (exact binomial test, 0.47±0.02, 95% CI, P± 0.20; Figures 4A–4C), distributed equally across hemispheres (proportion test, ${\chi }_1^2=1.85,$ P > 0.9 ; Figure S3F). Similar to relative-value neurons, total-value activity was not a consequence of past (t_173,617 = −0.92, P > 0.3) or future actions (t_173,617 = −0.96, P > 0.3; Figure 4C). Total-value neuron firing rate changes also fit the predicted changes in total value from the Q-learning model (Figure 4D). In contrast to relativevalue neurons, total-value neuron firing rates scaled with response time, but not choice ( P (c (t) = r) over z-scored firing rate logistic slope, 0.005±0.009, 95% CI; RT over z-scored firing rate linear slope, −0.033±0.005, 95% CI; Figure 4E). We did not find similar evidence for representations of action values alone (Figure S4). Thus, we demonstrate the existence of persistent activity in two groups of neurons that predicts choices and response times, quantitatively consistent with control signals used to drive flexible behavior.

Figure 4: Background, persistent activity in mPFC correlates with total value.

(A)-(E), the same as Figure 3A–E, but for total value.

Relative Value Signals are More Stable than Total Value Signals

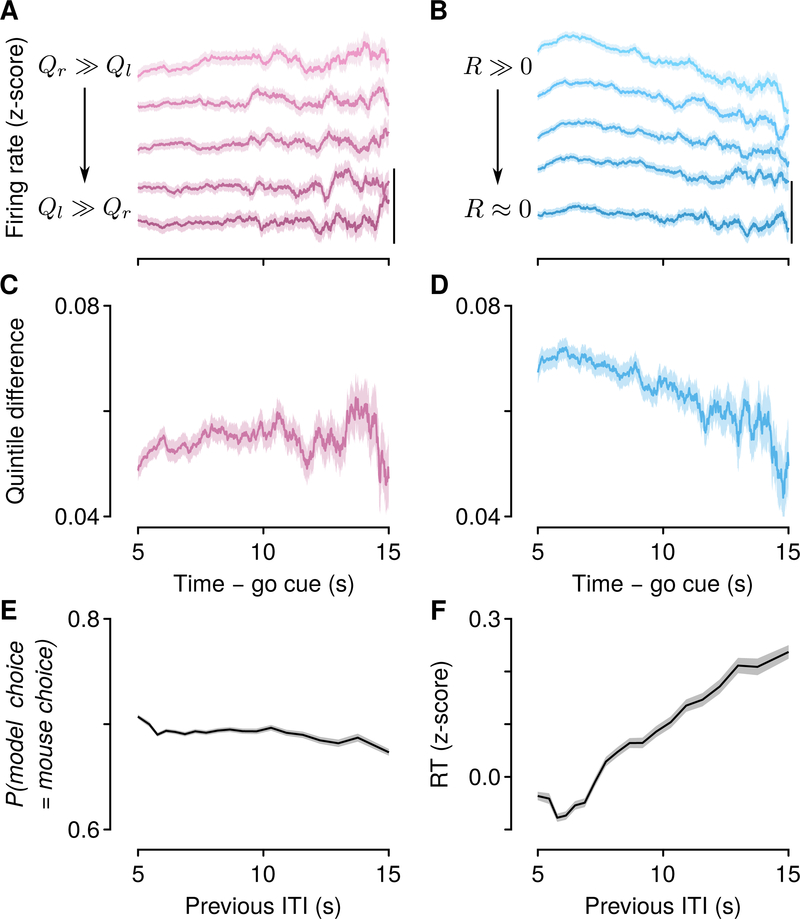
A key prediction of the behavioral model is that decision variables remain stable between the times of feedback. We asked how robust relative- and total-value representations were: did they decay during long ITIs, or were they stable? We split trials into quintiles of relative value, and analyzed the firing rates of all 1,548 relative-value neurons (Figures 5A and S5). We analyzed all relative-value neurons here to include as many long ITIs as possible. Relative-value neurons showed persistent activity that remained stable through ITIs as long as 15 s, consistent with model predictions (Figure 5C). We found similar stability in pure relative-value neurons (Figure S5E).

Figure 5: Relative-value signals are persistent and stable in time, while total-value signals are persistent but decay over time.

(A) Firing rates of relative-value neurons during ITIs, split by quintiles of relative value. Scale bar: 0.1 z-score. (B) Firing rates of total-value neurons during ITIs, split by quintiles of total value. The difference across quintiles (averaged across adjacent quintiles) remained stable over time for relative-value (C, linear slope, 2.600×10⁻⁴ ± 1.8×10⁻⁵ z-score s⁻¹, 95% CI) but not total-value (D, linear slope, −1.9×10⁻³ ±1.6×10⁻⁵ z-score s⁻¹, 95% CI) neurons. (E) The probability that the model choice matches the mouse’s choice remains stable as a function of previous ITI (linear slope, −1.3×10⁻³ ±4.6 × 10⁻⁴ probability s⁻¹ , 95% CI). (F) RT increases following longer ITIs (linear slope, 0.036±0.0019 z-score RT s⁻¹ , 95% CI). Shading denotes SEM. Neurons were sign-flipped as in Figures 3C and 4C. See also Figure S5.

We next split trials into quintiles of total value, and analyzed the firing rates of all 1,880 total-value neurons (Figures 5B and S5). Total-value neurons showed persistent activity that decayed during long ITIs (Figure 5D). We found a similar decay in pure total-value neurons (Figure S5F). This result indicates that the representation of total value was unstable, in contrast to the representation of relative value.

The observation that relative-value persistent activity was stable, whereas total-value persistent activity decayed, makes a specific prediction about the dependence of choices (computed from relative value) and response times (computed from total value): the probability of making an upcoming choice given a particular history of choices and rewards should not depend on the time elapsed since the previous choice. In contrast, the response time should vary with the time since the previous choice. Indeed, we found that model choices and mouse choices only weakly depended on previous ITI (Figure 5E), whereas response times slowed with increasing previous ITI (Figure 5F). Consistent with the prediction that the latter effect depended on total-value neurons, it was abolished following mPFC inactivation (Figures S5H–S5J).

Decision Variables are Only Weakly Represented in Premotor Cortex

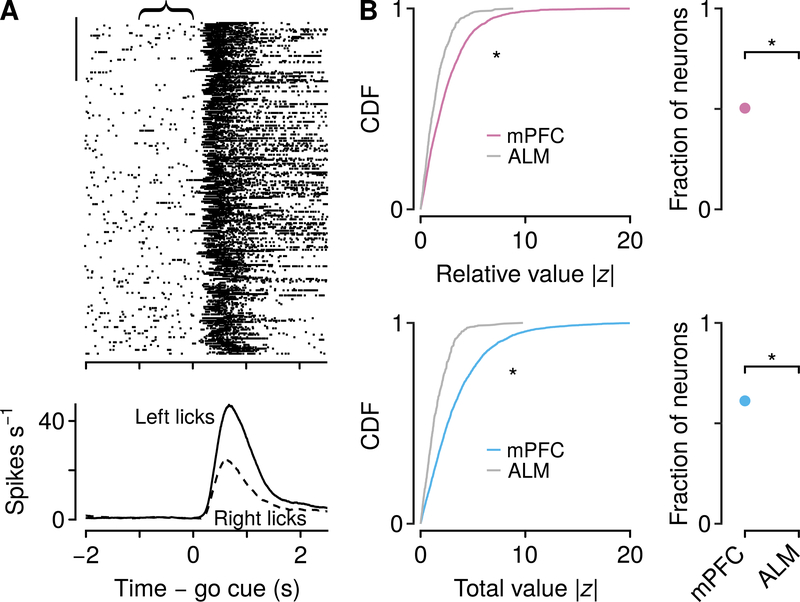
Where are decision variables in the temporal flow of information in neocortex? To address this, we measured activity in ALM (tongue premotor cortex), which is necessary for generating reward-guided licks (Komiyama et al., 2010; Guo et al., 2014; Li et al., 2015). Consistent with this observation, we observed firing rates at the time of the choice that distinguished between leftward and rightward licks (Figures 6A and S6A, 277 of 537 neurons, 52%). We compared the strength of relative- and total-value regressors in mPFC and ALM in the 1-s pre-cue window. Relative and total value were represented more strongly in mPFC than ALM, and fewer neurons in ALM showed persistent activity that tracked relative or total value (Figure 6B; 28.1% significant for relative value, 32.0% significant for total value). These findings demonstrate that decision variables are not robustly represented in premotor cortex.

Figure 6: ALM weakly represents relative and total value.

(A) Example neuronal activity relative to go cues (each tick is an action potential). Trials proceed downward. Scale bar: 50 trials. Curly brace indicates analysis window. Bottom, average firing rates of the same neuron during leftward and rightward choice trials. (B) Cumulative distribution functions (CDF) of | z | values from generalized linear models, for relative (top left) and total value (bottom left) were larger for mPFC than ALM (Wilcoxon rank sum tests, P <10⁻¹⁰ ). Poisson regressions use z statistics to determine significance. For reference, | z |=1.96 is significant at P= 0.05. Right: larger fraction of neurons significantly encoded relative (top, proportion test ${\chi }_1^2=90.9,$ P <10⁻¹⁰ ) and total value (bottom, ${\chi }_1^2=158.3,$ P<10⁻¹⁰ ) in mPFC than ALM. See also Figure S6.

Relative and Total Values are Sent to the Dorsomedial Striatum

If persistent decision variables are not inherited by premotor cortex, then what structures receive this information from mPFC to select actions? The mPFC contains diverse cell types, including neurons that project to multiple brain regions. A prominent projection target is the dorsomedial striatum, which is the main input structure of the basal ganglia, and is thought to be involved in action selection (Samejima et al., 2005; Balleine et al.,2007; Kim et al., 2009; Kimchi and Laubach, 2009; Stephenson-Jones et al., 2011; Seo et al., 2012; Tai et al., 2012; Kim et al., 2013; Ito and Doya, 2015; Morita et al., 2016; Shipp, 2017; Gerraty et al., 2018). We found these corticostriatal neurons across layers in mPFC (Figures 7A, 7B, and S7A), in agreement with previous work (Anastasiades et al., 2018).

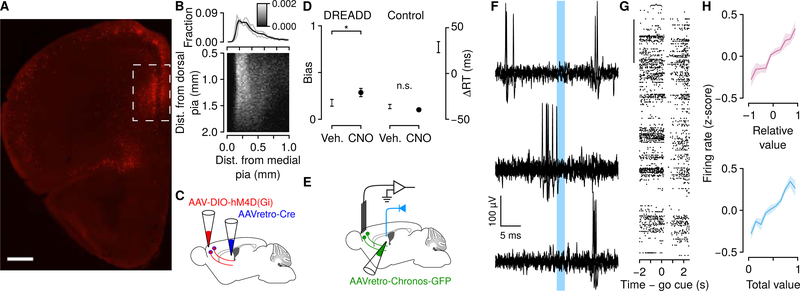
Figure 7: Neurons projecting to dorsomedial striatum encode decision variables using persistent activity.

(A) Localization of corticostriatal neurons. AAVretro-Cre was injected into an Ai9 mouse. Scale bar: 500μm. Box denotes region of recording sites. (B) Distribution of somata of labeled corticostriatal neurons. Marginal distributions are shown for each mouse (gray) and all mice (black). (C) Schema of inactivation of mPFC projections to dorsomedial striatum, using inhibitory designer receptors exclusively activated by designer drugs (DREADDs). (D) Left, inactivation of these neurons increased choice bias in DREADD, but not control, mice (Wilcoxon rank sum test, P < 0.05). Right, inactivation slowed response times. We calculated the change in response time induced by CNO relative to vehicle in DREADD and control mice. ΔRT is the difference between DREADD and control mice (95% bootstrapped CI). (E) Schema of experiment to identify corticostriatal neurons. (F) Example of a corticostriatal neuron, identified using collision tests. Top, action potentials evoked by optical axonal stimulation several milliseconds after spontaneous action potentials. Middle, failure to evoke action potentials briefly after spontaneous ones (“collisions”). Bottom, action potentials evoked following intervals without spontaneous firing. (G) Example corticostriatal neuron with persistent activity encoding decision variables. Scale bar: 50 trials. (H) Corticostriatal neurons encoded relative and total value using background firing rates. See also Figure S7.

First, we asked whether mPFC projections to dorsomedial striatum were critical for dynamic foraging. We expressed hM4D(Gi), an inhibitory receptor activated by clozapine-N-oxide (Krashes et al., 2011), exclusively in corticostriatal neurons (Figure S7B). Inactivation of corticostriatal neurons produced a significant increase in bias and slowed response times (Figures 7C and 7D), consistent with global inactivation of mPFC (Figure 2).

Next, we asked whether neurons projecting to the dorsomedial striatum represented the two decision variables we observed in mPFC. To record activity selectively from corticostriatal neurons, we expressed Chronos, a fast-activating light-sensitive protein (Klapoetke et al., 2014) in these neurons by injecting a retrogradely-infecting adeno-associated virus (AAVretro; Tervo et al., 2016) in the dorsomedial striatum (Figures 7E and S7C). This resulted in expression of Chronos in neurons across layers (Figure S7D). We implanted an optic fiber over striatum and delivered light stimuli (473 nm) to excite Chronos and retrogradely evoke action potentials.

Corticostriatal neurons were identified using collision tests (Figure 7F). Using this approach, axonal stimulation failed to evoke retrograde action potentials when there was a spontaneous action potential preceding the stimulation (“collision”). In total, we identified 20 corticostriatal neurons with this technique. We used somatic “tagging,” in which we stimulated cell bodies, in another set of experiments to identify an additional 15 corticostriatal neurons (Figures S7E–S7J). We found no differences in neurons identified with either method (Figure S7L) and therefore combined them into one dataset of 35 corticostriatal neurons. Consistent with our observations of unidentified mPFC neurons, 25 out of 35 corticostriatal neurons (71% ) showed long-lasting persistent activity that represented relative and total value (Figures 7G and 7H). Thus, two key decision variables from the theory, used to decide which option to choose and how fast to make the response, are sent from the mPFC into the striatum, a region thought to be involved in action selection itself (Figure 8).

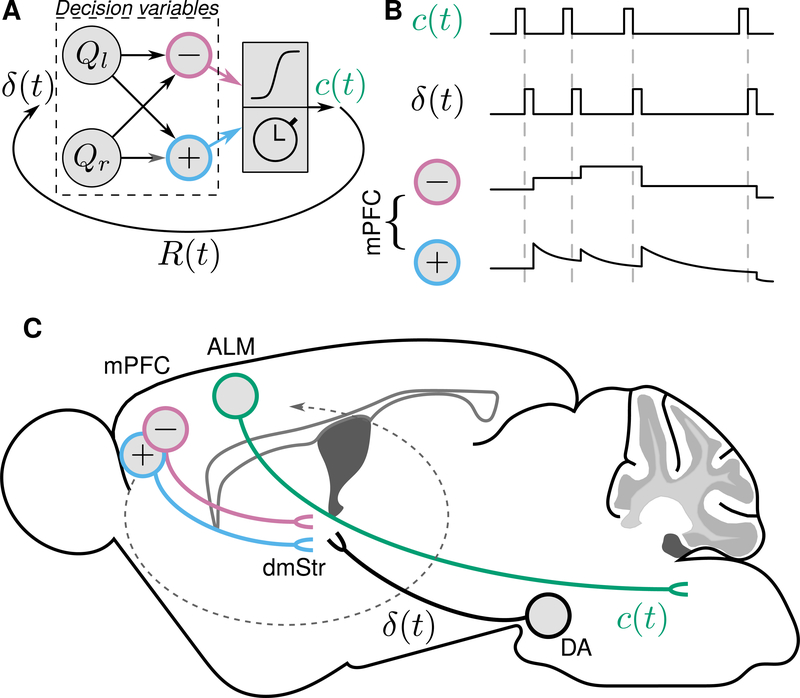
Figure 8: Summary of information flow during dynamic decision making.

(A) Model, reproduced from Figure 1B. (B) Schema of experimental results, in which choices (c (t)) and reward prediction errors (δ(t)) are brief, and induce stable changes in relative value, and decaying changes in total value. (C) Localization of persistent decision variables in mPFC projections to dorsomedial striatum, whereas brief signals in ALM and from dopaminergic (DA) neurons instantiate choices and reward prediction errors. Dashed arrow stylizes recurrent computations in cortico-basal-ganglia loops.

DISCUSSION

Theories of cognition propose that the nervous system maintains stable representations of decision variables used to guide action selection and to invigorate action execution. Here, we find that the firing rates of individual mPFC neurons quantitatively represent these key variables. We discovered a remarkably stable relative-value representation used to bias upcoming actions and a stable but decaying total-value representation used to drive the speed of actions.

What is the circuit logic that transforms relative and total value into actions? mPFC is not a premotor structure, as we demonstrated with a set of inactivation experiments (Figure 2). When we recorded from tongue premotor cortex, we observed a dramatic reduction in the persistent representation of decision variables. A similar dissociation was found in an action timing task between mPFC and secondary motor cortex (Murakami et al., 2017). This suggests that structures upstream of ALM inherit these value signals to bias actions. One major route from mPFC to ALM is through the basal ganglia and thalamus, where outputs can directly modulate ALM activity. Indeed, we discovered that mPFC projections to dorsomedial striatum are necessary for normal choices and response times, and that both relative and total value are sent along this pathway. Because the basal ganglia can add variability to input signals (Woolley et al., 2014), cortico-basal ganglia loops may function to stochastically convert relative value into discrete choices.

The dorsomedial striatum is likely only one of many downstream structures to receive relative- and total-value signals. For example, serotonergic neurons in the dorsal raphe maintain value representations over similarly long timescales (Cohen et al., 2015). Because mPFC projects monosynaptically to serotonergic neurons (Pollak Dorocic et al., 2014; Ogawa et al., 2014, Weissbourd et al., 2014), serotonergic neurons likely receive these decision variables as inputs. Indeed, stimulation of these neurons modulates decisions in a dynamic foraging task (Lottem et al., 2018).

The studies that inspired our work did not report similar persistent representations in ITIs (Sugrue et al., 2004; Lau and Glimcher, 2008; Tsutsui et al., 2016). A key difference between these tasks and ours is the manner in which they can be solved. In the primate experiments, monkeys made saccades to targets that changed position randomly, meaning specific actions to obtain reward could not be planned. This required monkeys to solve the task in object space, not action space. In our task, the lick ports (conceptually analogous to the saccade targets) remained fixed, meaning the task could be solved in action space. Interestingly, subtle persistent changes in firing rates have been reported in tasks that could be solved in action space (Stalnaker et al., 2010; Iwata et al., 2013). We hypothesize that this feature of our task, combined with a convincing generative model of behavior and the presence of long ITIs, allowed us to observe and quantify persistent activity. Importantly, this activity is qualitatively distinct from a population code in which information is tiled across neurons, across time—a phenomenon more typically observed in rodent cortex (Harvey et al., 2012).

We did not observe similar evidence for persistent action-value representations (that is, Q_r and Q_l ). Where are these action values represented? One possibility is the striatum, where action values have been observed as transient changes in firing rates (Samejima et al., 2005). Another possibility is that the brain may use a different algorithm to solve this task (Elber-Dorozko and Loewenstein, 2018). For example, a total-value-like signal can be obtained by leaky integration of rewards, without needing to compute action values. While we do not make any claims about the exact algorithm underlying behavior, our neural recordings, combined with inactivation of mPFC, allow us to conclude that mPFC contains information needed to bias the direction and response times of decisions. This logic has been seen before in sensory accumulation of evidence paradigms, in which one brain region supports both the direction and response times of decisions (Gold and Shadlen, 2007).

Many individual neurons jointly encoded relative and total value. Because action values, in principle, can be recovered as linear combinations of relative and total value, the lack of evidence for action-value neurons suggests that individual mPFC neurons nonlinearly represent relative and total value. Similar nonlinear coding has been proposed to underlie complex cognition, increasing the computational flexibility of PFC (Rigotti et al., 2013). We also observed an equal distribution of relative-value neurons with larger (or smaller) responses for Q_r – Q_l (or Q_l – Q_r) in both hemispheres. The lack of hemispheric specificity—what may be expected for motor regions— suggests that these relative-value representations are not hard wired and are instead converted into a motor plan by downstream regions. Indeed, actions may be arbitrary, requiring flexible circuitry to encode their relative values.

We found that removing relative value, by inactivating mPFC, disrupted flexible decision making. In primates, rostral cingulate motor area is crucial for reward-history-dependent actions, but not for cued actions (Shima and Tanji, 1998). This is remarkably consistent with our inactivation findings. It is well appreciated that decision making is under the control of several systems. Flexible, goal-oriented behavior is known to require mPFC and dorsomedial striatum. Inflexible, habitual behavior relies more on dorsolateral striatum (Balleine and O’Doherty, 2010). In our experiments, inactivating mPFC removed the goal-directed system, unmasking a suboptimal, likely stimulus-driven, strategy. This idea of separate controllers can explain why pupil dynamics can predict the direction of bias following mPFC inactivation. The pupil is known to encode variables such as effort (Varazzani et al., 2015), and differences in pupil dynamics for different choices may relate to a low-level bias. The multiplecontroller hypothesis also explains why mPFC inactivation had minimal effect in the two-alternative forced choice task, because stimulus-driven behavior maximizes reward.

What is the function of a total-value signal? We found that total value predicted trial-by-trial response times, consistent with theoretical predictions relating reward rates and response vigor (Niv et al., 2007; Yoon et al., 2018). Total value should invigorate behavior generally, not just response times. It is likely, then, that our movement measurements contain substantial information about the vigor state of the mouse. Interpreted this way, it makes sense why including movements as additional regressors should reduce total-value representations (which were reduced more than those of relative value): the two are correlated. This invigoration hypothesis also explains our inactivation experiments. Because total value modulates the speed of actions, its removal should uniformly slow response times, an effect we observed. One of our more intriguing findings was the slow decay of total-value neural signals, predicting the slowing of response times with increasing ITIs (Figures 5B, 5D, and 5F). This suggests that total value is computed as a rate, increasing upon receipt of reward and decaying in real time (Haith et al., 2012). Importantly, we observed the same effect in the two-alternative forced choice task, in which choices could not be prepared due to randomized stimulus presentation. This means the ITI-dependent reduction in response times was not due to disengagement of a motor preparatory signal. Our finding that mPFC inactivation disrupted this effect strongly supports our interpretation of the signal as representing total value.

Our results indicate that neuronal circuits in neocortex can adjust very flexibly to ongoing task demands, while nevertheless maintaining robustness over time. Ultimately, these decision variables, updated by feedback like that observed in dopaminergic neurons (Morris et al., 2006; Parker et al., 2016), could allow the brain to maximize reward in a dynamic world.

STAR METHODS

Animals and surgery.

We used 36 male C57BL/6J mice (The Jackson Laboratory, 000664), 6–20 weeks old at the time of surgery, for all electrophysiological (15 mice, 8 of which were used for identified corticostriatal recordings) and behavioral experiments. Mice were surgically implanted with custom-made titanium head plates using dental adhesive (C&B-Metabond, Parkell) under isoflurane anesthesia (1.0–1.5% in O₂ ). For electrophysiological experiments, we implanted a custom microdrive containing 8–16 tetrodes made from nichrome wire (PX000004, Sandvik) positioned inside 39 ga polyimide guide tubes. For identifying corticostriatal neurons, an optic fiber (200 μm diameter, 0.39 NA, Thorlabs) was implanted over dorsomedial striatum or mPFC for collision testing or somatic “tagging,” respectively. We targeted mPFC at 2.5 mm anterior to bregma and 0.5 mm lateral from the midline. We targeted ALM at 2.5 mm anterior to bregma and 1.5 mm lateral from the midline. Surgery was conducted under aseptic conditions and analgesia (ketoprofen, 5 mg/kg and buprenorphine, 0.05–0.1 mg/kg) was administered postoperatively. After at least one week of recovery, mice were water-restricted in their home cage with free access to food. Weight was monitored and maintained within 80% of their full body weight. All surgical and experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Johns Hopkins University Animal Care and Use Committee.

Behavioral tasks.

Water-restricted mice were habituated for 1–2 d while head-restrained before training on the task. Odors were delivered with a custom-made olfactometer (Cohen et al., 2012). Each odor was dissolved in mineral oil at 1:10 dilution. Diluted odors (30 μl) were placed on filterpaper housing (Whatman, 2.7 μm pore size). Odors were p-cymene, (−)-carvone, (+)-limonene, eucalyptol, and acetophenone, and differed across mice. Odorized air was further diluted with filtered air by 1:10 to produce a 1.0 L/min flow rate. Licks were detected by charging a capacitor (MPR121QR2, Freescale) or using a custom circuit. Task events were controlled with a microcontroller (ATmega16U2 or ATmega328). Mice were housed on a 12h dark/12h light cycle (dark from 08:00–20:00) and each performed behavioral tasks at the same time of day, between 08:00 and 18:00. Rewards were 2–4 μl of water, delivered using solenoids (LHDA1233115H, The Lee Co). All behavioral tasks were performed in a dark (except for sessions with pupil recordings), sound-attenuated chamber, with white noise delivered between 2–60 kHz (Sweetwater Lynx L22 sound card, Rotel RB-930AX two-channel power amplifier, and Pettersson L60 Ultrasound Speaker), with mice resting in a 38.1 mm acrylic tube.

Behavioral tasks: dynamic foraging.

In the dynamic foraging task, we delivered one of two odors, selected pseudorandomly on each trial, for 0.5 s (Figure 1). The first odor (presented with 0.95 probability) was a “go cue,” after which mice made a leftward or rightward lick toward a custom-built “lick port.” The second odor (presented with 0.05 probability) was a “no-go cue.” Licks after this cue were neither rewarded nor punished. The lick port consisted of two polished 21 ga stainless steel tubes separated by 4 mm, individually mounted to solenoids (ROB-11015, Sparkfun). The unchosen tube was retracted using the solenoid upon contact of the tongue to the chosen tube, and returned to its initial position after 1.5 s. If a lick was emitted within 1.5 s of cue onset, reward was delivered probabilistically.

Rewards were baited, so that if an unchosen action would have been rewarded, the reward was delivered upon the next choice of that alternative (Sugrue et al., 2004; Lau and Glimcher, 2005; Tsutsui et al., 2016). We did not use a “changeover delay,” in which there would have been a cost of switching. Inter-trial intervals (ITIs) were drawn from an exponential distribution with a rate parameter of 0.3, with a maximum of 30 s. This resulted in a flat ITI hazard function, ensuring that expectation about the start of the next trial did not increase over time (Luce, 1986). The mean ITI was 7.5 s (range 2.4–30.0 s). Miss trials (go cue trials with no response) were rare (less than 1% of all trials). Mice performed on average 399 trials per session (range 124–864 trials).

We used two task variants, a two-probability task (622 sessions) and a multiple-probability task (79 sessions). In the two-probability task, one lick port was assigned a high reward probability and one was assigned a low reward probability. For 98% of those sessions, reward probabilities were chosen from the set {0.4,0.1} (236 sessions), {0.4,0.05} (326 sessions), {0.4,0.07}, (28 sessions), or {0.5,0.05} (17 sessions). For the remaining 2% of two-probability sessions, one high reward probability was selected from {0.2,0.3,0.4,0.5} and one low reward probability was selected from {0,0.03,0.08,0.1}. In the multiple-probability task, for 92% of sessions, reward probabilities were chosen from the set {0.4 / 0.05,0.3857 / 0.0643,0.3375/ 0.1125,0.225/ 0.225} (73% sessions). These probabilities were chosen so the ratios would equal {8:1,6:1,3:1,1:1}, to match parameters from a previous study (Sugrue et al., 2004). The remaining 9% of those sessions used reward probabilities from {0.35/0.05,0.3/0.1,0.27/0.13,0.2/0.2} (2 sessions) or {0.4 / 0.1,0.34 / 0.16,0.3/ 0.2,0.25/ 0.25} (4 sessions). For both task variants, within individual sessions, block lengths were drawn from a uniform distribution that spanned a maximum range of 40–100 trials, although the exact length spanned a smaller range for individual sessions. Rarely, block lengths were manually truncated or lengthened if a mouse demonstrated a strong side-specific bias.

To minimize spontaneous licking, we enforced a 1 s no-lick window prior to odor delivery. Licks within this window were punished with a new randomly-generated ITI, followed by a 2.5 s no-lick window. Implementing this window within the first week of behavior significantly reduced spontaneous licking throughout the entirety of behavioral experiments. Across 321 sessions with neural recordings, 281 implemented the no-lick window. Within the 40 sessions that did not, mice licked in only 2.72% of 1 s pre-cue windows. Across all neural recording sessions with or without a no-lick window, only 0.43% of 1 s pre-cue windows contained licks.

Mice were initially trained with reward probabilities chosen from the set {0,1} and reversed every 15–25 trials. The solenoid was not energized during the task during this period of training. After 1–1.5 weeks of training, the solenoid was engaged as described above and the animal was trained for another several days. We implemented shaping routines to lengthen blocks if animals switched inappropriately, and automatically deliver reward if they perseverated. These routines were discontinued before further training. Depending on the mouse, reward probabilities were then gradually changed from {0,1} to the final set over the course of another 2 weeks or abruptly changed in 1 session. We observed no difference between either training protocol. To counteract the formation of directional lick bias, we mounted the lick ports onto a micromanipulator (DT12XYZ, Thorlabs) and built a custom digital rotary encoder system to reliably locate the position of the lick ports in XYZ space with 5–10 μm resolution. If mice showed a directional bias on a particular day, the lick ports were moved 50–100 μm in the opposite direction for the following session. The lick ports were only moved before individual sessions. Using this strategy, we did not need to use other techniques to train out a bias (for example, “bias-breaking” sessions). To test for the presence of a bias, at the beginning of some sessions, we required the mouse to choose one lick port for two trials, the opposite lick port for two trials, and the original lick port for two trials before beginning the session. Only these choices were rewarded. If no bias was observed, the session began normally. If a strong bias was observed, the lick ports were moved and the session was restarted.

Behavioral tasks: two-alternative forced choice.

We delivered one of two odors, selected pseudorandomly, for 0.5 s, after which mice made a leftward or rightward lick toward a lick port. A leftward lick was deterministically rewarded following one odor, and a rightward lick was rewarded following the other odor. ITIs were drawn from an exponential distribution with a rate parameter of 0.3, with a maximum of 10 s. The mean ITI was 7.9 s (range 6.0–11.0 s). A 1 s no-lick window was enforced to minimize spontaneous licking. Data were collected from 3 mice, 2 sessions each.

Behavioral tasks: dynamic classical conditioning.

We delivered one of two odors, selected pseudorandomly, for 1 s, followed by a delay of 1 s. For one odor (“CS+”, delivered with probability 0.95), this delay was followed by probabilistic reward delivery. The other odor (“CS −”, delivered with probability 0.05) was followed by nothing. Mice were allowed a 3 s water consumption period, followed by vacuum suction to remove any unharvested reward, followed by the ITI. ITIs were drawn from an exponential distribution with a rate parameter of 0.3, with a maximum of 30 s. The mean time between trials was 9.4 s (range 6.0–31.4 s). For the CS+ odor, rewards were delivered with probability 0.8 or 0.2, and reversed every 20 to 70 trials (uniform distribution) without explicit cues. Reward was delivered at the start of every session with probability 0.8. Behavior was quantified as the time of first lick within the cue or delay window (2 s after cue onset). Data were collected from 4 mice.

Video recording.

We recorded eye and face video using two CMOS cameras (Thorlabs, DCC1545M). We used a 1.0x telecentric lens (Edmund Optics, 58–430) to record the eye video and mounted the camera on a micromanipulator (DT12XYZ, Thorlabs) to reliably position it for each mouse. We used a manual iris lens (Computar, M1614-MP2) to record the face. The eye and face were illuminated with a custom-built infrared LED array (Digi-Key, QED234-ND) and the experimental rig was illuminated with white LED light to place the pupil diameter in the middle of its dynamic range. We only recorded the right eye and right side of the face. From the eye, we extracted pupil diameter (mm), horizontal pupil angle (°), and vertical pupil angle(°)The center of the eye was defined as 0 ° in both the horizontal and vertical planes. Nasal and upward movements were defined as positive angles. We used an eye diameter of 3.1 mm to convert to angle (Shupe et al., 2006). From the face video, we used an open-source Matlab GUI to extract the mean absolute motion energy (mean difference in absolute intensity between two consecutive frames) from regions of interest (ROI) encompassing the nose, whiskers, and jaw, and also extracted the first 10 dimensions of the singular value decomposition (SVD) of the whole frame (Stringer et al., 2019; https://github.com/MouseLand/FaceMap).

We used two regression models to account for behavioral and neuronal data using movements extracted from videos. In the first, which we call “movement model 1,” we used the pupil diameter, horizontal gaze angle, vertical gaze angle, nose motion, whisker motion, and jaw motion as regressors. In the second, which we call “movement model 2,” we used pupil diameter, horizontal gaze angle, vertical gaze angle, and the first 10 SVD dimensions as regressors. When analyzing data across multiple sessions, we z-scored movement variables.

To analyze left/right choice-related pupil dynamics (for comparison with muscimol inactivation), we measured pupil diameter on behavioral sessions without manipulation. Separately for left and right choices, we measured the pupil diameter in the 500 ms around its maximum and subtracted the baseline diameter in the 1 s preceding the trial. We report the difference between left and right choices for this metric. We were unable to record the pupil in one muscimol-injected mouse due to the presence of a pupil defect (coloboma) that resulted in a static pupil.

Pharmacological inactivation.

We inactivated mPFC reversibly by injecting muscimol, a GABA _A agonist. Muscimol hydrobromide (G019, Sigma-Aldrich) or muscimol powder (M1523, SigmaAldrich) was dissolved at 1 ng/nl in artificial cerebrospinal fluid (ACSF) and stored at 4° C. ACSF contained 119 mM NaCl, 2.5 mM KCl, 2.5 mM CaCl₂, 1.3 mM MgCl ₂ , 1 mM NaH ₂ PO₄, 11 mM glucose, and 26.2 mM NaHCO ₃. Muscimol was injected either prior to or during behavioral experiments. Vehicle injections consisted of ACSF only. For mPFC inactivation, we injected 100 nL of muscimol or vehicle into each hemisphere at a depth of 1 mm (relative to the brain surface) at a rate of 1 nl/s. If injected prior to behavior, we waited 10–20 min to allow the drug time to diffuse. In these experiments, we occasionally increased the response window from 1.5 s after the go cue to 2.5 or 3.5 s. For V1 inactivation, we bilaterally injected the same volume of muscimol at −3.5 mm posterior from bregma and 2.5 lateral, at a depth of 0.5 mm. To measure the spread of muscimol, we injected fluorescent muscimol (M23400, Sigma-Aldrich) into the mPFC of 3 mice and euthanized them after waiting 10 min.

Electrophysiology.

We recorded extracellularly (Digital Lynx 4SX, Neuralynx Inc., or Intan Technologies RHD2000 system with RHD2132 headstage) from multiple neurons simultaneously at 32 kHz using custom-built screw-driven microdrives with either 16 tetrodes (64 channels total) or 8 tetrodes coupled to a 200 μm fiber optic (32 channels total). All tetrodes were gold-plated to an impedance of 200–300 kΩ prior to implantation. Spikes were bandpass-filtered between 0.3–6 kHz and sorted online and offline using Spikesort 3D (Neuralynx Inc.) and custom software written in MATLAB. Individual channels were bandpass-filtered and inverted. Signals were median-filter subtracted (in the case of 64 channel recordings, this was done separately for each set of 32 channels).

Spikes were thresholded at 4σ_n where σ_n =median $(\left(\frac{|x|}{0.6745}\right)),$ where x is the bandpass-filtered signal (Quiroga et al., 2004). Waveform energy was used for initial clustering, followed by peak waveform amplitude if necessary to further split clusters. To measure isolation quality of individual units, we calculated the L-ratio (Schmitzer-Torbert et al., 2005) and fraction of interspike interval (ISI) violations within a 2 ms refractory period. All single units included in the dataset had an L-ratio less than 0.05 and fewer than 0.1% ISI violations. For both mPFC and ALM, we only included units that had a firing rate of greater than 0.1 spikes s ⁻¹ over the course of the recording session. Our classification of neurons was not critically dependent on either ISI or firing rate criteria (Figure S3G). In total, 3,073 mPFC neurons from 14 mice and 537 ALM neurons from 3 mice passed these criteria (mean of 241 neurons per mouse, range 87–649, mean of 11 neurons per session, range 1–59). For mPFC recordings, we typically recorded at microdrive-driven depths of 500 μm to 1,500 μm, relative to the brain surface. For ALM recordings, we recorded from the brain surface to microdrive-driven depths of 1,200 μm. We verified recording sites histologically with electrolytic lesions (15 s of 10 μA direct current across two wires of the same tetrode). We also functionally verified placement of ALM electrodes (at the end of data collection) by electrically microstimulating and observing jaw opening and contralateral tongue protrusions (Komiyama et al., 2010). We delivered pulses with 200 μs pulse width (cathode first, charge balanced) at 300 Hz and 70 μA. We recorded from right mPFC in 8 mice, bilateral mPFC in 4 mice, right ALM in 1 mouse, and simultaneously recorded from right mPFC and right ALM in 2 mice.

Viral injections.

To express Chronos in mPFC neurons projecting to dorsomedial striatum, we unilaterally pressure-injected 250 nl of AAVrg-Syn-Chronos-GFP (9×10 ¹² GC/ml) into the dorsomedial striatum of C57BL/6J mice at a rate of 1 nl/s (MMO-220A, Narishige). We injected at the following coordinates: 0.7 mm anterior of bregma, 1.2 mm lateral from the midline, and 2.8 mm (50 nl), 2.4 mm (100 nl), and 2.0 mm (100 nl) ventral to the brain surface. The injection pipette was left in place for 5 min between each injection. Five minutes after the last injection, the pipette was retracted 0.5 mm and left in place for 10 min before retracting fully. This significantly reduced release of the virus into primary/secondary motor cortex above dorsomedial striatum. AAVrg-Syn-Chronos-GFP was a gift from Edward Boyden (Addgene viral prep 59170-AAVrg; Klapoetke et al., 2014). The craniotomy was covered with silicone elastomer (Kwik-Cast, WPI) and dental cement. We quantified fluorescence of Chronos-GFP in mPFC in 4 mice. mPFC neurons were recorded in the hemisphere ipsilateral to the injection. For collision-testing, we implanted an optic fiber 2.0 mm ventral to the brain surface, above dorsomedial striatum.

To quantify the distribution of corticostriatal cell bodies, we injected AAVrg-pmSyn1-EBFP-Cre (5×10¹² GC/ml) into the dorsomedial striatum of 4 male B6.Cg-Gt(ROSA)26Sor ^{tm9(CAG−tdTomato)Hze} /J (also known as Ai9; Madisen et al., 2010) mice (The Jackson Laboratory, 007909). AAVrg-pmSyn1-EBFP-Cre (Madisen et al., 2015) was a gift from Hongkui Zeng (Addgene viral prep 51507-AAVrg). This resulted in a similar distribution of neurons as wild-type mice expressing virus chronically (Figures 7A, 7B, S7C, and S7D).

Inactivation of corticostriatal neurons.

To express hM4D(Gi) in corticostriatal neurons, we unilaterally pressure injected 250 nl of AAVrg-pmSyn1-EBFP-Cre (5×10¹² GC/ml) into the dorsomedial striatum of 6 male C57BL/6J mice. In 3 mice, we injected pAAV-hSyn-DIO-hM4D(Gi)mCherry into the mPFC (800 nl in each hemisphere across four injection sites). pAAV-hSyn-DIO-hM4D(Gi)-mCherry was a gift from Bryan Roth (Addgene viral prep 44362-AAV5). In 3 mice, we injected rAAV5-Ef1a-DIO-hChR2(H134R)-EFYP as a control. After training mice, we injected either 1.0 mg/kg clozapine-n-oxide dissolved in 0.5% DMSO/saline (NIMH Chemical Synthesis and Drug Supply Program) or an equivalent volume of vehicle (0.5% DMSO/saline alone) I.P. on alternating days in a pseudorandomized fashion (62 sessions).

Identification of corticostriatal neurons.

We used two techniques to optogenetically identify mPFC neurons projecting to the dorsomedial striatum: collision tests (Bishop et al., 1962; Fuller and Schlag, 1976; Li et al., 2015) and somatic tagging (Lima et al., 2009; Cohen et al., 2012). For collision tests (4 mice), at the end of daily recording sessions, we used Chronos excitation to observe stimulus-locked spikes by delivering 600 light pulses through an optic fiber implanted above the striatum using a diode-pumped solid-state laser (Laserglow), together with a shutter (Uniblitz). Stimulus parameters were 4 Hz, 2 ms pulses at 473 nm, and 60–80 mW. Identified neurons were reliably antidromically activated and did not show stimulus-locked spikes following spontaneous spikes (“collisions”). For somatic tagging (4 mice), at the end of daily recording sessions, we delivered 10 trains of light (10 pulses per train, 10 s between trains) at 10 Hz, 25 Hz, and 50 Hz, resulting in 300 total pulses. To limit the false positive rate of identification, we only included units that responded to light with a latency less than 3 ms (in response to 10 Hz pulses) and spiked in response to at least 80% of pulses at all frequencies. In total, we identified 20 corticostriatal neurons using collision tests and 15 corticostriatal neurons using somatic tagging. We combined all neurons into one identified dataset because there were no differences in either population (Figure S1L).

Data analysis.

All analyses were performed with MATLAB (Mathworks) and R (http://www.rproject.org/). All data are presented as mean ± SEM unless reported otherwise. All statistical tests were two-sided. For nonparametric tests, the Wilcoxon rank-sum test was used, unless data were paired, in which case the Wilcoxon signed-rank was used. For bootstrapped confidence intervals, we used 1,000 samples.

Data analysis: descriptive models of behavior.

To predict choice (c_r (t) =1 for a rightward choice and 0 for a leftward choice, and c_l (t) = 1−c_r(t)) as a function of reward and choice history, we calculated logistic regressions according to

$$\begin{array}{l}\log \left(\frac{P\left(c_r(t)\right)}{1-P\left(c_r(t)\right)}\right)=\sum _{i=1}^{15}{\beta }_i^R\left(R_r(t-i)-R_l(t-i)\right)\\ +\sum _{i=1}^{15}{\beta }_i^c\left(c_r(t-i)-c_l(t-i)\right)+{\beta }_0,\end{array}$$

and included mouse and session indicator variables, and a trial number variable. To predict z-scored response times, we fit the following linear regressions:

$$\begin{array}{l}\text{RT}(\text{t})=\sum _{i=1}^{15}{\beta }_i^R\left(R_r(t-i)+R_l(t-i)\right)\\ +\sum _{i=1}^{15}{\beta }_i^{RT}RT(t-i)+{\beta }_0,\end{array}$$

and included mouse and session indicator variables, and a trial number variable. Here, R (t)=1 if reward was delivered to that side on trial t and 0 if no reward was given. c (t) =1 if that action was emitted and 0 otherwise. Exponentials of the form $a{e}^{-{\beta }_{115}^R/\tau }$ were fit for the choice and response time models. We report fits using data from all mice combined (Figures 1E and 1F) and each mouse separately (Figure S1E).

To quantify choice bias in the dynamic foraging and two-alternative forced choice tasks, we defined $\text{Bias}=2\cdot |\frac{N_r}{N_r+N_l}-0.5|,$ where N_l and N_r are the total number of leftward and rightward choices, respectively. Bias =1 corresponds to exclusively left or right choices and Bias = 0 corresponds to an equal number of left and right choices.

Data analysis: generative model of behavior.

We developed a generative model of trial-to-trial behavior in the foraging task using Q-learning, a reinforcement-learning model that estimates the values of alternative actions, compares them, and generates choices (a random variable, c (t), leftward versus rightward, $c(t)\in \{l,r\}).$ In the model, each trial generated an action value for left ( Q_l ) and right (Q_r ) licks according to the following difference equations:

$$\begin{array}{l}{Q}_l(t+1)=\zeta Q_l(t)+\alpha \delta ,\\ Q_r(t+1)=\zeta Q_r(t),\\ ifc(t)=l,\text{where}\delta =R(t)-Q_l(t),\text{and}\\ Q_l(t+1)=\zeta Q_l(t),\\ Q_r(t+1)=\zeta Q_r(t)+\alpha \delta ,\end{array}$$

if c t(t) = r, where δ= R (t)−Q_r (t) . Learning and forgetting were implemented using the α and ζ parameters, respectively.

The Q-values were then fed into a softmax function (also known as a Boltzmann distribution; Daw et al., 2006) that generated choices, according to

$$\begin{array}{l}P(c(t)=r)=\frac{1}{1+e^{-\beta (Q_r(t)-Q_l(t)+b+\kappa a(t-1)}},\\ P(c(t)=l)=1-P(c(t)=r),\end{array}$$

where β is the so-called “inverse temperature” parameter that determines the balance of exploration versus exploitation given the relative action values, b is a bias term, and κ is a parameter to implement autocorrelation of the previous choice (a (t −1)= −1 for a leftward choice and 1 for a rightward choice). We used gradient descent to obtain maximum likelihood estimates of parameters. We used 10 randomly selected starting values for each parameter to avoid finding local minima.

To determine whether addition of each parameter improved the model without needlessly increasing model complexity, we compared the above model to ones in which we removed ζ, b, and κ. We then found the maximum likelihood estimates for each session and calculated the Bayesian information criteria. The above Q-learning model was the best model for the greatest number of mice (Figure S1F). The “base” model was one that excluded the b and κ terms.

In our formulation, forgetting decays action values to 0. To test whether action values decayed to a different baseline, we considered a model in which action values decayed to an arbitrary baseline. This model resulted in larger Bayesian information criteria than Q-learning. We also considered a number of other models, including the direct actor model (Dayan and Abbott, 2001), the stacked-probability model (Huh et al., 2009), and a “switch” model to test if animals switched when the reward rate dropped below a reference value. Each of these models included 8 variants, to fairly compare with the Q-learning model we selected. The Q-learning model outperformed these competing models. We argue against direct actor for a second reason. We found that response times were modulated by chosen value, in addition to total value (data not shown). This was independent of confounding variables such as | Q_r −Q _l | (which is related to decision confidence; Rolls et al., 2010), exploration, and switch trials. Since direct actor computes a relative-value-like decision variable directly, it is difficult to see how response times could be modulated by chosen value, which would require action-value-like representations.

Data analysis: relative-value and total-value persistent neurons.

We selected for relative-value and total-value persistently-firing neurons by calculating a Poisson generalized linear model which predicted spike counts in the 1 s pre-cue period as a function of relative value (Q_r −Q _l ), total value (Q_r +Q _l), and choice on the next trial (c (t+1)). We also considered a number of other models in which we used lagged choice regressors, autoregressive terms, and interactions between reward and choice, for both Poisson regressions of spike counts and linear regressions of z-scored firing rates. These other models did not qualitatively alter our findings. We used a P-value criterion of 0.05 to select for neurons. Neurons for which generalized linear models did not converge were discarded. This procedure removed 9 mPFC neurons and 0 ALM neurons. “Pure” relative-value neurons were those significant for relative value and non-significant for total value and future choice. “Pure” total-value neurons were defined similarly. Our selection of relative-value and total-value neurons was not sensitive to the P-value criterion, nor was it sensitive to the pre-cue window (Figure S4). The first 10 trials of each session were excluded from analysis to exclude effects of session initiation. These pure populations were used to calculate tuning curves in Figures 3 and 4. To generate tuning curves for corticostriatal neurons (Figures 7 and S7), due to smaller sample size, we regressed out total-value and future-choice signals to estimate relative-value tuning. Likewise, we regressed out relative-value and future-choice signals to estimate total-value tuning. To quantify persistence of relative- and total-value neurons (Figure 5), we included all neurons with significant regressors for each decision variable. Analyzing only pure relative- and total-value neurons yielded equivalent results (Figures S5E and S5F). To estimate firing rates, we convolved spikes with a causal half-Gaussian filter (SD, 250 ms). To analyze neurons independent of tuning, we transformed relative-value neurons with decreasing firing rates as Q_r −Q _l increased by multiplying their z-score firing rates by −1, and combined them with the neurons with increasing firing rates as Q_r −Q _l increased. Likewise, we multiplied z-score firing rates of total-value neurons with decreasing firing rates as Q_r +Q _l increased by −1 and combined them with the other total-value neurons.

Notably, we did not obtain similarly quantitative evidence for the presence of action-value (Q_-, Q_r ) coding neurons. Using established criteria (Seo and Lee, 2007; Ito and Doya, 2009; Kim et al., 2009; Cai et al., 2011) for defining relative-value, total-value, and action-value neurons, we found that relative- and total-value neurons were modulated by actions and outcomes in a manner consistent with model predictions. Action-value neurons, however, were both qualitatively and quantitatively inconsistent with model predictions, across a wide range of parameters. We also used another approach which has been advocated to minimize bias in selecting for action-value neurons (Wang et al., 2013). Again, relative- and total-value neurons were predictably modulated by actions and outcomes, but putative action-value neurons were not.

To determine whether neurons representing relative and total value may have arisen due to temporal correlations in neuronal data, we adapted a recently-proposed statistical method (Elber-Dorozko and Loewenstein, 2018). Briefly, this method identifies neurons that are more correlated with decision variables estimated from that session than from other sessions. For each neuron, we generated a z-value distribution by regressing spike counts onto estimated relative and total values for all sessions 300 trials or longer (sessions shorter than 300 trials were excluded; sessions longer than 300 trials were truncated). A regressor was considered significant if its z-value fell outside of the 5% significance boundary of this distribution. Using this method, we identified 221 of 2318 neurons significant for relative value (exact binomial test, 9.5%, P < 0.0001, where the percentage expected by chance is 5%) and 557 out of 2,318 significant for total value (exact binomial test, 24.0%, P < 0.0001). This is an exceedingly strict test and should be interpreted as a lower bound on the estimate of neurons correlated with decision variables, rather than a true estimate.

Analysis of single-neuron stability.

To rigorously test whether individual neurons persistently encoded relative and/or total value across long periods of time, we used a train/test encoding analysis. For individual neurons, we took spike counts in non-overlapping 1 s bins, starting at the cue (t = 0 s) and extending to 15 s after the cue, and fit Poisson generalized linear models to predict spike count as a function of relative value or total value. We then fixed this regression fit and calculated the root-mean-square error (RMSE) between predicted and actual spike counts at all other time points. We then repeated this procedure for all relative-value (1,548) and total-value (1,880) neurons. With this analysis, if individual neurons tile across time, encoding of relative and total value should only be significant near the diagonal (i.e., training time points) but decay rapidly off the diagonal. If, however, individual neuron firing rates are stable, then encoding should be significant for long periods of time. This appears as significant encoding off the diagonal. To obtain a noise distribution, we shuffled spike counts 10 times. RMSE values greater than the 99.9^th percentile and bins with fewer than 20 observations were discarded. Using the sign-rank test, a time bin was significant if the P-value was 0.05 less than $\frac{0.05}{{15}^2}$ (Bonferroni corrected).

Population analysis.

For each neuron, we performed a median split of relative value and generated two smoothed 15 s-long peri-stimulus time histograms (PSTHs, convolved with a causal half-Gaussian filter of SD 250 ms). We repeated this for all 3,073 neurons. We then performed a principal component analysis using only the 1 s pre-cue activity and projected the original PSTHs onto the first two principal components (accounting for 81% of the variance). We repeated this separately for total value (with the first two principal components accounting for 82% of the variance.)

Histology.

After recording, which lasted on average 42 d (range 16–61 d), mice were euthanized with an overdose of ketamine (100 mg/kg), exsanguinated with saline, perfused with 4% paraformaldehyde, and brains were cut in 100 μm-thick coronal sections. To localize the laminar distribution of corticostriatal neurons labeled with AAVretro injections into dorsomedial striatum in Ai9 mice, we acquired confocal images of mPFC (Zeiss LSM 800, ZEN acquisition software) at 10x and calculated distances from somata to the pial surface of the medial wall of cortex using Imaris software. We acquired epifluorescence images of mPFC (Zeiss Axio Zoom.V16) to quantify spread of fluorescent muscimol and to quantify the laminar distribution of corticostriatal cells labeled by AAVretro-Chronos-GFP injections into dorsomedial striatum. We included sections from 2.3–2.7 mm anterior to bregma. We used Fiji for image analysis (Schindelin et al., 2012).

Highlights.

• Medial prefrontal cortex (mPFC) persistently encodes value-based decision variables

• Relative value signals are stable and total value signals decay

• Persistent decision variables are weakly represented in premotor cortex

• mPFC projections to dorsomedial striatum persistently represent decision variables