Identifying Autism Spectrum Disorder with Multi-Site fMRI via Low-Rank Domain Adaptation

Abstract

Autism spectrum disorder (ASD) is a neurodevelopmental disorder that is characterized by a wide range of symptoms. Identifying biomarkers for accurate diagnosis is crucial for early intervention of ASD. While multi-site data increase sample size and statistical power, they suffer from inter-site heterogeneity. To address this issue, we propose a multi-site adaption framework via low-rank representation decomposition (maLRR) for ASD identification based on functional MRI (fMRI). The main idea is to determine a common low-rank representation for data from the multiple sites, aiming to reduce differences in data distributions. Treating one site as a target domain and the remaining sites as source domains, data from these domains are transformed (i.e., adapted) to a common space using low-rank representation. To reduce data heterogeneity between the target and source domains, data from the source domains are linearly represented in the common space by those from the target domain. We evaluated the proposed method on both synthetic and real multi-site fMRI data for ASD identification. The results suggest that our method yields superior performance over several state-of-the-art domain adaptation methods.

I. Introduction

AUTISM spectrum disorder (ASD) is one of the most common and heritable neurodevelopmental disorders, resulting in deficits in social interaction and social communication as well as restricted repetitive patterns of behavior, interests, and activities [1]. As reported by the Centers for Disease Control and Prevention (CDC), one in 68 American children is affected by a certain form of ASD [2]. The number of affected children has increased by 78% compared to a decade ago. The increasing prevalence of ASD poses a severe burden to the society and affected families. Early diagnosis and intervention are critical for improving the quality of life of ASD individuals [3]. Neuroimaging disease diagnosis has been shown to be effective in increasing our understanding of the underlying pathologic mechanisms of brain diseases [4]–[8] and has been used for early identification of ASD [9].

Resting-state functional magnetic resonance imaging (rs-fMRI) is one of the most extensively used imaging modalities for ASD identification [10]–[14]. Although machine learning has been shown useful for ASD identification based on rs-fMRI, most techniques typically assume that multi-site data are drawn from the same distribution [15], [16]. That is, existing studies for ASD identification often ignore the problem of data heterogeneity (e.g., different image contrasts, resolutions and noise levels) caused by inter-site variation in scanners or protocols among different sites [17], [18], thus cannot well handle multi-site heterogeneous data.

Existing efforts on brain disease diagnosis using multi-site heterogeneous data [19]–[23] roughly fall into two categories. The first category is single-site learning [15], [16], where a model is learned independently for each site or based on a pooled dataset from multiple sites. These methods ignore the problem of data heterogeneity among different cites. The second category is multi-site learning [19], [24], [25], aiming at reducing the negative influences of heterogeneous data. In this category, multi-site disease identification is usually formulated as a domain adaptation problem, by first training models based on a source data distribution (i.e., source domain) and then testing the learned model on a different but related target data distribution (i.e., target domain). According to whether or not the label information of the data in the target domain is available, domain adaptation can be categorized into two kinds: semi-supervised and unsupervised. In semi-supervised domain adaptation, there are usually limited labeled data in the target domain, whereas in unsupervised domain adaptation there are entirely unlabeled data in the target domain.

As a typical semi-supervised multi-site learning approach, classifier-based domain adaptation [26], [27] first learns the classifiers based on source domains, and then adjusts the parameters of trained classifiers according to the target domain. This method typically requires the source and a small portion of target data to be labeled. However, it is often difficult or expensive to obtain completely accurate and reliable labels for samples in both source and target domains, thus limiting the real-world applications of classifier-based adaptation methods. Recently, unsupervised Low-rank representation (LRR) [28], [29] has been proposed for domain adaptation. The source data are transformed via LRR to the target domain for tasks in the latter. In contrast to classifier-based methods [26], [27], LRR-based methods attempt to simultaneously adapt to both source and target domains, without using any label information for the target domain. However, existing LRR-based data adaptation methods are typically designed for a single source domain and not multiple source domains.

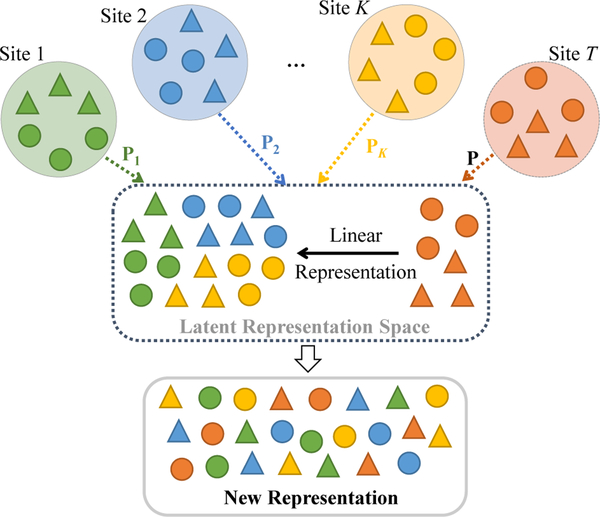
In this paper, we propose a general unsupervised domain adaptation framework for multi-site ASD identification, called multi-site adaptation based on low-rank representation (maLRR), which is designed to handle the situations with no labeled data available at the target domain. An overview of the method is shown in Fig. 1. Here, one site under analysis is treated as the target domain, and the remaining sites are treated as source domains. The aim is to learn a linear transformation to map the target and source domains to a common space such that each datum in the source domain can be linearly represented by samples from the target domain.

Fig. 1.

Illustration of the proposed method with K source domains and a target domain. Each source domain X_Si and the target domain X_T include samples from two categories (marked as triangles and circles). The first strategy of the proposed method is to transform each source domain and target domain into a latent representation domain via the specific projection P_i and the common projection P (with P_i = P + E_Pi, E_Pi is the sparse error term), respectively. Based on the transformed target domain data PX_T, the second strategy is to linearly represent each sample from each source domain using all samples from the target domain in the latent space (e.g., P_iX_Si = PX_TZ_Si + E_Si). Dotted arrows represent the first strategy, while the solid arrow represents the second strategy.

As shown in Fig. 1, we employ two strategies in our proposed method to adapt source data and target data, including 1) transforming data from both the target and source domains into a common latent space, and 2) linearly representing each sample from the source domains using all samples from the target domain in this latent space. Specifically, we first transfer samples from each source domain into a common latent space using a specific transformation matrix (e.g., P_i). Also, we would like to preserve the unique data structure from different sites. To this end, we disassemble the transformation matrix (i.e., P_i) of each source domain into a shared transformation matrix P and a site-specific matrix E_Pi by low-rank matrix decomposition. To reduce the difference between source domains and target domain, we also transform samples in the target domain into the common latent space via the shared transformation matrix P. Furthermore, in the common latent space, we linearly represent each transformed sample from source domains using samples from the target domain in an unsupervised manner, to further suppress the heterogeneity between target and source domains. In this way, we can generate new representations for samples from both the original target domain and multiple source domains in this common latent space. Finally, we construct a disease classification model using samples (with the new representation) from the source domains and their corresponding class labels as training data, and apply this disease classification model to samples (with the new representation) from the target domain to perform ASD identification. Notations used throughout this paper are defined in Table I.

TABLE I.

Notations and descriptions

Notation	Definition
XT	Target domain data.
XSi	The i-th source domain data.
ESi	The i-th sparse error matrix of data representation.
EPi	The i-th sparse error matrix of transformation matrix.
Zi	The i-th low-rank representation matrix.
Pi	The i-th specific transformation matrix.
P	The common transformation matrix.
d	The feature dimension.
nSi	The number of samples in the i-th source domain.
nT	The number of samples in the target domain.

It is worth noting that maLRR is an unsupervised domain adaptation approach, where no label information is required in the low-rank representation procedure. To the best of our knowledge, there is currently limited work to apply LRR-based domain adaptation method to ASD identification using multi-site fMRI data. That is, we provide a practical solution to perform data adaptation for multiple (> 2) imaging sites to build reliable ASD diagnosis systems. To evaluate the efficacy of our proposed model, we conduct experiments on both synthetic data and real multi-site ASD datasets with fMRI. The experiments demonstrate that our maLRR method can effectively improve the classification performances for automated ASD diagnosis. The preliminary work of this method was reported on MICCAI [30]. In this journal version, we 1) evaluate the proposed method on new synthetic data, 2) describe the optimization algorithm in detail and release the code, 3) employ an additional classifier for disease identification, and 4) study the influence of several important parameters on the performance of our method.

The remainder of this paper is organized as follows. In Section II, we review related work about low-rank representation, and domain adaptation in the field of computer-aided brain disease diagnosis. We present our proposed method as well as the alternating optimization algorithm in Section III. Experimental results and discussion are presented in Section IV and V, respectively. Finally, we conclude this paper in Section VI.

II. Related Works

Domain adaptation has attracted a lot of attention in the field of disease analysis recently. It arises when we need to leverage a relatively large amount of labeled data from source domains to train a classifier for unlabeled data drawn from a target domain. Generally, the source domain and target domain share the same task but follow different distributions. To reduce the distribution differences and achieve high performance, many research groups have devoted their efforts to this problem. For example, Moradi et al. [23] proposed a partial least squares regression based domain adaptation method to maximize the consistency of ASD imaging data across different sites. Heinsfeld et al. [17] developed an unsupervised denoising autoen-coder network (with two layers) for multi-site ASD identification, where the data distribution difference between different domains is reduced via the learned new representation. To improve the ability to segment MR brain scans of patients with variational imaging protocols, Kamnitsas et al. [21] developed a domain adaptation method based on adversarial neural networks to learn the invariant representation to reduce the data distribution difference between two domains. These studies have demonstrated the advantage of using domain adaptation for promoting the learning performance of medical image analysis. However, these studies usually tend to learn invariant features among multiple domains, thus ignoring the intrinsic structure characteristics of different data sites.

Low-rank representation (LRR) was proposed by Liu et al. [31] to recover the low-rank subspace structure of original data, which can better capture the global structure of data by suppressing the negative influences of outliers and noise corruption. Currently, LRR has been successfully applied to many neuroimaging-based disease analysis studies. For example, Schuler et al. [32] proposed to identify phenotypes associated with ASD via a generalized low-rank model to reduce the variation of data in two sources. Zhu et al. [33] designed a learning-based model with a sparsity-induced constraint and a low-rank constraint for ASD diagnosis, and obtained a significantly improved diagnostic accuracy. Adeli et al. [34] developed a feature selection framework to simultaneously de-noise features and samples for Parkinson’s disease diagnosis, where a low-rank matrix recovery strategy was employed in the model learning procedure to separate the noises from data. Vounou et al. [35] proposed to identify potential genetic data associated with Alzheimer’s disease via a two-step approach, where penalized linear discriminant analysis and sparse reduced-rank regression were used in turn. These studies have shown that low-rank representation-based approaches are effectively boosting the learning performance of neuroimaging-based brain disease diagnosis, by uncovering the inherent structure information of data.

Besides, Chang et al. [28] developed a robust domain adaptation model via low-rank reconstruction (RDALR) for latent domain leaning. Specifically, the RDALR method transformed multiple source domains to the target domain, and represented samples in each source domain using those in the target domain. That is, the RDALR method treated the target domain as the latent space, which is different from our proposed method that learns a common latent space for both the target and multiple source domains to remove noisy information. Ding et al. [36] proposed a deep low-rank coding (DLRC) method to incorporate the feature learning and knowledge transfer in a unified deep framework. To ensure the learned features to be more discriminative, the label information of source domain is always assumed to be accessible. Tang et al. [37] proposed a structure-constrained low-rank representation (SC-LRR), which provides a practical way for disjoint subspace segmentation. It’s worth noting that both the DLRC and SC-LRR methods preform semi-supervised learning for knowledge transfer between the target and source domains, while our maLRR method is designed in an unsupervised learning manner, which is suitable for more general scenarios. Ding et al. [38] designed a latent low-rank transfer subspace learning method (L²TSL) to guide the knowledge transfer between and within two domains for the missing modality problem. Note that the L²TSL method is designed for problems with only one single source domain, while our maLRR method can deal with problems with multiple source domains.

III. Proposed Method

A. Notation

Let ${\mathbf{X}}_T\in {ℝ}^{d\times n_T}\text{and}{\mathbf{X}}_{S_i}\in {ℝ}^{d\times n_{S_i}}$ be the target and i-th source domain data, respectively, where d is the feature dimension of data in both domains. Denote K as the number of source domains. Note that n_T and n_Si are the number of samples in target and i-th source domain, respectively. Denote $\mathbf{P}\in {ℝ}^{d\times d}\text{and}{\mathbf{P}}_i\in {ℝ}^{d\times d}$ as the common and specific transformation matrix for the target and each source domain. The sparse error matrix of data representation and transformation matrix are represented by ${\mathbf{E}}_{S_i}\in {ℝ}^{d\times n_{S_i}}\text{and}{\mathbf{E}}_{P_i}\in {ℝ}^{d\times d},$ respectively. Let ${\mathbf{Z}}_i\in {ℝ}^{n_T\times n_{S_i}}$ denote the i-th low-rank representation matrix. Denote σ_i(Z) as the i-th singular value of Z, and let $\Vert \mathbf{Z}{\Vert }_{*}={\sum }_i{\sigma }_i(\mathbf{Z})\text{and}\Vert \mathbf{Z}{\Vert }_1={\sum }_i{\sum }_j\left|{\mathbf{Z}}_{i,j}\right|$ represent the nuclear norm and ℓ₁ norm of matrix Z, respectively. Suppose all domains contain l classes, while samples in the target domain are unlabeled and those in each source domain are well labeled. To make the proposed model suitable for more general scenarios, in this work, we do not use any label information for samples in the target and source domains during the low-rank representation learning process.

B. Problem Formulation

In this paper, we focus on the problem of multi-site ASD identification by using low-rank representation (LRR) based domain adaptation. In the following, we first describe the general LRR-based framework for single source domain adaptation, where only one source domain needs to be adapted to the target domain. Then, we extend it to the problem of multiple source domain adaptation, by simultaneously adapting multiple source domains to the target domain.

In the problem with a single source domain X_S, our goal is to find a transformation matrix P to map the source domain into the target domain X_T, which can be described as

$$\mathbf{P}{\mathbf{X}}_S={\mathbf{X}}_T\mathbf{Z}+\mathbf{E}$$ (1)

where PX_S denotes the transformed matrix represented by the target domain, Z is the representation coefficient matrix, and E is the error matrix. In this way, each datum in the source domain can be linearly represented by samples in the target domain, which may reduce the data distribution difference between source and target domains [28]. However, the above formula is sensitive to sample-specific corruptions (e.g., different image contrast, resolution and noise level) of the source domain. To improve the robustness of models to undesirable noise data, the objective function of our LRR-based single source domain adaptation is formulated as follows:

$$\begin{gathered} \underset{\mathbf{P},\mathbf{Z},\mathbf{E}}{\min }\mathrm{rank}(\mathbf{Z})+\alpha \Vert \mathbf{E}{\Vert }_1 \\ \text{s.t.}\mathbf{P}{\mathbf{X}}_S={\mathbf{X}}_T\mathbf{Z}+\mathbf{E} \end{gathered}$$ (2)

where rank(·) is the rank of a matrix, ‖·‖₁ is the ℓ₁ norm, and α is a parameter to balance the contributions of two terms in Eq. (2).

For problems with multiple source domains, we aim to simultaneously adapt multiple source domains to the target domain to reduce the difference among multiple domains. Although the data distribution of each source domain may be different from the target domain, the underlying pathology of ASD patients from multiple imaging sites is similar. Intuitively, it is reasonable to assume that data drawn from multiple domains/sites share an intrinsic latent data structure. Therefore, we propose to map the source and target data into a common latent domain via the LRR-based adaptation method, which can be defined as follows:

$$\begin{gathered} \underset{{\mathbf{P}}_i,{\mathbf{Z}}_i,{\mathbf{E}}_{S_i}}{\min }\sum _{i=1}^K(\mathrm{rank}({\mathbf{Z}}_i)+\alpha {\Vert {\mathbf{E}}_{S_i}\Vert }_1) \\ \text{s.t.}{\mathbf{P}}_i{\mathbf{X}}_{S_i}={\mathbf{X}}_T{\mathbf{Z}}_i+{\mathbf{E}}_{S_i},i=1,\cdots ,K \end{gathered}$$ (3)

where S_i is i-th source domain. The rank minimization is a well-known NP-hard problem. Fortunately, the relaxation of rank minimization is well surrogated by the nuclear norm [31]. By minimizing the nuclear norm (rather than rank) of Z, we can rewrite Eq. (3) as the following equivalent problem:

$$\begin{gathered} \underset{{\mathbf{P}}_i,{\mathbf{Z}}_i,{\mathbf{E}}_{S_i}}{\min }\sum _{i=1}^K({\Vert {\mathbf{Z}}_i\Vert }_{*}+\alpha {\Vert {\mathbf{E}}_{S_i}\Vert }_1) \\ \text{s.t.}{\mathbf{P}}_i{\mathbf{X}}_{S_i}={\mathbf{X}}_T{\mathbf{Z}}_i+{\mathbf{E}}_{S_i},i=1,\cdots ,K \end{gathered}$$ (4)

where $\Vert \cdot {\Vert }_{*}$ is the nuclear norm of a matrix, equal to the sum of singular values of the matrix.

Besides reducing the data distribution difference among multiple site data via Eq. (4), we would like to further discover the intrinsic data structure of data acquired from different sites. Accordingly, we propose to disassemble the transformation matrix P_i of each source domain into a specific (i.e., E_Si) and common (i.e., P) term by low-rank matrix decomposition. The objective function of our proposed representation-based multi-site adaptation framework can be formulated as follows:

$$\begin{gathered} \underset{\mathbf{P},{\mathbf{P}}_i,{\mathbf{Z}}_i,}{\min }\Vert \mathbf{P}{\Vert }_{*}+\sum _{i=1}^K({\Vert {\mathbf{Z}}_i\Vert }_{*}+\alpha {\Vert {\mathbf{E}}_{S_i}\Vert }_1+\beta {\Vert {\mathbf{E}}_{P_i}\Vert }_1) \\ {\mathbf{E}}_{S_i},{\mathbf{E}}_{P_i} \\ \text{s.t.}{\mathbf{P}}_i{\mathbf{X}}_{S_i}=\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i+{\mathbf{E}}_{S_i}, \\ {\mathbf{P}}_i=\mathbf{P}+{\mathbf{E}}_{P_i},i=1,\cdots ,K \\ \mathbf{P}{\mathbf{P}}^T=\mathbf{I} \end{gathered}$$ (5)

where β is the balance parameter, and $\mathbf{I}\in {ℝ}^{d\times d}$ is the identity matrix. The orthogonal constraint PP^T = I is imposed to obtain the non-trivial solutions of the common transformation matrix P. Based on Eq. (5), we can transform data from multiple sites to the common domain in which the data of source domains can be linearly represented by the transformed target data. Once the above low-rank based preprocessing is complete, the new representation PX_T and PX_TZ_i for target and each source domain can be obtained.

C. Alternating Optimization Algorithm

The optimization of Eq. (5) is convex and can be solved by iteratively updating each variable separately [36]–[38]. Here, we employ the Augmented Lagrange Multiplier (ALM) algorithm [39] to solve the problem in Eq. (5). Specifically, by introducing two relaxation variables J and F_i, we can reformulate Eq. (5) as

$$\begin{gathered} \underset{\mathbf{J},\mathbf{P},{\mathbf{P}}_i,{\mathbf{Z}}_i,}{\min }\Vert \mathbf{J}{\Vert }_{*}+\sum _{i=1}^K\left({\Vert {\mathbf{F}}_i\Vert }_{*}+\alpha {\Vert {\mathbf{E}}_{S_i}\Vert }_1+\beta {\Vert {\mathbf{E}}_{P_i}\Vert }_1\right) \\ {\mathbf{E}}_{S_i},{\mathbf{E}}_{P_i}{\mathbf{F}}_i \\ \text{s.t.}{\mathbf{P}}_i{\mathbf{X}}_{S_i}=\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i+{\mathbf{E}}_{S_i}, \\ {\mathbf{P}}_i=\mathbf{P}+{\mathbf{E}}_{P_i},i=1,\cdots ,K \\ \mathbf{P}=\mathbf{J},{\mathbf{Z}}_i={\mathbf{F}}_i,\mathbf{P}{\mathbf{P}}^T=\mathbf{I} \end{gathered}$$ (6)

Then, we solve Eq. (6) by minimizing the following Augmented Lagrange Multiplier (ALM) [39] function $\mathcal{L}:$

$$\begin{gathered} \mathcal{L}=\Vert \mathbf{J}{\Vert }_{*}+\sum _{i=1}^K({\Vert {\mathbf{F}}_i\Vert }_{*}+\alpha {\Vert {\mathbf{E}}_{S_i}\Vert }_1+\beta {\Vert {\mathbf{E}}_{P_i}\Vert }_1 \\ +\langle {\mathbf{Y}}_{1,i},{\mathbf{Z}}_i-{\mathbf{F}}_i\rangle +\langle {\mathbf{Y}}_{2,i},{\mathbf{P}}_i{\mathbf{X}}_{S_i}-\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i-{\mathbf{E}}_{S_i}\rangle \\ +\langle {\mathbf{Y}}_{3,i},{\mathbf{P}}_i-\mathbf{P}-{\mathbf{E}}_{P_i}\rangle +\langle {\mathbf{Y}}_4,\mathbf{P}-\mathbf{J}\rangle \\ +\frac{\mu }{2}({\Vert {\mathbf{Z}}_i-{\mathbf{F}}_i\Vert }_F^2+{\Vert {\mathbf{P}}_i{\mathbf{X}}_{S_i}-\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i-{\mathbf{E}}_{S_i}\Vert }_F^2 \\ +{\Vert {\mathbf{P}}_i-\mathbf{P}-{\mathbf{E}}_{P_i}\Vert }_F^2+\Vert \mathbf{P}-\mathbf{J}{\Vert }_F^2\left)\right) \end{gathered}$$ (7)

where Y_1,i, Y_2,i, Y_3,i and Y₄ are Lagrange multipliers and μ > 0 is a penalty parameter. $\Vert \cdot {\Vert }_F^2$ denotes the matrix Frobenius norm, and $\langle \cdot ,\cdot \rangle$ is the inner product of matrices, i.e., $\langle \mathbf{A},\mathbf{B}\rangle =\mathit{tr}\left({\mathbf{A}}^T\mathbf{B}\right).$ Since there are five variables P, P_i, Z_i, E_Si, and E_Pi in Eq. (7), it is impossible to jointly update them using conventional ALM. Fortunately, we can optimize each variable in an iterative manner by fixing the others. For clarity, we denote the to-be-optimized variables in the t-th iteration as ${\mathbf{P}}^t,{\mathbf{P}}_i^t,{\mathbf{Z}}_i^t,{\mathbf{E}}_{S_i}^t,\text{and}{\mathbf{E}}_{P_i}^t.$ At the iteration t + 1(t ≥ 0), we can achieve the sub-solution using the following alternative optimization strategy:

• Update J: With others variables in Eq. (7) fixed, we can obtain the optimal J by solving the following objective function

  $${\mathbf{J}}^{t+1}=\underset{\mathbf{J}}{\mathrm{argmin}}\frac{1}{\mu }\Vert \mathbf{J}{\Vert }_{*}+\frac{1}{2}{\Vert \mathbf{J}-({\mathbf{P}}^t+{\mathbf{Y}}_{4,i}/\mu )\Vert }_F^2$$ (8)
• Update F_i: F_i can be updated by solving optimization problem (9)

  $${\mathbf{F}}_i^{t+1}=\underset{{\mathbf{F}}_i}{\mathrm{argmin}}\frac{1}{\mu }{\Vert {\mathbf{F}}_i\Vert }_{*}+\frac{1}{2}{\Vert {\mathbf{F}}_i-({\mathbf{Z}}_i^t+{\mathbf{Y}}_{1,i}/\mu )\Vert }_F^2$$ (9)
• Update E_Si : By fixing the remaining variables, We can update E_Si by solving the following optimization problem

  $$\begin{gathered} {\mathbf{E}}_{S_i}^{t+1}=\underset{{\mathbf{E}}_{S_i}}{\mathrm{argmin}}\frac{\alpha }{\mu }{\Vert {\mathbf{E}}_{S_i}\Vert }_1 \\ +\frac{1}{2}{\Vert {\mathbf{E}}_{S_i}-({\mathbf{P}}_i^t{\mathbf{X}}_{S_i}-{\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i^t+{\mathbf{Y}}_{2,i}/\mu )\Vert }_F^2 \end{gathered}$$ (10)
• Update E_Pi: With the other variables fixed, we can obtainthe optimal E_Pi by solving the following problem (11)

  $$\begin{gathered} {\mathbf{E}}_{P_i}^{t+1}=\underset{{\mathbf{E}}_{P_i}}{\mathrm{argmin}}\frac{\beta }{\mu }{\Vert {\mathbf{E}}_{P_i}\Vert }_1 \\ +\frac{1}{2}{\Vert {\mathbf{E}}_{P_i}-({\mathbf{P}}_i^t-{\mathbf{P}}^t+{\mathbf{Y}}_{3,i}/\mu )\Vert }_F^2 \end{gathered}$$ (11)
• Update Z_i: Z_i can be updated by solving the following optimization problem (12)

  $$\begin{gathered} {\mathbf{Z}}_i^{t+1}=\underset{{\mathbf{Z}}_i}{\mathrm{argmin}}\frac{\mu }{2}{\Vert {\mathbf{Z}}_i-{\mathbf{F}}_i^t\Vert }_F^2+\frac{\mu }{2}\Vert {\mathbf{P}}_i^t{\mathbf{X}}_{S_i} \\ -{\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i-{\mathbf{E}}_{S_i}^t{\Vert }_F^2+\langle {\mathbf{Y}}_{1,i},{\mathbf{Z}}_i-{\mathbf{F}}_i^t\rangle \\ +\langle {\mathbf{Y}}_{2,i},{\mathbf{P}}_i^t{\mathbf{X}}_{S_i}-{\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i-{\mathbf{E}}_{S_i}^t\rangle \end{gathered}$$ (12)
  The closed form solution of Eq. (12) is

  $$\begin{gathered} {\mathbf{Z}}_i^{t+1}={[{\mathbf{X}}_T^T{({\mathbf{P}}_i^t)}^T{\mathbf{P}}_i^t{\mathbf{X}}_T+\mathbf{I}]}^{-1}[{\mathbf{X}}_T^T{({\mathbf{P}}_i^t)}^T{\mathbf{G}}_1 \\ +{\mathbf{F}}_i^t-{\mathbf{Y}}_{1,i}/\mu ] \end{gathered}$$ (13)

  where ${\mathbf{G}}_1={\mathbf{P}}_i^t{\mathbf{X}}_{S_i}-{\mathbf{E}}_{S_i}^t+{\mathbf{Y}}_{2,i}/\mu .$
• Update P_i: By fixing the other variables, we can update P_i by solving the following optimization problem

  $$\begin{gathered} {\mathbf{P}}_i^{t+1}=\underset{{\mathbf{P}}_i}{\mathrm{argmin}}\frac{\mu }{2}{\Vert {\mathbf{P}}_i{\mathbf{X}}_{S_i}-{\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i^t-{\mathbf{E}}_{S_i}^t\Vert }_F^2 \\ +\frac{\mu }{2}{\Vert {\mathbf{P}}_i-{\mathbf{P}}^t-{\mathbf{E}}_{P_i}^t\Vert }_F^2+\langle {\mathbf{Y}}_{2,i},{\mathbf{P}}_i{\mathbf{X}}_{S_i}-{\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i^t \\ -{\mathbf{E}}_{S_i}^t\rangle +\langle {\mathbf{Y}}_{3,i},{\mathbf{P}}_i-{\mathbf{P}}^t-{\mathbf{E}}_{P_i}^t\rangle \end{gathered}$$ (14)
  The closed form solution of Eq. (14) is

  $${\mathbf{P}}_i^{t+1}=({\mathbf{G}}_2{\mathbf{X}}_{S_i}^T+{\mathbf{P}}^t+{\mathbf{E}}_{P_i}^t-{\mathbf{Y}}_{3,i}/\mu ){({\mathbf{X}}_{S_i}{\mathbf{X}}_{S_i}^T+\mathbf{I})}^{-1}$$ (15)

  where ${\mathbf{G}}_2={\mathbf{P}}^t{\mathbf{X}}_T{\mathbf{Z}}_i^t+{\mathbf{E}}_{S_i}^t-{\mathbf{Y}}_{2,i}/\mu .$
• Update P: Similarly, we can update P by solving the following objective function

  $$\begin{gathered} {\mathbf{P}}^{t+1}=\underset{\mathbf{P}}{\mathrm{argmin}}\sum _{i=1}^K(\frac{\mu }{2}{\Vert {\mathbf{P}}_i^t{\mathbf{X}}_{S_i}-\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i^t-{\mathbf{E}}_{S_i}^t\Vert }_F^2 \\ +\frac{\mu }{2}{\Vert {\mathbf{P}}_i^t-\mathbf{P}-{\mathbf{E}}_{P_i}^t\Vert }_F^2+\langle {\mathbf{Y}}_{2,i},{\mathbf{P}}_i^t{\mathbf{X}}_{S_i}-\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i^t \\ -{\mathbf{E}}_{S_i}^t\rangle +\langle {\mathbf{Y}}_{3,i},{\mathbf{P}}_i^t-\mathbf{P}-{\mathbf{E}}_{P_i}^t\rangle ) \\ +\langle {\mathbf{Y}}_4,\mathbf{P}-{\mathbf{J}}^t\rangle +\frac{\mu }{2}{\Vert \mathbf{P}-{\mathbf{J}}^t\Vert }_F^2 \end{gathered}$$ (16)
  The closed form solution of Eq. (16) is

  $${\mathbf{P}}^{t+1}=[{\mathbf{G}}_3/\mu +{\mathbf{G}}_4]{[\sum _{i=1}^K({\mathbf{X}}_T{\mathbf{Z}}_i^t{({\mathbf{Z}}_i^t)}^T{({\mathbf{X}}_T)}^T+\mathbf{I})+\mathbf{I}]}^{-1}$$ (17)

  where ${\mathbf{G}}_3={\sum }_{i=1}^M[{\mathbf{Y}}_{2,i}{({\mathbf{Z}}_i^t)}^T{({\mathbf{X}}_T)}^T+{\mathbf{Y}}_{3,i}]+\mu {\mathbf{J}}^t-{\mathbf{Y}}_4\text{and}{\mathbf{G}}_4={\sum }_{i=1}^M[({\mathbf{P}}_i^t{\mathbf{X}}_{S_i}^t-{\mathbf{E}}_{S_i}^t){({\mathbf{Z}}_i^t)}^T{({\mathbf{X}}_T)}^T+{\mathbf{P}}_i^t-{\mathbf{E}}_{P_i}^t].$
• Update multipliers: The to-be-optimized multipliers (i.e., Y_1,i, Y_2,i, Y_3,i, Y₄) and the parameter μ are updated as follows

  $$\{\begin{array}{l}{\mathbf{Y}}_{1,i}={\mathbf{Y}}_{1,i}+\mu ({\mathbf{Z}}_i-{\mathbf{F}}_i)\\ \begin{array}{l}{\mathbf{Y}}_{2,i}={\mathbf{Y}}_{2,i}+\mu ({\mathbf{P}}_i{\mathbf{X}}_{S_i}-\mathbf{P}{\mathbf{X}}_T{\mathbf{Z}}_i-{\mathbf{E}}_{S_i})\\ {\mathbf{Y}}_{3,i}={\mathbf{Y}}_{3,i}+\mu ({\mathbf{P}}_i-\mathbf{P}-{\mathbf{E}}_{P_i})\\ {\mathbf{Y}}_4={\mathbf{Y}}_4+\mu (\mathbf{P}-\mathbf{J})\end{array}\\ \mu =\min (\mu \rho ,{\mu }_{max})\end{array}$$ (18)

Especially, Eqs. (8) and (9) can be solved using Singular Value Thresholding (SVT) [40], while Eqs. (10) and (11) can be effectively addressed with the shrinkage operator [41]. Details of the proposed optimization algorithm and the convergence analysis can be found in the Supplementary Materials¹.

D. Computational Complexity

In the proposed optimization algorithm, the most time-consuming components include 1) the nuclear norm computation in Steps 3–4, and 2) the matrix multiplication and the inverse operation in Steps 7 − 9. Specifically, in Steps 3–4, the singular value decomposition (SVD) is performed on d × d and n_t × n_s matrix, and hence, the computational complexity is $\mathcal{O}(d^3)\text{and}\mathcal{O}(n_s^3),$ respectively. In Steps 7–9, the matrix inversions are operated for n_t × n_t, d × d and d × d, respectively. Then the computational complexity for Steps 7–9 are $\mathcal{O}(n_t{d}^2+n_t^{2}d+n_t^3+n_t^2{n}_s+n_t{n}_{s}d),\mathcal{O}(n_s{d}^2+d^3+n_t{d}^2),\text{and}\mathcal{O}(n_t{n}_{s}d+n_t{d}^2+d^3),$ respectively. For simplicity, we assume that d ≥ max(n_t, n_s). Thus, the computational complexity of our proposed optimization algorithm is $\mathcal{O}(\tau ((n_t+n_s)d^2+n_s^3+n_t^3+d^3)),$ where τ is the number of iterations.

E. Implementation Details

In the training stage, we first learn low-rank representation based on the different parameters (i.e., α and β in Eq. (5)) of the source and target domains. And then, by using the new representation source and target domains data, we train a k-nearest-neighbor (KNN) or a support vector machine (SVM) classifier [42] based on labeled source data to obtain the target data identification accuracy corresponding to different parameters. Finally, we can select the parameter values corresponding to the highest accuracy as the optimal low-rank representation model parameters. In the testing stage, for the testing source and target samples, we first preprocess its fMRI data, and obtain its representation under the optimal low-rank representation parameters learned in the training stage. We then train the KNN/SVM classifier using the new representation data of multiple source domains and the corresponding labels. Finally, we identify the final prediction of the representation target data through the well-trained KNN/SVM classifier.

IV. Experiments

In this section, we first introduce the materials used in this work, the competing methods, and the experimental setup. We then present the experimental results on both synthetic data and real-world multi-site fMRI data, as well as the comparison between our method and several state-of-the-art methods in ASD identification.

A. Materials

1). Data Acquisition:

To verify the effectiveness and efficiency of our proposed maLRR method, we conducted experiments on a real-world multi-sites dataset with rs-fMRI data, named Autism Brain Imaging Data Exchange (ABIDE) database [43], [44]. There are 1, 112 subjects in the baseline ABIDE database, including 539 ASD subjects and 573 normal controls (NCs). These subjects are acquired from 17 different sites. All participants have corresponding functional MRI and phenotypic information. The detailed scan procedures and protocols are described on the ABIDE website². Considering that several sites contain only a limited number of partici- pants, we use data from 5 different sites, each with more than 50 subjects, including NYU, Leuven, UCLA, UM and USM. Specifically, there are a total of 468 subjects, including 250 ASD patients and 218 NCs. The detailed demographic information is summarized in Table II, while such information of the whole ABIDE database is reported in Table SI of the Supplementary Materials.

TABLE II.

Demographic information of the studied subjects from five imaging sites in the ABIDE database. The values are denoted as mean±standard deviation. M/F: Male/Female.

Site	ASD		NC
	Age	M/F	Age	M/F
NYU	17.59 ± 7.84	66/5	16.49 ± 7.68	79/14
Leuven	13.10 ± 4.79	21/4	18.80 ± 9.00	24/8
UCLA	16.27 ± 6.48	28/8	14.65 ± 4.97	31/7
UM	17.05 ± 8.36	43/5	17.35 ± 7.12	56/9
USM	15.77 ± 7.21	30/8	17.34 ± 9.53	21/1

2). Data Pre-processing:

The rs-fMRI data used in this work are provided by the Preprocessed Connectome Project initiative³, and preprocessed by using the Configurable Pipeline for the Analysis of Connectomes (C-PAC) [45]. The image pre-possessing steps of this pipeline involve slice-timing and motion correction, nuisance signal regression and temporal filtering. Afterward, the derived rs-fMRI were normalized to Montreal Neurological Institute (MNI) space via a non-linear registration algorithm (i.e., ANTS [46]). Subsequently, we extract the mean time series for a set of brain regions based on the anatomical automatic labeling (AAL) atlas [47] that comprises 116 pre-defined regions-of-interest (ROIs). Finally, for each subject, we can generate a resting-state functional connectivity matrix expressed by a 116 × 116 symmetrical matrix where each element in this matrix denotes the Pearson correlation coefficient between a pair of ROIs. For simplicity, we remove the upper triangle and 116 diagonal elements (i.e., correlation of an ROI to itself), and convert the remaining triangles into a 6, 670-dimensional feature vector for representing each subject.

B. Competing Methods

In the experiments, we compare our maLRR method with the following seven methods, including two baseline methods and four representation-based methods.

• 1)Baseline-1: In this method, we use the SVM, one of the most widely used classification model in neuroimaging analysis [48], for neuroimaging-based ASD identification, based on the original data in multiple sites. Specifically, we directly train an SVM model on the combined/concatenated subjects in multiple source domains, and apply the trained model to subjects in the target domain to obtain the final classification decision. In the SVM classifier, we use the linear kernel and the penalty term C is selected by gird-search strategy from the range of [2⁻⁵, · · · , 2⁵] via cross-validation.
• 2)Baseline-2: Similar to Baseline-1, we simply use the original rs-fMRI features of subjects in multi-sites for classification in this method. To be specific, we use the KNN as the classifier for identifying ASD patients in the target domain, where subjects in source domains are used as training data. The parameter k for KNN is chosen from the range of [3, 5, 7, 9, 11, 15] via cross-validation.
• 3)Low-rank representation (LRR) [49]: This is a general feature transformation method, aiming to find the low-rank representation of original features. In LRR, we first discover the intrinsic representation for multiple domains via LRR separately, and then apply the SVM/KNN classifier to make the final decision for target data. The parameter α balances the contributions of the low-rank constraint and error term, and is selected from [10⁻³, · · · , 10³] via cross-validation.
• 4)Robust domain adaptation via low-rank reconstruction (RDALR) [28]: In this method, the low-rank representation constraint is used to directly transform data in source domains to the target domain, followed by KNN for classification. Note that, by introducing the ℓ_2,1 norm, RDALR is capable of capturing the relatedness of source domains during the adaptation process while suppressing the noises and outliers. The parameter α for the representation error is chosen from the set of [10⁻³, · · · , 10³] via cross-validation.
• 5)Geodesic flow kernel (GFK) [50]: The GFK method is an unsupervised kernel-based approach. It reduces the data distribution difference between the source and target domains by exploiting low-dimensional data structures that are invariant across different domains. In the experiments, we first employ GFK for learning low-dimensional representation based on source and target domains, and then feed the new features into the KNN classifier for target data identification. The parameter (i.e., dimensionality of the subspace) in GFK method is chosen from [5, 10, · · · , 100] via cross-validation.
• 6)Transfer component analysis (TCA) [51]: The TCA method is designed to make data distributions in different domains to be close to each other, by learning several transfer components across domains in a Reproducing Kernel Hilbert Space (RKHS) using Maximum Mean Discrepancy. In TCA, we also first learn the new representation in source and target domains, and then the SVM/KNN is used as the classifier to identify the final prediction of the target data, respectively. For simplicity, we use a linear kernel for new representation learning (i.e., feature extraction) in TCA, and the parameter of the new feature dimension is adjusted in the range of [5, 10, · · · , 100] via cross-validation.

Similar to our maLRR method, LRR, RDALR, GFK, and TCA are unsupervised approaches. To validate the advantage of our proposed representation using the common latent domain, we further compare our maLRR method with its simplified variant, called maLRR-1 in this paper. Different from maLRR, the maLRR-1 method simply transforms the source domains to the target domain (i.e., without learning the common transformation matrix). The objective function of maLRR-1 is shown in Eq. (4). The parameter of α in Eq. (4) is chosen from [10⁻³, · · · , 10³]. For the proposed maLRR method, the parameters α and β are selected from the range of [10⁻³, · · · , 10³]. Since both our methods (i.e., maLRR and maLRR-1) and four computing methods (i.e., LRR, RDALR, GFK, and TCA) only learn new representations for subjects in multiple domains, we further employ the KNN/SVM as classifier for ASD identification, where subjects in the target domain are selected as the testing data and those in source domains are treated as the training data. As the baseline classifiers, the linear kernel and the default penalty parameter (i.e., C = 1) is used for SVM. For KNN, the nearest neighbor is fixed to 5.

C. Experimental Setup

We adopt a 5-fold cross-validation strategy [52] to evaluate the performance of all methods. In brief, the subjects of each domain are randomly partitioned into 5 subsets (with each subset having a roughly equal size of subjects), and each time one subset is selected as the test data, while all other subjects in the remaining subsets are used as the training data. Note that, no testing data is used in such cross-validation process. In addition, to obtain the optimal parameters for different methods, we further perform an inner 5-fold cross-validation strategy using training data.

To evaluate the classification performance, seven evaluation metrics including classification accuracy (ACC), sensitivity (SEN), specificity (SPE), balanced accuracy (BAC), positive predictive value (PPV), negative predictive value (NPV), and the area under the receiver operating characteristic (ROC) curve (AUC) [53] are utilized, which have been widely used in neuroimaging analysis [54]. Denote TP, TN, FP and FN as True Positive, True Negative, False Positive, and False Negative, respectively. Those evaluation metrics can be defined as follows: ACC=(TP+TN)/(TP+TN+FP+FN), SEN=TP/(TP+FN), SPE=TN/(TN+FP), BAC=(SEN+SPE)/2, PPV=TP/(TP+FP), and NPV = TN/(TN+FN). For these metrics, higher values indicate better classification performance.

D. Results on Synthetic Data

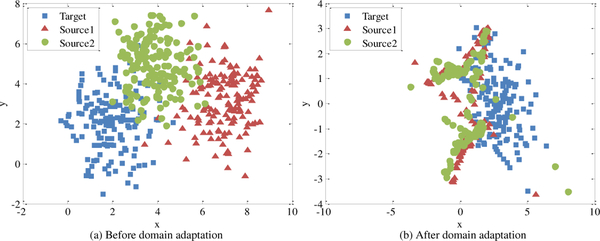
To illustrate the advantage (i.e., being able to transform multiple domains into a common latent domain such that the distribution variance is reduced) of the proposed maLRR method, we first conduct an experiment on unlabeled synthetic data. We generate three domains by Gaussian distributions with means [2, 2], [7, 3] and [4, 5] respectively, and covariance matrices [1 0; 0 2]. Each domain contains 150 samples. We simply treat the blue samples as the target domain while the green and red samples as two different source domains. As shown in Fig. 2 (a), the distributions of the three domains are significantly different before transformation, despite some partial overlap. After transform, as shown in Fig. 2 (b), we can observe that the data from three domains are mixed together into a compact region, which demonstrates the effectiveness of our proposed method in reducing the difference of domain distributions. Results of all methods on labeled synthetic data are reported in Section A of the Supplementary Materials.

Fig. 2.

Results on synthetic data achieved by our method, with the same color denoting data points from the same domain. (a) denotes the data distributions before transformation, and (b) denotes the data distributions after transformation (based on our proposed common domain transformation strategy). Here, samples represented by blue are treated as target domain, while samples represented by green and red are treated as source domains.

E. Results on ABIDE with Multi-site fMRI Data

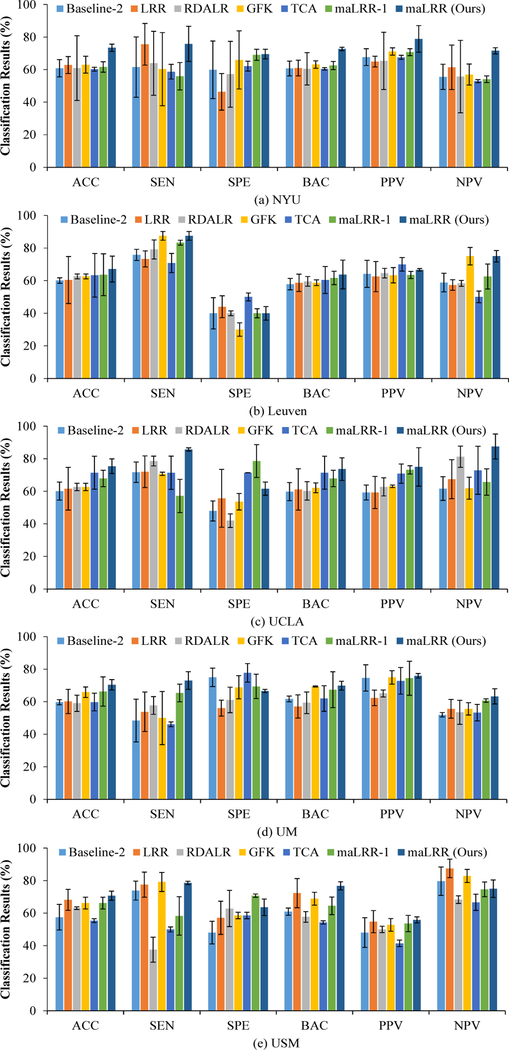
In this section, we conduct experiments on the real multi-site ASD dataset with five imaging sites (i.e., NYU, Leuven, UCLA, UM, and USM). Note that each domain can be selected as the target domain in turn, and the remaining ones are treated as the source domains. For four representation-based comparison methods (i.e., LRR, RDALR, GFK, and TCA) and our methods (including maLRR-1 and maLRR), the unsupervised adaptation experimental setting is adopted, where no label information is accessible during the new representation learning process. The labeled subjects in source domains are used as training data, and those in the target domain are treated as testing data. Also, the two baseline methods (i.e., Baseline-1 and Baseline-2) simply employ the original feature representation of subjects for model learning. We report the performance achieved by different methods using SVM and KNN classifiers in Table III and Fig. 3, respectively. In Fig. S3 of the Supplementary Materials, we further investigate the top 10 brain connectivity patterns identified by our maLRR method in ASD classification. Results on the whole ABIDE database (i.e., with all imaging sites) of all methods are reported in Tables SIII-SIV of the Supplementary Materials. More results on unbalanced ASD datasets are reported in Fig. S2 of the Supplementary Materials. From Table III and Fig. 3, we can make the following observations.

TABLE III.

Performance of five different methods in ASD classification using the SVM classifier on the multi-site ABIDE database. Here, each of multiple domains is alternatively used as the target domain, while the remaining ones are regarded as source domains.

Target Site	Method	ACC (%)	SEN (%)	SPE (%)	AUC (%)	BAC (%)	PPV (%)	NPV (%)
NYU	Baseline-1	57.16 ± 5.48	51.34 ± 6.94	64.79 ± 13.60	64.39 ± 2.58	58.07 ± 2.71	66.97 ± 4.68	54.55 ± 12.56
	LRR	66.49 ± 7.61	67.46 ± 4.59	65.48 ± 1.68	75.12 ± 0.17	66.47 ± 6.45	72.14 ± 2.19	60.93 ± 11.74
	TCA	68.92 ± 4.66	66.67 ± 1.00	72.14 ± 11.11	75.12 ± 6.90	69.40 ± 5.56	76.47 ± 8.32	61.58 ± 2.23
	maLRR-1	55.73 ± 3.68	59.13 ± 2.81	51.43 ± 12.12	49.80 ± 5.33	55.28 ± 4.66	62.28 ± 6.20	48.08 ± 2.72
	maLRR (Ours)	71.88 ± 4.42	66.67 ± 3.57	78.57 ± 10.20	80.75 ± 7.58	72.62 ± 1.68	82.50 ± 5.61	67.05 ± 1.25
Leuven	Baseline-1	60.96 ± 2.63	76.56 ± 7.4	41.00 ± 7.98	64.91 ± 4.80	58.78 ± 5.35	63.79 ± 5.88	62.81 ± 11.48
	LRR	58.74 ± 6.92	52.08 ± 6.20	70.00 ± 4.14	69.58 ± 4.12	61.04 ± 3.24	70.83 ± 5.89	52.22 ± 11.00
	TCA	59.09 ± 6.43	66.67 ± 3.57	50.00 ± 4.14	63.33 ± 1.00	58.33 ± 4.71	61.25 ± 1.77	58.33 ± 11.79
	maLRR-1	59.09 ± 6.43	41.67 ± 5.36	50.00 ± 8.28	65.00 ± 1.79	60.83 ± 3.54	63.33 ± 3.57	55.00 ± 7.07
	maLRR (Ours)	63.64 ± 2.86	75.00 ± 1.79	50.00 ± 4.14	71.67 ± 1.79	62.50 ± 2.96	64.29 ± 1.01	67.50 ± 7.68
UCLA	Baseline-1	65.20 ± 6.18	73.03 ± 5.10	56.94 ± 5.13	67.85 ± 4.70	64.99 ± 6.17	64.58 ± 5.53	68.07 ± 8.48
	LRR	69.84 ± 12.35	82.86 ± 4.04	54.46 ± 3.99	68.78 ± 2.41	68.66 ± 4.02	68.27 ± 9.52	71.67 ± 6.50
	TCA	63.49 ± 11.22	60.71 ± 5.15	66.96 ± 6.31	56.96 ± 10.46	63.84 ± 10.73	66.96 ± 6.31	60.71 ± 5.15
	maLRR-1	63.49 ± 11.22	46.43 ± 5.05	81.25 ± 6.52	55.55 ± 6.69	63.84 ± 10.73	81.25 ± 6.52	56.82 ± 9.64
	maLRR (Ours)	75.00 ± 5.05	64.29 ± 1.01	85.71 ± 2.00	77.55 ± 5.77	75.00 ± 5.05	85.71 ± 2.02	70.71 ± 1.01
UM	Baseline-1	55.09 ± 3.26	50.77 ± 6.02	68.02 ± 3.13	69.24 ± 2.50	59.40 ± 2.88	77.56 ± 4.24	48.48 ± 2.04
	LRR	61.27 ± 9.51	53.85 ± 2.50	69.44 ± 10.64	65.06 ± 1.36	61.65 ± 9.82	70.71 ± 10.00	53.98 ± 12.05
	TCA	65.91 ± 9.64	65.38 ± 5.44	66.67 ± 10.71	78.21 ± 6.65	66.03 ± 10.58	74.24 ± 10.71	56.82 ± 9.64
	maLRR-1	56.82 ± 3.21	46.15 ± 10.88	72.22 ± 7.86	56.84 ± 5.44	59.19 ± 1.51	70.71 ± 1.01	48.33 ± 2.36
	maLRR (Ours)	72.73 ± 6.43	76.92 ± 1.76	66.67 ± 7.14	80.77 ± 5.44	71.79 ± 2.69	83.33 ± 3.57	69.64 ± 7.58
USM	Baseline-1	66.67 ± 3.04	61.36 ± 5.53	69.74 ± 2.25	69.77 ± 1.56	65.55 ± 2.84	54.83 ± 4.42	76.54 ± 5.17
	LRR	70.74 ± 2.81	82.00 ± 2.00	53.57 ± 5.05	80.60 ± 3.20	76.79 ± 2.53	55.84 ± 1.84	83.00 ± 5.80
	TCA	71.86 ± 1.61	81.67 ± 1.79	63.57 ± 9.09	83.10 ± 3.81	77.62 ± 1.35	59.82 ± 3.79	83.75 ± 8.84
	maLRR-1	63.64 ± 1.00	50.00 ± 5.36	71.43 ± 2.00	51.79 ± 2.53	60.71 ± 7.58	50.00 ± 2.00	73.33 ± 9.43
	maLRR (Ours)	74.62 ± 5.32	86.11 ± 2.73	68.10 ± 4.30	83.10 ± 5.93	77.10 ± 2.14	66.94 ± 5.55	85.56 ± 5.11

Fig. 3.

Performance of seven different methods in ASD classification using the KNN classifier on the multi-site ABIDE database, where (a)-(e) denote the classification results using target domains.

First, in terms of the average (i.e., across multiple sites) ACC value, the results of two baseline methods (i.e., Baseline-1 and Baseline-2) are inferior to the competing representation- based methods. These results show that representation-based methods, which can reduce the distribution difference among multi-site ASD data sets, are useful in improving the performance of ASD diagnosis with multi-site fMRI data.

Second, the proposed maLRR method using SVM and KNN as classifiers consistently outperform the compared methods in terms of ACC, BAC, PPV and NPV. For instance, the average ACC values of maLRR with SVM and KNN classifiers are 71.57% and 71.43%, respectively, which are higher than the second-best ACC values of 64.08% (achieved by the GFK method using the KNN classifier) and 65.85% (yielded by the TCA method using the SVM classifier), respectively.

Third, our maLRR method is superior to RDALR in terms of six measures for multi-site ASD diagnosis using the KNN classifier. In particular, maLRR achieves an average SEN of 80.13% that is much better than the SEN (i.e., 63.36%) yielded by RDALR, suggesting that our method is more reliable in identifying ASD patients form the whole population when compared to RDALR. It is worth noting that, different from RDALR that transfers multiple source domains to the target domain, our maLRR method maps the target and source domains to a latent domain for removing noisy information. These results validate the efficacy of the proposed latent-space based strategy used in our method.

Finally, with SVM and KNN classifiers, maLRR achieves noticeably better performance than maLRR-1. These results imply that the low-rank matrix decomposition is beneficial to discover the intrinsic structures and further alleviate the heterogeneity among multiple sites.

F. Comparison with State-of-the-Arts

We further compare the results achieved by our maLRR with 5 state-of-the-art methods that use rs-fMRI data in the multi-site ABIDE dataset. Since very limited studies report average ASD classification results among multiple sites, we only report the results on the NYU site in Table IV. Also, we further list the details of each method in Table IV, including the type of features and classifiers. It is worth noting that in [15] and [18], the symmetrical functional connectivity matrix is directly used for ASD identification, while the vectorized functional network representation is applied in [17] and our method. In [15] and [18], they sample a certain proportion of data from each site as a training set, and train the corresponding deep model. Then the diagnostic performance on NYU site can be obtained by the well-trained model. The k values of the KNN classifier used in [15] and our maLRR method are fixed as 9 and 5 in our method, respectively.

TABLE IV.

Comparison with state-of-the-art methods for ASD identification using rs-fMRI ABIDE data on NYU site. HOA: Harvard Oxford Atlas. GMR: Gray Matter ROIS; AAL: Anatomical Automatic Labeling.

Method	Feature Type	Feature Dimension	Classifier	ACC (%)	SEN (%)	SPE (%)	AUC (%)
sGCN + Hing Loss [15]	HOA	111 × 111	KNN	60.50	−	−	57.00
sGCN + Global Loss [15]	HOA	111 × 111	KNN	63.50	−	−	61.00
sGCN + Constrained Variance Loss [15]	HOA	111 × 111	KNN	68.00	−	−	64.00
FCA [18]	GMR	7, 266 × 7, 266	t-test	63.00	72.00	58.00	−
DAE [17]	CC200 Atlas	19, 900	Softmax Regression	66.00	66.00	65.00	−
maLRR (Ours)	AAL	6, 670	KNN	73.44	75.79	69.52	−
maLRR (Ours)	AAL	6, 670	SVM	71.88	66.67	78.57	80.75

It can be seen from Table IV that our maLRR method generally outperforms the competing methods in ASD versus NCs classification. More specifically, maLRR achieves much higher accuracy (i.e., 71.88% and 73.44%) and specificity (i.e., 78.57% and 69.52%) with SVM and KNN classifiers, which are much better than five state-of-the-art methods, even though sGCN and DAE are two deep-learning methods. The possible reasons could be listed as follows. (1) To train reliable deep learning models generally needs massive samples. However, for multi-site ASD diagnosis, although the aggregate of multiple sites can generate a larger dataset, it is still difficult to train a robust depth neural network. (2) Deep learning models usually have to face the overfitting problem, especially when using noise data. In fact, the fMRI data is often accompanied by a large amount of noise information [55], and the deep learning models, while demonstrating the outstanding representational power to characterize the fMRI data set, tend to use brute-force to fit the noise component [56].

V. Discussion

In this section, we first analyze the influence of several essential parameters on the performance of the proposed method. We then discuss the limitations of the current work and present the possible future research directions.

A. Parameter Analysis

In our maLRR method, there are two parameters (i.e., α and β) to be tuned. In addition, in the above experiment settings, we adopt a 5-nearest neighbor classifier for disease classification. Here, we also discuss the effect of nearest neighbor value (i.e., k) on the performance of our method. Using each site as the target domain and the remaining ones as source domains, we conduct experiments using different parameters. Specifically, we independently vary the values of α, β and k, and α and β are selected from {10⁻³, · · · , 10³}, while k is chosen from {3, 5, 7, 9, 11, 13, 15}. The classification accuracies achieved by maLRR using different parameters are shown in Figs. 4–6, where we fix one parameter and vary the values of the other two parameters. From Figs. 4–5, we can clearly see that maLRR achieves good results with k = 5. Fig. 6 shows that the performance of maLRR slightly fluctuates within a very small range with the increase of values of α and β in each site. In most cases, the classification results of maLRR are stable with respect to α and β, demonstrating that our method is not very sensitive to parameters.

Fig. 4.

Classification accuracies with respect to different parameter values of β and k in the proposed maLRR model (with α = 0.1), where (a)-(e) denote results generated by maLRR using different target domains.

Fig. 6.

Classification accuracies with respect to different parameter values α and β in the proposed maLRR model (with k = 5), where (a)-(e) denotes different selection of target domain.

Fig. 5.

Classification accuracies with respect to different parameter values of α and k in the proposed maLRR model (with β = 1), where (a)-(e) denotes different selection of target domain.

B. Limitations and Future Work

Although our proposed maLRR method shows significant improvement in terms of multi-site ASD diagnosis over existing representation-based learning methods, several technical issues need to be considered in the future. First, even though we can partly alleviate data heterogeneity by learning shared features for multiple sites via the proposed maLRR method, fMRI feature extraction is still independent of classifier training, which may degrade the learning performance. Therefore, a unified framework for joint low-rank representation learning and classifier training will be studied in the future. Second, following previous studies [57], we simply extract edge weights from functional brain networks as the feature representation for each subject, ignoring the topological information of brain networks. It is interesting to take advantage of both edge weights and topological information of functional brain networks for multi-site disease analysis, which will be our future work. Third, besides the diagnostic labels (e.g., ASD patient or normal control), multiple clinical variables are generally acquired in ASD diagnosis [58], such as Autism Diagnostic Observation Schedule (ADOS) and Autism Diagnostic Interview (ADI). Since the clinical variables are helpful to reflect the status of ASD progression, using the continuous clinical values may help discover the disease-relevant markers, which will also be our future work.

VI. Conclusion

In this paper, we propose a multi-site adaptation framework with low-rank representation (maLRR) for ASD identification with rs-fMRI data. Specifically, we transform data from multiple sites into a common latent representation domain using low-rank matrix decomposition, through which subjects in each source domain can be linearly represented by those in the target domain. To efficiently solve the proposed objective function, we develop an alternating optimization algorithm using the classic augmented Lagrange method. We also analyze the computational complexity of the algorithm in detail and verify its convergence. Extensive experiments on both synthetic data and the real multi-site ABIDE datasets with fMRI demonstrate the effectiveness of the proposed method, in comparison to several state-of-the-art methods.