Quantum Chemical Investigation of Dimerization in the Schlenk Equilibrium of Thiophene Grignard Reagents

Abstract

The Schlenk equilibrium of Grignard reagents describes the intricate relationships between monomers, aggregates, and exchange products. The core step of the Schlenk equilibrium, formally 2RMgX ⇌ R₂Mg + MgX₂, has been subject to computational studies of simple methyl Grignards and NMR determination of thermodynamics. These studies neglect the effect the R group may have on the accessibility of intermediates in the Schlenk equilibrium. In this study, computational reaction discovery tools were employed to thoroughly search the chemical space for feasible dimerizations and pathways to ligand exchange for thiophene Grignards. Three bridged dimers, μ-(Cl, C), μ-(Cl, Cl), and μ-Cl, were found to be vital intermediates, which are stabilized by π-interactions involving the thiophene group. These dimers are approximately as thermodynamically stable as the Grignard monomers and its ligand exchange products, and therefore, their reactivity should be considered when examining mechanisms for aryl Grignard or cross-coupling reactions.

Graphical Abstract

INTRODUCTION

Grignard reagents of the form RMgX are widely used in organic reactions because of the high nucleophilicity of the R group. This nucleophilicity enables these reagents to react with electrophiles such as carbonyls in the Grignard reaction,^1–4 or with metal centers during transmetalation in Kumada cross coupling.^5–9 In particular, catalyst-transfer polymerization (CTP) is a powerful strategy that uses Kumada coupling to create polymers featuring π-conjugated backbones, such as poly(3-hexylthiophene), with control over molecular weight, end-group identity, and dispersity.^10–12 CTP has a limited monomer scope, with few reports of successful polymerizations of large or electron-deficient monomers.¹³ Significant progress has been made in understanding the nature of this catalytic cycle so as to expand the scope of monomers amenable to CTP;^10,14 however, a proper understanding of the catalytic cycle presupposes an understanding of the reactive species at the onset of catalysis. Because the transmetalation step may be rate-limiting,¹⁵ the polymerization rate will depend on the structure of the Grignard in solution.

Although often written down as a single RMgX structure (where X = Br, Cl, or I), Grignard reagents readily undergo aggregation and ligand exchange reactions, known as the Schlenk equilibrium.¹⁶ The behavior of the Schlenk equilibrium is difficult to predict, in part because of the extent of aggregation,^17–20 but also because of its dependence on concentration, R group structure, additives, and solvent.^21–23 One study by Peltzer et al. elucidated the mechanism of the Schlenk equilibrium of CH₃MgCl, using dynamics simulations, and found a variety of operative intermediates and pathways.²⁵ Other theoretical studies have also provided insight into the Schlenk equilibrium of CH₃MgBr and other alkyl Grignards,^20,24–26 but these have been hindered by competing factors of system-relevant parameters and low Grignard complexity. Experimental studies on Grignard reagents more sophisticated than methyl Grignard have been achieved,^18,19,21,27 but these have focused on NMR experiments, a method with limited sensitivity to the transient intermediates that are important for kinetics. The details of the kinetics of the Schlenk equilibrium for more complex reagents, such as aryl Grignards commonly used in cross-coupling reactions, are still unclear.

This gap in the literature concerning the mechanism and intermediates of the Schlenk equilibrium for complex Grignards, such as aryl Grignards, hinders chemists’ ability to understand structure and reactions of Grignards. Given the dependence of the equilibrium on interactions with solvent, complexity of aggregation modes, and the possible presence of radicals, a daunting number of possible pathways may exist for the equilibrium. To aid in exploring reactions that span a large chemical space, the Zimmerman group has developed computational methods for exhaustively searching reaction paths and elucidating nonintuitive reaction mechanisms.^28–32 These tools have already seen use on a variety of systems and have been instrumental in supplementing chemical intuition by providing mechanistic insight into poorly understood reaction networks.^33–37

Herein, we present a quantum chemical investigation of the Schlenk equilibrium of a thiophene Grignard reagent commonly used in Kumada CTP. This study examines the Grignard dimerization during Schlenk equilibrium to help elucidate structures present at the onset of catalysis. We leave investigation of the final extent of aggregation (identities of trimers, tetramers, and other oligomers) as a subject for future research. The modes of aggregation of these dimers were discovered through a search for kinetically feasible pathways using reaction discovery tools highlighted herein. Results indicate that several facile pathways exist for Schlenk product formation, all involving stable dimers of Grignard molecules bound by Lewis acid–base pairs (Scheme 1). Specifically, three bridged complexes were found to be kinetically accessible and may serve as key intermediates of the Schlenk equilibrium of aryl Grignards. These structures notably differ from those invoked for alkyl Grignard reagents and may serve as a starting point for investigation of the Schlenk equilibrium of other aryl Grignard reagents.

Scheme 1.

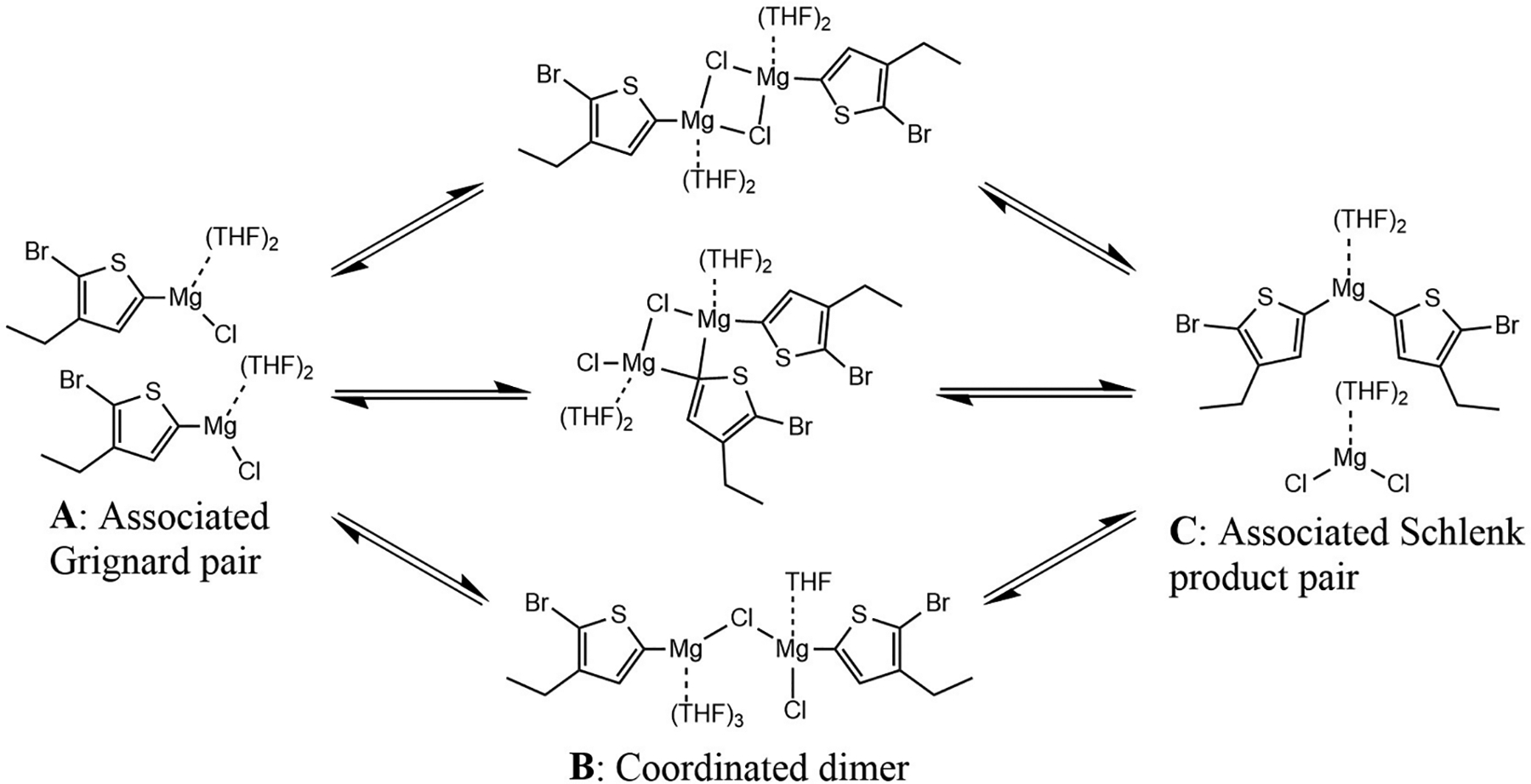
Schlenk Equilibrium of Thiophene Grignards, Including Operative Intermediates Discussed in This Study and Explicit Interactions with THF Solvent

Computational Methods.

All density functional calculations were carried out using the Q-Chem 5.0 software package.³⁸ All structures were optimized using the B3LYP functional^39–41 and the 6–31G* basis set,^42–46 using 0 to 4 tetrahydrofuran (THF) molecules bound to the Mg atoms. Structures 2B (both conformers) and C were also optimized using the dispersion-corrected ωB97X-D density functional⁴⁷ and the 6–31G* basis set to more accurately capture dispersion effects and long-range interactions such as C–H to π interactions present in these structures. For consistency, the energies of 2B and C relative to the other structures are derived from the structures optimized at the B3LYP/6–31G* level of theory, while detailed examination of C–H to π bonding uses the structures optimized at the ωB97X-D/cc-pVTZ level of theory. All intermediate and transition-state geometries were optimized to have the appropriate number of imaginary frequencies (frequency calculations done with B3LYP/6–31G*). Single-point Gibbs free energies were calculated using SMD implicit solvation model^48–50 and with thermodynamic corrections to vibrational entropy and enthalpy (at 298 K and 1 atm), where the ωB97X-D density functional and the cc-pVTZ basis set⁵¹ were used for the implicit solvation step. Atomic charges were calculated via the Natural Bond Orbital (NBO) formalism.⁵² To determine the presence of dispersive or hydrogen-bond interactions, absolutely localized molecular orbital-charge transfer analysis (ALMO-CTA) calculations were performed at the B3LYP/6–31G* level of theory to identify the orbitals responsible for the interaction as well as the interaction energy.^53,54

To explore the elementary steps responsible for the Schlenk equilibrium, ZStruct^28,29,55 generates reaction coordinates by enumerating all the possible reactions involving a set of “reactive” atoms. For this system, the reactive atoms were selected to be the Mg atoms, Cl atoms, C atoms attached to the Mg atoms, and the O atoms of each THF. From driving coordinates produced by ZStruct, the single-ended Growing String Method^30–32 acquired the chemically relevant pathways (Scheme 2). These methods generated and searched over 800 possible reaction pathways by reacting two disolvated Grignard monomers. Three pathways were selected as representative examples for further study, as these had low barriers and were the most stable intermediates of the 800 generated pathways (see SI Section 2 for a detailed description of how they were acquired).

Scheme 2.

Automated Reaction Discovery through ZStruct and the Growing String Method

RESULTS AND DISCUSSION

Structure of the Grignard Monomer in Solvent.

Grignard reagents are almost exclusively prepared and used in ethereal solvent, usually THF. For the Grignard reagent and the Schlenk products (R₂Mg and MgCl₂), THF molecules were bound to the Mg atom to determine the extent of solvation of these species in solution. Addition of one THF to unsolvated structures provided a stabilization, ΔG_bind, between −10.9 and −17.8 kcal/mol, and addition of a second THF to the monosolvated structures provided additional stabilization, with a ΔG_bind of −8.7 to −9.4 kcal/mol. Further solvation did not provide more than 2 kcal/mol stabilization (full details of the solvation energetics and analysis of electronics of these reagents can be found in SI Section 1). These results agree with previous studies²⁵ on methyl Grignard that found small differences in energy between the di-, tri-, and tetra-solvated species.

This study focuses on Mg bound to two THF molecules, as Mg species with more ligands are less likely to be reactive because of steric congestion. The reference state for this study therefore is two separated, disolvated Grignard monomers. For the ZStruct reaction pathway search, oxygen atoms in each THF molecule are considered reactive, allowing solvent dissociation as well as transfer to occur. None of the lowest-energy pathways contain THF unbinding, but THF transfer between Mg atoms does occur. Solvent association, however, was not considered, so the model does not permit additional THF to bind. All the species discussed below contain tetracoordinate or higher coordination number Mg atoms, so further solvent associations are expected to contribute minimally to the overall reaction mechanism.

Schlenk Equilibrium and Dimeric Intermediates.

Using ZStruct, a comprehensive reaction pathway search was performed to determine the kinetic accessibility of reaction paths between two solvated Grignard reagents (see Computational Methods). Over 800 reaction pathways were found starting from a pair of disolvated Grignard monomers, from which four categories of accessible dimers emerged, three of which were found to be more stable than the monomeric Grignard (Figure 1). These dimers are all formed through similar reactive processes: first, the separated reactants, SR, form an associated pair, A, via nearly barrierless rearrangement of <2 kcal/mol. A proceeds to produce coordinated intermediate, B, typically via barrierless processes involving the formation of weak, primarily ionic Mg–C or Mg–Cl bonds between the two Grignards.

Figure 1.

Structures of dimers discovered using ZStruct and the Growing String Method (ωB97X-D/cc-pVTZ//B3LYP/6–31G*). All these intermediates were found to be more stable than two separated, disolvated Grignards except for the μ-C bridged dimer. Energies for these intermediates referenced to SR.

The structures of the B intermediates differentiate the reaction paths that enable the Schlenk equilibrium. The formation of one Mg–Cl and one Mg–C bond leads to the μ-(Cl, C) bridged intermediate, 1B, which is stabilized by 0.4 kcal/mol relative to SR. The formation of two Mg–Cl bonds leads to 2B, a μ-(Cl, Cl) bridged intermediate which is stabilized by 3.3 kcal/mol. The formation of one Mg–Cl bond leads to a μ-Cl bridged intermediate, 3B, stabilized by 3.6 kcal/mol, and the formation of one Mg–C bond leads to a μ-C bridged intermediate, 4B, which is 1.8 kcal/mol less stable than SR. No μ-(C, C) bridged or THF bridged intermediates were observed, consistent with a prior study of CH₃MgCl that used AIMD to model dynamic solvation to identify intermediate structures.²⁵ The remainder of our study examines the properties and reactivity of the three most stable dimers (1B, 2B, and 3B). A deeper discussion on these three intermediates and similar intermediates can be found in SI section 2.

Structure 1B is approximately isoenergetic with SR, making it likely to be involved in the Schlenk equilibrium. This point is supported by prior experimental and theoretical studies, which suggested a Mg–C–Mg moiety may be present the Schlenk equilibrium of alkyl Grignard reagents, though they found it to be less stable than other aggregates.^19,20,23,26 To understand the stability of 1B compared to alkyl Grignards, the natural charge was computed. The natural charge on C2 was found to be −0.90 e⁻, and the natural charge on the corresponding carbon of a free Grignard monomer is −0.82 e⁻. This difference of 0.08 e⁻ is accompanied by a less-negative natural charge on the neighboring C and S relative to the free thiophene Grignard. This indicates that electron density is moved off the ring onto C2, and the Mg–C2 bonds are more ionic in character than in the free monomer. 1B is still less stable than a Cl-bridged species but more than an alkyl C-bridged species.²⁵ As will be discussed later, this stability has ramifications for the kinetics of the Schlenk equilibrium.

Structure 2B, the μ-(Cl, Cl) bridged dimer, is 3.3 kcal/mol more stable than SR, and nearly isoenergetic with 3B. Structures similar to 2B are commonly invoked as Schlenk equilibrium intermediates in the literature.^20,23,24 For example, in the Schlenk equilibrium of MeMgCl,²⁵ a similar structure computationally identified as the most stable aggregate had three THFs associated with the dimer, rather than the four in 2B. This difference in solvation may be a consequence of the increased electronegativity of sp² hybridized carbons, requiring the Mg to coordinate to another THF to stabilize its positive charge. Alternatively, this difference may be attributable to differences in level of theory, where a more accurate DFT functional is used herein or attributable to the use of an explicit solvation model in the case of MeMgCl. Structure 2B, as shown in Figure 2, is syn with respect to the thiophenes, which is 1.4 kcal/mol more stable than the analogous anti conformer when optimized at the ωB97X-D/6–31G* level of theory. The difference in energy between conformers and the positioning of the thiophene rings suggests that dispersion effects or π-interactions could be responsible for the conformational preference. ALMO-CTA analysis reveals that two C–H bonds, one on the thiophene ring as well as one on the ethyl group, accept electron density from the other thiophene ring (see Figure 3), providing a 1.0 kcal/mol stabilization, nearly the whole difference in energy between the syn- and anti- isomers. This interaction is expected to persist in other aryl Grignard aggregates, but is not expected to be present in alkyl Grignard aggregates, highlighting a difference in the Schlenk equilibrium of aryl Grignards.

Figure 2.

Key geometric parameters of intermediates 1B, 2B, and 3B (B3LYP/6–31G*).

Figure 3.

Orbitals from absolutely-localized molecular orbital analysis of 2B (B3LYP/6–31G*) showing the donation of electron density from one thiophene ring to two C–H bonds on the other thiophene ring. Occupied orbitals are shown with red/blue isosurfaces, while yellow/orange isosurfaces represent unoccupied orbitals.

Structure 3B is a μ-Cl bridged intermediate which is 3.6 kcal/mol more stable than two separated, disolvated Grignard reagents (SR), making it the most stable aggregate discussed in this study. This intermediate appears in previous literature,^20,23,25 and it has been hypothesized to form higher order aggregates by forming a chain of Mg–Cl–Mg bridges between Grignards.²³ 3B differs from the other associated pairs considered in this study because the coordinated solvent molecules are not evenly distributed between the two Mg centers.

During the formation of 3B from A, a THF molecule directly migrates from one Mg to the other. Since solvent binding and unbinding can affect the stability of these intermediates, this migration was studied further. Complex 3B-3THF, wherein one THF molecule solvates Mg1 and two THF are bound to Mg2 (Figure 4), was specifically examined. Depending on the site of coordination, addition of another THF to 3B-3THF can produce 3B (Mg atoms are unevenly solvated) or 3B′ (Mg atoms are evenly solvated). NBO calculations on 3B-3THF show that Mg1 has a more positive natural charge than the monosolvated Mg2 in 3B-3THF (1.64 compared to 1.59, respectively), suggesting that a THF molecule would form stronger interactions with Mg2 and therefore preferentially bind to Mg2, forming 3B. This is corroborated by the ΔG_bind of forming 3B, which is 4.8 kcal/mol more stable than 3B′. A reaction path finder that does not enable THF to migrate would have discovered 3B′ instead of 3B and underestimated the stability of the Cl-bridged aggregate. A pathway that involves a two-step THF binding and unbinding, similar to pathways invoked in dynamics simulations with explicit solvent,²⁵ is also possible. Since the reported intramolecular THF transfer (SI Figure S3, pathway S10) is close to barrierless, the two-step pathway was not investigated further.

Figure 4.

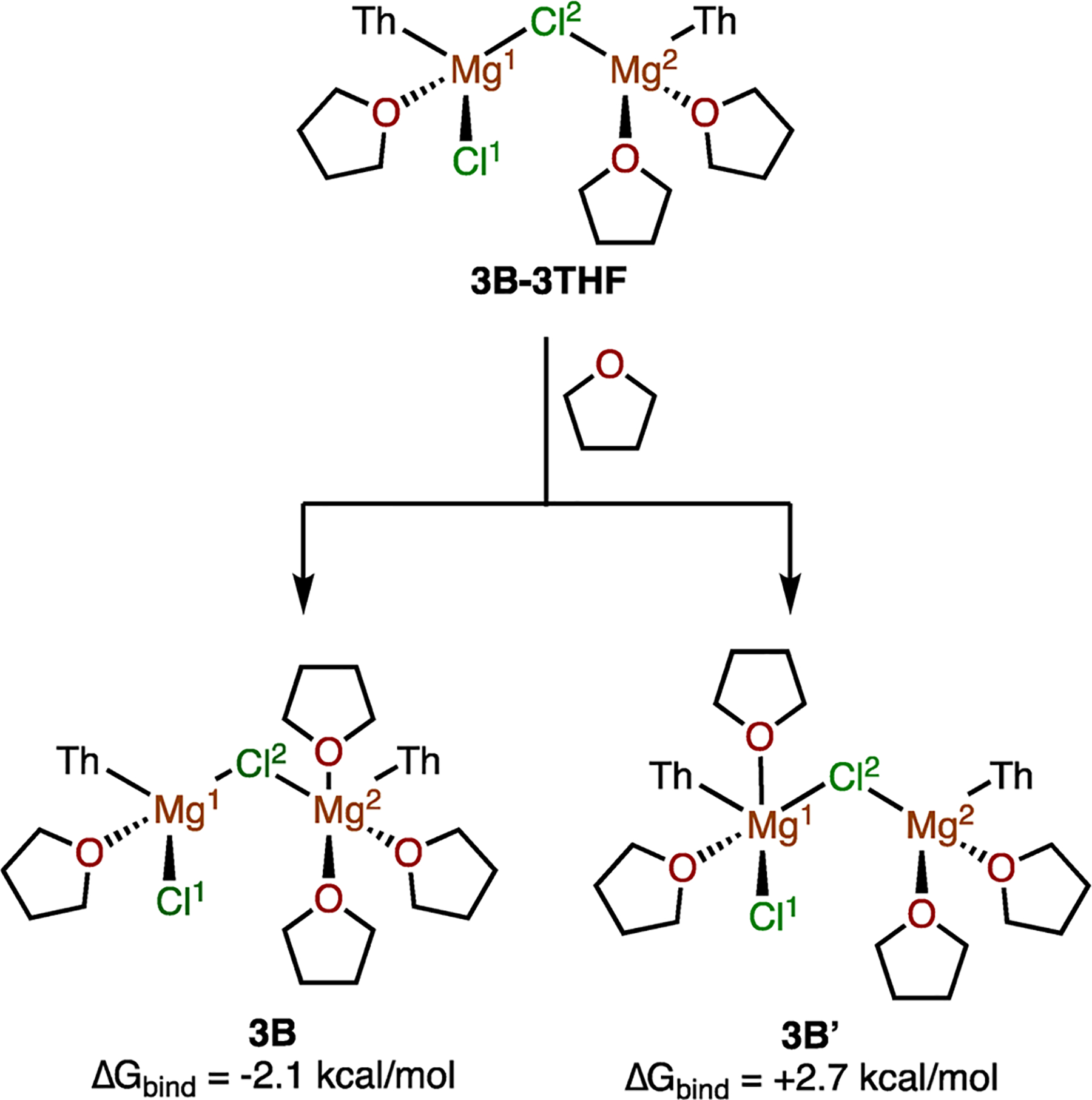
Reactions of 3B-3THF with THF to form 3B and 3B′ were compared to determine the relative stability of 3B and 3B′ (ωB97X-D/cc-pVTZ//B3LYP/6–31G*).

Transition States of the Schlenk Equilibrium.

From the associated Grignard dimers B, each of the 3 intermediates proceeds to its respective pair of associated Schlenk products, C. The B → C reactions are the only elementary steps of the Schlenk equilibrium found to have barriers. 1B to C proceeds through 1TS and requires only changes in Mg–C and Mg–Cl bond lengths. To form C from 2B or 3B, however, each dimer must rearrange to make the Mg–C bond that enables a μ-(C,Cl) bridge. Indeed, this folding does occur, but 2TS and 3TS occur after formation of this Mg–C bond, leading to transition states which resemble 1TS (see Figure 5). Since these transition states are defined by the same μ-(C,Cl) bridge as 1B, effects which alter the energy of 1B may also affect the energies of 1TS, 2TS, and 3TS.

Figure 5.

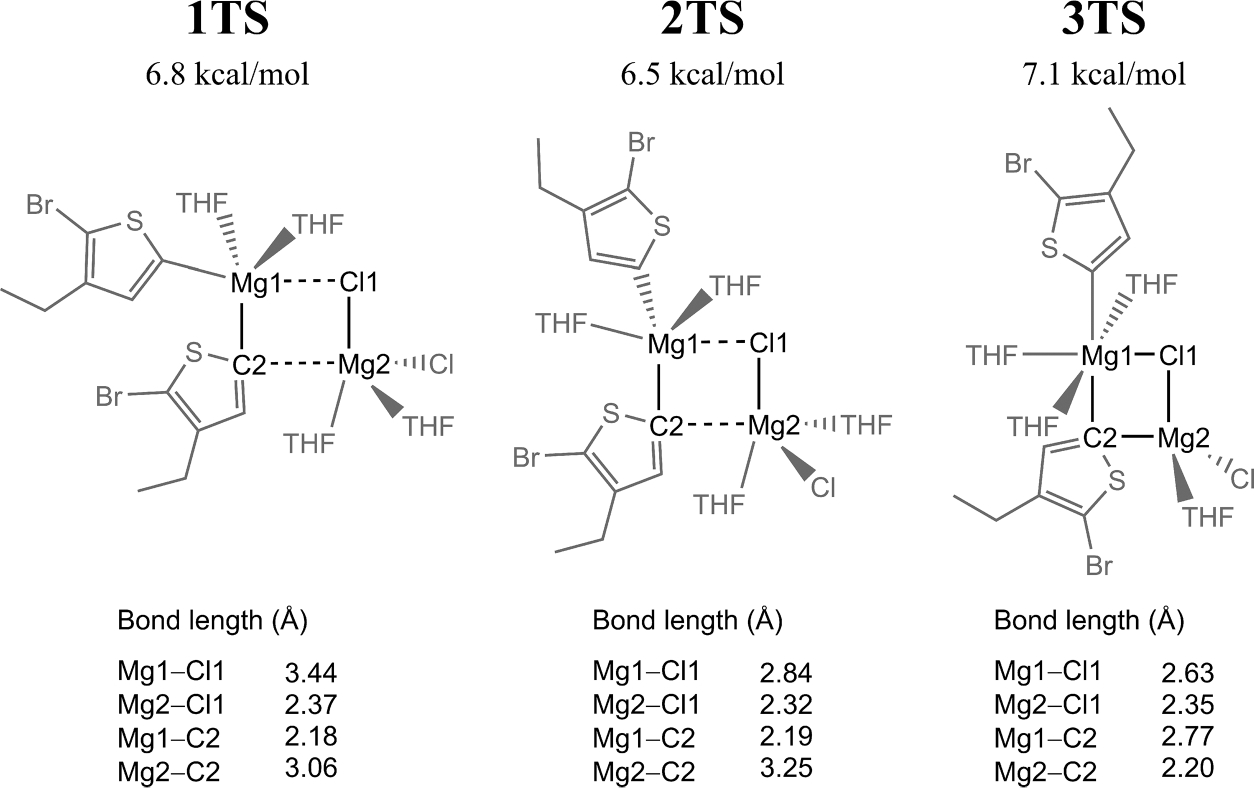
Key geometric parameters for the B → C transition states, along with the difference in energy between B and TS (ωB97X-D/cc-pVTZ//B3LYP/6–31G*).

The Mg atoms accommodate differences in geometry in the transition state, resulting in intrinsic barriers that are within 1 kcal/mol of each other (6.5 to 7.1 kcal/mol). The intrinsic barrier heights are therefore reflective of the similar energetic cost for each B intermediate to reach the activated μ-(C,Cl) square bridge, and the absolute barriers are dictated by the relative stability of the B intermediates.

The three B intermediates focused upon in this work are the lowest energy intermediates among many other possibilities. In SI sections 3 and 4, 11 pathways between the Grignard and the Schlenk products (including the three pathways addressed here) are examined. All pathways (forward and reverse) have barriers below 11.2 kcal/mol, suggesting that all thermodynamically plausible intermediates (SR, A, B, C, and SP) are in equilibrium with each other. Since the overall Schlenk behavior is driven by the thermodynamics of aggregates, only the most stable species are discussed in the main text, while a full discussion of other intermediates and pathways can be found in the SI.

The final step in the Schlenk equilibrium is the dissociation of C to yield the separated products, SP. This transition destabilizes the system by 1.9 kcal/mol, indicating the presence of long-range intermolecular interactions in C. ALMO-CTA analysis shows (Figure 6) pairs of localized molecular orbitals donating electron density from the thiophene rings into C–H bonds of the THF coordinated to MgCl₂. The charge-transfer analysis found these two interactions to stabilize the molecule by about 2.9 kcal/mol. This stabilization accounts for why intermediate C is more stable than the separated Schlenk products and explains the 3.8 kcal/mol gap between this structure and other structures discovered for the associated Schlenk products, where the latter lack C–H to π interactions (see SI section 2).

Figure 6.

Associated Schlenk products (C). Absolutely localized molecular orbitals (B3LYP/6–31G*) show the transfer of electron density from the thiophene rings to two C–H bonds in the THF molecules. Occupied orbitals are shown with red/blue isosurfaces, while unoccupied ones are yellow/orange. Centroids of each thiophene ring are labeled ct1 and ct2.

The C–H to π interactions in C reveal that the thiophene rings interact directly with bound solvent molecules. This type of interaction is expected to be present for thiophene Grignard monomers as well, as they will interact with nearby, unbound solvent molecules. Therefore, this interaction is only partially accounted for by our solvation model, through solute–solvent dispersion interactions. Since this solvent effect is accounted for in C, but less accurately treated in SP, the 1.9 kcal/mol gap in energy between C and SP is likely an artifact of the model. Additional bias may come from the fact that the number of THFs per structure was fixed to be no greater than 4; therefore, if additional THF binding is favorable for a reaction path, this would be unaccounted for in the model. The free-energy surface of the Schlenk equilibrium therefore must be interpreted in light of these two limitations: changes in relative energies from intramolecular C–H to π interactions with solvent and pathways that might be somewhat stabilized by additional THF binding.

Using the complete pathway between the Grignard reagents and the Schlenk products, a free-energy surface was constructed (Figure 7). The low barriers for TS place this system in equilibrium under standard reaction conditions. The Grignard monomer (SR) and the Schlenk products (SP) are nearly isoenergetic. This observation is in agreement with experimental measurements on aryl Grignards, indicating similar proportions of Grignard reagents and Schlenk products.²⁷ The overall profile of Figure 7 therefore appears realistic in comparison to expectations from experiment.

Figure 7.

Free-energy surface, with ωB97X-D/cc-pVTZ//B3LYP/6–31G* energies, showing three representative pathways for the Schlenk equilibrium.

To construct Figure 7, a small subset of a much wider scope of chemistry was selected. The figure contains 3 representative pathways out of the 11 delineated in the Supporting Information, which themselves were reduced from a search over 875 possible reaction steps. The full combinatorial set of possibilities was generated by a reaction discovery tool,^28,29 which provided a thorough search over the Schlenk equilibrium landscape. This means Figure 7 should be seen as a chemically descriptive subset of many more possibilities, including a handful more that occur with barriers under 10 kcal/mol (see Supporting Information). The core chemical characteristics of the 11 low-barrier pathways remain in Figure 7, so the preceding discussion therefore provides the important details of the Schlenk reaction, as the 3 primary reaction paths are representative of the others.

Before concluding the discussion of Figure 7, a limitation of the simulation protocol should be considered. Specifically, dimers of Grignard have intermolecular interactions that include additional THF molecules; these are absent in the Grignard monomers. A comprehensive solvent treatment including the second solvent sphere would be needed to fully refine the energetics of these species. Specifically, the relative energies of SR and SP are commensurately treated by solvent, being monomeric in nature, and the relative energies of A, B, TS, and C likewise. However, the energy differences between SR/SP and A/B/TS/C are likely biased toward stability of the dimeric species, as the latter contain additional specific, favorable weak interactions. This point is most clear in the relative energy of C and SP, where there is no specific bond between the product pair in C or SP, yet C appears more stable by 1.9 kcal/mol. Therefore, the relative energies appearing with change in number of associated Grignards should be no more accurate than this value. Likely, all dimeric intermediates should be shifted upward by as much as 2.9 kcal/mol, though this indication has no qualitative effect on the results or conclusions of the present study.

CONCLUSIONS

The Schlenk equilibrium for thiophene Grignard reagents was studied using quantum chemical reaction discovery tools, which revealed 11 representative pathways out of 875 investigated possibilities. The three pathways described in detail in this work show that this Schlenk equilibrium is complex and differs from that of alkyl Grignards because of the presence of new chemical interactions between the thiophene π systems. All Schlenk reactions pass through dimeric intermediates of varying structure, the most stable of which are Cl-bridged Grignard-dimers. Low barriers throughout the reaction profiles place the system firmly in equilibrium in most experimentally relevant reaction conditions.

The reaction discovery approach used in this work differs from prior studies, for example, where dynamics simulations were used to explore the Schlenk equilibrium of CH₃MgCl.²⁵ These simulations agreed qualitatively with the present study, showing that μ-(Cl, Cl) intermediates were important and THF exchange between Mg centers was operative. Our reaction discovery simulations, however, do not require extensive molecular dynamics, allowing this strategy to efficiently explore relevant regions of chemical space, even when complicated aggregation effects are in play. Key to the success of this strategy was including bound solvent in the structures of various Grignard species, as the monomer and dimer coordination environments depended sensitively on the specific attachment patterns of THF.

Due to the energetic closeness of Grignard monomers and dimers, we speculate that aggregation of Grignard reagents may account for the regioselectivity seen in CTP of thiophene Grignards or stereoselectivity of some asymmetric Grignard reactions.^3,10 Transmetalation in CTP might be slowed by the steric bulk of Grignard aggregates—in systems where this step is turnover-limiting, these Grignard aggregates will influence the rate of polymerization. This study thus motivates the consideration of the roles of aggregation and solvent effects in reactions of Grignard and similar organometallic reagents, especially in cross coupling and CTP. Further studies using the reaction discovery protocol used in this work will open up even more insight into these complicated, but highly useful reagents.