The Structure of Speed of Processing Across Cultures

Abstract

We examined whether a general processing factor emerges when using response times for cognitive processing tasks and whether such a factor is valid across three different cultural groups (Chinese, Canadian, and Greek). Three hundred twenty university students from Canada (n = 115), China (n = 110), and Cyprus (n = 95) were assessed on an adaptation of the Das-Naglieri Cognitive Assessment System (D-N CAS; Naglieri & Das, 1997). Three alternative models were contrasted: a distinct abilities processing speed model (Model 1) that is dictated by the latent four cognitive factors of planning, attention, simultaneous and successive (PASS) processing, a unitary ability processing speed model (Model 2) that is dictated by the response time nature of all measures, and a bifactor model (Model 3) which included the latent scores of Models 1 and 2 and served as the full model. Results of structural equation modeling showed that (a) the model representing processing speed as a collection of four cognitive processes rather than a unitary processing speed factor was the most parsimonious, and (b) the loadings of the obtained factors were invariant across the three cultural groups. These findings enhance our understanding of the nature of speed of processing across diverse cultures and suggest that even when cognitive processes (i.e., PASS) are operationalized with response time measures, the processing component dominates speed.

Introduction

The quest for a general measure of intelligence is older than the short history of psychology. A biological trait such as speed of processing could be a prime candidate. Individuals differ in their speed of processing information, and, hence, in their intelligence (e.g., Jensen, 2006). The current study addresses a continuing concern regarding the generality of speed and the increasing evidence in support of viewing speed, like accuracy, as a measure of the type of cognitive processing required rather than as an explanation (e.g., Das, Naglieri, & Kirby, 1994; Kirby & Williams, 1998).

The term speed of processing refers to the efficiency with which information is processed (Kail & Salthouse, 1994). Although research on speed of processing goes back to the early 1900s (Galton, 1907), several questions concerning the construct remain unanswered. A pre-eminently important one concerns the nature of speed of processing.For instance, even though influential psychometric models of intelligence, such as the three stratum Carroll-Horn framework (Carroll, 1997), include speed abilities, such as the cognitive processing speed (Gs) and the reaction time or decision speed (Gt), the nature of these constructs is still under investigation (e.g., Schneider & McGrew , 2012). The pragmatic use of a universal construct of processing speed is also an important concern, particularly since it may help us explore whether processing speed tasks offer a valid instrument for the study of cross-cultural similarities and/or differences in cognitive capacity (Kail, McBride-Chang, Ferrer, Cho & Shu, 2013). Thus, the purpose of the present study was to examine the nature of processing speed and to test whether processing speed, as a construct, is invariant across cultures (Chinese, Canadian, and Greek).

The exact nature of processing speed is still under debate (e.g., Cepeda, Blackwell, & Munakata, 2013; Danthiir et al., 2005; van den Bos, Zijlstra, & van den Broeck, 2003). On the one hand, some researchers have viewed processing speed as a unitary ability, a generic explanation for intelligence (e.g., Detterman, 1987; Jensen, 2006). On the other hand, some researchers have argued that processing speed represents cognitive strategies that are specific to particular tasks, abilities, and age (e.g., Eckert, Keren, Roberts, Calhoun, & Harris, 2010;McAuley, & White, 2011). In either case, processing speed has been assessed with a variety of measures. In a review of 172 studies, Sheppard and Vernon (2008) reported that these measures range from reaction time (e.g., Hick paradigm type-tasks) to general speed of information processing (e.g., visual search and trail making), or even speed of short- and long-term memory retrieval (e.g., Sternberg’s task;Sternberg, 1966). Sheppard and Vernon concluded that “there is a certain arbitrariness inherent to such a classification” (p. 537).

Evidence in favour of conceptualizing processing speed as a unitary ability comes from correlational studies focusing on mean response times (see Hunt, 2011, for a review), mental chronometry (e.g., Jensen, 2006; Levine, Preddy, & Thorndike, 1987), and their relation to intelligence (e.g., Hunt, 2011). These indexes of individual performance appear to produce different correlations with ability measures, depending on the tasks’ complexity (see Dodonova & Dodonov, 2013, for a review). Nevertheless, the results of several studies converge on the conclusion that reaction time is a unitary construct capturing individual differences in the efficiency of information processing and that processing speed is highly correlated with cognitive ability (e.g., Demetriou, Christou, Spanoudis, & Platsidou, 2002; Sheppard & Vernon, 2008). In fact, Jensen (2006) concluded that the use or addition of processing speed measures to the assessment of intelligence increases the predictive power of the extracted g. This occurs because cognitive speed does not only determine the duration of processing, but may also affect the efficiency of processing in simple (e.g., perceptual decision) or complex (e.g., working memory) cognitive tasks. In fact, studies that have espoused processing speed as a unitary ability have concluded that cognitive or processing speed refers to a wide variety of tasks (e.g., Levine, Preddy, & Thorndike, 1987; Michiels, de Gucht, Cluydts, & Fischler, 1999) utilized to measure information processing, and that simple and complex measures of reaction time share a general speed of information processing factor.

Evidence in favour of conceptualizing processing speed as a distinct set of abilities comes from studies examining the neurobiological explanations of age-related changes in processing speed (e.g., Allen et al., 2001; Salthouse, 2000; Schmiedek & Li, 2004) and the extent to which processing speed is treated as a possible mediator of age-related changes to other abilities, including those that are related to executive functions (e.g., McAuley & White, 2011; Span, Ridderinkhof, & van der Molen, 2004). The results of these studies have demonstrated that (a) processing speed does not involve a single neural system, but it is rather a reflection of coordinated activity across multiple neural networks, (b) age-related improvements in processing speed contribute to age-related improvements in other abilities, such as response inhibition and working memory, and (c) there is very little shared variance between simple and complex measures of reaction time (see, e.g., Chiaravalloti, Christodoulou, Demaree, & DeLuca, 2003).

We argue here that the hypothesis supporting processing speed as a unitary construct is likely untenable, particularly if we consider that there is no unitary speed for all neural processing (Eckert, Keren, Roberts, Calhoun, & Harris, 2010). Salthouse (1996) has further argued that the human cognitive system can be better conceptualized as having a relatively “small number of speed factors” (p. 417) that are related to age and contribute to the efficiency of many cognitive processes, including speed of processing, working memory, long-term memory, and reasoning. This hypothesis has been confirmed by examining how cognitive performance is degraded when processing is getting slower as a result of age (Schroeder & Salthouse, 2004). Likewise, Allen et al. (2001) concluded that models representing cognitive processing, such as processing speed, as a set of independent factors may be more empirically parsimonious than single common factor models.

Consequently, one could argue that speed may depend on the kind of information being processed (see Cepeda, Blackwell, & Munakata, 2013; Kazi, Demetriou, Spanoudis, Zhang, & Wang, 2012, for a similar argument). Some information may be processed fast and automatically (e.g., naming of single digits), other information may be processed slowly and intentionally (e.g., naming only the odd numbers among a string of digits). This task-specific view has two advantages: it defines processing in terms of certain kinds of tasks and provides further information regarding the specific cognitive processes involved in performing those tasks. For instance, although we know that, in broad terms, as learning occurs and automaticity is achieved, there is a form of decreased global activation and a change in activity from cortical to subcortical regions (e.g., Little, Klein, Shobat, McClure, & Thulborn, 2004), this pattern of activation also depends on the requirements of the tasks (Saling & Phillips, 2007). In fact, Dunst et al. (2014) recently examined the effect of person-specific and sample-based differences in task difficulty on neural efficiency¹ and concluded that neural efficiency reflects an (ability-dependent) adaptation of brain activation to the respective task demands. Therefore, increasing task difficulty requires stronger activation for participants, and thus, results in lower response rates. Interestingly, an interactive effect of culture and task on brain activation has also been reported (see Hedden, Ketay, Aron, Markus, & Gabrieli, 2008), showing an increase in sustained attentional control during tasks requiring a processing style for which individuals are less culturally prepared.

In light of these contrasting views of processing speed, it is surprising that no studies to date have contrasted these views in the same study rather than trying to find support in favour or against a specific view. Thus, in this study, we evaluated the fit of the above theory-driven models supporting either the distinct abilities processing speed hypothesis or the unitary ability processing hypothesis using the nested factor modelling approach, and we explored the measurement stability across cultures. We believe that testing competing alternative models in a single study is necessary and has obvious implications for directing the theory and applications on the speed of processing in explaining cultural-related cognitive differences, if any exist.

In addition, to our knowledge, no previous studies have examined if the same structure of processing speed applies to different cultures. Seeking cross-cultural universality as well as specificity for the structure of cognitive processes is certainly not new. Heine and Norenzayan (2006) proposed a distinction between evoked and transmitted cultures. On the one hand, as different groups and nationalities of people live in different ecological niches, they may evoke different ways to solve the same human problems. This may cause underlying cognitive mechanisms to be expressed differently. Transmitted culture, on the other hand, is acquired through social learning. Thus, cross-cultural comparisons, which consider both evoked and transmitted aspects of culture, are particularly useful for understanding the adaptive and functional aspects of cognitive processing (Demetriou et al., 2005).

Indeed, at a more fundamental level of cognitive processing, that of processing speed and working memory, Demetriou et al. (2005) reported that Greek and Chinese children performed equally well. Only in tasks requiring visual/spatial processing, Chinese children outperformed Greek children, a finding that is attributed to the extensive practice in visual/spatial processing that is required to learn the Chinese logographic writing system. Findings from reading studies also conclude that visual-spatial relationships predict unique variance in Chinese character recognition, even after controlling for vocabulary and speeded naming (McBride-Chang, Chow, Zhong, Burgess, & Hayward, 2005). They also highlight that visual-spatial skills and Chinese reading ability are significantly and reciprocally associated with each other (see, e.g., Lin, Sun, & Zhang, 2016). Similarly, Kazi et al. (2012) investigated the intellectual development in 4–7 years old Greek and Chinese children and reported that the differences between the two group in processing efficiency and representational capacity —as defined by the maximum amount of representations the mind can efficiently activate simultaneously—were limited only to aspects that could be directly associated with the writing system. Interestingly, Greek children outperformed Chinese children on the Simon task, which relies less on the early learning needs of the logographic writing. Nevertheless, there are also studies comparing Chinese with American or European participants on measures of processing speed which have reported significant differences in favor of the Chinese group (see, e.g., Kail, McBride-Chang, Ferrer, Cho, & Shu, 2013; Lynn & Vanhanen, 2002), although others have highlighted that these group differences disappear when tasks involve executive processes (e.g., Chincotta & Underwood, 1997; Hedden et al., 2002). Whether the superiority of Chinese participants in speed of processing measures translates to differences in the structure of processing speed remains to be examined.

The Present Study 

The purpose of this study was twofold: (a) to examine the nature of speed of processing by contrasting three competing theoretical models and (b) to examine if the findings can be replicated across three cultural groups (Chinese, Canadian, and Greek). Regarding the first objective, we operationalized speed of processing with response time measures of planning, attention, simultaneous and successive (PASS) processing. These measures were adapted from the Das-Naglieri Cognitive Assessment System (D-N CAS; see Naglieri & Das, 1997; see below for more information on the adaptation). The PASS theory of intelligence proposes that the maintenance of attention, the processing and storing of information, and the management and direction of mental activity comprise the activities of the operational units that work together to produce cognitive functioning (Das, Sarnath, Nakayama, & Janzen, 2013). Specifically, cognition is organized in three systems, namely, the planning, the attention and arousal, and the processing systems. The planning system involves executive functions responsible for regulating and programming behavior, selecting and constructing strategies, and monitoring performance, and is located in the frontal cortex. The attention system refers to the ability to demonstrate focused, selective, sustained, and effortful activity over time and resist distraction, and is located in the posterior parietal cortex. Finally, the third system includes simultaneous and successive coding of information and is located in the posterior (occipital, parietal, and temporal) cortex. Simultaneous processing involves the arrangement of incoming information into a holistic pattern that can be surveyed in its entirety. Successive processing, in turn, refers to coding information in discrete, serial order, where the detection of one portion of the information is dependent on its temporal position relative to other material. The operationalization of the PASS theory has been based on the identification of tests that are consistent with the process of interest which can be used to assess speed of processing.

Using PASS theory and the measures from the D-N CAS battery in the present study offers several advantages. First, PASS theory has been argued to provide an alternative look at intelligence Das, 2002; Papadopoulos, Parrila, & Kirby, 2015) and, in our study, we consider speed of processing as an index of intelligence. If Jensen’s (2006) argument that the use of response time measures is an index of a general g factor, then all D-N CAS response time measures should load on a common factor. Second, several previous studies have shown that the measures of PASS yield four separate factors that are linked to each of the cognitive processes (planning, attention, simultaneous and successive processing) and that these factors are invariant across different cultures, including the ones used in this study (Deng & Georgiou, 2015; Naglieri, Taddei, & Williams, 2013; Papadopoulos, 2013).

Third, several of the psychometric tests that have been used to measure processing speed can comfortably fit within the neurocognitive framework of PASS processes (Das, Naglieri, & Kirby, 1994). For example, in D-N CAS, the physical and name identity task by Posner and Boies (1971) that contrasts attention to physical and name identity is widely used as an index of lexical access time. Similarly, Planned Connections (PCn, a transparent adaptation of Trail Making) is part of the neuropsychological tests that index the integrity of frontal lobe functions associated with planning. Finally, because our study involves university students and D-N CAS was originally developed for ages 5–17 to assess accuracy in different cognitive processes, we have a unique opportunity to use the original measures in D-N CAS to obtain response times that are free from accuracy-speed trade-offs (assuming university students will not have problems answering correctly items that have been developed for younger children).

If the speed of processing is a unitary ability, then all measures of response rate, including simultaneous, successive, attention, and planning in the present study should load on one undifferentiated factor (or a common latent factor; see also Salthouse & Czaja, 2000). The possible parsimony of such as a model would indicate that all cognitive indicators share some degree of interrelationship with each other because they are all influenced by the same common factor, that is, speed of processing. Alternatively, if the indicators of speed of processing do not have a unifactorial structure, then all speeded tasks should be categorized under factors representing a variety of cognitive constructs that describe groupings of tasks sharing similar cognitive processing speed requirements. The unitary (e.g., Cella & Wykes, 2013; Chiaravalloti, Christodoulou, Demaree, & DeLuca, 2003; McAuley & White, 2011) and distinct abilities (e.g., Levine, Preddy, & Thorndike, 1987) hypotheses have been proposed and tested mostly in isolation. To the best of our knowledge, this is the first study to examine a third hypothesis, that of a bifactor or nested-factor model (see the Statistical Analysis section for a detailed description), which affords simultaneous estimations of the general and all specific group factors in a given data set, and thereby avoids fixing model parameters to presumably biased values. It is important to note that the differences in these three approaches may be smaller in practice than in theory. Although single or multiple correlated factor models and bifactor models differ considerably at a theoretical level, they are rarely distinguishable on the basis of fit (Mulaik & Quartetti, 1997). Thus, if the single or the multiple correlated factor models examined here have significantly poorer fit than the bifactor model, then that would indicate potential problems with the model specification, that is, the structure of processing speed as has been proposed and tested to date.

Regarding our second objective, we also intended to test the generalizability of the speed of processing construct. Given that the neurocognitive tests that are used in the present study for measuring information processing are founded on basic organization of cognitive functions (Luria, 1973), we hypothesize that they share a common framework of cortical functions. In a sense, that may justify our expectation of unity among different groups separated by geography and culture (Nisbett, 2003).

Method

Participants

Three hundred and twenty undergraduate students from Canada (n = 115; females = 95), China (n = 110; females = 69), and Cyprus (n = 95; females = 60) participated in our study. All participants were full-time third or fourth-year students recruited from the Departments of Elementary Education and Psychology at the University of Alberta (Canada), East China Normal University (China), and University of Cyprus (Cyprus). The elementary education and psychology students who comprised our sample were equally distributed across the three cultural groups and the admission processes in the three universities and departments were similar. All participants were native speakers of their respective language and none reported experiencing any intellectual, sensory, or developmental disorders. Participants received credit towards one of their undergraduate courses for their participation in the study. The mean age of each group was as follows. Canada: M_age = 23.39 years (SD = 6.42); China: M_age = 19.58 years (SD = 1.44), Cyprus: M_age = 20.75 years (SD = 1.40). Pairwise comparisons showed that the Canadian cohort was older than the other two groups. This result was expected given that almost 40% of Canadians enrolled in tertiary education are usually above the age of 22 (The Association of Universities and Colleges of Canada, 2011) and that students at the University of Alberta must enrol in a general program for two years prior to transferring into Education or Psychology. The groups were equivalent on gender, χ² (2, N = 320) = 3.36, p > .05. Ethics permission for the study was obtained from the ethics boards in each university and written consent was obtained from the participants prior to testing.

Measures

Participants were assessed on a computerized version of the D-N CAS (e-adaptation: Papadopoulos, Christoforou, Georgiou, & Das, 2013² ). The development of the computerized version of the D-N CAS was necessary for two reasons: First, most tasks in the traditional D-N CAS assess accuracy. Had we obtained accuracy scores, we would not be able to test Jensen’s (2006) hypothesis that different response time measures form one factor. Second, the D-N CAS allowed similar administration processes to be used across cultures. In the present study, we adapted the Basic Battery of the D-N CAS, in which the four cognitive processes were assessed with two subtests each (8 subtests total). Each task was preceded by two practice trials to ensure the participants understood the demands of the task. The e-version of the D-N CAS allowed us to collect both accuracy and RT data. Thus, time taken to complete each of the individual items and correct responses were recorded for all tasks.

Planning. Planning was assessed with Matching Numbers (MN) and PCn. In MN, participants were shown two pages containing eight rows of numbers each and were asked to click with a mouse the two identical numbers in each row as quickly as possible. There were six numbers of the same length per row, and the numbers increased in length from four to five (Item 1) or six to seven (Item 2) digits, respectively. In PCn, participants were required to connect by clicking with a mouse a series of numbers in numerical sequence (from 1–25; Item 1) or to shift between numbers (1–13) and letters (A–N) in their proper sequence (1 to A, A to 2, 2 to B, and so on; Items 2–3).

Attention. Attention was assessed with Expressive Attention (EA) and Number Detection (ND). In EA, participants were shown nine different frames, categorized into three conditions based on the nature of the targets, and were asked to select (i.e., responses were defined as mouse clicks on target stimuli): (a) the color words of a particular color (Condition 1: color naming condition, e.g., “select by clicking with the mouse all words written in blue color”), (b) a color word written in any color (Condition 2: word reading condition, e.g., “select by clicking with the mouse the word yellow written in any color”), and (c) the colour words written in different colours (Condition 3: interference group condition, e.g., “select by clicking with the mouse the word blue written in red color and the word red written in blue color”). The ratio score of absolute correct (correct - false detections) divided by the response time of the last three frames was used as the participants’ final score (i.e., following the typical procedure to obtain a Stroop interference score, according to the D-N CAS manual). In ND, participants were instructed to find and click the mouse on target numbers (e.g., the numbers 1, 2, and 3 printed in plain font) among several similar distracters printed in plain font (e.g., 4, 5, 6; Item 1) or among several distractors printed in a shadow font (e.g., numbers 1–6; Item 2).

Simultaneous processing. Simultaneous processing was assessed with Matrices (MAT) and Verbal-Spatial Relations (VSR). In MAT, participants were presented with a pattern of shapes/geometric designs that had a missing piece. Participants were asked to choose from six options the missing piece that would best complete the matrix. The task consisted of 32 items. In VSR, participants were required to listen to a question and then click with a mouse on one picture among six different illustrations that demonstrated the spatial relationship raised by the question (e.g., “which picture shows the ball in the basket on the table?”). The task consisted of 27 items.

Successive processing. Successive processing was assessed with Word Series (WS) and Sentence Questions (SQ). In WS, participants were asked to listen carefully to a series of words and then repeat them in the same order. The number of words in the string increased from two to nine throughout the 27 items. For this task, nine single syllable, high-frequency words were employed in all three languages. Time was recorded as soon as the participants pressed the spacebar on the keyboard to listen to the next item. Accuracy was recorded by the experimenter on an answer key form appearing on the computer screen. In SQ, participants heard, through headphones, 20 syntactically and grammatically correct, nonsensical sentences (presented sequentially) and were required to answer a question about the sentence as soon as its presentation was completed. To remove semantic meaning from the sentences and reduce the simultaneous processing load, the content words in these sentences were replaced by color words (e.g., “The blue is yellow. What is yellow?”). Time was recorded as soon as the participants pressed the spacebar on the keyboard to listen to the next item. Accuracy was recorded by the experimenter on an answer key form appearing on the computer screen.

Procedure

Participants were tested individually in a session lasting approximately 45 min in properly equipped rooms at the participating universities. The presentation of the tasks was similar for all three groups. Test administration was fully computerized and took place in the presence of trained graduate students who were familiar with the test administration and data recording of the e-version of the D-N CAS. Participants were asked to make themselves comfortable in front of a TFT-LCD monitor (aspect ratio: 16:9; optimum resolution 1920 x 1080 at 60 Hz) and were allowed to adjust the mouse and mousepad to a location that suited them. After completing the practice items in each task, the participants were asked if they had any questions before proceeding to the test items. Participants moved to the next item by clicking with a mouse on a “Done” button at the bottom of each screen. The data were saved on a local hard drive and were extracted and augmented into a single data file using a Matlab script (The MathWorks , 2012) to generate the files.

Statistical Analysis

Data preparation. To extract the response times in each task, we followed a three-step approach. First, response times associated with incorrect responses (4–7% of the data across tasks and cultures) were eliminated³ . Second, items within a given task to which fewer than 70% of our participants gave the correct answer were treated as missing and the response times associated with them were not used in the calculation of the response time. Again, this was done to avoid any interference of accuracy in the calculation of response times. In response time research, a speed-accuracy trade-off is typically presented as a positive relation between the proportion of correct items and the average time on these items (Van der Linden, 2009). Finally, response times less than 150 ms (technical/anticipation error) or higher than 180 s⁴ were also marked as missing. After these corrections had been made, the participants’ mean response times on each task were recalculated.

Data analyses. We used structural equation modeling (SEM) to test a number of theory-driven models with strong consonance (Mueller & Hancock, 2010): (a) a distinct abilities processing speed model (as dictated by the latent four cognitive processes of planning, attention, simultaneous and successive processing; Models 12, 22, and 32, for the Canadian, Chinese, and Greek groups, respectively; see Figure 1), (b) a unitary ability processing speed model (as dictated only by the latent speed factor; Models 13, 23, and 33; see Figure 2), and (c) a bifactor model, which served as the full model (as dictated by the latent four cognitive factors and the latent processing speed factor; Models 11, 21, and 31; see Figure 3). In the hypothesized models, circles represent latent variables and rectangles represent measured variables. We hypothesized that the latent variables were interrelated in the first two models (with a few exceptions in the full model). In the case of the subscale of latent cognitive processes, scores were expressed as a fraction of the correct responses divided by time. Speed of processing was the composite latent factor made up of all subscale scores (see Rodriguez, Reise, & Haviland, 2016, for calculating bifactor statistical indices).

Figure 1.

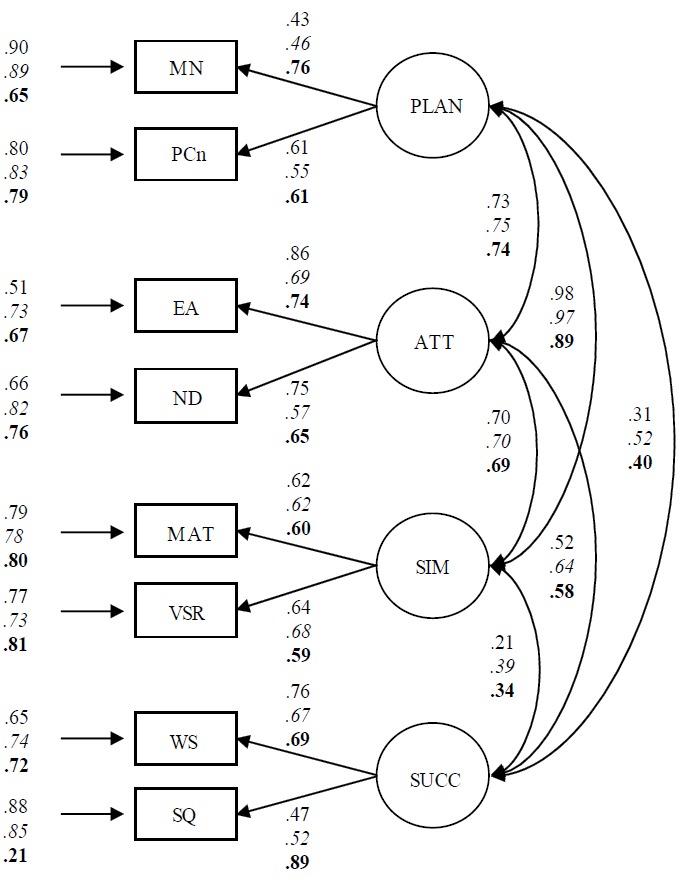
The hypothesized model of distinct abilities of processing speed: Models 12 (Canadian group, plain font), 22 (Chinese group, italics), and 32 (Greek group, bold). All coefficients but those smaller than 0.14 are statistically significant. MN = Matching Numbers; PCn = Planned Connections; EA = Expressive Attention; ND = Number Detection; MAT = Matrices; VSR = Verbal-Spatial Relations; WS = Word Series; SQ = Sentence Questions; PLAN = Planning; ATT = Attention; SIM = Simultaneous Processing; SUCC = Successive Processing.

Figure 2.

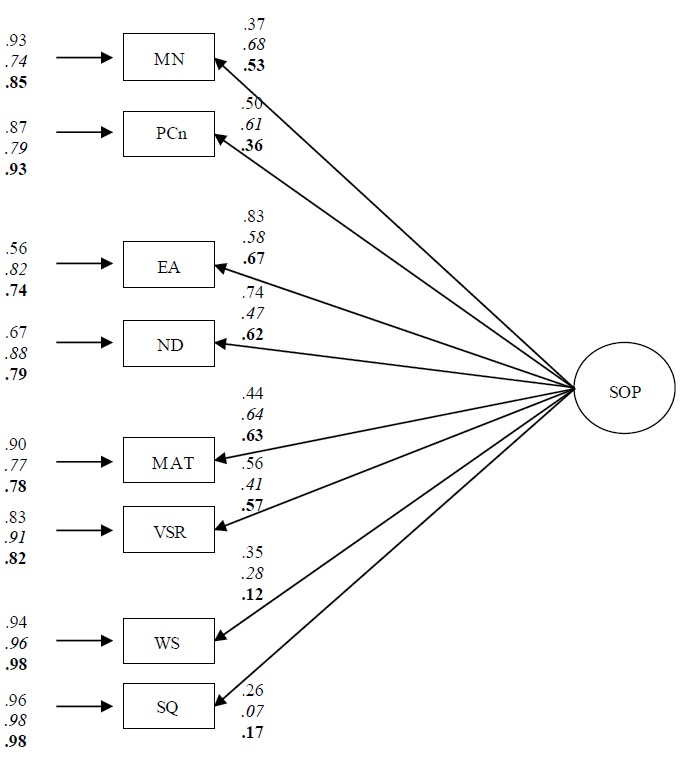
The hypothesized model of unitary ability of processing speed: Models 13 (Canadian group, plain font), 23 (Chinese group, italics), and 33 (Greek group, bold). All coefficients but those smaller than 0.14 are statistically significant. MN = Matching Numbers; PCn = Planned Connections; EA = Expressive Attention; ND = Number Detection; MAT = Matrices; VSR = Verbal- Spatial Relations; WS = Word Series; SQ = Sentence Questions; SOP = Speed of Processing.

Figure 3.

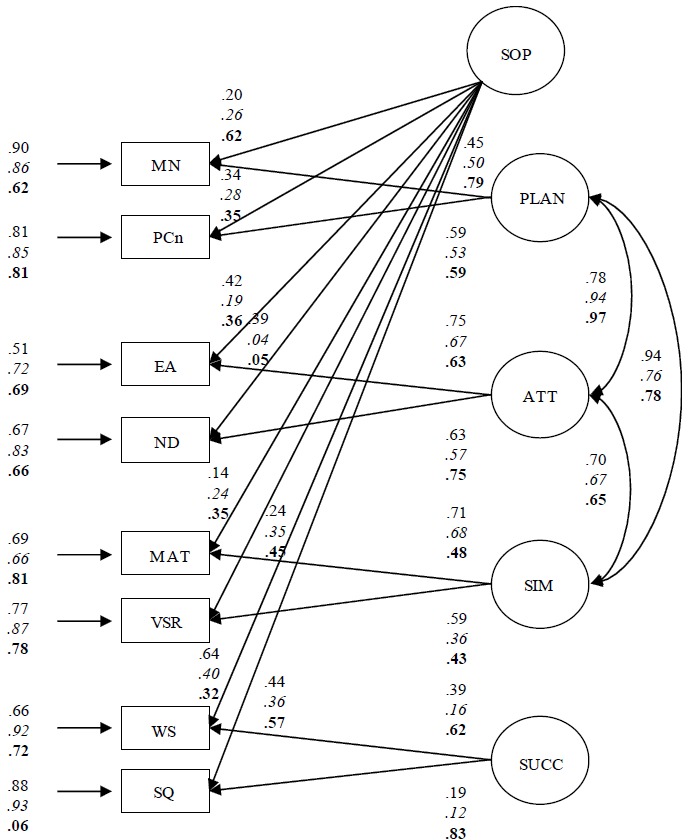
The hypothesized bifactor model of processing speed: Models 11 (Canadian group, plain font), 21 (Chinese group, italics), and 31 (Greek group, bold). All coefficients but those smaller than 0.14 are statistically significant. MN = Matching Numbers; PCn = Planned Connections; EA = Expressive Attention; ND = Number Detection; MAT = Matrices; VSR = Verbal-Spatial Relations; WS = Word Series; SQ = Sentence Questions; PLAN = Planning; ATT = Attention; SIM = Simultaneous Processing; SUCC = Successive Processing; SOP = Speed of Processing.

These models were nested (see Gustafsson & Balke, 1993; Papadopoulos, Kendeou, & Spanoudis, 2012) in that they could be derived by imposing constraints on the speed of processing factor in the case of the distinct abilities processing speed model, and on the latent cognitive factors in the case of the unitary ability processing speed model. These nested models were directly compared using a chi-square difference test, which, in turn, allowed for the selection of the most parsimonious, best-fitting model across the three groups. The difference between the chi-square values for the nested models was itself distributed as chi-square with k degrees of freedom, where k equalled the degrees of freedom for the more constrained model minus the degrees of freedom for the less constrained model. This means that it was possible to test directly whether more constrained models have a significantly poorer fit than less constrained models. In addition, we used fit indexes that take parsimony into account, namely, the Akaike information criterion (AIC) and the expected cross-validation index (ECVI). Although the AIC is more broadly used and accepted as an index reflecting the discrepancy between model-implied and observed covariance matrices (Browne & Cudeck, 1992), we also chose to use the ECVI as a cross-validation index. The ECVI penalizes for a number of free parameters and, therefore, is considered as a more robust index of model comparison. Lower AIC and ECVI indicate a better fit (Byrne, 2006; Hu & Bentler, 1999). Also, we adhered to the following criteria for evaluating good model fit: comparative fit indexes (CFIs) greater than .95 and root-mean-square errors of approximation (RMSEAs) below .07 (Byrne, 2006; Hu & Bentler, 1999).

By introducing and examining the bifactor model, which is parameterized to allow simultaneous indications of (a) the processing speed factor and (b) the four cognitive factors, we could examine whether the bifactor model would account for the intersubtests covariation of the cognitive abilities better than the distinct abilities processing and unitary ability processing speed factor models. These indications would allow for concurrent examination of which of the above, latent scores accounted for the largest portion of variance for all subtests.

Next, to investigate the measurement invariance of the most parsimonious model across the three groups, we used factorial invariance and partial factorial or metric invariance (Byrne, Shavelson, & Muthén, 1989) across groups (Meredith, 1993). Given that the type of processing could be established through the first set of analyses, the objective in this set of analyses was to test the degree to which the obtained model was the same across the three groups, that is, yielding identical factor structure.

In general, factorial invariance routine involves various levels from weaker forms of configural invariance to partial metric invariance (Horn & McArdle, 1992). It also involves testing and comparing nested models that impose successive restrictions on model parameters (Vandenberg & Lance, 2000). Four hierarchical steps of measurement invariance are commonly tested, from less to more constrained: configural, weak (or metric), strong (or scalar), and strict (Meredith, 1993). However, weak and strong invariance constitute at best sufficient evidence for measurement invariance (e.g., Vanderberg & Lance, 2000)⁵.

Results

Preliminary analysis. First, we examined the distributional properties of all measures. We found no significant departures from normality (Tabachnick & Fidell, 2007). The means, SDs, skewness, and kurtosis values for the entire sample are presented in Table 1. Standard scores (z-scores) were used in all further analyses to make dissimilar distributions comparable (Walrath , 2011). Next, we performed a correlational analysis (see Table 2). The correlation analysis showed that most measures were interrelated in all three cultures. As expected, the two measures used for each of the latent factors were strongly related to each other. Also, the attention tasks were found to be significantly related to all the other measures in the Canadian group and with a smaller number of measures in the other two groups (except the successive processing measures). In fact, successive processing measures revealed the smallest number of significant correlations with the other measures, particularly in the Chinese and Greek groups. Finally, the planning measures were significantly related to all measures except those of successive processing (particularly in the Greek group).

Table 1.

Descriptive Statistics on All the Measures

Table 2.

Correlations Among All Measures in All Cultures

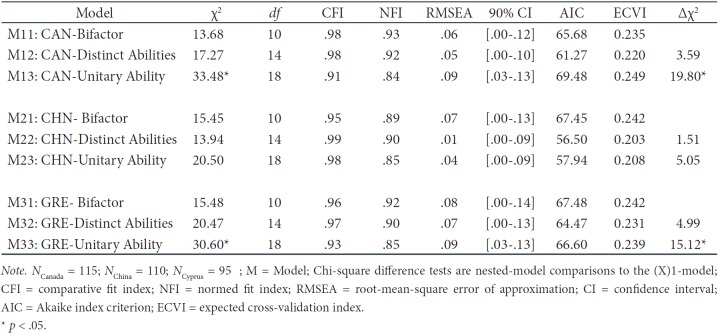
Results of structural equation modeling. In the case of the Canadian and Greek groups, the results of the measurement models indicated a good fit, for both the bifactor (Canadian: χ² [10, n = 115] = 13.68, p = .19; CFI = .98; RMSEA = .06 [CI.90 = .00 to .12]; Greek: χ² [10, n = 95] = 15.48, p = .12; CFI = .96; RMSEA = .08 [CI.90 = .00 to .14]) and the distinct abilities processing models (Canadian: χ² [14, n = 115] = 17.27, p = .24; CFI = .98; RMSEA = .05 [CI.90 = .00 to .10]; Greek: χ² [14, n = 95] = 20.47, p = .12; CFI = .97; RMSEA = .07 [CI.90 = .00 to .13]). The results also suggested that the observed variables had a poor fit to the data fitted in the unitary ability processing speed model for the Canadian and Greek groups. In fact, the unitary ability model produced a Δχ² that had a significantly worse fit to the data than the bifactor model in the Canadian group. In the case of the Chinese group, the distinct abilities (χ² [10, n = 110] = 13.94, p = .45; CFI = .99; RMSEA = .01 [CI.90 = .00 to .09]) and unitary abilities (χ² [14, n = 110] = 20.50, p = .31; CFI = .98; RMSEA = .04 [CI.90 = .00 to .09]) processing models fit the data well. These two models were similar to each other on the basis of the overall goodness of fit, in spite of the associated AIC and ECVI values that seemed to favour the distinct abilities processing model over the unitary model. It is likely that these negligible differences are better explained as a result of the complexity of each of the models (four vs. one parameters) rather than as a result of a statistical comparison of the two models (Brown, 2006). To conclude, the distinct abilities processing speed model had a better fit to the data and better represented the construct of processing speed compared with the unitary ability processing speed and bifactor models in all three groups.

To conclude, the distinct abilities processing speed model had a better fit to the data and better represented the construct of processing speed compared with the unitary ability processing speed and bifactor models in all three groups.

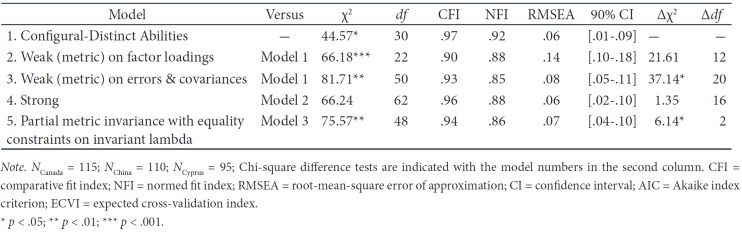
Model factorial invariance. To test the configural invariance of the type of processing across the three groups, we analyzed the data by fitting the three sets of data with the latent cognitive factors model (i.e., the distinct abilities processing, Models 12, 22, and 32). This initial baseline model provided the basis for the comparison with the three subsequent models in the invariance hierarchy, testing, in turn, for weak, strong, and partial metric invariance. Model fit was evaluated using chi-square difference tests and change in relative fit indices.

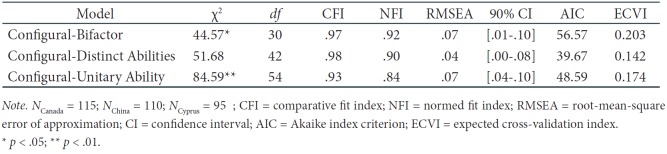
First, we determined which of the three models had a better model fit (see Table 3). The analysis showed that the models representing processing speed as a latent distinct abilities structure had a better model fit, χ² (42, n = 320) = 51.67, p = .15; CFI = .98; RMSEA = .04 (CI.90 = .00 to .08), with the pattern of fixed and free parameters being equivalent, producing the lowest AIC and ECVI among the three configural models that were tested.

Table 3.

Fit Indices for Models of Distinct Abilities Processing, Unitary Ability Processing Speed, and the Bifactor Model

Next, we tested the hierarchy of models.Table 4 describes the tests of factor and measurement invariance and provides evidence for similarities and differences across the three groups (Canadian, Chinese, and Greek groups): (a) same pattern of fixed and free parameters for each group (configural invariance or baseline model), (b) factor loadings invariant across the groups (weak or metric factorial invariance), (c) indicators’ intercepts invariant (strong factorial invariance), and (d) equality of indicator residual variances (partial metric invariance).

Table 4.

Fit Indices for All Three Configural Models

The analysis showed that factor loadings were invariant across groups. The intercept indicators were also invariant. Evaluation of fit indexes among the configural, weak, and strong models revealed a statistically significant difference in chi-square values and relative fit indexes between configural and weak models, suggesting that the configural model was the acceptable model based on the comparisons among the models and on the basis of robust criteria for model fit: Δχ² (1, N = 320) = 44.57, p < .05, CFI = .97 NFI = .92, RMSEA = .06 (90 % CI [.01 to .09]). This finding provides evidence that the obtained construct of distinct abilities processing speed as an index of cognitive processing was the same across groups.

Next, partial metric invariance was conducted because weak invariance produced a significant increase in model chi-square (Δχ² = 37.14, p < .01) when the invariance of errors and covariances were concurrently tested. This means that, although the results suggested that for all three groups the data were well described by the distinct abilities processing model as an index of cognitive processing, they did not necessarily imply that the actual factor loadings were the same across groups. Thus, the hypothesis of the equivalency of factor loadings across groups or of the parameters being invariant across groups was tested by imposing equality constraints on lambda between adjacent groups. This analysis was performed to further examine the parsimony of the distinct abilities processing model between adjacent groups. In essence, partial invariance evaluation of the model fit was used as a post hoc procedure so we could provide a compelling account for the parameters or the sources of noninvariance (Byrne, Shavelson, & Muthén, 1989). The analyses resulted in a better model fit compared with the initial models with no imposed parameter constraints (seeTable 5).

Table 5.

Fit Indices for the Distinct Abilities Model in the Invariance Sequence

This means that a particular variable caused the misfit in the adjacent groups. Specifically, the results indicated that the single one constraint that was significant for this outcome was the VSR test (χ² = 7.49, p < .01). This means that the VSR caused the misfit in this final model, being inconsistent between the Chinese and Canadian groups, with the former group outperforming the latter.

Discussion

The primary goal of the present study was to examine the nature of processing speed by contrasting three theoretical models, namely, a distinct abilities processing speed model, a unitary ability processing speed model, and a bifactor model. Our findings supported the distinct abilities hypothesis, showing that speeded tasks are better categorized under different cognitive processes. In this model, there were four latent cognitive processes of planning, attention, and information processing abilities which were strongly interrelated. In conjunction with the results from the factorial invariance analysis, the answer to the question regarding the nature of processing speed is clear and robust in supporting the presence of a distinct abilities construct.

Two aspects of the present findings significantly contribute to the existing literature. First, that processing speed is a nonunitary construct strengthens existing evidence showing that speed of processing represents cognitive strategies that are specific to particular tasks and abilities (e.g., Danthiir, Wilhelm, & Roberts, 2012; Kazi, Demetriou, Spanoudis, Zhang, & Wang, 2012; Roivainen, 2011). The divergence among tasks measuring planning, attention, and simultaneous and successive processing speed indicates that although all tasks may require speed of cognitive processing for successful completion, speed is not a general factor. Therefore, testing the nature of processing speed within a theoretical framework of cognitive abilities (in our case within the context of the PASS theory of intelligence) allowed us to confirm previous findings that processing speed does not involve a single neural system, but is rather a reflection of coordinated activity across multiple neural networks (Eckert, Keren, Roberts, Calhoun, & Harris, 2010).

More importantly, the finding that a significant improvement in model fit can be achieved by modeling a processing speed construct as a collection of cognitive processes rather than a unitary processing speed factor demonstrates the importance of this approach for the relevant research. The distinct abilities processing model that eventually emerged as metrically the most parsimonious was also theoretically superior to the unitary and bifactor abilities models for an important reason. The unitary and bifactor ability models add confusion about what kind of ability processing speed is. Processing speed, in the case of these two models, is a necessary consequence of a positive manifold. It is always possible to extract a single general speed factor (unitary model), and for this factor to correlate positively with all the manifest variables when there are positive entries in a correlation matrix (bifactor model). However, this is a mathematical necessity and not an empirical finding that explains how processing speed relates to cognitive processing. In contrast, with the use and acceptance of a distinct abilities model, thus treating speed as an integral component of cognitive abilities, it allowed for understanding how processing speed supports cognitive performance. Specifically, it challenged the idea that an underlying factor causes the across-abilities correlations between various speeded tests. Thus, our findings provide additional evidence to the argument that processing speed is a pervasive trait because all mental actions depend on neural processing (Hunt, 2011), and that processing speed should not be conceptualized as a separate factor. Simply put, the speed with which an individual performs a cognitive activity is a function of the processes required for that activity.

Second, using factorial invariance within SEM, our results showed that the distinct abilities hypothesis of processing speed remained invariant across three cultural groups (Chinese, Canadian, and Greek). This finding adds value to the search for the nature of the processing speed construct because it indicates that the latent constructs represented what was common among the constituent variables, and this representation was not different across cultures. This does not really deviate from the findings of previous studies that reported cross-cultural differences in processing speed subtests, particularly in favour of the Chinese groups compared to US groups (Kail, McBride-Chang, Ferrer, Cho, & Shu, 2013; Lynn & Vanhanen, 2002; Millar, Serbun, Vadalia, & Gutchess, 2013; Roivainen , 2010). If there are any, they are likely manifested only in speeded performance measures that are related to the role of language, as we partially observed in the case of the VSR task. McBride-Chang et al. (2011) have underscored the potential importance of the process of learning to read for shaping one’s visual-spatial skill development (see also Kazi, Demetriou, Spanoudis, Zhang, & Wang, 2012), a finding that has been also confirmed using functional magnetic resonance imaging (Tan et al., 2001). At any rate, again, the loadings of speed tests on four factors may be invariant, but differences in mean performance of speed tests can be significant⁶.

Certainly, following up on Nisbett’s (Nisbett, 2003) geography of thought, language, literacy environment, and cultural emphasis on types of processing are a few of the significant variables that explain diversity in cognitive processes (Das, 2015). Add to this that, in some cultures, accuracy is regarded as predominantly important rather than speed in the speed-accuracy tradeoff, and the discussion of such determinants of diversity could grow longer. Although it is beyond the scope of our present study, it is an important direction to pursue in future studies.

A similar issue which underscores the role of speed as an integral component rather than a separate factor of the processes required in an activity concerns research on the treatment of time as a separate factor in intelligence testing or learning conditions. For example, Chuderski (2013) has concluded that when fluid intelligence tests are administered with strong time restrictions, and thus, with processing speed as a separate factor which imposes high demands on working memory capacity, the internal and external reliability of the fluid intelligence measures are disrupted. In contrast, when liberal time restrictions are applied, iterative reasoning processes are promoted. Similarly, Ren, Wang, Sun, Deng, and Schweizer (2018) have shown that the consideration of processing speed as a separate latent factor leads to a decrease of the correlation between intelligence and working memory. Finally, intense time pressure during a learning episode has been found to prevent learning which is effective under no such pressure (Chuderski, 2016). Given all of the above, speed of processing can act as a critical processing constraint when it is treated as a separate (i.e., Model 3—bifactor model) or overarching (i.e., Model 2—latent factor speed) construct, as cognitive performance appears distorted due to speed factors unrelated to the individuals’ processing abilities (Estrada, Román, Abad, & Colom, 2017).

Two limitations of the present study are worth noting. First, we did not administer measures of speed of processing from existing psychometric batteries to examine how our measures related to them. We consider it necessary to generalize these findings to other cognitive tasks batteries. Second, we chose to conduct the study in early adulthood, when cognition begins to stabilize (Brizio, Gabbatore, Tirassa, & Bosco, 2015) and in line with previous response time studies based on homogeneous age groups of young adults (Jensen, 2006). However, it would have been interesting to explore the same hypothesis across different age groups. Finally, to the degree that these findings are replicable, a future direction of relevant research could focus on addressing the issue of factorial invariance of the distinct abilities processing speed construct in other different cultural groups and languages.

To conclude, our findings add to a growing body of research on processing speed by showing that it can be better understood as a collection of different cognitive processes rather than a unitary processing speed factor. We acknowledge that diversities in cognitive processes exist; these are as interesting as discovering the basis of unity (Demetriou & Papadopoulos, 2004) and exploring how cognitive processes develop and function within particular cultural contexts. However, we do not expect the argument in favor of speed of processing as a reflection of cognitive capacity to die anytime soon. As it has been said, theories do not die, they are merely superseded. In this case, particularly, by new findings from neuroscience.