Proper Orthogonal Decomposition-Based Method for Predicting Flow and Heat Transfer of Oil and Water in Reservoir

Abstract

Calculation process of some reservoir engineering problems involves several passes of full-order numerical reservoir simulations, and this makes it a time-consuming process. In this study, a fast method based on proper orthogonal decomposition (POD) was developed to predict flow and heat transfer of oil and water in a reservoir. The reduced order model for flow and heat transfer of oil and water in the hot water-drive reservoir was generated. Then, POD was used to extract a reduced set of POD basis functions from a series of “snapshots” obtained by a finite difference method (FDM), and these POD basis functions most efficiently represent the dynamic characteristics of the original physical system. After injection and production parameters are changed constantly, the POD basis functions combined with the reduced order model were used to predict the new physical fields. The POD-based method was approved on a two-dimensional hot water-drive reservoir model. For the example of this paper, compared with FDM, the prediction error of water saturation and temperature fields were less than 1.3% and 1.5%, respectively; what is more, it was quite fast, where the increase in calculation speed was more than 70 times.

1. Introduction

The aims of some reservoir engineering problems [1–7], such as optimal control of reservoir production and history matching, are to determine the optimal parameter sets (well controls or physical properties). Several methodologies [8–18] including ensemble-based optimization methodologies, quadratic interpolation, and gradient-based methodologies have been applied to determine the optimal parameter sets. The gradient-based algorithms [19] have been by far the most classical methods for calculating the optimal parameter sets, in which gradually approaching the optimal values is achieved via constantly calculating new gradients. However, calculating gradients [20] requires several passes of full-order numerical reservoir simulations which yield large amounts of partial differential equations. The computational time required is always very alarming, a typical reservoir model always contains 106−108 grid blocks, and the computational time for calculating the optimal well controls requires several days or even weeks, and this has been a hindrance for applying the reservoir numerical simulation technique in reservoir engineering problems [21,22]. In order to better apply the reservoir numerical simulation results in the reservoir engineering, a method that could not only save large amounts of computational time but also ensure physical accuracy for calculating physical fields in the reservoir is urged to be developed.

Model reduction [23] has been widely used for decreasing the computational costs in science and engineering fields. A few model reduction methods have been used in the physical system whether governing equations are linear or nonlinear. These methods generate the reduced order model by means of projecting the governing equations onto the subspace spanned by a reduced set of basis functions typically via the “Galerkin projection” [24], where the basis functions represent the dynamic characteristics of the original large-scale physical system and then the reduced order model is used to predict the behavior of the original physical system. These basis functions can be obtained from the Lagrange basis, the Taylor basis, the Fourier basis, and so on. However, these basis functions cannot accurately represent the dynamic characteristics of the original physical system, and this may lead to a large loss of computational accuracy for the reduced order model. In order to avoid this disadvantage, proper orthogonal decomposition (POD) [25] method is advised. POD method obtains basis functions from a large number of state solutions (snapshots) over a desired range of parameters from actual experimental data or high fidelity numerical simulations. The significant advantage of the POD basis functions is its energetic optimality: few POD basis functions may contain almost the total energy, so they can most efficiently approximate the dynamic characteristics of the original physical system. POD is also known as principal component analysis [26], which has been successfully applied in a number of fields, for example, signal analysis [27], fluid dynamics [28–30], inverse problems [31,32], and optimal control problems [33–35]. All of them indicated that POD helped to extract most dominant structures from the complex physical fields. In general, the previous work shows that there have been few reported results addressing that POD is applied in reservoir engineering fields.

This paper presents the application of POD in predicting flow and heat transfer of oil and water in the reservoir. The fundamentals of POD are described in Sec. 2. Then, the process of generating the reduced order model for the flow and heat transfer of oil and water in the reservoir is shown in Sec. 3. Thereafter, in Sec. 4, we show an example in which the reduced order model is applied in a two-dimensional hot water-drive reservoir model, and the performance of the POD-based method is examined by comparing its computational results with that of the finite difference method (FDM).

2. Fundamentals of the POD-Based Method

Mathematical description of POD. f(X, t_n) (n = 1, 2, …, N) is assumed to denote a solution (snapshot) of water saturation or temperature fields of the hot water-drive reservoir obtained by the numerical reservoir simulation. The variables X and t represent the space variable and the time variable, respectively. Snapshots are stored in a rectangular L × N matrix called F, where L and N denote the number of grid blocks and snapshot, respectively.

The purpose of POD is to obtain a reduced set of basis functions {φ_k(X), k = 1, 2, …, N} from the matrix F, where the φ_k(X) is just related to the space variable X. These basis functions can best correlate with the dynamic characteristics of the original physical fields. Then, f(X, t_n) can be reconstructed as

$$f(\mathbf{X},t_n)=\sum _{k=1}^N{c}_k(t_n){\phi }_k(\mathbf{X}),n=1,2,\dots ,N$$ (1)

where c_k(t_n) are spectral coefficients which are just related to the time variable t.

Snapshots method. According to the POD theory [36], the POD basis function φ(X) is calculated by maximizing the projection from f(X, t_n) to φ(X), which can be described by

$$\mathrm{MAX}\left\{\lambda ={\displaystyle \frac{⟨{(f(\mathbf{X},t_n),\phi (\mathbf{X}))}^2⟩}{(\phi (\mathbf{X}),\phi (\mathbf{X}))}}\right\}$$ (2)

where 〈 · , · 〉 denotes the ensemble average and ( · , · ) is the standard Euclidean inner product.

A linear operator R on φ(X) is defined as

$$\begin{array}{rl}R\phi (\mathbf{X})& ={\int }_{\mathrm{\Omega }}(f(\mathbf{X},t_n),f({\mathbf{X}}^{\prime },t_n))\phi ({\mathbf{X}}^{\prime })d{\mathbf{X}}^{\prime }\\ & ={\int }_{\mathrm{\Omega }}{\displaystyle \frac{1}{N}\sum _{n=1}^{N}f(\mathbf{X},t_n)f({\mathbf{X}}^{\prime },t_n)\phi ({\mathbf{X}}^{\prime })}d{\mathbf{X}}^{\prime }\end{array}$$ (3)

Therefore,

$$\begin{array}{rl}& (R\phi (\mathbf{X}),\phi (\mathbf{X}))\\ & ={\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}{\displaystyle \frac{1}{N}}\sum _{n=1}^{N}f(\mathbf{X},t_n)f({\mathbf{X}}^{\prime },t_n)\phi ({\mathbf{X}}^{\prime })d{\mathbf{X}}^{\prime }\phi (\mathbf{X})d\mathbf{X}\\ & ={\displaystyle \frac{1}{N}\sum _{n=1}^N{\int }_{\mathrm{\Omega }}f(\mathbf{X},t_n)\phi (\mathbf{X})d\mathbf{X}{\int }_{\mathrm{\Omega }}f({\mathbf{X}}^{\prime },t_n)\phi ({\mathbf{X}}^{\prime })d{\mathbf{X}}^{\prime }}\\ & ={\displaystyle \frac{1}{N}\sum _{n=1}^N{(f(\mathbf{X},t_n),\phi (\mathbf{X}))}^2}\\ & =⟨{(f(\mathbf{X},t_n),\phi (\mathbf{X}))}^2⟩\end{array}$$ (4)

Therefore, Eq. (2) can be further written as

$$\mathrm{MAX}\left\{\lambda ={\displaystyle \frac{⟨{(R\phi (\mathbf{X}),\phi (\mathbf{X}))}^2⟩}{(\phi (\mathbf{X}),\phi (\mathbf{X}))}}\right\}$$ (5)

Equation (5) results in an eigenvalue problem that the maximization problem in Eq. (5) is equivalent to how to obtain the eigenvalue λ in Eq. (6).

$${\displaystyle {\int }_{\mathrm{\Omega }}{\displaystyle \frac{1}{N}\sum _{n=1}^{N}f(\mathbf{X},t_n)f({\mathbf{X}}^{\prime },t_n)\phi ({\mathbf{X}}^{\prime })d{\mathbf{X}}^{\prime }=\lambda \phi (\mathbf{X})}}$$ (6)

For calculating λ, the number of grid blocks may be far larger than the number of snapshots; this requires very large computational resources in practical numerical simulation. To avoid this disadvantage, the “snapshots method” was proposed by Sirovich [37]. Sirovich assumes that each POD basis function is a linear combination of snapshots, that is

$${\phi }_k(\mathbf{X})=\sum _{n=1}^N{\alpha }_n^{k}f(\mathbf{X},t_n)$$ (7)

Substituting Eq. (7) into Eq. (6), we have

$$\begin{array}{rl}& {\int }_{\mathrm{\Omega }}{\displaystyle \frac{1}{N}}\sum _{i=1}^{N}f(\mathbf{X},t_i)f({\mathbf{X}}^{\prime },t_i)\sum _{j=1}^N{\alpha }_{j}f({\mathbf{X}}^{\prime },t_j)d{\mathbf{X}}^{\prime }=\lambda \sum _{i=1}^N{\alpha }_{i}f(\mathbf{X},t_i)\end{array}$$ (8)

Equation (8) can be further written as

$$\begin{array}{rl}& \sum _{i=1}^N\left[\sum _{j=1}^N{\displaystyle \frac{1}{N}{\int }_{\mathrm{\Omega }}f({\mathbf{X}}^{\prime },t_i)}f({\mathbf{X}}^{\prime },t_j)d{\mathbf{X}}^{\prime }{\alpha }_j\right]f(\mathbf{X},t_i)=\lambda \sum _{i=1}^N{\alpha }_{i}f(\mathbf{X},t_i)\end{array}$$ (9)

Thus, α can be obtained through solving

$$\mathbf{C}{\mathbf{\alpha }}^{(n)}={\lambda }_n{\mathbf{\alpha }}^{(n)},n=1,2,\dots ,N$$ (10)

where C is an N-dimensional matrix, λ_n is the eigenvalue of C, and α⁽ⁿ⁾ is the corresponding eigenvector.

According to Eq. (9), the element of C can be defined as

$${\mathbf{C}}_{i,j}={\displaystyle \frac{1}{N}{\int }_{\mathrm{\Omega }}f({\mathbf{X}}^{\prime },t_i)f({\mathbf{X}}^{\prime },t_j)d{\mathbf{X}}^{\prime }}$$ (11)

It can be easily seen from Eq. (11) that C is an N-dimensional positive and symmetric matrix, in that it has a set of orthogonal eigenvectors.

Now, the problem of how to obtain the POD basis function φ(X) in Eq. (6) can be attributed to how to calculate the eigenvalue λ_n and the corresponding eigenvector α⁽ⁿ⁾ of matrix C, which can be easily solved by the numerical method. This helps to construct the POD basis function using Eq. (7). In addition, it is easy to check

$$({\phi }_i(\mathbf{X}),{\phi }_j(\mathbf{X}))=\{\begin{array}{cc}1,& i=j\\ 0,& i\ne j\end{array}$$ (12)

Energy optimality of POD basis functions. The magnitude of λ_n represents the amount of energy captured by the corresponding POD basis function from the physical fields, and the energy represents the contribution of every POD basis function to the construction of the total physical fields [37]. Therefore, φ(X) are always ordered by arranging their corresponding eigenvalues in decreasing order as λ₁ > λ₂ > · · · > λ_N.

In order to quantitatively illustrate the contribution degree of every POD basis function to the total energy, the participant energy proportion ξ_n and cumulative energy proportion η_n are defined as follows:

$${\xi }_n={\displaystyle \frac{{\lambda }_n}{{\sum }_{n=1}^N{\lambda }_n},{\eta }_n={\displaystyle \frac{{\sum }_{n=1}^M{\lambda }_n}{{\sum }_{n=1}^N{\lambda }_n},M\le N}}$$ (13)

where ξ_n represents the ratio of energy contained in the nth POD basis function to the total energy and η_n denotes the ratio of energy contained in the first M POD basis functions to the total energy.

According to the energy optimality [36,37], only the first M (M ≪ N) POD basis functions can make η_n be more than 99.9%, and M means the truncation degree. Thus, only the first M POD basis functions are retained to approximate the total physical fields, that is

$$f(\mathbf{X},t_n)=\sum _{k=1}^M{c}_k(t_n){\phi }_k(\mathbf{X}),M\ll N$$ (14)

Reduced order model of the hot water-drive reservoir. In order to predict the physical fields in the hot water-drive reservoir by Eq. (14), evolution equations regarding c_k(t_n) should be generated, and the evolution equations are called the reduced order model; this can be obtained by the “Galerkin projection” method.

The fluid and rock in the reservoir are assumed incompressible and the effect of capillary pressure and gravity are neglected; the flow and heat transfer of oil and water in the reservoir in a practical grid block can be described by Jansen et al. [38].

Mass balance equation

Oil phase

$$\mathrm{\nabla }\cdot \left({\displaystyle \frac{\mathit{k}{k}_{ro}}{{\mu }_o}\mathrm{\nabla }{p}_o}\right)+q_o=\varphi {\displaystyle \frac{\mathrm{\partial }{S}_o}{\mathrm{\partial }t}}$$ (15a)

Water phase

$$\mathrm{\nabla }\cdot \left({\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}\mathrm{\nabla }{p}_w}\right)+q_w=\varphi {\displaystyle \frac{\mathrm{\partial }{S}_w}{\mathrm{\partial }t}}$$ (15b)

where the subscripts o and w denote the oil phase and the water phase, respectively; k, k_r, p, S, ϕ, and q are the absolute permeability of rock, the relative permeability of oil and water, the pressure, the saturation, the porosity of rock, and the external volumetric flow rate per unit reservoir volume, respectively.

Energy balance equation

$$\begin{array}{rl}& \mathrm{\nabla }\cdot ({\lambda }_R\mathrm{\nabla }T)+\mathrm{\nabla }\cdot \left(\sum _{i=o,w}{\rho }_i{e}_i{\displaystyle \frac{\mathit{k}{k}_{ri}}{{\mu }_i}\mathrm{\nabla }{p}_i}\right)-q_l+q_H\\ & ={\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left[(1-\varphi )M_{R}T+\varphi \sum _{i=o,w}{S}_i{\rho }_i{e}_i\right]}\end{array}$$ (15c)

where T, M_R, λ_R, ρ, and e are the temperature, the volumetric heat capacity of the rock, the thermal conductivity of the rock, the density of the fluid, and the internal energy of the fluid per unit mass, respectively, and e can be calculated by e = C_i(T − T_R) (i = o, w), in which C and T_R denote the heat capacity of the fluid and the initial reservoir temperature, respectively; q_l denotes the heat loss rate at the top and the bottom of reservoir per unit reservoir volume, and q_l = 0 because all boundaries are assumed adiabatic; q_H denotes the heat input or output rate from the injection wells or production wells per unit reservoir volume which should be calculated at every time step.

In addition, the saturations of oil and water are constrained by

$$S_o+S_w=1$$ (15d)

As the effect of capillary pressure is ignored, the pressures of oil and water are related by

$$p_o=p_w=p$$ (15e)

With the aid of Eq. (14), the pressure, water saturation, and temperature can be expressed as

$$p(\mathbf{X},t)=\sum _{k=1}^{M_p}{c}_k^p(t){\phi }_k^p(\mathbf{X})$$ (16a)

$$S_w(\mathbf{X},t)=\sum _{k=1}^{M_{S_w}}{c}_k^{S_w}(t){\phi }_k^{S_w}(\mathbf{X})$$ (16b)

$$T(\mathbf{X},t)=\sum _{k=1}^{M_T}{c}_k^T(t){\phi }_k^T(\mathbf{X})$$ (16c)

where M_p, $M_{S_w}$, and M_T denote the truncation degree of pressure, water saturation, and temperature, respectively.

If Eq. (15a) is added to Eq. (15b), we get

$$\mathrm{\nabla }\cdot \left(\left({\displaystyle \frac{\mathit{k}{k}_{ro}}{{\mu }_o}+{\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}}}\right)\mathrm{\nabla }p\right)+(q_o+q_w)=0$$ (17)

Substituting Eq. (16) into Eq. (17), Eq. (15b), and Eq. (15c), respectively, we have

$$\mathrm{\nabla }\cdot \left(\left({\displaystyle \frac{\mathit{k}{k}_{ro}}{{\mu }_o}+{\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}}}\right)\sum _{k=1}^{M_p}{c}_k^p(t)\mathrm{\nabla }{\phi }_k^p(\mathbf{X})\right)+(q_o+q_w)=0$$ (18a)

$$\begin{array}{r}\mathrm{\nabla }\cdot \left({\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}\sum _{k=1}^{M_w}{c}_k^{S_w}(t)\mathrm{\nabla }{\phi }_k^{S_w}(\mathbf{X})}\right)+q_w=\varphi {\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left(\sum _{k=1}^{M_w}{c}_k^{S_w}(t){\phi }_k^{S_w}(\mathbf{X})\right)}\end{array}$$ (18b)

$$\begin{array}{rl}& {\lambda }_R\sum _{k=1}^{M_T}{c}_k^T(t)\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^T(\mathbf{X}))\\ & +\sum _{k=1}^{M_p}{c}_k^p(t)\sum _{m=o,w}{\rho }_m{e}_m{\displaystyle \frac{\mathit{k}{k}_{rm}}{{\mu }_m}}\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X}))+q_H\\ & =\left[(1-\varphi )M_R+\varphi \sum _{i=o,w}{\rho }_i{S}_i{C}_i\right]{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}\sum _{k=1}^{M_T}{c}_k^T(t)\mathrm{\nabla }{\phi }_k^T(\mathbf{X})}\end{array}$$ (18c)

Projecting Eq. (18) on the reduced order space spanned by POD basis functions, we have

$$\begin{array}{rl}& \left({\displaystyle \frac{\mathit{k}{k}_{ro}}{{\mu }_o}+{\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}}}\right)\sum _{k=1}^{M_p}{c}_k^p(t)(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X})),{\phi }_i^p(\mathbf{X}))\\ & +((q_o+q_w),{\phi }_i^p(\mathbf{X}))=0(i=1,2,\dots ,M_p)\end{array}$$ (19a)

$$\begin{array}{rl}& \left(\mathrm{\nabla }\cdot \left\{{\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}\sum _{k=1}^{M_{S_w}}{c}_k^{S_w}(t)\mathrm{\nabla }{\phi }_k^{S_w}(\mathbf{X})}\right\},{\phi }_i^{S_w}(\mathbf{X})\right)+(q_w,{\phi }_i^{S_w}(\mathbf{X}))\\ & =\left(\varphi {\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left(\sum _{k=1}^{M_{S_w}}{c}_k^{S_w}(t){\phi }_k^{S_w}(\mathbf{X})\right),{\phi }_i^{S_w}(\mathbf{X})}\right)(i=1,2,\dots ,M_{S_w})\end{array}$$ (19b)

$$\begin{array}{rl}& {\lambda }_R\sum _{k=1}^{M_T}{c}_k^T(t)(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^T(\mathbf{X})),{\phi }_i^T(\mathbf{X}))\\ & +\sum _{k=1}^{M_p}{c}_k^p(t)\sum _{m=o,w}{\rho }_m{e}_m{\displaystyle \frac{\mathit{k}{k}_{rm}}{{\mu }_m}}(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X})),{\phi }_i^T(\mathbf{X}))+(q_H,{\phi }_i^T(\mathbf{X}))\\ & =\left(\left[(1-\varphi )M_R+\varphi \sum _{m=o,w}{\rho }_m{S}_m{C}_m\right]{\displaystyle \frac{\mathrm{\partial }}{\mathrm{\partial }t}\sum _{k=1}^{M_T}{c}_k^T(t)\mathrm{\nabla }{\phi }_k^T(\mathbf{X}),{\phi }_i^T(\mathbf{X})}\right)\\ & (i=1,2,\dots ,M_T)\end{array}$$ (19c)

Using the orthogonality of the POD basis function as shown in Eq. (12), the reduced order model is obtained as follows:

$$\begin{array}{rl}& \left({\displaystyle \frac{\mathit{k}{k}_{ro}}{{\mu }_o}+{\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}}}\right)\sum _{k=1}^{M_p}{c}_k^p(t)(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X})),{\phi }_i^p(\mathbf{X}))\\ & +((q_o+q_w),{\phi }_i^p(\mathbf{X}))=0(i=1,2,\dots ,M_p)\end{array}$$ (20a)

$$\begin{array}{rl}\varphi {\displaystyle \frac{d{c}_i^{S_w}(t)}{dt}}& ={\displaystyle \frac{\mathit{k}{k}_{rw}}{{\mu }_w}\sum _{k=1}^{M_{S_w}}{c}_k^p(t)(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X})),{\phi }_i^{S_w}(\mathbf{X}))}\\ & +(q_w,{\phi }_i^{S_w}(\mathbf{X}))(i=1,2,\dots ,M_{S_w})\end{array}$$ (20b)

$$\begin{array}{rl}& \left[(1-\varphi )M_R+\varphi \sum _{m=o,w}{\rho }_m{S}_m{C}_m\right]{\displaystyle \frac{d{c}_i^T(t)}{dt}}\\ & ={\lambda }_R\sum _{k=1}^{M_T}{c}_k^T(t)(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^T(\mathbf{X})),{\phi }_i^T(\mathbf{X}))\\ & +\sum _{k=1}^{M_p}{c}_k^p(t)\sum _{m=o,w}{\rho }_m{e}_m{\displaystyle \frac{\mathit{k}{k}_{rm}}{{\mu }_m}}(\mathrm{\nabla }\cdot (\mathrm{\nabla }{\phi }_k^p(\mathbf{X})),{\phi }_i^T(\mathbf{X}))\\ & +(q_H,{\phi }_i^T(\mathbf{X}))(i=1,2,\dots ,M_T)\end{array}$$ (20c)

By projecting the initial conditions of physical fields onto each POD basis function, the initial conditions are achieved as

$$\{\begin{array}{l}{c}_i^p(t=0)=(p(\mathbf{X},0),{\phi }_i^p(\mathbf{X})),i=1,2,\dots ,M_p\\ c_i^{S_w}(t=0)=(S_w(\mathbf{X},0),{\phi }_i^{S_w}(\mathbf{X})),i=1,2,\dots ,M_{S_w}\\ c_i^T(t=0)=(T(\mathbf{X},0),{\phi }_i^T(\mathbf{X})),i=1,2,\dots ,M_T\end{array}$$ (20d)

For calculating Eq. (20) at every time step, the water saturation coefficients $c^{S_w}(t)$ can be obtained from Eq. (20b) using the Euler method first. Then, the pressure coefficients c^p(t) can be obtained from Eq. (20a) using the Gauss–Seidel iterative method; finally, the temperature coefficients c^T(t) can be obtained from Eq. (20c) using the Runge–Kutta method together with the achieved c^p(t) and $c^{S_w}(t)$.

For a two-dimensional hot water-drive reservoir with 100 × 100 grid blocks, to obtain the physical fields, 3 × 100 × 100 algebraic equations are required to be solved simultaneously at each time step using FDM. However, using the reduced order model, the number of algebraic equations required to be solved at each time step is reduced from 3 × 100 × 100 to $M_p+M_{S_w}+M_T$, where M_p, $M_{S_w}$, and M_T are always less than 10. Therefore, significant computational time saving is expected to be achieved using the POD-based method.

The calculation process for the POD-based method for predicting flow and heat transfer of oil and water in the reservoir can be decomposed into two steps:

The offline calculation:

Collect snapshots by numerical reservoir simulation.

Construct matrix C using Eq. (11).

Solve Eq. (10) to obtain the eigenvalue λ and corresponding eigenvector α.

Determine the first M POD basis functions with Eq. (7).

The online calculation

Calculate the reduced order model (Eq. (20)) to obtain the spectral coefficients c(t).

Obtain the new physical fields using Eq. (14).

Thus, the calculation procedure to the POD-based method for predicting flow and heat transfer of oil and water in the reservoir is fully specified. The advantage of the POD-based method is that a reduced set of POD coefficients are used as intermediate calculational variables; there is no need to solve a large number of underlying full-order governing equations repeatedly in the online calculation, which considerably reduces the amount of calculation; therefore, a large amount of computational resources and CPU time saving are expected to be achieved in the online calculation. An underlying disadvantage is that the POD basis functions obtained in the offline step may not be able to be shared by multiple runs of the reduced order model corresponding to arbitrary times and parameters of interest, and this may influence the accuracy of the computational results. We will find that it is not a problem in the following example.

2.1. Example and Results.

Example description. A 2D hot water-drive reservoir model is considered. The geometric model and permeability fields are shown in Fig. 1. The reservoir has a dimension of 400 m by 400 m with a thickness of 10 m, in which both fluid (water is the wetting phase and oil is the nonwetting phase) and rock are incompressible. One injection well in which hot water is injected with constant temperature is located at the coordinate (200 m, 200 m) and four production wells are located at the coordinates (5 m, 395 m), (5 m, 5 m), (395 m, 395 m), and (395 m, 5 m), respectively. All boundaries of the domain are closed and adiabatic. The 2D domain is discretized into average meshes made of 40 × 40 rectangular grid blocks. The relevant rock and fluid properties data for this example are provided in Table 1. All fluid and rock properties are assumed constant, except for the oil viscosity which is related to temperature. For particular injection and production wells, WID (injection Index of injection well) and PID (production index of production well) are always constant. In addition, the capillary pressure at the interface of oil and water is neglected. The relative permeability curve of oil and water and the viscosity–temperature curve of crude oil are drawn in Figs. 2 and 3, respectively. The upper bound for the injection rates is limited to 150 m³/d. The lower and upper bounds for the bottom hole flowing pressure of production wells (BHPs) are specified as 0.5 MPa and 2.5 MPa, respectively.

Fig. 1.

Permeability fields of the hot water-drive reservoir model (1 d = 1 µm²)

Table 1.

Relevant data for the example

Meaning	Symbol	Value	Unit
Total porosity	ϕ	0.25	—
Thermal conductivity of the reservoir rock	λR	2.5	W/(m °C)
Volumetric heat capacity of the reservoir rock	MR	2520	kJ/(m3 °C)
Irreducible water saturation	Swc	0.25	—
Initial oil saturation	Soi	0.75	—
Residual oil saturation	Sor	0.2	—
Initial pressure	pi	5.0	MPa
Initial reservoir temperature	TR	25	°C
Initial oil viscosity	μoi	128	mPa s
Water viscosity	μw	1.0	mPa s
Oil density	ρo	930	kg/m3
Water density	ρw	1000	kg/m3
Heat capacity of oil	Co	3.08	kJ/(kg °C)
Heat capacity of water	Cw	4.2	kJ/(kg °C)
Temperature of injection water	Tin	80	°C
Injection index of the injection well	WID	12,000	md m
Production index of the production well	PID	10,000	md m

Fig. 2.

The relative permeability curve of oil and water

Fig. 3.

The viscosity–temperature curve of oil

3. Results

Offline calculation. The snapshots for calculating POD basis functions are obtained by simulating the governing equations (Eq. (15)) with FDM in the time interval (0 d, 1000 d) with the time step t (t = 1 d), where the water injection rate is 150 m³/d and the BHP for every production well is 1.0 Mpa, respectively. Two hundred pressure snapshots, 200 water saturation snapshots, and 200 temperature snapshots are recorded at constant time intervals t* (t* = 5t). Then, the matrix C_i (i denotes pressure, water saturation, and temperature) is formed using Eq. (11) and 200 eigenvalues together with 200 sets of corresponding eigenvectors of matrix C_i are obtained. Thus, the corresponding POD basis functions are obtained by Eq. (7). The 200 eigenvalues are arranged according to their magnitude as λ₁ > λ₂ > · · · > λ₂₀₀ and the first five largest eigenvalues together with their participant energy proportion ξ_n and cumulative energy proportion η_n are given in Table 2.

Table 2.

The first five eigenvalues and corresponding energy distributions of pressure, water saturation, and temperature

	n	1	2	3	4	5
λn	Pressure	205,271.085	134.828	31.782	4.683	1.380
	Water saturation	199.814	1.797	0.451	0.126	0.041
	Temperature	1,684,266.645	28,412.463	5976.681	1172.588	380.457
ξn (%)	Pressure	99.916	0.066	0.015	0.002	0.001
	Water saturation	98.790	0.888	0.223	0.062	0.020
	Temperature	97.898	1.651	0.347	0.068	0.022
ηn (%)	Pressure	99.916	99.982	99.997	99.999	99.999
	Water saturation	98.790	99.678	99.901	99.963	99.983
	Temperature	97.898	99.549	99.896	99.964	99.986

As shown in Table 2, the energy optimality of POD basis functions is obvious. For pressure, the first eigenvalue has the largest magnitude and captures 99.916% of the total energy alone. Then, the values of the other eigenvalues decrease dramatically, all eigenvalues except for the first one which only captures 0.084% of the total energy. In addition, only the first five largest eigenvalues can capture more than 99.99% of the total energy. Similarly, for water saturation and temperature, the variation trend is the same as that of pressure.

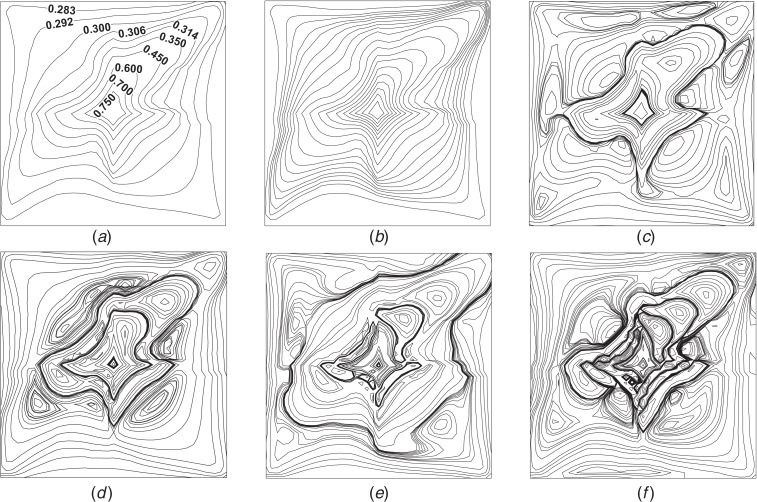
The average fields of 200 water saturation snapshots and 200 temperature snapshots are shown in Figs. 4(a) and 5(a), respectively, and the first 5 water saturation POD basis functions and temperature POD basis functions that correspond to their first 5 largest eigenvalues are given in Figs. 4(b)–4(f) and 5(b)–5(f), respectively. It can be seen in Figs. 4 and 5 that the POD basis function with the largest eigenvalue fit very well with the average physical fields, since it captures most of the energy from the original physical fields and best represent the dynamic characteristics of the original physical system. It is also observed that the corresponding POD basis function dramatically deviates from the average physical fields with the decrease of eigenvalue. This is because the POD basis functions with large eigenvalues represent the contribution of the dominant large-scale smooth structures to the total physical fields, and the POD basis functions with small eigenvalues represent the contribution of many small scale structures that cannot be captured by the POD basis functions with large eigenvalues to the total physical fields. Therefore, there is no need to keep more POD basis functions.

Fig. 4.

The average water saturation fields and the first five water saturation POD basis functions: (a) average water saturation fields, (b) the first POD basis function, (c) the second POD basis function, (d) the third POD basis function, (e) the fourth POD basis function, and (f) the fifth POD basis function

Fig. 5.

The average temperature fields and the first five temperature POD basis functions: (a) average temperature fields (°C), (b) the first POD basis function, (c) the second POD basis function, (d) the third POD basis function, (e) the fourth POD basis function, and (f) the fifth POD basis function

Since the numerical solutions of water saturation and temperature fields and the POD basis functions are obtained, the spectral coefficients c_k can be calculated by projecting the obtained physical fields onto the corresponding POD basis function, that is

$$c_k(t_n)=(f(\mathbf{X},t_n),{\phi }_k(\mathbf{X})),k=1,2,\dots ,N$$ (21)

Thus, the physical fields can be reconstructed using Eq. (14).

The temporal variations of the spectral coefficients c_k(t) for water saturation and temperature fields are shown in Figs. 6(a) and 6(b), respectively. It is obvious that the first spectral coefficients c₁(t) take the largest value and the spectral coefficients c_k(t) with larger index are closer to zero, which means that the POD basis function contributes less and less to the reconstruction of the original physical fields with the decrease of its corresponding eigenvalue.

Fig. 6.

The temporal variations of the spectral coefficients c_k(t) for water saturation and temperature fields: (a) variations of water saturation spectral coefficients with time and (b) variations of temperature spectral coefficients with time

In order to examine the accuracy of reconstruction solutions obtained by the POD-based method quantitatively, the relative error E is defined as

$$E={\displaystyle \frac{\parallel f-f_M\parallel }{\parallel f\parallel }\times 100\text{\%}}$$ (22)

where f denotes the solutions obtained by FDM and f_M denotes the reconstruction solutions obtained by the POD-based method.

The variations of the relative error E with the truncation degree M for water saturation and temperature fields are shown in Figs. 7(a) and 7(b), respectively. An overview of Fig. 7 shows that the relative error E decreases rapidly with the increase of the truncation degree M and then reduces to be almost constant. For water saturation fields, the relative error E has already reduced to 0.4% when M = 10. For temperature fields, the relative error E is less than 0.2% when M = 10. Therefore, the original physical fields can be reconstructed very accurately only using less POD basis functions.

Fig. 7.

The reconstruction error of water saturation and temperature fields: (a) the reconstruction error of water saturation fields and (b) the reconstruction error of temperature fields

Online calculation. To examine the performance of the POD-based method for predicting the new physical fields, we consider a case of the time-dependent well controls, as shown in Fig. 8, where the well controls vary constantly but in the ranges of interest with simulation time. The reduced order model (Eq. (20)) is used to predict the oil or water production rates in every time step, where the new coefficients c_k(t) are calculated using Eq. (20) with the truncation degree M = 10.

Fig. 8.

The different case of well controls for examining the performance of the POD-based method: (a) variation of water injection rate with time and (b) variation of BHP with time

It is noted that the case of well controls in Fig. 8 is set artificially, and our purpose is to examine the prediction accuracy of the reduced order model, and there is no need to consider the rationality of the varying form.

The solutions of water saturation and temperature fields on the 1000th day obtained by the FDM- and POD-based methods are shown in Figs. 9 and 10, respectively. From an overview of these solutions, it can be obviously seen that a remarkable qualitative agreement is obtained.

Fig. 9.

Comparison between water saturation solutions obtained by the FDM- and POD-based methods on the 1000th day: (a) solutions obtained by FDM and (b) solutions obtained by the POD-based method

Fig. 10.

Comparison between temperature solutions obtained by the FDM- and POD-based methods on the 1000th day: (a) solutions obtained by FDM and (b) solutions obtained by the POD-based method

The temporal variation of the relative error E for water saturation and temperature fields is shown in Figs. 11(a) and 11(b), respectively. It can be obviously discovered that the relative error E takes the largest value and decreases greatly in the initial stage, then increases gradually and slowly for both water saturation and temperature fields. This is because more and more new structures that are not contained in the original POD basis functions appeared in the physical fields due to well controls which are changed constantly. However, in 1000 days, the relative error E for water saturation and temperature fields is less than 1.3% and 1.5%, respectively. Namely, the POD basis functions are valid over a larger range of well controls and can be used repeatedly.

Fig. 11.

The temporal variation of the relative error E for water saturation and temperature fields

To demonstrate the advantage of “online calculation” for the POD-based method, we apply the FDM to simulate this example as well. The calculation procedure is completed in a computer with dual CPU of 8.0 G RAM. It can be easily seen from Table 3 that the POD-based method is very efficient. For simulating the physical fields on the 1000th day, more than 320 s is required using FDM but only less than 5 s is required using the POD-based method, and this brings about an increase of more than 30 times. It can be further expected that more advantage in computational CPU time may be achieved with the increase of the number of grid blocks.

Table 3.

Computational CPU time of the POD-based method and the finite difference method

Time	200 d	400 d	600 d	800 d	1000 d
FDM (s)	72.658	133.427	203.665	258.216	327.322
POD-based method (s)	0.983	1.856	2.766	3.492	4.612

It is worth pointing out that the computational time for the POD-based method does not contain the time that is consumed in the “offline calculation.” The offline calculation may consume a lot of computational time, but it is operated only once, and the POD basis functions obtained in the offline calculation can be used repeatedly in the “online calculation.” Therefore, the process of offline calculation can be attributed to the training process or the preparatory work for the later fast usage.

4. Conclusions

In this paper, we present the applications of the POD-based method in the prediction for flow and heat transfer of oil and water in the reservoir. A reduced set of POD basis functions are generated offline through full-order numerical reservoir simulations, then new physical fields corresponding to arbitrary well controls in the ranges of interest are obtained only through calculating a small amount of POD coefficients online, and this enables us to predict new physical fields online without directly solving the full-order governing equations. The performance of the POD-based method is examined by comparing its computational results with that of FDM. In the example, for the prediction accuracy, although well controls are changed constantly, in 1000 days, the relative error is not more than 1.3% and 1.5% for water saturation and temperature fields, respectively. Besides, as for the computational efficiency, the POD-based method is dozens of times faster than that of FDM in online calculation speed. It can be expected that the advantage of online calculation speed is greater as the number of grid blocks increases. Since the POD-based method proposed in this paper can accurately and efficiently predict the physical fields for flow and heat transfer of oil and water in the reservoir, it may be an appropriate approach to be applied in the reservoir engineering problems which involve several passes of full-order numerical reservoir simulations.