Postural Representations of the Hand in the Primate Sensorimotor Cortex

SUMMARY

Manual dexterity requires proprioceptive feedback about the state of the hand. To date, study of the neural basis of proprioception in the cortex has focused primarily on reaching movements to the exclusion of hand-specific behaviors such as grasping. To fill this gap, we record both time-varying hand kinematics and neural activity evoked in somatosensory and motor cortices as monkeys grasp a variety of objects. We find that neurons in the somatosensory cortex, as well as in the motor cortex, preferentially track time-varying postures of multi-joint combinations spanning the entire hand. This contrasts with neural responses during reaching movements, which preferentially track time-varying movement kinematics of the arm, such as velocity and speed of the limb, rather than its time-varying postural configuration. These results suggest different representations of arm and hand movements suited to the different functional roles of these two effectors.

In Brief

Goodman et al. show that, during grasping, individual neurons in the somatosensory and motor cortices of primates track the time-varying angles of joints distributed over the entire hand. This postural representation of the hand is well suited to support stereognosis.

INTRODUCTION

Proprioception—the ability to track the postures and movements of our limbs—is critical for our ability to move fluidly and interact effectively with our environment, as evidenced by the devastating impairments experienced by individuals who have lost this sense (Brochier et al., 1999; Cole, 2009; Cole et al., 2002; Cole and Paillard, 1998; Ghez et al., 1995; Kruger and Porter, 1958; Sainburg et al., 1995).Despite its importance, little is known about the basis of proprioception in the somatosensory cortex (SCx), particularly that of the hand. Indeed, the bulk of work on the neural basis of proprioception in primates has focused on representations of the proximal limb (upper arm and forearm) (Fromm and Evarts, 1982; Fromm et al.,1984; London and Miller, 2013; Prud’homme and Kalaska,1994; Weber et al., 2011), with few studies investigating proprioceptive representations of the digits (Costanzo and Gardner,1981; Gardner and Costanzo, 1981). However, the hand and arm differ fundamentally in their respective functions and biomechanical properties; the arm is more massive and functions to transport the hand in three-dimensional space, whereas the hand is lighter and functions to conform to objects to enable grasping and manipulation. Therefore, the neural mechanisms that control and track these two effectors may be fundamentally different.

In the present study, we investigated the neuronal representations of hand postures and movements in the SCx during the most common manual activity of daily living: grasping. Specifically, we had monkeys grasp objects of varying shapes, sizes, and orientations—designed to elicit a wide variety of hand postures—as we tracked the kinematics of the hand and measured neural activity in the SCx as well as the primary motor cortex (M1) using chronically implanted electrode arrays (Figures 1 and S1). Importantly, animals were trained to grasp objects without reaching toward them to permit study of neural coding of hand shape independent of a reaching component (cf. Saleh et al., 2010). In the SCx, we focused on cortical fields that are known to contain proprioceptive neurons (Brodmann’s areas 3a and 2) and verified electrode locations within these cortical fields with histology (Figure 1E). Our goal was to determine which aspects of hand movement and posture drive the responses of somatosensory neurons and to compare sensory response properties with their motor counterparts.

Figure 1. Experimental Methods and Histology.

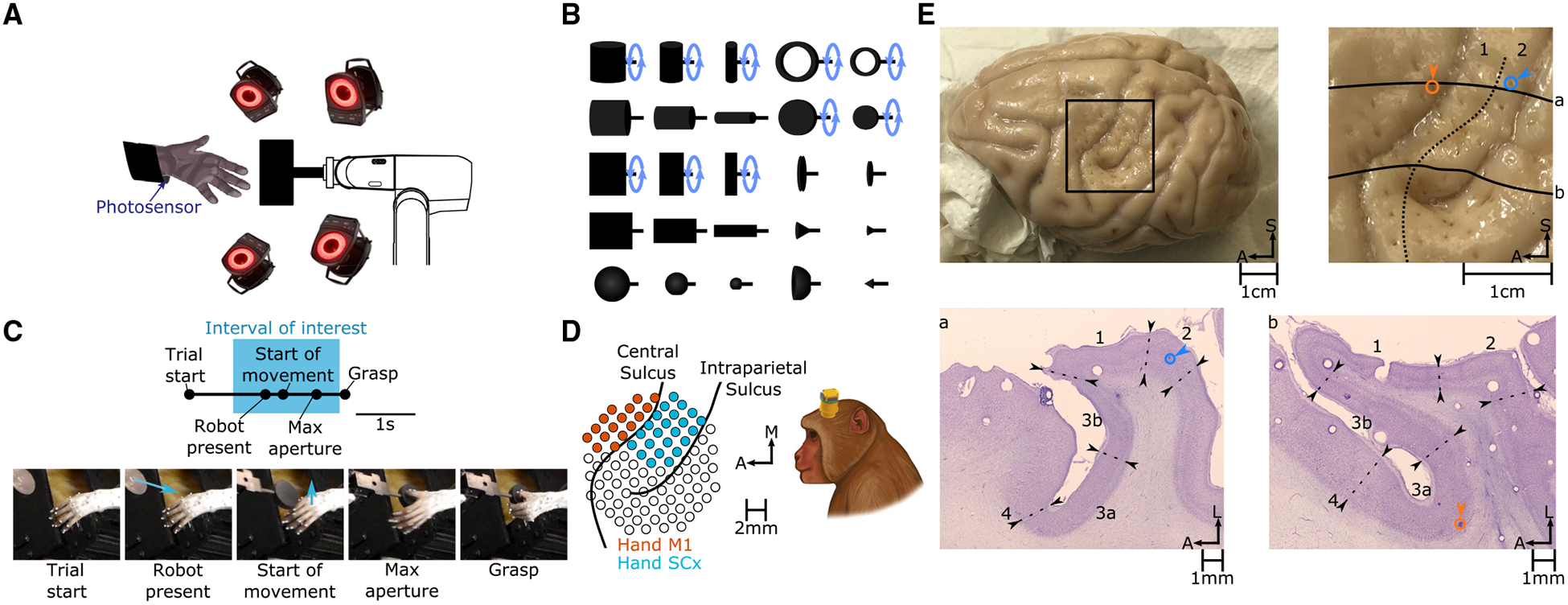
(A) Rhesus macaques grasp objects presented by a robotic arm. When the monkey lifts its arm to reach for the object, a photosensor is triggered, and the trial is aborted. A fourteen-camera motion-tracking system tracks the kinematics of the hand.

(B) The set of 25 shapes used in this study. Ten of these shapes (indicated by a blue circular arrow) were presented at different orientations, totaling 35 “objects.”

(C) Task progression. “Start of movement,” “Max aperture,” and “Grasp” were identified for each trial. Blue arrows indicate the motion of the robot (“Robot present”) or the hand (“Start of movement”). Analyses were confined to neural responses measured prior to “Grasp” (spanning the “Interval of interest”) to eliminate the confounding effects of object contact.

(D) Multi-electrode arrays were used to record neuronal activity. Pictured on the left are the reconstructed locations of electrodes relative to the surface of the cortex (left hemisphere) in monkey 4. See Figure S1 for array placements in other monkeys.

(E) Histological reconstruction of array placement. Top left: chronically implanted electrode tracks were clearly visible in the perfused cortex. Top right: enlarged view of the rectangular region at the top left. Registered to this view of the cortical surface are the architectonic boundary between areas 1 and 2 (dashed line), the locations of two electrodes impinging on areas 2 (blue) and 3a (orange), and the contours of the cortex along two horizontal slices pictured at the bottom (solid lines). Bottom: transverse slices are stained for Nissl substance, and boundaries between cortical fields are drawn on the basis of architectonic features. In scale bars, S indicates superior, A indicates anterior, and L indicates lateral.

RESULTS

Kinematics (and Neuronal Responses) Are Object Dependent

To characterize the neural representation of the hand, the space of hand postures and movements must be diverse. To verify that grasping occupies a sufficiently rich space of hand kinematics, we first examined the degree to which monkeys use different kinematics to grasp different objects. We found that hand posture trajectories diverged long before contact was established with the object (Figure 2A). That is, the animal preshaped its hand to each object to grasp it, and this preshaping began to emerge shortly after movement onset (Figure 2B). To characterize the object specificity of hand shape, we classified objects based on hand postures aligned to various events before object contact (Figure 2C). We found that classification performance evolved gradually over the course of the trial, was well above chance (2.8%) at maximum aperture, and peaked at around 60% just before grasping. This analysis confirms that animals preshape their hands over most of the duration of the trial in an object-specific manner.

Figure 2. Different Objects Give Rise to Different Hand Pre-shaping Kinematics.

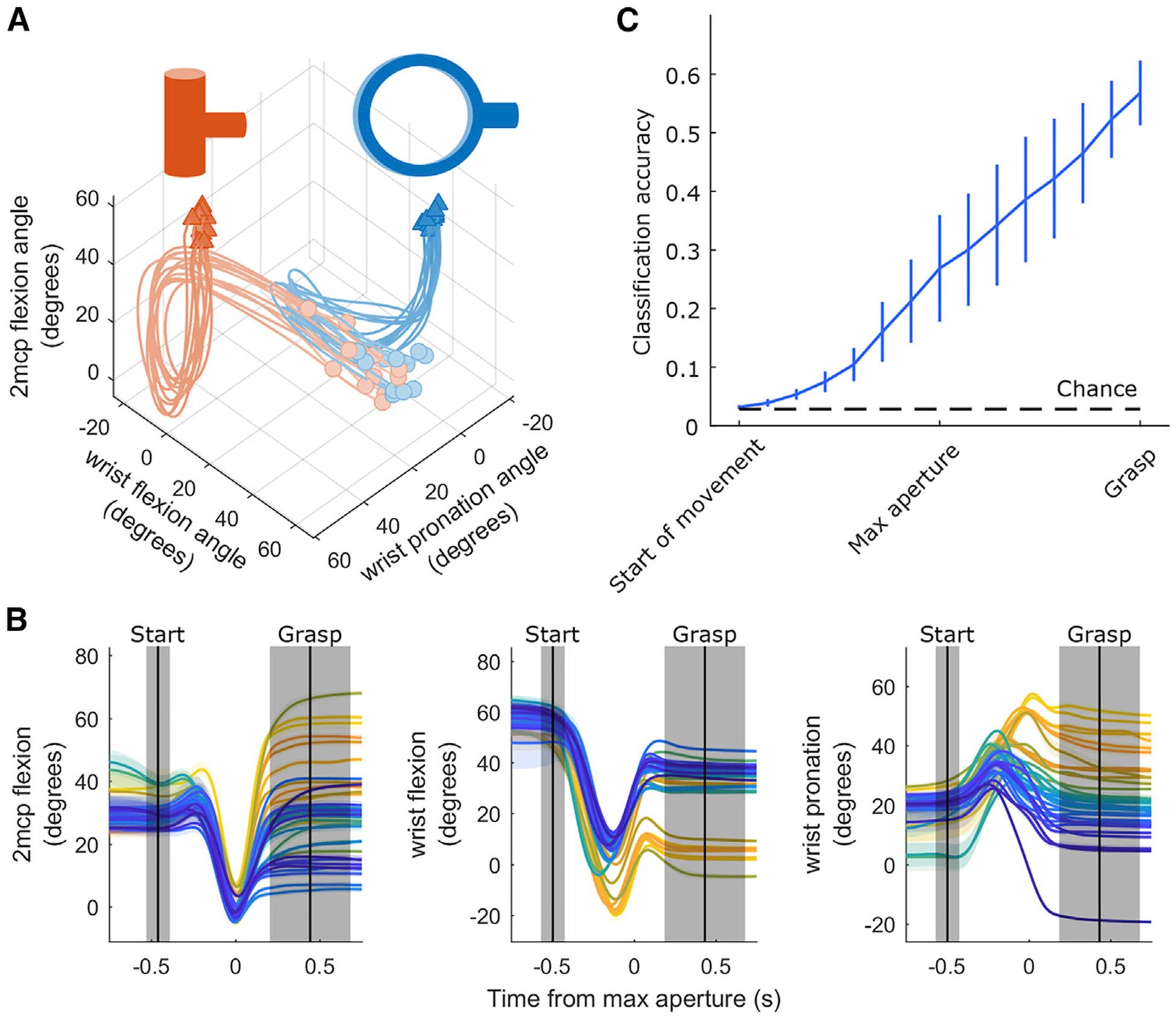
(A) Trajectories of three joints as an animal grasps two different objects over the course of a session. Each trace represents kinematics during a single trial. Circles indicate joint angles 750 ms prior to maximum aperture, and triangles indicate joint angles 750 ms after maximum aperture.

(B) The angles of the three joints shown in (A), plotted for the 35 objects, averaged across all presentations of each object (indicated by different colors). Shading denotes ± 1 SEM across trials. Vertical black lines indicate mean onset times for start of movement (left) and grasp (right) events; shaded regions indicate ± 1 SD across trials. All kinematic traces are aligned to maximum aperture. Figure S2 depicts the variety of neural responses that accompanied these kinematics.

(C) Time-varying object classification based on the posture of the hand, assessed across all sessions and averaged across monkeys. Error bars denote ± 1 SEM across monkeys. The black dashed line indicates chance performance.

Encoding Models Based on Kinematics Can Predict Neuronal Responses

We recorded from populations of neurons in the SCx and M1 as the animals performed the grasping task (Table 1). We found that the evoked responses varied widely across neurons and objects (Figure S2) and sought to determine the extent to which these responses reflected hand kinematics. To this end, we fit a generalized linear model (GLM) to predict the time-varying firing rate of each neuron from the time-varying joint angles and their derivatives. Importantly, these models were all regularized and cross-validated to minimize over-fitting (STAR Methods). GLMs often provided accurate predictions of neuronal responses (Figure 3A) with goodness of fit (Figure 3B) comparable with those achieved by similar models that fit M1 responses to two-degree-of-freedom proximal limb kinematics during reaching (Table S1; Hatsopoulos et al., 2007) Thus, neurons in the somatosensory and motor cortex encode hand kinematics with a comparable fidelity as arm kinematics.

Table 1.

Number of Neurons Recorded from Each Cortical Field

	Area 3a		Area 2		M1
	Sig.	>0.05	Sig.	>0.05	Sig.	>0.05
Monkey 1	1	1	17	13	77	51
Monkey 2	28	24	16	6	138	89
Monkey 3	1	1	6	4	15	11
Monkey 4	5	5	20	18	60	55
Total	35	31	59	41	290	206

Shown are the total numbers of neurons whose firing rates showed significant modulation with the task. Task modulation was assessed using ANOVA with task epoch (3 levels: 750 ms prior to start of movement to start of movement, start of movement to max aperture, and max aperture to grasp) and object identity (35 levels) as factors, along with their interaction. “Sig.” denotes statistical significance of at least one of these factors with > = 0.0167. In addition, the number of neurons with pseudo-R² > 0.05 (“>0.05”) for GLMs reported in Figures 3, 5, and 6, and Table S1 are provided in a separate column.

Figure 3. Performance of the Generalized Linear Model (GLM).

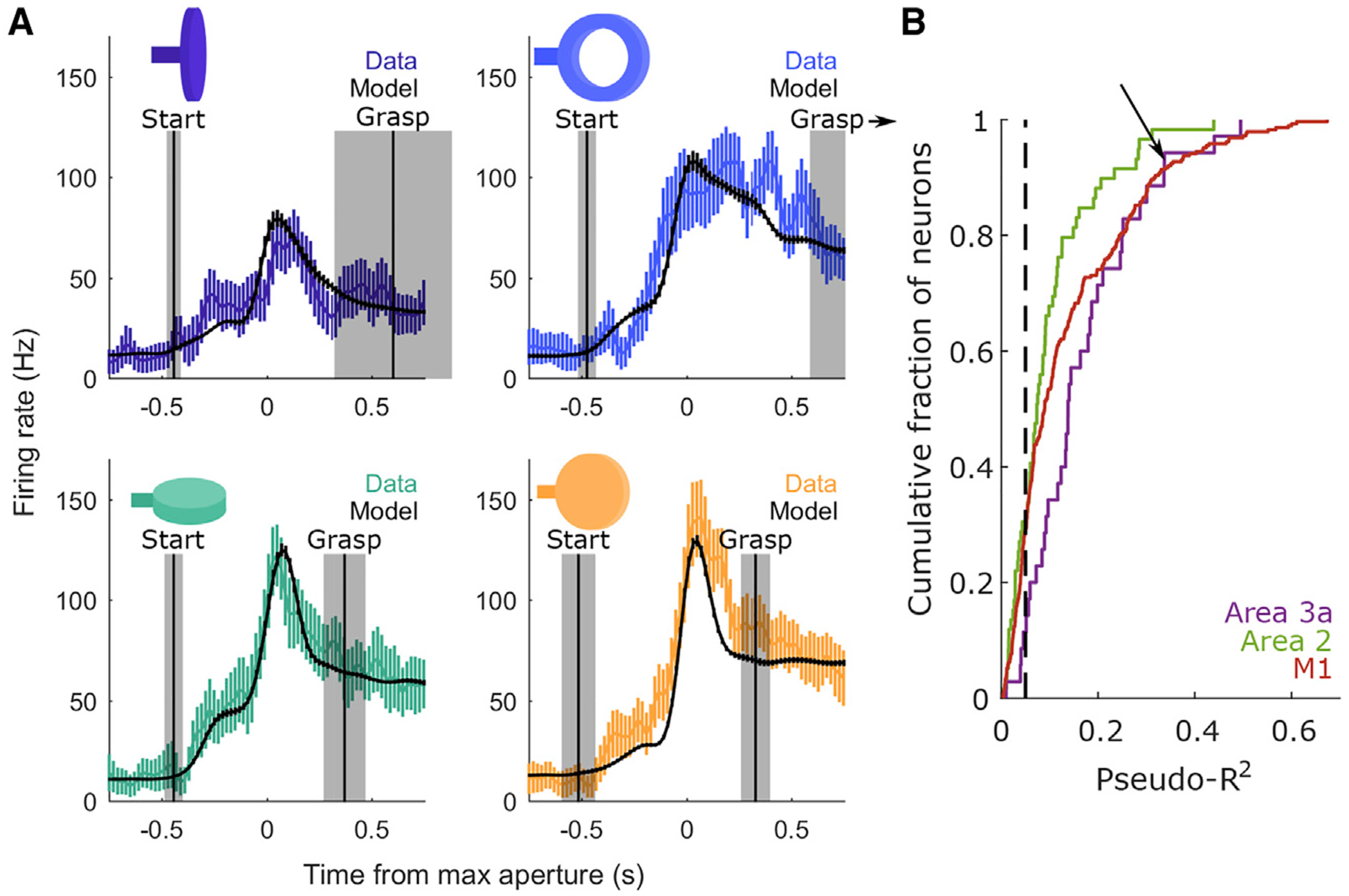
(A) Measured (colored) and predicted (black) peri-event time histograms (PETHs) for a single neuron in area 3a. Each plot depicts the PETH associated with a different object. The pseudo-R² of the GLM fit to this neuron is 0.34. Error bars denote ± 1 SEM across trials. Vertical lines mark the average onset of the start of movement (left) and grasp (right) across trials for each object. Shaded regions indicate ± 1 SD. All PETHs are aligned to maximum aperture. For the ring (top right), this distribution is truncated because the mean grasp time occurs 1.01 s following maximum aperture.

(B) Cumulative distributions of pseudo-R² values across neurons from each area. Neurons are pooled across sessions and monkeys. The black dashed line indicates a pseudo-R² cutoff of 0.05, which is used in subsequent analyses of RF structure. Neuron count statistics, including the subset of neurons that surpass this pseudo-R² threshold, are reported in Table 1. Importantly, the average goodness of fit is comparable with that reported for M1 neurons during reaching (Table S1). The arrow denotes the model fit to the responses of the neuron shown in (A).

Neuronal Response Fields Span Many Joints

Next we examined which movement features drive the responses of SCx and M1 neurons. First we assessed whether individual neurons encode the state of one joint or that of multiple joints. We found that neurons encode combinations of joints, with inferred multi-joint response fields (RFs) accounting for roughly twice the cross-validated deviance in spiking responses as single-joint RFs (Figure 4A). This substantial difference between multi- and single-joint pseudo-R² was observed in the M1 (paired-samples t test, t(205) = 16.27, p = 9.454e–39), area 3a (t(30) = 8.559, p = 1.504e–09), and area 2 (t(40) = 5.671, p = 1.371e–06).

Figure 4. RF Size for Neurons in the Somatosensory and Motor Cortex.

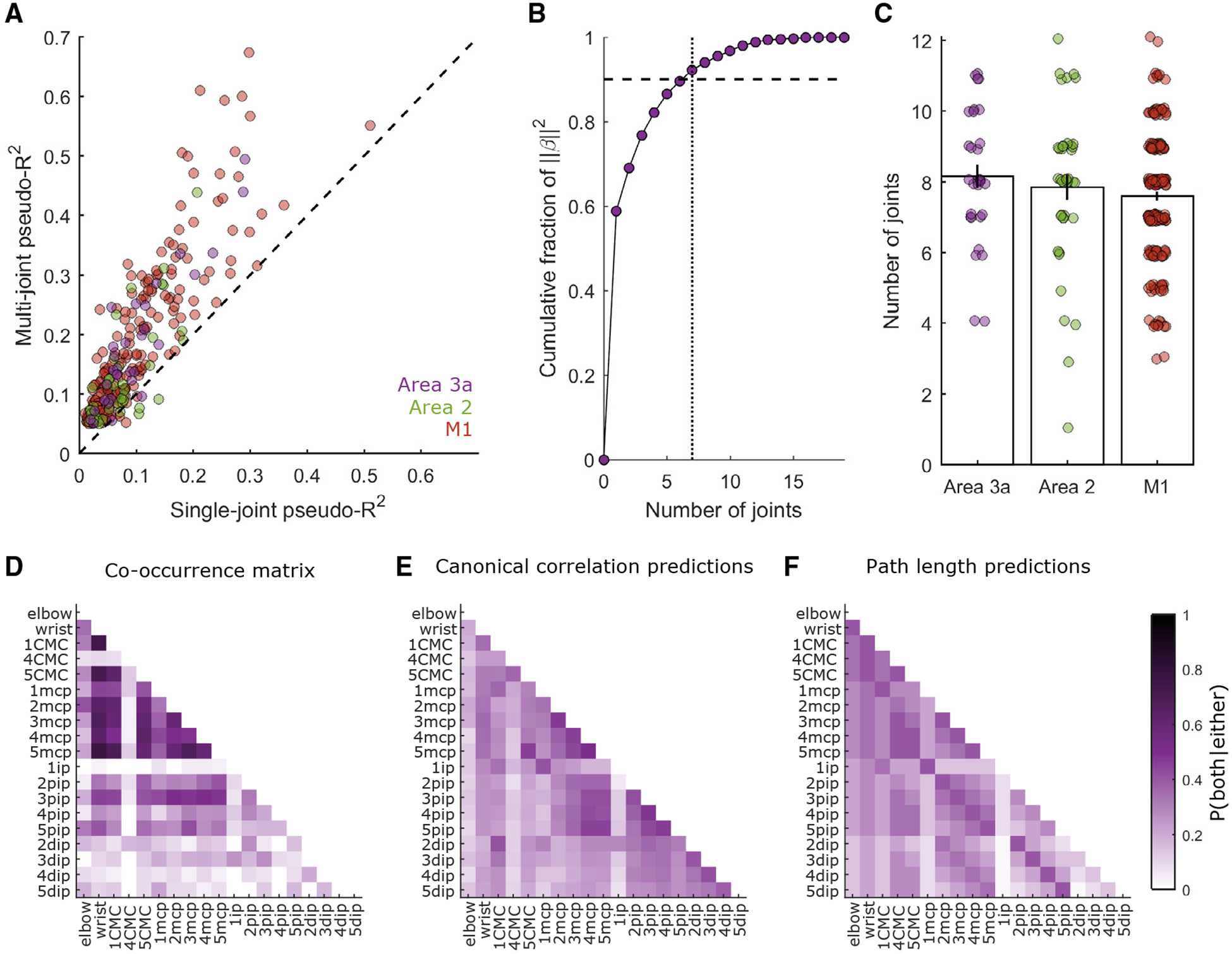
(A) Comparisons of each neuron’s best single-joint pseudo-R² (abscissa) against the corresponding multi-joint pseudo-R². Only neurons with pseudo-R² > 0.05 are included. The dashed line indicates the unity slope. Multi-joint models yield considerably better predictions than single-joint models.

(B) For each weight vector (β) defining a neuron’s RF, we calculate the contribution of each joint to the squared norm of b. The minimum number of joints (dotted vertical line) required to account for 90% of that squared norm (dashed horizontal line) is taken to be the set of joints defining that neuron’s RF. This panel illustrates this process for a single neuron from area 3a.

(C) Average number of joints in a neuron’s RF for each area. Around eight joints define the typical RF from each area. Individual points denote joint counts for the RFs of individual neurons. Vertical lines denote ± 1 SEM across neurons. Such distributions of joint counts are unlikely to emerge from neurons that only track or control a single joint (Figure S3A). Joint counts are similar when estimated with a sequential GLM procedure (Figures S3B–S3D).

(D) Co-occurrence matrix for area 3a. Co-occurrence is defined as the likelihood that two joints of a pair are contained within the same RF, given that at least one of them is present within that RF. Empirical co-occurrences are taken from the population of area 3a neurons with pseudo-R² > 0.05.

(E) Co-occurrences in the RFs of neurons in area 3a predicted from the correlations among joints. This model fails to explain a large fraction of the variance in the co-occurrence data (R² = 0.209).

(F) Co-occurrences in the RFs of neurons in area 3a, predicted from minimum path lengths between joints, as dictated by the skeletal and ligamentous anatomy of the hand (R² = 0.191). Similar analyses were also performed for area 2 and the M1, all yielding similar conclusions (Figure S4).

Axis tick labels in (D)–(F) mark joint identity. Apart from the elbow and the wrist joints, labels comprise a number (1–5) specifying the digit to which a joint belongs. CMC, carpo-metacarpal joint; MCP, metacarpo-phalangeal joint; ip, interphalangeal joint for digit 1; pip, proximal interphalangeal joint for digits 2–5; dip, distal interphalangeal joint for digits 2–5.

In fact, 8 joints were required, on average, to account for 90% of the neuron’s RF (STAR Methods), with little difference in RF size across somatosensory and motor cortical fields (Figures 4B and 4C). No substantial differences were noted across cortical fields in terms of the number of joints in the typical neuron’s RF (one-factor ANOVA, F(2,275) = 1.383, p = 0.2526). We verified that these large RFs were not artifacts of single-joint tuning in the presence of inter-joint correlations (Figure S3A). We also characterized RFs using a sequential GLM procedure and reached the same conclusion (Figures S3B–S3D).

RFs Span the Entire Hand

Next we examined how the joints in each RF were distributed over the hand. One might expect, especially at early stages of somatosensory processing, such as area 3a, that multi-joint RFs would be confined to just one digit or to two adjacent ones, controlled by a common muscle. To characterize the spatial extent of the RFs, we computed co-occurrence matrices, which show the likelihood that a given pair of joints is present in an individual neuron’s RF, conditioned upon at least one of those joints being present. We found that RFs spanned the entire hand (Figure 4D). That is, the metacarpo-phalangeal (MCP) joints of digits 1–5, the carpo-metacarpal (CMC) joints of digits 1 and 5, and the wrist all co-occurred with one another at similar rates as opposed to forming separate clusters of co-occurring joints.

We then examined whether patterns of co-occurrence in neuronal RFs trivially reflected kinematic correlations among joints (Figure 4E) or the anatomical proximity of those joints (Figure 4F). Anatomical proximity was determined by the number of bones between one joint and another (Table S2; STAR Methods). We found that neither model could account for the patterns of co-occurrence observed in area 3a (Figure 4), area 2, or the M1 (Figure S4).

To further test whether natural correlations among joints might be shaping the large RFs of proprioceptive neurons, we computed the principal components (PCs) of the kinematics, which reflect correlated patterns of joint postures and are sometimes inferred to be canonical “synergies” or “movement primitives” from which all movements arise (Santello et al.,1998). We regressed these, rather than the joint angles themselves, onto the neural responses. If such a coordinate frame were preferentially encoded, then one might expect multi-PC models to be more parsimonious (i.e., require fewer parameters) than multi-joint models. We found, however, that PC space did not provide a more parsimonious model of neuronal firing rates than joint space: the number of joints included in each neuron’s RF was similar to the number of PCs included he RF in both the M1 (paired-samples t test, t(205) = 0.839, p = 0.4022) and SCx (t(71) = 1.459, p = 0.1491) (Figure 5A) Multi-PC GLMs also did not yield better overall fits than multi-joint GLMs, as gauged by cross-validated pseudo-R² (M1: t(205) = 0.692, in p = 0.4895; SCx: t(71) = 0.9587, p = 0.3410). This was true in the SCx even when areas 3a and 2 were considered separately, and the results from the M1 are consistent with previous findings with a different manual task (Kirsch et al., 2014; Mollazadeh et al., 2014). Neurons in the sensorimotor cortex thus do not seem to preferentially represent kinematics in a principal-component coordinate frame relative to a joint coordinate frame. We also tested the hypothesis that RFs are large because neuronal tuning shifts between different joints or PCs during different task epochs (“hand opening” or “hand closing”) and found that the resulting models do not better account for the neuronal responses (Figure S5).

Figure 5. Lack of Parsimonious RF Description across Kinematic Coordinate Frames.

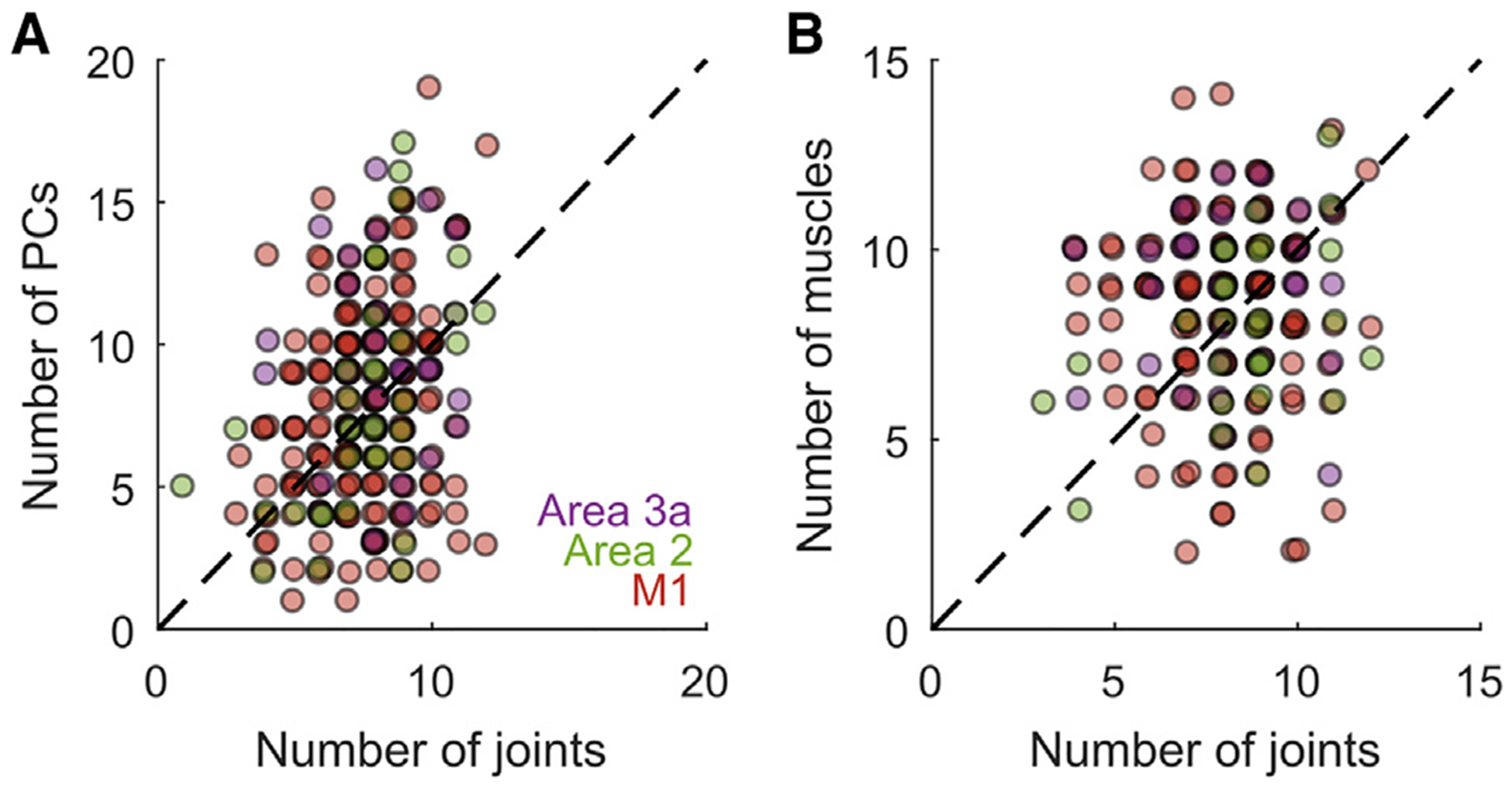
(A) Roughly the same number of PCs and joints are required to achieve similar levels of performance with multi-PC or multi-joint models (only neurons with pseudo-R² > 0.05 are considered). RFs are not better explained in terms of neural tuning that shifts over the course of grasping (Figure S5)

(B) Roughly the same number of predictors are required to achieve similar levels of performance with multi-muscle or multi-joint models (only neurons with pseudo-R² > 0.05 are considered).

Finally, as proprioceptive signals are thought to emanate primarily from muscle and tendon-associated receptors (spindles and Golgi tendon organs; Proske and Gandevia, 2012), we examined whether the musculotendon lengths of extrinsic hand muscles were preferentially encoded in cortical responses over joint kinematics. We found that multi-joint models of spiking activity were no less parsimonious than multi-muscle models; i.e., the number of joints in each neuron’s RF was similar to the number of muscles for both the M1 (paired-samples t test, t(154) = 1.891; p = 0.0604; average number of joints = 8.1; average number of muscles = 8.5) and SCx (t(57) = 0, p = 1) (Figure 5B). Multi-muscle and multi-joint RFs also yielded similar cross-validated pseudo-R² values for the M1 (t(154) = 1.608, p = 0.1099) and SCx (t(57) = 1.898, p = 0.0628, average pseudo-R² of joint models = 0.1613, average pseudo-R² of muscle models = 0.1630), even when areas 3a and 2 were considered separately.

Neurons Preferentially Encode Time-Varying Hand Postures Rather Than Movements

Individual neurons in the SCx and M1 respond more strongly to time-varying movement (i.e., velocity), rather than time-varying posture, of the proximal limb during reaching (London and Miller, 2013; Moran and Schwartz, 1999; Paninski et al., 2004; Reina et al., 2001; Wang et al., 2007; Weber et al., 2011). In light of this, we assessed whether hand representations preferentially encode movement (Figure 6A). To this end, we analyzed the partial pseudo-R² values for postural and movement-encoding models of each neuron’s responses (Movshon and Newsome,1996), termed here the fraction of unique deviance explained (FUDE) by each of these models. We found that spiking activity among proprioceptive neurons tracked time-varying postures better than movements; the FUDE of these postural models exceeded that of movement models in the M1 (paired-samples t test, t(205) = 11.43, p = 1.007e–23), area 3a (t(30) = 5.945, p =1.624e–06), and area 2 (t(40) = 5.338, p = 4.007e–06) (Figures 6B–6D). Our results therefore suggest that proprioceptive neurons preferentially track hand configuration for grasping, unlike their counterparts for reaching, which preferentially encode arm movements (Figure S6A; London and Miller, 2013).

Figure 6. Preferential Encoding of Time-Varying Joint Postures in the Somatosensory and Motor Cortex.

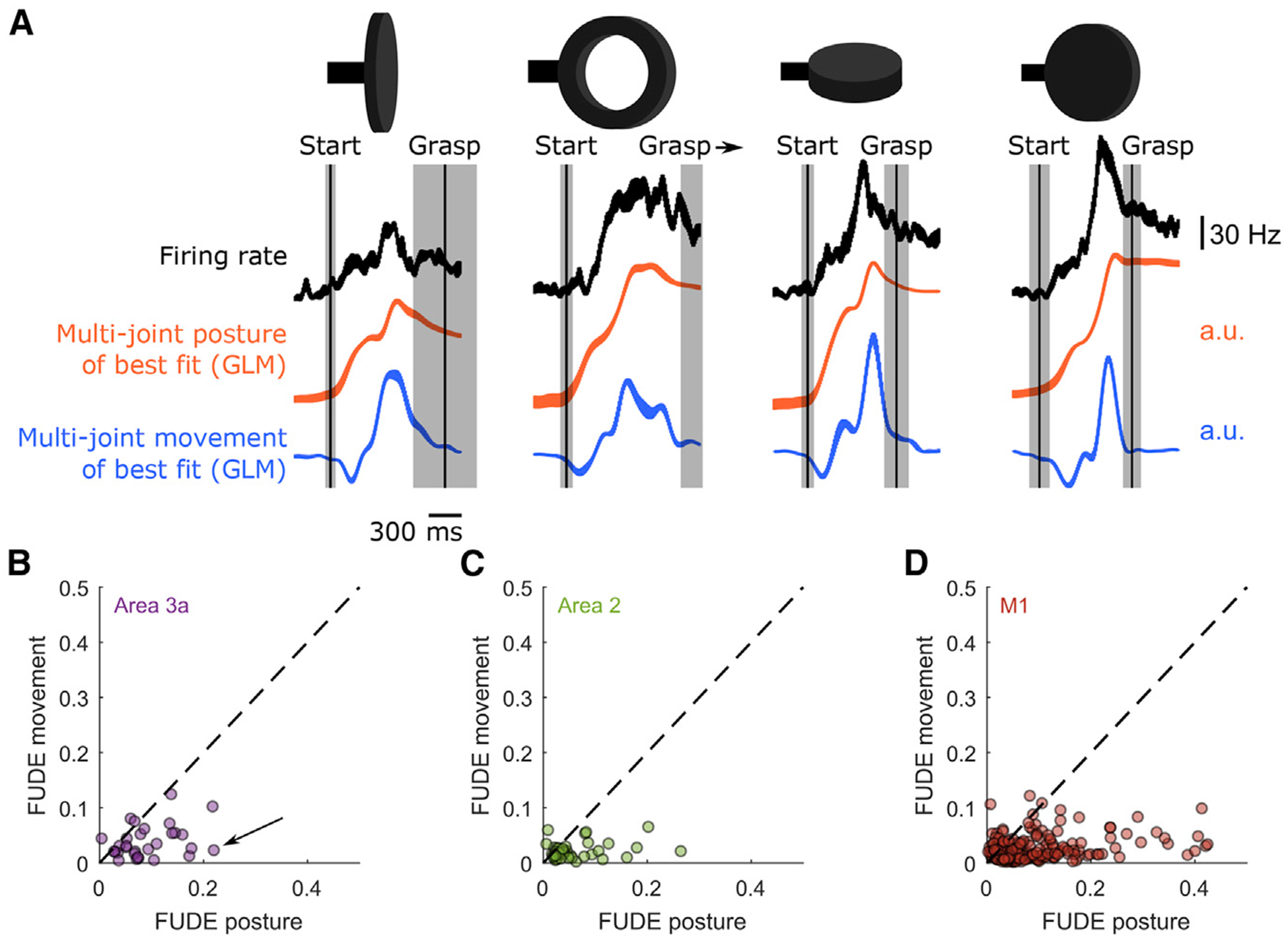
(A) PETHs from Figure 3A (top row), shown with hand posture (center row) or movement (bottom row) trajectories along the dimension most aligned with the neuron’s firing rate. Vertical lines and shaded regions indicate mean and ± 1 SD of the start of movement and grasping events. All PETHs are aligned to maximum aperture. Best dimensions for postures and movements are found using separate GLMs, one using only postural predictors and one using only movement ones. Posture and movement traces vary along different axes so movement is not derived from posture. The postural axis better matches the spiking profile.

(B–D) The fraction of unique deviance explained (FUDE) by time-varying joint angles (posture) and their derivatives (movement). Each point denotes a single neuron in (B) area 3a, (C) area 2, or (D) the M1. The arrow in (B) marks the neuron shown in (A). That most points fall well below the unity line (dashed line) suggests that postures rather than movements are preferentially encoded by these neurons. Note that this does not hold for the M1 during reaching movements (Figure S6).

See Figure S7 for further validation of the preferential tracking of time-varying postures.

Moreover, and surprisingly, M1 neurons also exhibited a strong preference for time-varying hand postures during grasping, in contrast to their extensively documented preference for time-varying velocities during reaching and earlier reports suggesting such a preference of M1 neurons during grasping (Saleh et al., 2010). In light of this previous report, we verified that preferential posture tracking emerges across a broad range of GLMs and found that movement tracking is observed only when velocity models can mimic postural ones (Figure S7).

One possibility is that the difference between arm and hand representations in the SCx and M1 is an artifact of the kinematics themselves. Indeed, movement-related responses are less dominant in the M1 (relative to their posture-related counterparts) during slow reaches or when the limb adopts a wide range of postures (Aflalo and Graziano, 2007; Caminiti et al., 1990; Scott and Kalaska, 1997). With this in mind, we compared the distributions of joint angular speeds and ranges of motion during reaching and grasping. We found that these distributions are largely overlapping, suggesting that the observed difference in the postural versus movement preference in grasping versus reaching is not a trivial consequence of differences in joint kinematics (Figures S6B–S6D).

Finally, we examined whether postural preference was uniform across the M1, following reports that neurons in the caudal M1 exhibit greater movement preference and neurons in the rostral M1 exhibit greater postural preference during reaching (Crammond and Kalaska, 1996). Given the specialization of the caudal M1 for hand control (Rathelot and Strick, 2009), a large fraction of our M1 sample stemmed from the caudal M1, which might account for our observation of postural preference in the M1. To text this possibility, we split M1 units into two groups based on the rostro-caudal location and depth of the electrode tips (the caudal M1 is located in the bank of the sulcus). We found that the FUDE achieved with postural models was consistently larger than the FUDE with movement models in both the caudal M1 (paired-samples t test: t(50) = 5.625, p = 8.326e–07) and rostral M1 (t(154) = 9.944, p = 2.646e–18). Moreover, the difference in FUDE between the postural and movement models was equivalent in the two subdivisions (two-sample equal-variance t test, t(204) = 0.5236, p = 0.6011). Postural preference thus does not stem from the spatial distribution of the sampled neurons.

DISCUSSION

Large Postural RFs in the Somatosensory and Motor Cortex

Proprioceptive and motor representations of the hand preferentially encode time-varying postures rather than movements during grasping, in contrast to their proximal limb counterparts during reaching (London and Miller, 2013; Moran and Schwartz, 1999; Paninski et al., 2004; Reina et al., 2001; Wang et al.,2007; Weber et al., 2011). These differences might reflect different constraints on movement imposed by the different inertial and biomechanical properties of the arm and hand (Gribble and Scott, 2002; Kalaska et al., 1989; Prud’homme and Kalaska, 1994; Sergio et al., 2005). Indeed, the mass of the entire arm is large, whereas that of the digits is negligible. The two effectors would thus require different muscle recruitment profiles to achieve similar kinematics. Therefore, these biomechanical factors may underlie the observed differences in neuronal firing profiles for reaching and grasping.

Another property of proprioceptive neurons in the SCx is that their RFs include several joints spanning the entire hand, as do their counterparts in the M1 (Costanzo and Gardner, 1981; Saleh et al., 2010, 2012; Schieber, 1996, 2001; Schieber and Hibbard, 1993). The large RFs in area 3a stand in stark contrast to the small tactile receptive fields in the somatosensory cortex (Pons et al., 1985) but are consistent with previous reports of larger RFs in area 3a relative to their tactile counterparts in area 3b (Krubitzer et al., 2004). However, we found that a much larger proportion of these neurons has large multi-digit RFs than reported previously (Costanzo and Gardner, 1981; Iwamura et al., 1983, 1993; Krubitzer et al., 2004), a difference that could be attributed to our analysis of responses of area 3a neurons during actively generated grasping movements rather than imposed joint movements.

Differences in proprioceptive and cutaneous RF sizes may reflect differences in the function of these two sources of somatosensory input. Indeed, cutaneous signals convey information about local shape features at the points of contact between hand and object, such as edge orientation (Bensmaia et al., 2008) and curvature (Yau et al., 2013). Smaller receptive fields lead to more acute tactile spatial representations. Proprioceptive signals convey information about the configuration of the hand, which, by definition, requires integrating information across the entire hand.

Ultimately, these two streams of information, tactile and proprioceptive, must be integrated. Indeed, local features of the object at each point of contact must be interpreted in terms of the relative positions of the contact points in three-dimensional space to culminate in stereognosis, a three-dimensional percept of the object (Delhaye et al., 2018). That individual neurons signal the time-varying postures of joints distributed over the entire hand is consistent with a view that the hand representation in the SCx and M1 emphasizes the configurations of the digits relative to one another, a representation that is ideally suited to support stereognosis.

Alternate Coordinate Frames Fail to Account Succinctly for Large RFs

We investigated whether the large proprioceptive and motor RFs could be better described in a different coordinate frame. One hypothesis is that multi-digit RFs arise from one or two extrinsic muscles of the hand. For example, the extensor digitorum communis inserts onto all digits and even influences wrist movements. We found, however, that models based on musculotendon lengths did not provide more accurate or parsimonious accounts of the neurons’ RFs.

One possibility is that limb forces or muscle activations are better encoded in the M1 than kinematics (Evarts, 1968; Morrow et al., 2007; Prud’homme and Kalaska, 1994; Sergio et al., 2005). Because we cannot accurately reconstruct forces and muscle activations from kinematics, we cannot directly test this hypothesis. However, the activity of single neurons in the motor cortex has been shown to drive facilitation and suppression of several muscles (Buys et al., 1986; Griffin et al., 2015; Hudson et al., 2017), consistent with our finding that M1 RFs are large. How forces are encoded in the proprioceptive SCx and how these force signals interact with kinematic ones is largely unknown.

Another possibility is that each neuron’s preferred kinematic features shift throughout the course of a grasp, akin to the shifting of M1 and premotor cortical neurons’ preferred directions during reaching (Mason et al., 1998; Sergio et al., 2005; Sergio and Kalaska, 1998). Such shifts in movement preference have been interpreted, alternately, as evidence for kinematic “trajectory” encoding (Hatsopoulos et al., 2007), for preferential encoding of muscle activations over limb kinematics (Sergio et al., 2005), or for a dominant role of intracortical dynamics in shaping neuronal responses (Churchland et al., 2012). One possibility, then, is that large RFs result from the enforcement of a static RF on neurons with shifting preferences. However, we found that multi-lag GLMs did not provide substantially better fits than their single-lag “static” counterparts (Figure S7A). Moreover, allowing neurons to adopt different preferences during different grasp epochs (Figures S5B and S5C) did not improve model performance. Thus, time-varying shifts in tuning do not explain the large RFs of sensorimotor neurons during grasping.

One more possibility is that proprioceptive neurons encode correlated combinations of joints. Indeed, according to some variants of the synergy hypothesis, neural control of the limb is restricted to a lower dimensional manifold than that afforded by its biomechanics to render its control simpler and more robust to motor noise (Flash and Hochner, 2005; Kutch and Valero-Cuevas, 2012; Tresch and Jarc, 2009). This putative manifold is revealed through standard dimensionality reduction approaches such as principal-component analysis. The efficient coding hypothesis (Barlow, 1961) would prescribe that the associated sensory system would also reflect this lower dimensional manifold to minimize redundancy in neuronal representations of the hand in the SCx. Such a representation would also be supported by Hebbian synaptic learning, which is known to give rise to neuronal representations that reflect correlated patterns of inputs (Friston et al., 1993; Miller and MacKay, 1994; Oja, 1982, 1992; Pehlevan et al., 2015); in this case, joint kinematics. Against these predictions, however, we found that models based on PCs of the kinematics, which collapse kinematic redundancy into a basis set of non-redundant signals, were no more accurate or parsimonious than models based on raw joint angles, consistent with previous findings in the M1 (Kirsch et al., 2014; Mollazadeh et al., 2014).

We note, however, that non-PCA transformation of the kinematics could, in principle, offer a parsimonious description of neural activity in the M1 and SCx. Such a transformation would itself likely comprise features defined by combinations of multiple muscles or joints and, therefore, fall under the broader definition of movement synergies. Such parsimonious models are likely to arise in a coordinate frame that captures behaviorally relevant features, such as hand aperture (Jeannerod, 2009; Jones and Lederman, 2006) or grip type (such as “power” and “precision”; Napier, 1956) or one that relative positions of the fingertips (Biggs et al., 1999). Similar transformations of coordinate frames have revealed parsimonious descriptions of otherwise complex neural response properties (e.g., Chang and Tsao, 2017). A major challenge moving forward is to understand the reference frame in which hand postures are encoded and discover how these postural representations interact with cutaneous representations of object contacts to give rise to stereognosis (Delhaye et al., 2018; Hsiao, 2008).

Proprioceptive and Motor Representations of the Hand Are Similar

Neurons in the SCx and M1 carry remarkably similar representations of action, as found for the proximal limb (London and Miller, 2013). The size of the RFs and the degree of posture preference is approximately equivalent across Brodmann’s areas 3a, 2, and 4 (M1). Note that one canonical difference between motor and sensory responses—that the former precede and the latter follow movement—is difficult to probe with natural movements given autocorrelations that stretch over long timescales. This is particularly difficult with respect to the highly autocorrelated hand postural kinematics preferentially tracked by somatosensory and motor cortices during grasping (Figure S7C).

The similarity between proprioceptive and motor representations may reflect their tight interplay in the neural control of movement. Indeed, the somatosensory cortex is essential for the execution of skilled movement (Brochier et al., 1999; Hikosaka et al., 1985; Jeannerod et al., 1984), and area 3a is known to send projections to and receive projections from the motor cortex in primates (Huerta and Pons, 1990; Huffman and Krubitzer, 2001; Jones et al., 1978). The bidirectional communication between somatosensory and motor cortices may be facilitated by a common representational scheme for the hand.

The Interplay between Reach and Grasp

Our results describe a postural representation of grasping in the absence of a typical reaching phase. In natural behavior, reaching and grasping are tightly linked: reaching and grasping kinematics co-vary systematically (Jeannerod, 1984), and perturbation of one can affect the timing of both (Saling et al., 1998). Moreover, premotor and posterior parietal cortical areas, typically thought to be specialized for grasp representations, carry information about reach location as well (Lehmann and Scherberger, 2013; Takahashi et al., 2017). M1 neurons exhibit a similar mixture of selectivity for proximal and distal limb movements (Rouse and Schieber, 2016; Saleh et al., 2012). In the present study, however, animals pre-shaped their hand despite the absence of reaching, as observed during standard reaching and grasping. Thus, the manual behavior did not seem to be affected by the absence of an arm movement. Furthermore, the neuronal representations of reaching and grasping have been shown to be relatively independent in time but carried by overlapping neuronal populations (Rouse and Schieber, 2018).

Conclusions

Proprioceptive representations of the hand encode time-varying joint postures distributed over the entire hand. This neural representation stands in contrast with its proximal limb counterpart, which preferentially encodes movement. Proprioceptive RFs in the SCx, similar to their counterparts in the M1, encompass multiple joints spanning the entire hand and cannot be easily explained by anatomical couplings between joints or patterns of correlations among their movements. The postural representation of the hand in the sensorimotor cortex is consistent with the primacy of tracking hand shape and a role of these representations in stereognosis.

STAR★METHODS

Detailed methods are provided in the online version of this paper and include the following:

LEAD CONTACT AND MATERIALS AVAILABILITY

This study did not generate new unique reagents. Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dr. Sliman Bensmaia (sliman@uchicago.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animals and surgery

We recorded neural data from four male Rhesus macaques (Macaca mulatta) ranging in age from 6 to 15 years and weighing between 8 and 11 kg. All animal procedures were performed in accordance with the rules and regulations of the University of Chicago Animal Care and Use Committee (IACUC). Monkeys received care from a full-time husbandry staff, and their health was monitored by a full-time veterinary staff.

Monkeys underwent a magnetic resonance imaging (MRI) scan to identify anatomic landmarks and stereotaxic coordinates in preparation for array implantation. Each monkey was then implanted with a head post fixed to the skull with bone screws. Monkey 1 was implanted with two Utah electrode arrays (UEAs, Blackrock Microsystems, Salt Lake City, UT), one in primary motor cortex, the other in somatosensory cortex and four floating microelectrode arrays (FMAs, Microprobes for Life Science, Gaithersburg, MD), two in the anterior and two in the posterior bank of the central sulcus (Figure S1A). Monkeys 2 through 4 were implanted with semi-chronic Microdrive electrode arrays (SC96, Gray Matter Research, Bozeman, MT), each spanning large swaths of primary motor and somatosensory cortex and comprising individually depth-adjustable electrodes (Figure 1D; Figures S1B, S1D, and S1E; Dotson et al., 2017). A second implant in Monkey 2 comprised two 64-channel Utah arrays, one in primary motor cortex and one in somatosensory cortex (Figure S1C). All procedures were performed under aseptic conditions and under anesthesia induced with ketamine HCl (20 mg/kg, IM) and maintained with isoflurane (10–25 mg/kg per h, inhaled).

METHOD DETAILS

Behavioral task and recording methods

Animals were trained to perform a grasping task. On each trial, one of 25 shapes was manually placed on the end of an industrial robotic arm (MELFA RV-1A, Mitsubishi Electric, Tokyo, Japan). Shapes were affixed to a magnetic base with a stem, and the magnetic base permitted the coupling of each shape to the robotic arm. The robot immediately moved to a “ready” state pointing the shape toward the monkey, but out of reach. To initiate the task from this “ready” state, the monkey was required to hold its arms still in the armrests of the chair in which it was seated, which was enforced using feedback from photosensors placed in the armrests. If the monkey lifted its arms out of the rests at this or any other point of the trial, that trial was aborted. After a 1–3 s delay, randomly drawn on a trial-by-trial basis, the robot translated the shape toward the animal’s stationary hand (Figure 1A). As the shape approached, the animal shaped its hand to grasp it. Some of the shapes were presented at different orientations, requiring a different grasping strategy, so the different orientations of the same shape will be referred to as different “objects” (Figure 1B). Each object was presented eight to eleven times in a given session. A set of 31 reflective markers was placed on bony landmarks straddling the joints of the hand and forearm (Figures S1F and S1G) and a 14-camera optical tracking system (MX T-Series, Vicon, Los Angeles, CA) (Figure 1A) tracked their time-varying three-dimensional positions at a sampling rate of 250 Hz (Monkey 1) or 100 Hz (Monkeys 2–4). Recorded marker positions were labeled (Nexus, Vicon, Los Angeles, CA) to specify their anatomical locations for further processing.

Different trial epochs could be divided based on five events (Figure 1C): trial start, when the cameras began to record kinematics; robot present, when the object began to move toward the monkey’s hand; start of movement, the time at which the hand began to move about the wrist joint; maximum aperture, the time at which the digits were maximally separated, a critical component of hand pre-shaping (Jeannerod, 2009; Jones and Lederman, 2006); and grasp, when object contact was finally established. Across all trials spanning all objects, sessions, and monkeys, the mean interval between the start of movement and maximum aperture was approximately 560 ms and the mean interval between maximum aperture and grasp was around 480 ms. Only neural data during pre-grasp epochs, extending from 750 ms prior to start of movement through 10 ms prior to grasp, were analyzed.

The timing of start of movement, maximum aperture, and grasp events were inferred on the basis of the recorded kinematics. A subset of trials from each session were manually scored for each of these three events. On the basis of these training data, joint angular kinematic trajectories spanning 200 ms before and after each frame were used as features to train a multi-class linear discriminant classifier to discriminate among these four classes: all three events of interest and “no event.” Log likelihood ratio was used to determine which “start of movement,” “maximum aperture,” and “grasp” times were most probable relative to “no event.” Events were sequentially labeled for each trial to enforce the constraint that start of movement precedes maximum aperture, and maximum aperture precedes grasp.

After grasp, monkeys were required to maintain contact with the object for another interval lasting between one and three seconds, randomly drawn on each trial. After this interval, the robot would retract. If the monkey maintained enough grip force to disengage the magnetic coupling between robot and object during the retraction of the robot, a water reward was administered. The object was then removed manually from the monkey’s hand, and a new object was manually attached to the robot to begin the next trial.

Because we wished to investigate coding of hand movements, we sought to eliminate movements of the proximal arm associated with reaching, which can overlap substantially with grasp representations, especially in motor representations of the limb (Donoghue et al., 1992; McKiernan et al., 1998; Park, et al., 2001; Saleh et al., 2012; Takahashi et al., 2017). However, the use of restraints to hold the arm in place would introduce cutaneous inputs and isometric forces exerted against those restraints, which might affect neural responses but not be reflected in the measured kinematics. To minimize these confounds while still isolating grasping movements, we trained monkeys to volitionally hold their arms stationary while grasping objects. This was achieved by placing a photosensor under each arm (Figure 1A) and only rewarding the monkeys when they performed the task without moving their arms off the sensors.

Neural data were recorded from single-units in somatosensory and primary motor cortex using multi-electrode arrays. Somatosensory cortex (SCx) comprises four cortical fields, each containing its own body map (Kaas et al., 1979; Pons et al., 1985): Brodmann’s areas 3a, 3b, 1 and 2. Measurements were focused on areas 3a and 2, which are known to contain neurons with proprioceptive responses (Jones and Porter, 1980; Kaas, 1983; Pons et al., 1985). In Monkey 1, UEAs targeted caudal M1 (anterior) and area 3a (posterior) (Figure S1A). In Monkeys 2–4, each SC96 array impinged on all relevant areas of SCx and M1 given the wide span of this implant and the fact that it comprises depth-adjustable electrodes (Figure 1D; Figures S1B, S1D, and S1E). A second implant in Monkey 2 comprised two 64-channel Utah electrode arrays, one in SCx (area 2) and one in M1 (Figure S1C). Histological reconstructions, obtained for one monkey (Monkey 4), verified the location of proprioceptive recordings in Brodmann’s areas 3a and 2 (Figure 1E).

Data Processing

We used the position of reflective markers placed on the animal’s hand to reconstruct joint angles and musculotendon lengths. Inverse kinematics were calculated using labeled marker kinematics and a musculoskeletal model of the human arm (https://simtk.org/projects/ulb_project; Anderson and Pandy, 1999, 2001; de Leva, 1996; Delp et al., 1990; Dempster and Gaughran, 1967; Holzbaur et al., 2005; Yamaguchi and Zajac, 1989) implemented in Opensim (https://simtk.org/frs/index.php?group_id=91; Delp et al., 2007) scaled to each subject (monkey) using the built-in Opensim scaling function, which sizes each segment (bone) according to the recorded placements of markers on the hand and arm. We modified the model to permit three degrees of freedom about the first and fifth carpo-metacarpal joints so that multi-axis oppositional movements could be captured. Inverse kinematics returned estimates of the time-varying joint angular coordinates—22 in Monkey 1 and 30 in Monkeys 2–4, spanning all degrees of freedom across 13 joints in Monkey 1, and 19 joints in Monkeys 2–4. Kinematic reconstruction of the extrinsic muscles of the hand was also possible for Monkeys 2–4. A diagram of the skeletal model and reconstructed joints is provided in Figure S1H. Further details of the joints and muscles we reconstructed are provided in Tables S2 and S3, respectively.

Inverse kinematic data were filtered first using a moving median filter (MATLAB movmedian) over a centered 83 ms window to remove outliers and sudden jumps in joint angle. The output of the moving median filter was then filtered using a 4^th order low-pass Butterworth filter with a 6 Hz cutoff frequency (MATLAB butter and filtfilt). Joint angular velocities were then calculated from these filtered kinematics (MATLAB diff).

Spikes in the neural data were detected by first identifying manually set threshold crossings in the raw voltage trace, sampled at 30 kHz and digitally high-pass filtered with a cutoff frequency of 200 Hz. Offline spike sorting (Offline Sorter, Plexon, Dallas, TX) was then used to isolate individual units from a trace if more than one action potential waveform was identified and to remove non-spike threshold crossings.

Functional hand mapping

As our interest was primarily in hand proprioceptive responses in somatosensory cortex, we functionally mapped somatosensory cortical units for proprioceptive responses. To this end, we first manually palpated the arm, hand, face, trunk, and legs and only accepted neurons responding selectively to palpations of the upper limb. We then applied light cutaneous stimulation by brushing the hand and arm tangentially with a cotton swab, and subsequently manipulated the joints of the hand and wrist and palpated the tendons and bodies of the forearm musculature. At joints where the overlying hairy skin was sufficiently loose (i.e., the elbow, wrist, and metacarpo-phalangeal joints), this skin was strained while maintaining the posture of the joint to confirm that a neuron’s response was indeed driven by proprioceptors and not a mere consequence of lateral shear of the skin. In some cases, tactile stimulation was applied to the tactile receptive field of the neuron while the hand was shaped in different postures or the wrist adopted positions at various degrees of flexion, extension, pronation, or supination, to confirm that the neurons indeed exhibited cutaneous responses. We recorded from somatosensory neurons that could be driven reliably by joint manipulations or forearm palpations.

Histology

At the conclusion of electrophysiological recordings in Monkey 4, we processed the cortex for histology to confirm the locations of electrodes relative to cytoarchitectonically defined cortical fields. Electrolytic lesions (10 μA monophasic pulses at 300 Hz for 10 s) were placed at strategic locations across the array to help locate selected electrode tracks. The animal was then euthanized (60 mg/kg pentobarbital sodium) and transcardially perfused with 0.9% saline followed by 3% paraformaldehyde. At the end of perfusion, the brain was removed from the cranium, blocked, and left to soak overnight in 30% sucrose phosphate buffer. Next, a cryostat was used to take transverse sections of blocked cortex at a thickness of 60 μm per slice. One of every 12 slices was stained for Nissl and VGlut2, and one of every 6 for Cytochrome Oxidase (CO), to aid in identifying boundaries between cortical areas using cell body morphology and density.

A three-dimensional reconstruction of histological sections, borders of cortical fields, and electrode tracks was achieved by registering transverse slices and histological sections using the Fiji distribution (https://imagej.net/Fiji) of ImageJ (https://imagej.nih.gov/ij/; Schneider et al., 2012) and the StackReg plugin (http://bigwww.epfl.ch/thevenaz/stackreg/; Thévenaz et al., 1998) then marking each electrode or cortical field border as a region of interest (ROI). Field borders were determined using previously defined architectonic features (Baldwin et al., 2018; Krubitzer et al., 2004). Progressing from rostral to caudal, the transition from area 4 to 3a coincides with a reduction in the frequency of pyramidal cells in the deepest cortical layers and an increase in the cell packing of layer 4; between 3a and 3b, a further sharp increase in the cell packing of layer 4; between 3b and 1, an increase in the spatial extent but decrease in the cell packing of layer 4; between 1 and 2, an overall reduction in cell packing contrast across layers; and at the caudal extent of area 2, a slight increase in the density of cell packing in layer 4. Example Nissl stains from two slices show electrode tracks in Brodmann’s areas 3a and 2, confirming the location of the recorded neurons initially estimated based on anatomical landmarks and response properties (Figure 1E).

QUANTIFICATION AND STATISTICAL ANALYSIS

Computing trial-averaged kinematics and firing rates

Kinematics and spike counts were collected across multiple presentations (~10) of each object and averaged to obtain an estimate of the time-varying hand shape (e.g., Figure 2B) or time-varying firing rates (e.g., Figure S2) associated with each object. Prior to averaging across trials, each time-varying joint angular or spike count trace was aligned to maximum aperture and smoothed with a Gaussian kernel (σ = 20 ms). Smoothed, trial-averaged kinematics and firing rates are only used for visualizing the activity of single neurons. All analyses are based on neuronal responses or kinematics that preserve trial-by-trial variability.

Kinematic object classification

To assess the degree to which the animals preshaped their hands in an object-specific way before grasp, we computed the accuracy with which classifiers could identify an object on the basis of joint angular postures at various epochs before object contact. First, we took 3 events and defined 12 additional pseudo-events, 6 evenly spaced between the start of movement and max aperture, and another 6 from max aperture to grasp, and extracted the instantaneous multi-joint posture at that event for each trial. The 12 pseudo-events simply mark alignment points that tile the time interval between the kinematically scored events and do not themselves correspond to features of grasp. Then, we fit multiclass linear discriminant classifiers (MATLAB fitcdiscr) using multiple trials (~350) across 35 objects, and assessed classification accuracy using leave-one-trial-out cross-validation. A separate classifier was used for kinematics aligned to each of these 15 events and pseudo-events.

We verified that individual monkeys used consistent grasping strategies for each object across sessions and pooled trials across sessions from each monkey to train and evaluate these classifiers. We did not pool across monkeys as different grasping strategies are used by different animals. We then averaged time-varying classification accuracy across monkeys (Figure 2C) to obtain an overall measure of the object specificity of hand postures during pre-shaping.

Generalized linear model (GLM)

One of the main goals of the present study was to establish which aspects of hand postures and movements drove the responses of individual sensorimotor neurons. To this end, we used Generalized Linear Models (GLMs) to predict the neuronal responses over the epochs of interest (Figure 1C), from 750 ms prior to start of movement through 10 ms prior to object contact. Kinematics were aligned with these neural data at different latencies, spanning 250-ms leads through 250-ms lags, in an attempt to find the latency that maximized the goodness-of-fit of each neuron’s GLM. In particular, we tested latencies of 0, ± 10, ± 20, ± 30, ± 50, ± 90, ± 150, and ± 250 ms.

Note that each of 15 single-lag models fit to each neuron imposed the same uniform latency across all kinematic predictors. We did, however, assess the extent to which kinematic trajectories spanning multiple latencies influenced goodness-of-fit (Figure S7A) and found a small, albeit significant, improvement with multiple lags. Because the effect of using multiple lags was small when expressed in terms of pseudo-R² (see below), and because single-lag models incorporate fewer parameters and are thus more readily interpretable, we used single-lag models to determine response field sizes and preferences for postural or movement kinematics.

We fit a number of different GLMs to the responses of each neuron: postural, movement, and combined. In Monkeys 2 through 4, a total of 30 predictors were used for “postural” GLMs: one for the time-varying angle about each joint degree of freedom (DOF). Similarly, 30 predictors were used for “movement” GLMs: one for the time-varying angular velocity about each joint DOF. Finally, the “combined” model used a total of 60 predictors, using both the time-varying joint angular and angular velocity predictors of the “posture” and “movement” models. In Monkey 1, 22 predictors were used in “posture” and “movement” models, and 44 in the “combined” model, as some joint degrees of freedom were not reconstructed for this monkey (Table S2).

We performed a similar analysis on neuronal responses evoked in M1 as the animal performed a planar reaching task with a KINARM (Hatsopoulos et al., 2007; Table S1; Figure S6A). The joint angular positions of shoulder flexion/extension and elbow flexion/extension (“posture”) or their derivatives (“movement”) were used to predict neuronal responses. “Combined” models included both the time-varying joint angles and their derivatives.

Neural data and kinematics were down-sampled to 50 Hz (20 ms bins) prior to running the GLMs. GLMs were fit using a Poisson noise model and a softplus inverse link function and implemented in MATLAB using the nonlinear input model (NIM) (http://neurotheory.umd.edu/nimcode; McFarland et al., 2013).

We used LASSO regularization to limit the number of predictors in the models. This approach introduces a hyperparameter, λ, that penalizes the L1-norm of the GLM predictor weight vector, β. Values of λ and β are fit using 60-20-20 cross-validation. For each λ tested, we fit the optimal β to a training set of 60% of our samples within a given session, chosen at random but kept consistent across different λ. We then estimated the Poisson log likelihood of each model on a validation set comprising 20% of our samples, chosen at random from the remaining 40% of samples not used to train each model. The λ and corresponding β that maximized the log likelihood of the validation set were then selected, and the log likelihood of the test set, comprising the final 20% of our samples, is reported.

The Poisson log likelihood, LL_ŷ|y, of a vector of predicted spike counts, ŷ, given a vector of observed spike counts, y, is

$$L{L}_{\widehat{y}|y}=\sum _{i=1}^N{y}_i\text{log\hspace{0.17em}}\left({\widehat{y}}_i\right)-{\widehat{y}}_i,$$ (Equation 1)

where N is the number of samples in each vector. The predicted spike counts, ŷ, were dependent on the model used to estimate them. For computing the log likelihood of “saturated” models (LL_saturated), ŷ by was set to be equal to y. For computing the log likelihood of “null” models (LL_null), ŷ was set to a single repeated value, namely the mean of y. For all other models (LL_model),

$$\widehat{y}=\text{log\hspace{0.17em}}\left[1+\text{exp\hspace{0.17em}}\left(X\beta +{\beta }_0\right)\right],$$ (Equation 2)

where log[1 + exp(ᐧ)] is the aforementioned softplus inverse link function; X is a N×d matrix of predictor values (e.g., angles), with d being the number of predictors (e.g., joint degrees of freedom); β is the aforementioned vector of optimal predictor weights; and β₀ is a scalar offset that is optimized alongside β.

For ease of interpretation, we then converted these log likelihoods into McFadden’s pseudo-R² values,

$$\mathit{\text{Pseudo\hspace{0.17em}}}{R}^2=1-\frac{L{L}_{\mathit{\text{saturated\hspace{0.17em}}}}-L{L}_{\mathit{\text{model\hspace{0.17em}}}}}{L{L}_{\mathit{\text{saturated\hspace{0.17em}}}}-L{L}_{\mathit{\text{null\hspace{0.17em}}}}}.$$ (Equation 3)

For typical linear regression, which assumes a Gaussian residual model, this pseudo-R² is precisely equivalent to the coefficient of determination, R². For a model with Poisson residuals, it quantifies the fraction of deviance, rather than variance, explained by the GLM. Note that pseudo-R² values tend to be much lower than their standard R² counterparts for fits that seem comparable upon visual inspection of trial-averaged PETHs.

In addition to LASSO GLM, we performed a stepwise GLM procedure (Figure S3B–D) on a subset of neurons (pseudo-R²>0.2 with the combined LASSO GLM model) using a built-in MATLAB routine (stepwiseglm). These GLMs used the same softplus inverse link function and Poisson noise model as the LASSO GLMs, but strictly optimized the log likelihood of the model rather than a penalized version of it. Stepwise GLMs were cross-validated in 80–20 train-test fashion, and the pseudo-R² of these models is reported for the test set, just as it is for the LASSO GLMs. Stepwise GLMs began from models that incorporated zero parameters, iteratively added new parameters if their addition resulted in a significantly smaller deviance of the model (chi-square test, α = 0.0083), and iteratively removed parameters from the previous iteration’s model if their removal did not significantly change the deviance of the model (chi-square test, α = 0.05)

Interpreting encoding models: size and extent of joint RFs

We computed a summary statistic to determine the number of joints in a typical neuron’s response field. We also computed partial pseudo-R² values of posture- and movement-based GLMs to determine their relative contributions to the model predictions. Summary statistics and partial pseudo-R² comparisons were computed only for the subset of neurons with a maximum cross-validated pseudo-R² value of at least 0.05. This criterion was chosen because it is close to the R² significance criterion of regression models fit to trial-averaged data (roughly R²> 0.08; cf. Paninski et al., 2004), is more conservative than one determined based strictly on statistical significance (Table 1), and ensures a baseline level of goodness-of-fit when analyzing RFs. In practice, the vast majority of neurons recorded from M1 and Brodmann’s areas 3a and 2 exceeded this criterion (Figure 3B). In some cases, namely the analyses associated with Figures S3B–S3D, S5B, S5C, and S7D–S7G, only the subset of neurons with pseudo-R² > 0.20 were considered.

The number of joints in a neuron’s response field was determined as follows. First, because we incorporated different axes of rotation as separate predictors, and because we used both the posture and movement of each joint angle as a separate predictor, we grouped standardized regression weights according to the joints with which they were associated and calculated the sum of their squares. Once the sum of squared regression weights was computed for each joint, we determined the minimal set of joints that cumulatively explained 90% of the sum of squared regression weights across all joints.

For stepwise GLMs, the number of joints is simply counted, as significance criteria set a categorical cut-off for which parameters were and were not included in the final model. For LASSO GLMs, no such clear cut-off exists, so the aforementioned 90% cut-off was devised as a proxy.

We also compared goodness-of-fit of these multi-joint models to those computed using a single joint as a predictor. There were 19 single-joint models for each neuron, each of which incorporated the angular position and velocity of each degree of freedom of that joint as a predictor (Table S2). For example, a single-joint model using the wrist would predict a neuron’s firing rate using the angle and angular velocity along the flexion/extension, abduction/adduction, and pronation/supination axes as separate predictors, yielding a model with a total of 6 predictors. A model using an interphalangeal joint would comprise just 2 predictors: angle and angular velocity along a single flexion/extension degree of freedom.

Surrogate data were also constructed to simulate responses of neurons whose response fields comprised just a single degree of freedom (Figure S3A). Each simulated neuron would respond to either the angle or angular velocity of a single, randomly selected degree of freedom of a joint. The time-varying firing rate of each simulated neuron was obtained by first multiplying the value of its preferred degree of freedom by a weight parameter, adding the value of an offset parameter to that, and then applying a softplus transformation to the resulting value. Time-varying spike counts were then simulated by drawing, for each 10-ms time bin, from a Poisson distribution with mean equal to the inferred firing rate for that bin. The weight and offset parameters were adjusted for each simulated neuron so that its expected pseudo-R² and overall mean firing rate would be equivalent to a randomly chosen neuron from which we recorded. Each neuron’s response was simulated to kinematics recorded during the same session as the recorded neuron to which its goodness-of-fit and overall mean rate were matched. RF sizes of these simulated neurons were then inferred using the same cross-validated LASSO GLM procedures as were recorded neurons.

The extent to which joints in a neuron’s response field (RF) were distributed across the entire hand was assessed by computing a co-occurrence matrix for each cortical field. For each pair of joints, we computed the number of neurons with both joints in their RFs, and normalized it by the number of neurons with either joint in their RFs.

We then used canonical correlation analysis to find the maximum correlation between each pair of joints — recall that individual joints can comprise separate predictors for different rotational degrees of freedom. We also determined the proximity of each pair of joints on the basis of the number of skeletal or ligamentous segments interposed between them. As a joint is defined as the junction between two or more bones (Table S2), two joints were deemed “adjacent” if both joints shared a bone or comprised adjacent metacarpal bones, the latter of which are connected by the transverse metacarpal ligament. This set of pairwise adjacencies formed an unweighted, undirected graph where nodes corresponded to joints and edges corresponded to links between adjacent joints. Minimum path lengths between all pairs of joints in this graph were then determined and served as a measure of the proximity of those two joints. Linear regression was then used to determine the extent to which minimum path length between each pair of joints predicted the rates with which those joints co-occurred within neural RFs: The R² of this regression is reported.

Interpreting encoding models: alternate coordinate frames

We assessed the degree to which two alternative kinematic coordinate frames might offer a more parsimonious description of neural activity than did joint angles: musculotendon lengths and principal components (PCs) of joint angular kinematics. Musculotendon lengths were obtained from the same OpenSim model as the joint angles and yielded 35 different coordinates spread across 22 different muscles; multiple insertions (“heads”) of multi-articulate muscles were modeled as separate musculotendon units (Table S3). When inferring the number of muscles in a neuron’s RF, squared regression weights across multiple “heads” of each muscle were summed to obtain each muscle’s contribution to the RF, just as they were across degrees of freedom of each joint. Musculotendon lengths were only reconstructed for Monkeys 2–4.

Joint PC scores were obtained by applying principal component analysis (PCA) to joint angular kinematics (cf. Thakur et al., 2008)) on a monkey-by-monkey basis, pooling across sessions within but not across animals. Both the positions and velocities (derivatives) along the resultant kinematic dimensions were used to fit GLMs using methods similar to those used for models in a joint coordinate frame. Each PC’s contribution to a neuron’s RF was quantified by summing over two squared regression weights: one for its “position,” and one for its “velocity.”

Interpreting encoding models: testing preferential encoding of posture or movement trajectories

Partial pseudo-R² of model X given model Y is computed using a calculation similar to that for partial coefficients of determination,

$$\mathit{\text{Partial\hspace{0.17em}pseudo\hspace{0.17em}}}{R}^2(X|Y)=1-\frac{L{L}_{\mathit{\text{saturated\hspace{0.17em}}}}-L{L}_{X,Y}}{L{L}_{\mathit{\text{saturated\hspace{0.17em}}}}-L{L}_Y},$$ (Equation 4)

where LL_X,Y is the cross-validated log likelihood of the combined model, and LL_Y is the cross-validated log likelihood of the model using only the set of predictors Y. In essence, these computations quantify the amount of unique deviance explained by including predictors X after first removing all deviance that can be explained solely by predictors Y. As such, these partial pseudo-R² values are reported as “fraction of unique deviance explained” (FUDE), followed by the predictor set (either “posture” or “movement”) that filled the role of X. To compute FUDE, we use LL_X,Y and LL_Y assessed at the latency that maximizes LL_X,Y. Using LL_Y assessed at its own best latency yielded similar results.

Testing for shifts in neural tuning

During hand movements, neuronal response fields (RFs) could conceivably shift between epochs of grasp in a similar manner that they have been shown to during reach (Mason et al., 1998; Sergio et al., 2005; Sergio and Kalaska, 1998). Such shifting tuning could artificially inflate the size of RFs, computed under the assumption of unchanging tuning throughout the movement. To test this hypothesis, we split each grasping epoch into two distinct phases: hand opening, which spanned the start of movement to maximum aperture; and hand closing, which spanned maximum aperture to grasp (Figure S5A). We then performed GLMs that fit one RF to both epochs (as we had previously done) or separate RFs to each epoch, and determined if separate RFs better accounted for the neuronal responses (Figures S5B and S5C).

More specifically, we fit four GLMs using the same LASSO regularization and 60-20-20 cross-validation methods as described previously. The first of these four models, the “fixed joint tuning” model, predicted firing rates across both hand opening and hand closing epochs using a single RF throughout the movement. Both joint angles and angular velocities were used as predictors for these models. We report pseudo-R² in the typical manner for these GLMs. The second model, “shifting joint tuning,” predicted firing rates using GLMs fit separately to neural activity occurring during the hand opening and hand closing epochs. Again, both angles and angular velocities were predictors. The deviances of these separated hand opening and closing GLMs are summed to compute a full-movement pseudo-R² which we report and compare with the fixed joint tuning model. The third model, “fixed PC tuning,” was computed by first projecting joint angular data onto the principal components (PCs) computed from the kinematics pooled across both epochs, incorporating the derivatives of these PC scores as predictors, then predicting firing rate throughout the movement using a single RF. Pseudo-R² is computed similarly to the fixed joint tuning model. The fourth model, “shifting PC tuning,” projected each epoch’s kinematics onto separately computed PCs, and predicted each epoch’s firing rates using a separate RF for each epoch. Again, both PC scores and their derivatives were used as predictors. Deviances across epochs are summed to obtain a pseudo-R² to compare with the fixed PC tuning models.

Testing spike history dependence and encoding of temporally extended hand trajectories

A previous report concluded that M1 neurons preferentially encode movements rather than postures of the hand (Saleh et al., 2010), in contradiction with our own conclusions. In an attempt to reconcile this apparent discrepancy, we examined differences in how the encoding models were implemented in the two studies. Indeed, the previous report used spike history terms and temporally extended kinematic trajectories as predictors.

We therefore fit additional GLMs that incorporated these additional features to determine how multi-lag models or spike history terms affected neurons’ apparent preference for postural or movement kinematics. Briefly, spike history terms were obtained by convolving spike trains with progressively wider causal filters, with each convolved trace acting as a separate predictor. These filters took the form of seven raised cosines whose phases and widths were defined on a logarithmic time axis, as described in the previous report (Saleh et al., 2010). Temporally extended kinematic trajectories were fit to each neuron’s response by treating each combination of kinematic degree of freedom and temporal lag as a separate predictor.

We assessed these GLMs using the same measures of pseudo-R², FUDE, and the number of predictors in each neuron’s RF (Figure S7) as used for other GLMs. We compared these measures among different GLMs comprising spike history predictors, multi-lag predictors, both, or neither to determine which sets of methodological differences, if any, were sufficient to change the relative posture or movement preferences of neurons. Moreover, for a subset of the GLMs (Figures S7D–S7G), we used the kinematic predictor set (comprising 6 degrees of freedom) described in the previous report (Saleh et al., 2010) to facilitate comparisons between those results and our own.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Rhesus macaque (Macaca mulatta)	• Covance (Monkeys 1 and 2)	N/A
	• University of Texas Health Sciences (Monkey 3)
	• PrimGen (Monkey 4)
Software and Algorithms
ImageJ (Fiji distribution) v1.52h	Schneider et al., 2012	https://imagej.nih.gov/ij/;https://imagej.net/Fiji
StackReg plugin for ImageJ	Thévenaz et al., 1998	http://bigwww.epfl.ch/thevenaz/stackreg/
OpenSim v3.3	Delp et al., 2007	https://simtk.org/projects/opensim
Upper Extremity Model (OpenSim model)	Holzbaur et al., 2005	https://simtk.org/projects/ulb_project
MATLAB R2017a	Mathworks	https://www.mathworks.com/products/matlab.html
Nonlinear input model (MATLAB code)	McFarland et al., 2013	http://neurotheory.umd.edu/nimcode
Offline sorter v2.8.8	Plexon	https://plexon.com/products/offline-sorter/
Nexus 2.6.0	Vicon	https://www.vicon.com/products/software/nexus
Other
Cerebus system	Blackrock Microsystems	https://www.blackrockmicro.com/neuroscience-research-products/neural-data-acquisition-systems/cerebus-daq-system/
Utah array	Blackrock Microsystems	https://www.blackrockmicro.com/electrode-types/utah-array/
Floating microelectrode array	Microprobes Life Sciences	https://microprobes.com/products/multichannel-arrays/fma
96 channel microdrive system (SC96)	Gray Matter Research	https://www.graymatter-research.com/96-channel-semi-chronic-microdrive-system/
MX T-Series motion capture system	Vicon	https://www.vicon.com/downloads/documentation/go-further-with-vicon-mx-t-series

Highlights.

• The response fields of sensorimotor neurons are distributed over the entire hand

• Response fields do not reflect kinematic synergies or hand anatomy

• For grasping, unlike reaching, neurons track joint angles rather than joint velocities

• Neuronal representation of hand posture is well suited to support stereognosis