Automating a Process Convolution Approach to Account for Spatial Information in Imaging Mass Spectrometry Data

Abstract

In the age of big data, imaging techniques such as imaging mass spectrometry (IMS) stand out due to the combination of data size and spatial referencing. However, the data analytic tools readily accessible to investigators often ignore the spatial information or provide results with vague interpretations. We focus on imaging techniques like IMS that collect data along a regular grid and develop methods to automate the process of modeling spatially-referenced imaging data using a process convolution (PC) approach. The PC approach provides a flexible framework to model spatially-referenced geostatistical data, but to make it computationally efficient requires identification of model parameters. We perform simulation studies to define optimal methods for specifying PC parameters and then test those methods using simulations that spike in real spatial information. In doing so, we demonstrate that our methods concurrently account for the spatial information and provide clear interpretations of covariate effects, while maximizing power and maintaining type I error rates near the nominal level. To make these methods accessible, we detail the imagingPC R package. Our approach provides a framework that is flexible and scalable to the level required by many imaging techniques.

1. Introduction

Imaging mass spectrometry (IMS) is a technique that measures the abundance of molecular fragments over a two-dimensional space. Data are collected over a regular grid, and at each point, the abundances of hundreds to thousands of fragments are measured to produce spectra. Each fragment is identified by its mass-to-charge ratio (m/z), and the relative abundance of fragments is measured as a ratio of abundances comparing fragments.

IMS results in considerable amounts of spatially-referenced data, but methods used to analyze such data have lagged. Commonly applied analysis methods include principal components analysis (PCA), segmentation analysis, and clustering algorithms [1, 2]. Though such methods can analyze the peaks from tens of thousands of spectra relatively quickly, they often ignore the inherent spatial correlation in IMS data and produce results with vague interpretations of covariate effects. Moreover, due to the complexities of combining data across experiments and incorporating covariate information, these analyses often focus on a single or a few regions of interest (ROIs) and lack population-level inference, thereby limiting the generalizability of results.

Here we develop and propose methods to automate the process of accounting for the spatial information inherent in imaging data while providing clear interpretations of covariate effects across multiple ROIs. Although our methods focus on IMS data, they are applicable to other forms of imaging data. Our methods require the outcome be a spatially-referenced continuous measure, collected on a regular grid. To account for the spatial information, we propose using a process convolution (PC) approach, which allows our methods to scale to large IMS datasets.

Thiébaux and Pedder [3] define generic moving average models for both spatial and temporal processes. Consider a two-dimensional space defined by domain D. They model the spatial process Z(s), where s is some location in D, by convolving a white noise (zero-centered) process, ε(s), with a continuous response function q(s),

$$Z\left(s\right)={\int }_{D}q\left(s^{\prime }\right)\epsilon \left(s-s^{\prime }\right)d{s}^{\prime }.$$ (1)

This continuous representation can be computationally intractable, and so Higdon offers a flexible and discrete form that he terms the PC approach [4]. Higdon convolves a zero-centered latent process u(s), with a smoothing kernel function, κ(s). u(s) is non-zero at M sites in D termed support sites, each at location ω_m (m = 1, 2, …M), such that u(s) = u(ω_m). The stochastic spatial process Z(s_i) is defined by the convolution

$$Z\left(s_i\right)=\sum _{m=1}^{M}u\left({\omega }_m\right)\kappa \left(s_i-{\omega }_m\right).$$

The latent process, u(ω_m), is typically assumed to be Gaussian, but that is not required. The smoothing kernel is a function of the shift from data location i to support site m, and it is often (though not necessarily) assumed to be distributed as bivariate normal with covariance Σ.

The focus of current research on modeling spatial information has shifted to developing methods that make minimal assumptions about underlying spatial processes and account for features like nonstationarity. The drawback to such methods is that they are computationally burdensome. For one such method that incorporates covariate information into the covariance structure, Risser and Calder report that 10,000 Markov Chain Monte Carlo (MCMC) iterations for a dataset of only 200 observations took approximately 20 hours to fit using a Xeon E5–2680 (2.7 GHz, eight cores) processor [5]. IMS experiments produce tens or hundreds of thousands of spectra per experiment. Moreover, investigators are often interested in numerous peaks across these spectra. Despite the appeal of methods that make minimal assumptions about the spatial process, such methods are currently limited in their scalability.

The advantages of the PC approach are flexibility and scalability. The latent process and smoothing kernel can each take the form of diverse continuous distributions to accommodate different spatial processes [6], though Gaussian distributions are typically assumed [7, 4, 8]. The PC approach can accommodate spatio-temporal [7, 9] and multivariate spatio-temporal data [10, 11], and the smoothing kernel can even develop over space to account for local nonstationarity [7].

The disadvantage of the PC approach is the need to specify model parameters about which little may be known in advance in order to make modeling computationally tractable. If the smoothing kernel is to be fixed and is assumed Gaussian, one needs to specify the variance-covariance matrix for that density. Furthermore, for an application of the PC approach, the locations of all support sites need to be assigned. Laying down support sites is a particular challenge, as there is little guidance about how many support sites are required and where they should be placed. For tissue microarrays (TMAs), in which hundreds of tissue samples can be arranged on a glass slide, the time required to manually place support sites for each ROI prohibits the efficient use of PC methods as they currently exist.

To make PC methods efficient and accessible, we seek to automate the process of placing support sites. We adopt an empirical Bayes (EB) approach by first estimating the variance of a Gaussian smoothing kernel. We overlay support sites on the ROIs and use MCMC to estimate the remaining model parameters. In Section 2 we specify the assumptions of the spatial process and describe simulation studies to specify PC parameters. In Section 3 we detail the results of simulations and establish a methodology for utilizing the PC approach with imaging data collected on a regular grid. We test the performance of that methodology in Section 4 using a simulation study that spikes in the spatial information from IMS data.

2. Methods

2.1. Assumptions

We assume that the spatial process Z(s) is second-order stationary, meaning that the expected value and covariance function are invariant to spatial shifts [12]. We assume Z(s) is isotropic, meaning κ(s_i − ω_m) is unaffected by changes in the angle between s_i and ω_m, and is only dependent on the distance between observation i and support site m [12]. The smoothing kernel, therefore, becomes $\kappa \left(\Vert s_i-{\omega }_m\Vert \right)$, where $\Vert \cdot \Vert$ is the L2-norm. We further assume that the smoothing kernel is univariate normal with variance ${\sigma }_{\kappa }^2$. Under this assumption the smoothing kernel is radially symmetric. We believe this to be an appropriate assumption as the tissue samples we’ve observed do not have strong directionality. Lastly, the latent process u(ω_m) is assumed to follow a zero mean normal distribution.

2.2. Procedure to Specify PC Parameters

2.2.1. Notation

For the discussions that follow we consider data in which y_ijk signifies the outcome of interest for subject i (i = 1, 2, …, N), ROI j (j = 1, 2, …, S_i), and raster k (k = 1, 2, …, R_ij) at location s_ijk. Furthermore, u(ω_ijm) is the latent process at location ω_ijm (m = 1, 2, …, M_ij). The number of ROIs per subject and the number of rasters and support sites per ROI are held constant in the simulations that follow. The methods described herein easily adapt to changing dimensions. We use the more generic term ROI instead of sample to recognize that investigators are sometimes interested in regions of tissue samples instead of the entire sample.

2.2.2. Computational Approach

In prioritizing computational efficiency, we fix the smoothing kernel, with standard deviation σ_κ, and treat the latent process as random. This allows for straightforward and efficient incorporation into a hierarchical modeling framework. In theory the parameters σ_κ, M_ij, and ω_ijm can all be estimated at each iteration of an MCMC chain, but that would require concurrently changing the dimensions and values of large matrices, making the task computationally inefficient for large datasets. By fixing the smoothing kernel, only the latent process is estimated. Compared to the smoothing kernel function, the latent process is much smaller in dimension, making computation more efficient.

2.2.3. Semivariogram-Based Estimation of σ_κ

With three parameters to specify for the PC approach (σ_κ, M_ij, ω_ijm), modeling these data begins by estimating σ_κ using a semvariogram-based approach. At every distance measured between observations that are within ROIs, we estimate the semivariance using the Cressie-Hawkins robust estimator [13]. We use the data across all ROIs to estimate the semivariance at each distance. Recall that the data are collected on a regular grid, and so distances between data are not unique. For the semivariogram function γ(h), where h is the distance between rasters with location s_ijk and $s_{ij{k}^{\prime }}$, and N(h) is the number of observations that are a distance h apart,

$$\widehat{\gamma \left(h\right)}=\frac{{\left[\frac{1}{\left|N\left(h\right)\right|}\sum _{N\left(h\right)}{\left|Z\left(s_{ijk}\right)-Z\left(s_{ij{k}^{\prime }}\right)\right|}^{1/2}\right]}^4}{0.457+0.494/\left|N\left(h\right)\right|},\hspace{1em}k\ne k^{\prime }.$$

We found that the Gaussian covariance model adequately fit the semivariance estimates for many m/z values (Figure F.20). We use a loss function weighted by the number of observations in each bin, and allow estimation of the nugget. From the fitted semivariogram, we recommend a value of ${\widehat{\sigma }}_{\kappa }$ according to the theoretical relationship between σ_κ and the range parameter $\varphi \left({\sigma }_{\kappa }=\varphi /\sqrt{2}\right)$ [14].

For IMS data, and in particular the IMS data described herein, it is important to estimate a nugget effect. Cressie identifies two processes that can contribute to a nugget effect: error in measurement and a microscale process [12]. We contend that both exist in our data. Many IMS techniques exist, and the data herein were collected using matrix-assisted laser desorption/ionization Fourier-transform ion-cyclotron resonance (MALDI FT-ICR). The FT-ICR mass analysis technique uses small changes in current induced by spinning ions to measure their abundance. The mass spectrometers using this technique are sensitive to electronic noise within the machine that can obscure the true measurements. While data processing steps attempt to account for this noise, this nonetheless provides evidence of measurement error. We also contend a microscale process contributes to a nugget effect, meaning the variance of measurements is non-zero as the distance between measurements approaches zero. Specifically, the laser used to release ions from the tissue surface in our experiments had a diameter of approximately 30µm. At this size, the laser samples relatively large cellular environments, and small shifts in that location can cause varied cellular environments to be sampled.

2.2.4. Choice of Support Structure

Our next task is to enumerate potential support structures, where support structures are the collections of support sites for ROIs. We consider two classes of support structures. The first, termed fixed support structures, positions five to twelve support sites at fixed locations across each ROI (Appendix A). These support structures are well-suited for regular shapes that are repeated, such as tissue punches on TMAs. We adopt the naming convention of combining the number of support sites with the letter “x,” used to signify the arrangement of four corner support sites (e.g., the fixed support structure with five support sites is called the 5x support structure). The second class of support structures is termed alternating and these are intended to scale up to larger samples that require more support sites. They are given the suffix alt, to distinguish them from the fixed support structures. In the alternating support structures, rows of alternating numbers of support sites are constructed such that each support site is equidistant to six other support sites, forming a hexagonal pattern (Appendix A). Among the fixed and alternating structures, we only consider structures where the total number of support sites across all ROIs is at most 50% of the total number of observations. We refer to this rule as the 50% rule, and we use it to limit the computational burden of models. In our experience, exceeding 50% adds little to the estimation of covariate effects, and ROIs that utilize support sites exceeding 50% often have spatial variation that approaches uncorrelated noise. From the structures considered, a structure must be chosen, which is the focus of this study.

2.2.5. Metric to Compare Support Structures

The value of σ_κ produces a weighting scheme that controls the relative importance of data in estimating nearby values of the latent process u(ω_ijm). For rough spatial processes, the value of σ_κ is small and only observations close to each ω_ijm have an appreciable impact on the estimation of u(ω_ijm). For smooth spatial processes, σ_κ is large and more distant observations impact the estimation of the u(ω_ijm) (Appendix B). To compare the performance of support structures, we require a metric that takes into account the distance between the data and support sites, relative to the value of σ_κ.

We define d as the maximum distance between a data point and its nearest support site. We scale d by ${\widehat{\sigma }}_{\kappa }$ to create $d^{\ast }=d/{\widehat{\sigma }}_{\kappa }$, which is interpreted as the number of smoothing kernel standard deviation units that encapsulate all the data. Finally, we note that Higdon recommends placing support sites external to the data [4]. Accordingly, we define c as the distance between the outermost data points and the corner support sites for each ROI, where the corner support sites extend beyond the bounds of the data.

2.3. Data Simulation

For the studies herein, data were simulated in the following manner. Consistent with our collaborations, we assume a paired data scenario in which five subjects each contribute two ROIs, one from a tumor sample and a second from the associated normal margin. It is common practice in surgical oncology to, whenever possible, remove a malignancy with a surrounding border of healthy tissue (referred to as the normal margin) to ensure complete removal of the cancerous tissue. We assume the investigator is interested in whether the abundance of an ionized fragment differs between the tumor and normal margin states. Each tissue sample was simulated as a 10x10 grid of lognormally distributed fragment abundances called peak intensities. On the log scale, subject-level intercepts and raster-level errors were drawn from zero-mean Gaussian distributions with variances of 0.25 and 0.09, respectively. The spatial information was generated by drawing 144 Gaussian process realizations, u(ω_ijm), per ROI, positioned on an equally-spaced 12x12 grid, from a standard normal distribution. The smoothing kernel was a normal distribution with a σ_κ of 0.5, 1, or 2, to produce increasingly smooth spatial processes. For example datasets see Figure C.6. The normal variances used to simulate data were chosen using estimates from early modeling.

After generating the spatial information, the tumor covariate effect was added to samples, where appropriate. We tested fold change (FC) values of 1 (null), 1.5, 2, and 3.

Simulations occurred in two distinct stages: (1) defining default support settings (σ_κ, M_ij, ω_ijm) and (2) defining structure selection. If the number of recommended support sites exceeds 50% of the number of observations, we require a default support structure to use instead. Stage (1) determines the settings for that structure, which allows us to recommend a support structure for all simulated data. In stage (2) we test different rules for choosing support structures to fully define our approach.

2.4. Model Fitting

We fit all models in a Bayesian framework to accommodate the large and complex random effects structures. We fit log-linear models that included subject-level intercepts to account for subject-level clustering. We assumed

$$\log \left(Y_{ijk}\right)|b_i,u\left({\mathbf{\omega }}_{ij}\right)~\text{N}\left({\mu }_{ijk},{\sigma }_{ij}^2\right)$$

$$b_i~\text{N}\left(0,{\sigma }_b^2\right)$$

$$u\left({\omega }_{ijm}\right)~\text{N}\left(0,{\sigma }_{uij}^2\right)$$

$$b_i╨u\left({\omega }_{i^{\prime }jm}\right),\forall i,i^{\prime },j,m,i\ne i^{\prime },$$

where

$$u\left({\mathbf{\omega }}_{ij}\right)=\left(u\left({\omega }_{ij1}\right),u\left({\omega }_{ij2}\right),\dots ,u\left({\omega }_{ij}{M}_{ij}\right)\right).$$

We modeled the conditional mean assuming a linear relationship with covariates and random effects, specifically

$${\mu }_{ijk}={\beta }_0+{\beta }_1{t}_{ij}+b_i+{\left[{\mathit{K}}_{ij}\right]}_{k}u\left({\mathbf{\omega }}_{ij}\right),$$

where

$$t_{ij}=\{\begin{array}{l}0,\hspace{0.17em}\text{ROI}\hspace{0.17em}j\hspace{0.17em}\text{from}\hspace{0.17em}\text{subject}\hspace{0.17em}i\hspace{0.17em}\text{is normal}\hspace{0.17em}\text{margin}\hfill \\ 1,\hspace{0.17em}\text{ROI}\hspace{0.17em}j\hspace{0.17em}\text{from}\hspace{0.17em}\text{subject}\hspace{0.17em}i\hspace{0.17em}\text{is}\hspace{0.17em}\text{tumor},\hfill \end{array}$$

and

$${\left[{\mathit{K}}_{ij}\right]}_k=\left(\kappa \left(\Vert s_{ijk}-{\omega }_{ij1}\Vert \right),\kappa \left(\Vert s_{ijk}-{\omega }_{ij2}\Vert \right),\dots ,\kappa \left(\Vert s_{ijk}-{\omega }_{ij}{M}_{ij}\Vert \right)\right).$$

By incorporating the PC approach into a mixed model framework, covariate effects have straightforward interpretations. Assuming peak intensities are lognormally distributed, exp(β₁) is interpreted as the peak intensity FC comparing the tumor to the normal margin state. To fully specify a Bayesian analysis, we assumed the following priors and hyperpriors:

$${\sigma }_{ij}~\text{U}\left(0,10\right)$$

$${\sigma }_b~\text{U}\left(0,10\right)$$

$${\sigma }_{uij}~\text{U}\left(0,10\right)$$

$${\beta }_0~\text{N}\left(0,{\sigma }_{{\beta }_0}^2\right);{\sigma }_{{\beta }_0}~\text{U}\left(0,10\right)$$

$${\beta }_1~\text{N}\left(0,{\sigma }_{{\beta }_1}^2\right);{\alpha }_{{\beta }_1}~\text{U}\left(0,10\right).$$

We found that we could reliably estimate the error and latent variances on the ROI level (${\sigma }_{ij}^2$ and ${\sigma }_{uij}^2$, respectively), and that doing so reduced type I error rates compared to estimating overall variances (Appendix D).

We fit all models using the R package NIMBLE [15, 16], which incorporates a C++ compiler to speed up the MCMC sampling. We used two chains with a 10,000 iteration burn-in, a 25,000 iteration sample, and thinned every 25th iteration for a chain length of 1,000 iterations per chain from which we conducted inference. Convergence was assessed using the Brooks-Gelman-Rubin (BGR) statistic [17] within the coda package [18]. Simulations were considered converged if β₁ had a BGR ≤ 1.10 [19]. We did not require convergence contingent on the intercept or variance components. The tumor coefficient converged more quickly and required less thinning than the intercept. The number of variance components prohibited using them in determining convergence. However, they consistently converged according to the BGR statistic and iteration plots. The simulations were run on a desktop with an Intel Core i7–8700 CPU (3.20 GHz).

2.5. Defining Default Support Structure Settings

If σ_κ is small, the underlying spatial process is rough, and large numbers of support sites are required to account for the spatial information. If σ_κ is too small, the number of support sites required to account for the spatial information can exceed that allowed under the 50% rule. When this occurs, we require default support structures (M_ij, ω_ijm) and default values in place of ${\widehat{\sigma }}_{\kappa }$. When we replace ${\widehat{\sigma }}_{\kappa }$ with a default value, we will refer to it as σ₀ to distinguish it from the estimate.

To determine what default support structures and default σ₀ should be used, we simulated 200 datasets each using a σ_κ of 0.5 and 1. We don’t use values of σ_κ greater than 1 because data simulated with a σ_κ of 1.5 or greater have not required default structures. For the cases in which we utilize default settings, we want to ensure we minimize type I errors. Therefore, to define default settings, we simulated data under the null, meaning no tumor effects were added.

We fit models in which we fixed c (the distance between the outermost data points and the corner support sites) at 0.5 and tested different default support structures and default values of σ₀. We tested two values for σ₀, 1 × d and 1.5 × d, where d is the largest observed distance between a data point and the nearest support site. We tested three default support structures, 5x, 10x, and the densest allowed, meaning the most support sites allowed under the 50% rule. We measured performance based on the model convergence rate, type I error rate of the tumor coefficient, and MSE. After determining optimal default settings, we fixed those settings for subsequent simulations.

2.6. Defining Support Structure Selection

Once we selected default settings and priors, we proceeded to specify the PC parameters ω_ijm and M_ij. This process can be framed by two questions: (1) How close do the outer support sites need to be to the data? and (2) How dense do the support structures need to be to account for the spatial information?

To answer these questions, we simulated datasets under the null (FC=1) and alternative (FC=1.5, 2, and 3) in which the spatial information was generated from either a rough (σ_κ = 1) or smooth (σ_κ = 2) spatial process, and we then controlled the placement and density of support sites. In early attempts at incorporating the PC approach, type I error rates were high (> 20%), so we focused on simulations under the null. For such simulations, we simulated 100 datasets from a rough or smooth process, and then we controlled the distance c and tested values of 0.1, 0.3, 0.5, 0.7, and 1. The distance between raster centroids where measurements are made is given an arbitrary distance of 1, so a c value of 0.5 is 50% of that arbitrary distance. To determine the density of support sites, we controlled the proximity of data to support sites in terms of the scaled distance $d^{\ast }\left(d^{\ast }=d/{\widehat{\sigma }}_{\kappa }\right)$. We used values of d^∗ = 0.5, 1, 1.5, and 2. For d^∗ = 1, a support structure is chosen such that all the data are within ${\widehat{\sigma }}_{\kappa }$ of a support site.

Upon running simulations under the null, we selected values of d^∗ that maintained low type I error rates and examined them further using simulations under the alternative. We simulated 100 datasets from either a smooth or rough process, and incorporated a FC of 1.5, 2, or 3 comparing the tumor to normal margin samples. For each set of simulations, we fixed c at the same values as null simulations. We measured performance using the percent significant, coverage, and bias for the tumor coefficient, as well as the MSE and computation time.

3. Results

3.1. Default Support Structure Settings

Table 1 shows the results for the default support settings. Recall that the default settings are only used if the number of support sites recommended across all samples exceeds 50% of the number of observations. All settings showed high convergence rates of at least 99%. Simulations differed meaningfully only in terms of type I error rate and MSE. As the number of support sites increased and more random effects were incorporated into the model, the MSE unsurprisingly decreased. For a given support structure, the MSE was lower for data simulated using a smoother spatial process (σ_κ = 1) compared to data simulated using a rougher spatial process (σ_κ = 0.5). Although the differences were not marked, using a default σ₀ of 1 × d consistently produced lower MSE values compared to using a default σ₀ of 1.5 × d. The lowest MSEs were produced by using the densest support structure available and a default σ₀ of 1 × d.

Table 1:

Convergence Rate, Type I Error Rate, and MSE for Default PC Settings

default structure	default σ0	σκ (simulation)	convergence rate (%, out of 200)	type I error rate (%)	MSE
5x	1.0 × d	0.5	100.0	0.0	0.649
		1.0	100.0	1.5	0.409
	1.5 × d	0.5	100.0	0.0	0.658
		1.0	100.0	19.0	0.432
10x	1.0 × d	0.5	100.0	1.0	0.623
		1.0	99.5	0.0	0.308
	1.5 × d	0.5	100.0	2.0	0.646
		1.0	99.0	3.0	0.348
densest	1.0 × d	0.5	100.0	1.5	0.425
		1.0	100.0	7.5	0.102
	1.5 × d	0.5	100.0	0.0	0.517
		1.0	100.0	0.0	0.116

Note: For a 10x10 grid of data, the densest support structure has 46 support sites.

The type I error rates produced results with a more muddled interpretation. When using 95% credible intervals, we expect the type I error rates to be approximately 5%. Specifying a default 5x support structure produced low type I error rates, except when using a default σ₀ of 1.5 × d with data generated from a σ_κ of 1. This produced a type I error rate of almost 20%. Because of this, we excluded the 5x from further consideration as a default support structure.

Using the densest support structure available produced a broad range of type I error rates. For simulations with a default σ₀ of 1.5 × d, there were no type I errors for either σ_κ. When a default σ₀ of 1 × d was used, the type I error rates increased to 1.5% and 7.5% for σ_κ = 0.5 and σ_κ = 1, respectively. Although the type I error rate for σ_κ = 1 exceeded 5%, it was closer to 5% than using a σ_κ of 1.5 × d.

In conjunction with the MSE values, the type I error rates for the densest support structure produced an interesting trend. For data simulated using a σ_κ of 0.5, a default σ₀ of 1 × d produced better fit according to the MSE but a higher type I error rate compared with a default σ₀ of 1.5 × d. The same trend occurred for data simulated with a σ_κ of 1. Smaller values for a default σ₀ capture more localized spatial effects (Figure B.5), and as the density of support sites increases, the default σ₀ decreases since it is defined by the distance between the data and support sites. If support structures get too dense, the model may overfit the data, leading to increased type I error rates and lower MSE. Although we observe higher type I error rates when using a default σ₀ of 1 × d, the models do not appear to be overfitting the data. In fact, from the default conditions tested, we selected a default structure of the densest available and a σ₀ of 1 × d. These conditions produced the lowest MSE values and type I error rates closest to 5% across both σ_κ values. We fixed the default structure and default σ₀ for subsequent simulations.

3.2. Support Structure Selection

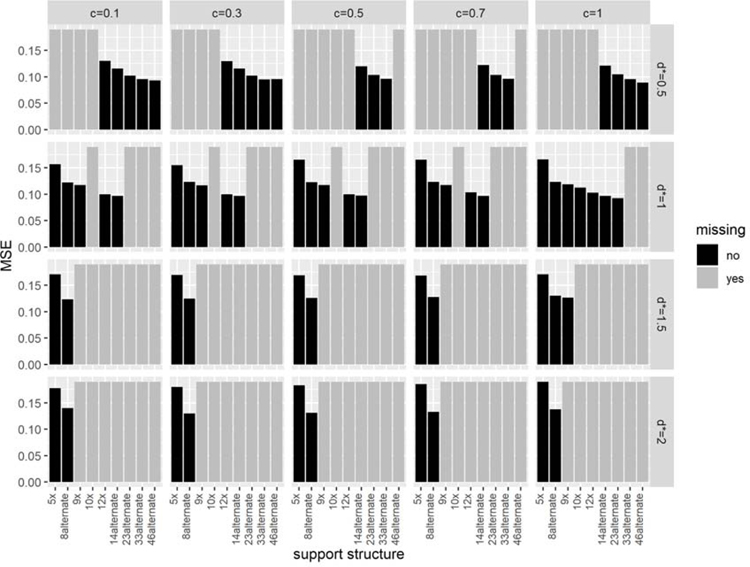
Figures 1 and 2 show the percent significant and MSE, respectively, from simulations in which we altered (1) the distance c between the outer support sites and the data and (2) the distance d^∗, the maximum allowed distance between the data and support sites, scaled by the standard deviation of the smoothing kernel ${\widehat{\sigma }}_{\kappa }$.

Figure 1:

Changes in the percent significant produced by changing the distance c and distance threshold d^∗. The rows of panels are differentiated by the log(FC), and the columns are differentiated by the σ_κ used to generate the simulated data. Each panel shows the percent significant, where the shapes distinguish between values of d^∗, the maximum allowed distance between any data point and the nearest support site, scaled by ${\widehat{\sigma }}_{\kappa }$. The values of c, the distance between the corner support sites and the outermost data points, are shown along the x-axis. For simulations under the null (FC=1), the area representing a type I error rate ≤ 5% is shaded.

Figure 2:

The effect of changing c, d^∗, and the tumor effect on the MSE. The figure is paneled by the log(FC) tumor effect (rows) and σ_κ used to generate the spatial information (columns). The MSE averaged across all simulations is plotted as a function of the distance c, where the shapes differentiate the d^∗ used to select support structures. All panels have the same y-axis limits to facilitate comparisons.

For simulations under the null, the percent significant is interpreted as the type I error rate (Figure 1, top panel). The trends in the type I error rate differed by σ_κ value. For data generated using the rougher spatial process (σ_κ=1), a d^∗ value of 1 provided the lowest type I error rate across all values of c, and d^∗ values of 0.5 and 1.5 produced type I error rates close to 5%. In general, the type I error rate decreased slightly as the outer support sites were pushed out farther from the data (c increased).

For data generated using a σ_κ of 2, selecting a support structure such that all data were within $0.5\times {\widehat{\sigma }}_{\kappa }$ of a support site (d^∗=0.5) produced the lowest type I error rate and the only type I error rate that fell below 5% for all values of c. The other d^∗ values produced type I error rates greater than 5%, with a d^∗ of 1 being the only other d^∗ value to produce type I error rates close to 5%. As c increased, there were no consistent trends for data generated by a σ_κ of 2.

Due to high type I error rates, we eliminated d^∗ values of 1.5 and 2 from further consideration, and for simulations under the alternative (Figure 1, bottom three panels), we only considered d^∗ values of 0.5 and 1. For data generated from the rough spatial process (σ_κ = 1), a d^∗ of 0.5 tended to produce higher power than a d^∗ of 1. This pattern flipped for data generated from the smooth spatial process, where a d^∗ of 1 produced higher power.

Interestingly, increasing the distance c between the outermost data points and the corner support sites had little impact on the MSE (Figure 2). However, as the density of support sites increased (d^∗ decreased), the MSE consistently decreased for both values of σ_κ.

In terms of coverage (Figure E.8) and for data generated using a σ_κ of 1, selecting a support structure using a d^∗ of 1 led to very high coverage (> 96%), while a d^∗ of 0.5 produced slightly lower coverage (≥86%). When a σ_κ of 2 was used to generate the spatial information, simulations using a d^∗ of 0.5 tended to have higher coverage (91 − 99%) than simulations using a d^∗ of 1 (86 − 98%).

Our last metric to compare values of d^∗ and c was the computation time. We approximated the average computation time for each set of conditions (Figure E.14) using the average computation time for a set of simulations using each support structure (Figure E.13), weighted by the proportion of converged simulations that used the structure (Figures E.11 and E.12). The simulations using a d^∗ of 0.5 almost exclusively utilized the three support structures with the highest number of support sites while the simulations using a d^∗ of 1 used a mix of all of the structures. The average computation time was consistently about 5 minutes less per simulation for a d^∗ of 1 compared to a d^∗ of 0.5. Though this may seem like a small amount of time, these simulations were relatively small. IMS experiments often produce tens or hundreds of thousands of observations per m/z, and so these small time differences would be more exaggerated with larger datasets.

To fully specify the PC parameters M_ij and ω_ijm, and therefore fully define our procedure, we chose to use a c of 0.1 and a d^∗ of 1. Only d^∗ values of 0.5 or 1 produced type I error rates consistently close to 5%, and so we only considered those values of d^∗. We selected a d^∗ of 1 based on a balance of the percent significant, MSE, computation time, and coverage. A d^∗ of 1 produced higher power for data generated from a σ_κ of 1 and lower power for data generated from a σ_κ of 2 (Figure 1), and this trend was reversed for coverage (Figure E.8). However, a value of 0.1 for c tended to minimize the differences in coverage. With regards to MSE, a d^∗ of 0.5 provided only minimal decreases.

3.3. Procedure to Specify PC Parameters

From the simulation studies, we recommend the following procedure to specify the PC parameters:

1. Estimate the range parameter and recommend a ${\widehat{\sigma }}_{\kappa }$. Estimate the semivariance at each distance that exists between data points. Fit a Gaussian semivariogram that allows estimation of the nugget, and estimate the range parameter. From the range parameter, recommend a ${\widehat{\sigma }}_{\kappa }$ based on the relationship ${\sigma }_{\kappa }=\varphi /\sqrt{2}$.

2. Enumerate the possible support structures. Generate all support structures in which the total number of support sites across all samples does not exceed 50% of the number of observations.

3. Select a support structure. Determine for which support structures all the data are within 1 ${\widehat{\sigma }}_{\kappa }$ of a support site. Among these support structures, choose the one with the smallest number of support sites. If the total number of support sites across all samples exceeds 50% of the number of observations, then choose the support structure with the largest number of support sites that does not exceed 50% of the number of observations and use a default σ₀ of 1 × d.

4. Application to N-Glycan IMS Data

4.1. Methods

We conducted a simulation study incorporating the spatial information from a single tissue sample to measure the ability of our methods to account for real spatial information. The tissue sample was a human prostate sample (Figure F.19) processed according to the methods outlined by Powers et al. [20] and using a Solarix 7T FT-ICR mass spectrometer (Bruker Daltonics). The data consist of approximately 18,000 spectra containing relative abundances for numerous N-glycans. N-glycans are protein modifications composed of branching chains of covalently bonded monosaccharides. Changes in N-glycan expression have consistently been associated with cancer [21, 22]. Consequently, they are viewed as potential biomarkers [23, 24] or prognostic indicators [25, 26].

In the work that follows, we refer to N-glycans by their assumed composition and approximate experimental m/z. Since N-glycans are composed of distinct monosaccharide units, each with known atomic mass, we can assume a composition with high confidence. The N-glycans we use are composed of hexose (Hex), N-acetylhexosamine (HexNAc), and neuraminic acid (NeuAc) residues. We chose four N-glycans (Figure 3): Hex5HexNAc2 + 1Na (1257.4663), Hex4HexNAc5 + 1Na (1704.6828), Hex9HexNAc2 + 1Na (1905.7403), and Hex5HexNAc4NeuAc1 + 2Na (1976.7573). We chose the N-glycans based on the presence of biological features and the amount of noise. By noise we mean the abrupt changes in log peak intensities that distort an underlying smooth surface. All the N-glycans exhibit biological features but differ in the amount of noise. Hex5HexNAc4NeuAc1 + 2Na (1976.7573) appears to have very little noise while Hex5HexNAc2 + 1Na (1257.4663) shows a much larger amount, and Hex4HexNAc5 + 1Na (1704.6828) and Hex9HexNAc2 + 1Na (1905.7403) fall in the middle.

Figure 3:

Log peak intensities for the four N-glycans. Each panel shows the same tissue sample shaded to represent the log peak intensities for the corresponding m/z at every spatial location. Blank dots represent peak intensity values of zero.

We randomly selected 10x10 grids of non-zero and non-missing peak intensities for each simulation. For each 10x10 grid, we centered the log peak intensities at an intercept of 5. We created the same data structure as previous simulations, in which five subjects each contributed two ROIs. We added subject-level intercepts and a tumor effect of increasing magnitude (log(1), log(1.1), log(1.25), log(1.5), log(2), and log(3)). In this way, we created data with the same structure as our simulations but with real spatial information. We conducted 200 simulations for each m/z and effect size in which we utilized our methodology defined in Section 3.3 to account for the spatial information while testing for differences in tumor status. We measured performance based on the convergence rate, percent significant, and coverage for the tumor coefficient.

4.2. Results

We found the Gaussian covariance model provided good fit to the semivariance estimates from simulations (Figure F.20). Table 2 shows the performance measures for simulations. We show the results for tumor effects < log(2) only because the results were similar for larger tumor effects. A full table of results is provided in Table F.6. Further results are provided in Appendix F.

Table 2:

Performance Measures for Simulations Using Real Spatial Information

experimental m/z	tumor effect	converged simulations	convergence rate (%)	percent significant	coverage (%)	MSE	average bias
1257.4663	log(1)	200	100.0	1.50	98.50	0.015	0.001
	log(1.1)	197	98.5	86.80	97.46	0.015	−0.004
	log(1.25)	198	99.0	97.98	97.47	0.016	−0.002
	log(1.5)	197	98.5	100.00	98.98	0.015	−0.001
1704.6828	log(1)	199	99.5	3.52	96.48	0.022	0.000
	log(1.1)	196	98.0	58.16	98.47	0.023	−0.006
	log(1.25)	200	100.0	94.00	98.00	0.022	−0.006
	log(1.5)	196	98.0	100.00	96.43	0.022	0.003
1905.7403	log(1)	195	97.5	4.10	95.90	0.020	0.003
	log(1.1)	200	100.0	61.50	95.00	0.020	−0.004
	log(1.25)	199	99.5	92.96	96.48	0.020	−0.006
	log(1.5)	194	97.0	100.00	97.42	0.020	0.000
1976.7573	log(1)	195	97.5	4.62	95.38	0.014	−0.003
	log(1.1)	192	96.0	65.62	82.81	0.014	−0.003
	log(1.25)	197	98.5	95.43	85.28	0.015	0.000
	log(1.5)	195	97.5	100.00	88.72	0.014	−0.004

Using a fixed burn-in, sample, and thinning interval, the simulations for all m/z values showed high convergence rates > 96%. Among the converged simulations, the type I error rates were low. None of the N-glycans exhibited type I error rates ≥ 5%. The power was high for all N-glycans and tumor effect sizes, as all simulation sets reached 100% power with a tumor effect of log(1.5). This is likely due to the strong autocorrelation in the prostate sample (Figure F.20) compared with the simulated data (Figure E.7), coupled with small estimates for the error variance (data not shown).

Across all simulations for the four N-glycans, only five support structures were selected: 5x, 8alt, 9x, 12x, and 46alt, where 46alt is the default support structure when the number of recommended support sites exceeds 50% of the number of observations. The simulations for Hex5HexNAc4NeuAc1 + 2Na (1976.7573), which exhibited clear biological features and little noise, very rarely used the default structure while Hex5HexNAc2 + 1Na (1257.4663), which exhibited much more noise, used the default support structure for approximately 60% of simulations (Table F.7). The default rates for the other two glycans fell between 5% and 20%.

When the type I error rates were broken down by support structure (Table F.8), we found that the 5x support structure had type I error rates of approximately 4–5% for each N-glycan. The 46alt support structure had a type I error rate of 0% across all simulations that used that structure, which is lower than the expected 5%. The other support structures (8alt, 9x, and 12x) had too few simulations select them to derive meaningful type I error rates.

The coverage appeared to be N-glycan-dependent. The coverages for Hex5HexNAc2 + 1Na (1257.4663), Hex4HexNAc5 + 1Na (1704.6828), and Hex9HexNAc2 + 1Na (1905.7403) were all approximately 95% and higher. For Hex5HexNAc4NeuAc1 + 2Na (1976.7573), simulations under the alternative produced coverages exceeding 80%.

5. Discussion

The experiments described herein establish a framework to account for the spatial information for continuous data collected on a regular grid. We use an empirical Bayes approach to specify the PC parameters and then estimate the latent process within an MCMC. This methodology automates the process of placing support sites and produces clear interpretations of covariates across ROIs. To make these methods accessible to investigators, we have released the R package imagingPC (https://github.com/cammiller/imagingPC). This package contains the methods described herein, as well as functions to process data and write and run models. For more information on this R package, see Appendix G.

Our methods performed well using simulated data. We constructed our methodology to keep type I error rates close to the nominal level, maximize power, and minimize the MSE and computational burden while accounting for spatial information. When we applied the methodology to spatial structure derived from a prostate sample, we found that it maintained type I error rates close to the 0.05 level. The computation times for simulations were also relatively short. The entire process, from estimating the range parameter through fitting a regression model, took 2.5–13.5 minutes, depending on the support structure chosen. Imaging experiments typically contain more than 1,000 observations, and so it will be necessary to further test our methods using real imaging data.

Aside from the automation, a secondary advantage of our approach is the straightforward interpretation. For current methods used to analyze imaging data, such as PCA, segmentation, and clustering algorithms, the interpretations of covariates are quite vague. By incorporating the PC approach into a likelihood-based modeling framework, the interpretations of covariates are clear.

Our methods have some limitations. To develop our methods we started with some restrictive assumptions about the underlying spatial process. We assumed the spatial process was stationary and isotropic, and that the smoothing kernel was univariate normal. Furthermore, we assumed the semivariogram model was Gaussian. We found these assumptions valid for much of the data we observed. They served as a good starting point for method development, and they performed well for our application to IMS data. However, these assumptions will certainly not be valid for all data, or even all IMS data. There is tremendous variety among biological samples that cannot be captured with such assumptions.

Additionally, we used a single data structure in which five subjects each contributed two ROIs, where all ROIs were comprised of the same number of rasters. Further testing is required to understand how our methods perform when using unpaired data, data with unbalanced numbers of tissue samples, or tissue samples of varying shapes and sizes. To test the ability of our methods to capture real spatial information, we used the data from a single tissue sample. While we used multiple m/z values and our methods performed well for all m/z values, the data are limited in terms of the diversity of the underlying spatial processes.

Lastly, our methods do not fully capture the multivariate nature of IMS data. Each IMS experiment produces spectra with dozens or hundreds of m/z values of interest. The molecular fragments for which abundances are measured are often interconnected in complex biological pathways. Though multivariate methods may capture the interdependence of these fragments, we take a one-at-a-time approach as a starting point, performing a separate analysis for each m/z.

Future research will focus on accounting for data features critical to imaging data, and in particular IMS data. In a typical IMS experiment utilizing the Fourier-transform ion-cyclotron resonance approach to mass analysis, the peak intensities for many m/z values are what are termed zero-heavy, where a large percentage of the measurements are zero. Multiple processes can contribute to the high percentages of zeros, which sometimes exceed 90%. Research will also focus on making our methods more flexible, not just in terms of the underlying spatial processes, but also with regard to the questions of interest. For IMS data, interest often lies in changes not only between samples, but also between regions of tissue samples and the spatial processes between regions.

While our work has focused on IMS data, it must be stressed that the methods herein are applicable to more than just IMS data. The only strict requirements are that the data be continuous, collected on a regular grid, and have no excess zeros. In addition to these requirements, users should check to make sure that Gaussian semivariogram model provides an adequate fit.

6. Conclusion

Imaging data present a modeling challenge due to the large numbers of observations and the inherent spatial structure. For techniques such as IMS, this challenge is furthered by their multidimensional nature. Here we develop methods to automate the incorporation of the PC approach to account for the spatial information in imaging data that’s collected on a regular grid. We make strong assumptions about the underlying spatial process in order to build a foundation for future method development. Despite these assumptions, our methods maintain low type I error rates for a null covariate effect when modeling real spatial structure. Our ultimate goal is to make methods of analysis for imaging data accessible to the investigators that require them. To this end we have released an R library that houses our methods.

Appendix A. Support Structures

The support structures considered are shown in Figure A.4. The fixed structures were named according to the number of support sites and the arrangement of the outside support sites. The structure 8x has 8 support sites with the outside sites at the corners.

The alternating structures started with 3 rows of alternating numbers of support sites. With each new alternating structure, a row was added, and an additional support site was added to each row. This was done until the number of support sites exceeded 50% of the average number of rasters per tissue sample.

Figure A.4:

The support structures considered for analysis. We considered two types of support structures, fixed (top) and alternating (bottom). The alternating support structures are iteratively built to accommodate tissue samples that may require a large number of support sites. Within the functions used for this study, they are constructed until the number of support sites across all ROIs exceeds 50% of the total number of observations.

Appendix B. K Matrix

Figure B.5:

Effect of choice for ${\widehat{\sigma }}_{\kappa }$. The grids represent rasters while the dots represent the locations of support sites. The color for each raster represents the value of the K matrix from row k and column m, where m is constant across each plot. For the same support structure (23alt), the plot on the left shows the values of a single column of the K matrix for ${\widehat{\sigma }}_{\kappa }=2$, and the right plot shows the same column of K matrix values for ${\widehat{\sigma }}_{\kappa }=5$.

Appendix C. Example Data

Figure C.6:

Example datasets under the null for each σ_κ. For all simulations, each subject (rows) contributed two ROIs (columns). The rasters are shaded by the log peak intensity.

Appendix D. Selecting Priors

We do not consider different distributional forms for priors in our model. We had excellent convergence rates for model coefficients using a zero-centered normal prior with a U(0,10) prior on the standard deviation. Furthermore, all variance components consistently converged using a noninformative U(0,10) prior on all standard deviations.

We do consider the level at which we estimate the error variance and latent variance. By level we mean the index from the simulated data structure. For the simulated data we can estimate single common, subject-level, or sample-level error and latent variances. To simulate data we used a single error variance and a single variance for the latent process. However, without a priori knowledge of the underlying processes that generated the data, we cannot necessarily assume that variance structure. Therefore, we conducted a simulation study in which we altered the assumed variance structure and measured performance using convergence rates, the MSE across all log peak intensities, and type I error rates for a tumor covariate.

We simulated 200 datasets each using a σ_κ of 0.5, 1, or 2. We then fit models in which, for each variance (error variance or variance of latent process), we estimated an overall variance, subject-level variances, or sample-level variances. We used all combinations of error and latent variances for a total of 9 variance structures. For each σ_κ we fit the 200 datasets to models assuming all 9 variance structures, for a total of 27 sets of 200 simulations.

Table D.3 shows the results for the simulations. The MSE was unaffected by the variance structure. The type I error rate for a σ_κ of 0.5 or 1 remained under 2% for all conditions tested. The type I error rate for a σ_κ of 2 was higher, with some variance structures producing type I error rates > 10%. To understand why the type I error rates increased so dramatically, we broke down the type I error rates by support structure (Table D.4). We found the type I error rates for one support structure, 8x, were particularly high. Due to the elevated type I error rates, we removed the 8x support structure from consideration for subsequent simulations.

Among the variance structures, we chose to estimate both the error variance and latent variance on the sample level, meaning these variances are estimated for each sample. Estimating these variances at the sample level produced comparable type I error rates (σ_κ of 0.5 or 1) or lower type I error rates (σ_κ of 2) compared with other variance structures. In fact, if the simulations that used the 8x structure were removed, the type I error rate for sample-level error and latent variance would be approximately 5%. Estimating sample-level error and latent variance also provides additional model flexibility by making less stringent assumptions about the variance structure.

Table D.3:

Type I Error Rate and MSE for Variance Structures

σκ	error variance	latent variance	total simulations	converged simulations	convergence rate (%)	type I error rate (%)	MSE
0.5	overall	overall	200	200	100.0	0.0	0.427
		subject	200	200	100.0	0.5	0.428
		sample	200	200	100.0	0.0	0.429
	subject	overall	200	200	100.0	0.5	0.429
		subject	200	200	100.0	0.5	0.431
		sample	200	200	100.0	0.0	0.432
	sample	overall	200	200	100.0	0.5	0.432
		subject	200	200	100.0	0.0	0.434
		sample	200	200	100.0	1.0	0.436
1.0	overall	overall	200	200	100.0	1.5	0.142
		subject	200	200	100.0	0.5	0.141
		sample	200	198	99.0	1.5	0.141
	subject	overall	200	198	99.0	1.5	0.142
		subject	200	200	100.0	1.0	0.142
		sample	200	198	99.0	1.5	0.142
	sample	overall	200	199	99.5	1.5	0.143
		subject	200	198	99.0	1.0	0.143
		sample	200	200	100.0	1.5	0.143
2.0	overall	overall	200	196	98.0	12.2	0.114
		subject	200	192	96.0	8.9	0.114
		sample	200	193	96.5	7.3	0.114
	subject	overall	200	192	96.0	12.0	0.114
		subject	200	196	98.0	8.7	0.114
		sample	200	187	93.5	9.6	0.114
	sample	overall	200	193	96.5	11.4	0.114
		subject	200	194	97.0	9.8	0.114
		sample	200	193	96.5	7.8	0.114

Table D.4:

Type I Error Rate (%) for Variance Structures, by Support Structure

			5x		8x		8alternate		12x		14alternate		23alternate		33alternate		46alternate
σκ	error var.	latent var.	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)	# sims	err rate (%)
0.5	overall	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0.5
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0
	subject	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0.5
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0.5
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0
	sample	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0.5
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	0
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0	199	1
1.0	overall	overall	-	-	1	100	1	0	-	-	10	0	56	0	132	1.5	-	-
		subject	-	-	1	0	1	0	-	-	10	0	56	0	132	0.8	-	-
		sample	-	-	1	100	1	0	-	-	10	0	54	0	132	1.5	-	-
	subject	overall	-	-	1	100	1	0	-	-	10	0	55	0	131	1.5	-	-
		subject	-	-	1	0	1	0	-	-	10	0	56	0	132	1.5	-	-
		sample	-	-	1	100	1	0	-	-	10	0	55	0	131	1.5	-	-
	sample	overall	-	-	1	100	1	0	-	-	10	0	55	0	132	1.5	-	-
		subject	-	-	1	0	1	0	-	-	10	0	56	0	130	1.5	-	-
		sample	-	-	1	100	1	0	-	-	10	0	56	0	132	1.5	-	-
2.0	overall	overall	5	0	14	35.7	106	15.1	36	2.8	33	6.1	2	0	-	-	-	-
		subject	5	0	14	42.9	105	10.5	34	0	32	0	2	0	-	-	-	-
		sample	5	0	14	42.9	103	7.8	36	0	33	0	2	0	-	-	-	-
	subject	overall	5	0	14	42.9	102	14.7	36	0	33	6.1	2	0	-	-	-	-
		subject	5	0	14	42.9	106	10.4	36	0	33	0	2	0	-	-	-	-
		sample	4	0	14	50	101	10.9	35	0	31	0	2	0	-	-	-	-
	sample	overall	4	0	14	42.9	104	14.4	36	0	33	3	2	0	-	-	-	-
		subject	5	0	14	42.9	105	10.5	35	0	33	6.1	2	0	-	-	-	-
		sample	4	0	14	42.9	106	8.5	35	0	32	0	2	0	-	-	-	-

Table D.5:

MSE for Variance Structures, by Support Structure

			5x		8x		8alternate		12x		14alternate		23alternate		33alternate		46alternate MSE
σκ	error var.	latent var.	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE
0.5	overall	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0.464	199	0.427
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0.468	199	0.428
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0.469	199	0.429
	subject	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0.466	199	0.429
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0.469	199	0.431
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0.47	199	0.432
	sample	overall	-	-	-	-	-	-	-	-	-	-	-	-	1	0.466	199	0.432
		subject	-	-	-	-	-	-	-	-	-	-	-	-	1	0.468	199	0.434
		sample	-	-	-	-	-	-	-	-	-	-	-	-	1	0.473	199	0.435
1.0	overall	overall	-	-	1	0.316	1	0.282	-	-	10	0.225	56	0.161	132	0.125	-	-
		subject	-	-	1	0.316	1	0.282	-	-	10	0.225	56	0.161	132	0.124	-	-
		sample	-	-	1	0.315	1	0.283	-	-	10	0.225	54	0.16	132	0.124	-	-
	subject	overall	-	-	1	0.316	1	0.282	-	-	10	0.226	55	0.162	131	0.125	-	-
		subject	-	-	1	0.316	1	0.283	-	-	10	0.226	56	0.162	132	0.125	-	-
		sample	-	-	1	0.316	1	0.284	-	-	10	0.226	55	0.161	131	0.125	-	-
	sample	overall	-	-	1	0.317	1	0.282	-	-	10	0.226	55	0.163	132	0.126	-	-
		subject	-	-	1	0.317	1	0.283	-	-	10	0.227	56	0.163	130	0.126	-	-
		sample	-	-	1	0.317	1	0.284	-	-	10	0.226	56	0.162	132	0.126	-	-
2.0	overall	overall	5	0.154	14	0.122	106	0.121	36	0.1	33	0.097	2	0.089	-	-	-	-
		subject	5	0.155	14	0.122	105	0.121	34	0.1	32	0.097	2	0.089	-	-	-	-
		sample	5	0.155	14	0.122	103	0.121	36	0.1	33	0.097	2	0.089	-	-	-	-
	subject	overall	5	0.155	14	0.122	102	0.121	36	0.1	33	0.097	2	0.089	-	-	-	-
		subject	5	0.155	14	0.122	106	0.121	36	0.1	33	0.097	2	0.089	-	-	-	-
		sample	4	0.157	14	0.122	101	0.121	35	0.1	31	0.097	2	0.089	-	-	-	-
	sample	overall	4	0.148	14	0.122	104	0.122	36	0.1	33	0.097	2	0.089	-	-	-	-
		subject	5	0.155	14	0.122	105	0.122	35	0.1	33	0.098	2	0.089	-	-	-	-
		sample	4	0.154	14	0.122	106	0.122	35	0.1	32	0.098	2	0.089	-	-	-	-

Appendix E. Defining Structure Selection

Figure E.7:

Gaussian covariance model fit for datasets simulated from σ_κ of 1 (left) and 2 (right). The top plots are semivariance estimates with the fitted Gaussian covariance model. The bottom plots are the number of data pairs used to estimate the semivariance at each distance. These plots are identical because both datasets are composed of 10x10 grids.

Figure E.8:

The coverage for simulations altering c and d^∗. The coverage is the percentage of simulations in which the true tumor effect is contained in the 95% credible interval.

Figure E.9:

The bias for simulations altering c and d^∗. The bias is averaged across all simulations.

Figure E.10:

Convergence rates for simulations that altered the distance c and d^∗. The figure is paneled by the value of σ_κ used to simulate the data and the magnitude of the tumor effect. Within each panel, the convergence rate is plotted for each value of d^∗ (the maximum allowable distance between any data point and the closest support site, scaled by ${\widehat{\sigma }}_{\kappa }$) and c (the distance between the outermost data points and the corner support sites).

Figure E.11:

Proportion of simulations that use each support structure (σ_κ = 1). The figure is paneled by the magnitude of the tumor effect and the value of d^∗, where d^∗ is the maximum allowable distance between any data point and the closest support site, scaled by ${\widehat{\sigma }}_{\kappa }$. Within each panel, a bar is plotted for each value of c tested, where c is the distance between the outermost data points and the corner support sites. Each bar is colored such that the height of each color segment represents the proportion of converged simulations that selected the corresponding support structure.

Figure E.12:

Proportion of simulations that use each support structure (σ_κ = 2). The figure is paneled by the magnitude of the tumor effect and the value of d^∗, where d^∗ is the maximum allowable distance between any data point and the closest support site, scaled by ${\widehat{\sigma }}_{\kappa }$. Within each panel, a bar is plotted for each value of c tested, where c is the distance between the outermost data points and the corner support sites. Each bar is colored such that the height of each color segment represents the proportion of converged simulations that selected the corresponding support structure.

Figure E.13:

Computation times for support structures. For each support structure, 10 simulations were run to estimate the computation time for each support structure. The individual computation times (in minutes) are plotted as a function of the number of support sites, and the average computation times are connected by a red line. The simulations were run on a desktop with an Intel Core i7–8700 CPU (3.20 GHz)

Figure E.14:

Approximated average computation times for changing c and d^∗. The average computation times for each structure from Figure E.13 were used to approximate the average computation times (in minutes) for simulations that altered c and d^∗. For each set of conditions, the average computation time was approximated by a weighted sum of the average support structure computation times.

Figure E.15:

Type I error rate by support structure for data simulated with σ_κ = 1. The figure is paneled by c and d^∗. The solid horizontal line is drawn at 5%, the expected type I error rate for 95% credible intervals. The bars are colored gray if no simulations used that structure. This is done to differentiate between missing values and 0% type I error rates.

Figure E.16:

Type I error rate by support structure for data simulated with σ_κ = 2. The figure is paneled by c and d^∗. The solid horizontal line is drawn at 5%, the expected type I error rate for 95% credible intervals. The bars are colored gray if no simulations used that structure. This is done to differentiate between missing values and 0% type I error rates.

Figure E.17:

MSE by support structure for data simulated with σ_κ = 1. The figure is paneled by c and d^∗. The MSE values are shown for a c of 0.1. The bars are colored gray if no simulations used that structure.

Figure E.18:

MSE by support structure for data simulated with σ_κ = 2. The figure is paneled by c and d^∗. The MSE values are shown for a c of 0.1. The bars are colored gray if no simulations used that structure.

Appendix F. Application to N-Glycan IMS Data

Figure F.19:

Human prostate sample

Table F.6:

Performance Measures for Simulations Using Real Spatial Information

experimental m/z	tumor effect	converged simulations	convergence rate (%)	percent significant	coverage (%)	MSE	average bias
1257.4663	log(1)	200	100.0	1.50	98.50	0.015	0.001
	log(1.1)	197	98.5	86.80	97.46	0.015	−0.004
	log(1.25)	198	99.0	97.98	97.47	0.016	−0.002
	log(1.5)	197	98.5	100.00	98.98	0.015	−0.001
	log(2)	200	100.0	100.00	97.50	0.015	0.001
	log(3)	200	100.0	100.00	97.00	0.015	−0.001
1704.6828	log(1)	199	99.5	3.52	96.48	0.022	0.000
	log(1.1)	196	98.0	58.16	98.47	0.023	−0.006
	log(1.25)	200	100.0	94.00	98.00	0.022	−0.006
	log(1.5)	196	98.0	100.00	96.43	0.022	0.003
	log(2)	200	100.0	100.00	97.50	0.022	−0.004
	log(3)	198	99.0	100.00	98.48	0.022	0.001
1905.7403	log(1)	195	97.5	4.10	95.90	0.020	0.003
	log(1.1)	200	100.0	61.50	95.00	0.020	−0.004
	log(1.25)	199	99.5	92.96	96.48	0.020	−0.006
	log(1.5)	194	97.0	100.00	97.42	0.020	0.000
	log(2)	198	99.0	100.00	94.95	0.020	0.003
	log(3)	198	99.0	100.00	95.96	0.020	0.006
1976.7573	log(1)	195	97.5	4.62	95.38	0.014	−0.003
	log(1.1)	192	96.0	65.62	82.81	0.014	−0.003
	log(1.25)	197	98.5	95.43	85.28	0.015	0.000
	log(1.5)	195	97.5	100.00	88.72	0.014	−0.004
	log(2)	194	97.0	100.00	89.69	0.014	0.004
	log(3)	193	96.5	100.00	86.01	0.014	0.003

Figure F.20:

Gaussian covariance model fit for two representative datasets. On the left are plots for one 1704.6828 dataset, and on the right are plots for one 1905.7403 dataset. For each m/z, on the top are semivariance estimates with the fitted Gaussian covariance model. On the bottom are plots of the number of data pairs used to estimate the semivariance at each distance. Note that the bottom plots are identical because all simulations used 10x10 grids of data, meaning the distance relationships are identical.

Table F.7:

Percent of Simulations that Utilized Default Settings

m/z	tumor effect	# converged simulations	# default simulation	default rate (%)
1257.4663	log(1)	200	118	59.00
	log(1.5)	197	123	62.44
	log(2)	200	128	64.00
	log(3)	200	114	57.00
1704.6828	log(1)	199	30	15.08
	log(1.5)	196	27	13.78
	log(2)	200	37	18.50
	log(3)	198	35	17.68
1905.7403	log(1)	195	23	11.79
	log(1.5)	194	17	8.76
	log(2)	198	19	9.60
	log(3)	198	16	8.08
1976.7573	log(1)	195	0	0.00
	log(1.5)	195	0	0.00
	log(2)	194	2	1.03
	log(3)	193	2	1.04

Table F.8:

Percent Significant Among Converged Simulations, by Structure

		5x		8alternate		9x		12x		46alternate
m/z	tumor efffect	# sims	% sign.	# sims	% sign.	# sims	% sign.	# sims	% sign.	# sims	% sign.
1257.4663	log(1)	76	3.9	5	0	1	0	0	-	118	0
	log(1.1)	61	57.4	7	100	0	-	0	-	129	100
	log(1.25)	70	94.3	10	100	0	-	0	-	118	100
	log(1.5)	64	100.0	9	100	1	100	0	-	123	100
	log(2)	65	100.0	6	100	0	-	1	100	128	100
	log(3)	81	100.0	5	100	0	-	0	-	114	100
1704.6828	log(1)	169	4.1	0	-	0	-	0	-	30	0
	log(1.1)	171	52.0	4	100	0	-	0	-	21	100
	log(1.25)	166	92.8	2	100	0	-	0	-	32	100
	log(1.5)	166	100.0	3	100	0	-	0	-	27	100
	log(2)	163	100.0	0	-	0	-	0	-	37	100
	log(3)	162	100.0	1	100	0	-	0	-	35	100
1905.7403	log(1)	166	4.8	6	0	0	-	0	-	23	0
	log(1.1)	173	55.5	6	100	0	-	0	-	21	100
	log(1.25)	179	92.2	3	100	0	-	0	-	17	100
	log(1.5)	175	100.0	2	100	0	-	0	-	17	100
	log(2)	174	100.0	5	100	0	-	0	-	19	100
	log(3)	178	100.0	4	100	0	-	0	-	16	100
1976.7573	log(1)	187	4.8	8	0	0	-	0	-	0	-
	log(1.1)	190	65.3	2	100	0	-	0	-	0	-
	log(1.25)	185	95.1	11	100	0	-	0	-	1	100
	log(1.5)	191	100.0	4	100	0	-	0	-	0	-
	log(2)	185	100.0	6	100	0	-	1	100	2	100
	log(3)	186	100.0	5	100	0	-	0	-	2	100

Table F.9:

Coverage Among Converged Simulations, by Structure

		5x		8alternate		9x		12x		46alternate
m/z	tumor efffect	# sims	coverage (%)	# sims	coverage (%)	# sims	coverage (%)	# sims	coverage (%)	# sims	coverage (%)
1257.4663	log(1)	76	96.1	5	100	1	100	0	-	118	100
	log(1.1)	61	91.8	7	100	0	-	0	-	129	100
	log(1.25)	70	92.9	10	100	0	-	0	-	118	100
	log(1.5)	64	96.9	9	100	1	100	0	-	123	100
	log(2)	65	92.3	6	100	0	-	1	100	128	100
	log(3)	81	92.6	5	100	0	-	0	-	114	100
1704.6828	log(1)	169	95.9	0	-	0	-	0	-	30	100
	log(1.1)	171	98.2	4	100	0	-	0	-	21	100
	log(1.25)	166	97.6	2	100	0	-	0	-	32	100
	log(1.5)	166	95.8	3	100	0	-	0	-	27	100
	log(2)	163	96.9	0	-	0	-	0	-	37	100
	log(3)	162	98.1	1	100	0	-	0	-	35	100
1905.7403	log(1)	166	95.2	6	100	0	-	0	-	23	100
	log(1.1)	173	94.2	6	100	0	-	0	-	21	100
	log(1.25)	179	96.1	3	100	0	-	0	-	17	100
	log(1.5)	175	97.1	2	100	0	-	0	-	17	100
	log(2)	174	94.3	5	100	0	-	0	-	19	100
	log(3)	178	95.5	4	100	0	-	0	-	16	100
1976.7573	log(1)	187	95.2	8	100	0	-	0	-	0	-
	log(1.1)	190	82.6	2	100	0	-	0	-	0	-
	log(1.25)	185	84.3	11	100	0	-	0	-	1	100
	log(1.5)	191	88.5	4	100	0	-	0	-	0	-
	log(2)	185	89.2	6	100	0	-	1	100	2	100
	log(3)	186	85.5	5	100	0	-	0	-	2	100

Table F.10:

MSE Among Converged Simulations, by Structure

		5x		8alternate		9x		12x		46alternate
m/z	tumor efffect	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE	# sims	MSE
1257.4663	log(1)	76	0.016	5	0.018	1	0.015	0	-	118	0.015
	log(1.1)	61	0.016	7	0.017	0	-	0	-	129	0.015
	log(1.25)	70	0.016	10	0.019	0	-	0	-	118	0.015
	log(1.5)	64	0.016	9	0.018	1	0.018	0	-	123	0.015
	log(2)	65	0.016	6	0.017	0	-	1	0.016	128	0.015
	log(3)	81	0.016	5	0.018	0	-	0	-	114	0.015
1704.6828	log(1)	169	0.023	0	-	0	-	0	-	30	0.02
	log(1.1)	171	0.023	4	0.021	0	-	0	-	21	0.021
	log(1.25)	166	0.023	2	0.022	0	-	0	-	32	0.02
	log(1.5)	166	0.023	3	0.022	0	-	0	-	27	0.02
	log(2)	163	0.023	0	-	0	-	0	-	37	0.02
	log(3)	162	0.023	1	0.02	0	-	0	-	35	0.021
1905.7403	log(1)	166	0.020	6	0.022	0	-	0	-	23	0.018
	log(1.1)	173	0.020	6	0.021	0	-	0	-	21	0.018
	log(1.25)	179	0.020	3	0.022	0	-	0	-	17	0.017
	log(1.5)	175	0.020	2	0.016	0	-	0	-	17	0.017
	log(2)	174	0.020	5	0.022	0	-	0	-	19	0.017
	log(3)	178	0.020	4	0.019	0	-	0	-	16	0.017
1976.7573	log(1)	187	0.014	8	0.015	0	-	0	-	0	-
	log(1.1)	190	0.014	2	0.01	0	-	0	-	0	-
	log(1.25)	185	0.015	11	0.014	0	-	0	-	1	0.013
	log(1.5)	191	0.014	4	0.018	0	-	0	-	0	-
	log(2)	185	0.014	6	0.018	0	-	1	0.009	2	0.011
	log(3)	186	0.014	5	0.016	0	-	0	-	2	0.011

Appendix G. imagingPC: an R Package to Analyze Imaging Data Using a Process Convolution Approach

The methods described are being made available in an R package called imagingPC. For processed data, meaning data that have been appropriately normalized and have single abundance measures for each m/z on the raster level, the imagingPC package uses the following work flow: (1) rescale the data (2) estimate the range parameter, (3) choose the support structure, (4) generate the smoothing kernel data and all information vectors needed to compile a Bayesian model, (5) write the model, and (6) run the model. Each step in the work flow uses a single function (Table G.11).

Table G.11:

imagingPC Functions

Task	Function
(1) rescale the data	rScale
(2) estimate the range parameter	estRange
(3) select support structure(s)	chooseStructures
(4) create data vectors for compiling a model	createPCData
(5) write model	writePCModel
(6) run model	runPCModel

The first step in the workflow is to rescale the data. The x- and y-coordinates often have long decimals associated with them. Theoretically this is not a problem, but it causes issues with downstream calculations due to the way numbers are stored, and so it is necessary to rescale the data. We rescale the data such that the distance between observations along the regular grid is 1.

In Step 2 the range is estimated using the estRange function, which is a wrapper for the variog and variofit functions from the geoR package [27]. For data collected on a regular grid, distances between data pairs are mostly non-unique. The estRange functions bins data at each distance and estimates the semivariance for each bin. It then fits a Gaussian semivariogram to the semivariance estimates in order to estimate the range parameter.

The estimated range parameter is used to choose a support structure in Step 3. The function chooseStructures enumerates support structures and selects one as explained in Section 3.3. While the simulated tissue samples were 10x10 grids, real data will certainly have ROIs of varying sizes and shapes. To accommodate such ROIs and for each ROI, the chooseStructures function places support sites across a square region encompassing the entire ROI and then removes support sites that are more than a multiplicative factor of ${\widehat{\sigma }}_{\kappa }$ away from data, with a default of $2\times {\widehat{\sigma }}_{\kappa }$. The total number of support sites across all ROIs is counted after removing support sites.

The last three steps in the workflow are concerned with running a model that incorporates the PC approach. The createPCData function is used to generate the K matrix, the result of the kernel smoothing function. Additionally, this function creates all the vectors of information necessary to compile a Bayesian model, such as a cumulative vector of the number of rasters per sample to navigate the K matrix.

The writePCModel writes a Bayesian model using NIMBLE [15], with all priors specified, and the runPCModel then runs that model. In the runPCmodel function, a model is considered converged if the BGR statistics for all model coefficients are ≤ 1.10. By default, other stochastic nodes are not monitored, but arguments allow the user to monitor all stochastic nodes and output the MCMC sample.

Currently, the writePCModel and runPCModel functions allow continuous, binary, and categorical covariates in the model. If a categorical covariate is input, dummy variables are generated, and differences between all subgroups are automatically calculated and monitored within the MCMC.

In addition to the functions described here, the imagingPC package includes plotting and summary functions, as well as functions to format IMS data for analyses. The imagingPC package is retained on GitHub at https://github.com/cammiller/imagingPC.