Validated Computational Framework for Evaluation of In Vivo Knee Mechanics

Abstract

Dynamic, in vivo evaluations of knee mechanics are important for understanding knee injury and repair, and developing successful treatments. Computational models have been used with in vivo experiments to quantify joint mechanics, but they are typically not predictive. The current study presents a novel integrated approach with high-speed stereo radiography, musculoskeletal modeling, and finite element (FE) modeling for evaluation of subject-specific, in vivo knee mechanics in a healthy subject performing a seated knee extension and weight-bearing lunge. Whole-body motion capture, ground reaction forces, and radiography-based kinematics were used to drive musculoskeletal and predictive FE models for load-controlled simulation of in vivo knee mechanics. A predictive simulation of knee mechanics was developed in four stages: (1) in vivo measurements of one subject performing a lunge and a seated knee extension, (2) rigid-body musculoskeletal modeling to determine muscle forces, (3) FE simulation of knee extension for knee-ligament calibration, and (4) predictive FE simulation of a lunge. FE models predicted knee contact and ligament mechanics and evaluated the impact of cruciate ligament properties on joint kinematics and loading. Calibrated model kinematics demonstrated good agreement to the experimental motion with root-mean-square differences of tibiofemoral flexion–extension <3 deg, internal–external <4 deg, and anterior–posterior <2 mm. Ligament reference strain and attachment locations were the most critical properties in the calibration process. The current work advances previous in vivo knee modeling through simulation of dynamic activities, modeling of subject-specific knee behavior, and development of a load-controlled knee model.

Introduction

Due to the high prevalence of knee pain and injury, and demand for higher functionality in total knee replacements, researchers construct computer models as a means to evaluate healthy function, pathology, and treatment [1,2]. Computational models enable efficient testing of new treatments and joint replacement designs in ways that are impractical with in vivo and in vitro experiments. Finite element (FE) models of the knee have been used to reproduce in vitro loading and boundary conditions from dynamic, mechanical knee simulators [3–6]. Mechanical in vitro joint simulators enable the evaluation of knee mechanics in a controlled and repeatable loading environment. FE models of mechanical simulators employ force-controlled simulations to predict joint or actuator motion due to changes in inputs such as knee alignment and muscle loading [3]. Force-controlled simulation means that joint forces and external loads are used to drive joint motion, which allows the prediction of knee kinematics when the joint is altered by interventions such as total knee arthroplasty. For example, Baldwin et al. [4] utilized an FE model with proportional–integral–derivative (PID)-controlled quadriceps force to follow the quadriceps excursion needed to flex the knee in simulations of TKR-implanted specimens in the Kansas Knee Simulator. Building computer simulations of cadaveric tests has the benefit that models may be calibrated to quantities that are not readily measurable in vivo, such as accurate measurement of joint loading inputs [5]. However, joint simulations that represent in vitro mechanical simulators may not represent in vivo conditions; applied muscle forces are typically limited to the quadriceps tendons, and in vitro loads and boundary conditions cannot be easily modified to represent different subjects and activities. For these reasons, researchers have sought to build force-controlled FE simulations that mimic in vivo conditions. Notably, Beillas et al. [7] incorporated radiography-based kinematics into an FE model to study in vivo knee mechanics of a single-leg hop, and Fernandez et al. [8] included kinematics from X-ray fluoroscopy and quadriceps force predictions from musculoskeletal modeling into an FE simulation for prediction of patellofemoral (PF) kinematics and contact mechanics during a step-up task. Unlike a substantial number of prior works that have employed generic knee models to represent subject-specific mechanics [9,10], the use of accurate knee kinematics from techniques such as radiography enables the calibration of subject-specific models.

Following the example of FE models of mechanical simulators, the goal of the current work was to create a force-driven computational simulation for the evaluation of healthy knee mechanics calibrated and driven with in vivo measurements. Similar to Fernandez et al. [8], the current study applies a sequential approach integrating in vivo stereo radiography kinematics and predicted joint motions and muscle forces from musculoskeletal modeling into detailed, subject-specific FE models of the knee. The current study expands on prior work through subject-specific calibration of soft tissue properties and simulation of the entire range of motion of the knee. Model calibration was performed using comparison to experimental in vivo tibiofemoral (TF) and PF kinematics during a knee extension task, and the predictive capability of the model was assessed through comparisons of experimental and model kinematics during a lunge task. The computational framework can be leveraged by implant manufacturers to optimize total knee arthroplasty designs for the restoration of natural knee mechanics.

Methods

A predictive simulation of knee mechanics was developed in four stages: (1) in vivo measurement of kinematics and ground forces of one subject performing a lunge and a seated knee extension, (2) rigid-body musculoskeletal modeling to determine muscle forces, (3) finite element simulation of knee extension for knee-ligament calibration, and (4) predictive finite element simulation of a lunge (Fig. 1).

Fig. 1.

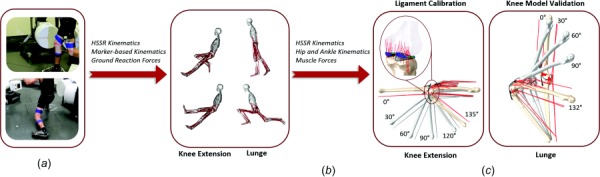
Experiment and computational modeling workflow including (a) data collection of HSSR images, motion capture, and ground reaction forces, (b) whole-body musculoskeletal modeling, and (c) detailed, subject-specific finite element modeling for knee extension and lunge activities

In Vivo Measurements.

Simultaneous marker-based motion capture, ground reaction forces, and high-speed stereo radiography (HSSR) images were collected for one healthy, older adult male (age = 52 years, height = 172 cm, weight = 57 kg, and BMI = 19.3 kg/m²) performing two activities: an unloaded, seated knee extension ranging from high knee flexion to full extension, and a single-leg weight-bearing lunge. This study was approved by the University of Denver Institutional Review Board and informed consent was provided by the subject. The motion capture system consisted of an eight-camera, passive marker, video photogrammetric system (Vicon Motion Systems, Centennial, CO) for measurement of whole-body motion. Ground reaction forces were recorded using four six-component, strain gaged force plates (Bertec Corp., Columbus, OH). High-speed stereo radiography was used to capture three-dimensional sub-mm measurement of bone motion for each activity [11]. The HSSR system is composed of two 40 cm diameter image intensifiers with high-speed, high-definition (1080 × 1080) digital cameras positioned at a relative 70 deg angle for collection of two images at a frequency of 50 Hz for the knee extension activity and 100 Hz for the lunge activity. Computed tomography (CT, 0.39 × 0.39 × 0.6 mm³, resolution: 512 × 512) and magnetic resonance (MR, 0.53 × 0.53 × 0.6 mm³, resolution: 320 × 320) images were captured for the subject. Bone and cartilage geometry were reconstructed from CT and MR imaging, respectively, using scanip (Simpleware, Exeter, UK). A femoral local coordinate system was defined by fitting a cylinder through the center of the medial and lateral femoral condyles; the medial–lateral (M–L) axis was defined by the most posterior points on each condyle; the superior–inferior (S–I) axis was parallel to the posterior edge of the femoral shaft; the anterior–posterior axis was defined by the cross product between the S–I and M–L axes. The relative positions of femur, tibia, and patella bones were tracked using Autoscoper (Brown University, Providence, RI) by manually aligning three-dimensional reconstructed geometry to the 2D images from radiography. TF and PF joint kinematics were described relative to a pose near full extension using a joint coordinate system defined by Grood and Suntay [12].

Musculoskeletal Modeling.

Muscle forces during the knee extension and lunge were calculated with a subject-specific, whole-body, musculoskeletal model developed in opensim (Stanford, CA). The model was based on that developed by Navacchia et al. [13] and consisted of 12 body segments (torso, pelvis, femurs, tibiae, tali, calcanei, and toes), and 92 Hill-type musculotendon units. Model segments were scaled based on the ratio of relative marker distances from motion capture and the virtual markers in the template model. Lower limb joint definition included a ball-and-socket hip joint, a revolute ankle joint, and a knee joint with prescribed TF and PF motion from the HSSR system. TF and PF kinematics were prescribed to a femoral coordinate system located at the midpoint of the femoral condyles using splines as a function of knee flexion [14]. All TF degrees of freedom (DOF) were prescribed, whereas the DOF prescribed to the PF joint were flexion–extension, superior–inferior translation, and anterior–posterior translation. The patellar tendon was represented in the model and applied the quadriceps force to the tibia so that the contribution of quadriceps muscle forces was included in the joint load calculations [15,16].

Motion capture and ground reaction forces were input into the musculoskeletal model for the prediction of joint kinematics and muscle forces. For simulation of the knee extension activity, the hip joint was constrained, and femoral motion was prescribed in all translational DOF to reproduce the support from the chair; the ankle/foot was unconstrained. Inverse kinematics of the marker-based motion was used to predict hip and ankle kinematics. Static optimization in OpenSim was used for the prediction of muscle forces.

Finite Element Modeling of the Lower Extremity.

Subject-specific finite element models were developed in Abaqus (Simulia, Providence, RI) for the knee extension and lunge activity (Fig. 1(c)). Models included hip (three DOF), ankle (one DOF), and knee joints (12 DOF), consistent with the joint definition described in the OpenSim musculoskeletal models. At the knee, bone and cartilage reconstructions from imaging were postprocessed in Hypermesh (v11.0, Altair, Troy, MI) using rigid, triangular, shell elements (R3D3) for bone, and hexahedral, continuum (C3D8R) elements for cartilage. Scaled mass and rotational inertial properties of the bones were obtained from musculoskeletal modeling and applied to the FE representations. Deformable contact was modeled between the articulating cartilage surfaces and the menisci with a frictional coefficient of 0.01.

Tibiofemoral ligament structures were represented using nonlinear tension-only springs (CONN3D2) and included the anteromedial-ACL bundle (ACLam), posterolateral-ACL bundle (ACLpl), anterolateral-PCL bundle (PCLal), posteromedial-PCL bundle (PCLpm), the lateral collateral ligament, popliteofibular ligament, medial collateral ligament (MCL), deep medial collateral ligament, posterior oblique ligament, anterolateral structure (ALS), and medial and lateral posterior capsule (PCAPm, PCAPl). TF ligament attachment locations were determined from MR imaging (cruciate and collateral ligaments) and anatomical bony landmarks. Initial estimates of ligament stiffness and reference strain were obtained from combined cadaveric experiments and modeling of four specimens by Harris et al. [17].

The meniscus was developed from MR reconstruction and modeled using hexahedral continuum elements (C3D8) and one-dimensional (1D) linear springs (CONN3D2) connecting the horns (N = 20) and periphery of the geometry (medial N = 24; lateral N = 12) to the tibia bone. Material properties utilized a Fung orthotropic hyperelastic material model [18–20].

Patellofemoral soft tissue structures (patellar and quadriceps tendons, and medial and lateral patellofemoral ligaments) were modeled using 2D fiber-reinforced membrane elements (M3D4R) and 1D, nonlinear, embedded springs (CONN3D2). Quadriceps tendon and patellar ligament properties were defined using a van der Waals hyperelastic model, calibrated to match uniaxial test data from the literature [21,22]. Medial and lateral patellofemoral ligaments were modeled using 1D nonlinear springs. Hard contact (zero surface-penetration) was defined between the PF soft tissue and bone to allow wrapping around the bony surfaces.

Quadriceps, hamstrings, and gastrocnemius muscles included the rectus-femoris, vastus-medialis, vastus-lateralis, vastus-intermedius, semimembranosus, biceps femoris, and gastrocnemius medial and lateral bundles. Quadriceps lines of action were estimated from reconstructions of muscle centroid path in the Visible Human Project, similar to Hume et al. [23]. A multifiber representation was adopted to better represent force generation over the entire excursion of the joint [24,25]. The vastus medialis and vastus lateralis were divided into three and two fibers, respectively, according to a previously described cadaveric dataset that grouped fibers based on function and sarcomere length [26]. A series of slipring connectors (CONN3D2) directed forces along the centroid of the muscle cross-sectional area. Hamstrings and gastrocnemius muscles were represented using a combination of point-to-point connectors (CONN3D2) and truss elements (T3D2). Truss elements allowed wrapping contact around analytical surfaces representing the femoral condyles and the posterior aspect of the tibia bone.

Simulation of Seated Knee Extension.

The loads and boundary conditions applied to the FE model replicated the experimental motion for seated knee extension (Fig. 1). The hip joint was constrained in all translational DOF to reproduce the support from the chair; the ankle/foot was unconstrained. Hip rotations were prescribed to match the rotations from the OpenSim musculoskeletal simulation. TF flexion–extension was prescribed from HSSR measurements; all other TF DOF and all DOF in the PF joint were unconstrained. The vector sum of quadriceps forces from the musculoskeletal simulation of knee extension was applied to the FE model, and the distribution of quadriceps force among the individual muscle groups was determined from Amis and Farahmand [27]. A static analysis, in the deep flexion-starting pose of the knee extension activity, was used to determine the peak magnitude of hamstrings and gastrocnemius forces. The static analysis utilized a proportional–integral–derivative controller to simultaneously solve for the combination of hamstrings and gastrocnemius loads required to maintain the deep flexion angle (∼135 deg) [28]. PID-controlled muscle forces were applied to the FE analysis using a user-defined VUAMP subroutine. Simulation of the knee extension activity was performed in reverse, such that the knee flexed from full extension to deep flexion, for improved computational efficiency. During the dynamic simulation of the knee extension activity, a ramped load from 15 N to the peak hamstrings and gastrocnemius loads (semimembranosus = 25 N, biceps femoris = 35 N, gastrocnemius medial and lateral = 200 N) was applied as the knee flexed.

Calibration of TF and PF soft tissue alignment and material properties was performed in simulations of the knee extension activity to match experimental joint kinematics using a design-of-experiments approach. Properties of the PF soft tissues were kept consistent with values reported in Baldwin et al. [21]; a sensitivity analysis doubled the stiffness of the quadriceps and patellar tendons, and found no significant differences in PF kinematics (<1 deg and 1 mm) [3]. Quadriceps and patellar tendon attachment locations on the patella were perturbed so that PF kinematics matched the measured motion from fluoroscopy. The PF soft tissue attachments and pretension in the medial and lateral PF ligaments were initially calibrated with the TF kinematics constrained to the subject motion. The TF soft tissue attachments and properties were then calibrated to reproduce the experimental TF motion, and the PF soft tissue properties were then calibrated again with the TF kinematics unconstrained. The perturbations primarily consisted of anterior–posterior translation of the patellar tendon attachment on the patella and also included internal–external rotations and medial–lateral translations of the quadriceps tendons and patellar tendon. For calibration of TF kinematics, the attachments and properties of the MCL, ACL, and PCL were modified. Ligament reference strain (EREF) [17], ACL stiffness (K) [29], and PCL stiffness [30] were perturbed within bounds described in the literature (Table 1). Table 1 describes the range of values, mean and standard deviations from literature, the initial set of parameters, and the calibrated values applied to the FE representations of the cruciate ligaments. Ligament attachment locations were varied within origin and insertion areas reconstructed from MRI and bony landmarks described in the literature. The calibration space was identified by simulating the knee extension activity with and without the ACL and PCL ligaments to establish the upper and lower bounds of TF anterior–posterior kinematics. Calibration was achieved through adjustment of ligament stiffness and reference strain until anterior–posterior kinematics matched the measured values from fluoroscopy. Hamstrings muscle attachments were adjusted to achieve agreement between experiment and model-predicted TF internal–external motion.

Table 1.

Cruciate ligament stiffness (K) and reference strain (EREF) properties applied to FE simulations Bounds and mean ±1 standard deviation for ACL stiffness [29], PCL stiffness [30], and reference strain [17] were obtained from the literature. Calibrated values describe the final set of parameters used for subject-specific simulation.

	ACLam		ACLpl		PCLal		PCLpm
	Stiffness (K, MPa)	Reference strain (EREF)	Stiffness (K, MPa)	Reference strain (EREF)	Stiffness (K, MPa)	Reference strain (EREF)	Stiffness (K, MPa)	Reference strain (EREF)
Bounds	50–240	0.85–1.15	45–240	0.85–1.15	30–300	0.85–1.15	30–100	0.85–1.15
Mean ± standard deviation	180 ± 25	0.99 ± 0.11	180 ± 29	0.98 ± 0.10	176 ± 57	0.95 ± 0.08	77 ± 32	0.97 ± 0.09
Initial estimate	100	1.04	47	1.01	35	0.93	60	1.00
Calibrated values	70	1.03	120	1.08	80	0.97	60	1.06

Predictive Simulation of Lunge.

In the FE simulation of the lunge activity, the dynamic, FE model was constrained at the foot in all DOF and the hip was free to move (Fig. 1). The kinematics of the TF and PF joints were load-driven, as the motions at the knee were driven by a combination of hip and ankle joint kinematics and loads, and quadriceps and hamstrings muscle forces. The foot was attached to an ankle revolute joint, which prescribed ankle flexion–extension based on inverse kinematics from musculoskeletal modeling. TF flexion–extension was driven using a PID-controlled quadriceps force, which tracked the experimental knee flexion profile. While TF internal–external rotation was primarily driven by geometry and soft tissue function in the knee extension activity, the lunge model included a PID-controlled internal–external torque to track the experimental TF internal–external rotation. Hip rotations were prescribed to match kinematics from the OpenSim musculoskeletal simulation, and a ramped, medial–lateral load (<40 N) was applied to the hip joint to stabilize the TF varus–valgus kinematics. Forces in the hamstrings and gastrocnemius were prescribed from the musculoskeletal simulation.

Outputs from FE simulations included predictions of TF and PF kinematics, contact mechanics, and ligament forces for the knee extension and lunge activities. Root-mean-square (RMS) differences between the model and experiment were calculated to describe model accuracy. Sensitivity analyses were performed in simulations of the lunge activity to evaluate the impact of cruciate stiffness and reference strain on TF anterior–posterior kinematics. Cruciate ligament parameters were perturbed for mean ±1 standard deviation of ligament stiffness and reference strain. Mean and standard deviations for reference strain [17], ACL stiffness [29], and PCL stiffness [30] were determined from cadaveric joint laxity experiments and mechanical testing described in the literature (Table 1). Total contact forces in the medial and lateral TF cartilage and PF cartilage were computed from simulation of the lunge activity. Also, the contribution of individual ligaments and total ligament tensile and anterior–posterior shear forces were described with respect to the tibial local coordinate system.

Results

Experimental Kinematics.

The subject achieved knee flexion angles of 135 deg in the knee extension activity and 132 deg in the lunge activity (Figs. 2 and 3). Differences in TF and PF kinematics between knee extension and lunge were small (RMS < 5 deg in rotations; RMS < 4 mm in translations). Similar to trends in kinematics reported in the literature [30], the tibia rotated internally (∼27 deg) and translated anteriorly (∼16 mm) with respect to the femur as the knee flexed. The patella flexed at approximately 60% of the knee flexion angle. Also, the patella rotated internally (∼7 deg) as the knee flexed and had a relatively small medial–lateral excursion (<3 mm).

Fig. 2.

Comparison of model and experimental TF and PF kinematics for the knee extension activity: experiment (-), initial estimate of soft tissue properties from Ref. [17] (--), ACL-deficient, PCL-deficient, and calibrated model predictions

Fig. 3.

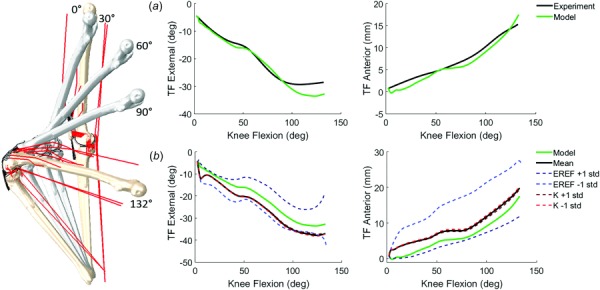
(a) Comparison of model and experimental TF kinematics for the lunge activity: experiment and calibrated model predictions (RMS difference of TF flexion–extension <3 deg, varus–valgus <2.5 deg, internal–external <4 deg, medial–lateral <3 mm, anterior–posterior <2 mm, superior–inferior <2 mm), (b) sensitivity analysis comparing the impact of mean ±1 standard deviation of ligament stiffness (K) and reference strain (EREF) on TF internal–external and anterior–posterior kinematics. Mean and standard deviations obtained from the literature (see Table 1).

Quadriceps and Hamstrings Forces.

Peak quadriceps force occurred near full extension (473 N at 15 deg TF flexion) in the knee extension activity, and forces decreased as the knee flexed. In the lunge activity, quadriceps forces increased as the knee flexed with the peak magnitude of load equal to 2972 N at 100 deg. The hamstrings muscles co-contracted with the quadriceps during the lunge activity, and peak hamstrings forces in the semimembranosus and biceps femoris were equal to ∼750 N. Gastrocnemius forces also increased as a function of flexion and reached a combined load of ∼300 N.

Knee Extension Model Kinematics.

To display the calibration space, experimental TF kinematics were compared to simulations of ACL-deficient and PCL-deficient behavior (Fig. 2). In the ACL-deficient condition, the model predicted an anterior shift of the tibia with respect to the femur through the entire range of motion, particularly in early flexion as differences between the model and experiment reached up to ∼13 mm at 30 deg knee flexion. In the PCL-deficient condition, the model predicted an increase in posterior tibial translation, primarily in deep flexion (∼6 mm maximum difference between model and experiment at 120 deg knee flexion).

TF and PF soft tissue properties and attachments were calibrated to match the experimental motion for the knee extension activity (Fig. 2). The initial estimate of soft tissue properties and alignment from Harris et al. [17] significantly under-predicted the anterior translation of the tibia with respect to the femur (RMS = 7.3 mm). The calibrated model matched experimental TF anterior–posterior kinematics with an RMS difference of 0.92 mm. Calibrated model PF kinematics predicted experimental motion with RMS differences of 5.2 deg in flexion–extension and 4.2 deg in patellar tilt, and 2.6 mm in medial–lateral translation (Fig. 2).

Lunge Model Kinematics.

In the simulation of the lunge activity, PID-controlled, TF flexion–extension and internal–external kinematics were accurate to within 1.5 deg and 2.4 deg of the experimental motion. The lunge model also showed good agreement to experimental TF kinematics in varus–valgus (RMS = 2.1 deg), medial–lateral (RMS = 3.0 mm), anterior–posterior (RMS = 1.2 mm), and superior–inferior (RMS = 2.1 mm) motions (Fig. 3(a)). Lunge model PF kinematics had similar accuracy to the knee extension model (RMS = 2.5 deg in flexion–extension, RMS = 2.3 deg in internal–external, and RMS = 4.3 mm in medial-lateral).

Joint Contact Forces.

In the knee extension activity, peak TF contact force (1001 N) occurred at full extension and decreased until ∼90 deg knee flexion, where TF contact forces then increased into deep flexion. TF contact forces were small near 90 deg (197 N) due to small quadriceps and hamstrings loads. PF contact forces were consistent with trends in quadriceps force such that the peak load (595 N) occurred at 15 deg knee flexion and decreased as the knee flexed. In the lunge activity, TF and PF contact forces increased as the knee flexed, consistent with increasing muscle and joint loads (Fig. 4). Peak TF contact force was 2367 N and occurred at 132 deg knee flexion, and peak PF contact force was 2505 N at 90 deg knee flexion.

Fig. 4.

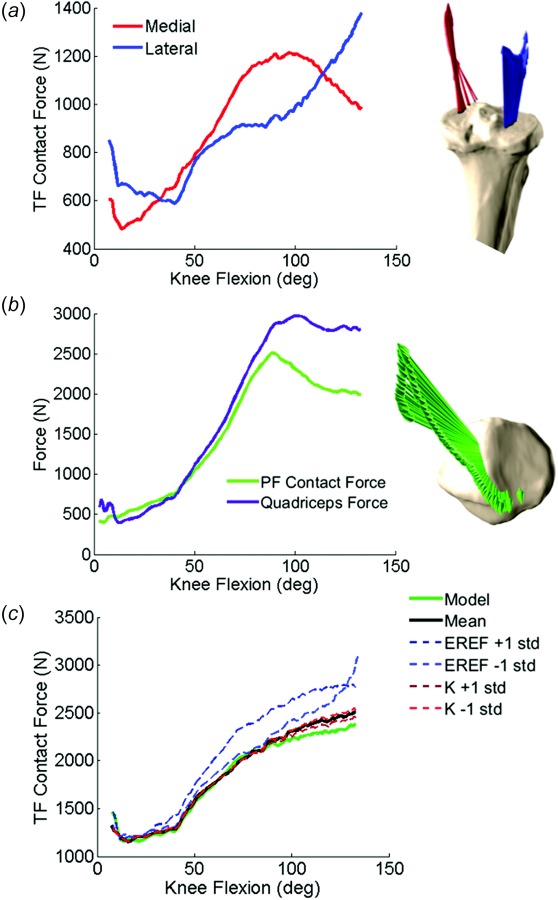
(a) Total TF contact force, (b) PF contact force and quadriceps force, and (c) comparison of TF contact forces between calibrated, mean, and ±1 standard deviation of ligament stiffness and reference strain analyses during the lunge activity. Mean and standard deviations obtained from the literature (see Table 1).

Ligament Forces.

The cruciate ligaments were the primary contributors to total ligament force in the knee extension and lunge activity. Trends in ligament force recruitment were consistent in both activities; ligament forces are shown for lunge only (Fig. 5). The ACL was active in early to midflexion (0 deg–60 deg), and the PCL was active in mid to deep flexion (60 deg–130 deg). In general, the posterolateral bundle of the ACL was more active in early flexion than the anteromedial bundle, which engaged in mid flexion. The anterolateral bundle of the PCL was the primary contributor to the posterior constraint of the tibia in deep flexion. The posterior capsule was active near full extension and quickly became inactive as the knee flexed (∼5 deg). In deep flexion, increased TF internal rotation of the subject resulted in constraint forces from the ALS and ACL. Ligament forces were highest near full extension and decreased as the knee flexed. Ligament shear forces dominated total ligament force in early-to-mid flexion, but tensile forces were greater in deep flexion.

Fig. 5.

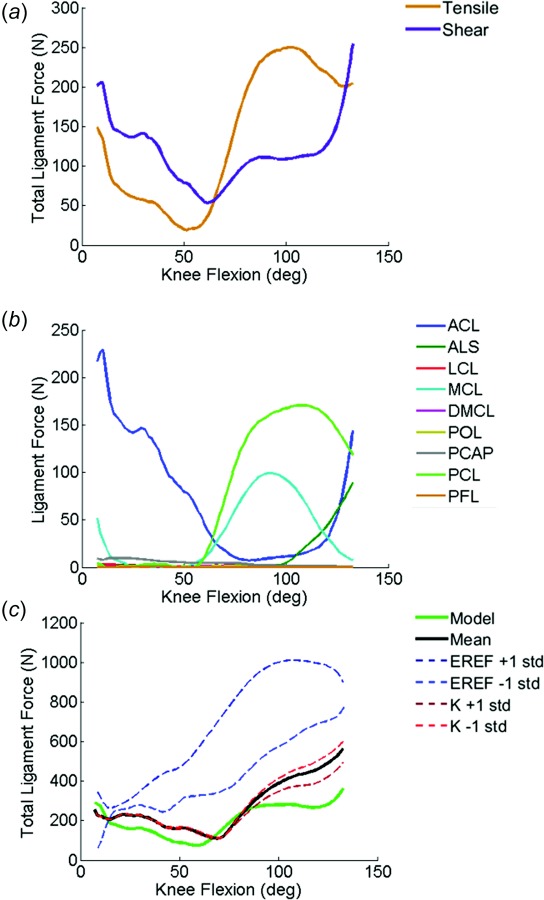
(a) Total tensile and shear ligament forces, (b) individual ligament forces, and (c) comparison of total ligament force between calibrated, mean, and standard deviation of ligament stiffness and reference strain analyses during the lunge activity. Mean and standard deviations obtained from the literature (see Table 1).

Sensitivity Analysis.

Sensitivity analyses evaluated the impact of cruciate ligament stiffness and reference strain properties on joint kinematics and loading during simulation of the lunge activity (Fig. 3(b); Table 1). Perturbations of ligament stiffness caused sub-mm and sub-degree differences in TF kinematics. Ligament reference strain had a greater impact on TF kinematics than ligament stiffness; 1 standard deviation in cruciate reference strain resulted in differences of up to 9 mm in TF anterior–posterior motion and 12 deg in TF internal–external rotation. Average RMS difference in TF anterior–posterior translation and internal–external rotation between mean and ±1 standard deviation of ligament reference strain was 6.2 mm and 6.4 deg, respectively.

Cruciate ligament stiffness had only minor effects on total TF contact force (∼50 N difference from the mean in deep flexion) in the lunge activity (Fig. 4(c)). In contrast, reference strains of +1 and −1 standard deviation increased TF contact force by an average 258 N from the mean across the lunge activity. The calibrated model had the lowest TF contact force with ∼216 N less force than the mean model at 132 deg knee flexion.

Similar to the sensitivity described in TF kinematics and contact forces, cruciate ligament stiffness had negligible effects on total ligament force (Fig. 5(c)). Perturbations of reference strain increased total ligament forces; reference strain values greater than 1 represented pretensioning of the ligament, so ligament forces were the largest in simulation of +1 standard deviation of the reference strain. While ACL and PCL ligament forces were small in the simulation of −1 standard deviation of reference strain, forces from the ALS and MCL increased due to posterior translation and internal rotation of the tibia with respect to the femur.

Discussion

The current study presents a novel approach to integrate stereo radiography, musculoskeletal modeling, and finite element modeling for evaluation of subject-specific, in vivo joint mechanics during knee extension and lunge tasks. Predictive FE models of the knee are typically developed using in vitro cadaveric tests but rarely simulate in vivo motion. Few studies have combined in vivo kinematic measurement and FE modeling for the evaluation of joint and soft tissue forces [7,8,28]. The current work advances previous in vivo knee modeling through simulation of dynamic activities including deep flexion, modeling of subject-specific knee behavior, and development of a load-controlled knee model. The validated computational framework provides a potential tool for investigating implant design and alignment strategies. The current study applied the computational modeling framework to investigate cruciate ligament function and its impact on joint kinematics and contact mechanics.

Subject-specific characteristics were implemented into the FE framework using CT and MR reconstructions of geometry and soft tissue landmarks, and calibration of ligament properties and alignment to match experimental knee motion. Model calibration was performed in the knee extension activity because the loading conditions are more easily measured and replicated relative to more complex weight-bearing activities. Calibrated model kinematics demonstrated good agreement to the experimental HSSR kinematics with similar RMS differences between model and experimental TF and PF kinematics shown in the literature [4,6,32]. Quadriceps force predictions from musculoskeletal and FE modeling were consistent with magnitudes and trends reported in the literature [33,34].

The application of soft tissue properties from an in vitro experiment resulted in poor representation of subject kinematics [17]. To explore the calibration space, the knee extension activity was simulated with and without the ACL and PCL ligaments. The initial estimate of cruciate properties from Harris et al. [17] predicted TF anterior–posterior kinematics beyond the bounds of the calibration space. While soft tissue attachment locations were informed by CT and MRI, the anterior–posterior position of the MCL, ACL, and PCL insertions and origins were modified, for example, the femoral, anterior–posterior attachment of the MCL relative to the knee joint center affected distribution of loading from the anterior to posterior bundles. In general, total ligament strain increased as the distance between the ligament attachment and knee joint center increased.

Ligament reference strain was the most critical material property in the calibration process, evidenced by the substantial differences in TF anterior–posterior kinematics, and TF contact and ligament forces (Figs. 3(b), 4(c), and 5(c)). While ligament stiffness affected the magnitude of contact and ligament forces, reference strain altered the trend and timing of ligament recruitment. Ligament strains were relatively small during the knee extension and lunge activity. As a result, perturbations of ligament stiffness had only minor effects on TF kinematics and contact mechanics during knee extension and lunge. Greater influence from ligament stiffness may occur in activities with extreme motions and loading, such as pivot or kneeling, because these activities may induce higher ligament strains. The calibrated model produced lower joint contact and soft tissue forces compared to the model with mean and ±1 standard deviation of ligament properties.

The experimental and computational workflow can be applied to alternative in vivo activities including chair rise, stepping up and down from stairs, and pivoting. A combination of hip and ankle joint loading, muscle force predictions from musculoskeletal simulation, and PID-control within the FE framework were used to develop external loads surrounding the knee for load-controlled simulation of the lunge activity. Although there is limited direct validation of joint and ligament mechanics, subject-specific calibration of soft tissue properties to experimental kinematics provides confidence in model predictions. The FE model accurately predicted joint kinematics in the lunge activity with RMS differences between model and experiment less than 5 deg and 4 mm. Joint and contact forces were qualitatively compared to measurements from subjects performing similar activities described in the Orthoload database [35]. Model-predicted TF contact force in our study was similar in trend and magnitude to average TF contact forces (700–2000 N from 0 deg to 100 deg knee flexion) for eight subjects performing a deep knee bend.

There are limitations to the proposed modeling framework. The FE models of the lower limb could be improved through subject-specific, continuum representations of muscle and soft tissue. For efficient evaluation of dynamic activity, the current study utilized 1D ligaments, which effectively capture overall joint stiffness, but do not model stress/strain distributions and wrapping contact around bone and soft tissue. Subject-specific muscle geometry could be reconstructed from MRI to provide more accurate direction of loading, and continuum representations could be used to model thigh–calf contact in simulations of deep flexion.

There are some limitations to the model loading and boundary conditions. The lunge model required a PID-controlled internal–external torque in addition to the muscle forces to accurately track the experimental TF internal–external kinematics. This demonstrated that the contribution of soft tissue and muscle forces to internal–external rotation may not have accurately reflected the physiological loading for this subject. Ligament calibration was performed in the knee extension activity, but future work could include passive laxity assessments under fluoroscopic surveillance as an alternative to using the knee extension activity for model calibration. While simulations of the knee extension and lunge activities included representations of the hip and ankle joints to provide a physiological reference for applied kinematics and loads from musculoskeletal models, the hip and ankle kinematics and forces were not predictive. The current study developed a model for subject-specific evaluation of in vivo knee mechanics, and future work should advance the capabilities of the FE model for prediction of hip and ankle mechanics.

The modeling framework was applied to only one subject and additional subject models would highlight the patient-specific differences in kinematics and soft tissue loading. Furthermore, simulation of additional activities would demonstrate that the ligament calibration was predictive of other measured activities in the same subject.

This work demonstrated an experimental and computational workflow that was used to investigate the effect of cruciate ligament properties on TF kinematics. A load-controlled model of the knee can be a powerful predictive tool for researchers, clinicians, and implant designers by allowing investigations of knee mechanics following simulated pathology or repair. The workflow can be used to evaluate total knee arthroplasty designs and surgical techniques (e.g., mechanical versus anatomic alignment) under dynamic, in vivo loading.

Funding Data

• Stryker Orthopedics (Funder ID: 10.13039/100008894).

• NIH National Institute of Arthritis and Musculoskeletal and Skin Diseases (Funder ID: 10.13039/100000002).

• National Institute of Biomedical Imaging and Bioengineering (Funder ID: 10.13039/100000002). National Institute of Child Health and Human Development (Grant No. U01 AR072989; Funder ID: 10.13039/100000002).