Computer-Controlled Biaxial Bioreactor for Investigating Cell-Mediated Homeostasis in Tissue Equivalents

Abstract

Soft biological tissues consist of cells and extracellular matrix (ECM), a network of diverse proteins, glycoproteins, and glycosaminoglycans that surround the cells. The cells actively sense the surrounding ECM and regulate its mechanical state. Cell-seeded collagen or fibrin gels, so-called tissue equivalents, are simple but powerful model systems to study this phenomenon. Nevertheless, few quantitative studies document the stresses that cells establish and maintain in such gels; moreover, most prior data were collected via uniaxial experiments whereas soft tissues are mainly subject to multiaxial loading in vivo. To begin to close this gap between existing experimental data and in vivo conditions, we describe here a computer-controlled bioreactor that enables accurate measurements of the evolution of mechanical tension and deformation of tissue equivalents under well-controlled biaxial loads. This device allows diverse studies, including how cells establish a homeostatic state of biaxial stress and if they maintain it in response to mechanical perturbations. It similarly allows, for example, studies of the impact of cell and matrix density, exogenous growth factors and cytokines, and different types of loading conditions (uniaxial, strip-biaxial, and biaxial) on these processes. As illustrative results, we show that NIH/3T3 fibroblasts establish a homeostatic mechanical state that depends on cell density and collagen concentration. Following perturbations from this homeostatic state, the cells were able to recover biaxial loading similar to homeostatic. Depending on the precise loads, however, they were not always able to fully maintain that state.

1 Introduction

Living soft tissues consist of cells embedded within an extracellular matrix (ECM). The ECM consists of a network of diverse proteins, often collagen and elastic fibers, as well as glycoproteins and glycosaminoglycans that together provide mechanical support and biological cues to the resident cells. Cells and ECM interact closely, and these interactions have a crucial impact on tissue health and disease [1–5]. Changes in matrix properties affect, for example, cell migration [6–8], differentiation [9–11], and survival [12–15]. At the same time, cells actively sense and regulate their surrounding ECM to establish or maintain a preferred (so-called homeostatic) state [16–18]. Understanding feedback mechanisms between cells and ECM is critical to advancing our understanding of mechanobiology.

Native ECM is a highly complex mixture of diverse fiber types and substances. To reduce parameters and interdependencies and focus on select mechanisms, cell-seeded collagen or fibrin gels, so-called tissue equivalents, often serve as simplified model systems for studying cell-matrix interactions (see Fig. 1). Most studies focus on free-floating gels [18,19] or the tension imposed on or developed within tissue equivalents in uniaxial settings [16,17,20–24]. Yet, in vivo most soft tissues are neither free from external loads nor subjected to simple uniaxial loading. Rather, most experience complex multiaxial loading. While some studies have examined biaxial loading cases, they have tended to focus on the analysis of fiber (re)orientation or passive mechanical properties [25–27], not cell-driven evolution of tension or deformation [28]. As demonstrated in computational studies [29,30], cell-mediated maintenance, adaptation, and repair of soft tissues in response to changes in mechanical environment over hours to days is critical for promoting both mechanobiological equilibrium and mechanobiological stability. A key reason why cell–matrix interactions have been studied in simple settings, such as free-floating or uniaxial gels, is the technical challenge associated with designing bioreactors for biaxial studies.

Fig. 1.

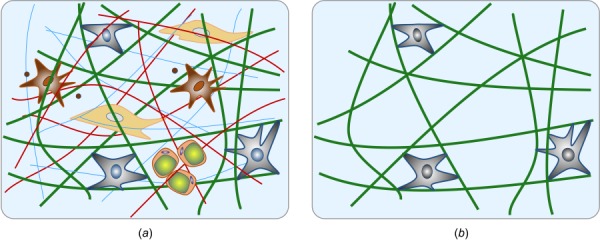
Schematic of native tissue consisting of various fiber and cell types, as well as additional constituents (a); cell-seeded collagen (Fig. 5(b)) gel as a simplified model system to study cell–matric interactions (b). In both cases, we emphasize the typical multiaxial geometry and loading that is important for in vivo relevance.

There is, therefore, a pressing need for a device that allows one to study cell-mediated changes in matrix, which give rise to stress–strain responses that characterize tissue behavior under loading conditions of interest and relevant time scales. Herein, we describe the development of such a device using paired high sensitivity, low drift force transducers and precision motors to allow diverse testing conditions, including static and cyclic uniaxial, strip-biaxial, and biaxial. Moreover, we report illustrative results obtained with this device, in particular, relations between cell density, matrix density, and loading state with a focus on the homeostatic stress level that is established and maintained in tissue equivalents in response to various perturbations in loading.

2 Design of Biaxial Culture Force Monitoring System

To mimic the multidimensional loading experienced by tissues in vivo, we designed a computer-controlled bioreactor for cell-seeded tissue equivalents capable of measuring mechanical metrics under a range of long-term (>24 h) biaxial stress/strain conditions. Here, we first overview the structure of the device before discussing its key features separately.

2.1 Overview.

An image of the custom device as well as a schematic drawing of its most important parts can be seen in Fig. 2. The core of the bioreactor is a square sample chamber (130 × 130 × 46 mm) made of glass-filled polycarbonate with a removable lid made of clear polycarbonate that prevents evaporation of culture medium and contamination of the sample during experiments. The samples are placed in the central region of the bath and attached to arms printed with a Form 2 printer (Formlabs, Somerville, MA). Both the x- and y-axes are equipped with high-resolution force transducers to allow accurate time-dependent measurements of force. A stepper motor (Advanced Micro-Systems, Liberty Hill, TX) is attached to each arm via a brass sled and stainless steel rods. The four motors, in combination with lead screws, have a resolution less than 1.0 μm, thus enabling precise loading (e.g., uniaxial, strip-biaxial, equi-biaxial, or non-equi-biaxial) of the gel sample. Each motor can be operated independently using a LabVIEW interface, allowing static or cyclic loading during load- or displacement-controlled tests while recording position and force. All components are attached to a polycarbonate base platform placed within a custom incubator (NU-5820, NuAire, Plymouth, MN, with sealed side ports for exteriorizing electrical cables) to provide appropriate environmental conditions (37 °C, 5% CO₂) and sterility for cell viability. A camera (V4K, IPEVO, Sunnyvale, CA) is mounted onto the base plate to image the specimens during testing.

Fig. 2.

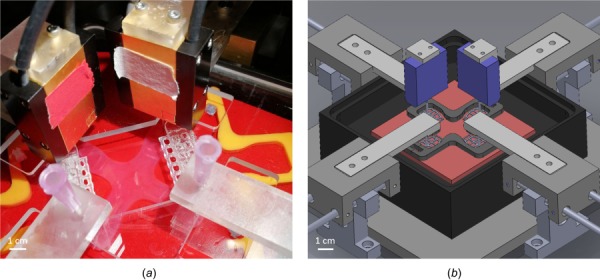
(a) Biaxial bioreactor and mechanical testing device with attached sample and (b) schematic drawing showing the inside of the bath chamber and the load cells mounted from above

2.2 Sample Preparation, Geometry, and Attachment.

A challenging step in the mechanical testing of collagen gels is their attachment to the testing device. Due to their fragility, every movement of the gel risks damage. Several approaches have been proposed for this coupling, including using sutures [31], wires [32], and by placing porous polyethylene bars in the mold before adding the gel solution so that the fiber network forming during gelation naturally surrounds and connects to these bars [28,33,34]. To ensure a simple mount and stable connection of the gel to the high-resolution force transducers, we developed a new design (Fig. 3(a)). Porous inserts stabilize the connection between the gel and device, avoiding problems like tearing at the transition between the holder and gel. These embedded inserts are 3D-printed using a Form 2 printer (Formlabs, Somerville, MA).

Fig. 3.

(a) A porous insert for attaching a gel to the testing device; (b) two-part mold having a cruciform shape to form gels; (c) floated cruciform gel attached to testing device; and (d) dog-bone shape mold for uniaxial experiments

Cruciform-shaped molds (Fig. 3(b)) are used to form the gels (Fig. 3(c)). Other shapes, including square or rectangular as widely used in testing native tissues, are more difficult to secure to the device when highly compliant as for collagen gels. The cruciform molds are 3D-printed from polylactide using a MakerBot Replicator+. To avoid stress concentrations, sharp edges in the molds were smoothed with filets. For a uniaxial setting, the cruciform mold can simply be replaced with a traditional “dog-bone” shaped mold (Fig. 3(d)) with analogously smoothed edges. A silicon rubber pad is used as a base for the mold to avoid leakage of the gel during gelation (Fig. 3(b)).

To avoid damage during experimental setup as well as to increase reproducibility and enable testing of delicate gels with low collagen concentrations (<1 mg/mL), the gel is set in the sample chamber, at the start of an experiment, already attached to the completely assembled testing frame while inside the incubator under sterile conditions (Fig. 2). This procedure also ensures a reproducible, stress-free configuration at the beginning of all experiments. To this end, a two-part cruciform mold (Fig. 3(b)) is placed inside the sample chamber and followed by a complete assembly of the testing device. Subsequently, the gel solution is prepared within a laminar flow hood and then transferred to the mold inside the chamber. After gelation for 30–45 min, the samples are floated with culture medium and the mold is detached from the gel with the help of four narrow slits in the chamber lid (Fig. 2(a)). The experiment starts directly after the mold is removed from the gel without the need for any relocation or attachment steps, which minimizes the probability of sample damage.

2.3 Force Measurement.

Cell-mediated forces acting within the gels tend to be low, in the order of 200 μN/million cells [16,17,20,21,22]. These small forces must be resolved by the transducer and measured accurately for long durations (e.g., 48 h) in a high humidity, 37 °C environment with negligible drift and a reasonable signal-to-noise ratio. We use two SI-H KG7 force transducers from World Precision Instruments (Sarasota, FL). These transducers detect force by optically measuring the deflection of a stiff beam, which limits the potential for damage from overloading as in traditional capacitive transducers. They have a force range of 0–5 mN (also allowing passive material tests of tissue equivalents) with noise less than 0.2 μN. These transducers demonstrated excellent performance with respect to physical as well as environmental requirements as described earlier. High accuracy, low noise, and low zero-level drift could be maintained up to the prescribed 40 h (Fig. S1 available in the Supplemental Materials on the ASME Digital Collection).

3 Materials and Methods

3.1 Cell Culture.

For illustrative purposes, NIH/3T3 fibroblasts (ATCC, Gaithersburg, MD) were maintained in culture medium consisting of Dulbecco's modified Eagle's medium (DMEM), 10% heat-inactivated fetal bovine serum (FBS) (Life Technologies, Carlsbad, CA), and 1% penicillin-streptomycin (ThermoFisher, Waltham, MA) in an incubator at 37 °C and 5% CO₂. Cells were grown in T75 flasks (ThermoFisher, Waltham, MA) and passaged at 70–80% confluence. Passages 4 and 5 were used in all experiments.

3.2 Cell Proliferation.

Pilot studies showed that NIH/3T3 fibroblasts have a tendency to proliferate strongly within the collagen gel, leading to a continuous increase in force rather than a force that tended to steady-state (Fig. S2(a) blue curve available in the Supplemental Materials on the ASME Digital Collection). To minimize cell proliferation, we used serum-starvation or treatment with Mitomycin C (Sigma, St. Louis, MO) to inhibit cell cycle progression (Fig. S2(a) available in the Supplemental Materials on the ASME Digital Collection). In the former, cells were starved in medium containing 0.5% FBS for 18 h prior to the experiment; in the latter, 0.12 mL of Mitomycin C (0.4 mg/mL, diluted in PBS, giving a final concentration of 4 μg/mL) was added to the cell culture flasks 2.5 h prior to the experiment. The influence of both treatments on cell number and force development was analyzed (Figs. S2(a) and S2(b) available in the Supplemental Materials on the ASME Digital Collection).

3.3 Collagen Gel Preparation.

Cell-seeded collagen gels were prepared on ice following a protocol modified slightly from Ref. [19]. Briefly, for 7.0 mL of gel solution (volume of the biaxial mold was ∼6.5 mL), 1.31 mL of 5× DMEM, 0.63 mL of a 10× reconstitution buffer (0.1 N NaOH and 20 mM HEPES; Sigma, St. Louis, MO), and 1.28 mL of high concentration, type I rat tail collagen (8.22 mg/mL; Corning, Corning, NY) were mixed with 3.78 mL of an experimental culture medium containing 7.0 × 10⁶ cells (a Neubauer chamber in combination with Trypan blue staining was used to count cells), giving a final collagen concentration of 1.5 mg/mL and a cell density of 1.0 × 10⁶ cells/mL. The experimental culture medium consisted of DMEM supplemented with 10% FBS, 10% porcine serum (Life Technologies, Carlsbad, CA), 1% penicillin-streptomycin, and 1% antibiotic/antimycotic (ThermoFisher, Waltham, MA). Acellular gels were prepared using the same protocol but omitting the cells.

The final gel solution was then pipetted into a uniaxial or biaxial mold placed within the bioreactor. The mold was removed after 30–45 min of gelation and the bath was filled with 100 ml of the experimental culture medium. This led to a detachment of the gel from the base of the bath, allowing it to float freely.

4 Results

Cells can sense and regulate their mechanical environment by, among other things, applying forces to the surrounding matrix. When cells are embedded in free-floating collagen gels, a strong compaction of the gel can be observed over multiple days [18,19] (Fig. 4). If gel compaction is prevented by uniaxial constraints, one observes a two-stage response consisting, first, of a steep increase in tension and, second, a near-constant tension in the gel [17,22,24,35]. Similar to prior uniaxial studies, our device allows one to study parameters such as cell density, collagen concentration, boundary conditions, and load amplitudes and directions on this general phenomenon.

Fig. 4.

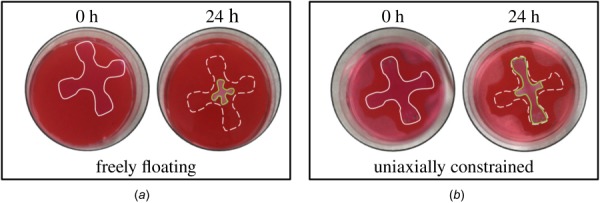
Compaction of a cruciform gel from an initial configuration (solid line at 0 h) to a deformed contour (solid line at 24 h) due to contractile forces imposed by resident cells (dashed line at 24 h indicates initial configuration): (a) freely floating gel and (b) uniaxially constrained gel

4.1 Influence of Cell Density and Collagen Concentration Under Uniaxial Constraint.

To confirm the influence of the number of cells/mL of gel on force buildup, three different cell densities, 0.2, 0.5 and 1.0 × 10⁶ cells/mL, were tested in a uniaxial setting for 17 h. As expected, a higher number of cells led to a steeper increase in force and thus a higher homeostatic force (Fig. 5(a)). However, the time needed to reach a steady-state was similar for the three cell densities. The relationship between cell density and steady-state force was nonlinear. Furthermore, the amplitude of the resulting force perturbation due to applied stretch is higher for a larger number of cells. The acellular gel shows typical viscoelastic relaxation behavior, which differs dramatically from the active relaxation/recovery mediated by cells (Fig. 6).

Fig. 5.

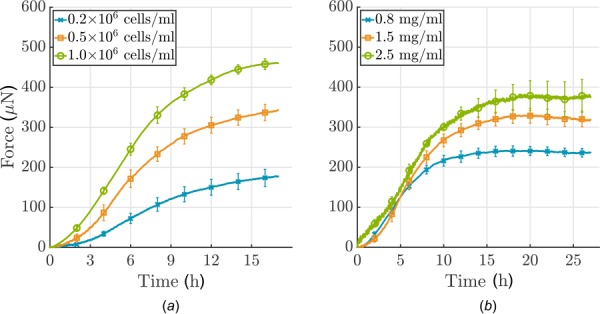
(a) Influence of cell density and (b) collagen concentration on force development in a uniaxial setting (cells were serum-starved; each curve shows the mean ± SEM for three identical experiments). (a) Note that force development depends nonlinearly on cell density: more cells/mL lead to higher forces; (b) force development depends nearly linearly on collagen concentration, higher concentrations lead to higher force.

Fig. 6.

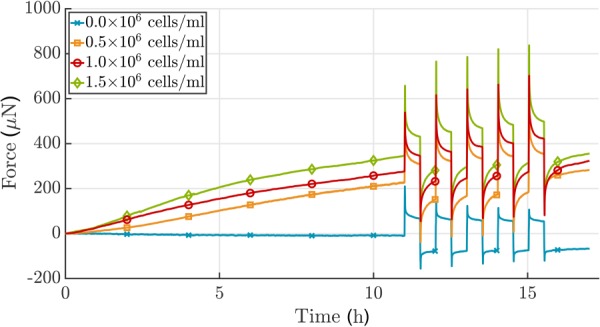
Analysis of the effect of 3T3 cell density on force development in case of a ±2.0% stretch alternating every 30 min after an initial 11 h culture period in uniaxial setting. The total force increases when the number of cells increases. Additionally, the amplitude of the resulting force perturbation due to applied stretch is higher for a larger number of cells. Since cells were not treated to prevent proliferation, no plateau in force was reached. The acellular gel shows typical viscoelastic relaxation behavior (collagen concentration 1.5 mg/mL), which differs dramatically from the active relaxation/recovery achieved via cell-mediation. Shown is one experiment for each cell density.

Analogously, force development was measured for 27 h in gels with three different collagen concentrations, namely, 0.8, 1.5, and 2.5 mg/mL. A higher concentration of collagen also leads to a higher plateau of force (Fig. 5(b)). Force development depends nearly linearly on collagen concentration. The steady-state level, with neither a further increase nor decrease of force, was reached earlier for lower collagen concentrations. Interestingly, the gradient of force increase was similar for these three concentrations, unlike the case of varying cell densities.

4.2 Influence of Load Amplitude Under Uniaxial Constraint.

As shown above, cells embedded in a collagen gel build up a certain force, often called homeostatic, which is then maintained for a prolonged period. It was shown previously that cells appear to seek to re-establish this state following mechanical perturbations [16,17]. However, prior data were restricted to 30 min relaxation intervals following such perturbations, not allowing confirmation of whether the force actually re-established completely or just partially. Our device allows measurements over extended relaxation times (e.g., 10+ h as shown in Figs. 7 and 8) when studying force development following mechanical perturbations (e.g., 10% and 20%, positive and negative perturbations in force) from the steady-state. We ran our experiments as semiforce controlled, that is, gels were stretched until force was perturbed by 10% or 20% with respect to the homeostatic value that had been reached. Subsequently, the stretch was fixed. The force recovery of the gels was dependent on the sign of the perturbation when gels were loaded to an extent corresponding to 10% of the steady-state level of force (Fig. 7(a)). For an increase in force caused by an increase in stretch, an offset remained after 10 h. When the force was decreased by a decrease in the stretch, the homeostatic state was re-established and then maintained. Our gels had an initial stiffness, that is Young's modulus, of about $10\hspace{0.17em}\mathrm{kPa}$.

Fig. 7.

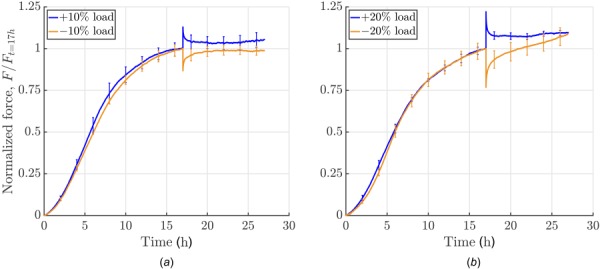
Influence of amplitude and direction of perturbation: force development was measured for 10 h following a perturbation in loading (uniaxial setting, cells were serum-starved; experiments were force-controlled: 10% load means application of a force that equals 10% of the homeostatic force; each curve shows the mean ± SEM of three identical experiments). (a) Increasing or releasing the load by 10%: a positive perturbation elicited a cell-mediated relaxation toward the prior steady-state force with a small residual offset whereas a negative perturbation resulted in a recovery of the homeostatic force. (b) Conversely increasing load by 20% led to a notable offset from homeostatic force after 10 h of cell-mediated relaxation whereas decreasing load by 20% led to a continuous increase in force, with a new plateau not reached over the subsequent 10 h.

Fig. 8.

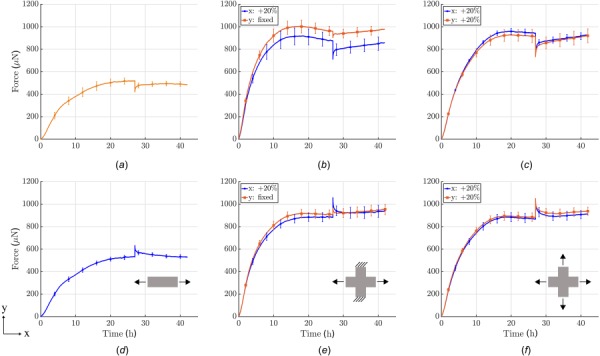
Influence of boundary conditions on force development prior to and after perturbing the load from steady-state (cells treated with Mitomycin C to minimize cell proliferation during testing; each curve shows the mean±SEM of three identical experiments). First row: 20% reduction in load after an initial 27 h culture period under uniaxial, strip-biaxial, or equi-biaxial ((a)–(c)) conditions. Second row: 20% increase in load after 27 h in uniaxial, strip-biaxial, and equi-biaxial ((d)–(f)) conditions.

To understand the effects of differing loads, we increased the magnitude of the applied force to 20% of the homeostatic value (Fig. 7(b)). Similar to the 10% perturbation, a notable offset to the prior steady-state value of force remained after 17 h. In contrast, if gels were released such that their internal force decreased by 20%, an increase in force above the value prior to load application was seen over the subsequent 17 h. This might be because cells in these experiments were only serum-starved prior to the experiment and cells may re-enter the cell cycle after 20 h in the apparatus, possibly triggered by external loading if a certain threshold is exceeded. An increased number of cells would then explain higher forces as shown before (Fig. 5(a)). This behavior could be prevented by treating cells with Mitomycin C, see Sec. 4.3. It is also worth noting that changes in the gel mechanical state are likely due to active tension generated by the cells. As there is a limit to the amount of tension generated by cells, it may be that longer time periods that allow for the production and degradation of extracellular matrix components are required to fully recover the basal state.

4.3 Influence of Boundary Conditions.

As described in Sec. 3, and in contrast to previous work by others [16,17,20,21,22], our new device can subject tissue equivalents to complex biaxial stress or strain conditions by stretching or releasing the two arms of the cruciform gel independently. To the best of our knowledge, the following results represent the first quantitative data of tension produced by cells within a collagen gel in a biaxial setting. For comparison, we performed experiments in uniaxial, strip-biaxial, and equi-biaxial protocols, with a ±20% perturbation of force after the homeostatic state was reached (Fig. 8). All experiments were performed with equal cell densities of 1.0 × 10⁶/mL and equal collagen concentrations of 1.5 mg/mL. As we suspected proliferation in the gels after 20% load perturbations prevented reestablishment of the homeostatic state, we used Mitomycin C to completely prevent cells from duplicating.

Due to in-plane coupling, homeostatic forces were approximately 1.8-times higher in both biaxial protocols than in the uniaxial protocols. Additionally, the rate of force increase was higher in the biaxial setting and homeostatic forces were reached almost 10 h earlier, after 17 h. In the strip-biaxial setup, the y-direction of the cruciform gel was kept at constant length while the x-direction was stretched or released (Figs. 8(b) and 8(e), also see Fig. S3 available in the Supplemental Materials on the ASME Digital Collection), again with a ±20% perturbation in force. Due to the in-plane coupling of the two directions, a small perturbation emerged in the y-direction (roughly one-third of the load perturbation in x-direction) even though stretch was applied in x-direction alone. In the direction of load perturbation (x-direction), force returned to a steady-state but with an offset of approximately 4–5% of the homeostatic force. The y-direction increased slowly without reaching a steady-state during the 15 h recovery period. A similar continuous increase was observed for both the x- and y-directions in the release case (Fig. 8(b))). In the equi-biaxial case, equal loading perturbations were applied in the x- and y-directions (Figs. 8(c) and 8(f)). This condition led to a compensatory response from the gel that depended on the sign of the perturbation: if gels were stretched, forces actively relaxed almost back to the homeostatic value, but a small offset remained in both directions; if gels were released, both directions showed an active restoration of force without reaching a steady-state within the considered period.

4.4 Identification of Relaxation Constants.

Following our previous work [36], a collagen gel can be modeled as a constrained mixture consisting of n collagen fiber families that can differ in their decay time constants $T^i$. Assuming the same homeostatic stress ${\sigma }_c$ for all fiber families and a nearly constant cross section over the considered 10 h time period, we can describe the recovery of the total Cauchy stress $\sigma \left(t\right)$ within the gel as a sum of relaxation processes

$$\sigma \left(t\right)-\hspace{0.17em}{\sigma }_c=\sum _{i=1}^n{\phi }^i\mathrm{e}\mathrm{xp}\left[-\frac{t-t_p}{T^i}\right]\left[\sigma \left(t_p^{+}\right)-{\sigma }_c\right]\hspace{0.17em}\mathrm{for}\hspace{0.17em}t>\hspace{0.17em}{t}_P$$ (1)

where ${\phi }^i$ is the volume fraction of the ith fiber family, with ${\sum }_{i=1}^n{\phi }^i=1$. ${\sigma }_c$ describes the value of homeostatic stress and $\sigma \left(t_p^{+}\right)$ the stress immediately after the perturbation at time $t_p$ when external loading is applied.

We used a sum of $n=2$ exponentials to fit the superimposed stress recovery data (hours 27–37) of three replicates of experiments that were performed for each setup shown in Fig. 8. The respective stress–time curves were normalized with respect to the initial perturbation from the homeostatic stress value $\left[\sigma (t_p^{+})-{\sigma }_c\right]$ and the respective time $t_p$ when external loading was applied. Figure 9 shows the best fit of Eq. (1) to both negative and positive recovery in the uniaxial setup, that is, to data in Figs. 8(a) and 8(d), respectively. Also, see Fig. S4 available in the Supplemental Materials on the ASME Digital Collection for the best fit of Eq. (1) to a strip-biaxial setup and Fig. S5 available in the Supplemental Materials on the ASME Digital Collection for the best fit of Eq. (1) to an equi-biaxial setup.

Fig. 9.

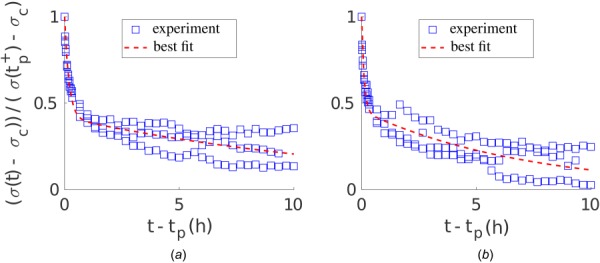
Best fit of Eq. (1) with n = 2 exponentials to stress recovery data (hours 27–37) of uniaxial experiments shown in Figs. 8(a) and 8(d). (a) Decreased load perturbation from the homeostatic state according to Fig. 8(a); (b) increased load perturbation from homeostatic state according to Fig. 8(d).

Table 1 lists volume fractions ${\phi }^i$, time constants $T^i$, and $L_2$-errors for the respective best fits of Eq. (1) to the experimental data in Fig. 8. The computed ${\mathrm{L}}_2$-errors are ∼15% (besides strip-biaxial), which was considered satisfactory given the standard error of the mean of the experimental data of ∼10%. Interestingly, as noted in Refs. [36] and [37], two relaxation time constants differing by about two orders of magnitude were needed for all fitted setups (besides for positive change in load in strip-biaxial setup due to re-increase in force after relaxation), thus suggesting two independently acting remodeling mechanisms within the gel.

Table 1.

Volume fractions ${\phi }^i$, time constants $T^i$ and $L_2$-errors for the best fit of Eq. (1) to experimental data shown in Fig. 8

		Uniaxial	Strip-biaxial		Equi-biaxial
		x	x	y	x	y
Negative change in load	${\phi }^1$	0.58	0.41	0.34	0.46	0.48
	${\phi }^2$	0.42	0.59	0.66	0.54	0.52
	$T^1\hspace{0.17em}$(h)	0.19	0.18	0.08	0.23	0.24
	$T^2$ (h)	14.11	13.00	5.95	11.41	7.12
	$L_2$-error (%)	14.86	9.44	26.30	8.62	8.04
Positive change in load	${\phi }^1$	0.54	0.67	0.53	0.70	0.64
	${\phi }^2$	0.46	0.33	0.47	0.30	0.36
	$T^1$ (h)	0.11	0.00	0.00	0.36	0.31
	$T^2$ (h)	7.18	4.2 × ${10}^{15}$	2.5 × ${10}^4$	14.98	22.60
	$L_2$-error (%)	18.60	14.80	40.31	12.83	10.90

5 Discussion

To date, the fundamental mechanisms underlying mechanobiological feedback loops between cells and ECM that ensure the viability and mechanical integrity of soft biological tissues remain poorly understood. In particular, few quantitative experimental data have been available that describe the cell-regulated evolution of stress and strain in soft tissues in response to perturbing forces. Moreover, the available data have also been restricted largely to free-floating gels or gels subjected to uniaxial loading. Because most soft tissues are subjected to multidimensional loads in vivo, we developed a computer-controlled biaxial bioreactor to create testing environments for both dogbone-shaped and cruciform-shaped tissue equivalents subjected to well-controlled uniaxial, strip-biaxial, or biaxial stress and strain states.

We demonstrated that our new device can measure forces produced by cells within collagen gels for up to 2 days within a 0–2000 μN range. Noise and drift were negligible (Fig. S1 available in the Supplemental Materials on the ASME Digital Collection). Although our device enables tests under load or stretch control, either statically or dynamically (Fig. S6 available in the Supplemental Materials on the ASME Digital Collection), we illustrated its utility via a subset of tests. One advantage of the cruciform-shaped samples is that they experience nearly homogeneous stress and strain fields in a central region under biaxial loads, with the added advantage that the cruciform arms of the sample also represent uniaxially loaded configurations. Another advantage of biaxial tests is that the effects of stresses can be studied in the absence of strains in the strip-biaxial test [31].

Our new device enables studies in a biaxial setting that focus on how cells establish a so-called homeostatic state within an initially stress-free gel and how they respond to perturbations to this state. Of course, one can study the effects of many parameters, including the impact of cell and fiber density, effects of exogenous cytokines and growth factors, and diverse loading conditions—uniaxial, strip-biaxial, equi-biaxial, and non-equi-biaxial—under static or dynamic stretching (see Fig. S6 available in the Supplemental Materials on the ASME Digital Collection). We emphasize, however, that the objective of this article was to present a new bioreactor design and to illustrate its utility, not to provide comprehensive data on the effects of one or more parameters.

Nonetheless, some of the illustrative gel results were provocative. When unperturbed, NIH/3T3 fibroblasts established and maintained a homeostatic state that depended on cell density, collagen concentration, and mechanical loading. Importantly, this stable homeostatic state was characterized by higher forces under biaxial conditions and it could only be maintained if cell proliferation was inhibited by either serum-starvation or treatment with Mitomycin C. In these cases, the cells were able to re-establish a force close to the preferred homeostatic state after a (single) step increase or decrease load perturbation, though, depending on the applied load, they were not fully able to maintain a stable state during the remaining course of the experiments. Although much more could be learned with the NIH/3T3 cells, there is a need to use cells that are of more interest biologically, including those with defects in cytoskeletal structure or integrin signaling, which would be expected to affect cell–matrix interactions dramatically.

In summary, this new biaxial bioreactor enables novel studies of cell–ECM interactions. It should help answer questions like: What does mechanical homeostasis mean in higher dimensions? What are cells sensing and how do they regulate their environment on the tissue scale? How does cell tension translate into tissue tension? How do cell–matrix interactions differ across different cell types on the tissue scale? Answering these and other key questions will help us to develop a rigorous theoretical foundation for understanding principles governing soft tissue mechanobiology.

Supplementary Material

Supplementary Material

Supplementary File

Funding Data

• Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—(Projektnummer 257981274; Projektnummer 386349077; Funder ID: 10.13039/501100001659).

• International Graduate School of Science and Engineering (IGSSE) of Technical University of Munich, Germany (Funder ID: 10.13039/501100005713).

• US National Science Foundation (Grant No. NSF DGE1122492; Funder ID: 10.13039/100000001).

• US National Institutes of Health (Grant No. P01 HL134605; Funder ID: 10.13039/100000002).