A numerical study to determine pericellular matrix modulus and evaluate its effects on the micromechanical environment of chondrocytes

Abstract

Chondrocyte biosynthesis is highly sensitive to mechanical strain. A thin pericellular matrix (PCM) surrounds the cell and plays an important role in mechanotransduction. PCM material properties are difficult to measure directly because of its size and connectivity to both cell and extracellular matrix (ECM). The purpose of this study was to develop a method of calculating linear elastic properties of the PCM using an inverse finite element approach with experimental properties of cell and chondron taken from the literature. Finite element models were constructed of both the equivalent chondron case and the chondrocyte-PCM structure, and a Fibonacci search obtained PCM moduli that matched the ECM strain field between the two cases. The most important result was that ECM strain adjacent to a chondron inclusion was sensitive to the chondron properties and may be used to calculate PCM mechanical properties, consistent with our strain field hypotheses. PCM moduli obtained through this method range from 43 to 240 kPa, were significantly higher than previously published but resulted in only a 0.5–21% decrease in relative effective cell strain. Similarities between effective strain ratios led to the conclusion that matching experimental techniques used to measure cell and PCM properties was more important than absolute values of the properties.

1. Introduction

Studies on the mechanobiology of cartilage and intervertebral disc have demonstrated a sensitivity of metabolism to cellular deformations. A pericellular matrix (PCM) surrounds the cells, and the chondrocytes combined with their PCM are referred to as chondrons. The PCM plays an important role in transferring mechanical signals between chondrocytes and their surrounding extracellular matrix (ECM) (Alexopoulos and Guilak, 2005; Poole, 1997). The mechanical properties of the PCM in the literature have a larger range in moduli with values from 1.5 to 66.5 kPa (Alexopoulos et al., 2003; Guilak et al., 1999), thereby suggesting challenges in obtaining these measurements and/or large variations in the chondron population and in isolation techniques. Chondrocytes have also shown variation in mechanical properties with different measurement techniques (Sheih and Athanasiou, 2003), and it is notable that seeded gel compression studies have consistently yielded significantly higher modulus values than micro-aspiration or cyto-indentation studies. While prior studies have sought to measure PCM stiffness based on the chondron’s response to mechanical loading, we proposed a hypotheses stating that the PCM stiffness may be inferred from the chondron’s mechanical influence on the strain field of the surrounding ECM under macroscopic deformation. This hypothesis was investigated through a series of numerical techniques combined with experimental data on compression of gels seeded with enzymatically isolated cells and chondrons from the literature. We further hypothesized that use of data from seeded gel compression of chondrons would yield PCM moduli that were greater than those obtained from chondrons using microaspiration, consistent with differences found for cell material properties reported in the literature. Our second goal was to evaluate the sensitivity of cell strains to the resulting PCM material properties and to compare cell strains with those calculate using reference PCM and chondrocyte material properties obtained using micro-aspiration as a validation. Experimental data from seeded agarose gels under compressive loading was used to determine cell and chondron mechanical properties because the strains were small, it utilized a 3-D culture environment, and mechanical data for chondrons and was available in the literature.

2. Methods

The PCM modulus was calculated through an inverse finite element method technique using a chondron modulus and chondrocyte cell properties from Kelly et al. (2004). The minimum, maximum, and mean values for equivalent modulus of enzymatically isolated chondrons were obtained using the bulk equilibrium stiffnesses of two chondron–agarose constructs with different cell concentrations from the literature (Kelly et al., 2004) and the rule of mixtures. For each concentration, the elastic modulus of the composite agarose/chondron construct was defined by

$$E=V_{\mathrm{\text{c}}}{E}_{\mathrm{\text{c}}}+V_{\mathrm{\text{a}}}{E}_{\mathrm{\text{a}}},$$ (1)

where V_i and E_i are the volume fractions and stiffnesses and subscripts c and a refer to chondrons and agarose, respectively. Solving (1) for E_a yields:

$$E_{\text{a}}=\frac{E-V_{\text{c}}{E}_{\text{c}}}{1-V_{\text{c}}}.$$ (2)

A constant modulus for the agarose gel between the samples was assumed because agarose concentrations were the same, yet the equivalent chondron/agarose constructs had distinct moduli, because the volume fraction of chondrons was increased from 1.8% to 10.6% in the work by Kelly et al. The equations were then rearranged to solve for the equivalent chondron modulus (3) where subscripts 1 and 2 associate the construct modulus with its associated chondron volume fraction.

$$E_{\text{c}}=\frac{E_1-E_1{V}_{\text{c}2}-E_2+E_2{V}_{\text{c1}}}{V_{\text{c1}}-V_{\text{c}2}}.$$ (3)

The PCM modulus was then obtained using an inverse finite element method that applied the determined equivalent modulus of the chondron and the modulus of the enzymatically isolated chondrocyte cell from the literature (Knight et al., 2002), which was obtained using confocal microscopy to correlate equilibrium stress with cell strains.

A strain-field hypothesis was proposed based on the following two assumptions. First, if a homogeneous medium with a spherical inclusion is subjected to a compressive load, the axial strain experienced by the medium surrounding the inclusion is unique to the elastic properties of the inclusion. Second, the strain field surrounding a bi-layered inclusion is the same as the field surrounding a continuous inclusion with equivalent material properties (Fig. 1). Since the properties of an equivalent inclusion (i.e., the chondron) were known as were those of one component of the bi-layered inclusion (i.e., the chondrocyte), then the properties of the second layer (i.e., the PCM) were determined by matching the surrounding strain field in the ECM. The strain fields were matched by minimizing the total difference between the axial strain profiles at z = 0 of the equivalent and test cases.

Fig. 1.

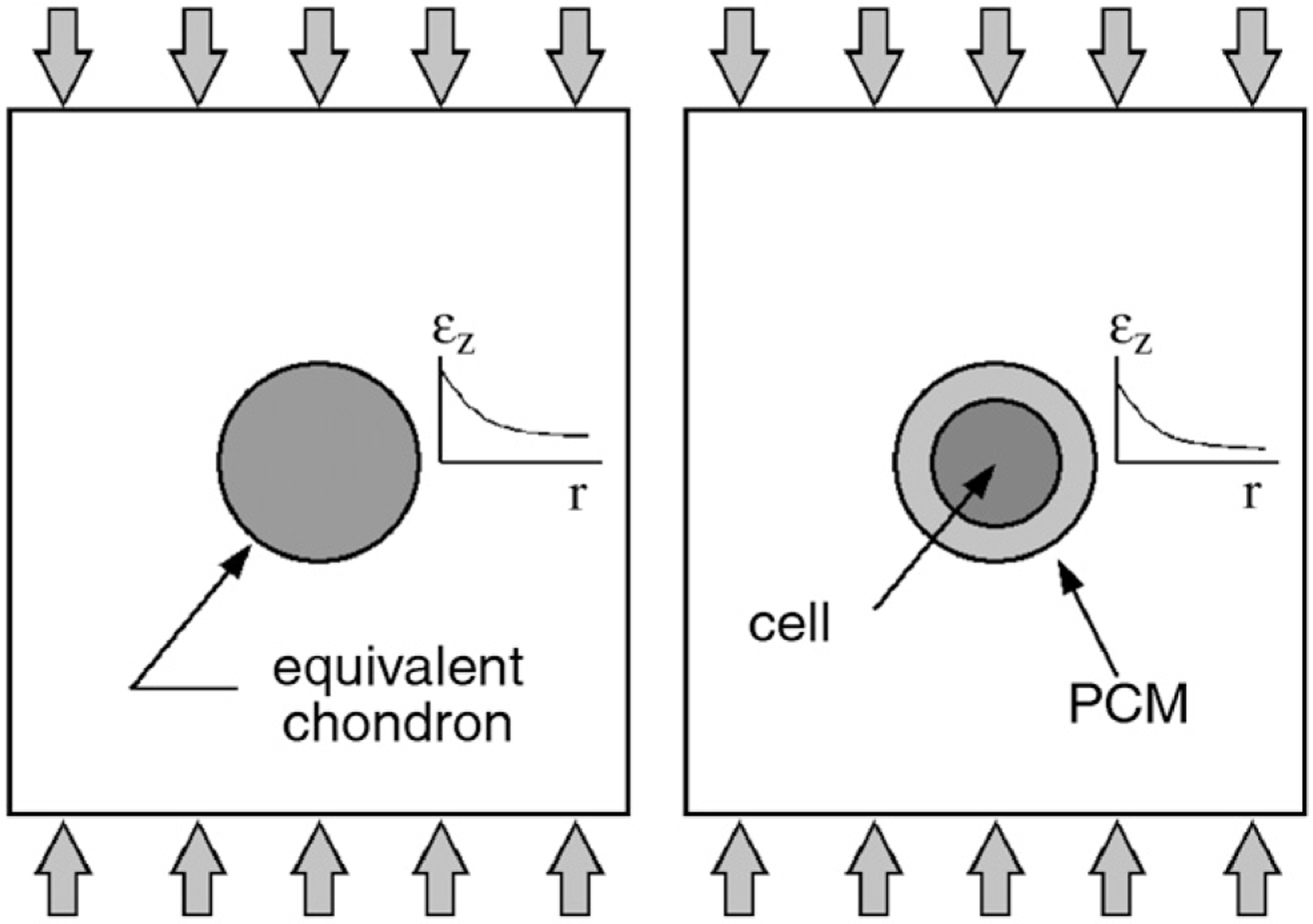
Axial strain profiles around solid (left) and bi-layered (right) inclusions under uniaxial compression.

The Fibonacci search method was used to vary the PCM modulus in order to minimize the difference in the axial strain field surrounding the equivalent case and the bi-layered case. Briefly, the Fibonacci search begins with lower and upper limits, x₁ and x₄, for the independent variable, and creates a pair of midpoints x₂ and x₃ to subdivide the domain according to:

$$\begin{gathered} x_2=x_4-\varphi (x_4-x_1);x_3=x_1+\varphi (x_4-x_1); \\ \varphi =2/(1+\sqrt{5}). \end{gathered}$$ (4)

If f(x₂) is greater than f(x₃), the limits of the domain become x₂ and x₄, and a new point is inserted between x₃ and x₄. Conversely, if f(x₃) is greater than f(x₂), the limits become x₁ and x₃, and the process is continued until a convergence criteria is met. The Fibonacci search is ideal for this application because it uses discreet point evaluations and does not require the gradient of the function, it requires fewer evaluation points than other discreet search techniques, and it is self-constraining and will not evaluate points outside initial limits. The search objective function for this study was defined as

$$f={\int }_a^b{(|{\epsilon }_{z:\text{ equivalent }}-{\epsilon }_{z:\text{bi}-\text{layered}}|)}_{z=0}\text{d}r,$$ (5)

where a and b are any two radial points outside of the chondron. A preliminary verification study found this objective function to be unimodal for all ratios of chondron modulus to matrix modulus.

The strain field in the chondron and surrounding ECM was computed using an axisymmetric and linearly elastic finite element model using FEMLAB (Comsol Inc., Burlington, MA). This analysis was carried out using FEA rather than analytically in order to more readily allow future work including multiphasic materials and non-spherical geometry. The chondron was modeled as a 5.5 μm radius sphere surrounded by an 8 mm radius sphere. Though the resulting strain fields are scale independent, the equivalent and bi-layered cases were given the same size for simplicity. No slip was permitted at the boundaries between the cell, PCM, and ECM. The mesh consisted of 1026 triangular elements with quadratic basis functions. To provide a more efficient solution, only the top half of the axisymmetric domain was modeled with a symmetry boundary condition at z = 0. A unit compressive load was applied to the top edge, and the outer radius was unconstrained.

The PCM modulus was computed using minimum, mean, and maximum values of the equivalent chondron modulus. Each case was also computed using Poisson’s Ratio 0.04 and 0.4, which approach the isotropic limits. The equivalent chondron modulus was calculated using stiffness data obtained through the compression of seeded gels, and mechanical properties obtained through gel compression techniques were likewise used for the chondrocyte. The chondrocyte was taken to have Young’s modulus of 3.4 kPa (Knight et al., 2002) and Poisson’s Ratio of 0.4 (Freeman et al., 1994). The ECM was assigned Young’s modulus of 0.15 MPa (Huang et al., 2005) and Poisson’s Ratio of 0.4, representative of superficial zone articular cartilage. The Fibonacci search was initialized with a range of PCM modulus from 0.01 to 1000 kPa, and terminated at E_PCM ± 5%.

The sensitivity of the chondrocyte cell to changes in PCM modulus was assessed by comparing effective cell strain to effective tissue strain. Effective strain is related to the three principal strains by the following:

$$\tilde{\epsilon }=1/3{[{\left({\epsilon }_1-{\epsilon }_2\right)}^2+{\left({\epsilon }_2-{\epsilon }_3\right)}^2+{\left({\epsilon }_3-{\epsilon }_1\right)}^2]}^{1/2}.$$ (6)

As a validation, the values for effective cell strain calculated using PCM properties obtained in this study were compared to a reference case which used cell (Jones et al., 1999) and PCM (Guilak et al., 1999) properties measured using microaspiration on cells and chondrons isolated enzymatically from the cartilage matrix.

3. Results

The Fibonacci search method was an efficient technique for finding PCM modulus given cell and effective chondron moduli. Convergence from the initial range to a final value ± 5% was attained within fewer than 20 iterations in all cases. Full results for v_PCM = 0.04 and v_PCM = 0.4 are shown in Table 1. The computed values of the mean PCM modulus ranged from 43 to 240 kPa. In order to determine the implications of these results and to provide a validation, they were used to measure the effective cell strain resulting from a 5% axial far-field tissue strain. Strain field results (Fig. 2) from the upper and lower cases were compared to the reference case, and the percent difference of effective cell strain ratio range from 0.5% to 21% when comparing values calculated using cell and PCM properties determined in this study and those from the reference case.

Table 1.

Results for chondron modulus, PCM modulus, effective strain relative to far field strain, and comparisons with effective strain values using properties obtained from microaspiration

	vPCM = 0.04			vPCM = 0.4
	Min	Mean	Max	Min	Mean	Max
Echondron (kPa)a	65	126	187	65	126	187
EPCM (kPa)b	0.04	43	150	82	240	400
${\tilde{\epsilon }}_{\text{cell}}/{\tilde{\epsilon }}_{\text{ECM}}$c	0.09	2.11	1.82	1.79	1.65	1.48
% Differenced	−95	+ 0.5	−13	−15	−21	−30

^aFrom seeded agarose construct (Kelly et al., 2004).

^bDetermined by the present method.

^cAverage cell strain relative to far-field tissue strain from FEA.

^dDifference in relative cell strains using the PCM modulus determined with the present method and a cell modulus of 3.4 kPa (Knight et al., 2002) versus cell (Guilak et al., 1999; Jones et al., 1999) and PCM (Guilak et al., 1999) properties determined using micro-aspiration.

Fig. 2.

Normalized equivalent strain fields using material properties obtained by microaspiration (left) and lower (center) and upper (right) limiting cases obtained by the present method.

4. Discussion

The most important result of this study was the finding that the ECM strain adjacent to a chondron inclusion was sensitive to the chondron properties and may be used to infer PCM mechanical properties from cell and equivalent chondron properties, consistent with our strain field hypotheses. An inverse finite element solution utilizing the Fibonacci search was demonstrated to be an efficient and effective tool for calculating the modulus of the chondrocyte PCM given the elastic properties of the cell and equivalent chondron. The computed values of the PCM modulus were approximately one order of magnitude higher than those previously published (Sheih and Athanasiou, 2003), consistent with our second hypothesis. We believe this difference is because the mechanical data obtained from 3-D culture experiments provided an effectively stiffer system than for the chondron under microaspiration. It was also seen that the relative differences in PCM and chondrocyte mechanical properties, as determined from seeded gel compression, yielded a cell strain ratio (cell strain to ECM strain) that was very similar to the reference case. This led to the conclusion that matching the experimental techniques used to measure the properties of the cell and PCM was more important than the absolute values of those properties. Therefore, our results further suggest that minimizing precision error may be more important than minimizing bias error when developing and using measurement techniques for obtaining cell and PCM mechanical properties.

Differences in cell and PCM measurements are associated with the distinct cellular environments inherent in 3-D agarose culture and microaspiration techniques. The broad range of the results presented (Table 1) was attributed to variance in the cell-seeded gel stiffness data, which may be associated with variations in the chondrocyte populations as well as potential experimental measurements. This study used experimental values from enzymatically isolated chondrons and cells properties because a full set of mechanical properties for both cell and chondron were available for microaspiration and because cell and equivalent chondron properties were available for gel compression. However, it is known that enzymatic digestion alters the natural properties of the chondron (Guilak et al., 1999; Knight et al., 2001) and future experimental studies on chondrons and chondrocytes that maintain 3-D pheno-type and do not use enzymatic isolation would provide additional data and allow researchers to further understand potential sources of variation in the chondrocyte and PCM mechanical property measurements. The spherical cell model geometry used in this study, while a simplification, was representative of cell morphologies in the experimental studies used in this paper, and is also a reasonable assumption based on symmetry of the geometry, lack of interactions between cells in agarose gel scaffolds, and has been used previously (Baer et al., 2003; Guilak et al., 1999). The domain presented represents a localized microscale where ECM properties are homogeneous. Some variations in effective cell strain ratio are anticipated if these techniques were applied to multiple regions with different ECM properties, PCM, and/or cell material properties and may be considered in the future. More specific cytomorphology of cells from cartilaginous tissues, such as processes or integrin connectivity (Bruehlmann et al., 2004; Hunter et al., 2004; Nettles et al., 2004) would affect boundary conditions and the mechanical and biological environment that affects cell metabolism, and future studies are warranted. Future modeling efforts also should account for biphasic or intrinsic viscoelasticity, and while Fibonacci search is often used with single variable problems its use may be extended for multivariable systems if the variables are independent. This study presented a novel method to obtain PCM material properties and may provide a tool for evaluating cell strains under tissue loading more accurately while improving our understanding of the cell microstructural environment.