Abstract
Mathematical programming has been widely used by professionals in testing agencies as a tool to automatically construct equivalent test forms. This study introduces the linear programming capabilities (modeling language plus solvers) of SAS Operations Research as a platform to rigorously engineer tests on specifications in an automated manner. To that end, real items from a medical licensing test are used to demonstrate the simultaneous assembly of multiple parallel test forms under two separate linear programming scenarios: (a) constraint satisfaction (one problem) and (b) combinatorial optimization (three problems). In the four problems from the two scenarios, the forms are assembled subjected to various content and psychometric constraints. Assembled forms are next assessed using psychometric methods to ensure equivalence about all test specifications. Results from this study support SAS as a reliable and easy-to-implement platform for form assembly. Annotated codes are provided to promote further research and operational work in this area.
Keywords: automated test assembly, SAS Operations Research, item response theory
Automated test assembly (ATA) is a process that uses mathematical procedures to first select items from an item bank and next package them into test forms subjected to content and psychometric constraints. ATA plays an important role in two stages of test creation: (a) test form generation and (b) item bank development (Armstrong, Jones, & Wu, 1992). Testing agencies oftentimes need to administer various tests at multiple locations, sessions, and examination days. Due to test security concerns, it is necessary to generate multiple parallel test forms that are maximally equivalent on content coverage and psychometric properties. The parallel forms can be assembled automatically as well as manually.
Automated methods are gaining popularity due to innovations in computer technology, psychometric theory, and the increasing need for large-scale assessment tools. ATA has great advantages over manual test assembly (Verschoor, 2007). Featuring improved effectiveness and efficiency, automated methods can streamline the optimal item selection and packaging process while factoring more constraints into forms. Therefore, automated methods can support the mass production of test forms for continuous test administration (Breithaupt & Hare, 2007, pp. 5-7; van der Linden & Adema, 1998, p. 190). Generally speaking, forms from automated methods tend to be more statistically parallel (i.e., more equivalent) than forms from manual assembly (Cor, Alves, & Gierl, 2009, p. 16; Luecht & Hirsch, 1992, pp. 46-47, 51; Stocking, Swanson, & Pearlman, 1991, 1993). Empirical evidence from the high-stakes medical licensing examinations also supports that automated methods generate forms which can assess examinees’ ability levels more accurately, particularly around the cutoff score for classifying examinees than manual methods (Choe & Denbleyker, 2014).
ATA can also work reversely to support the design and improvement of the item bank through investigating the maximum number of forms the item pool allows to be assembled. For instance, when item shortage causes one or more constraints not to be met, the ATA process will lead to an infeasible solution. Analysis of the item bank (e.g., checking item frequencies in various breakdowns from the blueprint, as recommend by Luecht, Champlain, and Nungester, 1998) may reveal the item shortage areas, which in turn guides future item writing.
Finally, ATA serves to establish test reliability and validity in various ways. In terms of test reliability, numerous measures have been proposed under either item response theory (IRT) or classical test theory (CTT) (e.g., Parshall, Spray, Kalohn, and Davey, 2002). When a reliability measure is operationalized in a test, it becomes a test specification. ATA allows one or more such specifications to be taken into consideration simultaneously. As for test validity, ATA supports the balance of content and psychometric properties by creating parallel test forms, a critical content validity consideration especially in criterion-referenced, credentialing examinations (e.g., medical licensing examinations) (Luecht et al., 1998; van der Linden, 2005, p. ix). Besides, ATA is able to more efficiently and rigorously satisfy test specifications from the test blueprint than manual assembly, which provides additional support for content validity, that is, easier to experiment with a larger number of test constraints and update constraint boundaries. In addition, ATA contributes to test security (e.g., effectively controlling item exposure and test overlap), which is another ultimate matter of test validity (Choe, 2017, pp. 5-7). In the end, ATA can automatically deal with enemy items (when one item gives away the answer to another through the stimulus or answer, one item is the enemy of the other) to prevent them from being administered to examinees on the same form, therefore contributing to test validity (Woo & Gorham, 2010).
Mathematical Programming for Binary Integers
There is extensive literature about ATA methods, which are largely based on mathematical programming (MP). Conceptually, different MP methods work in more or less a similar way (Drasgow, Luecht, & Bennett, 2006, p. 480). Given a mathematical target or criterion (if specified), an MP method searches for items optimizing the mathematical objective function (e.g., maximizing the test information function [TIF]) when simultaneously satisfying other test specifications formulated as constraints (Chen, Chang, & Wu, 2012; Drasgow et al., 2006; Luecht, 1998; Luecht & Hirsch, 1992; van der Linden, 2005).
ATA methods abound under the MP framework, such as mixed-integer linear programming (MILP), genetic algorithm (Finkelman, Kim, & Roussos, 2009; Sun, Chen, Tsai, & Cheng, 2008; Verschoor, 2007), simulated annealing (Veldkamp, 1999), normalized weighted absolute deviation heuristic (Luecht, 1998; Luecht & Hirsch, 1992), among many others. MILP is a most popular MP method for ATA to solve various test problems and has been implemented in many optimization software programs (Belov & Armstrong, 2005; Breithaupt & Hare, 2007; Chen et al., 2012; Cor et al., 2009; Diao & van der Linden, 2011; Luo & Kim, 2018; Luo, Kim, & Dickison, 2018; Theunissen, 1985, 1986; van der Linden, 2005).
Under MILP, ATA can be formulated as one of the following two problems: (a) constraint satisfaction (CS) and (b) combinatorial optimization (CO). With CO, the MILP program searches iteratively to identify the best possible solution to produce maximally equivalent test forms along the ability scale. The optimal solution here is in the form of feasible values of decision variables on test items that optimize the objective function while satisfying test constraints. By contrast, when ATA is formulated as CS, only test constraints need to be satisfied (no objective function is involved). So, CO and CS share two fundamental components: (a) decision variables and (b) constraints. For CO problems, the objective function needs to be specified as the third component. Methods to establish these components in an MILP-based ATA are elaborated below.
Test Specifications as Constraints
First, binary decision variables on item assignment are defined in the form of 1s and 0s:
| (1) |
where and . is the total number of items in the item pool, and is the total number of forms to be assembled. The values of these variables are iteratively updated by the optimization software to eventually find a feasible set of values with which to assign items to forms when meeting all test constraints. If an objective function is specified (CO problems), the objective function needs to be optimized at the same time.
Second, constraints are test specifications which are often formulated as linear equalities or inequalities on item assignment. Outlined below are typical constraints:
-
To restrict test length to be exactly items for form :
(2) -
To ensure item is selected no more than times across all forms:
(3) -
To limit the number of items on an attribute to be between and on each form, an attribute indicator is created for the ith item and the constraint is specified as follows:
(4)
An attribute is generally defined to indicate anything on which a constraint is to be specified, that is, whether or not an item covers a certain topic, belongs to the same testlet with other items or is an enemy item of others. can be either discrete (e.g., whether item covers a certain topic, number of items in a testlet) or continuous (e.g., item difficulty or response time).
Test Specifications as an Objective Function
Similar to constraints, the objective function represents test specifications as well. Whereas test specifications formulated as constraints typically cover attributes with lower and upper bounds, those in the objective function often deal with attributes that need to be either maximized or minimized. The formulation of an objective function depends largely on the goal of the ATA problem. Testing professionals could choose to minimize the length of the test while satisfying all other test specifications or attempt to maximize test reliability while keeping the lengths of all forms fixed at a certain number. In this study, the objective function is formulated by requiring the TIF of each assembled form to be as close to the selected target value at the cutoff ability score as possible. The cutoff score serves as the threshold with which to make a decision regarding each examinee: pass the test if an examinee’s ability estimate is equal to or greater than the cutoff and fail otherwise.
Calculated by summing all item information functions (IIFs) together under the local independence assumption, TIF is an instance of the Fisher information reflecting the information in an examinee’s responses to test items regarding his or her unknown ability. In other words, TIF is an indicator of the quality of a test form over the range of examinees’ ability levels and reflects how well the test distinguishes one examinee’s ability level from another across the ability continuum (de Ayala, 2009, pp. 27-31; van der Linden, 2005, pp. 16-17). When a test is designed to make decisions about examinees with a cutoff, it needs to reach a pre-specified information level both at the cutoff and around its neighborhoods so that the test allows an examinee whose ability level is above the cutoff to be clearly distinguished from another whose ability level is below the cutoff.
Following Theunissen (1985) and van der Linden (2005, p. 110), the objective function is defined as follows to minimize the distance between the TIF and a target TIF value at :
| (5) |
where is the IIF of the ith item evaluated at . Equation 5 represents a measure of test reliability under IRT (Parshall et al., 2002 p. 109). Since can only take binary values of 0 and 1, the product equals either 0 or , respectively. Thus, is the summation of the IIFs of all items assigned to form evaluated at . Under the assumption of local independence, IIFs are additive and the summation of all IIFs gives the TIF of the test. Next, the target value at any level along the ability scale (say, at the cutoff score as specified in Equation 5) is formulated as a weighted average IIF of the entire item pool evaluated at this ability level:
| (6) |
Since the objective function in Equation 5 is nonlinear with respect to due to the absolute value operation, an MILP solver capable of optimizing such a function is unavailable in many existing optimization software programs (including the software used in this article). Therefore, according to van der Linden (2005, p. 335), the nonlinear objective function is first approximated by a linear formulation before implementing MILP. This is done by minimizing the small tolerances with which the TIF at is allowed to be larger or smaller than the target value .
As noted by van der Linden (2005, p. 106), an objective function can also be approximated as constraints. Taking TIF as an example, it is a well-behaved smooth function for models such as Rasch. Therefore, if it is required that the TIF meets a smooth target at one point on the ability scale (say, ) with an objective function, it automatically approximates the target in a neighborhood of this point. It is recommended that TIF should reach a target value at multiple points (, ) along the ability continuum, effectively creating a multi-objective problem. Since the more the points selected to achieve a target, the slower it will be for a solution to be derived, van der Linden (2005) suggested that, from a practical perspective, at most three to five points should be selected where TIF is required to meet a target value. Besides reaching a target value at with an objective function, to allow the TIF to achieve an additional target value objective at another selected , the additional objective could be formulated into constraints (van der Linden, 2005, pp. 110-111) which need to be satisfied:
| (7) |
| (8) |
where is the target value for the TIF to reach at . In Equations 7 and 8, to avoid infeasibility, the tolerances and must be chosen realistically for a certain item pool.
Test Assembly Using SAS
A solution to a complicated MILP problem requires sophisticated optimization algorithms (i.e., solvers). The performance of the MILP method in ATA relies heavily on the software program that provides the solver. Therefore, choosing the right optimization software is critical in ATA. Moreover, given a large number of MILP solvers, the task can become overwhelming. A variety of solvers for linear programming have been made available and reviewed in the literature. For instance, Cor, Alves, and Gierl (2008) introduced the EXCEL-based Premium Solver version 7.0 platform. van der Linden (2005, p. 87) introduced multiple solvers including ConTEST, OPL Studio, OTD, LINDO/LINGO, AIMSS, and the linear programming options in EXCEL and solved all problems using CPLEX 9.0.
Many of these specialized tools are designed exclusively for optimization problems with little to no consideration of their ability to communicate with other software programs. R (R Core Team, 2018) is a likely exception here because it is versatile enough to communicate with many other software programs including SAS to transfer data and retrieve outputs, although some R optimization packages only provide wrapper functions serving as an interface to the well-known lp_solve version 5.5.2.5 program (Berkelaar, Eikland, & Notebaert, 2016) instead of offering their own solvers. To address this issue, the authors propose to use SAS as a possible one-stop shop to consolidate MILP-based ATA and many other psychometric analyses into one platform. Notably, SAS itself can be programmed to invoke other psychometrics and statistics software programs such as WINSTEPS (Linacre, 2018) for calibration and R for general statistical analyses and psychometric operational work. In other words, real-time data exchange and output sharing are possible between SAS and many of these other software programs.
SAS has been a popular analytic tool in the assessment industry and beyond. In many testing organizations, SAS has been used in various aspects of the operational work including test bank database query, initial response data cleaning, examinee scoring, score equating, score release, and reporting. However, SAS has not been widely utilized as a test form assembly platform. Many testing agencies have resorted to other programs for ATA work, such as LINDO/LINGO and EXCEL that cannot interact with SAS in any automated way to further process the data for form review and publishing purposes. Switching software significantly reduces work efficiency as it often incurs manual processes requiring many steps of pre-switch and post-switch data manipulation. It is therefore desirable to identify and utilize more effective and efficient tools in form assembly that can communicate with other psychometric analyses already conducted in SAS (and other software programs such as R).
In this article, the authors propose to use the SAS Operations Research (OR) software as a solution to linear programming in ATA. As the flagship procedure in SAS/OR, PROC OPTMODEL allows virtually unlimited numbers of decision variables and constraints (Pratt, 2018, September 25; SAS Institute, 2017a). The procedure integrates seamlessly and in real time with other SAS procedures and other software programs such as R and WINSTEPS to manage data and perform analysis while solving complex test assembly problems. In this study, the authors demonstrate the capabilities of SAS/OR in ATA by giving detailed information on how to code the objective function and various constraints under SAS/OR.
An empirical item bank is used to present four ATA exemplar problems formulated under CS (one problem) and CO (three problems) scenarios. PROC OPTMODEL is utilized to assemble forms. Form equivalence is evaluated by TIFs and test characteristic curves (TCCs). The authors conclude the study with findings, limitations, and recommendations for future work.
ATA Demonstrations in SAS
For the ATA demonstration here, an item bank of around 1,000 items is selected from the Comprehensive Osteopathic Medical Licensing Examination of the United States (COMLEX-USA). COMLEX-USA is a three-level computer-based series of examinations. Each level of the examination has multiple forms. The vast majority (around 90%) of items in this bank are standalone items and the rest are case items (i.e., a testlet of two or more items). In a sense, a standalone item can be treated as a special/fake case item (testlet) with only one item in it (vs. a true case item/testlet of two or more items). Finally, it is worthwhile mentioning how items are identified in the bank. Each and every item has an item ID (ITEM_ID) but those belonging to true testlets also share an additional case ID (CASE_ID). Although a standalone item can be viewed as a special case item with only one item in it, the bank does not assign a case ID to it.
Table 1 gives the information of 10 items in the pool including item and case IDs, sub-topics under the two dimensions of the COMLEX-USA master blueprint (BP1 and BP2: say, a 4 under BP1 indicates subtopic 4 under BP1 [BP1_4]; National Board of Osteopathic Medical Examiners [NBOME], 2018), calibrated Rasch difficulty parameters (RASCH_DIFF), and corresponding item IDs of enemies (ENEMY ITEM_ID). All items in the pool are also calibrated under CTT, but CTT difficulty and discrimination parameters are not displayed to save space. Finally, for programming purposes in SAS, a combo ID (COMBO_ID) is created for each item: for a standalone item, item ID prefixed with 888; for a true case item, case ID prefixed with 999. The combo ID allows each case to be uniquely identified and also distinguishes a true case item from a standalone item. As is to be seen, this new ID plays an important role in both the data preparation and the ATA processes.
Table 1.
Ten Select Items from the Empirical Item Bank.
| ITEM_ID | CASE_ID | COMBO_ID | BP1 | BP2 | RASCH_DIFF | ENEMY ITEM_ID |
|---|---|---|---|---|---|---|
| 100780 | 888100780 | 4 | 4 | 0.23 | ||
| 100781 | 888100781 | 8 | 3 | −0.61 | ||
| 100782 | 888100782 | 8 | 3 | −1.07 | 100783, 100784 | |
| 100783 | 888100783 | 8 | 2 | −1.16 | 100782, 100784 | |
| 100784 | 888100784 | 8 | 3 | −1.02 | 100782, 100783 | |
| 100785 | 2785 | 9992785 | 4 | 2 | 2.29 | |
| 100786 | 2785 | 9992785 | 4 | 2 | 2.32 | |
| 100787 | 2785 | 9992785 | 4 | 2 | 1.85 | |
| 100790 | 2790 | 9992790 | 7 | 2 | −0.96 | |
| 100791 | 2790 | 9992790 | 5 | 1 | 0.11 |
ATA Problems and Constraints
PROC OPTMODEL is used to solve four ATA problems: (a) Problem 1: CS, (b) Problem 2: CO under one objective (CO-O1), (c) Problem 3: CO under three objectives (CO-O3), and (d) Problem 4: CO under four objectives (CO-O4). The CS problem imposes no requirements on the TIFs of forms, whereas the other three optimization problems require the TIF of each form reach a target value at one or more selected values (one of the values is the cutoff score which, without losing generalizability for the purpose of this ATA demonstration, is selected to be 0.10). At , the authors specify an objective function as defined in Equation 5 to reach a target computed from Equation 6. Next, in CO-O3 and CO-O4 only, besides , the authors select additional points along the ability continuum which are in addition to : (a) and for CO-O3, ; (b) , , and for CO_O4, . Under each of these additional points besides , constraints as formulated in Equations 7 and 8 ( for CO_O4; for all other values under both CO_O3 and CO_O4) are specified in place of an objective function for the TIF to approximate its corresponding target computed from Equation 6 evaluated at , , and , respectively (van der Linden, 2005, pp. 106-107, 110-111). Finally, under each of the four problems, five equivalent forms are assembled satisfying the following (additional) content and psychometric constraints1:
Test length: 100 items for each form;
No item is used more than once across five forms (i.e., no overlap between forms);
Constraints on BP1, BP2, and life stage in clinical presentations. For example, subtopic 1 under BP1 (BP1_1) is at least 12%;
In each form, the average item difficulty under CTT should fall between 0.71 and 0.74;
In each form, the average item discrimination under CTT should be at least 0.15;
The difference between the average response time (average duration) of each assembled form and the average value of the item bank should not exceed 5%;
In each form, the number of (true) case items should be at most 10% of test length;
Items that are enemies to each other should not be assigned to the same form.
Programming in PROC OPTMODEL and Output
After data preparations (preparation details can be found in Supplemental Appendix A) are completed, PROC OPTMODEL can be used next to import data (READ DATA statement) from the case-level SAS dataset, solve the ATA problem under MILP, and export any CS/CO results (CREATE DATA statement) into a new SAS dataset for additional analyses. When writing the CS/CO code, the VAR declaration with the BINARY option is used to create binary decision variables outlined in Equation 1 (named as “included” in the code). The decision variables are laid out in an matrix. Next, regarding constraint coding, PROC OPTMODEL saves users the trouble of using the complicated, column-oriented Mathematical Programming System (MPS), still a standard in many commercial and open-source solvers. Instead, the procedure offers a more intuitive, row-oriented method using its own algebraic modeling language. In PROC OPTMODEL, test specifications are expressed in a form that corresponds in a natural and transparent way to its algebraic models (i.e., Equations 2-8; SAS Institute, 2017a, pp. 10-11). Finally, the stopping criterion is set as 0.01 using the ABSOBJGAP option in the SOLVE statement. This user-specified stopping threshold is more lenient than the default one of and is practically necessary in large-scale ATA problems to complete the optimization process in a reasonable amount of time and without notably compromising the extent to which form assemblies remain equivalent.
As a courtesy, sample SAS code (including specific constraint boundary percentages used in the study) is provided in Supplemental Appendix B. To fully understand the technical and syntactic details of the program, the authors recommend the official SAS guide on MP (SAS Institute, 2017a). Also, readers are welcome to contact the authors with questions, requests, and/or comments on the code.
Assessment of Form Equivalence
In all four problems, PROC OPTMODEL reached a feasible solution within 3 min on a regular desktop computer (CPU: Intel i5 2.40 GHz; Memory: 16.0 GB; OS: Windows 7 Professional 64-bit) under ABSOBJGAP = 0.01 using SAS version 9.4 and SAS/OR version 14.1. The feasible solution is in the form of an matrix of values for binary decision variables where a 1 includes the item in the form and a 0 excludes it from the form.
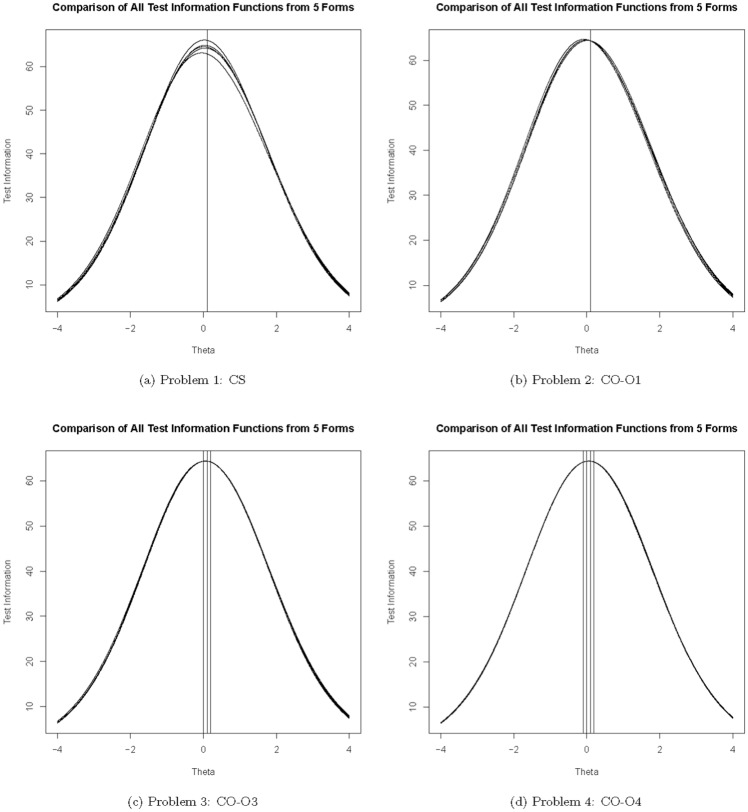
The authors begin with graphical means of assessing form equivalence. Figures 1 and 2 present the TIF and TCC overlays of the form assemblies for all four problems. Under each problem, the TIFs and TCCs, respectively, exhibit almost identical patterns over the examinee ability continuum across the forms. That the TIF/TCC curves closely overlap with each other suggests that they are statistically parallel and thus provides strong evidence of form equivalence. Notably, the TIFs of the CS problem have slightly more variability around the neighborhood of the cutoff (this is as expected since the CS problem imposes no requirements on the TIFs of forms), but this variability is not clearly visible in the TIF overlays of the other three problems. Because the CS problem does not implement an objective function, but the other three problems all have an objective function in place to minimize the distance between the TIF and a target value at , it is reasonable to conclude the objective function does improve the statistical equivalence of the forms. Next, among the three CO problems, reduction in variability can be observed but is not evident with the increase in selected points for achieving a target value.
Figure 1.
Test information functions for all five forms under each ATA problem.
Note. ATA = automated test assembly.
Figure 2.
Test characteristic curves for all five forms under each ATA problem.
Note. ATA = automated test assembly.
To supplement the TIFs and TCCs, the authors follow Luecht and Hirsch (1992) to further assess the extent to which the assembled forms are equivalent. To that end, the authors demonstrate the distributions (means and standard deviations) of CTT difficulty, CTT discrimination, and Rasch difficulty parameters (Table 2) and IIF values at selected ability levels (Table 3) across all five forms under each of the four problems. As is observed from the two tables, the between-form distributional differences on all three parameters and on IIF values at all selected ability levels are generally very minor. Evidently, PROC OPTMODEL is very consistent in matching item parameters and IIFs across test form assemblies. Besides, given that the CS problem does not impose any constraints on the TIF, it is probably not surprising to find that the five CS forms exhibit slightly more variability with regard to the average IIF value at than the five forms from any of the other three problems.
Table 2.
Distributions of Item CTT/Rasch Parameters Across Five Form Assemblies.
| CTT difficulty |
CTT discrimination |
RASCH_DIFF |
|||||
|---|---|---|---|---|---|---|---|
| Problem | Form | M | SD | M | SD | M | SD |
| CS | 1 | 0.72 | 0.15 | 0.16 | 0.05 | 0.08 | 0.77 |
| 2 | 0.71 | 0.18 | 0.15 | 0.05 | 0.06 | 0.92 | |
| 3 | 0.71 | 0.16 | 0.16 | 0.05 | 0.09 | 0.84 | |
| 4 | 0.71 | 0.16 | 0.16 | 0.05 | 0.07 | 0.84 | |
| 5 | 0.71 | 0.16 | 0.15 | 0.05 | 0.11 | 0.85 | |
| CO-O1 | 1 | 0.71 | 0.17 | 0.16 | 0.05 | 0.09 | 0.87 |
| 2 | 0.71 | 0.16 | 0.16 | 0.06 | 0.09 | 0.84 | |
| 3 | 0.71 | 0.17 | 0.16 | 0.05 | 0.09 | 0.85 | |
| 4 | 0.73 | 0.16 | 0.15 | 0.05 | 0.02 | 0.83 | |
| 5 | 0.72 | 0.16 | 0.16 | 0.06 | 0.04 | 0.85 | |
| CO-O3 | 1 | 0.71 | 0.16 | 0.16 | 0.06 | 0.09 | 0.84 |
| 2 | 0.71 | 0.16 | 0.15 | 0.05 | 0.11 | 0.85 | |
| 3 | 0.71 | 0.16 | 0.16 | 0.05 | 0.08 | 0.84 | |
| 4 | 0.72 | 0.15 | 0.15 | 0.06 | 0.05 | 0.84 | |
| 5 | 0.71 | 0.15 | 0.16 | 0.05 | 0.08 | 0.81 | |
| CO-O4 | 1 | 0.72 | 0.16 | 0.16 | 0.05 | 0.07 | 0.84 |
| 2 | 0.71 | 0.15 | 0.15 | 0.05 | 0.08 | 0.83 | |
| 3 | 0.71 | 0.15 | 0.16 | 0.06 | 0.08 | 0.82 | |
| 4 | 0.71 | 0.16 | 0.16 | 0.05 | 0.08 | 0.84 | |
| 5 | 0.71 | 0.16 | 0.16 | 0.06 | 0.09 | 0.84 | |
Note. CTT = classical test theory; CS = constraint satisfaction; CO = combinatorial optimization.
Table 3.
Distributions of IIF Values at Select Ability Levels Across Five Form Assemblies.
| IIF () |
IIF () |
IIF () |
IIF () |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Problem | Form | M | SD | M | SD | M | SD | M | SD |
| CS | 1 | 0.22 | 0.03 | ||||||
| 2 | 0.21 | 0.04 | |||||||
| 3 | 0.21 | 0.03 | |||||||
| 4 | 0.21 | 0.03 | |||||||
| 5 | 0.22 | 0.04 | |||||||
| CO-O1 | 1 | 0.21 | 0.04 | ||||||
| 2 | 0.21 | 0.03 | |||||||
| 3 | 0.21 | 0.03 | |||||||
| 4 | 0.21 | 0.03 | |||||||
| 5 | 0.21 | 0.04 | |||||||
| CO-O3 | 1 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | ||
| 2 | 0.21 | 0.04 | 0.21 | 0.03 | 0.21 | 0.03 | |||
| 3 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | |||
| 4 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | |||
| 5 | 0.21 | 0.02 | 0.21 | 0.02 | 0.21 | 0.02 | |||
| CO-O4 | 1 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 |
| 2 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | |
| 3 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.02 | 0.21 | 0.02 | |
| 4 | 0.21 | 0.04 | 0.21 | 0.03 | 0.21 | 0.03 | 0.21 | 0.03 | |
Note. IIF = item information function; CS = constraint satisfaction; CO = combinatorial optimization.
Notably, from time to time, PROC OPTMODEL may fail to find a feasible solution or cannot find one within a reasonable amount of time under specified constraints and/or the objective function. When that happens, it may be necessary to relax some constraint boundaries or adjust the threshold setting specified in ABSOBJGAP to give the procedure more flexibility in searching for the solution. Running an inventory analysis of the bank to see if there are enough items to meet a certain constraint is also recommended.
Discussion
The OPTMODEL procedure provides a general-purpose optimization modeling language and is capable of calling various solvers offered in SAS/OR to solve MP problems of many different types. Included solvers in PROC OPTMODEL are CLP for constraint logic programming, LP for linear programming, LSO for local search optimization, MILP for mixed-integer linear programming, Network for network optimization, NLP for general nonlinear programming, and QP for quadratic programming.
With PROC OPTMODEL, users can easily formulate an MP problem as an optimization model using a natural and transparent algebraic form that closely mimics the symbolic algebra of the formulation, pass the model together with the MP problem data directly to the appropriate solver, and review the solver results. Whether the problem data are encapsulated in SAS datasets or interweaved in the algebraic, optimization model in PROC OPTMODEL, the MP results can be saved, easily changed, and solved again. PROC OPTMODEL produces SAS data tables containing the solutions for users to view and interact with. Because the OPTMODEL procedure does not use a RUN statement but instead operates on an interactive basis throughout, users can continue to interact with PROC OPTMODEL even after invoking a solver. For example, users could modify the problem to update the model before issuing another SOLVE statement.
The OPTMODEL procedure is able to create and solve optimization problems of substantial scope and detail. For the test assembly problems in NBOME that vary in size and complexity (usually thousands of test specification constraints under hundreds of thousands of items in the item bank; regular desktop computers as outlined above), if the solution is feasible, PROC OPTMODEL typically reaches optimality in a reasonable amount of time (anywhere from a couple of seconds to 5-10 min, depending on the number of constraints, the value of the stopping criterion specified in the ABSOBJGAP option, among other things). If the solution is infeasible, the procedure spends no more than a couple of seconds figuring it out.
Also, the documentation admits that sometimes optimization models under PROC OPTMODEL can run out of memory during problem generation, and the authors have also encountered such a memory issue in this study. In the last problem, the authors planned to achieve objectives at five θ points (i.e., CO-O5) but due to the system running out of memory, they had to reduce the number of points to four (i.e., CO-O4). More generally, regarding the size of the MP problem that PROC OPTMODEL is able to handle and memory limits/requirements given an item bank and a specified set of test specification constraints, the authors recommend the official SAS documentation (SAS Institute, 2017a, pp. 19-21; 2018a, pp. 626-629), an online discussion within the SAS user community (Pratt, 2018, September 25), and a SAS usage note (SAS Institute, 2018b).
As for licensing and costs, PROC OPTMODEL is provided as part of SAS/OR, a component of SAS Optimization running on SAS Viya. To access PROC OPTMODEL, at least a SAS/OR license is required. In terms of system requirements, users should have at least SAS Base on which to run SAS/OR and other related SAS programs. Special features in SAS/OR may require additional SAS programs. For example, to enable graphics in SAS/OR, a SAS/GRAPH license is also required. To learn more about system requirements for SAS/OR, the authors recommend the official documentation such as SAS Institute (2017b, p. 27). Finally, when it comes to costs, like many other commercial optimization software packages (LINDO, IBM CPLEX, etc.), the license of SAS/OR and other related SAS programs needs to be purchased. The licensing costs depend on numerous factors and are subjected to change from time to time. The authors refer those interested to the SAS company sales department and authorized vendors for the most up-to-date information on SAS/OR pricing and licensing options. For users interested in free alternatives, there are several available, such as the R package xxIRT (Luo, 2018) and lp_solve version 5.5.2.5 and several of its API wrappers in R and Python.
Finally, the SAS-based ATA method proposed in this study focuses on in-house assembly of fixed forms that are to be administered (say, by computer) at a later point. Whether and how SAS/OR optimization can be extended to operationalize more complicated test designs (e.g., those requiring on-the-fly assembly during administration: adaptive testing, multi-stage testing, or a combination of both such as Chuah, Drasgow, and Luecht, 2006; Luecht, Brumfield, and Breithaupt, 2006; Zheng and Chang, 2014, 2015; Zheng, Wang, Culbertson, and Chang, 2014) need additional, dedicated investigations. Among the technical difficulties, the main one is likely to be how to combine the capabilities of PROC OPTMODEL with simultaneous test administration platforms.
Conclusion
The study implements ATA in the SAS/OR software program. The proposed approach is effective and efficient and can be integrated into other aspects of data analyses in SAS and/or R to streamline the entire ATA process including pre-assembly and post-assembly data query, item data management and manipulation, form equivalence assessment, scoring, result presentation, among other things. Although the scope of the study is restricted to a simultaneous assembly of fixed forms measuring a single ability, the authors hope their work will bring about more research in this area to harness the power of SAS and its optimization software to investigate form assembly in more complicated test designs. Finally, the study addresses to some extent the issue of test reliability under IRT through minimizing the distance between the TIF evaluated at the cutoff and a corresponding target. Additional research is needed to further examine how ATA contributes to test validity as well as reliability. Such an investigation is imperative in high-stakes medical licensing examinations tasked to protect the public by ensuring examinees possess the level of knowledge and skills necessary to provide high-quality, safe and effective patient care (NBOME, 2018).
Supplemental Material
Supplemental material, Finalization_File3_ATA_Online_Supplement for Automated Test Assembly Using SAS Operations Research Software in a Medical Licensing Examination by Can Shao, Silu Liu, Hongwei Yang and Tsung-Hsun Tsai in Applied Psychological Measurement
The constraints above only constitute a small subset of all those constraints taken into consideration in real COMLEX-USA form assembly. Also, the constraint boundaries in the study should not be taken as indicating the boundaries specified in real form assembly. The conclusions from the study have no implication whatsoever on the quality of NBOME products.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Can Shao  https://orcid.org/0000-0002-4528-6714
https://orcid.org/0000-0002-4528-6714
Supplemental Material: Supplemental material for this article is available online.
References
- Armstrong R. D., Jones H. J., Wu I.-L. (1992). An automated test development of parallel tests from a seed test. Psychometrika, 57, 271-288. [Google Scholar]
- Belov D. I., Armstrong R. D. (2005). Monte Carlo test assembly for item pool analysis and extension. Applied Psychological Measurement, 29, 239-261. [Google Scholar]
- Berkelaar M., Eikland K., Notebaert P. (2016). lp_solve_5.5.2.5 [Computer software]. Retrieved from https://sourceforge.net/projects/lpsolve/files/lpsolve/5.5.2.5/
- Breithaupt K., Hare D. R. (2007). Automated simultaneous assembly of multistage testlets for a high-stakes licensing examination. Educational and Psychological Measurement, 67, 5-20. [Google Scholar]
- Chen P. H., Chang H. H., Wu H. (2012). Item selection for the development of parallel forms from an IRT-based seed test using a sampling and classification approach. Applied Psychological Measurement, 72, 933-953. [Google Scholar]
- Choe E. M. (2017). Advancements in test security: Preventive test assembly methods and change-point detection of compromised items in adaptive testing (Unpublished doctoral dissertation). University of Illinois at Urbana-Champaign. [Google Scholar]
- Choe E. M., Denbleyker J. (2014). Quality psychometrics of Common Block Assembly: Summary report. Chicago, IL: National Board of Osteopathic Medical Examiners. [Google Scholar]
- Chuah S. C., Drasgow F., Luecht R. (2006). How big is big enough? Sample size requirements for CAST item parameter estimation. Applied Measurement in Education, 19, 241-255. [Google Scholar]
- Cor K., Alves C., Gierl M. J. (2008). Conducting automated test assembly using the Premium Solver Platform Version 7.0 with Microsoft Excel and the large-scale LP/QP solver engine add-in. Applied Psychological Measurement, 32, 652-663. [Google Scholar]
- Cor K., Alves C., Gierl M. J. (2009). Three applications of automated test assembly within a user-friendly modeling environment. Practical Assessment, Research and Evaluation, 14, 1-23. [Google Scholar]
- de Ayala R. J. (2009). The theory and practice of Item Response Theory. New York, NY: Guilford Press. [Google Scholar]
- Diao Q., van der Linden W. J. (2011). Automated test assembly using lp_Solve version 5.5 in R. Applied Psychological Measurement, 35, 398-409. [Google Scholar]
- Drasgow F., Luecht R. M., Bennett R. E. (2006). Technology and testing. In Brennan R. L. (Ed.), Educational measurement (4th ed., pp. 471-515). Westport, CT: Praeger. [Google Scholar]
- Finkelman M., Kim W., Roussos L. A. (2009). Automated test assembly for cognitive diagnosis models using a genetic algorithm. Journal of Educational Measurement, 46, 273-292. [Google Scholar]
- Linacre J. M. (2018). Winsteps® (Version 4.2.0) [Computer software]. Beaverton, Oregon: Winsteps.com; Available from https://www.winsteps.com/ [Google Scholar]
- Luecht R. M. (1998). Computer-assisted test assembly using optimization heuristics. Applied Psychological Measurement, 22, 224-236. [Google Scholar]
- Luecht R. M., Brumfield T., Breithaupt K. (2006). A testlet assembly design for adaptive multistage tests. Applied Measurement in Education, 19, 189-202. [Google Scholar]
- Luecht R. M., Champlain A. D., Nungester R. J. (1998). Maintaining content validity in computerized adaptive testing. Advances in Health Sciences Education, 3, 29-41. [DOI] [PubMed] [Google Scholar]
- Luecht R. M., Hirsch T. M. (1992). Item selection using an average growth approximation of target information functions. Applied Psychological Measurement, 16, 41-51. [Google Scholar]
- Luo X. (2018). xxIRT: Item Response Theory and Computer-Based Testing in R (R package version 2.1.0). Retrieved from https://CRAN.R-project.org/package=xxIRT
- Luo X., Kim D. (2018). A top-down approach to designing the computerized adaptive multistage test. Journal of Educational Measurement, 55, 243-263. [Google Scholar]
- Luo X., Kim D., Dickison P. (2018). Projection-based stopping rules for computerized adaptive testing in licensure testing. Applied Psychological Measurement, 42, 275-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NBOME. (2018). COMLEX-USA Master Blueprint. Retrieved from http://www.nbome.org/docs/Flipbooks/MasterBlueprint/index.html
- Parshall C. G., Spray J. A., Kalohn J. C., Davey T. (2002). Practical considerations in computer-based testing. New York, NY: Springer-Verlag. [Google Scholar]
- Pratt R. (2018, September 25). Re: Scale of capabilities of PROC OPTMODEL: Number of constraints, maximum dimension of input data [Online discussion group]. Retrieved from https://communities.sas.com/t5/Mathematical-Optimization/Scale-of-capabilities-of-PROC-OPTMODEL-Number-of-constraints/m-p/498794#M2412
- R Core Team. (2018). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/
- SAS Institute. (2017. a). SAS/OR 14.3 user’s guide: Mathematical programming. Cary, NC: Author. [Google Scholar]
- SAS Institute. (2017. b). System requirements for SAS 9.4 Foundation for Microsoft Windows for × 64. Cary, NC: Author. [Google Scholar]
- SAS Institute. (2018. a). SAS 9.4 language reference: Concepts (6th ed.). Cary, NC: Author. [Google Scholar]
- SAS Institute. (2018. b). SAS usage note 62892: Memory requirements for PROC OPTMODEL. Retrieved from https://support.sas.com/kb/62/892.html
- Stocking M. L., Swanson L., Pearlman M. (1991). Automatic item selection (AIS) methods in the ETS testing environment (Research Memorandum 91-5). Princeton, NJ: Educational Testing Service. [Google Scholar]
- Stocking M. L., Swanson L., Pearlman M. (1993). The application of an automated item selection method to real data. Applied Psychological Measurement, 17, 167-176. [Google Scholar]
- Sun K.-T., Chen Y.-J., Tsai S.-Y., Cheng C.-F. (2008). Creating IRT-based parallel test forms using the genetic algorithm method. Applied Measurement in Education, 21, 141-161. [Google Scholar]
- Theunissen T. J. J. M. (1985). Binary programming and test design. Psychometrika, 50, 411-420. [Google Scholar]
- Theunissen T. J. J. M. (1986). Some applications of optimization algorithms in test design and adaptive testing. Applied Psychological Measurement, 10, 381-389. [Google Scholar]
- van der Linden W. J. (2005). Linear models of optimal test design. New York, NY: Springer. [Google Scholar]
- van der Linden W. J., Adema J. J. (1998). Simultaneous assembly of multiple test forms. Journal of Educational Measurement, 35, 185-198. [Google Scholar]
- Veldkamp B. P. (1999). Multiple objective test assembly problems. Journal of Educational Measurement, 36, 253-266. [Google Scholar]
- Verschoor A. J. (2007). Genetic algorithms for automated test assembly (Unpublished doctoral thesis). University of Twente, Enschede, The Netherlands. [Google Scholar]
- Woo A., Gorham J. L. (2010). Understanding the impact of enemy items on test validity and measurement precision. CLEAR Exam Review, 21(1), 15-17. [Google Scholar]
- Zheng Y., Chang H.-H. (2014). Multistage testing, on-the-fly multistage testing, and beyond. In Cheng Y., Chang H.-H. (Eds.), Advancing methodologies to support both summative and formative assessments (pp. 21-39). Charlotte, NC: Information Age. [Google Scholar]
- Zheng Y., Chang H.-H. (2015). On-the-fly assembled multistage adaptive testing. Applied Psychological Measurement, 39, 104-118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y., Wang C., Culbertson M. J., Chang H.-H. (2014). Overview of test assembly methods in multistage testing. In Yan D., von Davier A. A., Lewis C. (Eds.), Computerized multistage testing: Theory and applications (pp. 87-99). New York, NY: CRC Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, Finalization_File3_ATA_Online_Supplement for Automated Test Assembly Using SAS Operations Research Software in a Medical Licensing Examination by Can Shao, Silu Liu, Hongwei Yang and Tsung-Hsun Tsai in Applied Psychological Measurement