CTRL – a label-free artificial intelligence method for dynamic measurement of single-cell volume

ABSTRACT

Measuring the physical size of a cell is valuable in understanding cell growth control. Current single-cell volume measurement methods for mammalian cells are labor intensive, inflexible and can cause cell damage. We introduce CTRL: Cell Topography Reconstruction Learner, a label-free technique incorporating the deep learning algorithm and the fluorescence exclusion method for reconstructing cell topography and estimating mammalian cell volume from differential interference contrast (DIC) microscopy images alone. The method achieves quantitative accuracy, requires minimal sample preparation, and applies to a wide range of biological and experimental conditions. The method can be used to track single-cell volume dynamics over arbitrarily long time periods. For HT1080 fibrosarcoma cells, we observe that the cell size at division is positively correlated with the cell size at birth (sizer), and there is a noticeable reduction in cell size fluctuations at 25% completion of the cell cycle in HT1080 fibrosarcoma cells.

Summary: A machine learning algorithm can predict the 3D mammalian cell volume to accurate quantify cell volume and cell growth trajectories in standard cell imaging conditions.

INTRODUCTION

Cell size plays a critical role during cell growth, division and proliferation (Björklund, 2019; Ginzberg et al., 2015; Lloyd, 2013; Pollizzi et al., 2015; Zlotek-Zlotkiewicz et al., 2015). Abnormalities in cell size regulation and growth control are thought to promote disease development (Björklund, 2019; Edens et al., 2013; Kozma and Thomas, 2002; Lloyd, 2013; Ginzberg et al., 2015; Stenkula and Erlanson-Albertsson, 2018). Accurately measuring single-cell size remains a challenge for mammalian cells due to their irregular shape. Existing techniques require specialized hardware, fluorescent labeling (Du and Wasser, 2009; Hevia et al., 2011) and/or cell suspension (Gray et al., 1983; Hirsch and Gallian, 1968; Kubitschek and Friske, 1986; Stern et al., 2017; Tzur et al., 2011). Fluorescent labeling or over-expression of a target marker can alter cell function. Cell suspension alters the cell shape and biochemical signaling from the extracellular matrix, and also potentially affects cell size. None of these methods has been successfully applied to measure mammalian cell growth at the single-cell level. While sensitive and accurate methods have been developed to measure single-cell mass over time (Cermak et al., 2016), the relationship between cell size and mass is not always clear.

An accurate and high throughput method of cell volume quantification is the fluorescence exclusion method (FXm), first proposed in 1983 (Gray et al., 1983) and subsequently developed and refined by several groups (Cadart et al., 2017; Perez Gonzalez et al., 2018, 2019). Cells are seeded in a micro-fabricated chamber and a membrane-impermeable high molecular weight fluorescent dye (e.g. FITC-dextran) is injected into the microchamber (Fig. 1A). The cell excludes its volume in the microchamber, therefore the total fluorescence loss is proportional to the cell volume. The FXm method obtains the cell volume from a single epifluorescence image, and therefore is high throughput (Cadart et al., 2017; Perez Gonzalez et al., 2018, 2019; Zlotek-Zlotkiewicz et al., 2015). However, due to endocytosis (Perez-Gonzalez et al., 2019; Zlotek-Zlotkiewicz et al., 2015) which occurs after several hours (common in many cell types), the dye eventually enters the cytoplasm, and therefore FXm generally cannot accurately report cell volume in time lapse without careful controls. Fluorescent imaging also introduces photobleaching, which alters the signal during time-lapse measurements. Moreover, microfluidic fabrication is needed to perform the experiment and the confinement of the microchamber may alter cell physiological processes over long periods. These drawbacks limit the use and applicability of FXm for studying cell growth.

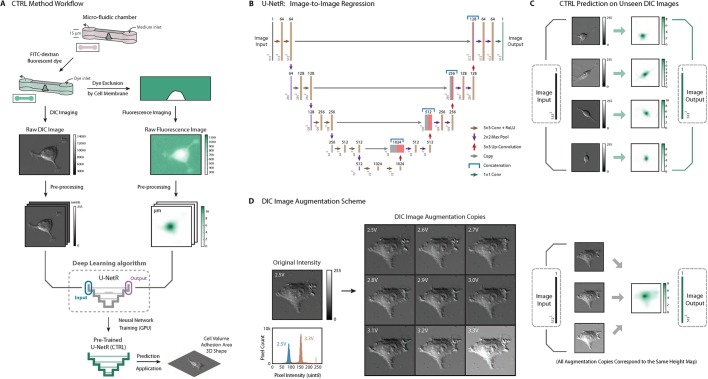
Fig. 1.

CTRL method overview. (A) CTRL method workflow. Cells are seeded into a micro-fabricated chamber for the fluorescence exclusion method (FXm). A membrane-impermeable fluorescent dye (dextran) is injected into the chamber for dye exclusion measurement. A DIC microscopy image is acquired. A cell topography image is reconstructed from the fluorescent image simultaneously acquired for the same cell. Two such images form an image pair and serve as the input and the output in the convolutional neural network: U-Net regression network (U-NetR). Training is performed with a graphics processing unit (GPU) to obtain a trained U-NetR based CTRL model. With the trained CTRL model, cell volume and topology can be computed and compared with training data as validation or test. (B) U-NetR structure. U-Net CNN structure was modified and applied according to the cell image size and output data type. The network has been modified to perform image-to-image regression, and we call the final network ‘U-NetR’. The structure starts with an image input of size 512×512, and two convolutional layers with kernel size 3×3 (each with a ReLU layer on top of it) are applied to the input layer and subsequently down-sampled to 256×256 with a max pool layer. The same procedure is applied four times in total to get a layer of size 32×32. After two further convolutional operations, the data are up-sampled using an up-convolutional layer and subsequently treated with two convolutional layers (each with a ReLU layer on top of it). The same procedure is again applied four times to ‘recover’ the image of size 512×512. For each of the four levels in U-Net, the image from the down-sampling layers is copied and concatenated to the corresponding image in the up-sampling layers in order to ‘record’ the information from the down-sampling layers (original image). After two further convolutional operations with kernel size 3×3 (each with a ReLU layer on top of it) to the layer after the last up-convolution, we applied a final convolutional layer with 64 kernels of size 1×1 to obtain an image of the same size but the third dimension of 1. In this output image, each pixel contains a real positive value, which is the prediction of cell height or cell topography. (C) Representative pre-processed DIC images and cell topography fluorescence images as network inputs and outputs. Four representative pre-processed DIC images and their corresponding cell topography fluorescence images are displayed. The DIC images serve as training input and the topography images serve as training output. (D) DIC image intensity augmentation using varying lamp voltages. Nine DIC images using lamp voltages from 2.5 V to 3.3 V with 0.1 V increments were taken as an augmentation on the intensity of the DIC image. Histograms of pixel intensity of the original image at 2.5 V and the augmented image copy at 3.3 V are displayed as a comparison. All DIC images correspond to one single output topography image as the DIC images are obtained from the same cell.

Convolutional neural networks (CNN) have been applied to microscopy images for both phenotype classification (Kihm et al., 2018; Yao et al., 2019) and image segmentation (Ibtehaz and Rahman, 2019; Ronneberger et al., 2015 preprint). CNNs trained on these tasks have proven to be accurate and predictive, and have demonstrated significant potential to generalize to a wide range of predictive tasks in biology. Here we present CTRL: Cell Topography Reconstruction Learner, a novel label-free technique that uses the U-Net regression network and FXm for reconstructing cell topography and estimating single-cell volume from differential interference contrast (DIC) microscopy images. The method requires a one-time training dataset of FXm single-cell images and their corresponding DIC images. Once trained, the method can be used to predict single-cell volume to quantitative accuracy without microchambers and fluorescence labeling. The method allows for continuous single-cell volume measurements in multiple types of cell culture platforms without time limit.

RESULTS

Deep learning enabled cell topography mapping from the DIC image

Deep learning algorithms are used to predict an outcome Y based on an input X, and deep learning models are trained based on hundreds to thousands of known X–Y pairs (training data). With a large amount of training data, a deep learning algorithm is able to ‘learn’ the complex mapping patterns from X to Y by finding the best model parameters during the training process. Once trained, the model with the best parameters can generate high accuracy predictions for inputs that were not in the training data set. The data formats of both X and Y are flexible. For instance, for classification of cats and dogs, a deep learning algorithm uses images as input and binary categories (0 or 1) as output. Prediction of disease uses information on lifestyle and genetics of a patient (a data vector) as the input and the probability of getting the disease (a scalar between 0 and 1) as the output. Here, we develop a specific image translation algorithm for predicting the three-dimensional (3D) volume of a single cell based on an input image. We use DIC images of the cell as input (X) and predict a cell height map (Y). For the training data set, the FXm approach is used to obtain a DIC image and a cell height map (image pair) for hundreds of cells.

The image translation CNN (U-Net) was first proposed by Ronneberger et al. (2015 preprint). As Fig. 1B shows, the CNN takes in a digital image as the input and generates a corresponding digital image as the output. The progressive structure between the first and last layer is composed of not only traditional convolution, ReLU, and down-sampling layers, but also up-convolution and up-sampling layers, enabling the network to ‘recover’ a parallel output image for the given the input image (image-to-image translation). The network structure starts with an image input of size 512×512; two convolutional layers with kernel size 3×3 (each with a ReLU layer on top of it) are applied to the input layer and subsequently down-sampled to 256×256 with a max pool layer. The same procedure is applied four times in total to get a layer of size 32×32. After two further convolutional operations, the data are up-sampled using an up-convolutional layer and subsequently treated with two convolutional layers (each with a ReLU layer on top of it). The same procedure is again applied four times to ‘recover’ the image of size 512×512. As shown in Fig. 1B, for each of the four levels in U-Net, the image from the down-sampling layers is copied and concatenated to the corresponding image in the up-sampling layers in order to ‘record’ the information from the down-sampling layers (original image). After two further convolutional operations with kernel size 3×3 (each with a ReLU layer on top of it) to the layer after the last up-convolution, we apply another final convolutional layer with 64 kernels of size 1×1 to get an image of the same size but the third dimension of 1 instead of 64. In this output image, each pixel contains a real positive value, which depicts the prediction of cell topography. U-NetR feature maps (activations) of two selected layers after the training of HEK-293A cells are displayed in Fig. 3C and Fig. S3. The computational code for U-NetR is available for download at: https://GitHub.com/sxslabjhu/CTRL.

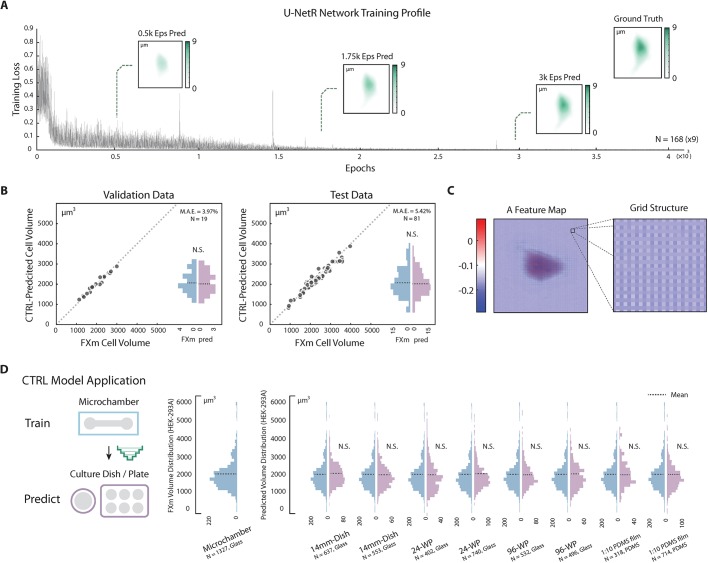
Fig. 3.

CTRL method validation and application. (A) U-NetR model training profile. Training profile of U-NetR based on training data of 1512 images (nine augmentations for each cell) on HEK-293A cells is shown with training loss progression over 80,000 training epochs. Predicted cell topography progression over the training course is shown for a representative cell at 0.5K, 1.75K and 3K epochs. Measured cell topography image (FXm data) for the cell is shown in the top-right corner. (B) CTRL model (HEK-293A) validation. Left: the trained CTRL model was applied on validation data (same microchamber, the other 20% of the cells); right: the trained CTRL model was applied on test data (cells in a different microchamber). CTRL-predicted volume is compared with FXm measured cell volume for every single cell. Volume distributions are shown as histograms. No statistical significance was found between measured volume and predicted volume. Cell number and mean absolute error (MAE) for both the validation and test cases are indicated in the top-right corner of each panel. (C) Feature maps display a grating-like structure. A representative feature map of the layer after the last up-convolutional operation in the up-sampling top level (the fourth last layer) with optical grating-like local structure is highlighted, potentially indicating that U-NetR is learning microscope optics. (D) CTRL model application across different cell culture platforms. A CTRL model trained from microchamber data can be applied to DIC cell images acquired on a variety of glass and PDMS substrates, eliminating the need for repeated FXm experiments. The only input for the CTRL model is a DIC image. HEK-293A cells were seeded in a 14 mm dish, a 24-well plate, a 96-well plate and a 1:10 PDMS membrane (two biological repeats, each biological repeat contains three technical repeats). Single-cell DIC images were inputs for the trained CTRL model. Distributions of the predicted volume in each condition are plotted in histograms, with the mean indicated by a dashed line. No statistical difference is found between the CTRL-predicted cell volume distribution and the measured volume distribution in any of the test conditions.

The application of U-Net in computational biology (Falk et al., 2019) has mainly focused on image segmentation by performing pixel classification (Ibtehaz and Rahman, 2019). Here we modify the last layer in traditional U-Net structure and present a U-Net network for pixel regression: U-Net regression network (U-NetR) (Fig. 1B). As opposed to predicting a categorical label, U-NetR predicts a positive real number for each pixel. For data collection, we acquire DIC image data and the corresponding microchamber fluorescence image data from the FXm experiment (Fig. 1A). Images are taken immediately after the introduction of fluorescent dye, therefore the data exclude potential effects of endocytosis. Pre-processing of DIC images and microchamber fluorescence images and the intensity augmentation for DIC images (Figs 1D and 2; Fig. S1) are detailed in the Materials and Methods section. For training data, the DIC image serves as the input and the fluorescence image serves as the output. U-NetR aims to uncover the hidden relationship between the image pair during network training. In other words, U-NetR learns to generate the cell height map (topography) from the DIC image, given hundreds to thousands of ‘image pairs’. The methodology is built upon the hypothesis that the intensity distribution over a DIC image contains information in the cell height map that is inexplicable to human eyes. Once trained, the CTRL model is capable of predicting a corresponding topography image from a previously unseen DIC image of any cell (Fig. 1C). Previous attempts have been made to model the optics of the DIC microscope to recover object 3D shape (Kagalwala and Kanade, 2003) by modeling the optical physics. Here we use the U-Net deep learning algorithm to optimize this mapping without knowledge of microscopy details.

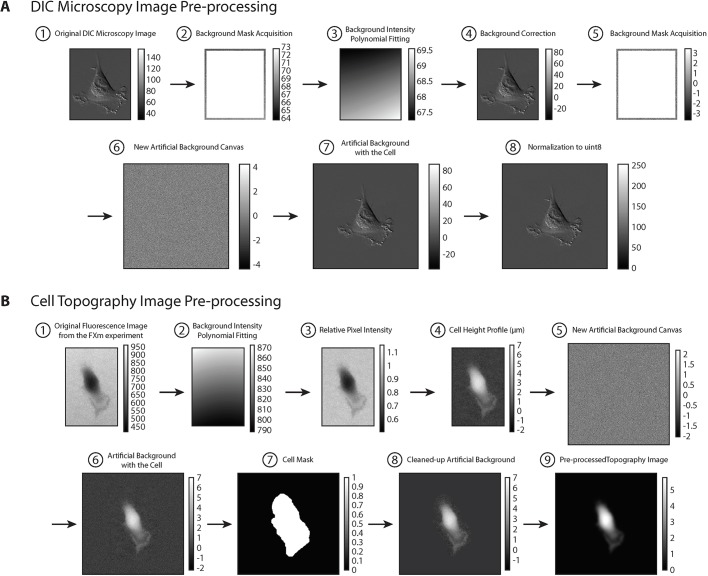
Fig. 2.

DIC image and cell topography fluorescence image pre-processing. (A) DIC image pre-processing. For each DIC image, we first cropped the image to obtain single cells with the least amount of background (A1). We then acquired a background mask by taking a 10 pixel band closest to the edge (A2). A polynomial fitting using the function ‘poly22’ in MATLAB was applied to perform an intensity fitting to the background mask (A3). The image in A3 is subtracted from the image in A1 to obtain a background-corrected image A4. The purpose of this background correction is to reduce the potential local intensity heterogeneity within one DIC image. After background correction, we acquired a new background mask A5 based on the background-corrected image with the same procedure and created a new artificial background ‘canvas’ for cell padding A6. The ‘canvas’ of size 512×512 was created by generating a Gaussian distribution with the same mean and standard deviation as the background mask acquired in A5. The background-corrected cell in A4 was then put into the middle of A6 to finalize the background padding (A7). Finally, we normalized the image to the data type of uint8 (8-bit) with integer values between 0 and 255 (A8). (B) Cell topography fluorescence image pre-processing. A background intensity polynomial fitting (B2) was first applied to the original fluorescence image (B1) using the same procedure as described in the ‘DIC image pre-processing’ section. The estimated height of the cell at each pixel h_pixel is directly proportional to the loss of intensity at the pixel. For instance, if the pixel intensity is 0, then the height at the pixel is the height of the microchamber; if the intensity is the maximum intensity, then the height of the cell at the pixel is 0:h_pixel = (1-I_pixel/I_channel) × h_channel. The relative pixel intensity (B3) I_pixel/I_channel was then obtained by dividing B1 by B2 for each pixel. The image B3 was then subtracted by 1 and multiplied by the value of microchamber height h_channel to reflect the height of the cell at each pixel (in μm units) as shown in B4. (Note due to optical effects, the intensity only estimates the height. However, the integrated intensity over the image reports the true volume image.) An artificial background ‘canvas’ (B5) was created for padding using the same procedure as described in the ‘DIC image pre-processing’ section. The cell image was put into the center of the ‘canvas’ as shown in B6, and a binary-valued cell mask was created by thresholding over the value of 0.05 and dilating approximately 30 pixels outwards (away from the cell) using MATLAB function ‘imdilate’ (B7). The binary mask with the value 0 in the background and the value 1 inside the dilated region was then multiplied to the image in B6 to obtain a cleaned cell image B8 with the intensity of all pixels in the artificial background cleared to zero. Finally, a Gaussian filter using MATLAB function ‘imgaussfilt’ with a 2D Gaussian smoothing kernel with standard deviation value of 3 was applied to the image to obtain a smoothed cell topography (B9). This step does not change the integrated cell volume.

The optimal parameters of our U-Net were obtained (trained) with the stochastic gradient descent (SGD) method as the learning algorithm to update model parameters. For SGD, the momentum was 0.9 and the learning rate was set to be fixed at 10⁻³. We observed a learning rate within 10⁻³ to 10⁻⁴ to be appropriate for the tests conducted in this work, and the application of learning rate decay did not have a meaningful impact on training outcomes. The loss function in the network was designed to measure the loss of ‘image volume’ per pixel, which is the ratio between the summation of all pixel values in an image and the number of total pixels in an image. SGD iteratively updates the model parameters to minimize the ‘image volume’ difference between the predicted topography image (Y_pred) and the ground truth topography (Y_true) image. Mini-batch size was set to be approximately 5% of the size of the dataset in each test, allowing the network to take a small batch of data from the training data at each iteration for parameter update. The mini-batches were designed to be shuffled randomly every epoch throughout the training process to enhance model validation performance. For training/validation set separation, in each test, 80% of the images were assigned as training data and 20% of the images were assigned as validation data randomly. L2 regularization was applied to the data in order to prevent overfitting of the U-Net algorithm.

Single-cell volume prediction is validated on multiple cell culture platforms

We applied U-NetR training to HEK-293A cells (Fig. 3A), which showed a gradual decrease of training loss over 80,000 epochs. The validation and test results (Fig. 3B; Fig. S2) show that the prediction mean absolute error (MAE) remains less than 4% for validation data (same microchamber, the remaining 20% of the cells) and 6% for test data with three biological repeats (cells from a different microchamber in a separate experiment) and the absolute error of the population average is less than 3% for both cases. These results suggest that a trained CTRL model can adequately predict cell volume for unseen DIC image data. The predicted cell volume distributions are also quantitatively similar to the measured cell volume distribution from FXm (Fig. 3B). The representative convolutional feature maps from the trained model are shown in Fig. S3. In particular, some of the feature maps show diffraction-grating-like grids (Fig. 3C; Fig. S2A), suggesting that U-NetR is learning optics to map the images in the training data. Comparing with the traditional FXm method, this computational approach achieves significant savings in laboratory work, requiring no micro-device fabrication and fluorescence imaging beyond the training data set. More importantly, it liberates cells from the confinement of microchambers and long-term incubation together with fluorescence dyes, and therefore ensures normal cell growth and eliminates errors from dye endocytosis. To test the applicability and robustness of the method to different substrates used during DIC imaging, we tested varying cell culture seeding platforms from glass to polydimethylsiloxane (PDMS) substrates and report the predicted cell volume distribution (Fig. 3D). Even though the training data were taking from microchambers with glass substrates, no significant variation was found between the predicted volume distributions of the populations across different platforms.

Artificial intelligence model generalization is achieved when global cell shape is preserved

To further explore the applicability of the method, we investigated the effect of pharmacological inhibition on model generalization. Rapamycin, a mammalian target of rapamycin (mTOR) pathway inhibitor, has been shown to decrease cell volume by ∼15% (Fingar et al., 2002; Inoki et al., 2005; Perez-Gonzalez et al., 2019; Pollizzi et al., 2015). We measured the cell volume data of rapamycin-treated (72 h, 1 nM) HEK-293A cells from the FXm method and applied the CTRL model trained on untreated cells to the corresponding DIC images. Results show that the predicted cell volume distribution matches cell volume distribution from FXm experiments (Fig. 4A). Next we tested HEK-293A CRISPR-mediated knockout of the Hippo pathway protein YAP (Plouffe et al., 2016, 2018), a nuclear transcription factor that regulates cell volume (Perez-Gonzalez et al., 2019) in an mTOR-independent manner. The CTRL model (trained on wild-type cells) predictions are again in excellent agreement with FXm (Fig. 4B). It is also known that biomechanical environment of the cell such as the substrate stiffness affects cell volume (Guo et al., 2017; Perez Gonzalez et al., 2018), and we found that the model trained on data from glass substrates (GPa) can predict cell volume on 3 kPa PDMS substrates (Fig. 4D).

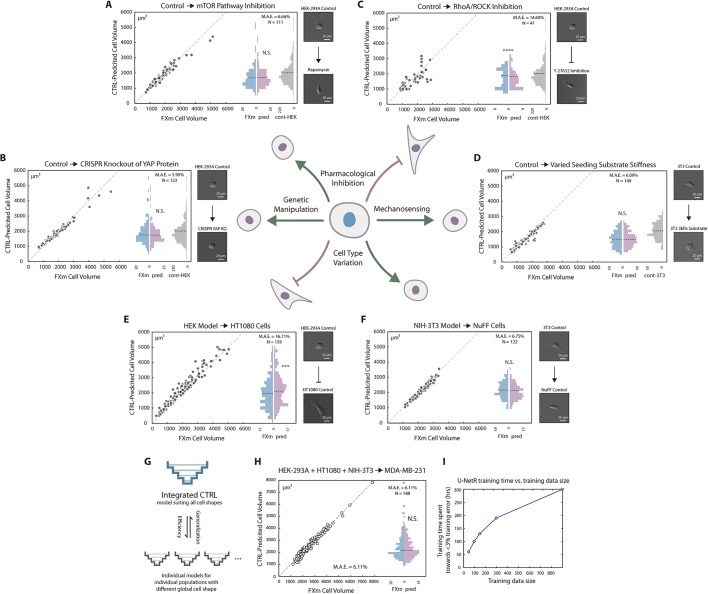
Fig. 4.

CTRL model generalization. (A) Generalization to cells with mTOR pathway inhibition via rapamycin. HEK-293A cells were treated with 1 nM rapamycin for 72 h before the FXm experiment. Cell volume was experimentally measured via the FXm and predicted by a CTRL model previously trained on data from untreated HEK-293A cells (Fig. 3B). No statistical difference was found between the measured volume and the predicted volume distributions. Cell volume distribution of control HEK-293A cells (training data) is plotted in gray as a reference. (B) Generalization to CRISPR knockout of YAP protein. YAP knockout of HEK-293A was generated previously (Plouffe et al., 2016, 2018). Cell volume was measured via the FXm and predicted by a CTRL model previously trained on data from WT HEK-293A cells (Fig. 3B). No statistical difference was found between measured volume and predicted volume. Measured cell volume distribution of control HEK-293A cells (training data) is shown in gray as a reference. (C) Generalization to cells with ROCK inhibition via Y-27632 cannot be achieved. HEK-293A cells were treated with 100 μM Y-27632 for 2 h before the FXm experiment. Cell volume was experimentally measured via the FXm and predicted by a CTRL model previously trained on data from untreated HEK-293A cells (Fig. 3B). Measured cell volume distribution of control HEK-293A cells (training data) is plotted in gray as a reference. (D) Generalization to PDMS substrate with different stiffness. 3T3 cells were seeded on a PDMS substrate with stiffness of 3 kPa. Cell volume was experimentally measured via the FXm and predicted by a CTRL model previously trained on data from NIH-3T3 cells on regular glass substrates (Fig. 3B). No statistical difference was found between FXm-measured volume and predicted volume. Measured cell volume distribution of 3T3 cells on regular glass substrate (training data) is plotted in gray as a reference. (E) Poor generalization to HT1080 cells with CTRL model trained on HEK-293A cells. U-NetR was trained on HEK-293A cells and tested on HT1080 cells. CTRL-predicted volume is compared with FXm-measured cell volume for every single cell. (F) Generalization to NuFF cells with CTRL model trained on NIH-3T3 cells. U-NetR was trained on NIH-3T3 cells and tested on NuFF cells. CTRL-predicted volume was compared with FXm-measured cell volume for every single cell. (G) Illustration of the relationship between an integrated model and individual models. Individual CTRL models trained on specific cell types may not generalize to other cell types with substantially different cell shapes, while an integrated model pooling training data from all cell types is able to achieve generalization. The trade-off for the integrated model will be greater training time. For panels A–F, DIC images of a representative cell of each training population and each test population are displayed. (H) Generalization to MDA-MB-231 cells with CTRL model trained on a combination of HEK-293A, HT1080 and NIH-3T3 cells. U-NetR was trained on a combination of HEK-293A, HT1080 and NIH-3T3 cells (N ∼900) and tested on MDA-MB-231 cells (N=148). CTRL-predicted volume was compared with FXm-measured cell volume for every single cell. Good generalization to a new cell type can be achieved when pooling data from multiple cell lines together as the training data. (I) The relationship between training time and the sample size of the training data. Five training data sizes were investigated: 50 cells, 100 cells, 150 cells, 300 cells and 900 cells (a random mixture of HEK-293A, HT1080 and NIH-3T3 cells). The training time is plotted against training data size. The training time here refers to the time spent until the training accuracy reaches 97% (training error reaches below 3%). The training time is in units of 10× hours as each training session takes 10 h.

We then sought to see if the model generalization persisted in situations where there is a dramatic change in cell shape. Y-27632 is known to inhibit (Claassen et al., 2009; Horani et al., 2013) Rho kinase activity and cell contractility, and change the cell shape. We found that the model (trained on untreated cells) can no longer predict the volume during Y-27632 treatment (Fig. 4C) with MAE greater than 14%. We then asked if a CTRL model trained on one cell type can generalize to a different cell type with a different cell shape. It was found that a CTRL model trained on data acquired for HEK-293A is able to predict larger average volume of HT1080 (fibrosarcoma cells) (Fig. 4E), but the MAE is too large to be quantitative at an individual level. However, a CTRL model trained on data from NIH-3T3 cells is able to predict cell volume accurately for newborn foreskin fibroblast (NuFF) cells (Fig. 4F), which is of the same cell types (fibroblast) as 3T3 and has a similar cell shape. These results (Fig. 4A–F) suggest that the CTRL model generalizes well to biological perturbation of the same cell type but fails when there is a dramatic cell shape change. It is reasonable to conjecture that pooling images from multiple cell types with different shape variations together with the training data will generate a general model (Fig. 4G). Indeed, a CTRL model trained on combined data of HEK-293A, HT1080 and NIH-3T3 cells can predict MDA-MB-231 cell volume accurately (Fig. 4H). However, a larger training data set also increases training time (Fig. 4I) and a balance must be found between generalizability and computational time. Depending on the U-NetR structure, hyperparameter selection, the data augmentation scheme, the volume of the training data and the graphics processing unit (GPU) used, the typical training time for a CTRL model can vary from days to weeks.

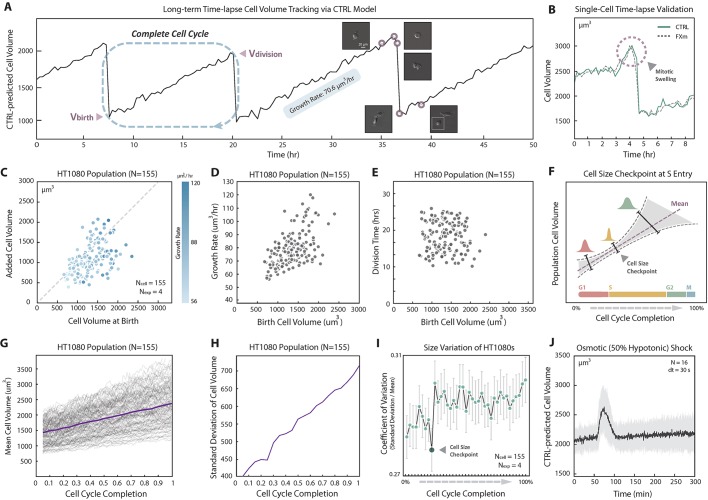
Long-term cell volume tracking reveals sizer behavior and cell size checkpoint

The proposed method is label free (no fluorescent dye is needed) and liberates the cell from the microchamber. These advantages allow us to track single-cell volume in standard cell culture dishes for an indefinite period with arbitrary time resolution. The method allows us to quantify cell volumetric growth rates over multiple generations of daughter cells. In particular, to gain greater insight into cell size regulation, we sought to correlate the added cell volume with the birth volume of the cell over several generations. Here we used HT1080 cells instead of HEK-293A cells because the daughter cells readily separate from mother cells. A CTRL model was trained for HT1080 cells and the achieved accuracy is shown in Fig. S1. The HT1080 CTRL model prediction for a 9 h time-lapse DIC movie is compared with the FXm volume measurement for the same cell (Fig. 5B). The model again demonstrates quantitative cell volume prediction even through cell division, including the phenomena of mitotic swelling (Zlotek-Zlotkiewicz et al., 2015). The prediction error over time (frames) for the entire population is shown in Fig. S4A, showing that the CTRL model is quantitatively accurate for all cells tracked. We then applied the CTRL model for a 50 h DIC movie of growing and dividing cells in a standard cell culture dish (Fig. 5A). The cell volume trajectory of a single cell and one of the daughter cells from each of its three divisions (generations) is shown in Fig. 5A. In order to quantify cell volume before and after cell division, it is essential to include images of cells undergoing division in the training data. Note that due to dye endocytosis, the experiment in Fig. 5A is not possible with FXm experiments. Results of added cell volume during a cell cycle versus the cell volume at birth (Fig. 5C) show that HT1080 adopts a sizer-like growth mechanism. The time-lapse experiment also revealed the correlation between the cell cycle length (division time), volume growth rate and cell birth volume (Fig. 5D,E). Moreover, the coefficient of variation, 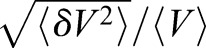, is generally constant over the cell cycle, but shows a visible decrease at 25% cell cycle completion (Fig. 5I). The mean and standard deviation of population cell volume throughout cell cycle completion are shown in Fig. 5G and H. This is indicative of a cell cycle checkpoint where size control would reduce cell size fluctuations (Fig. 5F). The CTRL model is also useful for quantifying rapid cell volume changes such as during an osmotic shock (Fig. 5J). Here the cell volume is tracked every 30 s, showing that HT1080 cells can re-adjust their volumes after a hypotonic shock (50%) in 15–30 min (single-cell trajectories are shown in Fig. S4B).

Fig. 5.

Time-lapse cell volume tracking via CTRL. (A) Representative long-term cell volume trajectory. Cell volume from CTRL prediction of a single HT1080 cell is plotted over time (50 h) with three visible divisions. DIC images of the cell before and after division at several time points are shown. The growth rate within one cell cycle is displayed. A linear growth law is assumed. (B) Time-lapse single-cell volume validation. Cell volume of HT1080 cells was quantified using CTRL model (continuous line) on DIC images and compared with experimental data from the FXm (dashed line) for the same cell. The time interval between adjacent frames is 20 min. (C) The relationship between added cell volume and cell volume at birth. From predicted HT1080 time-lapse cell volume trajectories, the added cell volume for one cell cycle is plotted against the cell volume at birth. To ensure that each cell has completed a full cell cycle, cells with two consecutive visible divisions were analyzed. The dashed line indicates added cell volume equal to birth volume. Data are from four biological repeats (N=155). The data indicate that HT1080 is a sizer. (D) Growth rate and cell birth volume. Growth rate is plotted against cell birth volume for each individual cell that has gone through a complete cell cycle (N=155). Larger cells consistently grow faster. (E) Cell cycle duration and cell birth volume. The overall duration of the cell cycle is plotted against birth cell volume for each cell through a complete cell cycle (N=155). (F) Cell size checkpoint concept illustration. The presence of a cell size checkpoint is a potential mechanism for maintaining size homeostasis for the entire population. Cells progress to a new cell cycle phase, e.g. S entry, only when the physical size of the cell reaches a size threshold (checkpoint). If there is such a checkpoint, cell size variation at the checkpoint should decrease due to feedback control. (G) Cell volume trajectories over the complete cell cycle. Mean cell volume as a function of cell cycle completion percentage (purple line). Raw cell volume trajectory over the complete cell cycle for every cell is also shown in gray (N=155). (H) Standard deviation of the cell volume vs cell cycle. Standard deviation of the cell volume is plotted by the purple line (N=155). (I) Cell volume coefficient of variation (CV) for the complete cell cycle. Individual single-cell volume was tracked for >70 h. To ensure each cell has completed a full cell cycle, only cells with two consecutive visible divisions were analyzed. The cell cycle is divided into 39 increments (2.5% for each increment), and we analyzed the collected volumes of all cells at each increment of cell cycle completion. The mean (G) and the standard deviation (H) of the cell volume, and the coefficient of variation (CV=standard deviation/mean) are shown. A visible decrease of CV was found at 25% cell cycle completion, indicating the presence of cell size checkpoint for HT1080 cells. Error bars represent standard deviations of CV generated from 1000 random sampling of 60 cells from 155 available cells. (J) Cell volume adaptation during osmotic shock. Hypotonic shock medium (50%) was added to HT1080 cells. DIC images were taken 60 min before the shock and 240 min after the shock with high time resolution (30 s). Average cell volume over all single cells in two biological repeats (N=19) is shown by the black line, and the standard deviation over all time points is supplied (gray interval). Single-cell volume trajectories are displayed in Fig. S4B.

DISCUSSION

Understanding the mechanisms controlling cell size and cell growth is a fundamental goal in cell and tissue biology. So far, the lack of a label-free and easy-to-use technique that can accurately measure cell volume has limited quantitative studies on factors influencing mammalian cell size and cell growth dynamics. The present methodology is quantitatively accurate in estimating both static and time-lapse single-cell size in standard cell culture conditions in a high throughput manner. The method requires a one-time data collection of training images using the FXm method, but subsequent volume predictions can be done in standard cell culture dishes without labeling. While the model generalization is problematic when there is a drastic change in the cell shape, the method has the potential to generalize to any cell type with sufficiently large input training data, perhaps from a global database. The average error in the estimated single cell volume when compared with FXm is in the range of 5–6%. Note that depending on the precision of fabrication and image analysis, FXm itself can also have errors of the order of 5–10%. Therefore the artificial intelligence (AI) method is quantitatively similar to FXm in its effectiveness. The proposed method can also be used to generate a predictive model based on other types of training data, making it broadly applicable to other methods of obtaining cell volume based on image data.

With the ability to measure cell volume over the entire cell cycle, a number of new features have been observed with our method. First, cells grow monotonically with bigger cells growing faster throughout the cell cycle. This might be explained by the fact that bigger cells have a larger surface area. However, the cell cycle duration is not correlated with cell size. For HT1080 cells, according to the CTRL prediction the added cell volume over the cell cycle is correlated with the initial cell volume, suggesting a sizer-like behavior. Cell volume variation increases over the cell cycle, but the coefficient of variation (CV) is roughly constant over the cell cycle, except at approximately 25% of the cell cycle (around where G1–S transition usually takes place for HT1080 cells), where there is a noticeable reduction in CV. Cell cycle reporters such as fluorescent ubiquitination-based cell-cycle indicator (FUCCI) are needed to further validate that the greatest growth control occurs at G1–S transition and the general relationship between cell volume and cell cycle. This noticeable reduction in CV is indicative of actions by a control system, which exerts a ‘corrective force’ on the cell size progression around this specific size control checkpoint. Growth of larger cells is slowed down while the growth of smaller cells speeds up around this size control checkpoint, as seen previously in HeLa cells (Kafri et al., 2013). The molecular mechanisms governing the size checkpoint are currently unknown, but are likely to be complex and worth exploration in future studies.

More generally, AI methods can provide new insights and opportunities for image-based biological discovery while reducing experimental time and cost. AI methods are especially useful for extracting quantitative data from images with high fidelity. Nevertheless, it is notable that AI methods cannot learn and make predictions on rare or unseen data. Therefore, the quality of the training data is the ultimate determinant of AI method effectiveness.

MATERIALS AND METHODS

Cell culture

HEK-293A (human embryonic kidney cells), HT1080 (fibrosarcoma tumor cells), NIH-3T3 (mouse embryonic fibroblasts), NuFF (neonatal foreskin fibroblasts) and MDA-MB-231 (breast cancer) cell lines were used in the present study. HT1080, NIH-3T3 and MDA-MB-231 cell lines were a gift from Denis Wirtz (Johns Hopkins University, Baltimore, MD, USA), neonatal foreskin fibroblasts (NuFF) were a gift from Sharon Gerecht (Johns Hopkins University, Baltimore, MD, USA). HEK-293A and its YAP CRISPR knockout cell line were a gift from the Kun-Liang Guan Laboratory (University of California, San Diego, CA, USA). Cells were grown inside the incubator in Dulbecco's modified Eagle’s medium (DMEM; 10-013-CV, Corning) with 10% v/v fetal bovine serum (FBS; 0-2020, ATCC) and 1% v/v penicillin streptomycin (PS; 15140163, Thermo Fisher Scientific) in a T75 flask with confluency <60% prior to all experiments.

Seeding substrate platforms

For cell culture platform validation experiments, we investigated three commonly used cell culture platforms with glass substrates and one culture platform with silicone substrate: (1) small dish: 29 mm glass bottom dish with 14 mm micro-well no. 1.5 cover glass (D29-14-1.5-N, CellVis, Mountain View, CA, USA), (2) 24-well plate: glass bottom plate with no. 0 cover glass 0.085–0.115 mm (P24-0-N, CellVis), (3) 96-well plate: glass bottom plates (P96-0-N, CellVis) and (4) polydimethylsiloxane (PDMS), a silicone-based organic polymer. For fabrication of the PDMS membrane, a silicone kit (Dow Sylgard 184 Silicone Encapsulant Clear 0.5 kg kit) containing the base and the curing agent was used. A 9:1 ratio between base and curing agent was applied, and the corresponding Young's modulus of the fabricated PDMS is 1000 kPa. Collagen was coated for 1 h in the following amounts: 200, 500 and 100 μl for the small dish, 24-well plates and 96-well plates, respectively. Collagen was then removed and the seeding dish/plate was washed with Dulbecco's phosphate-buffered saline (DPBS; 14190250, Thermo Fisher Scientific) twice. HEK-293A cells were trypsinized using Trypsin-EDTA (0.25%) (25200056, Thermo Fisher Scientific) and seeded onto the collagen-coated seeding platforms in the following amounts: 2 ml, 200 μl and 50 μl at a single-cell density of 10,000 cells per milliliter. Cells were then incubated with the dish/plate inside the incubator for 4 h prior to DIC microscopy imaging. Live cell DIC microscopy imaging was performed at a constant temperature of 37°C and 5% CO₂ inside the sealed microscope stage incubator. DIC images were taken using ZEN software.

Pharmacological inhibition

Rapamycin (37094, Sigma Aldrich) was used as an mTOR pathway inhibitor that decreases the cell volume at a concentration of 1 nM and assay time of 72 h. Y-27632 (72304, StemCell, Cambridge, MA) was used as a ROCK pathway inhibitor that decreases cell volume at a concentration of 100 μM and assay time of 2 h.

Extracellular matrix stiffness

For model generalization to cells on substrates of different stiffness, silicone elastomer was prepared by mixing a 1:1 weight ratio of silicone produce components CY52- 276A and CY52-276B (Dow Corning Toray) for 3 kPa (Style et al., 2014). In all cases, the elastomer was vacuum-degassed for ∼5 min to eliminate bubbles, and the polymer was then spin-coated onto the micro-well of the dish at 1000 r.p.m. for 60 s. The dish was cured overnight and resulted in a ∼50 µm thick layer of silicone. The devices were then rinsed with water, dried using compressed air, plasma-treated and bonded to the cell volume PDMS devices. The final devices were placed in an oven at 80°C for 45 min to enhance the bonding quality.

Osmotic shock experiment

HT1080 cells were seeded in 14 mm dishes 24 h prior to the experiment. During image acquisition, the dish was sealed onto the microscope stage to avoid excessive movement in order for single-cell data collection. The time resolution of the experiment (time interval between adjacent frames) is 30 s. Thirty-five frames were taken before applying the osmotic shock and 121 frames were taken after the shock. Cells were placed in 2 ml of DMEM+10% v/v FBS+1% v/v PS (regular medium) before osmotic shock. The osmotic shock application was conducted by changing the medium. For osmotic shock application, half of the regular medium (1 ml) in the dish was removed and 1 ml of filtered, deionized water was added and mixed with the regular medium. This creates a 50% water hypotonic solution for the osmotic shock investigation. The first frame was taken immediately after the osmotic shock application. Live cell DIC microscopy imaging was performed with a constant temperature of 37°C and 5% CO₂ inside the sealed microscope stage incubator. DIC images were taken using ZEN software.

Fluorescence exclusion method

Fabrication of microfluidic device

Silicon molds with the microfluidic chamber pattern were fabricated using standard photolithography procedures. Masks were designed using AutoCAD and ordered from FineLineImaging. Molds were made following the manufacturer's instruction for SU8-3000 photoresist. Two layers of photoresist were spin-coated on a silicon wafer (IWS) at 500 r.p.m. for 7 s with an acceleration of 100 r.p.m./s and 2000 r.p.m. for 30 s with an acceleration of 300 r.p.m./s, respectively. After a soft bake of 4 min at 95°C, UV light was used to etch the desired patterns from negative photoresist to yield feature heights that were approximately 15 µm. The length of the above-mentioned channels is 16.88 mm and the width is 1.46 mm.

A 10:1 ratio of PDMS Sylgard 184 silicone elastomer and curing agent were vigorously stirred, vacuum degassed, poured onto each silicon wafer and cured in an oven at 80°C for 45 min. Razor blades were then used to cut the devices into the proper dimensions, and inlet and outlet ports were punched using a blunt-tipped 21-gauge needle (76165A679, McMaster-Carr). The devices were then sonicated in 100% isopropyl alcohol for 15 min, rinsed with water and dried using a compressed air gun.

Glass-bottom Petri dishes (50 mm; FluoroDish Cell Culture Dish, World Precision Instruments) were cleaned with water and then dried using a compressed air gun. The Petri dishes and PMDS devices were then exposed to oxygen plasma for 1 min for bonding. Finally, the bonded devices were placed in an oven at 80°C for 45 min to further ensure enhanced bonding.

Fluorescence exclusion measurement

Micro-fluidic chambers were exposed to 30 s oxygen plasma before being incubated with 50 µg/ml of type I rat tail collagen (354236, Corning) for 1 h at 37°C. The chambers were washed with 1× PBS before approximately 50,000 cells were injected. The dishes were then immersed in a sufficient amount of medium to prevent evaporation from the microchambers. The cells were seeded along with 0.1 µg/ml of Alexa Fluor 488 Dextran dye (150 kDa; Thermo Fisher Scientific) and allowed to adhere to the substrate in the incubator at 37°C with 5% CO₂ at 90% relative humidity. Cells were then imaged within 8 h to avoid potential effects caused by dye endocytosis over time.

Every experiment on cell volume was repeated at least three times (biological repeats) with three technical repeats corresponding to the three individual channels in one micro-fluidic device. Experiments in glass gave around 50 single-cell measurements. Softer substrates often yielded smaller datasets per measurement. The sample size for volume measurements was at least 100 single cells.

Microscope image acquisition

For cell volume measurements via the FXm method, cells were imaged using a Zeiss Axio Observer inverted, wide-field microscope (Zeiss LSM 800) using a 20× air, 0.8 numerical aperture (NA) objective equipped with an Axiocam 560 mono charged coupled device (CCD) camera. The microscope was equipped with both DIC imaging and fluorescent imaging. DIC microscopy was used to accurately capture the cell area and shape, and epifluorescent microscopy was used to measure volume. The CO₂ Module S (Zeiss) was used and TempModule S (Zeiss) stage-top incubator (PeCon, Erbach, Germany) was set to 37°C with 5% CO₂ for all the live-cell imaging experiments. The imaging medium was DMEM with 10% FBS and 1% PS, and Alexa Fluor 488 dye was used as the fluorochrome for the FXm measurements. ZEN 2 (Zeiss) was used as the acquisition software. MATLAB 2018a (MathWorks, Natick, MA, USA) was used for image analysis subsequent to data acquisition. For DIC imaging, the prism was always reset before experiments so that the bottom-left corner of a cell was the brightest and the top-right corner of a cell the darkest for consistency. DIC images were taken under nine lamp voltage levels from 2.5 V to 3.3 V (Fig. 1D) as data augmentation as cell volume is invariant regardless of DIC light intensities. For each cell investigated, we adjusted the z-axis and focused well on the cell surface, and we avoided using out-of-focus cells for both training and test. For time-lapse imaging, we applied the ‘Definite Focus’ strategy of ZEN 2 software to focus well on the cells investigated.

Image pre-processing

DIC image pre-processing

For each DIC image, we first cropped the image to obtain single cells with minimal background area (Fig. 2A1). We then acquired a background mask by taking the 10-pixel region closest to the edge (Fig. 2A2). A polynomial fitting using the function ‘poly22’ in MATLAB was applied to perform a fitting to the background mask (Fig. 2A3). The image in Fig. 2A3 is subtracted from the image in Fig. 2A1 to obtain a background-corrected image (Fig. 2A4). The purpose of background correction was to reduce the potential local intensity heterogeneity within one DIC image. After background correction, we acquired a new background mask (Fig. 2A5) based on the background-corrected image with the same procedure described above, and created a new artificial background ‘canvas’ for cell padding (Fig. 2A6). The ‘canvas’ of size 512×512 was created by generating random intensities from a Gaussian distribution with the same mean and standard deviation as the background mask acquired in Fig. 2A5. The background-corrected cell in Fig. 2A4 was then put into the middle of Fig. 2A6 to finalize the background padding (Fig. 2A7). Finally, we normalized the image to the data type of uint8 (8-bit) with integer values between 0 and 255 (Fig. 2A8).

Cell topography image pre-processing

Fluorescence images were taken using an Axiocam 560 mono CCD camera under an inverted, wide-field microscope (LSM800, Zeiss) using a 20× air, 0.8 NA objective. Alexa Fluor 488 dye was used as the fluorochrome for the FXm measurements. A background intensity polynomial fitting (Fig. 2B2) was applied to the original fluorescence image (Fig. 2B1) using the same procedure as described in the ‘DIC image pre-processing’ section above. The height of the cell at each pixel (h_pixel) was calculated in this way: the height at each pixel is directly proportional to the loss of intensity at the pixel. For instance, if the pixel intensity is 0, then the height at the pixel is the height of the microchamber; if the intensity is the maximum intensity (at the background outside the cell), then the height of the cell at the pixel is 0:

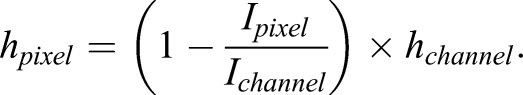The relative pixel intensity (Fig. 2B3) I_pixel/I_channel was then obtained by dividing Fig. 2B1 by Fig. 2B2 under pixel-wise operation (to be distinguished from matrix operation, in MATLAB, it is A./B instead of A/B). The image Fig. 2B3 was then subtracted by 1 and multiplied by the value of microchamber height h_channel to reflect the height of the cell at each pixel (in μm units) as shown in Fig. 2B4. An artificial background ‘canvas’ (Fig. 2B5) was created for padding using the same procedure as described in the ‘DIC image pre-processing’ section. The small image was put into the center of the ‘canvas’ as shown in Fig. 2B6, and a binary-valued cell mask was created by thresholding over the value of 0.05 and dilating approximately 30 pixels outwards (away from the cell) using MATLAB function ‘imdilate’ (Fig. 2B7). The binary mask with the value 0 in the background and the value 1 inside the cell was then multiplied to the image in Fig. 2B6 to get a cleaned-up cell image (Fig. 2B8) with the intensity of all pixels in the artificial background cleared to zero as the cell height outside the cell is zero. Finally, a Gaussian filter using MATLAB function ‘imgaussfilt’ with a 2D Gaussian smoothing kernel with standard deviation value 3 was applied to the image to obtain a smoother cell topography (Fig. 2B9).

Deep learning model

U-NetR

The U-Net CNN structure was applied and modified according to the cell image size and the desired output data type. The network has been modified to serve the use of image-to-image regression and we call the final network ‘U-NetR’. The detailed structure is displayed in Fig. 1B. The structure starts with an image input size of 512×512, and two convolutional layers with kernel size 3×3 (each with a ReLU layer on top of it) are applied to the input layer and subsequently down-sampled to 256×256 with a max pool layer. The same procedure is applied four times in total to get a layer of size 32×32. After two further convolutional operations, the data is up-sampled using an up-convolutional layer and subsequently treated with two convolutional layers (each with a ReLU layer on top of it). The same procedure is again applied four times to ‘recover’ the image of size 512×512. As shown in Fig. 1B, for each of the four levels in U-Net, the image from the down-sampling layers is copied and concatenated to the corresponding image in the up-sampling layers in order to ‘record’ the information from the down-sampling layers (original image). After two further convolutional operations with kernel size 3×3 (each with a ReLU layer on top of it) to the layer after the last up-convolution, we applied another final convolutional layer with 64 kernels of size 1×1 to get an image of the same size but the third dimension of 1 instead of 64. In this output image, each pixel contains a real positive value, which depicts the prediction of cell topography. U-NetR feature maps (activations) of two selected layers after the training of HEK-293A cells are displayed in Fig. 3C and Fig. S2.

Loss function

The loss function of U-NetR was designed to measure the loss of ‘image volume’ per pixel, which is the ratio between the summation of all pixel values in an image and the number of total pixels in an image (512×512=262,144). We applied L1 loss:

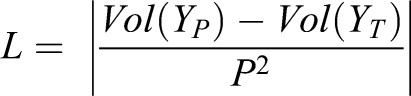where L is the loss function, 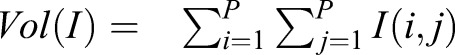is the volume of the cell from the topography map, I, Y_P is the prediction and Y_T is the ground truth. P is the total pixel number, and in our case, P=512². The neural network training aims to minimize the loss as much as possible over training epochs. The reason for adopting the volume of an image as the training loss function in the CTRL model for cell volume prediction is straightforward: as the topography image depicts the height of the cell at each pixel in µm units, the volume of the cell topography image is directly related to the volume of the cell by the formula: V_cell=α²×V_topo, where α is the actual length measure per pixel in a microscope image, and in our case, α=0.227 µm/pixel.

Training parameters

U-Net was trained with the stochastic gradient descent method as the learning algorithm. The momentum was 0.9 and the learning rate was set to be fixed at 10⁻³. We observed a learning rate within 10⁻³ to 10⁻⁴ to be appropriate for the tests conducted in this work, and the application of learning rate decay did not have a meaningful impact. Mini-batch size was set to be approximately 5% of the size of the dataset in each test and the mini-batches were designed to be shuffled randomly every epoch throughout the training process to enhance model validation performance. For training and validation set separation, in each test, 80% of the images were assigned as training data and 20% of the images were assigned as validation data randomly. L2 regularization was applied to the data.

The neural network training of this research project was conducted using scientific computational resources at the Maryland Advanced Research Computing Center (MARCC). The ConvNet training was performed using Nvidia K80 GPUs or Nvidia P100 GPUs depending on computation availability via FDR-14 InfiniBand interconnects. The GPU nodes at the MARCC are Dell PowerEdge R730 servers with dual Intel Haswell Xeon E5-2680v3 (12 core, 2.5 GHz, 120 W), 30 MB cache and 128 GB of 2133 MHz DDR4 RAM.

Statistical analysis

To obtain the statistical significance between distributions of cell volume (more specifically, between predicted cell volume and true cell volume), the non-parametric two-sample Kolmogorov–Smirnov test was performed without assuming Gaussian distribution of single-cell volume within a population (Figs 3 and 4; Figs S2 and S4). The Kolmogorov–Smirnov test is a statistical test based on comparing cumulative distributions and can be applied to two or more independent samples for testing whether the samples originate from the same distribution. The null hypothesis is that the samples are drawn from the same distribution. Statistical significance marks are as follows: N.S., P≥0.05; *P<0.05; **P<0.01; ***P<0.005; ****P<0.001.

Code availability

All MATLAB codes written and applied in convolutional neural network design and training, image pre-processing and validation analyses, as well as exemplary image data, are available online at: https://GitHub.com/sxslabjhu/CTRL.