A Late Critical Period for Frequency Modulated Sweeps in the Mouse Auditory System

Abstract

Neuronal circuits are shaped by experience during time windows of increased plasticity in postnatal development. In the auditory system, the critical period for the simplest sounds—pure frequency tones—is well defined. Critical periods for more complex sounds remain to be elucidated. We used in vivo electrophysiological recordings in the mouse auditory cortex to demonstrate that passive exposure to frequency modulated sweeps (FMS) from postnatal day 31 to 38 leads to long-term changes in the temporal representation of sweep directions. Immunohistochemical analysis revealed a decreased percentage of layer 4 parvalbumin-positive (PV⁺) cells during this critical period, paralleled with a transient increase in responses to FMS, but not to pure tones. Preventing the PV⁺ cell decrease with continuous white noise exposure delayed the critical period onset, suggesting a reduction in inhibition as a mechanism for this plasticity. Our findings shed new light on the dependence of plastic windows on stimulus complexity that persistently sculpt the functional organization of the auditory cortex.

Introduction

Auditory neural circuits are shaped by experience during time windows of enhanced plasticity in early postnatal development (Keuroghlian and Knudsen 2007; Kral 2013). Passive exposure of young mammals to a variety of sound features reveals a cascading series of developmental windows that open and close to define the long-lasting influences that early experiences have on the functional capability of the auditory cortex (Insanally et al. 2009; Sanes and Bao 2009; Popescu and Polley 2010). While the developmental plasticity for the simplest sounds—pure frequency tones—has been well characterized (de Villers-Sidani et al. 2007; Barkat et al. 2011), critical periods for more complex sound features, as well as potential mechanisms triggering the related enhanced plasticity, remain undefined.

Motivated by the importance of the direction of frequency modulated sweeps (FMS) for discriminating consonants like /ga/ (upward sweep) or /da/ (downward sweep) and for the understanding of speech and music in general (Altmann and Gaese 2014; Okamoto and Kakigi 2015), we used in vivo electrophysiological recordings and immunohistochemistry to determine whether responses to this sound feature could also be modified through passive FMS exposure, and if so, what the underlying mechanisms might be. We started by characterizing the temporal profile of upward and downward FMS responses in the two primary auditory cortices of mice: the primary auditory cortex (A1) and the anterior auditory field (AAF) (Stiebler et al. 1997). We then recorded A1 responses to FMS following passive FMS exposure, as well as across juvenile development, and identified postnatal day 31 (P31) to P38 to be the critical period for FMS. Finally, we perturbed cortical development through continuous white noise (WN) exposure to identify a decrease in layer 4 parvalbumin-positive (PV⁺) neurons as a potential mechanism for the developmentally restricted enhanced plasticity. Our results reveal a critical period for FMS correlated with a transient increase in firing rate of regular spiking neurons in A1 after the first month of life. The timing dependence of critical periods on stimulus complexity and the underlying mechanisms have strong implications for our understanding of developmental plasticity.

Materials and Methods

Experimental Subjects

All experimental procedures were carried out according to Basel University animal care and use guidelines. They were approved by the Veterinary Office of the Canton of Basel-Stadt, Switzerland. C57BL/6J mice (Janvier) were aged 20 days (P20) to 12 weeks old, and males and females were used without distinction. After weaning, they were housed in groups of 2–5 under a 12/12 h light/dark cycle and allowed to get food and water ad libitum.

Electrophysiological Recordings

Mice were anesthetized with an intraperitoneal (i.p.) injection of a mixture of 80 mg/kg ketamine (Narketan, Vetoquinol) and 16 mg/kg xylazine hydrochloride (Rompun 2%, Bayer). A subcutaneous injection of a mixture of 0.01 mg/mouse of bupivacaine and 0.04 mg/mouse of lidocain was used for analgesia. Ketamine (45 mg/kg) was supplemented during surgery as needed. The body temperature was kept at 37°C with a heating pad (FHC). A custom-made stainless-steel head-restraint post was fixed on the bone on top of the left hemisphere and used to head-fix the animals. Using a scalpel, a craniotomy (~2 × 2 mm²) was performed just above the auditory cortex. The dura was left intact and was covered with silicone oil. A 4 × 8 electrode (A4 × 8-5 mm-50-200-177-A32, Neuronexus) was inserted in the auditory cortex with a motorized stereotaxic micromanipulator (DMA-1511, Narishige) at a depth of (tip of electrode) 600 ± 50 μm from pia. Recording sites spanned 600 μm in the caudal-rostral axis and 350 μm in depth traversing the granular layer including sites in the supra- and subgranular layer. Recordings from A1 were confirmed in each animal by the increase in best frequency (BF) from the most caudal to the most rostral shaft of the 4-shaft electrodes (Fig. 1A), confirming the tonotopic organization typical of A1. AAF was identified based on the functional tonotopy, with a ventro-dorsal increase in BF (Fig. 1K). All recordings were performed in a sound-attenuating chamber (modified MAC-2 chambers, Industrial Acoustics Company nordics). For the developmental study, the group P20 included mice of P20 only, the group P30 included P29–P30 mice, the group P40 P39–P40 mice, and the group P50 mice P50 and above (P50–P78), considered adult.

Figure 1.

Temporal profiles of responses to FMS in A1 are topographically organized. (A) Schematic of A1 with the recording electrode at the surface of the mouse auditory cortex. The color code represents the tonotopy (blue: low BF, red: high BF). A 4 × 8 is the electrode design (4 shanks with 8 recording channels each, dimensions in the inset). (B) Spectrograms of + and −75 oct/s FMS displayed with frequencies linearly spaced as a function of time. (C) Two A1 example neuron responses to pure tones (FRA) and their PSTH to upward (+75 oct/s) and downward (−75 oct/s) FMS. The gray shaded area is the time window of the sweep stimulation. (D) Population PSTH for upward and downward 75 oct/s FMS, for A1 neurons of low (4–8 kHz, n = 102), middle (8–16 kHz, n = 123), and high (16–32 kHz, n = 86) BF (n = 8 mice). (E) Average population peak latencies for upward and downward sweep as a function of BF range. ^***P < 0.0001, n.s., P = 0.2559, 2-way ANOVA. (F, G, H) Comparison between upward and downward FMS responses expressed as DSI based on firing rate during FMS exposure +100 ms (F, DSI rate), DSI based on peak amplitude (G, DSI peak), and DSI based on firing rate during FMS exposure (H, DSI rate (short)), as a function of BF range. (I) Population PSTH for upward and downward 15 oct/s FMS, for A1 neurons of low (4–8 kHz) and high (16–32 kHz) BF (same neuronal population and color code as in C). (J) Difference in peak latency for FMS of different speeds for A1 neurons. The black bars are the data presented in D, for FMS at 75 oct/s. (K) Schematic of AAF with the recording electrode at the surface of the mouse auditory cortex. (L) PSTH of response to + and −75 oct/s FMS in AAF for units of 4–8 kHz BF range (n = 17). (M) Difference in peak latency between upward and downward FMS in A1 (black, n = 8 mice, 363 MU) and AAF (gray, n = 5 mice, 140 MU) for + and −75 oct/s FMS) as a function of BF range. Data show mean ± SEM.

Sound Exposure

Subsets of mice were placed in a custom-made sound-attenuating chamber and exposed to −75, +75 oct/s FMS (100 ms logarithmic sweeps from 50 kHz to 250 Hz or from 250 Hz to 50 kHz played at 2 Hz, 75 dB sound pressure level (SPL)) or continuous WN (bandwidth from 1 to 65 kHz, 75 dB SPL). The standard acoustic environment was the normal sound environment of the animal facility. Mice were otherwise reared under standard conditions (12:12 h light:dark cycle), had access to water and food ad libitum, and moved about freely in their cage. FMS sounds were generated with a function generator (model TG1000; TTi, Fort Worth). Continuous WN was generated by an arbitrary function generator (model AFG1022, Tektronix) and amplified by an integrated amplifier (model PM7005, Marantz). Both sounds were played through a magnetic speaker (MF1, Tucker Davis Technologies) positioned 35 cm above the bottom of the cage.

Auditory Stimulation

Sounds were generated with a digital signal processor (RZ6, Tucker Davis Technologies, 200 kHz sampling rate) and played through a free-field magnetic speaker (MF1, Tucker Davis Technologies) positioned at 10 cm from the mouse’s left ear. FMSs spanning in a logarithmic scale from 2 to 48 kHz (upward sweeps) or from 48 to 2 kHz (downward sweeps) at speeds of 15, 30, 45, 60, 75 or 90 oct/s (corresponding to durations of 51, 61, 76, 102, 153 or 306 ms, respectively; 4 ms cosine on/off ramps) were played with randomized intertone intervals of 1000–1500 ms at 60 dB SPL repeated 15 times. Stimuli were calibrated with a wide-band ultrasonic acoustic sensor (Model 378C01, PCB Piezotronics). For the establishment of frequency response areas (FRA), pure frequency tones (50 ms duration, 4 ms cosine on/off ramps) from 4 to 48.5 kHz in 0.1 octave increments and 0–80 dB SPL in 5 dB increments were played with randomized intertone intervals of 500–1000 ms repeated twice.

Immunohistochemistry

P20, P30, P40 and P50–P60 (called P50 group) mice of both genders were deeply anesthetized with an i.p. injection of pentobarbital (Esconarkon, 300 mg/mL, Streuli Pharma AG). Mice were transcardially perfused with saline followed by 4% paraformaldehyde (PFA; Sigma-Aldrich) in 0.1 M phosphate buffer (PBS; Sigma-Aldrich) pH 7.4 at 4°C. Brains were dissected out and postfixed overnight in 4% PFA, cryoprotected with 30% sucrose for 2 days, embedded in dry-ice frozen OCT (TissueTek, Sakura Finetek), and kept at −80°C. Coronal slices (45 μm) containing A1 were prepared with a cryostat (Leica CM3050 S). Slices were blocked in 0.05% Triton-X100 (Sigma-Aldrich) in PBS (PBS-T) for 1 h at room temperature. Double immunostaining for PV and vesicular glutamate transporter type 2 (VGlut2), which labels axonal thalamocortical terminals in L4 (Tatti et al. 2017b; Chang and Kawai 2018), was performed. Slices were incubated overnight in 10% Donkey Serum (cat# C06SBZ, Bio-Rad) in PBS-T containing the following primary antibodies: goat anti-PV (1:3000; cat# PVC-123, Swant) and guinea pig anti-VGlut2 (1:1000; cat# AB2251-I, Merck). On the following day, slices were immunoreacted for 2 h at room temperature with the following secondary antibodies: Alexa Fluor 594 donkey antigoat (1:1000; cat# A-11058, Thermo Fisher Scientific) and Alexa Fluor 488 donkey antiguinea pig (1:1000; cat# 706-546-148, Jackson ImmunoResearch). All slices were counterstained with fluorescent 4,6-diamidino-2-phenylindole, dihydrochloride (DAPI) (Thermo Fisher Scientific, D1306) to quantify the total number of cells and mounted with Fluoromount-G (Fluoromount-G, SouthernBiotech).

Images containing A1 were acquired with a slide scanner microscope (Zeiss AxioScan.Z1) using a 10× objective (Plan-Apochromat 10×/0.45 M27), and equal microscope settings were kept across animals. To ensure homogeneous sampling of PV cells, up to 7 images were taken per animal at the center depth of each slice. A1 was identified using the coordinates from the atlas for the mouse brain (Franklin and Paxinos 2013) corrected along the rostro-caudal axis (bregma −2.18 to −3.64 mm). Landmarks of the white matter and anatomy of hippocampus were also used as reference for A1 position.

Images were analyzed using the QuPath software (Open Source Digital Pathology, v0.2.1) in a blind manner. A1 boundaries and cortical layers (L2/3, L4, L5, L6) were outlined, and an automated quantification of DAPI⁺ cells and PV⁺ cells was run. All the measuring parameters were kept constant across animals to insure a homogenous quantification.

Data Processing

Responses from extracellular recordings were digitized with a 32-channel recording system (RZ5 Bioamp processor, Tucker Davis Technologies) at 24 414 Hz. Multiunit (MU) responses were band pass filtered at 300–5000 Hz. MU spikes were detected as threshold-crossing events using an adaptive threshold (4.5 SDs from the mean of a 10 s running average) and further analyzed using custom software in MATLAB (Mathworks). Sorted units (SUs) were identified from raw voltage traces using a semiautomated spike-detection and clustering algorithm (KiloSort, CortexLab, UCL) followed by a manual clustering according to their interspike interval distributions, waveform consistency, and presence in neighboring recording sites (phy, CortexLab, UCL) and further analyzed with custom software in MATLAB (Mathworks).

Data Analysis

FRAs were calculated in a fixed time window from tone onset (10–60 ms), smoothed with a median filter (4 × 4 sampling window), and thresholded to 20% of maximal response amplitude. To assess the tuning quality of the FRA, d′ was calculated as the difference in mean spike count within the FRA and mean spike count outside the boundary of FRA divided by their arithmetic average standard deviation (modified method from (Guo et al. 2012)). For all our analysis, we only selected units with d′ > 0.5. BF was defined as the tone frequency which evoked the highest response at all tested sound levels. A1 and AAF were identified based on the functional tonotopy (caudo-rostral increase in BF for A1 and ventro-dorsal increase in BF for AAF) and were bounded by BF reversal or unresponsive sites. Data that could not be identified to belong to one of these two primary auditory fields were excluded from the analysis. A topographic analysis of BF was achieved by dividing A1 into equal thirds along the tonotopic axis (Barkat et al. 2011) (Supplementary Figs 1C–E and 3A,D). Responses to FMS were quantified by peak latency (time from FMS onset to peak rate), firing rate (number of spike during the FMS presentation +100 ms divided by FMS duration +100 ms; Supplementary Fig. 1H), firing rate short (number of spike during the FMS presentation divided by FMS duration), or peak rate (number of spikes at the peak of the peristimulus time histogram (PSTH), the PSTH being constructed with 5 ms bins). Direction selectivity indices (DSI) were calculated as the response (rate or peak) of the upward FMS (U) minus response of the downward FMS (D) divided by the sum of both (DSI = (U − D)/(U + D)). A chi²-based statistic of DSI peak was also calculated (chi² DSI peak = (U − D) × abs(U − D)/(U + D)) (Insanally et al. 2009). Compared with DSI peak, this calculation transforms the data by decreasing small peak latency differences and increasing big peak latency differences. The depth of SUs was estimated knowing the depth of the tip of the electrode from the pia and the channel to which the SU was the closest to. The PSTH for the p2t profiles was established with 0.1 ms bin size. Onset latencies for pure tones were determined as the first time point in which the auditory evoked responses of all pure tones grouped together exceeded with 2 standard deviation the spontaneous activity (binning size: 1 ms). Onset latencies for FMS were determined as the first time point in which the auditory evoked responses of the specific FMS exceeded with 2 standard deviation the spontaneous activity. Bandwidth was calculated as the bandwidth (in octave) of the FRA 10 dB SPL above threshold (BW 10) or at 60 dB SPL (BW at 60 dB SPL). Tone rate was calculated as the mean response to the BF stimulation for all sound levels played. The spontaneous activity was calculated in a 100 ms window starting 150 ms before sound presentation.

Statistics

All statistical values were reported and plotted as mean ±standard error of the mean (SEM), with n representing the number of MUs (Figs 1, 2, 3 and 6D, Supplementary Figs 1, 3A–F, 4 and 5), SUs (Fig. 5, Supplementary Fig. 3G–I), or slices (Figs 4 and 6B) for the calculation of SEM. Statistical testing was carried out in GraphPad (GraphPad Software) using 2-way analysis of variance (ANOVA) with Sidak’s multiple comparison (Fig. 1D, Supplementary Figs 3A–E, 5G–E), 2-way ANOVA with Tukey’s multiple comparison (Figs 2, 4–6, Supplementary Figs 4 and 6), Student’s 2-sampled unpaired t-test to compare means, with no assumption of equal variance (Supplementary Figs 3I and 5F) or Spearman correlation (Supplementary Fig. 5D,E). The effects were named significant if the P value was smaller than 0.05 (^*), 0.01 (^**), or 0.001 (^***), for a confidence interval of 95, 99, or 99.9%, respectively. Tests to determine sample size were not performed, but our sample sizes were similar or bigger than those used in previous publications in the field.

Figure 2.

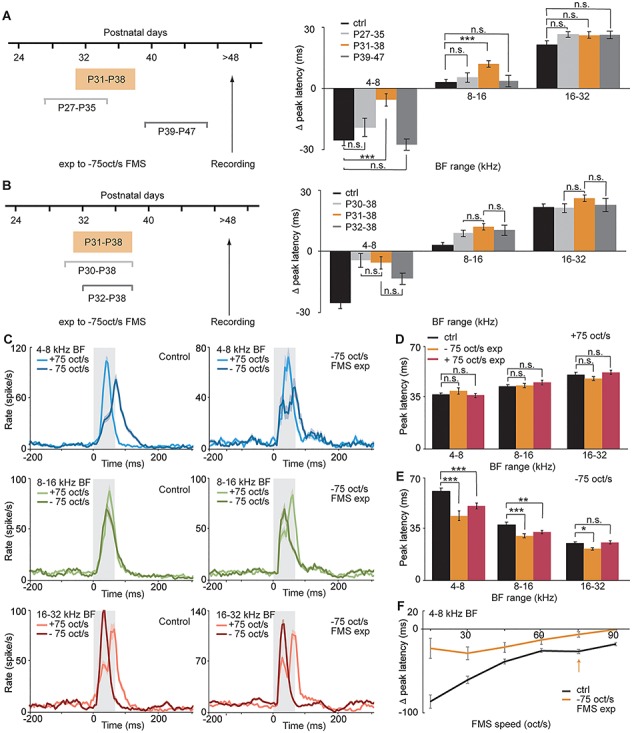
The critical period for FMS in mouse A1 is P31–P38. (A) Difference in peak latency for three −75 oct/s FMS exposure time windows: control (n = 8 mice, 102, 123, 86 MU with BF range of 4–8, 8–16, or 16–32 kHz, respectively), P27–P35 (n = 4 mice, 28, 72, 93; n.s., P = 0.3993, 0.9784, 0.4855, 2-way ANOVA), P31–P38 (n = 6 mice, 51, 131, 140, ^***P < 0.0001; ^**P = 0.0011; n.s., P = 0.5101, 2-way ANOVA), and P39–P47 (n = 5 mice, 56, 76, 91 MU; n.s., P = 0.8895, 0.9975, 0.4290, 2-way ANOVA). (B) Difference in peak latency for P30–P38 exposure time window (n = 8 mice, 38, 176, 79 MU; n.s., P = 0.999, 0.7322, 0.3323, 2-way ANOVA) or P32–P38 exposure time window (n = 4 mice, n = 46, 74, 50 MU; n.s., P = 0.3651, 0.9830, 0.9448, 2-way ANOVA). (C) PSTH of response to + and −75 oct/s FMS in control (left) and mice exposed to −75 oct/s between P31 and P38 (right) for units of 4–8, 8–16, or 16–32 kHz BF range (upper, middle, or lower row). (D) Peak latency for +75 oct/s FMS in control (black), P31–P38–75 oct/s exposed (orange; n.s., P = 0.6879, 0.9085, 0.7097, 2-way ANOVA), and +75 oct/s exposed mice (red; n = 8 mice, 128, 165, 176 MUs n.s., P = 0.9706, 0.1622, 0.3824, 2-way ANOVA). (E) Peak latency for −75 oct/s FMS in control (black), P31–P38–75 oct/s exposed mice (orange; ^***P < 0.00001, ^*P = 0.0197, 2-way ANOVA), and +75 oct/s exposed mice (^***P < 0.00001, ^**P = 0.0058, n.s., P = 0.9992, 2-way ANOVA). (F) Difference in peak latency between upward and downward FMS in control (black) and exposed mice (orange) for FMS of different speed in MU with a BF range of 4–8 kHz. The arrow indicates the exposed speed (75 oct/s) and the data represented in C–E. Data show mean ± SEM.

Figure 3.

FMS response timing differences are stable through postnatal development. (A) Schematic of recording time points through development. (B) Difference in peak latency between upward and downward FMS in P20 (n = 7 mice, 31, 83, and 100 MU), P30 (n = 8 mice, 48, 143, and 145 MU), P40 (n = 8 mice, 112, 166, and 176 MU), and adult (P50 and above, n = 8 mice, 102, 123 and 86 MU) mice as a function of BF range. Data show mean ± SEM. (C) PSTH of response to +(light blue) and 75 oct/s (dark blue) FMS in P30 and P40 mice for units of 4–8 kHz BF range (same data used in B).

Figure 6.

Preventing the decrease of L4 PV⁺ cells through WN exposure delays the critical period. (A) Schematic of the WN exposure and the critical period for FMS (CP FMS). (B) Quantification of PV⁺ cells in control P30 mice (n = 6 mice, 42 slices), control P40 mice (n = 4 mice, 28 slices), and in P40 mice exposed to WN from P30 to P40 (n = 5 mice, 35 slices; ^***P < 0.0001, ^*P = 0.012, 2-way ANOVA). (C) Schematic of the WN and FMS −75 oct/s exposure for electrophysiological experiments. (D) Peak latency differences in control (black, n = 8 mice, 102, 123, 86 MU), WN only exposed mice (gray, n = 7 mice, 105, 206 and 260 MU; n.s., P = 0.3836, 0.9085, 0.3438, 2-way ANOVA), and WN and FMS exposed mice (orange, n = 7 mice, 115, 145 and 221 MU; ^***P < 0.00001, ^*P = 0.0428, n.s., P = 0.999, 2-way ANOVA). Data show mean ± SEM.

Figure 5.

FMS responses of L4 regular spiking neurons increase transiently during the critical period. (A) Example of SU waveshape with p2t = 0.29 ms (narrow spiking) and p2t = 0.94 ms (regular spiking). (B) Distribution of SU as a function of p2t time at 350–500 μm from pia. The arrow represents the separation between narrow spiking and regular spiking SU (p2t = 0.6 ms). For P20, the value of p2t = 0.9 ms was used to separate the two populations. (C) Proportion of narrow spiking (NS, p2t < 0.6 ms for P30–P50, 0.9 ms for P20) SU across development (%). (D, E, F) Average firing rate for regular spiking SU in 150–350 (L2/3) or 350–550 μm (L4) from pia for responses to FMS (D), to pure tones (E), or spontaneous activity (F). P = 0.0019, 0.9999, 0.9387 between L4 P30 (n = 162 SU) and P40 (n = 176 SU), 2-way ANOVA. (G, H, I) Average responses for all SU across all recorded layers as average FMS firing rate (G), FMS peak amplitude (H), or spontaneous activity (I) across development (n = 7 mice, 332 SU (P20); 8 mice, 368 (P30); 8 mice, 376 SU (P40); 8 mice, 459 SU (P50)). Data in (D–I) show mean ± SEM.

Figure 4.

The number of PV⁺ neurons in L4 decreases during the critical period of FMS. (A) Confocal image taken with a 10× objective showing the location of A1. Landmarks of the white matter (WM) and anatomy of hippocampus (hip) were used to identify A1. Scale bar: 100 μm. (B) Brain slices were processed with antibody staining for VGlut2 (green) and fluorescent DAPI (blue) to measure L4 distance from the pia and identify layers. Scale bar: 170 μm. (C) From left to right: representative 10× confocal images showing the distribution of DAPI⁺, VGlut2⁺, and PV⁺ stainings in a P30 mouse across the A1 cortical layers. Scale bar: 150 μm. (D) Same as (C) in a P40 mouse. Brightness and contrast were adjusted to fit the purpose of the stainings. (E) Percentage of PV⁺ cells of the whole cell population across A1 layers quantified in 4 postnatal age groups (P20, n = 4 mice, 26 slices; P30, n = 6 mice, 42 slices; P40, n = 4 mice, 28 slices; P50, n = 4 mice, 28 slices). (F) Number of DAPI⁺ cells across A1 layers quantified in the 4 postnatal age groups. Data show mean ± SEM. Statistical significance was calculated by using 2-way ANOVA, and P-values were corrected for multiple comparisons. ^*P < 0.05; ^**P < 0.01; ^***P < 0.001.

Results

Temporal profiles of responses to FMS in A1 are topographically organized

To investigate whether responses to complex sound features display developmental plasticity, we used extracellular multichannel recordings in the mouse A1 (Fig. 1A) and characterized neuronal responses to FMS. We chose a set of FMS spanning in a logarithmic scale the range of 2–48 kHz in increasing (upward sweep) or decreasing (downward sweep) frequency (Fig. 1B, Supplementary Fig. 1A). Upward and downward sweeps were played at 60 dB SPL at 6 different speeds and were repeated 15 times (example recording in Supplementary Fig. 1B). Responses to pure frequency tones were also recorded and analyzed to determine the FRA of each MU recording site (see Methods). The BF, defined as the frequency triggering the strongest response across all tone levels, was then extracted from the FRA. Given the tonotopic organization of A1 (Stiebler et al. 1997; Hackett et al. 2011), we identified this primary cortical region through its increase in BF from the most caudal to the most rostral shaft of our 4-shaft multielectrode array recordings (see Methods, Supplementary Fig. 1C). The topographic organization of A1 was confirmed by plotting the mean BF as a function of topographic position within A1 (Supplementary Fig. 1C,D) (Barkat et al. 2011).

We then analyzed the responses to FMS and observed a striking difference in the temporal profile of responses between upward and downward sweeps. For a MU with a low BF, responses to +75 oct/s FMS reached their peak amplitude right after FMS onset, whereas responses to −75 oct/s FMS took much longer to reach their peak. The opposite was observed for a MU with a high BF (Fig. 1C). This observation was confirmed at the population level, where the upward and downward sweep peak latencies for MUs with low or high BF were significantly different (Fig. 1D,E; n = 102, P < 0.0001; n = 86, P < 0.0001, 2-way ANOVA for 4–8 kHz and 16–32 kHz BF, respectively). MU with intermediate BF responded more similarly to upward and downward sweeps (Fig. 1D,E; n = 123, P = 0.2559, 2-way ANOVA for 8–16 kHz BF). These results indicate that responses to FMS are correlated with BF and are thereby topographically organized along the tonotopic axis of A1, as confirmed by the quantification of peak latency difference as a function of the MUs position in A1 (Supplementary Fig. 1E). However, the temporal profile of an FMS response is only partially predictable based on how the FMS frequencies interact with the FRA. Indeed, when plotting peak latencies as a function of the MU’s BF temporal presentation in the FMS, responses to upward and downward sweeps were not symmetrically distributed along the unity line as would have been expected if their temporal profiles would have been a direct consequence of the neurons BF (Supplementary Fig. 2A; linear fit for +75 oct/s FMS responses: 0.26× + 33, r² = 0.055; linear fit for −75 oct/s FMS response: 1.08× + 12, r² = 0.48; a slope of 1 would have been expected if the MUs FRA was the only factor determining the FMS temporal profile). This asymmetry could not be explained by onset latencies to FMS (Supplementary Fig. 2B) nor pure tones (Supplementary Fig. 2C), suggesting that some intracortical mechanisms are involved and that FMS responses have emerging properties distinct from the neuron FRAs.

The topographic organization of sweep direction selectivity has been described previously with direction selectivity indexes (DSI, see Methods) in terms of response firing rate in a specific time window (Fig. 1F,H; DSI rate) (Zhang et al. 2003; Insanally et al. 2009; Trujillo et al. 2011; Issa et al. 2017; Sollini et al. 2018), of peak amplitude (Fig. 1G; DSI peak) (Razak et al. 2008; Kuo and Wu 2012) or its chi²-based values (Supplementary Fig. 6D; chi² DSI peak) (Insanally et al. 2009). The mechanisms behind these DSIs are not clear. One possible explanation is that they are a consequence of the asymmetric temporal profiles of responses to FMS of opposite directions. Indeed, most previous studies measured firing rates during the FMS stimulation for the calculation of DSI (DSI (short)). As can be seen from the peristimulus time histograms (PSTH, Fig. 1C,D), this ignores the spiking activity arriving after the stimulation has stopped. The FMS giving rise to a faster response will therefore result in a higher rate than the one with a slower response. Similarly, an FMS stimulation giving rise to a faster response will result in a higher peak amplitude than one whose response is slower and more spread out in time. Thus, the DSI might reflect the temporal profile differences between upward and downward FMS. This, together with the fact that the peak latency difference correlates more strongly with BF (Supplementary Fig. 1K, r² = 0.43) than DSI peak (Supplementary Fig. 1F, r² = 0.21), DSI rate (Supplementary Fig. 1G, r² = 0.13), or DSI rate measured in a shorter time window (DSI rate (short), see methods; Supplementary Fig. 1H, r² = 0.14), led us to use the difference in peak latency as a measure of FMS responses and their plasticity for the rest of the study.

We then asked whether the topographic organization of peak latency differences was specific to the speed of 75 oct/s (Fig. 1A–E) or whether it could be generalized to sweeps of different speeds. By plotting the PSTH of responses to 15 oct/s upward and downward sweeps, we concluded that peak latency is a robust parameter to distinguish responses to sweeps of different directions (Fig. 1I). This could be generalized to all FMS speeds, with a negative correlation between absolute peak latency difference and sweep speed (Fig. 1J).

Finally, we examined whether the topographic organization of FMS response timing differences could be observed in the AAF, another tonotopically organized cortical region receiving direct inputs from the auditory thalamus (Stiebler et al. 1997). Recordings from this region, identified with an increase in BF from the most ventral to the most dorsal shaft of our electrode arrays (Fig. 1K), indicated that responses to upward and downward sweeps cannot be distinguished as easily as in A1 (Fig. 1L,M, Supplementary Fig. 1I,J). This resulted in lower r² values as well as reduced slopes of the linear regressions (Supplementary Fig. 1K; n_AAF = 140 MU,  = 0.086, slope_A1 = 7.5 ms/oct; n_A1 = 363 MU,  = 0.43, slope_A1 = 17.8 ms/oct) and indicates a reduced topographic organization of peak latency differences in AAF compared with A1. This reinforces the observation made previously that FMS response timing differences are not only a direct consequence of tonotopy. Our data also indicate that FMS responses are distinct in A1 and AAF. They complement previous findings demonstrating that A1 and AAF process temporal information differently (Linden et al. 2003; Christianson et al. 2011; Solyga and Barkat 2019).

The Critical Period for FMS in Mouse A1 is P31–P38

A1 tonotopy can be modified following passive exposure to a pure tone during the time window from P12 to P15 (Barkat et al. 2011). We asked whether such developmental plasticity is also present for FMS passive exposure. We used in vivo extracellular recordings in adult mice reared in a standard acoustic environment (ctrl) or in mice exposed to a downward sweep of 75 oct/s during different time windows (FMS exp). Inspired by a previous study that found plasticity up to the sixth postnatal week (Insanally et al. 2009), we chose 1-week long time windows starting at P27, P31, or P39. Although exposure from P27–P35 or P39–P47 did not change peak latency differences compared with control mice (Fig. 2A; P27–P35, n = 4 mice, 28, 72, 93 MU; P39–P47, n = 5 mice, 56, 76, 72 MU for 4–8, 8–16 or 16–32 kHz BF range, respectively), exposure from P31 to P38 significantly changed it for responses with low and middle BFs (Fig. 2A; P31–P38, n = 6 mice, 51, 131, 140 MU; comparison with ctrl: P = 0.0001, 0.0011, and 0.5101 for MU of 4–8, 8–16, or 16–32 kHz BF, respectively, 2-way ANOVA).

We then examined whether the 7-day time window was the duration required for the maximum plasticity to happen. Exposing mice to FMS for 6 days (P32–P38) resulted in a smaller, although not significant, shift in peak latency difference than the 7-day exposure (Fig. 2B; n = 4 mice, n = 46, 74, 50 MU, P = 0.3651, 0.9830, 0.9448, 2-way ANOVA). Conversely, exposing mice to FMS for 8 days resulted in no further decrease in peak latency difference compared with that observed with the 7-day exposure (Fig. 2B; n = 8 mice, 38 176, 79 MU, P = 0.999, 0.7322, 0.3323, 2-way ANOVA). These results demonstrate that the critical period for FMS in mice is between P31 and P38, much later than the critical period for pure tones.

To address whether this late critical period could be an extension of the pure tone critical period, we first quantified responses to pure tones following FMS exposure from P31 to P38. The results demonstrate that neither the mean BF within each topographic region of A1 (Supplementary Fig. 3A) nor the bandwidth of FRAs was affected by the exposure, whether quantified for MUs (BW10, Supplementary Fig. 3B; BW at 60 dB SPL, Supplementary Fig. 3C) or for single unit clusters (SUs, Supplementary Fig. 3G–I for BF in the range of 4–8 kHz). We then showed that mice exposed to a pure tone (7 kHz; Supplementary Fig. 3D, n = 6 mice) or FMS (−75 oct/s; Supplementary Fig. 3E,F, n = 5 mice) during the critical period for pure tones have FMS response timing differences similar to control mice. Together, these results suggest that the time window from P31 to P38 displays a form of plasticity that is distinct from the critical period for pure tones.

To understand whether this plasticity was unique to downward sweeps or could be generalizable to the other sweep direction, we exposed mice to upward sweep during the same time window. This exposure lead to similar changes in FMS response timing differences (Supplementary Fig. 4A), allowing us to conclude that P31–P38 is the critical period for FMS and not for downward sweeps only.

We next examined how a passive sweep exposure during the critical period changed the response profile of auditory units. Comparing responses to upward and downward sweeps revealed that exposure to downward sweeps during P31–P38 changed the temporal profile of responses to downward sweeps only (Fig. 2C for responses to 75 oct/s FMS, Supplementary Fig. 5A,B for responses to 15 oct/s FMS). Peak latencies of responses to the downward (−75 oct/s) but not the upward sweep (+75 oct/s) were significantly shorter for exposed than for control mice (Fig. 2D,E; orange bars, P = 0.0001, 0.0001, 0.0197, 2-way ANOVA). Interestingly, similar changes were observed for exposure to upward sweeps (Fig. 2D,E; red bars, P = 0.0001, 0.0058, 0.9992, 2-way ANOVA), denoting that this acceleration did not depend on the direction of the overexposed sweep. This also reveals that changes in timing differences between upward and downward FMS upon sweep exposure (Fig. 2A,B, Supplementary Fig. 4A) are mainly due to an accelerated response to downward sweeps. The peak latency decrease was stronger for responses with low BF, those whose responses to downward sweeps were the slowest in control animals and therefore more susceptible to response acceleration. The fact that the timing shift was observed for one sweep direction but not the other rules out a possible shift in frequency tuning, confirming our previous results indicating that this plasticity is unique to FMS responses and does not affect pure frequency tone response properties (Supplementary Fig. 3A–C). In addition, the comparison of peak latencies of downward FMS responses as a function of the latency of the MU’s BF played in the sweep showed an accelerated response to MUs with a BF arriving later in the sweep in exposed (Supplementary Fig. 4B,C) compared with control mice (Supplementary Fig. 2A; for MU with a BF arriving after 30 ms in the −75 oct/s FMS, P < 0.0001 between control (n = 159) and −75 oct/s exposed mice (n = 107), P = 0.0499 between control and +75 oct/s exposed mice (n = 86), unpaired t-test). Together, this suggests that the plasticity does not influence the speed at which the sound responses reach A1 but rather the integration of the different frequencies present in the sweep. Based on this analysis of FMS response temporal profiles, we speculate that the intracortical connections from high BF to low BF, rather than subcortical connections, are strengthened by the passive FMS exposure.

FMSs can be characterized by sweep direction and sweep speed. We next asked whether mice exposed to a sweep of a certain direction at a certain speed would modify responses to that specific speed only, or whether the changes would generalize to speeds other than the one they were exposed to. We found that peak latency differences were strongly reduced for low BF MUs independently of sweep speed (Fig. 2F). Consistent with the idea of a change in intracortical connections, this would indicate that it is the direction rather than the speed of the exposed sweep that is determinant in this critical period.

Finally, we asked whether this plasticity could also be revealed when responses to FMS were quantified in terms of DSI instead of response timing differences. Although less stringent, the different ways of measuring DSI (DSI rate, DSI rate (short), DSI peak, or chi²-based DSI peak) showed the same trend as the FMS response timing differences (Supplementary Fig. 6): the difference between sweeps of opposite directions is decreased upon passive FMS exposure, for low BF neurons in particular.

FMS response timing differences are stable through postnatal development

We then asked whether this time window of enhanced plasticity was paralleled by changes in the FMS response timing differences during development. We compared responses with upward and downward 75 oct/s FMS from P20 to adulthood in mice exposed to a standard acoustic environment (Fig. 3A). We did not observe any significant change in peak latency differences around the critical period (Fig. 3B for the peak latency difference in the whole MU population, Fig. 3C for the PSTH of MU with 4–8 kHz BF at P30 and P40). These results demonstrate that FMS response timing differences are already present before the critical period starts and that they are stable in animals raised in a standard acoustic environment. The results also suggest that the developmental changes allowing for the critical period plasticity, if any, are subtle and cannot be observed in mean responses of the whole neuronal population.

The Number of PV⁺ Neurons in L4 Decreases During the Critical Period for FMS

Previous studies have shown that the maturation of inhibition, and of PV⁺ neurons in particular, is key to triggering critical periods for plasticity (Hensch 2005, 2014; Kuhlman et al. 2013; Takesian et al. 2018; Vickers et al. 2018). We asked whether a similar mechanism could explain the critical period for FMS by quantifying the number of PV⁺ cells through development. Using immunohistochemistry and antibody staining of PV⁺ cells, we counted the number of cells in the different A1 layers in P20, P30, P40, and P50 mice and normalized them to the number of DAPI⁺ cells in the same regions. The main thalamorecipient layer, defined as L4, was identified with an enrichment of VGlut2 staining (Tatti et al. 2017b; Chang and Kawai 2018) (Fig. 4A,B). Surprisingly, we found a significant decrease in the number of PV⁺ neurons in the thalamorecipient layer during the critical period, between P30 and P40 (Fig. 4C–E; n = 26, 42, 28, 28 slices for P20, P30, P40, and P50 mice, respectively. ^***P < 0.0001 between P30 and P40 in L4, 2-way ANOVA). This decrease between P30 and P40 was not paralleled by a change in the whole population of cells, as quantified by DAPI⁺ cell stainings (Fig. 4F). Although PV⁺ cells can be excitatory, the majority of them have been shown to be inhibitory and to represent the biggest population of cortical inhibitory neurons (Markram et al. 2004; Tremblay et al. 2016). Therefore, the decrease in the number of PV⁺ neurons could lead to a change in the excitation/inhibition ratio and also possibly explain the plasticity to the passive FMS exposure (Fagiolini et al. 2003, 2004). Our data can however not tell whether the decrease happens closer to the onset or offset of the critical period and therefore whether it could be related to triggering or to reducing the enhanced plasticity.

FMS Responses of L4 Regular Spiking Neurons Increase Transiently During the Critical Period

Would this change in PV⁺ population be paralleled by changes in neuronal activity around the critical period? In order to differentiate responses of PV⁺ cells and regular spiking cells as a function of cortical depth, we spike sorted our data to SU clusters (see methods) and quantified responses across development. We isolated neurons located between 350 and 550 μm below the pia surface as putative L4 neurons (Chang and Kawai 2018). Expanding on the PV⁺ cell counting results (Fig. 4), we estimated the amount of putative PV⁺ neurons present in our SU population by measuring the peak-to-trough (p2t) time of the SU waveforms. We observed the expected bimodal distribution of p2t time and approximated the number of PV⁺ neurons by the number of narrow spiking neurons (Lima et al. 2009). This revealed a decreased proportion of narrow spiking SUs (p2t < 0.6 ms) from P30 to P40 (Fig. 5A–C), which lines up with the decreased number of PV⁺ neurons we found at the anatomical level around the critical period for FMS (Fig. 4).

Furthermore, the quantification of L4 regular spiking SU (p2t > 0.6 ms) responses showed that their spike rates to FMS stimulation increased slightly from P30 to P40 (Fig. 5D, n = 162, 176 for L4 P30, P40 SU; P = 0.0019, 2-way ANOVA). Although this increase was small and did not linger at later developmental stages, it was not observed in responses to pure tones (Fig. 5E, P = 0.9999) nor in the spontaneous activity (Fig. 5F, P = 0.9387) of these SUs. This indicates that the changes happening between P30 and P40 might be particular to FMS processing. The same analysis for the whole SU population did not show any developmental changes, either in terms of FMS spike rates (Fig. 5G), FMS peak amplitudes (Fig. 5H), or spontaneous activity (Fig. 5I). Taken together, A1 responses are mostly stable from P20 until adulthood, with a transient and small increase in the firing rate of L4 regular spiking SUs to FMS, but not to pure tone or spontaneous activity, during the FMS critical period.

Preventing the Decrease of L4 PV⁺ Cells Through WN Exposure Delays the Critical Period

To probe whether the observed decrease in PV⁺ neurons could be the trigger for the critical period for FMS, we sought to manipulate these cells and determine the effect on the plasticity. As it is technically challenging to control this specific subpopulation within L4 PV⁺ neurons, we used a natural way to manipulate and delay the normal development of the auditory cortex and asked whether this would have any consequences on the critical period. Previous work showed that exposing mice to continuous WN, thereby masking most structured auditory inputs, could lead to a delay in A1 maturation (Chang and Merzenich 2003; Chang et al. 2005; Liang et al. 2018). We thus exposed mice to WN from P30 to P40 and compared the percentage of PV⁺ neurons in these mice with those in mice reared in standard acoustic environment (Fig. 6A). The quantification of PV stained slices showed that P40 WN exposed mice had a significantly higher number of PV⁺ cells than did controls, one that was similar to the number in P30 mice (Fig. 6B; n = 28, 35 slices in P40 control or WN exposed mice, respectively. ^***P < 0.0001, 2-way ANOVA).

We then asked whether delaying the decrease of L4 PV⁺ cells with WN had also an effect on the critical period. We exposed mice to WN from P30 to P40 and then to FMS (−75 oct/s) from P40 to P48 (Fig. 6C). If the critical period were to be delayed by the WN exposure, the following FMS exposure is expected to have an effect on the peak latency difference (Fig. 2A, P39–P47 case). Our prediction was confirmed by our results (Fig. 6D; n = 102, 155 for ctrl and WN + FMS MU with 4–8 kHz BF; P < 0.0001, 2-way ANOVA). We also verified that mice returning to a standard acoustic environment after WN had peak latency difference distributions similar to those in control mice (Fig. 6D, WN + ctrl, P = 0.3836, 2-way ANOVA). Taken together, our results offer more evidence that the decrease in L4 PV⁺ neuron population is correlated with the critical period for FMS. They also suggest that a change in L4 excitation/inhibition ratio is a potential mechanism for the presence of this critical period.

Discussion

We identified a critical period for FMS weeks later than the critical period for pure tones in the mouse A1. The cortical plasticity following 1 week passive exposure to FMS could be detected by a change in the temporal profile of FMS responses. A decrease in L4 PV⁺ cells and a correspondingly subtle increase in firing rate of regular spiking neurons in response to FMS stimulation both support the suggestion that this critical period reflects a developmental change in the excitation/inhibition ratio in the cortical neural circuits engaged by FMS. The dependence of the timing of critical periods on stimulus complexity has strong implications for the understanding of developmental plasticity, from birth until adulthood.

Responses to FMS of opposite directions have classically been characterized by DSIs. The topographic organization of DSI is debated, as some studies describe it clearly (Zhang et al. 2003; Insanally et al. 2009; Kuo and Wu 2012) while others denote its absence (Lui and Mendelson 2003; Atencio et al. 2007; Trujillo et al. 2011; Sollini et al. 2018). The reason for these contradictory results might be related to the way FMS responses were quantified. While direction selectivity has previously been measured in terms of spike rates in various time windows, or in terms of response peak amplitudes, we added the analysis of the temporal profile of the response and quantified the difference between upward and downward sweeps as the peak latency difference (Fig. 1). It would be interesting to test whether this way of characterizing the difference in responses between upward and downward sweeps would settle the controversy and confirm its topographic organization in all studies. Our results suggest that the temporal profile of the response can also be used to compare responses with sweeps of opposite direction. It is possible that rates or amplitudes are used in a manner complementary to this temporal representation to encode other features of complex sensory inputs (Lu et al. 2001; Bieler et al. 2017).

The analysis of the temporal profile of FMS responses allows us to suggest a mechanistic explanation of this late critical period. Passive exposure to FMS accelerates the peak responses to downward sweeps (Fig. 2E), whereas responses to upward sweeps are not affected (Fig. 2D). This suggests that the intracortical connections from high to low BF neurons become faster upon overexposure to FMS, independently of the direction of the exposed FMS. Overexposure to sweep could induce an increased activation of these connections that therefore become faster due to stronger or more numerous excitatory connections between high and low BF neurons. A possible explanation for the accelerated responses to downward sweeps only, and not to upward sweeps, could lie in an inherent asymmetry of connections in the caudo-rostral vs rostro-caudal direction of A1. For example, the different onset latencies of tone responses across the tonotopic axis (Supplementary Fig. 2C) (Solyga and Barkat 2019)—high BF neurons receiving inputs faster than low BF neurons—could make the responses to downward FMS more susceptible to acceleration than upward FMS. Alternatively, the intrinsic properties of pure tone soundwaves—their sinusoidal nature including periodicity of lower (f/2, f/4 etc.) but not higher frequency components—could account for this asymmetry.

A closer look at the temporal profile of low BF responses to downward sweeps indicates a biphasic response, with a first earlier peak likely reflecting sound onset with little frequency selectivity, and a second later peak reflecting the tuning of the neurons to the frequencies presented during the FMS (Fig. 2C, Supplementary Fig. 5A). The presence of this biphasic response does not seem to be due to two different populations of neurons, as most SUs show such profile (Supplementary Fig. 5C). It does not seem to be dependent neither on the depth of the SUs (Supplementary Fig. 5D) nor on their tuning width (Supplementary Fig. 5E). A similar biphasic response can be observed in the temporal profile of high BF responses to upward sweeps. Such observations can only be made in responses where the untuned and tuned responses do not overlap. The measure of the peak latency in the whole stimulation window, as done in this study, corresponds to the latency of the strongest of these two peaks. Upon FMS exposure during the critical period, the first peak increases its amplitude slightly—although not significantly—compared to the second peak (Supplementary Fig. 5D, P = 0.3808, unpaired t-test). The latencies of both peaks also decrease slightly, but only the latency of the peak over the whole FMS stimulation window does so significantly (Supplementary Fig. 5G–H, P = 0.9314, 0.1771, 0.0077, 2-way ANOVA). A possible interpretation of these observations is that FMS exposure leads to an increase in connection strength for all frequencies present in the sweep and therefore affects the first untuned response slightly more than the second tuned response.

If passive exposure to FMS accelerates the peak responses to downward FMS, it does so only during the critical period and not earlier nor later. But what is particular during this time window for allowing an enhanced plasticity? Our immunohistochemical experiments suggest that PV⁺ neurons may play a key role. In the auditory cortex, PV⁺ neurons have been shown to provide fast feedforward inhibition on excitatory cells (Li et al. 2014). Sweep exposure during the observed pruning of PV⁺ cells could decrease such fast feedforward inhibition and prevent adequate regulation of fast inputs, thereby degrading the encoding of FMSs into distinct sequences and making the difference between sweeps of opposite direction less clear. More generally, inhibition has been proposed to be a major determinant of FMS direction selectivity (Zhang et al. 2003; Kuo and Wu 2012), but that finding has been questioned by a more recent pharmacogenetic study indicating that silencing PV⁺ neurons has no effect on DSI (Sollini et al. 2018). Whether inhibition plays an important role in FMS direction selectivity or not might be independent of the role it plays in controlling the critical period. Here again, previous work has demonstrated that inhibition controls other critical periods in the visual (Fagiolini et al. 2004) and auditory systems (Kuhlman et al. 2013; Takesian et al. 2018). In both cases however, the critical periods were triggered by an increase in inhibition and not by a decrease in inhibition as suggested by a decrease in PV⁺ cells number and a transient increase in firing rate of regular spiking neurons described in our study. However, both a decrease in PV⁺ neurons and an increase in regular spiking neuron firing rate do not absolutely imply a decrease in inhibition or an increase in excitation/inhibition ratio. First, some PV⁺ neurons are glutamatergic, and our immunohistochemical experiments do not allow us to distinguish them from the PV⁺ neurons that are GABAergic. Second, regular spiking neurons are mainly composed of excitatory neurons, but interneurons other than narrow spiking neurons are also regular spiking, and our classification of cell type based on waveshape cannot isolate excitatory neurons only. Finally, a decrease in PV⁺ neurons has been shown in some cases to lead to a strengthening of inhibition (Tatti et al. 2017a). Altogether, although our results suggest that the excitation/inhibition ratio could be increased during the critical period, they do not demonstrate that this is really the case and other mechanisms could be at play. A detailed characterization of the subthreshold glutamatergic and GABAergic responses to FMS would be informative.

Our work raises the question as to whether it is a change in the excitatory/inhibitory ratio per se—it being positive or negative, and not an increase in inhibition only, that triggers an opportunity for change in a neural circuit, and hence a corresponding critical period. Excitatory/inhibitory balance refinement has been shown to play a role in the response to pure frequency tones earlier in development (Chang et al. 2005; Dorrn et al. 2010; Sun et al. 2010). The developmental changes described in our work could be related to a similar refinement, but for a different sound feature and for a different developmental time window. On the other hand, it might be that changes of the excitation/inhibition ratio in one direction or the other might be important for the specificity of the exposed sensory feature. While an increase in inhibition has been suggested as a model to increase synchrony and thereby allow ocular dominance plasticity in the visual system (Hensch 2005), a decrease in inhibition—and synchrony—might be important to bind asynchronous components of a sound, like the different frequency components of FMS. Alternatively, it might also simply be that a transient increase in firing rate in regular spiking neurons accentuates the overactivation of the connections engaged by FMS upon repeated exposure and thereby makes the response faster.

Among the different inhibitory cell types, our study focuses on the PV⁺ neuronal subpopulation because it is the largest group of interneurons, it has a strong influence on postsynaptic targets by inducing perisomatic inhibition (Markram et al. 2004), and it is the subtype that has been mostly involved in other studies of critical periods (Hensch 2005, 2014; Kuhlman et al. 2013; Takesian et al. 2018; Vickers et al. 2018). However, this does not imply that other subtypes do not play a role as well. For example, somatostatin (SOM) expressing interneurons have been shown to change their excitability during visual cortex development (Lazarus and Huang 2011) or to regulate spiny stellate cells in the developing thalamorecipient layer of the somatosensory cortex (Marques-Smith et al. 2016). The disinhibitory circuit containing vasoactive intestinal peptide (VIP) and SOM neurons has been shown to regulate plasticity in the adult visual cortex (Fu et al. 2015). L1—but not VIP—inhibitory neurons influence developmental plasticity in the auditory cortex by modulating thalamic drive onto L4 PV⁺ neurons (Takesian et al. 2018). Further studies will have to unravel how subpopulations of interneurons other than the PV⁺ neurons studied here are involved in this late critical period.

The results of our immunohistochemical experiments are based on the quantification of cells for which the PV fluorescence exceeded a certain fixed threshold (Figs 4 and 6B). They do not allow us to conclude whether the decrease in PV⁺ cells is due to a loss of cells or to a decreased PV immunoreactivity, nor whether this decrease is affecting glutamatergic and GABAergic PV⁺ cells equally. However, if one can assume that the spike waveshape is not influenced by the amount of PV in a cell, then the decreased proportion of narrow spiking SU (Fig. 5C) would indicate that it is a decrease in the number of GABAergic PV⁺ cells rather than the PV immunoreactivity that is affected in this critical period. One could then speculate whether the PV⁺ cells that disappear have their role replaced by the cells that remain in the circuit in a refinement step of the maturing cortex. This would result in a pool of PV⁺ neurons that remain low until adulthood, but in a transient increase in firing rates until the remaining PV synapses have stabilized, as observed in our results. The instability during this refinement phase could enable the auditory environment to modify circuits more easily than in earlier or later time windows, thereby delineating the critical period. In this context, a change in the dynamic and plasticity of these intracortical synapses could also play a role (Miao et al. 2016).

The sweep exposure modifies responses to one direction only, but to all FMS speeds tested (Fig. 2F). This could suggest, as previously indicated in the rat auditory cortex (Ricketts et al. 1998), thalamus (Lui and Mendelson 2003) and inferior colliculus (Lee et al. 2002), that speed and direction are processed independently by the brain and can therefore be regarded as independent sound features despite the fact that they are present in the same sound. These observations also reveal that P31–P38 is the critical period for FMS direction only and not for FMS speed. Given that previous studies indicated significant changes in speed tuning before P30 (Brown and Harrison 2011; Carrasco et al. 2013), it would be relevant to determine whether an earlier critical period for the speed of FMS exists.

Whether the processing of FMS during the described critical period is related to any changes in the production of FMS sounds is not known. FMS components of mouse vocalizations have been previously studied, and upward and downward sweeps have been recorded in P30 C57BL6/J mouse vocalizations (Lahvis et al. 2011). In CBA mice, a developmental change in the proportion of up- or downward FMS has been reported: pups up to P13 produce both downward and upward FMS equally, whereas P100 adults produce more upward than downward FMS (Grimsley et al. 2011). Whether these changes are related to the sound perception and do happen between P30 and P40 remain to be investigated.

What could such a critical period for complex sounds be good for? In the particular unnatural settings of our experimental design, having faster responses to downward sweeps might not lead to any advantages, especially since the overexposed sweeps are not linked to any behavioral relevance or meaning. In general however, one of the main advantages of critical periods could be to allow for an anticipated response to common sounds to be appropriately fitted to the environment in which the brain matures. The behavioral consequences of a change in FMS response timing differences will be important to understand. It is known from human studies that a poor judgment of sweep direction is observed in amusia and is leading to decreased linguistic and emotional judgments (Altmann and Gaese 2014). Inspired by translational approaches aimed at increasing pitch perception (Gervain et al. 2013), one could speculate whether an extended exposure to sweeps, combined with a subtle transient decrease in cortical inhibition, could be used as a rehabilitation strategy for people suffering from deficits in language or music processing like cochlear implanted adults.

Funding

Lundbeck Foundation (R139-2012-12375 to T.R.B.); Swiss National Science Foundation (ERC Transfer grant CRETP3-166735 to T.R.B.).

Notes

We thank Daniel Polley for assistance and discussions at the initial phase of the project. We thank Georg Keller, Hirofumi Morishita, and Gioia De Franceschi for comments and discussions on the article. We thank Nebojsa Bozanic for analytical assistance. We thank the Imaging Core Facility of the Biozentrum for their help with the imaging and quantification of the immunohistochemical experiments. Conflict of Interest: None declared.