Mechanical Regulation of Neurite Polarization and Growth: A Computational Study

Abstract

The densely packed microtubule (MT) array found in neuronal cell projections (neurites) serves two fundamental functions simultaneously: it provides a mechanically stable track for molecular motor-based transport and produces forces that drive neurite growth. The local pattern of MT polarity along the neurite shaft has been found to differ between axons and dendrites. In axons, the neurons’ dominating long projections, roughly 90% of the MTs orient with their rapidly growing plus end away from the cell body, whereas in vertebrate dendrites, their orientations are locally mixed. Molecular motors are known to be responsible for cytoskeletal ordering and force generation, but their collective function in the dense MT cytoskeleton of neurites remains elusive. We here hypothesized that both the polarity pattern of MTs along the neurite shaft and the shaft’s global extension are simultaneously driven by molecular motor forces and should thus be regulated by the mechanical load acting on the MT array as a whole. To investigate this, we simulated cylindrical bundles of MTs that are cross-linked and powered by molecular motors by iteratively solving a set of force-balance equations. The bundles were subjected to a fixed load arising from actively generated tension in the actomyosin cortex enveloping the MTs. The magnitude of the load and the level of motor-induced connectivity between the MTs have been varied systematically. With an increasing load and decreasing motor-induced connectivity between MTs, the bundles became wider in cross section and extended more slowly, and the local MT orientational order was reduced. These results reveal two, to our knowledge, novel mechanical factors that may underlie the distinctive development of the MT cytoskeleton in axons and dendrites: the cross-linking level of MTs by motors and the load acting on this cytoskeleton during growth.

Significance

A fundamental question of neurobiology is how the distinctive polarity profile of the microtubule array in neuronal cell projections establishes. We present computer simulations of cylindrical microtubule bundles cross-linked and powered by molecular motors; the bundles were subjected to an opposing load that resulted from actomyosin contractility in the surrounding cytoskeleton. The level of motor-induced connectivity between the microtubules and the load are found to be two determining factors of the bundles’ growth and structural characteristics. Highly connected microtubule motor bundles efficiently expanded and sorted, forming uniformly polarized bundles, as found in axons. In contrast, loosely connected bundles failed to expand and sort, remaining short and mixed, as in dendrites. These calculations provide important insight into the mechanical regulation of neuron development and growth.

Introduction

Axons and dendrites (together referred to as neurites) are the mature projections of neurons that transmit and receive information in the form of electrical signals. In contrast to dendrites, which remain short (∼100 μm long) and highly branched, axons may grow millimeters to meters long to reach their target site(s). These extreme axonal dimensions require sophisticated mechanisms that drive axonal growth and molecular transport to ensure proper supply while navigating through the complex extracellular environment. Neurites comprise a densely packed microtubule (MT) cytoskeleton that functions as a substrate for the transport of newly synthesized proteins, organelles, and RNA by molecular motor proteins (1). The MTs are polar filaments, having a rapidly polymerizing plus end and a more stable minus end (1). Molecular motors such as kinesins and dyneins recognize this polarity and preferentially move in one direction on the filament. In axons, most MTs orient uniformly with their plus ends away from the cell body (enabling efficient transport away from and toward the cell body), whereas in dendrites, this structural organization is not conserved. In vertebrates, the dendritic MT array is locally mixed with MTs pointing in either direction (2,3), whereas in Drosophila melanogaster and Caenorhabditis elegans, the MTs point their minus ends away from the cell body (“minus end out”) (4,5).

Apart from serving as tracks for directed molecular transport, the MT cytoskeleton also plays a part in generating pushing forces that drive neurite outgrowth (6). In addition to polymerization forces exerted by peripheral MTs at the growth-cone (GC) leading edge, experiments indicate that MTs also contribute to growth via their interaction with molecular motors, which slide the MTs along the membrane (7,8) or past each other (9,10) to eventually extend the MT cytoskeleton forward (7,9, 10, 11, 12). In particular, experiments have identified dynein (7,11,12) and kinesin-1 (7, 8, 9) to be essential for neurite outgrowth. Common to both motors is their tendency to dimerize asymmetrically, with a cargo domain on one end of the molecule and a moving domain on the other; this structural asymmetry has been shown to be essential for the motors ability to expand parallel bundles of MTs (see (13) and references therein). An important aspect of the molecular motors’ directional gliding on the filaments is that the forces they apply lead to filament sorting. The minus-end-directed motor dynein has been suggested to sort neuronal MTs by sliding plus-end-out MTs away from the cell body and minus-end-out MTs back into the cell body, thereby establishing the observed uniform MT polarity of the axon (7,10,14). In contrast, attenuated dynein activity and/or enhanced kinesin activity have been proposed to explain the mixed MT polarity of vertebrate dendrites (7,8,10,15).

The molecular-motor-generated forces that push the MTs into the GC are opposed by an actively generated load arising from the actomyosin cytoskeleton that envelops the MTs (see Fig. 1; (11,12,16, 17, 18, 19, 20)). Consistently, inhibition of myosin II motor activity (12,21) or interference with the neurites’ actin cytoskeleton (22, 23, 24) has been shown to facilitate neurite outgrowth, whereas depletion of MTs from the neurite core or inhibition of dynein or kinesin-1 molecular motors resulted in axon retraction and impaired growth (9,11,12,25,26). Because, however, F-actin and myosin II are also implicated in GC motility, their inhibition also yielded opposite effects on neurite outgrowth (27,28). The mechanical force balance in the neurite cytoskeleton has also been studied by applying external pulling forces on the cell membrane or GCs of emerging neurites. Threshold forces of ∼$1000\mathrm{p}\mathrm{N}$ in PC12 cells (29,30) and 15–100 pN in chick forebrain neurons (31) have been reported to facilitate stable axon outgrowth, presumably reflecting the load that normally suppresses the extension and growth of neuronal processes.

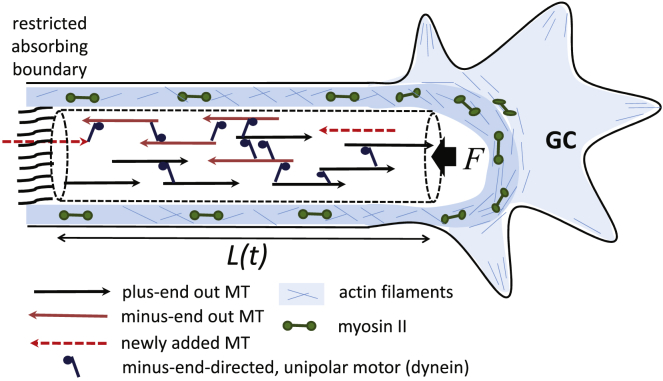
Figure 1.

Schematic illustration of major elements considered in the model. On the left is the neurite shaft comprising the cross-linked MT bundle that expands as asymmetric (unipolar) motors (dynein) slide the filaments. Filaments reaching the left boundary get absorbed into the cell body with some probability, which accounts for the restricted permeability of the entangled meshwork of cytoskeletal filaments (and organelles) present at the widened entry to the cell body (16,36). The MT bundle is subjected to a restoring (normal) force F on the right boundary arising from the actomyosin cytoskeleton enveloping the MTs (17,18,54). New MTs (dashed arrows) of either polarity enter arbitrary points in the bundle with a frequency ω_in. Adjacent MTs may or may not be cross-linked by motors. The probability that an overlapping region between adjacent MTs be cross-linked by motors is given by χ. To see this figure in color, go online.

Previous theoretical models (8,10,13,32,33) and experiments (10,12,34,35) have demonstrated that molecular motors can sort unorganized MT bundles as well as generate expansive forces against a resisting load. However, the effects of the load on the MT array expansion and sorting during growth are poorly understood. We here present a computational study of the consequences of the load on expanding bundles of MTs that are cross-linked by molecular motors and identify an important factor that enters the force-balance calculation: the level of MT connectivity by motors (governed by χ, below). We demonstrate that these two factors (force and MT connectivity) play important roles in dictating the structural and growth characteristics of the MT bundles. We define the local MT polarity along the bundle axis by the local excess of plus-end-out MTs over minus-end-out ones. Bundles subjected to stronger loads are shown to require more filaments in a cross section to overcome the load and thus become wider and extend more slowly. With a higher level of motor connectivity between the filaments, the bundles narrow in cross section and grow more quickly, whereas the MTs efficiently sort to form extended, thin, and uniformly polarized bundles, as found in axons. In contrast, loosely connected bundles fail to organize and expand against a load, and result in short, wide, and locally mixed bundles, as found in vertebrate dendrites (2,3). We also demonstrate that the load may play a role in clearing the neurite entry the from “ill”-oriented minus-end-out MTs that accumulate in that region because of their retrograde transport along the neurite shaft.

Materials and Methods

Cylindrical bundles of MTs, cross-linked by minus-end-directed unipolar molecular motors (e.g., cytoplasmic dynein), were simulated with one end (the distal GC end) subjected to an opposing normal load, F, and the other end containing an entangled meshwork of cytoskeletal filaments (16,36) (and organelles) that restrict MT absorption into the cell body while mechanically supporting the load. A similar algorithm has previously been used to investigate the sorting dynamics of force-free bundles (32) and then extended to investigate the expansion dynamics and force generation of parallel bundles using an impermeable left boundary (13). The impact of a load on the growth and establishment of the MT polarity profile along neurite-like MT-motor bundles, which are subjected to a load on their one end and open to MT exchange on their other end, has not yet been studied. The simulation algorithm, including the implementation of the boundary conditions, and the choice of parameters are described in detail in the Supporting Materials and Methods; we here outline the methodology and its major assumptions.

Neuronal MTs vary in length, and their length distribution varies broadly between neuron types, animal species, and developmental stages (37): a range between 1 and 30 μm has been reported for cultured rat hippocampal neurons (38), between 3 and 10 μm in C. elegans motor neurons (39), and much longer MTs, 100–400 μm, were reported in human adult sensory neurons in vivo (40). Because the mechanisms controlling the length distribution are still not fully understood (41), we here assumed, for simplicity, that all filaments have the same length, l = 10 μm, and the consequences of varying l are examined in the Supporting Materials and Methods (see Fig. S3). The filaments were arranged on a hexagonal lattice in the y-z plane, and their position along the x axis was propagated iteratively by solving a set of force-balance equations for the forces and velocities of all filaments in the bundle, as described in detail in the Supporting Materials and Methods. To investigate how the sliding dynamics and steady-state properties of MTs in the bundle are dictated by the motor-induced connectivity between MTs, we have defined the probability χ that a given overlap region between two adjacent MTs (independently of their orientations) is cross-linked by molecular motors and have simulated MT motion for varying values of χ. Motors within the same overlapping domain between MTs were assumed to be bound with the same orientation with respect to the MTs (see Fig. 1) because our calculations have indicated that in this configuration, the motors more efficiently cooperate to extend the bundle (13), and some evidence for this configuration exists (42,43). Explicit accounts of other MT accessory proteins (MAPs) and other types of motor proteins have been neglected for simplicity (however, their implicit effects are discussed below). The initial bundle had a length L₀ = 15 μm and comprised 20 MTs whose centers were randomly distributed along the x axis and the hexagonal lattice in the y-z plane. The MT orientation was chosen at random with equal probability. The motion of all MTs was then simulated while new MTs, with randomly chosen orientation, were added at a fixed rate, ω_in = 0.02 s⁻¹, to random positions along the bundle length to mimic either localized events of MT nucleation and severing within the bundle or transport of MTs from the cell body (1,10,15) (see Fig. 1). The fixed rate of mass addition was motivated by the observation that neurite growth rates are constant (30). This resulted in bundles with one to eight MTs per cross section, applicable to the thin neuronal processes of insects (7), worms (39), and other small animals (44); in Fig. S4, we show that our conclusions also hold with thicker bundles obtained with stronger forces and higher inward fluxes of MTs.

Results and Discussion

Effects of the load and MT-motor connectivity on bundle growth

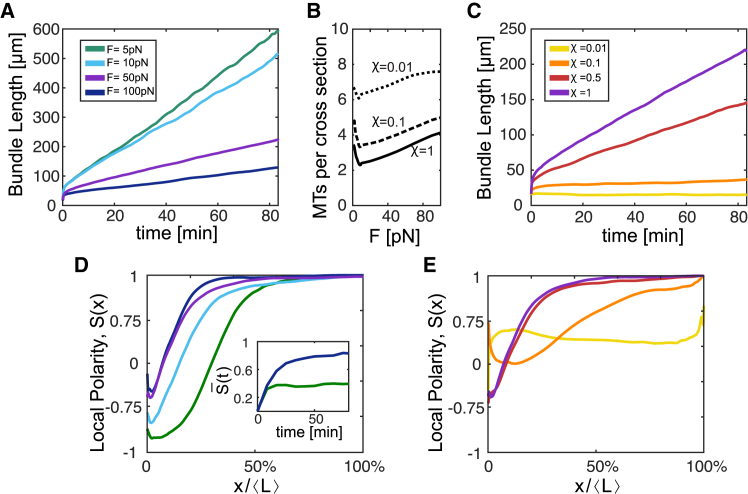
The gliding forces exerted by the motors on the MTs simultaneously act to expand the bundle against the load and sort the filaments according to their polarity. Fig. 2 demonstrates the predicted effects of the load (F) and connectivity (χ) on the bundles’ growth speed and MT polarity profile established along their length. As seen in Fig. 2 A, beyond a period of few seconds, the mean bundle length $\langle L\rangle$ increased at a fixed speed that decreased with the load on the bundle. The mean growth speed scaled as $d\langle L\rangle /dt\sim 1/F-const$; a similar scaling has been obtained with parallel bundles of filaments (13) but contained no constant term because the left boundary was impermeable (see below). Here, $\langle \cdots \rangle$ denotes ensemble averaging over thousands of bundle trajectories. To explain this scaling, we note that the overall MT volume is proportional to

$$L\overline{m}=Nl,$$ (1)

where N is the evolving number of MTs, l is their lengths, and $\overline{m}$ is the length-averaged number of MTs in a cross section. During linear growth, $\overline{m}$ adjusted to the load and maintained a fixed value that scaled as $\overline{m}\sim F$, for F > 10 pN (Fig. 2 B); taking the time derivative from Eq. 1, one finds

$$\frac{dL}{dt}=\frac{l\left({\omega }_{in}-{\omega }_{abs}\right)}{\overline{m}}.$$ (2)

Figure 2.

The effects of F and χ on bundle growth and polarity. (A) and (C) show the evolution of bundle length for varying levels of F and χ, respectively: green to blue correspond to F = 5, 10, 50, and 100 pN with χ = 1; and yellow to purple correspond to χ = 0.01, 0.1, 0.5, and 1 with F = 50 pN. (B) shows the effect of the load on a mean number of MTs per cross section for varying levels of χ. The load on the bundle dictates its width and thereby its growth speed. (D) and (E) show the effects of F and χ on the scaled MT polarity profile S(x) at t = 80 min; color coding is as in (A) and (C); the inset in (D) shows that the length-averaged order parameter, $\overline{S}\left(t\right)$, stabilizes within ∼10 min. The load on the bundle restrains growth and biases the polarity profile at the neurite entry. Highly interconnected MT bundles (large χ) more quickly expand (taper) and polarize under load, whereas loosely connected bundles fail to grow and remain short, wide, and mixed. To see this figure in color, go online.

Here, ω_in = dN_in/dt is the insertion rate of MTs into the bundle, ω_abs = dN_abs/dt is the rate of MT absorption into the cell body, and dN_in/dt – dN_abs/dt = dN/dT is the total rate of change in the number of MTs. We found ω_abs to linearly scale with the load, causing the second term on the right-hand side of Eq. 2 to be force independent. Accordingly, in our simulations, bundles that were subjected to stronger loads became wider and grew more slowly. This is supported by a number of experimental observations: 1) that thinner neurites grew faster than thicker ones (45), 2) that external pulling of the GC away from the cell body (i.e., in the direction that reduces the load on the MTs) increased neurite growth speed (30), 3) that myosin II inhibition (12,21) and F-actin depolymerization (22,23) facilitated growth, and 4) the evidence that dendrites are somewhat wider than axons (46) (although width control may have multiple mechanisms).

Another factor that significantly affected the bundles’ growth speed was the motor-induced connectivity between the MTs, dictated by χ. When χ was reduced, fewer MTs got pushed by motors, and more MTs accumulated in a cross section to balance the load (Fig. 2 B); consequently, the speed of growth decreased (Fig. 2 C). We found $\overline{m}$ to scale as ${\overline{m}}_a/\sqrt{\chi }$, and therefore, $d\langle L\rangle /dt=l\left({\omega }_{in}-{\omega }_{abs}\right)/\overline{m}\sim \sqrt{\chi }$, where ${\overline{m}}_a\sim F$ is the number of MTs in a cross section that are actively powered by unipolar motor proteins via interaction with other MTs. These findings are qualitatively consistent with the experimental observation that a downregulation of dynein motors caused axons to retract from weakly adhesive substrates (11) and led to a slowing down of neurite outgrowth (12).

Effects of the load and MT-motor connectivity on bundle polarity

To conveniently examine how F and χ govern the MT polarity profile along the bundle, we defined the normalized factor (order parameter):

$$S\left(x\right)=\langle \frac{n_R\left(x\right)-n_L\left(x\right)}{n_R\left(x\right)+n_L\left(x\right)}\rangle ,$$ (3)

where n_R(x) and n_L(x) denote the local number of MTs whose plus ends point to the right (GC direction) and left (cell-body direction), respectively. S(x) = 1 and S(x) = –1 imply that the bundle is locally polarized, with plus ends to the right and left, respectively, and S(x) = 0 implies a locally mixed region in the bundle. To analyze the changes in the profile of the order parameter during growth, we normalized the x axis by the overall length of the bundle and examined the order parameter as a function of $x/\langle L\rangle$. The scaled profile was found to settle at a steady state within a few tens of minutes (see Fig. S1), at which point the curves plotted in Fig. 2, D and E were calculated (t = 80 min). The length-averaged order parameter $\overline{S}\left(t\right)=1/L\left(t\right)\int S\left(x,t\right)dx$ stabilized within ∼10 min (see inset in Fig. 2 D).

The effect of the load on the polarity profile, S(x/L), is shown in Fig. 2 D for different values of F in case of high cross-linking probability, χ = 1; the qualitative shape of all curves is similar. Close to the cell body (left end of the bundle), the bundles are enriched with minus-end-out MTs (thus S < 0). Further away, the MT polarity profile is graded until the bundles eventually organize with all MTs pointing their plus ends toward the GC (S = 1). This graded polarity profile is consistent with the results of Sharp et al. (15) and Stepanova et al. (47), who found higher percentages of plus-end-out MTs distally from the cell body. The monotonic increase of the order parameter with the distance to the cell body arises because of the directed retrograde transport and gradual accumulation of minus-end-out MTs from all points along the shaft length. As the force on the bundle increases, the rate of MT absorption into the cell body (ω_abs) also increases. Consequently, the accumulated population of minus-end-out MTs next to the left boundary diminishes with the load on the bundle. This explains why both the length of the domain where S(x) < 0 and the absolute value |S(x)| (i.e., of the local MT polarity) in that region decrease as the load increases. In the limit of very weak forces (F $\underset{\sim }{<}$ 5 pN; see Video S4 and the corresponding kymograph in Video S1. Unstable Bundle Formed under Conditions of Weak Opposing Force, F = 2 pN, and Relatively Low Level of MT-Motor Connectivity, χ = 0.5, Video S2. Short and Mixed Bundle Formed under Conditions of Low MT Connectivity, χ = 0.1, and Relatively High Force, F = 50 pN, Video S4. Bipolar Bundle Formed under Conditions of Very Weak Opposing Force, F = 1 pN, and High Level of Connectivity, χ = 1, Video S5. Thick and Short Nonpolar Bundle Formed under High Force, F = 1000 pN, Enhanced Inward MT Flux, ωin = 0.1 s−1, but Reduced Connectivity Between the Filaments, χ = 0.1, Video S6. Thick, Rapidly Extending, Polar Bundle Forming under High Opposing Load, F = 1000 pN and High Inward MT Flux, ωin = 0.1 s−1, with High Motor Connectivity Between the MTs, χ = 1.0), we obtained a bipolar bundle having minus-end-out MTs segregated next to the left boundary and plus-end-out MTs next to the right boundary, similar to those found in our previous study of force-free bundles (32). We obtained more profound enrichment of minus-end-out MTs at the neurite entry also when simulating bundles with shorter MTs (Fig. S3). This resulted because shorter MTs get transported more quickly down the neurite shaft. This suggests an important role for the load in axon formation because it is found to contribute to the sorting out of ill-oriented (minus-end-out) MTs from the neurite entry.

Video S4. Bipolar Bundle Formed under Conditions of Very Weak Opposing Force, F = 1 pN, and High Level of Connectivity, χ = 1

Due to the weak load, and high level of connectivity the bundle extends and tapers relatively quickly, and minus-end-out MTs (red bars) rapidly get transported to the left from across the bundle length, accumulating next to the left boundary more rapidly than getting absorbed into the cell body. Consequently a bipolar bundle is formed with two subbundles of opposite polarity, a characteristic of this domain of weak forces. Due to the weak load and consequent tapering of the bundle, here too the bundle is unstable and often losses connectivity, breaking, retracting and regrowing again. Here, N₀ = 20, L₀ = 15μm and ω_in = 0.02 sec^–1.

The effect of χ on the bundles’ MT polarity profile is shown in Fig. 2 E. Decreasing χ is seen to lower the absolute value of the order parameter. For sufficiently small χ, we obtained bundles that were mixed throughout (yellow curve); these bundles also failed to grow because the motor-induced forces also act to expand the bundle. These results are consistent with the demonstration that minus-end-out MTs accumulate in the axon upon dynein inhibition (10).

To recapitulate the effects of χ and F on the bundles’ structural characteristics, we ran our simulations with loads ranging between 1 and 150 pN and χ between 0 and 1. The results are summarized in Fig. 3 in the form of two “phase” diagrams, showing the MT bundle length L (Fig. 3 A) and the length-averaged order parameter $\overline{S}=\left(1/L\right)\int S\left(x\right)dx$ (Fig. 3 B) as a function of F and χ at t = 80 min, beyond which both the growth speed and the MT polarity profile did not change (Fig. 2; Fig. S1). The diagrams reveal four distinct domains that we highlight in Fig. 3 B:

• 1)At low χ ($\underset{\sim }{<}$0.5) and 1 $\underset{\sim }{<}F\underset{\sim }{<}$ 3 pN, we obtained highly unstable bundles that rapidly tapered down to one to three MTs per cross section until frequently a critical MT-MT connection got disconnected and the bundle collapsed and regrew again. These bundles remained short on average and typically with mixed polarity (see Video S1 and the corresponding kymograph in Fig. S2 D).
• 2)For χ $\underset{\sim }{<}$ 0.1 and 3 $\underset{\sim }{<}F\underset{\sim }{<}$ 50 pN, we obtained short and mixed bundles that failed to grow and polarize, consistent with those found in vertebrate dendrites (2,3) (cf. yellow and orange curves in Fig. 2; Video S2; and the corresponding kymograph in Video S1. Unstable Bundle Formed under Conditions of Weak Opposing Force, F = 2 pN, and Relatively Low Level of MT-Motor Connectivity, χ = 0.5, Video S2. Short and Mixed Bundle Formed under Conditions of Low MT Connectivity, χ = 0.1, and Relatively High Force, F = 50 pN, Video S3. Long and Polar Bundle Formed with χ = 1, F = 100 pN, N0 = 20, L0 = 15 μm, and ωin = 0.02 s−1, Video S4. Bipolar Bundle Formed under Conditions of Very Weak Opposing Force, F = 1 pN, and High Level of Connectivity, χ = 1, Video S5. Thick and Short Nonpolar Bundle Formed under High Force, F = 1000 pN, Enhanced Inward MT Flux, ωin = 0.1 s−1, but Reduced Connectivity Between the Filaments, χ = 0.1, Video S6. Thick, Rapidly Extending, Polar Bundle Forming under High Opposing Load, F = 1000 pN and High Inward MT Flux, ωin = 0.1 s−1, with High Motor Connectivity Between the MTs, χ = 1.0).
• 3)With χ $\underset{\sim }{>}$ 0.1 and 10 $\underset{\sim }{<}F\underset{\sim }{<}$ 100 pN, the motor activity was efficient in sorting the MTs and expanding the bundles against the load. We consequently obtained long and uniformly polarized MT bundles as found in axons (3) (cf. red, violet, and dark blue curves in Fig. 2; Video S3; and the corresponding kymograph in Fig. S2 A).
• 4)With χ ≈ 0.5–1 and F $\underset{\sim }{<}$ 10 pN, we obtained rapidly extending thin bundles that segregated along their axis into two sub-bundles of opposite polarity (cf. green curve in Fig. 2; Video S4; and the corresponding kymograph in Video S1. Unstable Bundle Formed under Conditions of Weak Opposing Force, F = 2 pN, and Relatively Low Level of MT-Motor Connectivity, χ = 0.5, Video S2. Short and Mixed Bundle Formed under Conditions of Low MT Connectivity, χ = 0.1, and Relatively High Force, F = 50 pN, Video S4. Bipolar Bundle Formed under Conditions of Very Weak Opposing Force, F = 1 pN, and High Level of Connectivity, χ = 1, Video S5. Thick and Short Nonpolar Bundle Formed under High Force, F = 1000 pN, Enhanced Inward MT Flux, ωin = 0.1 s−1, but Reduced Connectivity Between the Filaments, χ = 0.1, Video S6. Thick, Rapidly Extending, Polar Bundle Forming under High Opposing Load, F = 1000 pN and High Inward MT Flux, ωin = 0.1 s−1, with High Motor Connectivity Between the MTs, χ = 1.0). MTs close to the cell body oriented with their plus ends toward the cell body and those further away oriented in the opposite direction. Unlike in the low χ regimes 1 and 2, in which $\overline{S}$ was low because the bundles were locally mixed (S(x) $\underset{\sim }{<}$ 0.7), the bundles here had low $\overline{S}$ because the averaging of S(x) over the bundle length integrated local regions with opposite polarity (S(x) ≈ ±0.9–1). This unique bidirectional segregation of MTs occurred because the load was insufficient to effectively push the accumulating minus-end-out MTs into the cell body.

Figure 3.

Diagrams recapitulating the effects of χ and F on (A) bundle length $\langle L\rangle$ and (B) mean polarity $\overline{S}$, as calculated at t = 80 min, beyond which the growth speed and $\overline{S}$ were stationary. White lines in both panels represent contours of equal bundle length (20 and 100 μm). The colored dots correspond to the respective colored curves in Fig. 2. Three regimes are distinguished in (B); see text for details. At low χ, MT bundles are short and mixed, as found in vertebrate dendrites. Axon-like, long, and uniformly polarized bundles are obtained with sufficient motor-induced connectivity between MTs (0.1 $\underset{\sim }{<}$χ < 1) and intermediate force (10 $\underset{\sim }{<}$F < 100 pN) that are low enough to enable growth but not too low to prevent accumulation of ill-oriented (minus-end-out) MTs at the neurite entry. With high connectivity, χ ≈ 0.5–1, and weak force, F$\underset{\sim }{<}$ 10 pN, the bundles elongate rapidly and taper, whereas the MTs segregate in two sub-bundles of opposite polarity along the bundle axis; minus-end-out and plus-end-out MTs accumulate next to the neurite entry and GC, respectively. To see this figure in color, go online.

We obtained similar trends and bundle types also with larger MT-motor bundles that comprised tens of MTs per cross section and hundreds of MTs in total (see Fig. S4 and Videos S5 and S6).

Video S5. Thick and Short Nonpolar Bundle Formed under High Force, F = 1000 pN, Enhanced Inward MT Flux, ω_in = 0.1 s⁻¹, but Reduced Connectivity Between the Filaments, χ = 0.1

Other factors were N₀ = 20, L₀ = 15μm.

Video S6. Thick, Rapidly Extending, Polar Bundle Forming under High Opposing Load, F = 1000 pN and High Inward MT Flux, ω_in = 0.1 s⁻¹, with High Motor Connectivity Between the MTs, χ = 1.0

Other factors were N₀ = 200, L₀ = 100μm.

Conclusions

Our calculations highlight two mechanical factors that may govern the growth speed, width, and MT polarity profile of growing neurites: the magnitude of the load upon the MTs, F, and the motor-induced connectivity between the MTs, as governed by χ. An enhanced load slowed down bundle extension because newly added MT mass distributed radially to balance the load rather than axially to extend the neurite. This explains the common observation that thinner neurites grow faster than thicker ones (45. In addition, our results are consistent with experiments which showed that myosin inhibition (12,21), actin depolymerization (22,23), and external GC pulling (30) accelerated growth and with the evidence that dendrites have larger diameters than axons (46). On the other hand, the bundles’ capacity to withstand a load also depends crucially on the motor-induced connectivity between the MTs; bundles with poor connectivity (small χ) became wide in cross section and failed to grow. Neurites comprise numerous other MAPs that passively cross-link the MTs and provide further structural support. However, they alone are not sufficient to extend the neurite, nor do they provide stability on long timescales. To expand and/or to withhold a long-standing load, the MTs must be cross-linked by motor proteins that exploit ATP molecules to actively counter the load. Indeed, experiments show that interference with dynein motor activity leads to neurite retraction in otherwise intact neurites, despite the presence of other passive MAPs (11,12).

Moreover, the gliding forces of the motors also act to sort the MTs according to their polarity because their motion on the filaments is directional. In our simulations, “mixing” of MTs was achieved via constant addition of new MTs with either polarity to arbitrary points along the bundle, thereby accounting for a few possible processes that might take place simultaneously in neurites (10), including transport of MTs by differently directed molecular motors, local MT nucleation, severing of long MTs, and flipping of short ones. Both χ and F were found to affect MT sorting along the bundle. In loosely connected bundles (small χ) the MTs remained with mixed polarity and failed to expand against the load. In contrast, highly connected bundles could expand against the load and polarize uniformly all along their length. Thus, the level of the MT-motor connectivity may be a determining property in the establishment of neurites’ major structural characteristics because it is found here to dictate the bundles’ length, width, and axial MT polarity profile.

We also found the load to have an important effect on the MT polarity profile. To obtain the uniform polarity observed in axons, the load needed to exceed a minimal level that could counter the accumulation of ill-oriented minus-end-out MTs at the neurite entry and push them into the cell body. This minimal level of force generally increases with the influx of MTs to the bundle (ω_in) and the transport speed of the minus-end-out MTs in the neurite shaft. Consequently, bundles comprising shorter MTs accumulated minus-end-out MTs more profoundly next to the neurite entry (see Fig. S3) because their transport down the bundle axis was faster. This suggests that the load on the neurite MT cytoskeleton should be optimized in some regime, which, on the one hand, enables growth and, on the other hand, is sufficiently strong to withdraw accumulating ill-oriented MTs into the cell body to ensure proper MT polarization.

Multiple factors may regulate the binding of dynein molecular motors to the MTs. In particular, the various MAPs that decorate the MT array in neurites are likely candidates. Axons and dendrites have been shown to differ in their MAP content; axons are rich in tau and MAP2C, and dendrites are rich in MAP2 (44). The effects of MAPs on molecular motor activity have been investigated in motility and binding assays as well as in single-molecule experiments. Although at high MAP/tubulin ratios, dynein binding to MTs (48) and gliding speed (49) are reduced, MAP2 and, to a lesser degree, tau were shown to sterically inhibit dynein gliding in motility assays in vitro (50). Interestingly, Chen et al. (44) found that the mean spacing between MTs differs between axons and dendrites, being ∼2-fold smaller (∼30 nm) in axons than in dendrites; for comparison, the MT spacing in dynein-induced MT bundles in vitro is ∼30 nm as well (43). It is thus tempting to speculate that through their steric modulation of the inter-MT separation, MAPs might govern the motor-induced connectivity between MTs and, in this way, modulate the arrays’ capacity to withstand the load and the molecular motors’ ability to sort the MTs.

The loss of cytoskeleton stability and collapse of neuronal processes is one of the hallmarks of neurodegenerative diseases such as Alzheimer’s and Parkinson’s (51), and both MAPs and dynein dysfunctions have been implicated in the progression of these diseases (41,52,53). We have quantitatively shown here that the motor-induced connectivity between the MTs may play a crucial role in establishing neurite mechanical stability and polarity. Whether and precisely how this property is tuned by MAPs is an intriguing question awaiting further experimental and theoretical investigation.

Author Contributions

A.Z. and M.A.H.J. wrote the simulation code. M.A.H.J. ran the calculations. M.A.H.J., K.F., and A.Z. designed the work and wrote the manuscript.

Editor: Dimitrios Vavylonis.