Measuring Stepwise Binding of Thermally Fluctuating Particles to Cell Membranes without Fluorescence

Abstract

Thermal motions enable a particle to probe the optimal interaction state when binding to a cell membrane. However, especially on the scale of microseconds and nanometers, position and orientation fluctuations are difficult to observe with common measurement technologies. Here, we show that it is possible to detect single binding events of immunoglobulin-G-coated polystyrene beads, which are held in an optical trap near the cell membrane of a macrophage. Changes in the spatial and temporal thermal fluctuations of the particle were measured interferometrically, and no fluorophore labeling was required. We demonstrate both by Brownian dynamic simulations and by experiments that sequential stepwise increases in the force constant of the bond between a bead and a cell of typically 20 pN/μm are clearly detectable. In addition, this technique provides estimates about binding rates and diffusion constants of membrane receptors. The simple approach of thermal noise tracking points out new strategies in understanding interactions between cells and particles, which are relevant for a large variety of processes, including phagocytosis, drug delivery, and the effects of small microplastics and particulates on cells.

Significance

The interaction of cells with nearby particles, e.g., bacteria, viruses, or synthetic material, is a very fundamental and complex process, often deciding cellular fate. The investigation of binding processes between particle and cell is typically investigated by fluorescence techniques, in which fluorophores often hinder the molecular interaction of specific binding partners. Therefore, alternative detection or imaging techniques are essential but are scarcely available, especially for live-cell investigations. Molecular binding is based on thermal position and orientation fluctuations of the binding partners to find the best interaction state. Here, we present a fluorescence-free measurement technique that allows us to detect multiple stepwise binding events of molecules on an optically trapped particle close to the cell membrane.

Introduction

The endocytic uptake of particles into cells is controlled by multiple biochemical and biophysical mechanisms. The most prominent cellular process, phagocytosis (1, 2, 3), comprises the engulfment, internalization, and intracellular transport of a particle, requiring energy for the deformation of the cell membrane, reorganization of the actin network (4), and phagosome transport by molecular motors (5,6). In many cases, endocytosis is receptor mediated, which means that ligands on particles, typically bacteria and viruses, trigger the recruitment of receptors in the cell membrane, such as the Fc receptor for immunoglobulins (Igs) or receptors of the complement system. The role of the spatial distributions of receptors, their diffusivity, and their kinetics of ligand binding are of superior interest to understand their dynamic function not only during endocytosis (7) but also during other fundamental cellular processes such as the formation of immunological synapses during antigen presentation (8) and the formation of focal adhesions (9).

However, the experimental investigation of such processes is difficult because they take place on very small length- and timescales. In addition, established optical techniques such immunocytochemical staining, Förster resonance energy transfer, and fluorescence recovery after photobleaching provide usually strong signals but often may influence the receptor ligand binding because of attachment of fluorophores or because they are based on genetic modifications of membrane proteins (10).

Against this background, various label-free optical detection methods have been developed or applied based on assay approaches using changes in local refractive indices within the membrane (11, 12, 13, 14, 15) or atomic-force-microscopy-based single-molecule studies, which allow detection of stepwise binding (16). Whereas many mechanistic insights into working and design principles of biomolecules are averaged out by bulk assay methods, single-molecule approaches provide more detailed information on both spatial and temporal scales. A large amount of information can be extracted when the thermal fluctuations between the binding partners are not suppressed but are measured on broad bandwidths with, e.g., optical tweezers or photonic force microscopes (PFMs) (17) and are analyzed by fluctuation variances (18,19) or with correlative or multispectral methods (20, 21, 22, 23).

A PFM (24) is an optical-tweezers-based apparatus able to bring binding partners in close vicinity of each other with the help of a steerable optical trap and to track the thermal motions of one or both binding partners in parallel. Using back-focal plane (BFP) interferometric tracking (25,26), the motions of a single bead (27) or bacterium (28) or several particles (29) can be recorded in three dimensions with nanometer precision and at rates of up to 2 MHz. Studies using PFMs have investigated individual streptavidin-biotin complexes on functionalized surfaces, revealing sequential bond formation (30), force-spectral bond ruptures (20), and intermediate states during membrane fusion (31).

In our study, we were able to expand this approach to investigate the successive binding of individual bonds of IgG-ligand-coated optically trapped beads and Fc-γ receptors in the plasma membrane of a living mouse macrophage.

Experimental and mechanistic principle

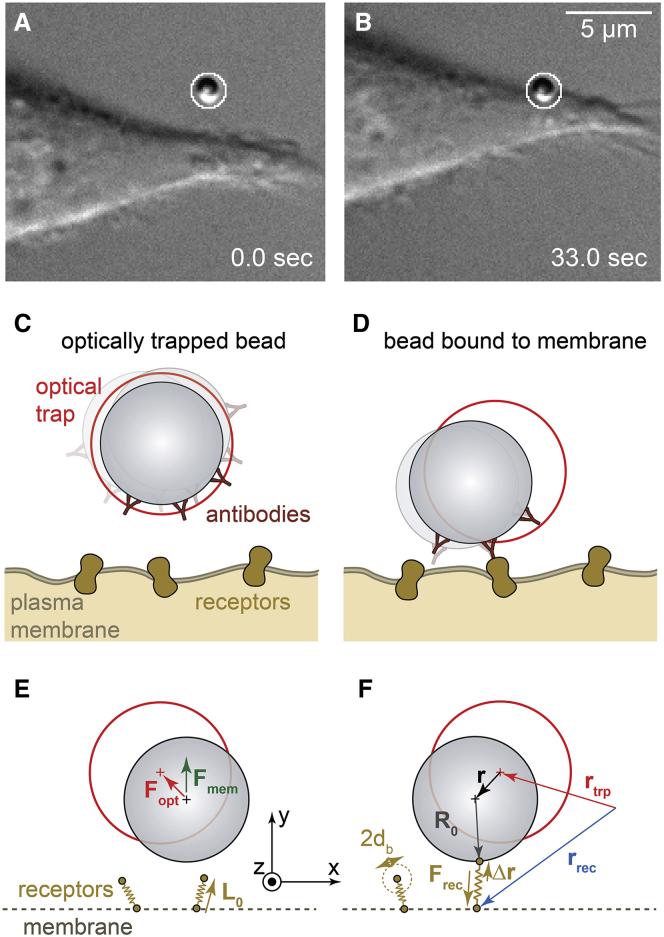
A 1-μm-sized polystyrene (PS) bead coated with IgG is approached by an optical trap to the periphery of an adherent J774 mouse macrophage. Care was taken to choose flat areas of the cell surface without any visible filopodia, here imaged by differential interference contrast (DIC) microscopy (see Fig. 1). In the first stage, the bead diffuses inside the stationary optical trap without being affected by the presence of the cell, as outlined by the sketch of Fig. 1 C. After some seconds, the bead’s motion is significantly changed in space and time because of subsequent binding of possible IgG ligands to the Fc-γ receptors in the plasma membrane. The change in the position fluctuations can barely be detected with conventional contrast enhancing microscopy methods (such as DIC) but can be tracked by BFP interferometry very precisely in three dimensions. The molecular scale fluctuation analysis of the temporal and spatial change of the bead center positions, which were measured by the PFM on one hand and simulated through Brownian dynamics (BD) on the other, define the underlying concept of the study. The mechanistic model as depicted in Fig. 1, E and F describes the relevant constituents: the optically trapped bead, the surface ligands, the membrane receptors, and the thermal driving forces. The temporal evolution of these counteracting forces can be described by a mathematical force equation, which represents the basis for our data analysis and the BD simulations.

Figure 1.

Measurement of the thermal motion of a microparticle during binding to a cell membrane. (A and B) DIC images of an optically trapped IgG-coated microparticle before (A) and after (B) binding to the membrane of a macrophage are shown. (C and D) Sketch (not to scale) of the optically trapped antibody-coated particle before (C) and after (D) binding to receptors in the cell membrane is given. (E and F) A schematic of the BD simulation of the binding process showing the particle in the optical trap before (E) and after (F) binding to receptors in the cell membrane is given. To see this figure in color, go online.

Materials and Methods

Cell culture and handling

The cells used for the experiments were J774A.1 murine mouse macrophages (17). Cells were cultivated as described previously (27). 1 day before the experiments, the cells were seeded on coverslips. To ensure access for the optical tweezers, an appropriate confluency is important. A cell coverage between 10 and 30% of the coverslips at the day of the experiments turned out to be most suitable because it ensured that there was enough space between the cells to move optically trapped particles. To provide physiological conditions during the experiment, the cells were kept heated at 37°C by a custom-built heating system.

IgG bead coating

Carboxylated 1 μm PS beads (Polysciences Europe GmbH, Hirschberg, Germany) were coated with IgG from mouse serum (I5381; Sigma-Aldrich, Darmstadt, Germany) as described previously (27).

Optical trapping and interferometric tracking

The experiments were performed on a self-developed PFM. The microscope was equipped with a three-dimensional (3D) piezo stage and is extended by the standard units for optical trapping and tracking (18) such as a 1064 nm laser (Crysta-Laser, Reno, NV).

The binding process was studied by tracking the 3D position of the bead using BFP interferometry at frequencies of 10–100 kHz. Before every experiment, the optical trap and the quadrant-photo-diode (QPD) detection system were calibrated with the methods described in (18, 19, 20). Scattering of the trapping laser light at the cell affects the mean value of the position signal (three-wave interference), but not the fluctuation width of the position signal (22), and therefore need not be considered in our analysis. Here, we assume that the refractive index at the cell periphery (overlapping with the trapping volume) does not change on a timescale of the bead position fluctuations.

Mathematical description of successive particle binding to the cell

In this section, we translate our mechanistic picture sketched in Fig. 1 into a mathematical description of the particle motion based on differential equations (DEs), which consider the most important forces influencing the particle. On the one hand, the DEs will be solved analytically to give a basis for the correlation analysis methods. On the other hand, the DEs will be solved in more detail numerically by BD simulations described in the second part of this section.

The bead’s stochastic motion in the vicinity of a cell surface can be described by an overdamped Langevin equation

$${\mathbf{F}}_{\gamma ,sol}\left(\dot{\mathbf{X}}\right)+{\mathbf{F}}_{opt}\left(\mathbf{X}\right)+{\mathbf{F}}_{cell}\left(\mathbf{X},\dot{\mathbf{X}},t\right)={\mathbf{F}}_{th}\left(t\right),$$ (1)

which we use to analyze and identify the cell binding characteristics. Here, the state vector X(t) = (x, y, z, α, β) describes both the center position r(t) = (x, y, z) and the orientation θ = (α, β) of the bead relative to the trap center at a given time t. F_γ,sol is the frictional force of the bead in the surrounding fluid, F_opt the optical force, and F_cell the force that the cell with membrane receptors exerts on the bead. The system is driven by a random thermal force F_th, which accounts for the Brownian motion of the particle.

The optical force is approximated to be linear for small bead displacements: F_opt(r) = −$-{\hat{\kappa }}_{opt}\cdot \mathbf{r}$, where ${\hat{\kappa }}_{opt}$ is a diagonal matrix containing the direction-dependent stiffnesses of the optical trap. The frictional force F_γ,sol = ${\mathbf{F}}_{\gamma ,sol}^{tra}+{\mathbf{F}}_{\gamma ,sol}^{rot}$ can be expressed by ${\mathbf{F}}_{\gamma ,sol}^{tra}=-{\gamma }_{sol}^{tra}\dot{\mathbf{r}}$ and ${\mathbf{F}}_{\gamma ,sol}^{rot}=-{\gamma }_{sol}^{rot}\dot{\mathit{\theta }}$, where ${\gamma }_{sol}^{tra}$ and ${\gamma }_{sol}^{rot}$ are the translational and rotational friction coefficients of the bead in the surrounding fluid solution.

The (3+2) dimensional forces are considered in the BD simulations. For the experimental data analysis and the analytical model description, we neglect the 2D bead rotation and proceed with a 3D description of translational motion because experimental data on the particle rotation are not available.

In first-order approximation, the binding of the bead to the membrane receptors is assumed to be harmonic. A single ligand-receptor bond is described by a harmonic potential with time-varying bond length L₀ ± Δr(t) and an elastic force F_κ,rec(r, t) = −κ_rec ⋅ Δr(t), where κ_rec denotes a time-independent isotropic bond stiffness between ligand and membrane receptor at position r_rec = r + R₀ + Δr + L₀ relative to the trap center r_trp = 0. R₀ is the vector from the bead center to the ligand position and hence the change in bond length is Δr(t) = r_rec(t) − R₀(t) − L₀(t) − r(t) (see Fig. 1 F). In addition to the elastic binding force, the ligand-receptor bond exerts a frictional force onto the bead, expressed by the linearized force F_γ,rec(r, t) = −γ_rec$\frac{\partial }{\partial t}$Δr(t), where γ_rec is an isotropic molecular friction coefficient influencing the temporal fluctuations of the bound bead. Hence, the receptor changes its position by diffusion and through the elastic force of its bond with the bead. For an increasing number N(t) of receptors (index n) that bind over time to the bead surface and successively change the fluctuation behavior of the bead, the linearized Langevin Eq. 1 for the bead position can be expressed by

$$\sum _{n=1}^{N\left(t\right)}\underset{\text{elastic and viscous force on bead from n-th receptor}}{\underbrace{\left({\kappa }_{rec}\cdot \Delta {\mathbf{r}}_n\left(t\right)+{\gamma }_{rec}\cdot \frac{\partial }{\partial t}\Delta {\mathbf{r}}_n\left(t\right)\right)}}+\underset{\text{bead repulsion}\text{from membran}}{\underbrace{\frac{F_0}{1+\exp \left(d/d_0\right)}{\mathbf{e}}_y}}+\underset{\text{bead friction}\text{in solution}}{\underbrace{{\hat{\gamma }}_{sol}\cdot \frac{\partial }{\partial t}\mathbf{r}\left(t\right)}}+\underset{\text{optical force}}{\underbrace{{\hat{\kappa }}_{opt}\cdot \mathbf{r}\left(t\right)}}={\mathbf{F}}_{th}\left(t\right).$$ (2)

To avoid an unrealistic transition of the bead through the membrane, a sigmoidally smoothed hard-core repulsion force F_mem ⋅ e_y of the bead at the membrane was introduced. This membrane force is$\left(1/2\right)$F₀, when the distance d to the bead surface (∼d + R₀ to the bead center) reaches the membrane deformation length d₀ ≈ 20 nm, which is on the order of ∼2–3 times the membrane thickness. At length d₀, the slope of F_mem is κ_mem = ${\frac{\partial }{\partial d}{F}_{mem}|}_{d0}=\frac{1}{4}{F}_0/d_0$.

Upon binding, the center position of the bead with radius R₀ mainly shifts in the y direction by the height h(t), which is the direction radial to the cell surface. Therefore, the mean position vector averaged over a time window Δt is approximated to $\langle \mathbf{r}\left(t\right)\rangle$ = (0, R₀ + h(t), 0) to estimate the number of receptors.

Number of receptors binding to the particle

Here, we describe a particle binding behavior before an active formation of the phagocytic cup. We use a simple, empirical model to describe the increase in binding area A_cap(t) through a passive, spherical cap-shaped indentation and the concentration increase c(t) of the receptors (transmembrane proteins such as FC-γ receptors) by fusion and binding to the spherical surface of the bead. In our simple model, both A_cap(t) and c(t) increase independently of each other in time.

In Eq. 2, the number N(t) of membrane receptors bound to the bead

$$N\left(t\right)=A_{cap}\left(t\right)\times c\left(t\right)=\left(2\pi R_{0}h\left(t\right)\right)\times c_0\left(1+k_{on}t\right)$$ (3)

is assumed to increase with time both because of an increase of the contact area of the spherical cap, A_cap(t) = 2πR₀ × h(t) with indentation height h, and the receptor concentration c(t).

The temporal increase of the indentation height h(t) (and thereby the spherical cap area A_cap(t)) is modeled by an exponential h(t) = h_max(1 − exp(−t/t₀)), which approaches a maximum indentation height h_max. This value is much smaller than the bead radius, i.e., h_max < R₀, and is reached when the adhesion energy between bead surface and membrane equals the deformation energy of both membrane and actin cortex. Our two-parameter approach is similar to a published power-law model (32,33), which was used for modeling the formation of a phagocytic cup.

We further assume an initial receptor concentration c₀ at time t = 0 and, as a first-order approximation, a linear increase in receptor concentration with time c₀k_ont through free diffusion. c(t) can vary with each cell. The receptors are assumed to bind to the bead with a rate k_on, which is in general limited by diffusion and by fluctuations. Furthermore, we assume that receptor unbinding is negligible. On the timescale of seconds, we assume that the contacting process is only diffusion limited and molecular binding occurs instantaneously, such that the binding rate k_on = 4D_rec/${\delta }_{rms}^2$ ≈ 4D_recc₀ depends on the diffusion constant D_rec of the receptors in the membrane and the root mean-square distance δ_rms ≈ $c_0^{-1/2}$between the receptors. In this approximation, the time-variant number of receptors in Eq. 3 can be refined to

$$N\left(t\right)=2\pi R_0{h}_{\max }\left(1-\exp \left(-t/t_{\mathit{0}}\right)\right)\times c_0\left(1+4D_{rec}{c}_{0}t\right)$$ (4)

Here, 4D_rect is the mean-square displacement for 2D free receptor diffusion with D_rec = k_BT/γ_rec defined by the receptor friction coefficient γ_rec introduced above.

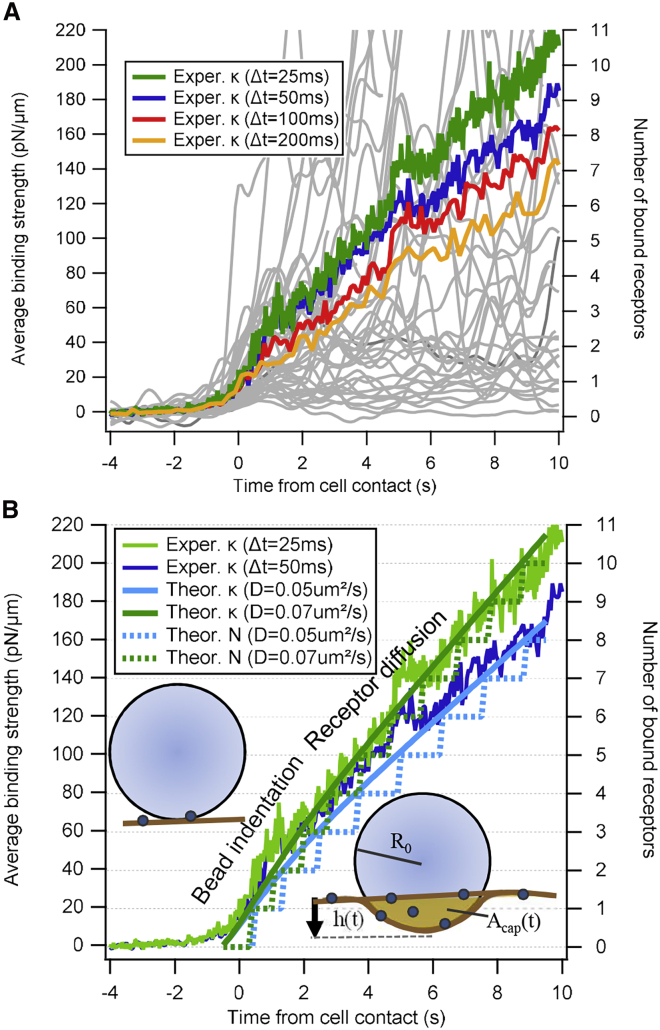
Solutions of Eq. 4 for various parameters will be compared to both experimental results and BD simulations and are presented in Fig. 6.

Figure 6.

Increase in binding strength between IgG-coated particles and J774 macrophages after particle-cell contact. (A) Measured binding strength traces κ_tot(t) − κ_opt for 45 different contacts (light gray) smoothed over Δt = 100 ms time window are shown. Averaged binding strength smoothed over time windows Δt = 25 ms, …, 200 ms is shown. (B) Two averaged binding strengths relative to traces κ_tot(t) − κ_opt obtained by the theoretical model. An assumed single receptor binding strength of κ_rec = 20 pN/μm leads to average binding of 10–11 receptors within 10 s (right ordinate). Model parameters: h_max = 80 nm, c₀ = 4/μm², D_rec = 0.05 μm²/s (0.07 μm²/s), R₀ = 0.5 μm, t₀ = 1 s. To see this figure in color, go online.

Increase in binding stiffness and friction

A suitable and common method to determine force constants κ and friction coefficients γ from fluctuation data of beads is correlation analysis (34). The bead experiences the harmonic potential of the optical trap and the sum of the harmonic potentials of each bound receptor, of which the number increases during the measurement time t_m. The resulting potential is again harmonic and can be described by the total stiffness or binding strength κ_tot(t_m), which is the sum of the trapping stiffness κ_opt and the increasing sum of all receptor stiffnesses N(t_m) × κ_rec. The total friction factor γ_tot(t_m) is the sum of friction factors experienced by the bead in the solution γ_sol and in contact with the receptors, N(t_m) × γ_rec.

Neglecting the directional dependency for a moment, the increase in binding strength and friction can be summarized as follows:

$$\begin{array}{l}{\kappa }_{tot}\left(t_m\right)\approx {\kappa }_{opt}+N\left(t_m\right)\times {\kappa }_{rec}\\ {\gamma }_{tot}\left(t_m\right)\approx {\gamma }_{sol}+N\left(t_m\right)\times {\gamma }_{rec}\end{array}$$ (5)

Both values can be measured for a small number N of receptors through autocorrelation analysis.

Autocorrelation analysis

One can assume quasithermal equilibrium for short time windows, within which stiffness and friction hardly change (see Eq. 2; (21,22)). For a linear force and friction acting on the particle, the autocorrelation (AC) function AC(x_j(t)) = AC_j(τ) = $\langle x_j\left(t\right)\times x_j\left(t+\tau \right)\rangle$ ≈ $\langle x_j{\left(0\right)}^2\rangle \times e^{-\tau /{\tau }_{0j}}$for the particle’s position in direction j = x, y, z is given by

$$\begin{array}{c}AC\left(x_j\left(t\right)\right)\approx \frac{k_{B}T}{{\kappa }_j}\times \exp \left(-\tau \times {\kappa }_j/{\gamma }_j\right)\\ \stackrel{\tau <<{\tau }_0}{\approx }\frac{k_{B}T}{{\kappa }_j}-\frac{k_{B}T}{{\gamma }_j}\times \tau \end{array}$$ (6)

Applying a two-parameter exponential fit to the second line of Eq. 6, each of the three parameters for stiffness κ_j and for friction γ_j can be extracted by determining the AC time τ_0j = γ_j/κ_j. For time delays τ much shorter than τ_0j, the autocorrelation can be well approximated to be linear in τ. The static part (τ = 0) of the AC yields the stiffness κ. The dynamical information extracted from the slope $\left(k_{B}T/{\gamma }_j\right)$ of the AC for short time delays τ yields the friction coefficient γ. The two parameters described in Eq. 5 can be analyzed within a time window Δt > τ_0j for each time point t_m as follows:

$${\kappa }_{tot,j}=k_{B}T\frac{1}{\langle x_j{\left(0\right)}^2\rangle },{\gamma }_{tot,j}\approx k_{B}T\frac{\Delta \tau }{\Delta A{C}_j\left(\tau \right)}$$ (7)

The stiffness can be obtained both from equilibrium information over the fluctuation width σ_j = ${\langle x_j\left(0\right)²\rangle }^{1/2}$ or through the exponential decay time τ₀ of the position autocorrelation function.

BD simulation

We used BD simulations to investigate the binding of a microparticle to the membrane of a cell as depicted in Fig. 2 A. Particles immersed in aqueous solution experience fluctuating thermal forces because of collisions with the water molecules. The autocorrelation time τ_w of these fluctuations is on the order of the average intermolecular separation divided by the mean molecular velocity, which yields ∼10⁻¹³ s at room temperature (35). On timescales that are large compared to τ_w, the motion of the center-of-mass coordinate x_j of a particle is described by the Langevin equation in the low Reynolds number limit. The translational and rotational Brownian motion of the particle is

$$\Delta x_j=\frac{1}{{\gamma }_{\text{sol}}^{\text{trans}}}\left(F_{\text{ext},j}+q_n\sqrt{24{\gamma }_{\text{sol}}^{\text{tra}}{k}_{\text{B}}T/\Delta t}\right)\Delta t$$

$$\Delta {\theta }_j=\frac{1}{{\gamma }_{\text{sol}}^{\text{rot}}}\left(M_{\text{ext},j}+q_n\sqrt{24{\gamma }_{\text{sol}}^{\text{rot}}{k}_{\text{B}}T/\Delta t}\right)\Delta t,$$ (8)

where in the upper equation, F_ext summarizes all additional deterministic external forces that act on the particle besides the translational viscous drag forces and the random thermal forces. In the lower equation, M_th represents the thermal torques acting on the bead, and M^ext summarizes all additional deterministic external torques besides the rotational viscous drag torques. The amplitude of the thermal force is described by the fluctuation-dissipation theorem $\langle F_{th}\left(t^{\text{'}}\right)F_{th}\left(t^{\text{'}}+t\right)\rangle =2{\gamma }_{\text{sol}}^{\text{tra}}$k_BTδ(t), where δ is the Dirac delta distribution (thermal torque M_th analogous). To simulate the Brownian motion of a particle, the thermal forces (and torques) can be calculated by using a random number generator. For evenly distributed random values q_n = [−0.5, …, 0.5], the maximal amplitude of the thermal force is (36) $\sqrt{24{\gamma }_{\text{sol}}^{\text{tra}}{k}_{B}T/\Delta t}$, where Δt denotes the temporal resolution of the simulation.

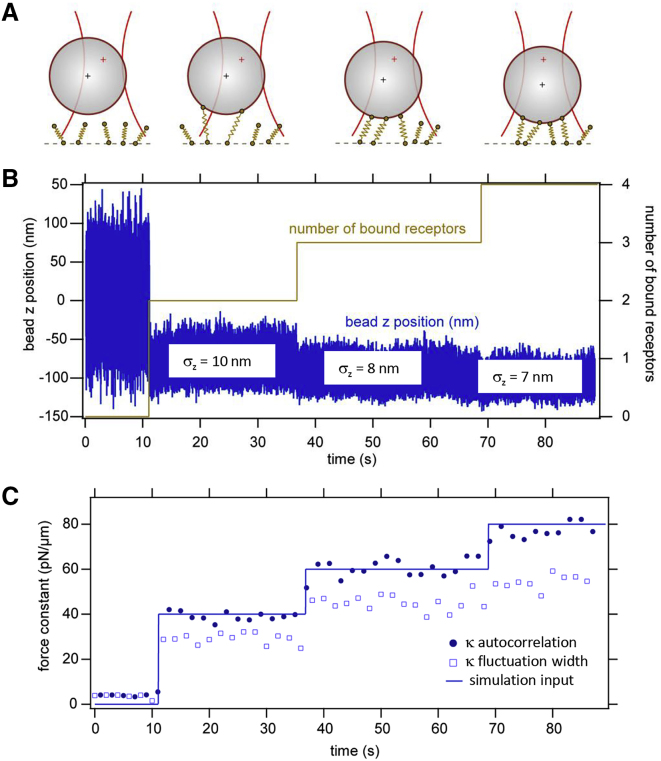
Figure 2.

BD simulation of sequential receptor binding. An optically trapped bead is moved toward a cell and binds sequentially to membrane receptors. (A) A sketch of the sequential binding process is given. (B) Bead position trace in the z direction is shown. (C) Total force constant κ_tot determined by the autocorrelation time and the fluctuation width is shown. To see this figure in color, go online.

Results

Simulations

The 1-μm-sized particle was simulated to diffuse in the 3D harmonic potential of an optical trap with typical trap stiffnesses κ_x = κ_y = 20 pN/μm and κ_z = 4 pN/μm (17). Membrane receptors were embedded in the membrane at an effective density of c₀ = 4/μm². This value is on the same order of magnitude, but lower than the reported experimental value of 10 Fc-γ receptors/μm² for neutrophils (37). We chose a lower value for the receptor density because we assume a binding probability of 100%, which means that in the simulation, each interaction between a receptor and the surface of a bead leads to a binding. However, experimentally, it is expected that not every interaction leads to a binding, for example, because of an incomplete coverage of the bead with antibodies (37). The receptors were allowed to diffuse freely in the plane of the membrane with diffusion coefficients ranging between D_rec = 0.03 μm²/s and D_rec = 0.07 μm²/s, which is in agreement with experimentally measured diffusion coefficients of membrane receptors (45). Based on our experimental results, the mechanics of a receptor was simulated in a first-order approximation as a linear spring with a spring constant of κ_rec = 20 pN/μm as described in Eq. 2. The orientation of the receptor was not restricted, but it was held in the membrane by a harmonic potential in the z direction (perpendicular to the plane of the membrane) with a force constant κ_mr = 20 pN/μm reflecting the embedding of the receptor in the membrane (see Video S1).

During the time course of the simulations, the particle was first fluctuating in the optical trap without any contact to the cell membrane. The trap was then moved slowly toward the cell until the bead was bound to the membrane (see Video S2). Binding to the membrane through a receptor was initiated when the surface of the bead was sufficiently close to the top part of the receptor. As sufficiently close, a binding distance of d_b = 20 nm was assumed. This value was determined by the size of an antibody of ∼10–15 nm (46) plus 5–10 nm to account for the Debye screening length and thermal fluctuations of the molecules. After one or more receptor bonds were formed, each receptor exerted a force and a torque onto the particle as depicted in Fig. 2 A.

Fig. 2 B shows an exemplary simulated trajectory of a particle that binds over the time course of several tens of seconds sequentially, at first to two receptors simultaneously, then to a third receptor, and subsequently to a fourth receptor. All simulations were performed in three dimensions, but only the z direction is shown here for simplicity.

It can be seen in the particle trajectory (Fig. 2 B) that the width of the fluctuations decreases with the first and second binding event. A quantitative analysis of the fluctuation width σ is shown in Fig. 2 C. In time intervals of 2 s, the standard deviation σ of the particle position fluctuations was calculated with a time window of Δt = 2 s, and the corresponding total force constant of the binding κ was calculated by κ_tot,y = k_BT/${\sigma }_y^2$ according to Eq. 7. This force constant (“binding strength”) is, in a first approximation, the sum of all the bound receptor stiffnesses. Because the optical trap and the membrane receptors form a parallel arrangement of damped springs, the optical trap stiffness provides a constant offset for κ and can be easily subtracted. The expected total force constant (labeled “total receptor κ”) is the sum of the bound receptor force constants, i.e., 40 pN/μm for N(t_m) = 2 bound receptors, 60 pN/μm for N(t_m) = 3, and 80 pN/μm for N(t_m) = 4 bound receptors at times t_m = 11 s, t_m = 38 s, and t_m = 70 s, respectively. This corresponds to fluctuation widths σ_z ≈10 nm, 8 nm, and 7 nm, which can be distinguished. However, it can be seen that the σ_z analysis underestimates the parameter κ. One reason for this underestimation is that the receptors are assumed to be held in the membrane by a harmonic potential in the y direction, i.e., perpendicular to the membrane. The resulting small diffusion of the receptors in the z direction increases σ and therefore decreases κ.

Instead of determining the total binding strength κ via the fluctuation width σ, it can also be calculated via the autocorrelation time τ of the fluctuations according to second line of Eq. 6. The result of this type of analysis is also shown in Fig. 2 C (filled circles). If the characteristic time of the receptor motion in the membrane potential separates sufficiently well from the characteristic time of the bead motion, this method for deriving κ gives more precise values. This can be seen by the good agreement between κ (autocorrelation method) and the expected value.

The results of the BD simulation presented in Fig. 2 demonstrate that it is in principle possible to extract single molecular binding events from 1-μm-sized beads fluctuating in position and orientation. The result is not obvious because our thermal noise analysis is based only on the fluctuations of the bead center positions, disregarding the orientation fluctuations and the torques induced by the receptors binding to the bead surface in a distance R₀ = 500 nm. The result is further surprising because the molecular springs, representing the receptors, also act in oblique directions, but only the vertical displacements along z directions of the 5D fluctuations are analyzed.

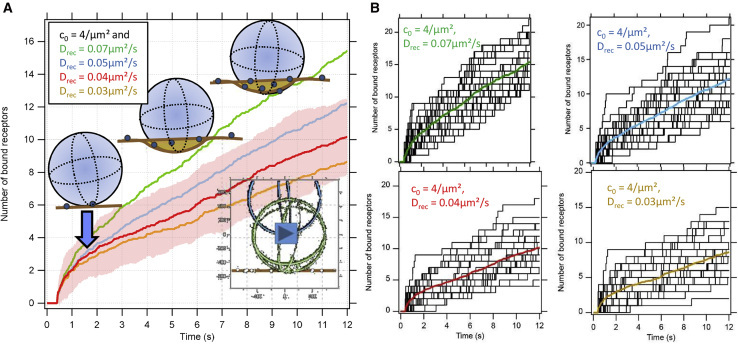
To enable further comparisons with experimental results (see next section), we ran the BD simulations repetitively over 12–20 s to simulate the number N(t) of receptors binding with time for the above mentioned membrane concentrations c₀ and receptor diffusion coefficients D_rec. Fig. 3 B displays 30 receptor binding traces N(t_m), which increase first nonlinearly, then linearly and stepwise with time. The colored traces indicate the average receptor numbers $\frac{1}{M}{\sum }_{m=1}^M{N}_m\left(t\right)$, where individual steps are no longer visible and which are summarized in Fig. 3 A. Here, the standard deviation is shown as an example only for the red trace.

Figure 3.

BD simulations of receptor binding as a function of time t_m. Model parameters were κ_rec = 20 pN/μm for single receptor binding strength and initial concentration c₀ = 4/μm², D_rec = 0.03, …, 0.07 μm²/s. (A) The mean number of bound receptors during subsequent stages of bead indentation and receptor diffusion is shown. See Videos S1 and S2. (B) Stepwise binding of single receptors on bead and analyzed from BD simulations (black tracks) and averaged trace in color are shown. To see this figure in color, go online.

Experiments

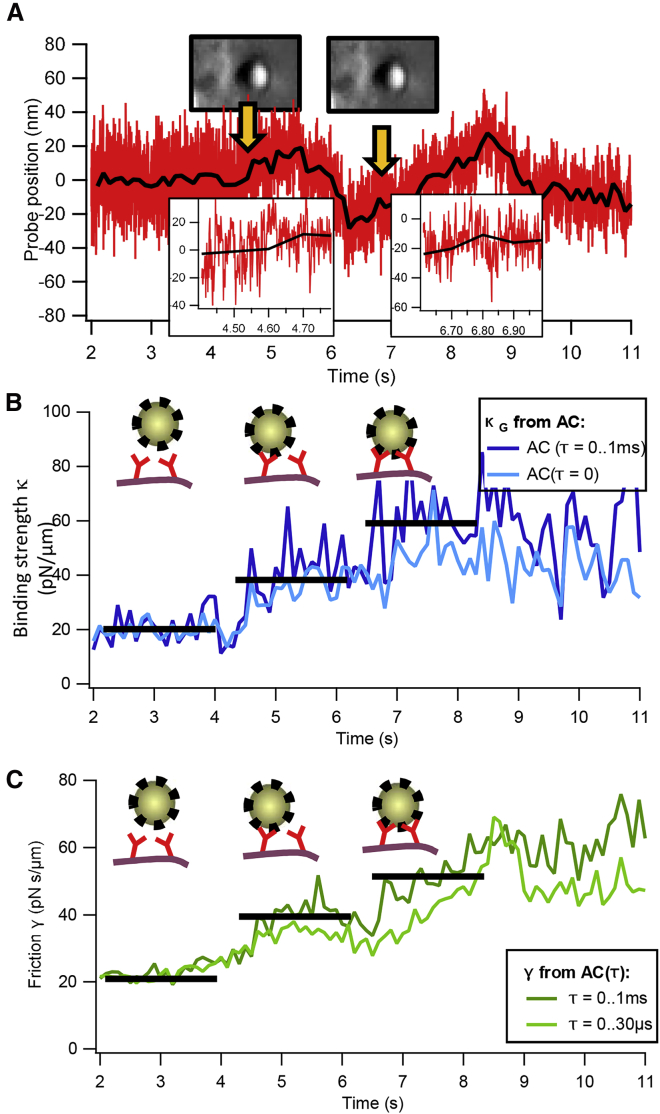
In a series of experiments, we measured the time course of the binding of IgG-coated microparticles to the membrane of macrophages. We trapped IgG-coated PS spheres and moved them within close vicinity of ∼100 nm to a visibly flat membrane of a macrophage (see Fig. 1). The thermal fluctuations of the particle’s position and orientation allowed the IgG ligands and the Fc-receptors in the membrane to find a preferable binding condition. Negative control experiments with nonfunctionalized particles showed no binding interactions. We measured the thermal motion of the bead center positions before and during the binding event by BFP interferometry with a spatial precision of several nanometers and a temporal resolution between 10 and 100 μs. A representative data set of the thermal motion of a particle during binding to a cell membrane is shown in Fig. 4 A, which typically does not allow to detect significant changes in the fluctuation behavior by pure eye observation.

Figure 4.

Binding dynamics between IgG-coated microparticles and cells. (A) Thermal motion of an optically trapped IgG-coated particle that binds stepwise to the membrane of a macrophage (see orange arrows and insets), which become visible in the plots below, is shown. (B) Autocorrelation analysis of the particle position fluctuations allows determining the binding force constant κ_tot(t). The binding force constant increases stepwise as the particle binds to the cell. A second abrupt increase a few seconds after the initial binding to the cell indicates a further bond formation between particle and cell membrane. (C) Stepwise change of the viscous drag γ_tot(t) experienced by the particle upon binding is shown. To see this figure in color, go online.

However, the analysis of the autocorrelation of the particle’s position fluctuations allows the determination of the total binding force constant κ_tot(t_m) and the friction constant γ_tot(t_m) as a function of measurement time t_m (see Eq. 5). This binding force constant (binding strength) is the sum of the optical trap stiffness κ_opt and the force constants of the receptors κ_rec(t_m), the friction constant reflects the damping of the bead at the membrane and the connection to the molecular spring with γ_rec(t_m), which both describe the binding to the cell in a two-parameter mechanistic model as introduced in the theory section.

Fig. 4, B and C show the temporal course of κ_tot(t_m) and γ_tot(t_m), which fluctuate depending on the strength of averaging and the chosen window size for each measurement point t_m. However, it can be seen in Fig. 4 B that the binding force constant fluctuates around a plateau value, which increases abruptly as the particle binds to the cell (to a value at around 40 pN/μm). About 2 s later, a second abrupt increase (the third plateau value at around 60 pN/μm) is visible, indicating an additional bond formation between the particle and the cell. Corresponding increases at related time points are visible in the time course of the friction constant in Fig. 4 C. Both binding events are marked by orange arrows in Fig. 4 A.

Based on the principles described in Eqs. 6 and 7, the varying decay of the position autocorrelation reflects the viscous drag γ experienced by the particle before binding, after the first binding, and after the second binding to the membrane. Both the binding force constant and the friction constant reveal a stepwise increase, which has been analyzed with the two different types of analysis. As demonstrated by the results of the BD simulations, the analysis of the whole correlation decay provides a reliable set of parameters.

A later series of experiments at higher sampling rate (at 1 MHz) allowed us to analyze both the stepwise increase in binding strength and friction as demonstrated by the exemplary results of Fig. 4.

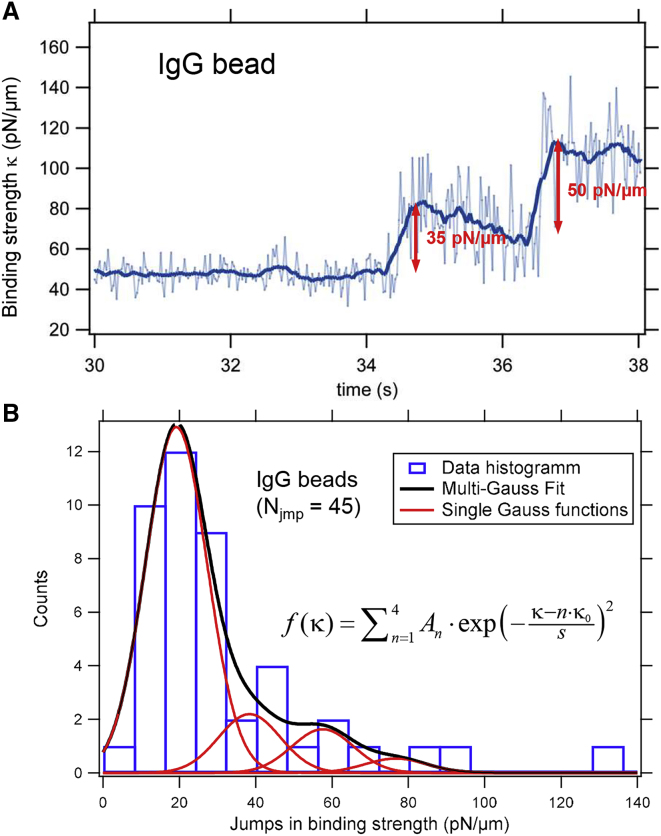
In an earlier series of experiments at a lower sampling rate (10–50 kHz), we performed binding experiments in which optically trapped IgG-coated particles of the same size were placed in close vicinity to the membrane of J774 macrophages. As shown in Fig. 5 A, we determined the initial stepwise increase of the binding force constant in experiments in which this was visible. In total, we identified 45 stepwise increases in the binding strength. Fig. 5 A displays the temporal course of the binding stiffness κ_tot(t_m) (using two different smoothing values), revealing two discrete steps with a height of ∼35 and 50 pN/μm. Before the time point t = 34 s, the particle was optically trapped with a force constant of ∼50 pN/μm. Analysis of all 45 binding events by fitting the multi-Gauss function f(κ) = ${\sum }_{n=1}^4{A}_n\exp {\left(-\frac{\kappa -n{\kappa }_0}{s}\right)}^2$ results in a distribution of force constant jumps n × κ₀ = n × (19 ± 1) pN/μm as shown in Fig. 5 B, with s = (11 ± 1) pN/μm and A = (13, 2, 1, 1) ± 1. Again, we associate these jumps in force constant with the binding of the particle to an individual Fc-γ receptor.

Figure 5.

Stepwise increase of the binding strength κ_tot(t) during binding of IgG-coated particles to J774 macrophages. (A) Temporal course of binding force constant with two distinct steps is shown. (B) A histogram of the observed stepwise increases of the binding force constants is given. The total number of measured jumps in force constant was N_jmp = 45. The histogram from the multi-Gaussian fit has peaks at n × κ₀ = n × 19 pN/μm. To see this figure in color, go online.

In addition to the stepwise increase of binding strength because of individual bond formation events, it is possible to determine the mean increase in binding strength between particles and cells as a function of time by averaging all measured time courses of the binding strength constants. Fig. 6 A shows the mean of the binding strength, which increases with time during the first 10 s after the initial binding event. Whereas the trajectories of single experiments fluctuate strongly, the average of 45 experiments shows a nearly linear increase with time, in which the slope slightly depends on the averaging time window. For four different smoothing parameters, corresponding to time windows Δt = 25 ms, …, 200 ms, the slope varies by not more than about ±20%. The association of an increase in binding strength of κ_rec = 20 pN/μm with each additional receptor leads to an average binding of N = 11 receptors during the first 10 s of particle-cell interaction (at Δt = 25 ms). Using a broad smoothing window of Δt = 200 ms, the analysis provides that N = 7 receptors bind in average within 10s (Fig. 6, right ordinate). For a reported receptor density of c₀ = 10…100/μm² with limited binding probability (37), we approximated c₀ ≈ 4/μm², assuming 100% binding probability in the BD simulation. In the analytical model, the cap area is A_cap(t_m = 1 s) = 0.1 μm² with receptor density c₀ ≈ 0.4/0.1 μm² in the first second and increases to N = 10 receptors after 10 s with a contact area A_cap(10 s) = 0.16 μm², such that c(10 s) ≈ 63/μm².

Using the initial concentration c₀ ≈ 4/μm², coincidence with the binding model described by Eq. 4 is achieved for a receptor diffusion constant of D_rec = 0.05, …, 0.07 μm²/s, which is at the lower limit in a list of experimentally obtained receptor diffusion constants (38), mainly measured by fluorescence recovery after photobleaching. A comparison between results obtained from experiments and theory is shown in Fig. 6 B for each of the two sets of curves, which all show a stronger increase directly after contact t_m = 0 s and slightly reduced increase after t_m = 1–2 s. Based on our model, only a small variation of free parameters fit the experimental analysis, which assumes a linear adding up of molecular springs constants. Here, the first phase is determined by an increase in contact area within t₀ = 1 s and at a small maximal bead indentation of h_max = 80 nm, corresponding to a maximal surface area of A_cap = 0.25 μm. The second phase is determined by the low receptor diffusion of D_rec = 0.05, …, 0.07 μm²/s at a receptor density c₀ = 4/μm², which was also used for the BD simulations.

Discussion

In the following section, we discuss our experimental approach with the underlying concept and the results presented in this work. Results include the analytical binding model, the BD simulations, the measured stepwise increase in binding strength, and the averaged linear increase in binding strength.

Experimental approach and concept

The usefulness of photonic force microscopy (PFM), especially in combination with BFP interferometric scattering, has been demonstrated in many publications. Decisive advantages relative to alternative interferometric tracking techniques such as iSCAT (39) are 1) that 3D tracking is well established, 2) that the manipulation (trapping) and the tracking beam typically is the same (40), and 3) that tracking at megahertz rates is possible and that even in the presence of other scatterers, 3D tracking is possible with nanometer precision (41).

Bead-based essays are commonly used to investigate interactions on a molecular scale especially between receptors and ligands. Based on this approach, only the technical advantages of PFM allow reliably tracking the nanometer-small changes in position fluctuations of optically trapped beads and to analyze them even in the presence of light-scattering cells. Although the presence of the cell influences the position signal at the QPD at low frequencies (typically <10 Hz), the particle’s position signal fluctuations at >10 kHz are not influenced by the cell (22). This allows a reliable analysis of high-frequency fluctuations, which decay exponentially in most cases in their temporal autocorrelation, confirming the assumption of linear forces and providing both the binding force constant (binding strength) and friction constant at subsequent time points of the experimental course. Because of the high sampling rate and 10³–10⁶ data points in time windows of 0.1–1 s, changes in fluctuation widths of only Δx = 1 nm can be well distinguished.

However, at this stage, orientation fluctuations of spherical particles cannot be measured with BFP interferometry (42,43). Although orientation fluctuations were estimated to be small, their influence on the measurement result could not be excluded, which required BD simulations.

BD simulations

The performed BD simulations turned out to be very helpful because they could answer a couple of questions that could not be answered by the experiments. The first question is whether orientation fluctuations influence the center position tracking of the 1-μm-large particle when one or several receptors bind to the bead surface at a distance of R₀ = 0.5 μm. It turned out that the hindered orientation fluctuations do not influence the strength of the position fluctuations because the output values for the binding force constant are close to the input values of the simulation. Second, it could be shown by the simulations (Fig. 3) that the position fluctuations of the membrane, and thereby of the receptors, hardly influence the binding force constant. However, it turns out that pure analyses of the fluctuation widths AC(τ = 0) provide a noticeable deviation from the input values, whereas correct results are obtained by analysis of the full autocorrelation decay AC(τ). This answers a third question: a dominant reason for the superior τ method is the larger amount of particle positions considered by correlating them at different delay times. Furthermore, there is a separation of timescales because slow movements of the membrane occur typically on longer timescales than the short autocorrelation times of optical traps and molecular bonds. In the simulation results presented in Fig. 4, we could demonstrate an increase of bound receptors with time, which consists of an initial indentation phase and a linearly increasing receptor diffusion phase and which coincides qualitatively and quantitatively with the experiments. In addition, it strengthens the assumptions of initial indentation and receptor diffusion made for the analytical model according to Eq. 4.

Stepwise change in fluctuation width

The stepwise changes in fluctuation widths shown in Figs. 4 and 5 were obtained by two independent measurement series performed at different setups demonstrating the reproducibility of the results, which is not self-evident with this type of experiment. Based on the theoretical approaches described above, especially on linear restoring forces and quasithermal equilibria, the total force constants analyzed within time windows of 25–200 ms were quite similar with only 20% variation. Whereas changes in the position traces (recorded at 1 MHz) are hardly visible by pure eyes, the stepwise increase in stiffness (Fig. 4 A) and friction (Fig. 4 B) is clearly visible for the first two binding events. Here, the pure analysis of the fluctuation width (correlation amplitude AC(τ = 0), light blue curve) results in less pronounced steps than in the case of an analysis in which time delays τ < 100 μs are considered (dark blue curve). This observation coincides very well with the BD simulations (autocorrelation method, Fig. 2 C) and can be explained by the much better statistics when correlating different time points AC(τ > 0) with each other. A similar behavior can be observed for the stepwise increase in the friction factor, which is better visible for larger time delays (τ < 100 μs, dark green curve) than for short time delay correlations in Fig. 4 B (τ < 30 μs, bright green curve). We interpret the increase in friction and damping as an increased viscous drag of the bead at the cell membrane or even the pericellular matrix (PCM).

The hypothesis that the change in fluctuations is not caused by single receptor bindings but by sudden movements of the cell periphery such as PCM filaments or filopodia cannot be fully excluded. Although filopodia were not detected in the DIC images, the small PCM filaments cannot be resolved with conventional microscopy. However, contact with the soft PCM is likely to result in a smooth increase in stiffness and friction, but not in a jump-like behavior (unpublished data).

Another hypothesis is that a bead movement out of the linear tracking regime results in a smaller fluctuation amplitude σ and thereby an erroneous increase in binding stiffness. Based on further BD simulations described in the supplementary material (Fig. S1), this effect was not relevant as long as the temporal decay of the AC(τ) was analyzed and not the pure fluctuation amplitude σ from AC(τ = 0) = k_BT/σ. The BD simulations also revealed (Fig. S2) that a smooth increase in viscosity and viscous drag of the bead toward the membrane (22) does not influence the correct analysis of the stiffness.

The exemplary experimental results of Fig. 5 show a stepwise increase of the binding stiffness independent of two different smoothing strengths, similar to Fig. 4 B. Upon each binding, a linear decay of the stiffness constant (i.e., the measured autocorrelation time τ = γ/κ) over 2 s is visible, which may be explained by an increase of the friction constant γ, resulting from a soft embedding of the bead into the PCM. Distinct jumps in stiffness of κ_rec = 35 and 50 pN/μm reflect the variety of the measurement results and may appear larger than the average stiffness jump by effects such as the aforementioned decay in κ. In total, 45 jumps in binding strength κ_tot are summarized by the histogram in Fig. 5 B, which reveals the most frequent stiffness jump at 19 pN/μm. Although measured higher stiffnesses can be a result of measurement uncertainty, the occurrence of stiffness jumps at a multiple of 19 pN/μm lead to the hypothesis that two or three binding events happen at the same time.

It will be of great interest for future experiments to correlate individual binding events measured through thermal position fluctuations with the underlying reorganization of the cytoskeleton using novel super-resolution microscopy methods operating at 100 Hz (44).

Conclusions

We could observe for the first time, to our knowledge, single successive binding events for IgG-coated beads to membrane receptors of living J774 macrophages using a fluorescence-free approach. The changes in the bead’s thermally driven position fluctuations during each binding event were tracked with quadrant photodiodes at rates of 10 kHz to 1 MHz. All experimental results coincide well with BD simulations and a simple analytical model, strengthening our interpretation of the results. We conclude that thermal noise encodes a variety of interactions that change with time, especially in living systems. Artificial probes such as coated beads turn out to be once more well suitable to measure molecular interactions at their surfaces because force transduction through the stiff bead and position tracking are very efficient. Future fluctuation binding experiments in combination with fluorescently labeled specific receptors might even reveal differences in the binding behavior under near physiological conditions, which may open new doors in toxicology, pharmacology, and immunology.

Author Contributions

A.R., E.H.K.S., and H.K. designed research. H.K., T.M., and A.R. performed research. H.K. and T.M. analyzed data. A.R. and H.K. wrote the manuscript.

Editor: Joseph Falke.