Abstract
At the end of December 2019, coronavirus disease 2019 (COVID-19) appeared in Wuhan city, China. As of April 15, 2020, >1.9 million COVID-19 cases were confirmed worldwide, including >120,000 deaths. There is an urgent need to monitor and predict COVID-19 prevalence to control this spread more effectively. Time series models are significant in predicting the impact of the COVID-19 outbreak and taking the necessary measures to respond to this crisis. In this study, Auto-Regressive Integrated Moving Average (ARIMA) models were developed to predict the epidemiological trend of COVID-19 prevalence of Italy, Spain, and France, the most affected countries of Europe. The prevalence data of COVID-19 from 21 February 2020 to 15 April 2020 were collected from the World Health Organization website. Several ARIMA models were formulated with different ARIMA parameters. ARIMA (0,2,1), ARIMA (1,2,0), and ARIMA (0,2,1) models with the lowest MAPE values (4.7520, 5.8486, and 5.6335) were selected as the best models for Italy, Spain, and France, respectively. This study shows that ARIMA models are suitable for predicting the prevalence of COVID-19 in the future. The results of the analysis can shed light on understanding the trends of the outbreak and give an idea of the epidemiological stage of these regions. Besides, the prediction of COVID-19 prevalence trends of Italy, Spain, and France can help take precautions and policy formulation for this epidemic in other countries.
Keywords: COVID-19, Infection disease, Pandemic, Time series, ARIMA, Forecasting
Graphical abstract
Highlights
-
•
Europe has become the epicentre of the virus and hit the continent harder than China.
-
•
The apparent mortality rate of COVID-19 is approximately 13% in Italy, 11% in Spain, and 15% in France.
-
•
Time series models are significant in predicting the prevalence of the COVID-19 pandemic.
-
•
ARIMA (0,2,1), ARIMA (1,2,0), and ARIMA (0,2,1) were chosen as the best models for Italy, Spain, and France, respectively.
1. Introduction
COVID-19 is defined as a new type of coronavirus that spreads rapidly from person to person and becomes a major epidemic that causes a great tragedy. COVID-19 has been identified from a family of zoonotic coronaviruses, such as the severe acute respiratory syndrome coronavirus (SARS-CoV) and the Middle East Respiratory Syndrome Coronavirus (MERS-CoV) seen in the past decade. The starting point of the virus is considered to be the Wuhan city of China, and the first fatal cases were reported in late 2019. At this point, this virus causes fatal effects, especially on the elderly and those with chronic diseases (Wang et al., 2020).
The disease has a very dynamic structure and spreads rapidly. Unfortunately, as of April 15, 2020, 123,010 deaths and approximately 2 million cases have been confirmed worldwide. The number of confirmed cases varies due to differences in epidemiological surveillance and detection capacities between countries. However, it can be said that the disease has spread all over the world as of today. Since there is no treatment method determined for this type of virus yet, it requires the effective planning of the health infrastructure and services, where the rate of disease spread should be controlled. For this reason, the estimation of the total confirmed cases and possible new cases in the future is vital for managing and directing the demand to the health system. Mathematical and statistical modeling tools that can be used for making short and long-term case estimates to plan the number of additional materials and resources are needed to deal with the outbreak. Estimating the expected burden of disease is essential for public health officials to effectively and timely manage medical care and other resources needed to overcome the epidemic. Also, such estimates can direct the intensity and type of interventions needed to alleviate the outbreak (Zhang et al., 2020).
Recently, different statistical methods such as time series models (Kurbalija et al., 2014), multivariate linear regression (Thomson et al., 2006), grey forecasting models (Wang et al., 2018a; Zhang et al., 2017), backpropagation neural networks (Liu et al., 2019; Ren et al., 2013; Zhang et al., 2013), and simulation models (Nsoesie et al., 2013; Orbann et al., 2017) were used to predict epidemic cases. Epidemics are affected by many different factors. For this reason, the general spread of the outbreak is characterized by tendencies and randomness. Therefore, the mentioned statistical tools are insufficient to analyze the epidemic randomness, and the models are difficult to generalize.
The Automatic Regressive Integrated Moving Average (ARIMA) model has been successfully applied in the field of health as well as in different fields in the past due to its simple structure, fast applicability and ability to explain the data set (Cao et al., 2020). As seen in Table 1 , ARIMA models have been successfully applied in the past to estimate the incidence and prevalence of influenza mortality, malaria incidence, hepatitis, and other infectious diseases. Besides, ARIMA models are widely used for time series prediction of epidemic diseases such as hemorrhagic fever with renal syndrome, dengue fever, and tuberculosis. ARIMA models are instrumental in modeling the temporal dependency structure of a time series, given the changing trends, periodic changes, and random distortions in the time series. It is relatively easy to explain to the end-user since ARIMA methods do not contain much mathematics or statistics. In this way, the end-user can have an idea of how the prediction model is developed and can rely more on the model during the decision-making process.
Table 1.
Various studies on disease prevalence/incidence prediction using the ARIMA model.
| Reference | Disease | Method(s) |
|---|---|---|
| (Guan et al., 2004) | HAV | ARIMA, ANNs |
| (Earnest et al., 2005) | SARS | ARIMA |
| (Gaudart et al., 2009) | Malaria | ARIMA |
| (Liu et al., 2011) | HFRS | ARIMA |
| (Zhang et al., 2013) | Typhoid Fever | SARIMA, BPNN, RBFNN, and ERNN |
| (Ren et al., 2013) | HEV | ARIMA, BPNN |
| (Nsoesie et al., 2013) | HPS | ARIMA |
| (Zheng et al., 2015) | Tuberculosis | ARIMA |
| (Wu et al., 2015) | HFRS | ARIMA, GRNN, and NARNN |
| (Zeng et al., 2016) | Pertussis | ARIMA, ETS |
| (Wei et al., 2016) | Hepatitis | ARIMA, GRNN |
| (Sun et al., 2018) | SFTS | ARIMA, NBM, and GAM |
| (Wang et al., 2018a) | HBV | ARIMA, GM (1,1) |
| (Wang et al., 2018b) | Pertussis | SARIMA, NAR |
| (He and Tao, 2018) | Influenza | ARIMA |
| (Wu et al., 2019) | Human Brucellosis | ARIMA, ERNN, and JNN |
| (Liu et al., 2019) | Pulmonary Tuberculosis | ARIMA, BPNN |
| (Chen et al., 2020) | Influenza | SARIMA |
| (Fang et al., 2020) | Infectious Diarrhea | ARIMA/X models, RF |
| (Polwiang, 2020) | Dengue Fever | ARIMA, ANN, and MPR |
| (Cao et al., 2020) | Brucellosis | ARIMA |
HAV: Hepatitis A Virus, HBV: Hepatitis B Virus, HEV: Hepatitis E Virus, SARS: Severe Acute Respiratory Syndrome, HFRS: Hemorrhagic Fever with Renal Syndrome, HPS: Hantavirus Pulmonary Syndrome, SFTS: Severe Fever with Thrombocytopenia Syndrome, ANN: Artificial Neural Networks, GM (1,1): Grey Model, SARIMA: Seasonal Autoregressive Integrated Moving Average, ETS: Exponential Smoothing, BPNN: Back Propagation Neural Networks, NARNN: Nonlinear Autoregressive Neural Network, RBFNN: Radial Basis Function Neural Networks, GRNN: Generalized Regression Neural Network, ERNN: Elman Recurrent Neural Networks, NBM: Negative Binomial Regression Model, GAM: Generalized Additive Model, NAR: Nonlinear Autoregressive Network, JNN: Jordan Neural Networks, RF: Random Forest, MPR: Multivariate Poisson Regression.
In recent studies different models have been used to predict COVID-19 incidence, prevalence, and mortality rate in China. For example, Li et al. (2020) developed a function to predict the ongoing trend with data-driven analysis and estimate the outbreak size of the COVID-19 in China (Li et al., 2020). Roosa et al. (2020) used validated phenomenological models during previous outbreaks to create and evaluate short-term forecasts of the cumulative number of confirmed cases in Hubei, China (Roosa et al., 2020). Fanelli and Piazza (2020) analyzed the temporal dynamics of the COVID-19 pandemic in mainland China, Italy, and France (Fanelli and Piazza, 2020). Roda et al. (2020) compared standard SIR and SEIR frameworks to model the COVID-19 in Wuhan Province, China (Roda et al., 2020). Wu et al. (2020) predicted the spread of COVID-19 for the national and global scale, to evaluate the effect of the metropolitan-wide quarantine of Wuhan and its neighbours (Wu et al., 2020). Al-qaness et al. (2020) improved the Adaptive Neuro-Fuzzy Inference System (ANFIS) by applying an Enhanced Flower Pollination Algorithm using the Salp Swarm Algorithm to estimate the number of confirmed COVID-19 cases in China (Al-qaness et al., 2020). Anastassopoulou et al. (2020) studied on the estimation of the critical epidemiological parameters as well as the modeling and predicting the spread of the COVID-19 epidemic in Hubei, China (Anastassopoulou et al., 2020). Wang et al. (2020) developed the Patient Information Based Algorithm for estimating the death rate of COVID-19 in real-time using publicly available data (Wang et al., 2020).
In summary, there are many studies in the literature to predict the spread of COVID-19 in China. However, Europe has become the epicenter of the virus and hit the continent harder than China. As of April 15, 2020, the apparent mortality rate of COVID-19 is 4% in China, 13% in Italy, 11% in Spain, and 15% in France. Therefore, it is significant to analyze the situation of the COVID-19 epidemic and predict the prevalence trend, especially in Italy and the two most affected countries, France and Spain.
The aim of this study is to estimate the prevalence of COVID-19 in Italy, Spain, and France, where the virus spreads fastest and causes tragic results. The data analyzed in this study correspond to the period between 21 February 2020 and 15 April 2020. The data set was used to perform and analyze a case estimation model by applying different ARIMA models. Thus, in addition to enlightening the characteristics of the spread of the epidemic, it was aimed to provide authorities with realistic estimates for the peak time and intensity of the epidemic using models based on simple quantitative models. These models can help predict the health infrastructure and material needs that patients will need in these countries in the near future.
2. Methods
2.1. Data collection
The prevalence data of COVID-19 was taken from the WHO website (https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/), and MS Excel was used to build a time-series database. Descriptive statistics of the COVID-19 data of the mentioned countries between 21/02/2020–15/04/2020 are given in Table 2 . To create a stable and effective ARIMA model, at least 30 observations are required (Box et al., 2015). Therefore, in this study, a time series containing at least 45 data was used to predict COVID-19 prevalence of Italy, Spain, and France over the next ten days with 95% relative confidence intervals.
Table 2.
Descriptive statistics on the prevalence and incidence of COVID-19 in Italy, Spain, and France.
| Case | Country | Mean | SE Mean | St. Dev | Minimum | Maximum | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|
| Prevalence | Italy | 57,262 | 7664 | 56,840 | 3 | 162,488 | 0.53 | −1.28 |
| Spain | 54,075 | 8641 | 61,098 | 2 | 172,541 | 0.73 | −1.06 | |
| France | 30,233 | 4822 | 34,097 | 12 | 102,533 | 0.82 | −0.83 | |
| Incidence | Italy | 3009 | 281 | 2065 | 6 | 6557 | −0.15 | −1.35 |
| Spain | 3521 | 432 | 3026 | 7 | 9222 | 0.28 | −1.35 | |
| France | 2092 | 269 | 1886 | 6 | 7500 | 0.69 | −0.29 |
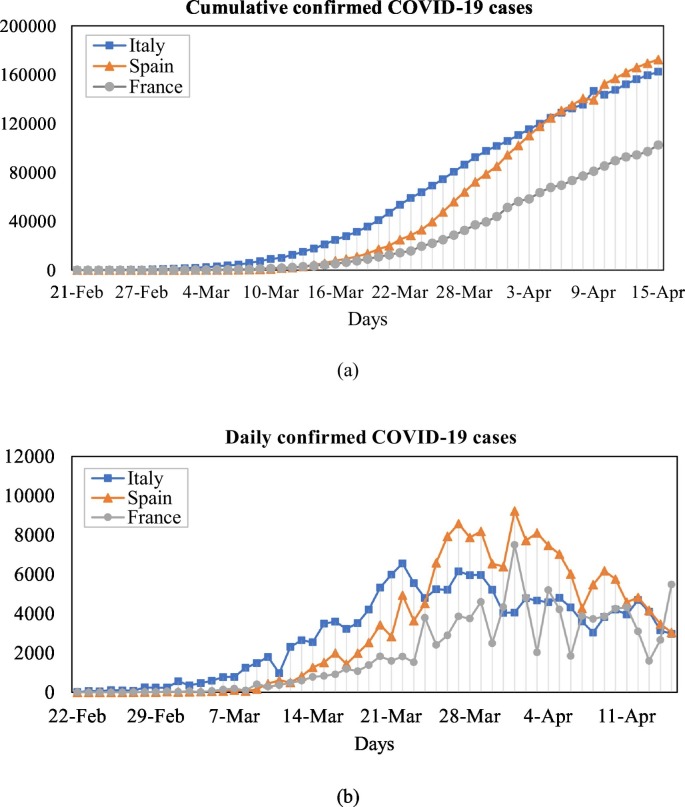
As seen from Fig. 1 , the COVID-19 outbreak in Spain and France started later than Italy. Italy reported its first COVID-19 case on January 31, 2020. In Italy, the total number of confirmed cases of COVID-19 reported during the period is 162,488, with an average of 3009 new cases per day. The north of the country was most affected, and the region with the highest number of cases was Lombardy, which recorded 62,153 cases. The neighbouring regions of Emilia-Romagna and Piedmont recorded 21,029 and 18,229 cases, respectively. The overall prevalence of COVID-19 in Spain and France follow Italy, the hardest-hit country in Europe. Spain is the second country with the highest number of deaths in Europe. The first COVID-19 case in Spain was reported about a month after Italy, and since then the number of confirmed cases has jumped to about 172,541. In France, the other most affected European country, the first COVID-19 incident was reported on January 24, 2020, the number of deaths reached to 15,708, and the reported total confirmed cases hit to 102,533.
Fig. 1.
The prevalence and incidence of the COVID-19 in Italy, Spain, and France.
2.2. ARIMA models
A time series is simply expressed as a set of data points ordered in time (Fanoodi et al., 2019). Time series analysis aims to reveal reliable and meaningful statistics and use this knowledge to predict future values of the series (Liu et al., 2011; Elevli et al., 2016; He and Tao, 2018; Benvenuto et al., 2020). The ARIMA model was introduced by Box and Jenkins in the 1970s (Box et al., 2015). The ARIMA is one of the most used time series models as it takes into account changing trends, periodic changes and random disturbances in the time series. ARIMA is suitable for all kinds of data, including trend, seasonality, and cyclicity. It is also flexible and useful in modeling the temporal dependency structure of a time series.
ARIMA model is generally referred to as an ARIMA (p,d,q) where p is the order of autoregression, d is the degree of difference, and q is the order of moving average (Li et al., 2019). The ARIMA model can be modified to perform the function of an ARMA model as well as a simple AR, I or MA model. AR (p) model refers to the current value of the time series Y t linearly in terms of its previous values Y t−1, Y t−2,..,Y t−p and the current residuals ε t. MA (q) model refers to the current value of the time series Y t linearly in terms of its current and previous residual series ε t−1, ε t−2,..,ε t−q.The general formula of AR (p) and MA (q) models can be expressed in Eqs. (1), (2), respectively.
| (1) |
| (2) |
where ϕ and θ are the autoregressive and moving average parameters, respectively. Y t is the observed value at time t and ε t is the value of the random shock at time t. It is assumed to be independently and identically distributed with a mean of zero and a constant variance of σ 2. ARMA(p,q) model is composed of AR and MA models, in which the current value of the time series is defined linearly in terms of its previous values as well as current and previous residual series. The ARMA(p,q) model can be presented as given in the Eq. (3).
| (3) |
where α is a constant, ε t−1 is the value of the previous random shock. The ARIMA model deals with non-stationary time series. The differenced stationary time series can be modelled as an ARMA model to perform the ARIMA model (He and Tao, 2018).
2.3. Model selection
The accuracy of a model can be tested by comparing the actual values with the predicted values. In this study, three performance criteria, namely Root Mean Square Error (RMSE), Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE) were applied to test the predictive accuracy of the developed ARIMA models. They are expressed mathematically in Eqs. (4), (5), (6).
| (4) |
| (5) |
| (6) |
where y t is the observed value at time point t, e t is the difference between the observed and estimated values. Also, n is the number of time points. Lower RMSE, MAE, and MAPE values indicate a better fit of the data. All analyses were performed using STATGRAPHICS Centurion XVI. I software with a statistically significant level of p < .05.
3. Results and discussion
3.1. Forecasting the prevalence of COVID-19 pandemic using the ARIMA model
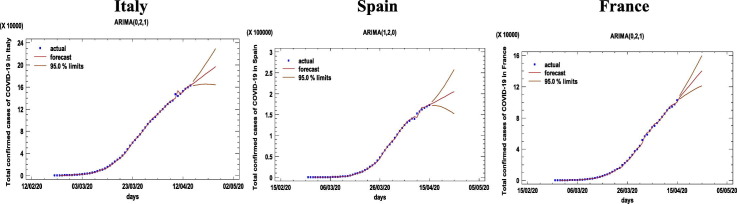
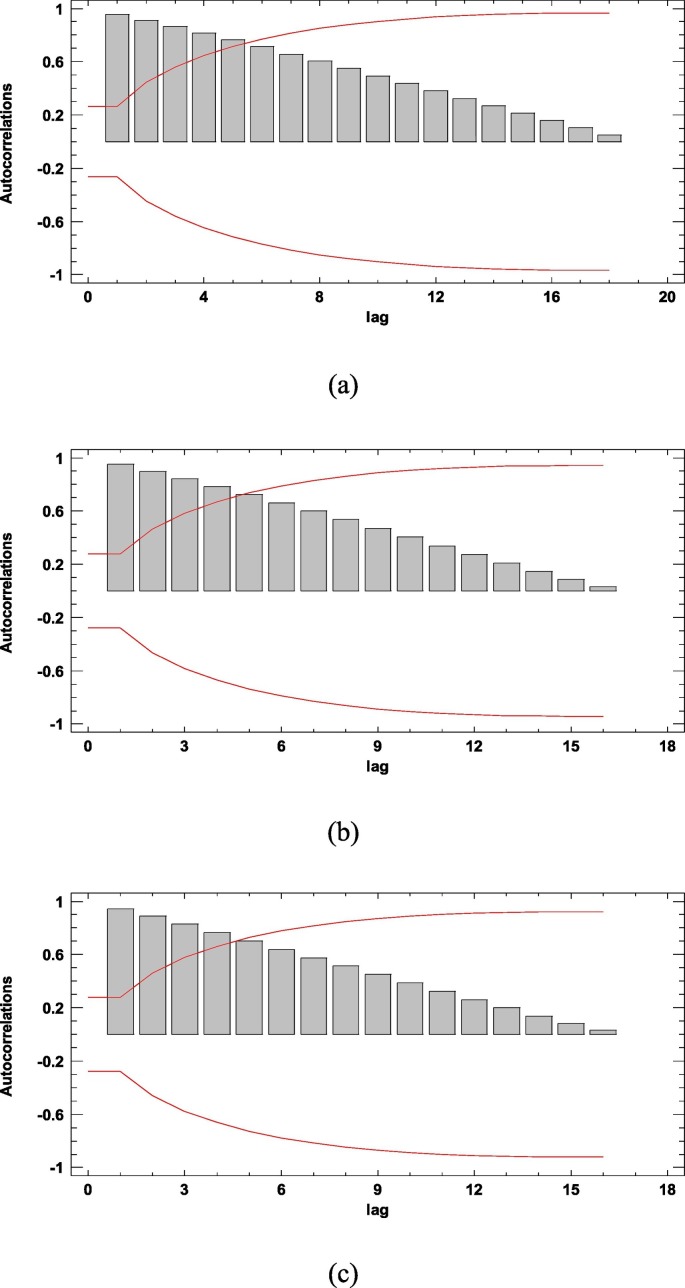
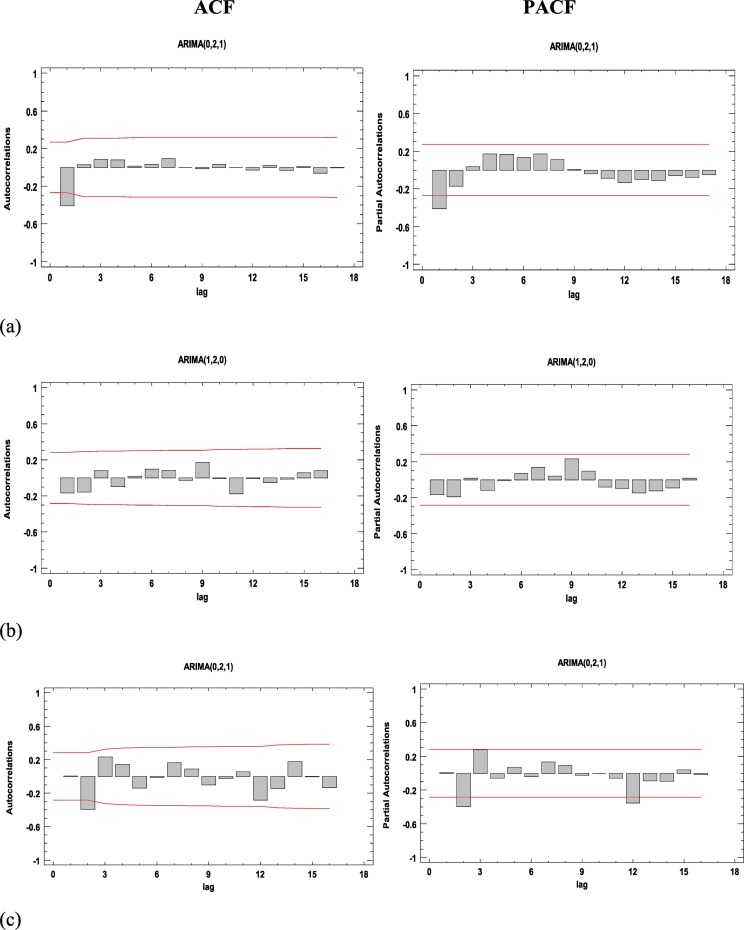
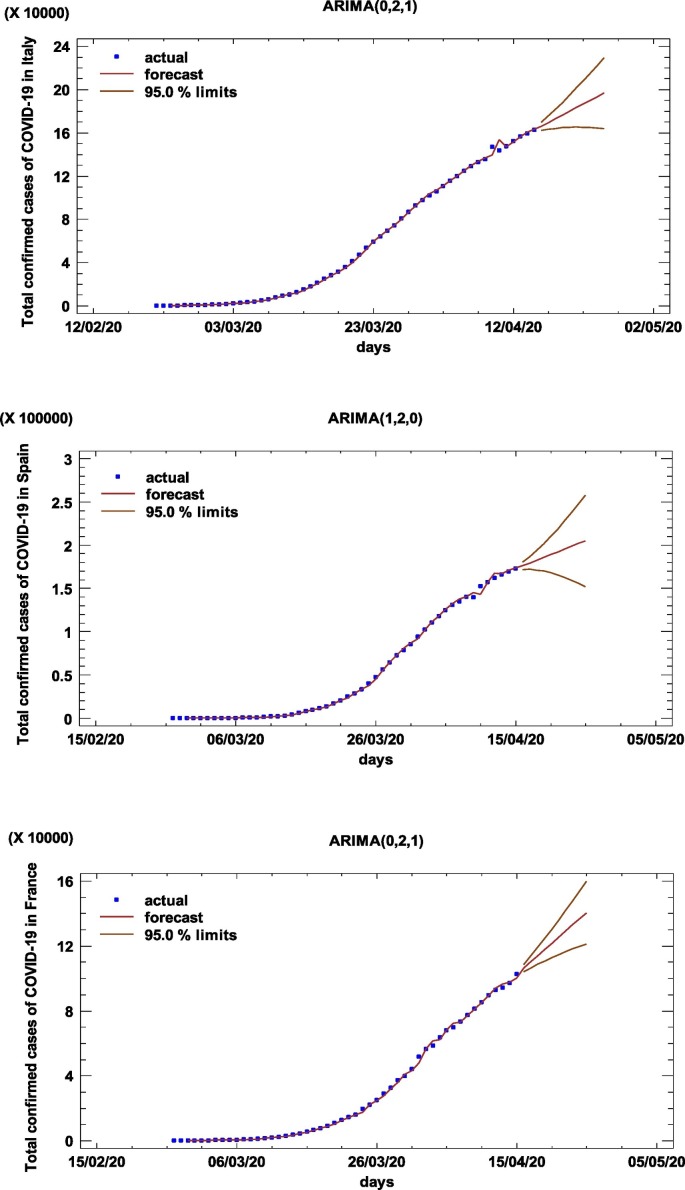
The ARIMA modeling procedure is composed of four iterative steps: assessment of the model, estimation of parameters, diagnostic checking, and prediction. The first step of the ARIMA model is to control whether the time series is stationary and seasonal. A time series is considered as stationary if its statistical properties such as mean, variance, autocorrelation are constant over time. The stationary of a time series observation is important as it will make it easier to get accurate estimates (Elevli et al., 2016). Time series plot, Autocorrelation Function (ACF), and Partial Autocorrelation Function (PACF) graphs were constructed to check the seasonality and stationarity. The ACF graph determines whether previous values in the series are related to the following values. The PACF graph finds out the degree of correlation between a variable and a lag of the said variable that is not explained by correlation at all low-order lags (He and Tao, 2018). Estimated autocorrelations for the time series of Italy, Spain, and France are shown in Fig. 2 . Straight lines on the graph are two standard deviations limits and allow to detect non-zero correlations. Bars that extend beyond the lines show statistically significant autocorrelations for the COVID-19 data. Fig. 1, Fig. 2 confirm that the overall prevalence of COVID-19 used in this study does not show seasonal patterns. However, the ACF plots in Fig. 2 shows that the prevalence of the COVID-19 is not stationary because autocorrelations reduce very slightly. Therefore, the first-order difference was taken to stabilize the mean of the COVID-19 prevalence. However, even after the first difference, it seems that the trends of all series not eliminated, so the second-order differences should be taken. All series became stationary after the second difference, and then parameters of ARIMA models were determined according to the ACF and PACF plots (see Appendix). In addition to the developed ARIMA models, different models were also created, and their performances were compared using various statistical tools. All statistical procedures were performed on the transformed COVID-19 data. ARIMA models with minimum MAPE values and statistically significant parameters were selected as the best models. Accordingly, the ARIMA (0,2,1), ARIMA (1,2,0), and ARIMA (0,2,1) models were chosen as the best models for Italy, Spain, and France, respectively. The models fitted the COVID-19 data reasonably well (Fig. 3 , Table 3 ) with a minimum MAPE Italy = 4.752, MAPE Spain = 5.849, and MAPE France = 5.634 values. Table 4 shows the parameter estimates for the best models. The p-values of the associated with the parameters are <0.05, so the terms are considerably different from zero at the 95.0% confidence level. The fitted and predicted values are presented in Fig. 4 . As seen in Table 5 , the next 10-day estimate of confirmed cases may be between 196,520–229,147 in Italy, 204,755–257,497 in Spain, and 140,320–159,619 in France.
Fig. 2.
Estimated autocorrelations for (a) Italy, (b) Spain, and (c) France.
Fig. 3.
The estimated ACF and PACF graphs to predict the epidemiological trend of COVID-19 prevalence for (a) Italy, (b) Spain, and (c) France.
Table 3.
Comparison of tested ARIMA models.
| Country | Model | RMSE | MAE | MAPE |
|---|---|---|---|---|
| Italy | ARIMA (0,2,1) | 1821.1800 | 850.4290 | 4.7520 |
| ARIMA (1,2,0) | 1939.5900 | 928.4860 | 4.8901 | |
| ARIMA (2,2,0) | 1729.4200 | 962.0600 | 5.1973 | |
| ARIMA (1,2,1) | 1687.1000 | 977.1580 | 5.2169 | |
| ARIMA (3,2,1) | 1654.6600 | 984.1700 | 5.4751 | |
| Spain | ARIMA (1,2,0) | 2082.7000 | 1043.1400 | 5.8486 |
| ARIMA (2,2,0) | 2037.0700 | 1123.8000 | 6.4824 | |
| ARIMA (3,2,0) | 2056.2100 | 1130.6600 | 6.5508 | |
| ARIMA (1,2,2) | 2054.1800 | 1150.7500 | 6.7158 | |
| ARIMA (1,2,1) | 2031.1200 | 1147.8900 | 6.6824 | |
| France | ARIMA (0,2,1) | 1106.8900 | 660.2550 | 5.6335 |
| ARIMA (1,2,1) | 1117.0700 | 664.5290 | 5.7458 | |
| ARIMA (1,2,0) | 1240.1300 | 733.2830 | 6.0335 | |
| ARIMA (3,2,0) | 972.5860 | 629.3750 | 6.2260 | |
| ARIMA (2,2,1) | 971.9250 | 635.8730 | 6.2467 |
Table 4.
Parameters of ARIMA models.
| Country | Best model | Parameters | Coefficient | Standart error | t-Statistic | p-Value |
|---|---|---|---|---|---|---|
| Italy | ARIMA (0,2,1) | MA (1) | 0.6389 | 0.1340 | 4.7661 | 0.0000 |
| Spain | ARIMA (1,2,0) | AR (1) | −0.6476 | 0.1112 | −5.8229 | 0.0000 |
| France | ARIMA (0,2,1) | MA (1) | 0.6545 | 0.1083 | 6.0439 | 0.0000 |
Fig. 4.
Time-series plots for the best ARIMA models.
Table 5.
Prediction of total confirmed cases of COVID-19 for the next ten days according to ARIMA models with 95% confidence interval.
| Date | Italy |
Spain |
France |
||||||
|---|---|---|---|---|---|---|---|---|---|
| ARIMA (0,2,1) |
ARIMA (1,2,0) |
ARIMA (0,2,1) |
|||||||
| Forecast | Lower limit | Upper limit | Forecast | Lower limit | Upper limit | Forecast | Lower limit | Upper limit | |
| 16/04/20 | 165,891 | 162,236 | 169,546 | 175,866 | 171,676 | 180,056 | 106,312 | 104,085 | 108,538 |
| 17/04/20 | 169,294 | 163,121 | 175,468 | 179,009 | 171,962 | 186,056 | 110,090 | 106,357 | 113,823 |
| 18/04/20 | 172,698 | 163,880 | 181,515 | 182,270 | 170,918 | 193,622 | 113,869 | 108,567 | 119,171 |
| 19/04/20 | 176,101 | 164,450 | 187,752 | 185,455 | 169,651 | 201,259 | 117,648 | 110,671 | 124,625 |
| 20/04/20 | 179,504 | 164,821 | 194,187 | 188,689 | 167,689 | 209,689 | 121,427 | 112,662 | 130,191 |
| 21/04/20 | 182,907 | 164,998 | 200,817 | 191,892 | 165,379 | 218,404 | 125,205 | 114,542 | 135,868 |
| 22/04/20 | 186,311 | 164,986 | 207,635 | 195,115 | 162,585 | 227,644 | 128,984 | 116,314 | 141,654 |
| 23/04/20 | 189,714 | 164,793 | 214,635 | 198,324 | 159,435 | 237,213 | 132,763 | 117,982 | 147,543 |
| 24/04/20 | 193,117 | 164,427 | 221,807 | 201,542 | 155,893 | 247,192 | 136,541 | 119,550 | 153,533 |
| 25/04/20 | 196,520 | 163,894 | 229,147 | 204,755 | 152,013 | 257,497 | 140,320 | 121,021 | 159,619 |
4. Discussion
Effective strategies are needed to prevent and control the spread of epidemics. Estimating the epidemiological trend of the prevalence of outbreaks is crucial for the allocation of medical resources, regulation of production activities, and even for the national economic development of countries. Thus, it is essential to create a reliable and suitable forecasting model that can help governments as a reference to decide on emergency macroeconomic strategies and medical resource allocation. Time series analysis is instrumental in developing hypotheses to understand the prevalence trend of various diseases and forecast the dynamics of observed phenomena, and then in the construction of a quality control system. ARIMA model is one of the most commonly used time series forecasting methods because of its simplicity and systematic structure and acceptable forecasting performance (Wang et al., 2018b). In this study, the current situation of the COVID-19 pandemic in Italy, Spain, and France was presented, and the ongoing trend and extent of the outbreak were estimated by the ARIMA model. To the best of our knowledge, this study is the first to implement ARIMA models to predict the prevalence of COVID-19 in Italy, Spain, and France.
There is great concern that European countries' health system capacity can effectively respond to the needs of infected patients who need intensive care for the COVID-19 pandemic. Especially in Italy, the number of patients infected since February 21 closely follows an exponential trend. Although the number of total confirmed cases of Italy is still increasing, the incidence of new confirmed cases is declining, and the government plans to return to normal life gradually. The daily new confirmed cases decreased to 2000–4500 over the last ten days. Meanwhile, Spain, Europe's second-worst-hit country with 18,056 deaths, has seen a drop in daily coronavirus deaths in the past five days. However, the total number of confirmed cases has overtaken Italy. On the other hand, there is no downward trend in new confirmed cases in France, and it seems that more days are needed to reach the plateau. This pattern will cause intensive care units to be at their maximum capacity. As a result, if the virus does not develop new mutations, the number of cases is expected to reach the plateau. Otherwise, clinical and social problems will be unmanageable, expected to result in disaster.
5. Conclusion
Forecasting the prevalence of the disease is important for health departments to strengthen surveillance systems and reallocate resources. Time series models play an important role in outbreak analysis and disease prediction. In this study, ARIMA time series models were applied to the overall prevalence of COVID-19 of three European countries most affected by COVID 19: Italy, Spain, and France. The results of the study can help politics and health authorities to plan and supply resources effectively, including staff, beds and intensive care facilities to manage the situation in these countries over the next few days and weeks. For more precise comparison and future perspectives, the data should be updated in real-time.
CRediT authorship contribution statement
Zeynep Ceylan:Writing - original draft, Writing - review & editing.
Acknowledgments
Acknowledgements
No funding to declare.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.scitotenv.2020.138817.
Appendix A. Supplementary material
Supplementary figures
References
- Al-qaness M.A.A., Ewees A.A., Fan H., Aziz Abd El, El M.A. Optimization method for forecasting confirmed cases of COVID-19 in China. J. Clin. Med. 2020;9:674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anastassopoulou C., Russo L., Tsakris A., Siettos C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS One. 2020;15 doi: 10.1371/journal.pone.0230405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benvenuto D., Giovanetti M., Vassallo L., Angeletti S., Ciccozzi M. Data in brief application of the ARIMA model on the COVID- 2019 epidemic dataset. Data Br. 2020;29 doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box G.E., Jenkins G.M., Reinsel G.C., Ljung G.M. John Wiley & Sons; 2015. Time Series Analysis: Forecasting and Control. [Google Scholar]
- Cao L. Ting, Liu H. Hui, Li J., Yin X. Dong, Duan Y., Wang J. Relationship of meteorological factors and human brucellosis in Hebei province, China. Sci. Total Environ. 2020;703 doi: 10.1016/j.scitotenv.2019.135491. [DOI] [PubMed] [Google Scholar]
- Chen Y., Leng K., Lu Y., Wen L., Qi Y., Gao W., Chen H., Bai L., An X., Sun B., Wang P., Dong J. Epidemiological features and time-series analysis of influenza incidence in urban and rural areas of Shenyang, China, 2010-2018. Epidemiol. Infect. 2020;148:e29. doi: 10.1017/S0950268820000151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Earnest A., Chen M.I., Ng D., Leo Y.S. Using autoregressive integrated moving average (ARIMA) models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore. BMC Health Serv. Res. 2005;5:1–8. doi: 10.1186/1472-6963-5-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elevli S., Uzgören N., Bingöl D., Elevli B. Drinking water quality control: control charts for turbidity and pH. Journal of Water, Sanitation and Hygiene for Development. 2016;6(4):511–518. [Google Scholar]
- Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos, Solitons and Fractals. 2020;134:1–12. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang X., Liu W., Ai J., He M., Wu Y., Shi Y., Shen W., Bao C. Forecasting incidence of infectious diarrhea using random forest in Jiangsu Province, China. BMC Infect. Dis. 2020;20:1–8. doi: 10.1186/s12879-020-4930-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fanoodi B., Malmir B., Firouzi F. Reducing demand uncertainty in the platelet supply chain through artificial neural networks and ARIMA models. Comput. Biol. Med. 2019;113 doi: 10.1016/j.compbiomed.2019.103415. [DOI] [PubMed] [Google Scholar]
- Gaudart J., Touré O., Dessay N., Dicko A.L., Ranque S., Forest L., Demongeot J., Doumbo O.K. Modelling malaria incidence with environmental dependency in a locality of Sudanese savannah area, Mali. Malar. J. 2009;8 doi: 10.1186/1475-2875-8-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan P., Huang D.S., Zhou B. Sen. Forecasting model for the incidence of hepatitis a based on artificial neural network. World J. Gastroenterol. 2004;10:3579–3582. doi: 10.3748/wjg.v10.i24.3579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Z., Tao H. International Journal of Infectious Diseases Epidemiology and ARIMA model of positive-rate of in fl uenza viruses among children in Wuhan, China: a nine-year retrospective study. Int. J. Infect. Dis. 2018;74:61–70. doi: 10.1016/j.ijid.2018.07.003. [DOI] [PubMed] [Google Scholar]
- Kurbalija V., Ivanovi M., Schmidt D., Lindemann G., Trzebiatowski V., Burkhard H., Hinrichs C. Time-series analysis in the medical domain: a study of Tacrolimus administration and influence on kidney graft function. Comput. Biol. Med. 2014;50:19–31. doi: 10.1016/j.compbiomed.2014.04.007. [DOI] [PubMed] [Google Scholar]
- Li X., Zhang C., Zhang B., Liu K. A comparative time series analysis and modeling of aerosols in the contiguous United States and China. Sci. Total Environ. 2019;690:799–811. doi: 10.1016/j.scitotenv.2019.07.072. [DOI] [PubMed] [Google Scholar]
- Li Q., Feng W., Quan Y.H. Trend and forecasting of the COVID-19 outbreak in China. J. Inf. Secur. 2020;80:469–496. doi: 10.1016/j.jinf.2020.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q., Liu X., Jiang B., Yang W. Forecasting incidence of hemorrhagic fever with renal syndrome in China using ARIMA model. BMC Infect. Dis. 2011;11 doi: 10.1186/1471-2334-11-218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q., Li Z., Ji Y., Martinez L., Zia U.H., Javaid A., Lu W., Wang J. Forecasting the seasonality and trend of pulmonary tuberculosis in Jiangsu Province of China using advanced statistical time-series analyses. Infect. Drug Resist. 2019;12:2311–2322. doi: 10.2147/IDR.S207809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nsoesie E.O., Beckman R.J., Shashaani S., Nagaraj K.S., Marathe M.V. A simulation optimization approach to epidemic forecasting. PLoS One. 2013;8 doi: 10.1371/journal.pone.0067164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orbann C., Sattenspiel L., Miller E., Dimka J. Defining epidemics in computer simulation models: how do definitions influence conclusions? Epidemics. 2017;19:24–32. doi: 10.1016/j.epidem.2016.12.001. [DOI] [PubMed] [Google Scholar]
- Polwiang S. The time series seasonal patterns of dengue fever and associated weather variables in Bangkok (2003-2017) BMC Infect. Dis. 2020;20:208. doi: 10.1186/s12879-020-4902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren H., Li J., Yuan Z.A., Hu J.Y., Yu Y., Lu Y.H. The development of a combined mathematical model to forecast the incidence of hepatitis E in Shanghai, China. BMC Infect. Dis. 2013;13:1–6. doi: 10.1186/1471-2334-13-421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J.M., Lu L., Liu K.K., Yang J., Wu H.X., Liu Q.Y. Forecast of severe fever with thrombocytopenia syndrome incidence with meteorological factors. Sci. Total Environ. 2018;626:1188–1192. doi: 10.1016/j.scitotenv.2018.01.196. [DOI] [PubMed] [Google Scholar]
- Thomson M.C., Molesworth A.M., Djingarey M.H., Yameogo K.R., Belanger F., Cuevas L.E. Potential of environmental models to predict meningitis epidemics in Africa. Trop. Med. Int. Heal. 2006;11:781–788. doi: 10.1111/j.1365-3156.2006.01630.x. [DOI] [PubMed] [Google Scholar]
- Wang Y. wen, Shen Z. zhou, Jiang Y. Comparison of ARIMA and GM(1,1) models for prediction of hepatitis B in China. PLoS One. 2018;13:1–11. doi: 10.1371/journal.pone.0201987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Xu C., Wang Z., Zhang S., Zhu Y., Yuan J. Time series modeling of pertussis incidence in China from 2004 to 2018 with a novel wavelet based SARIMA-NAR hybrid model. PLoS One. 2018;13:1–23. doi: 10.1371/journal.pone.0208404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Li J., Guo S., Xie N., Yao L., Day S.W., Howard S.C., Graff J.C., Gu T. Jo ur of. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W., Jiang J., Liang H., Gao L., Liang B., Huang J., Zang N., Liao Y., Yu J., Lai J., Qin F., Su J., Ye L., Chen H. Application of a combined model with autoregressive integrated moving average (ARIMA) and generalized regression neural network (GRNN) in forecasting hepatitis incidence in Heng County, China. PLoS One. 2016;11 doi: 10.1371/journal.pone.0156768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W., Guo J., An S., Guan P., Ren Y., Xia L., Zhou B. Comparison of two hybrid models for forecasting the incidence of hemorrhagic fever with renal syndrome in Jiangsu Province, China. PLoS One. 2015;10:1–13. doi: 10.1371/journal.pone.0135492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W., An S.Y., Guan P., Huang D.S., Zhou B. Sen. Time series analysis of human brucellosis in mainland China by using Elman and Jordan recurrent neural networks. BMC Infect. Dis. 2019;19:1–11. doi: 10.1186/s12879-019-4028-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Q., Li D., Huang G., Xia J., Wang X., Zhang Y., Tang W., Zhou H. Time series analysis of temporal trends in the pertussis incidence in Mainland China from 2005 to 2016. Sci. Rep. 2016;6:1–8. doi: 10.1038/srep32367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Liu Y., Yang M., Zhang T., Young A.A., Li X. Comparative study of four time series methods in forecasting typhoid fever incidence in China. PLoS One. 2013;8 doi: 10.1371/journal.pone.0063116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Wang L., Zheng Yanling, Wang K., Zhang X., Zheng Yujian. Time prediction models for echinococcosis based on gray system theory and epidemic dynamics. Int. J. Environ. Res. Public Health. 2017;14 doi: 10.3390/ijerph14030262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S., Diao M., Yu W., Pei L., Lin Z., Chen D. International Journal of Infectious Diseases Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: a data-driven analysis. Int. J. Infect. Dis. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Y.L., Zhang L.P., Zhang X.L., Wang K., Zheng Y.J. Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China. PLoS One. 2015;10:1–13. doi: 10.1371/journal.pone.0116832. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary figures