GIS-based spatial modeling of COVID-19 incidence rate in the continental United States

Abstract

During the first 90 days of the COVID-19 outbreak in the United States, over 675,000 confirmed cases of the disease have been reported, posing unprecedented socioeconomic burden to the country. Due to inadequate research on geographic modeling of COVID-19, we investigated county-level variations of disease incidence across the continental United States. We compiled a geodatabase of 35 environmental, socioeconomic, topographic, and demographic variables that could explain the spatial variability of disease incidence. Further, we employed spatial lag and spatial error models to investigate spatial dependence and geographically weighted regression (GWR) and multiscale GWR (MGWR) models to locally examine spatial non-stationarity. The results suggested that even though incorporating spatial autocorrelation could significantly improve the performance of the global ordinary least square model, these models still represent a significantly poor performance compared to the local models. Moreover, MGWR could explain the highest variations (adj. R²: 68.1%) with the lowest AICc compared to the others. Mapping the effects of significant explanatory variables (i.e., income inequality, median household income, the proportion of black females, and the proportion of nurse practitioners) on spatial variability of COVID-19 incidence rates using MGWR could provide useful insights to policymakers for targeted interventions.

Graphical abstract

1. Introduction

Coronavirus disease (COVID-19) caused by the SARS-CoV-2 virus, is a global health concern due to the rapid spread of the disease (WHO, 2020a). As of April 12, 2020, >105,000 deaths and nearly 1,700,000 incident cases have been globally confirmed (WHO, 2020b) and these figures are progressively increasing every day. The United Nations has described the disease as a social, human, and economic crisis (United Nations, 2020). The socioeconomic impacts and disease burden are especially evident in developing countries; however, the disease morbidity also impacts developed countries (United Nations, 2020). It is predicted that the annual global gross domestic product will decline by 24%, meaning that it is projected to decline by 2% each month (Congressional Research Service, 2020). The predictions also estimate a 13% to 32% decline in global trade (Congressional Research Service, 2020).

According to the World Health Organization (WHO, 2020c), COVID-19 was initially discovered in Wuhan, China, towards the end of 2019 before an outbreak of the disease was declared in January 2020. On March 11, 2020, the WHO officially declared the COVID-19 pandemic (WHO, 2020c). Shortly after, Iran and a few European countries, most notably Italy, experienced a significant increase in the number of cases and deaths (WHO, 2020c). In the United States, the first COVID-19 case was confirmed on January 19, 2020, in Washington State (Holshue et al., 2020). Thereafter, multiple states experienced an increased number of COVID-19 cases; New York State became one of the epicenters of the disease spread (Center for Infectious Disease Research and Policy, 2020). On March 17, 2020, all fifty states across the United States had confirmed cases of COVID-19 (Abir et al., 2020). On March 26, 2020, the United States became the leading country in the number of cases worldwide, replacing Italy that was previously in the lead of COVID-19 cases (Center for Infectious Disease Research and Policy, 2020). As of April 12, 2020, >20,000 deaths and >500,000 cases have been confirmed in the United States (The COVID Tracking Project, 2020).

Recent studies across the world have shown that multiple factors such as air pollution (Wu et al., 2020), smoking (Taghizadeh-Hesary and Akbari, 2020), and environmental conditions (Wang et al., 2020) may contribute to the severity and rate of spread pertaining to COVID-19. For example, Wu et al. (2020) showed that long-term air pollution exposure could potentially exacerbate the health outcomes of COVID-19 cases. Their findings also suggest that those with pre-existing conditions and air pollution exposure may suffer from higher mortality risk. In Iran, Taghizadeh-Hesary and Akbari (2020) suggest that smoking can negatively affect the health outcomes of COVID-19 patients due to potential decreased immune response. In China, Wang et al. (2020) indicated that environmental conditions such as humidity and temperature could influence the transmission of COVID-19 when compared to other respiratory viruses, suggesting a decline in disease spread.

Geographic information system (GIS) is an essential tool to examine the spatial distribution of infectious diseases (Mollalo et al., 2018, Mollalo et al., 2019), which can aid in the process of combating a pandemic and improving the quality of care (Lovett et al., 2014). GIS has become a vital tool in analyzing and visualizing the spread of COVID-19. For instance, Johns Hopkins University Center for Systems Science and Engineering (JHU CSSE) currently utilizes a GIS dashboard that provides live data of the worldwide spatial distribution of COVID-19, including the total number of confirmed cases, mortalities, and recovered patients (JHU CSSE, 2020). This nearly real-time database is readily accessible to the public, where they can keep track of the disease spread over time. The worldwide GIS map also accounts for the number of confirmed cases classified by country (JHU CSSE, 2020).

A limited number of GIS-based studies have been published since the initial outbreak of COVID-19. Boulos and Geraghty (2020), presented how various GIS applications and dashboards such as JHU CSSE, WHO dashboard, HealthMap, WorldPop, and EpiRisk are able to provide a clear representation of the COVID-19 spread. Lakhani (2020) utilized GIS mapping to identify COVID-19 health care priority locations pertaining to vulnerable populations, including elderly, palliative, and disabled patients in Melbourne, Australia. The findings suggest potential improvements in quality of care in the midst of the pandemic. Gibson and Rush (2020), utilized GIS technology to outline dwelling boundaries to detect the probability of COVID-19 spread in Cape Town, South Africa. Their results suggest that COVID-19 spread can be reduced through social distancing measures as supported by their buffer analysis and cluster identifications.

Spatial models are critical tools to statistically investigate the geographic relationship between several explanatory variables and disease outbreak (Mollalo et al., 2015; Mollalo and Khodabandehloo, 2016), such as COVID-19. In this study, we examine a few regressive and autoregressive spatial models to determine how well they can explain variations of COVID-19 in the continental United States based on several environmental, topographic, socioeconomic, behavioral, and demographic factors as explanatory variables. To our best knowledge, this paper provides the first attempt to use local geographic modeling of COVID-19 distribution across the United States and can provide useful insights for policymakers for targeted interventions.

2. Materials and methods

2.1. Data collection and preparation

The Centers for Disease Control and Prevention (CDC) continue to monitor state and county-level data of novel Coronavirus disease-daily and across the United States. For this study, the county-level counts of COVID-19 cases across the continental United States from January 22, 2020, to April 9, 2020, were retrieved from USAFacts (usafacts.org). Further, crude incidence rates were computed for the counties and joined to the administrative boundary shapefile of counties obtained from the TIGER/ Line database (www.census.gov) using ArcGIS Desktop 10.7.

A variety of 35 socioeconomic, behavioral, environmental, topographic, and demographic factors were compiled and considered as explanatory variables. Table 1 provides variable names together with their descriptions and the source of data. All variables were collected or prepared at the county-level and joined to the corresponding counties in ArcGIS environment.

Table 1.

Explanatory variables used in this study together with definitions and sources.

Theme	Variable Name	Description	Source
Socioeconomic	(1) Median household income (2) Income inequality (3) Uninsured (4) Unemployment rate (5) Food Insecurity (6) Fair or poor health	(2) The ratio of household income at the 80th percentile to income at the 20th percentile (2018) (3) Percentage of population under age 65 without health insurance (2018) (4) Number of people ages 16+ unemployed and looking for work (2018) (5) Food Environment Index (2018) (6) Percentage of adults that report fair or poor health (2018)	(1–2) Small Area Income and Poverty Estimates, American Community Survey, five-year Estimates (3) Small Area Health Insurance Estimates (4) Bureau of Labor Statistics (5) Map the Meal Gap (6) Behavioral Risk Factor Surveillance System
Behavioral	Adult smoking	Percentage of adults that reported currently smoking (2018)	Behavioral Risk Factor Surveillance System (BRFSS)
Environmental	(1) Road density (2) Particulate matter (PM) 2.5 (3) Air quality index (AQI) (4) Temperature (5) Precipitation	(1) The total length of primary and secondary roads for each county calculated/area of the corresponding county (2) Daily minimum, maximum and average (3) Minimum, maximum and average AQI; (4) Minimum, maximum and average temperature; (5) Total precipitation	(1) US Census Bureau TIGER/Line (2–3) US Environmental Protection Agency (EPA) (4-5) National Oceanic and Atmospheric Administration (NOAA)
Topographic	(1) Minimum, maximum, and average (2) Maximum slope	(1) Digital elevation model of the United States (1 km spatial resolution)	United States Geological Survey (USGS)
Demographic	(1) Percent of 65 years and over (2) Percent of Asian (3) Percent of Hispanic (4) The proportion of African American (5) Percent of black males and females; (6) Percent of white males and females (7) Net International migration rate (8) Total number of primary care physicians* (9) Total number of nurse practitioners* (10) Total number of physician assistants* (11) Total number of hospitals	*Assumed proportion to the fraction of state population living in the county	(1–7) US Census Bureau Population Estimates (2018) (8–10) Healthcare Capacity including Physicians, Nurse Practitioners, and Physician Assistants (2019) (11) Kaiser Family Foundation and AAMC

To examine the relationship between the potential explanatory variables and the dependent variable (COVID-19 incidence rate), we used five different models. The models include three global models: ordinary least squares (OLS), spatial lag model (SLM), spatial error model (SEM), and two local models: geographically weighted regression (GWR), and multiscale GWR (MGWR).

2.2. Global models

2.2.1. Ordinary least squares (OLS)

The OLS is a regression method that investigates the relationships between a set of explanatory or independent variables and a dependent variable and has the general form of (Ward and Gleditsch, 2018):

$${\mathit{y}}_{\mathit{i}}={\mathit{\beta }}_{\mathbf{0}}+{\mathit{x}}_{\mathit{i}}\mathit{\beta }+{\mathit{\epsilon }}_{\mathit{i}}$$ (1)

where at county i, y _i is the COVID-19 incidence rates, β ₀ is the intercept, x _i is the vector of selected explanatory variables, β is the vector of regression coefficients, and ε _i is a random error term. OLS optimizes regression coefficients (β) by minimizing the sum of squared prediction errors (Anselin and Arribas-Bel, 2013). OLS uses two major, implicit assumptions: that the observations are independent and constant across the study area and that the error terms are not correlated (Anselin and Arribas-Bel, 2013; Oshan et al., 2020).

OLS assumes that the observations at the county-level are independent of each other and does not consider spatial dependence. In reality, however, and in the case of COVID-19 spread, we know that variables are spatially correlated (as supported by the results of SEM and SLM later on). These interactions are omitted from OLS, and therefore OLS is a misspecified model in this case (Anselin and Arribas-Bel, 2013). Thus, we used SLM and SEM that are both variants of OLS (Anselin, 2003; Ward and Gleditsch, 2018) and both take spatial dependence into account, but model it differently.

2.2.2. Spatial lag model (SLM)

The SLM assumes dependency between the dependent variable and explanatory variables and incorporates spatial dependence into the regression model with a “spatially-lagged dependent variable” (Anselin, 2003; Ward and Gleditsch, 2018). SLM is denoted by:

$${\mathit{y}}_{\mathit{i}}={\mathit{\beta }}_{\mathbf{0}}+{\mathit{x}}_{\mathit{i}}\mathit{\beta }+\mathit{\rho }{\mathit{W}}_{\mathit{i}}{\mathit{y}}_{\mathit{i}}+{\mathit{\epsilon }}_{\mathit{i}}$$ (2)

where ρ is the spatial lag parameter (spatial autoregressive parameter), and W _i is a vector of spatial weights (a row of the spatial weights matrix). Eq. (2) is constructed by decomposing the error term in Eq. (1) (Ward and Gleditsch, 2018). The weight matrix (W) on the right-hand side of this equation specifies the neighbors at location i and, as such, relates the independent variable to the explanatory variables at that location (Anselin and Arribas-Bel, 2013). The presence of spatial lag suggests a potential diffusion process (Kostov, 2010).

2.2.3. Spatial error model (SEM)

The SEM assumes spatial dependence in the error term of OLS and decomposes the error term in Eq. (1) into two terms (λW _i ξ _i and ε _i below) (Anselin, 2003; Chen et al., 2016). The general form of this model is: (Ward and Gleditsch, 2018)

$${\mathit{y}}_{\mathit{i}}={\mathit{\beta }}_{\mathbf{0}}+{\mathit{x}}_{\mathit{i}}\mathit{\beta }+\mathit{\lambda }{\mathit{W}}_{\mathit{i}}{\mathit{\xi }}_{\mathit{i}}+{\mathit{\epsilon }}_{\mathit{i}}$$ (3)

where at county i, ξ _i indicates the spatial component of the error, λ indicates the level of correlation between these components, and ε _i is a spatially uncorrelated error term.

2.3. Local models

2.3.1. Geographically weighted regression (GWR)

Global regression models such as OLS, SEM, and SLM implicitly assume spatial stationarity in the relationships between explanatory variables and dependent variable(s), meaning that they assume these relationships do not vary over space (Brunsdon et al., 1996; Brunsdon et al., 1998). To relax this assumption and to allow for “parameters to vary spatially.” Brunsdon et al. (1996) introduced GWR as an extension of general regression models and based on kernel-weighted regression. Instead of estimating global values for regression parameters, GWR allows these parameters to be derived for each location separately, and in doing so, it incorporates geographic context (Oshan et al., 2020). GWR is denoted by (Fotheringham and Oshan, 2016)

$${\mathit{y}}_{\mathit{i}}={\mathit{\beta }}_{\mathit{i}\mathbf{0}}+\sum _{\mathit{j}=\mathbf{1}}^{\mathit{m}}{\mathit{\beta }}_{\mathit{ij}}{\mathit{X}}_{\mathit{ij}}+{\mathit{\epsilon }}_{\mathit{i}},\mathit{i}=\mathbf{1},\mathbf{2},\dots ,\mathit{n}$$ (4)

where at county i, y _i is the value for the COVID-19 incidence rate, β _i0 is the intercept, β _ij is the jth regression parameter, X _ij is the value of the jth explanatory parameter, and ε _i is a random error term. Parameter estimates for each explanatory variable and at each county in matrix form is given by (Fotheringham and Oshan, 2016):

$$\widehat{\beta }\left(i\right)={\left(X^{\prime }\mathrm{W}\left(i\right)X\right)}^{-1}{X}^{\prime }W\left(i\right)y$$ (5)

where $\widehat{\beta }$ is the vector of parameter estimates (m × 1), X is the matrix of the selected explanatory variables (n × m), W(i) is the matrix of spatial weights (n × n), and y is the vector of observations of the dependent variable (m × 1) (Fotheringham and Oshan, 2016). W(i) is a diagonal matrix that is constructed from the weights of each observation based on its distance from location i and is calibrated based on a locally weighted regression (Brunsdon et al., 1998; Fotheringham and Oshan, 2016). To calculate W(i), a kernel function and a bandwidth should be specified. The most commonly used kernel functions are Gaussian, and bi-square and the bandwidth is usually determined based on (Euclidean) distance or the number of nearest neighbors. Note that selecting different bandwidth types would affect the type of neighborhood in which local weighting happens.

2.3.2. Multiscale GWR (MGWR)

Even though GWR can be a great improvement compared to global regression in the context of spatial processes, it still assumes that the scale of all of the involved relationships are constant over space and thus does not allow for analyzing these relationships at different scales (Fotheringham et al., 2017; Oshan et al., 2019). Whereas, in many cases, including COVID-19 spread, this assumption is not valid because different processes are involved with varying spatial scales.

MGWR is an extension of GWR that allows studying the relationships at varying spatial scales and achieves that by using varying bandwidth as opposed to a single, constant bandwidth for the entire study area (Fotheringham et al., 2017; Yu et al., 2019). MGWR can be formulated as (Fotheringham et al., 2017):

$$y_i=\sum _{j=0}^m{\beta }_{\mathit{bwj}}{X}_{\mathit{ij}}+{\epsilon }_i,i=1,2,\dots ,n$$ (6)

where β _bwj is the bandwidth used for calibration of the jth relationship (Fotheringham et al., 2017), and the rest of the parameters are the same as Eq. (1). In practice, MGWR is usually treated as a generalized additive model (GAM), which as a result, allows it to be calibrated using back-fitting algorithms (Fotheringham et al., 2017; Hastie and Tibshirani, 1986; Buja et al., 1989). By reformulating MGWR as a GAM, we have:

$$y_i={\sum }_{j=0}^m{f}_{\mathit{ij}}+\epsilon$$ (7)

where f _ij (replacing β _bwj X _j in (3)) is the jth additive term and is a smoothing function applied to jth explanatory variable at county i (Fotheringham et al., 2017; Oshan et al., 2019). Calibrating the model will result in a set of bandwidth, one for each of the j explanatory variables. Differences in bandwidths represent differences in spatial scales, and by capturing the effect of scale in spatial processes, MGWR can more accurately capture spatial heterogeneity (Fotheringham et al., 2017; Oshan et al., 2019).

2.4. Models development

Due to the existence of a relatively large set of candidate variables, the stepwise forward procedure was applied to select a subset of variables by eliminating non-significant explanatory variables. Subsequently, Pearson's correlation analysis was applied to investigate the correlations between all pairs of selected variables. Variance inflation factor (VIF) was used to detect multi-collinearity, and therefore the most uncorrelated factors were selected as the input of the models. For comparison, OLS and all the following models were implemented with the same selected variables. All global models were run in GeoDa 1.14 software (geodacenter.github.io). The weight matrix was generated based on first-order Queens' contiguity. Local models were implemented in MGWR 2.2 (https://sgsup.asu.edu/sparc/mgwr). An (adaptive) bi-square kernel, which removes the effect of observations outside the neighborhood specified with the bandwidth and (minimized) corrected Akaike Information Criterion (AICc), was used to select optimal bandwidth (Oshan et al., 2020; Oshan et al., 2019). The adjusted R² and AICc were used to compare the performances of models in explaining COVID-19 incidence rates across the continental United States.

3. Results

After feature selection and correlation analysis (correlation coefficients <0.3), among the 35 collected candidate variables, only four variables were selected to be included in the final models. These variables are income inequality, median household income, the percentage of nurse practitioners, and the percentage of the black female population (to the total female population) at the county-level (Table 2 ). As seen in Table 2, in the OLS model, the selected variables have relatively low multi-collinearity since the VIFs for all of them are below the threshold of 5 (all VIFs <1.5) (O'Brien, 2007) and were positively associated with COVID-19 incidence rates (P < 0.001). Although the global OLS model presented a very low adjusted R², it provided a baseline for subsequent global and local models. Low adjusted R² implies that almost 87.3% of the COVID-19 incidence rates across the continental United States are caused by unknown variables to the model and likely due to the local variations which were not captured by the OLS model.

Table 2.

Summary statistics of the OLS model on selected variables in modeling COVID-19 incidence rates, continental United States.

Variable	Coefficient	T-statistic	P-value	VIF
Intercept	0.0007	0.0397	0.968338	–
Income inequality	0.2021	9.9015	0.000000*	1.4657
Median household income	0.2449	12.2474	0.000000*	1.4066
% of nurse practitioner	0.1365	7.4003	0.000000*	1.1963
% of black females	0.1095	5.7726	0.000000*	1.2667

According to Table 3 , by incorporating spatial dependence, SLM and SEM improve the performance of OLS in modeling the COVID-19 incidence rate in the United States. Both autoregressive lag coefficients (i.e., ρ and λ in Eqs. (2), (3), respectively) were found strongly significant (P < 0.000). However, spatial lag achieved a lower standard error of estimated parameters. Although both SEM and SLM significantly outperformed OLS, they still showed relatively poor performances in modeling the COVID-19 incidence rates in the United States. As mentioned before, this could be due to the neglected scale of spatial processes involved in modeling the disease incidence rate (Table 4 ).

Table 3.

Summary statistics of SLM and SEM in modeling COVID-19 incidence rates, continental United States.

Variable	Coefficient		Std. error		Z-score		P-value
	SLM	SEM	SLM	SEM	SLM	SEM	SLM	SEM
Intercept	−0.002	−0.003	0.016	0.027	−0.134	−0.098	0.893	0.922
Income inequality	0.172	0.189	0.019	0.021	8.98	9.158	0.000	0.000
Median household income	0.183	0.237	0.019	0.023	9.58	10.396	0.000	0.000
% of nurse practitioner	0.078	0.066	0.017	0.019	4.54	3.446	0.000	0.001
% of black females	0.064	0.123	0.018	0.0251	3.57	4.905	0.000	0.000
Rho	0.0402	–	0.024	–	16.99	–	0.000	–
Lambda	–	0.415	–	0.024	–	17.099	–	0.000

Table 4.

Measures of goodness-of-fit for OLS, SEM, SLM, GWR, and MGWR in modeling COVID-19 incidence rate, continental United States.

Criterion	OLS	SEM	SLM	GWR	MGWR
Adj. R2	0.127	0.238	0.242	0.674	0.681
AICc	8304.98	8063.52	8045.70	6134.19	`5796.53

To test potential local spatial differences, (M)GWR were employed. According to Table 3, Table 4, the value of adjusted R² significantly increased from 24.2% in the SLM (the most accurate general model in this study) to 67.4% in the GWR model. Moreover, the AICc dropped from 8045.70 to 6134.19. Among the employed models, the MGWR model showed the lowest AICc value (AICc: 5796.53), indicating the most parsimonious model. Moreover, MGWR obtained the highest adjusted R² (0.681), suggesting that the model could explain 68.1% of the total variations of COVID-19 incidence rates. This measure of goodness-of-fit was slightly lower for regular GWR (Adj. R²: 0.674), with higher AICc compared to MGWR (AICc: 6134.19).

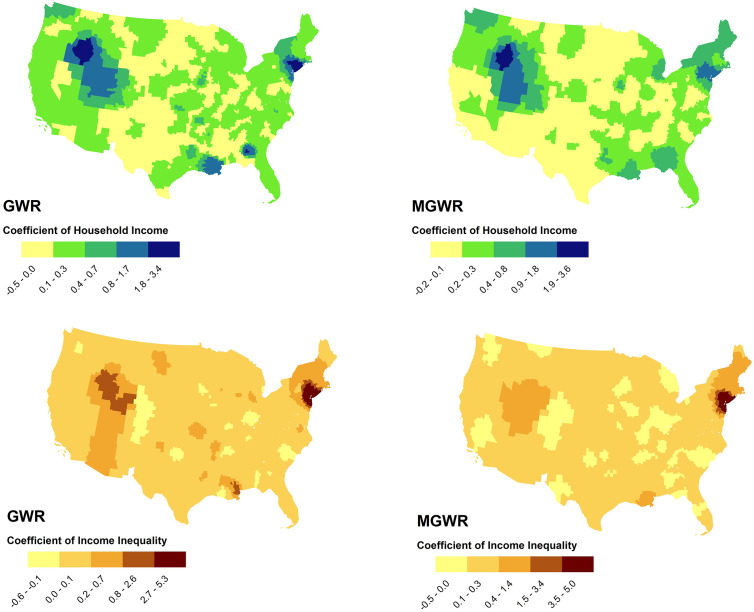
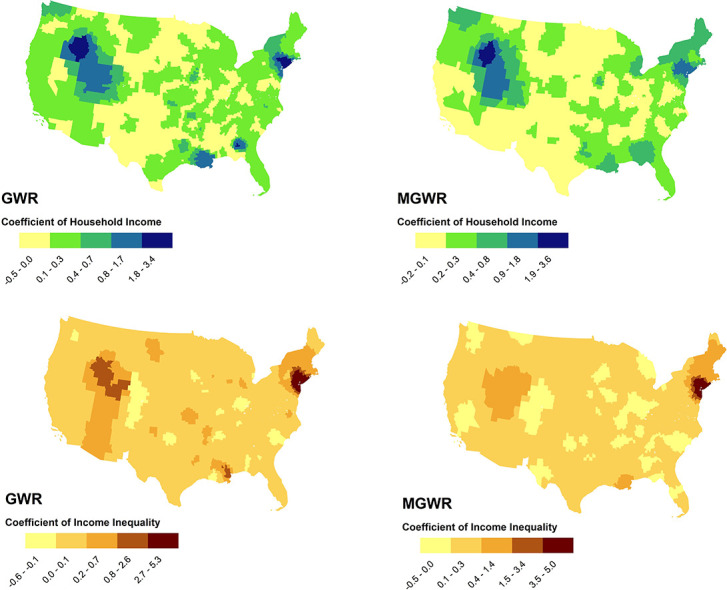
Fig. 1, Fig. 2 show the results of mapping coefficients of GWR and MGWR for the selected variables. As seen in Fig. 1, income inequality demonstrated almost similar patterns in describing the geographic distribution of COVID-19 incidence rates at the county-level in both GWR and MGWR. Income inequality was an influential factor in explaining disease incidence rates across counties in the tri-state area (i.e., New York, Connecticut, and New Jersey states), Massachusetts, and in parts of the Western United States, particularly in Nevada, Idaho, and Utah.

Fig. 1.

The effects of median household income (above) and income inequality (below) in describing COVID-19 incidence rates using GWR (left) and MGWR (right) models, continental United States.

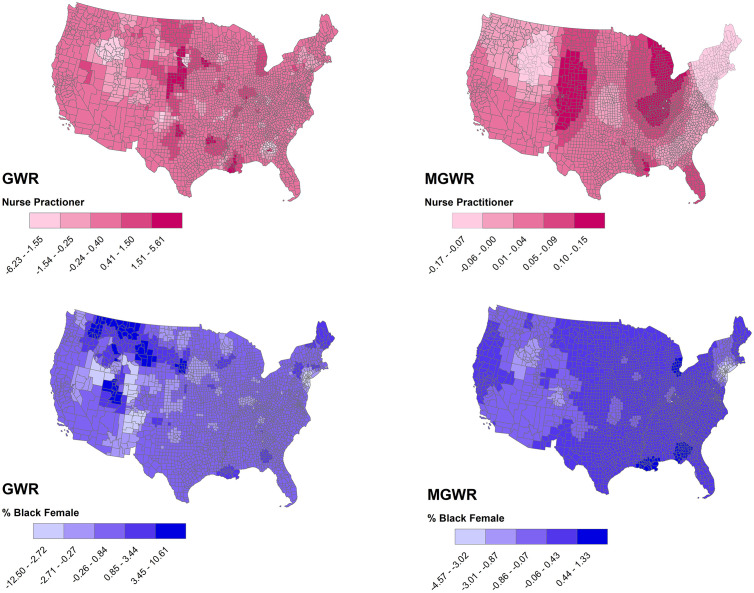
Fig. 2.

The effects of % of nurse practitioners (above) and % of black females (below) in describing COVID-19 incidence rates using GWR (left) and MGWR (right), continental United States.

On the contrary, both models represented poor performances at counties in the Southern United States, particularly in Arizona, Texas, and the New Mexico States, and also in most of the Northern Great Plains, particularly in North Dakota, South Dakota, and the Montana States. Median household income also revealed almost similar patterns to income inequality in both GWR and MGWR models.

In both GWR and MGWR, the percentage of nurse practitioners was a substantial factor in describing the geographic distribution of COVID-19 incidence rates in a number of counties in Louisiana, southern Mississippi, and a few counties in The Central United States and Midwest (Fig. 2). However, the impact of the percentage of black females on COVID-19 incidence rates was inconsistent between GWR and MGWR models.

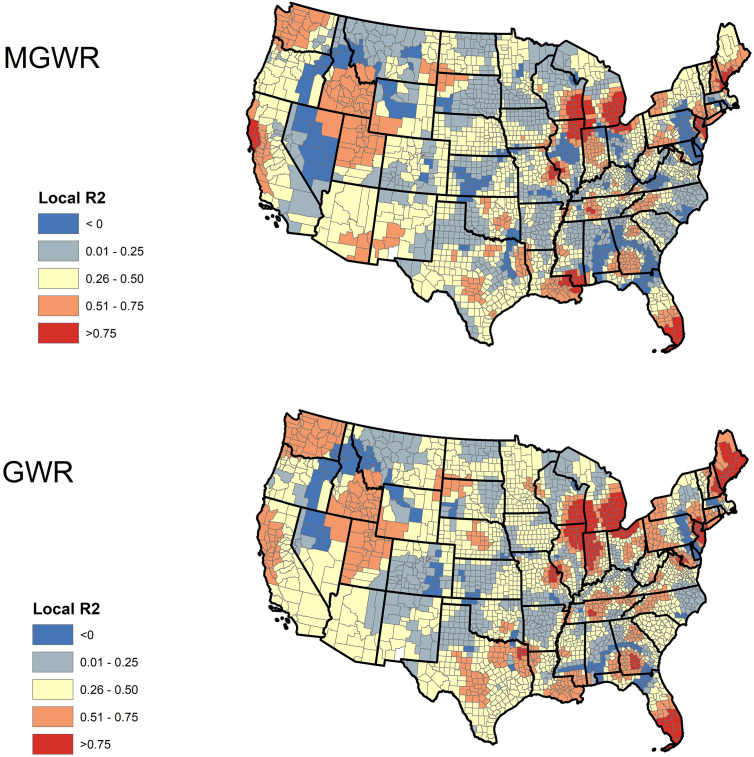
Fig. 3 illustrates the spatial distributions of local R² values in both GWR and MGWR models. In MGWR, several counties in southern Florida, southern Mississippi, eastern Wisconsin, and western California had very high local R², indicating a decent prediction of the model in these areas. On the contrary, the local R² values were low in most of the counties in Central and Southern United States, indicating the poor performance of the model across these counties. Although there is a clear consistency between the local goodness-of-fit of both GWR and MGWR, it is evident that MGWR was more conservative than GWR.

Fig. 3.

Geographic distribution of local R² of GWR and MGWR models for COVID-19 incidence rate associated with income inequality, median household income, % of nurse practitioners, and % of black females across the continental United States.

4. Discussion

In this GIS-based research, we compiled 35 variables that could potentially explain the spatial pattern witnessed in the COVID-19 incidence rate at the county-level across the continental United States. These variables were grouped into five different themes, namely socioeconomic, environmental, behavioral, topographic, and demographic. An ensemble of these variables was used to model the geographic distribution of COVID-19 incidence using a family of spatial regression and autoregressive models. Based on our findings, a combination of four variables of median household income, income inequality, percentage of nurse practitioners, and percentage of black female population could explain a relatively high variability of the disease incidence in the continental United States. Continued monitoring of these factors can aid in understanding the dynamics of disease spread. Among the implemented models, MGWR was shown to better explain the spatial context of COVID-19 incidence rates. Through the use of variable bandwidths, MGWR allowed for modeling the effect of neighboring counties in variable neighborhood sizes and provided more flexibility in studying the extent of spatial processes.

At the time of writing this manuscript, the states of New York, New Jersey, Louisiana, Massachusetts, and Connecticut respectively have the highest incidence of COVID-19 per population in the United States. Findings of GWR and MGWR suggested a strong positive relationship of disease incidence with income inequality and median household income in these areas. Ahmed et al. (2020) allude to the socioeconomic disadvantages and inequalities that arise during pandemics; COVID-19 is not an exception. As the disease continues to spread, the world has witnessed substantial vulnerabilities in healthcare systems, a steep decline in economies, and an increase in unemployment rates. For example, in the United States, those who become unemployed are at risk of losing their health insurance coverage, which can directly contribute to the health and economic disparities that already exist in the country (Gangopadhyaya and Garrett, 2020) and as such this pandemic can cause a feedback loop.

Furthermore, our findings support the substantial impact of healthcare professionals, such as nurse practitioners, during the pandemic. For instance, a recent article emphasized the presence of a significant number of healthcare professionals within 55 years old or over who are working on the frontline (Buerhaus et al., 2020). Their results suggest the importance of continued training for younger health care professionals in the United States. Yet, nurse practitioners and physician assistants may be limited in their health care practice due to state law limitations across numerous states (Bayne et al., 2020). Although we did not find consistent data pertaining to demographics, Dowd et al. (2020) emphasizes the importance of considering population dynamics and demographic data to mitigate the approaches to combat the pandemic.

Based on our study, environmental factors did not demonstrate to be substantially influential when compared to COVID-19 incidence. However, in China, Ma et al. (2020) found a significant association with diurnal temperature range and COVID-19, particularly pertaining to daily mortality. Further studies may consider temperature anomalies to analyze the severity of COVID-19 across the continental United States. While we did not find smoking to be significantly influential, Brake et al. (2020) emphasize that smoking contributes to the vulnerability of combating COVID-19. Their findings also highlight that smoking may not be limited to traditional cigarettes; other smoking methods and devices are to be further investigated, including electronic cigarettes and waterpipe smoking (Brake et al., 2020).

One of the limitations of this study was data availability. Due to unprecedented efforts in the global research community to provide and share public data regarding different aspects of the COVID-19 pandemic, access to disease data is not difficult. However, to the best of our knowledge, the finest spatial granularity at which nationwide COVID-19 data in the United States is available is at the county-level. Therefore making inferences at the sub-county and individual levels may not necessarily produce accurate results. Another limitation was modeling different statewide shelter-in-place or lockdown policies (or lack thereof) and the level at which such policies were implemented and enforced. Different states have had variations in policies and approaches ranging from a relatively early shelter in place orders in states such as New York and California to no limitations in Arkansas, Nebraska, and South Dakota. Such policies and their implementations could result in extraordinary impacts on disease incidence rates. However, isolating or modeling such effects would be a challenging task that was out of the scope of this study. Moreover, though we did not include pre-existing conditions as explanatory variables, they should be incorporated in further studies. Recent articles have considered comorbidities such as diabetes (Gupta et al., 2020) and cardiovascular conditions (Zheng et al., 2020) as potential risk factors for COVID-19. These risk factors may be significantly influential in COVID-19 health outcomes. Further analysis supporting the mentioned variables may aid in improving the quality of care, policy development, and an overall improvement in combating the pandemic.

5. Conclusions

Inspired by Oshan et al. (2019), who applied MGWR to study the spatial context of obesogenic process in the state of Arizona, and presuming that a multiscale approach would better explain the spatial variability of COVID-19 rate across the United States, we applied and compared the performance of MGWR to four other global or local models. Our results confirmed and extended the findings of the mentioned study as MGWR achieved the highest goodness-of-fit with the most parsimonious model, among others. The spatial variability of MGWR in different counties can reflect different behavior of COVID-19 incidence rates in response to the selected explanatory variables. To the best of our knowledge, there is a lack of nationwide researches on geographic modeling of COVID-19; thus, this study can be regarded as a basis for future geographic modeling of the diseases.

CRediT authorship contribution statement

Abolfazl Mollalo:Conceptualization, Data curation, Formal analysis, Writing - review & editing.Behzad Vahedi:Conceptualization, Writing - review & editing.Kiara M. Rivera:Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.