Self-straining of actively crosslinked microtubule networks

Abstract

Cytoskeletal networks are foundational examples of active matter and central to self-organized structures in the cell. In vivo, these networks are active and densely crosslinked. Relating their large-scale dynamics to the properties of their constituents remains an unsolved problem. Here, we study an in vitro active gel made from aligned microtubules and XCTK2 kinesin motors. Using photobleaching, we demonstrate that the gel’s aligned microtubules, driven by motors, continually slide past each other at a speed independent of the local microtubule polarity and motor concentration. This phenomenon is also observed, and remains unexplained, in spindles. We derive a general framework for coarse graining microtubule gels crosslinked by molecular motors from microscopic considerations. Using microtubule-microtubule coupling through a force-velocity relationship for kinesin, this theory naturally explains the experimental results: motors generate an active strain rate in regions of changing polarity, which allows microtubules of opposite polarities to slide past each other without stressing the material.

Active materials are made from energy-consuming constituents whose activity keeps the system out of equilibrium. Their study has deepened our understanding of self-organizing processes, both in vivo and in vitro^1,2. Its foundational examples include suspensions of microswimmers, in vitro assemblies of purified cellular components and the cell cytoskeleton³. Although notable progress has been made in deciphering the non-equilibrium physics of active materials by using experiments and symmetry-based phenomenological theories^4–6, there is far less understanding of how the large-scale dynamics actually devolves from microscopic activity. Such a theoretical framework would allow for rational design of new active materials and quantitative understanding of the cell cytoskeleton. We address this challenge for systems made of cytoskeletal polymers that are fully percolated by moving molecular motors. First, we describe the microscopic dynamics of a dense nematically aligned active gel made from purified microtubules and XCTK2 kinesin motors. Using photobleaching and second harmonic generation (SHG) microscopy, we show that the microtubule sliding speeds are independent of the local gel polarity and motor concentration, suggesting a robust internal coupling of the filamentous material. To investigate this phenomenon, we introduce a framework for systematically deriving continuum theories of densely crosslinked active gels from prescribed microscopic considerations. We use this framework to obtain a theory for the X CTK 2-microtu-bule system, which explains our experimental findings without adjustable parameters.

Many aspects of cell biology, including cell shape, motility and division, are driven by the cytoskeleton⁷. The cytoskeleton consists of polar filaments (mainly actin and microtubules) and the proteins that crosslink them and organize their behaviour. Molecular motors are active crosslinkers that use chemical energy to move filaments relative to each other. They play a central role in determining the architecture and dynamics of cytoskeletal structures such as the cell cortex and the spindle³. How large-scale behaviours of actively crosslinked networks emerge from the properties of their constituents is important for quantitative understanding of the cellular cytoskeleton^8–10. The in vitro XCTK2-microtubule system that we study recapitulates the previously unexplained polarity-independent sliding motion of microtubules that was observed using speckle microscopy in Xenopus meiotic spindles^11–13 and allows us to study how polarity-independent filament motion can emerge in actively crosslinked networks.

Phenomenological theories for actively crosslinked networks have been derived from conservation laws and symmetry considerations^1,4–6,14. They can reproduce the flow patterns observed in artificial¹⁵ and biological systems, such as the cell cortex^8,16–18, and quantitatively explain some aspects of spindle structure and dynamics¹⁹. However, such theories do not address how the large-scale behaviours of actively crosslinked networks emerge from the properties of their constituents. For this, an approach that derives macroscopic material laws from the properties of motors and filaments is needed.

Previous efforts to derive continuum theories for active gels from microscopic interactions have considered sparsely crosslinked systems, in which individual motor-filament clusters are thought of as disconnected objects^20–30. In contrast, actively crosslinked networks, such as the cytoskeleton3, are tightly coupled over length scales comparable to the system size and display behaviours different from those predicted for sparsely crosslinked active fluids. The rheologi-cal properties of highly crosslinked gels have been studied using combinations of numerical and analytical techniques^31–35. Here, we present an analytic framework for deriving continuum equations that capture their dynamics.

Experiments

To study the behaviour of heavily crosslinked active gels, we created one from purified microtubules and 0.4 μM of XCTK2, a minus-end directed kinesin-14 molecular motor capable of crosslinking and sliding aligned microtubules³⁶. Fluorescently labelled tubulin and fluorescently labelled XCTK2 were mixed together, and then paclitaxel was added, which nucleated and stabilized the microtubules. The sample was rapidly loaded into a 0.1 × 1 × 20mm³ rectangular microfluidic chamber (see Supplementary Information). The microtubule-motor mixture contracted within the first ~10 min and formed a macroscopic gel, with its microtubules nematically aligned parallel to the long axis of the microfluidic chamber. The sample remained in this macroscopically aligned state for ~1 h, after which the gel buckled and displayed complex dynamics for hours longer. Along the long axis, the boundaries of the material remained frictionally pinned at the chamber’s ends throughout the experiment. In this study, we characterize the motions of microtubules in the macroscopically aligned state of the gel, before buckling occurred.

We used a femtosecond laser to photobleach microtubules in the aligned gels, near the centre of the chamber, and investigate their dynamics. We generated multiple bleach lines orthogonal to the nematic director (Fig. 1a). Each of the bleached lines split into two parallel lines, which moved apart along the direction of alignment (Fig. 1b, left), indicating that microtubules in the gel are continually sliding relative to each other. Control experiments confirmed that the laser bleached, but did not ablate, the microtubules (see Supplementary Information).

Fig. 1 |. Bleaching of aligned active gels reveals microtubule sliding speed.

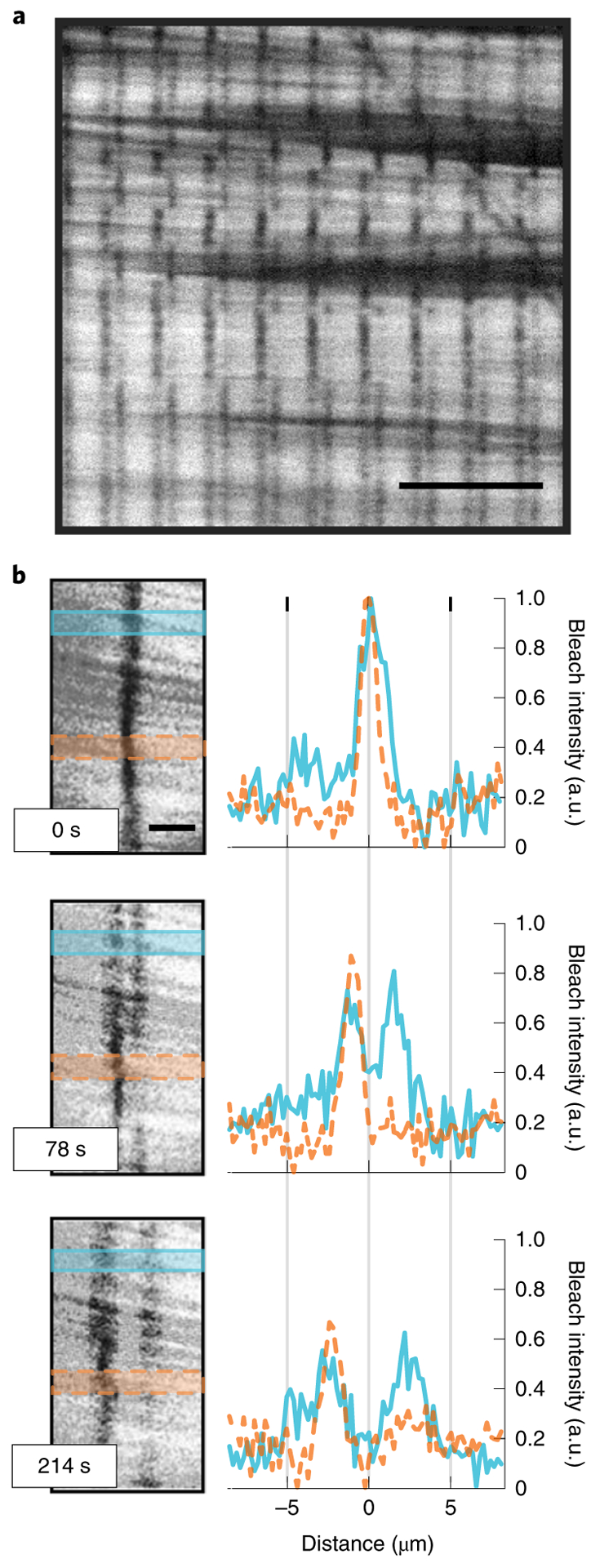
a, Aligned active gel after multi-line photobleaching. Scale bar, 20 μm. b, Left: higher magnification images of a bleached line taken at three different times. The bleached line with spatially varying polarity splits into two parallel lines as the microtubules slide apart. Solid blue and dashed orange shaded areas highlight regions of low and high polarity respectively. Right: intensity profiles of the high polarity (dashed orange, P_bleach = 0.63 ±0.12 standard error) and low polarity (solid blue, P_bleach = 0.08 ± 0.17 standard error) regions. Despite the difference in polarity, the peaks move apart at nearly identical speeds. Scale bar, 5 μm. XCTK2 concentration is 0.4 μM.

When a bleached line splits into two, the relative fluorescent intensity of the two new lines reflects the relative number of left-moving and right-moving microtubules. Hence, the relative bleach intensity provides a measure of the polarity at the initial location of the bleach. We define the bleach polarity, $P_{\text{bleach }}=\left|\frac{I_1-I_2}{I_1+I_2}\right|$, where I₁ and I₂ are the bleach intensities of the two lines (see Supplementary Information). The speed at which the two lines move apart provides a measure of the speed of microtubule sliding. Along the same bleach line, some regions have very high polarity (Fig. 1b, orange, P_bleach = 0.63 ± 0.12), while others have very low polarity (Fig. 1b, blue, P_bleach = 0.08 ± 0.17). Despite this difference in polarity, the speed of sliding is very similar (Fig. 1b, right, compare orange and blue). We next performed experiments with varying motor concentrations. We measured the polarity and sliding speeds for four different motor concentrations (0.3, 0.4, 0.5 and 0.75 μM), each at many different locations, and found that the speed of microtubule sliding was independent of both polarity and motor concentration (Fig. 2). For motor concentrations below 0.3 μM, the microtubules did not contract and did not spontaneously align. For motor concentrations above 0.75 μM the gels buckled before settling down into an aligned state. The average speed that microtubules slid apart in these XCTK2 active gels was 18.6 ± 0.9 nm s⁻¹, which is very close to the observed speed of 20 nm s⁻¹ at which XCTK2 slides apart isolated pairs of microtubules³⁶.

Fig. 2 |. Microtubule sliding speed is independent of polarity and motor concentration.

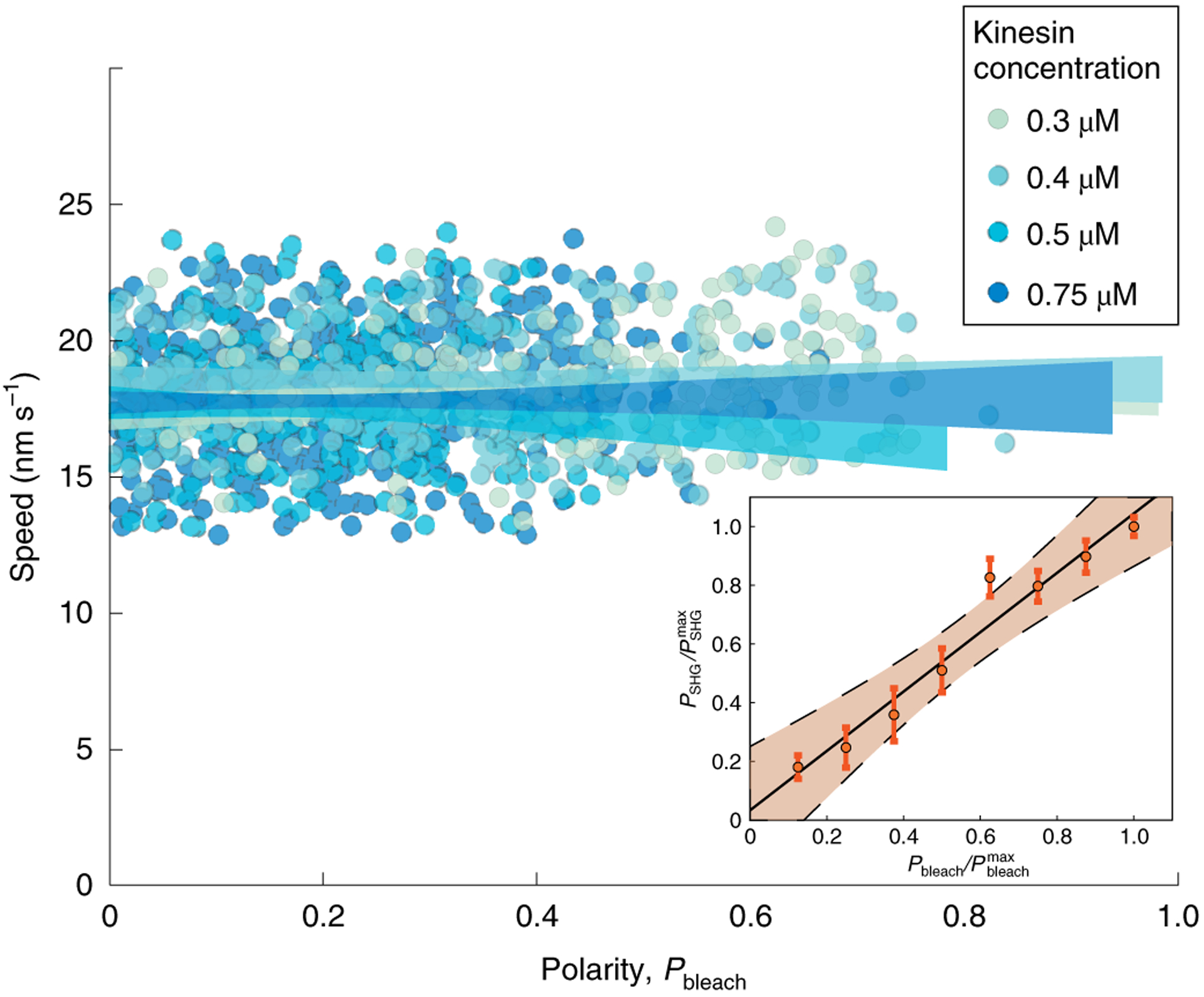
Local measurements (2μm bins) from photobleaching of microtubule sliding speed and polarity, P_bleach, for different XCTK2 concentrations. The shaded regions indicate the 95% confidence intervals of a linear regression for each motor concentration. Inset: correlation between local polarity P_bleach of microtubule motion measured by bleaching and local physical polarity P_SHG of microtubules measured by SHG. The black line is a linear regression and the shaded region indicates the corresponding 99% confidence interval.

P_bleach provides a local measure of the polarity of microtubule motion, that is, of the relative number of left-moving and right-moving microtubules. We next sought to determine to what extent this polarity of microtubule motion is related to the physical polarity of microtubules in the gel, that is, of the relative number of left-facing and right-facing microtubules. The physical polarity of microtubule arrays can be measured by simultaneous SHG, a nonlinear optical technique in which a signal can be produced from non-centrosym metric materials, and two-photon microscopy of fluorescent microtubules. The local physical polarity is proportional to $P_{\text{SHG}}=\sqrt{I_{\text{SHG}}/I_{\rho }^2}$, where I_SHG is the intensity measure from SHG and I_ρ is the intensity measure from two-photon microscopy³⁷. We simultaneously measured P_SHG and P_bleach at multiple locations, and found that they are highly correlated (Fig. 2, inset). Therefore, in this gel, the local dynamic polarity of microtubule motion reflects the local physical polarity of microtubules, and the microtubule sliding speed is independent of the local polarity. This is reminiscent of the independence of microtubule sliding speed and polarity observed in spindles^11–13.

The polarity-independent sliding speed of microtubules is difficult to reconcile with existing kinetic theories, which apply in the limit of dilute and sparsely crosslinked networks where the length scale over which filaments are interconnected is small compared to the system size. To illustrate the issue we describe previously presented arguments^20,28. In the absence of external driving forces, the balance of forces yields ρ⁺f⁺ + ρ⁻f⁻ = 0, where ρ^± are the densities of microtubules pointing along the nematic axis of the system in the positive and negative directions, respectively, and f^± are the forces acting on microtubules from their interactions with ∓ microtubules, respectively. In a sparsely crosslinked system the force exerted by a motor on a microtubule is balanced only by the drag between the microtubule and the surrounding medium. Assuming that the medium is locally at rest, the velocity of microtubules, v^±, will be given by v^±=μf^±, where μ is the microtubule mobility. A molecular motor crosslinking two microtubules moving at a speed V imposes v⁺−v⁻= 2V. Taken together, this leads to v^±=∓V(1∓P), where $P=\frac{{\rho }^{+}-{\rho }^{-}}{{\rho }^{+}+{\rho }^{-}}$ is the local microtubule polarity.

The argument described above predicts that the microtubule sliding velocity changes linearly with polarity, in conflict with our experimental measurements of reconstituted gels and spindle. Fundamentally, this prediction is a consequence of force balance in sparsely crosslinked systems: the mass fluxes of left moving and right moving microtubules locally balance because the momentum transfer in the system is dominated by fluid-mediated interactions. Polarity-dependent sliding generalizes to more sophisticated versions of dilute theories that include effects such as long-range hydrodynamics (see Supplementary Information). The disagreement between this theory and experiment suggests that microtu-bule-XCTK2 gels may not be in a sparsely crosslinked regime. To examine this possibility, we quantified the microtubule density in our gel by measuring the initial molarity of components in our mixture and then determined the percentage of components that were incorporated into the final gel via fluorescence microscopy. We estimate a 5% volume fraction of polymerized microtubules in the gels, with 17 microtubules per μm³ (see Supplementary Information) and ~25 XCTK2 dimers bound to each microtubule. Given that microtubules are significantly longer than their average spacing, this result argues that these networks are heavily crosslinked by molecular motors—far from the dilute theory described above. Motivated by such considerations, we developed a model of heavily crosslinked microtubule networks.

Theory for densely crosslinked microtubule gels

In our theory, microtubules are characterized by their length L, velocities v_i and orientations p_i. The distribution of microtubule positions and orientations $\psi (x,p)=\sum _i\delta \left(x-x_i\right)\delta \left(p-p_i\right)$ obeys the Smoluchowski equation ${\partial }_t\psi =-\nabla \cdot (\stackrel{.}{x}\psi )-{\partial }_p\cdot (\stackrel{.}{p}\psi )$. The microtubules’ translational and rotational fluxes, $\stackrel{.}{x}\left(x_i,p_i\right)=v_i$, and $\stackrel{.}{p}\left(x_i,p_i\right)={\stackrel{.}{p}}_i$, respectively, can be determined from the conditions F_i = 0 and T_i= 0, which state that the total force F_t and torque T_t on each microtubule are zero.

The forces and torques applied to microtubules are generated by the molecular motors that actively crosslink them. Here, motors are characterized by their force-velocity relation, the distance R (the motor size) over which they can crosslink filaments, and the crosslinking torque that they apply. The force that microtubule j exerts on microtubule i, via active crosslinks between x_t + s_tp_t and x_j + s_jp_j (Fig. 3a), is given by F_ijds_ids_j and the total force on microtubule i is

$$F_i=\underset{-L/2}{\overset{L/2}{\int }}\text{d}{s}_i\sum _j\underset{-L/2}{\overset{L/2}{\int }}\text{d}{s}_j\int \text{d}{p}_j\underset{\Omega \left(x_i+s,p_i\right)}{\int }\text{d}{x}^3\times \delta \left(x-x_j-s_j{p}_j\right)\delta \left(p-p_j\right)F_{ij}$$ (1)

where Ω(x) denotes a sphere of radius R centred at x (Fig. 3b). The force density can be written as the divergence of the network stress tensor Σ according to Kirkwood’s formula since F_ij = −F_ji (see Supplementary Information). The force balance of the network reads

$$\nabla \cdot \Sigma (x)=\sum _i{F}_i\delta \left(x-x_i\right)=0$$ (2)

In a dense and highly crosslinked system, the motion of the fluid in which microtubules are suspended follows the microtubule motion and can be ignored (see Supplementary Information). The torque that crosslinkers between filaments i and j exert on filament i is given by T_ijds_ids_j with T_ij= s_ip_i×F_ij+Γ_ij, where Γ_ij is the contribution stemming from an explicit crosslinker torque. The total torque T_i on microtubule i obeys an equation analogous to equation (1) (see Supplementary Information).

Fig. 3 |. Sketch of the microscopic model.

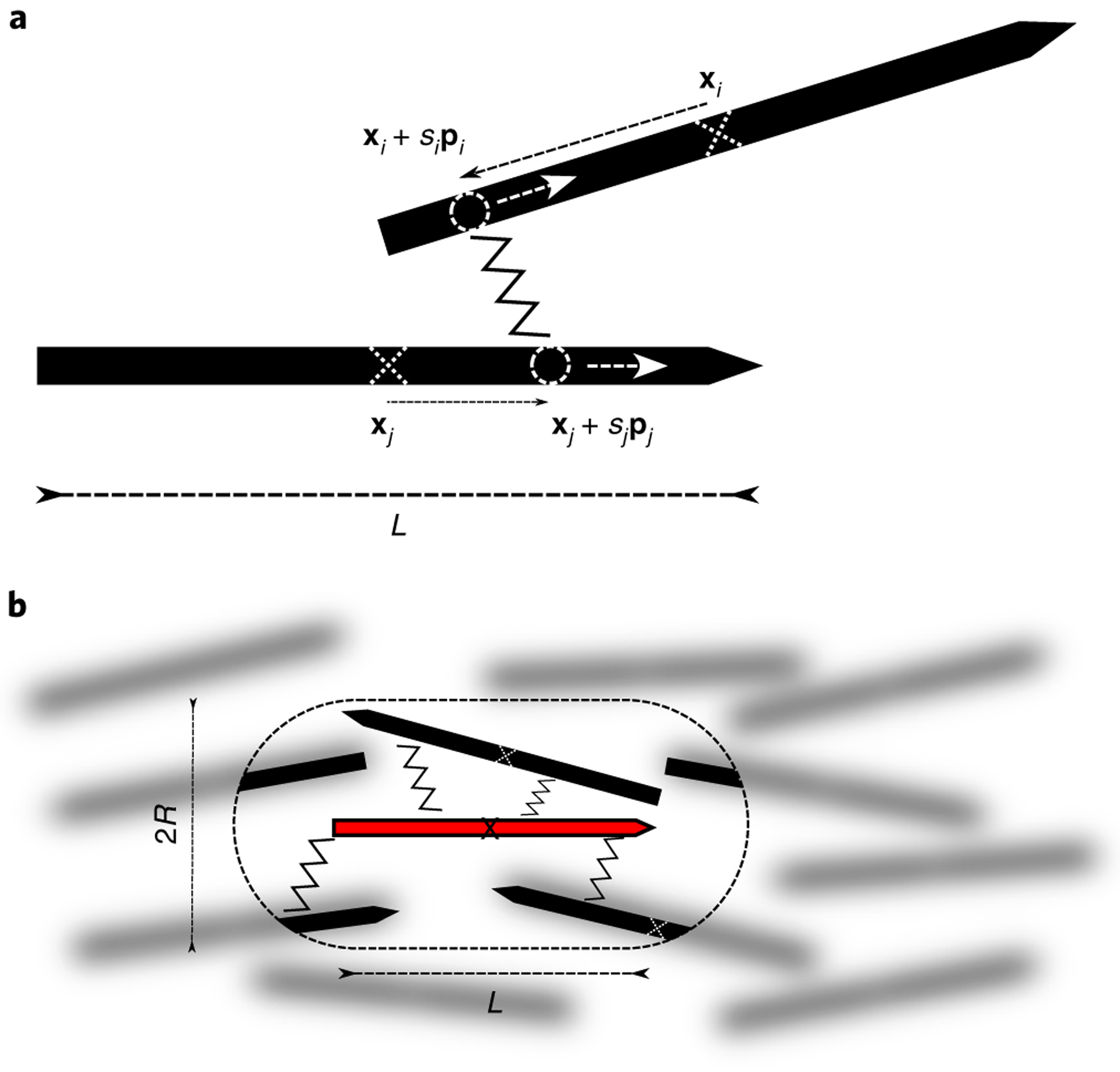
a, Each microtubule (black solid arrow) is characterized by its centre of mass position x (white crosses) and its orientation p. Microtubules interact via motor molecules (zigzag line), which connect them at arclength positions s_i, s_j (white circles) and walk towards their plus ends (white arrows). b, In the gel, crosslinkers of a test microtubule (red) explore all possible connections to other microtubules within reach (within the dashed capsule), that is, within a sphere of radius R around any position along the test microtubule.

We model the XCTK2 motors by a force-velocity relation and a crosslinking torque density. The force density F_ij(Δv_ij.) exerted by motors depends on the velocity difference Δv_ij between their two motor heads. The crosslinking torque density Γ_ij(p_i, p_j) depends on their orientations. For simplicity, we ignore the effects of non-uniform distributions of motors along microtubules. Furthermore, we do not account for the buildup of elastic strain in the motors, which is a good approximation on timescales that are large compared to motor binding/unbinding times. To linear order in Δv_ij

$$F_{ij}=-G\cdot \left[v_i+s_i{\stackrel{.}{p}}_i+V{p}_i-\left(v_j+s_j{\stackrel{.}{p}}_j+V{p}_j\right)\right]$$ (3)

where Vp_i is the velocity of the motor relative to the microtubule it is bound to. This choice renders the force between two microtubules dependent on their relative polarities. The linear response coefficient G is the motor friction and is in general a second rank tensor. In the following we choose G = γI for simplicity. Note that our results also hold for force velocity relations that are nonlinear in Δv_ij (see Supplementary Information). For the crosslinking torque density we choose Γ_ij = vp_i×p_j(p_i·p_j), which aligns microtubules, as would for example a torsional stiffness of the crosslinker. The coefficient v characterizes the magnitude of this effect. Note that, dimensionally, F_ij and T_ij are forces and torques per area, respectively. It is straightforward to generalize our formulation to include motor activity that varies along the length of a filament, say by pausing at microtubule ends. This effect has been linked to network contractions^20,27,35.

We next derive a continuum theory for our system. We start by expanding equation (1) around the centre-of-mass positions x_i and x_j:

$$F_i=-\gamma L^2\underset{\Omega \left(x_i\right)}{\int }\text{d}{x}^3\rho (x)\left[\left(v_i-v(x)\right)+V\left(p_i-P(x)\right)\right]-\gamma \frac{L^4}{12}\underset{\Omega \left(x_i\right)}{\int }\text{d}{x}^3\nabla \cdot \left[\rho (x)\left(p_i{\stackrel{.}{p}}_i+\mathcal{H}(x)\right)\right]$$ (4)

Here we have assumed that the length scale a of gradients in the system is large compared to the microtubule length L and dropped terms with more than two spatial derivative (see Supplementary Information). We also introduced density ρ(x) = ∫dpψ(x, p), the polarity P(x) = 〈p_i〉, the rotation rate tensor $\mathcal{H}(x)=p_i{\stackrel{.}{p}}_i$ and the velocity field v(x) = 〈v_i〉, where the angled brackets $\langle \dots \rangle =1/\rho {\sum }_i\int \text{d}p\delta \left(x-x_i\right)\delta \left(p-p_i\right)\dots$ denote local averaging. The force balance equation (2) becomes

$$\nabla \cdot \Sigma (x)=-\gamma L^2\underset{\Omega (x)}{\int }\text{d}{y}^3\rho (x)\rho (y)\left\{v(y)-v(x)+V(P(y)-P(x))\right\}-\gamma \frac{L^4}{12}\underset{\Omega (x)}{\int }\text{d}{y}^3\rho (x)(\nabla \cdot (\rho (y)\mathcal{H}(y))+(\nabla \rho (y))\cdot \mathcal{H}(x))$$ (5)

Now, using R/a≪1, we expand the integrand in equation (5) around x and perform the integration. In this way, for the gel stress tensor we obtain

$$\Sigma =\eta {\rho }^2(\nabla v+V\nabla P)-\alpha {\rho }^2\mathcal{H}$$ (6)

The coefficients $\eta =\gamma \frac{4\pi }{15}{L}^2{R}^5$ and $\alpha =\gamma \frac{4\pi }{36}{L}^4{R}^3$ have dimensions of viscosity by density squared. The first term of the stress tensor in equation (6) is viscous-like (that is, it depends on ∇v) and captures long-ranged coupling between microtubules. In contrast to a dilute suspension theory, in which a viscous coupling would be induced by the fluid, here it is induced by the crosslinkers. For active crosslinkers (V≠ 0) the stress-free state is self-straining and the gel’s spontaneous strain rate is ∇v = −V∇P. The second term of equation (6) is generated by microtubules reorienting in the gel and is analogous to a nematic alignment stress in liquid crystal theory. (We note that the ordering stress recovers the form derived for kinetic theories that approximate microtubule alignment by the Maier-Saupe free-energy²⁶ when using equation (8).) From equation (4), using ∇ · Σ= 0, we obtain the translational flux of microtubules:

$$v_i-v=-V\left(p_i-P\right)-\frac{L^2}{12}\frac{\nabla \rho }{\rho }\cdot \left(p_i{\stackrel{.}{p}}_i-\mathcal{H}\right)$$ (7)

An analogous calculation for the torque balance (see Supplementary Information) yields

$$\alpha p_i\times {\stackrel{.}{p}}_i=\widehat{\nu }{p}_i\times \left(p_i\cdot \mathcal{Q}\right)$$ (8)

which is reminiscent of Maier-Saupe theory, where $\widehat{\nu }=\nu L^2\frac{4\pi R^3}{3}$ and where $\mathcal{Q}(x)=p_i{p}_i$ is the nematic tensor order parameter. The force balance ∇ · Σ = 0 and equations (6), (7) and (8) fully specify the system’s dynamics and can be used to evolve the distribution of microtubule positions and orientations.

Comparison and interpretation

We next use the above described theory to investigate microtubule sliding in actively crosslinked networks. First we show that v_i = −Vp_i is the solution to an aligned network, which is the experimentally observed behaviour. Consider a fully aligned gel with all $p_i=\pm \widehat{e}$, for some unit orientation vector $\widehat{e}$. With this, equation (8) yields ${\stackrel{.}{p}}_i=0$. We make the ansatz v_i = −Vp_i+ C₀ + x_i × C₁, where C₀, C₁ denote constant rates of translation and rotation, respectively. After evaluating v = 〈v_i〉 and p = 〈p_i〉, this micro-scale ansatz obeys equation (7) and yields a macro-scale spatially uniform stress tensor satisfying Σ ≡ 0. It thus solves the force balance ∇ · Σ = 0 with stress free boundary conditions for any system geometry. To determine the constants C₀ and C₁ we impose that the gel be at rest in the lab frame, such that $\sum _i{v}_i=0$ and $\sum _i{x}_i\times v_i=0$, where we choose a coordinate system for which x = 0 is the system’s centre of mass. In our experiments, to good approximation $\sum _i{p}_i=0$ and $\sum _i{x}_i\times p_i=0$, that is the total number of left and right pointing microtubules are approximately equal and polar domains are distributed homogeneously throughout the system. With this, we find v_i =−Vp_i.

This means that all microtubules translate with the motor velocity in the direction of their plus end. The microtubule velocities are independent of the local polarity and only depend on the speed of the kinesin motors. This phenomenon is explained by motors generating an active strain rate in regions of varying polarity. Thus, microtubules can slide past each other without stressing the material because ∇v= −V∇P; see equation (6). This surprising behaviour is a collective effect, as can easily be seen when considering the case of two isolated microtubules: two parallel microtubules linked by motors will be at rest in the lab frame, while two anti-parallel ones will move. Ultimately, the system consists of two inter-penetrating gels of microtubules of opposite polarity that push against each other, with each gel held together by viscous coupling. In contrast, for sparsely crosslinked networks, the mass fluxes of left-moving and right-moving microtubules locally balance, leading to a strong dependence of sliding speed on the local polarity.

Thus our theory makes a series of quantitative predictions. First, the microtubules’ sliding speed should be independent of the local network polarity. Second, the sliding velocity should be independent of the motor concentration. We find both of these predictions to be accurate in our experiments (Fig. 2). Third, we predict the sliding speed is set by the speed of the motor itself. We measured speeds of 18.6 ± 0.9 nm s⁻¹, which are comparable to the single-molecule motor speeds of XCTK2 (~20 nms⁻¹)³⁶. Importantly, our predictions do not depend on adjustable parameters and arise directly from the form of equations (1) and (3). In turn, the form of equation (3) results from imposing that molecular motors act uniformly along the length of the microtubules, which is a good approximation for the XCTK2 motor at high enough densities³⁶.

Polarity-independent sliding velocities are also observed in spindles formed in Xenopus egg extracts. These spindles consist of an array of microtubules that are anti-parallel near the spindle centre and highly polar at the spindle poles^37–38. Microtubules in these spindles continually slide toward spindle poles, a motion believed to be driven by the molecular motor kinesin-5¹¹. Due to the symmetries observed in spindles³⁸, $\sum _i{v}_i\simeq 0$ and $\sum _i{x}_i\times v_i\simeq 0$, as in our in vitro experiments. Because motors in spindles are abundant, we speculate that spindles might be self-straining, like the XCTK2-micro-tubule gel presented here. If this were the case, the speed of sliding should be the speed of kinesin-5 itself and constant throughout the spindle. Very suggestively, this is exactly what has been observed. In spindles, and particularly so when dynein is inhibited, microtubules slide at a constant speed^12,13 that is approximately equal to the speed at which kinesin-5 slides apart pairs of anti-parallel microtubules in vitro³⁹. This suggests that, like our experimental system, spindles might consist of two inter-penetrating gels of microtubules of opposite polarity. Mechanically, this puts them in a regime between polymer suspensions and solid-like structures.

Our analytical framework can be used to investigate microtubule networks crosslinked by different motors. For example, dyneins pause and accumulate at microtubule minus ends⁴⁰. This motor dynamics can be implemented within our theory by modifying equation (3), which gives rise to $\mathcal{Q}$ and ρ dependent active stresses (the calculation that predicts stresses for a generalized force-velocity curve will be presented in a subsequent publication). Such active stresses explain dynein-driven contractions of microtubule networks^27,35,40. Thus, the described theory generalizes previous models for network contractions²⁷ by providing a rigorous framework to predict how different motor properties give rise to different active stresses.

The self-straining state depends only on the balance between activity and viscous material response. Elastic deformations of either microtubules or motors do not play a role in this behaviour. Elastic, active networks can behave quite differently from the purely viscous systems^31–33. For example, in elastic, active polymer gels, passive crosslinkers facilitate the buildup of contractile stresses³⁴, which do not arise in the purely viscous limit. In our viscous theory, adding passive crosslinkers turns out to be exactly equivalent to slowing the motor. The interplay between viscous and elastic effects can be studied in our framework by augmenting equation (3) with elastic, history-dependent terms.

Many cytoskeletal networks are densely crosslinked. For example, the contractility of acto-myosin networks has been explained as emerging from its heavily crosslinked nature^33,34. The work presented here is an important step towards predicting the material properties of actively crosslinked materials from the properties of their constituents and will enable the design of novel dynamics from first principles.