Gender and Parity in Statistical Prediction of Anterior Carry Hand-Loads from Inertial Sensor Data

Abstract

The objective of this study was to examine potential gender effects on the performance of a statistical algorithm for predicting hand-load levels that uses body-worn inertial sensor data. Torso and pelvic kinematic data was obtained from 11 men and 11 women in a laboratory experiment while they carried anterior hand-loads of 13.6 kg, and 22.7 kg, and during unloaded walking. Nine kinematic variables expressed as relative changes from unloaded gait were calculated and used as predictors in a statistical classification model predicting load-level (no-load, 13.6 kg, and 22.7 kg). To compare effects of gender on prediction accuracy, prediction models were built using both, gender-balanced gait data and gender-specific data (i.e., separate models for men and women) and evaluated using hold-out validation techniques. The gender-balanced model correctly classified load levels with an accuracy of 74.2% and 80.0% for men and women, respectively. The gender-specific models had accuracies of 68.3% and 85.0% for men and women, respectively. Findings indicated a lack of classification parity across gender, and possibly across other types of personal attributes such as age, ethnicity, and health condition. While preliminary, this study hopes to draw attention to challenges in algorithmic bias, parity and fairness, particularly as machine learning techniques gain popularity in ergonomics practice.

INTRODUCTION

Prolonged and frequent manual load carriage is an occupational risk factor for developing low back disorders such as a prolapsed lumbar disc (Kelsey et al., 1984). Knowledge about the magnitude of hand-load is essential information for assessing the longitudinal biomechanical impacts of load carriage on the musculoskeletal health of workers.

Prior studies about biomechanical adaptations to carrying hand-loads have shown that besides temporal changes in gait patterns, torso and pelvis postural sway and thoracic-pelvic coordination show significant changes with increasing hand load (Kinoshita, 1985; LaFiandra, Wagenaar, Holt, & Obusek, 2003). Utilizing this information, a novel prediction model of hand-loads that uses gait kinematics calculated from inertial sensor data was previously investigated (Lim & D’Souza, 2018, 2019). However, this work was limited to a cohort of young men.

Gait kinematics are also influenced by anthropometry resulting from differences in age (Nigg, Fisher, & Ronsky, 1994), gender (Mazzà et al., 2009) and strength. In a study on manual load carriage, Martin & Nelson (1986) reported that spatio-temporal gait parameters (e.g., stride length, swing duration) showed greater sensitivity to load magnitude in women compared to men. Gender differences in gait kinematics carrying hand-loads could potentially affect the performance of algorithms designed to predict hand loads during manual load carriage. This has practical concerns if such prediction algorithms either systematically under- or over-estimate the predicted load level differently for men vs. women.

The aim of this study was to examine potential gender effects on the performance of a statistical algorithm for predicting hand-load levels that uses body-worn inertial sensor data on torso and pelvic kinematics for classifying three hand-load levels (viz., no-load, 13.6 kg, and 22.7 kg). Gender bias was assessed by building a classification model with gait data from a gender-balanced sample of men and women. Gender-specific models (men- only vs. women-only) were also developed for comparing performance of the prediction model.

METHODS

Study Participants

Twenty-two healthy individuals (11 men, 11 women; 18-55 years old) were recruited for the study. Table 1 summarizes the average ± standard deviation age, stature, and mass of participants by gender. Participants reported no pre-existing back injuries or chronic pain in the last six months period by using a body discomfort questionnaire adapted from the body mapping exercise by NIOSH (Cohen, Gjessing, Fine, Bernard, & McGlothlin, 1997). The study was approved by the university’s institutional review board and written informed consent was obtained from participants prior to the study.

Table 1.

Summary statistics of the sample recruited in the study (n = 22).

	Gender
	Men (n=11)	Women (n=11)	Total (n=22)
Age (years)	34.8 ± 11.0	32.3 ± 10.2	34.2 ± 10.6
Stature (mm)	1803.9 ± 69.4	1677.2 ± 51.8	1734.2 ± 87.3
Mass (kg)	78.7 ± 13.8	70.3 ± 12.4	74.3 ± 13.4

Experiment Procedure

A laboratory experiment was conducted that required participants to carry a weighted box down a levelled corridor (12 m length x 1.5 m width) for a distance of 10 m done twice. Two box weights were evaluated (13.6 kg, and 22.7 kg) in random order, in addition to a no-load (i.e., unloaded reference) walk trial conducted first. Participants were allowed to self-select their walking speed across conditions in order to obtain their natural adaptation in walking patterns. A 2-minute rest break was provided between each trial.

Instrumentation

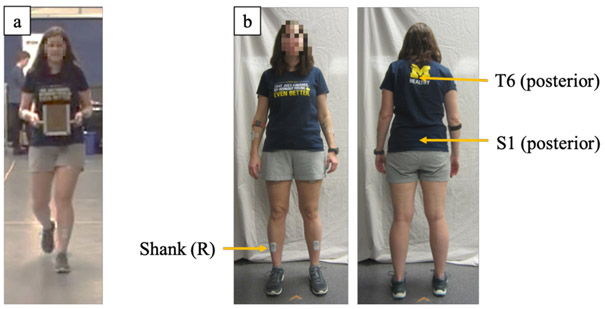
Three commercial inertial sensors (BiostampRC, mc10 Inc., Cambridge, MA, USA) were attached on the skin using double-sided tape at the sixth thoracic vertebra (T6), the first sacral vertebra (S1), and posterior-superior aspect of the right shank midway between the lateral femoral and malleolar epicondyles (Figure 1).

Figure 1.

Images showing (a) a sample participant carrying the weighted box (177.8 mm width x 228.6 mm depth x 203.3 mm height) in a two-handed anterior carry, and (b) locations for the three body-worn inertial sensors.

The inertial sensors recorded 3-D accelerometer and gyroscope data at a sampling frequency of 125 Hz. Sensor data was down-sampled to 80 Hz and filtered using a second-order low-pass zero-lag Butterworth filter with a cut-off frequency of 2-Hz. Gyroscope data (angular velocity, rad/s) were integrated and filtered using a second-order high-pass filter with a cut-off frequency of 0.75 Hz to reduce the effect of drift (Williamson & Andrews, 2001).

Algorithm to Classify Load Level

The statistical classification process was performed in four general steps to predict the outcome variable, namely, load level (i.e., no-load, 13.6 kg, or 13.6kg) for each walking trial (for details refer Lim & D’Souza, 2019). First, individual gait cycles were detected using a custom gait detection algorithm implemented in MATLAB R2016b (The MathWorks Inc.). Second, nine gait parameters were calculated over each gait cycle. Six torso and pelvis postural sway variables were obtained by calculating the range of angular displacement from the T6 and S1 sensors in each of the three anatomical planes, respectively (i.e., transverse, sagittal, and coronal planes). Mean relative phase angles between T6 and S1 sensor data in three planes were also calculated to represent the thoracic-pelvic coordination pattern (LaFiandra et al., 2003; van Emmerik & Wagenaar, 1996).

To account for inherent individual differences in gait patterns, all nine gait parameters were expressed in terms of the percent change from each individual’s average no-load gait parameters as follows:

$$X_{(i)relative}(\%)=\frac{X_{(i)}-{\overline{X}}_{noload}}{{\overline{X}}_{noload}}\ast 100$$ (1)

where:

X_(i)relative = Percent change in gait parameter at gait cycle i, X_(i) = Gait parameter at gait cycle i, ${\overline{X}}_{noload}$ = Average gait parameter across gait cycles in a no-load condition for each participant. Third, classification of load levels was performed for each gait cycle by using the Random forest method (Breiman, 2001), which is a nonparametric machine-learning algorithm based on a decision tree that grows using recursive binary partitioning at the nodes of the tree. A tree size of 500 was used for each prediction model in this study. The model was implemented using the randomForest package v.4.6-12 (Liaw & Wiener, 2002) in R v.3.3.1 (R Core Team, 2016). Fourth, the prediction results from each gait cycle within a walk trial were used to decide the final classification result for the walk trial using a Bayesian inference update (Box & Tiao, 2011).

Evaluating Model Performance

Model performance was evaluated by a hold-out validation test repeated 20 times. In each test, data from 2 randomly selected participants (1 man, 1 woman) was held out as a validation set while the remaining data (10 men, 10 women) was used to train the model. For comparison purposes, gender-specific models were also developed separately for men and women. The validation procedure was the same as the previous model except that each model was built and tested using data specific to each gender. Three measures of model prediction performance were calculated, namely, average prediction accuracy, precision, and sensitivity, and summarized in the form of a confusion matrix.

RESULTS

An average ± standard deviation of 7.5 ± 1.1 (range: 5 ~ 10) gait cycles were obtained in each repetition of the walk trials. A total of 132 walk trials were recorded across all participants and load levels (i.e., 22 participants x 3 load levels x 2 repetitions = 132 walk trials). In each hold-out test, 12 walk trials were selected for testing (i.e., 2 participants x 3 load levels x 2 repetitions = 12 walk trials). Subsequent results are based on this count.

Model Performance

Table 2 provides the confusion matrices from 20 hold-out tests for the model developed using gender-balanced data. When stratified by gender, the model’s overall prediction accuracy was 74.2% for men and 80.0% for women. For both men and women, most of the misclassifications occurred when distinguishing between load levels of 13.6 kg vs 22.7 kg. The higher load level (22.7 kg) was underestimated as the lower load (13.6 kg) more often in the data for men (19 of 40 trials) compared to women (7 of 40 trials).

Table 2.

Confusion matrices by gender for predicting load levels per walk trial using a gender-balanced statistical prediction model. Under- vs. over-estimated misclassifications are colored in red and green, respectively.

Men (prediction accuracy = 74.2%)
		Predicted Load Level			Total	Sensiti vity
		No-load	13.6 kg	22.7 kg
Actual Load	No-load	40	0	0	40	100%
	13.6 kg	7	29	4	40	72.5%
	22.7 kg	1	19	20	40	50%
Total		48	48	24	120
Precision		83.3%	60.4%	83.4%
Women (prediction accuracy = 80.0%)
		Predicted Load Level			Total	Sensiti vity
		No-load	13.6 kg	22.7 kg
Actual Load	No-load	40	0	0	40	100%
	13.6 kg	2	25	13	40	62.5%
	22.7 kg	2	7	31	40	77.5%
Total		44	32	44	120
Precision		90.9%	78.1%	70.5%

Conversely, the lower load level of 13.6 kg was more often overestimated as the high load among women (13 of 40 trials) compared to men (4 of 40 trials). None of the no-load trials were misclassified as “loaded” suggesting high sensitivity for the no-load condition. However, some of the loaded conditions were misclassified as the no-load condition, i.e., a precision of 83.3% and 90.9% at no-load for men and women, respectively.

Table 3 provides the confusion matrices from 20 hold-out tests for separate models developed and assessed for men and women. The classification accuracy of the model for men was 68.3%, and for women was 85.0%. Misclassifications still occurred when distinguishing between load levels of 13.6 kg vs 22.7 kg, more so among the model specific to men compared to women.

Table 3.

Confusion matrices for predicting load levels per walk trial using gender-specific statistical prediction models. Under- vs. over-estimated misclassifications are colored in red and green, respectively.

Men (prediction accuracy = 68.3%)
		Predicted Load Level			Total	Sensiti vity
		No-load	13.6 kg	22.7 kg
Actual Load	No-load	40	0	0	40	100%
	13.6 kg	7	23	10	40	57.5%
	22.7 kg	3	18	19	40	47.5%
Total		50	41	29	120
Precision		80%	56.1%	65.5%
Women (prediction accuracy = 85.0%)
		Predicted Load Level			Total	Sensiti vity
		No-load	13.6 kg	22.7 kg
Actual Load	No-load	40	0	0	40	100%
	13.6 kg	5	29	6	40	72.5%
	22.7 kg	0	7	33	40	82.5%
Total		45	36	39	120
Precision		88.9%	80.6%	84.6%

DISCUSSION AND CONCLUSIONS

Statistical prediction models for estimating hand-loads in load carriage from wearable inertial sensor data would allow ergonomists to quantify the external load without additional force measurement. This method can be effectively used where the hand-load level varies throughout a work-shift or is difficult to measure in field settings. In such situations, the predicted load levels combined with postural data can be used as inputs to a biomechanical model to estimate cumulative exposures or workload (e.g., joint moments, low-back compressive loads) and obtain quantitative indicators of work-related injury risk.

This study was performed to examine potential gender bias in statistical algorithm for classifying carried hand-load level using inertial sensor-derived torso and pelvis postural kinematics as predictors. The typical approach to creating a fair algorithm is by using a balanced and representative sample. Interestingly, despite a gender-balanced sample, model performance differed by gender. In male participants, the misclassification occurred mostly from underestimating the load level. In female participants, the most of the misclassifications occurred when the lower load condition was classified as the higher load condition. Furthermore, the men-specific model underperformed on accuracy compared to the gender-balanced model. However, the women-specific model out-performed the gender-specific model.

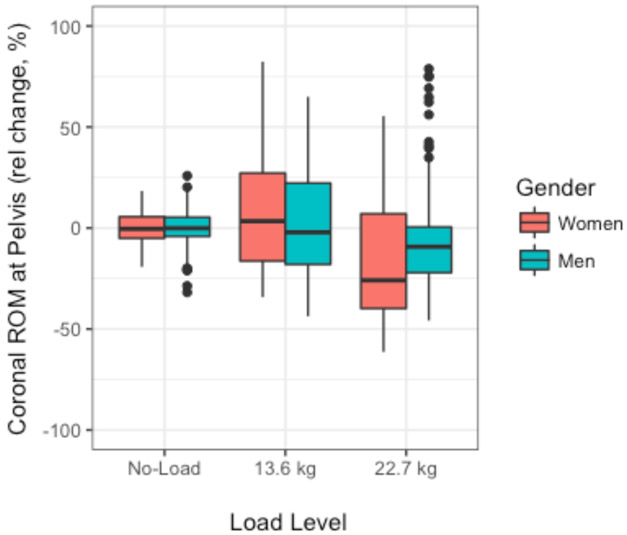
A likely explanation for these findings is that increasing hand-load produced smaller changes in torso and pelvis kinematics among men than women. As a result, kinematic data from men was less effective in discriminating between absolute load conditions. For example, Figure 2 depicts the relative change in pelvic range of motion (ROM) in the coronal plane. Both men and women showed relative decreases in coronal pelvic ROM with the increasing hand-load, but the change between different load levels were greater in women.

Figure 2.

Boxplot for coronal ROM at pelvis calculated as the percent change by load level and gender relative to no-load (unloaded) gait.

Implications for Practice

In terms of the practical implications of this study, two points are worth noting. First, the above case example could be remedied by normalizing the data to person-specific anthropometry (e.g., stature, strength) and other personal information (e.g., age, gender, race/ethnicity, health condition). For example, Silder, Delp, & Besier (2013) reported that men and women displayed similar adaptations in peak flexion angles at the hip, knee, and ankle during gait stance phase during load carriage after adjusting for body weight. Development of tailored statistical prediction algorithms using data normalized to individual anthropometry is underway. However, this implies that in practice, personal and sometimes protected information about a worker would be explicitly used to make decisions or predictions of workload. This could raise concerns of data privacy in some settings.

Second, while the scientific literature (especially in human factors and ergonomics) is seeing a proliferation of studies using statistical prediction (i.e., machine learning, deep learning), few studies explicitly examine potential issues of classification parity, fairness, and bias. A lack of attention to these issues could erode user trust and undermine the potential benefits of such novel techniques for improving worker health and safety. Examples of algorithmic bias from other domains such as social media, journalism, and banking have sparked tremendous interest in developing fair machine-learning algorithms (O’Neil, 2017; Zemel, Swersky, Pitassi, & Dwork, 2013). It is important that the ergonomics community also become cognizant of these issues and work towards productive solutions particularly as machine learning techniques gain popularity in ergonomics practice.