SBDiEM: A new mathematical model of infectious disease dynamics

Highlights

• •We introduce the SBDiEM approach for modeling, forecasting and nowcasting disease dynamics.
• •Our model can be adjusted to describe past outbreaks as well as COVID-19.
• •The novel methodology could have important implications for NHSs, international stakeholders and policy makers.
• •We aim at the improvement of outbreak control, vaccination and prevention strategies.
• •The model can be embedded into a global AI surveillance system for combating epidemic and pandemic outbreaks.

Abstract

A worldwide multi-scale interplay among a plethora of factors, ranging from micro-pathogens and individual or population interactions to macro-scale environmental, socio-economic and demographic conditions, entails the development of highly sophisticated mathematical models for robust representation of the contagious disease dynamics that would lead to the improvement of current outbreak control strategies and vaccination and prevention policies. Due to the complexity of the underlying interactions, both deterministic and stochastic epidemiological models are built upon incomplete information regarding the infectious network. Hence, rigorous mathematical epidemiology models can be utilized to combat epidemic outbreaks. We introduce a new spatiotemporal approach (SBDiEM) for modeling, forecasting and nowcasting infectious dynamics, particularly in light of recent efforts to establish a global surveillance network for combating pandemics with the use of artificial intelligence. This model can be adjusted to describe past outbreaks as well as COVID-19. Our novel methodology may have important implications for national health systems, international stakeholders and policy makers.

1. Introduction

The World Health Organization (WHO) reported on December 31, 2019 cases of pneumonia of undetected etiology in the city of Wuhan, Hubei Province in China. A novel coronavirus (CoViD-19) was identified as the source of the disease by the Chinese authorities on January 7, 2020. Eventually, the International Committee on Taxonomy of Viruses on 11 February, 2020 named the Severe Acute Respiratory Syndrome Coronavirus as SARS-CoV-2 [1]. Concerns on public health were dispersed on a global scale about potentially infected countries. The virus might have been generated by animal populations and transmitted via the Huanan wholesale market [2], [3], [4] albeit not proven, while clinical findings demonstrated that international spread was caused mainly by commercial air travel [4], [5], [6], [7]. The WHO declared SARS-CoV-2 a pandemic on March 11, 2020. Throughout the globe, huge efforts were in progress to limit the spread of the virus and find medications and vaccines. However, the scientific community could not fully comprehend the dynamics of the spread [8], [9], [10].

Several outbreaks of infectious diseases have occurred in the past with immense impact on public health. For instance, the Severe Acute Respiratory Syndrome (SARS) occurred in 2003, the swine flu in 2009 and the Middle East Respiratory Syndrome Coronavirus (MERS) in Saudi Arabia in 2012, which still survives at a sub-critical level causing some peaks [11], [12], [13], [14]. Additionally, the Ebola epidemic emerged between 2014 and 2016 and caused over 28,000 cases in West Africa [15]. Its temporal decline coincided with the outbreak of Zika virus in Brazil [16]. Consequently, the outbreak of severe pathogens such as the aforementioned, require global interdisciplinary efforts in order to decode key epidemiological features and their transmission dynamics, and develop possible control policies.

Insights from mathematical modelling can be extremely beneficial. Indeed, dealing with infectious diseases from a mathematical angle could reveal inherent patterns and underlying structures that govern outbreaks. Stakeholders utilize available data from current and previous outbreaks in order to forecast infection rates, identify how to restrict the spread of diseases, and eventually introduce vaccination policies that will be most effective. Epidemiology is essentially a biology discipline concerned with public health and as such, it can be heavily influenced by mathematical theory. Most phenomena observed at population level are often very complex and difficult to decode just by observing the characteristics of isolated individuals [17]. Statistical analyses of epidemiological data help to characterize, quantify and summarize the way diseases spread in host populations. Interestingly, mathematical models appear as efficient ways to explore and test various epidemiological hypotheses, mostly due to the existence of ethical and practical limitations when deducting experiments on living populations. Models provide conceptual results on e.g., the basic reproduction number, threshold effects or herd immunity. One additional element of epidemiological modeling is the link with data via statistical methods. Although simple epidemiological models are often used, viral and bacterial infections commonly require increased complexity. There are many models in the literature on single epidemics, endemic diseases and spatiotemporal disease dynamics. The aim is to develop robust public health policies in defining optimal vaccination strategies.

Our study presents for the first time a new stochastic mathematical model for describing infectious dynamics and tracking virus temporal transmissibility on 3-dimensional space (earth). This model can be adjusted to describe all past outbreaks as well as CoViD-19. As a matter of fact, it introduces a novel approach to mathematical modelling of infectious dynamics of any disease, and sets a starting point for conducting simulations, forecasting and nowcasting investigations based on real-world stereographic and spherical tracking on earth.

In short, a single epidemic outbreak as opposed to disease endemicity occurs in a time span short enough not to have the demographic changes perturbing the dynamics of contacts among individuals. The most popular mathematical model in this category is the Susceptible-Infected-Recovered (SIR) epidemic model, in which all individuals of a finite population interact in the same manner. Individuals at time t are susceptible (S), infected (I) or recovered (R). The final size of the epidemic will strongly depend upon the initial conditions of the number of susceptible and infected individuals as well as the infection parameter. The final size distribution of the simple SIR model in most cases is bimodal presenting two local maxima. This bimodal feature is caused by two likely scenarios; either the epidemic dies out quickly infecting few individuals, or it becomes long-lasting and substantial. However, stochasticity in the form of random walk transmission mechanisms related to spreading processes has never been explored in epidemiology widely [18], [19], [20]. For example, in computer science, some artificially created viruses propagate randomly by a plethora of online communication channels. To the best of our knowledge, we are the first to scrutinize extensively the role of random walks in epidemic spreading and provide the proper mathematical arsenal to model it robustly. Interestingly, random walk paths converge in distribution to Brownian motions [21]. In this work, we assume that a biological carrier of virus Y is at position X(t) at any given time t. We call this the inaugural contamination focal point on earth.

The path defined by its motion is considered infectious. X_t, t ≥ 0 is supposed to follow a Brownian motion on a 2-dimensional sphere S ² of radius a, i.e the sphere in $\mathbb{R}$ of dimension 3. We consider this a proxy for earth, spreading via spherical and stereographic coordinates. Next, using the Laplace-Beltrami operator we construct the Brownian motion infectious process on the 2-dimensional sphere, using spherical and stereographic coordinates as local coordinates. We evaluate explicitly certain quantities related to generated diffusion processes. In what follows, we compute the transition and transmission density for the X_t, t ≥ 0, and we derive the stochastic differential equations that govern the infectious disease dynamics for X_t, t ≥ 0 in those local coordinates. We continue with the calculation of expectations of outbreak exit times in time and space of specific domains, possessing certain symmetries. Moreover, the moment generating functions are produced. In mathematical terms, we derive the stochastic reflection principle on S ² for the infectious disease transmission process. Reflection points can be extremely useful to calculate the distribution functions of certain temporal quantities related to the dynamics. Additionally, we evaluate boundary local times of first hitting of the outbreak for an epidemic or a hybrid endemic-epidemic model. Hence, biological carrier(s) of a virus (infectious individuals) are tracked at any given time on earth coordinates, and the path(s) defined by each infectious dynamical motion. In the following two chapters we present a thorough literature review and a state-of-the-art analysis in order to pose clearly our novel approach optimally among the various methodologies followed thus far.

The rest of paper is organized as follows: Section 2 provides a brief literature review, past and recent, of mathematical epidemiology. Section 3 presents the state-of-the-art, and focal concepts and term definitions required to introduce our novel model. It also states which category the new model falls into, according to the official taxonomy of the various methodologies already utilized so far in the relevant literature. Next, section 4 exposes in detail the mathematical formulation of the model. Lastly, Section 5 discusses proposed policies and future paths of research, and concludes.

2. Literature review

The beginning of mathematical modeling in epidemiology dates back to 1766, when Bernoulli developed a mathematical model to analyze the mortality of smallpox in England [22]. Bernoulli used his model to show that inoculation against the virus would increase the life expectancy at birth by about three years. A revision of the main findings and a presentation of the criticism by D’Alembert, appears recently in Dietz and Heesterbeek [23]. Lambert in 1772 as well as Laplace in 1812 extended the Bernoulli model by incorporating age-dependent parameters [24], [25]. However, further systematic research was absent until the beginning of the twentieth century with the pioneering work of Ross in 1911, which is considered the inaugural study of modern mathematical epidemiology [26]. Ross used a set of equations to approximate the discrete-time dynamics of malaria via a mosquito-based pathogen transmission [27]. Importantly, the past century has witnessed the rapid emergence and development of substantial theories in epidemics. In 1927, Kermack and McKendrick [28] derived the celebrated threshold theorem, which is one of the key results in epidemiology. It predicts – depending on the transmission potential of the infection – the critical fraction of susceptibles in the population that must be exceeded if an epidemic is to occur. Kermack and McKendrick published three seminal papers, establishing what is called the deterministic compartmental epidemic modelling [29], [30], [31], wherein they addressed the mass–action incident in disease transmission cycles, assuming that the probability of infection of a susceptible is analogous to the number of its contacts with infected individuals. This deterministic representation was in line with the Law of Mass Action [32] introduced by Guldberg and Waage in 1864 and renders the basic most commonly used SIR model, which assumes homogeneous mixing of the contacts and conservation of the total population and low rates of interaction. MacDonald extended Ross’s model to explain in depth the transmission process of malaria. Utilizing modern computer power, the mathematical model for the dynamics and the control of mosquito-transmitted pathogens provided robust results in real-word applications. Overall, the family of models they introduced is known by now as Ross–MacDonald models [33]. Moreover, the classic work of Bartlett [34] examined models and data to explore the factors that determine disease persistence in large populations. Arguably, a landmark book on mathematical modelling of epidemiological systems was published by Bailey [35] and highlighted the importance of public health decision making [36]. Given the diversity of infectious diseases studied since the middle of the 1950s, an impressive variety of epidemiological models have been developed. In addition, we should highlight the 19th century works by Enko [37], [38], [39], who first published a probabilistic model for describing the epidemic of measles, yet in discrete time. This model is the precursor of the popular Reed-Frost chain binomial model introduced by Frost in 1928 in biostatistics’ lectures at Johns Hopkins University [40]. It assumes that the infection spreads from an infected to a susceptible individual via a discrete time Markov chain, and set the basis of contemporary stochastic epidemic modelling, on which we will also focus in our present work.

Moving to the 21st century, we mention some interesting works; Xing et al., [41] introduced a mathematical model on H7N9 influenza among migrant and resident birds, domestic poultry and humans in China. In this study they concluded that temperature seasonality might be a source of the disease, yet they suggested for the first time that controlling markets could help controlling outbreaks. Lee and Pietz [42] developed a mathematical model for Zika virus using logistic growth in human populations. Sun et al., [43] proposed a transmission model for cholera in China and observed that reducing the spread requires extensive immunization coverage of the population. Nishiura et al. [44] developed a Zika mathematical model which exhibited the same dynamics as dengue fever, and Khan et al. [45] introduced a model whereby a saturation function describes well the typhoid fever dynamics. Gui and Zhang [46], developed a modified SIR model demonstrating nonlinearities in recovery rates. Their model exhibited a backward bifurcation phenomenon, which in turn implied that a plain reduction of the reproduction number less than one, was not rendered sufficient to stop the disease spread. Li et al. [47] constructed a multi-group brucellosis model and found out that the best way to contain the disease is to avoid cross infection of animal populations. Moreover, Yu and Lin [48] identified complex dynamical behaviour in epidemiological models and particularly the existence of multiple limit cycle bifurcations using a predictor-prey model. Shi et al. [49] proposed an HIV model with a saturated reverse function to describe the dynamics of infected cells. Additionally, Bonyah et al. [50] developed a SIR model to study the dynamics of buruli ulcer and suggested policy measures to control the disease. Lastly, Zhang et al. [51] developed a model with a latent period of the disease wherein the person is not infectious with saturated incidence rates and treatment functions, called SEIR epidemic model.

3. State-of-the-art analysis and definitions

The SIR model is the basic one used for modelling epidemics. Kermack and McKendrick created the model in 1927 [29] in which they considered a fixed population with only three compartments, susceptible (S), infected (I) and recovered (R). There are a large number of modifications of the SIR model, including those that include births and deaths, the SIR without or with vital dynamics, a model where upon recovery there is no immunity called SIS and where immunity lasts for a short period of time, called SIRS model. Furthermore, a model where there is a latent period of the disease and where the person is not infectious is indentified as SEIS and SEIR respectively, or where infants can be born with immunity is named MSIR. Also, we mention the herd immunity model [52], [53].

Overall, the transmission mechanism from infective populations to susceptibles is not well-comprehended for many infectious diseases. Interactions in a population are very complex, hence it is extremely difficult to capture the large scale dynamics of disease spread without formal mathematical modeling. An epidemiological model uses microscopic effects - the role of an infectious individual - to forecast the macroscopic behavior of disease spread via a population.

Deterministic models do not incorporate any form of uncertainty and as such, they can be thought to account for the mean trend of a process, alone. On the other hand, stochastic models describe the mean trend as well as the variance structure of the underlying processes. Two basic types of stochasticity are commonly used: demographic and environmental. Within the context of demographic stochasticity, all individuals are subject to the same potential events with the exact same probabilities but differences in the fates of population individuals. Disease propagation in large populations obeys to the weak law of large numbers, thus effects of demographic stochasticity can be decreased significantly, and many times a deterministic model becomes more suitable. However, random events cannot be neglected and a stochastic model can be equally appropriate. Environmental stochasticity involves variations in the probability associated with an exogenous event. Model parameters of stochastic models are characterized by probability distributions, whilst for fixed parameter values deterministic models will always produce the same results, except when chaotic behaviour emerges.

In the classic SIR model it is assumed that the individuals leave the infectious class at a constant rate and even if this assumption seems most intuitive, it is not always the most realistic, regarding the duration individuals stay infective [54], [55], [56]. Usually, random variables describe the time of recovery since infection. For discrete random variables (e.g., number of individuals) it is easy to define a probability distribution, whilst for continuous variables the time of recovery since infection is modelled. Often, in this last category it is not possible to fix a probability as there is infinity of such times. Hence, we first define a cumulative distribution and then express a probability density function from this cumulative distribution. Infectious periods are exponentially distributed with a mean infectious duration, however as frequently real data does not back up this assumption, we rather use constant duration. To account for such more realistic distributions, the assumption that the probability of recovery does not depend on the time since infection, is often relaxed. Then, a common method of stages can be used to replace the infective compartment by a series of successive ones, each with an exponential distribution of the same parameter, leading to a total duration of the infectious period modelled by a gamma distribution [17].

Epidemic models presented above describe rapid outbreaks during which normally the host population is assumed to be in a constant state. For longer periods, deaths and births feed the population with new susceptibles, possibly allowing the disease to persist at a constant prevalence. This state renders an endemic state in the population [17]. In this case, we account for birth and death rate of the host population, whereby a good approximation is that the population size N = S + I + R is constant. When deterministic dynamics prevail a threshold on the value of the basic reproduction number exists. Conditions regarding this number guarantee the disease persistence, but in epidemic models such persistence can be dependent upon the magnitude of the stochastic fluctuations around the steady-state equilibrium. Furthermore, many times diseases are in an endemo-epidemic state. As endemic models exhibit damped oscillations which converge toward an endemic equilibrium, this equilibrium can be weakly stable with perturbations (intrinsic or extrinsic), which excite and sustain the inherent oscillation behaviour [57]. This behaviour is due to heterogeneity that is added temporally to the coefficient of transmission, spatially in the context of meta-populations, or by cohorts for age-structured models. Lastly, heterogeneity can be added statistically in case of stochastic versions. For example, a stochastic version of the endemic SIR model can utilize a Markov process, in which the future is independent of the past given the present, with a state space defined by the number of individuals in each of the three classes, and changes in the state space characterized by probabilistic transition events. And as future events are independent on past events, the time to the next event follows a negative exponential distribution.

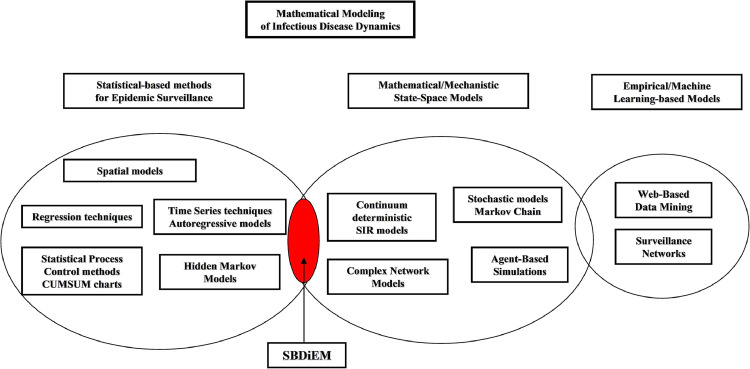
Over the years, a vast number of mathematical modeling approaches has been proposed, tackling the problem from different perspectives. The prevailing taxonomy proposed by Siettos and Russo [58] encompasses three general categories: (1) statistical methods of outbreaks and their identification of spatial patterns in real epidemics, (2) state-space models of the evolution of a “hypothetical” or on-going epidemic spread, and (3) machine learning methods, all utilized also for predictability purposes vis-à-vis an ongoing epidemic. In particular, the first category includes i) regression methods [59], [60], [61], [62], [63], [64], ii) times series analysis, namely ARIMA and seasonal ARIMA approaches [65], [66], [67], [68], iii) process control methods including cumulative sum (CUSUM) charts [69], [70], [71], [72], [73], [74] and exponentially weighted moving average (EWMA) methods [75], [76], as well as iv) Hidden Markov models (HMM) [77], [78]. The second category incorporates i) “continuum” models in the form of differential and/or (integro)-partial differential equations [79], [80], [81], [82], ii) discrete and continuous-time Markov-chain models [83], [84], [85], iii) complex network models which relax the hypotheses of the previous stochastic models that interactions among individuals are instantaneous and homogeneous [86], [87], [88], [89], [90], [91], and iv) Agent-based models [92], [93], [94], [95]. Lastly, the third category includes well-known machine learning approaches widely used in computer science, such as i) artificial neural networks [96], ii) web-based data mining [97], [98] and iii) surveillance networks [99], to name a few.

For the first time in the relevant literature, we introduce a new stochastic model laying in the intersection of categories (1) and (2), called “Stereographic Brownian Diffusion Epidemiology Model (SBDiEM)”. Fig. 1 presents a graphical overview of the models utilized so far, and the “positioning” of our novel approach for modelling infectious diseases.

Fig. 1.

Updated taxonomy of mathematical models for contagious diseases (source [58]). The new stochastic model lays in the intersection of categories (1) statistical methods and (2) state-space models of epidemic spreads.

4. Mathematical formulation

4.1. Preliminaries

4.1.1. The n-Sphere Sⁿ

Definition 4.1

Let $n\in {\mathbb{N}}^{*}=\{1,2,3,\dots \}$. The n-dimensional sphere Sⁿ with center $(c_1,\dots ,c_{n+1})$ and radius a > 0 is (defined to be) the set of all points  $x=(x_1,x_2,\dots ,x_{n+1})\in {\mathbb{R}}^{n+1}$ satisfying ${(x_1-c_1)}^2+\dots +{(x_{n+1}-c_{n+1})}^2=a^2$. Thus,

$$\begin{array}{ccc}\hfill S^n& =& \{(x_1,x_2,\dots ,x_{n+1})\in {\mathbb{R}}^{n+1}|{(x_1-c_1)}^2+\dots \hfill \\ & & +{(x_{n+1}-c_{n+1})}^2=a^2\}\hfill \end{array}$$

4.1.2. Stereographic projection coordinates

Definition 4.2

We consider ${\mathbb{R}}^n\subset {\mathbb{R}}^{n+1}$ to be the hyperplane given by  $x^{n+1}=0$. For convenience, we will let $(x_1,x_2,\dots ,x_n,x_{n+1})$ be coordinates on ${\mathbb{R}}^{n+1}$ and $({\xi }_1,{\xi }_2,\dots ,{\xi }_n)$ be coordinates on ${\mathbb{R}}^n\subset {\mathbb{R}}^{n+1}$. Let $S^n=\{(x_1,x_2,\dots ,x_{n+1})\in {\mathbb{R}}^{n+1}|x_1^2+\dots +x_n^2+{(x_{n+1}-a)}^2=a^2\}$. The stereographic projection coordinates of Sⁿ is the map $\Phi :S^n-\{0,0,\dots ,2a\}\to {\mathbb{R}}^n$ given by

$$\Phi (x_1,x_2,\dots ,x_n,x_{n+1})=(\frac{2a{x}_1}{2a-x_{n+1}},\dots ,\frac{2a{x}_n}{2a-x_{n+1}}).$$

This map defines coordinates $({\xi }_1,{\xi }_2,\dots ,{\xi }_n)$ on Sⁿ so that the point $(x_1,x_2,\dots ,x_n,x_{n+1})$ of Sⁿ has coordinates $({\xi }_1,{\xi }_2,\dots ,{\xi }_n),$ where

$${\xi }_1=\frac{2a{x}_1}{2a-x_{n+1}},\dots ,{\xi }_n=\frac{2a{x}_n}{2a-x_{n+1}}.$$

The inverse map is given by

$$\begin{array}{ccc}\hfill x_1& =& \frac{4a^2{\xi }_1}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2},\dots ,x_n=\frac{4a^2{\xi }_n}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2},\hfill \\ \hfill x_{n+1}& =& \frac{2a({\xi }_1^2+\dots +{\xi }_n^2)}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2}.\hfill \end{array}$$

4.1.3. Spherical coordinates

The points of the 2-sphere with center at the origin and radius a may also be described in spherical coordinates in the following way: $x_2=a\sin \phi ,$ where 0 ≤ φ < 2π.

$S^2=\{x=(a\cos \theta \sin \phi ,a\sin \theta \sin \phi ,a\cos \phi )\in {\mathbb{R}}^3|0\le \theta <2\pi ,0\le \phi \le \pi \}$ i.e.

$$x_1=a\cos \theta \sin \phi$$

$$x_2=a\sin \theta \sin \phi$$

$$x_3=a\cos \phi ,$$

where  0 ≤ θ < 2π and  0 ≤ φ ≤ π.

4.1.4. The Laplace-Beltrami operator

Definition 4.3

A C ^∞ differentiable manifold of dimension n is a set M together with a family of one-to-one maps x_α: U_α → M of open sets $U_{\alpha }\subset {\mathbb{R}}^n$ into M such that

• 1. ${\bigcup }_{\alpha }{x}_{\alpha }\left(U_{\alpha }\right)=M.$
• 2.For each pair α, β with $x_{\alpha }\left(U_{\alpha }\right)\bigcap x_{\beta }\left(U_{\beta }\right)=W\ne ⌀,$ we have that $x_{\alpha }^{-1}\left(W\right),x_{\beta }^{-1}\left(W\right)$ are open sets in ${\mathbb{R}}^n$ and that $x_{\beta }^{-1}\circ x_{\alpha },x_{\alpha }^{-1}\circ x_{\beta }$ are C ^∞ differentiable maps.
• 3.The family {U_α, x_α} is maximal relative to conditions 1 and 2.

Each pair (x_α, U_α) is called a coordinate chart on M. (For more details see [100])

Definition 4.4

A C^r function $f:M\to \mathbb{R},$ where M is a C ^∞ differential manifold is a function f, such that $f\circ x_{\alpha }:U_{\alpha }\to \mathbb{R}$ is C^r for every cordinate chart (x_α, U_α) on M.

Let $g=\left[g_{ij}\right]$ be the Riemmanian metric tensor on a Riemmanian manifold M. This means that, in any coordinate chart $(x_1,x_2,\dots ,x_n)$ on M, the length element can be computed by

$$d{s}^2=\sum _{j=1}^n\sum _{i=1}^n{g}_{ij}d{x}_{i}d{x}_j.$$

Given local coordinates $(x_1,\dots ,x_n),$ we can easily compute the matrix $g=\left[g_{ij}\right]$ by the inner product

$$g_{ij}=\frac{\partial x_a}{\partial x_i}·\frac{\partial x_a}{\partial x_j}$$

(see [100]). We denote by g^ij the elements of the inverse matrix $g^{-1}$.

Definition 4.5

The Laplace-Beltrami operator Δ_M associated with the metric g is defined by

$${\Delta }_{M}f=\frac{1}{\sqrt{det\left(g\right)}}·\sum _i\frac{\partial }{\partial x_i}(\sqrt{det\left(g\right)}·\sum _j{g}^{ij}\frac{\partial f}{\partial x_j}),$$ (4.1)

where f is a C^r function on M.

In this work we are interested in the case where $M=S^2,$ i.e., the 2 -dimensional sphere. We will denote the corresponding Laplace-Beltrami operator of S ² by Δ₂ or just Δ using the spherical coordinates. If $M=S^2,$ i.e.

$$\begin{array}{ccc}\hfill M=S^2& =& \{x=(a\cos \theta \sin \phi ,a\sin \theta \sin \phi ,a\cos \phi )\in {\mathbb{R}}^3|0\le \theta <\hfill \\ & & 2\pi ,0\le \phi \le \pi \},\hfill \end{array}$$

we have

$$x_{\theta }=\frac{\partial x}{\partial \theta }=(-a\sin \theta \sin \phi ,a\cos \theta \sin \phi ,0)$$

$$x_{\phi }=\frac{\partial x}{\partial \phi }=(a\cos \theta \cos \phi ,a\sin \theta \cos \phi ,-a\sin \phi )$$

$$g=\left[g_{ij}\right]=\left(\begin{array}{c}{x}_{\theta }{x}_{\theta }{x}_{\theta }{x}_{\phi }\\ x_{\phi }{x}_{\theta }{x}_{\phi }{x}_{\phi }\end{array}\right),$$

i.e.,

$$g=\left[g_{ij}\right]=\left(\begin{array}{cccc}{a}^2{\sin }^2\phi & 0\hfill & & \\ 0& a^2\hfill & & \\ & & \end{array}\right)$$

and

$$g^{-1}=\left[g^{ij}\right]=\left(\begin{array}{cccc}\frac{1}{a^2{\sin }^2\phi }& 0\hfill & & \\ 0& \frac{1}{a^2}\hfill & & \\ & & \end{array}\right).$$

Hence the Laplace-Beltrami operator of a smooth function f on S ² is

$${\Delta }_{2}f=\frac{1}{a^2\sin \phi }\sum _{i=1}^2\frac{\partial }{\partial x_i}\left(a^2\sin \phi \sum _{j=1}^2{g}^{ij}\frac{\partial f}{\partial x_j}\right),$$ (4.2)

where $x_1=\theta$ and $x_2=\phi .$ Thus

$${\Delta }_{2}f=\frac{1}{a^2\sin \phi }\sum _{i=1}^2\frac{\partial }{\partial x_i}\left[a^2\sin \phi (g^{i1}{f}_{\theta }+g^{i2}{f}_{\phi })\right]$$

or

$${\Delta }_{2}f=\frac{1}{a^2\sin \phi }(\frac{f_{\theta \theta }}{\sin \phi }+f_{\phi }\cos \phi +f_{\phi \phi }\sin \phi ).$$ (4.3)

In case where the function f is independent of θ the Laplace-Beltrami operator of f is

$${\Delta }_{2}f=\frac{1}{a^2\sin \phi }(f_{\phi }\cos \phi +f_{\phi \phi }\sin \phi ).$$ (4.4)

Generally the Laplace-Beltrami operator of a smooth function f on Sⁿ is

$${\Delta }_{n}f=\frac{1}{\sqrt{\det \left(g\right)}}·\sum _{i=1}^n\frac{\partial }{\partial {\theta }_i}(\sqrt{\det \left(g\right)}·\sum _{j=1}^n{g}^{ij}\frac{\partial f}{\partial {\theta }_j}),$$ (4.5)

where

$$\det \left(g\right)=a^{2n}\prod _{k=2}^n{\left(\sin {\theta }_k\right)}^{2(k-1)},$$ (4.6)

$$g^{ij}=0,\text{if}i\ne j,g^{ii}=\frac{1}{a^2{\sin }^2{\theta }_{i+1}·\dots ·{\sin }^2{\theta }_n}\text{and}{\theta }_n=\phi .$$

If f is independent of ${\theta }_1,{\theta }_2,...,{\theta }_{n-1}$,  the Laplace Beltrami operator of f is

$${\Delta }_{n}f=\frac{1}{a^2}((n-1)\cot \phi ·\frac{\partial f}{\partial \phi }+\frac{{\partial }^{2}f}{\partial {\phi }^2}).$$ (4.7)

Using Stereographic projection coordinates, if $M=S^n,$ i.e.

$$M=S^n=\{x=(\frac{4a^2{\xi }_1}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2},\dots ,\frac{4a^2{\xi }_n}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2},\frac{2a({\xi }_1^2+\dots +{\xi }_n^2)}{{\xi }_1^2+\dots +{\xi }_n^2+4a^2})\in {\mathbb{R}}^{n+1}|,{\xi }_1,\dots ,{\xi }_n\in \mathbb{R}\},$$

we have

$$\begin{array}{ccc}\hfill x_{{\xi }_k}& =& \frac{\partial x}{\partial {\xi }_k}=(\frac{-8a^2{\xi }_1{\xi }_k}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2},\dots ,\frac{-8a^2{\xi }_{k-1}{\xi }_k}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2},\frac{4a^2({\sum }_{i=1}^n{\xi }_i^2-2{\xi }_k^2+4a^2)}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2},\hfill \\ & & \frac{-8a^2{\xi }_{k+1}{\xi }_k}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2},\dots ,\frac{-8a^2{\xi }_n{\xi }_k}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2},\frac{16a^3{\xi }_k}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2}).\hfill \end{array}$$

Hence

$$g_{ii}=\frac{16a^4}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2}\text{and}{g}_{ij}=0,\text{if}i\ne j.$$

Thus we have

$$\begin{array}{ccc}\hfill g^{ii}& =& \frac{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^2}{16a^4},g^{ij}=0,\text{if}i\ne j,\text{and}\hfill \\ & & \sqrt{det\left(g\right)}=\frac{{\left(4a^2\right)}^n}{{({\xi }_1^2+\dots +{\xi }_n^2+4a^2)}^n}.\hfill \end{array}$$

Therefore, the Laplace Beltrami operator of a smooth function f on S ², using Stereographic projection coordinates is

$${\Delta }_{2}f=\frac{{({\xi }_1^2+{\xi }_2^2+4a^2)}^2}{16a^4}(\frac{{\partial }^{2}f}{\partial {\xi }_1^2}+\frac{{\partial }^{2}f}{\partial {\xi }_2^2})$$ (4.8)

4.1.5. Brownian motion on a riemannian manifold

Definition 4.6

Let M be a Riemannian manifold (see definition 1.5) and Δ its corresponding Laplace-Beltrami operator. Any function P(t, x, y) on (0, ∞) × M × M satisfying the differential equation

$$\frac{\partial P}{\partial t}-\frac{1}{2}{\Delta }_{x}P=0,$$ (4.9)

where Δ_x is Δ acting on the x-variables and the initial condition

$$P(t,x,y)\to {\delta }_x\left(y\right)\text{as},t\to 0^{+}$$ (4.10)

(where δ_x(y) is the delta mass at x ∈ M) is called a fundamental solution of the heat Eq. (4.9)on M.

The smallest positive fundamental solution of the heat Eqs. (4.9) and (4.10) is the heat kernel on M. It has been proved by J. Dodziak [101], that the heat kernel always exists, and is smooth in (t, x, y). Moreover the heat kernel possesses the following properties.

• 1.
  Symmetry in x, y, that is

  $$P(t,x,y)=P(t,y,x)$$
• 2.
  The semigroup identity: For any s ∈ (0, t)

  $$P(t,x,y)={\int }_{M}P(s,x,z)P(t-s,z,y)d\mu \left(z\right),$$

  where dμ is the area measure element of M. In polar coordinates $d\mu =\sqrt{\left|g\right|}d{\theta }_1\dots {\theta }_n,$ where ${\theta }_n=\phi$ and |g| is given by (4.6).
• 3.
  The total mass inequality, i.e., for all t > 0 and x ∈ M

  $${\int }_{M}P(t,x,y)d\mu \left(y\right)\le 1.$$ (4.11)

In case where M is compact and smooth, there is only one solution of (4.9) and (4.10) which is positive and satisfies

$${\int }_{M}P(t,x,y)d\mu \left(y\right)=1$$ (4.12)

Definition 4.7

A process  X_t, t ≥ 0 is a Markov process if for any  t, s ≥ 0, the conditional distribution of  $X_{t+s},$ given the information about the process up to time t, is the same as the conditional distribution of  $X_{t+s},$ given X_t.

Definition 4.8

The Brownian motion X_t, t ≥ 0, on a Riemannian manifold M is a Markov process with transition density function P(t, x, y) the heat kernel associated with the Laplace-Beltrami operator.

Remark 4.1

In the case where $M=S^n,$ n ≥ 2, the transition density function P(t, x, y) of the Brownian motion X_t depends only on t and d(x, y), the distance between x and y. Thus in spherical coordinates it depends on t and the angle φ between x and y. Hence, the transition density function of the Brownian motion can be written as

$$P(t,x,y)=p(t,\phi ),$$ (4.13)

where p(t, φ) is the solution of

$$\frac{\partial p}{\partial t}=\frac{1}{2}{\Delta }_{n}p=\frac{1}{2a^2}((n-1)\cot \phi ·\frac{\partial p}{\partial \phi }+\frac{{\partial }^{2}p}{\partial {\phi }^2})$$ (4.14)

and

$$\underset{t\to 0^{+}}{\lim }a{A}_{n-1}p(t,\phi )·{\sin }^{n-1}\left(\phi \right)=\delta \left(\phi \right).$$ (4.15)

Here δ( · ) is the Dirac delta function on $\mathbb{R}$ and A_n denotes the area of the n-dimensional sphere Sⁿ with radius a. It is well known that [102]

$$A_n=\frac{2{\pi }^{\frac{n+1}{2}}{a}^n}{\Gamma \left(\frac{n+1}{2}\right)},$$ (4.16)

where Γ( · ) is the Gamma function. More precisely

$$A_n=\frac{2{\pi }^{\frac{n+1}{2}}{a}^n}{\left(\frac{n-1}{2}\right)!}\text{for}\text{n}\text{odd}$$ (4.17)

$$A_n=\frac{2^n(\frac{n}{2}-1)!{\pi }^{\frac{n}{2}}{a}^n}{(n-1)!}\text{for}\text{n}\text{even}$$ (4.18)

Remark 4.2

The fact that Sⁿ is a compact and smooth manifold implies that (4.14) and (4.15) has a unique positive solution which also satisfies

$${\int }_{S^n}P(t,x,y)d\mu \left(y\right)=1.$$ (4.19)

Furthermore, as t → ∞,    P(t, x, y) approaches the uniform density on Sⁿ, i.e. P(t, x, y) → c, where

$$c=\frac{1}{A_n}.$$

In the sequel for typographical convenience we will write X_t instead of {X_t}_t ≥ 0.

4.2. Transition density function $p(t,\phi )$ of X_t, t > 0

In this section we shall represent the transition density function p(t, φ) of the position X(t) of a biological carrier (infected individual) of virus Y at any given time t. For the next sections we suppose that the infected individual is at position X(t) at any given time t, namely the path defined by its motion is considered infectious. X_t, t ≥ 0 describes a Brownian motion on a 2-dimensional sphere S ² of radius a. From the (4.14), (4.15) and (4.17) the transition density function p(t, φ) of X_t is the unique solution of

$$\frac{\partial p}{\partial t}=\frac{1}{2a^2\sin \phi }(\frac{{\partial }^{2}p(t,\phi )}{\partial {\phi }^2}\sin \phi +\frac{\partial p}{\partial \phi }\cos \phi )$$ (4.20)

and

$$\underset{t\to 0^{+}}{\lim }2\pi a^2\sin \phi ·p(t,\phi )=\delta \left(\phi \right).$$ (4.21)

The solution of the diffusion equation

$$\frac{\partial K(t,\phi )}{\partial t}=\frac{1}{\sin \phi }(\cos \phi \frac{\partial K(t,\phi )}{\partial \phi }+\sin \phi \frac{{\partial }^{2}K(t,\phi )}{\partial {\phi }^2})$$ (4.22)

with initial condition

$$\underset{t\to 0^{+}}{\lim }2\pi \sin \left(\phi \right)K(t,\phi )=\delta \left(\phi \right)$$ (4.23)

is given by the function

$$K(t,\phi )=\frac{1}{4\pi }\sum _{n\in \mathbb{N}}(2n+1)\exp (-n(n+1)\sqrt{2t})P_n^0\left(\cos \phi \right).$$ (4.24)

see[103]. Here $P_n^0,$ $n=0,1,2,\dots ,$ is the associated Legendre polynomials of order zero, i.e.

$$P_n^0\left(x\right)=\frac{1}{2^{n}n!}·\frac{d^n}{d{x}^n}\left[{(x^2-1)}^n\right]$$ (4.25)

This fact implies the following

Proposition 4.1

The transition density function of the Brownian motion X_t, t ≥ 0 on S ² with radius a it is given by the function

$$p(t,\phi )=\frac{1}{4\pi a^2}\sum _{n\in \mathbb{N}}(2n+1)\exp (-\frac{n(n+1)\sqrt{t}}{a})P_n^0\left(\cos \phi \right)$$ (4.26)

Proof

First we prove that p(t, φ) satisfies the differential equation

$$\frac{\partial p}{\partial t}=\frac{1}{2a^2\sin \phi }(\frac{{\partial }^{2}p(t,\phi )}{\partial {\phi }^2}\sin \phi +\frac{\partial p}{\partial \phi }\cos \phi ).$$

We have that

$$p(t,\phi )=\frac{1}{a^2}K(\frac{t}{2a^2},\phi ),$$

where K(t, φ) is given by the (4.24), therefore

$$\frac{\partial p(t,\phi )}{\partial t}=\frac{1}{2a^4}\frac{\partial K}{\partial t},$$

$$\frac{\partial p(t,\phi )}{\partial \phi }=\frac{1}{a^2}\frac{\partial K}{\partial \phi }\text{and}$$

$$\frac{{\partial }^{2}p(t,\phi )}{\partial {\phi }^2}=\frac{1}{a^2}\frac{{\partial }^{2}K}{\partial {\phi }^2}.$$

However from the (4.22)

$$\frac{\partial K}{\partial t}=\frac{1}{\sin \phi }(\cos \phi \frac{\partial K}{\partial \phi }+\sin \phi \frac{{\partial }^{2}K}{\partial {\phi }^2}),$$ (4.27)

hence

$$2a^4\frac{\partial p(t,\phi )}{\partial t}=\frac{1}{\sin \phi }(a^2\cos \phi \frac{\partial p(t,\phi )}{\partial \phi }+a^2\sin \phi \frac{{\partial }^{2}p(t,\phi )}{\partial {\phi }^2}),$$

i.e.

$$\frac{\partial p(t,\phi )}{\partial t}=\frac{1}{2a^2\sin \phi }(\cos \phi \frac{\partial p(t,\phi )}{\partial \phi }+\sin \phi \frac{{\partial }^{2}p(t,\phi )}{\partial {\phi }^2}).$$

Furthermore p(t, φ) satisfies the

$$\underset{t\to 0^{+}}{\lim }2\pi \sin \left(\phi \right)p(t,\phi )=\underset{t\to 0^{+}}{\lim }2\pi a^2\frac{1}{a^2}\sin \left(\phi \right)K(\frac{t}{2a^2},\phi )$$

and if we set $u=\frac{t}{2a^2}$ we imply that

$$\underset{t\to 0^{+}}{\lim }2\pi \sin \left(\phi \right)K(\frac{t}{2a^2},\phi )=\underset{u\to 0^{+}}{\lim }2\pi \sin \left(\phi \right)K(u,\phi )=\delta \left(\phi \right).$$

Therefore

$$\underset{t\to 0^{+}}{\lim }2\pi a^2\sin \left(\phi \right)p(t,\phi )=\delta \left(\phi \right).$$

and this complete the proof. □

4.2.1. Stochastic differential equation of the brownian motion in local coordinates

We recall the following well-known fact

Theorem 4.1

Let

$$\sigma \left(x\right)=\left[{\sigma }_{jk}\left(x\right)\right],\text{with}1\le j\le n,1\le k\le m,$$

be such that $a\left(x\right)=\sigma \left(x\right)·{\sigma }^T\left(x\right)$ is positive definite. If X_t is the Ito diffusion process

$$d{X}_t=b\left(X_t\right)dt+\sigma \left(X_t\right)d{B}_t,$$ (4.28)

then, its generator A is given by the formula

$$Af\left(x\right)=\sum _i{b}_i\left(x\right)\frac{\partial f}{\partial x_i}+\frac{1}{2}\sum _{i,j}{\left(\sigma {\sigma }^T\right)}_{i,j}\left(x\right)\frac{{\partial }^{2}f}{\partial x_i\partial x_j}.$$

Conversely, the operator A given above is the generator of diffusion (4.28). For the proof see [104].

Case of spherical coordinates

The generator of Brownian motion on S ² in spherical coordinates is

$$Af=\frac{1}{2}{\Delta }_{2}f,$$

i.e.

$$Af=\frac{\cos \phi }{2a^2\sin \phi }\frac{\partial f}{\partial \phi }+\frac{1}{2}(\frac{1}{a^2{\sin }^2\phi }\frac{{\partial }^{2}f}{\partial {\theta }^2}+\frac{1}{a^2}\frac{{\partial }^{2}f}{\partial {\phi }^2}).$$

Therefore, the Brownian motion on S ² in spherical coordinates is the solution of the stochastic differential equation

$$d{X}_t=(0,\frac{\cos \phi \left(t\right)}{2a^2\sin \phi \left(t\right)})dt+\left(\begin{array}{ccc}\frac{1}{a\sin \phi \left(t\right)}& 0& \\ 0& \frac{1}{a}& \\ & \end{array}\right)\left(\begin{array}{ccc}d{B}_1\left(t\right)& & \\ d{B}_2\left(t\right)& & \\ & \end{array}\right),$$

where

$$X_t=\left(\theta \right(t),\phi (t\left)\right).$$

Case of sterographic projection coordinates

Expressed in stereographic projection coordinates, the generator of Brownian motion on S ² is

$$Af=\frac{1}{2}\frac{{({\xi }_1^2+{\xi }_2^2+4a^2)}^2}{16a^4}(\frac{{\partial }^{2}f}{\partial {\xi }_1^2}+\frac{{\partial }^{2}f}{\partial {\xi }_2^2}).$$

Hence, the Brownian motion on S ² in stereographic projection coordinates is the solution of the stochastic differential equation

$$d{X}_t=\left(\begin{array}{ccc}\frac{(x_1{\left(t\right)}^2+x_2^2\left(t\right)+4a^2)}{4a^2}& 0& \\ 0& \frac{(x_1^2\left(t\right)+x_2^2\left(t\right)+4a^2)}{4a^2}& \\ & \end{array}\right)\left(\begin{array}{ccc}d{B}_1\left(t\right)& & \\ d{B}_2\left(t\right)& & \\ & \end{array}\right),$$ (4.29)

where

$$X_t=(x_1\left(t\right),x_2\left(t\right)).$$

4.3. Expectations of exit times of X(t)

We recall some basic definitions.

Definition 4.9

A measurable space $\{\Omega ,\mathcal{F}\}$ is said to be equipped with a filtration {$\mathcal{F}$ _t}, $t\in [0,+\infty ),$ if for every t ≥ 0 {$\mathcal{F}$ _t} is a σ-algebra of subsets of  Ω such that $\mathcal{F}$ _t $\subset \mathcal{F}$ and for every $t_1,t_2\in [0,+\infty )$ such that t ₁ < t ₂, we have that $\mathcal{F}$ ${}_{t_1}$ ⊂ $\mathcal{F}$ ${}_{t_2}$. (i.e. {$\mathcal{F}$ _t} is an increasing family of sub σ-algebras of $\mathcal{F}$).

Definition 4.10

Let us consider a measurable space $\{\Omega ,\mathcal{F}\}$ equipped with a filtration {$\mathcal{F}$ _t}. A random variable T is a stopping time with respect to the filtration {$\mathcal{F}$ _t}, if for every t ≥ 0

$$\{\omega \in \Omega |T\left(\omega \right)\le t\}\in {\mathcal{F}}_t.$$

Let X_t be the Brownian motion in Sⁿ and D ⊂ Sⁿ a domain. Then

$$T=\inf \{t\ge 0|X_t\notin D\}$$

is a stopping time with respect to $\mathcal{F}$ _t $=\sigma \{X_s|0\le s\le t\},$ called the exit time on ∂D.

Proposition 4.2

Let φ₀ ∈ [0, π) be fixed. We consider the set D in S ², such that

$$D=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi \in [0,{\phi }_0)\}.$$

Of course,

$$\partial D=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi ={\phi }_0\}.$$

If X_t is the position of the biological carrier of the virus Y at a given time t starting at the point

$$A=(\theta ,\phi )\in D,$$

and

$$T=\inf \{t\ge 0|X_t\notin D\},$$

then the expectation of T is given by

$$E^A\left[T\right]=2a^2\ln \left(\frac{1+\cos \phi }{1+\cos {\phi }_0}\right).$$ (4.30)

Proof

Based on [105],

$$u(\theta ,\phi )=E^A\left[T\right]$$

we have the unique solution of the differential equation

$$\frac{1}{2}{\Delta }_{2}u=-1,$$ (4.31)

with boundary condition as

$$u(\theta ,{\phi }_0)=0.$$

Here Δ₂ is the Laplace-Beltrami operator on S ². By symmetry of D, it follows that the expectation value of T is independent of θ. From (4.4) the differential Eq. (4.31) takes the form

$$\frac{1}{2a^2}[\cot \left(\phi \right)\frac{du}{d\phi }+\frac{d^{2}u}{d{\phi }^2}]=-1,$$ (4.32)

with boundary condition

$$u\left({\phi }_0\right)=0.$$ (4.33)

Set

$$f\left(\phi \right)=\frac{du}{d\phi }.$$

hence from (4.32)

$$\frac{1}{2a^2}[\cot \left(\phi \right)f\left(\phi \right)+\frac{df\left(\phi \right)}{d\phi }]=-1,$$

or

$$\cos \left(\phi \right)f\left(\phi \right)+\sin \left(\phi \right)\frac{df\left(\phi \right)}{d\phi }=-2a^2\sin \left(\phi \right),$$

Thus

$$f\left(\phi \right)=-\frac{2a^2}{\sin \phi }{\int }_0^{\phi }\sin \omega d\omega +\frac{c_1}{\sin \phi }.$$

Therefore,

$$u\left(\phi \right)=-2a^2{\int }_{{\phi }_0}^{\phi }\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx+c_1{\int }_{{\phi }_0}^{\phi }\frac{1}{\sin x}dx+c_2.$$ (4.34)

However (see [104])

$$u\left(\phi \right)=E^A\left[T\right]<\infty ,\text{for}\phi \in [0,{\phi }_0)$$

hence

$$c_1=0.$$

Furthermore, we have

$$u\left({\phi }_0\right)=0,\text{i.e.}{c}_2=0$$

thus,

$$u\left(\phi \right)=2a^2{\int }_{\phi }^{{\phi }_0}\frac{{\int }_0^x\left(\sin \omega \right)d\omega }{\left(\sin x\right)}dx.$$

Consequently,

$$E^A\left[T\right]=2a^2{\int }_{\phi }^{{\phi }_0}\frac{{\int }_0^x\left(\sin \omega \right)d\omega }{\left(\sin x\right)}dx.$$

Thus

$$E^A\left[T\right]=2a^2{\int }_{\phi }^{{\phi }_0}\frac{1-\cos x}{\sin x}dx,$$

or

$$E^A\left[T\right]=2a^2({\int }_{\phi }^{{\phi }_0}\frac{1}{\sin x}dx-{\int }_{\phi }^{{\phi }_0}\left(\cot x\right)dx),$$

hence

$$\begin{array}{ccc}\hfill E^A\left[T\right]& =& 2a^2[\ln \left(\tan \left(\frac{{\phi }_0}{2}\right)\right)-\ln \left(\tan \left(\frac{\phi }{2}\right)\right)\hfill \\ & & -\ln \left(\sin {\phi }_0\right)+\ln \left(\sin \phi \right)].\hfill \end{array}$$

Finally,

$$E^A\left[T\right]=2a^2\ln \left(\frac{1+\cos \phi }{1+\cos {\phi }_0}\right).$$ (4.35)

 □

Proposition 4.3

Let φ₁, φ₂ ∈ (0, π), such that φ₁ < φ₂, are both fixed. We consider the set D in S ², such that

$$D=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi \in ({\phi }_1,{\phi }_2)\}.$$

We have,

$$\partial D=\left\{\right(\theta ,\phi \left)\right|\theta \in [0,2\pi ),\text{and}\phi ={\phi }_1\text{or}\phi ={\phi }_2\}.$$

Let X_t be the position of the infectious individual Y is at a given time t starting at the point

$$A=(\theta ,\phi )\in D,$$

and

$$T=\inf \{t\ge 0|X_t\notin D\},$$

then the expectation of T is given by

$$\begin{array}{ccc}\hfill E^A\left[T\right]& =& \frac{4a^2}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}[\ln \left(\frac{\cos \left(\frac{{\phi }_1}{2}\right)}{\cos \left(\frac{{\phi }_2}{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{\phi }{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)}\right)\hfill \\ & & -\ln \left(\frac{\cos \left(\frac{{\phi }_1}{2}\right)}{\cos \left(\frac{\phi }{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{{\phi }_2}{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)}\right)]\hfill \end{array}$$ (4.36)

Proof

According to [105], E ^φ[t] satisfies the Poisson equation on D with Dirichlet boundary data. By uniqueness

$$u(\theta ,\phi )=E^A\left[T\right]$$

is the unique solution of the differential Eq. (4.31), i.e.,

$$\frac{1}{2}{\Delta }_{2}u=-1,$$

with boundary condition

$$u(\theta ,{\phi }_1)=u(\theta ,{\phi }_2)=0.$$

Here Δ₂ is the Laplace-Beltrami operator on S ². By the symmetry of D, it follows that the expectation value of T is independent of θ. From (4.4) the differential Eq. (4.31) takes the form (4.32) with boundary condition

$$u(\theta ,{\phi }_1)=u(\theta ,{\phi }_2)=0.$$ (4.37)

Hence from (4.34)

$$u\left(\phi \right)=-2a^2{\int }_{{\phi }_1}^{\phi }\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx+c_1{\int }_{{\phi }_1}^{\phi }\frac{1}{\sin x}dx+c_2.$$

However

$$u(\theta ,{\phi }_1)=u(\theta ,{\phi }_2)=0,$$

i.e.

$$-2a^2{\int }_{{\phi }_1}^{{\phi }_1}\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx+c_1{\int }_{{\phi }_1}^{{\phi }_1}\frac{1}{\sin x}dx+c_2=0$$

and

$$-2a^2{\int }_{{\phi }_1}^{{\phi }_2}\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx+c_1{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx+c_2=0.$$

Thus

$$c_1=2a^2\frac{{\int }_{{\phi }_1}^{{\phi }_2}\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx}{{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx}$$

and

$$c_2=0.$$

Consequently,

$$E^A\left[T\right]=2a^2({\int }_{\phi }^{{\phi }_1}\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx+\frac{{\int }_{{\phi }_1}^{{\phi }_2}\frac{{\int }_0^x\sin \omega d\omega }{\sin x}dx}{{\int }_{\phi 1}^{{\phi }_2}\frac{1}{\sin x}dx}·{\int }_{{\phi }_1}^{\phi }\frac{1}{\sin x}dx).$$

namely,

$$E^A\left[T\right]=2a^2({\int }_{{\phi }_1}^{\phi }\left(\cot x\right)dx-\frac{{\int }_{\phi 1}^{{\phi }_2}\left(\cot x\right)dx}{{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx}·{\int }_{{\phi }_1}^{\phi }\frac{1}{\sin x}dx),$$

hence

$$\begin{array}{ccc}\hfill E^A\left[T\right]& =& \frac{2a^2}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}[\ln \left(\frac{\sin \left(\frac{\phi }{2}\right)\cos \left(\frac{\phi }{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)\cos \left(\frac{{\phi }_1}{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{{\phi }_2}{2}\right)\cos \left(\frac{{\phi }_1}{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)\cos \left(\frac{{\phi }_2}{2}\right)}\right)\hfill \\ & & -\ln \left(\frac{\sin \left(\frac{{\phi }_2}{2}\right)\cos \left(\frac{{\phi }_2}{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)\cos \left(\frac{{\phi }_1}{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{\phi }{2}\right)\cos \left(\frac{{\phi }_1}{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)\cos \left(\frac{\phi }{2}\right)}\right)],\hfill \end{array}$$

from which we imply

$$\begin{array}{ccc}\hfill E^A\left[T\right]& =& \frac{4a^2}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}[\ln \left(\frac{\cos \left(\frac{{\phi }_1}{2}\right)}{\cos \left(\frac{{\phi }_2}{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{\phi }{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)}\right)\hfill \\ & & -\ln \left(\frac{\cos \left(\frac{{\phi }_1}{2}\right)}{\cos \left(\frac{\phi }{2}\right)}\right)·\ln \left(\frac{\sin \left(\frac{{\phi }_2}{2}\right)}{\sin \left(\frac{{\phi }_1}{2}\right)}\right)]\hfill \end{array}$$ (4.38)

 □

Proposition 4.4

We consider the 2-dimensional sphere S ² of radius a. Let two circles pass through the North pole, such that in stereographic coordinates are represented by the parallel lines ${\xi }_2=b$ and ${\xi }_2=c,$ where $b,c\in \mathbb{R},$ say b < c. We consider the set D in S ², whose stereographic projection is

$$D=\left\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2\in (b,c)\right\}.$$

Of course

$$\partial D=\left\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2=b\text{or}{\xi }_2=c\right\}.$$

If X_t is the position of the carrier of virus Y at a given time t starting at the point A, where the stereogrpaphic projection coordinates of A are

$$({\xi }_1,{\xi }_2)\in D.$$

and

$$T=\inf \{t\ge 0|X_t\in D\},$$

then,

$$E^A\left[T\right]=f({\xi }_1,{\xi }_2)-2a^2\ln ({\xi }_1^2+{\xi }_2^2+4a^2),$$ (4.39)

where

$$\begin{array}{ccc}& & f({\xi }_1,{\xi }_2)\hfill \\ & & =\frac{1}{\pi }{\int }_0^{\infty }\frac{g(\xi ,c)\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\sin \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)}{\exp \left(\frac{2\pi {\xi }_1}{c-b}\right){\sin }^2\left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+{(\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\cos \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+\eta )}^2}d\eta \hfill \end{array}$$

$$\frac{1}{\pi }{\int }_0^{\infty }\frac{g(\eta ,b)\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\sin \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)}{\exp \left(\frac{2\pi {\xi }_1}{c-b}\right){\sin }^2\left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+{(\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\cos \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)-\eta )}^2}d\eta$$ (4.40)

and

$$g(\xi ,t)=2a^2\ln (\frac{{(c-b)}^2{\ln }^2\left|\xi \right|}{{\pi }^2}+t^2+4a^2)$$ (4.41)

Proof

As we have seen the function

$$E^A\left[T\right]=U({\xi }_1,{\xi }_2)$$

satisfies the differential equation

$$\frac{1}{2}{\Delta }_{2}U=-1$$

with boundary conditions

$$U({\xi }_1,b)=U({\xi }_1,c)=0.$$

Here, Δ₂ is the Laplace-Beltrami operator on S ² expressed in stereographic projection coordinates. Hence, the differential equation takes the form

$$\frac{1}{2}\frac{{({\xi }_1^2+{\xi }_2^2+4a^2)}^2}{16a^4}·(\frac{{\partial }^{2}U}{\partial {\xi }_1^2}+\frac{{\partial }^{2}U}{\partial {\xi }_2^2})=-1,$$

or

$$\frac{{\partial }^{2}U}{\partial {\xi }_1^2}+\frac{{\partial }^{2}U}{\partial {\xi }_2^2}=-\frac{32a^4}{{({\xi }_1^2+{\xi }_2^2+4a^2)}^2}.$$ (4.42)

However the function

$$U_1({\xi }_1,{\xi }_2)=-2a^2\ln ({\xi }_1^2+{\xi }_2^2+4a^2)$$

satisfies the differential Eq. (4.42). Thus

$$U({\xi }_1,{\xi }_2)=-2a^2\ln ({\xi }_1^2+{\xi }_2^2+4a^2)+f({\xi }_1,{\xi }_2)$$

where f(ξ ₁, ξ ₂) satisfies

$$\frac{{\partial }^{2}f}{\partial {\xi }_1^2}+\frac{{\partial }^{2}f}{\partial {\xi }_2^2}=0,$$

with boundary conditions

$$f({\xi }_1,b)=2a^2\ln ({\xi }_1^2+b^2+4a^2)$$

and

$$f({\xi }_1,c)=2a^2\ln ({\xi }_1^2+c^2+4a^2).$$

If we take the transformation of variables $x={\xi }_1$ and $y={\xi }_2-b$ and set the function $\varphi (x,y)=f({\xi }_1,{\xi }_2),$ then ϕ(x, y) we satisfy

$$\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial y^2}=0,$$

with boundary conditions

$$\varphi (x,0)=2a^2\ln (x^2+b^2+4a^2)$$

and

$$\varphi (x,\beta )=2a^2\ln (x^2+c^2+4a^2)$$

where $\beta =c-b.$ Now let $z=x+yi$ and $w=\exp \left(\frac{\pi z}{\beta }\right),$ i.e. $z=\frac{\beta \ln w}{\pi }.$ Thus, if $w=u+vi,u,v\in \mathbb{R}$ then

$$u=\exp \left(\frac{\pi x}{\beta }\right)\cos \left(\frac{\pi y}{\beta }\right)\text{and}v=\exp \left(\frac{\pi x}{\beta }\right)\sin \left(\frac{\pi y}{\beta }\right).$$ (4.43)

Introducing the function $\psi (u,v)=\varphi (x,y).$ It follows that ψ(u, v) satisfies

$$\frac{{\partial }^2\psi }{\partial u^2}+\frac{{\partial }^2\psi }{\partial v^2}=0,$$

with boundary conditions

$$\psi (u,0)=2a^2\ln (\frac{{\beta }^2{\ln }^{2}u}{{\pi }^2}+b^2+4a^2),\text{for}u>0$$

and

$$\psi (u,0)=2a^2\ln (\frac{{\beta }^2{\ln }^2\left|u\right|}{{\pi }^2}+c^2+4a^2),\text{for}u<0.$$

This is the standard Dirichlet boundary value problem for the half line, and it is well known that (see e.g. [106]) its solution is given by the Poisson integral formula for the half-plane:

$$\psi (u,v)=\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{v\psi (\xi ,0)}{v^2+{(u-\xi )}^2}d\xi ,$$

or

$$\psi (u,v)=\frac{1}{\pi }{\int }_{-\infty }^0\frac{vg(\xi ,c)}{v^2+{(u-\xi )}^2}d\xi +\frac{1}{\pi }{\int }_0^{\infty }\frac{vg(\xi ,b)}{v^2+{(u-\xi )}^2}d\xi ,$$

where

$$g(\xi ,t)=2a^2\ln (\frac{{\beta }^2{\ln }^2\left|\xi \right|}{{\pi }^2}+t^2+4a^2).$$

Notice that $g(-\xi ,t)=g(\xi ,t).$ Hence,

$$\psi (u,v)=\frac{1}{\pi }v{\int }_0^{\infty }(\frac{g(\xi ,c)}{v^2+{(u+\xi )}^2}+\frac{g(\xi ,b)}{v^2+{(u-\xi )}^2})d\xi ,$$

where u, v are given in (4.43). Therefore

$$\varphi (x,y)=\frac{1}{\pi }\exp \left(\frac{\pi x}{\beta }\right)\sin \left(\frac{\pi y}{\beta }\right){\int }_0^{\infty }\frac{g(\eta ,c)}{\exp \left(\frac{2\pi x}{\beta }\right){\sin }^2\left(\frac{\pi y}{\beta }\right)+{(\exp \left(\frac{\pi x}{\beta }\right)\cos \left(\frac{\pi y}{\beta }\right)+\eta )}^2}d\eta$$

$$+\frac{1}{\pi }\exp \left(\frac{\pi x}{\beta }\right)\sin \left(\frac{\pi y}{\beta }\right){\int }_0^{\infty }\frac{g(\eta ,b)}{\exp \left(\frac{2\pi x}{\beta }\right){\sin }^2\left(\frac{\pi y}{\beta }\right)+{(\exp \left(\frac{\pi x}{\beta }\right)\cos \left(\frac{\pi y}{\beta }\right)-\eta )}^2}d\eta ,$$

i.e.

$$f({\xi }_1,{\xi }_2)=\frac{1}{\pi }{\int }_0^{\infty }\frac{g(\eta ,c)\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\sin \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)}{\exp \left(\frac{2\pi {\xi }_1}{c-b}\right){\sin }^2\left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+{(\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\cos \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+\eta )}^2}d\eta$$

$$+\frac{1}{\pi }{\int }_0^{\infty }\frac{g(\eta ,b)\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\sin \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)}{\exp \left(\frac{2\pi {\xi }_1}{c-b}\right){\sin }^2\left(\frac{\pi ({\xi }_2-b)}{c-b}\right)+{(\exp \left(\frac{\pi {\xi }_1}{c-b}\right)\cos \left(\frac{\pi ({\xi }_2-b)}{c-b}\right)-\eta )}^2}d\eta .$$

Finally

$$E^A\left[T\right]=f({\xi }_1,{\xi }_2)-2a^2\ln ({\xi }_1^2+{\xi }_2^2+4a^2).$$

 □

4.3.1. Hitting probabilities

Proposition 4.5

Let φ₁, φ₂ ∈ (0, π), such that φ₁ < φ₂, are both fixed. We consider the sets D ₁, D ₂ in S ², such that

$$D_1=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi \in ({\phi }_1,\pi ]\}$$

and

$$D_2=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi \in [0,{\phi }_2)\}.$$

We have,

$$\partial D_1=\{(\theta ,\phi )|\theta \in [0,2\pi ),\text{and}\phi ={\phi }_1\}$$

and

$$\partial D_2=\{(\theta ,\phi )|{\theta }_1\in [0,2\pi ),\text{and}\phi ={\phi }_2\}.$$

If X_t is the position of the infected (I) at a given time t starting at the point

$$A=(\theta ,\phi )\in D_1\cap D_2.$$

and in case

$$T_1=\inf \{t\ge 0|X_t\notin D_1\},$$

$$T_2=\inf \{t\ge 0|X_t\notin D_2\}$$

and

$$T=\inf \{t\ge 0|X_t\notin D_1\cap D_2\},$$

then the probabilities

$$P{r}^A\{T=T_1\}\text{and}P{r}^A\{T=T_2\}$$

are given by

$$P{r}^A\{T=T_1\}=\frac{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{\phi }{2}\right)}\right)}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}$$ (4.44)

and

$$P{r}^A\{T=T_2\}=\frac{\ln \left(\frac{\tan \left(\frac{\phi }{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}.$$ (4.45)

Proof

It is known that (see [21]),

$$u(\theta ,\phi )=P{r}^A\{T=T_1\}$$

is the unique solution of the differential equation

$$\frac{1}{2}{\Delta }_{n}u=0,$$ (4.46)

with boundary condition

$$u(\theta ,{\phi }_1)=1\text{and}u({\theta }_1,\dots ,{\theta }_{n-1},{\phi }_2)=0$$

Here Δ_n is the Laplace-Beltrami operator on S ². By the symmetry of D, it follows that the probability value of $T=T_1$ is independent of θ. From (4.7) the differential Eq. (4.46) takes the form

$$\frac{1}{2a^2}[(n-1)\cot \left(\phi \right)\frac{du}{d\phi }+\frac{d^{2}u}{d{\phi }^2}]=0,$$ (4.47)

with boundary condition

$$u\left({\phi }_1\right)=1\text{and}u\left({\phi }_2\right)=0.$$ (4.48)

In we set

$$f\left(\phi \right)=\frac{du}{d\phi },$$

hence from (4.47)

$$\frac{1}{2a^2}[\cot \left(\phi \right)f\left(\phi \right)+\frac{df\left(\phi \right)}{d\phi }]=0,$$

or

$$\cos \left(\phi \right)f\left(\phi \right)+\sin \left(\phi \right)\frac{df\left(\phi \right)}{d\phi }=0.$$

Thus

$$f\left(\phi \right)=\frac{c_1}{\sin \phi )},$$

i.e.

$$u\left(\phi \right)={\int }_{{\phi }_2}^{\phi }\frac{c_1}{\sin x}dx+c_2.$$ (4.49)

However,

$$u\left({\phi }_1\right)=1\text{and}u\left({\phi }_2\right)=0,$$

hence

$$c_1=-\frac{1}{{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx}$$

and

$$c_2=0.$$

Thus

$$u\left(\phi \right)=\frac{{\int }_{\phi }^{{\phi }_2}\frac{1}{\sin x}dx}{{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx}.$$

Consequently,

$$P{r}^A\{T=T_1\}=\frac{{\int }_{\phi }^{{\phi }_2}\frac{1}{\sin x}dx}{{\int }_{{\phi }_1}^{{\phi }_2}\frac{1}{\sin x}dx}.$$

or

$$P{r}^A\{T=T_1\}=\frac{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{\phi }{2}\right)}\right)}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}$$ (4.50)

Moreover,

$$P{r}^A\{T=T_2\}=1-P{r}^A\{T=T_1\},$$

hence

$$P{r}^A\{T=T_2\}=\frac{\ln \left(\frac{\tan \left(\frac{\phi }{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}{\ln \left(\frac{\tan \left(\frac{{\phi }_2}{2}\right)}{\tan \left(\frac{{\phi }_1}{2}\right)}\right)}.$$ (4.51)

 □

Proposition 4.6

We consider the 2-dimensional sphere S ² of radius a. Let two circles pass through the North Pole, such that in stereographic coordinates are represented by the parallel lines ${\xi }_2=b$ and ${\xi }_2=c,$ where $b,c\in \mathbb{R},$ with b < c. Next consider the sets D ₁, D ₂ in S ², for which the stereographic projections are

$$D_1=\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2\in (b,+\infty )\}$$

and

$$D_2=\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2\in (-\infty ,c)\}.$$

Of course,

$$\partial D_1=\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2=b\}$$

and

$$\partial D_2=\{({\xi }_1,{\xi }_2)|{\xi }_1\in \mathbb{R}\text{and}{\xi }_2=c\}.$$

Let X_t be the position of the carrier of virus Y at a given time t starting at the point A, and the stereographic projection coordinates of A are

$$({\xi }_1,{\xi }_2)\in D_1\cap D_2.$$

If

$$T_1=\inf \{t\ge 0|X_t\notin D_1\},$$

$$T_2=\inf \{t\ge 0|X_t\notin D_2\}$$

and

$$T=\inf \{t\ge 0|X_t\notin D_1\cap D_2\},$$

then

$$P{r}^A\{T=T_1\}=\frac{c-{\xi }_2}{c-b}\text{and}P{r}^A\{T=T_2\}=\frac{{\xi }_2-b}{c-b}.$$ (4.52)

Proof

It is known that (see [21]) the function

$$u({\xi }_1,{\xi }_2)=P{r}^A\{T=T_1\}$$

is the unique solution of the differential equation

$$\frac{1}{2}{\Delta }_{2}u=0$$ (4.53)

with boundary condition

$$u({\xi }_1,b)=1\text{and}u({\xi }_1,c)=0.$$ (4.54)

Here, Δ₂, is the Laplace-Beltrami operator on S ² expressed in the stereographic projection coordinates. Hence from (4.8) the differential Eq. (4.53) takes the form

$$\frac{1}{2}\frac{{({\xi }_1^2+{\xi }_2^2+4a^2)}^2}{16a^4}·(\frac{{\partial }^{2}u}{\partial {\xi }_1^2}+\frac{{\partial }^{2}u}{\partial {\xi }_2^2})=0,$$

or

$$\frac{{\partial }^{2}u}{\partial {\xi }_1^2}+\frac{{\partial }^{2}u}{\partial {\xi }_2^2}=0.$$ (4.55)

From (4.54) and (4.55) we see easily that

$$u({\xi }_1,{\xi }_2)=\frac{c-{\xi }_2}{c-b}.$$

Therefore,

$$P{r}^A\{T=T_1\}=\frac{c-{\xi }_2}{c-b}\text{and}P{r}^A\{T=T_2\}=\frac{{\xi }_2-b}{c-b}.$$

 □

4.3.2. Moment generating functions

Proposition 4.7

Let ${\phi }_0\in [0,\pi )$ be fixed. We consider the set D in S ², such that

$$D=\{(\theta ,\phi )|\theta \in [0,2\pi ),\text{and}\phi \in [0,{\phi }_0)\}.$$

Then,

$$\partial D=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi ={\phi }_0\}.$$

If X_t is the infectious position at a given time t starting at the point

$$A=(\theta ,\phi )\in D,$$

and

$$T=\inf \{t\ge 0|X_t\notin D\},$$

then the expectation of $\exp (-\lambda T)$ is given by

$$E^A\left[\exp (-\lambda T)\right]=\frac{P_{\nu }\left(\cos \phi \right)}{P_{\nu }\left(\cos {\phi }_0\right)},$$ (4.56)

where ν is such that $\nu (\nu +1)=-2a^2\lambda$ and P_ν( · ) is the Legendre function

$$P_{\nu }\left(z\right)=P_{-\nu -1}\left(z\right)=\frac{1}{\pi }{\int }_0^{\pi }{(z+\sqrt{z^2-1}\cos \phi )}^{\nu }d\phi ,$$

where the multiple-valued function ${(z+\sqrt{z^2-1}\cos \phi )}^{\nu }$ is to be determined in such a way that for $\phi =\frac{\pi }{2}$ it is equal to (the principal value of) z^ν (which is, in particular, real for positive z and real ν).

Proof

If $\lambda >-\frac{{\lambda }_1}{2},$ where λ ₁ is the first Dirichlet eigenvalue of D ⊂ S ², then

$$E^A\left[\exp (-\lambda T)\right]$$

it satisfies the differential equation

$$\frac{1}{2}{\Delta }_{2}u=\lambda u\left(\phi \right)$$ (4.57)

with boundary condition

$$u\left({\phi }_0\right)=1.$$ (4.58)

Here Δ₂ is the Laplace-Beltrami operator on S ². By the symmetry of D, it follows that the expectation of $\exp [-\lambda T]$ is independent of θ. Hence u is independent of θ. From (4.4) the differential equation (4.57) takes the form

$$\frac{1}{2a^2\sin \phi }(\frac{du}{d\phi }\cos \phi +\frac{d^{2}u}{d{\phi }^2}\sin \phi )=\lambda u\left(\phi \right),$$

i.e.

$$\frac{d}{d\phi }\left(\frac{du}{d\phi }\sin \phi \right)-\left(2\lambda a^2\sin \phi \right)u\left(\phi \right)=0.$$ (4.59)

If we set

$$z=\cos \phi ,$$

then

$$\frac{du}{d\phi }=-\sin \phi \frac{du}{dz}$$

and (4.59) transforms to

$$(1-z^2)\frac{d^{2}u}{d{z}^2}-2z\frac{du}{dz}-2\lambda a^{2}u=0,$$

or

$$(1-z^2)\frac{d^{2}u}{d{z}^2}-2z\frac{du}{dz}+\nu (\nu +1)u=0.$$

This is Legendre’s differential equation. However, u(φ) is bounded for all $\phi \in [0,\pi ]$ and $u\left({\phi }_0\right)=1$. Therefore (see [106]), the solution of (4.59) is

$$u\left(\phi \right)=\frac{P_{\nu }\left(\cos \phi \right)}{P_{\nu }\left(\cos {\phi }_0\right)},$$

i.e.

$$E^A[\exp (-\lambda T)=\frac{P_{\nu }\left(\cos \phi \right)}{P_{\nu }\left(\cos {\phi }_0\right)},$$

where ν is such that $\nu (\nu +1)=-2a^2\lambda .$  □

4.4. Reflection principle

Theorem 4.2

Let X_t be the position of the infectious carrier of virus Y at a given time t starting at the point

$$A=\left({\theta }_{,}\phi \right)\in D,$$

where

$$D=\{(\theta ,\phi )\in S^2|\theta \in [$$

If

$$T=\inf \{t\ge 0|X_t\notin D\},$$

then

$$P{r}^A\{T<t\}=2P{r}^A\{X_t\notin D\}.$$ (4.60)

Proof

$$P{r}^A\{T<t\}=P{r}^A\{T<t,X_t\notin D\}+P{r}^A\{T<t,X_t\in D\}.$$ (4.61)

However, if X_t ∉ D then of course T < t.

Thus,

$$P{r}^A\{T<t,X_t\notin D\}=P{r}^A\{X_t\notin D\}.$$ (4.62)

On the other hand, if we set

$$\widetilde{X_t}=\{\begin{array}{cccc}{X}_t,\text{if}t\le T& & & \\ \widehat{X_t},\text{if}t>T& & & \\ & & \end{array},$$

then by the strong Markov property of X_t

$$P{r}^A\{T<t,X_t\in D\}=P{r}^A\{T<t,\widetilde{X_t}\in D\},$$

but if $\widetilde{X_t}\in D$ then X_t ∉ D. Hence,

$$P{r}^A\{T<t,X_t\in D\}=P{r}^A\{T<t,X_t\notin D\},$$

or

$$P{r}^A\{T<t,X_t\in D\}=P{r}^A\{X_t\notin D\}.$$ (4.63)

Therefore from (4.61)–(4.63) we obtain that

$$P{r}^A\{T<t\}=2P{r}^A\{X_t\notin D\}.$$

 □

4.4.1. Applications of the reflection principle

The reflection principle can help to calculate the distribution functions of certain exit times.

Let X_t be the position of the infected individual at a given time t starting at the point N(0, 0) in spherical coordinates. If

$$D=\{(\theta ,\phi )\in S^2|\theta \in [0,2\pi ),\phi \in (\frac{\pi }{2},\pi ]\}$$

then

$$P{r}^N\{X_t\notin D\}={\int }_0^{\frac{\pi }{2}}{\int }_0^{2\pi }p(t,\phi )a^2\sin \left(\phi \right)d\theta d\phi ,$$

i.e.

$$P{r}^N\{X_t\notin D\}=2\pi a^2{\int }_0^{\frac{\pi }{2}}p(t,\phi )\sin \left(\phi \right)d\phi ,$$

where p(t, φ) is the transition density function of the Brownian motion on S ² of radius a. Hence from (4.26)

$$P{r}^N\{X_t\notin D\}=2\pi a^2{\int }_0^{\frac{\pi }{2}}\frac{1}{4\pi a^2}\sin \phi \sum _{n\in \mathbb{N}}(2n+1)\exp (-\frac{n(n+1)\sqrt{t}}{a})P_n^0\left(\cos \phi \right)d\phi ,$$

or

$$P{r}^N\{X_t\notin D\}=\frac{1}{2}+\frac{1}{2}\sum _{n\in {\mathbb{N}}^{*}}(2n+1)\exp (-\frac{n(n+1)\sqrt{t}}{a}){\int }_0^{\frac{\pi }{2}}{P}_n^0\left(\cos \phi \right)\sin \left(\phi \right)d\phi .$$ (4.64)

However for every $n\in {\mathbb{N}}^{*}$

$$I_n={\int }_0^{\frac{\pi }{2}}{P}_n^0\left(\cos \phi \right)\sin \left(\phi \right)d\phi ={\int }_0^1{P}_n^0\left(x\right)dx.$$

It is known that (see [106])

$$P_n^0\left(x\right)=\frac{1}{2n+1}\frac{d}{dx}[P_{n+1}^0\left(x\right)-P_{n-1}^0\left(x\right)].$$

However, $P_n^0\left(1\right)=1$ for every $n\in \mathbb{R}.$ Thus

$$I_n=\frac{1}{2n+1}(P_{n+1}^0\left(1\right)-P_{n-1}^0\left(1\right)-P_{n+1}^0\left(0\right)+P_{n-1}^0\left(0\right)),$$

or

$$I_n=\frac{1}{2n+1}(P_{n-1}^0\left(0\right)-P_{n+1}^0\left(0\right)).$$

It is also known that for every $n\in {\mathbb{N}}^{*}$

$$P_{2n}^0\left(0\right)={(-1)}^n\frac{\left(2n\right)!}{2^{2n}{(n!)}^2}\text{and}{P}_{2n+1}^0\left(0\right)=0.$$

Thus, if n is even then $I_n=0.$ If n is odd, i.e. $n=2k+1,$ then

$$I_n=\frac{1}{4k+3}(P_{2k}^0\left(0\right)-P_{2(k+1)}^0\left(0\right)),$$

i.e.

$$I_n=\frac{{(-1)}^n\left(2k\right)!}{(k+1){(k!)}^2{2}^{2k+1}}.$$ (4.65)

From (4.64) and (4.65) we get that

$$\begin{array}{ccc}\hfill P{r}^N\{X_t\notin D\}& =& \frac{1}{2}+\frac{1}{2}\sum _{n\in \mathbb{N}}{(-1)}^n\exp (-\frac{(2n+1)(2n+2)\sqrt{t}}{a})\hfill \\ & & \times \frac{\left(2n\right)!(4n+3)}{2^{2n+1}{(n!)}^2(n+1)}.\hfill \end{array}$$ (4.66)

Furthermore, if S(0, π) namely the South Pole of S ², then

$$P{r}^S\{X_t\notin D\}=P{r}^N\{\widehat{X_t}\notin D\}=P{r}^N\{X_t\in D\}=1-P{r}^N\{X_t\notin D\}.$$

Therefore

$$\begin{array}{ccc}\hfill P{r}^S\{X_t\notin D\}& =& \frac{1}{2}-\frac{1}{2}\sum _{n\in \mathbb{N}}{(-1)}^n\exp (-\frac{(2n+1)(2n+2)\sqrt{t}}{a})\hfill \\ & & \times \frac{\left(2n\right)!(4n+3)}{2^{2n+1}{(n!)}^2(n+1)}.\hfill \end{array}$$ (4.67)

By using Theorem 3.2, if $T=\inf \{t>0|X_t\notin D\},$ then

$$\begin{array}{ccc}\hfill P{r}^S\{T<t\}& =& 1-\sum _{n\in \mathbb{N}}{(-1)}^n\exp (-\frac{(2n+1)(2n+2)\sqrt{t}}{a})\hfill \\ & & \times \frac{\left(2n\right)!(2n+3)}{2^{2n+1}{(n!)}^2(n+1)}.\hfill \end{array}$$ (4.68)

4.5. Local time estimation

Definition 4.11

Let φ₁ ∈ [0, π]. We set

$$\begin{array}{ccc}\hfill D_1& =& \{({\theta }_1,\dots ,{\theta }_{n-1},\phi )\parallel {\theta }_1\in [0,2\pi ),{\theta }_i\in [0,\pi ]\text{for}\hfill \\ & & i=2,\dots ,n-1\text{and}\phi \in (0,{\phi }_1]\},\hfill \end{array}$$

is a subset of S ². The reflected Brownian motion in D ₁ is the diffusion Y_t whose generator is Δ_n in D ₁ with Neuman boundary condition at ∂D ₁.

Roughly speaking Y_t behaves like X_t inside D ₁ but when it reaches the boundary, it is reflected back in D ₁.

Definition 4.12

Let a fixed open set D ⊂ Sⁿ with $C^3-$boundary ∂D. If Y_t is the reflected Brownian motion in D, and D_δ the domain

$$D_{\delta }=\{x\in D:d(x,\partial D)<\delta \},$$

we define the boundary local time L_t of Y_t, as

$$L_t:=\underset{\delta \to 0^{+}}{\lim }\frac{1}{2\delta }{\int }_0^t{1}_{D_{\delta }}\left(Y_s\right)ds.$$

It can be shown that the limit exist in the L ₂ sense.

4.5.1. Boundary local time until first hitting

Proposition 4.8

Let φ₀, φ₁ ∈ (0, π), such that φ₀ < φ₁, both fixed. We consider the sets D, Γ₀ in S ², such that

$$D=\{(\theta ,\phi )|\theta \in [0,2\pi )\text{and}\phi \in ({\phi }_0,{\phi }_1)\}.$$

and

$${\Gamma }_0=\{(\theta ,{\phi }_0)|\theta \in [0,2\pi )\}.$$

Let Y_t be the reflected Brownian motion in Γ₀ starting at the point

$$A=(\theta ,\phi )\in D$$

if

$$T=\inf \{t\ge 0|X_t\in {\Gamma }_0\}$$

and  L_t is the boundary local time of  Y_t, then,

$$E^A\left[\exp \left(\lambda L_T\right)\right]=\frac{\frac{1}{\sin {\phi }_1}-\lambda \ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{\phi }{2}\right)}\right)}{\frac{1}{\sin {\phi }_1}-\lambda \ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)},\text{if}\lambda <\frac{1}{\sin \left({\phi }_1\right)\ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)}$$ (4.69)

and

$$E^A\left[\exp \left(\lambda L_T\right)\right]=+\infty ,\text{if}\lambda \ge \frac{1}{\sin \left({\phi }_1\right)\ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)}.$$ (4.70)

Proof

It is known that the function

$$z(\theta ,\phi )=E^A\left[\exp \left(\lambda L_T\right)\right]$$

satisfies the differential equation

$${\Delta }_{2}z=0$$

with boundary condition

$$z(\theta ,{\phi }_0)=1$$

and

$$-\frac{\partial z}{\partial \phi }(\theta ,{\phi }_1)+\lambda z(\theta ,{\phi }_1)=0.$$

as long as the function z is positive (see [107]). Here Δ₂ is the Laplace-Beltrami operator on S ². By the symmetry of D it follows that E^A[ exp (λL_T) ] is independent of θ. From (4.2) the differential equation takes the form

$$\cot \left(\phi \right)\frac{dz}{d\phi }+\frac{d^{2}z}{d^2\phi }=0.$$ (4.71)

We have shown that the solution of (4.71) is

$$z\left(\phi \right)=c_1{\int }_{{\phi }_0}^{\phi }\frac{1}{\sin x}dx+c_2,c_1,c_2\in \mathbb{R}.$$

However,

$$z(\theta ,{\phi }_0)=1$$

and

$$-\frac{\partial z}{\partial \phi }(\theta ,{\phi }_1)+\lambda z(\theta ,{\phi }_1)=0.$$

Hence

$$c_1=\frac{\lambda }{{\left(\sin {\phi }_1\right)}^{-1}-\lambda {\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}$$

and

$$c_2=1.$$

Thus

$$z\left(\phi \right)=\frac{{\left(\sin {\phi }_1\right)}^{-1}-\lambda {\int }_{\phi }^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}{{\left(\sin {\phi }_1\right)}^{-1}-\lambda {\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}.$$

However,

$$z\left(\phi \right)>0\text{if}\text{and}\text{only}\text{if}\lambda <\frac{{\left(\sin {\phi }_1\right)}^{-1}}{{\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}.$$

Therefore,

$$\begin{array}{ccc}& & E^A\left[\exp \left(\lambda L_T\right)\right]=\frac{{\left(\sin {\phi }_1\right)}^{-1}-\lambda {\int }_{\phi }^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}{{\left(\sin {\phi }_1\right)}^{-1}-\lambda {\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx},\hfill \\ & & \text{if}\lambda <\frac{{\left(\sin {\phi }_1\right)}^{-1}}{{\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}\hfill \end{array}$$

and

$$E^A\left[\exp \left(\lambda L_T\right)\right]=+\infty ,\text{if}\lambda \ge \frac{{\left(\sin {\phi }_1\right)}^{-1}}{{\int }_{{\phi }_0}^{{\phi }_1}{\left(\sin x\right)}^{-1}dx}$$

i.e

$$\begin{array}{ccc}& & E^A\left[\exp \left(\lambda L_T\right)\right]=\frac{\frac{1}{\sin {\phi }_1}-\lambda \ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{\phi }{2}\right)}\right)}{\frac{1}{\sin {\phi }_1}-\lambda \ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)},\hfill \\ & & \text{if}\lambda <\frac{1}{\sin \left({\phi }_1\right)\ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)}\hfill \end{array}$$

and

$$E^A\left[\exp \left(\lambda L_T\right)\right]=+\infty ,\text{if}\lambda \ge \frac{1}{\sin \left({\phi }_1\right)\ln \left(\frac{\tan \left(\frac{{\phi }_1}{2}\right)}{\tan \left(\frac{{\phi }_0}{2}\right)}\right)}.$$

 □

5. Discussion and conclusions

A worldwide multilevel interplay among a plethora of factors ranging from micro-pathogens and individual interactions to macro-scale environmental, socio-economic and demographic conditions, necessitate the development of highly sophisticated mathematical models for robust representation of contagious dynamics of infectious diseases that would lead to the establishment of effective control strategies and prevention policies.

Ethical and practical reasons defer from conducting enormous experiments in public health systems, hence mathematical models appear to be an efficient way to explore contagion dynamics. A key aspect of epidemiological models is their link to real data, which is of particular utility toward the design of vaccination policies. Two major vaccination strategies exist currently, i.e., the mass vaccination, which is most applied, and the recently developed pulse vaccination which is used in an increasing number of countries. However, most vaccination strategies are imperfect in the sense that they decrease the number of cases, without however eradicating the disease.

Public-health organizations in the world use the epidemiological models that fall in the three categories already presented in this work, to evaluate disease outbreak policies for epidemics. As we pointed out, many shortcomings exist for those models. All the models already used in the literature assume that the host population has constant size. However, this excludes diseases in exponentially growing populations as in most developing countries, or disease-induced mortality as childhood diseases in developing countries e.g., malaria. Modeling infectious dynamics in non-stationary host populations requires explicit modeling of the host population as well as of the disease per se. Models sometimes can be highly complicated in order to improve best fit to real data. Nonetheless, very complex models do not always perform optimally in real-world applications or in simulations. Real-world models allow for swift decision making, and suitable quantification of the spatiotemporal dynamics of an outbreak. Multidisciplinary research efforts are speeding up, integrating the advances in epidemiology, molecular biology, computational science and applied mathematics. Mathematical modeling allows better understanding of the transmission process of infectious diseases in space and time, by setting forth rigorously the proper assumptions, the variables, the equations and their parameters.

Due to the complexity of the underlying complex interactions, either deterministic or stochastic epidemiological models are built upon incomplete information about e.g., the basic reproduction number, threshold effects, intensity of spread, precise data of infected versus susceptible individuals, and other inaccuracies regarding the entire infectious network. Simulations or brute-force computational techniques have been implemented in that direction to provide approximate solutions with encouraging results. Nevertheless, some of the underlying generating processes of the outbreaks, such as the virus pathogenicity or variant social network topologies, ethnological characteristics and other quantities, may influence the spread of an outbreak. Simulations often prove to be inefficient for the systematic analysis of an emergent epidemic. New rigorous mathematical modeling methodologies, such as the one presented in this work for the first time, can be used to address inherent incomplete data structure and hidden nonlinear complex dynamics, with an aim to enhance forecastability in combating epidemic outbreaks.

In the present study we introduced a novel approach for surveillance and modeling of infectious disease dynamics, called SBDiEM. We explicitly described the mathematical framework underpinning the implementation and conceptualization of our new-age epidemiological model. Our goal is to contribute to the arsenal of models already developed so far. It can be of particular interest, in light of a recent intensive worldwide effort to speed up the establishment of a global surveillance network for combating pandemics of emergent and re-emergent infectious diseases. Toward this aim, mathematical modeling will play a major role in assessing, controlling and forecasting potential outbreaks. We have to better understand and model the impact of numerous variables on contagious dynamics, ranging from the microscopic host–pathogen level, to individual and population interactions, as well as macroscopic environmental, social, economic and demographic factors all over the world.

As a path for future research, we intend to conduct simulations, and empirical analyses based on real-time spatiotemporal datasets, in case of past outbreaks of infectious diseases as well as for COVID-19. Furthermore, we plan to convey an extensive comparative evaluation investigation of SBDiEM vis-à-vis the three major categories set forth by the taxonomy of Siettos and Russo [58], and more specifically versus (1) statistical methods for epidemic surveillance, (2) state-space models of epidemic spread and (3) machine learning methods. In this way, the forecasting and nowcasting capabilities of the new model will be thoroughly explored. We also intend to investigate embedding the proposed analytical model into integrated artificial intelligence systems in the near future.

Our novel methodology apart from offering a much better understanding of the complex and heterogeneous infectious disease dynamics could enhance predictability of epidemic outbreaks as well as have potentially important implications for national health systems, stakeholders and international policy makers.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.