Abstract

The coal-based reduction of fayalite was characterized using thermogravimetric (TG) and differential TG methods with reduction temperatures from 1123 to 1273 K. The results of fayalite isothermal reduction indicate that the reduction process is divided two stages. The corresponding apparent activation energy E was gained using the isoconversional and model-fitting methods. At the first stage, the effect of temperature on the reduction degree was not clear, and the phase boundary chemical reaction was the controlling step, with an apparent activation energy E value of 175.32–202.37 kJ·mol–1. At the second stage, when the temperature was more than 1123 K, the conversion degree and the reaction rate increased nonlinearly with increasing temperature, and two-dimensional diffusion, three-dimensional diffusion, one-dimensional diffusion, and phase boundary-controlled reaction were the controlling stages, with an apparent activation energy E ranging from 194.81 to 248.96 kJ·mol–1. For the whole reduction process, the average activation energy E and pre-exponential factor A were 185.07–225.67 kJ·mol–1 and 0.796–0.797 min–1, respectively.
Introduction
Flash smelting and converter smelting have been used in the copper industry for a number of years as a relatively advanced, most widely available technology for refining metallic copper from the copper ore.1 The main phases and compositions of the copper ore are chalcopyrite (CuFeS2), chalcocite (Cu2S), covellite (CuS), quartz (SiO2), and pyrite (FeS2).2 However, nearly all of the impurity metals enter the slag phase, under the action of oxygen-rich blowing, because the affinity of copper to oxygen is less than that of impurity metals. Therefore, a metal-rich fayalite is discharged as a byproduct with copper slag in the process of the matte smelting and refining of copper.3,4 Production of 1 ton of metallic copper generates approximately 2.2–3.0 tons of slag.
It is estimated that 19–26.7 million tons of copper slag is discharged into the environment annually in China. Generally, the compositions and contents of copper slag vary in the range of Fe2O3 35–65%, SiO2 20–45%, CaO 0.2–15%, MgO 0.5–12%, and so forth.5 Clearly, million tons of iron resources exist in the annually generated slag. However, only a little part of slag is used in construction materials, paving materials, and so forth.6,7 Recent research found that copper slag contains Cu in the form of sulfides, which can be recycled mainly by flotation,8−10 and Fe mainly in the form of fayalite, which can be difficult to recycle using conventional mineral processing methods. Compared to the natural raw ore, most secondary raw materials are of a higher grade11 but have a complicated structure and chemical phases, which seriously restrict the recycling efficiency of metals.
At present, the comprehensive use of resources, such as the coal-based reduction of copper slag, has become a topic of significant interest. The effects of reduction conditions such as reduction temperature, reduction time, and C/O ratio on the reduction and magnetic separation were investigated in detail, and metallic iron containing more than 90% Fe was obtained under optimal conditions.12−15 Although studying the effectiveness factors of the reduction process is very important, the kinetics of metal grain growth is more significant in prompting comprehensive utilization of iron. Three-dimensional (3D) diffusion model of the Jander equation16 and reaction geometry model,17 gas–liquid reaction theory and double membrane theory,18 and equilibrium model based on Gibbs free energy minimum principle19 usually can be used to describe the iron grain growth during the gas-based and oil-based reduction process, respectively. In the process of coal-based reduction, three models, that is, Hillert dynamics,20 integral method,21 and kinetic phenomenological theory,22 often describe the kinetics of the grain growth process. However, the formation and characterization of metallic iron grains during the copper slag reduction remain unclear, which are imperative for understanding and optimizing the coal-based reduction process. Furthermore, we might introduce a suitable model to describe the whole reduction process.
In this paper, as the main phase of the copper slag, fayalite would be considered. First, the granularity and composition of raw fayalite after magnetic separation were characterized by laser particle size analysis and X-ray diffraction (XRD). Second, the coal-based reduction process was identified by thermogravimetric analysis (TGA). Then, to illustrate the kinetics and mechanism of the coal-based reduction of fayalite, a relatively reasonable model was established via the isothermal thermal analysis kinetic method at 1123–1273 K.
Results and Discussion
TG and Reduction Degree Curves
Reduction degree curves and mass loss TG as a function of time at different reduction temperatures are shown in Figure 1. The reduction degree and mass loss increased sharply with increasing temperature. When the fayalite is reduced at relatively low temperatures (∼1123–1173 K), the reduction degree is strongly affected by the reduction temperature; the maximum degree of fayalite was 0.0816, 0.1935, 0.5566, and 0.9936 at 1123, 1173, 1223, and 1273 K, respectively. These experimental results indicate that when the temperature is less than 1173 K, the activation energy provided is inadequate to bring about a significant reduction; therefore, obvious reduction starts at 1223 K and above.
Figure 1.
(a) Mass loss and (b) reduction degree as a function of time at different temperatures.
Determination of Mode Function G(α)
ln–ln Analysis Method
The whole reaction process is divided into two stages on the basis of eqs 10 and 11 and the TG experimental data, and the range of corresponding reduction is shown in Table 1. The fitting data obtained at different temperatures are shown in Figure 2. The gained intercepts n ln k and slopes n are shown in Table 2. At the first stage, the slopes n are 0.98, 0.87, 0.83, and 0.77. These values are between 0.77 and 0.98, which accurately match (0.9933 ≤ R2 ≤ 0.9991) the values of F1(α) in Table 3. Therefore, the first stage can be described as the mode function F1(α). At the second stage, the slopes n are 0.58, 0.37, 0.79, and 1.39, which better match (0.9467 ≤ R2 ≤ 0.9997) the values of D2(α), D3(α), D1(α), and R2(α), respectively (Table 3). In the case of 1123 K, the second reduction stage is expressed by the mode function D2(α); thus, a two-dimensional (2D) diffusion process is proposed, described by the kinetic equation G(α) = (1 – α)ln(1 – α) + α. For the temperatures of 1173–1273 K, the second reduction stage is expressed by mode functions D3(α) and D1(α), respectively. In this case, a process from tridimensional particle shape Jander equation to one-dimensional (1D) diffusion is proposed, described by the kinetic equation G(α) = [1 – (1 – α)1/3]2 and G(α) = α2. For a temperature of 1273 K, the second stage is expressed by the mode function R2(α); in this case, a phase boundary-controlled reaction process is proposed, described by the kinetic equation R2(α) = 1 – (1 – α)1/2.
Table 1. Reduction Degree Range of Different Stages with Different Reduction Temperatures.
| T/K | 1173 | 1223 | 1273 | 1323 |
| first stage | 0.0000–0.0248 | 0.0000–0.0687 | 0.0000–0.1331 | 0.0000–0.3324 |
| second stage | 0.0248–0.0816 | 0.0687–0.1935 | 0.1331–0.5566 | 0.3324–0.9936 |
Figure 2.
Avrami transformation plots of ln[−ln(1 – α)] vs ln t at different temperatures. The reduction temperatures were (a) 1123, (b) 1173, (c) 1223, and (d) 1273 K, respectively.
Table 2. Data Fitting Values for Different Temperatures Determined by the ln–ln Analysis Method.
| reduction stage | T/K | slope/n | intercept/ln k | R2 |
|---|---|---|---|---|
| first stage | 1123 | 0.98 | –8.26 | 0.9991 |
| 1173 | 0.87 | –6.23 | 0.9966 | |
| 1223 | 0.83 | –5.60 | 0.9947 | |
| 1273 | 0.77 | –5.60 | 0.9933 | |
| second stage | 1123 | 0.58 | –6.44 | 0.9997 |
| 1173 | 0.59 | –4.12 | 0.9967 | |
| 1223 | 0.79 | –5.64 | 0.9941 | |
| 1273 | 1.39 | –7.74 | 0.9467 |
Table 3. Model Function G(α) of Different Stages at Different Temperatures.
|
T/K |
|||||
|---|---|---|---|---|---|
| reduction stage | mode function | 1123 | 1173 | 1223 | 1273 |
| first stage | G(α) | –ln(1 – α) | –ln(1 – α) | –ln(1 – α) | –ln(1 – α) |
| second stage | G(α) | (1 – α)ln(1 – α) + α | [1 – (1 – α)1/3]2 | α2 | 1 – (1 – α)1/2 |
Málek Method
We, in the Málek method, replaced the parameters in eq 12 with each of the 10 mechanism functions and tested the experimental data. Through a comparison of the experimental (α–y(α)) curves with theoretical ones, the most suitable f(α) was identified when the experimental (α–y(α)) values all matched with the theoretical line. Standard kinetic curves and fitting curves for fayalite samples at different reduction temperatures are shown in Figure 3. The experimental data accurately fit the value of F1 at the first stage, so the reaction follows the F1(α) model. An instantaneous nucleation and unidimensional growth (bimolecular decay law) process described by the kinetic equation G(α) = −ln(1 – α) is proposed. When the temperature is 1173 K, the second stage is expressed by the mode function D3(α), described by the kinetic equation G(α) = [1 – (1 – α)1/3]2. When the temperature is 1223 K, the second stage is described by the mode function D1(α), expressed by the kinetic equation G(α) = α2. When the temperature is 1273 K, the second stage is described by the mode function A2(α), expressed by the kinetic equation G(α) = 1 – (1 – α)1/2. Therefore, the second stage is a 2D diffusion, 3D diffusion, 1D diffusion, and phase boundary-controlled reaction process at the different reduction temperatures. The mechanisms controlling the fayalite reduction process are identical as determined by the two methods. The Málek method provides another evident reaction mechanism for the whole reduction process of fayalite, compared to the ln–ln analysis method.
Figure 3.

Standard kinetic curves and fitting curves for samples at various temperatures.
Apparent Activation Energy
Isoconversional Method
According to eq 13, the linear fitting of data is shown in Figure 4a, whose slope can usually obtain the apparent activation energy E. The apparent activation energy E values of the fayalite reduction process at different reduction degrees are shown in Figure 4b.
Figure 4.
Linear fitting of data (a) ln(dα/dt) vs 1/T and (b) E vs α.
Correlation coefficients (R2) and the slopes (−E/R) are shown in Table 4. The conversion degree and its corresponding correlation coefficients (R2) and apparent activation energy (E) values are also given in this table. The linear correlation coefficients range from 0.9123 to 0.9973 with 0.05 ≤ α ≤ 0.55, and the correlation is good for most of the linear graph (Table 4). The apparent activation energy E values of the first stage and the second stage are ∼175.32–202.37 and ∼173.45–297.71 kJ·mol–1, respectively. As shown in Figure 4b, the apparent activation energy E values increase linearly with the increase of reduction degree. Therefore, achieving higher reduction degree is a difficult process.
Table 4. Activation Energy Values Obtained by the Isoconversional Method.
| reduction stage | Α | slope | E/(kJ·mol–1) | R2 |
|---|---|---|---|---|
| first stage | 0.05 | –21,088 | 175.32 | 0.9795 |
| 0.10 | –27,595 | 229.42 | 0.9979 | |
| average | –24,341 | 202.37 | ||
| second stage | 0.15 | –20,863 | 173.45 | 0.9988 |
| 0.20 | –28,646 | 238.16 | ||
| 0.30 | –34,874 | 289.94 | ||
| 0.40 | –29,892 | 248.52 | ||
| 0.55 | –35,808 | 297.71 | ||
| average | –30,016 | 249.55 | ||
| all stage | average | 225.96 |
Model-Fitting Method
According to eq 8, linear fitting of G(α) versus t is shown in Figure 5, whose slopes are the corresponding reaction rates k(T) of various temperatures at various reduction stages. The reaction rates k(T) for various temperatures at various reduction stages are shown in Table 5.
Figure 5.
Fitting curves of G(α) vs t for different temperatures at different reduction stages.
Table 5. Reaction Rates k(T) for Different Temperatures at Different Reduction Stages.
| reduction stage | T/K | k(T)/10–3 | R2 |
|---|---|---|---|
| first stage | 1123 | 0.187 | 0.9896 |
| 1173 | 0.602 | 0.9693 | |
| 1223 | 1.060 | 0.9819 | |
| 1273 | 2.290 | 0.9903 | |
| second stage | 1123 | 0.0704 | 0.9937 |
| 1173 | 0.1120 | 0.9866 | |
| 1223 | 0.5530 | 0.9994 | |
| 1273 | 1.3800 | 0.9909 |
According to eq 14, linear fitting of ln k(T) versus 1/T is shown in Figure 6, which yields a straight line because that reduction degree (α) is a constant. From the slope of the line, we can calculate the apparent activation energy E values of the reaction reduction process at various reduction stages. The apparent activation energy E values of the first and second stages are 194.81 and 248.96 kJ·mol–1, respectively. For the whole reduction process, the average apparent activation energy E value is 221.88 kJ·mol–1, which is lower than the apparent activation energy E values gained by the isoconversional method.
Figure 6.
Linear fitting of data ln k vs 1/T at different temperatures in different reduction stages: (a) first stage and (b) second stage.
On the basis of the apparent activation energy E values, the k(T), and eq 14, the pre-exponential factor A was gained by the isoconversional method and the model-fitting method (Table 6). It can be seen that when the temperature ranges from 1123 to 1273 K, at the first stage, the values of pre-exponential factor A increase sharply with increasing temperature. The average values of A obtained by the isoconversional method and model-fitting method are 1.054 and 1.055, respectively. At the second stage, the values of pre-exponential factor A increase slightly with increasing temperature, and the average values of pre-exponential factor A were 0.538 and 0.539, respectively. Therefore, for the whole reduction process, the values of the pre-exponential factor A gained by the isoconversional method and the model fitting method are 0.796 and 0.797, respectively.
Table 6. Arrhenius Parameter (A) in the Two Stages at Different Temperatures.
| first stage |
Second stage |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| method | 1173 | 1223 | 1273 | 1323 | average | 1173 | 1223 | 1273 | 1323 | average |
| isoconversional method | 0.190 | 0.614 | 1.080 | 2.332 | 1.054 | 0.072 | 0.114 | 0.556 | 1.412 | 0.538 |
| model-fitting method | 0.191 | 0.615 | 1.081 | 2.334 | 1.055 | 0.072 | 0.115 | 0.557 | 1.413 | 0.539 |
Conclusions
Based on the results of our study, the following conclusions can be drawn.
-
(1)
The reduction process of fayalite was divided into two different steps, and the corresponding apparent activation energy was gained using a model-fitting method and the isoconversional method.
-
(2)
At the first stage (0.00 ≤ α ≤ 0.33), the reduction process follows the F1 model, and an instantaneous nucleation and unidimensional growth process is proposed, described by the kinetic equation G(α) = −ln(1 – α). At the second stage (0.33 ≤ α ≤ 0.98), the reduction process is controlled by 2D diffusion, 3D diffusion, 1D diffusion, and phase boundary-controlled reaction as the reduction temperature is increased from 1123 to 1273 K. The function model of coal-based reduction reactions matches the D2(α), D3(α), D1(α), and A2(α) models, respectively. The equations are G(α) = (1 – α)ln(1 – α) + α for T = 1123 K, G(α) = [1 – (1 – α)1/3]2 for T = 1173 K, G(α) = α2 for T = 1223 K, and G(α) = 1 – (1 – α)1/2 for T = 1273 K, respectively.
-
(3)
For the whole fayalite reduction process, the average apparent activation energy E value is 221.88–225.96 kJ·mol–1 and the average pre-exponential factor A value is 0.796–0.797 min–1, respectively.
The research method of the study can be applied to the reduction process of different kinds of smelting slag and difficult-to-float oxide ore. The research results can control the particle size of metal particles and can be applied to the fields of magnetic particle size control and metallurgical raw material preparation.
Experimental Section
Materials
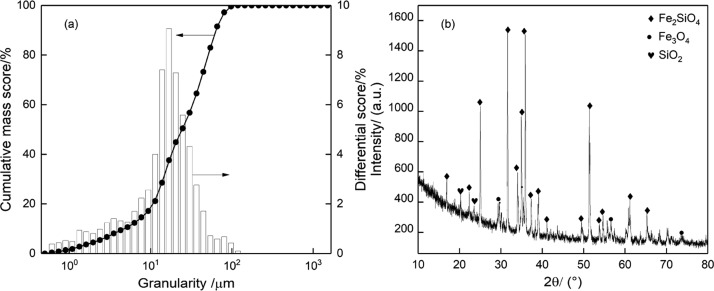
We obtained fayalite powder, using magnetic separation, from the copper slag provided by Zijin Copper Co., Ltd. (Fujian Province, China). The fayalite sample is subjected to particle size distribution analysis that was performed by a laser particle size analyzer (Malvern Mastersizer 2000). The analysis results indicate that more than 90% of the fayalite particles have a granularity less than 74 μm (Figure 7a). The chemical composition and material composition are shown in Table 7 and Figure 7a, respectively. The XRD pattern shows that fayalite (Fe2SiO4) is the dominant mineral in the copper slag and magnetite (Fe3O4) and quartz (SiO2) are minor components.
Figure 7.
Particle size distribution (a) and XRD pattern (b) of the copper slag.
Table 7. Chemical Composition of Fayalite.
| wt % | ||||||
|---|---|---|---|---|---|---|
| TFe | MFe | SiO2 | Al2O3 | CaO | S | P |
| 43.800 | 1.76 | 29.875 | 2.988 | 2.118 | 0.147 | 0.102 |
Reduction Mechanism
The Gibbs free energy as a function of temperature was calculated using the HSC Chemistry 7.0 software. As shown in Figure 8, the Gibbs free energy values of eqs 1 and 2 become increasingly negative with increasing temperature, while the values of eq 3 become increasingly positive with increasing temperature. In Figure 8, the evidence can be obtained easily; eq 1 is the predominant reaction, eq 2 cannot continue the reaction normally in a high temperature, and the reaction in eq 3 cannot continue during the given reduction temperature range, which resulted from the lack of CO in the initial stage of reaction and higher Gibbs free energy with the increasing temperature.
| 1 |
| 2 |
| 3 |
Figure 8.

ΔGθ vs T for the reaction system of fayalite.
Experimental Procedure
TGA experiments were performed on a TGA 2 thermogravimetric analyzer with a small furnace. The samples (fayalite) were reduced in the furnace as the mass was measured via a thermobalance with a sensitivity of ±10–4 g to make a better decision about whether or not to continue the reactions. The fayalite samples, which weighed (10 ± 0.5) mg, were placed in an Al2O3 crucible. When the fayalite samples were heated to the required temperature using a heating rate of 20 K·min–1, the fayalite samples were reduced under the flowing atmosphere of undiluted Ar (5 mL·min–1). The temperatures of isothermal reduction were 1123, 1173, 1223, and 1273 K, respectively.
Methods
The reduction degree, in the isothermal reduction process, is described as follows
| 4 |
where α is the reduction degree and wini, wt, and wend indicate the initial mass, the mass at time t, and the final mass of the sample, respectively. Generally, the method for the solid-state process can be expressed by a complex differential kinetic equation23,24
| 5 |
| 6 |
where t represents the time, k(T) indicates the temperature-dependent rate constant, and f(α) is a function that expresses the reaction model.
Combining eqs 5 and 6 results in the following description
| 7 |
An integration function of eqs 5 and 6 is expressed as25,26
| 8 |
where G(α) is the integral form of the reaction model (Table 8), T is the absolute temperature (K), R is the gas constant (J·mol–1·K–1), t is the time (min), A is the pre-exponential factor (min–1), and E is the apparent activation energy (kJ·mol–1).
Table 8. Nine Algebraic Expressions for G(α) Used To Describe Solid-State Reaction Mechanisms27,31.
| function | G(α) | n | mechanism |
|---|---|---|---|
| D1(α) | α2 = kt | 0.62 | 1D diffusion |
| D2(α) | (1 – α)ln(1 – α) + α = kt | 0.57 | 2D diffusion (bidimensional particle shape) |
| D3(α) | [1 – (1 – α)1/3]2 = kt | 0.54 | 3D diffusion (tridimensional particle shape Jander equation) |
| D4(α) | (1 – 2/3α) – (1 – α)2/3 = kt | 0.57 | 3D diffusion (tridimensional particle shape Ginstling–Brounshtein equation) |
| F1(α) | –ln(1 – α) = kt | 1 | bimolecular decay law (instantaneous nucleation and unidimensional growth) |
| R2(α) | 1 – (1 – α)1/2 = kt | 1.11 | phase boundary-controlled reaction (contracting area, e.g., bidimensional shape) |
| R3(α) | 1 – (1 – α)1/3 = kt | 1.07 | phase boundary-controlled reaction (contracting volume, e.g., tridimensional shape) |
| A2(α) | [−ln(1 – α)]1/2 = kt | 2 | random instant nucleation and 2D growth of nuclei (Avrami–Erofeev equation) |
| A3(α) | [−ln(1 – α)]1/3 = kt | 3 | random instant nucleation and 3D growth of nuclei (Avrami–Erofeev equation) |
Determination of the Reaction Model
ln–ln Analysis Method
The Avrami–Erofeev model often applies to analyze phase transformation kinetics, especially in isothermal kinetics analysis.25,27,28 The model can be defined as
| 9 |
where k indicates the reaction rate constant and n represents the Avrami exponent, which depends on the growth mechanism and geometry of the powder. The value of n provides information about the reduction mechanism related to the reaction process; the n values of each model are given in Table 8.
From eq 9, we can also obtain the calculated equation of n.
| 10 |
| 11 |
where ln[−ln(1 – α)] is plotted versus ln t. Eqs 10 and 11 are generally used to evaluate practical data. The slope and intercept of the resulting straight line are n and ln k, respectively. The index n is a criterion for distinguishing the model-fitting function. The algebraic expressions for g(α) used to describe the solid-state reactions are summarized in Table 8.
Málek Method
The Málek method describes that the f(α) function is proportional to the y(α) functions, which can usually be derived from a simple calculation of the TG data. With α = 0.5 as a reference point, in isothermal conditions, the function can be defined as29,30
| 12 |
According to the Málek method, we substituted the parameters in eq 12 with each of the nine mechanism functions shown in Table 8 and tested the experimental data. The most suitable f(α) was identified when the experimental (a, y(α)) values fell on the theoretical line, through a comparison of the experimental α–y(α) curves with theoretical ones.
Determination of the Apparent Activation Energy E
The kinetic method is expected to lead to the derivation of an appropriate kinetic description of the process in the light of the apparent activation energy. In this research, the apparent activation energy E values were gained by a model functional method and by an isoconversional method from experimental data. The isoconversional method relates to a number of experiments which are carried out at different temperatures. According to eq 5, the following equation can be obtained
 |
13 |
According to eqs 5 and 6, the logarithmic function of the Arrhenius equation is described as32
| 14 |
where a linear fitting of ln k(T) versus T–1 should result in a straight line whose slope and intercept can usually calculate the pre-exponential factor A and the apparent activation energy E, respectively.
Acknowledgments
The authors acknowledge the funding support by the National Natural Science Foundation of China (grant nos. 51674091 and 51604084), the Natural Science Foundation of Fujian Province of China (grant no. 2017J01483), and the National Training Program of Innovation and Entrepreneurship for Undergraduates (grant no. 201810386029).
The authors declare no competing financial interest.
References
- Yu H.; Wang L. Y.; Du T. Waste Heat Recovery and Reuse of Flue Gas in Copper Pyrometallurgy. Appl. Mech. Mater. 2011, 71–78, 2239–2242. 10.4028/www.scientific.net/AMM.71-78.2239. [DOI] [Google Scholar]
- Mihajlovic I.; Strbac N.; Zivkovic Z.; Kovacevic R.; Stehernik M. A Potential Method for Arsenic Removal from Copper Concentrates. Miner. Eng. 2007, 20, 26–33. 10.1016/j.mineng.2006.04.006. [DOI] [Google Scholar]
- Wang Z.; Zhao Z.; Zhang L.; Liu F.; Peng B.; Chai L.; Liu D.; Liu D.; Wang T.; Liu H.; et al. Formation mechanism of zinc-doped fayalite (Fe2-xZnxSiO4) slag during copper smelting. J. Hazard. Mater. 2019, 364, 488–498. 10.1016/j.jhazmat.2018.10.071. [DOI] [PubMed] [Google Scholar]
- Zhao Z. w.; Chai L. y.; Peng B.; Liang Y. j.; He Y.; Yan Z. h. Arsenic Vitrification by Copper Slag Based Glass: Mechanism and Stability Studies. J. Non-Cryst. Solids 2017, 466–467, 21–28. 10.1016/j.jnoncrysol.2017.03.039. [DOI] [Google Scholar]
- Shi C.; Meyer C.; Behnood A. Utilization of Copper Slag in Cement and Concrete. Resour., Conserv. Recycl. 2008, 52, 1115–1120. 10.1016/j.resconrec.2008.06.008. [DOI] [Google Scholar]
- Feng B.; Peng J.; Guo W.; Luo G.; Zhang W.; Wang H. The Depression Behavior and Mechanism of Carboxymethyl Chitosan on Calcite Flotation. J. Mater. Res. Technol. 2019, 8, 1036–1040. 10.1016/j.jmrt.2018.07.013. [DOI] [Google Scholar]
- Hu Y.; Li W.; Ma S.; Wang Q.; Zou H.; Shen X. The composition and performance of alite-ye’elimite clinker produced at 1300 °C. Cem. Concr. Res. 2018, 107, 41–48. 10.1016/j.cemconres.2018.02.009. [DOI] [Google Scholar]
- Feng B.; Zhang W.; Guo Y.; Wang T.; Luo G.; Wang H.; He G. The Flotation Separation of Galena and Pyrite Using Serpentine as Depressant. Powder Technol. 2019, 342, 486–490. 10.1016/j.powtec.2018.09.070. [DOI] [Google Scholar]
- Guo Z.; Zhu D.; Pan J.; Zhang F.; Yang C. Industrial Tests to Modify Molten Copper Slag for Improvement of Copper Recovery. JOM 2018, 70, 533–538. 10.1007/s11837-017-2671-5. [DOI] [Google Scholar]
- Huang H. J.; Lv D. L.; Cao X. F.; Hu Y. H. Research on New High Efficiency Recovery Process for Complex Refractory Copper Slag Resources. Adv. Mater. Res. 2014, 997, 592–598. 10.4028/www.scientific.net/AMR.997.592. [DOI] [Google Scholar]
- Ke Y.; Peng N.; Xue K.; Min X.; Chai L.; Pan Q.; Liang Y.; Xiao R.; Wang Y.; Tang C.; Liu H. Sulfidation Behavior and Mechanism of Zinc Silicate Roasted with Pyrite. Appl. Surf. Sci. 2018, 435, 1011–1019. 10.1016/j.apsusc.2017.11.202. [DOI] [Google Scholar]
- Sun Y.; Gao P.; Han Y.; Ren D. Reaction Behavior of Iron Minerals and Metallic Iron Particles Growth in Coal-Based Reduction of an Oolitic Iron Ore. Ind. Eng. Chem. Res. 2013, 52, 2323–2329. 10.1021/ie303233k. [DOI] [Google Scholar]
- Li S. F.; Sun Y. S.; Han Y. X.; Shi G. Q.; Gao P. Fundamental Research in Utilization of an Oolitic Hematite by Deep Reduction. Adv. Mater. Res. 2010, 158, 106–112. 10.4028/www.scientific.net/AMR.158.106. [DOI] [Google Scholar]
- Geng C.; Wang H.-j.; Hu W.-t.; Li L.; Shi C.-s. Recovery of Iron and Copper from Copper Tailings by Coal-Based Direct Reduction and Magnetic Separation. J. Iron Steel Res. Int. 2017, 24, 991–997. 10.1016/S1006-706X(17)30145-0. [DOI] [Google Scholar]
- Long H.; Meng Q.; Chun T.; Wang P.; Li J. Preparation of Metallic Iron Powder from Copper Slag by Carbothermic Reduction and Magnetic Separation. Can. Metall. Q. 2016, 55, 338–344. 10.1080/00084433.2016.1181313. [DOI] [Google Scholar]
- Jeong M. H.; Lee D. H.; Han G. Y.; Shin C.-H.; Shin M. K.; Ko C. K.; Bae J. W. Reduction-Oxidation Kinetics of Three Different Iron Oxide Phases for CO 2 Activation to CO. Fuel 2017, 202, 547–555. 10.1016/j.fuel.2017.04.076. [DOI] [Google Scholar]
- Kuila S. K.; Chatterjee R.; Ghosh D. Kinetics of Hydrogen Reduction of Magnetite Ore Fines. Int. J. Hydrogen Energy 2016, 41, 9256–9266. 10.1016/j.ijhydene.2016.04.075. [DOI] [Google Scholar]
- Bo L.; Wang X.; Wang H.; Wei Y.; Hu J. Smelting Reduction and Kinetics Analysis of Magnetic Iron in Copper Slag Using Waste Cooking Oil. Sci. Rep. 2017, 7, 2406. 10.1038/s41598-017-02696-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Zheng M.; Wang H.; Zhu D.; Feng X. Reduction of Fe3O4 in Copper Slag by Diesel Oil in the Presence of Nitrogen. Chem. Ind. Eng. Prog. 2014, 33, 1101–1107. 10.3969/j.issn.1000-6613.2014.05.005. [DOI] [Google Scholar]
- Zhu D.; Xiao Y.; Chun T.; Pan J. Growth Behavior of Metal Iron Grain during Direct Reduction of Low Grade Hematite. Chinese J. Nonferrous Met. 2013, 23, 3242–3247. 10.19476/j.ysxb.1004.0609.2013.11.031. [DOI] [Google Scholar]
- Wang G.; Xue Q.; Shen Y.; Wang J. Carbothermic Reduction Kinetics of Boron-Bearing Iron Concentrate. Chinese J. Eng. 2016, 38, 623–629. 10.13374/j.issn2095-9389.2016.05.005. [DOI] [Google Scholar]
- Feng Y.; Jia L.; Wu M.; Mi J. Grain Growth Kinetics of Nano-Sized Iron Oxide. Nat. Gas Chem. Ind. 2017, 42, 31–35. [Google Scholar]
- Vyazovkin S.; Wight C. A. Model-Free and Model-Fitting Approaches to Kinetic Analysis of Isothermal and Nonisothermal Data. Thermochim. Acta 1999, 340–341, 53–68. 10.1016/s0040-6031(99)00253-1. [DOI] [Google Scholar]
- Benoit P. M. D.; Ferrillo R. G.; Granzow A. H. Kinetic Applications of Thermal Analysis. J. Therm. Anal. 1985, 30, 869–877. 10.1007/BF01913314. [DOI] [Google Scholar]
- Starink M. J. Activation Energy Determination for Linear Heating Experiments: Deviations Due to Neglecting the Low Temperature End of the Temperature Integral. J. Mater. Sci. 2007, 42, 483–489. 10.1007/s10853-006-1067-7. [DOI] [Google Scholar]
- Starink M. J. The Determination of Activation Energy from Linear Heating Rate Experiments: A Comparison of the Accuracy of Isoconversion Methods. Thermochim. Acta 2003, 404, 163–176. 10.1016/S0040-6031(03)00144-8. [DOI] [Google Scholar]
- Sánchez-Jiménez P. E.; Perejón A.; Criado J. M.; Diánez M. J.; Pérez-Maqueda L. A. Kinetic Model for Thermal Dehydrochlorination of Poly(Vinyl Chloride). Polymer 2010, 51, 3998–4007. 10.1016/j.polymer.2010.06.020. [DOI] [Google Scholar]
- Mizoguchi T.; Perepezko J. H. Nucleation Behavior during Solidification of Cast Iron at High Undercooling. Mater. Sci. Eng. A 1997, 226–228, 813–817. 10.1016/S0921-5093(97)80085-8. [DOI] [Google Scholar]
- Málek J. Kinetic Analysis of Crystallization Processes in Amorphous Materials. Thermochim. Acta 2000, 355, 239–253. 10.1016/S0040-6031(00)00449-4. [DOI] [Google Scholar]
- Málek J. The Kinetic Analysis of Non-Isothermal Data. Thermochim. Acta 1992, 200, 257–269. 10.1016/0040-6031(92)85118-F. [DOI] [Google Scholar]
- Budrugeac P.; Segal E.; Pérez-Maqueda L. A.; Criado J. M. The Use of the IKP Method for Evaluating the Kinetic Parameters and the Conversion Function of the Thermal Dehydrochlorination of PVC from Non-Isothermal Data. Polym. Degrad. Stab. 2004, 84, 311–320. 10.1016/j.polymdegradstab.2004.01.017. [DOI] [Google Scholar]
- Ptáček P.; Kubátová D.; Havlica J.; Brandštetr J.; Šoukal F.; Opravil T. Isothermal Kinetic Analysis of the Thermal Decomposition of Kaolinite: The Thermogravimetric Study. Thermochim. Acta 2010, 501, 24–29. 10.1016/j.tca.2009.12.018. [DOI] [Google Scholar]