Abstract
The hot deformation behavior of an Al-Zn-Mg-Cu alloy was investigated by hot compression test at deformation temperatures varying from 320 to 440 °C with strain rates ranging from 0.01 to 10 s−1. The results show that the Mg(Zn, Cu)2 particles as a result of the sufficient static precipitation prior to hot compression have an influence on flow softening. A constitutive model compensated with strain was developed from the experimental results, and it proved to be accurate for predicting the hot deformation behavior. Processing maps at various strains were established. The microstructural evolution demonstrates that the dominant dynamic softening mechanism stems from dynamic recovery (DRV) and partial dynamic recrystallization (DRX). The recrystallization mechanism is continuous dynamic recrystallization (CDRX). The microstructure observations are in good agreement with the results of processing maps. On account of the processing map and microstructural observation, the optimal hot processing parameters at a strain of 0.6 are at deformation temperature range of 390–440 °C and strain rate range of 0.010–0.316 s−1 with a peak efficiency of 0.390.
Keywords: Al-Zn-Mg-Cu alloy, constitutive model, processing map, microstructural evolution, dynamic recrystallization
1. Introduction
Al-Zn-Mg-Cu alloys are extensively used for structural applications of aerospace, petroleum and gas, and automotive industries (aircraft fuselage, drill pipe, etc.) due to their high strength-to-weight ratio, good stress corrosion cracking resistance, and high fracture toughness [1,2,3,4,5]. Meanwhile, hot forming (rolling, forging, extrusion, etc.) is a significant processing technique for manufacturing these structural components. As a newly developed Al-Zn-Mg-Cu alloy used in oil drilling pipe, the studied alloy shows a relatively high strength and excellent thermal stability as compared to the conventional Al-Zn-Mg-Cu alloy with low Zn/Mg ratio. For the former alloy, high Zn/Mg ratio leads to a denser precipitation of η′ phase. Generally, oil drilling pipes are fabricated by hot extrusion. The performance of materials mainly depends on the final microstructure, which, in turn, is affected by the forming parameters. However, material flow behavior is often very complicated during hot extrusion. Various metallurgical phenomena often take place, which greatly influence the material flow behavior and final microstructure [6,7,8]. Therefore, an investigation of the hot deformation behavior, microstructural evolution, and corresponding mechanism of the studied alloy is quite crucial for industrial production, as the industrial manufacturing processes can benefit from the research results.
The flow behavior of alloys under different deformation conditions is usually described by the constitutive model. Many efforts have been performed to derive several suitable constitutive models to characterize the hot deformation behavior of aluminum alloys, such as 2026 [9], 7085 [10], and 7150 aluminum alloy [11]. However, the previous studies seldom concern the effect of strain, which possesses a significant influence on accurate prediction of the flow behavior of materials. Recently, Zhang et al. described the deformation behavior of Cu-Zr-Ce alloy and proposed a revised Arrhenius-type constitutive model by considering the compensation of strain. It was found that the developed constitutive equation exhibited an excellent prediction capability [12]. A similar method was employed by Cai et al. to develop two Arrhenius-type constitutive models with and without the strain compensation for AZ41M magnesium alloy. Their results stated that the revised model correlated well with the experimental results and accurately predicted the flow behavior of AZ41M [13]. Additionally, a revised Arrhenius-type constitutive model was used for predicting the flow behavior in Ti60 titanium alloy [14].
The grain structure varies greatly by different processing parameters, which leads to different recrystallization mechanisms. There are two main dynamic recrystallization (DRX) mechanisms (i.e., continuous dynamic recrystallization (CDRX) and discontinuous dynamic recrystallization (DDRX)). CDRX is characterized by progressive subgrain rotation, whereas DDRX is represented by nucleation and growth. Evolution of grain structures during hot deformation has attracted considerable interest in many investigations concerning recrystallization mechanism. In recent years, Luo et al. found numerous newly formed subgrains in the grain interiors as 7A09 aluminum alloy deformed at low temperatures (360–460 °C) with high strain rates (0.01–10 s−1), which was considered to be the result of CDRX [15]. The results obtained by Wang et al. showed that many recrystallized grains were found at grain boundaries as Al-Cu-Li alloy deformed at temperatures of 500 and 550 °C with two strain rates of 0.1 and 0.01 s−1, which were caused by DDRX [16]. Additionally, similar investigation was carried out for nickel-based superalloy [17].
Recently, many studies on Al-Zn-Mg-Cu alloy have been performed. Lin et al. found that the higher fatigue crack propagation (FCP) resistance of Al-Zn-Mg-Cu alloy was detected in T7351 condition rather than T7651 condition [18]. Cheng et al. proposed that the excellent mechanical properties of the nanocrystalline Al-Zn-Mg-Cu alloy resulted from the precipitated second-phase particles [19]. Furthermore, several investigations on the flow behavior and microstructure of Al-Zn-Mg-Cu alloy were performed. Shi et al. proposed a decline ratio map to study the hot deformation behavior of Al-Zn-Mg-Cu alloy, and they pointed out that the flow behavior was sensitive to the deformation temperature and strain rate [20]. Wang et al. developed the processing map and the constitutive model without considering the effect of strain for Al-Zn-Mg-Cu alloy and obtained the optimum parameters [21]. Zhao et al. investigated the hot deformation behavior and recrystallization behavior of Al-Zn-Mg-Cu alloy by considering the compensation of strain [22]. Zang et al. discussed the effect of initial microstructure on the hot deformation behavior of Al-Zn-Mg-Cu alloy. However, strain compensation was not considered in developing the constitutive model [23]. Despite the progress achieved in the abovementioned studies in exploring the flow behavior and recrystallization mechanism of Al-Zn-Mg-Cu alloys, few studies have focused on the hot deformation behavior considering strain effects and discussed the relationship between the second phase and the microstructural evolution in detail.
In present work, the hot compression test of the sample is performed under different deformation conditions. The constitutive model compensated with strain according to the Arrhenius-type model is developed and validated by experimental results. Then, the processing maps at various strains are established. In addition, the microstructural evolution and recrystallization mechanism of different deformation conditions are analyzed to confirm the processing map. The effect of the second phase on microstructural evolution is also discussed in detail. Finally, the optimal hot processing parameters of Al-Zn-Mg-Cu alloy are obtained.
2. Materials and Methods
In this work, the chemical composition of the studied Al-Zn-Mg-Cu alloy is listed in Table 1. The cast ingot was subjected to a two-step homogenization that consisted of a low-temperature step at 420 °C for 24 h followed by a high-temperature step at 465 °C for 72 h, after which it was machined to cylindrical compressive samples that were 10 mm in diameter and 15 mm in height. The initial microstructure of homogenized samples with a mean grain size approximately 60 μm is shown in Figure 1a. Figure 1b shows that few precipitates appear in the homogenized samples. The hot compression tests were performed at temperatures of 320, 350, 380, 410 and 440 °C with strain rates of 0.01, 0.1, 1 and 10 s−1 on a Gleeble-3500 testing system (Dynamic Systems Inc., New York, NY, USA). A graphite lubricant was utilized between the samples and the press indenters to maximize lubrication during the tests. Prior to loading, the samples were heated to the target temperature with 2 °C/s heating rate and then held for 3 min. The samples were compressed to 60% reduction and immediately water quenched.
Table 1.
Chemical compositions of the studied Al-Zn-Mg-Cu alloy (in wt %).
| Composition | Zn | Mg | Cu | Mn | Cr | Ti | Si | Fe | Al |
|---|---|---|---|---|---|---|---|---|---|
| Content | 7.00 | 2.37 | 1.66 | 0.40 | 0.15 | 0.11 | 0.026 | 0.046 | Bal. |
Figure 1.
Microstructures of the homogenized Al-Zn-Mg-Cu alloy: (a) EBSD and (b) TEM images.
The microstructures of samples were investigated at the center of the axial section by TEM and EBSD. The TEM foils were mechanically ground to 100 µm, punched subsequently into 3 mm discs, and then twin-jet electro-polished in a 20% HNO3 and 80% CH3OH solution with the temperature at about −25 °C. The samples for EBSD were prepared using the same method as those for TEM preparation, except that the twin-jet electro-polishing time was shorter than that of TEM samples. The observation of TEM samples were performed on a FEI Tecnai-G2 20 electron microscope (FEI Inc., Hillsboro, OR, USA) at 200 kV. The EBSD tests were operated on the ZEISS EVOMA instrument (ZEISS Inc., Oberkochen, Germany) equipped with an Oxford EBSD attachment (Oxford Instruments Inc., Abingdon, UK). TSL OIM Analysis 5 software (EDAX Inc., Mahwah, NJ, USA) was used for analyzing EBSD data.
3. Results and Discussion
3.1. Flow Stress Behavior
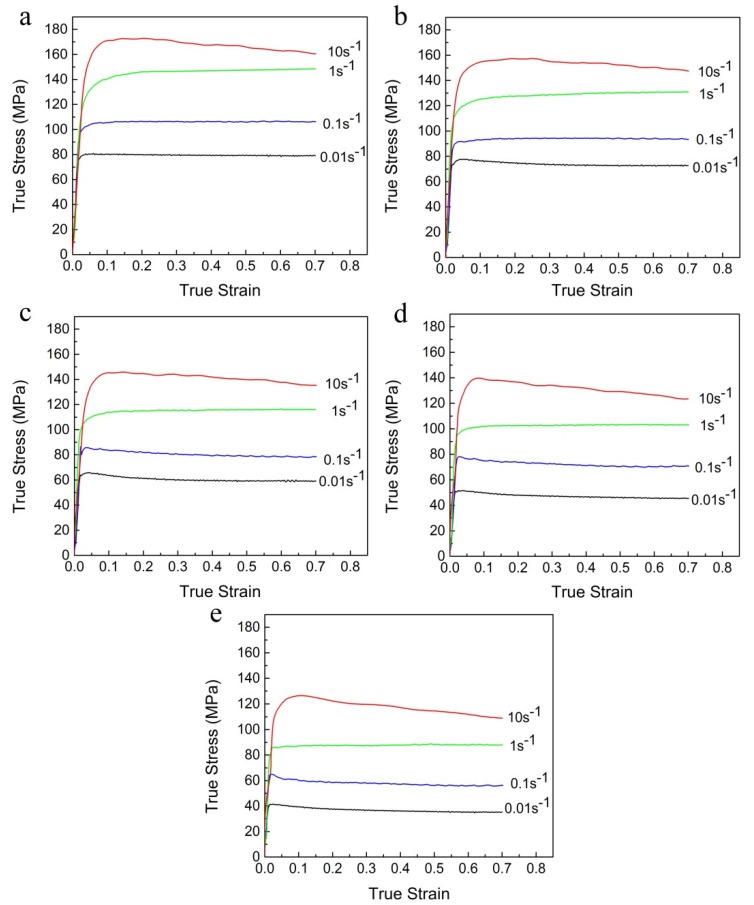
The experimental true stress–strain curves of Al-Zn-Mg-Cu alloy compressed under different deformation conditions are presented in Figure 2. It can be clearly observed that all the true stress–strain curves demonstrate a similar essential feature. The true stress–strain curves present initial work hardening (WH) followed by dynamic softening (DS) or inflexible state behavior. At the initial stage of deformation, the dislocation continually increases and multiplies rapidly. In addition, the formation of sufficient static precipitates occurs during the sample preheating and stabilization at the compression temperature [24,25]. Thus, the true stress dramatically increases, and the WH is dominant. At the softening stage of deformation, the density of accumulated dislocations exceeds a critical value, and the dislocation movement is sufficiently driven by the gradually accumulated energy. Moreover, severe deformation heating can also be generated as the hot compression tests are performed at high strain rates [26,27]. Consequently, the true stress decreases, and DS occurs at this stage. At the steady stage of deformation, the true stress keeps an inflexible state, owing to a dynamic equilibrium between the WH and DS.
Figure 2.
True stress–strain curves at deformation temperatures of (a) 320 °C, (b) 350 °C, (c) 380 °C, (d) 410 °C, and (e) 440 °C.
Meanwhile, Figure 2 shows that the peak flow stress decreases with the increasing deformation temperature or the decreasing strain rate. It should be associated with the fact that the increasing in deformation temperature can provide higher grain boundaries mobility for the nucleation and growth of DRX grains, and the decreasing in strain rate can obtain longer time for the movement of dislocations and the accumulation of deformation energy. Additionally, the thermal activation of atoms intensified with the increase of deformation temperature leads to further movement of dislocation and vacancy [28]. Thus, the dynamic recovery (DRV) and DRX caused by the slip and climb of dislocations are improved. In addition, with the increasing deformation temperatures, more and more potential second phases tend to continue dynamic coarsening or dissolution during hot compression, which lowers the alloy strength [10]. Therefore, the DS behavior is improved, causing a decrease in the peak flow stress.
3.2. Constitutive Model for Flow Stress
The Arrhenius-type model is widely used to represent hot deformation behavior [29], as shown in Equation (1).
| (1) |
where represents the strain rate (s−1); A1, A2, A, n1, n, α, and β are material constants, and α = β/n1; Q means the deformable activation energy (kJ mol−1); R represents the gas constant (8.314 J mol−1 K−1); T is the absolute temperature (K); σ is stress (MPa); and the peak stress σp is used as the term σ [30,31].
Equations (2)–(4) are obtained by taking the logarithm of both sides of Equation (1).
| (2) |
| (3) |
| (4) |
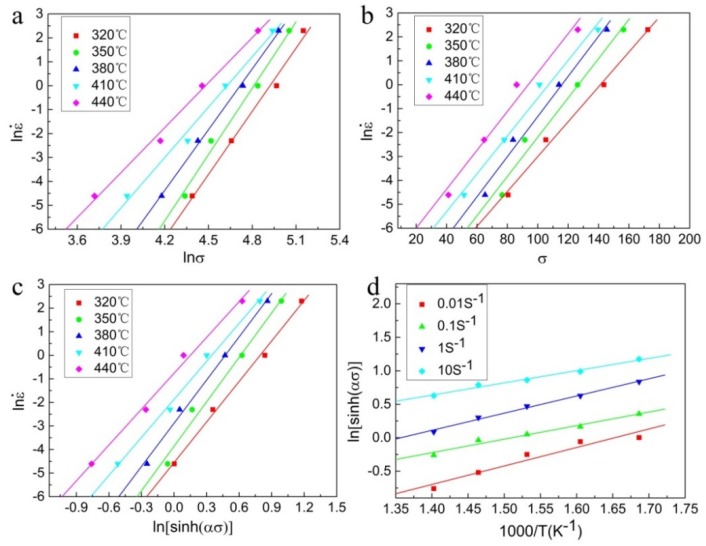
On account of the measured data, the relationship between lnσ, σ, and at different deformation temperatures is plotted in Figure 3a,b. After linear fitting, the values of n1 and β can be calculated to be 7.25583 and 0.07963 MPa−1, respectively. Therefore, α = β/n1 = 0.01097 MPa−1.
Figure 3.
Linear relationship fitting: (a) lnlnσ, (b) ln σ, (c) ln ln[sinh(ασ)], (d) ln[sinh(ασ)] 1000/T.
Differentiating Equation (4) gives the following equation:
| (5) |
Thus, the values of n and S can be obtained from the mean slope of the ln[sinh(ασ)] and ln[sinh(ασ)]1000/T plots, as shown in Figure 3c,d, respectively. The calculated Q is 189.07 kJ mol−1, which is lower than the value of 318 kJ mol−1 for the solution-treated 7085 alloy reported by Liu et al. [32] and similar to the value of 182.07 kJ mol−1 for the homogenized 7085 alloy revealed by Park et al. [33]. Moreover, the value of Q determined in present work is larger as compared to the value of 142 kJ mol−1 for the pure aluminum [34]. This difference may be ascribed to the dynamic precipitation, dissolution of precipitates, dislocation pinning effect, heat treatment conditions, and the amount of solute atoms (Zn, Mg, and Cu) in the alloy.
Moreover, the Zener-Hollomon (Z) parameter is as follows [35]:
| (6) |
Then, the logarithm of both sides of Equation (6) is taken. A best linear relationship of lnZ can be obtained. Hence, the value of A can be easily calculated as 3.79754 × 1013.
Thus, the constitutive model of the studied alloy can be expressed as follows:
| (7) |
3.3. Compensation of Strain
It has been reported by many researchers that the deformation behavior and material constants (i.e., α, β, n, lnA, and Q) among the entire strain range are significantly affected by the strain during hot deformation [25,36,37,38,39,40]. In addition, Figure 2 shows that the true stress is significantly sensitive to the strain, especially at the initial stage of the true stress–strain curves. However, the effect of strain is not taken into account in the above constitutive model. Thus, such model should consider the compensation of strain.
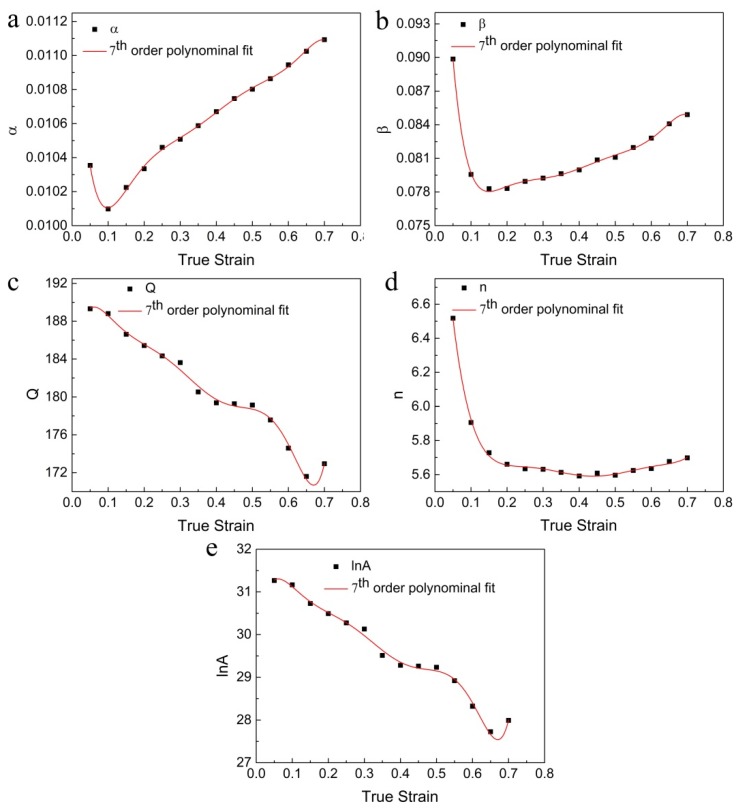
In previous reports, it has been shown that different order polynomials can be given to well express the effect of strain on these material constants [40,41,42]. So, a seventh-order polynomial is selected for present work, as seen in Equation (8). The values of material constants are computed at strains ranging from 0.05 to 0.7 with an interval 0.05. Then, the coefficients of α(ε), β(ε), n(ε), lnA(ε), and Q(ε) can be gained through polynomial fitting. Figure 4 shows the relationships of fitting, and corresponding values are listed in Table 2.
| (8) |
Figure 4.
Relationships between true strain and (a) α, (b) β, (c) Q, (d) n, and (e) lnA by a seventh-order polynomial fitting.
Table 2.
Coefficients of polynomial fit for α, β, Q, n, and lnA in Equation (8) for Al-Zn-Mg-Cu alloy.
| α | β | Q | n | lnA |
|---|---|---|---|---|
| B0 = 0.01173 | C0 = 0.12283 | D0 = 182.61081 | E0 = 8.09318 | F0 = 29.92634 |
| B1 = −0.04759 | C1 = −1.04332 | D1 = 299.84774 | E1 = −47.05679 | F1 = 59.96955 |
| B2 = 0.51783 | C2 = 9.73699 | D2 = −4614.03387 | E2 = 386.38381 | F2 = −922.80677 |
| B3 = −2.71861 | C3 = −47.39541 | D3 = 31,736.66147 | E3 = −1725.87388 | F3 = 6347.33229 |
| B4 = 7.90719 | C4 = 131.40288 | D4 = −117,379.43127 | E4 = 4480.68971 | F4 = −23,475.88625 |
| B5 = −12.95283 | C5 = −208.49173 | D5 = 236,927.83041 | E5 = −6756.57195 | F5 = 47,385.56608 |
| B6 = 11.18036 | C6 = 176.18315 | D6 = −244,644.91171 | E6 = 5491.34758 | F6 = −48,928.98234 |
| B7 = −3.95213 | C7 = −61.42370 | D7 = 100,787.54684 | E7 = −1859.00011 | F7 = 20,157.50937 |
After the material constants are calculated, the constitutive model considering strain compensation of the studied Al-Zn-Mg-Cu alloy is expressed as Equation (9).
| (9) |
3.4. Verification of Developed Constitutive Model
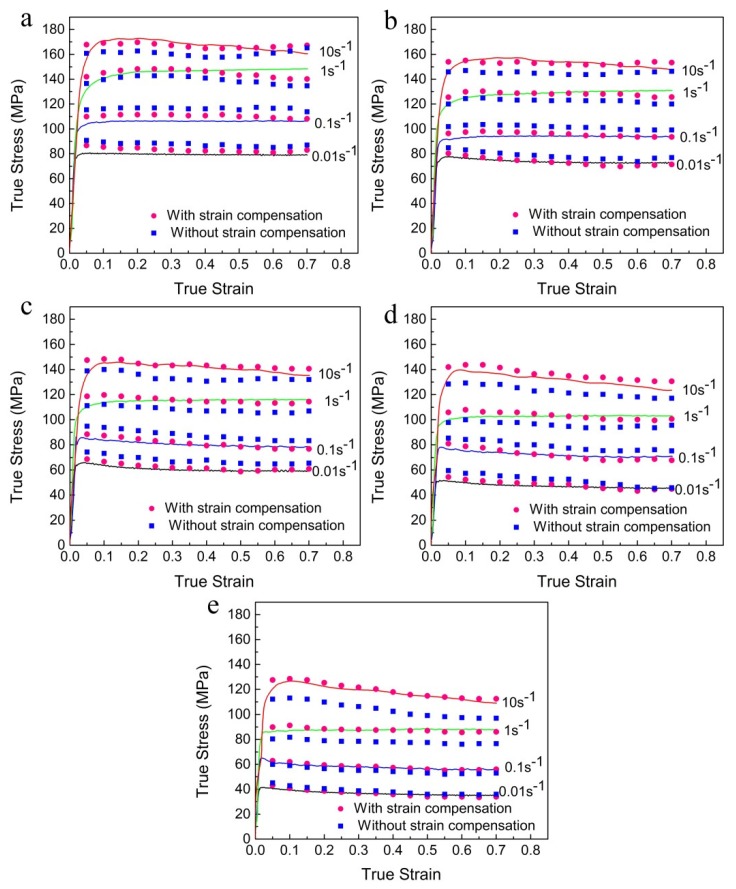
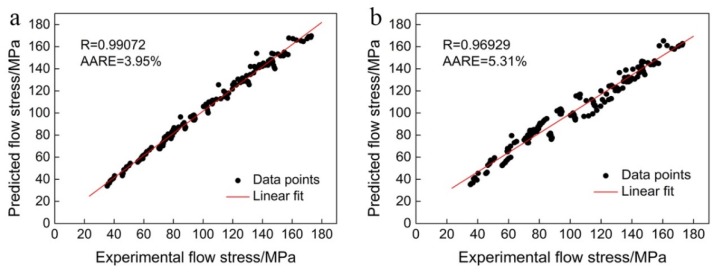
Figure 5 shows a comparison between the experimental flow stress and predicted values based on the model with and without strain compensation. It can be clearly found that the prediction accuracy of the model with strain compensation is better than that of the model without strain compensation.
Figure 5.
Comparison of the predicted and experimental flow stress curves by two models at deformation temperatures of (a) 320 °C, (b) 350 °C, (c) 380 °C, (d) 410 °C, and (e) 440 °C.
Meanwhile, the correlation coefficient (R) and the average absolute relative error (AARE) are selected to quantitatively evaluate the accuracy of two developed constitutive models. They can be represented as [43]:
| (10) |
| (11) |
where, is the experimental value and is the predicted value. and are the average values of and , respectively. N represents the total number of data used in the research.
Figure 6 shows the correlations between the experimental and predicted flow stresses by the model with and without strain compensation. It clear that the values of R and AARE for the model with strain compensation are 0.99072 and 3.95%, respectively, while those of the without strain compensation are 0.96929 and 5.31%, respectively. Obviously, the developed strain compensation constitutive model has higher accuracy than the model without strain compensation. Accordingly, taking the strain compensation into consideration is essential for precisely predicting the flow behavior.
Figure 6.
Correlations between the experimental and predicted flow stresses by models (a) with and (b) without strain compensation.
3.5. Processing Maps
3.5.1. The Principles of Processing Maps
The processing map is developed based on the DMM proposed by Prasad et al. [44]. According to the principles of DMM, as expressed in Equation (12), the total instantaneous power dissipation (P) is divided into the power dissipated by plastic deformation (G), and the power dissipated through microstructure evolution (J).
| (12) |
The strain rate sensitivity exponent m can be described by Equation (13).
| (13) |
The relationship between true stress and strain rate is given in Equation (14), according to irreversible thermodynamics [44].
| (14) |
where a, b, c, and d are the polynomial fitting coefficients. The third-order polynomial fitting curves of with strains of 0.3 and 0.6 are shown in Figure 7. Corresponding values of the polynomial fitting coefficients are listed in Table 3.
Figure 7.
Fitting curves to describe the relationship between and of Al-Zn-Mg-Cu alloy at strains of (a) 0.3 and (b) 0.6.
Table 3.
Polynomial fitting coefficients in Equation (14) for Al-Zn-Mg-Cu alloy.
| Strain | Temperature (°C) | Coefficient | |||
|---|---|---|---|---|---|
| a | b | c | d | ||
| 0.3 | 320 | 2.16450 | 0.11845 | −0.03227 | −0.01296 |
| 350 | 2.10561 | 0.12358 | −0.02061 | −0.01216 | |
| 380 | 2.06092 | 0.13526 | −0.02421 | −0.01172 | |
| 410 | 2.01119 | 0.12968 | −0.00947 | −0.00399 | |
| 440 | 1.94186 | 0.16220 | −0.01477 | −0.00183 | |
| 0.6 | 320 | 2.17009 | 0.11138 | −0.05082 | −0.01888 |
| 350 | 2.11574 | 0.12059 | −0.04041 | −0.01870 | |
| 380 | 2.06603 | 0.14718 | −0.04948 | −0.02495 | |
| 410 | 2.01444 | 0.13799 | −0.04029 | −0.01019 | |
| 440 | 1.94369 | 0.16558 | −0.04555 | −0.01477 |
According to Equations (13) and (14), the value of m can be easily derived from Equation (15).
| (15) |
For an ideal linear dissipater, m = 1 and. While, for a nonlinear dissipater, the power dissipation efficiency η can be represented by the following equation:
| (16) |
The variation of η with deformation temperatures and strain rates at constant strain constitutes the dissipation power map.
A continuum flow instability criterion is defined as:
| (17) |
Plotting as a function of deformation temperatures and strain rates at constant strain obtains the flow instability map. When is negative, flow instabilities occur during hot deformation.
The processing map is constituted by superimposing the flow instability map over the power dissipation map. In general, the good intrinsic workability should be in the “safe” domains with the peak efficiencies of power dissipation in a processing map [44,45].
3.5.2. Establishment and Analysis of Processing Maps
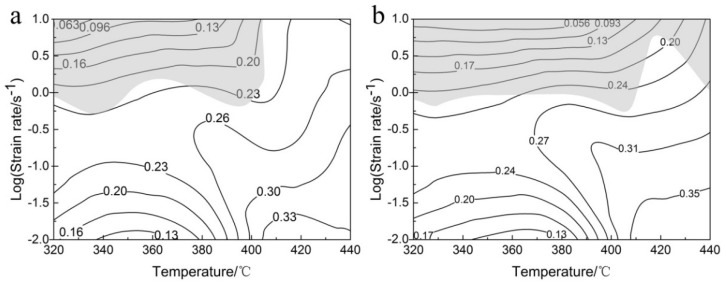
The processing maps of the samples at strains of 0.3 and 0.6 are shown in Figure 8. In Figure 8, the numbers on the contours are percentage of the power dissipation efficiency, and the shadowed regions represent the flow instability domains, while the white areas represent the “safe” processing domains.
Figure 8.
Processing maps of Al-Zn-Mg-Cu alloy at strains of (a) 0.3 and (b) 0.6.
As shown in Figure 8a,b, these processing maps demonstrate a common character that the flow instability domains nearly locate at their upper parts. However, there are differences in the shape of the flow instability domains. The instability domain gradually extends to the high temperature–high strain rate direction with increasing strain. This shows that the processing maps of sample are significantly affected by the strain. Liu et al. also found that the unstable region of 6063 alloy increases with increasing strain [40]. This is due to the concentration of stresses intensified with the increasing strain.
The highest power dissipation efficiency of the samples gradually increases as the strain increases from 0.3 to 0.6, with values of 0.35 and 0.39, respectively. This is ascribed to the microstructural evolution with the increase of strain. It is well known that DRV, DRX, and superplasticity are regarded as the “safe” deformation mechanisms. Previous literature has reported that DRV is identified as main deformation mechanism if the power dissipation efficiency is about 0.30, but DRX is correlated with the higher power dissipation efficiency [46]. Further discussion will be carried out in Section 3.6. When the power dissipation efficiency is greater than 0.6, superplasticity occurs during hot deformation [47]. However, in Figure 8a,b, the peak power dissipation efficiencies of the samples are lower than 0.6, indicating that no superplasticity occurs in these processing maps. Generally, the “safe” domains with the peak efficiencies of power dissipation in a processing map correspond to the ideal workability, where the hot processing parameters are considered as the optimal [44,45]. According to Figure 8b, when the strain is 0.6, the optimal hot processing parameters are deformation temperature of 390–440 °C and strain rate of 0.010–0.316 s−1 with a peak efficiency of 0.390.
3.6. Microstructural Evolution
Figure 9 exhibits the TEM results of several deformed samples. It is obvious that microstructural evolution is greatly affected by hot forming parameters. High density dislocation tangles in the deformed grain interior can be easily found when deformed under the condition of 320 °C/1 s−1 (Figure 9a). Increasing deformation temperature or decreasing strain rate (380 °C/0.1 s−1) (Figure 9b), can provide higher driving force or longer time for dislocation annihilation and rearrangement through climbing and sliding, reducing the dislocation density and forming the dislocation walls within the deformed grain. Subsequently, the dislocation walls convert to subgrain boundaries, segmenting the deformed grains into some subgrain structures; DRV occurs during this period. When the deformation temperature increases to 410 °C (Figure 9c), the sufficient atomic diffusion and dislocation migration lead to the merging of several grains. The low-angle grain boundaries (LAGBs) transform to high-angle grain boundaries (HAGBs) progressively by the absorption of dislocations, indicating that DRV is intensified with the increasing deformation temperature. With a further increase in temperature or a decrease in strain rate (440 °C/0.01 s−1) (Figure 9d), the dislocation density decreases, the straight and clear grain boundaries are found, and the recrystallization grains gradually grow through the migration of dislocations and HAGBs. On the basis of these microstructural observation, obviously, the dominant dynamic softening mechanism of the studied alloy is stemmed from DRV and partial DRX during hot deformation.
Figure 9.
TEM micrographs of Al-Zn-Mg-Cu alloy in various deformation conditions: (a) 320 °C/1 s−1, (b) 380 °C/0.1 s−1, (c) 410 °C/0.1 s−1, (d) 440 °C/0.01 s−1.
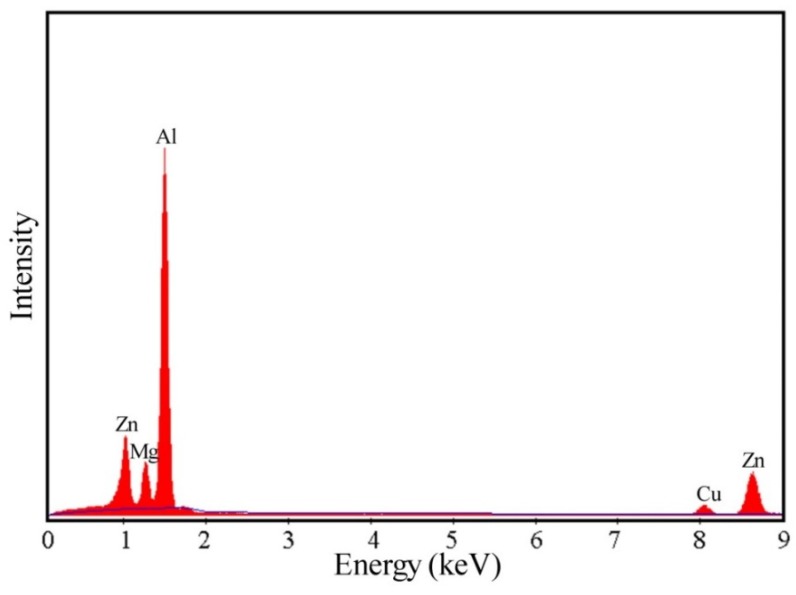
Additionally, another microstructural feature is precipitates. As shown in Figure 9a, many spherical and rod-shaped precipitates are found within subgrains when deformed at 320 °C/1 s−1. From Figure 1b and Figure 9, this is a direct result of the sufficient static precipitation prior to hot compression. In the studied alloy, Figure 10 shows the energy dispersive spectrometer (EDS) results of the particles, suggesting the particles contain more Mg, Zn and a small amount of Cu due to the different diffusive ability, with a composition approaching the stoichiometric Mg(Zn, Cu)2 phase. This finding is consistent with previous research [20,48,49,50]. These small precipitates induce a strong pinning effect on dislocations and then retard the movement of dislocations, leading to a great flow stress hardening at the initial stage of hot compression. However, in Figure 9, with the increasing deformation temperature or the decreasing strain rate, the precipitate size increases while its number density decreases. According to the Ashby-Orowan criterion, the pinning effect on dislocations will decrease [39]. Consequently, the degree of partial DRX is enhanced, leading to a significant flow stress softening. Moreover, it is noted that the precipitates begin the process of dynamic coarsening and even dissolve into the matrix when deformed at 380 °C/0.1 s−1 (Figure 9b), which can also result in a variation of the isoefficiency contours at about 390–440 °C in the processing maps, as shown in Figure 8. As reported by Wu et al. [25], the dissolution of the second phase leads the isoefficiency contours about at 387–427 °C to vary. Similarly, Luo et al.’s work [15] also shows that the isoefficiency contours at 417 °C are greatly affected by the dissolution of T phase.
Figure 10.
EDS analysis result of the particle marked with circle in Figure 9.
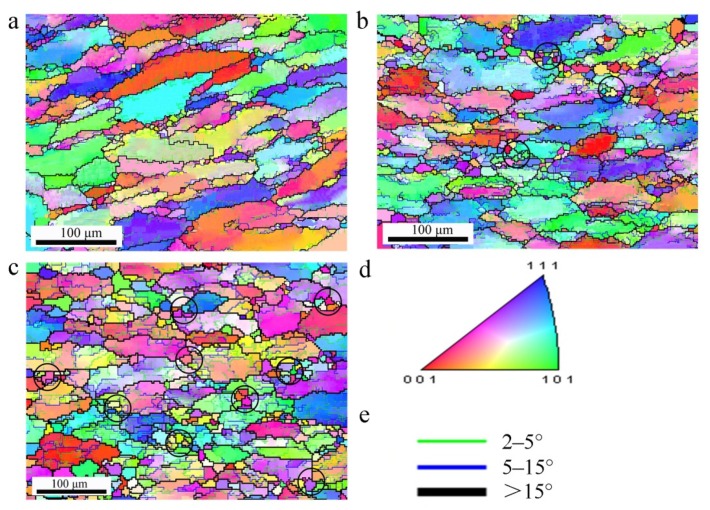
In general, EBSD maps are used to provide more information on microstructural evolution during hot deformation. Figure 11 shows EBSD results of several hot deformed samples. The initial large elongated grains containing equiaxed subgrains are dominant, and the deformed microstructure varies with hot processing parameters. When deformed at 380 °C/0.1 s-1 (Figure 11a), many new equiaxed subgrains appear in the form of LAGBs within the elongated grains. In addition, it can be clearly seen that the subgrains prefer to form around the boundaries of deformed grains, owing to the climb and cross-slip of dislocation being more thorough near the elongated grain boundary. When deformed at 410 °C/0.1 s−1 (Figure 11b), the LAGBs extend progressively towards the center of the deformed grain, suggesting that DRV is gradually enhanced with the increasing deformation temperature. Meanwhile, some fine DRX grains appear along the elongated original grain boundaries, indicating the transformation from LAGBs to HAGBs under such condition. This phenomenon arises from the fact that a higher deformation temperature accelerates the dislocation annihilation and rearrangement. As a result, the migration of subgrain boundaries and the polygonization are intensified; the degree of DRV is therefore enhanced and DRX occurs. When deformed at 440 °C/0.01 s−1 (Figure 11c), DRV further proceeds, the volume fraction of DRX increases, and some DRX grains grow up. The results are attributed to the facts that deformation at higher temperatures promotes the migration of subgrain boundaries, and deformation at lower strain rates provides enough time for the migration of subgrain boundaries. Besides, more precipitates coarsen and even dissolve into the matrix, leading to a weaker pinning effect on subgrain and grain boundaries [51,52,53], which is consistent with the TEM observation in this work. However, in Figure 11, it can also be clearly found that the DRV is still the main softening mechanism despite the occurrence of DRX.
Figure 11.
EBSD images of Al-Zn-Mg-Cu alloy in various deformation conditions: (a) 380 °C/0.1 s−1, (b) 410 °C/0.1 s−1, (c) 440 °C/0.01 s−1, (d) Inverse pole figure (IPF), (e) representation of different color lines used to identify the boundaries with different misorientation angles in (a–c).
As seen in Figure 11, a color gradient appears between neighboring subgrains in the interior of elongated grains. Additionally, the grain size of the new fine DRX grains is very close to that of the subgrains, and the orientation of DRX grains is different from their adjacent grains. This suggests that the progressive subgrain rotation by the gradual absorption of dislocations leads to a change in their misorientation. The progressive subgrain rotation gives rise to the misorientation rearrangement LAGBs and their gradual transformation to HAGBs, indicating that CDRX is the dominant DRX mechanism during deformation. Similar DRX mechanism has been observed in previous reports [16,17,49]. In general, the CDRX is considered to be an extended DRV, the dominant DRX mechanism for high stacking fault energy metals (e.g., aluminum alloy) is CDRX rather than DDRX owing to the dislocations climb and cross-slip that are prone to occur in such alloys. Moreover, the new fine DRX grains marked with black circles in Figure 11b,c form at triple junctions and original elongated grain boundaries, suggesting that DRX occurs preferentially at such sites.
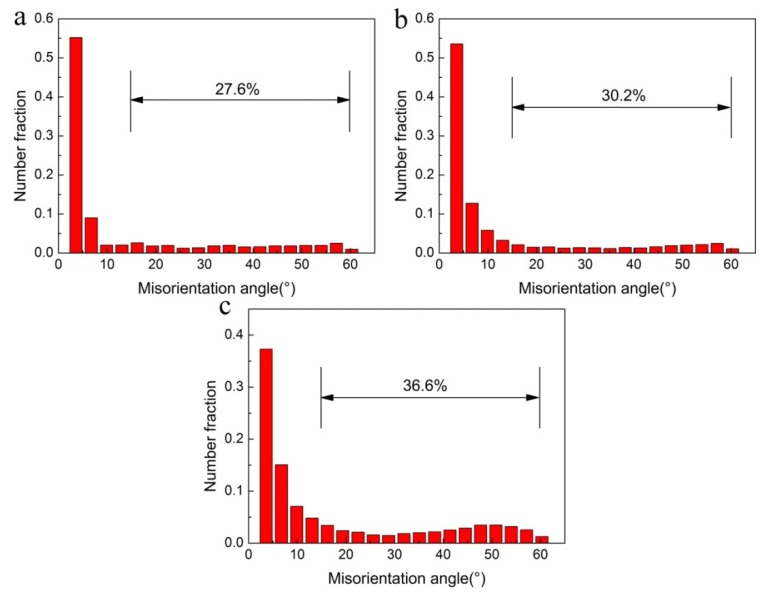
Figure 12 presents the misorientation angle distributions of the grain boundaries under different deformation conditions. According to Figure 12, the average misorientation angles of the deformation conditions of 380 °C/0.1 s−1, 410 °C/0.1 s−1, and 440 °C/0.01 s−1 are 12.3°, 13.6°, and 17.7°, respectively. Meanwhile, the fractions of HAGBs can be evaluated as 27.6%, 30.2%, and 36.6%, respectively. It is evident that the majorities (~70%) of the boundaries are LAGBs for all conditions, which indicates that DRV and slight DRX have taken place during the process of samples. The medium angle boundaries (MAGBs, 5–15°) usually reflect the occurrence of CDRX during the hot deformation [53,54,55]. According to the above result, this shows that some LAGBs gradually converted into MAGBs, which, in turn, evolved into HAGBs with the increasing deformation temperature or the decreasing strain rate. Therefore, this evolution can also be regarded as a process of CDRX, which is consistent with the analysis in Figure 11. Similar behavior is also reported in other alloys, such as 6099 alloy [8].
Figure 12.
Misorientation angle distributions of Al-Zn-Mg-Cu alloy under various deformation conditions: (a) 380 °C/0.1 s−1, (b) 410 °C/0.1 s−1, (c) 440 °C/0.01 s−1.
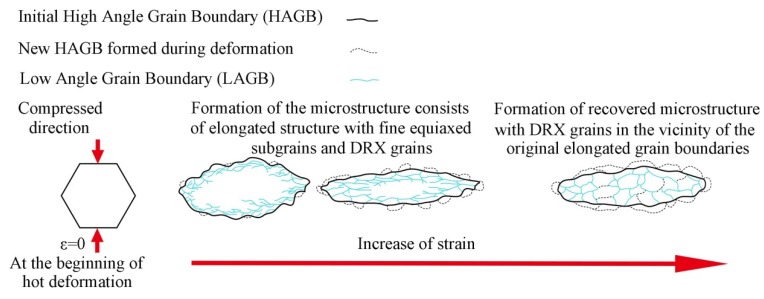
Based on the above analysis, the microstructural evolution of samples during hot compression is proposed in Figure 13. With the increasing strain, the equiaxed grains are obviously elongated perpendicularly to the compressed direction owing to hot deformation, and LAGBs transform to HAGBs, leading to the formation of new fine DRX grains. The new small grains with HAGBs are formed preferentially near the original elongated grain boundaries. The transformation of LAGBs to HAGBs is an indication of the occurrence of CDRX in studied alloy. In summary, both DRV and DRX occur during hot deformation. DRV is identified as main dynamic softening mechanism. The optimal hot processing parameters deduced from the stable domain of the processing map are reliable.
Figure 13.
Schematic illustration of the microstructural evolution of Al-Zn-Mg-Cu alloy during hot deformation.
4. Conclusions
In present work, the deformation behaviors considering strain effects and recrystallization mechanism of an Al-Zn-Mg-Cu alloy are investigated. The main results are summarized as follows:
The Mg(Zn, Cu)2 particles as a result of the sufficient static precipitation prior to hot compression have an influence on the flow behavior by effectively pinning the dislocation during hot compression. Both dynamic coarsening and even dissolution of Mg(Zn, Cu)2 particles can also cause the flow stress softening.
- The R and AARE values of the developed constitutive model compensated with strain are 0.99072 and 3.95%, respectively, suggesting a relatively high precision of the developed constitutive model. The constitutive model of the studied alloy can be expressed as:
(18) Both DRV and DRX occur, and DRV is identified as the main dynamic softening mechanism. The recrystallization mechanism is CDRX. CDRX prefers to occur at triple junctions and original elongated grain boundaries.
Based on the processing map and microstructural observation, the optimal hot processing parameters at a strain of 0.6 are in the deformation temperature range of 390–440 °C and the strain rate range of 0.010–0.316 s−1 with a peak efficiency of 0.390.
Acknowledgments
The authors are grateful for the financial support from the National Key Research and Development Program of China (2016YFB0300900), the National Key Fundamental Research Project of China (2012CB619506-3), and the National Natural Science Foundation of China (51171209).
Author Contributions
Z.L. and S.B. conceived the central idea; L.L. performed research, analyzed data, and wrote the paper; J.Z., D.Z., J.W., J.C. and Y.H. contributed to discussions of the results and review of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2016YFB0300900), the National Key Fundamental Research Project of China (2012CB619506-3), and the National Natural Science Foundation of China (51171209).
Conflicts of Interest
The authors declared that they have no conflicts of interest to this work.
References
- 1.Heinz A., Haszler A., Keidel C., Moldenhauer S., Benedictus R., Miller W.S. Recent development in aluminum alloys for aerospace applications. Mater. Sci. Eng. A. 2000;280:102–107. doi: 10.1016/S0921-5093(99)00674-7. [DOI] [Google Scholar]
- 2.Wang W.Y., Pan Q.L., Sun Y.W., Li X.D., Wang A.D., Song W.B. Study on hot compressive deformation behaviors and corresponding industrial extrusion of as-homogenized Al-7.82Zn-1.96Mg-2.35Cu-0.11Zr alloy. J. Mater. Sci. 2018;53:11728–11748. doi: 10.1007/s10853-018-2388-z. [DOI] [Google Scholar]
- 3.Williams J.C., Starke E.A., Jr. Progress in structural materials for aerospace systems. Acta Mater. 2003;51:5775–5799. doi: 10.1016/j.actamat.2003.08.023. [DOI] [Google Scholar]
- 4.Dixit M., Mishra R.S., Sankaran K.K. Structure-property correlations in Al 7050 and Al 7055 high-strength aluminum alloys. Mater. Sci. Eng. A. 2008;478:163–172. doi: 10.1016/j.msea.2007.05.116. [DOI] [Google Scholar]
- 5.Sun Y.W., Pan Q.L., Wang W.Y., Li A.D., Song W.B. Microstructural evolution and constitutive analysis combined with weight optimization method of Al-7.82 Zn-1.96 Mg-2.35 Cu-0.11 Zr alloy during hot deformation. J. Alloys Compd. 2018;732:902–914. doi: 10.1016/j.jallcom.2017.10.246. [DOI] [Google Scholar]
- 6.Puchi-Cabrera E.S., Guérin J.D., Barbier D., Dubar M., Lesage J. Plastic deformation of structural steels under hot-working conditions. Mater. Sci. Eng. A. 2013;559:268–275. doi: 10.1016/j.msea.2012.08.097. [DOI] [Google Scholar]
- 7.Lin Y.C., Dong W.Y., Zhou M., Wen D.X., Chen D.D. A unified constitutive model based on dislocation density for an Al-Zn-Mg-Cu alloy at time-variant hot deformation conditions. Mater. Sci. Eng. A. 2018;718:165–172. doi: 10.1016/j.msea.2018.01.109. [DOI] [Google Scholar]
- 8.Chamanfar A., Alamoudi M.T., Nanninga N.E., Misiolek W.Z. Analysis of flow stress and microstructure during hot compression of 6099 aluminum alloy (AA6099) Mater. Sci. Eng. A. 2019;743:684–696. doi: 10.1016/j.msea.2018.11.076. [DOI] [Google Scholar]
- 9.Huang X.D., Zhang H., Han Y., Wu W.X., Chen J.H. Hot deformation behavior of 2026 aluminum alloy during compression at elevated temperature. Mater. Sci. Eng. A. 2010;527:485–490. doi: 10.1016/j.msea.2009.09.042. [DOI] [Google Scholar]
- 10.Chen S.Y., Chen K.H., Peng G.S., Chen X.H., Ceng Q.H. Effect of heat treatment on hot deformation behavior and microstructure evolution of 7085 aluminum alloy. J. Alloys Compd. 2012;537:338–345. doi: 10.1016/j.jallcom.2012.05.052. [DOI] [Google Scholar]
- 11.Shi C.J., Mao W.M., Chen X.G. Evolution of activation energy during hot deformation of AA7150 aluminum alloy. Mater. Sci. Eng. A. 2013;571:83–91. doi: 10.1016/j.msea.2013.01.080. [DOI] [Google Scholar]
- 12.Zhang Y., Sun H.L., Volinsky A.A., Wang B.J., Tian B.H., Liu Y., Song K.X. Constitutive model for hot deformation of the Cu-Zr-Ce alloy. J. Mater. Eng. Perform. 2018;27:728–738. doi: 10.1007/s11665-018-3168-2. [DOI] [Google Scholar]
- 13.Cai Z.W., Chen F.X., Guo J.Q. Constitutive model for elevated temperature flow stress of AZ41M magnesium alloy considering the compensation of strain. J. Alloys Compd. 2015;648:215–222. doi: 10.1016/j.jallcom.2015.06.257. [DOI] [Google Scholar]
- 14.Peng W.W., Zeng W.D., Wang Q.J., Yu H.Q. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013;51:95–104. doi: 10.1016/j.matdes.2013.04.009. [DOI] [Google Scholar]
- 15.Luo J., Li M.Q., Ma D.W. The deformation behavior and processing maps in the isothermal compression of 7A09 aluminum alloy. Mater. Sci. Eng. A. 2012;532:548–557. doi: 10.1016/j.msea.2011.10.120. [DOI] [Google Scholar]
- 16.Wang Y.X., Zhao G.Q., Xu X., Chen X.X., Zhang C.S. Constitutive modeling, processing map establishment and microstructure analysis of spray deposited Al-Cu-Li alloy 2195. J. Alloys Compd. 2019;779:735–751. doi: 10.1016/j.jallcom.2018.11.289. [DOI] [Google Scholar]
- 17.Lin Y.C., Wu X.Y., Chen X.M., Chen J., Wen D.X., Zhang J.L., Li L.T. EBSD study of a hot deformed nickel-based superalloy. J. Alloys Compd. 2015;640:101–113. doi: 10.1016/j.jallcom.2015.04.008. [DOI] [Google Scholar]
- 18.Lin L.H., Liu Z.Y., Han X.N., Liu W.J. Effect of Overaging on Fatigue Crack Propagation and Stress Corrosion Cracking Behaviors of an Al-Zn-Mg-Cu Alloy Thick Plate. J. Mater. Eng. Perform. 2018;27:3824–3830. doi: 10.1007/s11665-018-3518-0. [DOI] [Google Scholar]
- 19.Cheng J.F., Cai Q.Z., Zhao B.Y., Yang S.F., Chen F., Li B. Microstructure and mechanical properties of nanocrystalline Al-Zn-Mg-Cu alloy prepared by mechanical alloying and spark plasma sintering. Materials. 2019;12:1255. doi: 10.3390/ma12081255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shi C.J., Lai J., Chen X.G. Microstructural evolution and dynamic softening mechanisms of Al-Zn-Mg-Cu alloy during hot compressive deformation. Materials. 2014;7:244–264. doi: 10.3390/ma7010244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang H.J., Wang C., Mo Y., Wang H., Xu J. Hot deformation and processing maps of Al-Zn-Mg-Cu alloy under coupling-stirring casting. J. Mater. Res. Technol. 2019;8:1224–1234. doi: 10.1016/j.jmrt.2018.08.009. [DOI] [Google Scholar]
- 22.Zhao J.H., Deng Y.L., Tang J.G., Zhang J. Influence of strain rate on hot deformation behavior and recrystallization behavior under isothermal compression of Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2019;809:151788. doi: 10.1016/j.jallcom.2019.151788. [DOI] [Google Scholar]
- 23.Zang Q.H., Yu H.S., Lee Y.S., Kim M.S., Kim H.W. Effects of initial microstructure on hot deformation behavior of Al-7.9 Zn-2.7 Mg-2.0 Cu (wt %) alloy. Mater. Charact. 2019;151:404–413. doi: 10.1016/j.matchar.2019.03.019. [DOI] [Google Scholar]
- 24.Chaudhuri A., Behera A.N., Sarkar A., Kapoor R., Suwas S. Hot deformation behaviour of Mo-TZM and understanding the restoration processes involved. Acta Mater. 2019;164:153–164. doi: 10.1016/j.actamat.2018.10.037. [DOI] [Google Scholar]
- 25.Wu H., Wen S.P., Huang H., Gao K.Y., Wang W., Nie Z.R. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy. J. Alloys Compd. 2016;685:869–880. doi: 10.1016/j.jallcom.2016.06.254. [DOI] [Google Scholar]
- 26.Mann R.E.D., Hexemer R.L., Jr., Donaldson I.W., Bishop D.P. Hot deformation of an Al-Cu-Mg powder metallurgy alloy. Mater. Sci. Eng. A. 2011;528:5476–5483. doi: 10.1016/j.msea.2011.03.081. [DOI] [Google Scholar]
- 27.Rajamuthamilselvan M., Ramanathan S. Hot deformation behaviour of 7075 alloy. J. Alloys Compd. 2011;509:948–952. doi: 10.1016/j.jallcom.2010.09.139. [DOI] [Google Scholar]
- 28.Lin Y.C., Chen M.S., Zhong J. Microstructural evolution in 42CrMo steel during compression at elevated temperatures. Mater. Lett. 2008;62:2132–2135. doi: 10.1016/j.matlet.2007.11.032. [DOI] [Google Scholar]
- 29.Sellars C.M., McTegart W.J. On the mechanism of hot deformation. Acta Mater. 1966;14:1136–1138. doi: 10.1016/0001-6160(66)90207-0. [DOI] [Google Scholar]
- 30.McQueen H.J., Ryan N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A. 2002;322:43–63. doi: 10.1016/S0921-5093(01)01117-0. [DOI] [Google Scholar]
- 31.Medina S.F., Hernandez C.A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996;44:137–148. doi: 10.1016/1359-6454(95)00151-0. [DOI] [Google Scholar]
- 32.Liu W.Y., Zhao H., Li D., Zhang Z.Q., Huang G.J., Liu Q. Hot deformation behavior of AA7085 aluminum alloy during isothermal compression at elevated temperature. Mater. Sci. Eng. A. 2014;596:176–182. doi: 10.1016/j.msea.2013.12.012. [DOI] [Google Scholar]
- 33.Park S.Y., Kim W.J. Difference in the hot compressive behavior and processing maps between the as-cast and homogenized Al-Zn-Mg-Cu (7075) alloys. J. Mater. Sci. Technol. 2016;32:660–670. doi: 10.1016/j.jmst.2016.04.006. [DOI] [Google Scholar]
- 34.Wu B., Li M.Q., Ma D.W. The flow behavior and constitutive equations in isothermal compression of 7050 aluminum alloy. Mater. Sci. Eng. A. 2012;542:79–87. doi: 10.1016/j.msea.2012.02.035. [DOI] [Google Scholar]
- 35.Zener C., Hollomon J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944;15:22–32. doi: 10.1063/1.1707363. [DOI] [Google Scholar]
- 36.Wan P., Wang K.L., Zou H., Lu S.Q., Li X. Study on hot deformation and process parameters optimization of Ti-10.2 Mo-4.9 Zr-5.5 Sn alloy. J. Alloys Compd. 2019;777:812–820. doi: 10.1016/j.jallcom.2018.10.399. [DOI] [Google Scholar]
- 37.Qin X.Y., Huang D.W., Yan X.J., Zhang X.Y., Qi M.J., Yue S. Hot deformation behaviors and optimization of processing parameters for Alloy 602 CA. J. Alloys Compd. 2019;770:507–516. doi: 10.1016/j.jallcom.2018.08.144. [DOI] [Google Scholar]
- 38.Tan Y.B., Ma Y.H., Zhao F. Hot deformation behavior and constitutive modeling of fine grained Inconel 718 superalloy. J. Alloys Compd. 2018;741:85–96. doi: 10.1016/j.jallcom.2017.12.265. [DOI] [Google Scholar]
- 39.Wang X.D., Pan Q.L., Xiong S.W., Liu L.L. Prediction on hot deformation behavior of spray formed ultra-high strength aluminum alloy-A comparative study using constitutive models. J. Alloys Compd. 2018;735:1931–1942. doi: 10.1016/j.jallcom.2017.11.331. [DOI] [Google Scholar]
- 40.Liu Y., Geng C., Lin Q.Y., Xiao Y.F., Xu J.R., Kang W. Study on hot deformation behavior and intrinsic workability of 6063 aluminum alloys using 3D processing map. J. Alloys Compd. 2017;713:212–221. doi: 10.1016/j.jallcom.2017.06.066. [DOI] [Google Scholar]
- 41.Mosleh A.O., Mikhaylovskaya A.V., Kotov A.D., Kwame J.S., Aksenov S.A. Superplasticity of Ti-6Al-4V Titanium Alloy: Microstructure Evolution and Constitutive Modelling. Materials. 2019;12:1756. doi: 10.3390/ma12111756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mosleh A., Mikhaylovskaya A., Kotov A., Pourcelot T., Aksenov S., Kwame J., Portnoy V. Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network. Metals. 2017;7:568. doi: 10.3390/met7120568. [DOI] [Google Scholar]
- 43.Haghdadi N., Zarei-Hanzaki A., Khalesian A.R., Abedi H.R. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013;49:386–391. doi: 10.1016/j.matdes.2012.12.082. [DOI] [Google Scholar]
- 44.Prasad Y.V.R.K., Gegel H.L., Doraivelu S.M., Malas J.C., Morgan J.T., Lark K.A., Barker D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A. 1984;15:1883–1892. doi: 10.1007/BF02664902. [DOI] [Google Scholar]
- 45.He D.G., Lin Y.C., Chen M.S., Chen J., Wen D.X., Chen X.M. Effect of pre-treatment on hot deformation behavior and processing map of an aged nickel-based superalloy. J. Alloys Compd. 2015;649:1075–1084. doi: 10.1016/j.jallcom.2015.07.213. [DOI] [Google Scholar]
- 46.Yan J., Pan Q.L., Li B., Huang Z.Q., Liu Z.M., Yin Z.M. Research on the hot deformation behavior of Al-6.2 Zn-0.70 Mg-0.3 Mn-0.17 Zr alloy using processing map. J. Alloys Compd. 2015;632:549–557. doi: 10.1016/j.jallcom.2015.01.228. [DOI] [Google Scholar]
- 47.Lin Y.C., Li L.T., Xia Y.C., Jiang Y.Q. Hot deformation and processing map of a typical Al-Zn-Mg-Cu alloy. J. Alloys Compd. 2013;550:438–445. doi: 10.1016/j.jallcom.2012.10.114. [DOI] [Google Scholar]
- 48.Berg L.K., Gjønnes J., Hansen V., Li X.Z., Knutson-Wedel M., Waterloo G., Schryvers D., Wallenberg L.R. GP-zones in Al-Zn-Mg alloys and their role in artificial aging. Acta Mater. 2001;49:3443–3451. doi: 10.1016/S1359-6454(01)00251-8. [DOI] [Google Scholar]
- 49.Sun Z.C., Wu H.L., Cao J., Yin Z.K. Modeling of continuous dynamic recrystallization of Al-Zn-Cu-Mg alloy during hot deformation based on the internal-state-variable (ISV) method. Int. J. Plast. 2018;106:73–87. doi: 10.1016/j.ijplas.2018.03.002. [DOI] [Google Scholar]
- 50.Zhang Y.D., Jin S.B., Trimby P.W., Liao X.Z., Murashkin M.Y., Valiev R.Z., Liu J.Z., Cairney J.M., Ringer S.P., Sha G. Dynamic precipitation, segregation and strengthening of an Al-Zn-Mg-Cu alloy (AA7075) processed by high-pressure torsion. Acta Mater. 2019;162:19–32. doi: 10.1016/j.actamat.2018.09.060. [DOI] [Google Scholar]
- 51.He H.L., Yi Y.P., Cui J.D., Huang S.Q. Hot deformation characteristics and processing parameter optimization of 2219 Al alloy using constitutive equation and processing map. Vacuum. 2019;160:293–302. doi: 10.1016/j.vacuum.2018.11.048. [DOI] [Google Scholar]
- 52.Lin Y.C., He D.G., Chen M.S., Chen X.M., Zhao C.Y., Mao X., Long Z.L. EBSD analysis of evolution of dynamic recrystallization grains and δ phase in a nickel-based superalloy during hot compressive deformation. Mater. Des. 2016;97:13–24. doi: 10.1016/j.matdes.2016.02.052. [DOI] [Google Scholar]
- 53.Sun Z.C., Zheng L.S., Yang H. Softening mechanism and microstructure evolution of as-extruded 7075 aluminum alloy during hot deformation. Mater. Charact. 2014;90:71–80. doi: 10.1016/j.matchar.2014.01.019. [DOI] [Google Scholar]
- 54.Li D.F., Guo Q.M., Guo S.L., Peng H.J., Wu Z.G. The microstructure evolution and nucleation mechanisms of dynamic recrystallization in hot-deformed Inconel 625 superalloy. Mater. Des. 2011;32:696–705. doi: 10.1016/j.matdes.2010.07.040. [DOI] [Google Scholar]
- 55.Chen K.Y., Tang J., Jiang F.L., Teng J., Fu D.F., Zhang H. The role of various Zr additions in static softening behavior of Al-Zn-Mg-Cu alloys during interval holding of double-stage hot deformation. J. Alloys Compd. 2019;792:1112–1121. doi: 10.1016/j.jallcom.2019.04.090. [DOI] [Google Scholar]