Na–Ni–H Phase Formation at High Pressures and High Temperatures: Hydrido Complexes [NiH₅]^3–Versus the Perovskite NaNiH₃

Abstract

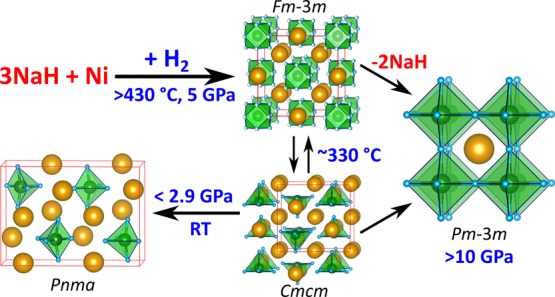
The Na–Ni–H system was investigated by in situ synchrotron diffraction studies of reaction mixtures NaH–Ni–H₂ at around 5, 10, and 12 GPa. The existence of ternary hydrogen-rich hydrides with compositions Na₃NiH₅ and NaNiH₃, where Ni attains the oxidation state II, is demonstrated. Upon heating at ∼5 GPa, face-centered cubic (fcc) Na₃NiH₅ forms above 430 °C. Upon cooling, it undergoes a rapid and reversible phase transition at 330 °C to an orthorhombic (Cmcm) form. Upon pressure release, Na₃NiH₅ further transforms into its recoverable Pnma form whose structure was elucidated from synchrotron powder diffraction data, aided by first-principles density functional theory (DFT) calculations. Na₃NiH₅ features previously unknown square pyramidal 18-electron complexes NiH₅^3–. In the high temperature fcc form, metal atoms are arranged as in the Heusler structure, and ab initio molecular dynamics simulations suggest that the complexes are dynamically disordered. The Heusler-type metal partial structure is essentially maintained in the low temperature Cmcm form, in which NiH₅^3– complexes are ordered. It is considerably rearranged in the low pressure Pnma form. Experiments at 10 GPa showed an initial formation of fcc Na₃NiH₅ followed by the addition of the perovskite hydride NaNiH₃, in which Ni(II) attains an octahedral environment by H atoms. NaNiH₃ is recoverable at ambient pressures and represents the sole product of 12 GPa experiments. DFT calculations show that the decomposition of Na₃NiH₅ = NaNiH₃ + 2 NaH is enthalpically favored at all pressures, suggesting that Na₃NiH₅ is metastable and its formation is kinetically favored. Ni–H bonding in metallic NaNiH₃ is considered covalent, as in electron precise Na₃NiH₅, but delocalized in the polyanion [NiH₃]⁻.

Introduction

The finding of high temperature superconductivity in highly compressed H₂S¹ stimulated intensive research efforts into binary metal–H systems at high pressures, leading to the discovery of hydrogen-rich hydrides, also called superhydrides, under extreme pressure conditions.²⁻⁵ Hydrogen-rich hydrides display a wide variety of unforeseen and previously unimaginable hydrogen structures, ranging from clathrate-like cages (e.g., LaH₁₀, CaH₆)⁶⁻⁸ and oligomeric chain fragments (e.g., NaH_n)⁹ to layer arrangements (e.g., FeH₅).¹⁰ Characteristically, binary superhydrides are only stable at very high pressures in the Mbar range (70–150 GPa) and cannot be retained at ambient pressure. In contrast, ternary compounds may be retained and might even form under low(er) pressure conditions. Recently, it has been shown that already the application of modest pressures of around 5 GPa can afford new complex transition metal hydrides (CTMHs) in which group five and six metals attain unusually high coordination numbers in homoleptic complex ions such as [CrH₇]^5– and [NbH₉]^4–.¹¹⁻¹³ Here, we demonstrate the accessibility of ternary hydrogen-rich hydrides in the Na–Ni–H system by using pressures up to 12 GPa and elevated temperatures up to 520 °C.

With the exception of Pd, late transition metals combine with elemental hydrogen only under high pressure conditions. The hydrogenation of Ni to γ-NiH requires about 1 GPa.¹⁴⁻¹⁶ A higher hydride, monoclinic Ni₂H₃, has been recently synthesized at 60 GPa.¹⁷ Both NiH and Ni₂H₃ cannot be quenched to ambient conditions. The situation changes radically when Ni is combined with an alkaline earth or rare earth metal. For example, the Ni-rich intermetallic compound LaNi₅ absorbs readily hydrogen into interstitial positions with varying occupancies (LaNi₅H_6.5), and Mg₂Ni is easily hydrogenated to yield the CTMH Mg₂NiH₄ featuring tetrahedral [NiH₄]^4– complexes.^18,19 The nature of Ni–H interactions in the metallic interstitial hydride LaNi₅H_6.5 and the semiconducting CTMH Mg₂NiH₄ is rather different. There is even a third class of Ni hydride compounds, namely, perovskites (i.e., CaNiH₃).²⁰ Similar to CTMHs, Ni–H bonding in perovskites is covalent but delocalized over a polyanionic framework.^21,22

In contrast with its heavier congeners Pd and Pt, Ni does not appear to combine easily with alkali metals in ternary hydrides. There is only one known representative, recently reported LiNiH₃ with the perovskite structure, which has been obtained by high pressure synthesis at 3 GPa.²³ Further, known hydrido complexes are restricted to tetrahedral [NiH₄]^4– with formally zero-valent Ni.²⁴ Again, this is different to Pd and Pt, for which oxidation states of II (d⁸) and even IV (d⁶) are known in CTMHs with square planar and octahedral hydrido complexes, respectively.^24,25 We will show that with pressure, the Na–Ni–H system affords not only d⁸-Ni hydrido complexes but also perovskite NaNiH₃.

Experimental Methods

In Situ Powder X-ray Diffraction Studies at High Pressures

The samples for the high pressure experiments were prepared in a glove box under an argon atmosphere because of air and moisture sensitivity of the starting materials. Powdered NaH (Sigma Aldrich, 90%) and powdered Ni metal (Sigma Aldrich, ≥99.9% trace metals basis) were carefully mixed at a molar ratio of 2:1 (NaH/Ni) and compressed into pellets. For the experiments at 5 and 10 GPa, sample pellets had an outer diameter (OD) of 2 mm and 1.5 mm height, while for the 12 GPa studies, dimensions were reduced to 1.4 and 0.75 mm, respectively. Ammonia borane (BH₃NH₃, Sigma-Aldrich, 97%) was used as hydrogen source. BH₃NH₃ has a well-defined decomposition behavior at high pressures and produces chemically inert BN as residual.²⁶ The amount of BH₃NH₃ used for each sample provided approx. 2.5 times molar excess of H₂ during the experiment with respect to nickel. NaH/Ni sample pellets were sandwiched between pelletized BH₃NH₃ and sealed inside NaCl capsules. The salt capsules employed at 5 and 10 GPa pressures had 3.0 mm OD and 3.8 mm height, while those used for 12 GPa runs were 2.4 mm OD and 2.8 mm height.

High pressure experiments at 5 and 10 GPa employed 14/8 multianvil assemblies. A detailed description of the 14/8 setup is provided elsewhere.²⁷ For reaching pressures above 12 GPa, the assembly was changed to a 10/5 type. Here, the sample capsules, protected by 2.8 mm OD BN sleeves, were inserted into 10 mm edge length Cr-doped MgO octahedra, along with two 2.8 mm OD ZrO₂ plugs and a nickel foil furnace (2.9 mm OD). Circular windows (2 mm OD) were cut in the Ni furnace along the beam direction to prevent the overlap with diffraction from the sample. Amorphous SiBCN rods (2 mm OD) and MgO rectangles (5 mm wide) were used as X-ray windows in the octahedra and gaskets, respectively, along the beam direction. Filled MgO octahedra were positioned between eight truncated tungsten carbide cubes (25 mm, Hawedia, ha7 grade) with 5 mm truncation edge length fitted with pyrophyllite gaskets. Both 14/8 and 10/5 assemblies were compressed at a rate of 1 bar/min oil pressure (∼2.5 and ∼3.2 GPa/h, respectively) to the target pressures and heated in the Voggenreiter-built modified-cubic press at beamline ID06-LVP, ESRF.²⁸ The heating was performed at various rates, ranging from 18 °C/min (comparatively fast) at T < 400 °C to <4 °C/min (comparatively slow) at higher temperatures or whenever a phase transition was expected. The heating was arrested each time the release of hydrogen from BH₃NH₃ was expected or the growth of ternary Na–Ni–H materials was detected. Pressure was estimated in situ from powder X-ray diffraction (PXRD) patterns using the equation of state (EOS) of NaCl, as reported by Birch.²⁹ For the 5 GPa experiments, temperature was evaluated from a D-type thermocouple calibration obtained in an independent run. The effect of pressure on the thermocouple EMF at 5 GPa is expected to be negligible.³⁰ During 10 and 12 GPa studies, the temperature was evaluated using the NaCl EOS.²⁹ Isobaric conditions were assumed during the heating, and the pressure was corrected after each >30 min dwell at constant power. Note that for the whole p, T range of the experiments, the Ni metal remained well below its melting curve.^31,32

Angle-dispersive PXRD patterns were collected continuously at a constant wavelength, selected by the Si (111) double-crystal monochromator from the emission of a U18 cryoundulator at ∼6 mm magnetic gap. For 5 and 10 GPa runs, the wavelength (λ) was 0.22542 Å (2.15–10.7° 2θ range) and for the 12 GPa experiment, λ = 0.2296 Å. At 12 GPa, data were collected in 1.66–10.18° and 2.86–11.34° 2θ intervals at different stages of the experiment. A Detection Technology X-Scan series 1 linear pixilated detector was used for data acquisition. A diffraction data set was typically saved every 32 s during compression and decompression and every 3.2 s during heating. This data set consists of 32 × 0.1 s sequential exposures, which were subsequently 32× rebinned. Sample-to-detector distance and detector offset were calibrated using LaB₆-SRM660a (NIST). The in situ data were integrated, visualized, and manipulated using Fit2D software.³³ The 2θ angular positions of the diffraction peaks for the Na–Ni–H compounds and NaCl as a function of time were extracted from the compiled in situ data via the multiple fitting (MFIT) function in Fit2D.³⁴ Unit cell dimensions and volumes were extracted from the MFIT results by the least squares method. Indexing of powder patterns was done using the DICVOL algorithm within the CRYSFIRE package.³⁵

Products from the high pressure experiments were recovered in a glove box under an argon atmosphere. Approximately half of the product from each run was sealed inside a glass capillary for ex situ characterization by PXRD.

Ex Situ PXRD Analysis

PXRD patterns of recovered samples were collected at the beamlines ID15B and ID22 at the ESRF, Grenoble. The measurements at ID15B were performed at a constant wavelength of 0.41127 Å with the beam focused on a sample to 30 × 30 μm size and using a Mar555 flat-panel detector. The integration of 2D data was performed using Fit2D software.³⁶ High resolution synchrotron PXRD data were collected at ID22 using monochromatic radiation selected by a Si(111) crystal (λ = 0.40008 Å for the 5 GPa product and λ = 0.3544 Å for the 12 GPa product). Data acquisition was typically performed over a 0.5–32.9° 2θ range (0.002° step size) with the dedicated multianalyzer stage operating nine detectors in parallel, each preceded by a Si(111) analyzer crystal.

Le Bail analysis³⁷ and Rietveld refinement³⁸ of in situ and ex situ PXRD data were performed using Jana2006 software.³⁹ Before analyzing the patterns, they were corrected for background by subtracting the minimal value of observed intensity from the entire I_obs column. For the data collected at ID22, the peak shape was fitted with a pure Lorentzian profile, while the rest of the refinements were performed using pseudo-Voigt peak profile function. In addition, ID22 data were thinned prior to the refinement so that only every second data point was used. In situ PXRD data were prepared for refinements by averaging 10–30 datapoints collected during the temperature dwell, which improved the signal-to-noise ratio and decreased possible contributions of texture to the refinement.

EOS Calculations

The calculation of the EOS for the NaNiH₃ perovskite was based on the in situ PXRD data collected on decompression during the 12 GPa experiment. The pressures were estimated from the cell volumes of NaCl using EOS, as reported by Birch.²⁹ The extracted data set of NaNiH₃ cell volumes as a function of pressure was introduced into EOSFit 5.2 software.⁴⁰ Data quality did not justify the use of the third order BM EOS model, and second order Birch–Murnaghan (BM) EOS was used instead. In addition, EOSfit 5.2 was employed to extract the EOS from the density functional theory (DFT) calculated p, V data. To make the resulting constants comparable with the fit of experimental data, a second order BM EOS model was used for the datasets obtained from DFT.

Theoretical Calculations

DFT enthalpy calculations were performed using the Vienna Ab Initio Simulation Package (VASP)^41,42 in the framework of the projector augmented wave method^43,44 within generalized gradient approximation and employing the Perdew–Burke–Ernzerhof parametrization of the exchange–correlation functional.^45,46 The cutoff energy for the plane wave basis set was 500 eV for all simulations. Structural relaxations employed a 3 × 4 × 5 Monkhorst–Pack (MP)⁴⁷k-point grid for Pnma Na₃NiH₅ (Z = 4), a 4 × 4 × 4 grid for Cmcm Na₃NiH₅ (Z = 4) and Na₂NiH₄ (Na₂PtH₄ structure, Z = 2), a 14 × 14 × 14 grid for the perovskites ANiH₃ (A = Li, Na, K), and 1 × 1 × 1 (Γ-point) for Z = 32 Na₃NiH₅ supercells. Relaxations were performed with total energies converged better than 10^–4 eV. Total energy calculations were carried out using the tetrahedron method with Blöchl correction⁴⁸ on a 4 × 4 × 4 MP k-point grid for Pnma and Cmcm Na₃NiH₅ and Na₂NiH₄, on a 14 × 14 × 14 grid for the perovskites ANiH₃, and on a 2 × 2 × 2 grid for Z = 32 Na₃NiH₅ supercells. For formation enthalpy calculations, total energy calculations were performed for NaH and Ni on 8 × 8 × 8 and 12 × 12 × 12 k-point grids, respectively. Molecular H₂ was considered with a pressure-independent enthalpy equal to −6.78 eV/molecule, as obtained from a total energy minimization of the H₂ molecule in a 10 × 10 × 10 ų box.

Electronic density of states (DOS) calculations used spheres around the atomic sites (parameter RWIGS in VASP) with radii Na = 1.4, Ni = 0.8, and H = 1.1 Å. Bader analysis of the charge densities⁴⁹ was performed according to refs (50) and (51). The phonon dispersions and the phonon partial DOS were calculated on 2 × 2 × 2 supercells using the small displacement method,^52,53 as implemented in PhonoPy.⁵⁴ Total energies were converged better than 10^–8 eV, referring to a 1 × 1 × 1 Γ-only (Na₃NiH₅) and a 8 × 8 × 8 k-point grid (NaNiH₃). The ionic positions were relaxed before the phonon calculations. The T_c estimation was performed using the Quantum Espresso code^55,56 and the Allen–Dynes-modified McMillan equation.⁵⁷ The cutoff energy for the plane waves was set to 60 Ry. The self-consistent calculations were performed on a 32 × 32 × 32 k-point grid. The electron–phonon coupling calculation was performed on a 4 × 4 × 4 k-point grid and using 0.1 as the value for the Coulomb pseudopotential μ*.

Ab initio molecular dynamics (MD) simulations of cubic Na₃NiH₅ in the NVT ensemble (i.e., maintaining the number of atoms N, volume of the system V, and temperature T) were performed using the Nosé–Hoover thermostat at 1000 K and the experimental volume at ∼5 GPa and 510 °C (a = 7.19 Å). The simulation was done on a 2 × 2 × 2 supercell (Z = 32, 288 atoms) of the cubic unit cell of the HT-HP Na₃NiH₅ phase. The Brillouin zone integration was done at the Γ-point.

Results and Discussion

Formation of Na₃NiH₅ at 5 GPa and Its Recovery to Ambient Pressure

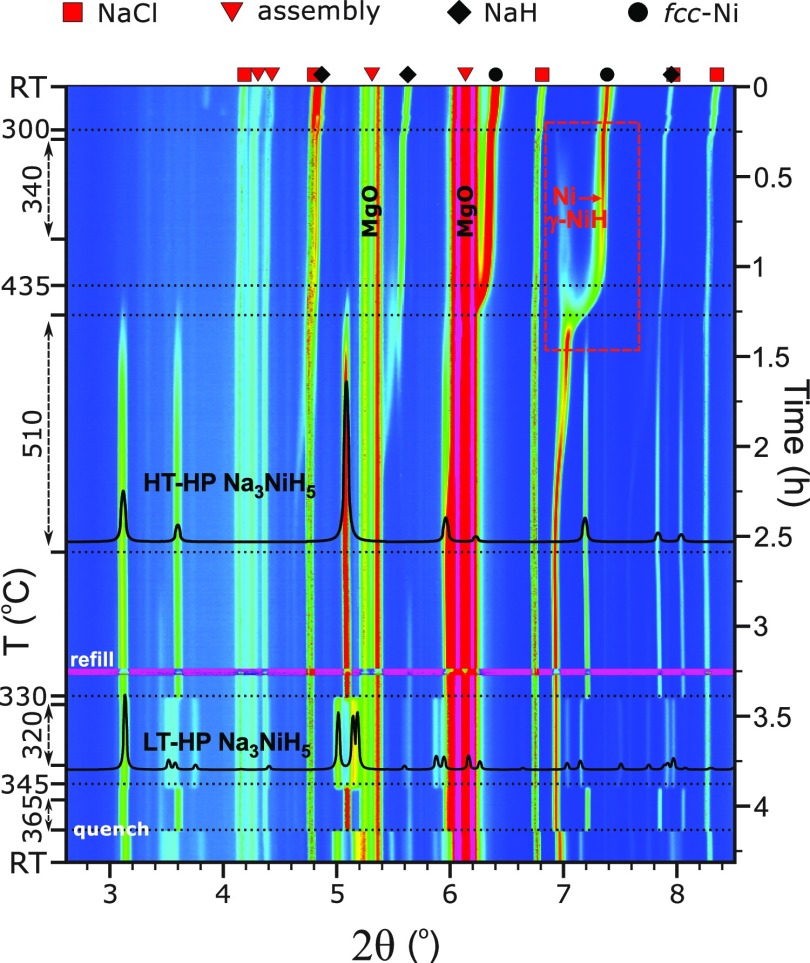
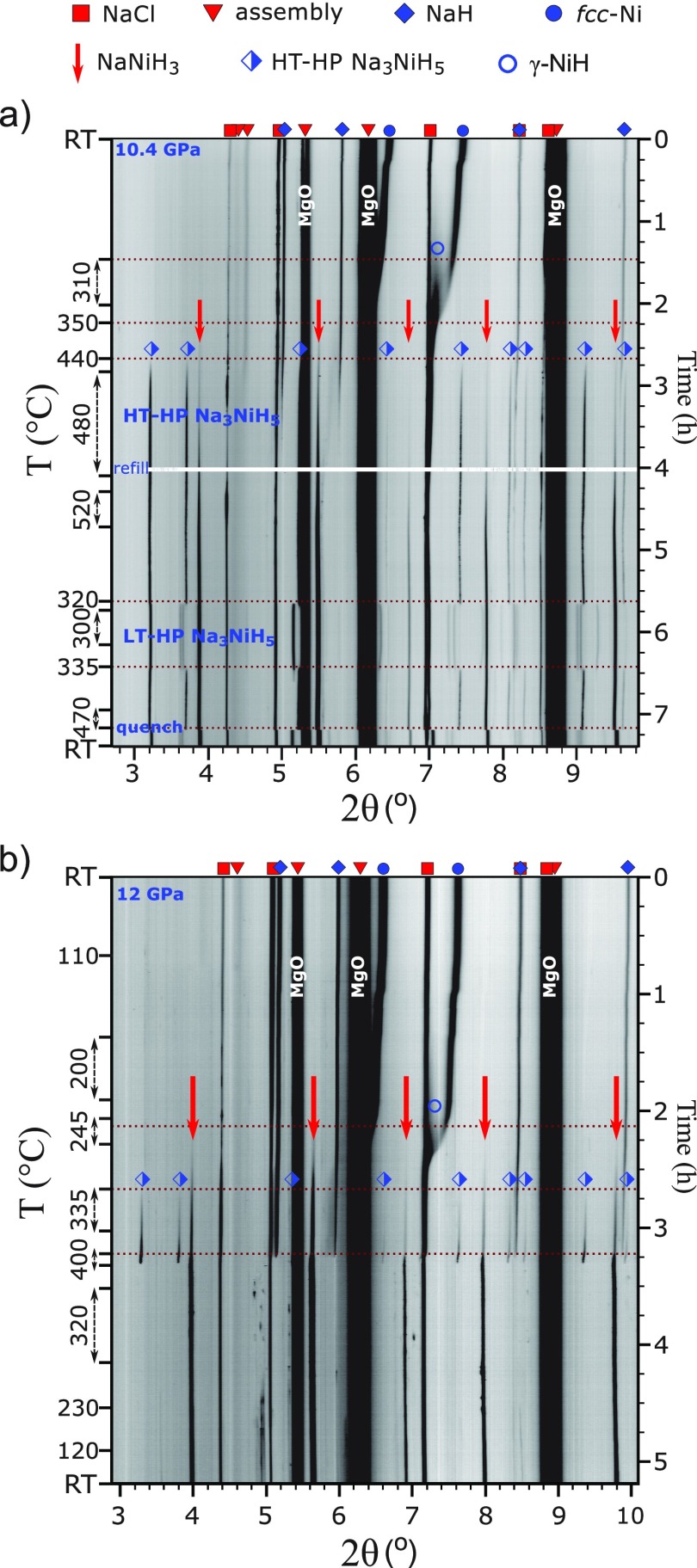
Throughout this study, reaction mixtures NaH/Ni/BH₃NH₃ 2:1:∼0.8 were employed which corresponded to a Ni/H₂ ratio 1:∼2.5. In total, three experiments were performed at pressures around 5 GPa. All experiments showed good reproducibility of observations. In the following, we describe an experiment, compiled in Figure 1, during which slow heating/cooling rates and prolonged annealing steps were applied, and diffraction data were acquired for structural analysis.

Figure 1.

Compilation of in situ PXRD patterns (λ = 0.22542 Å) showing the formation and polymorphic behavior of Na₃NiH₅ at ∼5 GPa. Diffraction peaks arising from the 14/8 multianvil assembly (MgO, h-BN, MgCr₂O₄) are marked with red triangles.

The sample was compressed to ∼5.4 GPa and then heated to ∼340 °C. At these p, T conditions, BH₃NH₃ is expected to be completely decomposed into BN and hydrogen fluid.²⁶ The sample was then kept at 340 °C for about 30 min in order to equilibrate the system in the presence of hydrogen fluid. Before the initial heating was finished, formation of γ-NiH (NiH_∼1) was noted at ∼300 °C as a set of diffuse peaks that appeared near the Ni metal reflections at lower 2θ angles. This is shown in the inset of Figure 1. In γ-NiH, the arrangement of metal atoms of face-centered cubic (fcc) Ni is retained, while H atoms are introduced in the octahedral voids of the metal structure, resulting in an expansion of the unit cell parameter.¹⁴ Upon further heating, at approx. 435 °C, a new set of reflections emerged in the PXRD patterns. The d-spacings of these reflections could not be matched to any known compound, and their presence was interpreted as formation of a ternary high pressure, high temperature phase, in the following denoted HT-HP Na₃NiH₅. These new diffraction lines became more pronounced, and their intensities increased further when dwelling at 510 °C for 80 min (Figure 1). The diffraction peaks from HT-HP Na₃NiH₅ were indexed to a fcc lattice, with a ≈ 7.19 Å at 510 °C.

After the dwell, the sample was slowly cooled at a rate of ∼5 °C/min. At about 330 °C, a new set of intense diffraction peaks replaced those of the HT-HP Na₃NiH₅ phase, indicating a transformation to a low temperature polymorph (LT-HP Na₃NiH₅). The transition completed almost instantly (within 60 s). The LT-HP phase was indexed to a C-centered orthorhombic lattice (extinction symbol C-c-) with the unit cell parameters a ≈ 7.34 Å, b ≈ 6.88 Å, and c ≈ 7.22 Å at 320 °C. The sample was dwelled for about 20 min and then slowly (3.5 °C/min) heated again to check the reversibility of the observed phase transition. The back-transformation of LT-HP Na₃NiH₅ to the HT-HP phase occurred at ∼345 °C. Again, the transition proceeded instantaneously. After the transformation, the sample was dwelled at ∼365 °C for 10 min and then quenched to room temperature. The HT-HP phase was not preserved by rapid cooling but was replaced with LT-HP Na₃NiH₅. The pressure was estimated as ∼4.4 GPa after the temperature quench.

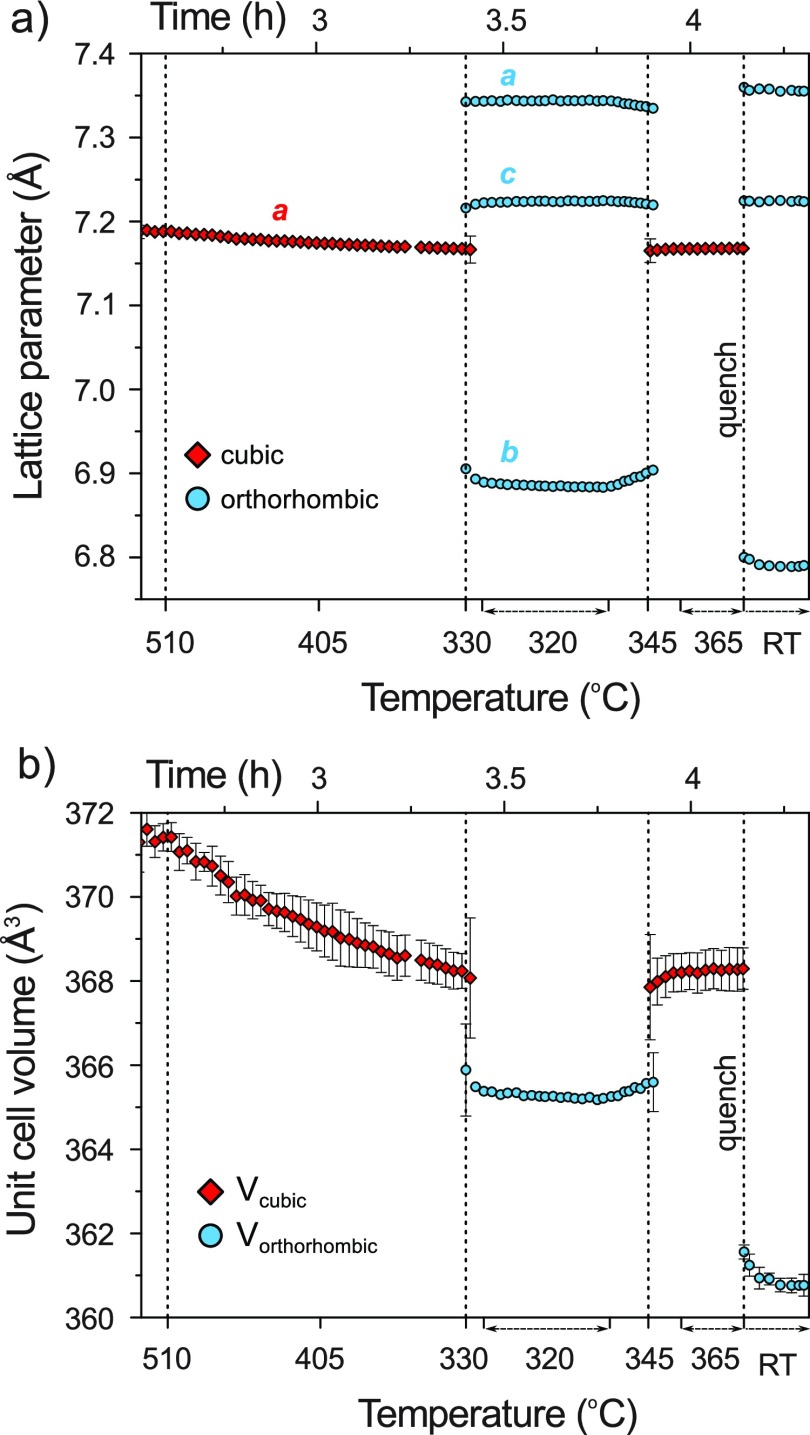
Figure 2a shows the unit cell parameters of both phases as a function of temperature and time as extracted from the in situ PXRD data. In addition, changes in the cell volumes are shown in Figure 2b. The average standard deviations for the cell parameters and unit cell volumes are within ±0.0052 Å (±0.461 ų) and ±0.0013 Å (±0.117 ų) for the HT-HP and LT-HP phases, respectively. The close numerical range of their cell parameters and volumes suggests that the two phases are polymorphs and that the orthorhombic lattice results from a distortion of the HT cubic cell on cooling. The splitting of the 220 reflection of the cubic HT phase during the transition to orthorhombic is shown in Figure S1. The volume change at the cubic to orthorhombic transition is approx. −2.1 ų (0.57%). The rapid character of the transformation and rather small temperature hysteresis are indicative of a first order displacive phase transition.

Figure 2.

Cell parameters (a) and volumes (b) of cubic HT-HP and orthorhombic LT-HP Na₃NiH₅ as a function of temperature at ∼5 GPa. Errors corresponding to the symbol size or smaller are not shown.

To conclude the experiment, the sample was decompressed to ambient conditions. At ∼2.9 GPa, new diffraction peaks emerged. At ∼2.6 GPa, the intensities of the new peaks increased, while the diffraction peaks of LT-HP Na₃NiH₅ became noticeably weaker, suggesting transformation to a different, low pressure, phase (LP Na₃NiH₅, see Supporting Information, Figure S2). At 1.4 GPa, the diffraction peaks of LT-HP Na₃NiH₅ were completely replaced. On final decompression, no significant further changes were observed, except for γ-NiH reverting back to fcc Ni. The sample was recovered at ambient conditions and used for ex situ PXRD examination. LP Na₃NiH₅ displayed a dark gray color, and when stored under Ar at room temperature, it decomposed over a period of several months.

Elucidating the Composition and Crystal Structures of Polymorphic Na₃NiH₅

For structural analysis of HT-HP and LT-HP Na₃NiH₅, PXRD data were prepared by averaging 20–40 patterns collected during the temperature dwell at 365 °C (cubic phase) as well as during the dwell at 320 °C and after the quench (orthorhombic phase). The HT-HP phase was analyzed using Le Bail fits to the space group Fm3̅m (225), whereas for the LT-HP phase space group Cmcm (63) was used. The a parameter for the cubic phase at 365 °C was refined to ≈7.169 Å. The cell parameters of the orthorhombic LT-HP phase at 320 °C were determined as a ≈ 7.344 Å, b ≈ 6.883 Å, and c ≈ 7.225 Å. Possible metal atom arrangements were then identified using the Superflip algorithm on the extracted intensities within the Jana2006 package.⁵⁸ For the HP-HT phase, an antifluorite arrangement of the metal atoms was suggested, with Ni and Na occupying 4a and 8c Wyckoff sites, respectively. However, this solution could not be fitted reasonably to the experimental data using Rietveld refinement (see Supporting Information for details). The fit improved significantly when an additional atom partially occupied the 4b site, resulting in a Heusler arrangement of metal atoms. However, the type of atoms at this site was ambiguous: the Rietveld fit was equally good if 4b was occupied by ∼0.3 Ni or ∼0.7 Na atoms, yielding metal atom compositions Na₂Ni_∼1.3 and Na_∼2.7Ni, respectively. An analogous result was obtained for the orthorhombic LT-HP phase (Cmcm): Na and Ni atoms were found to occupy 4c and 8e sites, respectively, with one more atom partially occupying a second 4c site. The resulting compositions for the LT-HP phase reproduced those of the cubic polymorph. The simulated patterns for both cubic and orthorhombic phases with a metal atom composition Na₂Ni_∼1.3 are overlaid in the in situ PXRD data in Figure 1 (cf. Figure S2 in the Supporting Information).

Further structural investigations then targeted the product LP Na₃NiH₅ recovered at ambient conditions. The structure determination and refinement were performed using integrated 2-dimensional PXRD data (cf. Supporting Information, Figure S3). Apart from leftover Ni metal and NaH, a set of reflections was present in the pattern, which could not be assigned to any known compound. The best indexing result suggested an orthorhombic unit cell with a Pn-a extinction symbol and approximate cell parameters a ≈ 10.41 Å, b ≈ 7.37 Å, and c ≈ 5.43 Å. Le Bail analysis was initially carried out within the P222 (16) space group. A subsequent space group test then suggested Pnma (62). Structure solution resulted in a metal arrangement with 3Na:1Ni stoichiometry (Ni on a Wyckoff site 4c, and Na on sites 4c and 8d) and atomic coordinates very similar to K and N atoms in Pnma K₃NO₄ (potassium orthonitrate),⁵⁹ see Supporting Information for details. The obtained structure was used for Rietveld refinement against the experimental data and fitted well to the observed diffraction pattern (R_obs ≈ 7.7%, see also Supporting Information for refinement procedure), which strongly indicated the correctness of the metal composition and metal atom arrangement in LP Na₃NiH₅. Consequently, the Na₃Ni stoichiometry was also assumed for the HP forms. A Na₃Ni metal composition suggested 5 H atoms and Ni in an oxidation state II (d⁸) or less likely 4 and 3 H atoms with Ni in the oxidation state I (d⁹) and 0 (d¹⁰), respectively.

In order to explore possible hydrogen atom arrangements, a simulated annealing (SA) global optimization algorithm in Endeavour 1.7 software was employed.⁶⁰ The previously refined “Na₃Ni” unit cell containing 12 Na⁺ and 4 Ni²⁺ cations was introduced as a base to which either 16 or 20 H^– atoms (4 or 5 H^– per f.u.) were added. A simple repulsion potential for the charged ions was used during the optimization, while the positions of metal cations were kept fixed. The minimal Ni–H and Na–H distances were constrained to 1.5 and 2.0 Å, respectively. Several SA global optimization runs with 50–100 seeds were performed, which produced a range of “Na₃NiH₄” and “Na₃NiH₅” structures with various H^– ligand arrangements. These structures were then subjected to DFT optimization and their stability was assessed by the formation energy with respect to NaH, Ni, and H₂. As expected, formation energies of Na₃NiH₄ structures were clearly unfavorable against Na₃NiH₅ ones. Most of the stable Na₃NiH₅ configurations returned unprecedented square pyramidal NiH₅^3– complexes, which is shared by the geometry of the d⁸-Co(I)H₅^4– complex in Mg₂CoH₅.⁶¹

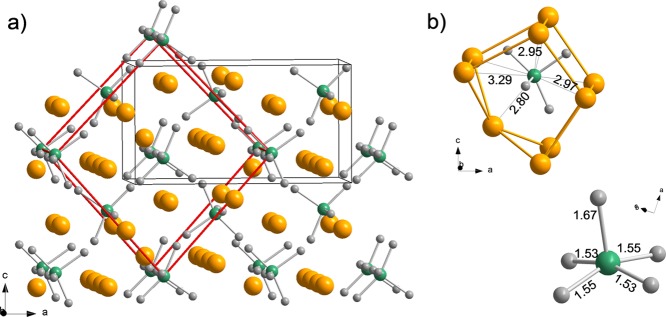
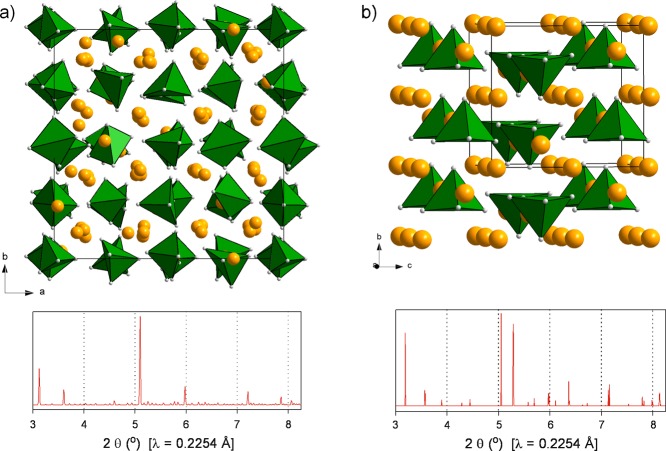
The most stable Na₃NiH₅ configuration found by DFT optimization is shown in Figure 3, and its parameters are compiled in Table 1. The structure can be interpreted as a cubic close packing of NiH₅^3– complexes with all tetrahedral and octahedral interstices filled by Na⁺ ions (Figure 3a). The distribution of Ni atoms follows the fcc metric; however, the location of cations deviates substantially from the ideal centers of interstices (i.e., 4b and 8c in Fm3̅m). The local coordination and geometry of a NiH₅^3– complex is shown in Figure 3b. In the NiH₅^3– complex, the four basal ligands have similar and short distances to Ni (1.53 × 2, 1.55 × 2 Å), whereas the bond to the apical ligand is rather elongated (1.67 Å).

Figure 3.

(a) Pnma structure of LP Na₃NiH₅ according to DFT optimization. Na, Ni, and H atoms are depicted as golden, green, and gray spheres, respectively. The arrangement of Ni atoms corresponds closely to a fcc structure (red unit cell). Na atoms are located in the vicinity of tetrahedral and octahedral voids. (b) Local coordination of a NiH₅^3– complex by 9 Na cations (top) and structure of a NiH₅^3– complex (bottom). Interatomic Na–Ni and Ni–H distances as obtained from DFT calculations are indicated (in angstroms).

Table 1. DFT Optimized Ambient Pressure Structure of LP Na₃NiH₅ (Space Group: Pnma (62); a = 10.2566 Å, b = 7.3388 Å, and c = 5.5697 Å).

atom	site	x	y	z
Ni	4c	0.8848	0.25	0.7670
Na1	8d	0.1562	0.0179	0.8467
Na2	4c	0.0580	0.25	0.3793
H1	4c	–0.0076	0.25	–0.0381
H2	4c	0.8251	0.25	0.5118
H3	8d	0.0947	–0.0447	0.2632
H4	4c	0.7512	0.25	–0.0607

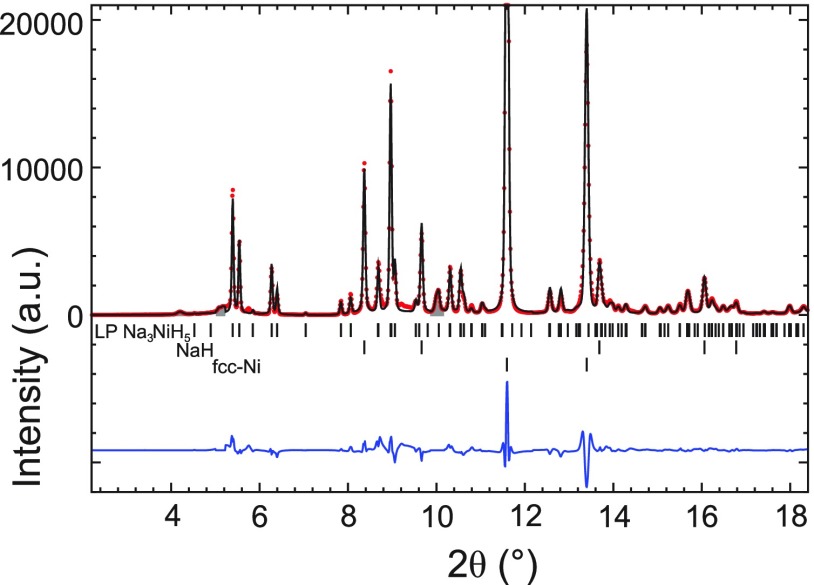
The optimized DFT structure of Pnma LP Na₃NiH₅ was then used as a model for a final Rietveld refinement against the experimental pattern. The hydrogen atom positions were kept unchanged during the refinement, and their U_iso parameters were fixed at 0.038 Ų (B_iso = 3 Ų). The refinement procedure is described in Supporting Information. The refinement details and obtained crystal structure parameters are included in Tables 3 and 4, and the final Rietveld fit is shown in Figure 4. A simulated PXRD pattern of Pnma LP Na₃NiH₅ is overlaid in the compilation of in situ PXRD patterns collected during decompression (Figure S2).

Table 3. Results of the Rietveld Refinement of Na₃NiH₅ Polymorphs under Different p, T Conditions.

phase	LP Na3NiH5	HT-HP Na3NiH5	LT-HP Na3NiH5	LT-HP Na3NiH5
temperature	RT (300 K)	365 °C (638 K)	320 °C (593 K)	RT (300 K)
pressure	ambient	∼5 GPa	∼5 GPa	∼4.4 GPa
crystal system	orthorhombic	cubic	orthorhombic	orthorhombic
space group	Pnma (62)	Fm3̅m (225)	Cmcm (63)	Cmcm (63)
Z	4	4	4	4
lattice parameters (Å)	a = 10.4131(9)	a = 7.16905(16)	a = 7.3444(9)	a = 7.3575(13)
	b = 7.3711(6)		b = 6.8828(9)	b = 6.7932(15)
	c = 5.4291(5)		c = 7.2247(8)	c = 7.2231(12)
V (Å3)	416.71(6)	368.456(15)	365.21(8)	361.02(12)
V/Z (Å3)	104.18	92.114	91.303	90.255
formula weight	132.7	132.7	132.7	132.7
dcalc (g/cm3)	2.115	2.392	2.413	2.442
Robs (%)	5.94	6.41	8.35	10.94
Rall (%)	5.94	6.41	8.71	11.10

Table 4. Fractional Coordinates and Atomic Displacement Parameters for the Various Na₃NiH₅ Polymorphs Obtained from Rietveld Refinement^a.

atom	site	x	y	z	Uiso (Å2)
LP Na3NiH5 (Ambient, RT)
Ni (Ni2+)	4c	0.8812(7)	0.25	0.7557(14)	0.0191(17)
Na1 (Na+)	8d	0.1528(12)	0.0151(13)	0.8209(18)	0.025(3)
Na2 (Na+)	4c	0.0731(13)	0.25	0.372(3)	0.025(3)
LT-HP Na3NiH5 (∼5 GPa, 320 °C)
Ni	4c	0	0.2427(15)	0.25	0.017(2)
Na1	8e	0.210(3)	0	0	0.070(6)
Na2	4c	0	0.691(4)	0.25	0.070(6)
LT-HP Na3NiH5 (∼4.4 GPa, RT)
Ni	4c	0	0.2391(16)	0.25	0.013(3)
Na1	8e	0.208(2)	0	0	0.046(6)
Na2	4c	0	0.675(3)	0.25	0.046(6)
HT-HP Na3NiH5 (∼5 GPa, 365 °C)
Ni	4a	0	0	0	0.0118(19)
Na1	8c	0.25	0.25	0.25	0.054(3)
Na2	4b	0.5	0.5	0.5	0.054(3)

^aHydrogen atoms for LP and LT-HP were introduced in the analysis from the DFT-optimized structures (Tables 1 and 2), and their positions were fixed during the refinement along with their ADPs [U_iso were set to 0.038 Ų (B_iso = 3 Ų)]. H atoms for HT-HP were placed at a site 48h with x = 0.15 (Ni–H = 1.521 Å) and an occupancy of 5/12. See Supporting Information for Rietveld refinement procedures and resulting plots (Figures S6 and S7).

Figure 4.

Rietveld fit of the DFT-optimized LP Na₃NiH₅ structure to the ambient synchrotron PXRD data of the product after depressurization of the 5 GPa run (λ = 0.41127 Å). Excluded regions are shown in gray (see Supporting Information for refinement details).

Following the results of the LP Na₃NiH₅ structure solution, the elucidation of the HT-HP and LT-HP structures was revisited using Na₃NiH₅ stoichiometry. For a more detailed analysis of the HT-HP phase, a 2 × 2 × 2 supercell (Z = 32) of the fcc Heusler arrangement of Na and Ni atoms was assembled and 5 H atoms were placed around each Ni atom. This was then used as the initial structure for NVTab initio MD simulations using the experimental volume at ∼5 GPa and 510 °C (a = 7.19 Å). The simulation temperature was 1000 K. The system equilibrated after 1 ps, as indicated in the almost zero hydrostatic stress attained after this time (see Supporting Information, Figure S4), and NiH₅^3– complexes were found to perform reorientational dynamics (Figure S5). Accordingly, the fcc HT-HP Na₃NiH₅ structure can be considered as a time-averaged Heusler arrangement of Na ions and dynamically disordered NiH₅^3– complexes. This arrangement of metal atoms is shared with K₃ReH₆ which possesses ordered octahedral d⁴ ReH₆^3– complexes.⁶²Figure 5a displays an MD snapshot and the corresponding simulated diffraction pattern. Upon cooling, the reorientational dynamics of NiH₅^3– complexes arrest and subsequent ordering causes an orthorhombic distortion of the Na⁺ counterion environment. To arrive at a model for the Cmcm structure, a range of trial structures with different orientations of NiH₅ complexes and Z = 4 were assembled inside a cubic simulation cell. DFT relaxation without using symmetry constraints yielded a robust lowest energy solution with orthorhombic lattice parameters very close to the experimentally observed ones and an atom arrangement with symmetry close to Cmcm. This is shown in Figure 5b, together with the simulated diffraction pattern. The structure parameters referring to a pressure of 5 GPa are given in Table 2.

Figure 5.

(a) Z = 32 MD snapshot of HT-HP Na₃NiH₅ at 1000 K (using the experimental volume at ∼5 GPa and 510 °C) after equilibration (top) and calculated powder diffraction pattern (bottom). (b) DFT relaxed model of Cmcm LT-HP Na₃NiH₅ at 5 GPa (top) and calculated powder diffraction pattern (bottom). NiH₅^3– complexes are drawn as green polyhedra.

Table 2. DFT-Optimized Structure of LT-HP Na₃NiH₅ at 5 GPa (Space Group: Cmcm (63); a = 7.24484 Å, b = 6.63230 Å, and c = 7.22221 Å).

atom	site	x	y	z
Ni	4c	0	0.24955	0.25
Na1	8e	0.21107	0	0
Na2	4c	0	0.67043	0.25
H1	8f	0	0.69735	0.5453
H2	8g	0.2075	0.27691	0.25
H3	8c	0	0.00196	0.25

The Rietveld refinement of HT-HP and LT-HP structures was repeated using the results of the computational simulations as starting models. The structure model for the refinement of the Fm3̅m HT-HP phase included Na atoms on 8c and 4b sites and Ni atoms occupying 4a sites. The hydrogen atoms were placed on a 48h Wyckoff site (and an occupancy of 5/12 was applied). This created a dodecahedral coordination around Ni atoms, which was intended to simulate the dynamically disordered situation. The Rietveld refinement was performed using the PXRD data collected at 365 °C (for the HT-HP phase) and at 320 °C and room temperature (for the Cmcm LT-HP phase), see Supporting Information for details about the refinement procedure. The refinements of the ∼5 GPa in situ data provided reasonable fits. The crystallographic results are given in Tables 3 and 4 as well as in Supporting Information, Figures S6 and S7.

Phase Stability of Na₃NiH₅ and the Electronic Structure of Pnma LP Na₃NiH₅

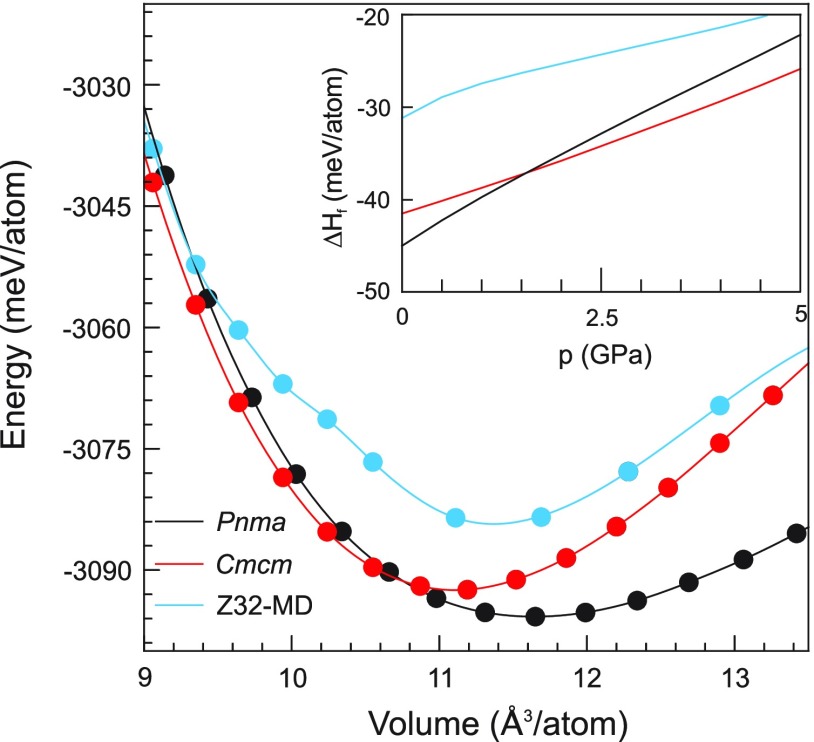
Next, we analyzed the phase and structure stability of polymorphic Na₃NiH₅ by DFT total energy calculations. Figure 6 shows E–V and ΔH–p relations for the three phases of Na₃NiH₅ (referring to 0 K). Formation enthalpies ΔH were calculated with respect to NaH, Ni, and H₂. The HT-HP model corresponded to an MD snapshot which was relaxed in the considered volume range. The kink in the E–V curve between 10 and 10.5 ų is attributed to an orientation change of complexes. The enthalpy difference between the HT-HP and LT-HP phases can be estimated as 10 meV/atom (8.6 kJ/mol). The equilibrium volume for both phases is near 11.1 ų/atom (note that both phases have also very similar volumes at the experimental conditions of the phase transition, cf. Figure 2), whereas the calculated equilibrium volume for Pnma LP Na₃NiH₅ is 11.6 ų/atom. Below 1.5 GPa the Pnma phase is more stable than the Cmcm one, which is in reasonable agreement with the decompression experiment where the phase transformation was observed in the range 2.5–3 GPa at room temperature.

Figure 6.

Total energy vs volume and formation enthalpy versus pressure relations of HT-HP Na₃NiH₅, Cmcm LT-HP Na₃NiH₅, and Pnma LP Na₃NiH₅. Formation enthalpies refer to 3NaH + Ni + H₂.

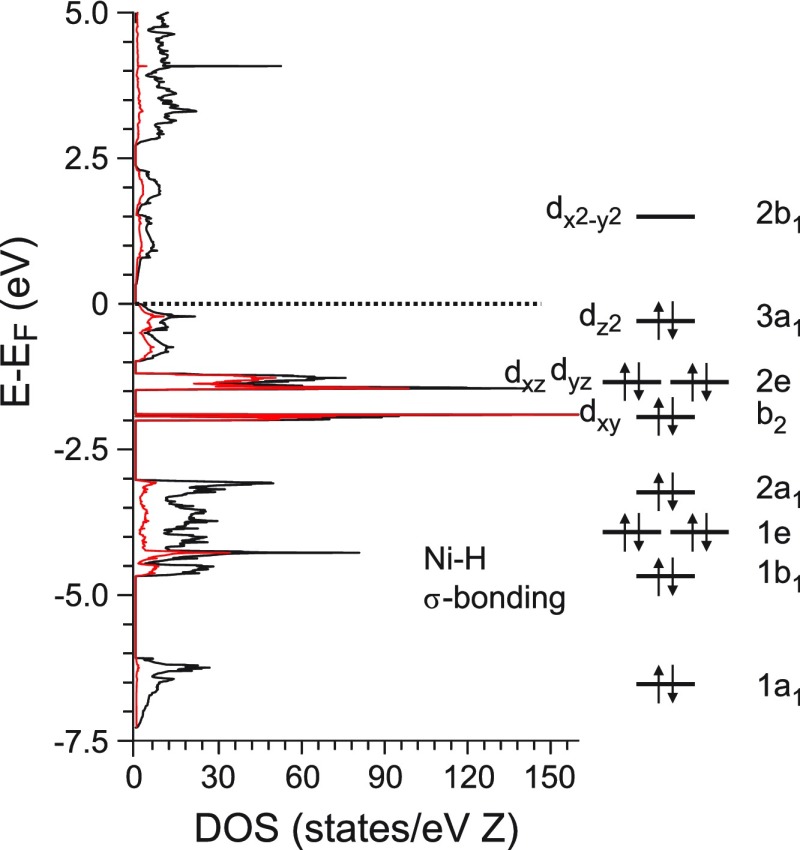
Figure 7 depicts the electronic structure of Pnma LP Na₃NiH₅ for the computed ambient pressure equilibrium structure (cf. Table 1). The occupied states in the electronic DOS mirror the MOs (and crystal field splitting) of an isolated, idealized, square pyramidal C_4v complex. The five bonding Ni–H σ-MOs possess the symmetry species 2A₁ + B₁ + E and would involve essentially d_x²–y² (A₁) among the Ni d orbitals. The lowest lying band, centered at around −7 eV below the Fermi level, has essentially s character and translates to the 1a₁ MO, and the remaining 4 Ni–H MOs are associated with states in the DOS region between −3 and −5 eV. The remaining occupied states, from about −2 eV up to the Fermi level, bear mainly Ni-d character. The narrow band at −2 eV is of nonbonding character and corresponds to a pure d_xy orbital (B₂), which is followed by weakly antibonding d_xz, d_yz (E) and d_z² (A₁)-based bands. Thus, with five occupied (Ni–H) bonding and four occupied (Ni-d) nonbonding/weakly antibonding states per formula unit, one obtains the picture of NiH₅^3– as an 18-electron complex.

Figure 7.

Electronic DOS of Pnma LP Na₃NiH₅ at the equilibrium volume corresponding to ambient pressure (left) and schematic MO diagram for the 18 electron complex, showing the sequence of 5 Ni–H σ-bonding orbitals, 4 nonbonding, d-based, orbitals and the antibonding lowest unoccupied molecular orbital (LUMO) (right). The latter maps the crystal field splitting of the d orbitals. (Total DOS: black line, Ni-partial DOS: red line. Energy is plotted with respect to the Fermi level, E_F = 0 eV).

The highest lying occupied band, associated with the 3a₁ (d_z²) HOMO, has a considerable dispersion which diminishes the band gap. The calculated band gap has a very small size (about 0.2 eV) which may be underestimated as typical for DFT calculations. From the dark gray color of the sample (which may be caused by the presence of Ni), one cannot draw any conclusions on the presence and size of a band gap in LP Na₃NiH₅. Above the Fermi level, a band stretches from 0.2 to about 2.5 eV. This band is associated with the antibonding 2b₁ LUMO, which completes the “1 over 4” crystal field splitting pattern of d orbitals for a C_4v complex.

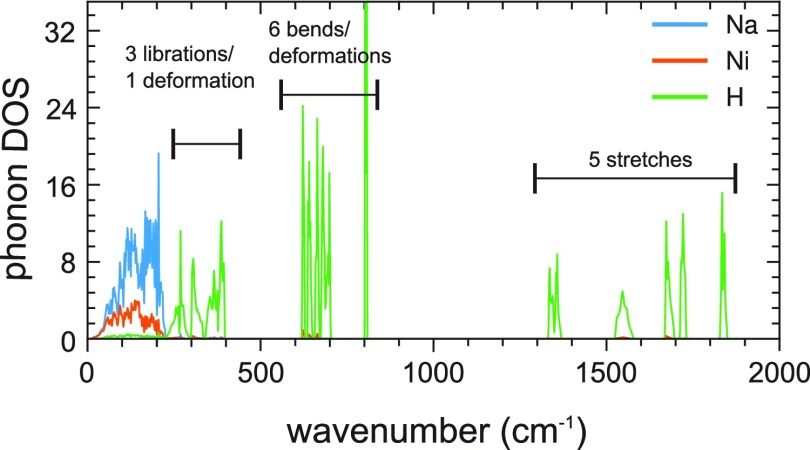
Figure 8 shows the phonon DOS for Pnma LP Na₃NiH₅ for the computed ambient pressure equilibrium structure. The absence of imaginary modes manifests the dynamic stability of LP Na₃NiH₅. A square pyramidal C_4v complex will give rise to 12 internal modes, of which five are classified as stretching modes (2 × A₁, B₁, E) and seven as bending and deformations (A₁, B₁, B₂, 2 × E). In addition, each complex will produce three libration (torsion) modes in the solid. Accordingly, the H-based modes in Na₃NiH₅ will distribute over three regions. Ni–H stretches are between 1300 and 1900 cm^–1. The two symmetric stretches (A₁) may be distinguished as apical (involving the apical H-ligand) and basal (involving the four basal H-ligands). The basal stretch is at the highest wavenumber (1830 cm^–1), whereas the apical one is at the lowest (1350 cm^–1). Six out of seven Ni–H bending/deformation modes are in the wavenumber range 600–800 cm^–1. One deformation mode attains a very low wavenumber (400 cm^–1) and falls in the spectral region of the libration modes (200–400 cm^–1).

Figure 8.

Phonon DOS (pDOS) of Pnma LP Na₃NiH₅ at the equilibrium volume corresponding to ambient pressure. pDOS is partitioned into atomic contributions of H, Na, and Ni.

Because of the sensitivity of Na₃NiH₅ toward decomposition, we were not able to corroborate the vibrational modes suggested from the calculated phonon DOS by IR/Raman measurements. It is therefore instructive to compare with isoelectronic and isostructural CoH₅^4– and also NiH₄^4– for which vibrational properties have been reported earlier.^63,64 For CoH₅^4 – in Mg₂CoH₅, Co–H stretches are in a range 1632–1834 cm^–1.⁶⁴ As in NiH₅^3–, the two symmetric stretches represent the extremes. However, the basal stretch is at considerably higher wavenumbers compared to NiH₅^3–. This is attributed to the large disparity of basal and apical Ni–H bond lengths. Bending modes for CoH₅^4– are between 766 and 1032 cm^–1 and thus higher than for NiH₅^3–, which indicates that Co–H bonds are more rigid with respect to angular displacements. For NiH₄^4–, stretching and bending modes are at lower wavenumbers compared to CoH₅^4– (1674–1691 and 620–791 cm^–1) and thus are more comparable to NiH₅^3–.⁶³ The libration modes of Mg₂CoH₅ and Mg₂NiH₄ are at considerably higher wavenumbers (420–580 cm^–1) which is expected because the divalent, polarizing Mg²⁺ ions will create a more rigid torsional potential for the complex ions.

Formation of NaNiH₃ at p > 10 GPa and Its Recovery to Ambient Pressures

The investigation of the Na–Ni–H system was then extended to 10 GPa in order to further explore the polymorphic behavior of Na₃NiH₅ compounds and the possibility of forming other Na–Ni–H phases. The sample was heated at a starting pressure of 10.4 GPa at which initial H₂ release and complete decomposition of BH₃NH₃ are expected at 260 and 310–330 °C, respectively.²⁶ The formation of γ-NiH became visible in PXRD patterns above 270 °C as a very diffuse peak near the 200 reflection of Ni (see upper part of Figure 9a). At 310 °C, the temperature was kept constant for about 35 min, after which heating was resumed at a slow rate (∼4 °C/min). Similar to the 5 GPa experiments, at about 440 °C, the growth of HT-HP Na₃NiH₅ was noted. However, at lower temperatures (350–380 °C), a set of very faint additional peaks was detected in the PXRD patterns (marked with red arrows in Figure 9a). The intensities of these new peaks continued to increase during further heating. To observe the development of the two phases, the sample was kept at ∼480 °C for ∼80 min. Intensities of the diffraction peaks for both HT-HP Na₃NiH₅ and the new phase noticeably increased during this time.

Figure 9.

(a) Compilation of in situ PXRD patterns (λ = 0.22542 Å and 0.2296 Å, respectively) showing formation of ternary hydrides from a NaH/Ni/H₂ = 2:1:2.5 reaction mixture at around 10 (a) and 12 GPa (b). The diffraction peaks arising from the 14/8 and 10/5 multianvil assemblies (MgO, h-BN, MgCr₂O₄) are marked with red triangles.

The sample was further heated to 520 °C and then dwelled for 25 min. As a result, the reflections of the new phase became even more pronounced. To find out if the polymorphic behavior of the Na₃NiH₅ phase is preserved at ∼10 GPa and to further observe the behavior of the new phase, the sample was cooled down to ∼300 °C. The phase transition of HT-HP Na₃NiH₅ to the LT-HP polymorph occurred at ∼320 °C, and upon reheating to 340 °C, the back-transformation was seen at ∼335 °C. The temperature interval and rapid nature of the order–disorder transition closely mimicked the experiments at 5 GPa. During the course of these temperature variations, lasting for about 3 h, it appeared that the new phase grows slowly over time at the expense of the initially formed Na₃NiH₅ (cf. Figure S8, Supporting Information).

Afterward, the sample was heated to ∼470 °C and subsequently temperature-quenched. As in the experiments at 5 GPa, the HT-HP phase underwent instant transformation to the orthorhombic LT-HP form on rapid cooling, whereas the diffraction peaks of the new phase remained unaltered. The pressure at room temperature was estimated as 8.9 GPa. The sample was then decompressed and recovered. PXRD characterization of the product revealed that the new compound was still present under ambient conditions, whereas LT-HP Na₃NiH₅ transformed to Pnma LP Na₃NiH₅, once again reproducing the behavior during the 5 GPa experiments.

The reflections of the new phase were indexed to a primitive cubic unit cell with no reflection conditions, and Pm3̅m space group was used for further evaluation. The unit cell parameter a varied within ∼3.32–3.33 Å during the temperature variations of this experiment. Le Bail analysis and subsequent structure solution via Superflip⁵⁸ resulted in a CsCl-type 1Na:1Ni metal arrangement. The cell parameter under ambient conditions was estimated as ≈3.43 Å, and the cubic perovskite structure NaNiH₃ was assumed for the new phase. This was confirmed by subsequent DFT calculations, which reproduced closely this cell parameter for the theoretical equilibrium structure. Consequently, it is inferred that at ∼10 GPa, Na₃NiH₅ is initially formed for kinetic reasons and then superseded by the more thermodynamically stable NaNiH₃. To further investigate the effect of pressure on NaNiH₃ formation, an experiment at 12 GPa was conducted.

The compilation of PXRD patterns at ∼12 GPa is shown in Figure 9b. The H release behavior of BH₃NH₃ at pressures above 10 GPa has not been explicitly determined. We estimate that complete decomposition at 12 GPa occurs around 350 °C. Growth of γ-NiH became apparent during ∼15 min dwell at ∼245 °C. During the same temperature dwell, extremely weak reflections of the NaNiH₃ phase appeared in the diffraction patterns. These peaks became increasingly prominent upon further heating. At ∼335 °C, the diffraction peaks of HT-HP Na₃NiH₅ also started to emerge in the PXRD patterns. At this point, the temperature was dwelled for 20 min, and during the dwell the intensities of reflections for both HT-HP Na₃NiH₅ and NaNiH₃ continued to increase. Their cell parameters under these conditions were estimated as ≈6.89 and ≈3.30 Å, respectively. When the heating was resumed and the estimated temperature reached 400 °C, diffraction peaks of HT-HP Na₃NiH₅, NaH, and γ-NiH almost instantly disappeared, while at the same time, the intensities of NaNiH₃ increased remarkably (lower part of Figure 9b). After a 5 min dwell at 400 °C, the sample was cooled to room temperature. No noticeable changes occurred to the NaNiH₃ pattern, and no other Na–Ni–H phases could be detected. At room temperature, the estimated pressure was 10.6 GPa. The cell parameter of NaNiH₃ after cooling corresponded to ≈3.295 Å.

The in situ PXRD data collected on decompression were further used to extract the unit cell volume of NaNiH₃ as a function of pressure. Figure S9 (Supporting Information) shows the pressure–volume EOS of NaNiH₃. The bulk modulus extracted from the experimental data is 69.9(1) GPa. This is somewhat lower than the DFT calculated value [80.8(4) GPa] and may indicate the presence of H defects in NaNiH₃, that is, NaNiH_3−δ. H deficiency in transition metal perovskite hydrides is especially known for the Pd-based representatives CaPdH_3−δ and SrPdH_3−δ (δ ≈ 0.1).⁶⁵⁻⁶⁷

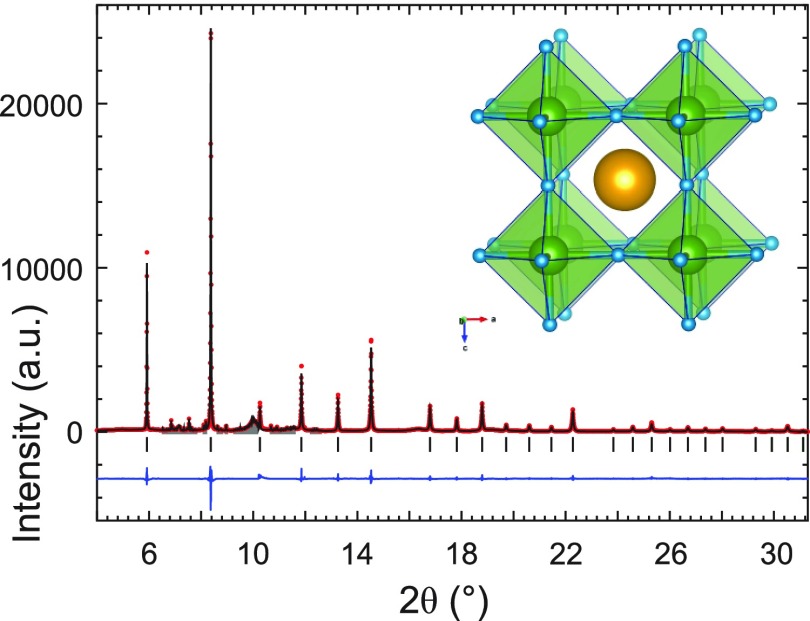
After the decompression, the sample was recovered for ex situ characterization. The sample color appeared brown with an orange tint and slight metallic luster. A high-resolution PXRD pattern confirmed Pm3̅m NaNiH₃ as the main product in the sample. The overall Rietveld fit is shown in Figure 10. A magnification of the high angle region and full width at half-maximum (FWHM) values for diffraction peaks as a function of 2θ, strongly corroborating a cubic metric for NaNiH₃, are shown as Supporting Information, Figures S10 and S11. Refinement details are given in Table 5 and as Supporting Information, Table S1. The lattice parameter at ambient pressure and room temperature is a = 3.43235(3) Å which implies a Ni–H distance of 1.716 Å.

Figure 10.

Rietveld fit of the NaNiH₃ cubic perovskite structure to the ambient synchrotron PXRD data of the product after depressurization of the 12 GPa run (λ = 0.3544 Å). Excluded regions are shown in gray (see Supporting Information for refinement details). Inset depicts the cubic perovskite structure.

Table 5. Results of the Final Rietveld Refinement of the Perovskite NaNiH₃ Structure under Ambient Conditions.

crystal system	cubic
space group	Pm3̅m (221)
Z	1
lattice parameters (Å)	a = 3.43235(3)
V (Å3)	40.4365(6)
formula weight	84.7
dcalc (g/cm3)	3.478
Robs (%)	2.39
Rall (%)	2.39

Na–Ni–H System at High Pressures: Hydrido Complexes Versus Perovskite

In situ synchrotron diffraction studies revealed that rather moderate pressures, 5–12 GPa, readily afford the formation of compounds in the ternary Na–Ni–H system. In the hydrides identified, Na₃NiH₅ and NaNiH₃, Ni formally attains the oxidation state II. Polymorphic Na₃NiH₅ represents a (presumably) semiconducting CTMH constituting isolated complex ions NiH₅^3–. NiH₅^3– represents the first homoleptic hydrido complex in which Ni possesses an oxidation state larger than 0 and binds to more than four ligands. In contrast, the perovskite NaNiH₃ is metallic (see discussion below). Ni is octahedrally coordinated by six H ligands, which, however, are shared between two Ni centers. It has been shown earlier that T–H bonding in transition metal perovskite hydrides is pronouncedly covalent.^21,22 In this respect, the corner-sharing octahedron framework in NaNiH₃ should be considered as a polyanion, [NiH_6/3]⁻, which is counterbalanced by Na⁺ cations. Compared to Na₃NiH₅ with localized Ni–H single bonds (with lengths of 1.53, 1.55, and 1.67 Å), the Ni–H distance in NaNiH₃ (with delocalized Ni–H bonding) is longer, at 1.72 Å. The presence of both types of hydrides, CTMH and perovskite, within a single binary metal combination is very rare and has previously been only found for the Sr–Pd–H, Eu–Pd–H, and Ca–Rh–H systems.⁶⁷⁻⁷⁰

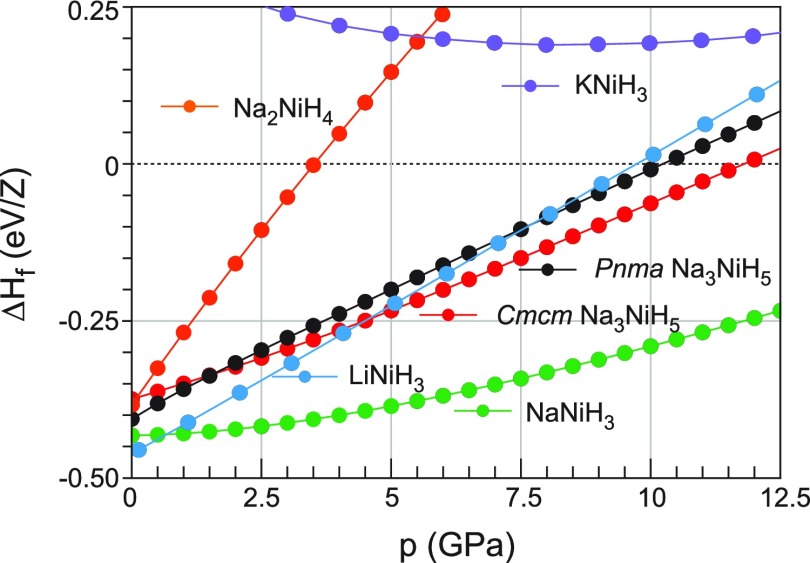
Figure 11 compares the (0 K) formation enthalpies of Na₃NiH₅ and NaNiH₃. Both systems are thermodynamically stable with respect to NaH + Ni + H₂, albeit weakly. The enthalpy change of the reactions NaH + Ni + H₂ → NaNiH₃ and 3NaH + Ni + H₂ → LP Na₃NiH₅ are estimated as −0.43 eV/Z (−41.5 kJ/mol) and −0.40 eV/Z (−38.6 kJ/mol), respectively, which is comparable to that of LaNi₅ hydrogenation (−32 kJ/mol H₂),⁷¹ that is, high pressures are actually not required to stabilize these compounds. The significance of pressure for the synthesis of Na₃NiH₅ and NaNiH₃ is however two-fold. First, with pressure, the decomposition temperature will shift to higher values, thus enabling the application of elevated temperature for synthesis (>430 °C at ∼5 GPa and reduced to ∼300 °C at ∼12 GPa). Second, kinetic barriers—present at ambient pressure—will be substantially reduced with increasing pressure. Importantly, the pressure dependence of the activity of molecular hydrogen is not well known (and thus not considered in our calculations). However, at pressures above 1 GPa, the activity of molecular hydrogen increases sharply,^72,73 which generally favors hydride formation.

Figure 11.

Compilation of formation enthalpies (with respect to NaH/AH + Ni + H₂) for Pnma LP Na₃NiH₅, Cmcm LT-HP Na₃NiH₅, Na₂NiH₄, and the perovskites ANiH₃ (A = Li, Na, K).

The calculated formation enthalpies also suggest that the formation of Na₃NiH₅ is kinetically driven. The decomposition according to Na₃NiH₅ → NaNiH₃ + 2NaH is favored at ambient pressure and becomes increasingly favorable with increasing pressure. Computed decomposition enthalpies as a function of pressure are shown in Figure S12 (Supporting Information). In Figure 11, we also included the formation enthalpy for hypothetical Na₂NiH₄ with the Na₂PtH₄ structure and square planar d⁸-NiH₄^2– complexes.⁷⁴ At ambient pressure, Na₂NiH₄ appears similarly stable as Na₃NiH₅ but becomes rapidly disfavored with increasing pressure.

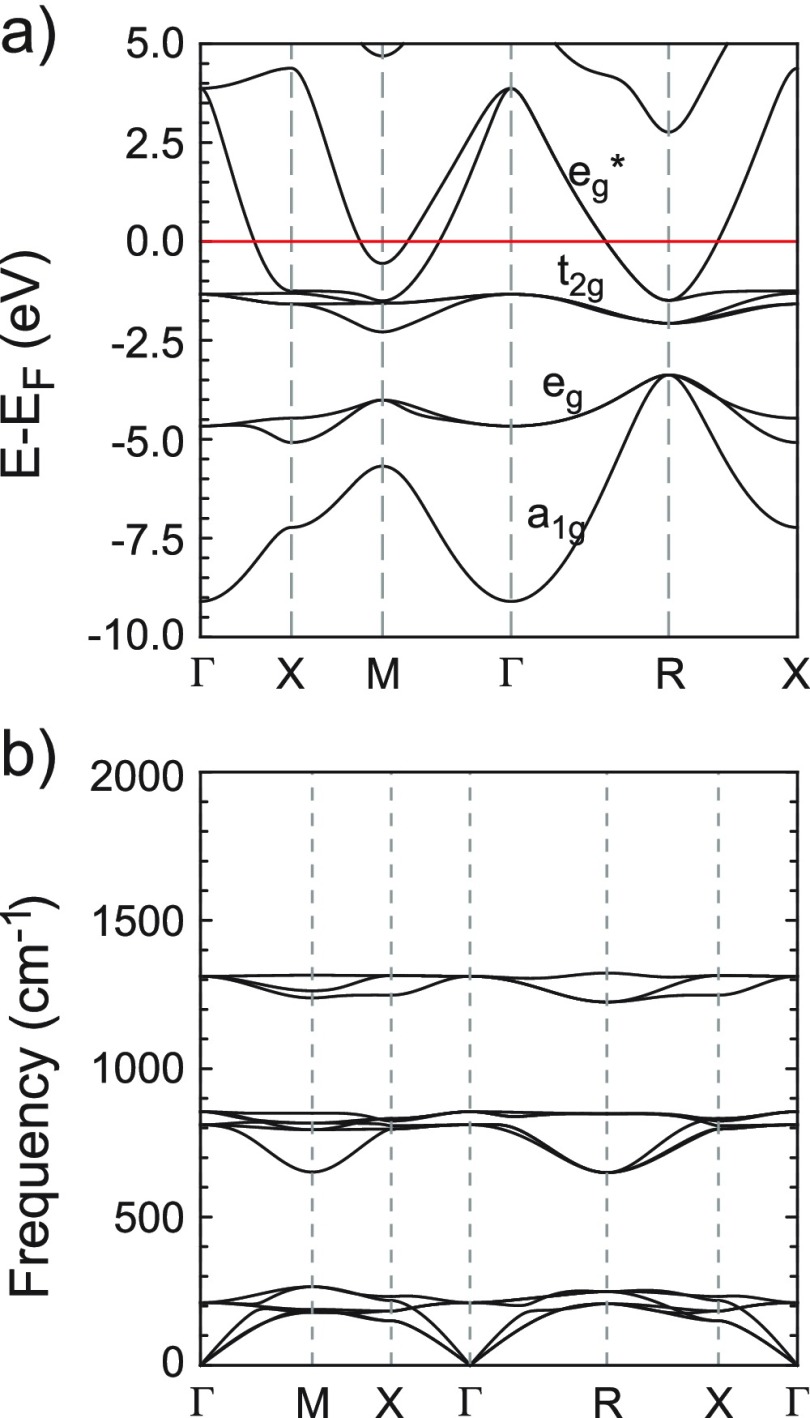
Transition metal perovskite hydrides are elusive. Including NaNiH₃ from this work, there are 10 known representatives. Most correspond to combinations of Ni and Pd with the divalent cations Ca, Sr, and Eu.⁷⁵ Lately, representatives with Co and Rh have been reported.^70,75 The electronic structure of transition metal perovskite hydrides has been analyzed earlier.^21,76,77Figure 12a depicts the band structure of NaNiH₃ at the computed equilibrium volume. Spin-polarized calculations revealed a nonmagnetic ground state. Occupied bands are divided into bonding a_1g and e_g, nonbonding t_2g, and antibonding e_g^*. The weakly dispersed t_2g band is completely filled for 12 e/Z. Accordingly, in NaNiH₃ with 14 e/Z, the e_g band is half-filled. The dispersion range of the Ni–H bonding and nonbonding bands relates well to the energy range of corresponding states for Na₃NiH₅ (cf. Figure 7). As initially mentioned, Ni–H bonding in NaNiH₃ is considered pronouncedly covalent. In this respect, it is instructive to discuss the result of a Bader analysis of charge densities⁴⁹ for the CTMHs LP Na₃NiH₅ and hypothetical Na₂NiH₄ with metallic NaNiH₃ and the ionic hydride NaH (NaCl-type). This is compiled in Table 6. Na attains a very similar (positive) charge, >0.8, irrespective of the system, which corroborates its cationic, Na⁺, character in all systems. Na–H distances are at 2.43 and 2.45 Å for NaNiH₃ and NaH, respectively, and in a range 2.45–2.81 Å for LP Na₃NiH₅. Compared to NaH, constituting hydridic H^–, Bader charges and volumes for H are considerably smaller in the Na–Ni–H materials with covalent Ni–H bonding. Yet, the state of covalent bonding, localized and delocalized (metallic), can be discriminated. The perovskite is distinguished by small volumes of all constituting atoms, manifesting its compact structure.

Figure 12.

Electronic DOS (a) and phonon dispersion (b) for NaNiH₃ at zero pressure.

Table 6. Compilation of Bader Charges and Volumes (ų).

compound	Na charge	Na volume	Ni charge	Ni volume	H charge	H volume
NaH	0.848	9.928			–0.848	17.824
NaNiH3	0.838	7.503	0.366	12.531	–0.401	6.374
Na2NiH4	0.841	9.622	0.323	19.633	–0.502	11.78
Na3NiH5	0.824	9.947	0.224	15.190	–0.539	11.95

Figure 12b depicts the phonon dispersions of NaNiH₃ at the computationally relaxed equilibrium volume. The 5 atoms in the unit cell give rise to 12 optic modes, of which 3 are Ni–H stretches and 6 are Ni–H bends and the remaining 3 correspond to Na translations. The H stretching modes are around 1300 cm^–1, which is considerably lower than the Ni–H stretches in LP Na₃NiH₅ (1350–1850 cm^–1) because of the larger Ni–H bond length in the perovskite (cf. Figure 8). The bending modes, however, are in a similar range, 600–800 cm^–1. Computation of the Eliashberg function and electron–phonon coupling integral show that electron–phonon coupling is negligible in NaNiH₃, and thus, superconductivity is not expected.

With respect to Na₃NiH₅, the formation of more stable NaNiH₃ is kinetically hindered. Here, it is important to compare with the Li–Ni–H system for which the perovskite LiNiH₃ was recently reported.^23,76 Similar to NaNiH₃, LiNiH₃ was obtained from the reaction of LiH and Ni at high pressures in the presence of H₂ fluid. However, this reaction already occurred at pressures around 3 GPa via an intermediate Li_yNi_1–yH solid solution (based on γ-NiH). There was no evidence for complex hydride formation in the Li–Ni–H system. Possibly, CTMH formation is suppressed because Li_yNi_1–yH enables a more favorable kinetics for LiNiH₃ formation.

As included in Figure 11, the formation enthalpy of LiNiH₃ is very similar to NaNiH₃ at ambient and slightly elevated pressures, but LiNiH₃ is destabilized considerably with respect to NaNiH₃ with increasing pressure. Because of the small size of Li, the equilibrium lattice parameter of LiNiH₃ is very small, 3.266(1) Å (cf. ≈3.432 Å for NaNiH₃). Accordingly, the Ni–H distance within the octahedral framework is reduced to ≈1.633 Å, which is comparable to the apical Ni–H distance in Na₃NiH₅. A further decrease of the Ni–H distance by external pressure will then destabilize LiNiH₃ with respect to NaNiH₃.

Despite the small Ni–H distance in LiNiH₃, Li⁺ remains loosely coordinated in the cuboctahedral cavity of the perovskite structure. Whereas the electronic structure of LiNiH₃ is very similar to NaNiH₃ (cf. refs (76) and (77)), phonon dispersions are rather different. In particular, the loose Li–H coordination is revealed in the Ni–H bends which are at considerably lower wavenumbers compared to NaNiH₃ (by 150 cm^–1 at Γ) and show a large dispersion, even merging with the phonons of Li translations at M and R (this is shown in Supporting Information, Figure S13). LiNiH₃ is clearly outside the Goldschmidt stability field for perovskite hydrides, as established by Ikeda et al.⁷⁵ Yet, its formation enthalpy is similar to NaNiH₃ which is situated inside the Goldschmidt stability field. In this respect, it is interesting to also investigate KNiH₃ which despite the considerably larger radius for K⁺ (1.64 Å as compared to 1.39 Å for Na⁺)⁷⁸ would also be located within the stability field. Again, the result is included in Figure 11. KNiH₃ has a positive formation energy for all pressures and is thus not expected to be thermodynamically stable. Note that KNiH₃ has a negative formation energy with respect to the elements, K + Ni + 3/2H₂.⁷⁷

Because transition metal perovskite hydrides are expected to be stable only as 14 and 15 e/Z systems,^21,22,76 an interplay between complex hydride and perovskite formation will be limited to hydrides of transition metals from groups 9 and 10. For Na–Ni–H, the CTMH Na₃NiH₅ forms initially but is unstable toward decomposition to the perovskite according to Na₃NiH₅ → 2NaH + NaNiH₃. In both forms of hydrides, Ni is present in the oxidation state II. A related interplay example has been reported for Ca–Rh–H. Here, Ca₂RhH_5+x is obtained from sintering mixtures of CaH₂ and Rh at temperatures between 250 and 500 °C in a slightly pressurized hydrogen atmosphere (several bars).^79,80 Mixed-valent Ca₂RhH_5+x (x ≈ 0.4) crystallizes with a hydrogen-disordered K₂PtCl₆ structure, featuring locally isolated octahedral Rh(II)H₆^4– and square pyramidal Rh(I)H₅^4– complexes. Furthermore, this synthesis strategy afforded also the more Rh-rich phases Ca₈Rh₅H₂₅ and Ca₈Rh₆H₂₄ in which additional Rh atoms are inserted in the K₂PtCl₆ structure and link previously isolated complexes through common H ligands. It has been conjectured that these more Rh-rich phases represent intermediates toward the perovskite CaRhH₃ according to Ca₂Rh(II)H₆ + Rh = 2 CaRh(I)H₃.⁷⁹ The synthesis of CaRhH₃ has not yet been achieved from reaction mixtures CaH₂ + Rh + H₂, and we suspect that, similar to NaNiH₃, its formation via Ca₂Rh_1+xH_6–y CTMHs is kinetically hindered but should be possible when using high pressures. Recently, the Kohlmann group reported the synthesis of CaRhH₃ from a different route, CaRh₂ + H₂ = CaRhH₃ + Rh, using the Laves phase CaRh₂ as a precursor.⁷⁰ This hydrogenation reaction proceeds under comparatively mild conditions, ∼250 °C and 50 bar H₂ pressure.

Metallic transition metal hydride perovskites have been investigated for superconductivity early on. Orgaz et al. performed a computational study on the electron–phonon coupling in the Pd hydrides MPdH₃ (M = Ca, Sr, Eu, and Yb) but found only moderate to weak coupling, suggesting low values of the superconducting transition temperature.⁸¹ Indeed, Ayukawa et al. did not observe superconductivity for CaPdH_3−δ above 2 K.⁶⁶ The superconducting properties of Ni hydride perovskites and CaRhH₃ are not known. Our calculations, however, indicate only a very weak electron–phonon coupling in NaNiH₃, and thus, superconductivity above 2 K is not expected.

Conclusions

The application of high pressures afforded for the first time ternary compounds in the Na–Ni–H system. Polymorphic Na₃NiH₅ featuring square pyramidal complex ions NiH₅^3– was obtained from reaction mixtures NaH–Ni–H₂ at pressures between 5 and 10 GPa. NiH₅^3– represents the first homoleptic hydrido complex in which Ni possesses an oxidation state larger than 0 and binds to more than four ligands. At temperatures above ∼335 °C, Na₃NiH₅ adopts a fcc structure in which NiH₅^3– complexes are dynamically disordered (HT-HP Na₃NiH₅); at lower temperatures, the structure distorts orthorhombically and complexes appear ordered (LT-HP Na₃NiH₅). Upon pressure release, LT-HP Na₃NiH₅ undergoes a phase transition to a low pressure form (LP Na₃NiH₅) which can be recovered at ambient p, T. Na₃NiH₅ is unstable with respect to decomposition into the perovskite NaNiH₃, according to Na₃NiH₅ → NaNiH₃ + 2NaH, and it is inferred that its formation is kinetically driven. NaNiH₃, in which Ni is octahedrally coordinated by six H atoms, was obtained at pressures 10–12 GPa. Also, this ternary hydride phase can be recovered at ambient conditions. It is conjectured that with pressure, a similar interplay between complex hydride and perovskite phases can be observed in the CaH₂–Rh–H₂ system. Na₃NiH₅ and NaNiH₃ are further examples of ternary hydrogen-rich hydrides that form under comparatively low pressure conditions and can be retained at ambient pressure.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00239.

• Splitting of 220 reflection during the transition of HT-HP Na₃NiH₅ to LT-HP polymorph, formation of LP Na₃NiH₅ polymorph upon decompression of the 5 GPa run at RT, fragment of a 2D-PXRD pattern of the recovered LP Na₃NiH₅ product, deviatoric stress as a function of the simulation time for HT-HP Na₃NiH₅, probability map of angular positions of H atoms in NiH₅^3– complexes in the HT-HP and LT-HP phases, results of the Rietveld fit of the cubic HT-HP Na₃NiH₅ and the Cmcm LT-HP Na₃NiH₅ models to in situ PXRD data, results of the Rietveld fit of the Cmcm LT-HP Na₃NiH₅ model, changes in phase fractions of Na−Ni−H products and nickel hydride during 10 GPa run, experimental and computed EOS for NaNiH₃, magnified high angle region of the NaNiH₃ perovskite structure Rietveld fit, FWHM values for NaNiH₃ diffraction peaks as a function of 2θ at ambient p, T, DFT-computed decomposition enthalpies for Na₃NiH₅ and Na₂NiH₄, comparison of the electronic band structure and phonon dispersions for NaNiH₃ and LiNiH₃, fractional coordinates and atomic displacement parameters obtained for the perovskite NaNiH₃, and details of the structure solution of the “Na₃Ni” arrangement for LP Na₃NiH₅ and the Rietveld refinement procedure for Na–Ni–H products (PDF)

• Crystallographic data of LP Na₃NiH₅ at ambient p, T (CIF)

• Crystallographic data of HT-HP Na₃NiH₅ at 638 K and ∼5 GPa (CIF)

• Crystallographic data of LT-HP Na₃NiH₅ at 593 K and ∼5 GPa (CIF)

• Crystallographic data of LT-HP Na₃NiH₅ at RT and ∼4.4 GPa (CIF)

• Crystallographic data of perovskite NaNiH₃ at ambient p, T (CIF)

The authors declare no competing financial interest.