Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Apr 7;5(15):9031–9040. doi: 10.1021/acsomega.0c01051

Elucidation of Selectivity Reversals for Binary Mixture Adsorption in Microporous Adsorbents

Rajamani Krishna 1,*, Jasper M van Baten 1
PMCID: PMC7178797  PMID: 32337468

Abstract

graphic file with name ao0c01051_0012.jpg

The adsorption selectivity, Sads, is a key metric that quantifies the efficacy of any adsorbent in mixture separations. It is common practice to use ideal adsorbed solution theory (IAST) for estimating the value of Sads, using unary isotherm data inputs. In a number of experimental investigations, the phenomena of selectivity reversals and adsorption azeotropy (Sads = 1) have been reported in the published literature; such reversals may result from changes in mixture compositions, pressures, or pore loadings. In many cases, IAST is unable to anticipate such selectivity reversals. In this article, configurational-bias Monte Carlo simulations are used to gain insights into the phenomena of selectivity reversals. Two fundamentally different scenarios of selectivity reversals have been identified. In the first scenario, selectivity reversals are caused by inhomogeneous distribution of adsorbates due to preferential location and siting of a guest species in the pore space. For example, CO2 locates preferentially in the side pockets of mordenite and in window regions of DDR, CHA, and LTA zeolites. CO2 also congregates around the extra-framework cations of NaX zeolite. IAST fails to anticipate such selectivity reversals because its development relies on the assumption that the competition between guest species is uniform within the pore space. In the second scenario, selectivity reversals are caused by entropy effects that manifest near pore saturation conditions; the component that is preferentially adsorbed is the one that has the higher packing efficiency. For a homologous series of compounds, the component with the smaller chain length is favored at high pore occupancies. For adsorption of mixtures of alkane isomers within the intersecting channel network of MFI zeolite, the linear isomer is favored on the basis of entropic considerations.

1. Introduction

Microporous adsorbents such as zeolites and metal–organic frameworks (MOFs) offer energy-efficient alternatives to conventional separation technologies such as distillation. There has been a tremendous upsurge in research on the development of MOFs for a variety of applications such as CO2 capture and alkene/alkane, alkyne/alkene, and water/alcohol mixture separations.1−6

A key metric that quantifies the efficacy of a microporous adsorbent for separation of a binary mixture consisting of components 1 and 2 is the adsorption selectivity, Sads, defined by

1. 1

where q1 and q2 are the molar loadings of the components 1 and 2 in the adsorbed phase in equilibrium with a bulk fluid phase mixture with partial fugacities f1 and f2.

The adsorption selectivity is dictated by dispersion and electrostatic interactions between the guest molecules and the framework material.7−10 The London–van der Waals dispersion interaction energies are largely dictated by the polarizabilities of the guest molecules and surfaces atoms of the adsorbent materials. The electrostatic interactions arise from charges (which create electric fields) of the extra-framework cations in zeolites or unsaturated metal atoms in MOFs. Because of the large quadrupole moment of CO2, cation-exchanged zeolites such as NaX, LTA-4A, and LTA-5A offer high selectivities in CO2-capture applications. Generally speaking, high values of Sads are desirable because this leads to sharper separations in fixed bed adsorption devices.11,12

A number of experimental investigations report the phenomena of reversal of selectivity values with changes in the operating conditions.13−17Figure 1a plots data on the selectivity for adsorption of CO2/hydrocarbon mixtures in a variety of cation-exchanged zeolites: LTA-5A,18 NaX,19 H-MOR,20 and ZSM-5;21 in all of these experiments, the total pressure and temperature are held constant and the bulk gas phase composition of CO2, y1, is varied. In each case, the values of Sads experience a selectivity reversal phenomenon at a certain value of y1.

Figure 1.

Figure 1

Open in a new tab

(a) Experimental data for the adsorption selectivity Sads for CO2–C2H4/LTA-5A,18 CO2–C3H8/NaX,19 CO2–C3H8/H-MOR,20 and CO2–C3H8/ZSM-5.21 (b) Experimental data on the adsorption selectivity Sads for adsorption of toluene/1-propanol mixture adsorption in de-aluminated Y zeolite,22 and p-xylene/1-butanol mixtures in high silica Y zeolite,23 plotted as a function of the mole fraction of the aromatic in the vapor phase. All calculation details and input data are provided in the Supporting Information accompanying this publication.

For adsorption of mixtures of toluene/1-propanol22 and p-xylene/1-butanol23 mixtures in Y zeolite, selectivity reversals occur as the mole fraction of the aromatic compound in the bulk vapor phase increases, see Figure 1b.

For adsorption of mixtures of homologous series of compounds, such as alkanes, alkenes, and 1-alcohols, the polarizability of the molecules increases with increasing chain length. Consequently, in the Henry regime of adsorption, the binding strengths of the molecules increase with increasing chain length.24−26 Remy et al.27 report data on transient breakthroughs of ethanol/1-propanol and ethanol/1-hexanol liquid mixtures in a fixed bed adsorber packed with SAPO-34 that has the same structural topology as CHA zeolite. The experiments show that the component that is eluted first from the adsorber is the alcohol with the longer chain length, implying that the selectivity is in favor of the shorter 1-alcohol.

Two major questions arise from the foregoing set of experimental observations: (i) what is the root cause of the selectivity reversals in the experiments mentioned in foregoing paragraphs? and (ii) what are the selectivity reversals amenable to quantitative description using ideal adsorbed solution theory (IAST) of Myers and Prausnitz28 that is widely used to estimate mixture adsorption characteristics? The primary objective of this article is to elucidate the phenomena of selectivity reversals. Toward this end, configurational-bias Monte Carlo (CBMC) simulations on mixture adsorption equilibrium were performed using the simulation methodology that is firmly established in the literature.29−33 The force field information is taken from García-Sánchez et al.34 and Dubbeldam et al.35

The Supporting Information accompanying this publication provides (a) detailed structural information on all of the zeolites and MOFs analyzed and discussed in the article, (b) details of the IAST and real adsorbed solution theory (RAST) methodologies and calculations for mixture adsorption equilibria, and (c) input data on unary isotherm fits for the wide variety of guest/host combinations examined in this article.

2. Results and Discussion

2.1. Thermodynamics of Mixture Adsorption

The appropriate starting point for setting up the theory for mixture adsorption is the Gibbs adsorption equation, written in the differential form7,13,14,28

2.1. 2

In eq 2, A represents the surface area per kg of framework, qi is the molar loading, μi is the molar chemical potential, and π is the spreading pressure. The spreading pressure π has the same unit as surface tension, that is, N m–1. At phase equilibrium, equating the component chemical potentials, μi, in the adsorbed phase equals that in the bulk fluid phase mixture. If the partial fugacities in the bulk fluid phase are fi

2.1. 3

In the Myers–Prausnitz development of IAST,28 the partial fugacities in the bulk fluid mixture are related to the mole fractions xi in the adsorbed phase mixture

2.1. 4

by the analogue of Raoult’s law for vapor–liquid equilibrium, that is,

2.1. 5

where Pi0 is the pressure for sorption of every component i, which yields the same spreading pressure π for each of the pure components, as that for the mixture

2.1. 6

In eq 6, qi0(f) is the pure component adsorption isotherm. Because the surface area A is not directly accessible from experimental data, the adsorption potential πA/RT, with the units mol kg–1, serves as a convenient and practical proxy for the spreading pressure π.

For multicomponent mixture adsorption, each of the equalities on the right hand side of eq 6 must be satisfied. These constraints may be solved using a suitable equation solver to yield the set of values of P10, P2, P30, ..., Pn, all of which satisfy eq 6. The corresponding values of the integrals using these as upper limits of integration must yield the same value of πA/RT for each component; this ensures that the obtained solution is the correct one.

The adsorbed phase mole fractions xi are then determined from

2.1. 7

In view of eq 7, we rewrite eq 1 as the ratio of the sorption pressures

2.1. 8

Applying the restriction specified by eq 6, it follows that Sads is uniquely determined by the adsorption potential πA/RT.

2.2. CO2/C3H8 Mixture Adsorption in Mordenite

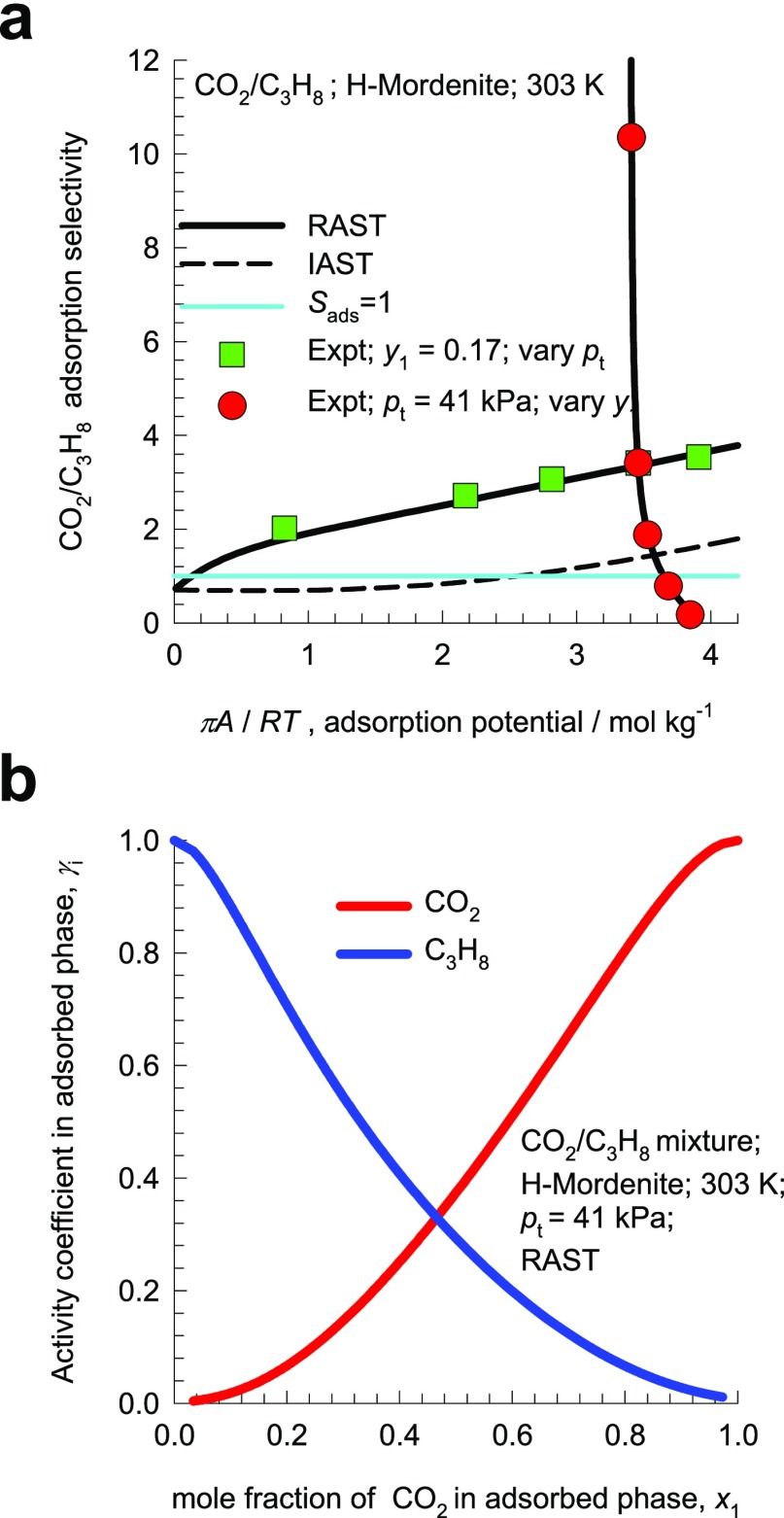
Talu and Zwiebel20 report two sets of experimental data for adsorption of CO2/C3H8 mixtures in H-MOR (=H-mordenite) at 303 K; this zeolite consists of 12-ring (7.0 Å × 6.5 Å;) 1D channels connected to 8-ring (5.7 Å; × 2.6 Å;) pockets, see pore landscapes and structural details in Figures S11 and S12. Figure 2a presents the data on the adsorption selectivity Sads for CO2(1)/C3H8(2) mixture adsorption as a function of the mole fraction of CO2 in the bulk gas phase, y1; the total gas phase pressure pt = p1 + p2 = 41 kPa. For y1 < 0.6, the selectivity is in favor of CO2(1), whereas for bulk gas phase mole fractions y1 > 0.6, Sads < 1 and the mixture adsorption is C3H8-selective. The experimental data clearly show the phenomenon of azeotropy, Sads = 1, at y1 ≈ 0.6. IAST estimations using the unary isotherm data (indicated by the dashed lines) do not anticipate selectivity reversal phenomena, and the adsorption is anticipated to be CO2-selective over the entire composition range.

Figure 2.

Figure 2

Open in a new tab

(a) Experimental data20 for the adsorption selectivity Sads for CO2(1)/C3H8(2) mixture adsorption in H-MOR as a function of the mole fraction of CO2 in the bulk gas phase, y1; the total gas phase pressure pt = p1 + p2 = 41 kPa. (b) Adsorption selectivity Sads for 17/83 CO2(1)/C3H8(2) mixture adsorption in which the total gas phase pressure pt = p1 + p2 is varied. Also shown in (a,b) are IAST (dashed lines) and RAST calculations (continuous solid lines). All calculation details and input data are provided in the Supporting Information accompanying this publication.

Figure 2b presents the data on Sads for 17/83 CO2(1)/C3H8(2) mixture adsorption in H-MOR in which the total gas phase pressure pt = p1 + p2 is varied. Over the entire range of total pressures, the experimental values of Sads > 1, and no selectivity reversal is experienced. It is interesting to note that the IAST estimations of Sads (indicated by dashed lines) for pt = p1 + p2 < 18 kPa show C3H8-selective adsorption; for pt = p1 + p2 > 18 kPa, the selectivity reverses in favor of CO2.

The two sets of experimental data for the adsorption selectivity in Figure 2a,b are replotted in Figure 3a as a function of πA/RT. The IAST calculations expect both sets of experimental data to coincide and follow the dashed lines. Contrary to this expectation, the experimental data follow two different trajectories on varying πA/RT.

Figure 3.

Figure 3

Open in a new tab

(a) Two sets of experimental data20 for the selectivity Sads for adsorption of CO2(1)/C3H8(2) mixtures in H-MOR, plotted as a function of the adsorption potential πA/RT. (b) RAST calculations of the activity coefficients in the adsorbed phase as a function of the mole fraction of CO2 in the adsorbed phase, x1.

To account for nonideality effects in mixture adsorption in H-MOR zeolite, we need to introduce activity coefficients γi in eq 5

2.2. 9

The implementation of the activity coefficients is termed as the RAST. With the introduction of activity coefficients, the expression for the adsorption selectivity for binary mixtures is

2.2. 10

Because γi is dependent on the adsorbed phase mole fractions, eq 10 implies that Sads is not uniquely determined by πA/RT. For quantification of nonidealities, the excess Gibbs free energy for binary mixture adsorption is modeled as follows20,28,36,37

2.2. 11

The Wilson model for activity coefficients is given for binary mixtures by

2.2. 12

In eq 12, Λ11 = 1; Λ22 = 1 and C is a constant with the unit kg mol–1. The choice of Λ12 = Λ21 = 1 in eq 12 yields unity values for the activity coefficients and reduces to IAST. The Wilson model has the right limiting behaviors: γi → 1; xi → 1. The introduction of 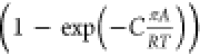Inline graphic imparts the correct limiting behaviors γi → 1; πA/RT → 0 for the activity coefficients in the Henry regime, pt → 0; πA/RT → 0. 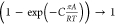As pore saturation conditions are approached, this correction factor tends to unity Inline graphic.13 The experimental data for CO2/C3H8 mixture adsorption in H-MOR are well-matched by the choice of the Wilson parameters Λ12 = 4.2; Λ21 = 6.5; C = 1 mol kg–1, as evidenced by the RAST calculations represented by the solid black lines in Figure 3a. The RAST calculations of the activity coefficients are plotted in Figure 3b as a function of the mole fraction of CO2 in the adsorbed phase. It is evident that both components are nearly equally influenced by thermodynamic nonidealities. The Wilson model must be viewed as providing a thermodynamically consistent approach to quantify the departures from the IAST estimates.

Having established the need to introduce activity coefficients in the description of mixture adsorption, the next step is to gain insights into the origins of nonidealities by resorting to CBMC simulations. Figure 4a presents CBMC simulation data for CO2(1)/C3H8(2) mixture adsorption in MOR zeolite at 300 K and total fugacity ft = 40 kPa, as a function of the mole fraction of CO2 in the bulk gas phase, y1. For y1 < 0.2, Sads > 1 and the selectivity is in favor of CO2. The CBMC simulation data, that are in remarkably good agreement with the experimental data plotted in Figure 2a, show that the adsorption selectivity Sads is increasingly lowered below unity, that is, in favor of the alkane, with increasing proportion of CO2 in the bulk gas phase. Computational snapshots are shown in Figure 4b. CO2 gets preferentially ensconced in the side pockets, but when the side pockets are fully occupied, the CO2 can also locate in the 12-ring 1D channels. The C3H8 molecules are unable to occupy the side pockets and are exclusively located in the 12-ring 1D channels.

Figure 4.

Figure 4

Open in a new tab

(a) CBMC simulations (symbols) of the component loadings for CO2(1)/C3H8(2) mixture adsorption in all-silica MOR zeolite at 300 K and total fugacity ft = 40 kPa, as a function of the mole fraction of CO2 in the bulk gas phase, y1. (b) Computational snapshots (for partial fugacities f1 = f2 = 20 kPa) showing the location of the guest molecules within the pore landscape. All calculation details and input data are provided in the Supporting Information accompanying this publication.

IAST anticipates Sads to be virtually independent of y1. The conventional IAST calculation assumes that C3H8 molecules compete with all of the CO2, making no allowance for segregation. Because of segregation effects, the competition faced by C3H8 molecules within the 12-ring channels, where C3H8 exclusively resides, is smaller than that in the entire pore space. IAST anticipates a stiffer competition between CO2 and C3H8 as it assumes a uniform distribution of composition; consequently, Sads is overestimated to a significant extent.

2.3. Segregated Mixture Adsorption in Cage-Type Zeolites

For separation of CO2 from gaseous mixtures, cage-type zeolites such as DDR, CHA, LTA, and ERI are of practical interest.4,30,38−40 These materials consist of cages separated by 8-ring windows in the 3.3–4.5 Å; range. For adsorption of CO2/CH4 mixtures, published CBMC simulations41 show that the window regions of cage-type zeolites have a significantly higher proportion of CO2 than within the cages. For all four zeolites, CO2 has the highest probability, about 30–40%, of locating in the window regions.41 As illustration, Figures 5a and 6a present computational snapshots for the location of CO2 and CH4 in DDR and CHA zeolites.

Figure 5.

Figure 5

Open in a new tab

(a) Computational snapshot showing the location of CO2 and CH4 within the cage/window structure of DDR zeolite. (b) CBMC simulations of the adsorption selectivity, Sads, for CO2(1)/CH4(2) mixture adsorption in all-silica DDR zeolite at 300 K. Two sets of simulation data are presented: (i) the bulk gas phase mole fractions are maintained at y1 = y2 = 0.5, and the mixture fugacity ft = f1 + f2 is varied, and (ii) the total bulk gas mixture fugacity is held constant, ft = f1 + f2 = 106 Pa, and the mole fraction of CO2 in the bulk gas mixture, y1, is varied. Both data sets are plotted as a function of the adsorption potential πA/RT. The dashed lines are the IAST calculations, and the continuous solid lines are the RAST calculations. All calculation details and input data are provided in the Supporting Information accompanying this publication.

Figure 6.

Figure 6

Open in a new tab

(a) Computational snapshot showing the location of CO2 and CH4 within the cage/window structure of CHA zeolite. (b) CBMC simulations of the adsorption selectivity, Sads, for CO2(1)/CH4(2) mixture adsorption in all-silica CHA zeolite at 300 K. Two sets of simulation data are presented: (i) the bulk gas phase mole fractions are maintained at y1 = y2 = 0.5, and the mixture fugacity ft = f1 + f2 is varied, and (ii) the total bulk gas mixture fugacity is held constant, ft = f1 + f2 = 106 Pa, and the mole fraction of CO2 in the bulk gas mixture, y1, is varied. Both data sets are plotted as a function of the adsorption potential πA/RT. The dashed lines are the IAST calculations; all calculation details and input data are provided in the Supporting Information accompanying this publication.

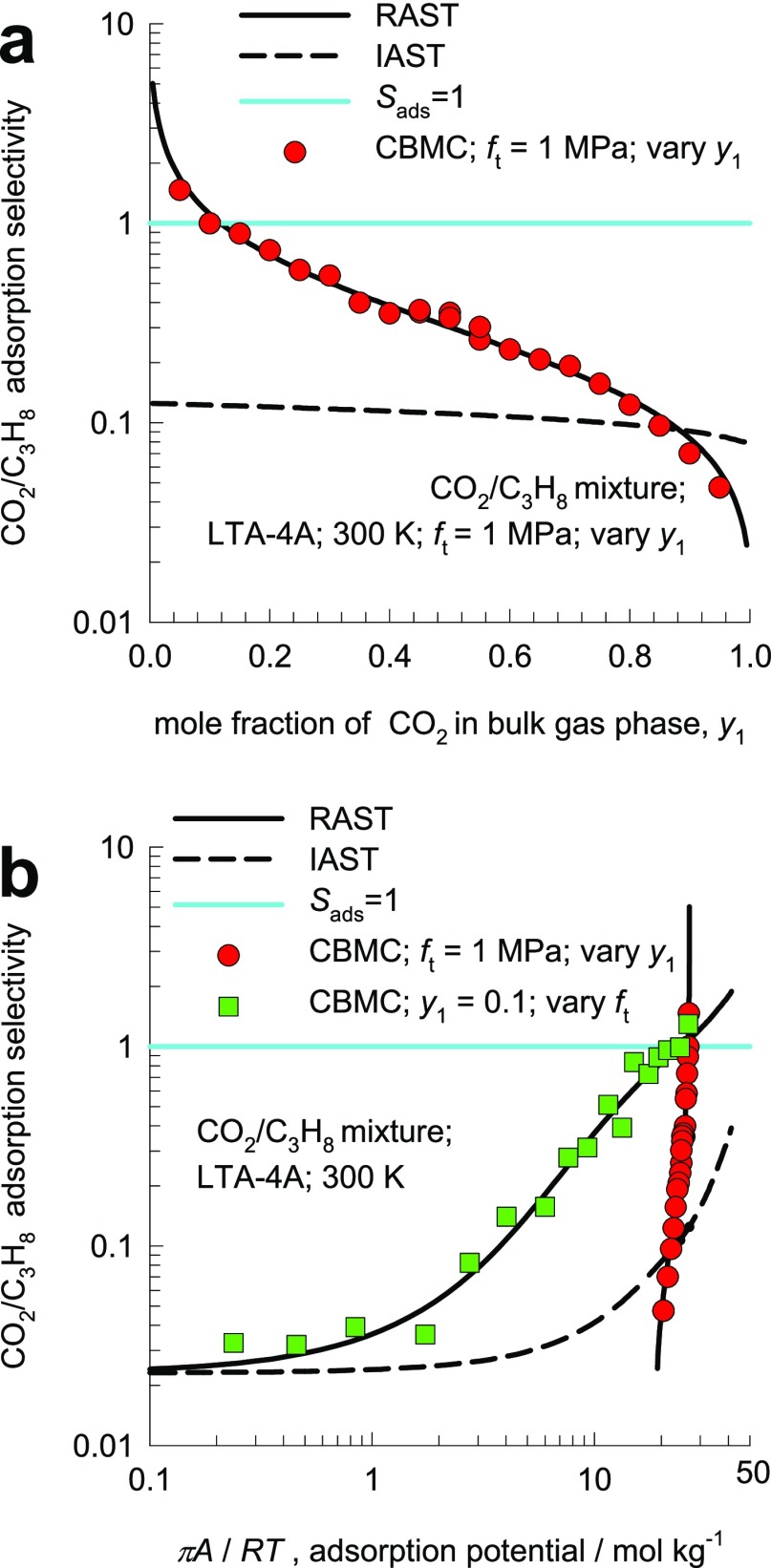
Figure 5b shows CBMC simulation data of the adsorption selectivity, Sads, for CO2(1)/CH4(2) mixtures in DDR zeolite that consists of cages of 277.8 Å;3 volume, separated by 3.65 Å; × 4.37 Å; 8-ring windows. Two sets of simulation data are presented: (i) the bulk gas phase mole fractions are maintained at y1 = y2 = 0.5, and mixture fugacity ft = f1 + f2 is varied, and (ii) the total bulk gas mixture fugacity is held constant, ft = f1 + f2 = 106 Pa, and the mole fraction of CO2 in the bulk gas mixture, y1, is varied. Both CBMC data sets on Sads are plotted as a function of the adsorption potential πA/RT. The IAST calculations (shown by the dashed line) anticipate that Sads is uniquely determined by πA/RT, whereas the CBMC data show that the two data sets for Sads do not coincide when plotted against πA/RT. Furthermore, IAST significantly overestimates the Sads values at πA/RT > 5 mol kg–1. The IAST calculation assumes that CH4 molecules compete with all of the CO2, making no allowance for segregation. Because of segregation effects, the competition faced by CH4 molecules within the cages, where they almost exclusively reside, is smaller than that in the entire pore space. The two sets of CBMC data are adequately captured by the choice of the Wilson parameters Λ12 = 0.81; Λ21 = 3; C = 0.34 mol kg–1, as evidenced by the RAST calculations indicated by the continuous solid lines in Figure 5b.

The corresponding CBMC simulation data for CO2/CH4 mixture adsorption in CHA zeolite that consists of cages of volume 316 Å;3 separated by 3.8 Å; × 4.2 Å; 8-ring windows are presented in Figure 6b. Because of segregation effects, IAST overestimates the Sads values for πA/RT > 0.5 mol kg–1.

Figure 7 shows snapshots of the location of CO2 and C3H8 molecules within the pore topology of LTA-4A zeolite that consists of cages of 743 Å;3 volume separated by 4.11 Å; × 4.47 Å; 8-ring windows. We note that the CO2 is almost exclusively located at the windows or near the window entrance regions. Because of configurational restraints, C3H8 can only be located at the cage interiors. Consequently, the competition between the adsorption of CO2 and C3H8 is less severe than assumed in the homogenous distribution that is inherent in the IAST prescription.

Figure 7.

Figure 7

Open in a new tab

Computational snapshot showing the location of CO2 and C3H8 within the cages of LTA-4A zeolite at 300 K and total fugacity ft = 1 MPa. The component partial fugacities are f1 = 0.8 MPa and f2 = 0.2 MPa.

Two different campaigns were carried out for CBMC simulations of CO2(1)/C3H8(2) mixture adsorption in LTA-4A zeolite at 300 K. The CBMC simulations for CO2(1)/C3H8(2) mixture adsorption in LTA-4A zeolite at ft = 1 MPa and varying mole fractions of CO2(1) in the bulk gas phase, y1, are shown in Figure 8a. For y1 < 0.1, Sads > 1, and the selectivity is in favor of CO2. The CBMC simulations show that the adsorption selectivity Sads is increasingly lowered below unity, that is, in favor of the alkane, with increasing proportion of CO2 in the bulk gas phase; IAST anticipates Sads to be virtually independent of y1. The observed selectivity reversal phenomena, arising out of inhomogeneous distribution of guest molecules in the cage/window structure of LTA, are entirely analogous to those observed for CO2/C2H4 mixture adsorption in LTA-5A reported by Basmadjian and Hsieh18 and plotted in Figure 1. Such selectivity reversals are also experienced in the transient breakthrough experiments reported by van Zandvoort et al.15,16

Figure 8.

Figure 8

Open in a new tab

(a) CBMC simulations (symbols) of the component loadings for CO2(1)/C3H8(2) mixture adsorption in LTA-4A zeolite at 300 K, plotted as a function of the mole fraction of CO2 in the bulk gas mixture, y1; the total mixture fugacity, ft = f1 + f2 = 106 Pa. (b) CBMC simulations (symbols) for CO2(1)/C3H8(2) mixture adsorption in LTA-4A zeolite at 300 K, plotted as a function of πA/RT. The dashed lines are the IAST calculations, and the continuous solid lines are the RAST calculations. All calculation details and input data are provided in the Supporting Information accompanying this publication.

The CBMC simulations for CO2/C3H8 mixture adsorption in LTA-4A zeolite in which the mole fraction of CO2 in the bulk gas phase is held constant, y1 = 0.1, and the bulk gas phase fugacity ft = f1 + f2 was varied are shown by the square symbols in Figure 8b. For πA/RT < 25 mol kg–1, the selectivity is in favor of C3H8; with increasing values of the adsorption potential πA/RT > 25 mol kg–1, the adsorption selectivity Sads switches in favor of CO2 because of strong Coulombic interactions with the extra-framework cations Na+. IAST does not anticipate this selectivity reversal in favor of CO2. The CBMC simulations can be matched by quantification of thermodynamic nonidealities using the Wilson parameters Λ12 = 1; Λ21 = 5.65; C = 0.1 mol kg–1: see RAST calculations indicated by continuous solid lines in Figure 8a,b.

The experimental data of Costa et al.19 for CO2/C3H8 mixture adsorption in NaX zeolite, which consists of cages of 786 Å;3 volume separated by 7.3 Å; 12-ring windows, demonstrate the selectivity reversal in favor of the saturated alkane at high mole fractions of CO2 in the bulk gas mixture: see Figure 1. Most likely, this selectivity reversal is caused by the inhomogeneous distribution of guest molecules, with CO2 congregating around the cations: see the computational snapshot in Figure 9. We note that the bottom cage contains only CO2 and there is no C3H8 present in that cage, underscoring the fact that the distribution of adsorbates is not uniform within the pore space. The competition faced by C3H8 in the entire pore space is effectively reduced, and this engenders a reversal in selectivity in favor of the alkane; for detailed analyses, see Figures S39–S42, S49, and S50 of the Supporting Information.

Figure 9.

Figure 9

Open in a new tab

Computational snapshots showing the location of CO2 and C3H8 within the cages of NaX zeolite at 300 K and partial fugacities are f1 = f2 = 0.5 MPa.

The experimentally observed selectivity reversals for aromatic/1-alcohol mixtures in Y zeolite (cf. Figure 1b) are most likely caused because of congregation of the aromatic molecules around the extra-framework cations; for detailed analyses, see Figures S53 and S54 of the Supporting Information.

2.4. Selectivity Reversals Caused by Molecular Packing Effects

We now attempt to gain insights into the selectivity reversals for ethanol/1-propanol and ethanol/1-hexanol mixture adsorption in SAPO-34 as evidenced in the liquid phase breakthrough experiments of Remy et al.27 For operations with feed mixtures in the liquid phase, the pore space of the adsorbent is expected to be saturated with guest molecules.24 Computational snapshots of the conformations of ethanol, 1-propanol, and 1-hexanol under pore saturation conditions in CHA (structural analogue of SAPO-34) are shown in Figure 10a. Because of the limited capacity of the cages of CHA, each having a volume of 316 Å;3, the maximum number of molecules that can be accommodated is, respectively, 4, 2, and 1 per cage. Near pore saturation conditions, entropic considerations favor the adsorption of the shorter ethanol because it is easier to fill in the few available vacant spaces.25,26

Figure 10.

Figure 10

Open in a new tab

(a) Snapshots showing the conformations of ethanol, 1-propanol, and 1-hexanol in CHA under saturation conditions in CHA zeolite. (b,c) Selectivity of adsorption of (b) ethanol/1-propanol and (c) ethanol/1-hexanol mixtures in CHA zeolite, Sads, plotted as a function of the adsorption potential πA/RT. The dashed lines represent the IAST calculations; all calculation details and input data are provided in the Supporting Information accompanying this publication.

The entropic preference for ethanol near saturation loadings is confirmed by the CBMC simulations for ethanol/1-propanol mixtures, as shown in Figure 10b. For adsorption potentials πA/RT < 30 mol kg–1, the adsorption selectivity is strongly in favor of the longer 1-propanol molecule that has the higher binding strength. However, πA/RT > 30 mol kg–1, corresponding to conditions in which the bulk fluid is in the liquid phase, we find a reversal of selectivity in favor of ethanol. This selectivity reversal is entropy-based and is ascribable to the significantly higher saturation capacity of ethanol (4 molecules per cage) in comparison with that of 1-propanol (2 molecules per cage). The IAST calculations, shown by the dashed lines, are in good agreement with the CBMC data.

The corresponding CBMC data for selectivity for ethanol/1-hexanol mixture adsorption are shown in Figure 10c. Selectivity reversal in favor of ethanol is realized for πA/RT > 20 mol kg–1. Although IAST also anticipates selectivity reversal, the agreement of IAST estimates of Sads is quantitatively poor. The reason for the poor IAST estimates is that only one molecule of 1-hexanol can occupy a single cage; consequently, within a single cage, there is no competitive adsorption with ethanol because of the inhomogeneous nature of the distribution of guest molecules in the pore space.

Analogous entropy-driven selectivity reversals are also found for methanol/ethanol mixture adsorption in CuBTC:42,43 see Figures S30 and S31.

CBMC simulations for adsorption of n-butane (nC4)/iso-butane (iC4) and n-hexane (nC6)/2-methylpentane (2MP) mixtures in MFI zeolite show that as saturation conditions are approached, the selectivity values are increasingly in favor of the linear isomers: see Figure 11a,b. The linear isomers pack more efficiently because these can be located along both the straight channels and zigzag channels. The branched isomers can only occupy the channel intersections because these demand more leg room: see computational snapshots in Figure 11c,d. Although IAST predicts the correct trends in the Sads versus πA/RT characteristics, the quantitative agreement with CBMC data is not very good because of the segregated nature of mixture adsorption with the intersecting network of channels.

Figure 11.

Figure 11

Open in a new tab

(a,b) CBMC simulations44 for the selectivity of adsorption of (a) nC4/iC4 and (b) nC6/2MP mixtures in MFI zeolite at 300 K, Sads, plotted as a function of the adsorption potential πA/RT. The dashed lines are the IAST calculations; all calculation details and input data are provided in the Supporting Information accompanying this publication. (c,d) Computational snapshots showing the location of guest molecules for adsorption of (c) nC4/iC4 and (d) nC6/2MP mixtures in MFI zeolite.

The experimental data of Titze et al.44 provide quantitative confirmation of the CBMC data and IAST estimates in Figure 11.

3. Conclusions

CBMC simulations have been used to gain insights into the phenomena of selectivity reversals for mixture adsorption in zeolites, as witnessed in a number of experimental investigations. Two fundamental different scenarios of selectivity reversals have been identified.

  • (1)

    In the first scenario, selectivity reversals are caused by inhomogeneous distribution of adsorbates because of preferential location and siting of a guest species in the pore space. For example, CO2 locates preferentially in the side pockets of MOR and in window regions of DDR, CHA, and LTA zeolites. CO2 also congregates around the extra-framework cations of NaX zeolite. IAST fails to anticipate such selectivity reversals because its development relies on the assumption that the competition between guest species is uniform within the pore space. For quantitative modeling, the use of the RAST with the introduction of activity coefficients becomes necessary.

  • (2)

    In the second scenario, selectivity reversals are caused by entropy effects that manifest near pore saturation conditions; the component that is preferentially adsorbed is the one that has the higher packing efficiency. For a homologous series of molecules, the component with the smaller chain length is favored at high values of the adsorption potential πA/RT. For adsorption of mixtures of alkane isomers within the intersecting channel network of MFI zeolite, the linear isomer is favored on the basis of entropic considerations. IAST is able to anticipate entropy-driven selectivity reversals but the IAST estimates of selectivities are not of adequate accuracy if there is nonuniform distribution of guest molecules in the pore space.

Acknowledgments

The authors acknowledge the constructive remarks and suggestions of the reviewers.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c01051.

  • Detailed structural information on all of the zeolites and MOFs analyzed and discussed in the article; details of the IAST and RAST methodologies and calculations for mixture adsorption equilibria, selectivities, and activity coefficients; and input data on unary isotherm fits for the wide variety of guest/host combinations examined in this article (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c01051_si_001.pdf (15.3MB, pdf)

References

  1. Cui X.; Chen K.; Xing H.; Yang Q.; Krishna R.; Bao Z.; Wu H.; Zhou W.; Dong X.; Han Y.; Li B.; Ren Q.; Zaworotko M. J.; Chen B. Pore Chemistry and Size Control in Hybrid Porous Materials for Acetylene Capture from Ethylene. Science 2016, 353, 141–144. 10.1126/science.aaf2458. [DOI] [PubMed] [Google Scholar]
  2. Cadiau A.; Adil K.; Bhatt P. M.; Belmabkhout Y.; Eddaoudi M. A Metal-Organic Framework–Based Splitter for Separating Propylene from Propane. Science 2016, 353, 137–140. 10.1126/science.aaf6323. [DOI] [PubMed] [Google Scholar]
  3. Bloch E. D.; Queen W. L.; Krishna R.; Zadrozny J. M.; Brown C. M.; Long J. R. Hydrocarbon Separations in a Metal-Organic Framework with Open Iron(II) Coordination Sites. Science 2012, 335, 1606–1610. 10.1126/science.1217544. [DOI] [PubMed] [Google Scholar]
  4. Krishna R. Methodologies for Screening and Selection of Crystalline Microporous Materials in Mixture Separations. Sep. Purif. Technol. 2018, 194, 281–300. 10.1016/j.seppur.2017.11.056. [DOI] [Google Scholar]
  5. Krishna R. Methodologies for Evaluation of Metal-Organic Frameworks in Separation Applications. RSC Adv. 2015, 5, 52269–52295. 10.1039/c5ra07830j. [DOI] [Google Scholar]
  6. Xiang S.; He Y.; Zhang Z.; Wu H.; Zhou W.; Krishna R.; Chen B. Microporous Metal-Organic Framework with Potential for Carbon Dioxide Capture at Ambient Conditions. Nat. Commun. 2012, 3, 954. 10.1038/ncomms1956. [DOI] [PubMed] [Google Scholar]
  7. Ruthven D. M.Principles of Adsorption and Adsorption Processes; John Wiley: New York, 1984. [Google Scholar]
  8. Yang R. T.Gas Separation by Adsorption Processes; Butterworth: Boston, 1987. [Google Scholar]
  9. Yang R. T.Adsorbents: Fundamentals and Applications; John Wiley & Sons, Inc.: Hoboken, New Jersey, 2003. [Google Scholar]
  10. Krishna R. Highlighting the Influence of Thermodynamic Coupling on Kinetic Separations with Microporous Crystalline Materials. ACS Omega 2019, 4, 3409–3419. 10.1021/acsomega.8b03480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Krishna R. Screening Metal-Organic Frameworks for Mixture Separations in Fixed-Bed Adsorbers using a Combined Selectivity/Capacity Metric. RSC Adv. 2017, 7, 35724–35737. 10.1039/C7RA07363A. [DOI] [Google Scholar]
  12. Ruthven D. M.; Farooq S.; Knaebel K. S.. Pressure Swing Adsorption; VCH Publishers: New York, 1994. [Google Scholar]
  13. Krishna R.; van Baten J. M.; Baur R. Highlighting the Origins and Consequences of Thermodynamic Nonidealities in Mixture Separations using Zeolites and Metal-Organic Frameworks. Microporous Mesoporous Mater. 2018, 267, 274–292. 10.1016/j.micromeso.2018.03.013. [DOI] [Google Scholar]
  14. Krishna R.; Van Baten J. M. Investigating the Non-idealities in Adsorption of CO2-bearing Mixtures in Cation-exchanged Zeolites. Sep. Purif. Technol. 2018, 206, 208–217. 10.1016/j.seppur.2018.06.009. [DOI] [Google Scholar]
  15. van Zandvoort I.; Ras E.-J.; Graaf R. d.; Krishna R. Using Transient Breakthrough Experiments for Screening of Adsorbents for Separation of C2H4/CO2 Mixtures. Sep. Purif. Technol. 2020, 241, 116706. 10.1016/j.seppur.2020.116706. [DOI] [Google Scholar]
  16. van Zandvoort I.; van der Waal J. K.; Ras E.-J.; de Graaf R.; Krishna R. Highlighting non-idealities in C2H4/CO2 mixture adsorption in 5A zeolite. Sep. Purif. Technol. 2019, 227, 115730. 10.1016/j.seppur.2019.115730. [DOI] [Google Scholar]
  17. Ritter J. A.; Bhadra S. J.; Ebner A. D. On the Use of the Dual-Process Langmuir Model for Correlating Unary Equilibria and Predicting Mixed-Gas Adsorption Equilibria. Langmuir 2011, 27, 4700–4712. 10.1021/la104965w. [DOI] [PubMed] [Google Scholar]
  18. Basmadjian D.; Hsieh S. T. Isothermal Column Sorption of Ethylene-Carbon Dioxide Mixtures with Azeotropic Behaviour. Can. J. Chem. Eng. 1980, 58, 185–189. 10.1002/cjce.5450580208. [DOI] [Google Scholar]
  19. Costa E.; Calleja G.; Jimenez A.; Pau J. Adsorption Equilibrium of Ethylene, Propane, Propylene, Carbon Dioxide, and Their Mixtures in 13X Zeolite. J. Chem. Eng. Data 1991, 36, 218–224. 10.1021/je00002a020. [DOI] [Google Scholar]
  20. Talu O.; Zwiebel I. Multicomponent Adsorption Equilibria of Nonideal Mixtures. AIChE J. 1986, 32, 1263–1276. 10.1002/aic.690320805. [DOI] [Google Scholar]
  21. Calleja G.; Pau J.; Calles J. A. Pure and Multicomponent Adsorption Equilibrium of Carbon Dioxide, Ethylene, and Propane on ZSM-5 Zeolites with Different Si/Al Ratios. J. Chem. Eng. Data 1998, 43, 994–1003. 10.1021/je9702100. [DOI] [Google Scholar]
  22. Sakuth M.; Meyer J.; Gmehling J. Vapor Phase Adsorption Equilibria of Toluene + 1-Propanol Mixtures on Y-Zeolites with Different Silicon to Aluminum Ratios. J. Chem. Eng. Data 1995, 40, 895–899. 10.1021/je00020a035. [DOI] [Google Scholar]
  23. Takeuchi Y.; lwamoto H.; Miyata N.; Asano S.; Harada M. Adsorption of l-butanol and p-xylene vapor with high silica zeolites. Sep. Technol. 1995, 5, 23–34. 10.1016/0956-9618(94)00101-w. [DOI] [Google Scholar]
  24. Krishna R. Separating Mixtures by Exploiting Molecular Packing Effects in Microporous Materials. Phys. Chem. Chem. Phys. 2015, 17, 39–59. 10.1039/c4cp03939d. [DOI] [PubMed] [Google Scholar]
  25. Krishna R. Elucidation and Characterization of Entropy Effects in Mixture Separations with Micro-porous Crystalline Adsorbents. Sep. Purif. Technol. 2019, 215, 227–241. 10.1016/j.seppur.2019.01.014. [DOI] [Google Scholar]
  26. Krishna R.; van Baten J. M. Commensurate-Incommensurate Adsorption and Diffusion in Ordered Crystalline Microporous Materials. Phys. Chem. Chem. Phys. 2017, 19, 20320–20337. 10.1039/c7cp04101b. [DOI] [PubMed] [Google Scholar]
  27. Remy T.; Cousin Saint Remi J.; Singh R.; Webley P. A.; Baron G. V.; Denayer J. F. M. Adsorption and Separation of C1-C8 Alcohols on SAPO-34. J. Phys. Chem. C 2011, 115, 8117–8125. 10.1021/jp111615e. [DOI] [Google Scholar]
  28. Myers A. L.; Prausnitz J. M. Thermodynamics of Mixed Gas Adsorption. AIChE J. 1965, 11, 121–127. 10.1002/aic.690110125. [DOI] [Google Scholar]
  29. Krishna R.; van Baten J. M. A comparison of the CO2 capture characteristics of zeolites and metal-organic frameworks. Sep. Purif. Technol. 2012, 87, 120–126. 10.1016/j.seppur.2011.11.031. [DOI] [Google Scholar]
  30. Krishna R.; van Baten J. M. In silico screening of metal-organic frameworks in separation applications. Phys. Chem. Chem. Phys. 2011, 13, 10593–10616. 10.1039/c1cp20282k. [DOI] [PubMed] [Google Scholar]
  31. Frenkel D.; Smit B.. Understanding Molecular Simulations: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, 2002. [Google Scholar]
  32. Smit B.; Krishna R. Molecular simulations in zeolitic process design. Chem. Eng. Sci. 2003, 58, 557–568. 10.1016/s0009-2509(02)00580-8. [DOI] [Google Scholar]
  33. Vlugt T. J. H.; Krishna R.; Smit B. Molecular Simulations of Adsorption Isotherms for Linear and Branched Alkanes and Their Mixtures in Silicalite. J. Phys. Chem. B 1999, 103, 1102–1118. 10.1021/jp982736c. [DOI] [Google Scholar]
  34. García-Sánchez A.; Ania C. O.; Parra J. B.; Dubbeldam D.; Vlugt T. J. H.; Krishna R.; Calero S. Development of a Transferable Force Field for Carbon Dioxide Adsorption in Zeolites. J. Phys. Chem. C 2009, 113, 8814–8820. 10.1021/jp810871f. [DOI] [Google Scholar]
  35. Dubbeldam D.; Calero S.; Vlugt T. J. H.; Krishna R.; Maesen T. L. M.; Smit B. United Atom Forcefield for Alkanes in Nanoporous Materials. J. Phys. Chem. B 2004, 108, 12301–12313. 10.1021/jp0376727. [DOI] [Google Scholar]
  36. Talu O.; Myers A. L. Rigorous Thermodynamic Treatment of Gas-Adsorption. AIChE J. 1988, 34, 1887–1893. 10.1002/aic.690341114. [DOI] [Google Scholar]
  37. Siperstein F. R.; Myers A. L. Mixed-Gas Adsorption. AIChE J. 2001, 47, 1141–1159. 10.1002/aic.690470520. [DOI] [Google Scholar]
  38. Krishna R.; van Baten J. M. In Silico Screening of Zeolite Membranes for CO2 Capture. J. Membr. Sci. 2010, 360, 323–333. 10.1016/j.memsci.2010.05.032. [DOI] [Google Scholar]
  39. Krishna R.; van Baten J. M. A molecular dynamics investigation of the diffusion characteristics of cavity-type zeolites with 8-ring windows. Microporous Mesoporous Mater. 2011, 137, 83–91. 10.1016/j.micromeso.2010.08.026. [DOI] [Google Scholar]
  40. Krishna R.; van Baten J. M. Using Molecular Dynamics Simulations for Elucidation of Molecular Traffic in Ordered Crystalline Microporous Materials. Microporous Mesoporous Mater. 2018, 258, 151–169. 10.1016/j.micromeso.2017.09.014. [DOI] [Google Scholar]
  41. Krishna R.; van Baten J. M. Segregation effects in adsorption of CO2 containing mixtures and their consequences for separation selectivities in cage-type zeolites. Sep. Purif. Technol. 2008, 61, 414–423. 10.1016/j.seppur.2007.12.003. [DOI] [Google Scholar]
  42. Gutiérrez-Sevillano J. J.; Calero S.; Krishna R. Selective Adsorption of Water from Mixtures with 1-Alcohols by Exploitation of Molecular Packing Effects in CuBTC. J. Phys. Chem. C 2015, 119, 3658–3666. 10.1021/jp512853w. [DOI] [Google Scholar]
  43. Gutiérrez-Sevillano J. J.; Calero S.; Krishna R. Separation of Benzene from Mixtures with Water, Methanol, Ethanol, and Acetone: Highlighting Hydrogen Bonding and Molecular Clustering Influences in CuBTC. Phys. Chem. Chem. Phys. 2015, 17, 20114–20124. 10.1039/c5cp02726h. [DOI] [PubMed] [Google Scholar]
  44. Titze T.; Chmelik C.; Kärger J.; van Baten J. M.; Krishna R. Uncommon Synergy Between Adsorption and Diffusion of Hexane Isomer Mixtures in MFI Zeolite Induced by Configurational Entropy Effects. J. Phys. Chem. C 2014, 118, 2660–2665. 10.1021/jp412526t. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c01051_si_001.pdf (15.3MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES