Quantification of Morphological Features in Non-Contrast-Enhanced Ultrasound Microvasculature Imaging

Abstract

There are significant differences in microvascular morphological features in diseased tissues, such as cancerous lesions, compared to noncancerous tissue. Quantification of microvessel morphological features could play an important role in disease diagnosis and tumor classification. However, analyzing microvessel morphology in ultrasound Doppler is a challenging task due to limitations associated with this technique. Our main objective is to provide methods for quantifying morphological features of microvasculature obtained by ultrasound Doppler imaging. To achieve this goal, we propose multiple image enhancement techniques and appropriate morphological feature extraction methods that enable quantitative analysis of microvasculature structures. Vessel segments obtained by the skeletonization of the regularized microvasculature images are further analyzed to satisfy other constraints, such as vessel segment diameter and length. Measurements of some morphological metrics, such as tortuosity, depend on preserving large vessel trunks. To address this issue, additional filtering methods are proposed. These methods are tested on in vivo images of breast lesion and thyroid nodule microvasculature, and the outcomes are discussed. Initial results show that using vessel morphological features allows for differentiation between malignant and benign breast lesions (p-value < 0.005) and thyroid nodules (p-value < 0.01). This paper provides a tool for the quantification of microvasculature images obtained by non-contrast ultrasound imaging, which may serve as potential biomarkers for the diagnosis of some diseases.

I. Introduction

Microvasculature architecture is known to be associated with tissue state and pathology. Various circumstances and diseases can alter such architecture at distinct size scales. Studies have demonstrated that the development of malignant tumors correlates with changes in the vascularity of healthy tissue [1]. Altered mechanical properties in malignant tumors are known to lead to the growth of more permeable and tortuous vessels [2], [3]. Vessel tortuosity has been found to reveal information about some diseases [4], [5]. Moreover, microvascular parameters, such as vessel diameter, segment length, and the number of branching points, correlate very well with tumor aggressiveness and angiogenesis [6].

Several preclinical studies are available to derive quantitative information from microvasculature images obtained by contrast agent ultrasound for diagnostic purposes and treatment monitoring [7]–[12]. Other studies on perfusion imaging [13] and molecular imaging [14], [15] provide some quantitative information of the vessels. Conventionally, these techniques endeavor to screen either the measure of blood flow inside a tissue volume by testing the increase in ultrasound signal from the blood pool contrast agents, or the presence of molecular markers of an ailment through imaging of the targeted contrast agent held in the blood flow. While a few studies have recently demonstrated the capacity of quantifying the architecture of the blood vessels in thyroid nodules and breast lesions, the use of contrast agents remains a barrier for extensive investigations [16]–[18]. On the other hand, analyzing vascular networks using ultrasound imaging devoid of contrast agent is a new framework made possible only recently, thanks to new clutter removal processing methods [19]–[21]. For example, Cohen et al. [22] demonstrated that vascular structures provide useful information for neuro-navigation in brain imaging. This framework exploits the coherence of the tissue data provided by fast plane wave imaging of a large field of view to enable detailed imaging of the microvasculature structure by integrating longer data ensembles.

Blood vessel segmentation and analysis techniques have been studied exhaustively in other imaging modalities, such as optical imaging of the retina [23], [24]. Retinal vessel segmentation algorithms are a principal component of automatic retinal infection screening frameworks. Different vessel analysis methods used in retinal images acquired by a fundus camera have been summarized in detail in the literature [23], [24]. Yousefi et al. introduced a hybrid Hessian/intensity-based method for segmentation and quantification of microvessel shape and diameter imaged by functional Optical coherence tomography (OCT) in vivo [25]. Moreover, methods for automatic or semi-automatic segmentation and quantification of blood vessel structure in OCT imaging have been introduced [26]. Application of the brain vessel segmentation has also been described in magnetic resonance imaging (MRI) [27]. A vessel analysis tool was reported for the morphometric measurement and representation of vessels in computed tomography (CT) and MRI data sets [28]. Methods of blood vessel segmentation algorithms have been reviewed widely in the literature [29]. The isotropic minimal path-based framework has been proposed for the segmentation and quantification of the vascular networks [30].

In this paper, we focus on the challenges of vessel quantification for 2-dimensional (D) label-free ultrasound Doppler imaging and propose solutions to overcome such challenges. We evaluate the performance of proposed solutions on the quantification of in vivo breast and thyroid data. As noted, vessel quantification has been widely used in a broad range of imaging modalities; however, adaptation for the analysis of the microvasculature images obtained by non-contrast ultrasound requires careful treatment. This imaging modality, while enabling a versatile mechanism for acquiring small vessel images, introduces some challenges. The main problem stems from the 2-D interpretation of 3-D vascular structures. The work in retinal vessel analysis, while performed in 2-D, only considers surface vascularity for which a 2-D model is well-justified. Considering vessels are distributed in a volume, 2-D cross-sectional ultrasound imaging may present erroneous branching and vessel crossings that can lead to incorrect interpretation of vessel segments. Morphological parameters such as vessel density and diameter are not significantly affected by this phenomenon. However, parameters such as tortuosity, branching points, and the number of vessel segments will be affected and the results may become inaccurate. Another difficulty arises from imaging vessels in the cross-sectional orientation, where vessels may appear as small segments with incorrect information regarding vascular tree segments. The main contribution of this paper is to address these issues using either vessel filtering or morphological operations such that the most dominant vascular features can be obtained from 2-D non-contrast ultrasound imaging. Finally, results of quantitative morphological parameters are tested on two in vivo patient populations, including benign and malignant breast lesions and thyroid nodules. Initial results show that the morphometrics extracted from ultrafast ultrasound imaging has the potential to help the diagnosis of cancerous breast lesions and thyroid nodules.

This paper is organized into four sections. Section II introduces the materials and methods, which includes 6 subsections to highlight A) the study sample and histopathological outcomes, B) image formation, C) morphological filtering/skeletonization, D) vessel quantification, and E) experimental setup. The results are presented in Section III. In Section IV, we conclude with a discussion, point out the limitations of the study, future research directions, and open problems related to the quantitative assessment of microvasculature morphological features obtained from non-contrast ultrasound images.

II. Material And Method

To demonstrate the potential clinical application of contrast-free quantitative ultrasound microvasculature imaging, we performed the technique on a group of patients with suspicious breast lesions or thyroid nodules. Before quantifying vessel morphological features from ultrasound microvasculature images, one must perform multiple preprocessing steps. The first step is image formation, which reconstructs the microvasculature image from a sequence of plane wave ultrasound images [20]. Second, vessel filtering is used to enhance the structure of vessels and provide adequate background separation for segmentation. Morphological filtering, vessel segmentation, and skeletonization occur last. The main contribution of this paper is in the use of spectral filtering, vessel segmentation, filtering and vessel quantification.

A. Study Sample And Histopathological Outcomes

Under an institutional review board-approved protocol, 15 patients with breast lesions (8 malignant and 7 benign) and 15 patients with thyroid nodules (9 malignant and 6 benign) participated in this study. Written, informed consent was obtained. The lesions from the breast and thyroid patients were manually segmented using the B-mode images obtained from the first frame in the imaging sequence. All patients underwent biopsy following the ultrasound examination, and pathology results were used as the final diagnosis.

B. Image Formation

Figure 1 demonstrates the sequence of processing steps of the microvasculature image formation, morphological operations, and vessel quantifications algorithm with an example of the output image in each processing step. Processing begins with the storage of ultrasound plane-wave data in the in-phase quadrature (IQ) format. This data can be characterized by the complex-valued variable s (x, z, t), where x and z denote the lateral and axial dimensions, respectively, and t denotes the ultrasound imaging slow time. This signal can be described as the sum of three components as follows:

$$s(x,z,t)=c(x,z,t)+b(x,z,t)+n(x,z,t),$$ (1)

where c (x, z, t), b (x, z, t) and n (x, z, t) represent the clutter signal, the blood signal, and the additive thermal noise, respectively. The spatial and temporal characteristics of these three components are different. n (x, z, t) The signal s (x, z, t) corresponds to tensor $\mathbf{S}\in {\mathbb{R}}^{n_x\times n_z\times n_t}$, where n_x and n_z are the number of spatial samples along the x-direction and z-direction, respectively, and n_t is the number of samples over time. The data tensor S is reshaped to form a Casorati matrix by transforming tensor S into a 2-D spatiotemporal matrix ${\mathbf{S}}_C\in {\mathbb{R}}^{(n_x\times n_z)\times n_t}$ to provide information from each frame in one column of the matrix. This transformation has also been proposed in other imaging modalities like MRI and CT [31]–[34].

Fig. 1.

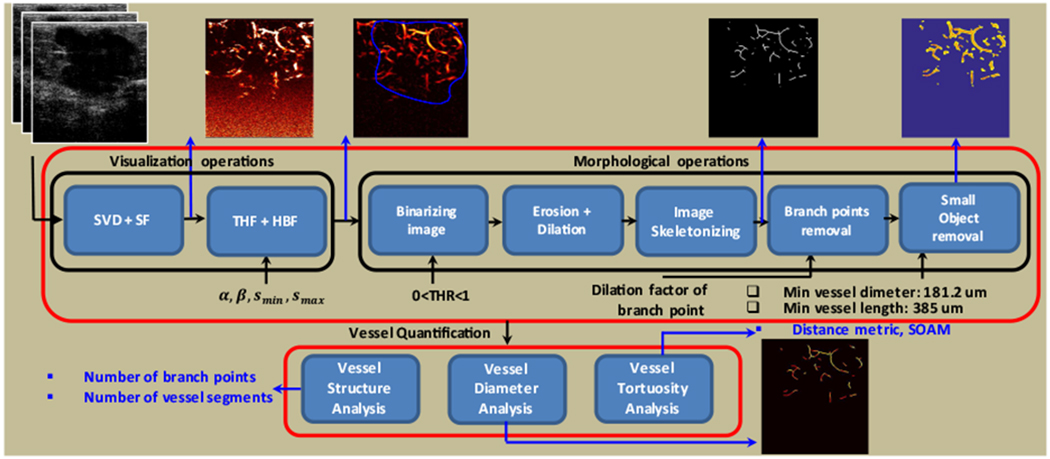
Block diagram of the microvasculature analysis system, including visualization and morphological operations and vessel quantification. SVD, singular value decomposition, SF, spectral filtering, THF, top hat filtering, HBF, hessian based filtering.

Using singular value decomposition (SVD) of S_C we have [35]

$${\mathbf{S}}_c={\mathbf{U}}^{\ast }\mathbf{V}$$ (2)

where $\Delta \in {\mathbb{R}}^{(n_x\times n_z)\times n_t}$ is a non-square diagonal matrix, $\mathbf{U}\in {\mathbb{R}}^{(n_x\times n_z)\times (n_x\times n_z)}$ and $\mathbf{V}\in {\mathbb{R}}^{n_t\times n_t}$ are orthonormal matrices, and indicates conjugate transpose. Columns of U and V matrices correspond to the spatial and temporal singular vectors of S_C. Based on the definition of SVD, the matrix S_C can be decomposed into the sum of rank-one matrices A_i = U_i ⊗ V_i as follows:

$${\mathbf{S}}_C={\sum }_i{\lambda }_i{\mathbf{A}}_i={\sum }_i{\lambda }_i{U}_i\otimes V_i$$ (3)

where U_i and V_i are i^th columns of U and V, respectively, λ_i is i^th ordered singular values of S_C, and ⊗ denotes outer product operation. Each column of V_i is a temporal signal with length n_t. Each column U_i is a spatial signal with the dimensionality of n_x × n_z. Each vector of U_i describes a 2-D spatial image I_i which is modulated by a temporal signal V_i. Hence, clutter removal based on a low-rank tissue assumption can be formed as

$$s_{\mathit{blood}}(x,z,t)=s(x,z,t)-\sum _{i=1}^n{\lambda }_i{I}_i(x,z)V_i(t).$$ (4)

In this paper, the threshold n is selected based on setting a limit on the slope of the second-order derivative of eigenvalues decay, as described by Bayat, et al. [36]. The filtered signal s_blood (x, z, t) is used to produce the power Doppler image as

$$I(x,z)=\sum _{k=1}^K{\mid s_{\mathit{blood}}(x,z,\mathit{kT})\mid }^2$$ (5)

where T is the sampling time between two successive ultrafast ultrasound frames. To further enhance clutter removal performance, an additional step is proposed before forming the intensity image in (5). This extra step enforces the unilateral Doppler shift which is expected to occur from the unidirectional flow in vessels. Hence, the final image can be formed as

$$I(x,z)=\mid I_p-I_n\mid$$ (6)

where I_p is the energy at the positive frequency side of the spectrum and is defined as

$$I_p={\int }_0^{\infty }{\mid S_{\mathit{blood}}(x,z,f)\mid }^2\mathit{df}$$ (7)

where S_blood (x, z, f) is Fourier transform of s_blood (x, z, t), and I_n is energy at the negative frequency side of the spectrum and is defined as

$$I_n={\int }_{-\infty }^0{\mid S_{\mathit{blood}}(x,z,f)\mid }^2\mathit{df}.$$ (8)

Finally, a top hat filter (THF) is applied on I (x, z) to remove the background noise. A THF is comprised of a background estimation, followed by a background subtraction operation [37]. The resulting output image of THF is denoted by I_T (x, z), which represents the intensity at coordinates (x, z). Details about the application of this filter for background removal of non-contrast ultrasound microvasculature images have been previously described [20].

Hessian-based filtering:

Morphological filtering based on a THF was used to enhance the visibility of the microvasculature image in the presence of strong background signals. Due to background noise, random patterns will also be present at the output of a THF. Hence, vessel enhancement filters are used to penalize background noise and further enhance vessel structure. Enhancement filters based on the analysis of eigenvalues of the Hessian matrix applied on a 2-D image selectively amplify a specific local intensity profile or structure in an image. Hessian-based filters [38] distinguish between different local structures by analyzing the second order intensity derivatives at each point in the image. The analysis is typically performed on a Gaussian scale space of the image to enhance the local structures of various sizes, as previously described [20].

For 2-D images, the following vessel likeliness measure has been proposed [38] and used [20] for vessel filtering of ultrasound microvasculature images:

$${\upsilon }_o(s)=\{\begin{array}{cc}0\hfill & \text{if}{\lambda }_2>0\hfill \\ \exp \left(-\frac{R_B^2}{2{\beta }^2}\right)\left(1-\exp \left(-\frac{s^2}{2{\alpha }^2}\right)\right)\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (9)

where R_B = λ₂/λ₁ is the “blobness” measure in the 2-D image and represents the eccentricity of the second order ellipse, λ₁ and λ₂ are the eigenvalues the Hessian matrix, α and β are filter parameters and s_min ≤ s ≤ s_max is the scaling parameter of the Hessian-based filter with minimum and maximum size scales of s_min and s_max, respectively. To be consistent, we kept these parameters constant at α = 1 and β = 0.6 across all examples. The effect of these parameters were extensively discussed in [38], and re-discussed and fine-tuned for current application in [20].

For consistency in notation, the output image of the Hessian-based filter is denoted by I_H (x, z).

C. Morphological Filtering, Vessel Segmentation And Skeletonization

Each step of the morphological operations described in this subsection is listed in Table 1. In morphological operations, the size of each pixel in an output image is correlated with the respective pixel in the input image, along with its neighbors. By selecting the size and shape of the areas in the neighborhood, we can develop a morphological operation that is sensitive to the particular shapes in the input image.

TABLE I:

Morphological Operations

begin
	Converting the grayscale image to the binary image (C-I)
	Erosion following by dilation (C-II)
	Removing small holes (C-III)
	Finding the skeleton image (C-IV)
	Removing isolated pixels
	Removing spur pixels
	Finding branch points
	Dilating branch points
	Removing branch points
	Labeling connected components
	Removing small objects
	• Removing vessels with length less than a threshold
	• Removing vessels with diameter less than a threshold
end

Morphological filtering and vessel segmentation include the following steps: converting the microvasculature image (output of Hessian filter) to a binary image, removing small noise-like objects through an erosion and dilation operation, removing small holes, filling small holes with a dilation and erosion operation, finding the image skeleton, cleaning the skeleton image, removing spur pixels, labeling connected components, finding branch points, dilating branch points, removing branch points, and removing small objects. In the remainder of this section, each step will be briefly described. After these steps, the output image includes the vessel segments. Those segments are analyzed in the vessel quantification module to estimate the desired quantitative parameters of the vessels. The following preprocessing steps are included: a) Converting grayscale to binary: The input image to the morphological operation module, I_H (x, z), is converted to a binary image I_B (x, z) using the global threshold (THR). b) Erosion followed by dilation: We use erosion followed by dilation to remove some noise-like small objects in the image after amplitude thresholding [39]. c) Removing small holes: The spectral subtraction in equation 6, while providing additional clutter suppression, may induce erroneous intensity nulling in the image at isolated points along the vessels with horizontal orientation due to symmetric Doppler spectra. A morphological “hole-filling’ step is added to avoid erroneous splitting of the vessels at these points; this step sets a pixel to 1 if five or more pixels in its 3-by-3 neighborhood are 1s; otherwise, it sets the pixel to 0. After this operation, some small holes with larger sizes remain. To remove the remaining small holes in the vessels, we use the operation of a dilation followed by erosion with a structure element size of 4 pixels (0.85 λ). d) Finding the skeleton image: To estimate the centerline of vessel structure, the next step in the morphological operations on binary images is removing pixels so that an object without holes shrinks to a line, and an object with holes shrinks to a connected ring halfway between each hole and the outer boundary. Finding the skeleton image is based on a thinning algorithm [40].

D. Vessel Quantification

Vessel segments (e.g., overlaid on the binary vessel image in Figure 1) are used for vessel quantification. The processing steps of the vessel quantification are shown in Figure 1. The quantification parameters include number of vessel segments, vessel density, number of branch points, vessel diameter, and vessel tortuosity. Two different tortuosity metrics are considered: the distance metric (DM) and the sum of the angle metric (SOAM). We use the Moore-Neighbor tracing algorithm modified by Jacob’s criteria [41] to track vessels. Each vessel is defined by a “location vector” whose elements represent the pixels within the vessel. The location vector for the vessel j is defined as P_j := [p_1j, .…, p_Njj], where p_i,j := [x_ij, z_ij]^T is the point i in the vessel j, and N_j is the length (number of points) of vessel j.

1). Distance Metric’ (DM):

The DM of the vessel j is the most common parameter used to measure vascular tortuosity in 2-D [23], [24]. The DM of a vessel is defined as the ratio between the actual path length of a meandering curve and the linear distance between endpoints. The DM for vessel j is denoted by τ in the following equation:

$${\tau }_j=\sum _{k=2}^N\mid {\mathbf{p}}_{k,j}-{\mathbf{p}}_{k-1,j}\mid /\mid {\mathbf{p}}_{N,j}-{\mathbf{p}}_{1,j}\mid .$$ (10)

2). Sum Of Angle Metric (SOAM):

The displacement vectors between points p_k−1,j, p_k,j on vessel j are defined by

$${\mathbf{d}}_{k,j}={\mathbf{p}}_{k,j}-{\mathbf{p}}_{k-1,j},$$ (11)

where k ∈ {2, … , N_j − 2}, and N_j is the length of the vessel in pixels. The in-plane angle at the point p_k,j is given by

$$I_{\mathit{kj}}≔{\cos }^{-1}\left(\left({\mathbf{d}}_{k,j}∕\mid {\mathbf{d}}_{k,j}\mid \right)\cdot \left({\mathbf{d}}_{k+1,j}∕\mid {\mathbf{d}}_{k+1,j}\mid \right)\right).$$ (12)

Since we are performing 2-D imaging, we only have the in-plane angle. Therefore, the total angle at point p_kj and vessel j is given by

$$C{P}_{\mathit{kj}}=\mid {\mathit{I}}_{\mathit{kj}}\mid .$$ (13)

The SOAM calculates the total tortuosity of the vessel j and is defined as in [4].

$${\mathit{SOAM}}_j=\sum _{k=2}^{N_j-2}\mathit{C}{\mathit{P}}_{\mathit{kj}}/\sum _{k=2}^N\mid {\mathbf{p}}_{\mathit{kj}}-{\mathbf{p}}_{k-1j}\mid .$$ (14)

3). Estimating Diameter:

To acquire localized vessel diameter, we first invert the binary image. Next, we obtain the Euclidean distance in the inverted image between pixels corresponding to vessel segments and the nearest pixel corresponding to the background of the image. For all pixels corresponding to vessels, the distance to the most adjacent non-vessel pixel is dedicated to that pixel. The set of points inside of the vessel region and the background region is denoted by V and B, respectively. For any point of (x, z) ∈ V, the Euclidian distance between (x, z) and all points (x_b, z_b) ∈ B are calculated, and the minimum distance value is obtained as follows:

$$d(x,z)=\underset{(x_b,z_b)}{\min }\sqrt{{(x-x_b)}^2+{(z-z_b)}^2}\mathrm{s}.\mathrm{t}.(x_b,z_b)\in \mathit{B}.$$ (15)

The vessel image is then skeletonized using a thinning algorithm [40] so that the distances along the centerlines can be calculated. The i^th point at centerline of the vessel j is denoted by (x_ij, z_ij. Vessel diameter is D (x_ij, z_ij = 2d (x_ij, z_ij). For each vessel segment, the average diameter of the vessel segment over points related to that vessel is reported as vessel segment diameter D_j.

4). Quantification Of Vessel Trunks:

In 2-D imaging of 3-D vascular structures, some vessels are only partially visible in the imaging plane. Moreover, it is possible that vessels may appear to cross each other when they do not cross in 3-D space. This crossing occurs because of the slice thickness of an ultrasound image. The vessels seem to cross if both are within the slice thickness of B-mode and they are not parallel. Most often, one vessel goes out of the imaging plane, making it look like a small branch. One of the consequences of the branching for vessel quantification is that the main trunk breaks into short vessel segments, which may adversely impact the quantification of the morphological features of the trunk. To resolve this problem, we propose two strategies and compare the results: (1) Hessian-based filtering with different minimum size scales, and (2) morphological operations to recover large trunk segments after branching of the small vessel segments. In the first method, the minimum size scale of the Hessian-based filtering, i.e. S_min, controls the formation of small vessels in the image. In the second method, we create a disk-shaped structuring element with radius r μm. Morphological operations using disk approximation run much faster when the structuring element uses other approximations, such as octagon or diamond approximations. We perform erosion followed by dilation using the same structuring element for both of the operations (i.e., disk-shaped structuring element). We define the erosion/dilation (ED) factor as

$$\mathit{ED}≔r$$ (16)

to remove small objects and analyze trunks inside the lesion. Using this method, vessel structures with a size less than r are removed from the image. In dilation, only structures larger than r that remain in the image are dilated and converted to their original size. Therefore, we expect only vessel trunks to appear in the final image. In the tortuosity analysis, our goal is to analyze the vessels that are fully located in the imaging plane. Therefore, by removing small vessel segments connected to main vessel trunks, it is possible to analyze the main vessel trunk.

5). Contribution Of Small Vessel Segments In Tortuosity Analysis:

The microvasculature image is constructed from a sequence of 2-D ultrasound plane wave images in which some vessels are only partially visible in the imaging plane. This, in turn, results in observing small vessel segments in the image. The residual noise, when passed through the Hessian-based filtering, might also result in structures that are perceived as short vessel segments. Hence, an additional step is required to remove unwanted erroneous or partial vessel segments; this is accomplished by enforcing a minimum vessel segment length constraint as part of the quantification tool. This operation alone can considerably change some morphometric values (e.g., DM representing vessel tortuosity), as small vessel segments may skew the distribution of such morphometric values with no added information.

E. Experimental Setup

To assess the performance of the proposed methods for morphological analysis of the microvasculature images obtained by contrast-agent-free ultrasound, an Alpinion Ecube12-R ultrasound machine (ALPINION Medical Systems, Seoul, Korea) and a linear array transducer L3-12H (ALPINION Medical Systems, Seoul, Korea) were used. For each patient, 3 seconds of high frame rate, 5-angle compounded plane wave imaging data were acquired at 680 frames per second. Vasculature images were obtained using SVD clutter removal filtering, followed by THF background removal and Hessian-based vessel filtering, as described previously in the literature [20]. The THF was employed using a disk structuring element of size 577.5 μm (15 pixels equal to 3.2 λ, where λ is the wavelength of imaging). Vessel filtering was applied using size scales in the range of 115.5 μm (3 pixels corresponding to 0.65 λ) to 346.5 μm (9 pixels corresponding to 1.9 λ). The ED factor selected was 154 μm (4 pixels corresponding to 0.85 λ) based on the system specifications. Values outside this range are explicitly noted in the results section. The vessel’s filter parameters α and β were set to 1 and 0.6, respectively. Vessel images were further analyzed to acquire morphological parameters using the proposed method. The minimum length for a vessel segment was considered 385 μm; the minimum diameter for a vessel segment was considered to be 181.2 μm (i.e. λ). To convert the grayscale images to binary, a THR of 0.15 was used, which is obtained empirically for removing noise fluctuations.

III. Results

We applied the vessel quantification algorithm on the microvasculature images obtained from vascularized breast lesions and thyroid nodules. Fifteen different breast lesions, 8 malignant and 7 benign, were studied, along with 15 different thyroid nodules, 9 malignant and 6 benign. We derived quantitative parameters of the microvasculature images for these lesions to study and address the challenges of vessel quantification using contrast-agent-free ultrasound imaging.

To examine the effect of small vessel branches connected to the main vessel trunk on vessel quantification, we studied a malignant breast lesion. Figures 2(a) and (b) show the output of the Hessian-based filtering for this lesion with different minimum size scales. As Figure 2(a) shows, there are some branches connected to the main vessel trunk, and these branches cause the main trunk to break down into small vessel segments at branching points. When the minimum size scale of the vessel filter is increased to 462 μm, these branching vessels are not visible, as shown in Figure 2(b). Hence, the multiple scale size processing capabilities of the vessel filter enable removal of the smaller vessel branches so that large trunks can be more accurately analyzed for tortuosity. The apparent disadvantage of increasing the minimum size scale is losing fine vessel segments with diameters smaller than the minimum allowed. Figures 2(c) and (d) show the corresponding binary images of Figures 2(a) and (b), with extracted vessel segments shown in red color overlaid on the binary segmentation of the vasculature skeleton (yellow). Figure 2(e) shows the mean of the DM [mean(τ)] over different vessel segments of the malignant breast lesion as a function of the minimum size scale of the Hessian-based filter (maximum size scale of 500.5 μm).

Fig. 2.

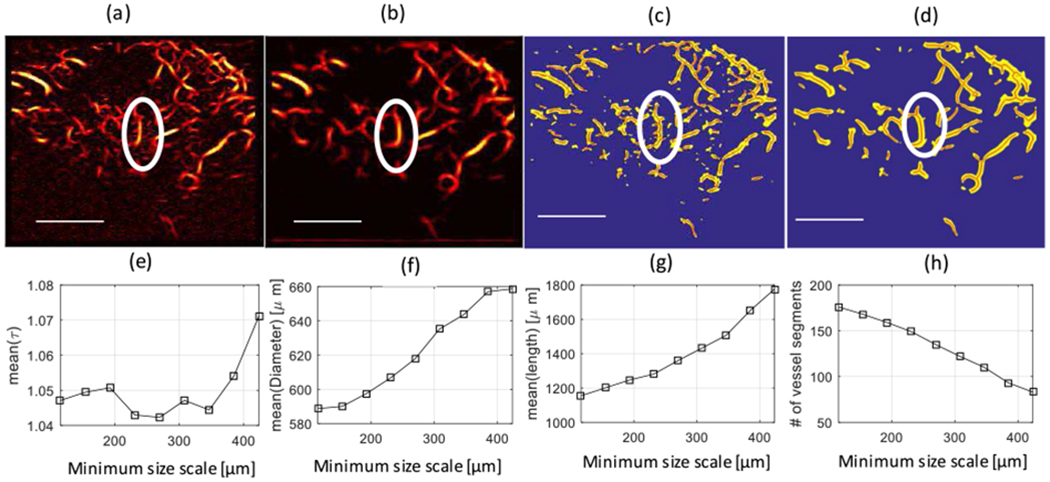
Top Row- Microvasculature images: (a) Microvasculature image of a malignant breast lesion after Hessian-based filtering with a minimum size scale of 115.5 μm (equivalent to 3 pixels), and (b) after Hessian-based filtering with a minimum size scale of 423.5 μm (equal to 12 pixels). Both (a) and (b) have a maximum size scale of 500.5 μm (equivalent to 15 pixels). (c) Binary image of (a) (in yellow) with extracted vessel segments (in red). (d) Binary image of (b) (in yellow) with extracted vessel segments (in red). The white ellipse shows an area to identify branches connected to the main vessel trunk. Lower row-Morphological parameters of the lesion as a function of the minimum size scale: (e) Mean of the distance metric [mean(τ)] over different vessel segments. (f) Mean of the diameter of vessel segments [mean(Diameter)]. (g) Mean of the length of vessel segments. (h) Number of vessel segments.

Note that the mean(τ) increases with an increasing minimum size scale. The advantage of using a higher value for the minimum size scale is that the contribution of small vessel segments, which may partially appear in the imaging plane, on the calculation of the mean(τ) is reduced. Moreover, vessel trunks do not break into smaller vessels, and vessels with larger tortuosity contribute to calculating the mean(τ). Therefore, the mean(τ) does not reduce artificially due to the contribution of partially-appearing vessels in the imaging plane or broken vessel trunks. The mean(τ), though, is not necessarily an increasing function of the minimum size scale, s, in different microvasculature images, since vessel trunks may not be tortuous naturally in all microvasculature images. Figure 2(f) shows the mean diameter of the vessel segments as a function of the minimum size scale of the Hessian-based filter. As expected, the mean diameter of vessel segments is an increasing function of the minimum size scale. Figure 2 (g) shows the mean length of the vessel segment as a function of the minimum size scale. As we expected, due to the removal of the small vessel segments, the mean length of vessel segments is an increasing function of the minimum size scale. Figure 2(h) shows the number of vessel segments as a function of the minimum size scale. It is evident that the number of vessel segments is a decreasing function of the minimum size scale, as fewer branching points are expected to occur when small vessel segments are discarded. Additionally, using higher values for the minimum size scale of vessels for tortuosity analysis provides a more accurate estimation of vessel trunk tortuosity. This effect results from keeping vessel trunks while removing small vessel segments connected to the main vessel trunk, which consequently prevents the breaking of the vessel trunk during the branching procedure.

To illustrate the effect of ED on removing the small vessel segments connected to a trunk and its impact on the DM, we applied different values for this parameter on the microvasculature image post Hessian-based filtering, shown in Figure 2(a). This process removes small vessel segments connected to the vessel trunk, as seen inside the white ellipse in Figure 2(a). Figure 3 shows the corresponding binary image of the microvasculature image of a malignant breast lesion with a minimum size scale of 0.65 λ and maximum size scale of 1.9 λ for different levels of the ED factor with λ = 181.2 μm. As can be observed in Figure 3(a–d, inside the white ellipse), by increasing the ED factor, small vessel branches disappear while large vessel trunks are preserved in the image. Additionally, a very large ED factor can incur significant distortion in the binary image in comparison with the SVD image. Figure 3(e) depicts the mean of the DM [mean(τ)] over different vessel segments of the malignant breast lesion as a function of the ED factor in μm. The mean(τ) is shown to be an increasing function of the ED factor. Figure 3(f) demonstrates the mean diameter of vessel segments [mean(diameter)] as a function of the ED factor. As expected, the mean diameter is an increasing function of the ED. Figure 3(g) shows the mean length of vessel segments [mean(length)] as a function of the ED factor. As expected, by removing small vessel segments, the mean length of vessel segments is an increasing function of the ED factor. Figure 3(h) shows the number of vessel segments as a function of the ED. It is evident that the number of vessel segments is a decreasing function of the ED, mainly due to the removal of the small vessel segments. By comparison, the results seen in Figure 3(e) and Figure 2(e) demonstrate that using ED for removing small vessel segments provides a smoother increment in the DM than changing the minimum size scale of the Hessian filter; however, large ED values (≥ 6 pixels, equivalent to 231 μm) should be avoided to prevent adding unwanted distortion to the image. In the remainder of this paper, vessel filtering was applied using size scales in the range of 115.5 μm (3 pixels) to 346.5 μm (9 pixels). The ED factor 154 μm (4 pixels) was selected based on the system specifications.

Fig. 3.

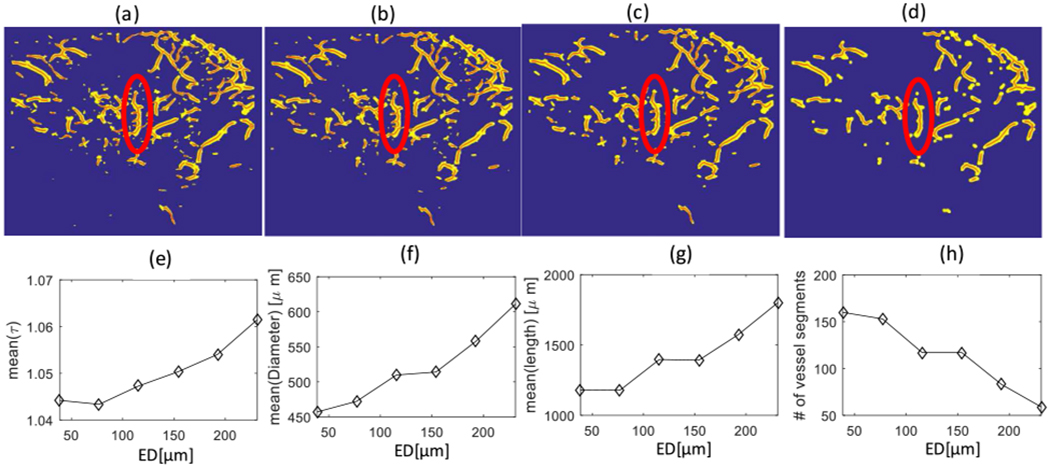
(a) Binary images of a breast malignant lesion for different levels of the erosion-dilation factor: (a) Without the erosion-dilation factor, (b) With a 77 μm ersion-dilation factor, (c) With a 154 μm erosion-dilation factor, and (d) With a 231 μm erosion-dilation factor. (e) Mean of the distance metric [mean(τ)] over different vessel segments (b) Mean of the diameter of vessel segments [mean(Diameter)] (c) Mean of the length of vessel segments, and (d) Number of vessel segments all in terms of erosion-dilation (ED) factor.

To demonstrate the potential diagnostic applications of microvessel quantification in breast lesions, it is helpful to study examples of vessel quantification applied to in vivo data from benign and malignant breast masses with fixed parameters, as described in the experimental setup subsection. Figures 4(a–d) depict the steps from the B-mode image (a) to the skeleton image (d) of the malignant breast lesion. Figures 4(e–h) depict the steps from the B-mode image (a) to the skeleton image (d) of the benign breast lesion. Based on these results, we estimated the quantitative parameters of vessels (e.g., diameter, number of vessel segments, number of branch points, DM, and SOAM) for these two lesions. Figures 4(d) and (h) show the vessel diameter map for malignant and benign breast lesions, respectively, where the heat map represents the local diameter variations across different parts of the vascular structure. The remaining Figure 4 images provide the morphological finding for the same lesions.

Fig. 4.

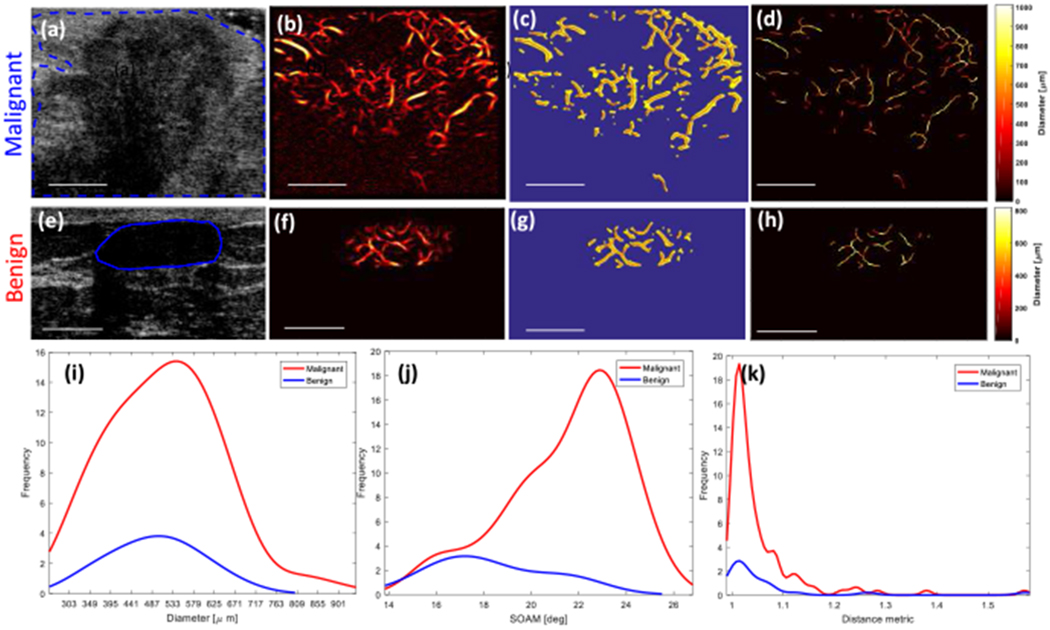
(a-d) and (e-h) show images from malignant and benign breast lesions, respectively. (a) and (e) Ultrasound B-mode images. (b) and (f) Microvasculature images after Hessian-based filtering. (c) and (g) Binary images (yellow) and extracted vessel segments (skeleton of image denoted by red overlay). (d) and (h) Diameter map of the vessels. (i) Histogram of the diameter. (j) Histogram of the distance metric. (k) Histogram of the sum of angle metric (SOAM). White line denotes a scale of 1cm.

Along the same line, to show the potential diagnostic applications of microvessel quantification in thyroid nodules, it is helpful to study examples of vessel quantification applied to in vivo data from benign and malignant thyroid nodules. Figure 5 presents the quantification of the vasculature for the thyroid malignant and benign nodules. Results of the morphological analysis are summarized in Figures 5 (i) to (k). Quantitative assessment of these two breast lesions and two thyroid nodules are summarized in Table 2. In this table, the normalized number of vessel segments (NNV) and branch points (NNB) are calculated by dividing the number of vessel segments (NV) and branch points (NB), respectively, to the geometric area of the lesion in the imaging plane. Of the breast lesions and thyroid nodules, the number of vessel segments and branch points in the benign cases are smaller than those of the malignant cases. Mean and standard deviation vessel diameter values are lower in the benign breast lesion in comparison with those values from the malignant breast. Figures 6(a)–(d) show the box plots for vessel density, number of vessel segments, number of branch points, and mean of distance metric in benign and malignant breast lesions. Malignant lesions had higher vessel density compared to benign cases, and the difference was statistic ally significant (p < 0.01). Benign lesions had a significantly lower number of vessel segments (median 6) compared to malignant (median 31, p<0.05). Malignant cases had a significantly higher number of branch points compared to the benign cases (p<0.01). Also, the mean(τ) was significantly higher in the malignant cases compared to the benign cases (p<0.01). It is noteworthy that if the ED selected is smaller (i.e. ED < 155 μm), the difference in the mean of distance metric between the two groups is no longer significant (i.e. if ED = 77 μm, then p = 0.68).

Fig. 5.

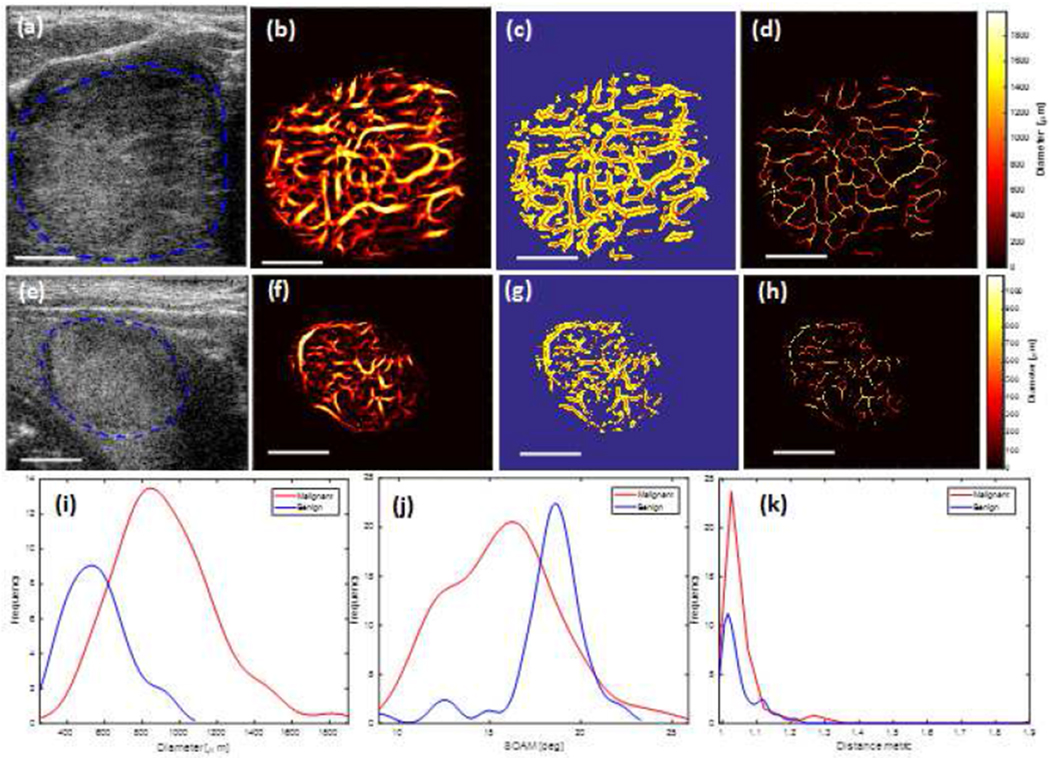
(a-d) and (e-h) show images from malignant and benign thyroid nodules, respectively. (a) and (e) Ultrasound B-mode images. (b) and (f) Microvasculature images after Hesian-based filtering. (c) and (g) Binary images (yellow) and extracted vessel segments (skeleton of image denoted by red overlay). (d) and (h) Diameter map of the vessels. (i) Histogram of the diameter. (j) Histogram of the distance metric. (k) Histogram of sumof angle metric (SOAM). The white line denotes scale of 1cm.

TABLE II:

Estimated quantification parameters for four different lesions.

Vessel	Breast Lesion		Thyroid Nodule
Parameter	Malignant	Benign	Malignant	Benign
Vessel density	0.11	0.18	0.40	0.26
Mean τ	1.05±0.08	1.06±0.12	1.07±0.36	1.06±0.1
Max τ	1.57	1.56	2.9	1.91
Mean SOAM [deg/μm]	21.5±2.5	18.1±2.6	15.7±3.0	18.1±2.4
Max SOAM [deg]	25.8	22.7	24.9	22.6
Mean Diameter [μm]	514±125	494±99	923±273	560±163
Max Diameter [μm]	914	697	1875	957
Mean length [μm]	1391±1065	1504±973	1749±1114	1331±983
Max length [μm]	7182	3897	6637	6887
NV	117	24	178	87
NNV	10.76	18.48	19.69	24.08
NB	59	11	132	64
NNB	5.42	8.47	14.17	17.33

NV: number of vessel segments, NB: Number of branch points, NNV: normalized number of vessel segments, NNB: Normalized number of branch points

Fig. 6.

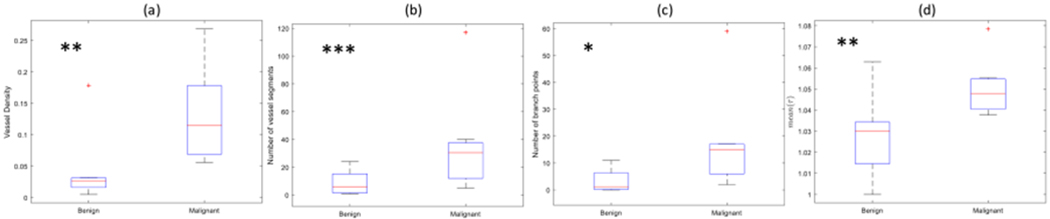
Box plots of the (a) vessel density (b) number of vessel segments (c) number of branch points (d) mean of distance metric (mean(τ)) in the two groups of benign and malignant breast lesions, the malignant lesions had a significantly higher morphological parameter compared to the benign lesions. * p < 0.05; ** p < 0.01, *** p < 0.005.

Figures 7 (a) – (c) show the box plots for the vessel density, number of vessel segments, and number of branch points in thyroid nodules. The vessel density is higher in malignant lesions in comparison to benign lesions, but the difference between the two is not statistically significant (p<0.18). Benign lesions had a significantly lower number of vessel segments (median 31) compared to malignant (median 101, p<0.01). Also, malignant cases had a larger number of branch points compared to the benign lesions (p<0.01).

Fig. 7.

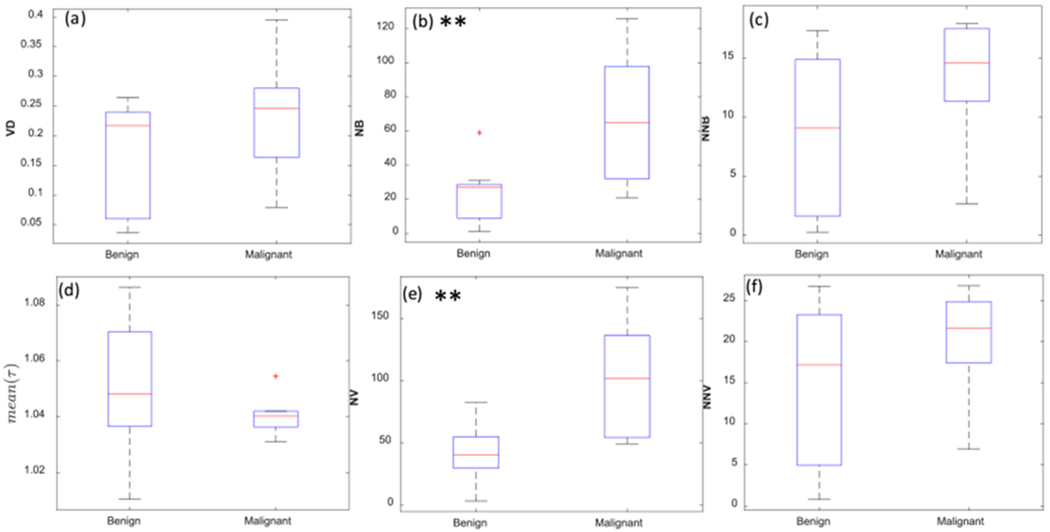
Box plots of the (a) vessel density (VD), (b) number of branch points (NB), (c) normalized number of branch points (NNB), (d) mean of distance metric (mean(τ)), (e) number of vessel segments (NV), and (f) normalized number of vessel segments (NNV) in the two groups of benign and malignant thyroid nodules. Malignant lesions had significantly higher morphological parameters of NB and NV compared to benign lesions. ** p<0.01.

IV. Discussion & Conclusion

Using our proposed vessel quantification algorithm on the microvasculature images obtained from vascularized breast lesions and thyroid nodules, the results are in agreement with other studies, such as contrast-enhanced acoustic angiography technique [42]. Gessner, et al. [7] showed that the morphological features can function as potential biomarkers for the detection of cancerous lesions using acoustic angiography. our findings agree with the results of shelton, indicating that the morphometric analysis of microvessels of malignant tumor using acoustic angiography reveal significant vessel tortuosity irregularities associated with tumor evolution [8].

It has been noted that ultrasound measurement of vessel density using acoustic angiography could evaluate the response to anti-angiogenic therapy in renal cell carcinoma [43]. Although we do not have the complete results, we are investigating these quantitative changes in our ongoing research. In [44] the investigators demonstrated the quantitative assessment of microvasculature using microbubble contrast agents, confirming increased vessel density in tumors compared to controls, which concurs with our results. The quantification of morphological parameters is subjective or impossible in conventional ultrasound without contrast-enhancement, due to poor quality of the final vessel image. in this paper, we introduced a method using ultra-fast ultrasound imaging to enhance tumor microvessels without using a contrast agent, which makes it possible for quantitative analysis of microvessel structures.

In this paper, a set of methods for quantification of the tissue microvasculature obtained by non-contrast ultrasonic microvasculature imaging was presented. The microvasculature map comprises vessel segments resulting from blood activity. We introduced procedures to acquire morphometric parameters with additional morphological constraints to reduce erroneous data. As shown in a photoacoustic imaging study [45], vascular structures were accepted as vessel segments when multiple constraints on the amplitude, diameter, and length of the vessel segments were satisfied. We addressed challenges in acquiring segmentation-ready microvasculature images and showed that a combination of background removal and vessel enhancement filtering allows vessel segmentation and skeletonization, in turn enabling morphological analysis. The quantitative parameters may include tortuosity measures, (DM and SOAM), diameter of vessel segments, length of vessel segments, number of vessel segments, number of branching points, and vessel density. Given the 2-D nature of B-mode ultrasound imaging, accurate interpretation of 3-D microvascular features like branching and vessel crossings can be difficult. While quantitative evaluation of parameters, such as vessel density and diameter, are not significantly affected by this phenomenon, measures of the tortuosity, number of branching points, and number of vessel segments may become inaccurate. In this paper, we introduced several strategies to enable the extraction of several morphological features by adding additional constraints. The most important contribution was to devise methods to preserve large vessel trunks that may be broken into small pieces due to an intersection with out-of-plane vessel segments, namely by removing small size-scales from the vessel filtering and small vessel segments connected to large trunks via morphological operations. Another limitation in ultrasonic microvasculature images is related to small vessel segments which may result from cross-sectional imaging of the vessels. These may appear as small vessel segments with incorrect information regarding the vascular tree segments. We addressed this issue by enforcing vessel segment length and diameter constraints to removed partially visible vessel segments from the quantification analysis. The methods presented in this paper provide a set of tools for quantitative assessment of microvasculature morphological features. These features may be associated with certain diseases or different health conditions. In cancer, for example, malignant tumors have been shown to give rise to tortuous vessels. The initial results in this paper suggest that quantitative morphological parameters allow differentiation of certain lesions, such as benign and malignant breast lesions and thyroid nodules. Therefore, we conclude that the quantitative assessment of microvasculature morphological features obtained from non-contrast ultrasound images results in potential biomarkers for cancer detection and other disease diagnoses.

Biographies

Siavash Ghavami, PhD received his B.S. and M.S. degrees (with Honors) in electrical engineering from the Iran University of Science and Technology, Tehran, Iran, in 2006 and 2009, respectively, and the Ph.D. degree in electrical engineering from the University of Tehran in 2014. From 2012 to 2014, he was a research scholar with the Department of System Biology and Bioinformatics, Laboratory of Adaptive and Regenerative Software Systems, both in Faculty of Computer Science and Electrical Engineering, University of Rostock, Rostock, Germany, and the School of Electrical and Computer Engineering (ECE), University of Toronto, Toronto, ON, Canada. After that, he was a Research Associate with the School of ECE, the University of Tehran in 2015. From 2015 to 2017, he was a Post-Doctoral Associate with the School of ECE, University of Minnesota, Minneapolis, MN, USA, and from 2017 to 2019 he was a Research Fellow at the Department of Radiology, College of Science and Medicine, Mayo Clinic, Rochester, MN, USA. His research interests include wireless communications, molecular communications, neural communications, medical imaging, biomedical engineering, ultrasound, and network information theory.

Mahdi Bayat, PhD Mahdi Bayat received his Ph.D. degree in Electrical Engineering from the University of Minnesota in 2014. He then joined the Mayo Clinic Ultrasound Research Lab as a Post-Doctoral Research Fellow where he became a Research Associate in 2016. He is currently a Research Assistant Professor and an Adjunct Assistant Professor in the Department of Electrical Engineering and Computer Science at Case Western Reserve University. The focus of his research is broadly in signal and data processing for novel imaging methods with applications in diagnostic and therapeutic ultrasound. He is the recipient of 2016 American Institute of Ultrasound in Medicine early investigator recognition award. He has served as the organizer and session chair in a number of national and international technical meetings including 173^rd and 175^th meetings of the Acoustical Society of America in 2017 and 2018 respectively.

Mostafa Fatemi, PhD (S ’M’77–SM’07-F’12-LF’18)) received his Ph.D. degree in Electrical Engineering from Purdue University. He joined Mayo in 1994, and currently, he is a Professor of Biomedical Engineering at the Department of Physiology and Biomedical Engineering of Mayo Clinic College of Medicine in Rochester, MN. At the Mayo Clinic, he is also an active member of the Mayo Clinic Cancer Center and the Center for Clinical and Translational Science. Dr. Fatemi’s current research areas include developing novel ultrasonic methods for cancer imaging, microvasculature imaging, and bladder function evaluation. His research program is continuously supported by multiple major federal grants funded by the National Institute of Health (NIH) and Komen Breast Foundation for the Cure and Department of Defense. He is a Life Fellow of IEEE and holds Fellow membership at these institutions: American Institute of Medical and Biological Engineering (AIMBE), Acoustical Society of America (ASA), and American Institute of Ultrasound in Medicine (AIUM). Dr. Fatemi is recipient of the IEEE-UFFC Distinguished Lecturer award.

Azra Alizad, MD (M’06–SM’15) received her medical degree and fellowship from Tehran University Medical Sciences. Currently, Dr. Alizad is a professor of Radiology, Department of Radiology and Professor of Biomedical Engineering as well as an associate professor of Medicine at the Mayo Clinic College of Medicine in Rochester MN. In addition to her training in Medicine, she has a broad background and expertise in medical ultrasound research. She directs a translational research laboratory, involving development and application of novel ultrasound technologies such as microvasculature imaging, functional ultrasound, elastography, vibro-acoustic imaging for diagnosis of abnormalities in breast, thyroid, prostate, neck masses, and axillary lymph nodes, brain and bone. Dr. Alizad is the principal investigator of multiple major federal grants funded by the National Institute of Health (NIH) and recipient of grant funded by Komen Breast Foundation for the Cure. She is an elected Fellow of American Institute for Medical and Biological Engineering (AIMBE) and American Institute of Ultrasound in Medicine (AIUM). In addition to senior member of Institute of Electrical and Electronics Engineers-UFFC. At the Mayo Clinic, she is also an active member of the Mayo Clinic Cancer Center and the Center for Clinical and Translational Science.