Abstract
The nuclear protein poly (ADP-ribose) polymerase-1 (PARP-1) inhibitors have been proven effective to potentiate both chemotherapeutic agents and radiotherapy. However, a major problem of most current PARP inhibitors is their lack of selectivity for PARP-1 and its closest isoform PARP-2. NMS-P118 is a highly selective PARP inhibitor that binds PARP-1 stronger than PARP-2 and has many advantages such as excellent pharmacokinetic profiles. In this study, molecular dynamics (MD) simulations of NMS-P118 in complex with PARP-1 and PARP-2 were performed to understand the molecular mechanism of its selectivity. Alanine scanning together with free energy calculation using MM/GBSA and interaction entropy reveal key residues that are responsible for the selectivity. Although the conformation of the binding pockets and NMS-P118 are very similar in PARP-1 and PARP-2, most of the hot-spot residues in PARP-1 have stronger binding free energy than the corresponding residues in PARP-2. Detailed analysis of the binding energy shows that the 4′4-difluorocyclohexyl ring on NMS-P118 form favorable hydrophobic interaction with Y889 in PARP-1. In addition, the H862 residue in PARP-1 has stronger binding free energy than H428 in PARP-2, which is due to shorter distance and stronger hydrogen bonds. Moreover, the negatively charged E763 residue in PARP-1 forms stronger electrostatic interaction energy with the positively charged NMS-P118 than the Q332 residue in PARP-2. These results rationalize the selectivity of NMS-P118 and may be useful for designing novel selective PARP inhibitors.
Keywords: PARP, NMS-P118, selectivity, interaction entropy, binding free energy, alanine scanning
Introduction
DNA damage occurs constantly in organisms and may lead to disease if not repaired in time (Hosoya and Miyagawa, 2009). Therefore, cells have evolved sophisticated DNA damage detection and repair systems to maintain normal physiological functions. Blocking the DNA repair pathway has become important in many anti-cancer chemotherapeutic drugs (Staibano et al., 2005) that aim to kill tumor cells by damaging DNA (Jones and Plummer, 2008; Drew and Plummer, 2009).
Poly (ADP-ribose) polymerase (PARP) is an enzyme that locates in the nucleus and is involved in the synthesis of poly ADP-ribose, a multimer of ADP-ribose linked by ribosylation-ribose bonds. Since the discovery of the first poly ADP ribose polymer (PAR) (Sabau et al., 1999; Qiu et al., 2014), at least 17 members of the PARP family that share a homologous catalytic region have been identified (Peralta-Leal et al., 2009). The PARP family has gained much attention because of their involvement in genomic stability, DNA damage response, apoptosis by DNA damage, cell division, transcriptional regulation, and chromatin remodeling (Ame et al., 2004; Schreiber et al., 2006; Hakmé et al., 2008; Anwar et al., 2015). PARP-1 is the first discovered and most thoroughly studied family member with core repair function during base excision repair (BER) (Bennett and Xie, 1988). When DNA single-strand break occurs in the cell, PARP-1 actively participates in the repair process with BER (Lord and Ashworth, 2017; Berger et al., 2018). Inhibition of PARP-1 impairs the DNA damage repair and causes apoptosis of cancer cells, and therefore reduces the intensity of chemotherapy and eventually the damage to human body (Davar et al., 2012; Lupo and Trusolino, 2014). So far, many potent PARP-1 inhibitors such as olaparib (Rottenberg et al., 2008), rucaparib (Tikhe et al., 2004; Thomas et al., 2007), tatzoparib (Timonen et al., 2011; Shen et al., 2013), and veliparib (Donawho et al., 2007) have been discovered. However, an important problem of these inhibitors is the lack of selectivity to PARP-1 and PARP-2 (Papeo et al., 2015).
PARP-2 is the closest homolog of PARP-1 and shares 84% identity and 90% similarity within the PARP signature motif (Krishnakumar and Kraus, 2010), it only contribution 5–10% to the total DNA damage induced PARP activity (Yélamos et al., 2008). Moreover inhibition of PARP-2 would affect important cellular functions such as genome surveillance, spermatogenesis, adipogenesis, and T cell development (Yélamos et al., 2008; Papeo et al., 2015). However, all PARP-1 inhibitors discovered so far also inhibit PARP-2. Therefore, it is important to develop efficient selective PARP-1 inhibitors that do not bind PARP-2.
Recently, a potent, orally available, and highly selective PARP-1 inhibitor named NMS-P118 was discovered and in preclinical studies for cancer therapy (Figure 1A). It has a selective ratio (PARP-2 Kd/PARP-1 Kd) of 154 and mitigates toxicities arising from cross-inhibition of PARP-2 with excellent pharmacokinetic profiles and high oral availability in mouse and rat (Papeo et al., 2015). Quantitative understanding of the different binding modes of NMS-P118 to PARP-1 and PARP-2 is important to design novel selective PARP-1 inhibitors. However, the crystal structure of PARP-1 and PARP-2 show very similar binding pose with a pocket RMSD of 0.80 Å (Figure 1B). Therefore, it is difficult to rationalize the selectivity based on the static crystal structures alone.
Figure 1.

(A) 2D skeleton structure of the compound NMS-P118. The plus sign indicates the positive charge on the N atom in the 1,4-dimethylpiperidin-1-ium group. (B) The binding pocket of NMS-P118 in PARP-1 and PARP-2. The PARP-1 is colored with aquamarine and PARP-2 is colored with light orange.
Computational simulation and accurate calculation of protein-ligand binding free energy is a powerful approach in understanding ligand binding mechanisms from a dynamic perspective (Sun et al., 2013). Although some methods such as free energy perturbation (FEP) (Bash et al., 1987; Rao et al., 1987; Kollman, 1993; Kita et al., 1994; Jorgensen and Thomas, 2008) and thermodynamic integration (TI) (Beveridge and DiCapua, 1989; Zacharias et al., 1994) are rigorous for binding free energy calculation, they are not routinely used due to high computational demand for large protein-ligand system. On the other hand, the Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) is a widely used method because of its efficiency in the absolute free energy calculation (Massova and Kollman, 1999, 2000; Kollman et al., 2000; Moreira et al., 2007; Sun et al., 2014). It is important to note that in MM/GBSA calculation, the entropy contribution can be obtained by the normal mode approach (Nguyen and Case, 1985; Brooks et al., 1995) which is often neglected because of its high computational cost and rough accuracy (Sun et al., 2018). On this regard, a recent method called interaction entropy (IE) (Duan et al., 2016) for calculating entropy contribution has been developed and successfully used in protein-ligand and protein-protein systems (Cong et al., 2017; Yan et al., 2017; Liu et al., 2018).
In general, only a few important residues play a major role in protein-ligand binding (Burgoyne and Jackson, 2006; Barillari et al., 2008; Cheung et al., 2012; Bauman et al., 2016). Therefore, it is crucial to identify these key residues and explore the binding mechanism of protein-ligand to improve the binding potency and selectivity of ligand. To this end, the alanine scanning (AS) approach has been combined with the MM/GBSA_IE method to obtain binding free energies of specific residues (Yan et al., 2017; Qiu et al., 2018). In this approach, a single-trajectory MD simulation is performed starting from the initial complex structure. Alanine scanning is then carried out on individual residues in the trajectory and the enthalpy and entropic component are calculated with the MM/GBSA and IE method, respectively (Gohlke et al., 2000).
In this study, to gain quantitative understanding of the selectivity of NMS-P118, MD simulations were performed on the complex structures of NMS-P118 with PARP-1 and PARP-2. Binding free energy calculation was carried out and showed that NMS-P118 binds PARP-1 3.04 kcal/mol stronger than PARP-2, which agrees with the experimental affinity. Based on our calculations, the hot-spot residues that are responsible for the different binding affinity were identified, and the detailed molecular interactions were analyzed. These results explain the selectivity of NMS-P118 and may provide guidance for future study and design of novel PARP inhibitors.
Method
MD Simulation
The initial structures for MD simulation and alanine scanning were obtained from the Protein Databank (PDB) (Berman et al., 2000). The PDB IDs for PARP-1-NMS-P118 and PARP-2-NMS-P118 were 5A00 and 4ZZY (Papeo et al., 2015). The AMBER ff14SB force field (Maier et al., 2015) and the general AMBER force field (GAFF) (Wang et al., 2004) were used to parameterize the system. The complexes were solvated in truncated octahedron TIP3P (Jorgensen et al., 1983) boxes with a 10.0 Å buffer distance. Chloride and sodium ions were added as counterbalance ions to neutralize the system. To eliminate the bad contacts between solute and solvent water molecule, we used the conjugate gradient minimization followed by the steepest descent method to minimize the energy. During minimization, the solvent water molecules were optimized first by restraining the coordinates of other molecules with a force constant of 500 kcal/(mol *Å2). The restrains were then removed in a subsequent minimization step to optimized the whole system.
The minimized system was slowly heated to 300 K within 300 ps with all solute atoms restrained with a force constant of 10 kcal/(mol *Å2). After equilibration at 300 K, a production simulation was carried out in NPT ensemble for 100 ns, where the Langevin dynamics was used to maintain the temperature and Berendsen barostat was used to control the pressure at 1.0 atm. All bonds involving hydrogen atoms were constrained by the SHAKE (Ryckaert et al., 1977), and the cutoff distance for the non-bonded interactions was 10.0 Å. The simulation time step was 2 fs and the trajectory were recorded every 1 ps. Each complex structure was simulated with three 100 ns replicates. Hydrogen bond was identified with a distance cutoff of 3.5 Å and angle cutoff of 120°.
Computational Alanine Scanning
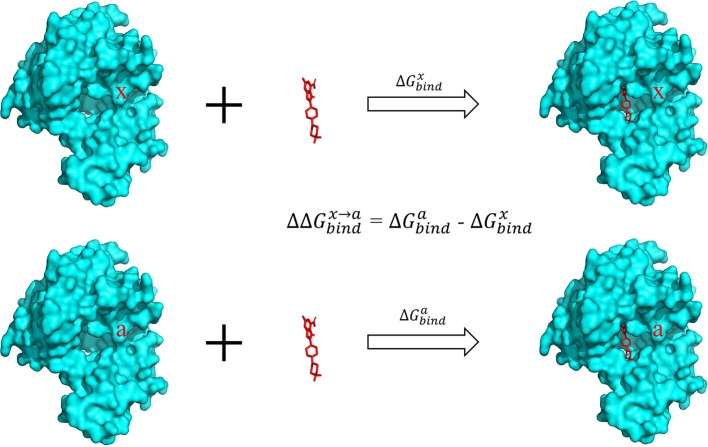
The alanine scanning method was used to calculate the binding free energy. In this approach, a residue was mutated to alanine and the difference of binding free energy before and after the mutation was calculated (Figure 2). In generally, the mutated alanine has negligible contribution to the binding free energy. Therefore, the difference of binding free energy before and after the mutation is equivalent to the contribution of the mutated residue to the total binding free energy.
Figure 2.
Calculation of binding free energy with the alanine scanning approach. The contribution of a specific residue x in the pocket was calculated by mutating this residue to alanine and calculating the difference of the binding energy in the two complexes.
The difference of binding free energy between wild type (WT) and alanine-mutated complex structure is defined by the following formula:
| (1) |
where
| (2) |
and similar for
| (3) |
In the above equations, “P” and “L” represent the protein and ligand, respectively. The superscript “x” represents a residue on the surface of protein, and superscript “a” represents the mutation of residue x into alanine. is the binding free energy of wild type complex while is the binding free energy of the mutant. P(x) and P(a) represent the wildtype residue x and the mutated alanine in the protein. ΔGgas(P(x) − L) and ΔGsol(P(x) − L) represent the gas-phase component and the solvation free energy component of total binding free energy of the wild-type, similarly to the mutant.
Hence, formula (1) can be written as
| (4) |
Here, is the difference of binding free energy before and after mutation. The relative binding free energy can be divided into a gas-phase term and a solvation term .
The gas phase can be obtained in the following way:
| (5) |
Here, and indicates the gas-phase binding free energy of the mutated alanine and the wildtype residue to the ligand, respectively. During alanine scanning, other residues remained unchanged, so the difference between and is the contribution of x residue to the total binding free energy.
The solvation energy was obtained with the following formula
| (6) |
Here Gsol(P(x) − L) represents the solvation energy of P(x) − L complex, and similar for Gsol(P(a) − L).
Finally, the difference of solvation energy becomes
| (7) |
Where the Gsol(P(x) − L) means the solvation energy of wild type complex P(x)-L, and Gsol(P(x)) means the solvation energy of wild type protein.
Interaction Entropy Method
The gas-phase component of binding free energy is composed of two parts: molecular mechanics interaction energy and entropic contribution. In this study, the entropy was obtained by the IE method which is more efficient than the conventional normal mode method (Duan et al., 2016; Yan et al., 2017; Liu et al., 2018). The gas-phase component of the binding free energy is derived as follows:
| (8) |
Ep, El, and Ew repsesent internal energies of protein, ligand, and waters, respectively. , , and are interaction energies of protein-ligand, protein-water, and ligand-water, respectively. represents the fluctuation of the energy and therefore:
| (9) |
Thus, can be calculated by the following formula:
| (10) |
Based on the IE method:
| (11) |
and similar for
| (12) |
Among the formulas above, represents the fluctuation of the energy. The average of Eint was calculated on the MD trajectory:
| (13) |
therefore
| (14) |
and similar for the mutated trajectory:
| (15) |
Finally, the difference of gas phase binding free energy is
| (16) |
MM/GBSA Method
For the solvation energy,
| (17) |
The solvation energy was calculated with the GBSA method
| (18) |
Here, ΔGgb, ΔGnp represent the generalize-born and non-polar solvation free energy, respectively.
ΔGgb is obtained by OBC GBSA model with igb = 2 (Ryckaert et al., 1977; Onufriev et al., 2000, 2004), with the dielectric constants of 1, 3, and 10 for non-polar, polar and charged residues, respectively (Qiu et al., 2018; Li et al., 2020). ΔGnp is obtained by empirical solvent-accessible surface area formula:
| (19) |
In this study, the constants γ and β adopted the values of 0.00542 kcal/(mol*Å2) and 0.92 kcal/mol, respectively.
The total binding free energy was calculated by summation of the contribution of residues within 5 Å of the ligand in the crystal structure:
| (20) |
Binding Free Energy Difference () in Alanine Scanning
Five 5-ns windows that have a stable complex structure were selected from each of the 100-ns trajectories to calculate binding free energy. Therefore, the reported energy values were averaged over 15 windows. The mutant trajectories were obtained by removing sidechain atoms that are beyond the Cβ atom in the wild-type trajectories. The solvation free energy was calculated using the GB model with igb = 2. There are 100 equally distributed frames in every 5-ns window were extracted for calculation of enthalpy. Entropy was obtained by Equation (11) using all 5,000 frames for every 5-ns window. To eliminate noises and ensure convergence, energy values that are within three standard deviation of the average value were used to calculate IE (Qiu et al., 2018).
Results and Discussion
Stability of the Complex Systems
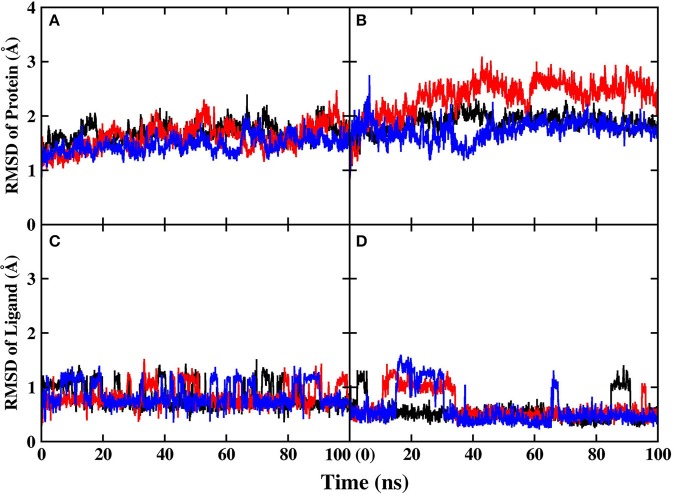
Before performing energy calculations and alanine scanning, the root-mean-square-deviation (RMSD) of the protein backbone atoms and ligand with respect to the initial crystal structure was calculated to exam whether the systems are stable in the MD simulations (Figure 3).
Figure 3.
RMSD of protein and ligand in MD simulations. Different colors represent different replicates. (A) Protein backbone in PARP-1 (B) protein backbone in PARP-2 (C) ligand in PARP-1 (D) ligand in PARP-2.
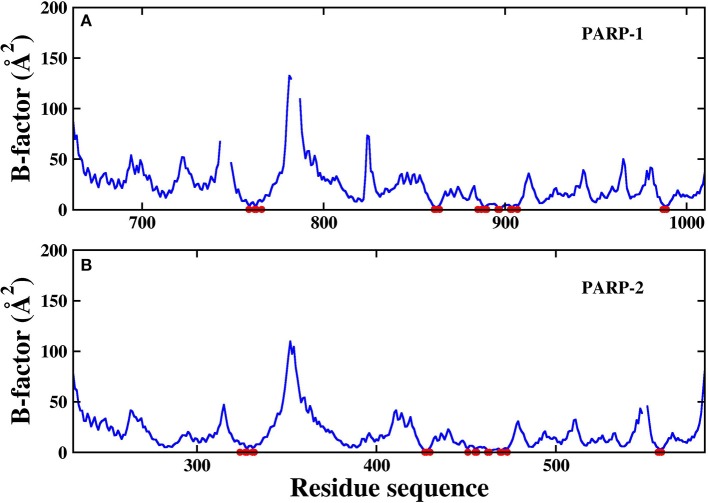
The RMSD of the protein backbone in PARP-1 is around 1.5 Å and the RMSD in PARP-2 is around 2.0 Å. The RMSD of ligand in PARP-1 and PARP-2 is <1 Å in most of the time, although there are some fluctuations due to small conformational change of the ligand. Besides, the isotropic temperature factor (B-factor) was calculated to reveal the mobility of each residue around its mean position in the simulations (Figure 4). The B-factor values of the residues in the pocket are relatively low, which shows that they are very stable throughout the simulation. These results suggest that the complex structures are overall stable in the simulations.
Figure 4.
The calculated B-factor of protein Cα atoms in the simulations. The residues in the pocket are marked with red circle. (A) PARP-1 (B) PARP-2.
To exam the difference between the binding pockets of PARP-1 and PARP-2 during simulation, the 2D-RMSD of backbone atoms in the binding pockets is calculated (Figure 5). It is clear that the similarity of the PARP-1 and PARP-2 pockets are decreased during simulation, and suggests that it is important to study the binding interaction from a dynamic perspective instead of a static structure.
Figure 5.
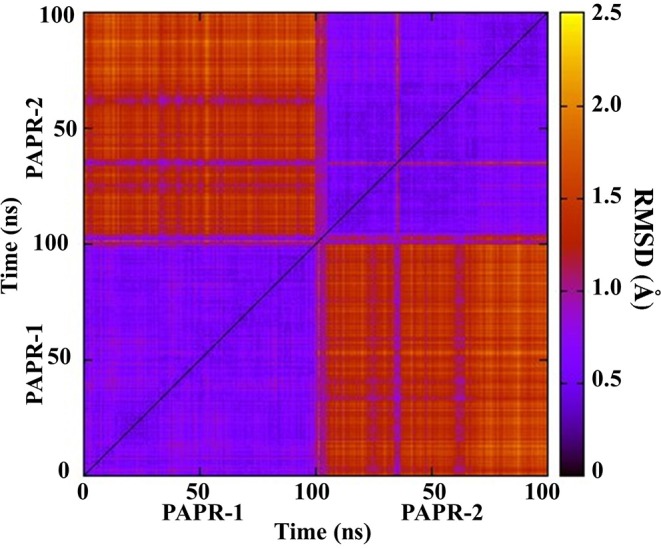
2D-RMSD of PARP-1 and PARP-2 during simulations.
Comparisons Between Calculated and Experimental Binding Free Energy
Five stable 5-ns segments from each trajectory are selected for the calculation of binding free energy. The computational alanine scanning was carried out using the MM/GBSA_IE method on the residues that are within 5 Å of the ligand in the two complexes. The total binding free energy is obtained by adding up binding free energy of each pocket residue (Table 1). The calculated binding free energy of PAPP-1 is 3.04 kcal/mol stronger than that of PARP-2, which is consistent with the experimental value of 3.00 kcal/mol.
Table 1.
Overall binding free energy of NMS-P118 with PARP-1 and PARP-2 using the MM/GBSA_IE method.
| PARP-1 | PARP-2 | Difference | |||||
|---|---|---|---|---|---|---|---|
| ΔH | −TΔS | ΔG | ΔH | −TΔS | ΔG | ||
| Mean | −24.31 | 5.11 | −19.20 | −22.29 | 6.13 | −16.16 | 3.04 |
| SD | 0.43 | 0.53 | 0.48 | 0.43 | 0.83 | 0.85 | |
| ΔGexp | −10.90 | −7.90 | 3.00 | ||||
All energy values are given in kcal/mol. SD represents the Standard Deviation.
Residue-Specific Binding Free Energies
To explore the reasons for the stronger binding ability of PARP-1, the contribution of binding free energy of each pocket residue was analyzed to study the differences between PARP-1 and PARP-2 (Table 2). The residue-specific binding free energy were obtained by MM/GBSA_IE method and averaged on the 15 MD segments for each system. Residues that contribute more than 1 kcal/mol are classified as hot-spot residues.
Table 2.
Computational alanine scanning for PARP-1 and PARP-2 with the MM/GBSA_IE method.
| PARP-1 | |||||||
|---|---|---|---|---|---|---|---|
| Mutation | ΔΔEvdw | ΔΔEele | ΔΔGgb | ΔΔGnp | ΔΔH | −TΔΔS | ΔΔG |
| Y907A | 6.41 ± 0.15 | −0.09 ± 0.19 | −0.25 ± 0.24 | 0.27 ± 0.04 | 6.33 ± 0.15 | −0.73 ± 0.13 | 5.60 ± 0.26 |
| Y889A | 4.05 ± 0.14 | 0.09 ± 0.30 | −0.04 ± 0.26 | 0.24 ± 0.02 | 4.35 ± 0.18 | −0.66 ± 0.23 | 3.69 ± 0.24 |
| Y896A | 3.33 ± 0.09 | 0.90 ± 0.05 | −0.86 ± 0.04 | 0.13 ± 0.01 | 3.51 ± 0.09 | −0.41 ± 0.05 | 3.10 ± 0.13 |
| H862A | 1.53 ± 0.16 | −0.44 ± 0.12 | 0.67 ± 0.12 | 0.06 ± 0.00 | 1.81 ± 0.16 | −0.17 ± 0.04 | 1.64 ± 0.19 |
| E988A | 1.04 ± 0.13 | 4.94 ± 0.11 | −4.43 ± 0.10 | 0.09 ± 0.02 | 1.65 ± 0.14 | −0.28 ± 0.11 | 1.37 ± 0.25 |
| E763A | 1.20 ± 0.21 | 4.90 ± 0.28 | −4.43 ± 0.27 | 0.16 ± 0.04 | 1.83 ± 0.25 | −0.87 ± 0.29 | 0.96 ± 0.23 |
| K903A | 1.38 ± 0.21 | −3.59 ± 0.23 | 3.15 ± 0.20 | 0.07 ± 0.02 | 1.00 ± 0.17 | −0.13 ± 0.05 | 0.87 ± 0.16 |
| D766A | 0.19 ± 0.08 | 4.00 ± 0.21 | −3.54 ± 0.20 | 0.01 ± 0.01 | 0.67 ± 0.10 | −0.15 ± 0.08 | 0.52 ± 0.03 |
| V762A | 0.56 ± 0.03 | −0.19 ± 0.02 | 0.19 ± 0.02 | 0.03 ± 0.01 | 0.60 ± 0.03 | −0.11 ± 0.03 | 0.49 ± 0.05 |
| Q759A | 0.84 ± 0.05 | 0.35 ± 0.26 | −0.41 ± 0.23 | 0.05 ± 0.02 | 0.83 ± 0.04 | −0.39 ± 0.31 | 0.44 ± 0.30 |
| F897A | 0.23 ± 0.01 | 0.24 ± 0.02 | −0.18 ± 0.03 | 0.00 ± 0.00 | 0.30 ± 0.02 | −0.02 ± 0.01 | 0.28 ± 0.02 |
| S904A | −0.55 ± 0.29 | 1.87 ± 0.29 | −0.58 ± 0.14 | 0.00 ± 0.00 | 0.74 ± 0.13 | −0.46 ± 0.14 | 0.28 ± 0.21 |
| W861A | 0.06 ± 0.00 | −0.01 ± 0.02 | 0.12 ± 0.01 | 0.00 ± 0.00 | 0.17 ± 0.01 | 0.00 ± 0.00 | 0.17 ± 0.01 |
| T887A | 0.16 ± 0.06 | 0.12 ± 0.15 | −0.09 ± 0.13 | 0.01 ± 0.00 | 0.20 ± 0.09 | −0.03 ± 0.04 | 0.17 ± 0.10 |
| Y989A | 0.07 ± 0.01 | −0.02 ± 0.01 | 0.05 ± 0.01 | 0.00 ± 0.00 | 0.10 ± 0.01 | 0.00 ± 0.00 | 0.10 ± 0.01 |
| P885A | 0.04 ± 0.02 | 0.09 ± 0.02 | −0.08 ± 0.02 | 0.00 ± 0.00 | 0.05 ± 0.02 | −0.01 ± 0.01 | 0.04 ± 0.02 |
| N987A | 0.01 ± 0.00 | 0.02 ± 0.02 | −0.02 ± 0.02 | 0.00 ± 0.00 | 0.01 ± 0.00 | 0.00 ± 0.00 | 0.01 ± 0.00 |
| S864A | 0.03 ± 0.01 | −0.05 ± 0.12 | 0.03 ± 0.12 | 0.00 ± 0.00 | 0.02 ± 0.01 | −0.02 ± 0.02 | 0.00 ± 0.02 |
| PARP-2 | |||||||
| Mutation | ΔΔEvdw | ΔΔEele | ΔΔGgb | ΔΔGnp | ΔΔH | −TΔΔS | ΔΔG |
| Y473A | 6.34 ± 0.13 | 0.18 ± 0.10 | −0.55 ± 0.11 | 0.34 ± 0.01 | 6.31 ± 0.12 | −0.91 ± 0.08 | 5.40 ± 0.16 |
| Y455A | 3.35 ± 0.70 | 0.32 ± 0.25 | −0.18 ± 0.24 | 0.19 ± 0.08 | 3.67 ± 0.76 | −0.53 ± 0.19 | 3.14 ± 0.58 |
| Y462A | 3.40 ± 0.39 | 0.92 ± 0.08 | −0.94 ± 0.07 | 0.16 ± 0.05 | 3.54 ± 0.40 | −0.43 ± 0.09 | 3.11 ± 0.42 |
| E558A | 1.08 ± 0.08 | 4.99 ± 0.11 | −4.46 ± 0.11 | 0.11 ± 0.02 | 1.71 ± 0.09 | −0.27 ± 0.07 | 1.44 ± 0.14 |
| H428A | 1.32 ± 0.21 | −0.10 ± 0.31 | 0.29 ± 0.31 | 0.06 ± 0.01 | 1.57 ± 0.25 | −0.18 ± 0.05 | 1.39 ± 0.28 |
| K469A | 1.10 ± 0.08 | −3.41 ± 0.07 | 3.00 ± 0.07 | 0.09 ± 0.01 | 0.77 ± 0.08 | −0.07 ± 0.02 | 0.69 ± 0.08 |
| I331A | 0.81 ± 0.08 | −0.31 ± 0.12 | 0.31 ± 0.04 | 0.08 ± 0.05 | 0.88 ± 0.12 | −0.38 ± 0.07 | 0.51 ± 0.17 |
| L327A | 0.41 ± 0.30 | −0.02 ± 0.07 | 0.06 ± 0.07 | 0.04 ± 0.03 | 0.49 ± 0.31 | −0.06 ± 0.05 | 0.43 ± 0.29 |
| P451A | 0.24 ± 0.15 | 0.03 ± 0.02 | −0.01 ± 0.03 | 0.02 ± 0.02 | 0.28 ± 0.17 | −0.04 ± 0.03 | 0.24 ± 0.15 |
| F463A | 0.22 ± 0.02 | 0.25 ± 0.03 | −0.22 ± 0.04 | 0.00 ± 0.00 | 0.25 ± 0.04 | −0.03 ± 0.01 | 0.23 ± 0.05 |
| W427A | 0.06 ± 0.00 | −0.01 ± 0.02 | 0.12 ± 0.02 | 0.00 ± 0.00 | 0.17 ± 0.01 | 0.00 ± 0.00 | 0.17 ± 0.01 |
| S470A | −0.60 ± 0.26 | 1.83 ± 0.29 | −0.61 ± 0.11 | 0.00 ± 0.00 | 0.63 ± 0.10 | −0.47 ± 0.08 | 0.16 ± 0.14 |
| S328A | 0.38 ± 0.15 | 0.65 ± 0.50 | −0.73 ± 0.51 | 0.05 ± 0.04 | 0.35 ± 0.16 | −0.26 ± 0.29 | 0.09 ± 0.17 |
| Y559A | 0.06 ± 0.01 | −0.03 ± 0.01 | 0.06 ± 0.01 | 0.00 ± 0.00 | 0.09 ± 0.01 | 0.00 ± 0.00 | 0.09 ± 0.01 |
| N557A | 0.01 ± 0.00 | 0.04 ± 0.01 | −0.04 ± 0.01 | 0.00 ± 0.00 | 0.01 ± 0.00 | 0.00 ± 0.00 | 0.01 ± 0.00 |
| Q332A | 0.69 ± 0.56 | −0.39 ± 1.11 | 0.26 ± 1.15 | 0.07 ± 0.08 | 0.64 ± 0.57 | −0.63 ± 0.73 | 0.01 ± 0.29 |
| S430A | 0.03 ± 0.01 | −0.02 ± 0.07 | 0.01 ± 0.07 | 0.00 ± 0.00 | 0.02 ± 0.01 | −0.02 ± 0.00 | 0.00 ± 0.01 |
All energy values are given in kcal/mol. ΔΔEvdw, ΔΔEele, ΔΔGgb, and ΔΔGnp represent the difference of van der waals interaction, electrostatic interaction, generalize-born and nonpolar solvation free energy between WT and the mutant.
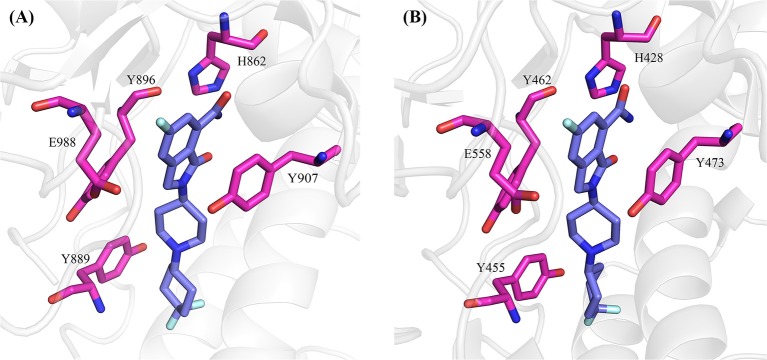
Decomposition of the binding free energy shows that PARP-1 and PARP-2 both have five hot-spot residues: Y907, Y889, Y896, H862, and E988 for PARP-1, and Y473, Y455, Y462, E558, and H428 for PARP-2.
The positions of these residues in the two complexes are plotted side-by-side (Figure 6). The NMS-P118 occupies the nicotinamide-ribose sites90 (NI-sites) and displays a similar pose in the two complexes, and therefore forms similar interactions with PARP-1 and PARP-2. For example, it forms π-alkyl hydrophobic interaction with Y889 and Y896 in PARP-1 and Y455 and Y462 in PARP-2, and π-π stacking with Y907 in PARP-1 and Y473 in PARP-2.
Figure 6.
The hot-spot residues in PARP-1 (A, PDB ID: 5A00) and PARP-2 (B, PDB ID:4ZZY). The proteins are shown in cartoon, and the hot-spot residues and ligand are shown in sticks.
Although the two complexes have the same hot-spot residues, most of the residues in the PARP-1 have stronger binding free energy than the corresponding residues in PARP-2. To compare the difference between the corresponding residues in PARP-1 and PARP-2 clearly, the residues that contributed most to the binding free energy are shown in Figure 7.
Figure 7.

The residues that contributed the most to the binding free energy in PARP-1 and PARP-2. Red represents the residue in PARP-1 and black represents the residue in PARP-2. Stars indicate statistically significant difference (t-test, p-value < 0.01).
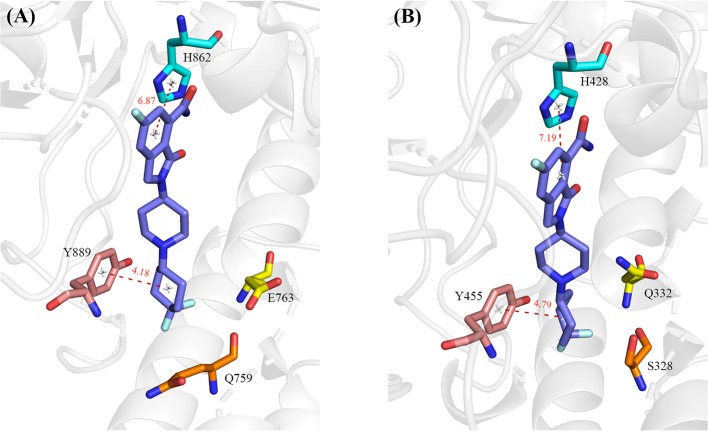
A number of hot-spot residues in PARP-1 such as Y889, H862, E763, and Q759 show stronger contributions to binding free energy compared to the corresponding residues in PAPR2, revealing the origin of the stronger binding of PARP-1 (Figure 8).
Figure 8.
The hot-spot residues that are responsible for the different binding affinity in PARP-1 (A, PDB ID: 5A00) and PARP-2 (B, PDB ID: 4ZZY). The protein is shown in cartoon, and the residues and ligand are shown in sticks. The red dashed lines indicate distance between PARP1/2 residues and the ligand.
Y889 in PARP-1 contributes 0.55 kcal/mol more than the corresponding residue Y455 in PARP-2. We calculated the average distances between center of mass of benzene ring between Y889/Y445 and 4′4-difluorocyclohexyl in NMS-P118. The average distance of Y889 is 4.18 Å while the distance of Y445 in PARP-2 complex is 4.79 Å. The shorter distance in PARP-1 may account for the stronger van der Waals interaction of Y889 in PARP-1. H862 in PARP1 is 0.25 kcal/mol stronger than the corresponding residue H428 in PARP2. H862 is more strongly bound to the ligand because the distance with ligand is 6.87 Å, which is closer than the 7.19 Å distance of H428 in PARP2 complex. Moreover, a hydrogen bond exists between the ligand and backbone of H862 in PARP-1 and H428 in PARP-2. The occupancy of hydrogen in PARP-1 and PARP-2 is 54.31% and 44.14% in MD simulations, respectively, which can partly account for the stronger interaction in PARP-1 (Table 3). The binding free energy of E763 is 0.95 kcal/mol larger than that of Q332, which is likely due to the favorable electrostatic interactions of E763 and the positively charged 1,4-dimethylpiperidin-1-ium group in the ligand.
Table 3.
Occupancy of hydrogen bonds between Q759/S328 and the ligand during MD simulation.
| System | Acceptor | Donor | Ave Distance (Å) | Ave Angle (°) | Occupancy (%) |
|---|---|---|---|---|---|
| PARP-1 | NMS-P118O28 | H862CA-HA | 3.50 | 144.92 | 54.31 |
| NMS-P118F27 | Q759CB-HB3 | 3.08 | 126.79 | 77.93 | |
| NMS-P118F26 | Q759CA-HA | 3.68 | 134.10 | 27.08 | |
| PARP-2 | NMS-P118O28 | H428CA-HA | 3.55 | 147.82 | 44.14 |
| NMS-P118F27 | S328CB-HB2 | 4.77 | 104.31 | 10.53 | |
| NMS-P118F27 | S328CA-HA | 3.91 | 123.98 | 25.61 |
It is believed that the Q759 and V762 in PARP-1 and S328 and I331 in PAPP-2 are responsible for the selectivity of NMS-P118 in PARP-1 and PARP-2 (Papeo et al., 2015). However, our results show that there is no obvious difference between V762 and I331, and slightly stronger contribution from Q759 in PARP-1 than that of S328 in PARP-2. Therefore, the hydrogen bonds between ligand and Q759 in PARP-1 and S328 in PARP-2 are analyzed (Table 3). The occupancy of hydrogen bonds in PARP-1 are both larger than those of corresponding hydrogen bonds in PARP-2, which contribute to the larger binding free energy.
Conclusion
The MM/GBSA_IE method that combines the MM/GBSA method and the IE method was used to obtain the quantitative binding free energy between NMS-P118 and PARP1/PARP2. Analysis of hot-spot residues explores the differences in the binding mechanism between NMS-P118 with PARP-1 and PARP-2.
PARP-1 has the same number of hot-spot residues with PARP-2, but the relative binding free energy of most hot-spot residues in PARP-1 is greater than that of the corresponding residues in PARP-2. Especially, Y889 in PARP-1 has 0.55 kcal/mol greater binding free energy than Y455 in PARP-2 because of the stronger π-alkyl interaction with 4′4-difluorocyclohexyl ring in ligand. Furthermore, H862 in PARP-1 is 0.25 kcal/mol stronger than H428 in PARP-2 because of the shorter distance with the ligand and more stable hydrogen bonds. Besides the stronger electrostatic interaction between E763 and positively charged ligand induces the 0.95 kcal/mol greater binding free energy than Q332 in PARP-2, which may also contribute to the selectivity. Moreover, the hydrogen bonds between Q759/S328 and 4′4-difluorocyclohexyl ring also cause the energy difference of 0.35 kcal/mol.
Selective PARP-1 inhibitors can not only be used as radiotherapy and chemotherapy sensitizers to enhance anti-tumor efficacy, but also would mitigate toxicities arising from cross-inhibition of PARP-2. The results of this study partly reveal the reasons for stronger binding of PARP-1 with NMS-P118, which may provide guidance for further improvement and design of potent selective PARP inhibitors.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
RW performed main calculation study and wrote the draft paper. YC, ML, and JB helped coding the program and participated in discussion. YQ supervised and helped to write the paper. JZ designed and supervised the entire project.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We also thank the ECNU Public Platform for Innovation 001 for providing supercomputer time.
Footnotes
Funding. This work was supported by National Key R&D Program of China (Grant no. 2016YFA0501700), National Natural Science Foundation of China (Grant nos. 21433004, 31700646, 91753103), and NYU Global Seed Grant.
References
- Ame J. C., Spenlehauer C., de Murcia G. (2004). The PARP superfamily. Bioessays 26, 882–893. 10.1002/bies.20085 [DOI] [PubMed] [Google Scholar]
- Anwar M., Aslam H. M., Anwar S. (2015). PARP inhibitors. Hered. Cancer Clin. Pract. 13:4. 10.1186/s13053-014-0024-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillari C., Marcou G., Rognan D. (2008). Hot-spots-guided receptor-based pharmacophores (HS-Pharm): a knowledge-based approach to identify ligand-anchoring atoms in protein cavities and prioritize structure-based pharmacophores. J. Chem. Inf. Model. 48, 1396–1410. 10.1021/ci800064z [DOI] [PubMed] [Google Scholar]
- Bash P. A., Field M. J., Karplus M. (1987). Free energy perturbation method for chemical reactions in the condensed phase: a dynamic approach based on a combined quantum and molecular mechanics potential. J. Am. Chem. Soc. 109, 8092–8094. 10.1021/ja00260a028 [DOI] [Google Scholar]
- Bauman J. D., Harrison J. J. E. K., Arnold E. (2016). Rapid experimental SAD phasing and hot-spot identification with halogenated fragments. IUCrJ 3, 51–60. 10.1107/S2052252515021259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett G. J., Xie Y. K. (1988). A peripheral mononeuropathy in rat that produces disorders of pain sensation like those seen in man. Pain 33, 87–107. 10.1016/0304-3959(88)90209-6 [DOI] [PubMed] [Google Scholar]
- Berger N. A., Besson V. C., Boulares A. H., Burkle A., Chiarugi A., Clark R. S., et al. (2018). Opportunities for the repurposing of PARP inhibitors for the therapy of non-oncological diseases. Br. J. Pharmacol. 175, 192–222. 10.1111/bph.13748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., et al. (2000). The protein data bank. Nucleic Acids Res. 28, 235–242. 10.1093/nar/28.1.235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks B. R., Janežič D., Karplus M. (1995). Harmonic analysis of large systems. I. Methodology. J. Comput. Chem. 16, 1522–1542. 10.1002/jcc.540161209 [DOI] [Google Scholar]
- Burgoyne N. J., Jackson R. M. (2006). Predicting protein interaction sites: binding hot-spots in protein–protein and protein–ligand interfaces. Bioinformatics 22, 1335–1342. 10.1093/bioinformatics/btl079 [DOI] [PubMed] [Google Scholar]
- Cheung S.-L., Kanwar M., Ostermeier M., Konstantopoulos K. (2012). A hot-spot motif characterizes the interface between a designed ankyrin-repeat protein and its target ligand. Biophys. J. 102, 407–416. 10.1016/j.bpj.2012.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong Y., Li M., Feng G., Li Y., Wang X., Duan L. (2017). Trypsin-ligand binding affinities calculated using an effective interaction entropy method under polarized force field. Sci. Rep. 7:17708. 10.1038/s41598-017-17868-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beveridge D. L., DiCapua F. M. (1989). Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 18, 431–492. 10.1146/annurev.bb.18.060189.002243 [DOI] [PubMed] [Google Scholar]
- Davar D., Beumer J. H., Hamieh L., Tawbi H. (2012). Role of PARP inhibitors in cancer biology and therapy. Curr. Med. Chem. 19, 3907–3921. 10.2174/092986712802002464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donawho C. K., Luo Y., Luo Y., Penning T. D., Bauch J. L., Bouska J. J., et al. (2007). ABT-888, an orally active poly(ADP-Ribose) polymerase inhibitor that potentiates DNA-damaging agents in preclinical tumor models. Clin. Cancer Res. 13, 2728–2737. 10.1158/1078-0432.Ccr-06-3039 [DOI] [PubMed] [Google Scholar]
- Drew Y., Plummer R. (2009). PARP inhibitors in cancer therapy: two modes of attack on the cancer cell widening the clinical applications. Drug Resist. Updates 12, 153–156. 10.1016/j.drup.2009.10.001 [DOI] [PubMed] [Google Scholar]
- Duan L., Liu X., Zhang J. Z. H. (2016). Interaction entropy: a new paradigm for highly efficient and reliable computation of protein–ligand binding free energy. J. Am. Chem. Soc. 138, 5722–5728. 10.1021/jacs.6b02682 [DOI] [PubMed] [Google Scholar]
- Gohlke H., Hendlich M., Klebe G. (2000). Predicting binding modes, binding affinities and ‘hot spots’ for protein-ligand complexes using a knowledge-based scoring function. Perspect. Drug Discov. Des. 20, 115–144. 10.1023/A:1008781006867 [DOI] [Google Scholar]
- Hakmé A., Wong H.-K., Dantzer F., Schreiber V. (2008). The expanding field of poly(ADP-ribosyl)ation reactions. EMBO Rep. 9, 1094–1100. 10.1038/embor.2008.191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosoya N., Miyagawa K. (2009). Clinical importance of DNA repair inhibitors in cancer therapy. Memo-Mag. Eur. Med. Oncol. 2, 9–14. 10.1007/s12254-008-0081-7 [DOI] [Google Scholar]
- Jones C., Plummer E. R. (2008). PARP inhibitors and cancer therapy — early results and potential applications. Br. J. Radiol. 81, S2–S5. 10.1259/bjr/30872348 [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L., Thomas L. L. (2008). Perspective on free-energy perturbation calculations for chemical equilibria. J. Chem. Theory Comput. 4, 869–876. 10.1021/ct800011m [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L. (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. 10.1063/1.445869 [DOI] [Google Scholar]
- Kita Y., Arakawa T., Lin T.-Y., Timasheff S. N. (1994). Contribution of the surface free energy perturbation to protein-solvent interactions. Biochemistry 33, 15178–15189. 10.1021/bi00254a029 [DOI] [PubMed] [Google Scholar]
- Kollman P. (1993). Free energy calculations: applications to chemical and biochemical phenomena. Chem. Rev. 93, 2395–2417. 10.1021/cr00023a004 [DOI] [Google Scholar]
- Kollman P. A., Massova I., Reyes C., Kuhn B., Huo S., Chong L., et al. (2000). Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 33, 889–897. 10.1021/ar000033j [DOI] [PubMed] [Google Scholar]
- Krishnakumar R., Kraus W. L. (2010). The PARP side of the nucleus: molecular actions, physiological outcomes, and clinical targets. Mol. Cell 39, 8–24. 10.1016/j.molcel.2010.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z., Bao J., Qi Y., Zhang J. Z. H. (2020). Computational approaches to studying methylated H4K20 recognition by DNA repair factor 53BP1. Phys. Chem. Chem. Phys. 10.1039/C9CP05635A [DOI] [PubMed] [Google Scholar]
- Liu X., Peng L., Zhou Y., Zhang Y., Zhang J. Z. H. (2018). Computational alanine scanning with interaction entropy for protein–ligand binding free energies. J. Chem. Theory Comput. 14, 1772–1780. 10.1021/acs.jctc.7b01295 [DOI] [PubMed] [Google Scholar]
- Lord C. J., Ashworth A. (2017). PARP inhibitors: synthetic lethality in the clinic. Science 355, 1152–1158. 10.1126/science.aam7344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lupo B., Trusolino L. (2014). Inhibition of poly(ADP-ribosyl)ation in cancer: old and new paradigms revisited. Biochim. Biophys. Acta Rev. Cancer 1846, 201–215. 10.1016/j.bbcan.2014.07.004 [DOI] [PubMed] [Google Scholar]
- Maier J. A., Martinez C., Kasavajhala K., Wickstrom L., Hauser K. E., Simmerling C. (2015). ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 11, 3696–3713. 10.1021/acs.jctc.5b00255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massova I., Kollman P. A. (1999). Computational alanine scanning to probe protein–protein interactions: a novel approach to evaluate binding free energies. J. Am. Chem. Soc. 121, 8133–8143. 10.1021/ja990935j [DOI] [Google Scholar]
- Massova I., Kollman P. A. (2000). Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discov. Des. 18, 113–135. 10.1023/A:1008763014207 [DOI] [Google Scholar]
- Moreira I. S., Fernandes P. A., Ramos M. J. (2007). Computational alanine scanning mutagenesis—an improved methodological approach. J. Comput. Chem. 28, 644–654. 10.1002/jcc.20566 [DOI] [PubMed] [Google Scholar]
- Nguyen D. T., Case D. A. (1985). On finding stationary states on large-molecule potential energy surfaces. J. Phys. Chem. 89, 4020–4026. 10.1021/j100265a018 [DOI] [Google Scholar]
- Onufriev A., Bashford D., Case D. A. (2000). Modification of the generalized born model suitable for macromolecules. J. Phys. Chem. B. 104, 3712–3720. 10.1021/jp994072s [DOI] [Google Scholar]
- Onufriev A., Bashford D., Case D. A. (2004). Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 55, 383–394. 10.1002/prot.20033 [DOI] [PubMed] [Google Scholar]
- Papeo G., Posteri H., Borghi D., Busel A. A., Caprera F., Casale E., et al. (2015). Discovery of 2-[1-(4,4-Difluorocyclohexyl)piperidin-4-yl]-6-fluoro-3-oxo-2,3-dihydro-1H-isoindole-4-carboxamide (NMS-P118): A potent, orally available, and highly selective PARP-1 Inhibitor for cancer therapy. J. Med. Chem. 58, 6875–6898. 10.1021/acs.jmedchem.5b00680 [DOI] [PubMed] [Google Scholar]
- Peralta-Leal A., Rodríguez-Vargas J. M., Aguilar-Quesada R., Rodríguez M. I., Linares J. L., de Almodóvar M. R., et al. (2009). PARP inhibitors: new partners in the therapy of cancer and inflammatory diseases. Free Radical Biol. Med. 47, 13–26. 10.1016/j.freeradbiomed.2009.04.008 [DOI] [PubMed] [Google Scholar]
- Qiu L., Yan Y., Sun Z., Song J., Zhang J. Z. H. (2018). Interaction entropy for computational alanine scanning in protein–protein binding. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8:e1342 10.1002/wcms.1342 [DOI] [Google Scholar]
- Qiu W., Lam R., Voytyuk O., Romanov V., Gordon R., Gebremeskel S., et al. (2014). Insights into the binding of PARP inhibitors to the catalytic domain of human tankyrase-2. Acta Crystallogr. Sect. D Struct. Biol. 70, 2740–2753. 10.1107/S1399004714017660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao S. N., Singh U. C., Bash P. A., Kollman P. A. (1987). Free energy perturbation calculations on binding and catalysis after mutating Asn 155 in subtilisin. Nature 328, 551–554. 10.1038/328551a0 [DOI] [PubMed] [Google Scholar]
- Rottenberg S., Jaspers J. E., Kersbergen A., van der Burg E., Nygren A. O. H., Zander S. A. L., et al. (2008). High sensitivity of BRCA1-deficient mammary tumors to the PARP inhibitor AZD2281 alone and in combination with platinum drugs. Proc. Natl. Acad. Sci. U. S. A. 105, 17079–17084. 10.1073/pnas.0806092105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryckaert J.-P., Ciccotti G., Berendsen H. J. C. (1977). Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341. 10.1016/0021-9991(77)90098-5 [DOI] [Google Scholar]
- Sabau A., Frahm C., Pfeiffer M., Breustedt J.-M., Piechotta A., Numberger M., et al. (1999). Age-dependence of the anticonvulsant effects of the GABA uptake inhibitor tiagabine in vitro. Eur. J. Pharmacol. 383, 259–266. 10.1016/S0014-2999(99)00628-7 [DOI] [PubMed] [Google Scholar]
- Schreiber V., Dantzer F., Ame J.-C., de Murcia G. (2006). Poly(ADP-ribose): novel functions for an old molecule. Nat. Rev. Mol. Cell Biol. 7, 517–528. 10.1038/nrm1963 [DOI] [PubMed] [Google Scholar]
- Shen Y., Rehman F. L., Feng Y., Boshuizen J., Bajrami I., Elliott R., et al. (2013). BMN 673, a novel and highly potent PARP1/2 inhibitor for the treatment of human cancers with DNA repair deficiency. Clin. Cancer Res. 19, 5003–5015. 10.1158/1078-0432.Ccr-13-1391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staibano S., Pepe S., Muzio L. L., Somma P., Mascolo M., Argenziano G., et al. (2005). Poly(adenosine diphosphate-ribose) polymerase 1 expression in malignant melanomas from photoexposed areas of the head and neck region. Hum. Pathol. 36, 724–731. 10.1016/j.humpath.2005.04.017 [DOI] [PubMed] [Google Scholar]
- Sun H., Duan L., Chen F., Liu H., Wang Z., Pan P., et al. (2018). Assessing the performance of MM/PBSA and MM/GBSA methods. 7. entropy effects on the performance of end-point binding free energy calculation approaches. Phys. Chem. Chem. Phys. 20, 14450–14460. 10.1039/C7CP07623A [DOI] [PubMed] [Google Scholar]
- Sun H., Li Y., Li D., Hou T. (2013). Insight into crizotinib resistance mechanisms caused by three mutations in ALK tyrosine kinase using free energy calculation approaches. J. Chem. Inf. Model. 53, 2376–2389. 10.1021/ci400188q [DOI] [PubMed] [Google Scholar]
- Sun H., Li Y., Shen M., Tian S., Xu L., Pan P., et al. (2014). Assessing the performance of MM/PBSA and MM/GBSA methods. 5. improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 16, 22035–22045. 10.1039/C4CP03179B [DOI] [PubMed] [Google Scholar]
- Thomas H. D., Calabrese C. R., Batey M. A., Canan S., Hostomsky Z., Kyle S., et al. (2007). Preclinical selection of a novel poly(ADP-ribose) polymerase inhibitor for clinical trial. Mol. Cancer Ther. 6, 945–956. 10.1158/1535-7163.Mct-06-0552 [DOI] [PubMed] [Google Scholar]
- Tikhe J. G., Webber S. E., Hostomsky Z., Maegley K. A., Ekkers A., Li J., et al. (2004). Design, synthesis, and evaluation of 3,4-Dihydro-2H-[1,4]diazepino[6,7,1-hi]indol-1-ones as inhibitors of Poly(ADP-Ribose) polymerase. J. Med. Chem. 47, 5467–5481. 10.1021/jm030513r [DOI] [PubMed] [Google Scholar]
- Timonen J. M., Nieminen R. M., Sareila O., Goulas A., Moilanen L. J., Haukka M., et al. (2011). Synthesis and anti-inflammatory effects of a series of novel 7-hydroxycoumarin derivatives. Eur. J. Med. Chem. 46, 3845–3850. 10.1016/j.ejmech.2011.05.052 [DOI] [PubMed] [Google Scholar]
- Wang J., Wolf R. M., Caldwell J. W., Kollman P. A., Case D. A. (2004). Development and testing of a general amber force field. J. Comput. Chem. 25, 1157–1174. 10.1002/jcc.20035 [DOI] [PubMed] [Google Scholar]
- Yan Y., Yang M., Ji C. G., Zhang J. Z. H. (2017). Interaction entropy for computational alanine scanning. J. Chem. Inf. Model. 57, 1112–1122. 10.1021/acs.jcim.6b00734 [DOI] [PubMed] [Google Scholar]
- Yélamos J., Schreiber V., Dantzer F. (2008). Toward specific functions of poly(ADP-ribose) polymerase-2. Trends Mol. Med. 14, 169–178. 10.1016/j.molmed.2008.02.003 [DOI] [PubMed] [Google Scholar]
- Zacharias M., Straatsma T. P., McCammon J. A. (1994). Separation-shifted scaling, a new scaling method for Lennard-Jones interactions in thermodynamic integration. J. Chem. Phys. 100, 9025–9031. 10.1063/1.466707 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.