Intelligent Labeling Based on Fisher Information for Medical Image Segmentation Using Deep Learning

Abstract

Deep Convolutional Neural Networks (CNN) have recently achieved superior performance at the task of medical image segmentation compared to classic models. However, training a generalizable CNN requires a large amount of training data, which is difficult, expensive and time consuming to obtain in medical settings. Active Learning (AL) algorithms can facilitate training CNN models by proposing a small number of the most informative data samples to be annotated to achieve a rapid increase in performance. We proposed a new active learning method based on Fisher information (FI) for CNNs for the first time. Using efficient backpropagation methods for computing gradients together with a novel low-dimensional approximation of FI enabled us to compute FI for CNNs with large number of parameters. We evaluated the proposed method for brain extraction with a patch-wise segmentation CNN model in two different learning scenarios: universal active learning and active semi-automatic segmentation. In both scenarios, an initial model was obtained using labeled training subjects of a source data set and the goal was to annotate a small subset of new samples to build a model that performs well on the target subject(s). The target data sets included images that differed from the source data by either age group (e.g. newborns with different image contrast) or underlying pathology that was not available in the source data. In comparison to several recently proposed AL methods and brain extraction baselines, the results showed that FI-based AL outperformed the competing methods in improving performance of the model after labeling a very small portion of target data set (< 0.25%).

I. Introduction

Image segmentation is an important component of automatic medical image analysis. Given the segmentation, important quantitative imaging markers of disease can be extracted for improved diagnosis, personalized treatment planning and monitoring response to therapy. Supervised deep learning models, including convolutional neural networks (CNNs) have gained tremendous success in performing segmentation tasks in the last few years [1]–[4]. These models have also been among the highest ranked competitors in medical image segmentation challenges.

Deep CNNs require a large amount of labeled data in order to generalize well to unseen test data. However, labeled samples are not available for many populations in medical settings, such as patients that come from different age groups (e.g., newborns) or have different pathological conditions. This mismatch between labeled data sets and target populations arises frequently in clinical applications and degrades the performance and generalization capacity of deep models. To address this problem, we must label additional samples from the targeted, unlabeled data set, which is very costly, especially in medical applications where both time and expertise are needed for labeling. In contrast, obtaining unlabeled data is becoming less expensive. Simply labeling all of these data is not affordable. The first and simplest solution, i.e. random selection of samples to label, is sub-optimal leading to an unnecessarily large labeled data set. To address these issues, active learning (AL) methods aim to intelligently select a limited number of most informative samples to be annotated by an expert, maximizing the prediction performance for large, unlabeled data sets.

A. Related Work

Among AL methods developed for CNNs, uncertainty sampling (US) has been one of the most popular methods [5]–[12], which queries the most uncertain samples to be labeled. Various uncertainty measures have been used. Gal et. al [7] measured uncertainty via Monte-Carlo dropout and used it in a Bayesian setting in order to consider both aleatoric uncertainity —the noise in the data and epistemic uncertainty —the uncertainty over the parameters of the CNN. Heteroscedastic aleatoric uncertainties were also considered for selecting uncertain samples by [8] through building Bayesian neural networks that predict sample-dependent variance [13]. Zhou et. al [9] utilized uncertainty together with Kullback-Leibler metric to query slices for labeling. Recently, Beluch et. al [10] showed that estimating uncertainty based on network ensembles resulted in a better performing AL algorithm. Similarly, Kou et. al [12] computed disagreement between an ensemble of networks through Jensen-Shannon entropy (as opposed to classic Shannon entropy) as an estimate for uncertainty in their AL technique. Uncertainty-based AL techniques were successful in training models with fewer labeled samples in comparison to passive learning (i.e. random query selection). Nevertheless, these methods are prone to 1) redundancy among queries and 2) outliers. Although some of the work mentioned above attempted to address these issues with ad-hoc solutions, the question that remains to be answered is whether one can solve these issues more principally by using an information theory based objective.

Other information gain measures have been proposed to address shortcomings of US, such as mutual information between unlabeled samples and the model parameters [7], [14], [15], which, however, did not improve uncertainty results for CNNs, and mutual information between query candidates and unlabeled samples [16], which is computationally intractable for CNN models. Geometrical AL algorithms that use geometrical measures to select the most informative samples are more suitable for large learning models. Group of methods combined uncertainty with pair-wise similarities between candidates and the rest of unlabeled population to address the issue of outlier selection [17], [18]. Iterative optimization of such similarity-based objectives could be used instead of simply ranking the candidates to address the redundancy as well [19], [20]. Moreover, recently Sener et. al [21] chose queries that best covered various parts of the feature space occupied by the rest of the unlabeled samples. Although these algorithms are scalable to complex CNN models, they become very slow for large pool of unlabeled samples, and as we will show in our experiments, their performance do not differ significantly from the US methods.

B. Contributions

Here, we proposed to use a more sophisticated objective based on Fisher information (FI) for active learning in deep CNNs. FI has been shown to be theoretically beneficial for active learning in classical shallow models such as the logistic regression classifier [22]–[24]. In statistics, FI is known to measure the amount of information that a single sample carries about the parameters of the underlying distribution from which it is drawn. Intuitively, FI-based AL selects those queries that are expected to carry more information about the optimal model parameters. Recent studies showed FI-based objectives outperformed US when applied in AL on logistic regression [25], [26]. However, FI-based AL has not previously been applied to CNN models. The main reason is the significantly large parameter space of the CNN models which leads to very large FI matrices that are difficult to form and manipulate. Here, we developed the first FI-based AL method for deep CNNs by means of a method that exploits dimensionality reduction in parameter space. This paper is an extension of our short preliminary work that was recently presented [27].

FI has been previously used with deep models for purposes different than active learning including natural gradient descent [28], [29] and parameter weighting [30]. Computing FI, or Hessian matrix of the loss function as an approximation to FI, is not practical for most neural network architectures with millions of parameters. In some specific applications, formation of the entire FI matrix can be avoided [31], but in others, including our FI-based AL problem, FI matrix needs to be explicitly computed. Few approximate formations have been proposed which usually impose certain structural assumptions over the model parameters. For example, (block) diagonal approximations of FI [30], [32] assume that (blocks of) the parameters are uncorrelated, and Kronecker factorization of the matrix blocks [29], [33] makes an extra assumption of independence between pre- and post-activations of the layers’ outputs.

Our contribution in this paper is threefold:

• We developed a FI-based AL for CNNs by applying a tractable approximation of FI that is based on an implicit re-parameterization of the model. Our approximation technique makes no assumptions about the structure of the model parameters.

• We used and evaluated AL for CNNs in two transfer learning scenarios, where we fine-tuned a pre-trained model obtained from a source data set to 1) build a model that is generalizable to a target data set of multiple subjects with different properties than the source (Universal AL), and 2) specialize a model for a specific patient with different anatomy or pathology by personalized refinement of an insufficient initial segmentation (active semi-automatic segmentation). We showed that our proposed FI-based AL achieve at least 99.7% accuracy of a fully trained model by only labeling a small portion (less than 0.25%) of the target data in the universal AL.

• We evaluated a comprehensive list of the most recently proposed AL approaches and state-of-the-art segmentation methods for patch-wise brain extraction to 1) compare the relative effectiveness of different AL methods and objectives in a widely-studied, benchmark medical image segmentation task, and 2) assess whether our proposed FI-based AL method can outperform the other methods in both segmentation scenarios considered here.

The semi-automatic segmentation scenario is tightly related to interactive image segmentation. Despite the advances in segmentation methods, interactive tools are still needed in practice because the automated segmentation results on clinical medical images are rarely flawless. This is due to several sources of variation in data such as inter-subject variations and/or variations due to use of different scanners or protocols [34]–[36]. Hence, user interaction is often needed to refine the segmentation results before they are used in clinic. Traditionally, the user’s interactions for refinement of the results are fully manual, which include scrolling through all slices and exhaustively searching for mis-segmented regions to correct. Unfortunately, this process can be very labor intensive and time-taking. Instead, we proposed an intelligent system that can learn from the users limited feedback at any given time and automatically refines the algorithm so that the algorithm automatically correct similar mistakes in other parts of the image. In this scenario, AL was used to accelerate the process of interactive image segmentation by converting its fully manual process into a semi-automatic workflow. There are existing semi-automatic interactive segmentation methods, however, they either lack any AL component [37], [38], or simply use uncertainty sampling [39], [40]. In this paper, an interactive image segmentation framework is proposed based on our FI-based AL algorithm.

II. Methods

This section is organized as follows. Section II-A gives a short introduction to active learning, Section II-B explains our FI approximation methods. Lastly, Section II-C describes the recently introduced AL methods that we compare our approach with.

A. Preliminaries

Active learning (AL) is usually done in an iterative fashion. The pseudo-code of this algorithmic process is shown in Figure 1. Each AL iteration consists of two phases: (1) query selection from a pool of unlabeled samples, and (2) model update using the newly labeled queries possibly mixed with the previously labeled samples. In line 3, $\mathcal{A}$ denotes a querying module that takes the current model and the unlabeled pool of samples and select a subset of unlabeled samples of size k (query batch size). The selected queries are then labeled by an expert (line 4) and added to the labeled data set (line 5). The expanded labeled data are then used in the second phase to update ${\mathcal{M}}_{t-1}$ to ${\mathcal{M}}_t$ (line 6). Previous research has shown that fine-tuning ${\mathcal{M}}_{t-1}$ with the labeled queries converges faster and to a more robust model than training all layers of the model from scratch [9], [41].

Fig. 1.

General pool-based AL iterations

While the initial labeled samples ${\mathcal{L}}_0$ can be considered a non-empty set, e.g. those samples that are used to train ${\mathcal{M}}_0$, in this paper we start from an empty ${\mathcal{L}}_0$. This is because our goal is not necessarily to preserve the performance of the model with respect to the source data set. Instead, we aim to adapt the network to achieve highest accuracy possible in the target data set with minimum number of additional samples to be queried and labeled. Moreover, if size of the initial training data is much larger than $k\left(\left|{\mathcal{L}}_0\right|\gg k\right)$, the new labeled queries from the target data set will be overwhelmed by ${\mathcal{L}}_0$ and consequently ${\mathcal{M}}_t$ will be too close to ${\mathcal{M}}_{t-1}$.

The family of models that we focus here include CNNs. Any model $\mathcal{M}$ in this family is capable of outputting class posterior probabilities for a given input x, i.e. $\mathbb{P}(y|\mathbf{x},\mathit{\theta })$. Let us denote the ordered set of model parameters by θ = {θ₁, …, θ_L}, where θ_i is the parameter set of the i-th layer and L is the number of hidden layers. We use d_i to represent number of the parameters involved in the i-th layer, that is ${\mathit{\theta }}_i\in {ℝ}^{d_i}$, and d = ∑_i d_i indicates total number of model parameters. We also define $\ell (\mathit{\theta })=\ell (\mathit{\theta };\mathbf{x},y)≔\log \mathbb{P}(y|\mathbf{x},\mathit{\theta })$, where we skip writing the dependence to x and y for simplifying the notations. The gradient of this function with respect to θ, i.e. ∇_θℓ(θ), is called the score function and plays key role in defining the FI.

Fisher information (FI) I(θ) is defined as ${\mathbb{E}}_{\mathbf{x},y}[{\nabla }_{\mathit{\theta }}\ell (\mathit{\theta }){\nabla }_{\mathit{\theta }}^{\top }\ell (\mathit{\theta })]$. Assuming that the underlying distribution of the data has the form $p(\mathbf{x},y)=p(\mathbf{x})\mathbb{P}\left(y|\mathbf{x},{\mathit{\theta }}_0\right)$ with a conditional in the same parametric family as the model posterior $\mathbb{P}\left(y|\mathbf{x},\mathit{\theta }\right)$, the FI I(θ₀) measures the amount of information that an observation carries about the true model parameter θ₀. Trace of (inverse) FI serves as a useful active learning objective [23], [24]. We optimize this objective with respect to a query distribution q defined over the pool $\mathcal{U}$ (hence q_i is the probability of querying ${\mathbf{x}}_i\in \mathcal{U}$):

$$\underset{\mathbf{q}\in {[0,1]}^n}{\arg \min }\mathrm{tr}\left[{\mathbf{I}}_{\mathbf{q}}{\left({\mathit{\theta }}_0\right)}^{-1}\right]\text{s.t.}\sum _i{q}_i=1.$$ (1)

where I_q denotes the FI when the underlying data distribution is $q(\mathbf{x})\mathbb{P}\left(y|\mathbf{x},{\mathit{\theta }}_0\right)$ for some query distribution q. In pool-based AL, there is a finite number of unlabeled samples from which the queries are chosen, and therefore q is a probability mass function (PMF). Furthermore, since θ₀ is not known, it is replaced by the available estimate $\widehat{\mathit{\theta }}$ in ${\mathcal{M}}_{t-1}$. The matrix inversion in optimization (1) makes the objective highly nonlinear and hard to solve. Simply removing this non-linearity by discarding the inversion will lead to an objective that scores samples independently based on the expected ℓ₂-norm of their gradients (hence, expected gradient length AL [42]). However, such simplified objective ignores the interaction between the queries resulting in poor AL performance. Fortunately, the optimization (1) can be reformulated in the form of a semidefinite programming (SDP) problem [26], [43]. Therefore, in FI-based AL, the querying module $\mathcal{A}(\mathcal{U},\mathcal{M},k)$ (line 3 in Figure 1) consists of two steps: (1) solving this SDP for a query distribution q(x), and (2) choosing distinct samples of k draws from this distribution.

B. Approximate FI-based AL

For large models with millions of parameters, including deep CNNs, forming FI matrix explicitly is prohibitively expensive. Furthermore, computational complexity of solving the resulting SDP increases quadratically with sample size n and super-quadratically with respect to the number of parameters [26]. Therefore, even if we can find a way of forming exact FI matrix, tractability of FI-based AL is very sensitive to size of the model’s parameter space and can easily become intractable for CNNs with even intermediate number of layers. To address this problem, we propose our method of approximating FI matrix with reduced dimensionality. Our approximation decreases dimensionality of the FI matrix from the number of parameters to the number of hidden layers in the neural network.

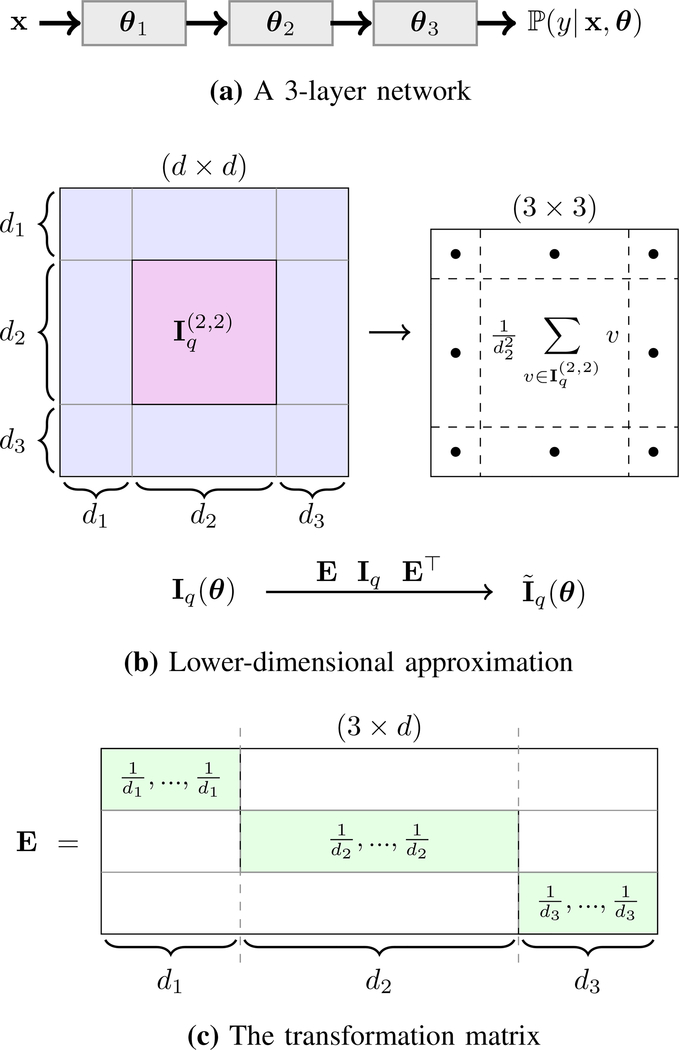
Suppose ${\mathbf{I}}_q\in {ℝ}^{d\times d}$ is the full FI matrix of the model, where d denotes the overall number of parameters in the network. This matrix can be partitioned into L² sub-matrices, where the (i,j)-th sub-matrix ${\mathbf{I}}_q^{(i,j)}$ has dimensionality of n_i × n_j (for some 1 ≤ i, j ≤ L) and includes all interactions between elements of θ_i and θ_j (Figure 2, first and second rows).

Fig. 2.

Illustration of our FI approximation for a 3-layer network (L = 3). Parameters of the model are denoted by θ = {θ₁, θ₂, θ₃} such that the i-th layer has d_i parameters, i.e. ${\mathit{\theta }}_i\in {ℝ}^{d_i}$ (row (a)). The full FI matrix I_q(θ) has dimensionality d×d, where d = d₁+d₂+d₃, and it can be partitioned into 3×3 = 9 sub-matrices each of which corresponds interactions between a pair of layers. For example, the marked sub-matrix ${\mathbf{I}}_q^{(2,2)}$ contains all interlayer terms of θ₂. In this example, the second layer is assumed to have more parameters than the other two (d₂ > d₁, d₃). The approximated FI matrix is 3×3, where the (i, j)-th element is the average of all elements in the (i, j)-th block in I_q (row (b)). This transformation can be done through a matrix multiplication of form EI_q(θ)E^⊤ where E is a 3 × d matrix structured according to the size and order of the layers, for example its second row has value $\frac{1}{d_2}$ in elements indexed by d₁ + 1, …, d₁ + d₂ and zero elsewhere (row (c)).

We transform down the full FI to a smaller matrix with a non-uniform average-pooling of I_q. More specifically, we form L × L matrix ${\tilde{\mathbf{I}}}_q$ such that its (i, j)-th element is the average of all elements in sub-matrix ${\mathbf{I}}_q^{(i,j)}$. It is easy to verify that this transformation can be written as the following matrix multiplication:

$${\tilde{\mathbf{I}}}_q=\mathbf{E}{\mathbf{I}}_q{\mathbf{E}}^{\top }$$ (2)

where E is a sparse L × n matrix. Considering the same ordering in block-wise set of parameters θ shown above, the i-th row of E is an all-zero vector except for d_i-th block of elements with indices (d₁+…+d_i−1+1), …, (d₁+…+d_i−1+d_i), which have value $\frac{1}{d_i}$ (Figure 2, third row). This matrix can be viewed as the Jacobian of the re-parameterization that transforms I_q to ${\tilde{\mathbf{I}}}_q$.

It is easy to show that ${\tilde{\mathbf{I}}}_q$ can be computed without explicitly forming I_q. Indeed, it is equivalent to Fisher information of a model with a score function equal to $\tilde{\mathbf{s}}(\mathit{\theta })={\left[\frac{1}{d_1}{\sum }_{\theta \in {\mathit{\theta }}_1}{\nabla }_{\theta }\ell (\mathit{\theta }),\dots ,\frac{1}{d_L}{\sum }_{\theta \in {\mathit{\theta }}_L}{\nabla }_{\theta }\ell (\mathit{\theta })\right]}^{\top }$, which contains layer-wise average of the original scores. Now, then the (i, j)-th element of the new model’s FI is

$$\begin{gathered} {\mathbb{E}}_{\mathbf{x},y}{\left[\tilde{\mathbf{s}}(\mathit{\theta })\tilde{\mathbf{s}}{(\mathit{\theta })}^{\top }\right]}_{i,j} \\ ={\mathbb{E}}_{\mathbf{x},y}\left[\left(\frac{1}{d_i}\sum _{\theta \in {\mathit{\theta }}_i}{\nabla }_{\theta }\ell (\mathit{\theta })\right)\left(\frac{1}{d_j}\sum _{\theta \in {\mathit{\theta }}_j}{\nabla }_{\theta }\ell (\mathit{\theta })\right)\right] \\ =\frac{1}{d_i{d}_j}\sum _{\theta \in {\mathit{\theta }}_i}\sum _{{\theta }^{\prime }\in {\mathit{\theta }}_j}{\mathbb{E}}_{\mathbf{x},y}\left[{\nabla }_{\theta }\ell (\mathit{\theta }){\nabla }_{{\theta }^{\prime }}\ell \left({\mathit{\theta }}^{\prime }\right)\right], \end{gathered}$$ (3)

which is, by definition, equal to the (i, j)-th element of ${\tilde{\mathbf{I}}}_q(\mathit{\theta })$. Hence, in order to form ${\tilde{\mathbf{I}}}_q$ we only need to form $\tilde{s}(\mathit{\theta })$ from the current model and use its outer-product from (3).

As mentioned before, computational complexity of solving (1) also depends on size of the unlabeled pool and increases quadratically with n. Hence, in practice it will be slow for large n values. In order to further accelerate our AL framework, we downsample the unlabeled pool to a subset that contains the most β uncertain samples (β < n). Such downsampling of the large pools via uncertainty filtering has already been used in accelerating pool-based AL methods [26], [44].

Gathering everything in one place and introducing L auxiliary variables, $t_1,\dots ,t_L\in ℝ$, similar to the shallow version of FI-based AL [26], we get the following SDP for our approximate FI-based AL:

$$\begin{gathered} \underset{q_1,\dots ,q_{\beta },t_1,\dots ,t_L}{\arg \min }{t}_1+\dots +t_L \\ \text{s.t.}\sum _{i=1}^{\beta }{q}_i=1,\underset{j=1}{\overset{L}{\oplus }}\left[\begin{array}{cc}{\sum }_i{q}_i{\tilde{\mathbf{I}}}_q(\widehat{\mathit{\theta }};{\mathbf{x}}_i)& {\mathbf{e}}_j\\ {\mathbf{e}}_j^{\top }& t_j\end{array}\right]⪰0, \end{gathered}$$ (4)

where ⊕ denotes matrix direct sum, q_i denotes the probability of querying the i-th unlabeled sample x_i after uncertainty filtering, and ${\tilde{\mathbf{I}}}_q({\mathbf{x}}_i;\widehat{\mathit{\theta }})$ is the conditional FI at the single sample x_i, defined as

$$\begin{gathered} {\tilde{\mathbf{I}}}_q({\mathbf{x}}_i;\widehat{\mathit{\theta }})={\mathbb{E}}_{y|{\mathbf{x}}_i,\widehat{\mathit{\theta }}}\left[\tilde{\mathbf{s}}(\mathit{\theta })\tilde{\mathbf{s}}{\left(\mathit{\theta }\right)}^{\top }\right] \\ =\sum _{y_i}\mathbb{P}(y_i|{\mathbf{x}}_i,\widehat{\mathit{\theta }})\tilde{\mathbf{s}}(\mathit{\theta })\tilde{\mathbf{s}}{\left(\mathit{\theta }\right)}^{\top }. \end{gathered}$$ (5)

C. Non-FI AL Methods

Here, we list and briefly describe the non-FI AL methods that we will compare against the FI-based AL in the next section. The name with which each paragraph starts represent the label that we will use to represent the corresponding method in the results section.

random: randomly querying k samples without replacement from the unlabeled pool $\mathcal{U}$;

entropy [6]: uncertainty sampling method with uncertainty measured by means of Shannon entropy function computed over the network’s class posterior probabilities; suppose the posterior of a sample x_i is denoted by p_i ∈ [0,1]^c where $p_{ij}=\mathbb{P}(y=j|{\mathbf{x}}_i,\widehat{\mathit{\theta }})$, then its uncertainty is measured by $H_S({\mathbf{p}}_i|\widehat{\mathit{\theta }})≔-{\sum }_{j=1}^c{p}_{ij}\log p_{ij}$.

MC drop-out [7]: uncertainty sampling method with uncertainty measured as the Shannon entropy of the average of class posterior probabilities in T = 20 Monte-Carlo (MC) parameter sets drawn from dropout distribution [7]; suppose the resulting posterior probability of the i-th sample in the τ-th MC run is denoted by ${\mathbf{p}}_i^{(\tau )}$, then the model’s uncertainty for the i-th sample would be estimated as $H_S\left(\frac{1}{T}{\sum }_{\tau =1}^T{\mathbf{p}}_i^{(\tau )}\right)$.

ensemble-S [10]: an uncertainty sampling method where the uncertainty is measured as the average of Shannon entropies based on an ensemble of networks; in each AL iteration, an ensemble of T = 7 networks was created as the following: in the first iteration where no labeled target sample was observed yet, multiple pre-trained models were obtained by repeatedly training models over the source data set with different random initializations and drop-out; in the intermediate t-th AL iteration (t ≥ 2), an ensemble was obtained by fine-tuning ${\mathcal{M}}_{t-2}$ with ${\mathcal{L}}_{t-1}$ for multiple times, each time using drop-out for the FC layers in order to get a slightly different model. After creating the ensemble $\left\{{\widehat{\mathit{\theta }}}^{(1)},\dots ,{\widehat{\mathit{\theta }}}^{(T)}\right\}$, the uncertainty is measured by computing Shannon entropy over the average of posterior probabilities of the ensemble, i.e. $H_S\left(\frac{1}{T}{\sum }_{\tau =1}^T{\mathbf{p}}_i^{(\tau )}\right)$, where $p_{ij}^{(\tau )}≔\mathbb{P}\left(y=j|{\mathbf{x}}_i,{\widehat{\mathit{\theta }}}^{(\tau )}\right)$.

ensemble-JS [12]: an uncertainty model similar to ensemble-S, except it uses Jensen-Shannon entropy over the ensemble posteriors rather than Shannon entropy; for the i-th sample, Shannon-Jensen entropy is defined as $H_{JS}\left({\mathbf{p}}_i^{(1)},\dots ,{\mathbf{p}}_i^{(T)}\right)≔H_S\left(\frac{1}{T}{\sum }_{\tau =1}^T{\mathbf{p}}_i^{(\tau )}\right)-\frac{1}{T}{\sum }_{\tau =1}^T{H}_S\left({\mathbf{p}}_i^{(\tau )}\right)$. This entropy measures the amount of disagreement among a given ensemble of posteriors, hence this algorithm can be viewed as a query by committee technique [45].

RepU [19], [20]: an AL algorithm that combines uncertainty with representativeness to query the most uncertain samples that also represent the unlabeled pool best [19]; although this algorithm was originally proposed for fully convolutional networks but it can be applied to patch-wise segmentation as well. It has the following steps: (1) selecting a certain number of most uncertain candidates B (size of B is set to 200 in our experiments in order to be consistent with our uncertainty filtering), (2) choosing a subset Q ⊂ B of size k which is most similar to the rest of the unlabeled pool $\mathcal{U}\backslash B$, with set-wise similarity defined as $\mathrm{sim}(Q,\mathcal{U}\backslash B)≔{\sum }_{\mathbf{z}\in Q}{\max }_{{\mathbf{z}}^{\prime }\in \mathcal{U}\backslash B}\cos \left(\mathbf{z},{\mathbf{z}}^{\prime }\right)$, where cos(·,·) is the cosine similarity, and z, z′ are features extracted from the second FC layer of our network. Since choosing Q that maximizes this similarity is an NP-hard problem, a forward greedy selection algorithm is used.

core-set [21]: this AL approach selects queries that best covers feature space of the data, which is shown to be equivalent to the k-center problem (facility location problem) [46]; this algorithm requires computing similarities between the pool samples and the labeled data set ${\mathcal{L}}_{t-1}$ that is obtained until the t-th iteration, and greedily adding unlabeled samples that have the largest distance to their nearest neighbor in ${\mathcal{L}}_{t-1}$. This similarity can be computed using the same set-wise similarity that was used for performing RepU. In the first iteration, we do not have any labeled sample from the target subjects $({\mathcal{L}}_0=Ø)$, hence we consider labeled voxels from the source subjects. Note that here it is assumed that we still have access to the source data set, which is not always the case in practice.

Among the competing methods explained above, entropy, MC dropout, ensemble-S and ensemble-JS are examples of different US techniques, and RepU and core-set are geometrical AL algorithms.

III. Experimental Settings

We evaluated performance of the proposed AL framework in the application of patch-wise brain extraction using T1- and T2-weighted MR images. Our experiments had flavor of transfer learning: given a CNN model pre-trained over a source data set, the goal was to fine-tune this model to a target data set with different properties than the source, using the smallest number of additional target data to be labeled. Depending on the number of target subject(s), we had the following two scenarios:

• Universal AL, where subjects of the target data set were divided into pool and test partitions. We used voxels of the pool subjects as the unlabeled pool from which the voxel queries were selected, whereas the test subjects were used only to evaluate the performance of the resulting model on the target data set.

• Active semi-automatic segmentation, where individual subjects of each data set were considered separately. We selected the queries from the same subject to refine the model for that specific subject by labeling only a small number of new samples from that subject. We evaluated the final model by comparing the resultant segmentation for each subject with the corresponding ground truth segmentation.

A. Data

We used brain images of 10 healthy adolescent subjects as our source data set to train ${\mathcal{M}}_0$. We considered four pediatric data sets as target: newborns and subjects with tuberous sclerosis complex (TSC) divided into three age groups of (Gr1) younger than six months, (Gr2) between six months and one year old, and (Gr3) older than one year. The latter data set contained 25 normal newborn subjects provided by the Developing Human Connectome Project [47], and the other three groups contained 26 subjects from 2 months old to 2.5 years old, whose MRI images were acquired in five TSC centers throughout the United States (data set with different health conditions). The three age groups of this data set had nine, nine and eight subjects, respectively. Sample 2D axial slices from each data set are shown in Figures 3a to 3c, indicating different visual characteristics. Pediatric brain presents specific challenges for segmentation because of marked intra- and inter-variation in head size and shape in early life, rapid changes in tissue contrast associated with myelination, and low contrast to noise ratio compared to adult brain MRIs. Newborn MR images in particular have different intensity contrast compared to older children and adult brain images.

Fig. 3.

Sample axial slices of T1-weighted (first row) and T2-weighted (second row) MRI images from the data sets used in the experiments. The interior region of the green boundary is the ground-truth brain mask. These samples show contrast differences between source and target populations, especially between newborns and adolescents.

B. Technical Details

In patch-wise segmentation, any voxel is a data sample represented by a patch around it containing the voxel itself and some of its neighbors. In our initial experiments of brain extraction, we examined different patch sizes from axial slices and chose 2D patches of size 25×25 as the best choice. Having two modalities of T1- and T2-weighted images, each voxel is represented by a 25 × 25 × 2 patch from each modality. Architecture of the CNN model that we used is shown in Figure 4. This model has four convolutional layers and three fully connected (FC) layers (L = 7). Furthermore, there exists a ReLU activation function after each layer, except the last layer that is followed by a soft-max activation to give class posteriors.

Fig. 4.

Architecture of the CNN model used in our experiments. The input is concatenation of two 25 × 25 patches from T1w and T2w images, and the output is a binary posterior probability. The numbers shown in “Conv.” blocks represent the size and number of the kernels, and those in “FC” blocks show the number of output nodes.

An initial model ${\mathcal{M}}_0$ was trained with the network’s parameters initialized according to [48]. Then, we ran various AL algorithms to make improvement on ${\mathcal{M}}_0$ with k = 50 until the total number of queries reach 600. Note that in practice, our algorithm requires a single click for labeling the central voxel of a query patch. In other words, each AL iteration consists of k user clicks. In the t-th AL iteration, the model got updated by fine-tuning ${\mathcal{M}}_{t-1}$ for 60 epochs using all labeled samples available from the previous iterations. In both initial training of ${\mathcal{M}}_0$ and partial fine-tuning of ${\mathcal{M}}_t$, we used Adam optimizer with learning rate of 10⁻⁵ and drop-out rate of 0.5 only for FC layers. The CNN models were built using the TensorFlow package and the SDP of FI-based AL in (4) was solved using MOSEK solver [49] of CVXPY package [50], [51].

We compared our FI-based AL algorithm with a list of other AL algorithms explained in Section II-C. In addition to these techniques, we also compared the results of the networks trained using the competing AL algorithms with several brain extraction baseline methods from the literature, including BET [52], ROBEX [53] and volBrain [54]. When running BET, we set the fractional intensity threshold to 0.1 and the vertical gradient of fractional intensity to −0.1. The results of volBrain algorithm were obtained through their online automated system¹.

For evaluating any given model resulted from AL iterations or baseline methods, we compared the corresponding predicted segmentation map after post-processing with the ground-truth mask. The post-processing steps included 3D connected component analysis, i.e., keeping only the largest 3D component, and morphological operations for filling its holes. We used Dice score and average surface distance (ASD) as two evaluation metrics.

IV. Results

In this section, we demonstrated the results of our experiments using the proposed FI-based AL, other competing AL methods and the brain extraction baselines. See section III for more details on the experimental setting.

A. Universal Active Learning

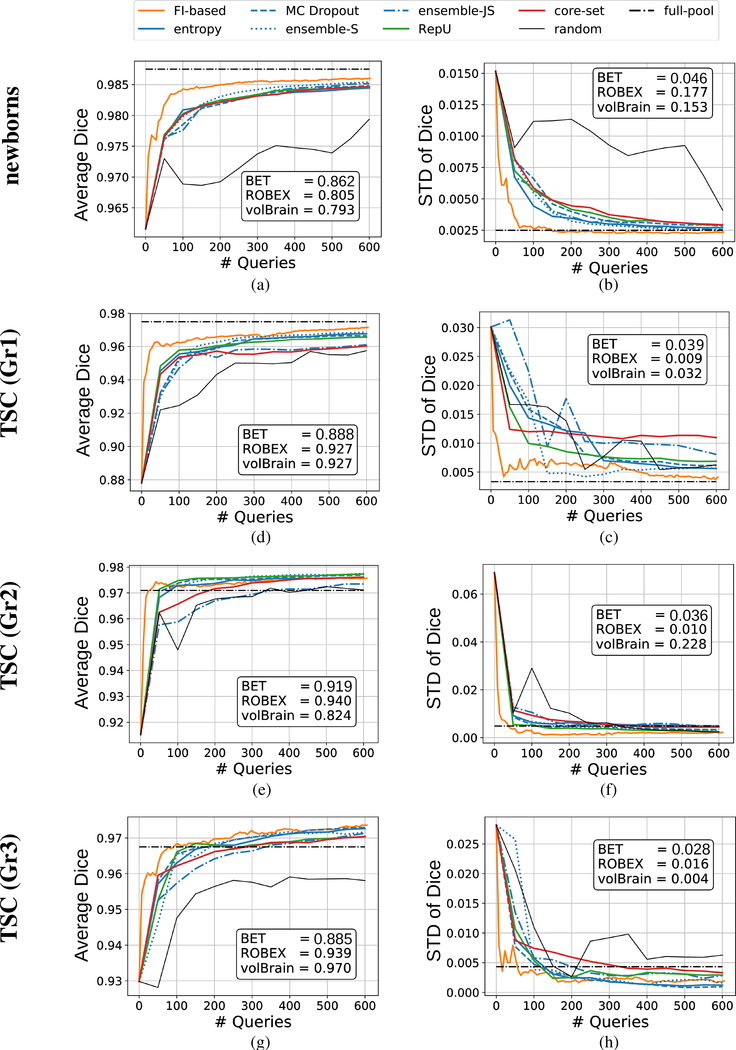
Average values and standard deviation of the two evaluation metrics, i.e. Dice coefficient and ASD, computed for all universal AL iterations are shown in Figures 5 and 6. For each AL iteration, the statistics are taken over the test subjects of the corresponding target data set. These curves show that based on both metrics, FI-based AL could converge to a high-accuracy model faster (i.e. using less samples to be annotated) than other AL methods. The converged accuracy of the proposed FI-based AL is comparable to that of the full-pool training, when the number of labeled samples at the end of the AL experiments is less than 0.5% of size of the pool. Indeed, for two data sets the AL models could achieve even higher accuracy than the model that used all the pool samples for training. Moreover, observe that all the baseline methods resulted in significantly weaker performance, in some cases even worse than the pre-trained model².

Fig. 5.

Evaluating Dice coefficients of the models obtained from universal AL algorithms that were executed to select up to 600 queries (colored curves), models that were trained using all unlabeled samples in the pool (the horizontal dash-dotted line labeled as “full-pool”), and the baseline methods (reported in text-boxes within the figures).

Fig. 6.

Evaluating Average Surface Distance (ASD) criterion for the models obtained from universal AL algorithms that were executed to select up to 600 queries (colored curves), models that were trained using all unlabeled samples in the pool (the horizontal dash-dotted line labeled as “full-pool”), and the baseline methods (reported in text-boxes within the figures).

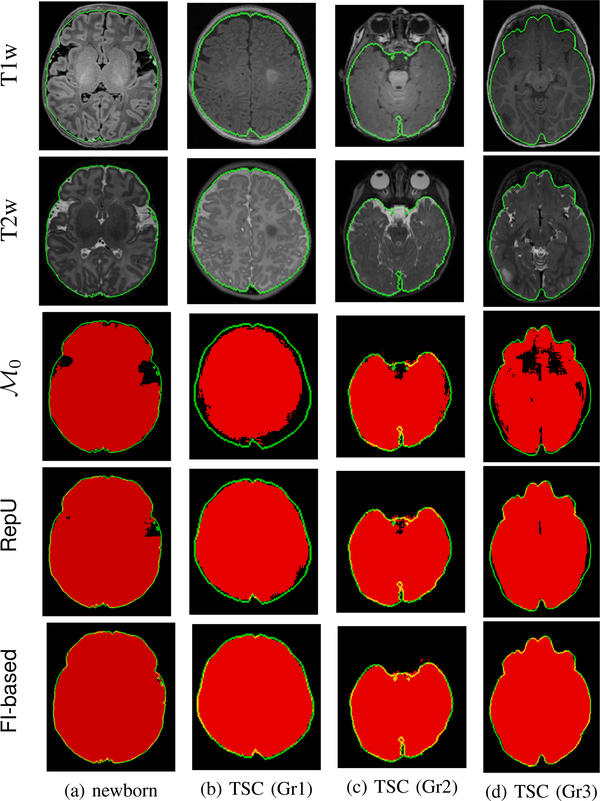
We also visualized segmentation of sample slices by different AL models in Figure 7. These are the results of early AL iterations. More specifically, for a given target data set, we took models obtained after labeling up to 50 queries from the corresponding target data set and used them to segment a sample slice from a test subject. The results indicate the fine details where FI-based AL outperformed other methods. The difference is obvious for the newborn’s sample slice where T1w image was not enough for extracting several parts of the brain. Visualizing the same slice from T2 modality (see Figure 8a) reveals that T2w image can be used to remove this ambiguity. However, only FI-based AL was successful in creating a model which could properly grasp information from both modalities. Failure of baseline methods to segment this slice is also demonstrated in Figures 8b to 8d. BET and ROBEX missed the main structure by undersegmenting and oversegmenting the brain in the selected slice, respectively. Moreover, volBrain could distinguish the overall structure but resulted in too many false positives.

Fig. 7.

Segmentation of a sample test slice from each target data set using models from early AL iterations (after labeling up to 50 queries by each method). Each row corresponds to a single target data set, where the first image is the original slice from the T1-weighted MRI image together with the ground-truth mask (interior region of the green boundary), and the rest show the segmentation results. The red voxels represent those that are marked as brain by the corresponding models. Ideally, all the voxels inside the green boundaries should be red.

Fig. 8.

T2-weighted image and the baseline results of the newborn slice shown in Figure 7.

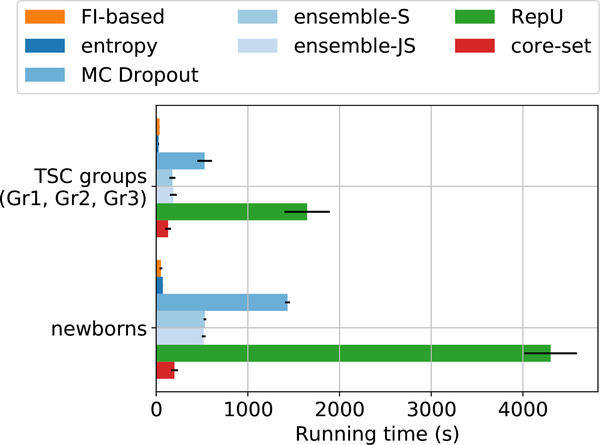
We noticed that FI-based AL algorithm was faster than other methods in all the experiments. Figure 9 shows average running time duration of all the AL techniques used in this paper. All the experiments were run on a 2.6GHz Intel Xenon CPU and an NVIDIA GeForce GTX 1070 Ti GPU. The slowest AL method was RepU which showed best performance among the other non-FI AL algorithms based on Figure 5.

Fig. 9.

Average running time of a single AL iteration for different methods. The average values are reported for the three TSC groups and newborns data sets separately as the image dimensions in the latter are larger. Notice that FI-based AL is significantly faster than most other competents.

B. Active Semi-automatic Segmentation

Average and standard deviation of Dice coefficients computed for all the AL iterations are reported in Figure 10. Similar to universal active learning, we observed that FI-based AL in average achieved higher model accuracy with less number of queries. Among other non-FI AL methods, ensemble-JS was significantly worse than others, and RepU and ensemble-S were comparable to FI-based approach. Furthermore, note that the convergent Dice scores in semi-automatic segmentation experiments were generally better than those in universal AL. This is expected because specializing a learning model to smaller data set (e.g., a single subject) is generally easier than training a model that is generalizable to large data sets.

Fig. 10.

Evaluating models obtained from semi-automatic segmentation AL algorithms that were executed to select up to 400 queries (colored curves), and the baseline methods (reported in text-boxes within the figures). For each metric, the first row shows the average values and second row shows the standard deviations (taken over all the subjects in target data set).

Segmentation of sample slices with different models in these experiments are shown in Figure 11. One subject per group was chosen to visualize segmentation results obtained by the pre-trained model ${\mathcal{M}}_0$, and the models achieved by two AL methods in early iterations (after labeling up to 50 queries): FI-based and the best non-FI AL method in terms of the average Dice scores, which was RepU. It is clear that FI-based AL resulted in more accurate segmentation results with much fewer false negatives.

Fig. 11.

Segmentation of sample slices from different subject groups in active semi-automatic segmentation experiments. Each column corresponds to a single subject. The first two rows show the slice from T1- and T2-weighted images together with the ground truth mask (green boundaries). The third row shows the results obtained by the initial pre-trained model, and the last two rows show the results of RepU method, as the best method among non-FI AL techniques in terms of average Dice scores, and FI-based AL. For the subjects considered in columns (a) to (d) and the AL iterations whose results were shown, the FI-based AL (considering all slices) improved Dice scores of ${\mathcal{M}}_0$ by 3.16%, 8.21%, 1.19% and 6.54%, respectively.

V. Conclusion

In this paper, we proposed to use an active learning (AL) objective based on Fisher information (FI) for CNN models. In order to make FI-based computations tractable for deep models, we shrunk the parameter space by an implicit model reparametrization. Our experiments included various transfer learning scenarios, where we started from a pre-trained model obtained from a source data set and executed AL for intelligent labeling of small number of target samples in order to fine-tune the initial model. We used 10 adolescent subjects as our source, and considered four target data sets: newborn subjects and patients with TSC lesions that came from 3 different age groups. We evaluated the proposed AL framework in the context of patch-wise brain extraction. The results were presented in two scenarios of (1) universal AL to build a model for multiple target subjects, and (2) active semi-automatic segmentation to personalize a model for a single subject. The results showed that FI-based AL outperformed a comprehensive list of recently proposed AL techniques and brain extraction baseline approaches in reducing the number of samples that need to be labeled for training a high-quality patch-wise segmentation method. We saw that, in the worst case of universal AL, labeling only a 0.25% of the target subjects with FI-based AL achieved about 99.7% of the model that used all target subjects for training. Furthermore, in best the case of universal AL, the FI-based model even improved the fully-trained model by around 0.6% of Dice score.

There are still some difficulties in implementing FI-based AL. One of them is the computational complexity of the SDP that is involved. Here, we did uncertainty filtering in order to downsample the unlabeled pool and speed-up solving this optimization. The downside of this filtering is that the true performance of FI-based AL cannot be reached because such filtering could also throw away useful samples. Future work involves developing other approaches to reduce the complexity of optimization while realizing the full capacity of FI-based deep AL. Another important direction of future work is to extend FI-based AL to fully convolutional networks (FCNs). In contrast to CNNs with fully connected final layers that output only a single probability distribution, FCNs output a map of class probabilities associated with the full segmentation map of the input. Therefore, computing FI matrix for FCNs will require modeling the joint distribution of class labels of all voxels.