Efficient Pharmacokinetic Modeling Workflow With the MonolixSuite: A Case Study of Remifentanil

Abstract

MonolixSuite is a software widely used for model‐based drug development. It contains interconnected applications for data visualization, noncompartmental analysis, nonlinear mixed effect modeling, and clinical trial simulations. Its main assets are ease of use via an interactive graphical interface, computation speed, and efficient parameter estimation even for complex models. This tutorial presents a step‐by‐step pharmacokinetic (PK) modeling workflow using MonolixSuite, including how to visualize the data, set up a population PK model, estimate parameters, and diagnose and improve the model incrementally.

Drug development is increasingly supported by mathematical models that allow one to better understand the drug’s behavior and to optimize the next development steps, for example, during clinical trials. Examples of applications include the characterization of the pharmacokinetics (PK), pharmacodynamics (PD), disease progression, or patient survival.

The data supporting these models are typically patient‐level longitudinal (i.e., over time) data. A powerful framework to capture this type of data is the population approach, which aims at describing the typical drug behavior in the population as well as the variability observed from individual to individual. These two aspects are best described using nonlinear mixed effect (NLME) models. The term nonlinear refers to the function describing the physical and biological mechanisms, also called “structural model.” The structure of the structural model is the same for all individuals, but its parameter values vary between individuals. “Mixed effect” refers to the probabilistic description of the individual parameter values, which includes fixed effects (same for all individuals), random effects, and possibly individual characteristics called covariates. Together with the measurement error model (also called residual error), this constitutes the statistical part of the NLME model.

The NLME framework is a rigorous environment to model and simulate different types of data, but it requires (i) efficient algorithms to fit possibly complex models to large data sets and (ii) a user‐friendly way to define and interpret the models. Monolix (Lixoft, Antony, France) was developed after a 7‐year research program to meet both requirements. It incorporates many innovations, such as the stochastic approximation expectation‐maximization (SAEM) estimation algorithm1 and its extension to censored data,2 numerous diagnostic tools,3 and automatic model‐building procedures. The combination of quick and efficient algorithms with a clear and interactive interface leads to a particularly fast learning curve for the user.

Monolix is now part of MonolixSuite—a set of interconnected software applications that covers all stages of drug development. These applications help in data visualization (Datxplore), noncompartmental analysis of the data (PKanalix), NLME model development and parameter estimation (Monolix), simulations of new situations (Simulx), and workflow management (Sycomore). Moreover, MonolixSuite satisfies regulatory requirements and it has been routinely and successfully used for regulatory submissions.

The aim of this tutorial is to show step‐by‐step a modeling workflow using MonolixSuite on a typical PK data set. We assume that the reader has no familiarity with the software, but we recommend basic knowledge of population PK/PD modeling. For a didactic and comprehensive introduction to this topic, we refer the reader to previous tutorials presented in this journal.4, 5

OUTLINE

This tutorial is structured in four sections. We first give a brief introduction of the software applications of MonolixSuite. Then we show step by step how to develop a model on a typical PK data set. This includes the structural model definition, its diagnosis, and a covariate search. More advanced features, not directly used in this tutorial, are also briefly reviewed.

All the material necessary to reproduce the results from this tutorial is available as Supplementary Material : data set, step‐by‐step instructions with numerous screenshots, all Monolix runs and the Sycomore project, as well as a video showing the main modeling steps.

SOFTWARE

MonolixSuite is composed of several interconnected applications that enable a very efficient modeling and simulation workflow.6 A project can be carried from one application to another without having to redefine the project’s fundamental features such as the data set or model. The role of each application is presented next. In this tutorial, we use Datxplore, Monolix, and Sycomore.

Datxplore

Datxplore is an interactive software for the exploration and visualization of longitudinal data. It provides various graphics (spaghetti plots, survival curves, covariates histograms, etc.) to give insights about the data at hand. Plots can easily be customized by splitting/filtering/coloring.

Monolix

Monolix is dedicated to NLME modeling. Its graphical user interface, large library of built‐in models, and robust and fast parameter estimation make it an easy to use and efficient application. Moreover, it includes automated generation of diagnostic plots, statistical tests to guide the model development, and automatic model‐building procedures. Monolix also comes with an R API (http://monolix.lixoft.com/monolix-api/) and thus can be used via R scripts. In addition, the R package Rsmlx (R Speaks Monolix; http://rsmlx.webpopix.org) provides further methods for model building and evaluation, such as bootstrap and likelihood profiling.

Sycomore

Sycomore enables the visual and interactive explorations of a modeling workflow. It allows users to keep an overview of the Monolix runs and their hierarchy and launch and compare them side by side.

Simulx

Simulx is a powerful and flexible simulator to study new situations and plan clinical trials. It is also used for interactive exploration and visualization of complex models.

PKanalix

PKanalix is a user‐friendly and fast application for compartmental and noncompartmental analysis. It uses industry‐standard methods within a straightforward workflow, which includes clear settings, output tables, and automatic plots.

MonolixSuite is available for all major operating systems, and a free license can be requested for academic usage at http://httpRequestLicense://lixoft.com/downloads/#RequestLicense. Readers from industry can ask for a trial license.

TUTORIAL

Introduction

This tutorial shows how to use MonolixSuite to build a population PK model for remifentanil. Remifentanil is an opioid analgesic drug with a rapid onset and rapid recovery time. It may be used alone for sedation or be combined with other medications for general anesthesia. It is given in adults via continuous intravenous (i.v.) infusion with doses that may be adjusted depending on the age and weight of patients. The goal of the PK analysis is to determine the influence of the patient’s covariates on the individual parameters.

The model development makes use of a publicly available data set of remifentanil’s PK.7 The data comprise dense remifentanil concentration measurements for 65 healthy adults following an i.v. infusion at a constant infusion rate. The infusion rate varies between subjects from 1 to 8 µg/kg/minutes and lasts from 4 to 20 minutes.

The plan of this tutorial is as follows: The data set is first visualized with Datxplore to identify general trends of the data and to promote the formulation of modeling hypotheses. These hypotheses are then implemented in a population PK model, which is evaluated using Monolix. Sycomore is used to keep an overview of the stepwise model development.

Data set format

The data must be formatted as.txt or.csv text file with tabulation, comma, space, or semicolon delimiters. It follows the usual format for patient‐level data sets for pharmacometrics: Each row corresponds to a dose or an observation record for one patient. In each row, separate columns record the subject identifier, the dose information (in this example time in minutes, dose amount in µg, and rate of infusion in µg/minutes), the observations (PK measurements in µg/L), and the patient characteristics (age in years, sex (M = male, F = female), lean body mass (LBM) in kg, and infusion duration in minutes). Columns names are written in a header and can be freely chosen. An extract of the data set used in this tutorial can be seen in the Supplementary Material .

When applicable, the data set can contain further information such as the limit of quantification, several types of observations (PK and PD or parent and metabolite, for instance), or flags to ignore specific lines from the analysis. A full description of all possible column types and their format rules is presented online (http://www.dataset.lixoft.com).

Note that MonolixSuite does not handle units, and it is the user’s responsibility to ensure the consistency of the data set’s units and to infer the units of the thereafter estimated model parameters.

Data set visualization with Datxplore

As a first step of this tutorial, Datxplore is used to display a graphical representation of the data set. After opening Datxplore, the data set must first be loaded (menu: Project > New > Browse). The data set table is displayed in the interface and drop‐down menus allow to tag each column from a predefined set of column types. Columns with standard header names are automatically tagged. In this example, it is the case for the following columns: ID tagged as ID, TIME as TIME, AMT as AMOUNT, RATE as INFUSION RATE, DV as OBSERVATION, AGE as CONTINUOUS COVARIATE, and SEX as CATEGORICAL COVARIATE. The LBM and TINFCAT (infusion duration) columns can be manually tagged as CONTINUOUS COVARIATE and CATEGORICAL COVARIATE, respectively.

MonolixSuite allows the user to specify and save (menu: Settings > Preferences) data set header names that should be automatically associated with given column types.

Clicking on “accept” automatically generates several plots to visualize the data. The Data Viewer tab shows the observations vs. time as a spaghetti plot (i.e., dots corresponding to the same individual are connected by lines). In all MonolixSuite applications, the panel on the right of the interface offers many customization options. The “Settings” tab allows to choose what to display: Linear/log scale, display of dosing times as vertical lines, display of the number of individuals, etc. The “Preferences” tab allows to choose the size of labels, the background color, etc. The “Stratify” tab allows to split, color, or filter the plot using the columns tagged as continuous or categorical covariates.

In Figure 1a , the spaghetti plot of concentrations vs. time is split in four stratification groups using the infusion duration categorical covariate TINFCAT. The stratification is created by selecting TINFCAT in the Stratify panel with the “split” option and rearranging the seven TINFCAT categories into four groups (see the Supplementary Material for the click‐by‐click instructions). For the purpose of the tutorial, the data are also colored according to two LBM groups with an equal number of individuals in each group.

Figure 1.

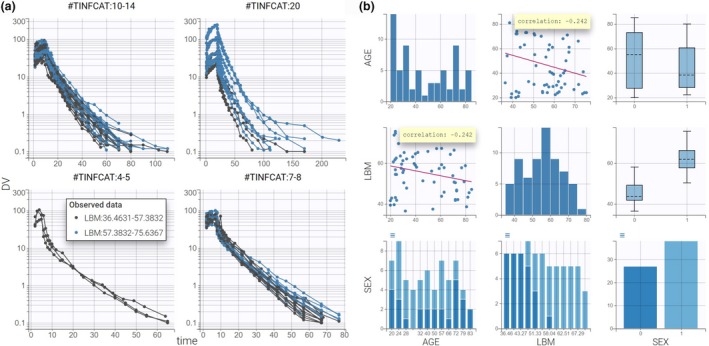
Data visualization with Datxplore. (a) Spaghetti plot of remifentanil concentrations (y axis) with respect to time (x axis) split by TINFCAT and colored by LBM. (b) Covariate viewer with LBM, AGE, and SEX selected. Correlation coefficients are overlaid on the scatterplots. DV, observed concentrations; LBM, lean body mass.

These plots show that the remifentanil concentration increases during the infusion and decreases afterward. The elimination phase of the remifentanil’s concentration in a y‐log scale has several slopes over time, which suggests using a PK model with several compartments. Moreover, LBM seems to influence the PK as the PK curves corresponding to the high values of LBM (in green) appear mostly above the others (in red).

The “Covariate Viewer” (Figure 1b ) tab presents a matrix of the covariate‐by‐covariate plots. The subplots on the diagonal show the distribution of each covariate. The off‐diagonal subplots are useful to identify correlations between covariates, such as between LBM and AGE, and LBM and SEX.

Upon saving the Datxplore project, all settings, preferences, and stratifications options are stored and can be retrieved by loading the saved.datxplore file into Datxplore.

In summary, the data exploration in Datxplore has revealed the following insights:

• A model with several compartments is probably necessary to describe this data set.

• LBM might influence the PK.

• LBM and AGE are negatively correlated, and males have higher LBM values than females.

These insights will guide the model‐building process detailed in the next sections.

Model development and diagnosis using Monolix

Monolix run setup. The Monolix interface is organized in successive tabs that guide the user to define a run.

Definition of the data. The Datxplore project can be directly exported into Monolix with “Export > Export to Monolix.” This opens Monolix and transfers the data set information (i.e., path to data set file and column tagging) from Datxplore to Monolix. Clicking on “Next” leads the user to the next Monolix tab “Structural model.”

Alternatively, the user could open Monolix, start a new project, load the data set, and tag the column as described for Datxplore. For data visualization, it is also possible to open Datxplore from Monolix using the “Data Viewer” button.

Definition of the structural model. In Monolix, the structural model is defined in a separate text file. It is possible to write a new model file from scratch or pick a model file from the wide collection of predefined models, which are available in the following seven model libraries: PK, PD, joint PKPD, PK with double absorptions (with any combination of absorption types), target‐mediated drug disposition, time‐to‐event, and count models. Each library can be easily browsed using filters.

For this tutorial data set, a two‐compartment model is chosen as a first try because data visualization in Datxplore suggested a model with several compartments. This model is available under the name infusion_2cpt_ClV1QV2.txt in the Monolix PK library via “Load from library” and selecting the following filters: “infusion,” “2 compartments,” and “linear elimination.” Once the model is selected, it is displayed within the interface in the tab “Structural model”:

DESCRIPTION:
The administration is via an infusion (requires INFUSION RATE or INFUSION DURATION column‐type in the data set). The PK model has a central compartment (volume V1), a peripheral compartment (volume V2, intercompartmental clearance Q), and a linear elimination (clearance Cl).

[LONGITUDINAL]
input = {Cl, V1, Q, V2}
EQUATION:
; Parameter transformations
V = V1
k = Cl/V1
k12 = Q/V1
k21 = Q/V2
; PK model definition
Cc = pkmodel(V, k, k12, k21)
OUTPUT:
output = Cc

Library and user‐defined models are written using the Mlxtran language, which has been developed to ease the definition of pharmacometric models. The input line contains the parameters to estimate, whereas the output line defines the model variable(s) corresponding to the observations recorded in the data set. In between, the model can be defined using either a system of ordinary differential equations or macros, which are simple shortcuts to define the model components. In the previous example, the model definition relies on the macro pkmodel (documentation: http://mlxtran.lixoft.com/pkmodel/), which allows one to define standard PK models based on the list of parameters acting as recognized keywords. In the backend, the pkmodel macro is automatically replaced by the closed‐form analytical solution written in efficient C++ code.

To write user‐defined models, it is often convenient to start from a library model and modify it in the MlxEditor. This Mlxtran dedicated editor allows to check the model consistency by clicking on the button “compile.” Syntax errors prompt clear messages to help the user identify the mistakes. A comprehensive documentation of the Mlxtran language with numerous examples is available online (http://mlxtran.lixoft.com/).

When a model contains several outputs, the mapping panel on the right‐hand side of the “structural model” tab allows to flexibly map the model outputs to the several observation types present in the data set.

Finally, it has to be noted that the model file contains only the structural model. The statistical part of the model, which includes the error model and parameter distributions, is defined via the interface at next steps. Moreover, the likelihood objective function is always inferred by Monolix automatically, for any type of data (continuous, time to event, count, categorical, and any combination of those). This is also the case for censored data: Data below the lower limit of quantification, for instance, are automatically taken into account in the likelihood as the probability of having an observation within an interval.

Selection of the initial values. Selecting the structural model leads the user to the next tab “Initial estimates” to set the initial values for the population parameters. The “Check initial estimates” subtab displays individual plots to easily compare the predictions, based on the given initial values, with the individual data. Although Monolix is quite robust with respect to initial parameter values as a result of its efficient implementation of SAEM, choosing reasonable initial estimates is a good practice to speed up the convergence of the parameter estimation. The key is to find initial values such that the predictions display the key features of the model. For a two‐compartment model, this corresponds to two slopes in the elimination phase on log‐scale. For models from the PK library, initial values are found automatically by Monolix, when clicking on the “autoinit” button, via computation of noncompartmental analysis–like empirical rules followed by an optimization step on the pooled data.

To finalize this step, the initial values must be applied by clicking “Set as initial values.” This also brings the user to the next tab: “Statistical model & Tasks.”

Definition of the statistical model. The “Statistical model & Tasks” tab is used to define the statistical model and run estimation tasks. The statistical model is composed of the residual error model (also called observation model) and the individual model for the parameters.

By default, the observation model is set to a combined residual error model with an additive and a proportional term. Its formula, which can also be seen in the interface, is:

$$\text{DV}=\text{Cc}+(\mathrm{a}+\mathrm{b}\ast \text{Cc})\ast \mathrm{e}$$

where DV represents the observations from the data set (its name comes from the header of the observation column), Cc is the output of the structural model, and a and b are the parameters of the residual error model. e is a standard normal random variable generating the residual error.

A combined error model is usually a good choice for the first run. If necessary, the error model can later be changed to constant, proportional, or combined2 (which includes a square root in the formula) from the drop‐down menu. It is also possible to define a transformation of the observations and model outputs directly via the interface, for instance, to implement an exponential error model.

The default choice for the individual parameters Cl, V1, Q, and V2 is a log‐normal distribution within the population because their values should stay positive. Other available distributions are normal, logit‐normal, and probit‐normal. More complex distributions are also possible but must be encoded directly in the structural model.

By default, no correlations between random effects are assumed. This corresponds to a diagonal variance–covariance matrix. Similarly, covariate effects are not included at first. The set of formulas describing the parameter distribution can be seen in the interface. For example, the formula for the parameter Cl is the following:

Chemical Formula: $\log (\text{Cl})=\log (\text{Cl}\_\text{pop})+\text{eta}\_\text{Cl}\iff \text{Cl}={\text{Cl}}_{\text{pop}}{e}^{\mathrm{\eta }\text{cl}}$

where eta_Cl represents the random effect defining the interindividual variability for Cl. It is automatically defined in Monolix as a normal random variable with zero mean and a standard deviation to be estimated. The distribution of Cl is thus defined with two population parameters: Cl_pop, the typical value of Cl in the population, and omega_Cl, the standard deviation of eta_Cl.

Running the estimation tasks. Once all of the elements of the model have been specified, several tasks can be run in the “Statistical model & Tasks” tab. It is important to save the project before running (Project > Save as) because it will save the results as text files in the same folder. In this tutorial, the first run is saved as PK_01.mlxtran. This human‐readable text file contains all the elements necessary to define the run, ensuring the reproducibility.

Tasks can either be run one by one by clicking on the corresponding buttons, or several tasks can be run at once by selecting all desired tasks and clicking on the green arrow “Run scenario.” Below each task is described in detail.

Estimation of the population parameters. The estimation of the population parameters is the first and a mandatory task. It is run by clicking on “Population parameters” (http://monolix.lixoft.com/tasks/population-parameter-estimation-using-saem/). Monolix relies on a very efficient implementation of the SAEM algorithm1 to find the population parameters that maximize the likelihood, i.e., the objective function. When launching the task, a pop‐up window opens so that the user can follow the evolution of the population parameter estimates over each of the algorithm iterations (Figure 2a ).

Figure 2.

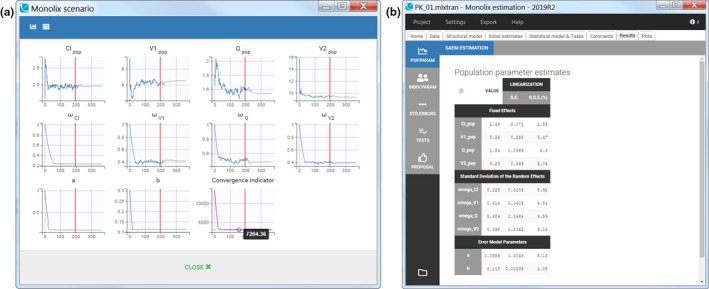
First Monolix run. (a) Scenario window with the convergence of population estimates. (b) Table of population parameter estimates and their standard errors.

The SAEM algorithm is split in two phases separated by the vertical red line on each subplot. During the first phase, called exploratory, the algorithm explores the parameter space and gets to a neighborhood of the maximum likelihood estimate. In the second phase, called smoothing, the estimates stabilize toward the maximum likelihood. The switch from the exploratory to the smoothing phase is done according to convergence criteria, which take among other into account the stability of the parameter estimates. In case the algorithm fails to converge, a warning message appears and the convergence trajectories for each parameter help the user spot which parameter did not stabilize and might be unidentifiable.

Once the task is completed, the estimated values can be found in the tab “Results” (Figure 2b ) as well as in a text file in the result folder created by Monolix next to the saved.mlxtran file.

Estimation of the empirical Bayes estimates (EBEs). The EBEs are the modes of the conditional distributions for the parameters of each individual (conditional on the estimated population parameters and on the individual data). They represent the most likely parameter values for each individual. They can be calculated by clicking on the task “EBEs” (http://monolix.lixoft.com/tasks/ebes/). The estimated individual parameter values are displayed in the tab “Results” as well as saved in the result folder. These values are used to calculate the individual predictions in the plots “individual fits” and “observations vs. predictions.”

Estimation of the conditional distribution. The conditional distribution represents the uncertainty of the individual parameter value given the estimated population parameters and the data for each individual. The task “conditional distribution” allows to sample sets of individual parameters from the conditional distributions via a Monte Carlo Markov Chain procedure (http://monolix.lixoft.com/tasks/conditional-distribution/). These sets are plausible parameter values for each individual, whereas the EBEs presented previously are the most probable parameter values. They are useful to calculate the corresponding random effects used for instance in the plots “correlation between random effects” or “individual parameters vs covariates.” Because they take into account the uncertainty of the individual parameters, they circumvent the phenomenon of shrinkage, which can affect EBEs when the data are sparse. In this way, they increase the reliability of diagnostic plots.3

Estimation of the standard errors. The standard errors correspond to the uncertainty of the estimated population parameters. In Monolix, they are determined via the calculation of the Fisher Information Matrix. To calculate the standard errors using bootstrap instead, a function is provided in the R package Rsmlx (for “R speaks Monolix”) to generate case‐resampled data sets and run Monolix on each.

When clicking on the task “standard errors” (http://monolix.lixoft.com/tasks/standard-error-using-the-fisher-information-matrix/), the Fisher Information Matrix is calculated either via a linear approximation based on the Taylor expansion around the EBEs (if the option “use linearization method” is checked) or via a stochastic approximation using the exact model. The linearization method is usually faster but can be less accurate than the stochastic approximation.

After running the task, the standard errors and relative standard errors associated with each parameter are displayed in the table of population parameters in the tab “Results.” Small relative standard errors (RSEs), e.g., RSE < 15%, mean that parameters are estimated with good confidence. In the “Std.Errors” tab, the correlation matrix of the estimates is shown. Values close to 1 or −1 on off‐diagonal terms indicate that the corresponding population parameter values are highly correlated. Strong correlations often suggest a poorly identifiable model. The condition number is displayed in the same tab as “max/min eigenvalue” and can also be used to detect overparameterization.

Estimation of the likelihood. The likelihood is the objective function used during the population parameter estimation. Although the likelihood is maximized during the population parameter estimation task, its final value is not known because the SAEM algorithm does not require to compute it explicitly during the optimization. Therefore, there is a dedicated task to calculate the likelihood (link to documentation) using importance sampling or a linearization method to speed up the calculation.

Once the task is completed, the value of −2 log‐likelihood (−2LL), the Akaike information criteria (AIC), the Bayesian information criteria (BIC), and a corrected version of the BIC (BICc) are displayed in the “Result” tab. In opposition to the −2LL, the information criteria include a penalty based on the number of parameters.8

Generation of diagnostic plots. Monolix provides a large set of built‐in diagnostic plots that greatly help the user to diagnose the model. The plots are generated by running the “Plots” task (http://monolix.lixoft.com/graphics/). By default, a subset of possible plots is generated and other plots can be selected via the list icon next to the button “Plots.” The following plots are available:

• Data

  1. Observed data

• Model for the observations

  1. Individual fits

  2. Observations vs. predictions

  3. Scatter plot of the residuals

  4. Distribution of the residuals

• Model for the individual parameters

  1. Distribution of the individual parameters

  2. Distribution of the random effects

  3. Correlation between random effects

  4. Individual parameters vs. covariates

• Predictive checks and predictions

  1. Visual predictive check

  2. Numerical predictive check

  3. Below level of quantification predictive check

  4. Prediction distribution

• Convergence diagnosis

  1. Population parameters (SAEM) convergence

  2. Conditional distribution (Monte Carlo Markov Chain) convergence

  3. Likelihood (via importance sampling) convergence

• Tasks results

  1. Likelihood individual contributions

  2. Standard errors of the estimates

The plots are interactive. For instance, if the user clicks on any point belonging to an individual, all points of this individual will be highlighted in all plots. This greatly helps to identify misspecifications and understand their causes. Furthermore, the user can customize plots: Display additional elements, modify scales and axes, and define colors and sizes. The plots have publication quality and can be exported as images (PNG or SVG format).

Finally, the tab “Comments” can be used both before and after the run to record the user’s comments, which is useful to note the key characteristics of a run for future work.

Development and diagnosis of the structural model

A two‐compartment model has been chosen in PK_01.mlxtran. The first goal is to assess if this structural model properly captures the data.

After running the tasks, the estimated parameters and standard errors are displayed in Figure 2b . The small RSE values indicate that the parameters are estimated with a good confidence. Among the diagnostic plots, the “individual fits” and the “observations vs. predictions” are particularly useful to assess the structural model. Figure 3a shows the observations vs. predictions plot in log–log scale. A deviation from the y = x line is clearly visible for small concentrations, which suggests that the two‐compartment model is not sufficient. The user can use the interactivity of the plots to clicks on any outlier point to highlight all points corresponding to this individual. The coloring is applied to all plots, which allows to easily find the individual fit plot corresponding to this individual (Figure 3b ). This plot shows that low remifentanil concentrations at large time points are not well fitted because of the two‐compartment model being unable to capture the third slope of remifentanil’s elimination phase. This suggests trying a structural model with three compartments.

Figure 3.

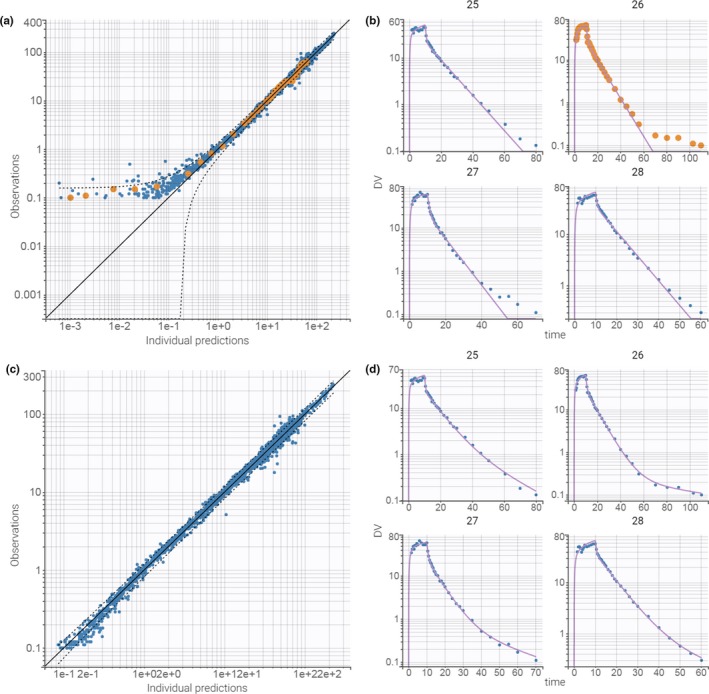
Assessment of the structural model. (a) Plot of observations vs individual predictions for PK_01.mlxtran. The dots are not symmetrically spread around the diagonal, suggesting that the model does not properly captures the data. Clicking on any underpredicted point colors all the points from the same individual (id 26). (b) Plot of individual fit for the id 25 to 28 for PK_01.mxtran. The misspecification is visible with underpredictions at the end of the elimination. (c) Plot of observations vs. individual predictions for PK_02.mlxtran. No misspecification is visible. (d) Plot of individual fit for the id 25 to 28 for PK_02.mxtran. No misspecification is visible. DV, observed concentrations.

The second run is setup by loading the model infusion_3cpt_ClV1Q2V2Q3V3.txt from the PK library, which corresponds to a three‐compartment model with i.v. infusion and linear elimination. As previously, reasonable initial values for the parameters are automatically computed with the “auto‐init” button. The default “combined1” error model and log‐normal distributions for all parameters are kept unchanged. The modifications are saved in a new file PK_02.mlxtran to avoid overwriting the results of the previous run. All estimation tasks are then run again. The diagnostic plots reveal that the three‐compartment model captures the data much better (Figure 3 c,d). The individual fits, observations vs. predictions, or residuals plots do not reveal any misspecification. In addition, all parameters have a low RSE. Hence, the three‐compartment model seems to be an appropriate structural model.

Development and diagnosis of the statistical model

The next step of the model development is the investigation of the statistical model, which includes the individual parameter distributions with their covariates and correlations as well as the residual error model. Before, to speed up the convergence of the next runs, the estimated parameters are saved as new initial values. This is done by clicking on the button “Use last estimates: all” in the “Initial estimates” tab.

Covariates. Investigation of the relationships between individual parameters and covariates aims at better understanding how the PK depends on easily measurable patient characteristics, such as age or body weight. Adding informative covariates in the definition of the individual parameter distributions reduces the unexplained interindividual variability, which is represented by the standard deviations of the random effects. To identify the informative covariates, the user can rely on the correlations between covariates and individual parameters, which are displayed as diagnostic plot and are analyzed in the tab “Results > Tests.”

The plot “individual parameters vs. covariates” (Figure 4a ) displays all possible pairs of random effects and covariates. Trends indicate a possible covariate effect. The random effects are by default calculated using the samples from the conditional distribution. This method produces more reliable trends and avoids the spurious correlations that may occur when using EBEs affected by shrinkage. Figure 4a shows a strong trend between the random effects of the clearance Cl and the AGE covariate, for instance.

Figure 4.

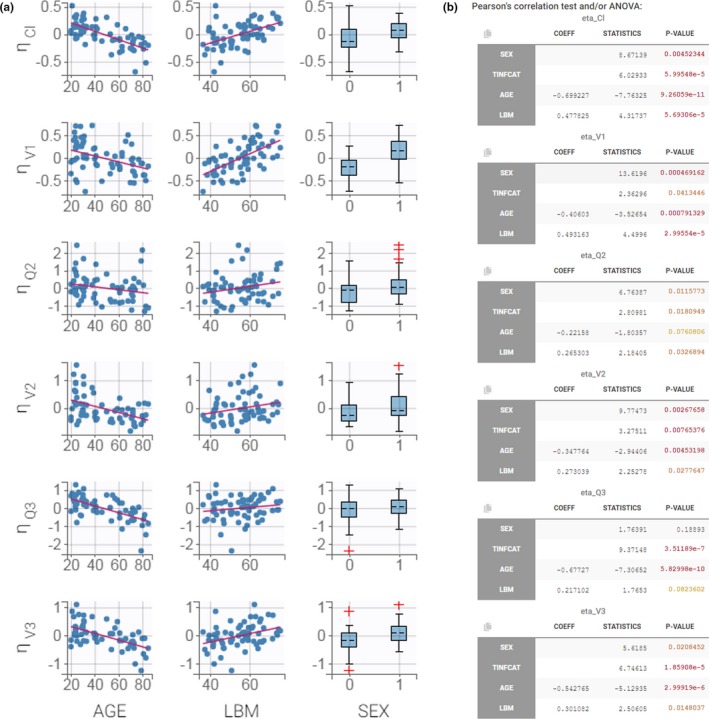
Assessment of the covariate model. (a) Plot of correlations between random effects and covariates. (b) Statistical tests of the correlations between random effects and covariates. ANOVA, analysis of variance; COEFF, coefficient; LBM, lean body mass; η_Cl, η_Q2, η_Q3, η_V1, η_V2, η_V3, random effects for Cl, Q2, Q3, V1, V2 and V3.

In parallel of the diagnostic plots, Monolix performs statistical tests to help the user identify significant correlations. Pearson’s correlation tests for continuous and analysis of variance tests for categorical covariates are displayed in the tab “Results > Tests” for each pair of random effects and covariates (Figure 4b ). The samples from the conditional distribution are again used to avoid bias in the statistical tests. Small P values are colored in yellow/orange/red and highlight significant correlations. In the case of remifentanil, many correlations appear significant, but they may not all be needed in the model. Once a covariate is added on a parameter, a correlation between another covariate and the random effects of this parameter may disappear as the covariates themselves may be correlated with each other.

In this tutorial, the workflow for the covariate search will be the following: Covariates are added one by one, starting with the strongest significant correlation and checking at each step that the likelihood improves. This stepwise manual method is suited for relatively simple models with few covariates. It allows the user to control each step of the model building process and to decide which covariate to include based on statistical criteria as well as physiological plausibility. It is also possible to use an automatic covariate search procedure, which is explained later.

The first step in the covariate search is to add AGE as a covariate on clearance, as it has the smallest P value and is reasonable biologically. In Monolix, adding a covariate effect is easily done by clicking on the corresponding box in the individual model part of the tab “Statistical model & Tasks.” This creates automatically a linear relationship between the transformed parameter and the covariate, with a new parameter named β_{Cl_AGE}. For the lognormally distributed parameter Cl, the transformed parameter is log(Cl). The default relationship between Cl and AGE is thus exponential:

$$\log \left(\text{Cl}\right)=\log \left({\text{Cl}}_{\text{pop}}\right)+{\mathrm{\beta }}_{\text{Cl\_AGE}}\ast \text{AGE}+{\mathrm{\eta }}_{\text{Cl}}$$

Chemical Formula: $\iff {\text{Cl}=\text{Cl}}_{\text{pop}}{e}^{{\mathrm{\beta }}_{\text{Cl\_AGE}}\ast \text{AGE}}{e}^{{\mathrm{\eta }}_{\text{Cl}}}$

Another option is to implement the typical power law relationship. For this, AGE needs to be log‐transformed first. Clicking on the arrow icon next to AGE and then on “Add log‐transformed” automatically creates a new covariate named logtAGE defined by the following formula $\text{logtAGE}=\log \left(\frac{\text{AGE}}{36.6299}\right)$, where AGE is divided by the weighted mean, i.e., the average from the individual AGE values of the data set weighted by the number of observations per individual. The centering value can be modified by the user by clicking on “EDIT.”

Selecting logtAGE for the covariate effect defines the desired relationship:

$$\log \left(\text{Cl}\right)=\log \left({\text{Cl}}_{\text{pop}}\right)+{\mathrm{\beta }}_{\text{Cl\_logtAGE}}\ast \log \left(\frac{\text{AGE}}{36.6299}\right)+{\mathrm{\eta }}_{\text{Cl}}$$

Chemical Formula: $\iff \text{Cl}={\text{Cl}}_{\text{pop}}{\left(\frac{\text{AGE}}{36.6299}\right)}^{{\mathrm{\beta }}_{\text{Cl\_logtAGE}}}{e}^{\text{Cl}}$

This formula involves a new population parameter to estimate named ${\mathrm{\beta }}_{\text{Cl\_logtAGE}}$ and can be displayed with a click on “Formula.”

The modified model is saved as PK_03.mlxtran, and all estimation tasks are run again. Monolix provides different ways to assess the performance of the new statistical model. The following list of observations show that the covariate effect is relevant.

• The relative standard error of ${\mathrm{\beta }}_{\text{Cl\_logtAGE}}$ is low, so the confidence in the estimation is good.

• The estimate of ${\mathrm{\omega }}_{\text{Cl}}$ has decreased from 0.228 to 0.164, meaning that the interindividual variability for Cl is now partly explained by the covariate.

• Low P values of the Pearson’s correlation test, which checks whether the correlation between Cl and logtAGE is significant, and of the Wald test, which checks if the estimate of ${\mathrm{\beta }}_{\text{Cl\_logtAGE}}$ is significantly different from 0, mean that the covariate effect is relevant.

• The −2LL has decreased by 64 points and the BICc by 52 points.

Once the first covariate effect has been confirmed, the new population parameter estimates are set as initial values by clicking on the button “use last estimates” in the “Initial Estimates” tab, and the stepwise covariate search procedure can be continued.

Table 1 summarizes the successive steps in the covariate search and indicates the difference in AIC and BICc values between two successive runs. The effects of the continuous covariates AGE and LBM are always added with power laws. Adding covariates does not always improve the model. For example, a relationship between SEX and V2 in the run PK_10.mlxtran increases the BICc value. This relationship is thus not kept in the model. The final covariate model is PK_09.mlxtran and includes the effect of logtAGE on Cl, Q2, Q3, and V3, logtLBM on Cl and V1, and SEX on V3.

Table 1.

Workflow for the manual covariate and correlation search

Project name	Covariate effect or correlation	ΔBICc (by linearization)	Keep the effect
PK_03	PK_02 + AGE on Cl	52	Yes
PK_04	PK_03 + LBM on V1	47	Yes
PK_05	PK_04 + AGE on Q3	35	Yes
PK_06	PK_05 + AGE on V3	17	Yes
PK_07	PK_06 + LBM on Cl	23	Yes
PK_08	PK_07 + AGE on Q2	18	Yes
PK_09	PK_08 + SEX on V3	5	Yes
PK_10	PK_09 + SEX on V2	−0.4	No
PK_11	PK_09 + LBM on V2	−7	No
PK_12	PK_09 + Q3−V3	60	Yes
PK_13	PK_12 + Cl−Q3−V3	29	Yes
PK_14	PK_13 + V1−V2	−10	No
PK_15	PK_13 + Q2−V2	10	Yes

Each row represents a Monolix run with a new covariate effect or a new correlation between random effects added in the statistical model.

ΔBICc, difference in BICc from the previous run; LBM, lean body mass.

Correlations between random effects. Correlations between random effects take into account that individuals with a large value of one parameter (for instance, the volume V1) tend to also have a large value for another parameter (for instance, the clearance Cl), independently of the effect of the covariates on these parameters. Significant correlations can be identified for each pair of random effects in the matrix scatter plot “correlations between random effects” plot (see Supplementary Material ) and with the P values of the Pearson correlation tests. When random effects appear correlated, it is important to estimate this correlation as part of the population parameters to include the correlation when sampling new individuals in later simulations.

Correlations between random effects can be defined via tickboxes in the Monolix graphical user interface. Several groups of correlated random effects are possible, which is equivalent to a block‐diagonal variance–covariance matrix.

Following the same approach as for the covariate search, relevant correlations are added to the model one by one. The highest significant t‐test (i.e., lowest P value) is between Q3 and V3. After adding the correlation, the scenario is run to update the population parameters, the scatter plots for pairs of random effects, and the results of correlation tests. Table 1 summarizes the steps that lead to the final correlation model, saved as PK_15.xmltran. It includes correlations between Cl, Q3, and V3 and a correlation between Q2 and V2.

Error model. The last step is the assessment of the error model. In the table of estimated population parameters in the section “Pop. Parameters” of the tab “Results,” the estimate for the constant part of the combined residual error (parameter a) is low compared with the concentration range in the data set (a = 0.00076 vs. concentrations in 0.1–300 in the data set). In addition, the RSE for a is high (209%). This suggests that a simpler observation model, with a proportional residual error, may be more appropriate. The procedure is the same as when changing other elements of the statistical model: First the last estimates are set as new initial values, then the error model is changed to “proportional” using the drop‐down menu, and finally the modified model is saved under a new name, as PK_16.mlxtran.

After executing the scenario, the BICc decreased (ΔBICc = 9.74), so the proportional error model is indeed more appropriate for this data set.

Final model overview. The final model is composed of a three‐compartment structural model with a proportional error model. All parameters follow a lognormal distribution. AGE is included as a covariate on Cl, Q2, Q3, and V3; LBM on Cl and V1; and SEX on V3. The random effects of Cl, Q3, and V3 are correlated as well as those of Q2 and V2.

The ability of this model to capture the data can be assessed using the visual predictive check (VPC) available in the list of plots (see Supplementary Material ). The VPC (Figure 5 ) is based on multiple simulations with the model and the design structure of the observed data grouped in bins over successive time intervals with optimized binning criteria.9 It is a useful tool to assess graphically whether simulations from the model can reproduce both the central trend and variability in the data. The median and percentiles of the observed data are plotted in blue curves and can be compared with the corresponding prediction intervals in blue and pink, respectively. Discrepancies are highlighted in red.

Figure 5.

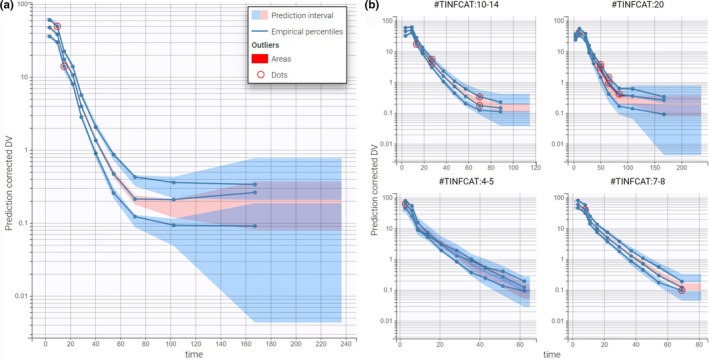
Final evaluation of the PK model. (a) Visual predictive check on the whole population. (b) Visual predictive check stratified by TINFCAT. DV, observed concentrations.

In Figure 5a , corrected predictions10 have been selected in “Settings” to take into account the high heterogeneity in doses. The y axis is in log‐scale, and the number of bins is set to 10. The plot shows a good predictive power of the model. In Figure 5b , the same VPC plot is split according to groups of similar infusion durations using the covariate TINFCAT. This allows one to better see the predictions for more homogeneous subpopulations.

Advanced features of Monolix

Monolix implements advanced options for automatic covariate search, automatic statistical model building, and convergence assessment. Although their usage is beyond the scope of this tutorial, this section gives a brief summary of the available approaches. For more information, the user can see the http://monolix.lixoft.com/model-building/.

Automatic covariate search. The manual search for significant covariates is a tedious process, but it can easily be automatized after defining a search strategy and acceptance rules. Several automatic covariate strategies are available in Monolix. They are located in the “Model building” tab, which is opened with the first gray button next to the green “RUN” button in the tab “Statistical model & Tasks.”

The first strategy is the well‐known stepwise covariate modeling method. It performs forward selection among all possible parameter–covariate relationships followed by backward elimination. This method is effective but expensive in terms of number of runs, as it tests all possible parameter–covariate relationships at each step. A second method, called Conditional Sampling use for Stepwise Approach based on Correlation tests, selects which covariates to test using the information contained in the correlation statistical tests between random effects and covariates of the current run. This greatly reduces the number of iterations required to optimize the covariate model.

The automatic covariate search applied to PK_02.mlxtran requires 133 iterations for the stepwise covariate modeling method and 25 for Conditional Sampling use for Stepwise Approach based on Correlation tests. The BICc values of the final covariate models are comparable with those of the manual covariate search (< 2 points of difference). A detailed comparison table is given in the Supplementary Material .

Automatic statistical model building. The section “Proposal” in the tab “Results” identifies the best improvements to the statistical part of the model (residual error model, covariate effects, correlations between random effects) by comparing many correlation, covariate, and error models. For example, in the case of covariates, the evaluated models correspond to linear regressions between the random effects sampled from the conditional distribution and the covariates. Selection is done according to a BIC criterion relative to the linear regression and not the full model. Because these linear regressions use the random effects of the current run and are fast to calculate, the Proposal takes a negligible computing time. The proposed statistical model is displayed in a compact table format and can be applied with a single click before reestimating the population parameters with this new model.

Going one step further, in the “Model building” tab, Monolix proposes also an automatic statistical model building. The procedure is named SAMBA and performs iteratively the same procedure as the Proposal: It applies at each step the best proposed model that is then reestimated. Thus, this method allows one to find a good statistical model in very few iterations.

Convergence assessment. The SAEM algorithm is a stochastic method, which means that the exact values of the estimated parameters depend on the sequence of random numbers set via the seed (the seed value can be seen in the global menu Settings > Project settings). The estimated parameters may also depend on the initial values, for example, if different local minima are found. To assess the robustness of the SAEM convergence, a so‐called convergence assessment can be run. This built‐in tool executes a workflow of estimation tasks several times with different initial values for the fixed effects and/or different seeds.

The convergence assessment tool can be launched with the second gray button next to the green “RUN” button in the tab “Statistical model & Tasks.” The user can choose in the interface the number of runs used for the assessment, the estimation tasks performed during each run, and the parameters whose initial values should be sampled randomly. The convergence assessment task returns a graphical report with the convergence of each parameter estimation as well as with a comparison of the estimates and their standard errors for all runs.

In this tutorial case study, the good convergence of the SAEM algorithm is clear (Figure 2a ). The convergence assessment is performed for a didactic purpose only. The report in Figure 6 compares five replicates of the estimation of the population parameters, the standard errors, and log‐likelihood for randomly picked initial values for all parameters. The report is composed of three plots. The first overlays the five trajectories of the population parameters estimates with respect to the iterations of the SAEM algorithm (Figure 6a ). The second compares the final estimates with their standard errors (Figure 6b ). The third compares the estimation of the log‐likelihood by importance sampling across replicates ( Supplementary Material ). The results confirm a good convergence of all replicates to the same −2LL minimum.

Figure 6.

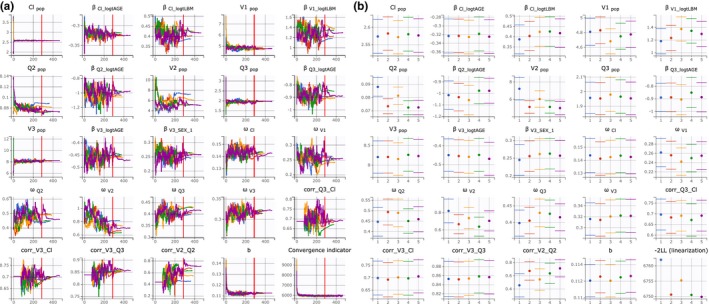
Convergence assessment. (a) Plots of population parameters estimates with respect to the iterations of stochastic approximation expectation‐maximization. (b) Final estimates with their standard errors for the five runs.

Keeping track of the modeling workflow using Sycomore

Sycomore is designed to keep track of the modeling process and to compare runs side by side. It is interconnected with Monolix, allowing to export and import runs to and from Monolix directly from the Sycomore interface.

Following the instructions described in the Supplementary Material , all Monolix runs are loaded into Sycomore. The runs are displayed in a table that includes an overview of each run (likelihood and BICc, structural model file, summary of the statistical model, comments). In the tree view panel located below the table, the runs can be added to the tree representation of the model development process. Defining parent–child relationships between models is done via drag and drop. Action buttons allow to load new runs, open a run in Monolix, duplicate a run, and select models to be run in batch mode. Moreover, the tab “Comparison” ( Supplementary Material ) compares two or more runs in detail, in particular the parameter estimates and exported diagnostic plots.

A Sycomore project that contains an overview of the whole modeling process in shown in Figure 7 . On this figure, the tree diagram is zoomed on the steps after the run PK_09.mlxtran.

Figure 7.

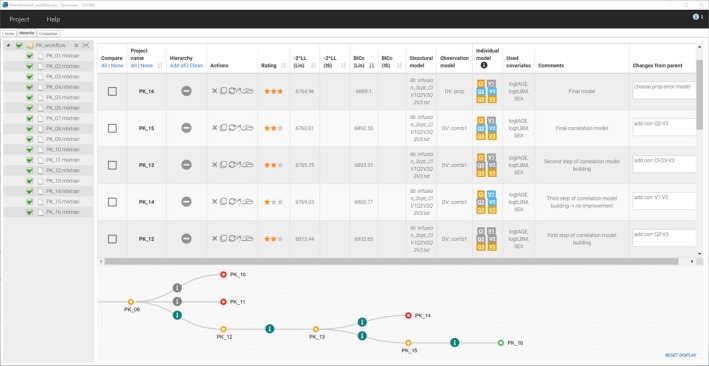
Overview of the modeling workflow in Sycomore with the summary table and tree diagram (zoomed on the last nodes). In this example, the user‐defined ratings mean the following: red = no improvement compared with previous step, orange = improvement compared with previous step, green = final model. The table has been sorted by decreasing values of the corrected version of the Bayesian information criteria.

CONCLUSION

In this tutorial, MonolixSuite has been used to build a population model for remifentanil’s PK. With Datxplore, the data have been visualized to identify their key properties. With Monolix, a model has been developed stepwise: First the structural model and then the covariates and correlations between random effects. Each model modification was guided by the diagnostic plots and statistical tests to assess the performance of the model and the improvement compared with the previous runs. The successive steps were tracked with Sycomore for a clear overview.

Population models provide a summary of the PK of a molecule (typical half‐life, variability from individual to individual, etc.). They can be used to explore new situations via simulations. Examples of applications include clinical trial simulations to determine the best dosing protocol or assessing the uncertainty of an end point depending on the number of individuals per arm. For this purpose, the MonolixSuite includes the simulation application Simulx. Monolix runs can be imported into Simulx, and the simulation definition can efficiently reuse its elements. The user can also specify new elements, such as different treatments, number of subjects, or covariate values representing different populations.

MonolixSuite provides a unified suite of applications for the analysis, modeling, and simulation of pharmacometric data. Its ease of use through a clear graphical user interface and its efficient solvers and algorithms makes it a powerful software for both beginner and advanced users.

Funding

No funding was received for this work.

Conflict of Interest

All authors are employees of Lixoft. Lixoft licenses the MonolixSuite software.

Supporting information

Supinfo 1. Word document detailing all steps to perform the tutorial with illustrative screenshots from MonolixSuite2019R1 and links to the online documentation.

Supinfo 2. Zip file containing the data set and all Monolix runs used in the modeling workflow.

Video. Video file showing the mains steps of the model development in real time.