Predictive model of spread of Parkinson’s pathology using network diffusion

Abstract

Growing evidence suggests that a “prion-like” mechanism underlies the pathogenesis of many neurodegenerative disorders, including Parkinson’s disease (PD). We extend and tailor previously developed quantitative and predictive network diffusion model (NDM) to PD, by specifically modeling the trans-neuronal spread of alpha-synuclein outward from the substantia nigra (SN). The model demonstrated the spatial and temporal patterns of PD from neuropathological and neuroimaging studies and was statistically validated using MRI deformation of 232 Parkinson’s patients. After repeated seeding simulations, the SN was found to be the most likely seed region, supporting its unique lynchpin role in Parkinson’s pathology spread. Other alternative spread models were also evaluated for comparison, specifically, random spread and distance-based spread; the latter tests for Braak’s original caudorostral transmission theory. We showed that the distance-based spread model is not as well supported as the connectivity-based model. Intriguingly, the temporal sequencing of affected regions predicted by the model was in close agreement with Braak stages III-VI, providing what we consider a “computational Braak” staging system. Finally, we investigated whether the regional expression patterns of implicated genes contribute to regional atrophy. Despite robust evidence for genetic factors in PD pathogenesis, NDM outperformed regional genetic expression predictors, suggesting that network processes are far stronger mediators of regional vulnerability than innate or cell-autonomous factors. This is the first finding yet of the ramification of prion-like pathology propagation in Parkinson’s, as gleaned from in vivo human imaging data. The NDM is potentially a promising robust and clinically useful tool for diagnosis, prognosis and staging of PD.

Introduction

Parkinson’s disease (PD) is a progressive neurodegenerative disease classically defined by the presence of four cardinal symptoms: bradykinesia, rigidity, tremor and postural instability. As it progresses, the majority of patients develop dementia, depression or other neuropsychiatric symptoms (1). PD is histopathologically characterized by loss of dopaminergic cells in the substantia nigra pars compacta (SN) with widespread co-occurrence of intracytoplasmic protein inclusions, termed Lewy bodies, composed primarily of misfolded α-synuclein (αS) (2). It has long been hypothesized based on histopathological studies first reported by Braak, that Parkinson’s pathology spreads in specific stages according to a stereotypic pattern, starting from the lower brainstem (dorsal motor nucleus of the vagus nerve) locus coeruleus and olfactory nucleus (Braak stages I-II); subsequently appearing in a predictable sequence in mesencephalic regions, especially the substantia nigra (stage III); limbic areas (amygdala and hippocampus, stage IV); and neocortical regions (stages V- VI); (3,4) – see Figure S1. The 6 Braak stages are based on Lewy pathology, and do not always concord with atrophy observable on MRI, especially in the striatum, which has high atrophy but modest concentration of Lewy bodies.

Recently multiple reports suggest that misfolded αS can spread via a direct trans-neuronal “prion-like” mechanism (5–7), like other protein species involved in neurodegenerative disorders: tau, Aβ, TDP-43 and Huntingtin (8–11). Misfolded proteins appear to undergo a corruptive templating process, whereby it can trigger misfolding of adjacent same-species proteins, which in turn is thought to cascade along neuronal pathways (12,13). Wild type mice receiving synthetic αS injection in the dorsal striatum exhibited Lewy pathology in anatomically connected regions and selective loss of dopaminergic neurons in the SN (5). Lewy pathology then spreads sequentially to ventral striatum, thalamus, occipital cortex, along with commissural and brainstem fibers. These data suggest that the transmission of misfolded synuclein follows network projections, hence connectivity is a mediator of susceptibility (5).

While these qualitative findings are becoming entrenched, we had proposed a connectivity-based graph-theoretic network-diffusion model (NDM) to convert these findings into quantitatively testable models. This model was successful in capturing the network-wide ramification of trans-neuronal transmission in Alzheimer’s and other dementias (14) and in predicting future longitudinal progression (15). In summary, misfolded pathology transmits across brain regions by transport processes along axonal projections, followed by trans-neuronal transmission between cells. Therefore, these processes can be modeled approximately by a process of diffusion, restricted to the network and governed by inter-regional structural connectivity. The NDM mathematically encapsulates this using a first-order graph diffusion equation, the solution of which deterministically gives the evolution of pathology starting from any given initial (e.g. seeding) pathology distribution. Similarly, network based analysis has been applied to PD populations showing a network of atrophy supporting the role of S propagation in disease spread (16).

Here we show that this network-restricted diffusive mechanism also applies to PD and provides a deterministic framework for capturing the spatiotemporal progression of PD topography. Hence we re-encoded the NDM as described in (14) to capture αS-driven trans-neuronal pathology spread in PD. The concept is illustrated in Figure S1. Since no in vivo imaging currently exists that specifically targets synuclein deposits, we test instead whether a model based on pathology progression can fit MRI-derived regional atrophy. Although the pattern of atrophy in PD is roughly associated with pathological Braak stages, synuclein pathology and atrophy are not congruent (17,18). Some areas show Lewy pathology without appreciable atrophy (e.g. locus ceruleus, raphe nucleus, amygdala), and atrophy without Lewy pathology (the striatum). Nevertheless, we fit our model to atrophy due to its immediate clinical relevance. We reason that proliferation of cell loss must have a pathological basis, if not locally then at the network level. If the overall model succeeds in fitting to atrophy, then deviations between local atrophy and NDM-predicted pathology pattern would provide additional insights into regional vulnerability. We compare our connectivity-based model with two alternative hypotheses: transmission along random pathways and distance-dependent spread. We also test the cell-autonomous theory of PD progression: the idea that certain brain regions are innately vulnerable to PD, for instance dopaminergic areas. To test this hypothesis, we computed the spatial distribution of PD-implicated genes, under the plausible assumption that their regional profiles must reflect innate cellular and regional vulnerability.

The main contribution of this study is that it synthesizes the qualitative trans-neuronal hypothesis of synucleinopathy into a statistically validated deterministic model of Parkinson’s progression. We report strong fits that provide quantitative evidence that human Parkinson’s progression is undergirded by trans-neuronal prion-like pathology spread. This spread is best explained by connectivity-driven processes rather than distance-based or random spread. More importantly, overall connectivity-pattern dominates in determining spatial patterns, even if some genes help to mediate spread of pathology across neural pathways. This indicates that the NDM is more significant as a predictor of regional atrophy patterns than gene expression. Intriguingly, the temporal sequencing of affected regions predicted by the NDM was in close agreement with Braak stages III-VI. This opens the door to a “computational Braak” staging scheme that requires only in vivo imaging, not pathology on autopsy series.

Materials and Methods

Building a parcellated atlas from healthy subjects

For the current study a brain parcellation with 78 regions has been used. Details have been reported previously (16). Briefly, supratentorial regions were included from Hammers atlas i.e. cortical and basal ganglia related regions (19). Furthermore, three midbrain structures, SN, subthalamic nucleus (STN), and red nucleus (RN) were manually segmented using the high-resolution MRI template (T1-weighted ICBM152 template, resolution = 0.5 mm³), the BigBrain (20), and the brainstem anatomical atlas of Duvernoy 1995. The accuracy of the segmentations was confirmed using subcortical atlas based on ultrahigh-field MRI (22).

Building the connectivity network or connectome of healthy subjects

For structural connectivity, we used Illinois Institute of Technology Human Brain atlas v.3 constructed from high resolution diffusion weighted MRI (DW-MRI) data from 72 young healthy subjects. The measure of connectivity used in this paper is the anatomical connection density (ACD), defined as the fraction of the connected superficial nodes with respect to the total number of superficial nodes of both areas, as proposed in Iturria-Medina et al., 2007 (23). ACD is obtained by dividing the raw connection strength value by the sum of region-pair surface areas, hence ACD corrects for varying brain region sizes. We refer to this network using the connectivity matrix C = {c_i,j}, whose elements c_i,j, represent the connection strength of white matter fiber pathways between i^th and j^th GM regions. Connections are assumed to be bidirectional since directionality is not deducible from DTI tractography data. The process has been explained in detail previously in (16,24).

A network diffusion model for Parkinson’s disease

We modeled PD progression as a diffusion process on C From Figure S1 and (14) the transmission of pathology from R1 to R2 is asserted to satisfy $\frac{d{x}_1}{dt}=\beta c_{1,2}\left(x_2-x_1\right)$ where x₁ and x₂ are pathology concentration in each region, and β is a global diffusivity constant. Assembling pathology from all regions into a vector x (t) = {x_i (t)}, the above equation extends to become:

$$\frac{dx(t)}{dt}=-\beta Hx(t)$$ (1)

where H is the well-known symmetric normalized graph Laplacian

$$H=I-D^{-\frac{1}{2}}C{D}^{-\frac{1}{2}}$$ (2)

where D is a diagonal matrix whose diagonal entries contain the degree of each node, degree being defined as the sum of weighted connections emanating from the node. Note, in order to accommodate regions having widely different out-degrees, we used the degree-normalized version of the Laplacian matrix (15). Eq. 1 admits a closed-form solution $x(t)=e^{-\beta Ht}{x}_0$ where x₀ is the initial pattern of the disease process, and we call term e^−βHt the diffusion kernel since it acts essentially as a spatial and temporal blurring operator on x₀. This diffusion kernel represents the operation of an equivalent random walk, and is similar to the “state transition matrix” used in linear systems theory to model Markovian processes on graphs. The unit of model’s diffusion time t is arbitrary (a.u.). Global diffusivity β is unknown and its exact value is arbitrary, hence we chose a value that would roughly span Parkinson’s progression (10–20 years). Specifically, we chose a β such that the peak correlation of the NDM against empirical atrophy will occur, over all seeded regions, in the range t_max ∈ [10,20] years. We ran NDM for multiple β values that would satisfy above criteria. In our experimentation, we achieved this for β = 0.15. In future, both t and β would be estimated by fitting to longitudinal data and would then acquire correct dimensions and units.

Subsequent diffusion of PD pathology out of SN is given at any time point t by

$$x_{PD}(t)=e^{-\beta Ht}{e}_{SN}$$ (3)

where e_SN is a unit vector with 1 at the index of the SN and zeros elsewhere. The NDM code is publically available at www.rajlab.ucsf.edu/projects/.

From pathology to atrophy.

Regional MRI-derived atrophy is modeled as being proportional to the pathology vector, hence we assert Φ(t) = const ⋅ x(t).

Alternate model: distance-based spread.

Next, we build an alternate model of network spread, where pathology diffusion is dependent on the Euclidean distance between any two brain regions. To achieve this mathematically, we replaced connectivity matrix C with a distance-matrix F = {f_i,j}, with entries

$$f_{i,j}=e^{-d_{i,j}/\sigma }$$ (4)

where d_i,j, is the distance between the centers of mass of ROI i and j, and σ = mean ({d_i,j })⁄2 is a scale parameter. Entries f_i,j may be considered probabilities of two regions being connected based on their distance. To maintain sparsity entries less than 0.15 were set to zero (that is, remote nodes are not connected). Although any monotonically decreasing relationship could in theory be used, the exponential has several desirable properties: its decay rate is easily controlled by σ and its range [0, 1] is fixed and intuitive. Now that we have a distance-based adjacency matrix F which is equivalent to the fiber connectivity C, we now apply the same equation (2) to compute a distance-based Laplacian of F, to give H_F. Finally, a “distance diffusion” model is obtained, mirroring exactly the network-based evolution of Eq (3):x_d (t) = exp (−βtH_F) x₀. This equation should be capable of encoding, for instance, the proximity-based caudorostral spread postulated by Braak (3).

Parkinson’s disease patient data

To test our model we used cross-sectional imaging data from the Parkinson’s Progression Markers Initiative (PPMI) (www.ppmi-info.org/data). PPMI is a publicly available, multi-center, and multi-scanner dataset. In order to measure PD related regional atrophy, 3T high resolution T1-weighted MRI images from the baseline visit of 232 de-novo Parkinson’s patients as well as 117 age-matched normal controls (NC) were obtained from PPMI. This data is acquired as part of PPMI imaging dataset using GE medical systems, Siemens, and Philips medical systems and the acquisition parameters are detailed in (http://www.ppmi-info.org/wp-content/uploads/2017/06/PPMI-MRI-Operations-Manual-V7.pdf). Table 1 demonstrates motor and cognitive data at the time of the study of PPMI cohort. The images were pre-processed including denoising, intensity non-uniformity correction, and normalization. After pre-processing, all images were first linearly and then non-linearly registered to the MNI-ICBM 152 template. All the preprocessing steps are implemented as part of our center’s standard pipeline (25). The standard pipeline is publicly available on github server (https://github.com/vfonov/nist_mni_pipelines). Deformation based morphometry (DBM) (i.e. the determinant of the Jacobian transformation matrix obtained from nonlinear transformation fields) maps were calculated to measure regional brain atrophy. After calculating voxel-wise DBM maps, we extracted mean regional DBM values per subjects and calculated the effect size of PD related regional atrophy represented by the vector $t_{PPMI}=\left\{t_{PPMI}(i)|i\in \text{[1, N]}\right\}$, (N=112) using a two tailed t-test between PD and NC mean DBM values. The t-statistic was converted to the natural range [0,1] using the logistic transform, following (15). Resulting logistically transformed PD atrophy is given by $t_{rescaled}=1/(1+\exp \left(-\left(t_{PPMI}-\text{a}0\right)/\alpha /\mathrm{std}\left(t_{PPMI}\right)\right)$, where, α = 1 and a0 = 0.5*α. This logistic non-linear transform serves to convert atrophy from a t-stat to a number bounded between 0 and 1 which is an analytically desirable and biophysically interpretable quantity. This strategy has been widely used in our prior work as well as in other publications (26,27). These atrophy measures were then used to test the propagation modeling analyses.

Table 1:

Demographic and clinical details of PPMI cohort. MoCA = Montreal Cognitive Assessment, UPDRS = Uniform Parkinson’s Disease Rating Score

	Male	Female	Age	MoCA	UPDRS-III	Hoehn and Yahr stage
HC (n=117)	74	43	59.7 ± 11.3	28.2 ± 1.2	-	-
PD (n=232)	155	77	61.2 ± 9.1	27.3 ± 2.2	21.9 ± 9.1	1.6 ± 0.5

Statistical Analysis

The network diffusion model is described by x (t) and Φ(t), two 112×100 tables that represent the theoretical pathology and its resulting theoretical atrophy in all 112 ROIs over 100 points in time. Label number and names of these 112 ROIs are listed in Supplementary Table S1. Thirty-four cerebellar regions were removed, leaving regional PD atrophy statistics on 78 cerebral regions. Pearson correlation strength (R statistic) and p-values were calculated between the (static) empirical atrophy t-statistic measured on the PPMI’s PD group, t_rescaled and ) Φ(t) at all 100 model timepoints t. These cerebellar regions were removed because, 1) There is a higher individual variability in cerebellum of the subject compared to the rest of the brain 2) there is high bias in estimation of the brainstem connectivity with cerebellum compared to the cortical connectivity with both cerebellum and brainstem. The 1) causes lower estimation of the atrophy in cerebellum based on MRI imaging whereas 2) causes higher model estimation of the atrophy in cerebellum. Future studies to accurately delineate the connectivity between cerebellum and brainstem/cortical regions will help us to overcome the bias and include the cerebellum in our model.

Repeated seeding.

Next, the NDM was run 78 times, each time starting from a different ROI, in order to deduce the most likely seed regions. For each node i, we start the model with x₀ = e_i, where e_i is a unit vector with 1 at the i-th location and zero elsewhere. We observed that the atrophy pattern in our group was generally bilateral, hence for repeated seeding experiments, we chose to seed bilaterally, so that two entries in the “unit” vector were assigned 1. This was repeated for each region in turn, and the NDM-predicted atrophy pattern Φⁱ (t) was calculated from Eq. (3). This gave 78/2 = 39 different Φ(t) matrices. Label number and names of these bilateral 39 regions are listed in Supplementary Table S2. For each predictor matrix the corresponding Pearson’s R was calculated at all model times t, giving Rⁱ (t). These Rⁱ (t) values were plotted on common axis, giving what we denote as “R-t curves”. From each Rⁱ (t), we recorded the maximum value $R_{max}^i$, which is used here as an indicator of model evidence reflecting the likelihood of the region i being the true region of pathology onset. This effectively “ran the NDM backwards”, allowing us to determine which seeded ROI would serve as the most likely origination site to subsequently yield the regional patterns closest to empirical data.

Nigral seeding.

Given that SN seeding consistently produced the best R against empirical data (see Results), we explored nigral seeding, given by the initial vector x₀ = e_SN, which yields the model predictor $x^{SN}(t)=\exp (-\beta Ht)e_{SN}$. Snapshots of the evolving $x^{SN}(t)$ vector were recorded and plotted in glassbrain renderings at selected model times t = 6,12,18 (AU).

Arrival time.

We define arrival time as the model time required for NDM pathology $X^{SN}(t)$ to reach 98% of the maximum value of pathology diffusion into a given brain region, starting from the seeding event in SN. The 98% value is used instead of 100% because many regions get maximum diffusion at the steady state distribution at infinite time. A similar arrival time table was compiled for amygdala seeding.

Random scrambling.

In order to build a null distribution for assigning significance to the NDM, we performed two levels of randomization experiments. 1) We ran the NDM on 2000 randomly scrambled versions of the connectivity matrix C. C was scrambled using a symmetric transformation of the network’s nodes by randomly permuting entire rows and columns, and the NDM was evaluated for each shuffled network after bilateral SN seeding. This scrambling procedure maintains the edge and node statistics of the true connectivity C. The NDM evaluated on these 2000 randomly scrambled networks therefore constitute null or reference models which supplied significance values to results of the true model. 2) We ran the NDM on 2000 randomly scrambled PD atrophy vector. Atrophy values in t_rescaled vector were randomly assigned amongst the 78 cerebral regions with 2000 different permutations. This scrambling method maintained the true connectivity C, but replaced true regional atrophy pattern with a random distribution of atrophy.

Association between network diffusion patterns and individual patients’ motor and clinical scores

While DBM measures brain shrinkage or expansion compared to the standard atlas, the underlying mechanism resulting in the deformation is manifold and not disease specific (e.g. partly due to normative aging). NDM provides us with a disease specific map of the brain, based on the transmission of pathology from a seed region to the rest of the brain. Here we use this disease specific map to calculate a weighted average of each individual’s deformation map as the PD-related atrophy measure.

$$PD–atrophy\left(sbj\right)={\Sigma }_{j\in region}DiseaseSpecificMap\left(j\right)\times DBM(sbj,j)$$

We examined how this PD-specific atrophy measure relates to motor related disease severity (measured by UPDRS-III) and cognitive measures (measured by MoCA) using Pearson correlation. For detailed procedure of the clinical assessments please refer to the PPMI study protocol (http://www.ppmi-info.org/wp-content/uploads/2018/02/PPMI-AM-13-Protocol.pdf).

Atrophy prediction with combined network diffusion and genetic expression modeling

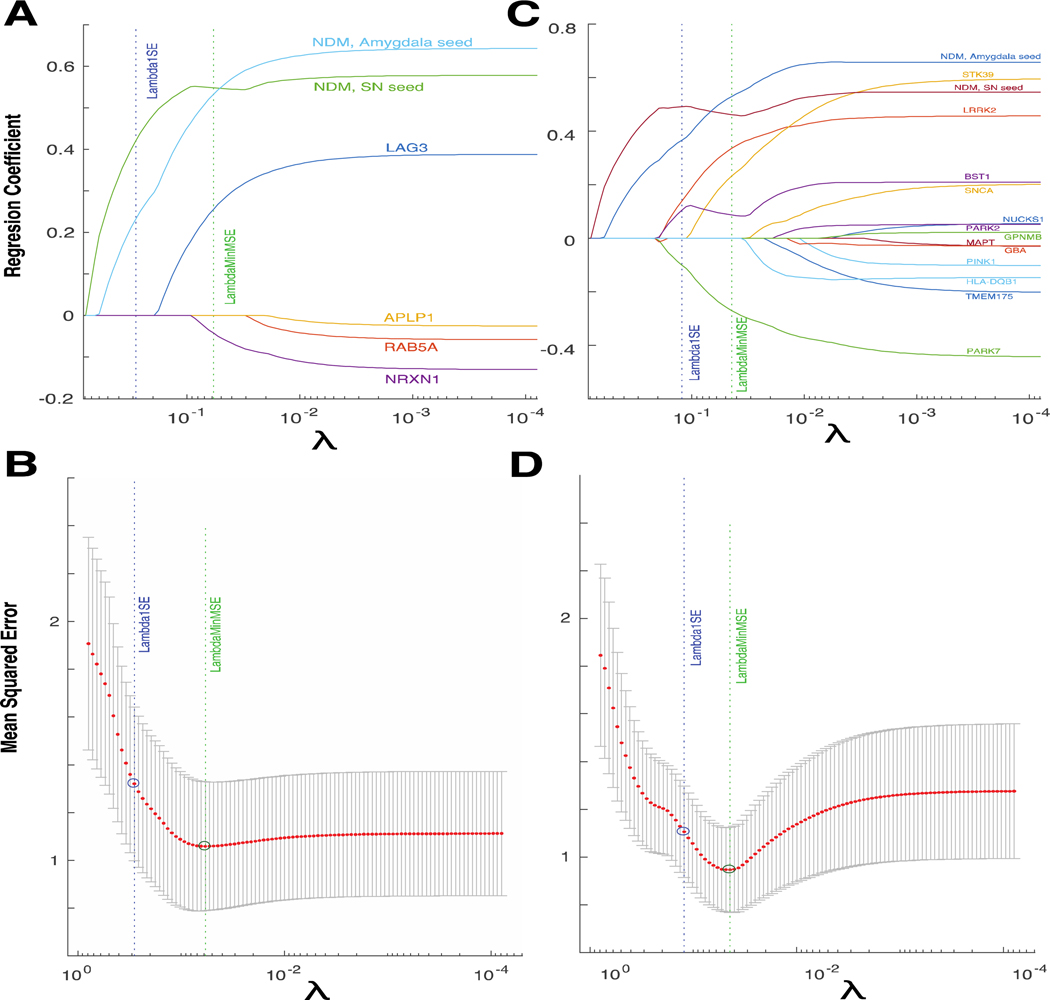
17 genes of interest implicated in PD were selected for expression analysis as in Freeze et al., 2018. Four genes identified as having roles in trans-synaptic synuclein transfer in Mao et al., 2016 were included (LAG3, APLP1, NRXN1 and RAB5A). The ten genes with the lowest p-values from the Nalls et al., 2014 GWAS meta-analysis for which Allen Brain Atlas (ABA) expression data was available were included: BST1, GBA, GPNMB, HLA-DQB1, LRRK2, MAPT, NUCKS1, SNCA, STK39 and TMEM175. The three genes strongly associated with typical autosomal recessive PD were also included (PINK1, PARK2 and PARK7). For each gene, data was obtained from the publicly available human ABA (31) . The ABA includes 926 brain regions, with each region having microarray expression levels from a set of 58,692 probes that correspond to 29,181 distinct genes. Expression data for each of the 926 regions was manually mapped to the 78 region parcellation using region name identification and comparison of atlas coordinates. L₁ regularized regression models were created containing R_max NDM predictors from the SN and amygdala, and regional genetic expression profiles, averaged across all subjects and probes. Ten-fold cross-validation was performed for each model across a range of values for the tuning parameter λ using the Matlab script ‘lasso’.

Results

Cross-sectional spatial distribution of PD atrophy

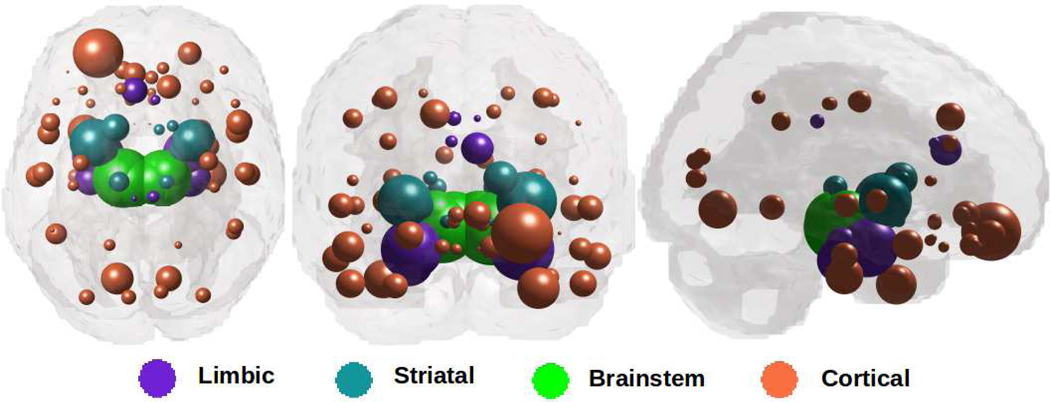
Figure 1 illustrates “glass brain” renderings of the spatial distribution of PD atrophy. The spheres are located at the centroid of each of 78 brain regions, their size is proportional to the t-statistic of PD atrophy after logistic transform and color-coded as per: limbic = purple, striatal = cyan, midbrain = green, and cortex = coral. The most atrophied regions (midbrain, striatum, amygdala, thalamus, nearby cortices) are consistent with other imaging studies (16,32–36) and with PD pathophysiology (17,18).

Figure 1: Spatial distribution of PD atrophy.

Measured regional PD atrophy are depicted by “glass brain” visualization, with spheres placed at the centroid of each brain region, and their diameter proportional to effect size.

Model-free correlation analysis

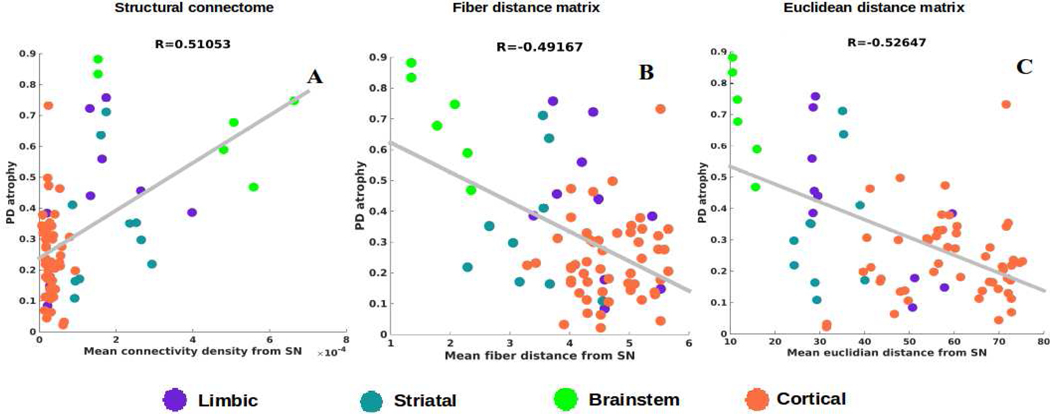
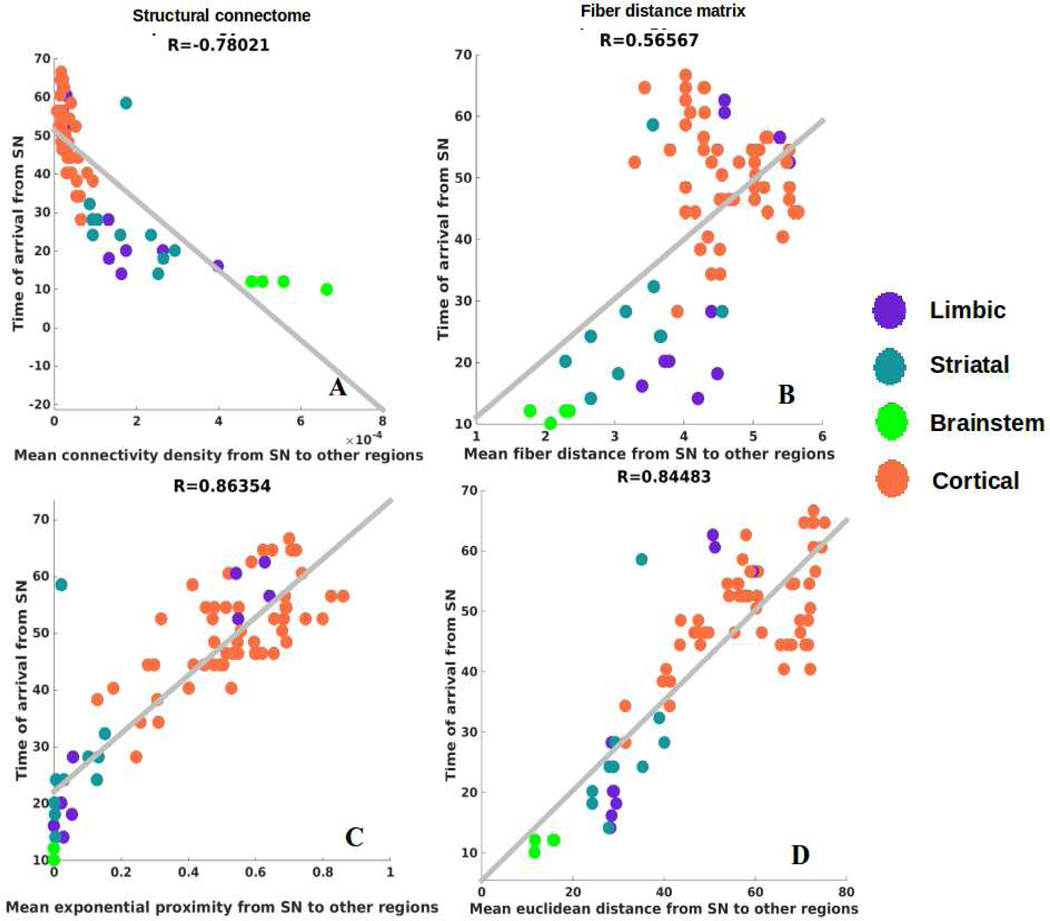
First, we establish the role played by proximate anatomic features involving the nigral system in governing the regional patterns of PD atrophy, in a model-free analysis. Given that SN is considered one of the earliest hotspots of PD pathology outside of the lower brainstem, we chose the following anatomic predictors: a) connectivity to SN, b) fiber (i.e. along connecting fiber tracts) distance to SN, c) Euclidean distance to SN. Each covariate is a 78-long vector, covering the entire brain. Since the group atrophy t-statistic is generally bilateral, we removed lateralization effects by averaging the left- and right-hemispheric values of these vectors, giving predictor vectors of size 39×1. Linear bivariate correlation analyses of regional PD atrophy with these SN-proximate predictors are shown in Figure 2. Dots are color coded as per (limbic = purple, striatal = cyan, midbrain = green, and cortex = coral). We see a significant positive correlation between PD atrophy and connectivity from bilateral SN (R = 0.51, p < 0.001), a significant negative correlation between PD atrophy and fiber distance from bilateral SN (R = −0.49, p < 0.001) and a significant negative correlation between PD atrophy and Euclidian distance from bilateral SN (R = −0.53, p < 0.001). Given the closeness of the two distance models and their high level of collinearity, we chose in all subsequent analyses to exclude Euclidian distance model, with the understanding that distance along fiber projections is perhaps the more plausible descriptor, given the strongly synaptic localization of synuclein and extensive evidence of deposits following neural projections (37).

Figure 2: Correlations of PD atrophy with network and non-network metrics.

Scatter plot of mean connectivity, fiber distance, and Euclidian distance from SN versus empirical PD atrophy. Dots are color coded by lobe – supratentorial = purple and brainstem = green.

Repeated seeding of the Network Diffusion model

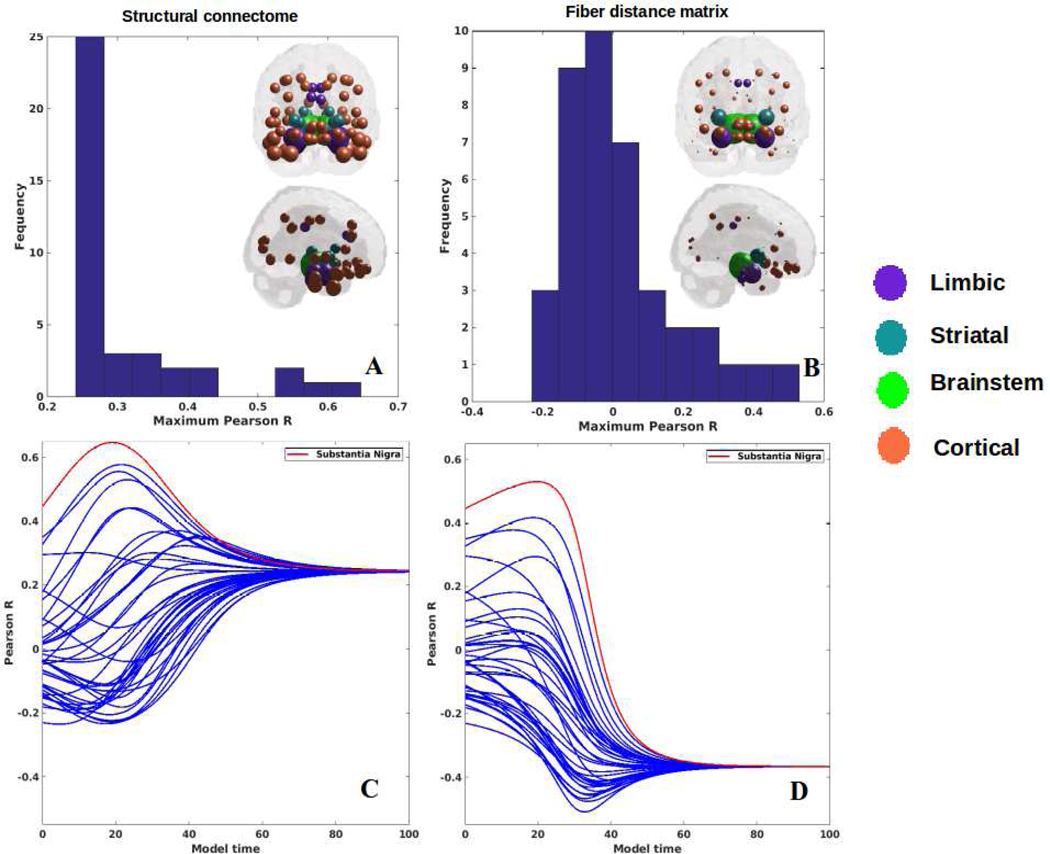
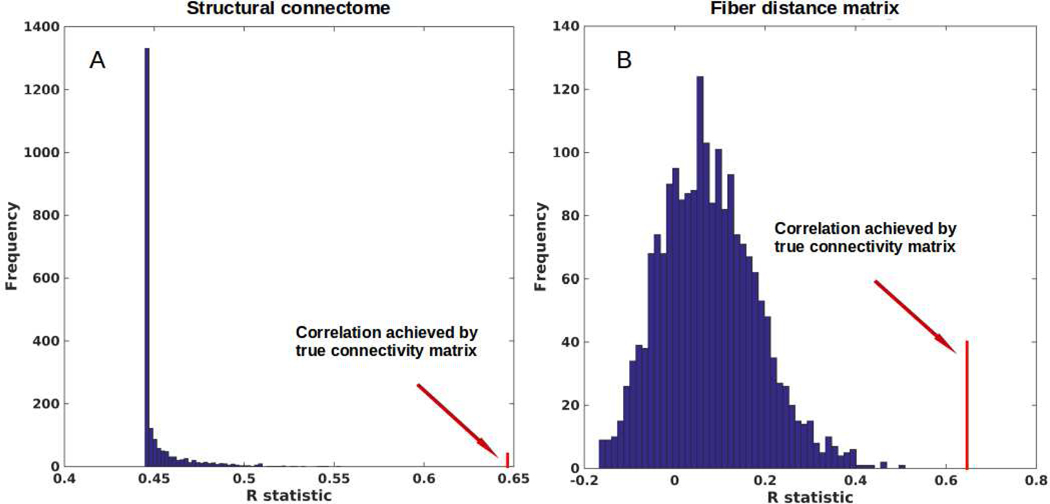
Each region was computationally “seeded” in turn and NDM was played out over time. The histogram of the maximum Pearson correlation strength $R_{max}^i$ between empirical data and the NDM seeded at region i is shown in Figure 3A,B. Since $R_{max}^i$ serves as a measure of the likelihood of each region being a seed, this information is spatially depicted in the “glass-brain” insets. Table 2 shows top 20 regions with maximum correlation strength for each region seeded in turn. Clearly, the SN, RN, amygdala, STN and limbic structures serve as the best seed regions; this is true whether we consider connectivity or distance network. However, the connectivity-based NDM always gives better model evidence compared to proximity. Figure 3C,D shows the R-t curves between empirical atrophy and model evolution (Eq. 2), one for each seeded region. As noted above, the highest R was achieved by the SN, for both the connectome and fiber distance-based network diffusion. In order to determine that our choice of β did not affect maximum correlations, we also re-evaluated our results with two different choices of β and are shown in Supplementary Figure S2. In addition, to conclude that the highest correlation from the seed is not entirely driven by its strong association with PD atrophy, we further explored the entire Rt-curve at the model time where the peak is achieved after excluding the seeds. These results are demonstrated in Supplementary Figure S3 and Supplementary Table S3. Furthermore, we re-examined our Rt-curves without logistic transform and with a different steepness parameter (α=3) to assess if it affected the linear relationship and correlation values in our results. These results are shown in Supplementary Figure S4.

Figure 3: Results for repeated seeding analysis.

Each region was seeded in turn and network diffusion model was played out for all time points. Pearson’s R was recorded at each time point between the model and PD atrophy vector. As the diffusion time increases, more and more of the pathogenic agent escapes the seed region and enters the rest of the network. A: The point of maximum correlation with measured atrophy using structural connectome was recorded with glassbrains of measured R shown inset B: Maximum correlation strength for bilaterally seeded ROIs. The maximum correlations are achieved by seeding the substantia nigra. The fact that SN achieves the best performance in almost all these seeding experiments provides a level of validation of the ND model, since nigral origin is a universal hallmark of classic Parkinson’s disease. C: ND model seeded at bilateral regions using structural connectome indicates that the SN (shown by red curve) is the most plausible candidate for Parkinson’s disease seeding – it has the highest peak R, and the characteristic intermediate peak indicative of true pathology spread. D: ND model seeded at the bilateral SN using fiber distance connectivity matrix yields the best R curve of all, indicating that it is the most plausible seed region for Parkinson’s disease spread.

Table 2:

Top 20 regions with maximum correlation strength for bilaterally seeded ROIs

Regions from structural connectome		Regions from effective distance connectome
Substantial Niagra	0.65	Substantial Niagra	0.53
Red Nucleus	0.58	Red Nucleus	0.42
Amygdala	0.56	Amygdala	0.38
Subthalamic Nucleus	0.53	Putamen	0.30
Parahippocampal gyrus	0.44	Subthalamic Nucleus	0.29
Hippocampus	0.44	Orbitofrontal Cortex-Anterior Orbital Gyrus	0.18
Anterior middle temporal lobe	0.37	Parahippocampal gyrus	0.18
Lateral Occipital temporal gyrus	0.37	Hippocampus	0.13
Inferiolateral temporal lobe (anterior part)	0.35	Anterior middle temporal lobe	0.10
Anterior superior temporal gyrus	0.34	Occipital lobe lingual gyrus	0.09
Inferior middle temporal gyrus	0.32	Pallidum	0.06
Putamen	0.30	Lateral Occipital temporal gyrus	0.06
Thalamus	0.30	Anterior inferior temporal lobe (lateral part)	0.03
Pallidum	0.28	Inferior middle temporal gyrus	0.03
Superior central temporal gyrus	0.27	Anterior superior temporal gyrus	0.02
Insula	0.24	Thalamus	0.02
Nucleus accumbens	0.24	Superior temporal gyrus (central part)	0.01
Subcallosal area	0.24	Caudate Nucleus	−0.02
Orbitofrontal Cortex-Anterior Orbital Gyrus	0.24	Posterior temporal lobe	−0.03
Caudate Nucleus	0.24	Anterior superior cingulate gyrus	−0.04

Network diffusion out of SN recapitulates regional atrophy in Parkinson’s disease

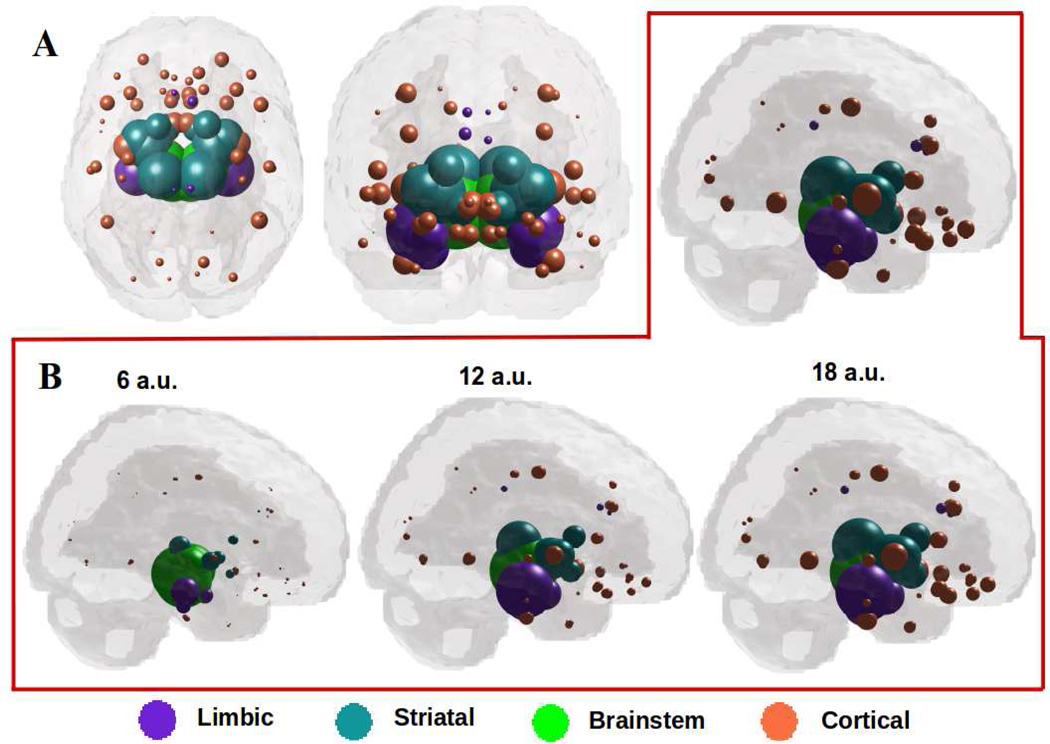
Since bilateral SN gives the best seeding, we plot the spatiotemporal evolution of x_SN (t). The maximum of R^SN(t) occurs at t_max = 19, hence x_SN (t_max) is shown in Figure 4A. The model’s regional pattern is a good match visually against the empirical atrophy pattern in Figure 1, and statistically very strong and significant (R=0.65, p < 1e-5). Figure 4B shows the evolution of x_SN (t), from early (t=6) through mature stage (t=18), the model increasingly resembling empirical atrophy of Figure 1: early involvement of RN and STN, shown in green, followed by limbic areas: amygdala, hippocampus shown in purple. Next affected are the basal ganglia (caudoputamen, accumbens and globus pallidus) shown in cyan. This is followed by thalamus, shown in purple. NDM predicts eventual spread to wider cortices, especially anteromedial temporal regions, and anterior/subgenual cingulate, shown in coral.

Figure 4: A: ND prediction from bilaterally seeded SN at t_max = 19.

Glassbrains of network diffusion model seeded at the bilateral SN at t_max = 19 shows spatial evolution of Parkinson’s from SN to connected striatal areas, especially RN and STN shown in green, and limbic areas like amygdala, hippocampus, and thalamus shown in purple. The next regions to be affected includecaudoputamen, accumbens and globus pallidus shown in cyan. Finally, the NDM predicts spread to wider cortices, especially inferotemporal and middle temporal regions as shown in coral. B: Spatiotemporal evolution of model Parkinson’s pathology. Evolution of SN-seeded network diffusion exhibits the classic striatal and limbic areas as early affected regions, followed by somewhat slower diffusion into the caudate and inferotemporal gyrus. This temporal sequencing predicted by the model is a close match with Parkinson’s progression, assuming that spread into limbic regions, typically in dementia with Lewy bodies and PD with dementia, are part of the same continuum as classic Parkinson’s.

Perhaps the prominence of SN is because it is so pervasively and well connected to other structures that our result is reflecting merely a deafferentation process involving direct one-hop connectivity rather than a true pathology diffusion process. We have already noted that connectivity to SN by itself can explain regional atrophy (R=0.51, Figure 2), although the association is not as high as for NDM seeded at SN (R=0.65, Figure 3). To rule out this explanation we plot the connectivity from SN to various cortical structures (Supplementary Figure S5). From Figure S5A, we can see that SN is well connected with midbrain/diencephalon, limbic and striatal regions and poorly with the rest of cortex. Thus, network spread in later stages into frontal and neocortical regions cannot be simply explained by one-hop connectivity from SN. Histogram of node strength (Figure S5B) shows that SN does not have especially high connectivity in comparison to other well-connected structures. Thus, the outcome that SN is the most likely seed region is not because of especially strong or pervasive connectivity or a direct deafferentation process, but rather due to its location within the brain’s network topology.

Testing for significance against alternate randomized models

We evaluated the NDM against alternate network models to show its specificity to PD atrophy and to the connectome on which it evolves. We evaluated this in two ways and recorded the best R achieved by each model against the PD. First, we randomly scrambled the healthy average connectivity matrix C 2000 times and ran the NDM on each scrambled network. Second, we randomly scrambled the group t-statistic of regional PD atrophy vector and ran the NDM on original connectivity matrix C. The distribution of Pearson’s R over 2000 scrambled matrices is shown in Figure 5A, and clearly indicates that our correlation results are unlikely to be due to chance. There is a hard limit on the left of this plot at R~0.45, which corresponds to the zero-diffusion time value of R^SN(t) curve in Figure 3A. The second random scrambling experiment, where the atrophy vector was scrambled instead of the connectome, gave an R distribution shown in Figure 5B. This distribution was approximately Gaussian, with mean 0.07, standard deviation 0.11. Random model’s R was much lower than the maximum R of 0.65 achieved by the true model; statistically outside the 95% confidence interval, or p < 0.05. Hence, the reported SN-seeded NDM prediction is unlikely to be explained by chance. We have also re-evaluated our results with two different choices of β and are shown in Supplementary Figure S6. Since our method for randomization only preserves edge and node statistics for the whole network, but not edge statistics for the node sequence, we re-evaluated our results by using a null model that preserves the node degree sequence by including a null model as a) the Laplacians of a distribution of degree sequence preserving connectivity matrices, and b) the degree sequence preserving permutations of the single Laplacian computed from C. These results are shown in Supplementary Figure S7.

Figure 5: Scrambled networks and PD atrophy.

A: Histogram of correlation strength between ND model and PD data over 2000 shuffled networks. B: Histogram of correlation strength between ND model and 2000 shuffled PD data over using unshuffled structural connectome. The true connectome was shuffled by symmetrically permuting its rows and columns randomly, and the ND model was evaluated for each shuffled network after bilateral SN seeding. The best R achieved by each model was recorded and entered into the histogram. The null models are distributed well below the true model, indicating that the latter is highly unlikely to arise by chance (p < 0.05).

NDM-predicted arrival time from SN to other regions recapitulates Braak staging of Lewy pathology in PD

Next, we determined arrival times from SN to other regions to demonstrate the temporal sequencing of progression predicted by NDM. Table 3 contains mean arrival time of pathology via network diffusion seeded at both SN nuclei, of top 20 structures, averaged between left and right regions. Supplementary Table S4 contains mean arrival time from SN-seeding of pathology of top 20 structures with different choice of β parameters and Supplementary Table S5 contains mean arrival time of pathology from SN-seeding for all 78 regions with β=0.15. RN and STN, which are closest to SN, have the smallest arrival times followed by striatal, amygdala and limbic structures. Further innervation of NDM from these regions proceeds into anterior cingulate, frontoinsular and occipitotemporal cortex, roughly in accordance with their connectivity and proximity to the SN. Figure 6A shows NDM’s arrival time against connectivity to SN. This confirms the intuition that regions with a higher degree of anatomical connectivity to SN experience earlier pathology arrival. We observed a significant exponentially decaying pattern between connectivity-to-SN and NDM arrival time (R = −0.78, p < 1e-5). Figure 6B,D shows arrival time from SN using an equivalent NDM evolved on the fiber “distance network” and Euclidean distance network, respectively, indicating a significant positive linear association. The strong exponential association in Figure 6A further motivated us to test an alternate model _{defined by proximity=} e^−ci,j⁄σ. A better fit with R = 0.86 (p < 1e-5) was achieved with this model between arrival time and connectivity from SN to other regions as shown in Figure 6C.

Table 3:

Top 20 mean arrival time of pathology through network diffusion seeded at SN

Regions	Arrival Time
Red Nucleus	11.11
Subthalamic Nucleus	12.12
Parahippocampal gyrus	16.16
Hippocampus	18.18
Pallidum	19.19
Thalamus	19.19
Amygdala	24.24
Nucleus accumbens	26.26
Caudate nucleus	30.30
Subcallosal area	31.31
Occipital lobe (lateral part)	36.36
Inslula	39.39
Putamen	41.41
Inferior frontal gyrus	42.42
Orbitofrontal Cortex-Lateral Orbital Gyrus	43.43
Precentral gyrus	44.44
Straight gyrus	45.45
Middle frontal gyrus	46.46
Orbitofrontal Cortex-Anterior Orbital Gyrus	46.46
Anterior Cingulate	46.46

Figure 6: Association between pathology arrival time, connectivity and distance from SN to other regions.

A: Arrival time vs connectivity from SN to other regions. The curve appears to describe an exponential decay of arrival with increase in connectivity from SN. B,D: Linear association between arrival time and distances from SN. C: Linear association between arrival time and exp(−connectivity). The slight improvement in R from panel A to panel C suggests that the exponential decay assumption has merit.

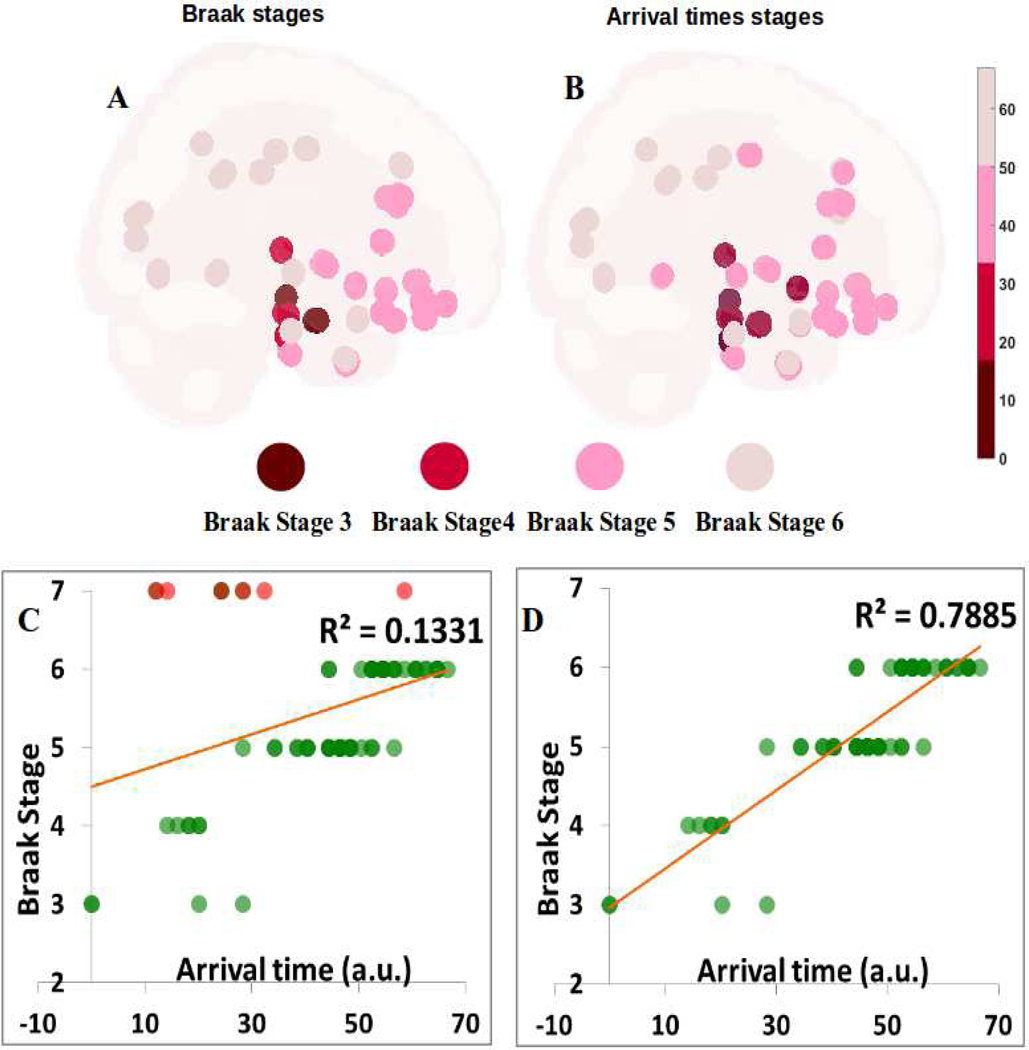
Given that the above arrival time data implicate many structures known to be sites of PD pathology, next we explored whether it can also predict the classic Braak stages of Lewy pathology (3). To this end we created a Braak staging model for each of the 78 non-cerebellar, non-brainstem structures available in our atlas, and assigned each an approximate Braak stage from 3 to 6, starting with SN and amygdala at stage 3, and most of the neocortex at stage 6. The resulting Braak map is shown in Figure 7A; its comparison against NDM arrival time (Figure 7B) can be visually appreciated. The correlation between Braak and NDM arrival time are shown in Figure 7C,D. The only interesting deviations from the Braak model include the striatum and the RN; the latter we believe is due to tractography and spatial resolution limitations whereby connectivity out of SN may be erroneously imputed to RN, which just happens to be in the vicinity of nigral projections. Therefore we did not include RN in Fig 7C,D. Since striatum is not a part of Braak staging scheme, we arbitrarily assign it stage 7 (i.e. outside the 6 accepted stages). Figure 7C clearly shows that striatal areas are outliers (depicted in red) in that their arrival time from NDM would predict them to be involved at early stages. Possible reasons for the lack of observed pathology in the striatum are enumerated in Discussion. When striatal areas are removed (Fig 7D), the agreement between NDM arrival time and Braak stages becomes very strong (R² = 0.79, p < 1e-6). The amygdalae are below the linear fit, and appear as weak outliers. We therefore also tested amygdala-seeding (Supplementary Figure S8A,B); this gave a significant association with Braak stage (R² = 0.39, p < 1e-5), but far weaker than SN-seeding. Supplementary Table S6 contains mean arrival time from amygdala-seeding for all 78 regions.

Figure 7: Braak staging and Arrival time predicting the Braak staging of Lewy pathology in PD from SN-seeding.

A: The Braak stage from 3–6 for each of the 78 non-cerebellar, non-brainstem structures available in our atlas. We can see that Stage 3 which is indicated by dark red starts with SN and amygdala, to Stage 4 with blood red spheres showing temporal mesocortical involment, and finally to Stage 5 and 6 showing most of the neocortex. Color sphere represents stage 4–6 of the Braak’s staging. B: Comparison of the Braak stage against NDM’s arrival time. We can see that arrival time can also predict the classic Braak stages of Lewy pathology as it involves many structures which are known to be sites of PD pathology. Color sphere represents time of arrival through stage 4–6 of the Braak’s staging. Scale represents time of arrival range, ranging from 0–67. C, D: Correlations between Braak and NDM arrival time with (C) and without (D) the striatum and RN with SN seeding. Correlation in (C) shows the striatal areas in red are clear outliers and by removing them we obtain a better correlation (R² = 0.79, p < 1e-6) between NDM arrival time and Braak stages.

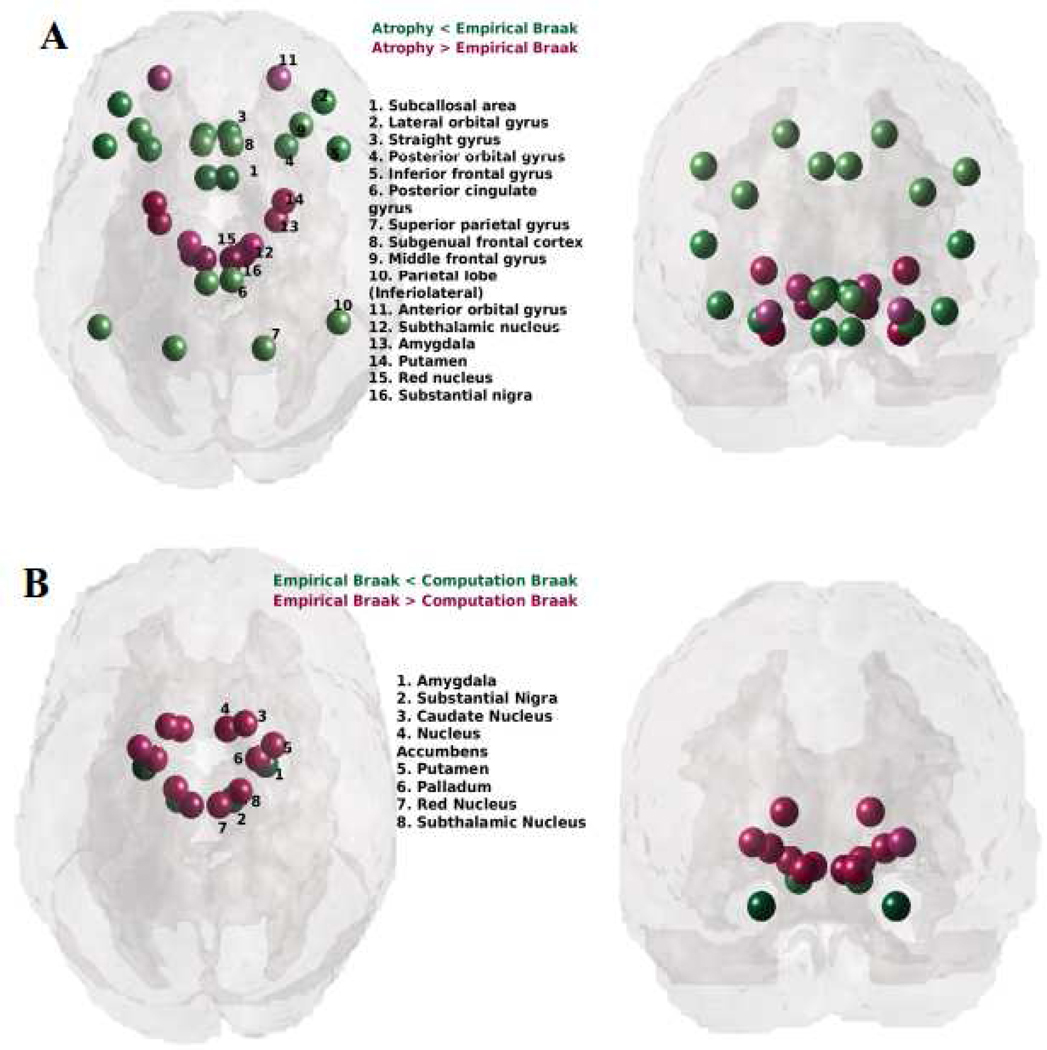
We further identified discrepant regions between PD regional atrophy, Braak staging and the proposed “computational Braak” staging based on the NDM. Figure 8 shows glassbrain renderings of the residuals of a linear fit between empirical regional atrophy and Braak stages (A), and Braak stages and the NDM-predicted arrival time from the SN (B). Spheres are color coded by residual value – negative in green and positive in red. Only the top most discrepant regions (|residual| > 0.15 for panel A and (|residual| > 1.5 for panel B) are shown. The empirical Braak staging underestimates the cell loss seen in the striatum (panel A) in contrast to the proposed computational Braak staging via NDM arrival time shows no discrepancy with striatal atrophy (panel B).

Figure 8: Discrepancies between PD regional atrophy, Braak staging and the proposed “computational Braak” staging based on the NDM.

A: Glass-brain rendering of the residuals of a linear fit between empirical regional atrophy and Braak stages. Spheres are color coded by residual value – negative in green (empirical atrophy is less than that predicted by Braak) and positive in red. Only the top most discrepant regions are shown. Braak staging shows a systematic bias, under-estimating the cell loss seen in the striatum and brainstem. B: Residuals of a linear fit between Braak stages and the NDM-predicted arrival time from the SN. Negative residuals are shown in green (empirical Braak is less than that predicted by NDM arrival time) and positive in red. Clearly, the proposed computational Braak staging via NDM arrival time under-estimates empirical Braak stage in the striatum, where NDM predicts early stage in the striatum whereas Braak reported little early synuclein in the striatum. A comparison with panel A suggests that the discrepancy between NDM arrival time and Braak in the striatum is reflective of the discrepancy between striatal atrophy and its Braak stage (panel A). Hence the proposed computational Braak staging may be considered a more relevant staging system for PD-related atrophy.

Network diffusion is more predictive of atrophy than expression of PD-related genes

Multiple genes have been associated with PD in biochemical and genome wide association studies (GWAS). A recent study by our group identified several genes with regional genetic expression profiles predictive of the atrophy pattern, including LAG3 and RAB5A - which are implicated in trans-synaptic αS transfer (38). To determine the relative contributions of NDM and genetic expression to regional atrophy prediction, we employed two cross-validated L₁ regularized regression models. We chose this approach as it allows for selection of the most important predictive variables by driving coefficients of unimportant variables to zero. The best fit (maximum R) NDM predictors for the SN and amygdala were included in each model, as these are the most biologically plausible seed regions. The first model also contained the regional genetic expression profiles for LAG3, APLP1, NRXN1 and RAB5A; genes implicated in trans-synaptic αS transfer. The second model contains 13 other genetic expression profiles, including those for well-validated PD-risk genes such as SNCA (αS), GBA and LRRK2. Genetic expression profiles were obtained from the ABA and mapped to the same regions used for NDM.

The cross-validated model with minimum mean squared error (MSE) in each case contained both NDM variables (Figure 9A,C), indicating that they are important predictors of the atrophy pattern. Both NDM predictors were also the only variables retained at very high values of the tuning parameter λ, indicating that the maximally sparse model contains only NDM predictors and no genetic expression profile predictors. However, the models with minimal MSE did contain multiple genetic expression profiles, suggesting that genetic factors are relevant but are less predictive of the atrophy pattern. In the trans-synaptic transfer model, LAG3 and NRXN1 were important predictive variables (Figure 9A,C), in keeping with previous reports from us and others (28,39). In the model containing other functional class genes, BST1, STK39, LRRK2 and PARK7 were important predictive variables (Figure 9B,D). Interestingly, the profile for the gene encoding αS (SNCA) was not predictive of atrophy, similar to previous findings (28).

Figure 9: Network diffusion is a more important predictor of atrophy than genetic expression profiles.

(A) Cross-validated L₁ regularized regression coefficients as a function of tuning parameter λ for a model containing both SN and amygdala NDM predictors; and expression profiles for genes implicated in trans-synaptic alpha-synuclein transfer. Both NDM predictors, and expression profiles of LAG3 and NRXN1 have non-zero coefficients at minimum model MSE, indicating that these are important predictive variables. (C) Regression coefficients for a model containing both NDM predictors and expression profiles for genes from other functional classes. Both NDM predictors, and expression profiles of BST1, STK39, LRRK2 and PARK7 have non-zero coefficients at minimum model MSE. Both NDM predictors are the only variables retained at very high values of λ in both models. (B, D) Ten-fold cross validated mean squared error curves for the corresponding models in A and C, respectively.

Can network diffusion predict individual patients’ regional atrophy and clinical scores?

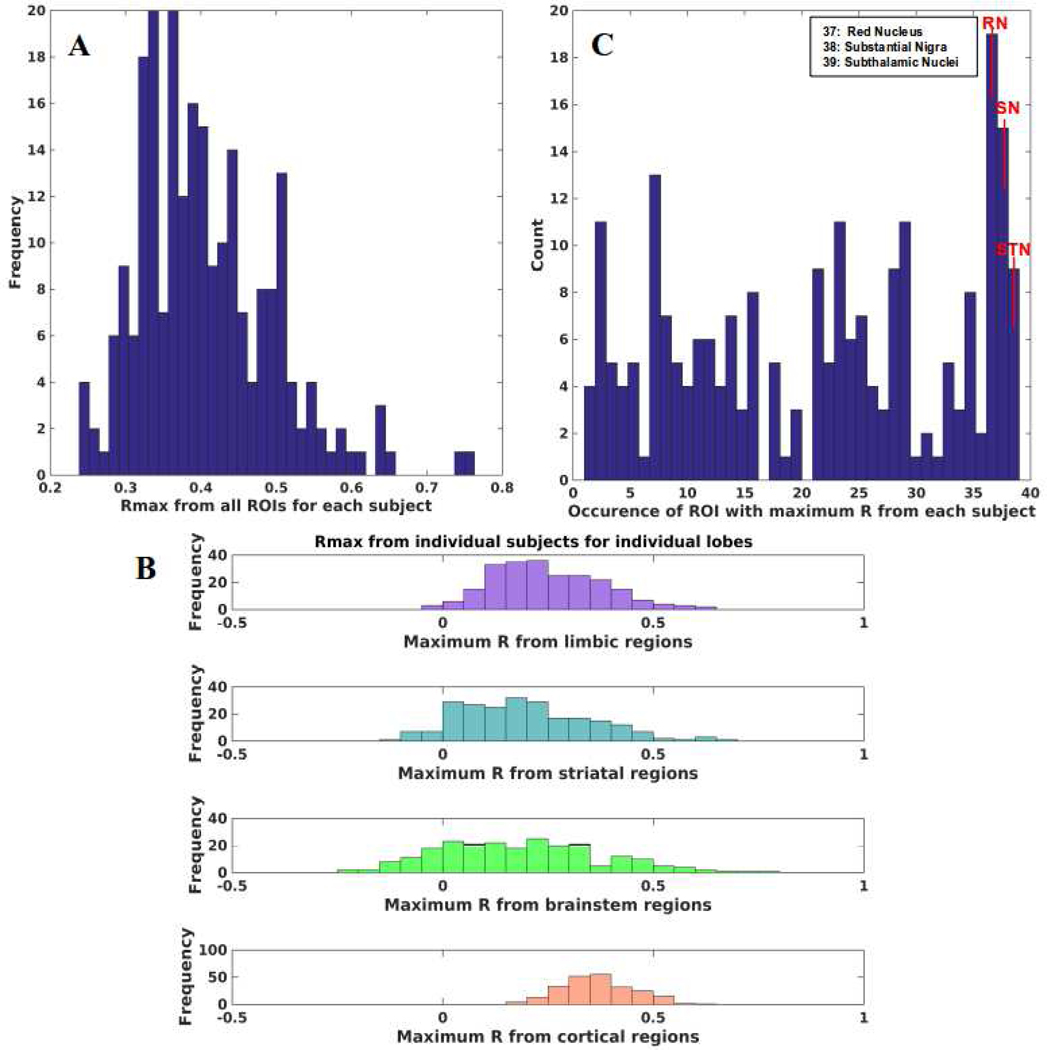
To assess clinical impact, we tested if NDM could reproduce cortical PD atrophy in individual subjects. We ran NDM on 232 PD individuals and calculated maximum Pearson’s R after seeding each of 39 bilateral ROIs for each subject (Figure 10A). We can see that NDM can reproduce individualized regional atrophy with peak R as high as 0.75–0.76. From Figure 10B,C we can see that maximum R is achieved by midbrain regions (RN, SN), and the striatal STN. In Figure 10B, each color bar is representative of maximum R achieved from limbic (purple), striatal (cyan), midbrain (green), and cortical (coral) regions respectively from all individual subjects. Maximum R achieved from limbic and striatal regions are around 0.62–0.66, whereas maximum R achieved from midbrain regions is around 0.65–0.76. RN and SN achieved maximum R from most subjects as seen in Figure 10C, followed by STN. RN result may in fact reflect SN projections, as noted before. We also re-evaluated our results with two different choices of β parameters to verify that our choice of β did not affect maximum correlations in individual subjects, and are shown in Supplementary Figure S9.

Figure 10: PD atrophy on individual subjects with NDM.

A: Histogram of maximum R achieved from all ROIs seeded bilaterally from each individual subjects. Single Rmax is obtained from 232 individuals from all bilaterally seeded ROIs. Rmax is well distributed with mean Rmax ~ 0.41 demonstrating that NDM can reproduce PD atrophy in most of the subjects. B: Maximum R achieved from four major regions (limbic = purple, striatal = cyan, midbrain = green, and cortex = coral) from individual subjects. Rmax values were attained for each of these regions from 232 individual subjects. We can see that for most of the subjects’ maximum R was achieved from the midbrain (yellow bars) compared to other regions. C: Count of number of times a specific ROI was identified with maximum R. We can see that midbrain regions (37–39) were identified with maximum R multiple times than other regions. Red nucleus (RN) occurred the most followed by substantia nigra (SN) and subthalamic nucleus (STN).

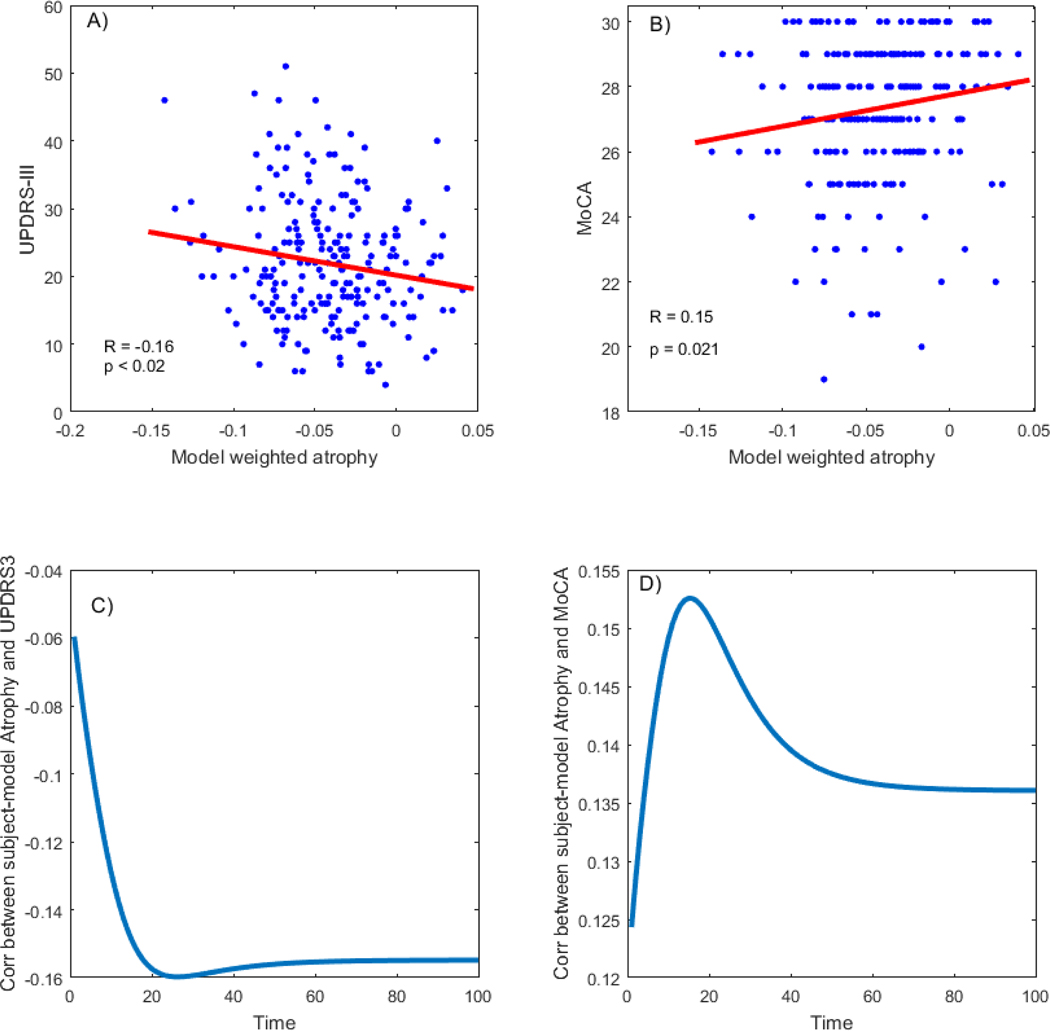
After calculating the PD spread pattern, we used the PD maps to calculate disease specific atrophy measures per subject, reflecting subjective disease related brain alterations. We found a significant relationship between the subjective atrophy and motor related disease severity measured by UPDRS-III (R = − 0.16, p < 0.02) as seen in Figure 11, where negative correlation indicates higher deformation (more negative) relates to higher motor related disease severity (more positive). The relationship between PD-related atrophy and cognitive decline measured by MoCA was also significant (R = 0.15, p < 0.022) indicating lower cognitive score for higher deformation.

Figure 11: Association between PD-related deformation score and disease severity,

A: PD-related deformation is significantly correlated with motor related disease severity (r = −0.16, p<0.02). The higher the model weighted atrophy in the brain (more negative score), the higher the disease severity score B: PD-related deformation is significantly correlated with cognitive related disease severity (r = 0.15, p=0.021). The higher the model weighted atrophy in the brain, the lower the cognitive score. C: Correlation between UPDRS-III and model-weighted atrophy over time D: Correlation between MoCA and model-weighted atrophy over time.

Discussion

Key findings

PD-related regional atrophy follows a stereotyped spatiotemporal progression in a caudorostral fashion from early loss of cells in the brainstem, to limbic, striatal, and finally neocortical atrophy. The causative mechanisms behind this progression are not fully understood. Here we proposed that a mathematical model of network spread, Network Diffusion, could correctly recapitulate the classic progression of PD. The NDM is based on the trans-neuronal transmission of misfolded pathological proteins, in this case αS, whose aggregates form Lewy bodies, which are the classic hallmark of PD and the related human dementia with LBs (DLB). Since in vivo Lewy body imaging is currently unfeasible, we asked instead whether the model’s prediction of pathological progression can also explain regional atrophy, under the assumption that downstream cell loss must be underpinned by upstream pathological processes. By applying the NDM to PD subjects’ regional atrophy data, we were able to assess whether network-based spread of pathology is a good model for predicting downstream atrophy phenotype in PD.

We reported that the ND model agreement with group-level cross sectional atrophy patterns from the PPMI database was strong and highly significant (R=0.65, Figures 3,4, Table 2). Repeated seeding of the NDM yielded the SN as the most likely seed region, mirroring its role as one of the most atrophied and Lewy body-rich regions in PD. We noted that our results are not due to SN having an especially strong or pervasive connectivity, or a direct deafferentation process, but due to its unique location in the brain’s network topology (Figure S5). Therefore, our data are better explained by the idea that synuclein misfolding, starting in the brainstem nuclei but prominently accumulating in SN, causes misfolding in nearby regions, which then act a secondary sources of synucleinopathy. Our result is also not due to chance, based on randomized network scrambling simulations (Figure 5). The analysis was regionally unbiased, whereby each region was seeded in turn. Some of the other regions that have high likelihood of seeding (parahippocampal, hippocampus and amygdala: Table 3) are also early and consistent participants in PD and DLB etiology. The thalamus also has high seeding likelihood, in agreement with reports of thalamic pathways involved in generating movement and in monitoring movement action (40); thalamic pathology contributes directly to Parkinson’s symptoms (41).

That the central role of SN was imputed in an unbiased, data-driven manner without explicit knowledge of the pathological staging scheme, serves to confirm the ability of the NDM to model the pathological progression underlying frank atrophy progression in PD. Note however that due to methodological limitations, our study was not designed to access lower brainstem regions. Therefore, the inference involving SN does not imply that synuclein pathology begins in SN, but that amongst all regions reliably quantifiable on MRI, SN is the most likely seed. Pre-SN Braak stages are the subject of some controversy, especially the role of medullary and olfactory nuclei in early pathology (Burke et al., 2008; Jellinger, 2009; Gagnon et al., 2006; Boucetta et al., 2016). Higher resolution MRI data will be needed to address this question using the presented methodology.

Another intriguing finding was that the temporal sequencing of pathology “arrival times” (Table 3) into implicated regions predicted by the NDM seeded at SN is capable of closely recapitulating (with some adjustments, see below) Braak’s famous Lewy body-based staging scheme, in particular of stages III (nigral) to VI (neocortical). A highly significant association was found between NDM and Braak stage (R² = 0.79, p < 1e-6) – see Figure 7. This opens the door for the use of models like NDM as a computational Braak-like staging scheme using only MRI instead of post mortem pathology scoring. We also tested amygdala-seeding, since it was empirically the second most likely seed region, and is known as a parallel branch of synuclein ramification at Braak stage 3 (46). Although amygdala-seeded arrival times were significantly associated with Braak stages (R² = 0.39, p < 1e-5), the amygdala-seeded NDM produced far weaker results than SN-seeding. These findings are further discussed below in the context of existing literature and future applications.

Given that multiple genes have been associated with PD, and our previous report suggesting that some genes exhibit regional expression profiles that correlate with atrophy (28), we attempted to understand whether innate gene expression can explain atrophy better than NDM. Here we demonstrated using a L₁ regularized regression model that the relative contribution of NDM vastly exceeds that of regional genetic expression in determining the regional atrophy of PD (Figure 9). Employing various rigorous cross-validation approaches we were able to show that the most important predictive variables are the NDM predictors derived from seeding at the SN and amygdala. Gene expression profiles did not survive as significant predictors at the highest levels of the model’s sparsity-inducing parameter. However, the most important trans-synaptic genes under less stringent sparsity conditions were LAG3 and NRXN1. Our previous work (28) also identified LAG3 as an important genetic factor predictive of atrophy, possibly related to the ability of LAG3 to bind αS preformed fibrils (39). Amongst other functional class genes, BST1, STK39, LRRK2 and PARK7 were important predictive variables. Interestingly, the profile for the SNCA was not predictive of atrophy under any relevant model conditions, similar to previous findings (28).

This combined gene and NDM analysis was designed to answer specifically: what role does healthy (as compared to environment- or age-induced) gene expression, as a proxy for innate molecular properties of brain regions, plays in governing their selective vulnerability to PD? Our interpretation of these data is that, apart from the obvious interpretation that genetics plays a secondary role in PD progression, they indirectly support cell non-autonomous mechanisms of PD progression and raise questions about the cell-autonomous hypothesis involving innate vulnerability. In the latter view the apparent progression of PD pathology and atrophy might be unrelated to inter-regional connectivity, and instead come about simply in the order of their innate cellular and molecular vulnerability. We have demonstrated that innate vulnerability holds only moderate explanatory power in comparison to the cell non-autonomous processes, especially the role of trans-neuronal cell-cell interaction based on network based NDM. These results are concordant with the “molecular nexopathy” paradigm (47) in that a central role is noted for network spread, but also discordant in that we find no evidence for selective vulnerability based on cell-type, architectonic and other intrinsic properties of brain regions that may be reflected in innate gene expression. It is noteworthy however that the nexopathy paradigm enumerates a more diverse set of potential mechanisms by which molecular dysfunction might interact with the neural architecture than is possible to explore in a single study. Possibly, the seed regions inferred by our NDM approach (SN and amygdala) may have specific molecular vulnerability that remained undiscovered by our study design. In future work we will explore the genetic correlates of likely seed regions of PD, rather than PD-associated atrophy as done here. Finally, we reported the ability of NDM to predict individual patients’ atrophy data; the agreement in individual cases varied greatly but was on average moderate, with Pearson’s R varying in the range 0.25 to 0.75 (Figure 10). The NDM-derived disease severity scores of patients gave rather modest albeit significant predictor of cognitive and motor scores (Figure 11), with R=−0.16 for UPDRS and R=0.15 for MoCA scores (p=0.02 for both). This is not unexpected, as clinical measures are known to correlate weakly with regional atrophy in PD, in particular in this de novo cohort.

The conclusion that a network spread model, NDM, based on diffusive prion-like propagation, adumbrates the stereotypical pattern of Parkinson’s spread across the brain also serves to independently bolster the etiologic theory of trans-neuronal transmission of Parkinson’s pathology – something that is currently not possible directly on human in vivo data. We previously demonstrated that a similar network spread model recapitulated the classic patterns of Alzheimer’s disease (AD) (14). This broad applicability attests to the NDM’s robustness and bolsters the hypothesis that all neurodegenerative diseases share a common prion-like mode of transmission.

Diagnostic and prognostic applications

Diagnostics.

NDM results largely corroborate what is known from neuroimaging studies about the archetypal patterns of damage in PD, including resting-state functional MRI, structural MRI, MR susceptibility, magnetization transfer, DTI, ASL perfusion (16,32–36) and metabolic FDG-PET (32,33,48). Although these imaging studies may provide promising diagnostic biomarkers, there is a need to combine these phenomenological markers with a model-based approach that is informed by how disease actually progresses in the brain. Computational and statistical methods have been employed in identifying the patterns of damage in PD and successfully used for automatic classification (49), but they too are phenomenological.

We demonstrated that individual subjects’ atrophy (Figure 10), cognitive and motor scores (Figure 11) can be predicted moderately but significantly using NDM-based projections. Although this is insufficient for immediate diagnostic applications, with future enhancements including machine learning, more sensitive and multiple imaging modalities, and subject-specific connectomes, the power of the NDM approach can be harnessed into a fully quantitative diagnostic tool. This will signify a dramatic break from current practice, where PD is diagnosed purely by history and physical exam, and neuroimaging exams are only used to exclude other neurologic causes such as stroke and tumors.

Prognostics.

An important application of our model is the potential to provide prognostic information, including the prediction of individual disease progression, starting from baseline MRI. Model dynamics encapsulated in Eq. 2 can “play out” future atrophy patterns. Since the prediction is fully spatially resolved, predictions regarding specific regions and pathways are possible, facilitating prognoses regarding specific functional deficits. Future risk of dementia in Parkinson’s patients could therefore be quantifiably ascertained, which would inform treatment and non-clinical lifestyle decisions.

Regionally targeted therapies.

The deterministic, hence reversible, nature of our model raises the possibility of inferring likely originating sites from a patient’s current disease topography. This was demonstrated on group data in the seeding results of Figure 2, but future adaptation on individuals could prove valuable in localizing targeted therapies like deep brain stimulation.

Towards a “Computational Braak Staging” scheme.

Seminal autopsy studies by Braak revealed that S deposits followed a caudal-rostral pattern, beginning in the olfactory and peripheral enteric system, ascending the brainstem, then moving into the anteromedial temporal mesocortex, then neocortical sensory association and prefrontal areas, and finally the premotor and primary sensory/motor fields (3). Some aspects of Braak staging are noteworthy from a modeling viewpoint. Pathology-based scoring is by nature qualitative rather than quantitative. Braak’s is the most well-known, but by no means universally accepted staging scheme for synuclein pathology in PD. A recent study of 208 pathology-confirmed cases found that of 76 with Lewy pathology, only half conformed to Braak staging (50). Other related pathologies, DLB prime among them, do not properly fit Braak staging, although DLB and PD with dementia (PDD) may be thought to represent advanced (5–6) stages of the Braak model (46).

The NDM-predicted arrival time (Figure 7C,D) gives a strong association with Braak stage (R² = 0.79, p < 1e-6) – see Figure 7, when striatal areas are excluded. Given the limitations of qualitative pathology scoring, such a strong association with Braak is intriguing, and suggests that NDM can be used to obtain a computational Braak staging from in vivo imaging data. Since the current PPMI data are not pathology-confirmed, the validation of such a tool will require a different study on an autopsy series. We note also that our computational model is based on general pathology spread and is incapable for differentiating between different synucleinopathy. Since our NDM begins at Braak stage 3, it may more successfully recapitulate advanced disease, like PDD and DLB, rather than pure PD.

The proposed computational Braak staging via NDM arrival time shows no discrepancy with striatal atrophy (Figure 8, panel B), in contrast to empirical Braak staging (Figure 8, panel A). This suggests that the discrepancy between arrival time and Braak in the striatum (panel B) is reflective of the discrepancy between striatal atrophy and its Braak stage (panel A). Hence the proposed computational Braak staging may be considered a more relevant staging system for PD-related atrophy.

Striatal synuclein pathology.

The key discrepancy between our model and Braak stages is in the striatum, where our model imputes a strong involvement, with arrival times shortly after limbic infiltration, whereas Lewy pathology is entirely absent from Braak staging. In fact, our empirical atrophy data (Figure 1) suggests a strong striatal involvement, mirroring other wellknown studies in the field. Therefore, the real mystery is, why is striatal atrophy not accompanied by striatal Lewy pathology? There are several possible explanations. First, recent studies have in fact revealed significant striatal involvement in synucleinopathies. In spite of the fact that association of the neostriatum was not considered in the originally proposed PD staging by Braak et al., 2003, in another study they reported presence of neostriatal lesion in stage VI of PD (Fig. 3d in Braak et al., 2006). Mild striatal αS burden was associated with Braak stage 3, and very mild striatal αS lesions were seen in PD brains scoring Braak stages 3–5. Of PDD cases presenting initial parkinsonian symptoms, 29% had positive synuclein lesions in the striatum. Mild to moderate synuclein pathology in caudate nucleus and putamen was seen in 76.5% of DLB brains. Almost 60% of DLB cases with initial PD phenotype (mean PD stage, 5.2) had some striatal synuclein lesions than PDD with mean PD stage, 4.0 (52). In addition, Saito et al., 2003 reported numerous Lewy dots in the putamen in the neocortical form DLB and neuritic αS lesions in the neostriatum which appear in the limbic form DLB. A study done by Mori et al., 2008 showed strong nonlinear correlation between PD stages and neostriatal inclusions, especially in medium spiny projection neurons. They reported that αS accumulates in the neostriatum at stage III initially and neostriatal αS pathology severity is correlated with the PD stage. Second, the reliance on Lewy bodies and neurites in the classic staging model leaves open the possibility of oligomeric or soluble synuclein being abundant in non-Braak areas. In PD and DLB there has been only limited examination of striatal pathology (52). Only the use of novel monoclonal antibodies raised against altered synuclein uncovered an extensive burden of synuclein pathology in the striatum of Lewy body disorders, the highest density of striatal lesions being observed in patients with a combination of AD and DLB or pure DLB (55).

We also cannot rule out limitations in our approach. Striatal atrophy may not directly result from synuclein accumulation, and could instead result from deafferentation of nigrostriatal dopaminergic projections (52). The NDM is based on DW-MRI tractography, which can only give undirected connectivity amongst brain regions. This can limit the predictive power of the ND model in the striatum, because the striatum in particular is a highly directional region. Regardless of these possibilities, that striatal atrophy is prominent in de novo PD, that the NDM fits well to the observed regional patterns of atrophy, and that atrophy rather than Lewy distribution might be a better correlate of downstream dysfunction, suggests that despite variance from Braak staging in the striatum, the NDM gives clinically relevant recapitulation of PD progression.

Limbic synuclein pathology.

Both amygdala and hippocampus play a prominent role in the NDM seeded at SN, and the amygdala was the second most likely seed region (Table 2), except for the RN, which we discount, see Limitations. SN-seeded network diffusion affects both striatal and limbic areas early, consistent with MRI studies that have reported an atrophic amygdala in early PD (56). Hippocampal involvement is sometimes used as a differentiator of Parkinson’s cases with or without dementia. Amygdala-seeded NDM recapitulated PD atrophy to some extent but not as strongly as SN-seeding, suggesting against a primary limbic involvement at least in de novo PD. The NDM is a general model of transmission and is not specific to PD; hence it might be capturing processes involved in other Lewy disorders like DLB. Our data does not rule out that pathology spread could follow the classic pure Parkinson’s pathway (through striatum to the neocortex) or the DLB/PDD pathway (via amygdala and hippocampus). If further confirmed, this would reinforce the emerging notion that there may be no special distinction between PD, PDD and DLB; these might instead be variants along a pathophysiological continuum reflecting slightly different striatal/limbic routes of the same transmission mechanism (see e.g. Burke et al., 2008; Jellinger, 2009). A separate study would be necessary to quantitatively demonstrate this on variant cohorts.

Alternative hypotheses

Other alternative spread models were also evaluated for comparison, specifically, random spread and distance-based spread. Random spread is not a realistic model but serves as a statistical reference that was used to provide a significance level to the model results. Distance-based spread on the other hand is highly plausible; in fact, Braak’s original staging model relied on caudorostral spread that placed adjacency and distance of affected structures at the center of Parkinson’s progression. This theory has been criticized on the grounds that there is little in vivo evidence of brainstem pathology and that adjacent structures are not always affected (42). Although our data favor connectivity-driven rather than distance-driven mechanism of pathology spread, the difference is not stark, and distance-based spread cannot be definitively ruled out due to strong collinearity between connectivity and proximity.

Epidemic spread model, an alternate disease spread model analogous to the spread of epidemics in populations mathematically describe the interdependence between intra-brain misfolded proteins propagation and the brain’s defense response. Mathematical models like this have been studied in recent years for AD (24) but not much research has been done to apply these models to PD. It would be interesting to compare the present results with this model, however it is noted that the two generally give similar results, as both are based on network-based spread.

The NDM did not differentiate between pathways of dopamine and other neurotransmitter systems, which are thought to be differentially impacted by PD. While the NDM prominent effect in dopamine-rich regions is certainly consistent with the hypothesis that Parkinson’s topography simply reflects the targeting of synuclein-rich dopaminergic systems (42,43), our data points to a network-driven mechanism that is not limited to the dopaminergic neurotransmitter system.

Limitations and future work

The PPMI volumetric data were not confirmed by histopathology, opening the possibility of misdiagnosis. Validating the full temporal dynamics of the NDM will require longitudinal data of a sufficiently long follow up period, which is currently unavailable. The model uses a canonical connectivity matrix derived from the white matter tract tracings of healthy subjects, but it is possible that PD itself alters the brain’s connectome and thus changes the pattern of progression. This might account for some of the variability in individual patterns that our model is unable to capture. Downstream cognitive and clinical outcomes are simply too high-order, noisy, variable and suffer from inter-operator variance, to be capable of being predicted accurately by imaging-based measures. In particular, this cohort of de novo patients does not have a sufficiently high effect size in regional atrophy, which makes the association with downstream dysfunction even more difficult to detect. In addition, there is a disconnect between what the brain’s morphological state tells us (whether observed or predicted by a model such as ours) and its downstream dysfunction, which is influenced by so many other factors including age, sex, demographics, environment, genetics, etc. This does not mean that the proposed NDM model is not valuable in a prognostic sense, but it does mean that a neurologist should be careful when interpreting our quantitative predictions and should consider extraneous phenomena like resilience and reserve. Given this our model will require future enhancement to be considered for diagnostic purposes, however much is still unknown about the exact mechanistic details of network transmission in PD and other synucleinopathies. Further, the limited spatial and contrast resolution of T1 weighted MRI and DW-MRI make it difficult to localize atrophy to small nuclei with complete certainty. Spatial inaccuracy in atlas generation and normalization of subject images to MNI space may compound this problem. This is especially relevant to small structures of the basal forebrain and midbrain. For example, using propagator analysis the RN appears to have high connectivity to the SN, causing it to be a prominent early site of SN-seeded NDM, but there are few if any nigral afferents into RN, and it is more likely that RN is simply in the proximity of nigrostriatal projections. Unfortunately, the current state of DW-MRI and tractography do not allow us to fully resolve these structures. Furthermore, because T1-weighted MRI is sensitive to iron content, changes in iron accumulation, for example, in SN, globus pallidus, or RN, may be interpreted as volume changes by the DBM methodology. In our model the striatum shows high discrepancy, but at its root we think there is a hitherto unexplored process at play, which our future work will target. As we have thoroughly discussed in our study, recent studies suggest that oligomeric species are indeed abundant in the striatum, even though Lewy bodies are not. If either oligomeric species or other mediators like microglia are implicated by ongoing and future studies, the discrepancy we are reporting will be resolved. If and when that happens, a mathematical model like ours will be critical in quantitatively testing these hypotheses. Finally, this study captures only mid-to-late PD. It describes how disease localized to the SN spreads through the brain over time, but is unable to access upstream Braak stages I/II due to lack of access to medullo-pontine and olfactory nuclei which are difficult to reliably identify on MRI.