Evaluation of RF interactions between a 3T birdcage transmit coil and transcranial magnetic stimulation coils using a realistically-shaped head phantom

Abstract

Purpose

Multichannel Transcranial Magnetic Stimulation (mTMS)(1) is an emerging technology that allows multiple sites to be stimulated simultaneously or sequentially under electronic control without movement of the coils. A mTMS/MRI head coil array for 3T is currently under development to mitigate challenges of concurrent TMS/fMRI as well as to enable potential new applications. The influence of the mTMS system on the MR image quality and safety must be carefully investigated.

Methods

A standard birdcage volume coil for 3T systems was simulated using a commercial numerical electromagnetic solver. Two setups consisting of i) a MR compatible TMS coil and ii) a 3-axis TMS coil array were simulated to quantify changes in the transmit field $B_{1 }^{+}$ and the specific absorption rate (SAR). A realistically shaped homogeneous head model was used in the computations.

Results

The stimulation coils produced enhancements and attenuations on the transmit field with effects greater than 5% up to 2.4 cm and 3.3 cm under the scalp for the MR compatible TMS coil and 3-axis TMS coil array respectively. The 10-gSAR distribution did not change significantly in either of the cases, however the nominal SAR maximum locus was shifted between existing hot spots.

Conclusion

The simulated B₁⁺ variations found near the TMS coils indicate the possibility of inducing sequence-dependent image artefacts predominatly limited to the vicinity of the coil(s). However, we conclude that neither the MR compatible commercial TMS coil nor the 3-axis TMS coil array siginificantly elevate SAR in the head or neck beyond accepted safety limits.

Introduction

Concurrent imaging and stimulation of the brain is a rapidly expanding field that has the potential to drastically improve the understanding of brain function in healthy and diseased state. The combination of non-invasive stimulation techniques such as transcranial magnetic stimulation (TMS) with functional magnetic resonance imaging (fMRI), presented for the first time twenty years ago (2), offers the possibility to localize the TMS-induced activations with high spatial resolution in the millimetre scale. It also provides the unique benefits of studying the causal relationships between the cortical and subcortical nodes of large-scale brain networks. This approach can be used to address unresolved questions about the functional connectivity vs. causality in fMRI studies. Furthermore, it can be employed to map how the effects of TMS propagate from the primary target to the secondary areas that are functionally and/or anatomically connected to it (3–5). This is particularly important as the therapeutic efficacy of TMS may be related to the intrinsic connectivity between the TMS cortical ‘hot spot’ and a target brain region (6).

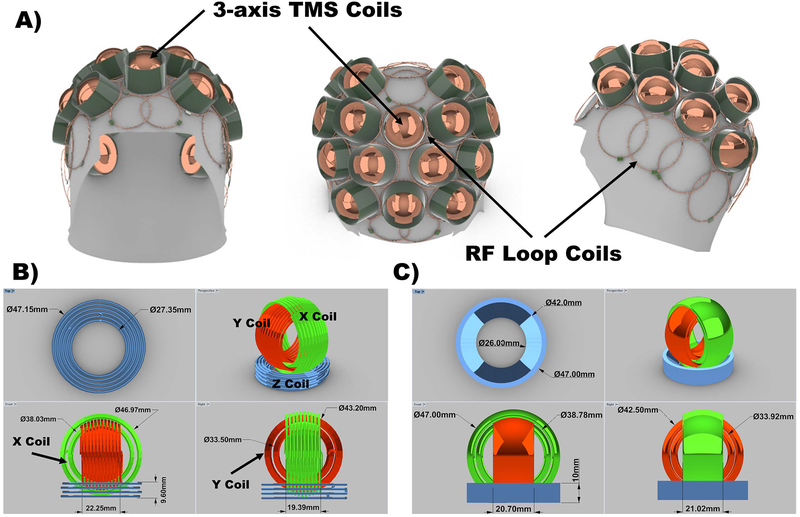
The state-of-the-art setup to conduct concurrent TMS/fMRI experiments uses large head coils (usually head birdcage coils driven in quadrature) placing the magnetic resonance (MR) compatible TMS coil between the imaging coil and the subject. Improved methods using a dedicated thin receive-only MR coil array underneath the TMS coil have been proposed to boost the sensitivity of the experiments(7). In the latter set up, the built-in body coil of the scanner is used for RF excitation of the sample. Even though this approach allows a more flexible positioning of the TMS coil, keeping the precise placement of the stimulation coil over the desired target fixed respective to the subject’s head over the course of the entire exam remains a challenge. To address this limitation as well as to widely expand the scope of possible TMS-fMRI protocols, a multichannel TMS system (mTMS) integrated with a whole head MR coil has been proposed and is under development (see Figure 1A). The building block element of the stimulation system is a novel 3-axis TMS coil (see Figure 1B). The principle of mTMS(1) enables a more flexible targeting of the brain as it allows the stimulation pulse or pulses to be steered to the desired cortical location for accurate delivery without any physical repositioning of the TMS coils. Additionally, it will allow multiple sites to be targeted either simultaneously or sequentially using electronic control. The multichannel approach therefore has the potential to overcome the main challenge TMS/fMRI experiments are currently facing: changing the target stimulation area ‘on-line’ during the imaging session. Combining the emerging mTMS technology with a close-fitting, high-SNR MR receive brain array coil could significantly advance this promising multimodal imaging/stimulation methodology to become a standard and easy-to-use tool for both research and clinical applications.

Figure 1.

A) First prototype design of the mTMS integrated with a whole-head MR coil. The RF coil array elements will be routed around the TMS coils to allow the stimulation system to be positioned directly on top of the subject’s head. B) 3D-CAD complex model of the 3-axis TMS coil prototype. The model dimensions are shown in the figure. The wire diameter of the model is 1.5 mm. This element is the building-block component of the mTMS array and it consists of three independently driven coils in three perpendicular planes. The design offers additional degrees of freedom on the generated electric field shapes in comparison with a single Z-coil unit. C) 3D-CAD simplified model of the 3-axis TMS as four rings and a tube with two heights representing the inner and outer X and Y coil windings and the Z coil windings, respectively. The model dimensions are shown in the figure. For the X and Y rings the thickness was 2 mm.

The combination of TMS in the MR environment presents many technological challenges. Many of the interactions and effects that might have an impact on the image quality have already been investigated. First, the homogeneity of the B₀ field is affected by the presence of the TMS coil in the bore. Susceptibility effects produced by the plastic housings encapsulating the stimulation coils touching the scalp as well as the TMS coil windings (typically copper conductors) can increase distortions and signal drop-outs in fMRI data (8). Any leakage current from the stimulator to the coil may disturb the spatial encoding of magnetization to be measured (9). RF interactions between receive only coil elements and an overlaying MR compatible TMS coil has already been investigated and shown to be negligible (7). Finally, the effects of the TMS timing with respect to the acquisition on the image quality were carefully investigated (10) and practical rules were proposed to minimize the imaging artefacts when the TMS is interleaved with EPI acquisition. The effects of receive-only coil inserts on the RF field of a volume transmit coil have also been previously addressed (11). However, the interactions of TMS coils with the transmit field of the RF coils used for transmission, whether it is a head birdcage coil, or the built-in body coil integrated into most 3 T commercial scanners, have not yet been systematically investigated to the best of our knowledge. These interactions could in principle have an influence not only on image quality but more importantly on safety. The distribution of the specific absorption rate (SAR) of the radiofrequency (RF) energy, responsible for potential heating of the tissue, might at least in theory change and/or produce new focal ‘hot spots’ in the subjects due to interactions of the TMS coils with the transmit electric field. As these effects are potentially more pronounced in mTMS systems where the entire head of the subject is covered with the TMS coil array, their careful study is necessary to assess the safety and feasibility of the mTMS integration in the MR environment.

To quantitatively characterize the effects of the commercially available MR compatible TMS coils on the $B_1^{+}$ field and on the SAR distribution, both electromagnetic simulations (EM) and measurements could be done. For the mTMS system however, only a first prototype of the 3-axis TMS coil is available. For this reason, here we focus on the simulations to answer the fundamental safety and design questions for the integrated whole-head MR coil planned for the system. To support our simulations, we validated the simplified 3-axis TMS coil model used for the mTMS simulations with experimental data. Our overarching goal was to determine if the $B_1^{+}$ and SAR distribution are significantly changed by the presence of the TMS coils when the birdcage (body) coil of the 3T systems is used as transmit coil.

Methods

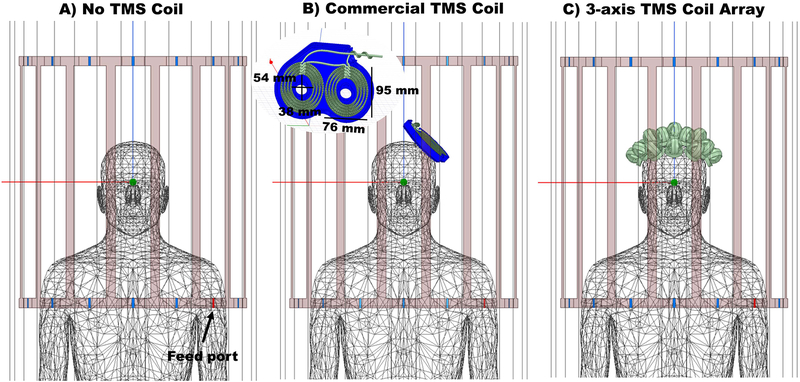
Finite element simulations were performed to assess the interaction of the RF fields of a 3T scanner (123.2 MHz) with (a) a realistic model of a commercially available MR compatible TMS coil, and (b) the prototype multichannel 3-axis TMS coil system under development (not including the RF receive elements) based on a simplified model of the 3-axis TMS coil. The reference simulation set up was a generic birdcage body coil loaded with a homogenous human phantom (relative permittivity ε’ = 78 and conductivity σ =0.47 Siemens/m) with the head positioned at the centre of the coil as used for brain imaging. A second set of simulation was performed modelling a commercial MR compatible figure-of-eight TMS coil positioned over the left hemisphere of the phantom’s head. Finally, an array of sixteen 3-axis TMS coils was modelled and placed on the top of the phantom’s head, following a hexagonal pattern similar to that of the actual multichannel system under development. The distance between the coils and the surface of the head was set to 5 mm to approximate the expected thickness of the housing of the elements. Illustrations of the three set ups considered are shown in Figure 2.

Figure 2.

Simulation set ups as seen in the simulation software HFSS. A) Reference model, with birdcage coil and the homogenous realistic human phantom. B) Setup showing the birdcage coil, the human phantom and the MR compatible commercial TMS coil, with bottom housing over the left hemisphere. C) Setup showing the birdcage coil, the human phantom and the sixteen 3-axis TMS coils over the phantom’s head distributed in a hexagonal pattern. No housing was drawn for this setup and therefore the elements are placed 5 mm above the scalp surface to account for the expected distance added by the chassis. For all three simulations, the feed ports are shown in red. One of the two ports is shown in the figure, the other is on the left side of the phantom and not visible.

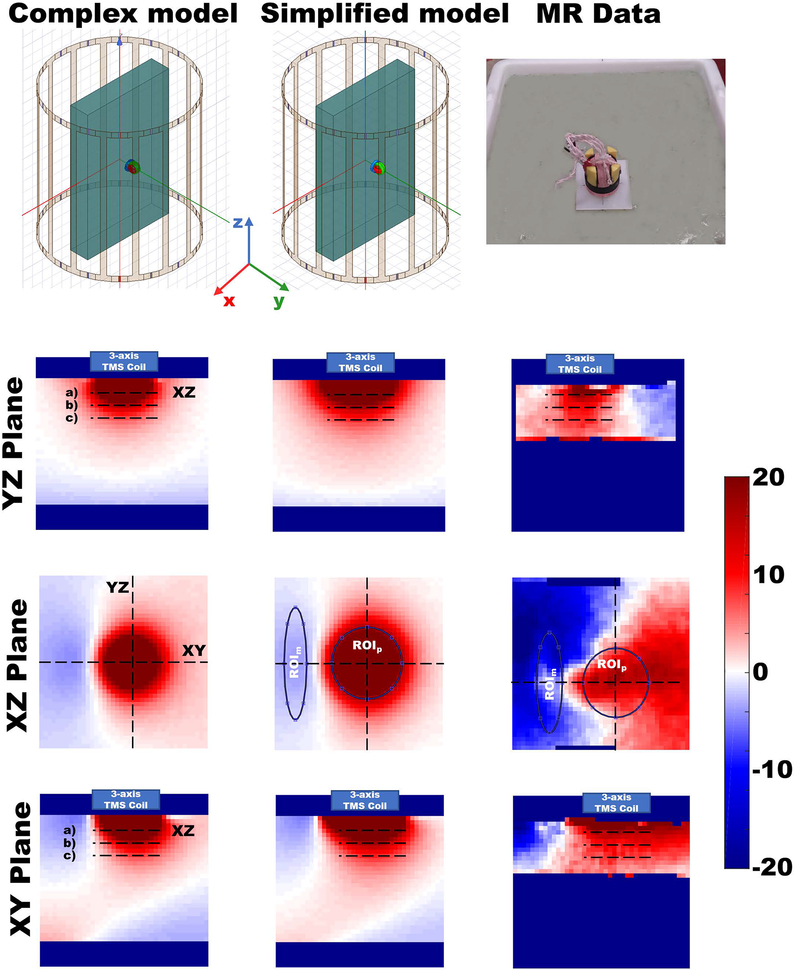
In order to make the computational simulation of the multichannel 3-axis TMS system feasible and to avoid making the model and meshing overly complex, the 3-axis TMS coils were simulated based on the simplified model shown in Figure 1C. For the validation of the simplified model, a more realistic 3-axis TMS model (see Figure 1B) consisting of three “orthogonal” solenoids was simulated over a ASTM block-phantom (American Society for Testing and Material) inside the same generic birdcage coil at 3T (see Supporting Information Figure S1A). The “X,Y, and Z” coil unit were geometrically accurately represented by copper wire windings with interlaced “X” and “Y” coil units. The results of the complex and simplified model were compared in terms of $B_1^{+}$ field change results (reference case is always without the TMS coil present) and currents surface distributions J_surf. To validate the model experimentally, simulation results were compared to $B_1^{+}$ field change maps acquired base on MR data using a 3-axis TMS coil prototype on an in-house built gel block phantom.

Simulations

Simulations were done following the previously published methods (12,13) as a combination of electromagnetic simulations and lumped circuit co-simulations. Ansys Electronic Desktop 18.0.0 (Ansys, Canonsburg, PA, USA) was used, which integrates High Frequency Structure Simulator (HFSS) for the 3D-EM simulations and Circuit Designer for the circuit level simulations. First, the RF coil was modelled as an HFSS design replacing all lumped elements with 50 Ω ports and loaded with the phantom and with the different TMS coil configurations as described below. The EM simulations were run on a Dell PowerEdge R740xd server with 1.5TB of RAM and 2 Intel Xeon Gold 6140, 18-core processors. Electric and magnetic fields were obtained as well as the S-parameter matrix corresponding to the RF coil and the load. The calculated multiport S-parameter matrix was used in the integrated circuit design simulator. Lumped elements were implemented at the ports to tune and match the coil at 123 MHz similar to our previous work (14–16). The optimization process to tune and match the coil was only done for the reference setup with no TMS coil present inside the birdcage coil (Figure 2A) for both the homogenous human phantom and the ASTM block-phantom load simulations. Once these values were calculated, they were kept the same for the simulations with stimulation devices present.

To assess possible shifts of the birdcage coil resonace frequency for the homogenous human phantom investigations, a sweep simulation covering from 118 MHz to 128 MHz with 200 points was performed for all three set ups.

RF Coil and TMS Coil Models

The MR body coil was modelled as a high-pass, 16-rung birdcage coil with 60 cm diameter and a length of 67 cm. The shield of the coil was modelled as a 65.7 cm diameter cylinder with a length of 122 cm. The coil was driven in quadrature.

For the commercial MR compatible TMS coil, a 3D-CAD drawing of the bottom part of the housing was imported into HFSS. The housing material was modelled as polyamide (relative permittivity ε’ = 4.3 and dielectric loss tanδ = 0.004). The coil itself was modelled as two wings separated 3 mm from each other forming a figure-eight placed 8 mm away from the bottom part of the housing as specified by the manufacturer. The wings themselves consisted of two 4-turn coils separated 5.5 mm vertically from each other. The winding in the plane are separated 2.5 mm horizontally. Dimensions of the TMS coil model are shown in Figure 1B. The wire of the coil was modelled as a rectangular conductor of dimension 2.3mm × 3.5mm. The coil together with the bottom part of the housing were placed directly over the left hemisphere of the phantom to emulate the real application (see Figure 2B).

The approximate realistic geometry of the 3-axis TMS element is shown in Figure 1B as a 3D-CAD model. This model will be referred from now on as the complex model. It consists of three orthogonally wound coils. The “Z” coil is placed at the bottom and “X” and “Y” coils are positioned above it and wound together in an interlaced fashion. The simplified 3-axis TMS coil was modelled as i) one solid copper conductor for the Z-coil with radially increasing cross-sectional height, and ii) two solid copper rings for the X-coil and two for the Y-coil, representing the separate layers of the windings of the X and Y coils. The geometry as well as the dimensions of the coils are shown Figure 1C.

The simplified model of the 3-axis TMS coil was duplicated 16 times and positioned over the phantom’s head following a hexagonal pattern to model the 3-axis TMS coil array (see Figure 2C).

For the human phantom simulations, sources were connected through ports 23 and 27 and for the ASTM block-phantom simulations, through ports 19 and 23 (marked in red in Figure 2 and Supporting Information Figure S1 respectively). In both cases the birdcage coil was fed with 130 V sinusoidal sources at 123 MHz with 50 Ω source impedance. The input power for all simulations was 84.5 Watts.

Numerical Convergence

The human phantom was divided into two parts: (i) the upper part consisting of head, shoulders and part of the chest that lies inside the birdcage coil and (ii) the lower part outside the birdcage coil. At the start of each simulation, the algorithm started with a user-defined initial tetrahedral mesh which forced a fine resolution in the upper part of the human phantom (maximum tetrahedron edge < 10mm) and a coarser one for the lower part of the human phantom (maximum tetrahedron edge < 20mm). For the commercial MR compatible TMS coil, the mesh size was forced to be less than 5 mm on the surface of the stimulation coil. The same condition was applied for the 3-axis TMS coil array for each stimulation coil. For the model validation simulations employing the ASTM block-phantom, both the simplified and the complex model were forced to have a mesh length less than 1mm. For the ASTM block-phantom itself the mesh condition was set to be less than 10mm.

The adaptive algorithm then refined the mesh by 30% between each two iterative simulations. At each step, the maximum change in the magnitude of S-parameters, ΔS, was defined as $\mathrm{\Delta }S=ma{x}_{ij}\left|S_{ij}^N- S_{ij}^{N-1}\right|$, where i and j index all S-matrix entries (ports) and N represents the iteration number. The adaptive simulation continued until the threshold of ΔS<0.02 was reached.

Once the simulations reached the convergence condition the mesh was visually inspected to check if the TMS coils and their surroundings were accurately represented.

${\mathit{B}}_1^{+}$, J_surf and SAR Calculations

The counter-clockwise rotating component of the RF magnetic field produced by the birdcage coil, responsible for the excitation of the spins in the MR experiment (17) was calculated as $B_{1 }^{+}= \frac{B_{1x}+ j{B}_{1y}}{2}$. The complex magnitude of the $B_{1 }^{+}$ field was exported on a cartesian grid with 2 mm and 3 mm resolution for the human phantom simulation and the ASTM block phantom respectively. The percentage of the field difference was calculated as:

$${\mathrm{\Delta }B}_{1\mathrm{ }}^{+}=\mathrm{ }\frac{B_{1\mathrm{ }REF+\mathit{\text{STIM COIL}}}^{+}-B_{1REF}^{+}}{B_{1REF}^{+}}\bullet 100\mathrm{\%}$$

Field differences in percentage were calculated and plotted in MATLAB (Mathworks, Natick MA, USA).

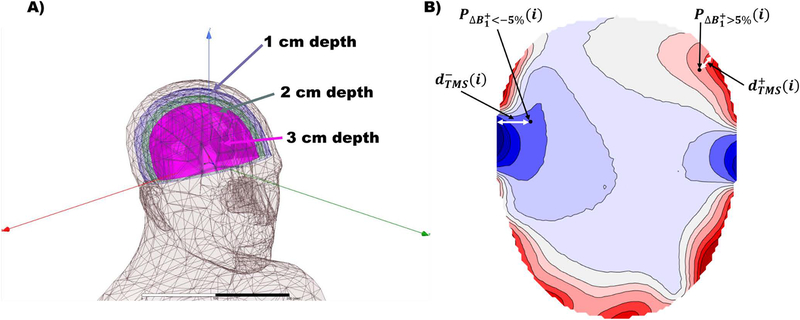
To quantify the extent of the effects of the TMS coils on the $B_{1 }^{+}$ field, the “effect depth plus/minus” was defined and calculated using in-house MATLAB scripts for the simulations with the realistic phantom. This measure ($d_{TMS}^{+}\left(i\right), d_{TMS}^{-}\left(i\right)$) is defined as the minimal Euclidean distance from the points P in the phantom affected by either an increase ($P_{\mathrm{\Delta }{B}_{1 }^{+}>5\%}\left(i\right)$) or a decrease ($P_{\mathrm{\Delta }{B}_{1 }^{+}<-5\%}\left(i\right)$) of the $B_{1 }^{+}$ larger than 5% to the scalp:

$$d_{TMS}^{+}\left(i\right)={\text{min}}_j\Vert P_{\mathit{\text{scalp}}}\left(j\right)-P_{\mathrm{\Delta }{B}_{1\mathrm{ }}^{+}>5\mathrm{\%}}\left(i\right)\Vert \mathrm{ };\mathrm{ }{d}_{TMS}^{-}\left(i\right)={\text{min}}_j\Vert P_{\mathit{\text{scalp}}}\left(j\right)-P_{\mathrm{\Delta }{B}_{1\mathrm{ }}^{+}<-5\mathrm{\%}}\left(i\right)\Vert$$

where j index corresponds to points that belong to the scalp and i index corresponds to the region(s) where ${\mathrm{\Delta }B}_{1 }^{+}$ is greater/less than ±5% (for illustration of the defined metric, see Figure 3B)

Figure 3.

A) Definition of parallel scalp surfaces for the evaluation of the $B_1^{+}$ field at distances of 1 cm, 2 cm and 3 cm. B) Illustration of the defined “effect depth” metrics ${\mathit{d}}_{\mathit{T}\mathit{M}\mathit{S}}^{+}\left(\mathit{i}\right),\mathit{ }{\mathit{d}}_{\mathit{T}\mathit{M}\mathit{S}}^{-}\left(\mathit{i}\right).\mathbf{ }{\mathit{P}}_{\mathrm{\Delta }{\mathit{B}}_{1\mathit{ }}^{+}>5\%}\left(\mathit{i}\right)$ and ${\mathit{P}}_{\mathrm{\Delta }{\mathit{B}}_{1\mathit{ }}^{+}<-5\%}\left(\mathit{i}\right)$ are points in the phantom affected by either an increase or decrease of the $B_{1 }^{+}$ larger than 5% respectively. The effect depth is the distance between those points and the closest point on the scalp.

For points in the phantom where the field changes by less than 5%, the “effect depth” is defined as zero. Subsequently, the maximal effect depth was calculated and reported to characterize the worst-case scenario.

Parallel surfaces to the phantom’s scalp were defined at 1 cm, 2 cm and 3 cm as shown in Figure 3A to evaluate the change in the field homogeneity over depth. Standard deviation of the $B_{1 }^{+}$ over the defined surfaces were calculated for the three sets of simulations using MATLAB.

The surface current density J_surf on both models of the 3-axis TMS coil were calculated directly by the commercial EM simulation software for the block-phantom simulations and visualized using the built-in tools.

The 1g-averaged and 10g-averaged SAR values in the head of the phantom were calculated to assess SAR enhancements or formation of new hot spots due to the presence of either the MR compatible commercial TMS coil or the 3-axis TMS coil array. The values were exported on a cartesian grid with 2 mm resolution and processed with MATLAB.

Experimental model validation

In order to experimentally validate the simplified 3-axis TMS model used in the simulations of the human phantom, $B_{1\mathrm{ }}^{+}$ field maps were obtained using the birdcage coil of the Skyra 3T (Siemens, Erlangen, Germany). As load, an in-house built phantom (0.82% NaCl, 1.7% Agar-Agar, Magnevist Gadolinium solution diluted down to 1ml/L (Bayer Healthcare, Wayne, NJ, USA)) with the dimensions 40cmx60×5cm was used, similar to the ASTM Phantom included in the simulations. Two setups were employed: (i) the phantom alone and (ii) the phantom with one 3-axis TMS prototype placed 5 mm over the center and placed in the isocenter. To account for the TMS coil housing, the TMS coil prototype with exposed wire windings was placed on a 5 mm plastic plate. The reference transmit voltage was set in both cases to 300 V. A picture of the phantom with the prototype on the top of it is shown in Figure 4 top right. Gradient Echo (GRE) images with 6 different flip angles (FA) (TR=600ms, TE=10ms, FA=20,40,60,80 and 90, 40 slices, 3mmx3mmx3mm, MA=64×64, 4 averages) were acquired for each setup to calculate $B_{1 }^{+}$ maps. The measured data was fitted pixel-wise to $B_1^{+}\bullet \text{sin}(FA)$ to calculate the field (18) using in-house written MATLAB scripts. The final $B_{1 }^{+}$ maps were smoothed with a 6 mm gaussian kernel. The percentage of the field difference was calculated as defined in the equation above.

Figure 4.

Comparison of the relative field change patterns between the simulated data using either the complex or the simplified 3-axis TMS coil and the experimental data. Left column) Relative $B_1^{+}$ field change produced when placing the complex 3-axis TMS coil model on the ASTM block-phantom. Orientation of the axes corresponding to the YZ, XZ, and XY planes are shown in the top right panel. The positions of the YZ, XZ, and XY planes are indicated by the corresponding labels in the images. Red color is used to indicate field enhancement while blue shows field decrease. The blue box over the phantom shows the position and extent of the TMS coil model. Dashed lines marked with a), b), and c) denote the positions being used for evaluation of the field changes at 1.2 cm, 2.1 cm and 3 cm depths, respectively. The XZ plane depicted is at depth 1.2 cm. Center column) Relative $B_1^{+}$ field change produced when placing the simplified 3-axis TMS coil model on the ASTM block-phantom over the same slices as shown for the complex model. Right column) Relative $B_1^{+}$ field change pattern produced when placing the 3-axis TMS coil prototype on a physical gel phantom inside the MRI scanner. Slices depicted correspond to the ones shown for the complex and simplified model simulations. A picture of the experimental setup is shown on the top right part of the picture.

Results

Mesh statistic, convergence and simulation time

The mesh statistics for the three sets of simulations is given in Table 1 and for the ASTM block-phantom simulations in Supporting Information Table S1. The total number of tetrahedrons increased by factors of 1.25 and 3.92 for the MR compatible commercial TMS coil and the 3-axis TMS coil array simulations respectively. For the ASTM block-phantom simulations the total number of tetrahedrons increased by 18.5% for the complex 3-axis TMS coil compared to the simplified model.

Table 1.

Mesh statistics of the reference commercial TMS Coil and the 3-axis prototype TMS Coil Array simulations. Convergence as quantified by the maximal change in the magnitude of S-parameters at the final step and the simulation time for each condition are listed in the last two columns.

Mesh statistics	No. Total Elements	No. Elements (Body_up)	Max. Edge Length (Body_up)	Min. Edge Length (Body_up)	RMS Edge Length (Body_up)	Max ΔS	CPU Time
No TMS Coil	1479927	618981	11.25mm	4.05mm	8.13mm	0.010452	11:00:45
Commercial TMS Coil	1843506	641752	11.31mm	3.69mm	8.06mm	0.011268	14:17:25
3-axis TMS Coil Array	5798036	679926	11.47mm	1.81mm	7.93mm	0.011689	54:31:01

All simulations converged after 2 passes. From the simulation time, the 3-axis TMS coil array required a factor of 3.15 time more CPU time than the commercial TMS coil simulation. For the model validation simulations, the complex 3-axis TMS coil model required 26.4% more CPU time than the simplified model.

3-axis TMS coil model validation: Surface current density and relative field change patterns

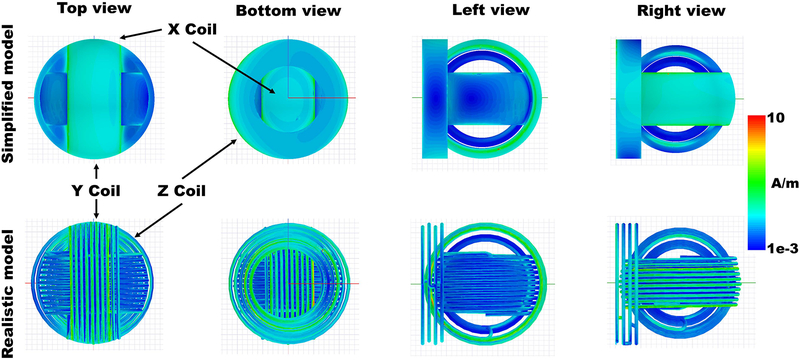
For the model validation simulations, the surface current density distributions for both models were plotted in HFFS and are shown in Figure 5. Both models follow a similar pattern. The values are higher on the bottom part of the “Z” coil and the outer part of the “X” coil. However, the simplified model shows higher current surface distribution on the edges of the rings while the complex model shows the high values distributed over the single windings. For the complex coil, the current density in the “Z” coil is more concentrated in the inner windings than in the outer ones. The “Y” coil showed lower surface current density than the other coils with slightly higher values on the edges in both cases.

Figure 5.

Induced surface current distribution on the 3-axis TMS coils. Top row) On the simplified model. Higher values are on the edges and on the X Coil. Different views. Bottom row) On the complex model. Higher values are distributed on the windings of the X Coil and more inner windings of the Z coil. Different views.

The calculated birdcage coil field difference percentage values ($\mathrm{\Delta }{B}_{1\mathrm{ }}^{+}$) over the ASTM block-phantom in the TMS coil vs. no TMS coil cases are shown in Figure 4. Results for both simulations models, the complex and the simplified model are shown for comparison in the left and the center columns of the figure. Results for the acquired MR data are shown in the right column. The selected slices are 12 cm long to show the effects on the field under the stimulations coils. Position of the XY and YZ planes are marked with dashed lines on the XZ Plane plots. The XZ plots show the results at 1.2 cm distance from the surface.

The average field differences over the lines under the coils marked as a), b) and c) corresponding to depths of 1.2 cm, 2.1 cm and 3.0 cm respectively are listed in Table 2 for all three cases. Over the XZ planes, regions-of-interest (ROIs) were marked (ROI_m and ROI_p) and the average field differences were calculated for all three cases. In the simulated cases, both ROIs are placed at the same position. For the experiment, the ROIs were placed at corresponding locations based on the coil position. The data evaluated over the ROIs are listed in Table 2.

Table 2.

Average percentage $B_1^{+}$ field change evaluated over the profiles and ROIs depicted in Figure 4. First two columns show the results of the simulated data (complex and simplified model) and the third column shows the results obtained based on the calculated $B_1^{+}$ based on the MR data.

	Phantom depth	${\mathrm{\Delta }\mathit{B}}_1^{+}$ Complex Model (%)	${\mathrm{\Delta }\mathit{B}}_1^{+}$ Simplified Model (%)	${\mathrm{\Delta }\mathit{B}}_1^{+}$ MR Data (%)
XY Plane	a) 1.2 cm	32.87%	31.17%	15.47%
	b) 2.1 cm	13.36%	14.69%	9.58%
	c) 3.0 cm	6.31%	7.67%	7.35%
YZ Plane	a) 1.2 cm	30.47%	29.56%	10.85%
	b) 2.1 cm	12.51%	14.07%	7.61%
	c)3.0 cm	5.91%	7.45%	6.74%
XZ Plane	ROIp	25.40%	27.73%	11.29%
	ROIm	−3.36%	−2.95%	−8.96%

The simulation results show that the simplified model produces a broader effect under the coil. The values reported in the table imply that the simplified model slightly underestimates (less than 1 percentage point) the 3-axis TMS coil effects on the field at 1.2 cm from the phantom surface. However, for further distances, the simplified model overstimates the effects slightly (around 1.5 percentage points). The ROI evaluation of the enhancement (ROI_p) at 1.2 cm of the simplified model shows the broadening effect under the coil with a higher average value of the field difference, but the same underestimation for the field decrease (ROI_m) (less than 1 percent point).

From the experimental data evaluation we conclude that enhancement values obtained close to the surface (1.2 cm) differ from the simulations by 15 to 20 percentage points. However, this difference decreases with depth to 4 to 6.5 percentage point at 2.1 cm and to less than 1 percentage point at 3 cm. On the other hand, the field decreases due to the presence of the 3-axis TMS coils are more prominent in the MRI data (up to 6 percentage points more) than in the simulation data. Taken together, these results show that i) the simplified model can be used to calculate the effects with high accuracy at > 1 cm from the phantom surface and ii) the overall agreement of the computational model with the experimental data is adequate suggesting that the numerical simulations provide resonable estimates of the TMS/RF coil interactions.

${\mathit{B}}_{1 }^{+}$ field evaluation on the realistic phantom head

Tuning of the birdcage coil did not change significantly when placing the TMS coils inside the birdcage coil. The resonance frequency changed less than −0.1 MHz in both cases.

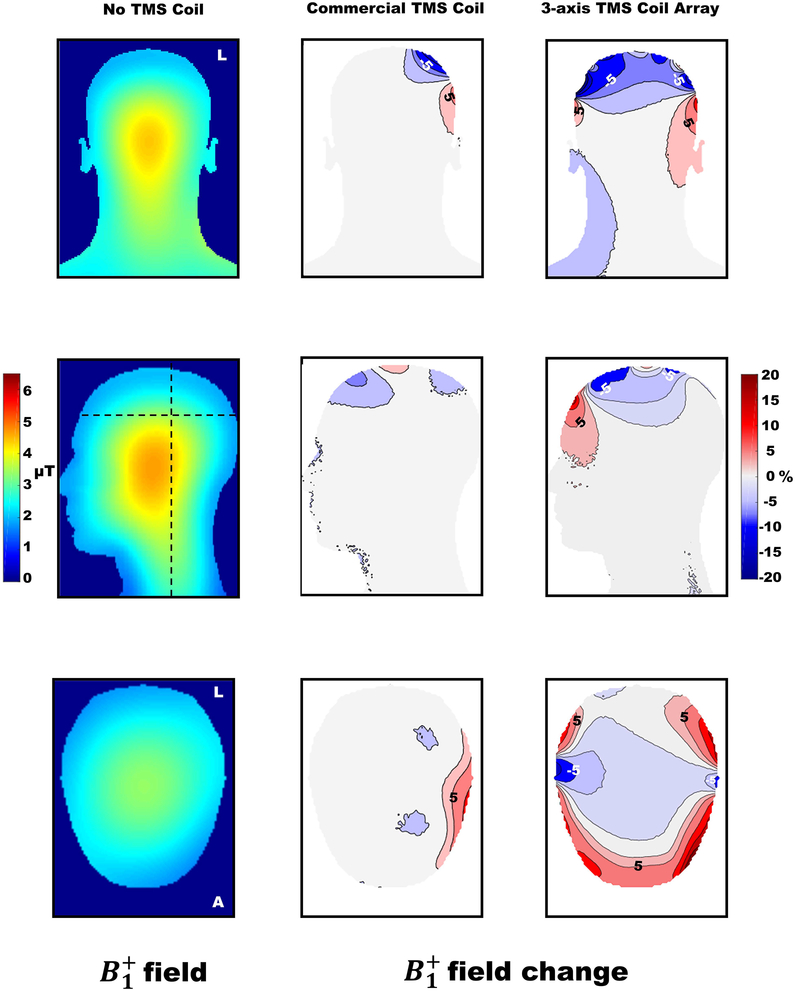
Field results for the reference simulation, the “no TMS coil” set up, are shown in Figure 6 on the left part for the coronal, sagittal and transversal planes. The percentage of change in the $B_{1 }^{+}$ with respect to the reference is shown as a contour plot to better visualize the effects of the MR compatible TMS coil and the 3-axis TMS coil array. The change in $B_{1 }^{+}$ field when the MR compatible commercial TMS coil was present ranged from −15% to +24% and from −41% to 44% for the 3-axis TMS coil array. The field enhancement/attenuation was observed to be maximal directly under the TMS coils and to decrease in amplitude with depth.

Figure 6.

Coronal, sagittal and transverse sections to illustrate $B_1^{+}$ field and field change percentage. The absolute $B_1^{+}$ field magnitude is shown only for the reference simulation with no TMS coil present in the birdcage coil. For the simulations placing TMS coils into the birdcage coil, the calculated field difference percentages based on the “no TMS coil” condition as the reference are shown. Contour lines are plotted for both cases. The main sagittal view (through the middle of the phantom), a coronal view and the transversal plane at 6 cm depth from the top of the head are shown. Dotted lines in the field images of the no TMS coil condition show the coronal and transversal planes depicted.

For the MR compatible commercial TMS coil, the main coronal plane showed that the upper wing of the coil produced a field decrease and the lower wing produced field enhancement. The maximal effect depth over the whole head producing a field enhancement ($d_{TMS}^{max+}$) was 1.76 cm while for field decrease ($d_{TMS}^{max-}$) was 2.38 cm. The location where the changes occurred depends on the position of the MR compatible commercial TMS coil over the head.

For the 3-axis TMS coil array, the main coronal plane showed predominantly a decrease in the ${\mathrm{B}}_{1\mathrm{ }}^{+}$ field of the birdcage coil due to the presence of the TMS coils. This effect was observed over the top part of the head while the field was slightly increased on the rest of the head area of the phantom. Over the scalp, a pattern of enhancement/attenuation of the field was observed that also in this case decayed with depth. The main sagittal plane showed field enhancement in the anterior part and field attenuation more posterior. The maximal effect depth over the whole head producing a field enhancement in the 3-axis coil array case ($d_{3-axi{s}_{TMS}}^{max+}$) was 2.51 cm while for field decrease ($d_{3-axi{s}_{TMS}}^{max-}$) it was 3.32 cm.

The percentage increase in the standard deviation of the field over the three surfaces introduced in the Methods section are listed in Table 3. The values increased in both cases, for the 3-axis TMS coil array the increase is almost 20 percentage points more than for the MR compatible commercial TMS coil. In both cases, the homogeneity of the transmit field decreases due to the TMS coils, but the effect decreases in both cases with depth.

Table 3.

Results of the standard deviation of the field over the 3 defined surfaces parallel to the scalp (see Figure 3). The colors are related to the surface depth as shown in the figure.

	% standard deviation field increase
Depth	1cm	2cm	3cm
Commercial TMS Coil	12.8	9.75	8.4
3-axis TMS Coil Array	32.5	28.6	25

SAR evaluation

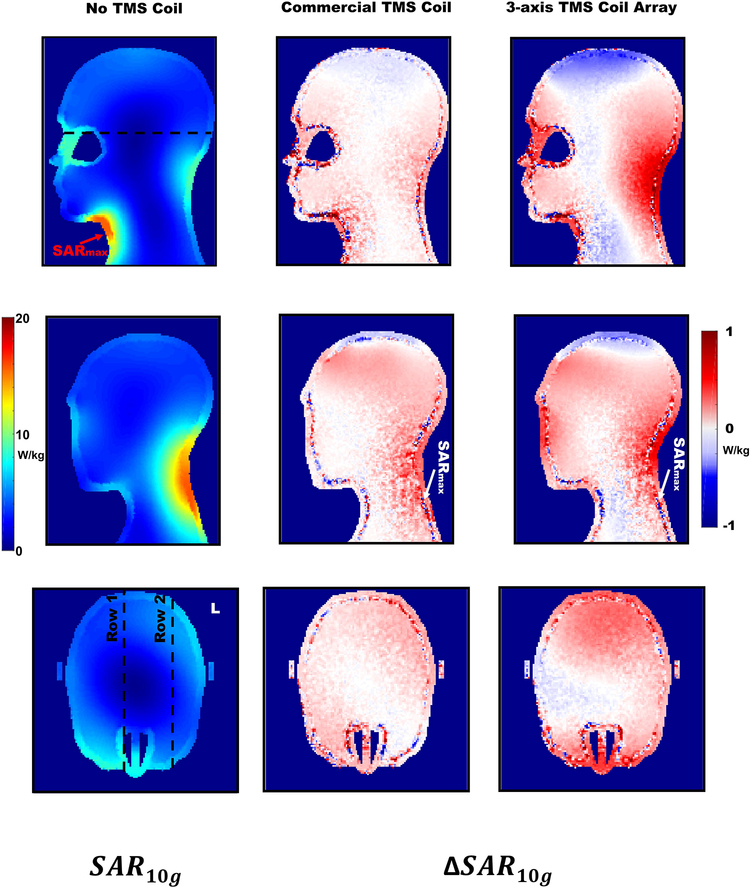
The 10g-averaged SAR distribution for the reference simulation is shown for two sagittal and one transversal planes in Figure 7. Additionally, the relative changes to the reference simulation were plotted for the same slices for both stimulation coil cases.

Figure 7.

Left column) 10g-average SAR distribution for the reference simulation with no TMS coil. For the sagittal views, the planes were the maximal nominal values were found for the reference case, and the commercial TMS coil and 3-axis TMS coil array were selected. The transverse plane at 12 cm depth from the top of the head is shown. Dotted lines in the SAR distribution show the planes selected for visualization with the TMS coils included. Center column) Relative 10g-averaged SAR changes for the commercial TMS coil. Same slices are shown as for the 10g-averaged SAR distribution. Right column) Relative 10g-averaged SAR changes for the 3-axis TMS coil Array. Same slices are shown as for the 10g-averaged SAR distribution.

For the 1g-averaged SAR (not shown), the maximal value (i.e., the “hot spot”) for the reference simulation with no TMS coil was found in the top part of the neck with a value of 25 W/kg. For both cases where TMS coils were placed inside the birdcage coil, the 1g-averaged SAR distribution remained very similar. When placing TMS coils into the imaging coil, both “hot spots” were found very close to the location of the reference case “hot spot”. For the MR compatible commercial TMS coil the SAR maximum was found 4.9 mm from the reference SAR maximum and the value was 26 W/kg. For the simulation case of the 3-axis TMS coil array the maximum SAR value was found 3.5 mm away from the reference SAR maximum and the value was 26 W/kg.

For the 10-g averaged SAR, the nominal maximal SAR values were in all three cases the same: 16 W/kg. For the reference simulation, two hot spots were found with the same value, 16 W/kg: (i) on the top part of the neck and (ii) at the left posterior part of the neck. The highest nominal value (if the values were evaluated with two decimals precision) was found 2 cm away from the hot spot found at the 1g-averaged SAR distribution. For the MR compatible commercial TMS coil, a very similar SAR pattern was obtained, with comparable two hot spots. In this case the highest nominal value was found in the second hot spot at the left posterior part of the neck (Figure 7, second row, central column), 13.1 cm from the nominal maximum value of the reference simulation. For the 3-axis coil array, the results showed again comparable SAR distribution with two analogous hot spots. Again in this case, the highest nominal value (Figure 7, second row, left column) was found in the second hot spot, 12.9 cm from the maximum found in the reference simulation. No new hot spots were observed in any of the simulation conditions placing the stimulation devices into the birdcage coil.

From the plots of the relative 10g-averaged SAR values, changes were found in the range of ±1W/kg. Only some voxels at the boundary of the phantom were found to have larger changes than 1W/kg in magnitude. This is most likely due to the averaging process involved in calculating the SAR.

Discussion

In this article, we present for the first time a set of realistic electromagnetic simulations of interactions between TMS coils and the ${\mathrm{B}}_{1\mathrm{ }}^{+}$ field of a 3 T volume transmit RF coil as well as experimental data validating the computational model. This topic was investigated in the context of the ${\mathrm{B}}_{1\mathrm{ }}^{+}$ field effects of a 3-axis TMS coil array to illuminate fundamental design questions pertaining to safety and image quality for the planned integrated whole head multi-channel integrated TMS/MRI system.

The simplified 3-axis TMS coil model used for the simulations with the realistically shaped phantom was validated by comparing the results of the field effects using a more complex coil model as well as experimental data using a block phantom. The simplified model understimates marginally the field effects at 1.2 cm compared to the complex model but is a slightly overestimating the changes for the deeper regions of the phantom. The experimental data shows a reasonable agreement with the simulated field change patterns. The asymmetry of the B₁⁺ field effect on the XZ plane is observed in both simulation cases and in the experiment. This effect is directly related to the asymmetric pattern of the induced surface current density on the 3-axis TMS coil produced by the birdcage coil as shown in Figure 5. We should note that the exact pattern depends on the orientation of the coil with respect to the E field generated by the birdcage coil.

There are some discrepancies between the simulations and experiments such as the higher field enhancement values close to the coil that were observed in the simulations. These might be explained due to lower overall image intensities obtained close to the top of the phantom produced by susceptibility effects caused by i) the plastic plate used to elevate the TMS coil prototype or ii) the surface inhomogeneities and bubbles on the phantom. At a distance of 3 cm from the surface of the phantom, the experimental data and the simulations show a high level of agreement.

The results obtained for both commercial TMS coil as well as a three-axis TMS coil array showed transmit field enhancement/attenuation directly under the stimulation coils. Overall, these effects decay with depth and at ~ 3 cm below the surface of the head the changes are mainly reduced to less than 5%. In case of the commercial MR compatible TMS coil the effects diminish around 2.4 cm to less than 5% absolute field change and they only affect the stimulation site where the coil is placed. For the 3-axis TMS coil array the extent of the effects reaches in some locations even the 3.3 cm depth because overlapping effects of neighbouring stimulation coil elements. However, for this configuration, the impact on the transmit field is independent of the site of stimulation and the effect pattern or map is not expected to significantly change over different experiments. The homogeneity of the transmitted field is affected mainly close to the stimulation coils, but the impact may still considerable at 3 cm as shown in Table 3.

The simulation study presented here is based on a realistically-shaped homogeneous head phantom and simplified 3-axis TMS coil models to analyze the effects of the stimulation coils on the transmit field. The focus of this study was to quantify the relative change of the field and the effects of these changes on image quality and safety. We chose to use a homogenous phantom with a single compartment without any internal tissue boundaries and the simplified 3-axis TMS coil model for the multichannel TMS system for the sake of keeping numerical simulations relatively fast and robust. The ${\mathrm{B}}_{1\mathrm{ }}^{+}$ field results obtained showed higher brightening effect in the center of the head than reported results using compartmental models at 3T (19). However, we consider that a multi-compartment model would not yield much additional information on the relative ${\mathrm{B}}_{1\mathrm{ }}^{+}$ field changes but it might be informative for investigating the SAR values using a more detailed head model. Validation of the simplified 3-axis TMS coil model was done by comparing the results produced using the complex 3-axis TMS coil model and the experimental B₁⁺ maps using a 3-axis TMS coil prototype. Due to the fact that the field differences between the simulations with different coil models are lower than 2 percentage points at a phantom depth of 1.2 cm, the results discussed above in terms of effect depth, homogeneity and SAR appear valid and not dominated by coil modelling effects.

Data acquired for fMRI experiments are limited to the brain tissue which are at most at a distance of 1.2 to 1.5 cm to the scalp (20,21). The increase of the inhomogeneity of the transmitted field has consequences on the quality of the acquired data. The $B_{1 }^{+}$ inhomogeneities produce a non-uniform flip angle distribution that is seen in the images as reduced or enhanced image sensitivity and is a key issue in quantitative MRI. ${\mathrm{B}}_{1\mathrm{ }}^{+}$ inhomogeneity also reduces the effectiveness of the fat saturation pulses for lipid suppression, which can can cause fat to shift into the brain along phase encoding direction in EPI fMRI images. These additional challenges together with the increased B₀ inhomogeneities produced by the presence of the TMS coils may diminish the intrinsic low dynamic range of the time series data from the brain.

Traditionally, the focus of TMS-induced artefacts in the concurrent TMS/MRI experiments has been on the B₀ (susceptibility) effects. For the case of the MR compatible commercial TMS coil, passive shimming of the coil was proposed (8). For the 3-axis TMS coil array B₀ effects have not been systematically assessed yet and could also potentially degrade the fMRI signal. New methods to correct B₀ effects directly in the acquisition process (22) could be implemented in the integrated RF whole head coil to minimize this problem. In light of the results of the present study, the $B_{1 }^{+}$ effects may also influence the TMS-fMRI signal quality and should be taken into consideration. Methods to correct $B_{1 }^{+}$ inhomogeneities artefacts have been previously proposed (23–26). These methods are based on acquiring reliable $B_{1 }^{+}$ field maps to correct the image intensities biased by the transmit field inhomogeneity. Such methods could be employed for TMS-fMRI setups as well. Unfortunately, these post-processing correction methods do not help to increase the effectiveness of the lipid suppression so alternative solutions may need to be sought.

The simulated birdcage coil in this work is the integrated body coil in 3T scanners which is typically used in concurrent TMS/fMRI experiments when signal reception is performed using a dedicated MR array coil under the TMS coil (27) or other receive-only MR coils placed away from the stimulation spot (28–30). The RF coil used in other studies (5,30) was a head birdcage coil working as a transmit/receive MR coil. In these experiments, significant signal drop-outs under the coil were usually reported. Additional simulations should be done to clarify if the loss of sensitivity on the target for this case could be explained as stronger effects on the $B_{1 }^{+}$ field due to the closer proximity of the TMS coil to the MR transmit coil.

From the safety point of view, our results show that none of the SAR distributions change significantly when placing the TMS coils into the birdcage coil. No new hot spots are created and while those spots are slightly higher for the 1g-averaged SAR distribution when placing the stimulation devices inside the transmit coil, the increase of 4% does not raise substantial safety concerns. For the 10-g averaged SAR distribution the maximal values obtained were the same for all three cases (no TMS coil, single MR compatible TMS coil, 3-axis TMS coil array). However, the nominal maximal value changed from the hot spot under the neck to the hot spot at the left posterior part when placing stimulation devices inside the birdcage coil. The relative 10g-averaged SAR change plots showed that the increase in SAR in those regions are limited to 1 W/kg. The maximal value found, 16 W/kg is nominally higher than the limits given in the IEC 60601-2-33 (31). However, if the birdcage coil in the scanner meets the safety requirements, our results confirm that the TMS coils do not significantly increase the maximal SAR value. Nevertheless, SAR results should be validated with additional MR-thermography experiments (32) or other methods to finally assess safety.

The work presented in this paper does not include neither the cabling from stimulators to the TMS coil(s) nor the load of the stimulator. There are different reasons for this decision. First, there is no standard way in which the TMS cable(s) are positioned inside the scanner and unlike the TMS coil wire windings, its length can be chosen in multiple different ways. This will potentially have quite significant effect on the current induced, and therefore a rather large number of possible configurations and cable lengths would have to be simulated to capture the expected variability. Second, potential issues with the cables in the MR bore can be minimized using cable traps tuned to the Larmor frequency. This strategy has been largely used for the receive RF coil arrays cables (33) and will be utilized for the TMS cables in concurrent TMS/MR. Using cable traps effectively in the MR bore blocks the induced RF signal on the cables and no RF impedance transformation of the stimulator would be effective. Additionally, cables will be run through the center of the bore where the birdcage transmit coil E field is theoretically close to zero in absence of a human body, to minimize interactions.

Concurrent TMS/fMRI studies can help us to understand the underlying mechanisms of TMS and explain its therapeutic efficacy in some common pathologies like major depressive disorder (34–36), enabling individualized treatment protocols to be developed based on experimentally determined dose-response characteristics. This approach may significantly benefit from the development of integrated multichannel TMS/MRI systems with multi-target stimulation and whole-head imaging capabilities. Our results show that while the interactions between the TMS coils and $B_{1 }^{+}$ transmit field need to be carefully considered, we conclude that from both safety and imaging standpoint the mTMS system can be integrated with receive-only MR coil array in 3T and used with the body transmit coil. While B₁⁺ variations introduced near the TMS coils may cause sequence-dependent image artifacts, we conclude that neither the MR compatible commercial TMS coil nor the 3-axis TMS coil array would elevate SAR in the head or neck beyond accepted safety limits.

Supplementary Material

supp info

Supporting Information Figure S1. A) Simulation setup of the ASTM block-phantom with the complex 3-axis TMS coil as seen in the simulation software HFSS. A zoomed view of the complex 3-axis TMS coil is shown in the top right corner as an inset. The birdcage coil is the same as the one used with a homogenous realistic human phantom. B) Simulation setup of the ASTM block-phantom with a simplified

Supporting Information Table S1. Mesh statistics of the ASTM block-phantom simulation with the simplified and the complex 3-axis TMS coil model. Convergence information as the maximal change in the magnitude of S-parameters at the final step and simulation time for each condition are listed in the last two columns.