Phase-based T₂ Mapping with Gradient Echo Imaging

Abstract

Purpose:

Transverse relaxation time (T₂) mapping with MRI has a plethora of clinical and research applications. Current T₂ mapping techniques are based primarily on spin-echo (SE) relaxometry strategies that rely on the signal magnitude, and often suffer from lengthy acquisition times. In this work we propose a phase-based T₂ mapping technique where T₂ information is encoded into the signal phase of rapid gradient echo (GRE) acquisitions.

Theory:

Bloch equation simulations demonstrate that the phase of GRE acquisitions obtained with a very small inter-repetition RF phase increment has a strong monotonic dependence on T₂, resulting from coherent transverse magnetization. This T₂-dependent phase behavior forms the basis of the proposed T₂ mapping technique. To isolate T₂-dependent phase from background phase, at least two datasets with different RF phase increments are acquired. The proposed method can also be combined with chemical shift encoded MRI to separate water and fat signals.

Methods:

The feasibility of the proposed technique was validated in a phantom experiment. In vivo feasibility was demonstrated in the brain, knee, abdomen and pelvis. Comparisons were made with SE-based T₂ mapping, spectroscopy and T₂ values from the literature.

Results:

The proposed method produced accurate T₂ maps compared with SE-based T₂ mapping in the phantom. Good qualitative agreement was observed in vivo between the proposed method and the reference. T₂ measured in various anatomies agreed well with values reported in the literature.

Conclusion:

A phase-based T₂ mapping technique was developed and its feasibility demonstrated in phantoms and in vivo.

Introduction

The transverse relaxation time (T₂) is associated with important microscopic tissue properties such as the concentration and cluster-size of paramagnetic particles and the mobility of hydrogen atoms. Importantly, T₂ is well known to characterize a plethora of important disease processes such as iron deposition, fibrosis, edema, malignancy, and inflammation, among others. As a result, quantitative T₂ mapping with MRI has many applications, including assessment of neuro-degenerative diseases and characterization of malignant lesions¹, detection of myocardial edema², detection of chronic rejection after heart transplant^3,4, detection of early cartilage degeneration⁵, quantification of liver iron overload⁶ and even identification of myofascial trigger points⁷ .

Spin-echo (SE) based methods are commonly used to map T₂. By varying the echo time and fitting the signals to a mono-exponential decay model (multi-exponential if a multi-component model is appropriate^8,9), T₂ can be estimated. Unfortunately, lengthy exams are needed due to the long repetition time (TR) to minimize T₁ weighting. Acquisition times can be reduced by acquiring multiple echoes (multi-echo SE) in a single TR^10,11, although the use of multi-echo methods may lead to different measurement of T₂¹².

Magnetization prepared T₂ contrast (“T₂-prep”) is a method used to encode T₂ relaxation into the longitudinal magnetization¹³. This technique is advantageous for imaging blood vessels and the heart¹³, and relies on modulation of the longitudinal magnetization prior to a readout acquisition. Although faster than SE-based acquisitions, T₂-prep-based T₂ quantification also suffers from relatively long acquisition times^14,15.

Steady-state short TR methods based on spoiled gradient echo (SGRE), balanced-steady state free precession (bSSFP)¹⁶, and gradient-refocused acquisition in the steady-state (GRASS)^17,18 are time efficient compared to spin-echo (SE) T₂ mapping techniques. For example, two SGRE acquisitions with varying flip angle combined with bSSFP contain the necessary information for joint T₁ and T₂ estimation¹⁶. Due to the use of short TR acquisitions, these methods can deliver simultaneous T₁ and T₂ quantification of spatially resolved 3D volumes within clinically acceptable acquisition times¹⁶.

To further reduce acquisition time for T₂ mapping, Welsch et al. proposed a multi-echo GRE acquisition known as double echo steady-state (DESS)¹⁷. This approach can also be extended for joint estimation of T₁ and T₂ using the triple echo steady-state (TESS) method proposed by Heule el al.¹⁸. In these methods, T₂ information is encoded into the relative magnitude between echoes. In vivo feasibility of these methods has been demonstrated^11,19. A variation of the DESS T₂ mapping technique developed by Staroswiecki et al.²⁰, has demonstrated high potential for accurate in vivo T₂ mapping. Although only a single gradient echo (GRE) acquisition is required, these methods rely on water specific RF pulses for fat suppression, which may be unreliable in the setting of B₀ inhomogeneities¹⁸. Differential T₂* weighting in the various echoes can also confound T₂ estimates.

We note that none of the above methods exploit signal phase to encode T₂ relaxation. In this work, we propose a major modification of an RF phase scheme first proposed by Zur et al²¹ to achieve robust spoiling of transverse magnetization for GRE acquisitions. As we propose below, the use of very small RF phase increments, rather than large RF phase increments needed for RF spoiling, can create T₂-dependent changes in both the phase and magnitude of the GRE signal. In this work we propose a novel quantitative T₂-mapping technique that encodes T₂ information into the phase of the GRE signal by manipulating the RF phase increment.

Theory

Complete spoiling of transverse magnetization is generally assumed when using spoiled gradient echo (SGRE) acquisitions. RF spoiling is a well-known approach used for spoiling transverse magnetization^21,22. As first proposed by Zur et al.²² , RF spoiling methods use a pseudo-random sequence of phases of the RF excitation. The phase sequence is defined by the difference between the n^th and the (n+1)^th RF excitation, i.e.: Φ_RF(n) = Φ_RF(n-1) + Φ₀ + n·ΔΦ (n=0, ….). If the RF phase increment (ΔΦ) is chosen carefully, transverse magnetization accumulates in an incoherent manner and is effectively spoiled.

The choice of RF phase increment is important for effective RF spoiling. Specific choices of RF phase increment (e.g. 117°) lead to excellent RF spoiling and the signal closely approximates the ideal SGRE signal magnitude²¹. Other choices of RF phase increment may lead to less effective RF spoiling²¹. Importantly, we note that the phase of gradient echo signals in the context of RF spoiling has not been well described.

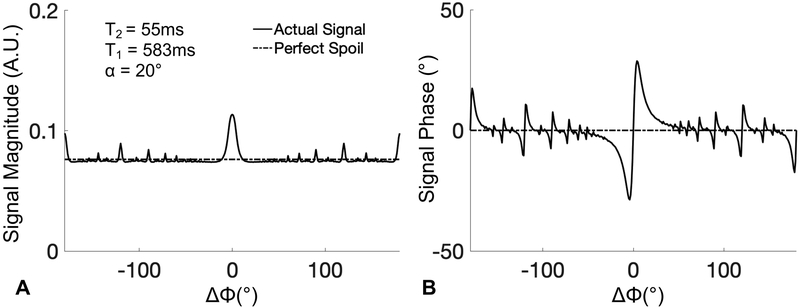
In this study, we investigate the effects of the RF phase increment on the phase of the complex-valued gradient echo signal. Figure 1 plots the results of a Bloch equation simulation showing both the signal magnitude (η) and phase (θ) of the gradient echo signal, using the RF phase increment method proposed by Zur et al.²². In this computer simulation, an ensemble of 1000 spins periodically experienced a sequence consisting of an RF pulse, T₁ and T₂ relaxation, and at the end of each repetition, a 2π phase dispersion across the isochromats due to an unbalanced readout gradient. Note that the acquisition reference frame matches the excitation phase.

Figure 1.

GRE signal magnitude (A) and phase (B) over the full range of RF phase increments (ΔΦ), according to the method of Zur et al.²² By varying the RF phase increment, large variations in the magnitude and phase of the GRE signal are observed. Signal shown in this plot was generated using a Bloch equation simulation assuming T₁=583ms and T₂=55ms to simulate normal liver tissue²¹ at 1.5T, with TR=10ms and flip angle=20°.

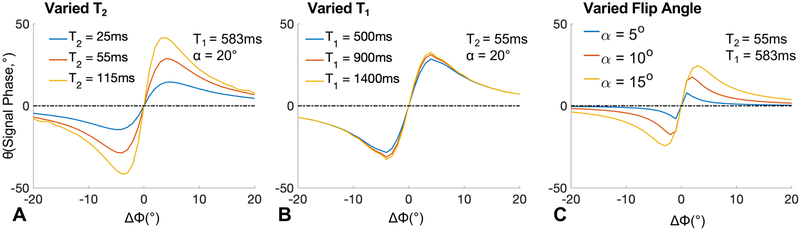
Figure 2 focuses on a narrow range of small RF phase increments, also with varying T₁, T₂ and flip angle. As can be seen in Figure 2, significant variations in the signal phase occur with changes in T₂ and flip angle, and to a much lesser extent with T₁. The largest signal phase was observed with small RF phase increments between 1° to 4°. Various combinations of T₂ (25ms, 55ms, 115ms), T₁ (500ms, 900ms, 1400ms) and flip angle (5°, 10°, 15°) are used in the simulation assuming a TR of 10ms and simulated TE of 0ms to ignore the effects of T₂* decay, for simplicity.

Figure 2.

GRE signal phase is heavily influenced by T₂ (A), but only minimally by T₁ (B) for very small RF phase increments (ΔΦ), forming the basis for the proposed T₂ mapping method. The phase of the GRE signal over the low range of RF phase increments were generated using Bloch equation simulations with physiological T₁ and T₂ values and TR=10ms. The dotted lines are the case where transverse magnetization is spoiled perfectly.

The effects of T₂, T₁ and flip angle are also plotted in Figure 3, demonstrating not only a strong dependence of the signal phase on T₂ and flip angle, but also a relatively weak dependence on T₁. We can express the steady-state gradient echo signal acquired with an RF phase increment as:

$$\mathrm{S}(\Delta \Phi ,\alpha ,\text{TR};{\mathrm{M}}_0,{\mathrm{T}}_1,{\mathrm{T}}_2)={\mathrm{M}}_0\cdot \eta (\Delta \Phi ,\alpha ,\text{TR};{\mathrm{T}}_1,{\mathrm{T}}_2)\cdot {\mathrm{e}}^{\mathrm{i}[\theta (\Delta \Phi ,\alpha ,\text{TR};{\mathrm{T}}_1,{\mathrm{T}}_2)+{\theta }^{\prime }]}$$ (1)

where η(ΔΦ,α,TR; T₁, T₂) is the signal magnitude relative to M₀, θ(ΔΦ, α,TR; T₁, T₂) is the signal phase immediately after excitation and is dependent on T₂, T₁, flip angle (α) and θ′, which is the local background phase caused by complex coil sensitivity, eddy currents, magnetic field inhomogeneities, etc.

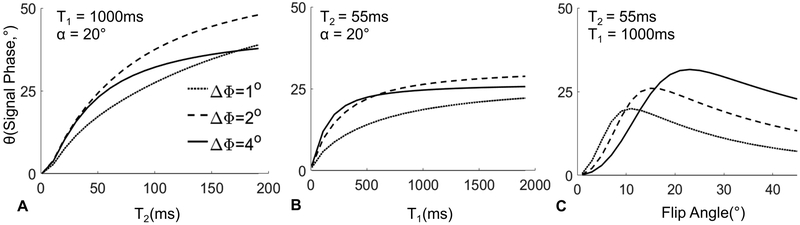
Figure 3.

GRE signal phase (A) increases monotonically with increasing T₂ for small RF phase increments (ΔΦ), e.g. 1-4°. Using a small RF phase increment (e.g. 2°), the signal phase is sensitive to T₂ over a wide range of T₂ values, a property that is favorable for encoding T₂ information. Note also that the signal phase is relatively insensitive to varying T₁ (B) and flip angle (for midrange flip angles such as 18°) for phase increments of 1° and 2°. The phase and magnitude of the GRE signal over the low range of RF phase increments were generated using Bloch equation simulations with physiological T₁ and T₂ values and TR=10ms.

To the best of our knowledge, simple analytical forms of η(ΔΦ,α,TR;T₁, T₂) and θ(ΔΦ, α,TR;T₁,T₂) have not been derived. In this work, calculation of these two functions is based on the use of a lookup table. Lookup tables are constructed from Bloch equation simulations based on wide ranges of possible T₁ and T₂ values, and the known acquisition parameters used in the experiment: ΔΦ, α, TR. All lookup tables used in this work are constructed using the same Bloch equation simulation described above.

Figure 3 depicts in greater detail the dependence of the signal phase with respect to T₂, T₁ and flip angle over a few small RF phase increments. A pronounced monotonic increase in the observed phase with T₂ is noted over a wide range of physiological T₂ values²³ with RF phase increments between 1° and 4°. For an RF phase increment of 2°, the signal phase is consistently sensitive to T₂ over a wide range of T₂ values (Figure 3, A). Unlike the strong dependence on T₂, the signal phase changes minimally over a wide range of T₁ values between 1000ms and 2000ms (Figure 3, B). Given these observations, a small RF phase increment such as 2° will encode the tissue T₂ into the signal phase.

In actual MRI acquisitions the received signal phase contains an additional background phase term, i.e.: θ′(Eq. 1). Estimates of the signal phase resulting from T₂ of the tissue must be isolated from the background phase. In this work we propose the following method to isolate θ from θ′, and subsequently estimate tissue T₂.

Proposed phase-based T₂ mapping:

In principle, two identical acquisitions with equal and opposite RF phase increments will generate equal but opposite phase responses (Figure 2), i.e.: θ(ΔΦ, α,TR ;T₁, T₂) = - θ(-ΔΦ, α,TR ;T₁, T₂). Using two such acquisitions, θ can be isolated from M₀, η and θ′ in Eq.1 by taking the phase difference of two gradient echo signals acquired with opposite RF phase increments, and with all other acquisition parameters identical, i.e.:

$$\widehat{\theta }(\Delta \Phi ,\alpha ,\text{TR};{\mathrm{T}}_1,{\mathrm{T}}_2)=(\angle \mathrm{S}(\Delta \Phi ,\alpha ,\text{TR};{\mathrm{T}}_1,{\mathrm{T}}_2)-\angle \mathrm{S}(-\Delta \Phi ,\alpha ,\text{TR};{\mathrm{T}}_1,{\mathrm{T}}_2))∕2$$ (2)

Using a well-chosen RF phase increment (e.g. ΔΦ=2 °) and a relatively large flip angle (e.g. α=18 °), the estimated signal phase can be used to estimate T₂. Based on the model presented above, it is expected that only a small error might occur in the T₂ estimate related to T₁ and unanticipated errors in flip angle (Figure 3 B,C). Note that the same figure shows a maximum signal phase of 50°, which will result in a phase difference of 100° between two signals. This phase difference is well below 2π, suggesting that even with higher T₂ values, there should be no risk of phase wrap in the proposed method.

In this work, we propose to estimate T₂ from $\widehat{\theta }$ through the use of a lookup table generated from a Bloch equation simulation that uses the known TR and flip angle of the acquisition. We note that the phase is weakly dependent on T₁, and therefore T₁ values measured using other methods or values reported in the literature for the anatomy of interest can be used to generate the lookup table.

Synthetic T2-weighted images:

In addition to the phase maps used to generate the T₂ map, magnitude images are also acquired. By multiplying these magnitude images with the inferred T₂ decay from the phase-based T₂ map, synthetic T₂-weighted images can be generated. The synthesis of the signal in each voxel can be expressed as:

$${\mathrm{S}}_{syn}=\mid \mathrm{S}\mid \times {\mathrm{e}}^{-{\text{TE}}_{\mathrm{V}}∕\widehat{{\mathrm{T}}_2}}$$ (3)

where S_syn is the synthesized T₂-weighted signal, TE_v is the virtual echo time, S denotes the signal acquired with one (or a combination) of the images acquired at the two phase increments. $\widehat{{\mathrm{T}}_2}$ denotes the estimated phase-based T₂ value.

Methods

Phantom experiments:

The accuracy of the proposed method was evaluated using a phantom constructed with varying concentrations of agarose and NiCl₂ to modulate the T₂ and T₁ relatively independently²⁴. The T₁ was varied such that the confounding effect of T₁ variation in the proposed method can be demonstrated. A 4×4 grid of cylindrical vial agarose gel phantom was constructed for this experiment. Each vial is approximately 3cm in diameter and 4.8cm in height. Each column was constructed with a varying concentration of agarose (0.5%, 1%, 2%, 4%) to modulate T₂. Each row is doped with a varying concentration of NiCl₂ (0mM, 0.5mM, 1mM, 2mM) to modulate T₁.

All phantom experiments were performed on a clinical 3.0T MRI system (Signa Premier, GE Healthcare, Waukesha, WI) using a high channel density posterior and anterior receive array coil with up to 90 independent coil elements (Air coil, GE Healthcare, Waukesha, WI). Single-echo SE-based T₂ mapping was performed to provide a reference standard. Echo times of 11ms, 50ms, 100ms, 150ms were acquired with TR of 6000ms. Other acquisition parameters include: axial acquisition; field of view (FOV)=18cm×18cm; matrix=128×128; slices=1; slice thickness=15mm; receiver bandwidth=±83.33kHz. Signals were fit to a mono-exponential decay signal model offline in Matlab (MathWorks, Natick, MA) to estimate T₂ on a voxel by voxel basis. A circular ROI was drawn in each vial. The T₂ measurements were averaged in each ROI for comparison with the proposed method.

T₁ maps of the phantoms were generated using inversion recovered fast spin-echo (FSE-IR) MRI. Acquisition parameters were as follows: inversion time=50ms, 500ms, 1000ms, 1500ms, 2500ms, 3500ms, 4000ms; TR=6000ms; FOV=18cm×18cm; matrix=256×256; slices=1; slice thickness=15mm; receiver bandwidth=±25kHz. T₁ estimation was performed on a voxel by voxel basis using the standard inversion recovery signal model²⁵.

GRE images for phase-based T₂ map were acquired using an axial acquisition; TR=5.0ms; FOV=18cm×18cm×24cm; matrix=128×128×24; receiver bandwidth=±50.1kHz; number of signal averages=4. Two complex GRE datasets with ΔΦ=2° and −2°, each with 18° flip angle were acquired for the proposed method. The sum of squares image was used as a virtual body coil image. The complex sensitivity map was generated using the source images with one RF phase schedule (the first echo if multiple echoes are acquired) and used to combine complex channel images for both sets of images with difference RF phase schedule, and all acquired echoes. This process was used to generate complex coil combined images. T₂ maps were reconstructed as described in the theory section. For the reconstruction of phase-based T₂ maps_, a T₁ of 1850ms was assumed (mid-point of the range of the T₁ measured in the phantom, as reported in the Results section).

For each reconstruction by the proposed method, T₂ measurements were averaged in a circular ROI in each vial, on the center slice. Linear regression was used to compare the T₂ measurements obtained using the proposed phase-based method and SE-based T₂ mapping.

In vivo experiments:

The proposed methods were also evaluated in healthy volunteers to demonstrate in vivo feasibility. All human imaging was performed after obtaining approval from our institutional review board (IRB) and informed written consent. All in vivo experiments were performed on 3.0T clinical MRI systems (abdomen, pelvis, brain experiments on Signa Premier; knee experiments on Discovery MR 750w, GE Healthcare, Waukesha, WI). Various phased array receive coils appropriate for the specific anatomy were used including: 8-channel head coil (brain), 8-channel knee coil (knee) and high channel density posterior and anterior receive array coils with up to 90 independent coil elements (Air coil, GE Healthcare, Waukesha, WI) for the abdomen and pelvis.

For the proposed method, the choice of RF phase increment and flip angle are as follows: ΔΦ = 2° and −2°, each with an 18° flip angle.

In the knee volunteer experiments, a total of 6 knees were scanned in 4 volunteers (4 males, ages 28-35). The acquisition parameters of the proposed method are as follows: 3D acquisition; sagittal plane; FOV=14cm×14cm×9.6cm; TR=5.9ms; matrix=256×256×32; bandwidth=±90.91kHz; signal averages=3; acquisition time=4:48 minutes. Due to the difficulty of limiting motion over long acquisition times, a commercial multi-echo SE T₂ mapping was used as reference instead of single-echo SE. Acquisition parameters include: sagittal plane; FOV=14×14cm; slice thickness=2.7mm; gap=0.3mm; slices=28; TR=1.0s; acquisition matrix=256×256; echo times=8.6ms, 14.8ms, 22.2ms, 29.5ms, 36.9ms, 44.3ms, 51.7ms, 59.1ms; bandwidth=±31.25kHz; signal averages=1; exam time=12:56 minutes. The acquisition volumes of the two methods were precisely colocalized.

Phase-based T₂ maps were reconstructed as described in the theory section. T₁ of 1198ms was assumed (midpoint between the T₁ of the medial femoral cartilage and patella)²⁶. The reference T₂ map from multi-echo SE images were calculated by fitting the signal to a single-exponential decay model to minimize least square error on a voxel by voxel basis. To compare the proposed method and the reference, T₂ measurements were averaged inside ROIs drawn directly on the T₂ maps in the following regions described by Fang Liu et, al²⁷: medial femoral central (MFC) condyle, medial femoral posterior (MFP) condyle, medial tibial plateau (MTP), patella-deep (PAT-D), patella-superficial (PAT-S), lateral femoral central (LFC) condyle, lateral femoral posterior (LFP) condyle, lateral tibial plateau (LTP), as well as T₂ measurements from the gastrocnemius muscle (MUS). For each individual region, box-whisker plots were created to demonstrate the distribution of T₂ measurements by the two compared methods. A Student’s t-test was performed for paired samples. For measurements across all the regions, the Pearson coefficient was computed.

A brain study was performed on one volunteer (male, age 30). The acquisition parameters of the proposed method were as follows: 3D acquisition; axial plane; FOV=24cm×24cm×12.8cm; TR=5.6ms; acquisition matrix=256×256×32; bandwidth=±90.91kHz; signal averages=3; exam time=4:30 minutes. Single-echo SE T₂ mapping was used as reference for T₂ measurements, acquisition parameters include: axial plane; FOV=24cm×24cm; slice thickness=3.6mm; slice spacing=0.4mm; number of slices=22; TR=5s; acquisition matrix=256×256; echo times=11ms, 70ms; bandwidth=±31.25kHz; signal averages=1; acquisition time=24:00 minutes. The acquisition volumes of the two methods were precisely colocalized.

Phase-based T₂ maps were reconstructed as described in the theory section. T₁ of 915ms was assumed (midpoint between the T₁ of white matter and the putamen at the age of 20) ²⁸. The reference T₂ map was reconstructed using least square error fitting to a single-exponential model. Synthetic T₂-weighted images were also generated with virtual TE values of 70ms and 100ms as described in the theory section.

For imaging in the abdomen and pelvis, separation of water and fat signals was performed by combining the proposed method with a multi-echo 3D GRE chemical shift encoded (CSE) acquisition. Abdomen (male, age 54) and pelvis (male, age 47) experiments were conducted on one volunteer respectively. The acquisition parameters in the abdomen included: axial plane; FOV=40cm×32cm×26cm; TR=6.5ms; acquisition matrix=100×80×26; 5 echoes with echo times=0.9ms, 2.0ms, 3.0ms, 4.0ms, 5.1ms; bandwidth=±100kHz; signal averages=1; exam time=20 seconds in a single breath-hold. In the pelvis, the same acquisition parameters were used with the following exceptions: slice thickness=8mm; slices=32, TR=6.4ms; bandwidth=±90.91kHz; exam time of 25 seconds in a breath-hold.

For the image reconstruction, the proposed method was combined with CSE-MRI. Using complex fitting with single R2* least-squares fitting reconstruction²⁹ from the ISMRM Fat-Water Toolbox³⁰ (http://ismrm.org/workshops/FatWater12/data.htm), water and fat signals were separated. The magnitudes and phases of each chemical species were then used to reconstruct individual T₂ maps for each chemical species.

Single voxel multi-TE stimulated echo acquisition mode (STEAM)-MR spectroscopy³¹ (MRS) was acquired in the liver and the spleen to provide reference values for phase-based T₂ measurements. STEAM-MRS data was acquired with the following parameters: TR=3500ms; TE=10ms, 15ms, 20ms, 25ms, 30ms; number of points=2048; spectral width=5000Hz; 5ms mixing time. The voxel size was 15mm×15mm×20mm in the liver and 15mm×15mm×10mm in the spleen. Signal magnitude as well as T₂ of water and fat signal was estimated jointly using non-linear least square fitting³².

Simulation experiment to evaluate the sensitivity of phase to motion:

Although no apparent effect of motion was observed in vivo (below), it is well known that GRE acquisitions with unbalanced gradients and no RF spoiling (i.e. unspoiled GRE) can be sensitive to motion^33,34. In the presence of unbalanced gradients, moving spins will accrue a different phase during each TR. This phase accrual may impact the T₂-dependent phase of the method proposed in the current work, potentially confounding T₂ measurements.

For the proposed method, phase accrual resulting from the unbalanced readout gradient is a linear function of the voxel location. Assuming that the phase dispersion from the unbalanced gradient is 2π across the voxel in the readout direction, the additional phase accrual from the overall voxel can be written as: n×TR×Vx×2π/ΔX, for a voxel moving from the image isocenter, where Vx is the velocity of the voxel in the readout direction and ΔX is the voxel dimension in the readout direction. This effect potentially confounds quantification of the phase shift used to encode T_2.

To assess the magnitude of velocity effects on T₂ quantification, we performed a Bloch equation simulation experiment where the effects of the first order motion (velocity) in the readout direction were modeled. This simulation was performed using a modification of the simulation described in the Theory section. In addition to a 2π phase dispersion, a velocity dependent common phase was added to all isochromats in a voxel at the end of each repetition. This simulation experiment was conducted with velocity values ranging from −1mm/s to 1mm/s, with a 2mm voxel dimension. Other parameters used in the simulation included: flip angle = 18°, TR = 5ms, ΔΦ=±2°, T₂=50ms, and T₁=1000ms. Signal phase attributed to T₂ was estimated from the phase difference between the two signals (i.e. with ΔΦ=±2°) divided by 2, and compared with a T₂ lookup table for T₂ estimation, using the proposed method described in the Theory section. The lookup table was generated using Bloch equation simulation without motion and the same acquisition parameters over a wide range of tissue relaxation parameters.”

Results

Phantom experiments:

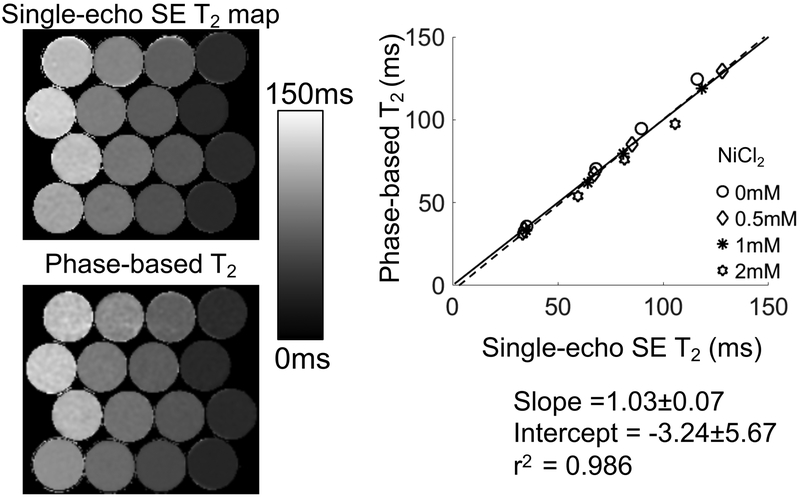
In the phantom experiment the T₁ of the phantom vials were estimated by FSE-IR to be 873ms, 932ms, 829ms, 925ms, corresponding to agar concentrations of 0.5%, 1%, 2%, 4% in phantoms with 2mM NiCl₂; 1390ms, 1315ms, 1279ms, 1332ms in phantoms with 1mM NiCl₂; 1725ms, 1698ms, 2053ms, 1792ms in phantoms with 0.5mM NiCl₂; 2848ms, 2902ms, 2788ms, 2888ms in phantoms with 0mM NiCl₂. The proposed method (which did not correct for T₁ effect in the signal phase) demonstrated close agreement with reference T₂ estimates (Figure 4) (slope=1.03±0.07, intercept=−3.24±5.67). For vials of vastly different T₁ measurements (2mM NiCl₂ and 0.5mM NiCl₂), the T₂ measurements show slightly higher deviation from the reference at high T₂ values.

Figure 4.

T₂ maps generated using the proposed method provided accurate T₂ measurements agreeing closely with spin-echo T₂ mapping. Phantom T₂ maps generated using single-echo SE MRI and the center slice of the phase-based T₂ mapping are shown. The agreement between the phase-based T₂ map and single-echo SE MRI was evidenced by linear regression between T₂ values averaged in ROIs drawn in the center of the vials, with a slope and intercept statistically equal to one and zero, respectively.

In vivo experiments:

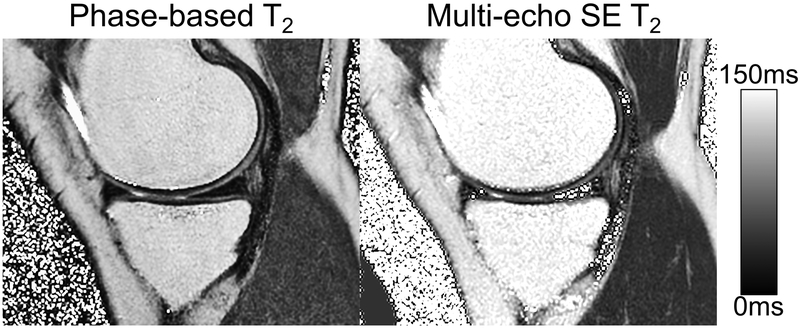
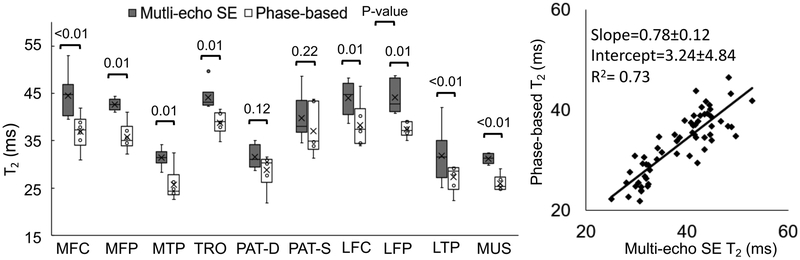
In the knee imaging experiments, the proposed method produced high quality T₂ maps in all knees (Figure 5), including high apparent SNR and excellent depiction of anatomical detail. In areas where water signal is dominant (cartilage and muscle), similar T₂ values were observed between the proposed method and the multi-echo SE T₂ map used as a reference. In Figure 6, the box-whisker plot and scatter plot showed strong correlation between the phase-based T₂ and the reference T₂ measurements (Pearson correlation coefficient = 0.86), with slope=0.78±0.12 and intercept=3.24±4.84. Quantitative T₂ values measured using the proposed method were very similar to the multi-echo SE based T₂ measurements, although many of these measurements showed statistical differences.

Figure 5.

T₂ map generated with the phase-based T₂ mapping showed excellent image quality in all six knees. Similar intensities can be observed in regions with dominant water signal such as cartilage and the muscle. An example of T₂ maps generated using multi-echo SE MRI and the proposed method are shown.

Figure 6.

The box and whisker plot and scatter plot showed strong correlation between the phase-based T₂ and the multi-echo SE T2 with a high Pearson correlation coefficient (0.86). Measurements made in 10 different regions on each of six different knees. The regions measured were medial femoral central condyle (MFC), medial femoral posterior condyle (MFP), medial tibial plateau (MTP), patella-deep (PAT-D), patella-superficial (PAT-S), lateral femoral central condyle (LFC), lateral femoral posterior (LFP), lateral tibial plateau (LTP), gastrocnemius muscle (MUS).

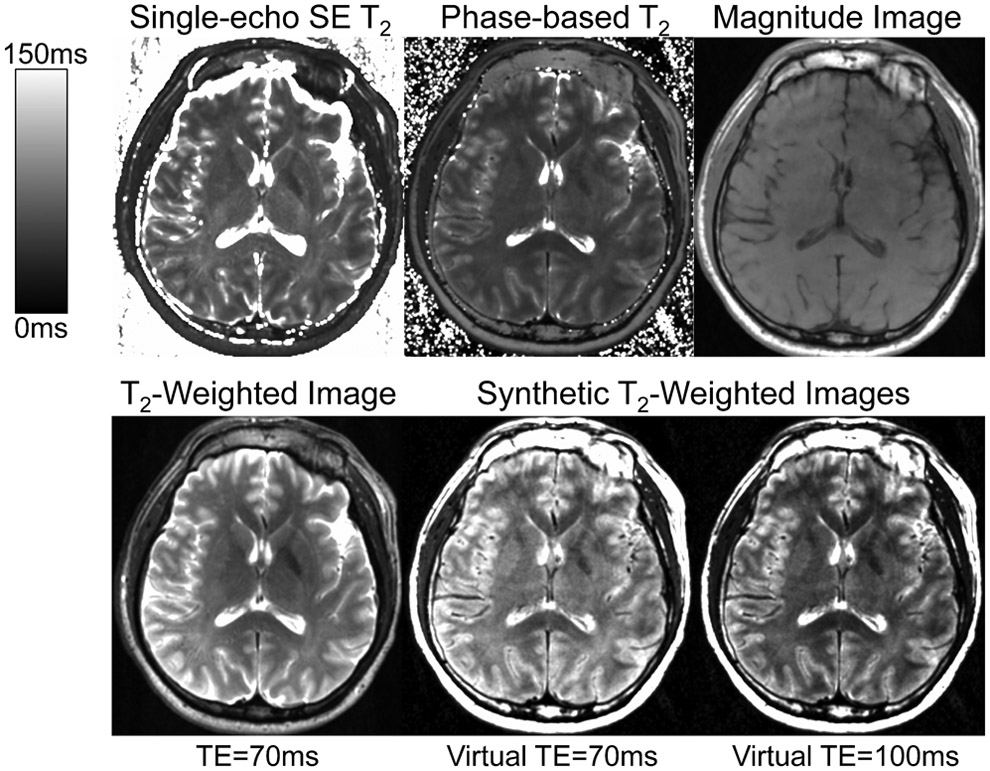
Similarly, high quality T₂ maps were generated by the proposed method in the brain (Figure 7). However, some discrepancies in T₂ values were observed between the two methods, especially in the grey matter. Average T₂ values in regions of interest (ROIs) were 39ms (phase-based) and 53ms (SE) in the genu of corpus callosum; 40ms (phase-based) and 61ms (SE) in the splenium of corpus callosum; 47ms (phase-based) and 59ms (SE) in the white matter; 35ms (phase-based) and 40ms (SE) in the globus pallidus of basal ganglia; 45ms (phase-based) and 54ms(SE) in the putamen of basal ganglia.

Figure 7.

High quality T₂ maps were generated in the brain using the proposed phase-based method. The phase-based T₂ appeared lower than the reference T₂ map especially in the grey matter. The magnitude image used in the proposed method is also shown. Synthesized T₂-weighted images (virtual TE=70ms, TE=100ms) showed overall similar appearance although with less grey-white matter contrast than T₂-weighted SE at the same TE (70ms).

Synthetic T₂-weighted images generated from the phase-based T₂ map and the simultaneously acquired magnitude images are also shown with two different virtual echo times (70ms, 100ms). Compared with a T₂-weighted SE image with TE of 70ms, the synthesized T₂-weighted image with virtual TE of 70ms showed overall similar appearance, although with slightly reduced apparent grey-white matter contrast..

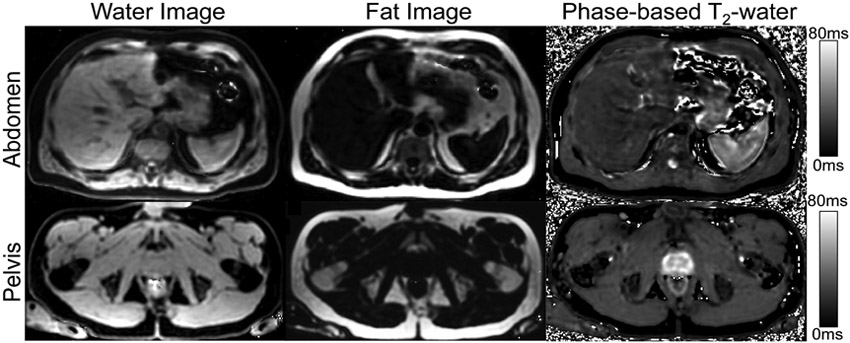
In the abdomen and pelvis, 3D spatially resolved T₂ maps generated from separated water signal were successfully reconstructed after water-fat separation (Figure 8). Close agreement between T₂ value of the water signal estimated by the proposed method and MRS was observed, with estimates of 20ms and 22ms respectively, using a co-localized voxel. Similarly, in the spleen, the proposed method measured a T₂ value of 38ms compared to 34ms with MRS.

Figure 8.

The proposed phase-based 3D T₂ mapping combined with CSE-MRI water-fat separation is feasible over the entire abdomen or the pelvis within a single breath-hold. Water and fat images were calculated from multi-echo gradient echo images with varied RF phase increments. A phase-based T₂ map for water signal was also generated from the water phase of different RF phase increments. Simultaneous R₂* and B₀ field maps were also generated, but not included for brevity.

Finally, in the peripheral zone of the prostate, phase-based T₂ measurements (72ms) were comparable to values reported in literature (74±9ms in the prostate)²³.

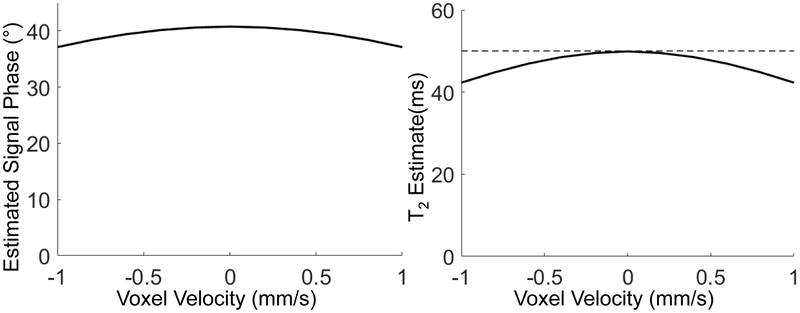
Simulation experiment to study the sensitivity of signal phase to motion:

As shown in Figure 9, the signal phase in the proposed method was sensitive to motion. For example, a velocity of 1mm/s lead to a 3.6° change in the signal phase, relative to no motion. Accordingly, the apparent T₂ estimation was reduced from 50ms to 42ms.

Figure 9.

Sensitivity of the proposed method to motion. Signal phase generated using Bloch-equation simulation modeling constant velocity leads to small errors in the apparent T₂-dependent phase and subsequent underestimation of T₂.

Discussion

We have proposed and successfully demonstrated preliminary feasibility of a phase-based T₂ mapping technique based on GRE imaging. The theory and technique for encoding T₂ information into the signal phase of a gradient echo acquisition were developed. We demonstrated that using a small RF phase increment in gradient echo acquisitions, a signal phase that increases monotonically with the transverse relaxation time can be generated. This behavior forms the basis of the proposed method for encoding information into the GRE signal phase. The feasibility of the proposed method was successfully demonstrated in phantoms and in vivo experiments, including in combination with chemical shift encoded water-fat separation. Further, the proposed approach can be used to generate high quality synthetic T₂-weighted images that can be acquired in relatively short acquisition times.

Compared with traditional SE-based T₂ mapping and T₂-prep-based methods, the proposed method reduces acquisition time and would potentially render quantitative T₂ mapping feasible for many clinical applications, including those that require short breath-holds. Compared with DESPOT2, the proposed method requires fewer GRE source images for parametric mapping and consequently shorter acquisition time. Further, the proposed method is also immune to signal voids caused by banding artifacts seen with bSSFP methods. Compared with the TESS T₂ mapping technique, T₂ weighting and T₂* weighting in the signals of the proposed method are naturally separated, because the T₂ information is contained in the signal phase, which is not affected by T₂* effects. The proposed technique is also compatible with CSE-MRI, which is useful in many extra-cranial imaging applications, particularly in the abdomen and pelvis. This feature would enable simultaneous generation of T₂ maps for both water and fat signals as well as the R₂* and B₀ field map.

In this work, the proposed GRE-based method was able to shorten the minimum acquisition time compared to spin-echo-based T₂-mapping methods. Among the steady-state methods, DESPOT2 requires at least three of more acquisitions. The proposed phase-based T₂ mapping technique requires two acquisitions, while DESS and TESS require only one. The number of acquisitions required would normally determine the minimum acquisition time needed to create a T₂ map of a certain resolution and FOV. However, it is worth noting that the relative advantage of DESS and TESS in this comparison is offset by their generally longer TR (14ms, 20ms, 26ms, 21ms) ^17-20 compared to DESPOT2 (e.g. 3.6ms) ¹⁶ and the phase-based T₂ mapping (e.g. 5.9ms, 5.6ms and 6.5ms in this work). Further, depending on the application, multiple signal averages are often acquired, when there is sufficient acquisition time (e.g. in the knee and in the brain). In such applications, the SNR efficiency is a more important measure of acquisition speed. Rigorous evaluation of the SNR performance of the proposed method is beyond the scope of this work but will be an important component of future investigations.

Small discrepancies between the T₂ measured with the proposed method and SE-based methods was observed, particularly in the brain. While the reasons for these discrepancies are unclear, possible reasons include multi-component T₂ effects, magnetization transfer, B₁ inhomogeneities, motion, or combinations of these factors. Further work will be needed to determine the cause of these discrepancies.

Previous studies have demonstrated that motion can lead to change in the signal magnitude in steady-state acquisitions using unbalanced gradient echo acquisitions and pseudo-random RF phase spoiling. In this work, we have performed preliminary Bloch equation simulations modeling constant linear motion, demonstrating that small changes in the signal phase may result from motion, leading to underestimation of T₂. Although no definite effects of motion on artifacts or T₂ estimation accuracy were observed in the experimental studies, some underestimation of T₂, relative to references standard measurements was observed in cartilage and in the brain. It is uncertain whether this apparent underestimation in T₂ was related to motion or not. Future rigorous evaluation of the potential effects of motion on T₂ estimation is warranted, especially for applications where tissue motion may be an important factor, eg. heart, flowing blood

There are several limitations of this work. First, although the feasibility of this method has been successfully demonstrated, considerable technical optimization and substantial further clinical validation is needed. Further studies will be needed to evaluate the technical accuracy and noise performance of the proposed method, as well as to optimize acquisition parameters. In addition, the precise impact of B₁ inhomogeneities, motion, variation in T₁ of the tissues, magnetization transfer effects³⁵ and multi-exponential relaxation²⁷ requires further evaluation. These effects may explain the apparent discrepancies between the T₂ measurements in the brain between the proposed phase-based method and conventional SE-based T₂ mapping.

Another major limitation of the proposed method is that the T₂ mapping algorithm requires knowledge or assumption of the T₁ of tissue to map the signal phase into a T₂ value. Although the signal phase is relatively independent of T₁ for long T₁ values, this is not the case for shorter T₁ values. Thus, the overall accuracy of this method is unknown for T₂ quantification, especially in tissues with short T₁ values.

Further, the proposed method can be used to generate synthetic T₂-weighted images. However, due to the relatively large flip angle in the proposed method, the source magnitude images are T₁-weighted. For this reason, the T₂-weighted images synthesized from the phased-based T₂ maps and simultaneously acquired magnitude images will be T₁-weighted as well, similar to short tau inversion recovery (STIR) based methods.

In addition, the proposed method currently requires the use of 3D acquisitions, due to the need for a uniform flip angle across the tissue of interest. Extension to 2D imaging should be feasible but will require more complex lookup table construction that accounts for acquisition slice profiles.

In conclusion, we have presented and successfully demonstrated the feasibility of a novel phase-based T₂ mapping method based on gradient echo imaging. This approach has the potential for rapid, 3D mapping of T₂ in tissue. Further technical development, optimization and clinical validation are needed.