Cardiac-gated steady-state multifrequency magnetic resonance elastography of the brain: Effect of cerebral arterial pulsation on brain viscoelasticity

Abstract

In-vivo brain viscoelasticity measured by magnetic resonance elastography (MRE) is a sensitive imaging marker for long-term biophysical changes in brain tissue due to aging and disease; however, it is still unknown whether MRE can reveal short-term periodic alterations of brain viscoelasticity related to cerebral arterial pulsation (CAP). We developed cardiac-gated steady-state MRE (ssMRE) with spiral readout and stroboscopic sampling of continuously induced mechanical vibrations in the brain at 20, 31.25, and 40 Hz frequencies. Maps of magnitude |G*| and phase ϕ of the complex shear modulus were generated by multifrequency dual visco-elasto inversion with a temporal resolution of 40 ms over 4 s. The method was tested in 12 healthy volunteers. During cerebral systole, |G*| decreased by 6.6 ± 1.9% (56 ± 22 Pa, p < 0.001, mean ± SD), whereas ϕ increased by 0.5 ± 0.5% (0.006 ± 0.005 rad, p = 0.002). The effect size of CAP-induced softening slightly decreased with age by 0.10 ± 0.05% per year (p = 0.04), indicating lower cerebral vascular compliance in older individuals. Our data show for the first time that the brain softens and becomes more viscous during systole, possibly due to an effect of CAP-induced arterial expansion and increased blood volume on effective-medium tissue properties. This sensitivity to vascular-solid tissue interactions makes ssMRE potentially useful for detection of cerebral vascular disease.

Introduction

Compliance of cerebral arteries is a key element of cerebral pulsation and brain hemodynamics.¹ Many neurological disorders such as vascular dementia have been related to an impaired vascular function of the brain, eventually leading to chronically hypoxic regions, dysregulated metabolic activity or cerebral amyloid deposition.^2–5 Yet, viable biomarkers which can directly quantify in vivo arterial stiffness and vascular compliance in the brain are still lacking.⁶

Vascular compliance is an adaptive change in blood volume in response to an altered blood pressure.⁷ Changes in cerebral blood volume during cerebral arterial pulsation (CAP) can be measured by specialized magnetic resonance imaging (MRI) sequences such as arterial spin labeling (ASL)^8,9 or by transcranial Doppler ultrasound (TDC).¹⁰ While ASL-based blood volume measurement is precise but time-consuming,¹¹ TDC is a routine clinical method despite limitations in that it cannot measure arterial volume or diameter directly.¹² Both methods have in common the inability to assess changes in intracranial pressure, leaving them with surrogate pressure parameters measured outside the brain.⁸

Measurement of pressure, as volumetric, isotropic mechanical stress, requires a counteracting mechanical force, preferably applied in a noninvasive fashion for medical imaging examinations.⁶ Today, magnetic resonance elastography (MRE) uses noninvasive stress fields induced by acoustic shakers for quantitative in vivo mapping of mechanical parameters of biological soft tissues.¹³ MRE measures the effective (macroscopic) shear modulus of the tissue including all solid–fluid interactions of compartments contained in an imaging voxel. According to the theory of poroelastography, such biphasic tissue interactions communicate vascular pressure into the MRE-measured effective shear modulus and make MRE potentially sensitive to properties of the vasculature including vascular compliance.^14,15

The aim of this study was to test whether MRE is sensitive enough to detect viscoelasticity changes in the brain related to CAP. In conventional brain MRE, any influence of CAP on brain viscoelasticity is eliminated by long-term signal averaging over multiple cardiac cycles. To overcome this limitation, we here introduce cardiac-gated steady-state MRE (ssMRE) with spiral readout and stroboscopic sampling of time-harmonic mechanical vibrations at multiple frequencies. This method will allow us to test the hypothesis that CAP, which relies on vascular compliance, is mirrored by shear modulus (inverse compliance) of brain tissue as quantified by cardiac-gated cerebral ssMRE.

CAP and shear modulus will be derived from a single scan comprising 100 snapshots obtained with 25-Hz frame rate. The method will be tested in healthy volunteers and analyzed for effect size, relative timing and age effects. Our data are intended as first reference for shear modulus variations in the healthy brain over the cardiac cycle.

Materials and methods

Subjects

The study was approved by the ethics committee of Charité – Universitätsmedizin Berlin based on the WMA Declaration of Helsinki (Ethical Principles for Medical Research Involving Human Subjects) and each volunteer gave written informed consent. Twelve healthy male volunteers without any history of neurological events were investigated (mean age ± SD: 36 ± 11 years, age range: 23 to 58 years). Heart rate and peripheral blood pressure were recorded for each subject (heart rate: 65 ± 8 1/min, systolic blood pressure: 123 ± 9 mmHg, diastolic blood pressure: 73 ± 10 mmHg). Due to the nature of the pilot study, volunteers and the researcher collecting data were not blinded to study group assignment.

MRI scanner and mechanical actuator setup

All measurements were performed on a 1.5-T clinical MRI scanner (Siemens Magnetom Sonata, Erlangen, Germany). Continuous harmonic vibrations were induced by a pressurized air driver comprising two pipelines and two air bottles placed inside the standard head coil (single-element, birdcage coil), directly underneath the subject’s head (Figure 1). The two bottle drivers were switched in opposed-phase mode to induce predominantly left-to-right motion. A forerun of vibrations prior to the start of the imaging sequence of at least 3 s was maintained in order to ensure the establishment of a mechanical steady state. Three vibration frequencies of 20 Hz, 31.25 Hz, and 40 Hz were applied consecutively during the entire MRE experiment. The waveform generator was automatically configured by a ‘smart trigger’ from the MRE sequence, the length of which identified a set of vibration parameters stored in a library of the waveform generator.¹⁶ The clock of the wave generator was locked to the MRI clock to avoid any drift between wave excitation and the MRI sequence over the course of the MRE examination.

Figure 1.

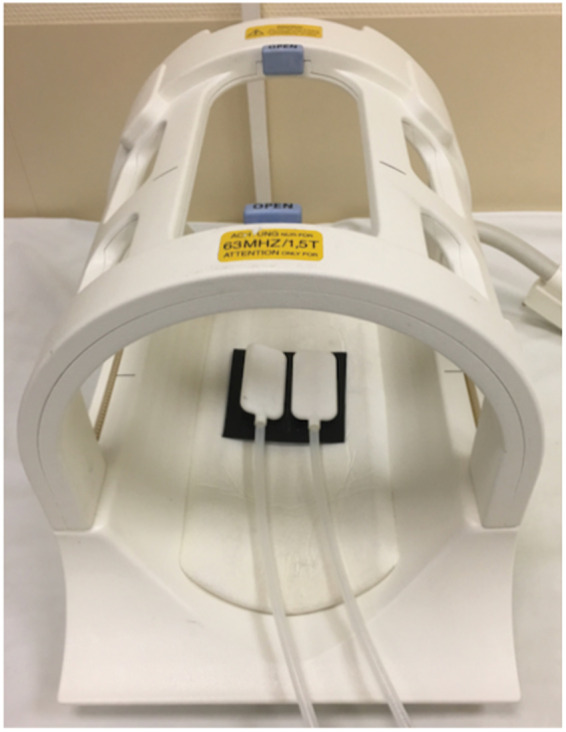
Mechanical actuators for brain stimulation based on pressurized air pads.

ssMRE pulse sequence

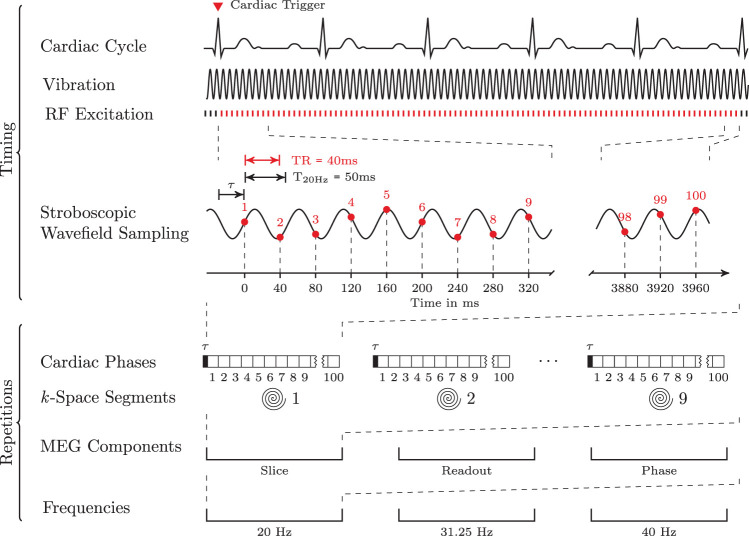
Acardiac-gated steady-state MRE (ssMRE) sequence was developed based on a gradient echo pulse sequence with segmented spiral readout (spiral-out trajectories starting from the center of k-space). Nine spiral trajectories were combined to obtain one full k-space. The repetition time (TR) for one trajectory was 40 ms including RF excitation (25° flip angle), motion encoding within 20 ms echo time (TE), and signal spoiling. The same motion-encoding gradient (15 ms, 30 mT/m amplitude) was applied for all three frequencies according to the principle of fractional encoding¹⁷ and corresponding to a velocity encoding efficiency (VENC) of 0.7 cm/s. The first of the nine k-space segments was consecutively acquired 100 times so that a total interval of 4 s was sampled with 25 frames per second. Thereafter, the next k-space segment was acquired and so forth until the complete k-space was sampled (Figure 2). The experiment was repeated nine times to acquire three orthogonal wave field components at three frequencies (Figure 3). For each of the 12 experiments, the first of the 100 phases was used to perform voxel-wise phase correction in all images. This phase correction eliminates any static phase offsets and improves the performance of the phase-unwrapping algorithm or even makes it obsolete. When multi-channel receive coils are used, phase correction optimizes the signal-to-noise ratio (SNR) in the combined phase images. The data were acquired in a transverse image slice through the center of the cerebrum, parallel to a line from the genu to the rostrum of the corpus callosum. Slice thickness, field of view (FoV), and matrix size were 5 mm, 220 × 220 mm², and 192 × 192, respectively.

Figure 2.

ssMRE sequence for the stroboscopical encoding of continuous harmonic vibration fields (three Cartesian components of wave deflection) at three frequencies within a single image slice. A spiral readout trajectory was used; 100 images were acquired at instances demarcated by red vertical bars, while RF excitation was also applied when no signals were acquired (black bars) in order to maintain the steady state of magnetization. Vibration was initiated at the beginning of the sequence running continuously through the entire experiment for every driving frequency. All TR’s were synchronized to the vibration by adapting time τ, so that the wave phase was consistent throughout the accumulation of interleaved k-space trajectories. Each τ was computed by real-time analysis of pulse trigger and total vibration phase.

Figure 3.

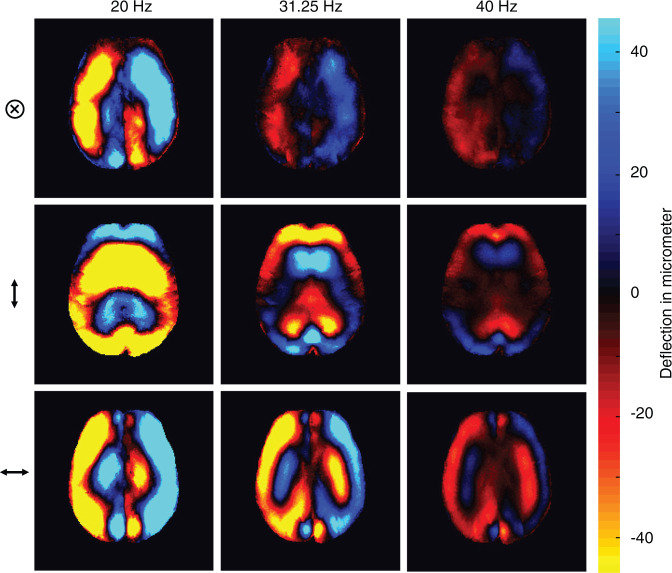
Representative wave fields for three frequencies and three deflection components (⊗, ↕, ↔ denote deflections through-plane [head-to-feed], up-down [anterior-posterior], and left-right, respectively).

Steady-state synchronizations and stroboscopic sampling

RF excitation and data sampling were started immediately after the 3-s mechanical forerun and upon receipt of a trigger signal from a fingertip pulse oximeter. The relative phase between mechanical wave and motion encoding was locked by a delay time τ between the pulse wave of the cardiac trigger and the first TR (see Figure 2). The TR of 40 ms was intentionally mismatched to vibration periods of 50 ms, 32 ms, and 25 ms, corresponding to the excitation frequencies of 20 Hz, 31.25 Hz, and 40 Hz, respectively. By this principle of stroboscopic sampling, a harmonic cycle of 50 ms (20 Hz) is 10 ms shorter than the data acquisition, so that five TRs are required to capture a full cycle. In the same fashion, vibrations with 32 ms (31.25 Hz) and 25 ms (40 Hz) can be sampled within four and five TRs, respectively. We note that there is no further repetition required for capturing the wave dynamics. Instead, 20 or 25 full vibration cycles are encoded within 100 TR’s for all applied frequencies. To maintain a steady state of magnetization, RF excitation was continuously deployed, even after 100 TR’s while waiting for the next pulse trigger and no signal was acquired (black vertical bars in Figure 2 indicate RF-excitation without signal acquisition). Overall, our cardiac-gated ssMRE sequence ensured (i) a mechanical steady state of uninterrupted time-harmonic shear vibrations, (ii) a steady state of magnetization, and (iii) that both steady states (i and ii) remained synchronized (by waiting delay τ), regardless of the number of cardiac cycles or their duration.

Depending on the heart rate, the total image acquisition time was approx. 8 min for 900 images recording the propagation of shear waves of three frequencies and three components within an image slice.

Parameter reconstruction

Postprocessing was based on the multifrequency dual elasto-visco (MDEV) inversion algorithm as detailed in Hirsch et al.¹⁸ and publicly available on https://bioqic-apps.charite.de. The algorithm was adapted to account for stroboscopic sampling: a temporal Hilbert transform was applied across all 100 time-resolved wave images, yielding 100 complex-valued wave images after complex smoothing of the wave phase by a Gaussian kernel with sigma = 0.65 pixels and gradient unwrapping.¹³ The Hilbert transform extracted the fundamental driving frequency by a Gaussian bandpass with σ = 0.2 Hz. A total of 18 (2 × 3 × 3) complex strain images were obtained for each of the 100 time points, mapping the in-plane spatial derivative components (2) of each wave component (3) and frequency (3).¹⁹ These 18 strain images per time point were further processed according to the standard MDEV pipeline. In brief, a 2D-Butterworth lowpass filter with a threshold of 50 1/m was used to suppress compression wave offsets, followed by combining all 18 images in the inversion equations (equation (2) in Streitberger et al.¹⁹) to obtain compound parameter maps depicting the magnitude |G*| and the phase ϕ of the complex shear modulus. Of note, we discarded the first and last six times points (i.e. 240 ms at the beginning and 240 ms at the end of the temporal window) from our analysis to avoid any temporal boundary artifact due to the Hilbert transform.

Parameter analysis and statistical tests

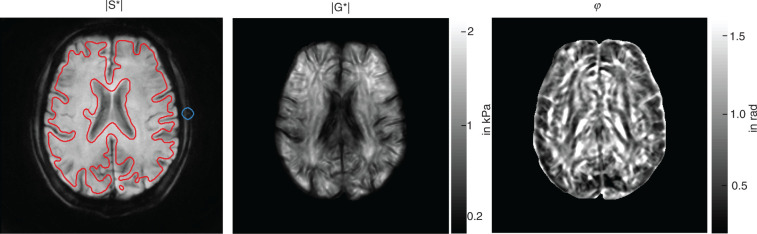
Time-dependent |G*| and ϕ parameters were further analyzed by referring to the entire brain parenchyma shown in our image slice without the ventricles and larger sulci. This region of interest (ROI) was selected based on the T2* signal of our ssMRE sequence (S*) applying an intensity threshold of the magnitude signal |S*|. SNR analysis was performed for all |S*| images and for all wave displacement images over measure time as detailed in Bertalan et al.²⁰ and based on the same brain region addressed by |G*| and ϕ. A representative |S*| image with overlaid ROI is shown in Figure 4. |G*| and ϕ were averaged within the ROI and correlated with the time course of CAP. The CAP paradigm was obtained from the signal modulation in |S*| within regions of the pulsating temporal arteries in subcutaneous tissue (blue circle in Figure 4). The signal modulations arose from the influx of blood carrying fully relaxed magnetization. This ‘fresh’ magnetization gave a periodically increased signal intensity when the arterial pulse wave passed through the arteries. Of note, only |S*|-images with in-plane motion sensitization (mainly A-P) were used to avoid signal artifacts related to intra-voxel phase dispersion. To double-check the CAP-paradigm, we also deduced periodic CAP-related signal modulations from the phase contrast provided by ssMRE without external vibrations in a deep-gray matter region (Supplementary Figure 1). However, since measurement of the phase-contrast CAP-signal required extra experiments, we further used the signal of temporal arteries for analyzing the timing of CAP.

Figure 4.

ssMRE images averaged over the full acquisition window (4 s, 99 images) for display of anatomical structures in a volunteer. |S*|: magnitude of the complex MRI signal, |G*|: magnitude of the complex shear modulus, ϕ: phase angle of the complex shear modulus. Red lines demarcate the whole-parenchyma region of interest, while the blue circle indicates the region of the temporal artery from which the CAP paradigm was derived in |S*| images.

To analyze the correlation between the MRE and CAP signals, we performed a normalized cross-correlation to obtain a correlation coefficient and the time shift between MRE and CAP. To test the significance of the correlation, we computed the slopes of the time-shifted signals in each volunteer using a linear model. A one-sample (two-tailed) t-test was used to test whether the slopes are significantly different from zero across all volunteers. Averaged effect sizes between diastole and systole were calculated by manually selecting the cardiac phases. Paired t-tests were applied assuming normally distributed data residuals (Shapiro–Wilk normality test, p = 0.49). Statistical significance was assumed at p values < 0.05. All statistical analysis was done in R (version 3.4.2).

Results

MRE data consistency

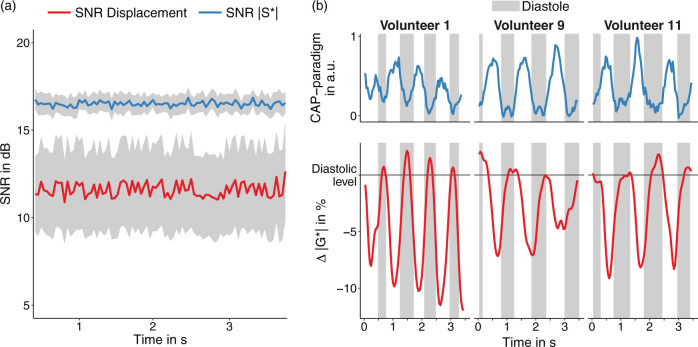
Figure 5(a) shows group-mean SNR values over acquisition time for both the MRI signal (|S*|, mean SNR = 17 ± 1 dB) and wave displacement (mean SNR 12 ± 4 dB) averaged within the full brain parenchymal ROI (red line in |S*| of Figure 4). Neither SNR measure changed significantly over acquisition time, suggesting stability of both steady-state magnetization amplitudes and steady-state vibration amplitudes for further analysis. Furthermore, no subject motion or slice displacement was visible in our data over the entire measure time. The stability of anatomical boundaries is demonstrated in a movie provided as supplementary material (supplementary_mov_1.gif).

Figure 5.

Time courses of ssMRE signals. (a) Averaged SNR time series for |S*| images (blue) and displacement fields (red). The gray area indicates the confidence interval. (b) Time course of relative stiffness changes (|G*| in %, red lines) and CAP paradigm (blue lines, |S*| signal from the temporal artery) for three volunteers investigated in this study. The 0%-baseline was defined based on mean |G*| during diastole as identified by the CAP-paradigm (gray vertical bars).

CAP paradigm

The CAP rate, which was derived from periodic signal intensity variations in the temporal artery as seen in the |S*| images (Figure 4), was 69 ± 11 1/min and correlated with the heart rate of 65 ± 8 1/min (r = 0.80 p = 0.002). Arrival time of first CAP-systole was 570 ± 210 ms relative to the pulse wave recorded in the radial arteries by our fingertip pulse oximeter which is in agreement to the literature.²¹ Mean durations of CAP systole and CAP diastole were 287 ± 105 ms and 610 ± 150 ms, which is in the normal range.¹³ There was no age effect in CAP-related times (CAP-rate vs. age: r = −0.19, p = 0.55). Demographic data and physiological parameters of all volunteers are listed in Table 1.

Table 1.

Individual data for physiology and ssMRE including statistical description.

#	Age in years	Systole/ diastole blood pressure in mmHg	Weight in kg	Sex	Pulse- rate in 1/min	|G*| -rate in 1/min	CAP- rate in 1/min	|G*| Diastole in Pa (SD)	|G*| Systole in Pa (SD)	Δ |G*| in % (SD)	Slope |G*| vs. CAP (p-value)	ϕ Diastole in rad (SD)	ϕ Systole in rad (SD)	Δ ϕ in % (SD)	Slope ϕ vs. CAP (p-value)	MRE vs. CAP time shift in ms
1	23	106/59	74	M	77	83	83	898 (12)	813 (13)	−9.5 (2.6)	−1.4 (p < .001)	1.108 (0.004)	1.112 (0.004)	0.4 (0.7)	0.4 (p = .1)	−40
2	25	115/70	70	M	60	68	68	672 (5)	630 (8)	−6.3 (1.8)	−2.0 (p < .001)	1.16 (0.003)	1.162 (0.002)	0.2 (0.5)	0.6 (p = .03)	−80
3	27	121/77	88	M	75	75	83	812 (6)	768 (8)	−5.4 (1.7)	−1.4 (p < .001)	1.144 (0.003)	1.15 (0.005)	0.5 (0.7)	1.8 (p < .001)	40
4	28	126/63	98	M	60	56	54	684 (8)	631 (11)	−7.9 (2.8)	−1.0 (p < .001)	1.197 (0.005)	1.203 (0.008)	0.5 (1.1)	−0.4 (p < .01)	40
5	29	129/65	75	M	71	71	60	939 (13)	856 (14)	−8.8 (2.7)	−0.6 (p = .03)	1.019 (0.005)	1.029 (0.009)	0.9 (1.3)	1.0 (p < .001)	200
6	32	123/69	84	M	68	63	71	1050 (7)	989 (9)	−5.8 (1.5)	−1.6 (p < .001)	0.962 (0.006)	0.976 (0.006)	1.4 (1.2)	0.6 (p = .016)	−40
7	34	126/77	71	M	55	58	56	1036 (10)	940 (23)	−9.2 (3.1)	−1.7 (p < .001)	1.095 (0.004)	1.103 (0.003)	0.8 (0.7)	1.2 (p ≤ .001)	−40
8	35	120/81	90	M	67	79	79	791 (13)	742 (9)	−6.1 (2.7)	−0.9 (p < .001)	1.094 (0.003)	1.101 (0.005)	0.6 (0.7)	−0.4 (p = .08)	−40
9	44	127/65	93	M	55	60	63	995 (9)	942 (11)	−5.3 (2.0)	−1.0 (p < .001)	1.098 (0.003)	1.11 (0.007)	1.1 (0.9)	0.9 (p ≤ .001)	200
10	45	125/90	82	M	75	75	83	566 (5)	544 (6)	−3.8 (1.9)	−1.7 (p < .001)	1.198 (0.003)	1.196 (0.006)	−0.2 (0.8)	0.8 (p ≤ .01)	80
11	48	118/79	80	M	57	60	58	719 (5)	667 (10)	−7.1 (2.1)	−1.4 (p < .001)	1.143 (0.003)	1.143 (0.004)	0.0 (0.7)	−0.1 (p = .8)	120
12	58	143/85	87	M	65	65	65	753 (6)	722 (15)	−4.1 (2.7)	0.0 (p = .91)	1.125 (0.006)	1.125 (0.008)	0.0 (1.2)	−0.5 (p = .1)	40
Mean (SD)	36 (11)	123/73 (9/10)	83 (9)	M	65 (8)	68 (9)	69 (11)	826 (157)	770 (141)	−6.6 (1.9)	−1.23 (0.56) (p < 0.001)	1.112 (0.068)	1.117 (0.064)	0.5 (0.5)	0.5 (0.71) (p = 0.03)	40 (100)

ssMRE: steady-state magnetic resonance elastography

Viscoelastic parameters

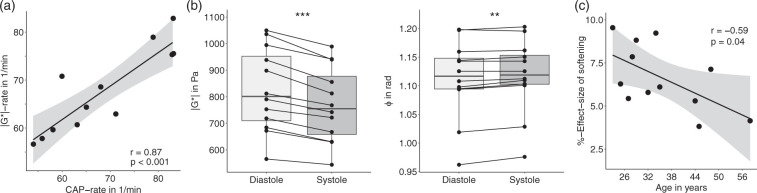
We found a decrease in |G*| during cerebral systole as identified by the CAP paradigm in all volunteers. Figure 5(b) shows for three representative cases the changes of |G*| relative to a baseline defined as diastolic stiffness that is |G*| averaged within all diastolic time periods. The decrease of |G*| during CAP-systole was also apparent by phase-contrast-derived pulsation velocity as shown in the Supplementary Figure 1. Both time series, |G*|, and the CAP paradigm were highly inversely correlated with a mean linear slope of normalized |G*| versus CAP of −1.23 ± 0.56 (p < 0.001). The relative lag between |G*| and CAP measured at peak intensity changes during CAP-systole (40 ± 100 ms) was not significantly different from zero (p = 0.18), indicating the synchrony of |G*| and CAP at the temporal resolution used here. Compared to |G*|, the correlation between ϕ and CAP was weaker with a mean linear slope of ϕ versus CAP of 0.5 ± 0.71 (p = 0.03). Mean durations of systole and diastole observed in the modulation of |G*| and estimated from the inflection points of the parameter changes were 323 ± 104 ms and 577 ± 135 ms. The rate of periodic change in |G*| signals (corresponding to the heart rate) was 68 ± 9 1/min and significantly correlated with the aforementioned CAP rate of 69 ± 11 1/min (r = 0.87, p < 0.001; Figure 6(a)). Based on ϕ, no period durations could be derived due to the weak correlation between ϕ and CAP. The overall effect size of parameter changes between systole and diastole was −6.6 ± 1.9% (−56 ± 22 Pa, p < 0.0001) for |G*| and 0.52 ± 0.49% (0.006 ± 0.005 rad, p = 0.002) for ϕ, meaning that |G*| decreases with CAP while ϕ increases (Figure 6(b)). Mean values of |G*| and ϕ were 770 ± 141 kPa and 1.117 ± 0.064 rad during systole and 826 ± 157 kPa and 1.112 ± 0.068 rad during diastole. Viscoelastic parameters and effect sizes for each subject are listed in Table 1.

Figure 6.

Quantification of the effect of cerebral pulsation on brain viscoelasticity. (a) Linear correlation of heart rates estimated from |G*| and CAP paradigm in 1/min. The gray areas indicate confidence intervals. (b) Total change in MRE parameters from cerebral diastole to systole in all volunteers; left: |G*|, right: ϕ. (c) Relative changes in cerebral |G*| induced by arterial pulsation over age. The black line is the linear regression line and the gray area indicates the confidence range based on Pearson’s linear correlation.

Effect of age and blood pressure on MRE parameters

Figure 6(c) shows that the effect of softening (reduced |G*|) during CAP systole decreases moderately with age with 0.1 ± 0.05% relative effect size per year (r = −0.59, p = 0.042). By contrast, neither time-averaged stiffness nor ϕ showed any age-related effect (mean |G*|: r = −0.18, p = 0.58; mean ϕ: r = 0.14, p = 0.66). No significant correlation was observed between any MRE parameter and blood pressure.

Discussion

The notion of soft tissue as an effective medium in which vascular pressure and vascular compliance influence the macroscopic shear modulus was introduced into cerebral MRE by Paulsen et al.^22–24 Since then, a number of studies have been published investigating the sensitivity of MRE to perfusion, pressure, and arterial pulsation.^25–29 None of these studies quantified cerebral shear modulus in a time-resolved manner over the cardiac cycle.

Reasons for the lack of quantitative data include challenges of harmonic wave field encoding without interruption of the RF sequence and/or mechanical vibration due to cardiac triggering. Such transient scan imposes variations in SNR, shear wave amplitude and eventually parameter maps. Our approach of using (i) twofold steady states, of magnetization and vibration, both locked to each other by adaptation of delay time τ through real-time analysis of wave phase and ECG in conjunction with (ii) stroboscopic wave sampling, allowed us, for the first time, to observe softening of brain parenchyma during cerebral systole. We believe that (i) and (ii) are crucial technical steps towards time-resolved cerebral MRE. While the spiral readout used in our experiment reduced the sensitivity of ssMRE to unwanted motion, our technique might have been similarly effective with Cartesian sampling. Also, the number of frequencies (three) might have been reduced to shorten overall scan time; however, our previous experience with wideband MRE (nine frequencies from 10 to 50 Hz)³⁰ and perfusion-sensitive cerebral MRE (three frequencies from 30 to 50 Hz)^27,29 suggests that the consistency of brain MRE increases by taking more than one vibration frequency into account. The optimum number of frequencies and the frequency dependence of our results deserve further investigation in future studies.

So far, we have demonstrated that our data are consistent with respect to SNR and wave amplitudes. Averaging |G*| and ϕ maps over the full acquisition window of 4 s (99 images) allowed us to produce visco-elastograms which are unprecedentedly rich in detail (see Figure 4). In particular, |G*| reveals the spatial alignment of prominent white matter tracts by higher intensities (stiffness) which, however, deserves further in-depth analysis. In contrast to the clear stiffness contrast among anatomical regions, we found no higher consistency and effect size by regional analysis of CAP-induced parameter changes. Regional analysis of occipital lobe, frontal lobe, temporal lobe, and periventricular spaces including deep gray matter (data not shown) gave similar results as whole-brain analysis, however, with higher interindividual variability due to smaller averaging regions. The global nature of disseminated shear softening points to a rapidly propagating wave as the underlying mechanism of the observed CAP effect on MRE data. Whether such a wave reflects compression (pressure) or shear cannot be decided due to the limited time resolution of our data. In this context, it is worthwhile to clarify terms regarding cerebral compression modulus, shear modulus, and tissue compliance, which are frequently used in the literature, sometimes in an inconsistent manner.

Cerebral compression compliance versus shear compliance

The initial phase of the intracranial pressure pulse wave is primarily generated when the ascending arterial pulse from the heart arrives at the midbrain through the large cerebral arteries.³¹ That pressure wave propagates throughout the brain parenchyma at a speed which is dictated by the effective-medium compression modulus of the brain. The inverse compression modulus is the tissue’s compression compliance C, which is the ratio of volume (V) change to pressure (P) change (C = ΔV/ΔP).³² C relates to a change in total brain volume through the cardiac cycle and is linked to high incompressibility of water, the confinement of the brain inside the skull as well as in- and outflow of blood and CSF, making C largely dependent on frequency. Dynamic volumetric expansion of the brain at peak arterial pulsation is on the order of 0.5 mL³³ and is larger under static conditions (approx. 3 mL upon Valsalva maneuver³⁴). For peak-systolic whole brain volumetric strain, a range of (2.8–4.5) × 10^{−4 25,33} was reported, suggesting a compression wave speed on the order of 50 m/s assuming a 6 mmHg CAP pressure amplitude. Consequently, the CAP-related pressure wave traverses the brain almost instantaneously for a time scale of ssMRE. By contrast, CAP-driven pulsatile fluid flow is a shear wave that spreads throughout the brain, from the arteries into the capillary bed. The speed of that fluid pulse wave is influenced by the shear modulus and the distensibility of vascular walls and, within the brain, can vary from 0.4 m/s (in proximal segments of the middle cerebral artery³⁵) down to very small values of 0.3 mm/s in the neocortical capillaries of the mouse brain.³⁶ Passage of the fluid pulse wave during CAP systole is associated with a transient increase in the fluid fraction, which could explain the observed systolic brain softening and increased viscosity in our study. Furthermore, the observed disseminated effect could be explained by the fluid pulse wave speed within perforating arteries in WM, which is 0.5–1.0 cm/s³⁵ and is still too fast for a spatially resolved analysis in ssMRE.

It is worthwhile to note that our present study is not in conflict with previous studies reporting a positive correlation between brain stiffness and ICP or perfusion pressure.^28,29,37 As outlined above, we believe that our technique is insensitive to short-term transient tissue compression induced by CAP, while static changes in the effective compression modulus of the brain, e.g. related to hypercapnia or the Valsalva maneuver, could impact MRE values differently from the effect we report here.

Interestingly, the arterial blood volume constitutes only approx. 2.0% of total brain volume.³⁸ Given our effect size of approx. 7% for |G*|, this relatively small proportion of expandable compartments in the brain sheds light on the importance of liquid–solid poroelastic interactions for the effective shear modulus of brain parenchyma. This poroelastic effectiveness renders ssMRE potentially sensitive to cerebral vascular compliance (CVC). CVC is an important clinical marker to assess brain function and potential risks for vascular dementia and stroke.⁷ It is known that CVC decreases with age as elastin loses its functionality, leading to stiffer, less compliant cerebral arteries.³⁹ Therefore, the observed decrease in effect size (relative change in |G*| between systole and diastole) with age could point towards an overall stiffening of the vessels (both large and small vessels) and reduced distensibility of cerebral arterial walls related to ageing. Albeit preliminary, this observation might indicate that ssMRE could serve as a marker for cerebrovascular compliance in clinical diagnostic applications.

Although we obtained encouraging results, our study has limitations. The sample size of a pilot study is naturally small and covers a limited age range. Furthermore, volunteers and researchers collecting data were not blinded to study group assignment. More subjects including patients with impaired CVC need to be examined, and the results should be compared with established imaging markers determined by TDC or ASL MRI. Furthermore, we used a finger pulse trigger, which is less precise than ECG gating. Our current hardware was not able to suppress electrical artifacts induced by motion-encoding gradients, masking the weaker ECG signals. This might have increased the variability of the timing of our ssMRE sequence with respect to the cardiac phases. Finally, general limitations of MRE inversion methods also apply to our MDEV reconstruction method, similar to all approaches which cannot fully account for the 3D nature of shear wave fields, the heterogeneity of brain tissue, the anisotropy of white matter bundles, and the viscoelastic dispersion of the shear modulus. Studies have been designed to selectively address these issues^30,40–43; however, none of these studies took cerebral artery pulsation into account.

In summary, using novel cardiac-triggered steady-state spiral MRE, we have shown that CAP results in a short transient softening of brain tissue on the order of 7% while viscosity increases at the same time. This effect might be explained by pulsation-induced arterial expansion and increased blood volume and could make MRE potentially useful for the detection of cerebral vascular disease.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: IS and JB received funding from the German Research Foundation (Sa 901/16). Furthermore, IS received funding from the German Research Foundation (Graduiertenkolleg BIOQIC, GRK 2260, SFB1340 Matrix in Vision) and from the European Union’s Horizon 2020 Programme (ID 668039, EU FORCE – Imaging the Force of Cancer). TE received funding from the German Research Foundation (EL606/2).

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Authors’ contributions

FS and IS conceived and designed the experiments. CW developed the sequence. FS, CW, BK and IS performed the experiments. JB built the actuators. SH and HT, IS, and TE were involved in the analysis and interpretation of the data. IS and FS wrote the manuscript and all authors provided critical revisions.

Supplementary material

Supplemental material for this article is available online.