Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 4;142(16):7591–7597. doi: 10.1021/jacs.0c01712

Polyamorphism Mirrors Polymorphism in the Liquid–Liquid Transition of a Molecular Liquid

Finlay Walton †, John Bolling †, Andrew Farrell †, Jamie MacEwen †, Christopher D Syme †, Mario González Jiménez †, Hans M Senn †, Claire Wilson †, Gianfelice Cinque ‡, Klaas Wynne †,*
PMCID: PMC7181258  PMID: 32249557

Abstract

graphic file with name ja0c01712_0005.jpg

Liquid–liquid transitions between two amorphous phases in a single-component liquid have courted controversy. All known examples of liquid–liquid transitions in molecular liquids have been observed in the supercooled state, suggesting an intimate connection with vitrification and locally favored structures inhibiting crystallization. However, there is precious little information about the local molecular packing in supercooled liquids, meaning that the order parameter of the transition is still unknown. Here, we investigate the liquid–liquid transition in triphenyl phosphite and show that it is caused by the competition between liquid structures that mirror two crystal polymorphs. The liquid–liquid transition is found to be between a geometrically frustrated liquid and a dynamically frustrated glass. These results indicate a general link between polymorphism and polyamorphism and will lead to a much greater understanding of the physical basis of liquid–liquid transitions and allow the systematic discovery of other examples.

Introduction

It is well known that substances have mesophases: phases in between the crystal and the isotropic liquid in which the liquid has partial orientational or translational ordering. However, over the years numerous examples have been found of mesophases with no apparent long-range order that give rise to a liquid–liquid transition (LLT). Many examples have been found in strongly interacting liquids such as in Al2O3–Y2O3,1 germanium,2 silicon,3 and phosphorus.4 The suggestion that an LLT in water would be able to explain many of its anomalous properties5 initiated a hunt to find the LLT in water as well as in other more weakly interacting molecular liquids. To date only four molecular liquids have been found with compelling evidence for a LLT: water,6n-butanol,7,8d-mannitol,9,10 and triphenyl phosphite.11−13 However, the LLT in molecular liquids remains highly controversial and has found alternative explanations in terms of arrested crystallization14,15 or a defect ordered phase.11,16,17 Therefore, the LLT remains shrouded in mystery, hampering efforts to explain the basic physics or to find other examples of LLTs in a systematic fashion.

All known LLTs in molecular liquids take place in the supercooled state, suggesting a strong connection with supercooling and vitrification.18 It has been suggested that supercooled liquids resist crystallization because of the existence of locally favored structures or frustration-limited domains that differ greatly from the packing in the thermodynamically most stable crystal.18−20 In the simplistic example of a liquid of Lennard-Jones particles, the locally favored structure is known to be a regular dodecahedron,21 which has 5-fold axes and therefore cannot tile space, and hence geometrically frustrates the nucleation of a crystal. It is tempting to suggest a link between such locally favored structures and LLTs; however, nothing is known about the actual local molecular packing associated with them except in simple cases.22

Here we will present comprehensive new data using various forms of spectroscopy and microscopy on the crystallization, supercooling, and LLT in triphenyl phosphite (TPP). Our results rule out that the transition in the supercooled liquid is due to the formation of nanocrystals in an otherwise untransformed phase and unequivocally establish that it is a true LLT between two amorphous states. A new crystal polymorph of TPP was discovered, and its crystal structure determined. Using its spectroscopic signature, it was established that the locally favored structure in the supercooled liquid has a molecular packing similar to this metastable polymorph. Finally, we established that the LLT in TPP is associated with a change in local packing in the liquid similar to the change in molecular packing between the two crystal polymorphs. However, we find that the LLT leads to a glassy state that kinetically frustrates the formation of the thermodynamically most stable crystal polymorph. Therefore, the polyamorphism in TPP mirrors its crystal polymorphism. This indicates LLTs are more widely associated with polymorphism and provides an avenue for a better physical understanding of LLTs and for finding new examples of LLTs.

Results

Crystallinity and Crystal Polymorphs

Our experiments were carried out by quenching room-temperature liquid TPP to a given quench temperature, holding that temperature for a given duration, and observation using phase contrast or polarization microscopy and IR and Raman spectroscopy and imaging. For Raman or IR imaging experiments, the temperature is dropped to the glass-transition temperature23 of 203 K to arrest all dynamics, allowing images to be collected at a leisurely rate. (Experimental details are provided in the Supporting Information.)

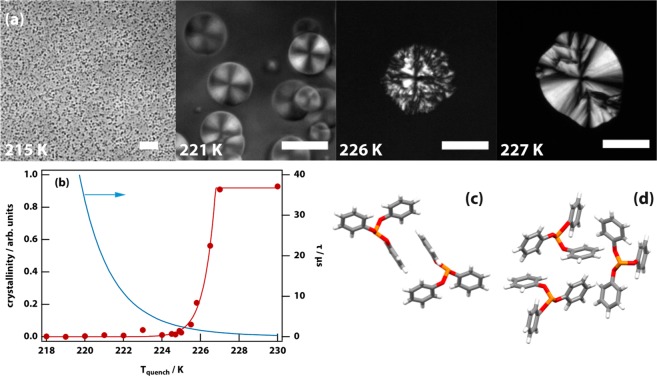
The LLT in TPP has been studied previously using microscopy, and the observations here (see Figure 1(a)) are consistent with previous work.12,13,23 The thermodynamically stable crystalline phase of TPP has a melting temperature of Tm = 298 K, and the liquid is readily supercooled. On quenching the samples to temperatures in the range 216–226 K, TPP undergoes an LLT from the high-temperature liquid 1 by nucleating droplets of liquid 2 (also sometimes referred to as the glacial phase11), which continue to grow until the entire sample is converted to the new phase. Below 216 K, but above the liquid 1 glass transition at 203 K, the LLT proceeds by spinodal decomposition. The LLT becomes progressively slower for lower quench temperatures as the viscosity increases.

Figure 1.

Figure 1

Open in a new tab

Microscopy of the liquid–liquid transition (LLT) in triphenyl phosphite (TPP) was used to determine the degree of crystallinity and to discover a new crystal polymorph. (a) Microscopy images of the formation of the liquid 2 phase of TPP at different quench temperatures. The phase-contrast image taken at 215 K shows high probability nucleation. The remaining polarization-microscopy images show the transition proceeding by nucleation and growth. A faint Maltese cross visible at 221 K indicates weak long-range ordering. The scale bar is 50 μm. (b) Liquid 2 droplet crystallinity as a function of quench temperature (red disks, the red line is a guide to the eye). The brightness of the droplet relative to the surrounding untransformed liquid under crossed polarizers is a proxy for crystallinity. Above ∼225.5 K the crystallinity shoots up, indicating that the droplet is composed largely or entirely of crystalline TPP. Droplet size varies inversely with quench temperature, and droplets <217 K are too small to be measured reliably; see (a). Also shown is a Vogel–Fulcher–Tammann fit to the experimentally determined relaxation time in liquid 1 (blue line).25 (c) The molecular packing in the new crystal polymorph (crystal 1) exhibits parallel π-stacking of the phenoxy rings. (d) In contrast, the packing in the thermodynamically most stable crystal polymorph (crystal 2) exhibits T-shaped π-stacking.

It was previously observed that the droplets of liquid 2 displayed a faint Maltese cross under polarization microscopy, suggesting contamination with crystalline TPP.24 Hence, we carried out a systematic study of the degree of crystallinity in the liquid 2 droplets as a function of quench temperature. Figure 1(b) shows the degree of crystallinity as determined using the contrast observed under polarization microscopy (normalized with the result at 230 K where the droplets are fully crystalline, see Figure 1(a)). The degree of crystallinity is very small (<2%) at low temperature but rapidly rises to 100% at 226 K. Also shown in Figure 1(b) is a Vogel–Fulcher–Tammann fit (T0 = 186 K) to the relaxation time of liquid 1 determined experimentally using dielectric relaxation spectroscopy.25

In the interval 227–260 K crystallization occurs in the form of spherulitic growth as seen previously. However, here two types of growth pattern were observed: a regular smooth spherulite with a clear Maltese cross vs an irregular multicolored spherulite (see Supplementary Figure 1), suggesting two crystal polymorphs. It was determined that the irregular spherulitic growth of (what we will refer to as) crystal 1 dominates at T > 239 K, while the regular spherulitic growth of crystal 2 dominates at 226 K < T < 239 K (see Supplementary Figure 1). While crystal 2 melts at Tm = 298 K, crystal 1 melts at Tm = 289 K, confirming these are crystal polymorphs. Crystal 1 melts to form the supercooled liquid; it does not convert to the thermodynamically most stable crystal 2.

Single-crystal X-ray diffraction (XRD) was carried out to determine that crystal 2 is the well-known thermodynamically most stable polymorph,26 while crystal 1 is a new polymorph different from a third polymorph (crystal 3) described previously.27Figure 1(c) and (d) show the difference in packing in crystal 1 and 2. In the well-known crystal 2 (Figure 1(d)), TPP molecules π-stack in a T-shape fashion, while in the new crystal 1 they parallel π-stack (see also Supplementary Figures 2 and 3).

Vibrational Spectroscopy

Time-resolved infrared experiments (on a minute to hour time scale) were carried out to follow structural changes during a quench, leading to a LLT or crystallization. The spectrum of liquid 1 did not change during the quench itself. Interesting changes during the transitions are seen around 860 cm–1, but experimental limitations do not allow meaningful analysis. Hence, the main range of interest was 1150–1250 cm–1, where significant changes are observed during the transitions.

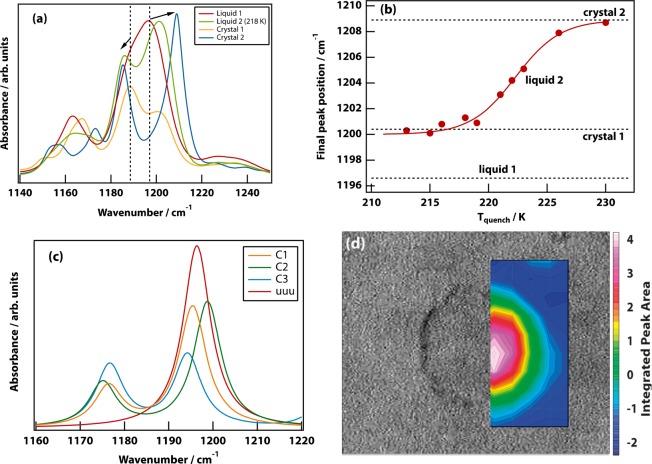
Four canonical spectra are shown in Figure 2(a). In liquid 1, a large peak with a shoulder is seen centered on 1197 cm–1. After the LLT, in liquid 2, the shoulder has shifted to slightly lower frequency, while the main peak has split off and shifted to much higher frequency. The magnitude of the latter shift depends on the quench temperature (see Figure 2(b)), with the greatest shift seen at the highest temperature (226 K). The spectrum of crystal 2 has a larger shift still. Finally, the spectrum of crystal 1 is characterized by a reduction in amplitude of the main peak.

Figure 2.

Figure 2

Open in a new tab

The infrared spectrum can be used as a proxy for the local molecular packing in the liquid or crystal. (a) Infrared spectra of liquid 1, liquid 2, crystal 1, and crystal 2 in the 1140–1250 cm–1 range. Liquid 1 shows a band with an intense peak at 1197 cm–1 and a shoulder at 1188.5 cm–1. During the LLT from liquid 1 to 2, one observes increased splitting of this band, which becomes even more pronounced in crystal 2. On the formation of crystal 1, the spectrum narrows, the peaks change intensity, while the shoulder remains in the same position as in liquid 1. (b) The final position of the intense peak is plotted as a function of quench temperature and is also shown (dotted lines) for liquid 1, crystal 1, and crystal 2. The data are fit to a sigmoid function shown as a solid line. (c) Normal-mode spectra for crystals 1, 2, and 3, as well as the uuu configuration of TPP. (d) Infrared image overlaying a bright field image of a droplet of liquid 2 produced at a quench temperature of 224 K. The color scale corresponds to the integrated area of the main peak in the interval 1200–1215 cm–1. Point spectra can be found in the SI, which match the bulk infrared measurements of liquid 1 and liquid 2.

In the time-resolved spectra (see Supplementary Figures 4, 5, and 6) it is clear that each transition (both LLT and crystallization) has associated and unique isosbestic points. These time-resolved experiments showed no perceptible changes in the liquid 2 spectrum for at least 10 h after the completion of the LLT, which is characteristic of a glass.

DFT normal mode calculations show (Figure 2(c)) that the bands around 1200 cm–1 are due to P–O–C bend vibrations that are sensitive to the molecular conformation. The low-energy conformers (in the single-molecule DFT calculations, which do not incorporate the effects of packing) all have two phenyl rings pointing up and one of the rings pointing down with respect to the phosphorus atom (uud). This is the conformation found in all three crystal polymorphs. The conformer from crystal 3 is thermodynamically most stable; however, the conformers from crystals 1 and 2 lie within just 3 kJ mol–1 (see Supplementary Table 1). The uud arrangement of the rings gives rise to a split band with the degree of splitting and intensities dependent on the exact conformation. By contrast, a uuu conformer, in which all three phenyl rings are pointing up, gives rise to a single vibrational peak for the P–O–C bend.

From these results, it can be concluded that liquid 1—having the smallest splitting of the bands around 1200 cm–1—is a uud conformer with predominantly crystal-1-like packing. Liquid 2 on the other hand—having the largest splitting—has the uud conformer with predominant crystal-2-like packing.

Infrared imaging experiments were carried out (Figure 2(d)) in the same spectral region, showing that the spectral changes are strictly confined to the growing droplets of liquid 2 rather than being a gradual change of the entire sample. This is consistent with the isosbestic points seen in the time-resolved infrared spectra.

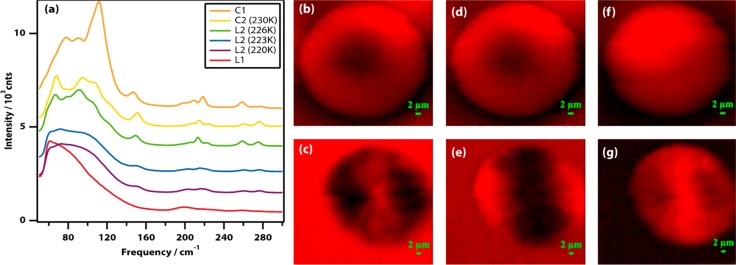
Confocal Raman spectroscopy was used to examine the low-frequency part of the vibrational spectrum, where one expects to observe phonon modes in the presence of crystals. Figure 3(a) shows Raman spectra taken inside the nucleating droplets of liquid 2 and the spherulites of crystals 1 and 2 (see also Supplementary Figure 7). Liquid 1 has a low-frequency spectrum typical of organic liquids28,29 with a smooth band due to molecular librations peaking at 60 cm–1 (2 THz), as confirmed by optical Kerr-effect spectroscopy (Supplementary Figures 8 and 9). Liquid 2 (quenched at 220 and 223 K) also has a smooth spectrum characteristic of a liquid peaking at a surprisingly high frequency of 105 cm–1 (3.5 THz) characteristic of relatively strongly interacting liquids. The spectrum at 226 K is starting to display a lot more structure and is starting to resemble the spectrum of crystal 2 at 230 K. The spectra of both crystals 1 and 2 display significant fine structure due to phonon modes associated with crystals.

Figure 3.

Figure 3

Open in a new tab

Raman spectroscopy and imaging in the low-frequency region can be used to determine the presence or absence of spherulitic crystal growth. (a) Raman spectra of liquid 1, liquid 2 (quenched at 220, 223, and 226 K), crystal 2 (230 K), and crystal 1. The traces have been displaced vertically for clarity. (b–g) Raman images of liquid 2 droplets in the spectral regions 65–73 (b, c), 85–90 (d, e), and 145–156 (f, g) cm–1 made by quenching to 220 K (b, d, f) and 226 K (c, e, g).

To confirm the conclusions that can be drawn from the spectra, confocal Raman imaging experiments were carried out. Spherulitic growth inevitably leads to alignment of the constituent nano/microcrystals30 and therefore to spatial anisotropy in the Raman intensity of phonon bands. As can be seen in Figure 3(b), (d), and (f), anisotropy is not observed in droplets of liquid 2 quenched at 220 K (nor at 223 K, not shown), but clear anisotropy is seen in Figure 3(c), (e), and (g) in droplets quenched at 226 K, demonstrating that the latter are mostly crystalline and spherulitic in nature.

Discussion

Nature of the Liquid–Liquid Transition

There is considerable discussion on whether the LLT is a real transition12,23,31−34 or instead the arrested growth of nanocrystals.15,26,35,36 In this nanocrystal hypothesis, as the temperature is lowered, the probability for nucleation of crystal 2 increases; however, the viscosity also increases on approaching the glass transition temperature, resulting in “a heavily nucleated state composed of nanocrystals of the stable crystalline phase embedded in the matrix of non-transformed supercooled liquid”.14 The data presented here are inconsistent with such a nanocrystal hypothesis.

Microscopy shows the formation of a relatively small number of “droplets” below 226 K, with the numbers increasing as the quench temperature is lowered (Figure 1(a)). This observation is inconsistent with a high crystal-nucleation rate in the bulk liquid. However, it could be consistent with a high rate of secondary nucleation of new grains at the interface of existing (nano)crystals. This so-called growth front nucleation would lead to spherulitic growth.30 Polarization microscopy shows a sudden drop in crystallinity below 226 K inconsistent with the nanocrystal hypothesis as the viscosity of liquid 1 gradually increases following a Vogel–Fulcher–Tammann dependence on approaching Tg (Figure 1(b)).37 This result is consistent with previous X-ray and neutron scattering,31 NMR,32 and dielectric relaxation experiments.38 The low contrast Maltese cross pattern observed in the droplets generated below 226 K (low crystallinity) is inconsistent with spherulitic growth. However, the long-range order below 226 K must be due to the alignment of some micro/nanostructures on the growth front. The infrared spectra of liquid 1 and liquid 2 are distinct from those of crystal 1 and crystal 2 (Figure 2), with the states converting into each other as shown by the presence of multiple isosbestic points. This implies conversion between distinct (meta)stable states and is inconsistent with the nanocrystal hypothesis. The Raman spectra of liquid 1 and 2 and those of crystal 1 and 2 are also distinct (Figure 3(a)). The spectra of liquid 2 at 220 and 223 K are smooth, while that at 226 K has distinct narrow bands due to phonon modes. The Raman images in the phonon region are isotropic at 220 and 223 K, while they are anisotropic at 226 and 230 K, consistent with spherulitic growth at the higher temperatures only (Figure 3(b)). Thus, all these experimental results are only consistent with crystalline spherulitic growth at T ≥ 226 K and the formation of an amorphous phase below 226 K. This emphatically rules out the nanocrystal hypothesis.

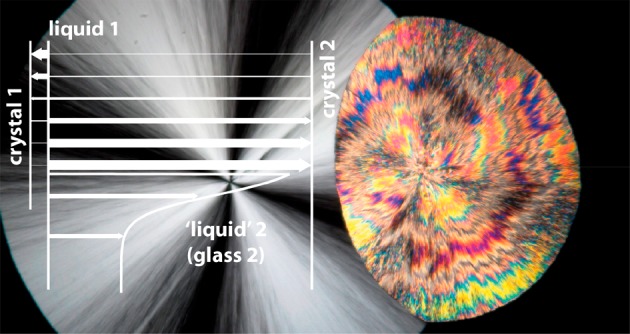
The data presented here allow us to gain insight into the molecular scale structures that give rise to the LLT and to describe the order parameter of the transition (see Figure 4). The infrared data and DFT calculations show that liquid 1 is most like crystal 1, while liquid 2 is more like crystal 2. On quenching in the liquid 1 region, the probability for nucleating a crystal increases on lowering the quench temperature as expected. However, for T > 239 K the metastable crystal 1 is most likely to nucleate, while for T < 239 K crystal 2 is most likely to nucleate. This strongly suggests that the crystal-1-like infrared spectrum we observe in liquid 1 reflects the locally favored structure that frustrates the formation of the thermodynamically most favored state (crystal 2). This locally favored structure involves parallel π-stacking of the phenoxy rings (indicated as simply “π” in Figure 4), while crystal 2 requires T-shaped π-stacking (indicated as “τ” in Figure 4). Thus, in simplistic terms, the order parameter of the LLT is the π to τ transition in local packing (as shown in Figure 4).

Figure 4.

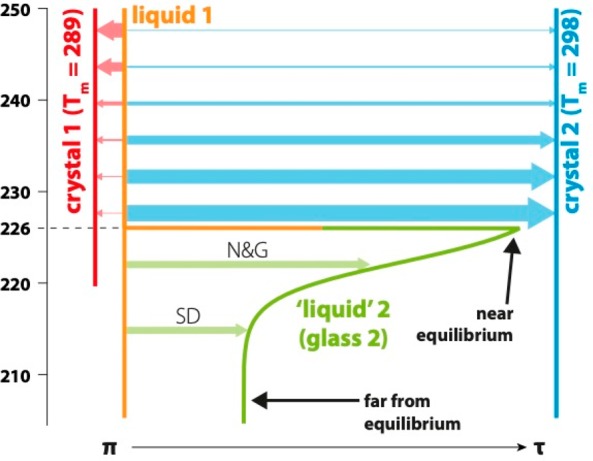
Figure 4

Open in a new tab

Cartoon depicting the order parameter of the LLT and crystallization in TPP. The horizontal axis is the order parameter, which goes from parallel π-stacking of the phenoxy rings on neighboring molecules on the left (π) to T-shaped stacking on the right (τ). The vertical axis represents the quenching temperature. Solid lines show the four relevant forms of TPP (liquid 1, liquid 2, crystal 1, and crystal 2), and colored arrows the transitions between them, with the thickness of the arrow indicating the relative probability of a transition. Liquid 2 is formed from liquid 1 through nucleation and growth (N&G) and spinodal decomposition (SD). Liquid 1 has a glass-transition temperature Tg,1 ≅ 203 K,23 while that of liquid 2 is Tg,2 ≅ 226 K.

For quench temperatures below 226 K, the crystallinity discontinuously drops from 100% to <2% (Figure 1(b)) even though the liquid 1 viscosity is continuous and there is no sign of having reached the homogeneous nucleation temperature.39,40 This discontinuous behavior is fully consistent with an LLT occurring below 226 K. However, the time-resolved infrared spectroscopy experiments (Figure 1(a), Supplementary Figures 4, 5, and 6 and the stability of liquid 2 for as much as 10 h) show that liquid 2 is, in fact, a glass. This conclusion may appear at odds with recent dielectric relaxation experiments23 that purport to show α-relaxation and therefore liquid-like behavior in liquid 2. However, in that work the relaxation process can only be fitted to a Cole–Cole function with a small stretching parameter (β ≈ 0.36) implying significant inhomogeneity. Therefore, this relaxation peak cannot be due to α-relaxation41 and must be due to β-relaxation or a fast β-process.42 This means that either the α-relaxation peak is invisible (unlikely as it would require stable clusters in which the dipole moment is somehow canceled) or liquid 2 is a glass. The latter is consistent with the data presented here.

The quench-temperature dependence of the infrared spectra (Figure 2(b)) shows that this liquid 2 glass has a structure somewhere in between liquid 1 and crystal 2. This temperature dependence is characteristic of a glass: at the lowest quench temperatures glassy liquid 2 is closest to liquid 1 (more π-like and most out of equilibrium) and becomes closer to crystal 2 (more τ-like and closer to equilibrium) as the temperature approaches 226 K. Thus, we conclude that the glass transition temperature of liquid 2 is Tg,2 = 226 K.

Outlook

A debate has been raging for decades on whether the glacial phase in TPP represents a true LLT or aborted crystallization. The experiments presented here have allowed us to demonstrate that both points of view are correct at the same time. There is an LLT in TPP that starts below 226 K as evidenced by the sudden changes in properties that we have shown are inconsistent with (nano)crystals. This LLT has all the requisite physical properties of a first-order phase transition including nucleation, spinodal decomposition, and reversibility.33 However, the new phase, liquid 2, is a metastable glass in between liquid 1 and crystal 2 that kinetically frustrates the formation of the thermodynamically most stable state, crystal 2. This is very similar in general nature to the LLT in n-butanol as described recently8 as well as the LLT in germanium at 7.9 GPa,2 suggesting this is a general principle behind LLTs. It also explains the recently observed drastic enhancement of crystal nucleation caused by the LLT.43

We have also been able to show that the LLT in TPP is caused by competition between local liquid structures that mirror the structures of two crystal polymorphs. The local structure in liquid 1 is most like that in metastable polymorph crystal 1 (parallel π-stacked), which acts as an effective locally favored structure geometrically frustrating the formation of the thermodynamically most stable crystal 2. At sufficiently low temperature, T-shape π-stacking becomes thermodynamically favored over parallel π-stacking even in the liquid (giving rise to the LLT), but by then the temperature is so low that liquid 2 is already a glass, thereby kinetically frustrating crystallization.

There are a number of other examples of LLTs or polyamorphic transitions where a link with polymorphism is suggested. For example, the pressure-induced polyamorphic transition in amorphous silica has been associated with a change in the structure from tetrahedral to octahedral coordination.18 This is mirrored by corresponding polymorphs, α-quartz at low pressure vs stishovite and seifertite at high pressure. Another example is the LLT in germanium and silicon, which are associated with the diamond cubic and β-tin polymorphs.2,18 The results presented here and these previous examples suggest that polymorphism as a cause for polyamorphism is also a general principle behind LLTs.

These new insights based on firm experimental results may underpin a new phase of research into the physical basis of LLTs in molecular liquids, their more general occurrence, and more generally into supercooling and vitrification, and the interplay of geometric and kinetic frustration. It may also contribute to a better understanding of the LLT in water,6 which is known to have many crystal polymorphs. Liquid–liquid phase separation of aqueous solutions of proteins and nucleic acids in vitro and in vivo has witnessed a lot of interest in recent years.44−46 Some of the insights gained here will apply to these systems too and play a role in protein crystallization.

Acknowledgments

We thank the Engineering and Physical Sciences Research Council (EPSRC) for support through grants EP/J004812/1, EP/J004790/1, EP/J009733/1, EP/J014478/1, and EP/N007417/1. This work was partly funded by Leverhulme Trust Research Project Grant RPG-2018-350 and received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 832703). We thank the Diamond Light Source for access to beamline B22 (proposal number SM20351). We also greatly acknowledge discussions with Richard Buchner (University of Regensburg) regarding the interpretation of the dielectric relaxation peak in liquid 2 of triphenyl phosphite.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c01712.

  • Materials and methods, supplementary references, supplementary figures (PDF)

  • Crystallographic data (CIF)

The authors declare no competing financial interest.

Notes

The data that support the findings of this study are available in Enlighten: Research Data Repository (University of Glasgow) with the identifier: http://dx.doi.org/10.5525/gla.researchdata.993. CCDC 1920486 contains the supplementary crystallographic data for crystal 1 and can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/.

Supplementary Material

ja0c01712_si_001.pdf (3.4MB, pdf)
ja0c01712_si_002.cif (122KB, cif)

References

  1. Aasland S.; Mcmillan P. Density-driven liquid-liquid phase-separation in the system Al2O3-Y2O3. Nature 1994, 369, 633–636. 10.1038/369633a0. [DOI] [Google Scholar]
  2. Bhat M. H.; Angell C. A.; Molinero V.; Soignard E.; Solomon V. C.; Sastry S.; Yarger J. L. Vitrification of a monatomic metallic liquid. Nature 2007, 448, 787–790. 10.1038/nature06044. [DOI] [PubMed] [Google Scholar]
  3. Mcmillan P.; Wilson M.; Daisenberger D.; Machon D. A density-driven phase transition between semiconducting and metallic polyamorphs of silicon. Nat. Mater. 2005, 4, 680–684. 10.1038/nmat1458. [DOI] [PubMed] [Google Scholar]
  4. Katayama Y.; Mizutani T.; Utsumi W.; Shimomura O.; Yamakata M.; Funakoshi K. A first-order liquid-liquid phase transition in phosphorus. Nature 2000, 403, 170–173. 10.1038/35003143. [DOI] [PubMed] [Google Scholar]
  5. Mishima O.; Stanley H. E. The relationship between liquid, supercooled and glassy water. Nature 1998, 396, 329–335. 10.1038/24540. [DOI] [Google Scholar]
  6. Gallo P.; Amann-Winkel K.; Angell C. A.; Anisimov M. A.; Caupin F.; Chakravarty C.; Lascaris E.; Loerting T.; Panagiotopoulos A. Z.; Russo J.; Sellberg J. A.; Stanley H. E.; Tanaka H.; Vega C.; Xu L.; Pettersson L. G. M. Water: A Tale of Two Liquids. Chem. Rev. 2016, 116, 7463–7500. 10.1021/acs.chemrev.5b00750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kurita R.; Tanaka H. On the abundance and general nature of the liquid-liquid phase transition in molecular systems. J. Phys.: Condens. Matter 2005, 17, L293–L302. 10.1088/0953-8984/17/27/L01. [DOI] [Google Scholar]
  8. Syme C. D.; Mosses J.; González Jiménez M.; Shebanova O.; Walton F.; Wynne K. Frustration of crystallisation by a liquid–crystal phase. Sci. Rep. 2017, 7, 42439. 10.1038/srep42439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Tang W.; Perepezko J. H. Polyamorphism and liquid-liquid transformations in D-mannitol. J. Chem. Phys. 2018, 149, 074505–9. 10.1063/1.5041757. [DOI] [PubMed] [Google Scholar]
  10. Zhu M.; Yu L. Polyamorphism of D-mannitol. J. Chem. Phys. 2017, 146, 244503–6. 10.1063/1.4989961. [DOI] [PubMed] [Google Scholar]
  11. Cohen I.; Ha A.; Zhao X.; Lee M.; Fischer T.; Strouse M. J.; Kivelson D. A Low-Temperature Amorphous Phase in a Fragile Glass-Forming Substance. J. Phys. Chem. 1996, 100, 8518–8526. 10.1021/jp953785h. [DOI] [Google Scholar]
  12. Kurita R.; Tanaka H. Critical-like phenomena associated with liquid-liquid transition in a molecular liquid. Science 2004, 306, 845–848. 10.1126/science.1103073. [DOI] [PubMed] [Google Scholar]
  13. Mosses J.; Syme C. D.; Wynne K. Order Parameter of the Liquid–Liquid Transition in a Molecular Liquid. J. Phys. Chem. Lett. 2015, 6, 38–43. 10.1021/jz5022763. [DOI] [PubMed] [Google Scholar]
  14. Hedoux A.; Guinet Y.; Derollez P.; Hernandez O.; Lefort R.; Descamps M. A contribution to the understanding of the polyamorphism situation in triphenyl phosphite. Phys. Chem. Chem. Phys. 2004, 6, 3192–3199. 10.1039/B401262C. [DOI] [Google Scholar]
  15. Tarnacka M.; Madejczyk O.; Dulski M.; Maksym P.; Kaminski K.; Paluch M. Is There a Liquid–Liquid Phase Transition in Confined Triphenyl Phosphite?. J. Phys. Chem. C 2017, 121, 19442–19450. 10.1021/acs.jpcc.7b05336. [DOI] [Google Scholar]
  16. Demirjian B. G.; Dosseh G.; Chauty A.; Ferrer M.-L.; Morineau D.; Lawrence C.; Takeda K.; Kivelson D.; Brown S. Metastable Solid Phase at the Crystalline-Amorphous Border: The Glacial Phase of Triphenyl Phosphite. J. Phys. Chem. B 2001, 105, 2107–2116. 10.1021/jp000765t. [DOI] [Google Scholar]
  17. Tarjus G.; Alba-Simionesco C.; Grousson M.; Viot P.; Kivelson D. Locally preferred structure and frustration in glass-forming liquids: a clue to polyamorphism?. J. Phys.: Condens. Matter 2003, 15, S1077–S1084. 10.1088/0953-8984/15/11/329. [DOI] [Google Scholar]
  18. Mcmillan P. Polyamorphic transformations in liquids and glasses. J. Mater. Chem. 2004, 14, 1506–1512. 10.1039/b401308p. [DOI] [Google Scholar]
  19. Kivelson D.; Kivelson S. A.; Zhao X.; Nussinov Z.; Tarjus G. A thermodynamic theory of supercooled liquids. Phys. A 1995, 219, 27–38. 10.1016/0378-4371(95)00140-3. [DOI] [Google Scholar]
  20. Machon D.; Meersman F.; Wilding M. C.; Wilson M.; McMillan P. F. Pressure-induced amorphization and polyamorphism: Inorganic and biochemical systems. Prog. Mater. Sci. 2014, 61, 216–282. 10.1016/j.pmatsci.2013.12.002. [DOI] [Google Scholar]
  21. Frank F. C. Supercooling of liquids. Proc. Royal Soc. London A 1952, 215, 43–46. 10.1098/rspa.1952.0194. [DOI] [Google Scholar]
  22. Hirata A.; Guan P.; Fujita T.; Hirotsu Y.; Inoue A.; Yavari A. R.; Sakurai T.; Chen M. Direct observation of local atomic order in a metallic glass. Nat. Mater. 2011, 10, 28–33. 10.1038/nmat2897. [DOI] [PubMed] [Google Scholar]
  23. Murata K.-I.; Tanaka H. Link between molecular mobility and order parameter during liquid-liquid transition of a molecular liquid. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 7176–7185. 10.1073/pnas.1822016116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kobayashi M.; Shimizu R.; Tanaka H. Time-Resolved Light Scattering Study on the Kinetics of the Liquid–Liquid Transition in Triphenyl Phosphite. J. Phys. Chem. B 2015, 119, 11768–11782. 10.1021/acs.jpcb.5b05402. [DOI] [PubMed] [Google Scholar]
  25. Schiener B.; Loidl A.; Chamberlin R. V.; Bohmer R. Dielectric study of supercooled triphenylphosphite and butyronitrile: Comparison with a mesoscopic model. J. Mol. Liq. 1996, 69, 243–251. 10.1016/S0167-7322(96)90018-5. [DOI] [Google Scholar]
  26. Derollez P.; Hernandez O.; Hedoux A.; Guinet Y.; Masson O.; Lefebvre J.; Descamps M. Structural and microstructural description of the glacial state in triphenyl phosphite from powder synchrotron X-ray diffraction data and Raman scattering investigations. J. Mol. Struct. 2004, 694, 131–138. 10.1016/j.molstruc.2004.03.033. [DOI] [Google Scholar]
  27. Golovanov D. G.; Lyssenko K. A.; Antipin M. Y.; Vygodskii Y. S.; Lozinskaya E. I.; Shaplov A. S. Long-awaited polymorphic modification of triphenyl phosphite. CrystEngComm 2005, 7, 465–468. 10.1039/b505052a. [DOI] [Google Scholar]
  28. Reichenbach J.; Wynne K. Frustration vs. prenucleation: understanding the surprising stability of supersaturated sodium thiosulfate solutions. J. Phys. Chem. B 2018, 122, 7590–7596. 10.1021/acs.jpcb.8b04112. [DOI] [PubMed] [Google Scholar]
  29. Reichenbach J.; Ruddell S. A.; González Jiménez M.; Lemes J.; Turton D. A.; France D. J.; Wynne K. Phonon-like Hydrogen-Bond Modes in Protic Ionic Liquids. J. Am. Chem. Soc. 2017, 139, 7160–7163. 10.1021/jacs.7b03036. [DOI] [PubMed] [Google Scholar]
  30. Gránásy L.; Pusztai T.; Tegze G.; Warren J.; Douglas J. Growth and form of spherulites. Phys. Rev. E 2005, 72, 011605 10.1103/PhysRevE.72.011605. [DOI] [PubMed] [Google Scholar]
  31. Mei Q.; Ghalsasi P.; Benmore C. J.; Yarger J. L. The Local Structure of Triphenyl Phosphite Studied Using Spallation Neutron and High-Energy X-ray Diffraction. J. Phys. Chem. B 2004, 108, 20076–20082. 10.1021/jp046762o. [DOI] [Google Scholar]
  32. Senker J.; Sehnert J.; Correll S. Microscopic description of the polyamorphic phases of triphenyl phosphite by means of multidimensional solid-state NMR spectroscopy. J. Am. Chem. Soc. 2005, 127, 337–349. 10.1021/ja046602q. [DOI] [PubMed] [Google Scholar]
  33. Kobayashi M.; Tanaka H. The reversibility and first-order nature of liquid-liquid transition in a molecular liquid. Nat. Commun. 2016, 7, 1–8. 10.1038/ncomms13438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Murata K.-I.; Tanaka H. Impact of surface roughness on liquid-liquid transition. Sci. Adv. 2017, 3, e1602209 10.1126/sciadv.1602209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Hedoux A.; Guinet Y.; Derollez P.; Hernandez O.; Paccou L.; Descamps M. Micro-structural investigations in the glacial state of triphenyl phosphite. J. Non-Cryst. Solids 2006, 352, 4994–5000. 10.1016/j.jnoncrysol.2006.02.155. [DOI] [Google Scholar]
  36. Shmytko I. M.; Ramos M. A. Structural and thermodynamic studies of n-butanol. J. Phys.: Condens. Matter 2010, 22, 195102. 10.1088/0953-8984/22/19/195102. [DOI] [PubMed] [Google Scholar]
  37. Wiedersich J.; Kudlik A.; Gottwald J.; Benini G.; Roggatz I.; Rossler E. On Polyamorphism of Triphenyl Phosphite. J. Phys. Chem. B 1997, 101, 5800–5803. 10.1021/jp970848i. [DOI] [Google Scholar]
  38. Mizukami M.; Kobashi K.; Hanaya M.; Oguni M. Presence of Two Freezing-In Processes Concerning α-Glass Transition in the New Liquid Phase of Triphenyl Phosphite and Its Consistency with “Cluster Structure” and “Intracluster Rearrangement for α Process” Models. J. Phys. Chem. B 1999, 103, 4078–4088. 10.1021/jp983926q. [DOI] [Google Scholar]
  39. Gebauer D.; Wolf S. E. Designing Solid Materials from Their Solute State: A Shift in Paradigms toward a Holistic Approach in Functional Materials Chemistry. J. Am. Chem. Soc. 2019, 141, 4490–4504. 10.1021/jacs.8b13231. [DOI] [PubMed] [Google Scholar]
  40. Davey R. J.; Schroeder S. L. M.; ter Horst J. H. Nucleation of organic crystals--a molecular perspective. Angew. Chem., Int. Ed. 2013, 52, 2166–2179. 10.1002/anie.201204824. [DOI] [PubMed] [Google Scholar]
  41. Turton D. A.; Hunger J.; Stoppa A.; Hefter G.; Thoman A.; Walther M.; Buchner R.; Wynne K. Dynamics of imidazolium ionic liquids from a combined dielectric relaxation and optical Kerr effect study: evidence for mesoscopic aggregation. J. Am. Chem. Soc. 2009, 131, 11140–11146. 10.1021/ja903315v. [DOI] [PubMed] [Google Scholar]
  42. Tanaka H. Two-order-parameter model of the liquid–glass transition. III. Universal patterns of relaxations in glass-forming liquids. J. Non-Cryst. Solids 2005, 351, 3396–3413. 10.1016/j.jnoncrysol.2005.09.010. [DOI] [Google Scholar]
  43. Kurita R.; Tanaka H. Drastic enhancement of crystal nucleation in a molecular liquid by its liquid–liquid transition. Proc. Natl. Acad. Sci. U. S. A. 2019, 114, 201909660. 10.1073/pnas.1909660116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shin Y.; Brangwynne C. P. Liquid phase condensation in cell physiology and disease. Science 2017, 357, eaaf4382–13. 10.1126/science.aaf4382. [DOI] [PubMed] [Google Scholar]
  45. Ianiro A.; Wu H.; Rijt M. M. J.; Vena M. P.; Keizer A. D. A.; Esteves A. C. C.; Tuinier R.; Friedrich H.; Sommerdijk N. A. J. M.; Patterson J. P. Liquid–liquid phase separation during amphiphilic self-assembly. Nat. Chem. 2019, 268, 1–9. 10.1038/s41557-019-0210-4. [DOI] [PubMed] [Google Scholar]
  46. Le Ferrand H.; Duchamp M.; Gabryelczyk B.; Cai H.; Miserez A. Time-Resolved Observations of Liquid–Liquid Phase Separation at the Nanoscale Using in Situ Liquid Transmission Electron Microscopy. J. Am. Chem. Soc. 2019, 141, 7202–7210. 10.1021/jacs.9b03083. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja0c01712_si_001.pdf (3.4MB, pdf)
ja0c01712_si_002.cif (122KB, cif)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES