Balancing Multiple Goals and Making It Work for Materials Research

We face decisions every day where we balance competing objectives. For example, “Do I have time to shop and get to work in 40 minutes?” We try it one day and find out that we need at least 50 minutes to do both. We take this information, learn what works best, and refine such decision-making throughout our life. However, the emulation of a lifelong learning process is a major challenge for an artificial learning approach. The complex issue of handling multiple objectives is addressed by Janet et al. in this issue of ACS Central Science.¹ It is all the more impressive then to appreciate that our brain quickly manages this rationalization of multiple objectives using about 15 W. Compare that to IBM’s supercomputer Watson, which required about 85,000 W and 90 servers to defeat human contestants on Jeopardy.

Scientific problems in chemistry and engineering invariably require the optimization of multiple objectives. For example, in the solution processing of hybrid organic–inorganic perovskites, we effectively balance solubilizing a salt against our desire to use a green solvent, or favor components with greater stability. These choices affect the optimal choice of the material’s composition. Similarly, drug discovery searches look for molecules that are maximally potent, but minimally toxic. Artificial intelligence (AI) tools are being developed to satisfy one objective, e.g., to optimize the choice of solvent via machine learning tools such as Bayesian optimization in situations where data are scarce and costly.² Satisfying more than one objective at a time has received far less attention, with a notable example by Haghanifar et al.³ using Bayesian optimization. Their goal was to emulate the glasswing butterfly’s ability to exhibit high antifogging capabilities and transmission with low haze.

In this issue of ACS Central Science, we see a fine example of multiobjective optimization in the paper by Kulik and co-workers, which takes a new approach to encoding the physical data. An interesting outcome emerged from their paper, namely, that the underlying Gaussian process can be superseded by a suitably trained artificial neural network (ANN) to handle the multiobjective prediction. The authors provide a joint prediction via a “black box” ANN rather than assuming independent variables (as in the glasswing case) or trying to understand the joint probability distribution of the problem at hand. The main issue is that, in each iteration, the system has to be “retrained.” This could be achieved fast and easily with a Bayesian Gaussian Process Regression. However, the system that uses ANN needs to be retrained in every iteration, which takes time. The design of a neural network involves important decisions such as how many nodes are used, how these are connected, choice of hyperparameters, etc. Changing the number of nodes, for instance, delivers different results. To make sense of these different results typically involves employing determination of the root mean squared error from a “hold out” set (not used to train the system). We might finesse the need for retraining each iteration using a Bayesian approach to train the next neural network point. As it stands, the approach taken by Janet et al. offers a fresh perspective, and it would be reasonable to imagine that the field will move toward adopting this sort of strategy.

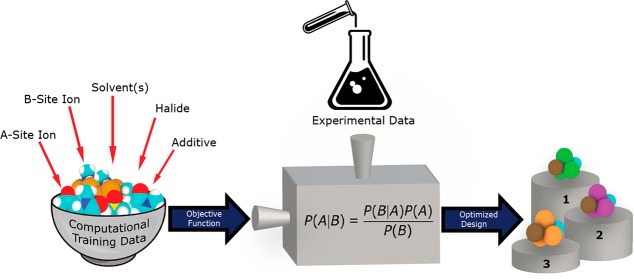
Looking ahead to the future of multiobjective approaches, we will increasingly have to consider the way we represent the objectives that drive the optimization (shown schematically in Figure 1). The approach to creating so-called “surrogate models” tends to involve considering the system’s true objective with a scalar noise term. However, the reality is that we frequently have to find an ersatz for the objective we want, since the true objective may be hard to measure or calculate in a cost-effective way. For example, calculating the enthalpy of solvation is a computationally expensive task that would make the use of a Bayesian optimization approach encumberingly costly. However, learning that a cheaply available experimental substitute for the enthalpy of solvation (like the Gutmann donor number or a fast computation of the Mayer bond order, a measure of dative bonding) correlates well with the enthalpy of solvation has a dramatic effect on our ability to use a machine learning approach in a computationally efficient manner.² Uncovering these substitutes for the true objectives will impart new richness in how we understand the underlying physics and chemistry of the process under investigation and how this relates to our understanding of composition (or processing)–structure–function relationships. Moving forward, our challenge will be to formalize this approach for model generation. Ultimately, the goal will be to automate, or partially automate, the determination of objective substitutes. This implies that we have to find a way to incorporate what domain experts know by intuition, or their long experience, of the mechanisms and likely the solutions drawn by inference from other experiences.

Figure 1.

Schematic representation of a Bayesian optimization-based pipeline from (left) the creation and selection of objective functions that are fed to the Bayesian optimization algorithm (middle) to produce ranked predictions of the best solutions to meet those objectives. Experimental sources of information are represented by the top middle icon.

There are a small number of multiobjective Bayesian optimization methods in the literature, and very few of them applied to chemical systems. However, the consideration of even two objectives simultaneously incurs a great need for data. The consideration of three objectives is essentially impossible if we attempt to calculate the entire “Pareto front.” We are starting to see the emergence of new methods^4,5 that avoid these constraints by understanding that only part of the Pareto front is likely to be important for performance. This, in turn, implies that we can determine how to prioritize which part(s), or subset, of the Pareto front is going to be the most important for optimization. Information to help this determination may come from experiments, or computation, or the expertise of a decision-maker.

Finally, in our human experience as decision-makers, we frequently make the determination that solving one objective is more important than solving another. For instance, recalling the drug discovery example mentioned above, practitioners prioritize low toxicity over efficacy. Methods are starting to emerge in which satisfying the constraint to favor one objective over another is used as a determiner for selecting those Pareto-optimal points.⁶ We are edging closer to being able to exploit the potential of AI to make complex decisions that lead to optimal, and, perhaps, disruptive solutions.