Modality-specific attention attenuates visual-tactile integration and recalibration effects by reducing prior expectations of a common source for vision and touch

Stephanie Badde; Karen T Navarro; Michael S Landy

doi:10.1016/j.cognition.2019.104170

. Author manuscript; available in PMC: 2020 Apr 24.

Published in final edited form as: Cognition. 2020 Feb 6;197:104170. doi: 10.1016/j.cognition.2019.104170

Modality-specific attention attenuates visual-tactile integration and recalibration effects by reducing prior expectations of a common source for vision and touch

Stephanie Badde ^a,^*,¹, Karen T Navarro ^b,¹, Michael S Landy ^a

PMCID: PMC7182122 NIHMSID: NIHMS1558008 PMID: 32036027

Abstract

At any moment in time, streams of information reach the brain through the different senses. Given this wealth of noisy information, it is essential that we select information of relevance - a function fulfilled by attention - and infer its causal structure to eventually take advantage of redundancies across the senses. Yet, the role of selective attention during causal inference in cross-modal perception is unknown. We tested experimentally whether the distribution of attention across vision and touch enhances cross-modal spatial integration (visual-tactile ventriloquism effect, Expt. 1) and recalibration (visual-tactile ventriloquism aftereffect, Expt. 2) compared to modality-specific attention, and then used causal-inference modeling to isolate the mechanisms behind the attentional modulation. In both experiments, we found stronger effects of vision on touch under distributed than under modality-specific attention. Model comparison confirmed that participants used Bayes-optimal causal inference to localize visual and tactile stimuli presented as part of a visual-tactile stimulus pair, whereas simultaneously collected unity judgments - indicating whether the visual-tactile pair was perceived as spatially-aligned - relied on a sub-optimal heuristic. The best-fitting model revealed that attention modulated sensory and cognitive components of causal inference. First, distributed attention led to an increase of sensory noise compared to selective attention toward one modality. Second, attending to both modalities strengthened the stimulus-independent expectation that the two signals belong together, the prior probability of a common source for vision and touch. Yet, only the increase in the expectation of vision and touch sharing a common source was able to explain the observed enhancement of visual-tactile integration and recalibration effects with distributed attention. In contrast, the change in sensory noise explained only a fraction of the observed enhancements, as its consequences vary with the overall level of noise and stimulus congruency. Increased sensory noise leads to enhanced integration effects for visual-tactile pairs with a large spatial discrepancy, but reduced integration effects for stimuli with a small or no cross-modal discrepancy. In sum, our study indicates a weak a priori association between visual and tactile spatial signals that can be strengthened by distributing attention across both modalities.

Keywords: Visual-tactile, Multisensory integration, Recalibration, Causal inference, Attention, Ventriloquism

1. Introduction

On their own, the senses provide only noisy and sometimes systematically distorted information. Yet, the different senses can support each other. Integration of information from different senses can improve the precision of sensory estimates and consistent discrepancies between the sensory signals can trigger recalibration of one sense by the other. To measure cross-modal integration and recalibration of spatial information, experimenters often induce an artificial discrepancy between the senses, for example, using an optical prism to shift the apparent visual location of a hand-held object (von Helmholtz, 1909). Cross-modal spatial integration leads to shifts in the perceived location of stimuli that are part of a cross-modal, spatially-discrepant stimulus pair. Spatial recalibration induces perceptual shifts of stimuli presented via a single modality after exposure to cross-modal stimulus pairs with a constant spatial discrepancy. These shifts are often called the ventriloquism effect and aftereffect, respectively, in analogy to the perceptual illusion that a puppeteer’s speech sounds appear to originate from the puppet’s mouth (Howard & Templeton, 1966; Pick, Warren, & Hay, 1969; Jack & Thurlow, 1973; Thurlow & Jack, 1973; Bertelson & Aschersleben, 1998; Lewald & Guski, 2003; reviewed in Bertelson & De Gelder, 2004; Chen & Vroomen, 2013). Ventriloquism-like shifts in cross-modal localization are not limited to pairings of visual and auditory stimuli: the perceived locations of auditory stimuli are shifted toward concurrently presented spatially discrepant tactile stimuli (Caclin, Soto-Faraco, Kingstone, & Spence, 2002; Bruns & Röder, 2010a, 2010b; Renzi et al., 2013) and the perceived locations of tactile stimuli are shifted toward concurrently presented visual stimuli (Pavani, Spence, & Driver, 2000; Spence & Driver, 2004; Samad & Shams, 2016). Also ventriloquism aftereffects are not limited to the visual-auditory domain (Radeau & Bertelson, 1974, 1977, 1978; Bermant & Welch, 1976; Bertelson & Radeau, 1981; Recanzone, 1998; Lewald, 2002; Frissen, Vroomen, de Gelder, & Bertelson, 2005; Bertelson, Frissen, Vroomen, & de Gelder, 2006; Kopco, Lin, Shinn-Cunningham, & Groh, 2009; Bruns, Liebnau, & Röder, 2011; Frissen, Vroomen, & de Gelder, 2012; Bruns & Röder, 2015; Zierul, Röder, Tempelmann, Bruns, & Noesselt, 2017; Bosen, Fleming, Allen, O’Neill, & Paige, 2017). Artificial shifts of visually perceived limb locations lead to subsequent changes of proprioceptive and motor space (von Helmholtz, 1909; Mather & Lackner, 1981; Kornheiser, 1976; Hay & Pick, 1966; Welch & Warren, 1980; van Beers, Wolpert, & Haggard, 2002; Redding & Wallace, 1996; Redding, Rossetti, & Wallace, 2005; Cressman & Henriques, 2009, 2010; Henriques & Cressman, 2012; Welch, 2013). Moreover, the spatial perception of tactile stimuli shifts after exposure to pairings with synchronous but spatially discrepant visual stimuli (Samad & Shams, 2018), whereas exposure to spatially discrepant audio-tactile stimulus pairs recalibrates auditory space (Bruns, Spence, & Röder, 2011).

During a ventriloquist’s performance, the perceived sound location will be fully shifted toward the puppet. The far higher spatial precision of vision as compared to audition results in complete capture of the auditory by the visual signal. Yet, when the spatial reliability of the visual stimulus is artificially degraded, the degree of influence each modality has on the perceived location depends on the relative reliability of the two sensory signals (Battaglia, Jacobs, & Aslin, 2003; Hairston et al., 2003; Alais & Burr, 2004; Charbonneau, Véronneau, Boudrias-Fournier, Lepore, & Collignon, 2013) as predicted by optimal cue integration (Landy, Maloney, Johnston, & Young, 1995; Yuille & Bülthoff, 1996; Trommershäuser, Körding, & Landy, 2011). In turn, the apparent dominance of vision over audition, proprioception, and touch in spatial recalibration matches the typically greater spatial reliability of vision (Welch & Warren, 1980) and task-dependent variations in visual and proprioceptive reliability are reflected in the direction of visual-proprioceptive spatial recalibration (van Beers et al., 2002).

Reliability-weighted cross-modal integration and recalibration leads to more precise sensory estimates, but only if the sensory signals provide corresponding information. If the signals do not correspond – usually because they stem from different sources – the sensory signals should be kept separate and should not prompt recalibration. Thus, the brain should perform causal inference to establish whether sensory signals from different modalities originate from the same source (Körding et al., 2007), and that inference should modulate integration and recalibration.

Causal inference takes two types of information into account: sensory data and prior knowledge (Körding et al., 2007; Sato, Toyoizumi, & Aihara, 2007; Wei & Körding, 2009; Wozny, Beierholm, & Shams, 2010; Rohe & Noppeney, 2015a; Gau & Noppeney, 2016). First, cross-modal signals with a large spatial (Gepshtein, Burge, Ernst, & Banks, 2005) or temporal discrepancy (Holmes & Spence, 2005; Parise & Ernst, 2016) are not integrated, because they are unlikely to share a common source (reviews in Alais, Newell, & Mamassian, 2010; Shams & Beierholm, 2010; Chen & Spence, 2017). Second, a priori knowledge about the origin of the sensory signals can impact causal inference. For example, knowledge that visual and haptic signals have a common source can promote integration even in the absence of spatial alignment between the signals (Helbig & Ernst, 2007), and knowledge about random discrepancies between two signals can reduce the strength of multisensory integration (Debats & Heuer, 2018). However, in most situations, explicit knowledge about the correspondence of the two current signals is unavailable and the brain must rely on expectations based on previous experience.

Another means to improve perception in the face of competing sensory signals is selective attention, the “differential processing of simultaneous sources of external information” (Johnston & Dark, 1986). Within one modality, selective attention to a spatial location, object, or perceptual feature improves perception in the focus of attention (Shinn-Cunningham, 2008; Carrasco, 2011), likely because it amplifies the neural responses to that signal and suppresses irrelevant responses (Desimone & Duncan, 1995; Kastner & Ungerleider, 2001; Gazzaley, Cooney, McEvoy, Knight, & D’Esposito, 2005). Yet, selective attention to a modality does not necessarily improve perception, because modality-specific attention counteracts cross-modal integration, which itself can be beneficial for perception. Evidence indicating that the distribution of attention across modalities enhances cross-modal integration comes from behavioral and neuroscientific studies (reviews in Talsma, Senkowski, Soto-Faraco, & Woldorff, 2010; Tang, Wu, & Shen, 2016). Visual-tactile integration, measured by the tap-flash illusion, is reduced when the task emphasizes only one of the modalities (Werkhoven, van Erp, & Philippi, 2009) and cross-modal congruency effects in visual-tactile pattern matching are weaker when participants attend to only one modality (Göschl, Engel, & Friese, 2014). Integration of visual-auditory stimulus pairs, measured either by means of multisensory enhancement effects in color discrimination (Mozolic, Hugenschmidt, Peiffer, & Laurienti, 2008) or by a change in event-related scalp potentials (Talsma, Doty, & Woldorff, 2007), even depended on distributed attention: cross-modal enhancements were only present when both modalities were attended. Thus, current evidence suggests that cross-modal integration is attenuated or even eliminated when participants attend to only one of the stimulus modalities. However, the mechanism behind these attentional modulations remains speculative. The focus of attention could affect either of the two types of information that govern causal inference – the sensory signals themselves and prior expectations about the shared source of the signals – or even change the way in which cross-modal information is processed.

In this paper, we present the results of two experiments involving visual and tactile cues for the estimation of spatial location. In both experiments we manipulate the focus of attention on each modality and measure the impact of distributed versus modality-specific attention on integration (Expt. 1) and recalibration (Expt. 2). We find that the distribution of attention across vision and touch is required to maximize both integration and recalibration. Subsequent modeling reveals an impact of attention on the participant’s expectation that the two signals share a common source and consequently provide corresponding information as well as on the reliability of the individual stimuli. However, model simulations also reveal that only the attention-induced change in the common-cause prior can explain the observed enhancements of visual-tactile integration and recalibration effects.

2. Expt. 1: Attention effects on the integration of vision and touch

In Expt. 1, we investigated whether visual-tactile spatial integration is sensitive to the attentional context. Participants were presented with visual-tactile stimulus pairs of variable spatial discrepancy. Visual-tactile ventriloquism, the indicator for the strength of integration effects, can be measured in two ways, either by means of localization shifts or by means of binary judgments about the unity or spatial alignment of the two stimuli. In general, unity judgments show a similar pattern to localization shifts (Wallace et al., 2004; Hairston et al., 2003; Rohe & Noppeney, 2015b). However, shifts in the perceived locations of two spatially discrepant stimuli do not always result in the observer misperceiving the two stimuli as spatially aligned. There can be substantial but incomplete shifts of perceived auditory location toward a concurrently presented visual stimulus even though the stimuli are perceived as spatially misaligned (Bertelson & Radeau, 1981; Körding et al., 2007; Wozny et al., 2010). Therefore, we measured visual-tactile ventriloquism based on both localization estimates and unity judgments.

We hypothesized that the integration of vision and touch would be affected by the focus of attention with larger effects when attention was distributed across both modalities. In every trial, participants indicated the location of one modality, either the felt or the viewed stimulus. The response-relevant modality was either cued before the stimulus pair was presented, allowing participants to focus attention on one modality (modality-specific attention), or after the stimulus pair had been presented, encouraging participants to attend to both modalities (distributed attention).

2.1. Methods

2.1.1. Participants

A group of 12 individuals participated in Expt. 1 (19–30 years old, mean age: 21 years; 7 female; 11 right-handed). All participants reported having no sensory or motor impairments and normal or corrected-to-normal vision. Participants were rewarded with course credit or $10 per hour for participation. The study was conducted in accordance with the guidelines laid down in the declaration of Helsinki and approved by the New York University institutional review board. All participants gave written informed consent prior to the start of the experiment.

2.1.2. Apparatus and stimuli

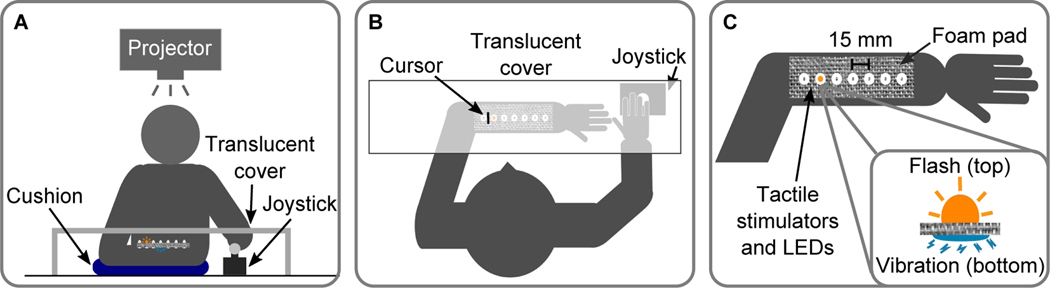
Participants sat in front of a table with the head supported by a chin rest. The non-dominant arm was positioned parallel to the front of the body, palm-down, and lay on an arm-length pillow that both provided comfort and leveled the arm (Fig. 1A, B). A custom-made sleeve was attached to the non-dominant arm using velcro straps. The sleeve held 7 LEDs and 7 tactile stimulators (ERMs, Precision Microdrives, UK) spaced 15 mm apart, positioned along the top of the forearm (Fig. 1C). LEDs and tactile stimulators were aligned so that one LED and one tactile stimulator were located at each of 7 positions (Fig. 1C); the LEDs faced upward and the tactile stimulators were in contact with the arm. The sleeve was made of foam and rubber, ensuring that the vibration of an activated tactile stimulator was not transmitted to the LEDs or neighboring tactile stimulators. A translucent cover was placed above the arm to obstruct vision of the arm but allow activated LEDs to be seen. An LCD projector (Hitachi CPX3010, Tokyo, Japan), mounted so that it projected onto the translucent cover (Fig. 1A), was used to display task instructions, a fixation cross (aligned with the center LED at the beginning of each block), a cursor (vertical line, Fig. 1B), and a color cue. For localization responses, a joystick (Fig. 1A, B) enabled participants to move the cursor along the horizontal axis; to confirm a chosen location the joystick was pressed down. For categorical responses, participants used a custom-made button box (not shown). All custom-made peripherals, i.e., stimulators, joystick, and button box were controlled by microcontrollers (Arduino R3, Somerville, MA) that interfaced with the experimental computer via serial connections. The experimental program was written in Matlab (The Mathworks, Inc., Natick, MA) and used the Psychophysics Toolbox (Brainard, 1997; Kleiner, Brainard, & Pelli, 2007).

Fig. 1. — Experimental setup. (A) Front view. The non-dominant arm was placed under a translucent cover and supported with a cushion. The dominant hand held a joystick. A projector mounted overhead was used to display task instructions, a fixation cross, a cursor, and colored response cues on the translucent cover. (B) Top view. During the response phase a cursor controlled by the joystick was used to indicate the perceived stimulus location. C) Close up. Seven LEDs and seven tactile stimulators were placed along the top of the forearm (15 mm spacing) using a custom-made sleeve. The LEDs faced upward and the tactile stimulators were in contact with the arm. When activated, the LEDs would shine through the translucent cover and the tactile stimulators would vibrate.

Prior to the main experiment, each participant’s tactile detection threshold was determined as a function of stimulus duration using an adaptive procedure (accelerated stochastic approximation; Robbins & Monro, 1951; Kesten, 1958). In each trial of the thresholding procedure, a tactile stimulus was presented in one of two successive time intervals, delimited by auditory beeps. The participant indicated via button press whether the stimulus was presented in the first or the second interval. The algorithm was set to converge to 75% correct responses. It was determined that the procedure had converged after participants’ accuracy averaged over the last 15 trials lay within the range of 70–80%. The procedure was repeated three times, and the resulting three duration estimates, the average duration over the last 10 trials, were averaged for the final threshold estimate. In the main experiment, tactile stimulus duration was jittered (sampled from a Gaussian with a standard deviation of 2 ms) around 2.5 times the participant’s tactile detection threshold (mean duration: 57 ms, SD across participants: 16 ms). Visual stimulus duration was the same as tactile stimulus duration in visual-tactile trials; in visual-only trials duration was jittered in the same way as tactile stimulus duration.

2.1.3. Task and procedure

Participants localized visual and tactile stimuli presented either alone or as part of a visual-tactile stimulus pair with random inter-modal spatial discrepancy. Visual and tactile stimuli presented alone and visual-tactile stimulus pairs were randomly interleaved. A color cue (color change of the projected background image) signaled the to-be-localized modality (blue: tactile, red: visual). Participants indicated the perceived location of the cued stimulus by moving a visually presented cursor to that location. After confirming the localization response, participants reported whether they had perceived the visual and the tactile stimulus as spatially aligned or misaligned (or whether they only perceived one stimulus modality) by choosing the respective option from a drop-down menu using the joystick.

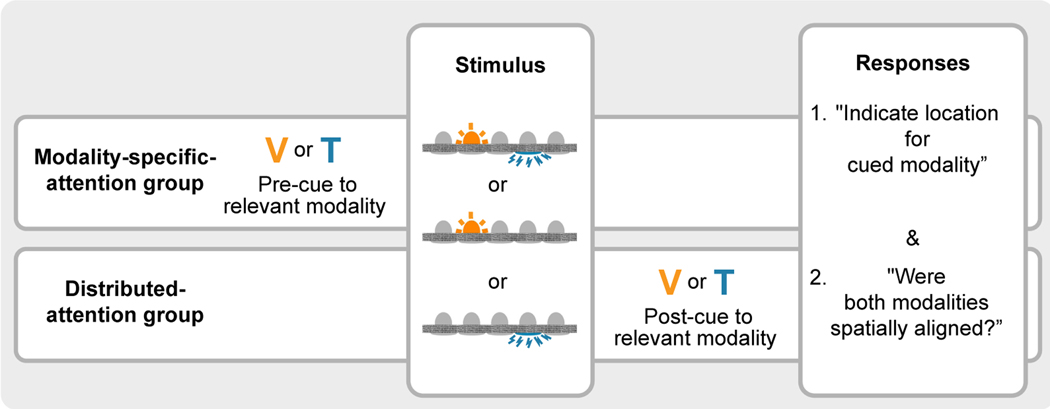
The time point at which the relevant modality was cued varied across groups (Fig. 2); one group of participants received the cue before the stimulus was presented (modality-specific-attention group; n = 5), the other group afterward (distributed-attention group; n = 7). Otherwise,trial timelines were as similar across groups as possible. A trial began with the display of a fixation cross for 1 s. 0.5 s after the removal of the fixation cross, an auditory start cue was presented. In the modality-specific-attention group, this auditory cue was paired with the visual color cue indicating the response-relevant modality. 1 s later, the stimulus was presented. In the distributed-attention group, the color cue to the response-relevant modality was presented 1 s after stimulus onset. The cursor appeared 200 ms after the stimulus or the post-cue, if one was presented. 300 ms after the localization response had been confirmed, the drop-down menu for the spatial-alignment response appeared. Response times were not limited and the next trial started immediately after the response was given.

Visual and tactile stimuli were presented with equal probability at each of 5 possible locations (the inner 5 of the 7 possible ones). For visual-tactile stimulus pairs, the location of each modality was chosen independently. Thus, all 25 different spatial combinations were presented with equal probability, but consequently the 9 resulting visual-tactile spatial discrepancies were presented with unequal probabilities (p(0 cm) = 0.2, p(±1.5 cm) = 0.32, p(±3 cm) = 0.24, p(±4.5 cm) = 0.16, and p(±6 cm) = 0.08). Stimulus locations were pseudo-randomized across trials such that one full set of locations was completed before the next set began. Within each set, visual and tactile stimuli presented alone and visual-tactile stimulus pairs were presented twice at all possible locations, i.e., a set comprised 10 visual and 10 tactile stimuli presented alone and 50 visual-tactile stimulus pairs. For visual-tactile stimulus pairs, the visual stimulus was response-relevant in one repetition and the tactile stimulus in the other. Every participant completed at least 13 blocks with 50 trials in each block for a total of 650 trials per participant. However, most participants completed 28 blocks or more. The experiment was divided into multiple sessions of self-determined length.

2.1.4. Data analysis

Trials in which the alignment response indicated that the participant had misperceived the number of stimuli were excluded from all analyses (6.6% of trials; raw data are available at https://osf.io/epcqv/?view_only=ab4d5bc816b54548918b3548bb7eed7d; Badde et al., 2019). First, we compared between groups the size of the ventriloquism effect measured via localization responses. We subtracted participants’ average localization response in trials in which the stimulus had been presented alone from their average localization response for the same stimulus, but in trials in which a visual-tactile stimulus pair had been presented. This difference was calculated for each location of the task-relevant stimulus and each inter-modal discrepancy, and then averaged across all locations of the task-relevant stimulus. We regressed the resulting difference values against the inter-modal discrepancy (with negative values representing stimulus pairs in which the visual stimulus was closer to the elbow than the tactile stimulus). The estimated slope indicates the size of the ventriloquism after (distributed-attention group) the effect relative to the inter-modal discrepancy, with a slope of 0 indicating no ventriloquism effect and a slope of ±1 indicating a full shift toward the non-cued modality. For this analysis, we split localization responses by task-relevant modality, and by whether the unity judgment indicated that the two modalities were perceived as spatially aligned.

To compare these relative localization shifts across groups, an analysis of variance was computed on the estimated regression slopes. We tested one within-participants factor (perceived spatial alignment) and one between-participants factor, group (modality-specific vs. distributed attention). Significant interaction effects were followed-up by t-tests comparing the size of the ventriloquism effect between groups. Once all interactions were resolved, one-sample t-tests against zero were conducted to test the significance of the (relative) ventriloquism effect. As the dependent variable, the regression slopes, might not be normally distributed, we used permutation tests to determine the significance of the F- and t-statistics. For the analysis of variance, we permuted labels across conditions and participants (Anderson, 2001), for group effects we permuted labels across participants, and for condition effects we permuted labels within participants. Please note, the pattern of statistical results was nearly identical to that based on the F- and t-distributions.

We further compared between groups the ventriloquism effects as indicated by the proportion of spatial-alignment responses. We calculated the overall proportion of visual-tactile trials in which the visual and the tactile stimulus were perceived as spatially aligned. We compared the resulting proportions across groups using unpaired t-tests. For this analysis, the data were split by task-relevant modality. We again used permutation tests to derive robust p-values.

We adjusted for multiple comparisons according to Holm (1979) and assumed significance at a Type I error rate of 5%.

2.2. Results

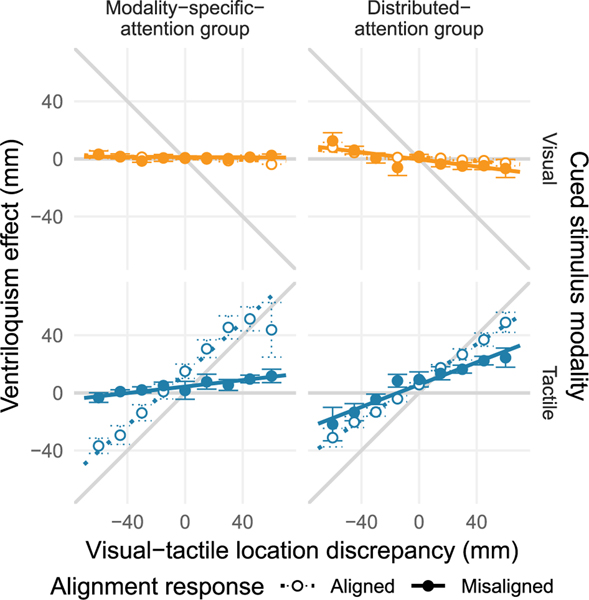
We first analyzed localization performance. We compared the size of the ventriloquism effect – in the form of relative localization shifts – between the two attention groups. We did so separately for each to-be-localized modality and separated trials in which the visual and the tactile stimuli were perceived as spatially aligned from trials in which they were perceived as misaligned (Fig. 3). The slope of a regression line through the data provides an estimate of the degree of the relative ventriloquism effect, i.e., the relative amount of shift of perceived location toward the location of the other modality’s stimulus.

Fig. 3. — Expt. 1: Ventriloquism effect — localization shifts. The ventriloquism effect was measured by subtracting localization responses in trials in which only one stimulus was presented from localization responses for stimuli of the same modality and location but in trials in which a visual-tactile stimulus pair was presented. The averaged differences in perceived location are shown as a function of the spatial discrepancy within the visual-tactile stimulus pair (five possible locations for each modality resulting in nine visual-tactile discrepancies; negative numbers indicate pairs with the visual stimulus located closer to the elbow than the tactile stimulus). The data are separated into trials in which the visual and tactile stimuli were perceived as spatially aligned (open circles and dotted lines) or misaligned (solid circles and lines; see Fig. S1 for undivided data). Visual (top row, orange) and tactile (bottom row, blue) stimuli were response-relevant with equal probability. The modality-specific-attention group (left column) was informed about the response-relevant modality before the stimulation; the distributed-attention group (right column) was informed about the relevant modality after the stimulation. Regression lines are based on group averages of individual participants’ intercept and slope parameters. The grey diagonal line indicates the maximal possible localization shift, the horizontal line indicates the absence of a localization shift, and error bars are standard errors of the mean. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

An analysis of variance on the visual localization data (the estimated slopes) revealed solely a main effect of group, F(1,10) = 6.18, p = 0.041, η² = 0.259. Follow-up one-sample t-tests against zero revealed a marginally significant relative shift (M = −0.013, SE = 0.005) in the modality-specific-attention group, t(4) = 3.65, p = 0.059, d = 1.35, and a significant relative shift (M = −0.097, SE = 0.027) in the distributed-attention group, t(6) = 3.65, p < 0.001,d = 1.49, both indicative of a ventriloquism effect in visual localization independent of the perceived spatial alignment of the stimulus pair.

An analysis of variance on tactile localization data revealed a main effect of perceived visual-tactile alignment, F(1,10) = 28.35, p < 0.001, η² = 0.600, which differed across groups, F(1,10) = 7.75, p = 0.018, η² = 0.291. To follow up on the interaction, we conducted unpaired t-tests between groups separately for trials with and without perceived visual-tactile alignment. For trials in which the visual and the tactile stimulus were perceived as spatially aligned, no significant difference between groups emerged, t(10) = 1.53, p = 0.160, d = 0.683. A one-sample t-test against zero conducted across groups confirmed a ventriloquism effect on tactile localization in these trials, M = 0.759, SE = 0.082, t(11) = 9.25, p < 0.001, d = 2.79. For trials in which the stimuli had been perceived as misaligned, a significant difference between groups was present, t(10) = 3.14, p = 0.026, d = 1.403. Follow-up t-tests indicated a significant ventriloquism effect in both the modality-specific-attention group, M = 0.113, SE = 0.045, t(4) = 2.51, p < 0.001, d = 1.25, and in the distributed-attention group, M = 0.388, SE = 0.066, t(6) = 5.86, p = 0.001, d = 2.39 even though the stimuli were perceived as misaligned. In sum, both groups showed a nearly complete shift of perceived tactile locations toward the locations of concurrently presented visual stimuli in trials in which they indicated perceptual alignment of the stimuli. However, the distributed-attention group showed a stronger ventriloquism effect than the modality-specific-attention group in trials in which the visual and the tactile stimuli had been perceived as spatially misaligned.

We further compared the proportion of trials in which visual and tactile stimuli were perceived as spatially aligned across groups, separately for each cued modality (Fig. 4). Unpaired t-tests indicated a significantly lower proportion of perceived spatial alignment responses in the modality-specific compared to the distributed-attention group for trials in which the visual stimulus had to be localized, t(10) = 3.47, p = 0.012, d = 1.55, and for trials in which the tactile stimulus had to be localized, t(10) = 3.19, p = 0.012, d = 1.43.

Fig. 4. — Expt. 1: Ventriloquism effect — perceived spatial alignment. Group mean proportion of responses indicating that the stimuli of a visual-tactile stimulus pair were perceived as spatially aligned. Data from trials in which the visual (orange) or tactile (blue) stimulus had to be localized are shown separately for the modality-specific-attention group (left side), which was informed about the response-relevant modality before the stimulation, and the distributed-attention group (right side), which was informed about the relevant modality after the stimulation. Error bars show standard errors of the mean. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.3. Summary

The first experiment tested whether the integration of visual and tactile spatial information is influenced by the necessity to attend to the locations of both stimuli. Participants localized visual or tactile stimuli presented either alone or with random spatial discrepancies between the two modalities. To manipulate attention, we varied the time point at which the response-relevant modality was cued, either before the stimulus pair was presented – modality-specific attention – or afterward — distributed attention. A small shift of visual localization toward a concurrently presented tactile stimulus emerged in both groups, but the effect was stronger in the distributed-attention group. The perceived location of tactile stimuli shifted considerably toward the location of a concurrently presented visual stimulus. When participants perceived visual-tactile stimulus pairs as spatially aligned, the relative tactile ventriloquism effect was maximal, that is, the perceived tactile stimulus location was completely shifted toward the physical location of the visual stimulus in both groups. However, in trials in which the visual-tactile stimulus pairs were perceived as misaligned, the distributed-attention group showed a larger tactile ventriloquism effect than the modality-specific-attention group. Moreover, participants in the distributed-attention group perceived the stimuli more often as spatially aligned than participants in the modality-specific-attention group. In sum, the results are in agreement with our hypothesis that the integration of vision and touch can be enhanced by attending to both modalities at the same time.

3. Expt. 2: Attention effects on visual recalibration of touch

The second experiment tested the sensitivity of cross-modal recalibration to the attentional context. Previous studies indicate that the effect of modality-specific attention on cross-modal recalibration depends on the pair of sensory modalities involved. Auditory spatial perception is recalibrated independent of which modality is attended during the adaptation phase (Canon, 1970); proprioceptive space is only recalibrated when attention during the adaptation phase is directed toward vision (Kelso, Cook, Olson, & Epstein, 1975). Yet, whether the distribution of attention across both modalities strengthens cross-modal recalibration in the same way as cross-modal integration has, to our knowledge, not been tested for any combination of modalities.

Moreover, neither the spatial recalibration of touch by vision (Cardini & Longo, 2016; Samad & Shams, 2018) nor the recalibration of visual bumpiness (Ho, Serwe, Trommershäuser, Maloney, & Landy, 2009), slant (Ernst, Banks, & Bülthoff, 2000; van Beers, van Mierlo, Smeets, & Brenner, 2011), size (Atkins, Jacobs, & Knill, 2003; Gori, Mazzilli, Sandini, & Burr, 2011), gloss (Wismeijer, Gegenfurtner, & Drewing, 2012), motion (Atkins, Fiser, & Jacobs, 2001), and texture (Atkins et al., 2001) by haptics (active touch, Gibson, 1962) have been probed using any attentional manipulations. Based on our results on visual-tactile integration, we hypothesized that the spatial recalibration of touch by vision would be sensitive to the attentional context. We probed this hypothesis by varying the task participants performed during the adaptation phase in which they were exposed to spatially discrepant visual-tactile stimulus pairs in the same way as in Expt. 1. Additionally, we introduced a task that did not require participants to attend to the location of the stimuli. Participants either monitored the stimulus pairs for stimuli with a longer duration in both modalities (non-spatial-attention task) or they indicated the location of either the felt or the viewed stimulus (spatial task). Crucially, in the spatial task the response-relevant modality was again either cued before the stimulus pair was presented, allowing participants to attend to one modality (the modality-specific-attention task), or after the stimulus pair had been presented, encouraging participants to attend to both modalities (the distributed-attention task). We hypothesized that the need to attend to the locations of both signals at the same time would result in larger recalibration effects.

3.1. Methods

3.1.1. Participants

36 newly-recruited persons (18–45 years old, mean age: 22.5 years; 17 male; 5 left-handed) participated in Expt. 2. Data of 17 additional participants were excluded or only partially collected either due to problems following the task instructions (3 participants) or problems localizing the tactile stimuli (14 participants, indicated by localization performance indistinguishable from chance level). Note that difficulty localizing the tactile stimuli was independent of the participant’s age, sex, and task during the adaptation phase. High exclusion rates are common in studies requiring tactile localization (e.g., Azañón, Mihaljevic, & Longo, 2016; Schubert, Badde, Röder, & Heed, 2017).

3.1.2. Apparatus and stimuli

Apparatus and stimuli were the same as in Expt. 1. As in Expt. 1, the duration of visual and tactile stimuli was set based on individual tactile detection thresholds.

3.1.3. Tasks and procedure

Expt. 2 consisted of three phases (Fig. 5).

In the pre-adaptation phase, participants localized visual and tactile stimuli presented alone at one of the inner 5 of the 7 possible locations. Visual and tactile stimuli were randomly interleaved. The pre-adaptation phase comprised 5 blocks of 40 trials for a total of 200 trials. Each block consisted of 4 replications of each combination of location and tested modality.

In the adaptation phase, visual-tactile stimulus pairs were presented with the visual stimulus located 30 mm closer to the elbow than the tactile stimulus. The stimulus pair was presented in one of 5 different locations, randomized across trials. The task during the adaptation phase differed between groups (Fig. 5, center panel). In the non-spatial task, participants indicated whether the current stimulus had a longer duration than the majority of the stimuli. These deviant stimulus pairs were presented in 10% of the trials and were 30 ms longer in duration than standard stimulus pairs. In the spatial, modality-specific-attention task, participants localized either the visual or the tactile stimulus of the stimulus pair. The cue indicating the to-be-localized modality was displayed prior to stimulus presentation. In the spatial, distributed-attention task, participants again localized either the visual or the tactile stimulus, but the cue – indicating the response-relevant modality – was displayed after stimulus presentation. Participants were pseudo-randomly assigned one of the three tasks, resulting in 12 participants per group. The non-spatial adaptation task comprised 12 blocks of 50 trials for a total of 600 trials. The two spatial adaptation tasks comprised 7 blocks of 50 trials for a total of 350 trials. Responses in the spatial adaptation tasks (joystick-controlled positioning of a cursor) took longer to complete than those in the non-spatial adaptation task (button presses). The number of repetitions was chosen so that the duration of the adaptation phase was similar across tasks. Within each task, trials were pseudo-randomized such that all possible stimulus pairs and, for the attention tasks, cued modalities were presented equally often per block.

In the post-adaptation phase, participants performed 5 blocks of 40 trials of the same task as in the pre-adaptation phase, i.e., they localized visual and tactile stimuli presented alone.

Trial timing was identical to Expt. 1. In the non-spatial attention task, a response cue rather than a cursor was presented 200 ms after the stimulus. Participants could rest briefly after each phase of the experiment. On average participants completed the experiment within 120 min; pre- and post-adaptation phases took around 25 min each and the adaptation phase took 40 min.

3.1.4. Data analysis

To measure the recalibration effect, we compared localization performance for visual and tactile stimuli presented alone during the preand post-adaptation phases. For each participant, testing phase, and stimulus modality, we regressed reported stimulus locations against true stimulus locations. To this aim, the center of the possible stimulus locations was coded as location zero, and locations closer to the elbow were coded as negative locations (that is, leftward for right-handed participants tested using their non-dominant left arm and rightward for left-handed participants). A ventriloquism aftereffect shifts perceived location and hence was predicted to impact the regression intercept. For each stimulus modality, an analysis of variance was conducted on the regression intercepts with two factors: testing phase (pre- and post-adaptation) and group (non-spatial, spatial with modality-specific attention, and spatial attention distributed across modalities). Significant interaction effects were followed up with paired t-tests comparing the intercept between pre- and post-adaptation phases separately for each adaptation task group. We were equally interested in testing for the presence and for the absence of differences between pre- and post-adaptation phases. Therefore, non-significant comparisons were further followed-up by a t-test for equivalence (Wellek, 2010), which enabled us to formulate the absence of a difference as an alternative hypothesis and consequently rendered it testable within the null-hypothesis significance-testing framework. For this test, we used a liberal region of similarity, comparable to 0.5 SD. We again used permutation tests to derive distribution-independent p-values, adjusted for multiple comparisons according to Holm (1979), and assumed significance at a Type I error rate of 5%.

3.2. Results

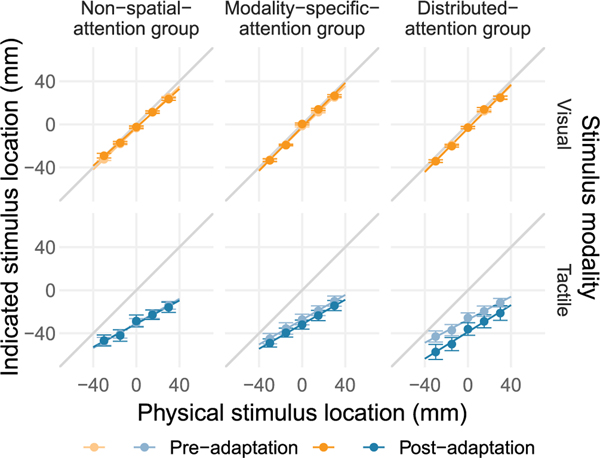
We compared the localization of visual and tactile stimuli presented alone between the pre- and post-adaptation phases (Figs. 6 and 7). If visual-tactile recalibration is enhanced by distributing attention across both modalities, this predicts a larger shift from pre- to post-adaptation for the distributed-attention than for the modality-specific-attention group.

Fig. 6. — Expt. 2: Visual and tactile localization performance in the pre- and post-adaptation phases. Group mean localization responses are shown as a function of the physical stimulus location for visual (top row, orange hues) and tactile stimuli (bottom row, blue hues). Negative numbers indicate locations closer to the elbow. Localization responses are shown for the pre- (light shades) and post-adaptation (dark shades) phases. Lines are based on group averages of individual participants’ regression intercept and slope parameters. The unity line indicates perfect localization. Error bars show standard errors of the mean. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7. — Expt. 2: Ventriloquism aftereffect. Group mean adaptation-induced shifts in the perceived location of visual (orange) and tactile (blue) stimuli. The shifts are calculated as the difference between the pre- and post-adaptation regression intercepts from Fig. 6. Negative numbers indicate a shift of localization responses toward the elbow. Error bars show standard errors of the mean. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

For the localization of visual stimuli, neither significant main effects nor an interaction between testing phase and adaptation task group emerged.

For the localization of tactile stimuli, analysis of variance revealed a main effect of testing phase, F(1,33) = 12.05, p = 0.003, η² = 0.028. This effect was modulated by the task during the adaptation phase as indicated by a significant interaction between testing phase and adaptation task group, F(2,33) = 4.45, p = 0.020, η² = 0.021. We followed up on this significant interaction by comparing tactile localization or after (distributed attention) the stimulus. between the pre- and post-adaptation phases separately for each group. No significant difference between testing phases was found for the non-spatial attention group, t(11) = 0.18, p = 0.882, d = 0.052, or for the spatial, modality-specific-attention group, t(11) = 1.29, p = 0.480, d = 0.372. Follow-up t-tests for equivalence confirmed equivalent tactile localization performance in pre- and post-adaptation trials for the non-spatial attention group, T = 0.18, p<0.05, but not for the modality-specific-attention group, T = 1.29, p>0.05. A significant difference in tactile localization performance between testing phases was found for the distributed-attention group, t(11) = 4.31, p = 0.006, d = 1.243. In this group, a ventriloquism aftereffect emerged: after adaptation, tactile localization was shifted toward the elbow, that is, in the direction of the location of the visual stimulus during the adaptation phase.

3.3. Summary

Expt. 2 tested whether visual-tactile spatial recalibration is sensitive to the focus of attention during the adaptation phase. To this aim, we varied the task-relevance of spatial and modality-specific information during the adaptation phase across groups. A significant tactile ventriloquism aftereffect – indicated by a shift in the localization of tactile stimuli presented alone after the adaptation phase – emerged only when participants were required to attend to the location of both visual and tactile stimuli during the adaptation phase. A smaller, non-significant effect emerged when participants had the possibility to focus on spatial information from one modality alone, and equivalent tactile localization in pre- and post-adaptation phases was found when the task during the adaptation phase required no spatial encoding. We found no significant visual ventriloquism aftereffects. One possible explanation for this is that any visual shift would have shifted both the stimulus and the cursor display used for reporting of the perceived location. Alternatively, recalibration might have been restricted to the tactile modality due to the far higher visual than tactile reliability. Our results indicate that it is necessary to attend to spatial information from both modalities to elicit reliable visual-tactile recalibration.

4. Model: causal inference and attention effects on visual-tactile integration and recalibration

Both experiments demonstrated an increase of visual-tactile interaction effects with distributed compared to modality-specific attention. Yet, distributing attention across both modalities might have enhanced visual-tactile interactions in different ways: (1) bottom-up, by affecting the sensory data, and (2) top-down by changing participants’ prior expectation of a shared source for vision and touch, i.e., the stimulus-independent expectation that the signals correspond and should be integrated.

First, our manipulation of attention might have influenced visual-tactile interactions by affecting the reliability of the sensory signals. If attention toward both modalities uses a common, limited resource (Lavie, 1995; Driver & Spence, 1998; Spence & Driver, 2004; Alsius, Navarra, & Soto-Faraco, 2007), the need to attend to both modalities could reduce the resources allocated to each modality. In contrast, under modality-specific attention most resources can be allocated to the response-relevant modality. Hence, the reliability of the response-relevant modality might be higher in the modality-specific than in the distributed-attention condition (Mishra & Gazzaley, 2012), similar to the reduction of sensory noise that is achieved by allocating selective attention within one modality (Carrasco, 2011).

Second, distributed attention might have affected participants’ a priori expectation of whether the two signals originate from the same source and thus belong together. When attending to only one modality, humans might not expect and simply check whether signals from other modalities come from the same source and should be integrated with the attended signal. Consistent with this idea, frontal cortical areas that have been associated with causal inference (Cao, Summerfield, Park, Giordano, & Kayser, 2019) are active under distributed but not under modality-specific attention (Johnson & Zatorre, 2006; Degerman et al., 2007; Salo, Salmela, Salmi, Numminen, & Alho, 2017).

Consistent with an attenuating effect of distributed attention on sensory reliability, activity in the sensory cortices is reduced when attention is distributed across modalities compared to modality-specific attention (Mishra & Gazzaley, 2012). In turn, modality-specific attention seems to improve the reliability of sensory signals: the weighting of auditory stimuli during auditory-tactile integration increases when attention is directed toward audition (Vercillo & Gori, 2015) and the direction of modality-specific attention influences the attended signal’s neural weight (Rohe & Noppeney, 2018). However, a change in modality weighting only provides conclusive evidence of an impact of attention on reliability if participants could be sure that the stimuli came from the same source and, thus, integrated both signals in every trial of the experiment. In causal-inference studies like ours, participants cannot assume that in every trial both stimuli originated from the same source. Thus, a change in modality weighting could result from changes in reliability as well as from changes in the expectation of a shared source for both signals. Hence, the effect of attention on both variables needs to be estimated. A previous visual-auditory ventriloquism study that estimated both parameters found that focusing attention on one rather than both modalities changed only the sensory reliability of the visual stimulus (Odegaard, Wozny, & Shams, 2016). However, the model used to estimate these parameters assumed the same visual and auditory reliability whether modality-specific attention was directed toward the visual or toward the auditory stimulus. The analysis thus compared the average of modality-specific, focused and averted attention with distributed attention, which renders the results difficult to interpret.

We modeled the data from Expt. 1 on visual-tactile integration to determine whether the need to attend to both modalities affected participants’ causal-inference strategy, each modality’s sensory noise, participants’ expectation of a common source for visual and tactile signals, or all of these. We first compared a large set of models to determine participants’ causal-inference strategy. We then evaluated the parameters of the best-fitting model, to test whether our attentional manipulation affected visual and tactile sensory noise and the prior expectation of a common cause for both sensory signals. Finally, we used simulations with the best-fitting model and a corresponding model of cross-modal recalibration to characterize the influence of changes in both sensory reliability and the expected probability of a common source on visual-tactile integration and recalibration effects.

4.1. Model comparison

In Appendix A, we describe twenty models for the data of Expt. 1. We begin with the ideal-observer causal-inference model of cue integration (Körding et al., 2007; Sato et al., 2007), but also include multiple variants of the model (for an overview about the model elements and variants, see Fig. 12). Data from both groups were fitted best by the same model, which suggests that the distribution of attention across modalities had no effect on participants’ causal inference strategy. The best-fitting model indicated that localization data in both groups were in accordance with optimal Bayesian causal inference (Körding et al., 2007). Yet, both groups based their spatial-alignment responses on a heuristic: they reported the stimuli as being spatially aligned when the two optimal location estimates were sufficiently close.

4.2. Model parameters

The parameters of the best-fitting model revealed that our manipulation of modality-specific attention affected both the sensory noise and the common-cause prior, participants’ expectation of a shared source for visual and tactile signals (Fig. 8). Participants who were forced to attend to both stimuli showed higher tactile sensory uncertainty and a stronger expectation of the two signals sharing the same source (see Appendix A for statistical results). Prior studies demonstrated that changes in sensory noise do not induce changes in the probability a priori assigned to a common source (Beierholm, Quartz, & Shams, 2009), suggesting that modality-specific attention influenced sensory reliabilities and the expectation of a shared source independent of each other.

Fig. 8. — Group means of parameter estimates for the best-fitting model. (A) σ_v,VT,att+ and σ_v,VT, indicative of the reliability of attended visual stimuli that were presented with a tactile stimulus. (B) σ_t,VT,att+ and σ_t,VT, indicative of the reliability of attended tactile stimuli that were presented in the context of visual-tactile stimulation. (C) p_CC: participants’ a priori probability that both stimuli share a common source. Error bars show standard errors of the mean. See Tables S1 and S2 for single-participant parameter estimates

4.3. Model simulations — visual-tactile integration

Our simulations using the best-fitting model revealed that even though both reliabilities and common cause priors were affected by our attentional manipulation, only an increase in the prior probability of vision and touch sharing a source predicted increases across all conditions for both measures of visual-tactile ventriloquism (Figs. 9 and 10). In contrast, changes in sensory reliability affected both measures of visual-tactile integration differently, dependent on the stimulus condition, and mostly at sensory reliabilities higher than the ones identified for touch in our experiments (see Appendix A, Figs. 9 and 10). In sum,the simulation results indicate that the influence of attention on visual-tactile integration effects in Expt. 1 is driven mostly by an attention-induced modulation of participants’ prior expectation that visual and tactile signals originate from the same source.

Fig. 9. — Simulations of the influence of sensory reliabilities and common-cause priors on the ventriloquism effect — localization shifts. Simulated shifts in the perceived locations of (A) visual and (B) tactile stimuli presented as part of a visual-tactile stimulus pair with varying degree of cross-modal spatial discrepancy (columns; negative numbers indicate pairs with the visual stimulus located closer to the elbow than the tactile stimulus). The intensity and direction of the perceptual shifts (color scale; negative numbers indicate a shift toward the elbow) are shown as a function of the standard deviation of visual (σ_v) and tactile (σ_t) sensory noise and the prior probability of visual and tactile signals sharing a source (p_CC, rows). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 10. — Simulations of the influence of sensory reliabilities and common-cause priors on the tactile ventriloquism effect — perceived spatial alignment. Simulated probabilities of perceiving visual-tactile stimulus pairs with varying degree of cross-modal spatial discrepancy (columns; negative numbers indicate pairs with the visual stimulus located closer to the elbow than the tactile stimulus) as originating from a common source. Probabilities (color scale) are shown as a function of the standard deviation of visual (σ_v) and tactile (σ_t) sensory noise and the prior probability of visual and tactile signals sharing a source (p_CC, rows). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.4. Model simulations — visual-tactile recalibration

Simulations using a recalibration version of the best-fitting model (Appendix A) with three different learning rules all predicted higher recalibration of touch with an increasing expectation of the two signals sharing a source and with increasing learning rate (Fig. 11). In contrast, the observed decrease in the reliability of the to-be-localized modality predicted an increase in recalibration effects for sensory signals with a comparably high reliability, but not for sensory signals with a low reliability as was the case for touch in our study (see Appendix A for a discussion of the rationale behind the effect). Consequently, the simulation results indicate that the influence of attention on visual-tactile recalibration that we observed in Expt. 2 was driven solely by an increase in participants’ prior expectation that the visual and tactile signals share a source.

Fig. 11. — Simulated tactile ventriloquism aftereffect. Estimated shifts in the localization of tactile stimuli after recalibration (color scale) are shown as a function of participants’ estimates of the probability of visual and tactile signals sharing a source (p_CC) and the standard deviation of the (attended) tactile stimulus (σ_t,VT for the distributed-attention group, σ_t,VT,att+ for the modality-specific-attention group) in visual-tactile trials during the adaptation phase. We additionally varied the decrease in tactile reliability (i.e., the increase in tactile standard deviation, σ_t,att− − σ_t,att+) associated with attention toward the visual stimulus and the learning rate α. (A,B) Results from the optimal Bayesian causal-inference model of adaptation (Sato et al., 2007), for (A) the distributed- and (B) the modality-specific-attention group. (C, D) Results from a model variant in which recalibration only occurs in trials in which the two sensory signals were judged as sharing a source. (E, F) Results from a model variant in which the learning rate is modulated by the posterior probability of a common cause. The red markers indicate the parameter estimates derived for visual-tactile integration (squares: distributed-attention group, circles: modality-specific-attention group). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

5. General discussion

The current study demonstrated enhanced visual-tactile integration and recalibration effects under distributed attention across modalities compared to selective attention toward one modality. Causal-inference modeling revealed that the enhancement of both effects under distributed attention was due to an increase in participants’ common-cause prior, the stimulus-independent estimate of the probability of a shared source for visual and tactile signals. Distributed attention additionally led to a decrease in sensory reliability of the attended modality compared to modality-specific attention. However, our simulations indicate that this reduced reliability cannot account for the enhanced integration and recalibration effects we observed with distributed attention.

5.1. Prior expectations of a shared source for vision and touch

Cross-modal integration and recalibration should occur only if both signals share the same source; sensory signals from different sources should be kept separate (Welch & Warren, 1980; Körding et al., 2007; Sato et al., 2007, reviewed in Shams & Beierholm, 2010; Deroy, Spence, & Noppeney, 2016; Chen & Spence, 2017). Thus, the brain should base cross-modal integration and recalibration on causal inference about the source of the two signals, which for localization responses was confirmed by our modeling efforts. Causal inference is top-down influenced by the prior probability of a common cause, the signal-independent expectation that the two signals belong together because they originate from the same event or object. Here, the need to attend to both vision and touch strengthened the common-cause prior for vision and touch compared to modality-specific attention.

Priors allow observers to use their knowledge about the structure of the world to achieve the best interpretation of the sensory signals they receive. Thus, priors are typically characterized as long-term statistics of the environment (Girshick, Landy, & Simoncelli, 2011). From this viewpoint, the observed effect matches an environment in which we encounter visual-tactile signals from the same source more often when we attend to both modalities than when we switch attention between vision and touch. Such a statistical relation is impossible to verify but appears reasonable. Touch is tied to the body, but our gaze is usually directed toward objects in the world. Thus, most of the time concurrently arriving visual and tactile signals will have different sources. Moreover, most of the time attention will likely be directed only toward one of these modalities, as vision and touch draw from shared attentional resources (Wahn & König, 2017). To perceive visual-tactile signals from the same source, gaze has to be shifted toward the body. Thus, visual-tactile spatial information from the same source is rarely perceived coincidentally but rather requires an action that would imply some degree of attention to both modalities.

Our results reveal that observers do not use a single, fixed prior probability of vision and touch sharing a source, but adapt their expectation to the situation. Consistently, previous studies showed that common-source priors vary with the external context. The expectation of a common source for cross-modal signals is higher in situations that participants learned to associate with corresponding cross-modal signals (Gau & Noppeney, 2016). In turn, our results suggest that distributed attention across vision and touch forms an internal context associated with visual and tactile signals from the same source.

Our finding of a relatively weak link between visual and tactile locations in the case of modality-specific attention stands in marked contrast to findings indicating that visual and tactile texture (Lunghi, Binda, & Morrone, 2010) and motion (Hense, Badde, & Röder, 2019) information are even integrated in the absence of awareness. This contrast suggests that prior assumptions about the shared origin of visual and tactile signals depend on the feature in question, again pointing toward flexible rather than rigid priors about the relation between visual and tactile signals.

5.2. Sensory reliability

Distributed attention across vision and touch was associated with a decrease in sensory reliability for the attended, response-relevant sensory modality. However, our model simulations revealed that a reduction in reliability does not predict a universal enhancement of visual-tactile integration and recalibration effects. Localization shifts resulting from visual-tactile integration and recalibration increased initially with a reduction in tactile reliability, but declined with greater reductions. Thus, there is a ‘sweet spot’ in which the effects of cross-modal integration and recalibration are maximal. This non-linearity clearly distinguishes cases of optimal cue integration (Landy et al., 1995; Yuille & Bülthoff, 1996; Ernst & Banks, 2002; Trommershäuser et al., 2011) from causal-inference-based cue integration (Körding et al., 2007; Sato et al., 2007) as optimal cue integration predicts a monotonic increase in effects with a decrease in the reliability of the response-relevant modality. Hence, apparent mismatches between changes in sensory reliability and the size of cross-modal integration effects (Helbig & Ernst, 2008) might indicate that participants performed causal inference and did not fully rely on the integrated estimate as is the case for optimal cue integration.

Moreover, in our simulation a decrease in sensory reliability led to an increase in the perceived alignment between the two modalities for stimuli with large cross-modal discrepancies but had the opposite effect on stimuli with small cross-modal discrepancies. Thus, the effects of changes in reliability on integration and recalibration depend crucially on the size of the cross-modal conflict. Attention increases cue reliability and thus, for congruent stimuli, will decrease integration effects, whereas for incongruent stimuli, attention will enhance integration effects.

5.3. Attentional resources

Our study reveals that visual-tactile interactions vary with the modality-focus of selective attention. Yet, only the distribution but not the amount of attentional resources should have been affected by our manipulation. The influence of a withdrawal of attentional resources on cross-modal interactions has been studied repeatedly to investigate whether cross-modal integration and recalibration functionally depend on attentional resources (for reviews on the interplay between attention and multisensory integration in general, see Talsma et al., 2010; Koelewijn, Bronkhorst, & Theeuwes, 2010; Tang et al., 2016; Macaluso et al., 2016; Wahn & König, 2017).

One of the best-known arguments that audio-visual integration depends on attentional resources is the breakdown of the McGurk effect, an indicator of the integration of visual and auditory speech information, when attentional resources are withdrawn from both modalities by an additional task (Alsius, Navarra, Campbell, & Soto-Faraco, 2005; Alsius et al., 2007). Yet, this breakdown can be explained by the decrease of visual and auditory reliabilities that accompanies the withdrawal of attention (Carrasco, 2011; Shinn-Cunningham, 2008). Our simulations show that for cross-modal stimuli with little conflict between the sensory signals, such as the stimuli in a McGurk task, a reduction in reliability will lead to a decrease in the inferred probability that the two signals originated from the same source. As a consequence, binary effects in which the two sensory signals are either fused or separated such as the McGurk effect will be reduced or eliminated under increased attentional load.

In contrast, our simulations predict hardly any effect of a with-drawal of attention from both modalities, i.e., a decrease in both sensory reliabilities, on cross-modal interaction effects that reflect the relative weighting of the two sensory signals. Consistent with this prediction, ventriloquism-like shifts in the localization of auditory stimuli were unaffected by the direction of an additional attention-demanding task (Bertelson, Vroomen, de Gelder, & Driver, 2000), and vision recalibrates auditory spatial perception even when attentional resources are reduced by an additional attention-diverting task (Eramudugolla, Kamke, Soto-Faraco, & Mattingley, 2011), or absent altogether, such as in the non-attended hemifield of hemineglect patients (Passamonti, Frissen, & Làdavas, 2009). Thus, the absence of an attentional modulation of cross-modal integration or recalibration effects does by no means imply that attention had no effect on the sensory signals.

Moreover, our study reveals that the focus of attention influences the prior expectation of a common source for vision and touch. A withdrawal of attention might well be associated with even lower prior expectations that vision and touch or vision and other body-related senses share a common cause, simply because observers might even be less likely to evaluate whether signals that are not currently relevant originate from the same source. This potential reduction in the observer’s common-cause prior, coupled with the low reliability of proprioception might explain why visual-proprioceptive recalibration declines substantially when attentional resources are diverted using a mental-arithmetic task (Redding, Clark, & Wallace, 1985; Redding & Wallace, 1985, although see Redding, Rader, & Lucas, 1992, for a conflicting result).

In sum, our modeling results demonstrate that it is not necessary to assume a functional role of attention in cross-modal integration and recalibration, our and previous results can be explained through the influence of attention on sensory reliabilities and common-cause priors.

5.4. Relationship between recalibration and integration

Our manipulations of the ventriloquism aftereffect, as well as the model we employed to simulate this effect, assume a close connection between cross-modal recalibration and cross-modal integration. The results support this assumption: both integration and recalibration effects were strengthened by distributing attention across both modalities, and both of these effects were reproduced using a causal-inference model (Körding et al., 2007; Sato et al., 2007). Indeed, not only Bayesian but also neural-network models can predict both effects of recalibration and integration (Magosso, Cuppini, & Ursino, 2012; Ursino, Cuppini, & Magosso, 2014). However, in apparent contrast to our results, recalibration and integration of visual-proprioceptive (Welch, Widawski, Harrington, & Warren, 1979) and visual-auditory (Radeau & Bertelson, 1977) spatial information show diverging sensitivity to task manipulations. Moreover, the size of visual-auditory recalibration effects cannot be predicted based on the size the integration effects (Bosen et al., 2017), and in visual-motor tasks, the presence of sensory integration does not necessarily lead to recalibration (Smeets, van den Dobbelsteen, de Grave, van Beers, & Brenner, 2006). Finally, whereas some studies find that the direction and degree of cross-modal recalibration depend on the relative reliability of the two sensory signals (van Beers et al., 2002; Burge, Girshick, & Banks, 2010) – the core principle of cross-modal integration – other studies suggest that it is cue accuracy rather than cue reliability that determines the direction of cross-modal recalibration (Zaidel, Turner, & Angelaki, 2011). However, as discussed above, our simulations indicate that changes in sensory reliability can affect integration and recalibration differently, depending on the overall reliability levels and the degree of conflict between the modalities. Thus, recalibration can be based on integration even if both effects are not correlated within persons or across tasks.

5.5. Spatial-alignment responses

Model comparison revealed that participants in both modality-specific- and distributed-attention groups based their localization responses on ideal-observer-like causal inference, but spatial-alignment judgments were based on a heuristic decision strategy. Thus, these two measures, localization shifts and alignment judgments, provided related but distinct information. Consistently, in previous studies, in which both responses were collected and modeled separately, parameter estimates diverged with the measure that was fitted (Bosen et al., 2016; Acerbi, Dokka, Angelaki, & Ma, 2018) even though qualitatively the two measures agree widely (Wallace et al., 2004; Hairston et al., 2003; Rohe & Noppeney, 2015b). In the best-fitting model, spatial-alignment responses were based on comparisons of the optimal location estimates of the two sensory signals (a decision rule not included in previous models). This suggests greater cognitive influence on spatial-alignment (or common-source) judgments as compared to localization responses. Indeed, such binary judgments of ventriloquism vary according to the wording of the instructions (Lewald & Guski, 2003), indicating that these measures are cognitively penetrable. In sum, by combining localization and spatial-alignment judgments within the same trial, as we have done here for the first time, we revealed spatial-alignment responses to be cognitive heuristics based on the optimal location estimates that characterize localization responses.

5.6. Tactile biases

Participants exhibited strong biases in tactile localization. Biases toward anatomical landmarks are a known feature of tactile localization (de Vignemont, Majid, Jola, & Haggard, 2009). Model fitting attributed these biases to modality-specific priors, meaning that participants expected to feel a touch with greater probability at the elbow or the wrist than along the length of the lower arm. These tactile biases influenced not only localization responses but also the perceived spatial alignment of visual-tactile stimulus pairs (Fig. 14). Thus, our study indicates that priors about the location of events and objects in the world depend on the sense through which we perceive them, which is consistent with previous reports on discrepancies between visual and auditory spatial priors (Odegaard, Wozny, & Shams, 2015; Bosen et al., 2016). The modality-specificity of spatial priors is consistent with the variability of the common-cause prior revealed by our study, both results suggest priors to be situation-dependent.

5.7. Working-memory demands

Our manipulation of modality-specific attention affects the working-memory demands of the task. In the modality-specific-attention condition, the localization response was given immediately after stimulus presentation, whereas in the distributed-attention condition participants had to memorize both locations for one second, until the relevant modality was cued. Thus, task difficulty might have been higher for participants who had to distribute their attention across modalities than for the modality-specific-attention group. Yet, whereas varying task difficulty can explain differences in overall performance, the specific effects on integration and recalibration found here are difficult to link to task difficulty. However, the retention of both sensory signals in working memory might influence integration and recalibration independent of task difficulty. Working memory for visual and for tactile stimuli is governed by the same brain network (Ricciardi et al., 2006) and cross-modal information tends to be stored as one integrated object (Lehnert & Zimmer, 2006). Thus, holding both signals in working memory might foster the association between them while at the same time decreasing the reliability of the sensory signals. Yet, given that the retention interval of one second used in our study is comparatively short, we assume that concurrent attention toward both modalities is the major driving force behind our effects.

6. Conclusion

Our study shows that visual-tactile integration and recalibration effects are enhanced under distributed compared to modality-specific attention. Using causal-inference models we revealed that the need to concurrently attend to both vision and touch increased the expectation of visual and tactile sensory signals sharing a source and thus belonging together while reducing their sensory reliability. The gain in the prior expectation about the origin of visual-tactile signals explained the observed enhancement of integration and recalibration effects. The decrease in sensory reliability however predicted reduced recalibration effects while enhancing integration effects for pairs with a large spatial discrepancy only. In sum, our study indicates a weak default link between spatial vision and touch that can be strengthened by distributing attention across both modalities.

Supplementary Material

NIHMS1558008-supplement-1.pdf^{(1.1MB, pdf)}

Acknowledgements

This work was supported by the National Institute of Health, grant NIH EY08266 to MSL and the German Research Foundation, grant BA 5600 1/1 to SB. We thank the Landylab for valuable comments on a previous version of the manuscript.

Appendix A

A.1. Causal-inference models of visual-tactile integration

The ideal-observer causal-inference model (Körding et al., 2007; Sato et al., 2007) is a Bayesian inference model. Thus, it is based on a generative model (Fig. 12) describing the world situation that the observer expects to encounter. Here, the generative model consists of the following elements. First, visual and tactile stimuli either arise from a single source (C = 1) or two sources (C = 2), with p(C = 1) = p_CC being the a priori probability of a common cause, i.e., the probability of a single, shared source for visual and tactile stimuli. The locations of the visual (s_v) and tactile (s_t) sources vary randomly from trial to trial. In the original version of the model, visual and tactile sources are sampled from the same Gaussian prior distribution (e.g., $s_{v t} ~ N (μ_{p \cdot v t}, σ_{p \cdot v t}^{2})$ ). In other words, a visual and a tactile stimulus have the same probability of originating from any given location. We will consider alternative priors below. If the visual and the tactile stimulus arise from the same source (C = 1), both stimuli originate at a single random location (s_v = s_t = s_vt); if they arise from separate sources (C = 2), two independent samples of the Gaussian distribution determine the source locations (s_v, s_t). Finally, the observer receives noisy measurements usually centered on these world locations (e.g., $x_{v} ~ N (s_{v}, σ_{v}^{2})$ ), but we tested alternatives, too. The ideal-observer model assumes the observer has full knowledge of the generative model and performs Bayesian inference, that is, the observer determines the posterior probability of each possible location given the noisy measurements by inverting the generative model.

Fig. 12. — Causal-inference models of cue integration. The schematic depicts the generative or world model. Visual and tactile signals either arise from a single source (C = 1) or two sources (C = 2). The locations of the visual (s_v) and tactile (s_t) sources vary randomly from trial to trial. In the original version of the model, the distribution of visual and tactile sources over space is described by one Gaussian distribution (e.g. $s_{v t} ~ N (μ_{p \cdot v t}, σ_{p \cdot v t}^{2})$ ). Guided by our experimental data, we tested differently shaped modality-specific distributions of visual and tactile sources over space (“Type of sensory prior”). If the visual and the tactile stimulus arise from the same source C = 1, both stimuli originate at a single random location (s_v = s_t = s_vt); if they arise from separate sources C = 2, the two signals have two independent source locations (s_v,s_t). Finally, the observer receives noisy measurements either distributed around these world locations or shifted in one direction (“Type of likelihood”). Moreover, the level of noise perturbing the measurements can vary with attention (“Sensory reliability”). The ideal-observer model assumes the observer performs Bayesian inference, that is, inverts the generative model and determines the posterior probability of each possible location given the noisy measurements. The ideal observer has knowledge about the structure of the world model as well as about the parameters of this world such as the amount of sensory noise, form of sensory priors, and the probability that visual and tactile signals arise from the same source (“Common-source prior”). The observer can use an optimal or heuristic “decision rule” to turn the posterior probability over space into a response indicating either the location of the response-relevant stimulus or the spatial alignment of both stimuli. Variations in the model elements (printed in black) constitute the different model variants we tested to find the best model description of the specific world scenario and the rules our participants employed. Having established the best-fitting model variant, we tested for attention-dependent variations in several model parameters (printed in red). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

If the observer knew the signals shared a common source, the optimal location estimate $({\hat{s}}_{v t, C = 1})$ would be a combination of the measurements and the mean of the prior, each weighted by its respective reliability (Landy et al., 1995; Yuille & Bülthoff, 1996; Ernst & Banks, 2002). This estimate is optimal in the sense that it minimizes squared localization error and maximizes the a posteriori probability of the estimate:

{\hat{s}}_{v t, C = 1} = \frac{x_{v} σ_{v}^{- 2} + x_{t} σ_{t}^{- 2} + μ_{p \cdot v t} σ_{p \cdot v t}^{- 2}}{σ_{v}^{- 2} + σ_{t}^{- 2} + σ_{p \cdot v t}^{- 2}} .

(1)

However, when the visual and the tactile measurements are known to originate from different sources (C = 2), the estimated location of the visually perceived object $({\hat{S}}_{v, C = 2})$ should be independent of the tactile measurement and vice versa:

{\hat{s}}_{v, C = 2} = \frac{x_{v} σ_{v}^{- 2} + μ_{p \cdot v t} σ_{p \cdot v t}^{- 2}}{σ_{v}^{- 2} + σ_{p \cdot v t}^{- 2}} and {\hat{s}}_{t, C = 2} = \frac{x_{t} σ_{t}^{- 2} + μ_{p \cdot v t} σ_{p \cdot v t}^{- 2}}{σ_{t}^{- 2} + σ_{p \cdot v t}^{- 2}} .

(2)

Thus, an ideal observer’s estimate of the location of a tactile sensation might vary considerably depending on whether she judged the touch to stem from the same source as a concurrent flash. A final estimate of the source location depends on determining the probability of a common cause given the noisy measurements. Bayes’ rule and the generative model yield:

p (C = 1 | x_{v}, x_{t}) = \frac{p (x_{v}, x_{t} | C = 1) p_{C C}}{p (x_{v}, x_{t} | C = 1) p_{C C} + p (x_{v}, x_{t} | C = 2) (1 - p_{C C})},

(3)

where

p (x_{v}, x_{t} | C = 1) = \int p (x_{v}, x_{t} | s_{v t}) p (s_{v t}) d s_{v t} = \int p (x_{v} | s_{v t}) p (x_{t} | s_{v t}) p (s_{v t}) d s_{v t} = \frac{1}{2 π \sqrt{σ_{v}^{2} σ_{t}^{2} + σ_{v}^{2} σ_{p \cdot v t}^{2} + σ_{t}^{2} σ_{p \cdot v t}^{2}}} \exp (- \frac{1}{2} \frac{{(x_{v} - x_{t})}^{2} σ_{p \cdot v t}^{2} + {(x_{v} - μ_{p \cdot v t})}^{2} σ_{t}^{2} + {(x_{t} - μ_{p \cdot v t})}^{2} σ_{v}^{2}}{σ_{v}^{2} σ_{t}^{2} + σ_{v}^{2} σ_{p \cdot v t}^{2} + σ_{t}^{2} σ_{p \cdot v t}^{2}})

(4)

and

p (x_{v}, x_{t} | C = 2) = \iint p (x_{v}, x_{t} | s_{v}, s_{t}) p (s_{v}, s_{t}) d s_{v} d s_{t} = \int p (x_{v} | s_{v}) p (s_{v}) d s_{v} \int p (x_{t} | s_{t}) p (s_{t}) d s_{t} = \frac{1}{2 π \sqrt{(σ_{v}^{2} + σ_{p \cdot v t}^{2}) (σ_{t}^{2} + σ_{p \cdot v t}^{2})}} \exp (- \frac{1}{2} (\frac{{(x_{v} - μ_{p \cdot v t})}^{2}}{σ_{v}^{2} + σ_{p \cdot v t}^{2}} + \frac{{(x_{t} - μ_{p \cdot v t})}^{2}}{σ_{t}^{2} + σ_{p \cdot v t}^{2}})) .

(5)

An ideal observer then uses these inferences about the origins of the two measurements to weigh the two conditional location estimates relative to the likelihood of the underlying scenario, resulting in the Bayesian least-squares estimates:

\begin{array}{l} {\hat{s}}_{v} = p (C = 1 | x_{v}, x_{t}) {\hat{s}}_{v t, C = 1} + p (C = 2 | x_{v}, x_{t}) {\hat{s}}_{v, C = 2} \\ {\hat{s}}_{t} = p (C = 1 | x_{v}, x_{t}) {\hat{s}}_{v t, C = 1} + p (C = 2 | x_{v}, x_{t}) {\hat{s}}_{t, C = 2} . \end{array}

(6)

Finally, we assume there is additional zero-mean, i.e., unbiased Gaussian noise that perturbs the report of perceived location so that, e.g., the report of the location of the visual stimulus is

r_{v} = {\hat{s}}_{v} + ϵ, where ϵ ~ N (0, σ_{ϵ}^{2}) .

(7)

Crucially, the estimates described so far are all conditional on the noisy sensory measurements (x_v,x_t), but these are unobservable. As an experimenter, all we know are the stimuli we supplied ($s_v, s_t$) and the participant’s response (r_v,r_t). To infer the likelihood of an observed response, we have to marginalize over all possible measurements (x_v,x_t) and values of the response noise (ϵ):

\begin{array}{l} p (r_{v} | s_{v}, s_{t}) = ∭ p (r_{v} | {\hat{s}}_{v}, ϵ) p ({\hat{s}}_{v} | x_{v}, x_{t}) p (x_{v} | s_{v}) p (x_{t} | s_{t}) d x_{v} d x_{t} d ϵ \\ p (r_{t} | s_{v}, s_{t}) = ∭ p (r_{t} | {\hat{s}}_{t}, ϵ) p ({\hat{s}}_{t} | x_{v}, x_{t}) p (x_{v} | s_{v}) p (x_{t} | s_{t}) d x_{v} d x_{t} d ϵ, \end{array}

(8)

where the second term in each equation is a Dirac δ function based on Eqs. (6) and (7). That is, for given pair of measurements x_v and x_t, the estimated locations ${\hat{s}}_{v}$ and ${\hat{s}}_{t}$ are deterministic.

We further assume that our observer judges both stimuli as coming from the same source if $p (C = 1 | x_{v}, x_{t}) > 0.5$ , but lapses with rate λ ∈ [0,1] when indicating via button press whether the stimuli were spatially aligned. Thus, the probability for a response indicating that the stimuli were perceived as aligned is^² $p (I_{‘aligned’ response} = 1 | x_{v}, x_{t}) = λ I_{p (C = 1 | x_{y}, x_{t}) \leq 0.5} + (1 - λ) I_{p (C = 1 | x_{v}, x_{t}) > 0.5}$ . But again, we can neither know the actual measurements in the observer’s head nor whether she lapsed in a specific trial. Therefore, we marginalize:

p (I_{‘aligned’ response} = 1 | s_{v}, s_{t}) = λ \int \int I_{p (C = 1 | x_{v}, x_{t}) \leq 0.5} p (x_{v} | s_{v}) p (x_{t} | s_{t}) d x_{v} d x_{t} + (1 - λ) \int \int I_{p (C = 1 | x_{v}, x_{t}) > 0.5} p (x_{v} | s_{v}) p (x_{t} | s_{t}) d x_{v} d x_{t}

(9)

A.1.1. Causal-inference model — reliabilities

The goal of our modeling efforts was to pinpoint the effects of our attentional manipulation. The basic model assumes equal sensory noise in all trials (model parameters σ_v and σ_t). However, directing attention toward one modality might change the sensory noise associated with both the attended and unattended sensory signals. Further, attending to a stimulus in the context of a cross-modal stimulus pair could result in a different reliability than attending to a visual or tactile stimulus presented alone. Thus, rather than two reliability parameters, one for each modality, we allowed for four different reliability levels per modality. For vision, for example, there are visual reliability parameters for a stimulus 1) presented alone (σ_{v, V}), presented in a visual-tactile stimulus pair 2) with both modalities attended (σ_v,VT, distributed-attention group only), 3) with vision attended, i.e., when vision was known in advance to be task-relevant (σ_v,VT,att+, modality-specific-attention group only) and 4) with vision unattended, when touch was known ahead to be task-relevant (σ_v,VT,att−, modality-specific-attention group only). An analogous set of four parameters were used for the reliability of tactile signals.

A.1.2. Causal-inference model — priors

The basic causal-inference model assumes that in the case of two separate origins, the ideal observer still relies on her prior knowledge about the distribution of visual-tactile objects in the world (p(s_vt)). Yet, the observer’s prior experiences might differ for locations of visually and tactually perceived objects. To test this second possibility we extended the model to include modality-specific priors $p (s_{v}) ~ N (μ_{p \cdot v}, σ_{p \cdot v})$ and $p (s_{t}) ~ N (μ_{p \cdot t}, σ_{p \cdot t})$ ) (Odegaard et al., 2015; Bosen et al., 2016). These priors are used when separate causes are inferred, whereas p(s_vt) is used when a common cause is inferred. Eq. (2) then becomes

{\hat{s}}_{v, C = 2} = \frac{x_{v} σ_{v}^{- 2} + μ_{p \cdot v} σ_{p \cdot v}^{- 2}}{σ_{v}^{- 2} + σ_{p \cdot v}^{- 2}} and {\hat{s}}_{t, C = 2} = \frac{x_{t} σ_{t}^{- 2} + μ_{p \cdot t} σ_{p \cdot t}^{- 2}}{σ_{t}^{- 2} + σ_{p \cdot t}^{- 2}}

(2a)

and Eq. (5) becomes

p (x_{v}, x_{t} | C = 2) = \frac{1}{2 π \sqrt{(σ_{v}^{2} + σ_{p \cdot v}^{2}) (σ_{t}^{2} + σ_{p \cdot t}^{2})}} \exp (- \frac{1}{2} (\frac{{(x_{v} - μ_{p \cdot v})}^{2}}{σ_{v}^{2} + σ_{p \cdot v}^{2}} + \frac{{(x_{t} - μ_{p \cdot t})}^{2}}{σ_{t}^{2} + σ_{p \cdot t}^{2}})) .

(5a)

Consistent with modality-specific priors, our participants showed biases in tactile but not in visual localization (Fig. 6). Overall tactile localization was shifted toward the elbow, yet, some participants showed shifts toward the wrist. Such biases toward anatomical landmarks are a known feature of tactile localization (de Vignemont et al., 2009) and have been attributed to the categorization of the body into parts (Knight, Longo, & Bremner, 2014). To accommodate biases toward either one or both joints, we consider models that include a bimodal tactile prior $(p (s_{t}) ~ ω N (μ_{p \cdot t_{ellow}}, σ_{p \cdot t_{elbow}}) + (1 - ω) N (μ_{p \cdot t_{wrist}}, σ_{p \cdot t_{wrist}}), ω \in [0, 1])$ over tactile space.

Eq. (2) becomes

{\hat{s}}_{v, C = 2} = \frac{x_{v} σ_{v}^{- 2} + μ_{p \cdot v} σ_{p \cdot v}^{- 2}}{σ_{v}^{- 2} + σ_{p \cdot v}^{- 2}} and {\hat{s}}_{t, C = 2} = \overset{mode}{s_{t}} (\frac{1}{\sqrt{2 π σ_{t}^{2}}} \exp (\frac{- {(s_{t} - x_{t})}^{2}}{2 σ_{t}^{2}}) (\frac{ω}{\sqrt{2 π σ_{p \cdot t_{elbow}}^{2}}} \exp (\frac{{- (x_{t} - μ_{p \cdot t_{elbow}})}^{2}}{2 σ_{p \cdot t_{elbow}}^{2}}) + \frac{1 - ω}{\sqrt{2 π σ_{p \cdot t_{wrist}}^{2}}} \exp (\frac{{- (x_{t} - μ_{p \cdot t_{wrist}})}^{2}}{2 σ_{p \cdot t_{wrist}}^{2}})))

(2b)

and Eq. (5) becomes

p (x_{t}, x_{v} | C = 2) = \frac{1}{\sqrt{2 π (σ_{v}^{2} + σ_{p \cdot v}^{2})}} \exp (\frac{- {(x_{v} - μ_{p \cdot v})}^{2}}{2 (σ_{v}^{2} + σ_{p \cdot v}^{2})}) \frac{ω}{\sqrt{2 π (σ_{t}^{2} + σ_{p \cdot t_{elbow}}^{2})}} \exp (\frac{- {(x_{t} - μ_{p \cdot t_{elbow}})}^{2}}{2 (σ_{t}^{2} + σ_{p \cdot t_{elbow}}^{2})}) + \frac{1}{\sqrt{2 π (σ_{v}^{2} + σ_{p \cdot v}^{2})}} \exp (\frac{- {(x_{v} - μ_{p \cdot v})}^{2}}{2 (σ_{v}^{2} + σ_{p \cdot v}^{2})}) \frac{(1 - ω)}{\sqrt{2 π (σ_{t}^{2} + σ_{p \cdot t_{wrist}}^{2})}} \exp (\frac{- {(x_{t} - μ_{p \cdot t_{wrist}})}^{2}}{2 (σ_{t}^{2} + σ_{p \cdot t_{wrist}}^{2})}) .

(5b)

A.1.3. Causal-inference model — shifted likelihoods

As stated above, the base model assumed that an ideal observer has a correct representation of the Gaussian noise that distorts the sensory measurements and uses this knowledge for inferences about the location of the stimulus. The likelihood function assigns a probability to each world location based on the sensory measurement. If that sensory noise is assumed to have zero mean, the likelihood function is centered at the measurement

L (s_{v} | x_{v}) = ϕ (s_{v}; x_{v}, σ_{v}^{2}) and L (s_{t} | x_{t}) = ϕ (s_{t}; x_{t}, σ_{t}^{2}),

(10)

where ϕ is the Gaussian density function. Yet, cross-modal recalibration, such as the ventriloquism aftereffect, is often implemented as a shift in the sensory likelihoods (Sato et al., 2007; Wozny & Shams, 2011). If the likelihoods are shifted, the same sensory measurement is interpreted as evidence for a different location in the world than without the shift. We tested the possibility that due to naturally occurring recalibration the visual and tactile sensory likelihoods were shifted in Expt. 1 (Odegaard et al., 2015; Bosen et al., 2016). Thus, we also consider models with shifted likelihoods, so that Eq. (10) becomes

L (s_{v} | x_{v}) = ϕ (s_{v}; x_{v} - Δ_{v}, σ_{v}^{2}) and L (s_{t} | x_{t}) = ϕ (s_{t}; x_{t} - Δ_{t}, σ_{t}^{2}) .

(10a)

A.1.4. Causal-inference model — localization response

An ideal observer that strives to minimize squared error (Bayesian least squares) performs model averaging (Eq. (6)), weighting the two conditional location estimates (Eqs. (1) and (2)) by the posterior probability of each scenario (e.g., Eq. (3)). We will also consider models using suboptimal, heuristic strategies for estimating the location. In the first such model, the observer reports the combined location estimate (Eq. (1)) whenever the distance between the visual and the tactile measurements (x_v, x_t) is smaller than a fixed threshold value (κ), and the segregated location estimate (Eq. (2)) otherwise (Rohe & Noppeney, 2015b; Acerbi et al., 2018).

{\hat{s}}_{v} = {\begin{array}{l} {\hat{s}}_{v t, C = 1} & if | x_{v} - x_{t} | < κ \\ {\hat{s}}_{v, C = 2} & otherwise \end{array}, {\hat{s}}_{t} = {\begin{array}{l} {\hat{s}}_{v t, C = 1} & if | x_{v} - x_{t} | < κ \\ {\hat{s}}_{t, C = 2} & otherwise . \end{array}

(11)

In a second heuristic model, the observer bases this choice on the distance between the segregated location estimates for vision and touch (Eq. (2)). This heuristic, unlike the first one, takes into account the observer’s knowledge about sensory noise and the distribution of stimuli in the world:

{\hat{s}}_{v} = {\begin{array}{l} {\hat{s}}_{v t, C = 1} & if | {\hat{s}}_{v, C = 2} - {\hat{s}}_{t, C = 2} | < κ \\ {\hat{s}}_{v, C = 2} & otherwise \end{array}, {\hat{s}}_{t} = {\begin{array}{l} {\hat{s}}_{v t, C = 1} & if | {\hat{s}}_{v, C = 2} - {\hat{s}}_{t, C = 2} | < κ \\ {\hat{s}}_{t, C = 2} & otherwise. \end{array}

(12)

A.1.5. Causal-inference model — spatial-alignment response

The ideal observer reports the visual and tactile stimuli to be spatially aligned if the probability of a common source (Eq. (3)) exceeds 50%. We additionally consider three heuristic decision rules for the alignment judgment. An observer might base the spatial-alignment response on the distance between the two measurements (x_v,x_t):

I_{intended ‘aligned’ response} = {\begin{array}{l} 1 & if | x_{v} - x_{t} | < κ \\ 0 & otherwise \end{array}

(13)

or on the distance between the two segregated location estimates:

I_{intended ‘aligned’ response} = {\begin{array}{l} 1 & if | {\hat{s}}_{v, C = 2} - {\hat{s}}_{t, C = 2} | < κ \\ 0 & otherwise . \end{array}

(14)

We assumed that observers who based their localization response on a heuristic would base the spatial-alignment response on the same heuristic. Alternatively, an observer might use optimal Bayesian inference to derive the localization response, but base the alignment response on a heuristic. Such observers could rely on the first two heuristics or on the distance between the two optimal location estimates for vision and touch:

I_{intended ‘aligned’ response} = {\begin{array}{l} 1 & if | {\hat{s}}_{v} - {\hat{s}}_{t} | < κ \\ 0 & otherwise \end{array}

(15)

As for the optimal decision rule, we again assume that the observer chooses the non-intended alignment-response with probability λ, so that the probability of a response indicating that the stimuli were perceived as aligned is $p (I_{‘aligned’ response} = 1 | x_{v}, x_{t}) = λ p (I_{intended ‘aligned’ response} = 0 | x_{v}, x_{t}) + (1 - λ) p (I_{intended ‘aligned’ response} = 1 | x_{v}, x_{t})$

A.1.6. Model fitting

We fitted the models to the data using maximum-likelihood estimation, that is, by determining the parameter vector $θ \in Θ$ that maximizes the likelihood $p (data | Θ, M)$ for any given model M. Models were fit separately to data from individual participants. We did this by maximizing the log-likelihood $L L (Θ, M) = \log (p (data | Θ, M)) = \sum_{i = 1}^{N_{trials}} \log (p (response in trial i | Θ, s_{t}^{i}, s_{v}^{i}))$ , thus assuming that responses were independent across trials. Data from visual, tactile, and visual-tactile trials were evaluated simultaneously. To improve model-based inference, we further fitted the models simultaneously to localization and spatial-alignment responses. That is, we maximized the joint likelihood

\begin{array}{l} p (r_{v}, I_{‘aligned’ response} | s_{t}, s_{v}, Θ) = p (r_{v} | I_{‘aligned’ response}, s_{t}, s_{v}, Θ) p (I_{‘aligned’ response} | s_{t}, s_{v}, Θ) \\ p (r_{t}, I_{‘aligned’ response} | s_{t}, s_{v}, Θ) = p (r_{t} | I_{‘aligned’ response}, s_{t}, s_{v}, Θ) p (I_{‘aligned’ response} | s_{t}, s_{v}, Θ) . \end{array}

(16)

We approximated the integrals in Eqs. (8) and (9) using 30,000 Monte Carlo simulations. To determine the conditional probabilities of the localization responses $(e.g., p (r_{v} | s_{t}, s_{v}, I_{‘aligned’ response} = 1, Θ))$ , the simulated localization responses were quantized into 41 bins of 5 mm width and two larger bins containing all responses more than 100 mm to the left and to the right of the center location. The empirical distribution of simulated responses across those bins was determined separately for each simulated spatial alignment response. The conditional probability $p (I_{‘aligned’ response} = 1 | s_{t}, s_{v}, Θ)$ that the observer indicated spatial alignment when the visual and the tactile stimuli were presented at locations s_v and s_t was obtained from the simulated data by calculating the empirical probability of each alignment response. We additionally assumed that participants would indicate a random location (a randomly chosen bin) in a very low percentage of trials. This reasonable assumption prevented numerical problems during fitting that arise from empirical probabilities of zero. Finally, the observed localization responses were quantized in the same way as the simulated ones to determine the likelihood of the response in a single trial as a function of the parameter vector Θ.

The parameter space Θ was high-dimensional with potential collinearities between some parameters. Consequently, a convex likelihood function was not expected. We fitted the data in a two-step process. In the first step we cast a wide net of grid points within Θ. In a second step, we used the ten best-fitting parameter sets per model as starting points for a conditional maximization procedure. In every step of the conditional-maximization procedure, the parameter set was randomly divided into two subsets, one of fixed and one of variable parameters. The number of variable parameters was randomly determined in every step, however, smaller sets were chosen with larger probability. The fixed parameters were set to their values from the previous step of the procedure while we searched for the values of the variable parameters that maximized log likelihood. Due to the stochastic nature of our model, we used a mesh algorithm with a generalized pattern search polling strategy (as implemented in Matlab’s pattern-search function) to find the best estimates for the variable parameters within one step of the conditional-maximization procedure. 100 repetitions of this procedure were run for each model and starting point. To check the fitting procedure, we conducted a parameter recovery for the best-fitting model. Given that the time needed to fit the model increased considerably with each additional parameter, we limited the recovery to our parameters of interest and cast a wide net for these parameters. The parameter recovery revealed no problems (see Fig. S4). We used Akaike’s information criterion (AIC), separately averaged across participants from the modality-specific- and distributed-attention groups, for model comparison. Please note, model rankings based on BIC were identical.

A.1.7. Parameter analysis

We compared the estimates of the reliability parameters ( $σ_{v, V T}, σ_{t, V T}, σ_{v, V}, σ_{t, T}$ in the distributed-attention group and $σ_{v, v T, a t t +}, σ_{t, V T, a t t +}, σ_{v, V}, σ_{t, T}$ in the modality-specific-attention group) and estimates of participants’ common-cause prior (p_CC) across attention groups using unpaired t-tests.

A.1.8. Model simulations

Our parameter analysis served to reveal changes in the top-down and bottom-up factors that control causal inference and accompany the observed change in behavior. However, changes in causal-inference parameters and in observed behavior might have been independent of each other. To characterize the influence of sensory reliabilities and common-source priors on visual-tactile integration effects, we simulated both measures of visual-tactile ventriloquism using the causal-inference model. To render these simulation results as general as possible, we used a wide range for the parameters of interest $(σ_{v, V T}, σ_{t, V T}, σ_{v, V T, a t t +}, σ_{t, V T, a t t +} \in [0, 80]; p_{C C} \in [0, 1])$ , but assumed uninformative modality-specific or supramodal priors $(N (0, 5000))$ and no likelihood shifts. The combination of uninformative priors and unshifted likelihoods has the additional consequence that simulated localization responses to visual and tactile stimuli presented alone are centered on the physical stimulus location. Thus, we simulated ventriloquism effects in the form of localization shifts by calculating the difference between the simulated physical and estimated stimulus location. For the second measure of ventriloquism, spatial-alignment responses, we report the estimated probability of a common cause $(P (C = 1 | s_{v}, s_{t}))$ to avoid information loss by transforming these probabilities into binary values. For each combination of parameters, we conducted 100 simulations. For each condition (location of the visual stimulus, s_v × location of the tactile stimulus, s_t × response-relevant modality), we simulated an observer’s location estimate ( ${\hat{s}}_{t | s_{v}, s_{t}}$ ) and the probability of a common cause $(P (C = 1 | s_{v}, s_{t}))$ by sampling 30,000 measurements (x_v, x_t) from the measurement distributions ( $N$ (s_v, σ_v), $N$ (s_t, σ_t)), deriving the corresponding 30,000 location and probability estimates ( ${\hat{s}}_{t | s_{v}, s_{t}}$ and $P (C = 1 | x_{v}, x_{t})$ , respectively) and taking the mean.

A.2. Results — causal-inference models of visual-tactile integration

A.2.1. Model comparison

Data from both the modality-specific- and distributed-attention groups were best fit by a model in which localization responses were derived in an ideal-observer fashion (Tables 1 and 2). Thus, participants performed Bayes-optimal causal inference to indicate the location of the cued stimulus. In contrast, spatial-alignment judgments were derived sub-optimally, based on the difference between visual and tactile location estimates. In the best-fitting model, likelihoods could be shifted and the prior over tactile locations was potentially bimodal, with one mode shifted toward the elbow and one toward the wrist. Simulations with the best-fitting model using the maximum-likelihood estimates of the parameters reproduce all of the qualitative aspects of the data and fit the data well (Figs. 13 and 14; see Fig. S3 for data from individual participants).

The second-best-fitting model was identical across both groups and differed from the best-fitting model only in one component: spatial-alignment responses were based on the difference between visual and tactile location estimates given separate sources.

Table 1.

Group	Prior	Likelihood	Decision Rule Localization	Decision Rule Fusion	# Parameters	AIC	ΔAIC
Modality-specific attention	modality-specific; tactile: mixture	shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	21	3563	0
Modality-specific attention	modality-specific; tactile: mixture	shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	21	3570	7
Modality-specific attention	modality-specific; tactile: mixture	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	20	3578	15
Modality-specific attention	modality-specific; tactile: mixture	shifted	model averaging	p_CC < 0.5	20	3592	30
Modality-specific attention	modality-specific; tactile: mixture	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	20	3595	33
Modality-specific attention	modality-specific	shifted	model averaging	p_CC < 0.5	17	3603	41
Modality-specific attention	modality-specific; tactile: mixture	non-shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	19	3625	62
Modality-specific attention	modality-specific; tactile: mixture	non-shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	19	3643	80
Modality-specific attention	modality-specific	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	15	3646	84
Modality-specific attention	modality-specific	non-shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	16	3651	88
Modality-specific attention	modality-specific; tactile: mixture	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1,} if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	18	3657	95
Modality-specific attention	modality-specific; tactile: mixture	non-shifted	model averaging	p_CC < 0.5	18	3678	116
Modality-specific attention	modality-specific	non-shifted	model averaging	p_CC < 0.5	15	3693	130
Modality-specific attention	modality-specific; tactile: mixture	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	18	3723	161
Modality-specific attention	modality-specific	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	15	3726	164
Modality-specific attention	modality-specific	shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	18	3966	403
Modality-specific attention	modality-specific	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1,} if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	17	4071	509
Modality-specific attention	modality-specific	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1,} if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	17	4080	518
Modality-specific attention	modality-specific	non-shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	16	5819	2256
Modality-specific attention	modality-specific	shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	18	6190	2628

Open in a new tab

Table 2.

Group	Prior	Likelihood	Decision Rule Localization	Decision Rule Fusion	# Parameters	AIC	ΔAIC
Distributed attention	modality-specific; tactile: mixture	shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	19	4135	0
Distributed attention	modality-specific; tactile: mixture	shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	19	4147	12
Distributed attention	modality-specific; tactile: mixture	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	18	4164	29
Distributed attention	modality-specific; tactile: mixture	non-shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	17	4179	44
Distributed attention	modality-specific; tactile: mixture	non-shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	17	4179	44
Distributed attention	modality-specific; tactile: mixture	shifted	model averaging	p_CC < 0.5	18	4193	58
Distributed attention	modality-specific; tactile: mixture	non-shifted	model selection	$\| x_{t} - x_{v} \| < κ$	16	4199	64
Distributed attention	modality-specific; tactile: mixture	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	18	4206	71
Distributed attention	modality-specific; tactile: mixture	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	16	4217	82
Distributed attention	modality-specific	shifted	model averaging	p_CC < 0.5	15	4220	85
Distributed attention	modality-specific; tactile: mixture	non-shifted	model averaging	p_CC < 0.5	16	4242	107
Distributed attention	modality-specific	non-shifted	model averaging	p_CC < 0.5	13	4259	123
Distributed attention	modality-specific	shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	16	4746	611
Distributed attention	modality-specific	non-shifted	model averaging	$\| {\hat{s}}_{t} - {\hat{s}}_{v} \| < κ$	14	4799	664
Distributed attention	modality-specific	shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	16	5188	1052
Distributed attention	modality-specific	non-shifted	model averaging	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	14	5316	1181
Distributed attention	modality-specific	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	15	5367	1232
Distributed attention	modality-specific	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| {\hat{s}}_{t, C = 2} - {\hat{s}}_{v, C = 2} \| < κ$	13	5368	1233
Distributed attention	modality-specific	shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	15	5807	1672
Distributed attention	modality-specific	non-shifted	model selection ${\hat{s}}_{t} = {\hat{s}}_{v t, C = 1}, if \| x_{t} - x_{v} \| < κ {\hat{s}}_{t} = {\hat{s}}_{t, C = 2}, otherwise$	$\| x_{t} - x_{v} \| < κ$	13	5850	1715

Open in a new tab

Fig. 13. — Simulated ventriloquism effect — localization shifts. Simulated and observed group mean localization responses as a function of the physical stimulus location (negative numbers indicate locations closer to the elbow) split by inter-modal discrepancy (negative numbers indicate that visual stimuli were closer to the elbow than the tactile stimulus; ‘none’ indicates that only one modality was presented). For each participant, we simulated 2000 trials per location using participant-level parameter estimates for the overall best-fitting model. Error bars show standard errors of the mean.

Fig. 14. — Simulated ventriloquism effect — perceived spatial alignment. Simulated and observed group mean proportions of alignment responses as a function of the inter-modal discrepancy (negative numbers indicate that visual stimuli were closer to the elbow than the tactile stimulus). For each participant, we simulated 2000 trials per location using participant-level parameter estimates for the overall best-fitting model. Error bars show standard errors of the mean.

A.2.2. Parameter estimates

We then analyzed the best-fitting model to test whether attention affected sensory reliabilities and the a priori expectation about visual and tactile signals sharing a common source.

The reliability of visual stimuli presented in the context of visual-tactile stimulus pairs (measured as standard deviations σ_v,VT and σ_v,VT,att+ for the distributed- and modality-specific-attention group, respectively) did not differ significantly between groups, t(10) = 1.74, p = 0.113, d = 0.78 (Fig. 8A). The reliability of tactile stimuli presented in the context of visual-tactile stimulus pairs was significantly higher for the modality-specificattention than for the distributed-attention group (measured as standard deviations σ_t,VT and σ_t,VT,att+), t(10) = 2.4, p = 0.037, d = 1.07 (Fig. 8B). Neither the reliability of visual nor of tactile stimuli presented alone differed significantly between groups, t(10) = 1.38, p = 0.197, d = 0.62 and t(10) = 1.14, p = 0.280, d = 0.51. Participants in the distributed-attention group assumed a significantly higher probability that visual and tactile signals share the same source (p_CC) than participants in the modality-specific-attention group, t(10) = 2.29, p = 0.045, d = 1.02 (Fig. 8C). A similar pattern of parameter estimates was obtained for the second-best-fitting model (Fig. S2).

A.2.3. Model simulations

After having established that the focus of attention changed sensory reliabilities and the prior probability that vision and touch share a common source, we tested how changes in either of these parameters affect visual-tactile integration. To this aim, we simulated visual-tactile ventriloquism effects based on a wide range of each of these parameters. An increase in the prior probability of a shared source was associated with larger shifts in the perceived locations (Fig. 9) and higher probabilities of perceiving the stimuli as sharing a source and thus as spatially aligned (Fig. 10).

Moreover, localization shifts (Fig. 9) generally became larger with decreases in the reliability of the to-be-localized modality and increases in the reliability of the other modality. In contrast, comparable changes in the reliabilities of both modalities hardly influenced localization shifts across a large range of reliabilities. However, if the reliability of the non-task-relevant modality was high (small σ_t in Fig. 9A and small σ_v in Fig. 9B) localization shifts decreased again with very low reliabilities of the to-be-localized modality (σ_v in Fig. 9A and σ_t in Fig. 9B). Thus, there is a ‘sweet spot’ of visual and tactile reliabilities in which localization shifts are maximal. For an intuition for this effect, consider a case in which there is high visual reliability (e.g., σ_v = 5), a much lower tactile reliability (e.g., σ_t = 20), and a small discrepancy between visual and tactile stimulus locations (e.g., −15, the visual stimulus being located 15 mm closer to the elbow than the tactile stimulus). Fig. 9B shows that the shifts in the perceived location of touch will decrease if the reliability of touch decreases further, relatively independent of the prior probability of a common cause. If the reliability of touch decreases, tactile measurements will spread further around the true location. Due to the higher visual reliability, the fused location estimates ( ${\hat{s}}_{t, C = 1}$ ) will be close to the physical location of the visual stimulus in the majority of trials. However, the weight assigned to the fused estimate on average decreases with decreasing tactile reliability (Eq. (4)). Thus, in the case of already low tactile reliabilities as in our study, if reliability decreases further, the final location estimates are more influenced by the tactile measurements and less by the fused location estimates, resulting in smaller shifts of the perceived location of touch toward the visual stimulus.

The influence of sensory reliabilities on the estimated probability of perceiving the stimuli as sharing a source depended critically on the spatial discrepancy of the visual-tactile stimulus pair. In the case of large spatial cross-modal discrepancies (Fig. 10, outer columns), a decrease in sensory reliability (increase in σ_v or σ_t) led to an increase in the probability of perceiving the stimulus pair as originating from the same source. If sensory reliabilities are high, it is very unlikely that two measurements with a considerable distance originated from the same source. If reliabilities decrease, measurements spread wider around their source and it becomes more likely that two measurements with the same considerable discrepancy between them originated from the same source. In contrast, in the case of small or absent spatial cross-modal discrepancies, (Fig. 10, inner columns) a decrease in sensory reliability (increase in σ_v and σ_t) would lead to a decrease in the estimated probability of perceiving the stimuli as sharing a source. If the physical stimuli are spatially aligned or very similar, most measurements will be similar across modalities if both sensory reliabilities are high. However, if the reliabilities decrease, measurements will spread wider, resulting in greater perceived discrepancies across modalities. As a consequence, the average estimated probability that the two measurements originated from the same source will decrease. Both effects were symmetrical across both sensory reliabilities, and restricted to high and moderate reliabilities. For low sensory reliabilities, the estimated probability of perceiving the stimuli as coming from a shared source slightly decreased with further decreases in reliability and depended mostly on the prior probability of a common cause.

A.3. Causal-inference models of visual-tactile recalibration.

Finally, we explored the influence of the sensory reliabilities and the common-cause prior on cross-modal recalibration. The causal-inference model of recalibration (Sato et al., 2007) builds on the causal-inference model of integration. In every trial of the adaptation phase, an ideal observer derives a visual and a tactile location estimate ( ${\hat{s}}_{v}$ , ${\hat{s}}_{t}$ ) based on the conditional location estimates $({\hat{s}}_{v t, C = 1}, {\hat{s}}_{v, C = 2}, {\hat{s}}_{t, C = 2})$ and the probabilities of the underlying scenarios $(p (C = 1 | x_{v}, x_{t}), p (C = 2 | x_{v}, x_{t}))$ . The difference between each measurement and the optimal location estimate updates the shifts of the likelihoods (Δ_v, Δ_t, Eq. (10a)):

\begin{array}{l} Δ_{v} (n + 1) = (1 - α) Δ_{v} (n) + α (x_{v} (n) - {\hat{s}}_{v} (n)) \\ Δ_{t} (n + 1) = (1 - α) Δ_{t} (n) + α (x_{t} (n) - {\hat{s}}_{t} (n)), \end{array}

(17)

where α controls the learning rate.

This learning rule (Eq. (17)) indirectly depends on the observer’s assessment of the source of the two measurements, because the optimal location estimate does so. However, observers might employ additional precautions to avoid recalibration based on non-corresponding cross-modal signals. In one alternative model, observers recalibrate only in trials in which they judge the two measurements as sharing the same source:

Δ_{v} (n + 1) = {\begin{matrix} (1 - α) Δ_{v} (n) + α (x_{v} (n) - {\hat{x}}_{v} (n)) & if P (C = 1 | x_{v} (n), x_{t} (n)) > 0.5 \\ Δ_{v} (n) & otherwise \end{matrix} Δ_{t} (n + 1) = {\begin{matrix} (1 - α) Δ_{t} (n) + α (x_{t} (n) - {\hat{x}}_{t} (n)) & if P (C = 1 | x_{v} (n), x_{t} (n)) > 0.5 \\ Δ_{t} (n) & otherwise . \end{matrix}

(18)

In an alternative model, observers modulate the learning rate in every trial according to the posterior probability that the two signals share the same source:

\begin{array}{l} Δ_{v} (n + 1) = (1 - α P (C = 1 | x_{v} (n), x_{t} (n))) Δ_{v} (n) + α P (C = 1 | x_{v} (n), x_{t} (n)) (x_{v} (n) - {\hat{x}}_{v} (n)) \\ Δ_{t} (n + 1) = (1 - α P (C = 1 | x_{v} (n), x_{t} (n))) Δ_{t} (n) + α P (C = 1 | x_{v} (n), x_{t} (n)) (x_{t} (n) - {\hat{x}}_{t} (n)) . \end{array}

(19)

A.3.1. Model simulations

We simulated visual-tactile recalibration effects using each of the three learning rules and parameter estimates derived for data from Expt. 1. Fitting the model to the data was not feasible because of the serial dependencies across trials during the adaptation phase. Recalibration changes the shifts applied to the sensory measurements arriving in the brain based on the discrepancy between the initial sensory measurements and the final location estimate. Consequently, the shift of a sensory measurement in trial n will vary according to the discrepancy between the measurement and estimate in trial n − 1, which in turn depend on the previous trial. The problem is that this serial dependency involves the measurements, to which we have no access. As long as trials are independent, we can marginalize over all measurements, which we did via Monte Carlo simulations. However, in the case of serial dependence on the measurements it is not possible to do so separately for each trial. Rather we would have to draw 30,000 samples for trial 1 and 30,000 × 30,000 for trial 2 (30,000 for each sample in trial 1), etc.

In the model simulations, we varied three parameters susceptible to our attentional manipulation: participants’ estimate of the probability that both signals share the same source (p_CC ∈ [0,1]), the reliability of the (attended) tactile signal in a visual-tactile context (σ_t,TV ∈ [5 mm,120 mm] in the distributed-attention group, σ_t,TV,att+ ∈ [5 mm,120 mm] in the modality-specific-attention group), and the effect of withdrawing attention from touch toward vision on the reliability of the same tactile signal (σ_t,TV,att− − σ_t,TV,att+ = 40, 80, or 120 mm in the modality-specific-attention group only). For every model variant, we used two learning rates (α) one roughly matched to the size of the recalibration effect in the distributed-attention group (a different value for each model) and one 0.003 lower. All other parameters were held constant. We used Monte Carlo simulations to marginalize across the noisy visual and tactile measurements. As in the behavioral experiment, per group we simulated twelve observers performing 350 adaptation trials, 70 repetitions at each of the five possible stimulus locations. The order of stimuli was randomized across observers and 100 simulations were conducted per parameter set.

To quantify the estimated recalibration effect, we simulated 1000 trials for the localization of visual and tactile stimuli presented alone before and after the adaptation, i.e., with updated shifts. As for our observed data, we fitted a linear regression model to each simulated observer’s data and quantified the ventriloquism aftereffect by comparing the regression intercepts between the pre- and post-adaptation phases.

A.3.2. Model simulations — visual-tactile recalibration

The results of our simulations are shown in Fig. 11. All three model variants predict higher recalibration of touch with increasing expectation of the two signals sharing a source (p_CC) and with increasing learning rate (α). The influence of the reliability of the attended, tactile stimulus (i.e., σ_t,VT,att+ in the modality-specific-attention group, σ_t,VT in the distributed-attention group) on tactile recalibration is non-monotonic. Below the reversal point (located at around 20 mm), a decrease in reliability (i.e., an increase in standard deviation) is associated with an increase in recalibration effects. Above this reversal point, a further decrease in reliability is associated with smaller recalibration effects. This behavior can be explained as follows. If tactile reliability is very high (e.g., a standard deviation of 2 mm), the optimal location estimate ( ${\hat{s}}_{t}$ ) is hardly influenced by the measured location of the visual stimulus. As a consequence, barely any discrepancy between measurement (x_t) and location estimate ( ${\hat{s}}_{t}$ ) will be noticed by the tactile system and, thus, if at all, only a small recalibration shift will occur. If tactile reliability decreases (e.g., to a standard deviation of 15 mm), the optimal tactile location estimate will be shifted closer toward the location of the visual stimulus. This leads to higher discrepancies between measured and estimated touch location and, thus, larger correcting shifts. Thus, in this range recalibration effects should increase with decreasing reliability. However, if tactile reliability is reduced further (e.g., to a standard deviation of 60 mm), optimal tactile location estimates will be shifted less toward the visual stimulus (Fig. 9), leading to smaller discrepancies between measured and estimated touch locations and thus smaller recalibration effects. In our experiments, touch had a relatively low spatial reliability (Fig. 8). Consequently, the simulation results indicate that the increase in recalibration with the need to attend to both stimuli that we found in Expt. 2 is driven solely by an increase in participants’ expectation that the visual and tactile signals share a source.

All model variants predicted larger recalibration effects for the distributed- than for the modality-specific-attention group. However, only the model in which recalibration was conditional on a shared source between the two signals predicted an effect large enough to be in agreement with the observed results (the predicted shifts at the red squares and red circles in Fig. 11).

Appendix B. Supplementary data

Raw data are available at https://osf.io/epcqv/?view_only=ab4d5bc816b54548918b3548bb7eed7d. Supplementary data to this article can be found online at https://doi.org/10.1016/j.cognition.2019.104170.

Footnotes

IA denotes the indicator function. I_A = 1 if A is true, I_A = 0 otherwise.

References

Acerbi L, Dokka K, Angelaki DE, & Ma WJ (2018). Bayesian comparison of explicit and implicit causal inference strategies in multisensory heading perception. PLoS Computational Biology, 14, e1006110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Alais D, & Burr D. (2004). The ventriloquist effect results from near-optimal bimodal integration. Current Biology, 14, 257–262. 10.1016/j.cub.2004.01.029. [DOI] [PubMed] [Google Scholar]
Alais D, Newell FN, & Mamassian P. (2010). Multisensory processing in review: From physiology to behaviour. Seeing and Perceiving, 23, 3–38. 10.1163/187847510X488603. [DOI] [PubMed] [Google Scholar]
Alsius A, Navarra J, Campbell R, & Soto-Faraco S. (2005). Audiovisual integration of speech falters under high attention demands. Current Biology, 15, 839–843. 10.1016/j.cub.2005.03.046. [DOI] [PubMed] [Google Scholar]
Alsius A, Navarra J, & Soto-Faraco S. (2007). Attention to touch weakens audiovisual speech integration. Experimental Brain Research, 183, 399–404. 10.1007/s00221-007-1110-1. [DOI] [PubMed] [Google Scholar]
Anderson MJ (2001). Permutation tests for univariate or multivariate analysis of variance and regression. Canadian Journal of Fisheries and Aquatic Sciences, 58, 626–639. [Google Scholar]
Atkins JE, Fiser J, & Jacobs RA (2001). Experience-dependent visual cue integration based on consistencies between visual and haptic percepts. Vision Research, 41, 449–461. [DOI] [PubMed] [Google Scholar]
Atkins JE, Jacobs RA, & Knill DC (2003). Experience-dependent visual cue recalibration based on discrepancies between visual and haptic percepts. Vision Research, 43, 2603–2613. [DOI] [PubMed] [Google Scholar]
Azanon E, Mihaljevic K, & Longo MR (2016). A three-dimensional spatial characterization of the crossed-hands deficit. Cognition, 157, 289–295. 10.1016/j.cognition.2016.09.007. [DOI] [PubMed] [Google Scholar]
Battaglia PW, Jacobs RA, & Aslin RN (2003). Bayesian integration of visual and auditory signals for spatial localization. Journal of the Optical Society of America. A, Optics, Image Science, and Vision, 20, 1391–1397. [DOI] [PubMed] [Google Scholar]
Beierholm UR, Quartz SR, & Shams L. (2009). Bayesian priors are encoded independently from likelihoods in human multisensory perception. Journal of Vision, 9, 23.1–23.9. 10.1167/9.5.23. [DOI] [PubMed] [Google Scholar]
Bermant RI, & Welch RB (1976). Effect of degree of separation of visual-auditory stimulus and eye position upon spatial interaction of vision and audition. Perceptual and Motor Skills, 42, 487–493. 10.2466/pms.1976.42.2.487. [DOI] [PubMed] [Google Scholar]
Bertelson P, & Aschersleben G. (1998). Automatic visual bias of perceived auditory location. Psychonomic Bulletin & Review, 5, 482–489. 10.3758/BF03208826. [DOI] [Google Scholar]
Bertelson P, & De Gelder B. (2004). The psychology of multimodal perception. Crossmodal Space and Crossmodal Attention, 141–177. [Google Scholar]
Bertelson P, Frissen I, Vroomen J, & de Gelder B. (2006). The aftereffects of ventriloquism: Patterns of spatial generalization. Perception & Psychophysics, 68, 428–436. [DOI] [PubMed] [Google Scholar]
Bertelson P, & Radeau M. (1981). Cross-modal bias and perceptual fusion with auditory-visual spatial discordance. Perception & Psychophysics, 29, 578–584. [DOI] [PubMed] [Google Scholar]
Bertelson P, Vroomen J, de Gelder B, & Driver J. (2000). The ventriloquist effect does not depend on the direction of deliberate visual attention. Perception & Psychophysics, 62, 321–332. [DOI] [PubMed] [Google Scholar]
Bosen AK, Fleming JT, Allen PD, O’Neill WE, & Paige GD (2017). Accumulation and decay of visual capture and the ventriloquism aftereffect caused by brief audio-visual disparities. Experimental Brain Research, 235, 585–595. 10.1007/s00221-016-4820-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bosen AK, Fleming JT, Brown SE, Allen PD, O’Neill WE, & Paige GD (2016). Comparison of congruence judgment and auditory localization tasks for assessing the spatial limits of visual capture. Biological Cybernetics, 110, 455–471. 10.1007/s00422-016-0706-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brainard DH (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]
Bruns P, Liebnau R, & Röder B. (2011). Cross-modal training induces changes in spatial representations early in the auditory processing pathway. Psychological Science, 22, 1120–1126. 10.1177/0956797611416254. [DOI] [PubMed] [Google Scholar]
Bruns P, & Röder B. (2010a). Tactile capture of auditory localization: an event-related potential study. The European Journal of Neuroscience, 31, 1844–1857. 10.1111/j.1460-9568.2010.07232.x. [DOI] [PubMed] [Google Scholar]
Bruns P, & Röder B. (2010b). Tactile capture of auditory localization is modulated by hand posture. Experimental Psychology, 57, 267–274. 10.1027/16183169/a000032. [DOI] [PubMed] [Google Scholar]
Bruns P, & Röder B. (2015). Sensory recalibration integrates information from the immediate and the cumulative past. Scientific Reports, 5, 12739 10.1038/srep12739. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bruns P, Spence C, & Röder B. (2011). Tactile recalibration of auditory spatial representations. Experimental Brain Research, 209, 333–344. 10.1007/s00221-011-2543-0. [DOI] [PubMed] [Google Scholar]
Burge J, Girshick AR, & Banks MS (2010). Visual-haptic adaptation is determined by relative reliability\ The Journal of Neuroscience, 30, 7714–7721. 10.1523/JNEUROSCI.6427-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
Caclin A, Soto-Faraco S, Kingstone A, & Spence C. (2002). Tactile “capture” of audition. Perception & Psychophysics, 64, 616–630. [DOI] [PubMed] [Google Scholar]
Canon LK (1970). Intermodality inconsistency of input and directed attention as determinants of the nature of adaptation. Journal of Experimental Psychology, 84, 141–147. [DOI] [PubMed] [Google Scholar]
Cao Y, Summerfield C, Park H, Giordano BL, & Kayser C. (2019). Causal inference in the multisensory brain. Neuron, 102, 1076–1087. 10.1016/j.neuron.2019.03.043e8. [DOI] [PubMed] [Google Scholar]
Cardini F, & Longo MR (2016). Congruency of body-related information induces somatosensory reorganization. Neuropsychologia, 84, 213–221. 10.1016/j.neuropsychologia.2016.02.013. [DOI] [PubMed] [Google Scholar]
Carrasco M. (2011). Visual attention: The past 25 years. Vision Research, 51, 1484–1525. 10.1016/j.visres.2011.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Charbonneau G, Véronneau M, Boudrias-Fournier C, Lepore F, & Collignon O. (2013). The ventriloquist in periphery: Impact of eccentricity-related reliability on audio-visual localization. Journal of Vision, 13, 20 10.1167/13.12.20. [DOI] [PubMed] [Google Scholar]
Chen L, & Vroomen J. (2013). Intersensory binding across space and time: a tutorial review. Attention, Perception & Psychophysics, 75, 790–811. 10.3758/s13414-013-0475-4. [DOI] [PubMed] [Google Scholar]
Chen Y-C, & Spence C. (2017). Assessing the role of the ‘unity assumption’ on multisensory integration: A review. Frontiers in Psychology, 8, 445 10.3389/fpsyg.2017.00445. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cressman EK, & Henriques DYP (2009). Sensory recalibration of hand position following visuomotor adaptation. Journal of Neurophysiology, 102, 3505–3518. 10.1152/jn.00514.2009. [DOI] [PubMed] [Google Scholar]
Cressman EK, & Henriques DYP (2010). Reach adaptation and proprioceptive recalibration following exposure to misaligned sensory input. Journal of Neurophysiology, 103, 1888–1895. 10.1152/jn.01002.2009. [DOI] [PubMed] [Google Scholar]
Badde S, Navarro KT, & Landy MS (2019). Modality-specific attention and visual-tactile ventriloquism. Open Science Framework. 10.17605/OSF.IO/EPCQV. [DOI] [Google Scholar]
de Vignemont F, Majid A, Jola C, & Haggard P. (2009). Segmenting the body into parts: Evidence from biases in tactile perception. The Quarterly Journal of Experimental Psychology (Hove), 62, 500–512. 10.1080/17470210802000802. [DOI] [PubMed] [Google Scholar]
Debats NB, & Heuer H. (2018). Explicit knowledge of sensory non-redundancy can reduce the strength of multisensory integration. Psychological Research. 10.1007/s00426-018-1116-2. [DOI] [PubMed] [Google Scholar]
Degerman A, Rinne T, Pekkola J, Autti T, Jääskeläinen IP, Sams M, & Alho K. (2007). Human brain activity associated with audiovisual perception and attention. NeuroImage, 34, 1683–1691. 10.1016/j.neuroimage.2006.11.019. [DOI] [PubMed] [Google Scholar]
Deroy O, Spence C, & Noppeney U. (2016). Metacognition in multisensory perception. Trends in Cognitive Sciences, 20, 736–747. 10.1016/j.tics.2016.08.006. [DOI] [PubMed] [Google Scholar]
Desimone R, & Duncan J. (1995). Neural mechanisms of selective visual attention. Annual Review of Neuroscience, 18, 193–222. 10.1146/annurev.ne.18.030195.001205. [DOI] [PubMed] [Google Scholar]
Driver J, & Spence C. (1998). Cross-modal links in spatial attention. Philosophical Transactions of the Royal Society B: Biological Sciences, 353, 1319–1331. 10.1098/rstb.1998.0286. [DOI] [PMC free article] [PubMed] [Google Scholar]
Eramudugolla R, Kamke MR, Soto-Faraco S, & Mattingley JB (2011). Perceptual load influences auditory space perception in the ventriloquist aftereffect. Cognition, 118, 62–74. 10.1016/j.cognition.2010.09.009. [DOI] [PubMed] [Google Scholar]
Ernst MO, & Banks MS (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature, 415, 429–433. 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
Ernst MO, Banks MS, & Bülthoff HH (2000). Touch can change visual slant perception. Nature Neuroscience, 3, 69–73. 10.1038/71140. [DOI] [PubMed] [Google Scholar]
Frissen I, Vroomen J, & de Gelder B. (2012). The aftereffects of ventriloquism: The time course of the visual recalibration of auditory localization. Seeing and Perceiving, 25, 1–14. 10.1163/187847611X620883. [DOI] [PubMed] [Google Scholar]
Frissen I, Vroomen J, de Gelder B, & Bertelson P. (2005). The aftereffects of ventriloquism: Generalization across sound-frequencies. Acta Psychologica, 118, 93–100. 10.1016/j.actpsy.2004.10.004. [DOI] [PubMed] [Google Scholar]
Gau R, & Noppeney U. (2016). How prior expectations shape multisensory perception. NeuroImage, 124, 876–886. 10.1016/j.neuroimage.2015.09.045. [DOI] [PubMed] [Google Scholar]
Gazzaley A, Cooney JW, McEvoy K, Knight RT, & D’Esposito M. (2005). Topdown enhancement and suppression of the magnitude and speed of neural activity. Journal of Cognitive Neuroscience, 17, 507–517. 10.1162/0898929053279522. [DOI] [PubMed] [Google Scholar]
Gepshtein S, Burge J, Ernst MO, & Banks MS (2005). The combination of vision and touch depends on spatial proximity. Journal of Vision, 5, 1013–1023. 10.1167/5.11.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gibson JJ (1962). Observations on active touch. Psychological Review, 69, 477–491. [DOI] [PubMed] [Google Scholar]
Girshick AR, Landy MS, & Simoncelli EP (2011). Cardinal rules: Visual orientation perception reflects knowledge of environmental statistics. Nature Neuroscience, 14, 926–932. 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gori M, Mazzilli G, Sandini G, & Burr D. (2011). Cross-sensory facilitation reveals neural interactions between visual and tactile motion in humans. Frontiers in Psychology, 2, 55 10.3389/fpsyg.2011.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
Göschl F, Engel AK, & Friese U. (2014). Attention modulates visual-tactile interaction in spatial pattern matching. PloS One, 9, e106896 10.1371/journal.pone.0106896. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hairston WD, Wallace MT, Vaughan JW, Stein BE, Norris JL, & Schirillo JA (2003). Visual localization ability influences cross-modal bias. Journal of Cognitive Neuroscience, 15, 20–29. 10.1162/089892903321107792. [DOI] [PubMed] [Google Scholar]
Hay JC, & Pick HL (1966). Visual and proprioceptive adaptation to optical displacement of the visual stimulus. Journal of Experimental Psychology, 71, 150–158. [DOI] [PubMed] [Google Scholar]
Helbig HB, & Ernst MO (2007). Knowledge about a common source can promote visual-haptic integration. Perception, 36, 1523–1533. 10.1068/p5851. [DOI] [PubMed] [Google Scholar]
Helbig HB, & Ernst MO (2008). Visual-haptic cue weighting is independent of modality-specific attention. Journal of Vision, 8, 21–21. [DOI] [PubMed] [Google Scholar]
Henriques DYP, & Cressman EK (2012). Visuomotor adaptation and proprioceptive recalibration. Journal of Motor Behavior, 44, 435–444. 10.1080/00222895.2012.659232. [DOI] [PubMed] [Google Scholar]
Hense M, Badde S, & Röder B. (2019). Tactile motion biases visual motion perception in binocular rivalry. Attention, Perception & Psychophysics. 10.3758/s13414-019-01692-w. [DOI] [PubMed] [Google Scholar]
Ho Y-X, Serwe S, Trommershäuser J, Maloney LT, & Landy MS (2009). The role of visuohaptic experience in visually perceived depth. Journal of Neurophysiology, 101, 2789–2801. 10.1152/jn.91129.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Holm S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 6, 65–70. [Google Scholar]
Holmes NP, & Spence C. (2005). Visual bias of unseen hand position with a mirror: spatial and temporal factors. Experimental Brain Research, 166, 489–497. 10.1007/s00221-005-2389-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Howard I, & Templeton W. (1966). Human spatial orientation. John Wiley & Sons. [Google Scholar]
Jack CE, & Thurlow WR (1973). Effects of degree of visual association and angle of displacement on the “ventriloquism” effect. Perceptual and Motor Skills, 37, 967–979. 10.2466/pms.1973.37.3.967. [DOI] [PubMed] [Google Scholar]
Johnson JA, & Zatorre RJ (2006). Neural substrates for dividing and focusing attention between simultaneous auditory and visual events. NeuroImage, 31, 1673–1681. 10.1016/j.neuroimage.2006.02.026. [DOI] [PubMed] [Google Scholar]
Johnston WA, & Dark VJ (1986). Selective attention. Annual Review of Psychology, 37, 43–75. [Google Scholar]
Kastner S, & Ungerleider LG (2001). The neural basis of biased competition in human visual cortex. Neuropsychologia, 39, 1263–1276. 10.1016/s00283932(01)00116-6. [DOI] [PubMed] [Google Scholar]
Kelso JA, Cook E, Olson ME, & Epstein W. (1975). Allocation of attention and the locus of adaptation to displaced vision. Journal of Experimental Psychology. Human Perception and Performance, 1, 237–245. [DOI] [PubMed] [Google Scholar]
Kesten H. (1958). Accelerated stochastic approximation. The Annals of Mathematical Statistics, 29, 41–59. [Google Scholar]
Kleiner M, Brainard D, & Pelli D. (2007). What’s new in psychtoolbox-3? ECVP abstract supplement. [Google Scholar]
Knight FLC, Longo MR, & Bremner AJ (2014). Categorical perception of tactile distance. Cognition, 131, 254–262. 10.1016/j.cognition.2014.01.005. [DOI] [PubMed] [Google Scholar]
Koelewijn T, Bronkhorst A, & Theeuwes J. (2010). Attention and the multiple stages of multisensory integration: A review of audiovisual studies. Acta Psychologica, 134, 372–384. 10.1016/j.actpsy.2010.03.010. [DOI] [PubMed] [Google Scholar]
Kopco N, Lin I-F, Shinn-Cunningham BG, & Groh JM (2009). Reference frame of the ventriloquism aftereffect. The Journal of Neuroscience, 29, 13809–13814. 10.1523/JNEUROSCI.2783-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Körding KP, Beierholm U, Ma WJ, Quartz S, Tenenbaum JB, & Shams L. (2007). Causal inference in multisensory perception. PloS One, 2, e943. 10.1371/journal.pone.0000943. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kornheiser AS (1976). Adaptation to laterally displaced vision: A review. Psychological Bulletin, 83, 783–816. [PubMed] [Google Scholar]
Landy MS, Maloney LT, Johnston EB, & Young M. (1995). Measurement and modeling of depth cue combination: In defense of weak fusion. Vision Research, 35, 389–412. [DOI] [PubMed] [Google Scholar]
Lavie N. (1995). Perceptual load as a necessary condition for selective attention. Journal of Experimental Psychology: Human Perception and Performance, 21, 451–468. [DOI] [PubMed] [Google Scholar]
Lehnert G, & Zimmer HD (2006). Auditory and visual spatial working memory. Memory & Cognition, 34, 1080–1090. [DOI] [PubMed] [Google Scholar]
Lewald J. (2002). Rapid adaptation to auditory-visual spatial disparity. Learning & Memory, 9, 268–278. 10.1101/lm.51402. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lewald J, & Guski R. (2003). Cross-modal perceptual integration of spatially and temporally disparate auditory and visual stimuli. Brain Research. Cognitive Brain Research, 16, 468–478. [DOI] [PubMed] [Google Scholar]
Lunghi C, Binda P, & Morrone MC (2010). Touch disambiguates rivalrous perception at early stages of visual analysis. Current Biology, 20, R143–R144. 10.1016/j.cub.2009.12.015. [DOI] [PubMed] [Google Scholar]
Macaluso E, Noppeney U, Talsma D, Vercillo T, Hartcher-O’Brien J, & Adam R. (2016). The curious incident of attention in multisensory integration: Bottom-up vs. top-down. Multisensory Research, 29, 557–583. [Google Scholar]
Magosso E, Cuppini C, & Ursino M. (2012). A neural network model of ventriloquism effect and aftereffect. PloS One, 7, e42503. 10.1371/journal.pone.0042503. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mather JA, & Lackner JR (1981). Adaptation to visual displacement: contribution of proprioceptive, visual, and attentional factors. Perception, 10, 367–374. 10.1068/p100367. [DOI] [PubMed] [Google Scholar]
Mishra J, & Gazzaley A. (2012). Attention distributed across sensory modalities enhances perceptual performance. The Journal of Neuroscience, 32, 12294–12302. 10.1523/JNEUROSCI.0867-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mozolic JL, Hugenschmidt CE, Peiffer AM, & Laurienti PJ (2008). Modality-specific selective attention attenuates multisensory integration. Experimental Brain Research, 184, 39–52. 10.1007/s00221-007-1080-3. [DOI] [PubMed] [Google Scholar]
Odegaard B, Wozny DR, & Shams L. (2015). Biases in visual, auditory, and audio-visual perception of space. PLoS Computational Biology, 11, e1004649 10.1371/journal.pcbi.1004649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Odegaard B, Wozny DR, & Shams L. (2016). The effects of selective and divided attention on sensory precision and integration. Neuroscience Letters, 614, 24–28. [DOI] [PubMed] [Google Scholar]
Parise CV, & Ernst MO (2016). Correlation detection as a general mechanism for multisensory integration. Nature Communications, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Passamonti C, Frissen I, & Làdavas E. (2009). Visual recalibration of auditory spatial perception: Two separate neural circuits for perceptual learning. The European Journal of Neuroscience, 30, 1141–1150. 10.1111/j.1460-9568.2009.06910.x. [DOI] [PubMed] [Google Scholar]
Pavani F, Spence C, & Driver J. (2000). Visual capture of touch: Out-of-the-body experiences with rubber gloves. Psychological Science, 11, 353–359. [DOI] [PubMed] [Google Scholar]
Pick HL, Warren DH, & Hay JC (1969). Sensory conflict in judgments of spatial direction. Perception & Psychophysics, 6, 203–205. [Google Scholar]
Radeau M, & Bertelson P. (1974). The after-effects of ventriloquism. The Quarterly Journal of Experimental Psychology, 26, 63–71. 10.1080/14640747408400388. [DOI] [PubMed] [Google Scholar]
Radeau M, & Bertelson P. (1977). Adaptation to auditory-visual discordance and ventriloquism in semirealistic situations. Perception & Psychophysics, 22, 137–146. [Google Scholar]
Radeau M, & Bertelson P. (1978). Cognitive factors and adaptation to auditory-visual discordance. Perception & Psychophysics, 23, 341–343. [DOI] [PubMed] [Google Scholar]
Recanzone GH (1998). Rapidly induced auditory plasticity: The ventriloquism aftereffect. Proceedings of the National Academy of Sciences of the United States of America, 95, 869–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
Redding GM, Clark SE, & Wallace B. (1985). Attention and prism adaptation. Cognitive Psychology, 17, 1–25. [DOI] [PubMed] [Google Scholar]
Redding GM, Rader SD, & Lucas DR (1992). Cognitive load and prism adaptation. Journal of Motor Behavior, 24, 238–246. 10.1080/00222895.1992.9941619. [DOI] [PubMed] [Google Scholar]
Redding GM, Rossetti Y, & Wallace B. (2005). Applications of prism adaptation: A tutorial in theory and method. Neuroscience and Biobehavioral Reviews, 29, 431–444. 10.1016/j.neubiorev.2004.12.004. [DOI] [PubMed] [Google Scholar]
Redding GM, & Wallace B. (1985). Cognitive interference in prism adaptation. Perception & Psychophysics, 37, 225–230. [DOI] [PubMed] [Google Scholar]
Redding GM, & Wallace B. (1996). Adaptive spatial alignment and strategic perceptual-motor control. Journal of Experimental Psychology. Human Perception and Performance, 22, 379–394. [DOI] [PubMed] [Google Scholar]
Renzi C, Bruns P, Heise K-F, Zimerman M, Feldheim J-F, Hummel FC, & Röder B. (2013). Spatial remapping in the audio-tactile ventriloquism effect: A TMS investigation on the role of the ventral intraparietal area. Journal of Cognitive Neuroscience p. (epub). [DOI] [PubMed] [Google Scholar]
Ricciardi E, Bonino D, Gentili C, Sani L, Pietrini P, & Vecchi T. (2006). Neural correlates of spatial working memory in humans: A functional magnetic resonance imaging study comparing visual and tactile processes. Neuroscience, 139, 339–349. 10.1016/j.neuroscience.2005.08.045. [DOI] [PubMed] [Google Scholar]
Robbins H, & Monro S. (1951). A stochastic approximation method. The Annals of Mathematical Statistics, 22, 400–407. [Google Scholar]
Rohe T, & Noppeney U. (2015a). Cortical hierarchies perform Bayesian causal inference in multisensory perception. PLoS Biology, 13, e1002073. 10.1371/journal.pbio.1002073. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rohe T, & Noppeney U. (2015b). Sensory reliability shapes perceptual inference via two mechanisms. Journal of Vision, 15, 22 10.1167/15.5.22. [DOI] [PubMed] [Google Scholar]
Rohe T, & Noppeney U. (2018). Reliability-weighted integration of audiovisual signals can be modulated by top-down attention. eNeuro, 5 10.1523/ENEURO.0315-17.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Salo E, Salmela V, Salmi J, Numminen J, & Alho K. (2017). Brain activity associated with selective attention, divided attention and distraction. Brain Research, 1664, 25–36. 10.1016/j.brainres.2017.03.021. [DOI] [PubMed] [Google Scholar]
Samad M, & Shams L. (2016). Visual–somatotopic interactions in spatial perception. Neuroreport, 27, 180–185. [DOI] [PubMed] [Google Scholar]
Samad M, & Shams L. (2018). Recalibrating the body: Visuotactile ventriloquism after effect. PeerJ, 6, e4504 10.7717/peerj.4504. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sato Y, Toyoizumi T, & Aihara K. (2007). Bayesian inference explains perception of unity and ventriloquism aftereffect: Identification of common sources of audiovisual stimuli. Neural Computation, 19, 3335–3355. 10.1162/neco.2007.19.12.3335. [DOI] [PubMed] [Google Scholar]
Schubert JTW, Badde S, Röder B, & Heed T. (2017). Task demands affect spatial reference frame weighting during tactile localization in sighted and congenitally blind adults. PloS One, 12, e0189067 10.1371/journal.pone.0189067. [DOI] [PMC free article] [PubMed] [Google Scholar]
Shams L, & Beierholm UR (2010). Causal inference in perception. Trends in Cognitive Sciences, 14, 425–432. 10.1016/j.tics.2010.07.001. [DOI] [PubMed] [Google Scholar]
Shinn-Cunningham BG (2008). Object-based auditory and visual attention. Trends in Cognitive Sciences, 12, 182–186. 10.1016/j.tics.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Smeets JBJ, van den Dobbelsteen JJ, de Grave DDJ, van Beers RJ, & Brenner E. (2006). Sensory integration does not lead to sensory calibration. Proceedings of the National Academy of Sciences of the United States of America, 103, 18781–18786. 10.1073/pnas.0607687103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Spence C, & Driver J. (2004). Crossmodal space and crossmodal attention. USA: Oxford University Press. [Google Scholar]
Talsma D, Doty TJ, & Woldorff MG (2007). Selective attention and audiovisual integration: Is attending to both modalities a prerequisite for early integration? Cerebral Cortex, 17, 679–690. 10.1093/cercor/bhk016. [DOI] [PubMed] [Google Scholar]
Talsma D, Senkowski D, Soto-Faraco S, & Woldorff MG (2010). The multifaceted interplay between attention and multisensory integration. Trends in Cognitive Sciences, 14, 400–410. 10.1016/j.tics.2010.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tang X, Wu J, & Shen Y. (2016). The interactions of multisensory integration with endogenous and exogenous attention. Neuroscience and Biobehavioral Reviews, 61, 208–224. 10.1016/j.neubiorev.2015.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thurlow WR, & Jack CE (1973). Certain determinants of the “ventriloquism effect” Perceptual and Motor Skills, 36, 1171–1184. 10.2466/pms.1973.36.3c.1171. [DOI] [PubMed] [Google Scholar]
Trommershäuser J, Körding K, & Landy MS (2011). Sensory cue integration. Oxford University Press. [Google Scholar]
Ursino M, Cuppini C, & Magosso E. (2014). Neurocomputational approaches to modelling multisensory integration in the brain: A review. Neural Networks, 60, 141–165. 10.1016/j.neunet.2014.08.003. [DOI] [PubMed] [Google Scholar]
van Beers RJ, Wolpert DM, & Haggard P. (2002). When feeling is more important than seeing in sensorimotor adaptation. Current Biology, 12, 834–837. [DOI] [PubMed] [Google Scholar]
van Beers RJ, van Mierlo CM, Smeets JB, & Brenner E. (2011). Reweighting visual cues by touch. Journal of Vision, 11, 20–20. [DOI] [PubMed] [Google Scholar]
Vercillo T, & Gori M. (2015). Attention to sound improves auditory reliability in audio-tactile spatial optimal integration. Frontiers in Integrative Neuroscience, 9, 34 10.3389/fnint.2015.00034. [DOI] [PMC free article] [PubMed] [Google Scholar]
von Helmholtz H. (1909). Handbuch der physiologischen Optik. Hamburg: Voss. [Google Scholar]
Wahn B, & König P. (2017). Is attentional resource allocation across sensory modalities task-dependent? Advances in Cognitive Psychology, 13, 83–96. 10.5709/acp-0209-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wallace MT, Roberson GE, Hairston WD, Stein BE, Vaughan JW, & Schirillo JA (2004). Unifying multisensory signals across time and space. Experimental Brain Research, 158, 252–258. 10.1007/s00221-004-1899-9. [DOI] [PubMed] [Google Scholar]
Wei K, & Körding KP (2009). Relevance of error: What drives motor adaptation? Journal of Neurophysiology, 101, 655–664. 10.1152/jn.90545.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Welch RB (2013). Perceptual modification: Adapting to altered sensory environments. Elsevier. [Google Scholar]
Welch RB, & Warren DH (1980). Immediate perceptual response to intersensory discrepancy. Psychological Bulletin, 88, 638–667. [PubMed] [Google Scholar]
Welch RB, Widawski MH, Harrington J, & Warren DH (1979). An examination of the relationship between visual capture and prism adaptation. Perception & Psychophysics, 25, 126–132. [DOI] [PubMed] [Google Scholar]
Wellek S. (2010). Testing statistical hypotheses of equivalence and noninferiority. CRC Press. [Google Scholar]
Werkhoven PJ, van Erp JBF, & Philippi TG (2009). Counting visual and tactile events: the effect of attention on multisensory integration. Attention, Perception & Psychophysics, 71, 1854–1861. 10.3758/APP.71.8.1854. [DOI] [PubMed] [Google Scholar]
Wismeijer DA, Gegenfurtner KR, & Drewing K. (2012). Learning from vision-totouch is different than learning from touch-to-vision. Frontiers in Integrative Neuroscience, 6, 105 10.3389/fnint.2012.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wozny DR, Beierholm UR, & Shams L. (2010). Probability matching as a computational strategy used in perception. PLoS Computational Biology, 6 10.1371/journal.pcbi.1000871. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wozny DR, & Shams L. (2011). Computational characterization of visually induced auditory spatial adaptation. Frontiers in Integrative Neuroscience, 5, 75 10.3389/fnint.2011.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yuille A, & Bülthoff H. (1996). Bayesian theory and psychophysics In Knill D, & Richards W. (Eds.). Perception as Bayesian inference (pp. 123–161). Cambridge University Press. [Google Scholar]
Zaidel A, Turner AH, & Angelaki DE (2011). Multisensory calibration is independent of cue reliability. The Journal of Neuroscience, 31, 13949–13962. 10.1523/JNEUROSCI.2732-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zierul B, Röder B, Tempelmann C, Bruns P, & Noesselt T. (2017). The role of auditory cortex in the spatial ventriloquism aftereffect. NeuroImage, 162, 257–268. 10.1016/j.neuroimage.2017.09.002. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS1558008-supplement-1.pdf^{(1.1MB, pdf)}

[R1] Acerbi L, Dokka K, Angelaki DE, & Ma WJ (2018). Bayesian comparison of explicit and implicit causal inference strategies in multisensory heading perception. PLoS Computational Biology, 14, e1006110. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Alais D, & Burr D. (2004). The ventriloquist effect results from near-optimal bimodal integration. Current Biology, 14, 257–262. 10.1016/j.cub.2004.01.029. [DOI] [PubMed] [Google Scholar]

[R3] Alais D, Newell FN, & Mamassian P. (2010). Multisensory processing in review: From physiology to behaviour. Seeing and Perceiving, 23, 3–38. 10.1163/187847510X488603. [DOI] [PubMed] [Google Scholar]

[R4] Alsius A, Navarra J, Campbell R, & Soto-Faraco S. (2005). Audiovisual integration of speech falters under high attention demands. Current Biology, 15, 839–843. 10.1016/j.cub.2005.03.046. [DOI] [PubMed] [Google Scholar]

[R5] Alsius A, Navarra J, & Soto-Faraco S. (2007). Attention to touch weakens audiovisual speech integration. Experimental Brain Research, 183, 399–404. 10.1007/s00221-007-1110-1. [DOI] [PubMed] [Google Scholar]

[R6] Anderson MJ (2001). Permutation tests for univariate or multivariate analysis of variance and regression. Canadian Journal of Fisheries and Aquatic Sciences, 58, 626–639. [Google Scholar]

[R7] Atkins JE, Fiser J, & Jacobs RA (2001). Experience-dependent visual cue integration based on consistencies between visual and haptic percepts. Vision Research, 41, 449–461. [DOI] [PubMed] [Google Scholar]

[R8] Atkins JE, Jacobs RA, & Knill DC (2003). Experience-dependent visual cue recalibration based on discrepancies between visual and haptic percepts. Vision Research, 43, 2603–2613. [DOI] [PubMed] [Google Scholar]

[R9] Azanon E, Mihaljevic K, & Longo MR (2016). A three-dimensional spatial characterization of the crossed-hands deficit. Cognition, 157, 289–295. 10.1016/j.cognition.2016.09.007. [DOI] [PubMed] [Google Scholar]

[R10] Battaglia PW, Jacobs RA, & Aslin RN (2003). Bayesian integration of visual and auditory signals for spatial localization. Journal of the Optical Society of America. A, Optics, Image Science, and Vision, 20, 1391–1397. [DOI] [PubMed] [Google Scholar]

[R11] Beierholm UR, Quartz SR, & Shams L. (2009). Bayesian priors are encoded independently from likelihoods in human multisensory perception. Journal of Vision, 9, 23.1–23.9. 10.1167/9.5.23. [DOI] [PubMed] [Google Scholar]

[R12] Bermant RI, & Welch RB (1976). Effect of degree of separation of visual-auditory stimulus and eye position upon spatial interaction of vision and audition. Perceptual and Motor Skills, 42, 487–493. 10.2466/pms.1976.42.2.487. [DOI] [PubMed] [Google Scholar]

[R13] Bertelson P, & Aschersleben G. (1998). Automatic visual bias of perceived auditory location. Psychonomic Bulletin & Review, 5, 482–489. 10.3758/BF03208826. [DOI] [Google Scholar]

[R14] Bertelson P, & De Gelder B. (2004). The psychology of multimodal perception. Crossmodal Space and Crossmodal Attention, 141–177. [Google Scholar]

[R15] Bertelson P, Frissen I, Vroomen J, & de Gelder B. (2006). The aftereffects of ventriloquism: Patterns of spatial generalization. Perception & Psychophysics, 68, 428–436. [DOI] [PubMed] [Google Scholar]

[R16] Bertelson P, & Radeau M. (1981). Cross-modal bias and perceptual fusion with auditory-visual spatial discordance. Perception & Psychophysics, 29, 578–584. [DOI] [PubMed] [Google Scholar]

[R17] Bertelson P, Vroomen J, de Gelder B, & Driver J. (2000). The ventriloquist effect does not depend on the direction of deliberate visual attention. Perception & Psychophysics, 62, 321–332. [DOI] [PubMed] [Google Scholar]

[R18] Bosen AK, Fleming JT, Allen PD, O’Neill WE, & Paige GD (2017). Accumulation and decay of visual capture and the ventriloquism aftereffect caused by brief audio-visual disparities. Experimental Brain Research, 235, 585–595. 10.1007/s00221-016-4820-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Bosen AK, Fleming JT, Brown SE, Allen PD, O’Neill WE, & Paige GD (2016). Comparison of congruence judgment and auditory localization tasks for assessing the spatial limits of visual capture. Biological Cybernetics, 110, 455–471. 10.1007/s00422-016-0706-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Brainard DH (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]

[R21] Bruns P, Liebnau R, & Röder B. (2011). Cross-modal training induces changes in spatial representations early in the auditory processing pathway. Psychological Science, 22, 1120–1126. 10.1177/0956797611416254. [DOI] [PubMed] [Google Scholar]

[R22] Bruns P, & Röder B. (2010a). Tactile capture of auditory localization: an event-related potential study. The European Journal of Neuroscience, 31, 1844–1857. 10.1111/j.1460-9568.2010.07232.x. [DOI] [PubMed] [Google Scholar]

[R23] Bruns P, & Röder B. (2010b). Tactile capture of auditory localization is modulated by hand posture. Experimental Psychology, 57, 267–274. 10.1027/16183169/a000032. [DOI] [PubMed] [Google Scholar]

[R24] Bruns P, & Röder B. (2015). Sensory recalibration integrates information from the immediate and the cumulative past. Scientific Reports, 5, 12739 10.1038/srep12739. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Bruns P, Spence C, & Röder B. (2011). Tactile recalibration of auditory spatial representations. Experimental Brain Research, 209, 333–344. 10.1007/s00221-011-2543-0. [DOI] [PubMed] [Google Scholar]

[R26] Burge J, Girshick AR, & Banks MS (2010). Visual-haptic adaptation is determined by relative reliability\ The Journal of Neuroscience, 30, 7714–7721. 10.1523/JNEUROSCI.6427-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Caclin A, Soto-Faraco S, Kingstone A, & Spence C. (2002). Tactile “capture” of audition. Perception & Psychophysics, 64, 616–630. [DOI] [PubMed] [Google Scholar]

[R28] Canon LK (1970). Intermodality inconsistency of input and directed attention as determinants of the nature of adaptation. Journal of Experimental Psychology, 84, 141–147. [DOI] [PubMed] [Google Scholar]

[R29] Cao Y, Summerfield C, Park H, Giordano BL, & Kayser C. (2019). Causal inference in the multisensory brain. Neuron, 102, 1076–1087. 10.1016/j.neuron.2019.03.043e8. [DOI] [PubMed] [Google Scholar]

[R30] Cardini F, & Longo MR (2016). Congruency of body-related information induces somatosensory reorganization. Neuropsychologia, 84, 213–221. 10.1016/j.neuropsychologia.2016.02.013. [DOI] [PubMed] [Google Scholar]

[R31] Carrasco M. (2011). Visual attention: The past 25 years. Vision Research, 51, 1484–1525. 10.1016/j.visres.2011.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] Charbonneau G, Véronneau M, Boudrias-Fournier C, Lepore F, & Collignon O. (2013). The ventriloquist in periphery: Impact of eccentricity-related reliability on audio-visual localization. Journal of Vision, 13, 20 10.1167/13.12.20. [DOI] [PubMed] [Google Scholar]

[R33] Chen L, & Vroomen J. (2013). Intersensory binding across space and time: a tutorial review. Attention, Perception & Psychophysics, 75, 790–811. 10.3758/s13414-013-0475-4. [DOI] [PubMed] [Google Scholar]

[R34] Chen Y-C, & Spence C. (2017). Assessing the role of the ‘unity assumption’ on multisensory integration: A review. Frontiers in Psychology, 8, 445 10.3389/fpsyg.2017.00445. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Cressman EK, & Henriques DYP (2009). Sensory recalibration of hand position following visuomotor adaptation. Journal of Neurophysiology, 102, 3505–3518. 10.1152/jn.00514.2009. [DOI] [PubMed] [Google Scholar]

[R36] Cressman EK, & Henriques DYP (2010). Reach adaptation and proprioceptive recalibration following exposure to misaligned sensory input. Journal of Neurophysiology, 103, 1888–1895. 10.1152/jn.01002.2009. [DOI] [PubMed] [Google Scholar]

[R37] Badde S, Navarro KT, & Landy MS (2019). Modality-specific attention and visual-tactile ventriloquism. Open Science Framework. 10.17605/OSF.IO/EPCQV. [DOI] [Google Scholar]

[R38] de Vignemont F, Majid A, Jola C, & Haggard P. (2009). Segmenting the body into parts: Evidence from biases in tactile perception. The Quarterly Journal of Experimental Psychology (Hove), 62, 500–512. 10.1080/17470210802000802. [DOI] [PubMed] [Google Scholar]

[R39] Debats NB, & Heuer H. (2018). Explicit knowledge of sensory non-redundancy can reduce the strength of multisensory integration. Psychological Research. 10.1007/s00426-018-1116-2. [DOI] [PubMed] [Google Scholar]

[R40] Degerman A, Rinne T, Pekkola J, Autti T, Jääskeläinen IP, Sams M, & Alho K. (2007). Human brain activity associated with audiovisual perception and attention. NeuroImage, 34, 1683–1691. 10.1016/j.neuroimage.2006.11.019. [DOI] [PubMed] [Google Scholar]

[R41] Deroy O, Spence C, & Noppeney U. (2016). Metacognition in multisensory perception. Trends in Cognitive Sciences, 20, 736–747. 10.1016/j.tics.2016.08.006. [DOI] [PubMed] [Google Scholar]

[R42] Desimone R, & Duncan J. (1995). Neural mechanisms of selective visual attention. Annual Review of Neuroscience, 18, 193–222. 10.1146/annurev.ne.18.030195.001205. [DOI] [PubMed] [Google Scholar]

[R43] Driver J, & Spence C. (1998). Cross-modal links in spatial attention. Philosophical Transactions of the Royal Society B: Biological Sciences, 353, 1319–1331. 10.1098/rstb.1998.0286. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Eramudugolla R, Kamke MR, Soto-Faraco S, & Mattingley JB (2011). Perceptual load influences auditory space perception in the ventriloquist aftereffect. Cognition, 118, 62–74. 10.1016/j.cognition.2010.09.009. [DOI] [PubMed] [Google Scholar]

[R45] Ernst MO, & Banks MS (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature, 415, 429–433. 10.1038/415429a. [DOI] [PubMed] [Google Scholar]

[R46] Ernst MO, Banks MS, & Bülthoff HH (2000). Touch can change visual slant perception. Nature Neuroscience, 3, 69–73. 10.1038/71140. [DOI] [PubMed] [Google Scholar]

[R47] Frissen I, Vroomen J, & de Gelder B. (2012). The aftereffects of ventriloquism: The time course of the visual recalibration of auditory localization. Seeing and Perceiving, 25, 1–14. 10.1163/187847611X620883. [DOI] [PubMed] [Google Scholar]

[R48] Frissen I, Vroomen J, de Gelder B, & Bertelson P. (2005). The aftereffects of ventriloquism: Generalization across sound-frequencies. Acta Psychologica, 118, 93–100. 10.1016/j.actpsy.2004.10.004. [DOI] [PubMed] [Google Scholar]

[R49] Gau R, & Noppeney U. (2016). How prior expectations shape multisensory perception. NeuroImage, 124, 876–886. 10.1016/j.neuroimage.2015.09.045. [DOI] [PubMed] [Google Scholar]

[R50] Gazzaley A, Cooney JW, McEvoy K, Knight RT, & D’Esposito M. (2005). Topdown enhancement and suppression of the magnitude and speed of neural activity. Journal of Cognitive Neuroscience, 17, 507–517. 10.1162/0898929053279522. [DOI] [PubMed] [Google Scholar]

[R51] Gepshtein S, Burge J, Ernst MO, & Banks MS (2005). The combination of vision and touch depends on spatial proximity. Journal of Vision, 5, 1013–1023. 10.1167/5.11.7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Gibson JJ (1962). Observations on active touch. Psychological Review, 69, 477–491. [DOI] [PubMed] [Google Scholar]

[R53] Girshick AR, Landy MS, & Simoncelli EP (2011). Cardinal rules: Visual orientation perception reflects knowledge of environmental statistics. Nature Neuroscience, 14, 926–932. 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Gori M, Mazzilli G, Sandini G, & Burr D. (2011). Cross-sensory facilitation reveals neural interactions between visual and tactile motion in humans. Frontiers in Psychology, 2, 55 10.3389/fpsyg.2011.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Göschl F, Engel AK, & Friese U. (2014). Attention modulates visual-tactile interaction in spatial pattern matching. PloS One, 9, e106896 10.1371/journal.pone.0106896. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] Hairston WD, Wallace MT, Vaughan JW, Stein BE, Norris JL, & Schirillo JA (2003). Visual localization ability influences cross-modal bias. Journal of Cognitive Neuroscience, 15, 20–29. 10.1162/089892903321107792. [DOI] [PubMed] [Google Scholar]

[R57] Hay JC, & Pick HL (1966). Visual and proprioceptive adaptation to optical displacement of the visual stimulus. Journal of Experimental Psychology, 71, 150–158. [DOI] [PubMed] [Google Scholar]

[R58] Helbig HB, & Ernst MO (2007). Knowledge about a common source can promote visual-haptic integration. Perception, 36, 1523–1533. 10.1068/p5851. [DOI] [PubMed] [Google Scholar]

[R59] Helbig HB, & Ernst MO (2008). Visual-haptic cue weighting is independent of modality-specific attention. Journal of Vision, 8, 21–21. [DOI] [PubMed] [Google Scholar]

[R60] Henriques DYP, & Cressman EK (2012). Visuomotor adaptation and proprioceptive recalibration. Journal of Motor Behavior, 44, 435–444. 10.1080/00222895.2012.659232. [DOI] [PubMed] [Google Scholar]

[R61] Hense M, Badde S, & Röder B. (2019). Tactile motion biases visual motion perception in binocular rivalry. Attention, Perception & Psychophysics. 10.3758/s13414-019-01692-w. [DOI] [PubMed] [Google Scholar]

[R62] Ho Y-X, Serwe S, Trommershäuser J, Maloney LT, & Landy MS (2009). The role of visuohaptic experience in visually perceived depth. Journal of Neurophysiology, 101, 2789–2801. 10.1152/jn.91129.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Holm S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 6, 65–70. [Google Scholar]

[R64] Holmes NP, & Spence C. (2005). Visual bias of unseen hand position with a mirror: spatial and temporal factors. Experimental Brain Research, 166, 489–497. 10.1007/s00221-005-2389-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Howard I, & Templeton W. (1966). Human spatial orientation. John Wiley & Sons. [Google Scholar]

[R66] Jack CE, & Thurlow WR (1973). Effects of degree of visual association and angle of displacement on the “ventriloquism” effect. Perceptual and Motor Skills, 37, 967–979. 10.2466/pms.1973.37.3.967. [DOI] [PubMed] [Google Scholar]

[R67] Johnson JA, & Zatorre RJ (2006). Neural substrates for dividing and focusing attention between simultaneous auditory and visual events. NeuroImage, 31, 1673–1681. 10.1016/j.neuroimage.2006.02.026. [DOI] [PubMed] [Google Scholar]

[R68] Johnston WA, & Dark VJ (1986). Selective attention. Annual Review of Psychology, 37, 43–75. [Google Scholar]

[R69] Kastner S, & Ungerleider LG (2001). The neural basis of biased competition in human visual cortex. Neuropsychologia, 39, 1263–1276. 10.1016/s00283932(01)00116-6. [DOI] [PubMed] [Google Scholar]

[R70] Kelso JA, Cook E, Olson ME, & Epstein W. (1975). Allocation of attention and the locus of adaptation to displaced vision. Journal of Experimental Psychology. Human Perception and Performance, 1, 237–245. [DOI] [PubMed] [Google Scholar]

[R71] Kesten H. (1958). Accelerated stochastic approximation. The Annals of Mathematical Statistics, 29, 41–59. [Google Scholar]

[R72] Kleiner M, Brainard D, & Pelli D. (2007). What’s new in psychtoolbox-3? ECVP abstract supplement. [Google Scholar]

[R73] Knight FLC, Longo MR, & Bremner AJ (2014). Categorical perception of tactile distance. Cognition, 131, 254–262. 10.1016/j.cognition.2014.01.005. [DOI] [PubMed] [Google Scholar]

[R74] Koelewijn T, Bronkhorst A, & Theeuwes J. (2010). Attention and the multiple stages of multisensory integration: A review of audiovisual studies. Acta Psychologica, 134, 372–384. 10.1016/j.actpsy.2010.03.010. [DOI] [PubMed] [Google Scholar]

[R75] Kopco N, Lin I-F, Shinn-Cunningham BG, & Groh JM (2009). Reference frame of the ventriloquism aftereffect. The Journal of Neuroscience, 29, 13809–13814. 10.1523/JNEUROSCI.2783-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Körding KP, Beierholm U, Ma WJ, Quartz S, Tenenbaum JB, & Shams L. (2007). Causal inference in multisensory perception. PloS One, 2, e943. 10.1371/journal.pone.0000943. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] Kornheiser AS (1976). Adaptation to laterally displaced vision: A review. Psychological Bulletin, 83, 783–816. [PubMed] [Google Scholar]

[R78] Landy MS, Maloney LT, Johnston EB, & Young M. (1995). Measurement and modeling of depth cue combination: In defense of weak fusion. Vision Research, 35, 389–412. [DOI] [PubMed] [Google Scholar]

[R79] Lavie N. (1995). Perceptual load as a necessary condition for selective attention. Journal of Experimental Psychology: Human Perception and Performance, 21, 451–468. [DOI] [PubMed] [Google Scholar]

[R80] Lehnert G, & Zimmer HD (2006). Auditory and visual spatial working memory. Memory & Cognition, 34, 1080–1090. [DOI] [PubMed] [Google Scholar]

[R81] Lewald J. (2002). Rapid adaptation to auditory-visual spatial disparity. Learning & Memory, 9, 268–278. 10.1101/lm.51402. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R82] Lewald J, & Guski R. (2003). Cross-modal perceptual integration of spatially and temporally disparate auditory and visual stimuli. Brain Research. Cognitive Brain Research, 16, 468–478. [DOI] [PubMed] [Google Scholar]

[R83] Lunghi C, Binda P, & Morrone MC (2010). Touch disambiguates rivalrous perception at early stages of visual analysis. Current Biology, 20, R143–R144. 10.1016/j.cub.2009.12.015. [DOI] [PubMed] [Google Scholar]

[R84] Macaluso E, Noppeney U, Talsma D, Vercillo T, Hartcher-O’Brien J, & Adam R. (2016). The curious incident of attention in multisensory integration: Bottom-up vs. top-down. Multisensory Research, 29, 557–583. [Google Scholar]

[R85] Magosso E, Cuppini C, & Ursino M. (2012). A neural network model of ventriloquism effect and aftereffect. PloS One, 7, e42503. 10.1371/journal.pone.0042503. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] Mather JA, & Lackner JR (1981). Adaptation to visual displacement: contribution of proprioceptive, visual, and attentional factors. Perception, 10, 367–374. 10.1068/p100367. [DOI] [PubMed] [Google Scholar]

[R87] Mishra J, & Gazzaley A. (2012). Attention distributed across sensory modalities enhances perceptual performance. The Journal of Neuroscience, 32, 12294–12302. 10.1523/JNEUROSCI.0867-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R88] Mozolic JL, Hugenschmidt CE, Peiffer AM, & Laurienti PJ (2008). Modality-specific selective attention attenuates multisensory integration. Experimental Brain Research, 184, 39–52. 10.1007/s00221-007-1080-3. [DOI] [PubMed] [Google Scholar]

[R89] Odegaard B, Wozny DR, & Shams L. (2015). Biases in visual, auditory, and audio-visual perception of space. PLoS Computational Biology, 11, e1004649 10.1371/journal.pcbi.1004649. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R90] Odegaard B, Wozny DR, & Shams L. (2016). The effects of selective and divided attention on sensory precision and integration. Neuroscience Letters, 614, 24–28. [DOI] [PubMed] [Google Scholar]

[R91] Parise CV, & Ernst MO (2016). Correlation detection as a general mechanism for multisensory integration. Nature Communications, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R92] Passamonti C, Frissen I, & Làdavas E. (2009). Visual recalibration of auditory spatial perception: Two separate neural circuits for perceptual learning. The European Journal of Neuroscience, 30, 1141–1150. 10.1111/j.1460-9568.2009.06910.x. [DOI] [PubMed] [Google Scholar]

[R93] Pavani F, Spence C, & Driver J. (2000). Visual capture of touch: Out-of-the-body experiences with rubber gloves. Psychological Science, 11, 353–359. [DOI] [PubMed] [Google Scholar]

[R94] Pick HL, Warren DH, & Hay JC (1969). Sensory conflict in judgments of spatial direction. Perception & Psychophysics, 6, 203–205. [Google Scholar]

[R95] Radeau M, & Bertelson P. (1974). The after-effects of ventriloquism. The Quarterly Journal of Experimental Psychology, 26, 63–71. 10.1080/14640747408400388. [DOI] [PubMed] [Google Scholar]

[R96] Radeau M, & Bertelson P. (1977). Adaptation to auditory-visual discordance and ventriloquism in semirealistic situations. Perception & Psychophysics, 22, 137–146. [Google Scholar]

[R97] Radeau M, & Bertelson P. (1978). Cognitive factors and adaptation to auditory-visual discordance. Perception & Psychophysics, 23, 341–343. [DOI] [PubMed] [Google Scholar]

[R98] Recanzone GH (1998). Rapidly induced auditory plasticity: The ventriloquism aftereffect. Proceedings of the National Academy of Sciences of the United States of America, 95, 869–875. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R99] Redding GM, Clark SE, & Wallace B. (1985). Attention and prism adaptation. Cognitive Psychology, 17, 1–25. [DOI] [PubMed] [Google Scholar]

[R100] Redding GM, Rader SD, & Lucas DR (1992). Cognitive load and prism adaptation. Journal of Motor Behavior, 24, 238–246. 10.1080/00222895.1992.9941619. [DOI] [PubMed] [Google Scholar]

[R101] Redding GM, Rossetti Y, & Wallace B. (2005). Applications of prism adaptation: A tutorial in theory and method. Neuroscience and Biobehavioral Reviews, 29, 431–444. 10.1016/j.neubiorev.2004.12.004. [DOI] [PubMed] [Google Scholar]

[R102] Redding GM, & Wallace B. (1985). Cognitive interference in prism adaptation. Perception & Psychophysics, 37, 225–230. [DOI] [PubMed] [Google Scholar]

[R103] Redding GM, & Wallace B. (1996). Adaptive spatial alignment and strategic perceptual-motor control. Journal of Experimental Psychology. Human Perception and Performance, 22, 379–394. [DOI] [PubMed] [Google Scholar]

[R104] Renzi C, Bruns P, Heise K-F, Zimerman M, Feldheim J-F, Hummel FC, & Röder B. (2013). Spatial remapping in the audio-tactile ventriloquism effect: A TMS investigation on the role of the ventral intraparietal area. Journal of Cognitive Neuroscience p. (epub). [DOI] [PubMed] [Google Scholar]

[R105] Ricciardi E, Bonino D, Gentili C, Sani L, Pietrini P, & Vecchi T. (2006). Neural correlates of spatial working memory in humans: A functional magnetic resonance imaging study comparing visual and tactile processes. Neuroscience, 139, 339–349. 10.1016/j.neuroscience.2005.08.045. [DOI] [PubMed] [Google Scholar]

[R106] Robbins H, & Monro S. (1951). A stochastic approximation method. The Annals of Mathematical Statistics, 22, 400–407. [Google Scholar]

[R107] Rohe T, & Noppeney U. (2015a). Cortical hierarchies perform Bayesian causal inference in multisensory perception. PLoS Biology, 13, e1002073. 10.1371/journal.pbio.1002073. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R108] Rohe T, & Noppeney U. (2015b). Sensory reliability shapes perceptual inference via two mechanisms. Journal of Vision, 15, 22 10.1167/15.5.22. [DOI] [PubMed] [Google Scholar]

[R109] Rohe T, & Noppeney U. (2018). Reliability-weighted integration of audiovisual signals can be modulated by top-down attention. eNeuro, 5 10.1523/ENEURO.0315-17.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R110] Salo E, Salmela V, Salmi J, Numminen J, & Alho K. (2017). Brain activity associated with selective attention, divided attention and distraction. Brain Research, 1664, 25–36. 10.1016/j.brainres.2017.03.021. [DOI] [PubMed] [Google Scholar]

[R111] Samad M, & Shams L. (2016). Visual–somatotopic interactions in spatial perception. Neuroreport, 27, 180–185. [DOI] [PubMed] [Google Scholar]

[R112] Samad M, & Shams L. (2018). Recalibrating the body: Visuotactile ventriloquism after effect. PeerJ, 6, e4504 10.7717/peerj.4504. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R113] Sato Y, Toyoizumi T, & Aihara K. (2007). Bayesian inference explains perception of unity and ventriloquism aftereffect: Identification of common sources of audiovisual stimuli. Neural Computation, 19, 3335–3355. 10.1162/neco.2007.19.12.3335. [DOI] [PubMed] [Google Scholar]

[R114] Schubert JTW, Badde S, Röder B, & Heed T. (2017). Task demands affect spatial reference frame weighting during tactile localization in sighted and congenitally blind adults. PloS One, 12, e0189067 10.1371/journal.pone.0189067. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R115] Shams L, & Beierholm UR (2010). Causal inference in perception. Trends in Cognitive Sciences, 14, 425–432. 10.1016/j.tics.2010.07.001. [DOI] [PubMed] [Google Scholar]

[R116] Shinn-Cunningham BG (2008). Object-based auditory and visual attention. Trends in Cognitive Sciences, 12, 182–186. 10.1016/j.tics.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R117] Smeets JBJ, van den Dobbelsteen JJ, de Grave DDJ, van Beers RJ, & Brenner E. (2006). Sensory integration does not lead to sensory calibration. Proceedings of the National Academy of Sciences of the United States of America, 103, 18781–18786. 10.1073/pnas.0607687103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R118] Spence C, & Driver J. (2004). Crossmodal space and crossmodal attention. USA: Oxford University Press. [Google Scholar]

[R119] Talsma D, Doty TJ, & Woldorff MG (2007). Selective attention and audiovisual integration: Is attending to both modalities a prerequisite for early integration? Cerebral Cortex, 17, 679–690. 10.1093/cercor/bhk016. [DOI] [PubMed] [Google Scholar]

[R120] Talsma D, Senkowski D, Soto-Faraco S, & Woldorff MG (2010). The multifaceted interplay between attention and multisensory integration. Trends in Cognitive Sciences, 14, 400–410. 10.1016/j.tics.2010.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R121] Tang X, Wu J, & Shen Y. (2016). The interactions of multisensory integration with endogenous and exogenous attention. Neuroscience and Biobehavioral Reviews, 61, 208–224. 10.1016/j.neubiorev.2015.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R122] Thurlow WR, & Jack CE (1973). Certain determinants of the “ventriloquism effect” Perceptual and Motor Skills, 36, 1171–1184. 10.2466/pms.1973.36.3c.1171. [DOI] [PubMed] [Google Scholar]

[R123] Trommershäuser J, Körding K, & Landy MS (2011). Sensory cue integration. Oxford University Press. [Google Scholar]

[R124] Ursino M, Cuppini C, & Magosso E. (2014). Neurocomputational approaches to modelling multisensory integration in the brain: A review. Neural Networks, 60, 141–165. 10.1016/j.neunet.2014.08.003. [DOI] [PubMed] [Google Scholar]

[R125] van Beers RJ, Wolpert DM, & Haggard P. (2002). When feeling is more important than seeing in sensorimotor adaptation. Current Biology, 12, 834–837. [DOI] [PubMed] [Google Scholar]

[R126] van Beers RJ, van Mierlo CM, Smeets JB, & Brenner E. (2011). Reweighting visual cues by touch. Journal of Vision, 11, 20–20. [DOI] [PubMed] [Google Scholar]

[R127] Vercillo T, & Gori M. (2015). Attention to sound improves auditory reliability in audio-tactile spatial optimal integration. Frontiers in Integrative Neuroscience, 9, 34 10.3389/fnint.2015.00034. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R128] von Helmholtz H. (1909). Handbuch der physiologischen Optik. Hamburg: Voss. [Google Scholar]

[R129] Wahn B, & König P. (2017). Is attentional resource allocation across sensory modalities task-dependent? Advances in Cognitive Psychology, 13, 83–96. 10.5709/acp-0209-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R130] Wallace MT, Roberson GE, Hairston WD, Stein BE, Vaughan JW, & Schirillo JA (2004). Unifying multisensory signals across time and space. Experimental Brain Research, 158, 252–258. 10.1007/s00221-004-1899-9. [DOI] [PubMed] [Google Scholar]

[R131] Wei K, & Körding KP (2009). Relevance of error: What drives motor adaptation? Journal of Neurophysiology, 101, 655–664. 10.1152/jn.90545.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R132] Welch RB (2013). Perceptual modification: Adapting to altered sensory environments. Elsevier. [Google Scholar]

[R133] Welch RB, & Warren DH (1980). Immediate perceptual response to intersensory discrepancy. Psychological Bulletin, 88, 638–667. [PubMed] [Google Scholar]

[R134] Welch RB, Widawski MH, Harrington J, & Warren DH (1979). An examination of the relationship between visual capture and prism adaptation. Perception & Psychophysics, 25, 126–132. [DOI] [PubMed] [Google Scholar]

[R135] Wellek S. (2010). Testing statistical hypotheses of equivalence and noninferiority. CRC Press. [Google Scholar]

[R136] Werkhoven PJ, van Erp JBF, & Philippi TG (2009). Counting visual and tactile events: the effect of attention on multisensory integration. Attention, Perception & Psychophysics, 71, 1854–1861. 10.3758/APP.71.8.1854. [DOI] [PubMed] [Google Scholar]

[R137] Wismeijer DA, Gegenfurtner KR, & Drewing K. (2012). Learning from vision-totouch is different than learning from touch-to-vision. Frontiers in Integrative Neuroscience, 6, 105 10.3389/fnint.2012.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R138] Wozny DR, Beierholm UR, & Shams L. (2010). Probability matching as a computational strategy used in perception. PLoS Computational Biology, 6 10.1371/journal.pcbi.1000871. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R139] Wozny DR, & Shams L. (2011). Computational characterization of visually induced auditory spatial adaptation. Frontiers in Integrative Neuroscience, 5, 75 10.3389/fnint.2011.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R140] Yuille A, & Bülthoff H. (1996). Bayesian theory and psychophysics In Knill D, & Richards W. (Eds.). Perception as Bayesian inference (pp. 123–161). Cambridge University Press. [Google Scholar]

[R141] Zaidel A, Turner AH, & Angelaki DE (2011). Multisensory calibration is independent of cue reliability. The Journal of Neuroscience, 31, 13949–13962. 10.1523/JNEUROSCI.2732-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R142] Zierul B, Röder B, Tempelmann C, Bruns P, & Noesselt T. (2017). The role of auditory cortex in the spatial ventriloquism aftereffect. NeuroImage, 162, 257–268. 10.1016/j.neuroimage.2017.09.002. [DOI] [PubMed] [Google Scholar]

PERMALINK

Modality-specific attention attenuates visual-tactile integration and recalibration effects by reducing prior expectations of a common source for vision and touch

Stephanie Badde

Karen T Navarro

Michael S Landy

Abstract

1. Introduction

2. Expt. 1: Attention effects on the integration of vision and touch

2.1. Methods

2.1.1. Participants

2.1.2. Apparatus and stimuli

Fig. 1.

2.1.3. Task and procedure

Fig. 2.

2.1.4. Data analysis

2.2. Results

Fig. 3.

Fig. 4.

2.3. Summary

3. Expt. 2: Attention effects on visual recalibration of touch

3.1. Methods

3.1.1. Participants

3.1.2. Apparatus and stimuli

3.1.3. Tasks and procedure

Fig. 5.

3.1.4. Data analysis

3.2. Results

Fig. 6.

Fig. 7.

3.3. Summary

4. Model: causal inference and attention effects on visual-tactile integration and recalibration

4.1. Model comparison

4.2. Model parameters

Fig. 8.

4.3. Model simulations — visual-tactile integration

Fig. 9.

Fig. 10.

4.4. Model simulations — visual-tactile recalibration

Fig. 11.

5. General discussion

5.1. Prior expectations of a shared source for vision and touch

5.2. Sensory reliability

5.3. Attentional resources

5.4. Relationship between recalibration and integration

5.5. Spatial-alignment responses

5.6. Tactile biases

5.7. Working-memory demands

6. Conclusion

Supplementary Material

Acknowledgements

Appendix A

A.1. Causal-inference models of visual-tactile integration

Fig. 12.

A.1.1. Causal-inference model — reliabilities

A.1.2. Causal-inference model — priors

A.1.3. Causal-inference model — shifted likelihoods

A.1.4. Causal-inference model — localization response

A.1.5. Causal-inference model — spatial-alignment response

A.1.6. Model fitting

A.1.7. Parameter analysis

A.1.8. Model simulations

A.2. Results — causal-inference models of visual-tactile integration

A.2.1. Model comparison

Table 1.

Table 2.

Fig. 13.

Fig. 14.

A.2.2. Parameter estimates

A.2.3. Model simulations

A.3. Causal-inference models of visual-tactile recalibration.

A.3.1. Model simulations

A.3.2. Model simulations — visual-tactile recalibration

Appendix B. Supplementary data

Footnotes

References

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES