Vitrification decoupling from α-relaxation in a metallic glass

For a metallic glass, vitrification kinetics takes place at temperatures lower than expected from the α-relaxation.

Abstract

Understanding how glasses form, the so-called vitrification, remains a major challenge in materials science. Here, we study vitrification kinetics, in terms of the limiting fictive temperature, and atomic mobility related to the α-relaxation of an Au-based bulk metallic glass former by fast scanning calorimetry. We show that the time scale of the α-relaxation exhibits super-Arrhenius temperature dependence typical of fragile liquids. In contrast, vitrification kinetics displays milder temperature dependence at moderate undercooling, and thereby, vitrification takes place at temperatures lower than those associated to the α-relaxation. This finding challenges the paradigmatic view based on a one-to-one correlation between vitrification, leading to the glass transition, and the α-relaxation. We provide arguments that at moderate to deep undercooling, other atomic motions, which are not involved in the α-relaxation and that originate from the heterogeneous dynamics in metallic glasses, contribute to vitrification. Implications from the viewpoint of glasses fundamental properties are discussed.

INTRODUCTION

A class of materials as diverse as viscous liquids and colloidal suspensions can both solidify in a nonequilibrium state under conditions that are still not fully understood. This process, known as the glass transition or vitrification, has been a topic of extraordinary importance in the last decades and one of the most fascinating and still unsolved problems in condensed matter physics (1). Decreasing temperature is usually the parameter triggering viscous liquids through the transition, while packing fraction or waiting time plays the same role for soft glassy materials. One of the major questions is whether vitrification in viscous liquids— that is, the transformation from a supercooled liquid in metastable equilibrium into a nonequilibrium glass—and devitrification—taking place on heating the glass through its glass transition—are exclusively related to the primary structural relaxation process, i.e., the α-relaxation process, which is attributed to cooperative motion of several structural units, or rather other atomic motions play a role. The conventional wisdom, based on experimental evidences in glasses of various nature (2–5), indicates that the cooling rate dependence of the glass transition temperature exhibits the same behavior as the temperature dependence of viscosity or the structural α-relaxation time, τ. In the case of so-called kinetically fragile liquids, the equilibrium viscosity and τ start to develop a super-Arrhenius temperature dependence below a temperature of about twice the calorimetric glass transition temperature, T_g (6).

Recent experiments (7–11) and simulations (12, 13), mostly on polymer glasses under geometrical confinement, challenged the connection between vitrification kinetics and α-relaxation. They showed that, on reducing the typical length scale of confinement, vitrification of the supercooled liquid is shifted to lower temperatures with respect to the bulk material, indicating T_g reduction. In contrast, the α-process remained essentially size independent. These results pointed toward a decoupling between vitrification kinetics and the α-relaxation (14, 15), and the role of other mechanisms of relaxation, beyond the α-process, was recalled. For bulk glasses, that is, unconstrained by geometrical confinement and at relatively short observation times, corresponding to standard calorimetric cooling rates, i.e., several K/min, this role is not evident. In this case, much longer observation time scales, for instance, long annealing times in the glassy state (16, 17), are required to highlight effects beyond the α-process in the (de)vitrification kinetics (18–21). In contrast, polymers subjected to some specific conditions of geometrical confinement can exhibit heterogeneity of vitrification kinetics on much shorter time scales (22–24).

Contrary to polymeric and molecular systems, bulk metallic glasses (BMGs) are often considered model candidates to investigate the glass transition process as they do not have any reorentational or intramolecular motion, which could influence their vitrification. They are typically multicomponent alloys with large size mismatch and heterogeneous chemical affinity between the constituents. It results that the liquid structure is highly densely packed with a pronounced structural and chemical short- and medium-range order. In these glass-forming alloys, both diffusion and viscous flow start to develop solid-like features upon cooling far above the liquidus temperature and several hundreds degrees above the mode coupling critical temperature (25, 26). Already at the melting point, viscosities of BMG formers are several orders of magnitude larger than those of regular metals and alloys (27). Experiments demonstrated that dynamics in deeply undercooled liquids are heterogeneous, even in single-component systems, and there is the evidence that the length scale of the dynamic heterogeneities grows on approaching the glassy state (28).

For what specifically concerns metallic glasses, these observations highlight how their multicomponent nature should reflect on heterogeneous dynamic behavior and imply that, apart from the α-relaxation, there exist multiple different atomic motions exhibiting a variety of time scales. These atomic motions may be profoundly decoupled from the α-relaxation as shown by tracer diffusion experiments (25, 29, 30) and nuclear magnetic resonance (NMR) (31) on BMGs. Furthermore, the presence of multiple heterogeneous relaxation in atomic motion may be evidenced even in experiments probing macroscopic dynamics, such as those monitoring the stress decay (32), and in molecular dynamics simulations showing the structural origin of secondary relaxations (33).

Here, we show that multicomponent bulk metallic glasses can display heterogeneity of vitrification kinetics in standard conditions, i.e., without any geometrical restriction or prolonged annealing. The evidence for this is based on two exhaustive studies by fast scanning calorimetry (FSC), one to determine vitrification kinetics and the other to probe the atomic mobility of an Au-based BMG former in a broad time and temperature range. The former aspect is characterized in terms of the limiting fictive temperature, T_f (34), i.e., the temperature at which a glass formed after cooling at a given rate would be at equilibrium. Through the step response analysis (35), which is completely independent of the T_f analysis, FSC conveys information on the atomic mobility via the temperature and frequency dependence of the complex-specific heat. The employment of FSC allows attaining this characterization over a wide range of time scales, otherwise inaccessible by other techniques. Furthermore, FSC allows circumventing crystallization by applying fast cooling from the melting temperature down to the glass transition. We find that the cooling rate dependency of the vitrification kinetics, as identified by T_f, is decoupled from the temperature dependence of the α-relaxation. In particular, the former follows milder temperature dependence in comparison to the α-relaxation. This result implies that the T_f of a glass can be tuned by changing preparation conditions, for instance, the cooling rate or the annealing time in the glassy state, over a considerably larger range than it would be allowed by the α-process alone. The deep implications on the effect on properties of fundamental importance are discussed.

RESULTS

Atomic mobility by means of the step response analysis

We start presenting the frequency-dependent reversing specific heat: C_p(rev)(ω) = (C_p′(ω)² + C_p′′(ω)²)^0.5, shown in the inset of Fig. 1 (top), which conveys insights on atomic mobility associated to the α-relaxation and secondary relaxation processes (see Materials and Methods). This provides information on the dynamic glass transition. C_p(rev) is normalized accounting for the glass and melt reversing specific heats as follow

$$C_{\mathrm{p}(\text{rev})}^{\text{norm}}(\mathrm{\omega })=\frac{C_{\mathrm{p}(\text{rev})}(\mathrm{\omega })-C_{\mathrm{p}(\text{rev},\text{glass})}(\mathrm{\omega })}{C_{\mathrm{p}(\text{rev},\text{melt})}(\mathrm{\omega })-C_{\mathrm{p}(\text{rev},\text{glass})}(\mathrm{\omega })}$$ (1)

Fig. 1. Reversing specific heat as a function of temperature and frequency in relation to mechanical compliance.

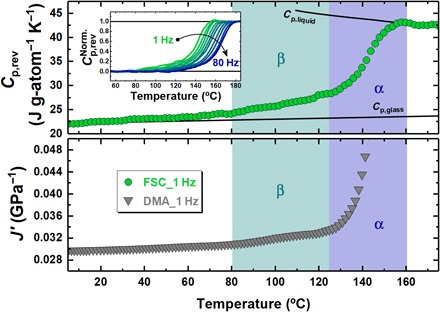
Frequency-dependent response for the Au₄₉Cu_26.9Si_16.3Ag_5.5Pd_2.3 glass former: (Top) Reversing specific heat as a function of temperature obtained from step response analysis at 1 Hz by FSC. The lines show the glass and liquid reversing specific heat taken from (17). The inset shows the normalized reversing specific heat as a function of temperature at frequencies from 1 to 80 Hz. (Bottom) Real part of the mechanical compliance as a function of temperature obtained from dynamic mechanical analysis (DMA) at 1 Hz taken from (36).

C_p(rev) is approximately equal to C_p′(ω), given the fact that the latter is generally at least one order of magnitude larger than C_p′′. As expected, a frequency increase induces a shift to higher temperature of the step in C_p(rev).

The Fig. 1 (top) shows the temperature dependence of C_p(rev) for a frequency of 1 Hz. Although these results were obtained on cooling, it is worth pointing out that similar experiments conducted on heating from the glass delivered the same behavior, provided that samples were immediately characterized after cooling. Apart from the main step, associated to the α-process, a second smooth increase in C_p(rev) is observed between 80° and 120°C. We attribute this to the slow β-relaxation process, which, differently from the cooperative motion responsible for the α-relaxation, is generally attributed to localized atomic motion. This attribution well agrees with the dynamic mechanical analysis (DMA) data shown in Fig. 1 (bottom), which reports the temperature dependence upon heating at a frequency of 1 Hz of the mechanical equivalent of C_p^′, i.e., the real part of the compliance, J^′ (36). This equivalence comes from the fact that $C_{\mathrm{p}}^{*}$ is the complex thermal compliance and, therefore, is equivalent to the complex mechanical compliance, J*. Note that the step response analysis using FSC is able to detect the slow β-relaxation process, and this is consistent with DMA studies. This calorimetric approach could be exploited in the future for its large frequency range of measurement.

Vitrification kinetics by means of fictive temperature determination

Vitrification kinetics is characterized by assessing T_f considering heating scans after cooling at different rates. Figure 2 shows selected heat flow scans at 1000 K/s after cooling at the indicated rates. Three zones can be distinguished: (i) a low temperature region in the range from <150° to ∼180°C, magnified in the inset and related to the glass transition; (ii) an intermediate range where cold crystallization takes place; and (iii) the temperature range of melting above 320°C. Inspection of the glass transition region indicates that, apart from the expected increase of the endothermic overshoot connected to a larger enthalpy recovery, the step in the specific heat remains constant when the applied cooling rate is decreased from 1000 down to 0.7 K/s. The associated heat of crystallization, which is the area associated to the exothermic signal, remains constant as well (see fig. S6 for the rigorous quantification of the heat of crystallization). In contrast, when the liquid is cooled with a rate of 0.5 K/s or slower, the heat flow rate step at the glass transition appears to drop and the exothermic signal becomes gradually smaller until it disappears, indicating that partial to total crystallization takes place upon cooling at these slow rates.

Fig. 2. Heat flow rate for Au₄₉Cu_26.9Si_16.3 Ag_5.5Pd_2.3 as a function of temperature upon heating with 1000 K/s after cooling at the indicated rates in the range from 1000 to 0.1 K/s.

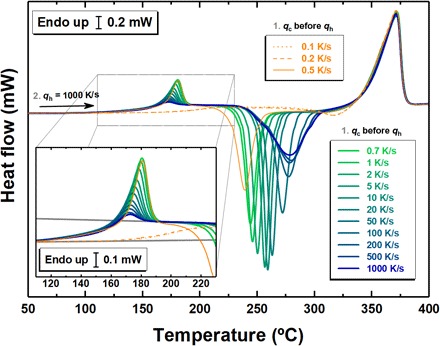
The inset is a magnification in the glass transition region.

The application of the Moynihan method (34) allows extracting cooling rate–dependent T_f values from the heat flow rate signals of Fig. 2 (see Materials and Methods). The so-obtained cooling rate–dependent T_f values are plotted in Fig. 3. Here, the cooling rate q_c is converted to a characteristic time scale for vitrification based on the equation: τ = ΔT/q_c, where the ΔT is the width of the glass transition, which is independent of the applied heating rate (see fig. S7). This equation was proposed independently in (2, 37) and subsequently successfully applied to BMG formers (38–42).

Fig. 3. Time scale of vitrification extracted from T_f data (filled orange stars) and relaxation time τ (filled green circles) as a function of the inverse of temperature obtained by FSC for Au₄₉Cu_26.9Si_16.3Ag_5.5Pd_2.3 glass.

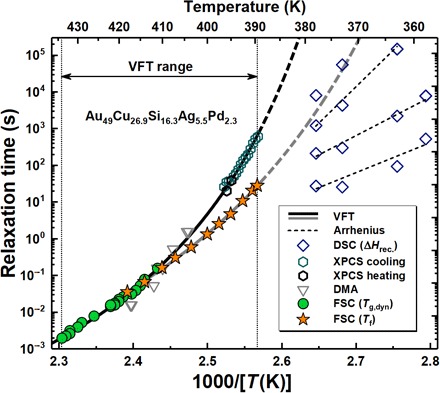
Additional relaxation time values from literature are displayed with open symbols based on XPCS (hexagons) (43), DMA (triangles) (36, 43), and enthalpy recovery studies after isothermal annealing (diamonds) (17).

DISCUSSION

Figure 3 plots time scale values associated to the Au₄₉Cu_26.9Si_16.3Ag_5.5Pd_2.3 glassy dynamics. In particular, apart from the characteristic time scale for vitrification related to T_f (star symbols), it reports the time scale of the α-relaxation (filled circles) obtained from the FSC step response analysis of Fig. 1 considering the temperature of the midpoint of the step in C_p(rev) in the glass transition region as the dynamic glass transition temperature, T_{g, dyn}. Figure 3 also includes atomic relaxation times based on DMA (36, 43) (triangles) and x-ray photon correlation spectroscopy (XPCS) in the liquid state (hexagons) (43). Furthermore, characteristic time scales based on previous calorimetric enthalpy recovery studies (17) are reported with diamond symbols. These likely bear an intimate relation with different diffusivities previously identified in BMG (31, 44).

The temperature dependence of τ from FSC by step response analysis (green circles) agrees with DMA- and XPCS-based τ(T) data, as it was also found in other glasses (45). All of these data are associated to atomic mobility and are fitted through the Vogel-Fulcher-Tammann (VFT) equation

$$\mathrm{\tau }(T)={\mathrm{\tau }}_0\text{exp}\left(\frac{T_0{D}^{*}}{T-T_0}\right)$$ (2)

where τ₀ is a pre-exponential factor, T₀ is the temperature at which τ would become infinite, and D* is the so-called kinetic fragility index (46). The fit of atomic mobility data to the VFT equation delivers T₀ = 348 K, log τ₀ = − 18, and D* = 6.8 ± 0.2. The latter is characteristic of a fragile liquid (38, 47) and is in agreement with the high-temperature liquid fragility for this glass former reported elsewhere (17, 43).

The temperature dependence of τ associated with cooling rate–dependent T_f values from FSC experiments (star symbols) also exhibits super-Arrhenius behavior but with different parameters. The data obtained by applying fast cooling rates, which correspond to high values of T_f, match with those of the α-relaxation. In contrast, upon the application of lower cooling rates, substantial deviations from the temperature dependence of the α-relaxation can be observed. The fragility index obtained from the VFT fit of the time scales for vitrification (fit of star symbols only) is D* = 11. This would correspond to lower kinetic fragility than that of the α-relaxation. The same considerations apply to the fragility index exclusively associated to the cooling rate–dependent T_f data, which is D* = 10.3 (see the Supplementary Materials). This would correspond to the fragility of a stronger liquid, although not enough to advocate a fragility crossover. For this composition, this crossover was found at a considerably lower critical temperature in the ultraviscous liquid state connected to relaxation times in the order of 1000 s based on XPCS and high-energy x-ray diffraction analyses (17, 43). At the lowest temperature for which vitrification kinetics and atomic mobility data are available (389 K), the characteristic time connected to vitrification kinetics is 1.5 orders of magnitude faster than the relaxation time of the α-process, indicating a significant decoupling between them. The onset of this decoupling is observed for τ ∼ 0.1 s, which corresponds to the moderate cooling rate of 200 K/s. It results that, for deeper undercooling (in this case, connected to slower cooling rates), the liquid vitrifies at a T_f that is lower than expected according to the VFT behavior associated to the α-relaxation. Together, these observations indicate that, at time scales greater than 0.1 s, other atomic motions—not involving appreciable atomic rearrangement connected to the α-relaxation—contribute to maintain the system at equilibrium, and thereby, vitrification is delayed to lower temperatures. Further corroboration to this important conclusion can be drawn comparing the temperature width of the α-relaxation with that of the transformation from glass into melt, an approach recently followed by Schawe (4). This relies on the fact that, in those cases where the α-relaxation and vitrification are fully coupled, the ratio of these widths, the so called “vitrification function,” κ, must be independent of the relaxation time (or equivalently the cooling rate). The outcome of this analysis, shown in section S4, shows that κ actually increases with the relaxation time, indicating that glass transformation into melt encompasses a much larger temperature range than expected on the base of the α-relaxation alone. The increase of κ is evident at values of τ larger than ∼0.1 s, which is equal to that for which the decoupling α-relaxation/vitrification kinetics is observed.

This finding is not typically observed in other glass-forming systems at these moderate time scales (2–5), unless the system is subjected to geometrical confinement, as widely reported for polymeric glasses (11, 22–24, 48). Glasses subjected to extremely long annealing would also present a decoupling. In this case, much longer time scales are required to allow the observation of a significant separation between vitrification kinetics and the α-relaxation for bulky polymeric specimens, e.g., when the liquid is quasi-static cooled with a rate of ∼10⁻⁴ K/s (49).

The outcome of the present study hints toward the existence of multiple mechanisms involved in relaxation in the glassy state. In the case of the present metallic glass, the separation of these mechanisms has been recently unveiled by monitoring how equilibrium is recovered in the glassy state following the time evolution of the enthalpy (17). The associated time scales are reported in Fig. 3 as blue open diamonds. These exhibit mild Arrhenius temperature dependence, and thereby, each of these mechanisms can be responsible for the reduction of the activation energy of the vitrification process, highlighted by the VFT behavior of τ(T_f) data. Furthermore, the role of the secondary relaxation identified by step response analysis (see Fig. 1) may also be of relevance, and further investigation in this sense is warranted. Different mechanisms of devitrification were also observed in other metallic glasses aged over prolonged time (19, 50, 51), where the fast mechanisms, providing early devitrification, were associated to fluctuations of local regions (19). Similar results were observed for nonmetallic glass-forming systems as well, such as a plastic crystal aged over 7 years (18), polystyrene aged for months (20), and several polymers aged over about 30 years (21). Our study provides, in addition, the observation that, in a bulk glass (that is, unrestricted by geometrical confinement) and for time scales as short as a few seconds (i.e., without any specific annealing), vitrification can take place according to the atomic mobility of processes different from the α-relaxation. This separation becomes more pronounced at larger undercooling, suggesting a significant contribution of the additional dynamical processes. These have been identified by enthalpy recovery experiments (17) (see diamonds in Fig. 3) and, in line with our conjectures, actually tend to merge with the α-relaxation in the temperature range where the decoupling vitrification kinetics/α-relaxation begins to be visible.

According to the previous discussion, the existence of multiple mechanisms of vitrification is a general pattern in all kinds of glasses. While, depending on the kind of glass, the connection with specific relaxational processes (52, 53) is inevitably glass specific, it is worth pointing out that the shear transformation zone (STZ) theory (54, 55) or, more generally, the existence of spatially heterogeneous events (56) may convey a general framework for the presence of mechanisms different from the α-process in the vitrification kinetics, a fact, as discussed, actually found in glasses of different nature. The STZ theory predicts the existence of a highly disordered state with a large population of low activation barriers, whose hierarchical relaxation precedes that associated to the α-process.

The results of the present study prove that T_f of metallic glasses can be tuned at wish through the activation of additional mechanisms of atomic mobility, which differ from the α-process. If vitrification was driven only by the latter, as a consequence of its very high activation energy, then only limited variations of the T_f with the cooling rate, or equivalently limited variations of the annealing time in aging experiments, would be allowed. In contrast, even for deep undercooling, access to low values of T_f can be assisted by atomic mobility mechanisms that do not involve the α-process. This result implies a reconsideration of the glass transition mechanism and suggests a previously unknown way for tuning mechanical (57, 58) and optical (59) properties of glasses, recently shown to be intimately connected to T_f.

In summary, using FSC, we have characterized for a metallic glass former the α-relaxation in terms of the dynamic glass transition temperature, T_{g, dyn}, and the vitrification kinetics in terms of the limiting fictive temperature, T_f, upon cooling. Combining FSC results with those of other techniques, we were able therewith to characterize the α-relaxation time over more than four decades. Challenging conventional wisdom based on a one-to-one correlation between vitrification kinetics and the α-relaxation, we show that these two aspects of glassy dynamics are decoupled. In particular, vitrification is delayed with respect to what it would be expected, accounting exclusively for the α-relaxation. This result implies that fast atomic mechanisms that do not contribute to the α-relaxation and that they can be identified by tracer diffusion (25, 29, 30), NMR (31), or enthalpy recovery experiments in the glassy state (17), steer vitrification at deep undercooling. Last, it is important to point out that while our results are specific for a single metallic glass, the existence of different relaxation mechanisms has been proved for other metallic glasses and glass formers of different nature. Hence, the presence of the decoupling α-relaxation/vitrification kinetics can be anticipated in a wide variety of glasses. The decoupling that we observe at moderate rates may remain an open question, thus it will promote a large impact and engagement in science. We expect new impetus to further exploration of the decoupling through the employment of new generation advanced calorimetry.

MATERIALS AND METHODS

FSC experiments were performed with the Au₄₉Cu_26.9Si_16.3Ag_5.5Pd_2.3 composition by using the Flash DSC 1 of Mettler Toledo based on chip calorimetry technology, equipped with a two-stage intracooler, allowing for temperature control between −90° and 450°C. FSC specimens were obtained from an as-spun ribbon of 7 ± 1 μm of thickness, which was prepared using the procedures described in (17). The ribbon was shown to be amorphous by x-ray diffraction and homogeneous by scanning electron microscopy. The FSC specimen was manually placed onto the active area of a chip sensor, and the actual mass was determined by comparing the heat of fusion obtained by this technique to that obtained by conventional DSC with a known mass. For the sake of reproducibility, different masses, implying different sample sizes, were used. This ranged between 500 and 1000 ng. In all cases, both atomic mobility and vitrificaton kinetics exhibited the same behavior. This implies that, at least until the lowest used sample mass, no size effects exist, and therefore, the glassy dynamics response of our metallic glass is bulk like. The FSC cell was constantly fluxed by nitrogen gas with a rate of 20 ml min⁻¹. Calibration of the FSC was ensured through the melting of a standard indium at different rates placed onto the reference chip area afterward.

Step response analysis was used to assess the atomic mobility (35). This consisted of 2 K temperature down jumps followed by isotherms of duration 0.05 or 1 s. In such a way, the complex specific heat, $C_{\mathrm{p}}^{*}(\mathrm{\omega })={C_{\mathrm{p}}}^{\prime }(\mathrm{\omega })-i{C_{\mathrm{p}}}^{\prime \prime }(\mathrm{\omega })$, is obtained by Fourier transformation of the heat flow rate [HF(t)] and the instantaneous cooling rate [q_c(t)]

$$C_{\mathrm{p}}^{*}(\mathrm{\omega })=\frac{{\int }_0^{t_{\mathrm{p}}}\mathit{HF}(t)e^{-i\mathrm{\omega }t}\mathit{dt}}{{\int }_0^{t_{\mathrm{p}}}{q}_{\mathrm{c}}(t)e^{-i\mathrm{\omega }t}\mathit{dt}}$$ (3)

By changing the duration of the period, t_p, and accessing higher harmonics: ω = k2π/t_p, where k is an integer, a frequency range from 1 to 80 Hz could be accessed. Experiments on a wide variety of glasses show that thermal fluctuations are generally larger than 2 K (60). On the basis of our experiments of Fig. 1 (top), the thermal fluctuations for this metallic glass are approximately 9 K (see the Supplementary Materials), thereby, the chosen temperature jump guarantees linearity. Hence, in such a way, the so-called frequency-dependent dynamic glass transition temperature, T_{g, dyn}, is obtained.

The kinetics of vitrification was characterized over a range of cooling rates between 0.7 to 1000 K/s. To avoid crystallization, before applying these rates, quenching of the melt was always carried out with a cooling rate of 4000 K/s from well above the liquidus temperature down to 170°C. The limiting T_f attained after applying different cooling rates below 170°C was calculated applying the Moynihan method (see the Supplementary Materials) (34) to heat flow rate scans obtained at a rate of 1000 K/s. The T_f calculated by this method is characteristic for the applied cooling rate and, therefore, independent of the subsequent heating rate. As T_f is calculated on heating, we checked whether there exist superheating effects, as previously reported (61). In the Supplementary Materials, we show in details, also making reference to pertinent works (62, 63), that these effects are negligible in the conditions used in our work.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/17/eaay1454/DC1