Individual Variation in Functional Topography of Association Networks in Youth

SUMMARY

The spatial distribution of large-scale functional networks on the cerebral cortex differs between individuals, and is particularly variable in association networks that are responsible for higher-order cognition. However, it remains unknown how this functional topography evolves in development and supports cognition. Capitalizing upon advances in machine learning and a large sample imaged with 27 minutes of high-quality fMRI data (n = 693, ages 8-23y), we delineate how functional topography evolves during youth. We found that the functional topography of association networks is refined with age, allowing accurate prediction of unseen individuals’ brain maturity. The cortical representation of association networks predicts individual differences in executive function. Finally, variability of functional topography is associated with fundamental properties of brain organization including evolutionary expansion, cortical myelination, and cerebral blood flow. Our results emphasize the importance of considering both the plasticity and diversity of functional neuroanatomy during development, and suggest advances in personalized therapeutics.

INTRODUCTION

During childhood, adolescence, and young adulthood, the human brain must develop to support increasingly complex cognitive and behavioral capabilities. One broad domain of cognition that undergoes particularly protracted development is executive function, which encompasses diverse cognitive processes including working memory, performance monitoring, and task switching (Best and Miller, 2010; Gur et al., 2012). Individual differences in executive function have been linked to meaningful functional outcomes such as academic achievement (Arffa, 2007; Best et al., 2011), and deficits of executive function are associated with violence, initiation of drug use, and risk taking behaviors (Reynolds et al., 2019). Executive dysfunction is also associated with most major neuropsychiatric diseases (Shanmugan et al., 2016), including attention deficit hyperactivity disorder and psychosis (Barkley, 1997; Wolf et al., 2015).

Executive processes rely upon a spatially distributed set of brain regions that span frontal, parietal, and temporal cortex (Alvarez and Emory, 2006; Niendam et al., 2012; Rottschy et al., 2012). These regions have low cortical myelin content (Glasser and Van Essen, 2011), receive a disproportionate amount of cerebral blood flow (Satterthwaite et al., 2014b; Taki et al., 2011), and have greater areal expansion compared to other cortical regions in humans (Reardon et al., 2018) and analogous regions in non-human primates (Hill et al., 2010). Non-invasive studies using functional MRI (fMRI) in humans have shown that these distributed regions activate together during cognitively demanding executive tasks and also show coherent signal fluctuations at rest (Cole and Schneider, 2007; Marek and Dosenbach, 2018; Satterthwaite et al., 2013b), allowing them to be understood as large-scale functional networks. Typically, these networks have been compared across individuals by alignment with brain structure, which assumes that there is a stable correspondence between functional and structural anatomy across individuals (Laumann et al., 2015). However, recent evidence from multiple independent efforts has demonstrated that there is marked inter-individual variability in the spatial topography of functional brain networks even after accurate alignment of brain structure (Bijsterbosch et al., 2018; Braga and Buckner, 2017; Glasser et al., 2016; Gordon et al., 2017a; Gordon et al., 2017b; Gordon et al., 2017c; Kong et al., 2018; Laumann et al., 2015; Li et al., 2019; Wang et al., 2015).

Studies of highly-sampled individuals for whom numerous sessions of scanning data were acquired have established that an individual’s functional topography is highly reproducible across scanning sessions (Gordon et al., 2017c; Laumann et al., 2015). Furthermore, several studies have reported that topographic variability across individuals is maximal in association networks (Gordon et al., 2017b; Gordon et al., 2017c; Kong et al., 2018; Li et al., 2019; Wang et al., 2015). This finding aligns with work showing that association networks also show the greatest inter-individual variation in their connectivity profiles (Gratton et al., 2018; Kong et al., 2018; Li et al., 2019; Mueller et al., 2013), and can be used for accurate identification of individuals (Finn et al., 2015; Miranda-Dominguez et al., 2014). Understanding subject-specific functional topography also allows prediction of an individual’s spatial pattern of activation across diverse tasks (Gordon et al., 2017c; Laumann et al., 2015; Li et al., 2019; Tavor et al., 2016; Wang et al., 2015). Failure to account for such individual variation in functional topography may lead differences in spatial distribution to be aliased into measurement of inter-regional functional connectivity, potentially biasing both inference and interpretation (Bijsterbosch et al., 2018; Li et al., 2019).

Despite such rapidly accruing evidence for the importance of individual differences in functional neuroanatomy, to our knowledge no studies have characterized variation of functional topography in youth. To address this gap, here we tested three inter-related hypotheses. First, we hypothesized that functional topography would be systematically refined during development, with developmental changes being concentrated in association cortex. Second, we expected that variation in the functional topography of association networks would predict individual differences in executive function. Third and finally, we anticipated that variability in functional topography would be constrained by fundamental properties of brain organization, including evolutionary expansion and cortical myelination. To test these hypotheses, we capitalized upon recent advances in machine learning and a large sample of youth who participated in the Philadelphia Neurodevelopmental Cohort (PNC; Satterthwaite et al., 2014a).

RESULTS

We studied 693 youths aged 8-23 years who completed imaging as part of the PNC with over 27 minutes of high-quality fMRI data. To delineate person-specific functional networks, we used a spatially-regularized form of non-negative matrix factorization (NMF; Lee and Seung, 1999) that has previously been shown to accurately identify functional networks in individuals (Li et al., 2017) (Figure S1). To facilitate comparison to other methods (Kong et al., 2018), we identified 17 functional networks in each participant (Figure 1). In contrast to methods that discretely assign each vertex to a single network, NMF yields a probabilistic (soft) parcellation. This probabilistic parcellation can be converted into discrete (hard) network definitions for both display and comparison with other methods by labeling each vertex according to its highest loading. Visual inspection suggested that these discretized networks showed a high correspondence with a widely-used 17-networks solution (Yeo et al., 2011). Using a spin-based spatial permutation test (see STAR Methods), we found a significant alignment (P_spin < 0.001) between our group atlas and the canonical 17 networks from the Yeo atlas (Yeo et al., 2011). We also verified that individualized networks improve functional homogeneity compared to group averaged networks as expected (See STAR Methods and Figure S2A & B).

Figure 1.

Group atlas of 17 networks. The networks in the group atlas include visual networks (numbers 6 and 10); somatomotor networks (2: foot motor; 4: face motor; 11 and 13: hand motor); an auditory network (16); dorsal attention networks (5 and 14); cingulo-opercular/ventral attention networks (7 and 9); fronto-parietal control networks (3, 15, and 17), and default mode networks (1, 8, and 12). In this atlas, there are 17 loadings for each vertex, which quantify the extent it belongs to each network. For each loading map, brighter colors indicate greater loadings. Vertices can be assigned to the network with the highest loading, yielding a discrete network parcellation (center).

We named each of these networks by comparing the overlap with the Yeo atlas (Yeo et al., 2011) (Figure 1). However, some networks could have alternate labels when considering another widely-used network parcellation (Power et al., 2011). Specifically, we refer to network 7 and network 9 as cingulo-opercular/ventral attention networks, as suggested by other functional atlases (Dosenbach et al., 2007; Power et al., 2011). Network 15 aligns with a fronto-parietal network in the Yeo atlas (Yeo et al., 2011), but has also been referred to as the medial parietal network (Gilmore et al., 2015; Power et al., 2011). Network 8 encompasses the temporo-parietal network and aligns with the default mode network in the Yeo atlas, but would be categorized as the ventral attention network by Power et al. (2011). Finally, network 16, which primarily encompassed the auditory cortex, was not present in the Yeo atlas. As such, we named it an auditory network as in Power et al. (2011).

Across-subject variability of network topography is maximal in association cortex

Visual examination of individual subjects revealed that while the gross spatial distribution of networks was consistent across participants, distinct person-specific topographic features could be readily observed across the age range studied (Figure 2). Heterogeneity in the spatial distribution of networks was particularly apparent in association networks such as the fronto-parietal, cingulo-opercular/ventral attention, and default mode networks. In contrast, participant-level representations of the visual and somatomotor networks appeared to be much more consistent across individuals.

Figure 2.

Individuals display distinct functional network topography. The group network parcellation and four example network parcellations are displayed. The four participants include a child with low executive function (EF), a child with high EF, an adult with low EF, and an adult with high EF. The topmost row represents the whole-brain discrete network parcellation, while the subsequent five rows represent the fronto-parietal, cingulo-opercular/ventral attention, default mode, visual, and somatomotor networks. For each network, both the loading map and the corresponding discrete networks are displayed. While the gross spatial distribution of networks was consistent across participants, distinct person-specific topographic features could be readily observed. In particular, heterogeneity in the spatial distribution of networks was apparent in association networks including fronto-parietal, cingulo-opercular/ventral attention, and default mode networks. In contrast, participant-level representations of visual and somatomotor networks appeared to be more consistent across individuals.

In order to quantitatively evaluate this observation in the entire sample, we calculated the across-subject variance in network loadings using a non-parametric statistic (the median absolute deviation). We observed the highest across-subject variability in frontal, parietal, and temporal cortex (Figure 3A). When variability was ranked by network, we found that association networks had the highest topographic variability across subjects, whereas sensorimotor networks had the lowest (Figure 3B). Additionally, we evaluated whether across-subject variability was stable over the age range studied. To do this, we split the sample into age tertiles (n = 231 each), and calculated the topographic variability for each group. We found that variability was highly similar in each age group (r = 0.99; Figure 3C). Results were highly similar when the variability of discrete networks derived using NMF or MS-HBM were examined (Figure S2C & D). Having confirmed that functional topography is most variable in association networks, we next evaluated whether this variation was related to brain maturation during youth.

Figure 3.

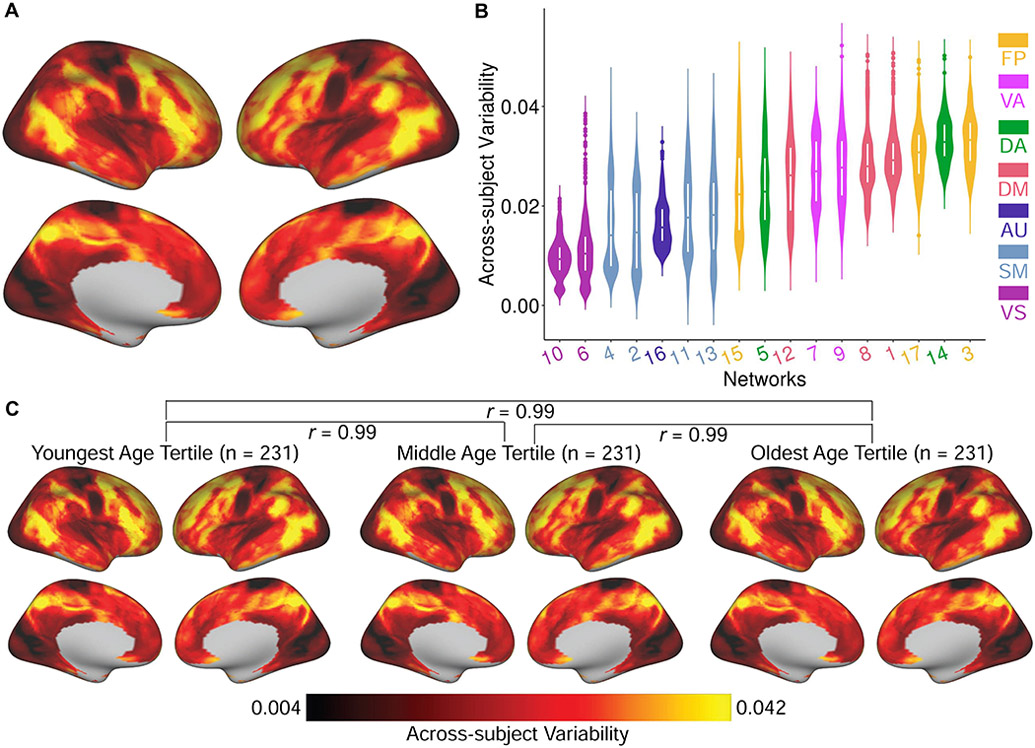
Across-subject variability of functional network topography is highest in association cortex. (A) A non-parametric measure of variability revealed that functional topography was most variable across individuals in association cortex and least variable in sensorimotor cortex. (B) Summarizing variability by network revealed that across-subject variability was highest in association networks including fronto-parietal, dorsal attention, default mode, and cingulo-opercular/ventral attention networks. (C) Variability of functional topography was nearly identical in each of three age-based tertiles (n = 231 each). FP: fronto-parietal; VA: cingulo-opercular/ventral attention; DA: dorsal attention; DM: default mode; AU: auditory; SM: somatomotor; VS: visual.

Functional topography is refined with age and encodes brain maturity

As an initial step, we examined whether the total cortical representation of each network was associated with age. Specifically, for each network, we summed the loadings of all vertices to concisely summarize the total cortical representation of each probabilistic network. Notably, as networks were derived in template space, this measure controls for individual differences in total surface area, which varies across development (Tamnes et al., 2017). As brain development is known to be a nonlinear process (Blakemore, 2012; Grayson and Fair, 2017; Tamnes et al., 2017), we used general additive models (GAMs; Wood, 2004) to capture both linear and nonlinear associations with age, while covarying for sex and in-scanner motion. After correcting for multiple comparisons with the Bonferroni method, these analyses revealed that the cortical representation of the face motor network (network 4, Z = −3.72, P_Bonf = 0.003, partial r = −0.14, Confidence Interval (CI) = [−0.21 −0.07]) and occipital pole visual network (network 10, Z = −3.06, P_Bonf = 0.038, partial r = −0.12, CI = [−0.19, −0.04]) significantly declined with age (Figure 4).

Figure 4.

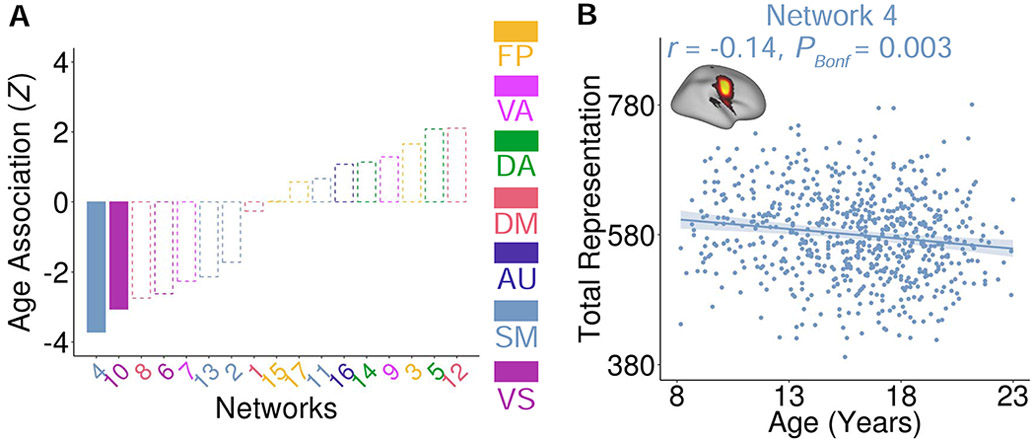
Associations between total cortical representation and age in youth. (A) The total cortical representation of two networks – the face motor network (network 4) and occipital pole visual network (network 10) – declined with age (P_Bonf < 0.05; dashed lines indicate networks with non-significant age effects). (B) Scatter plot of the relationship between age and the total cortical representation of the face motor network.

Notably, a coarse summary measure such as the total network representation does not capture complex patterns of topographic reconfiguration. We further used mass-univariate analysis to evaluate the relationship between network loading and age for each vertex (see Figure S3A). Due to the relatively large number of tests conducted, relatively few vertices survived FDR correction (q < 0.05). Previous studies have demonstrated that multivariate analyses can leverage such high dimensional data and integrate spatially distributed patterns (Haynes, 2015; Kong et al., 2018; Norman et al., 2006). Accordingly, we used a multivariate approach to understand the degree to which the overall pattern of functional topography encoded developmental information. Specifically, we used ridge regression with a nested two-fold cross validation (2F-CV) to predict the brain maturity of an unseen individual based on the functional topography of all networks (see STAR Methods). Using training and testing sets that were matched on age, we calculated both the mean absolute error (MAE) and the partial correlation between the predicted age (“brain maturity index”) and chronologic age in the testing set, while controlling for sex and in-scanner motion. This multivariate analysis revealed that the complex pattern of network topography could accurately predict an unseen individual’s brain maturity with a high degree of accuracy (Figure 5A): the partial correlation between the predicted age and chronological age was 0.66 (P_perm < 0.001), while MAE was 1.92 years (P_perm < 0.001). We repeated this procedure while reversing the training and testing sets, and found very similar results (partial r = 0.65, P_perm < 0.001; MAE = 2.00 years, P_perm < 0.001). In order to ensure that our matched split of the data was representative, we repeated this procedure 100 times, each time randomly splitting subjects into two subsets. Such random, repeated cross-validation returned highly consistent results (mean partial r = 0.65, P_perm < 0.001; mean MAE = 1.98 years, P_perm < 0.001; Figure 5B).

Figure 5.

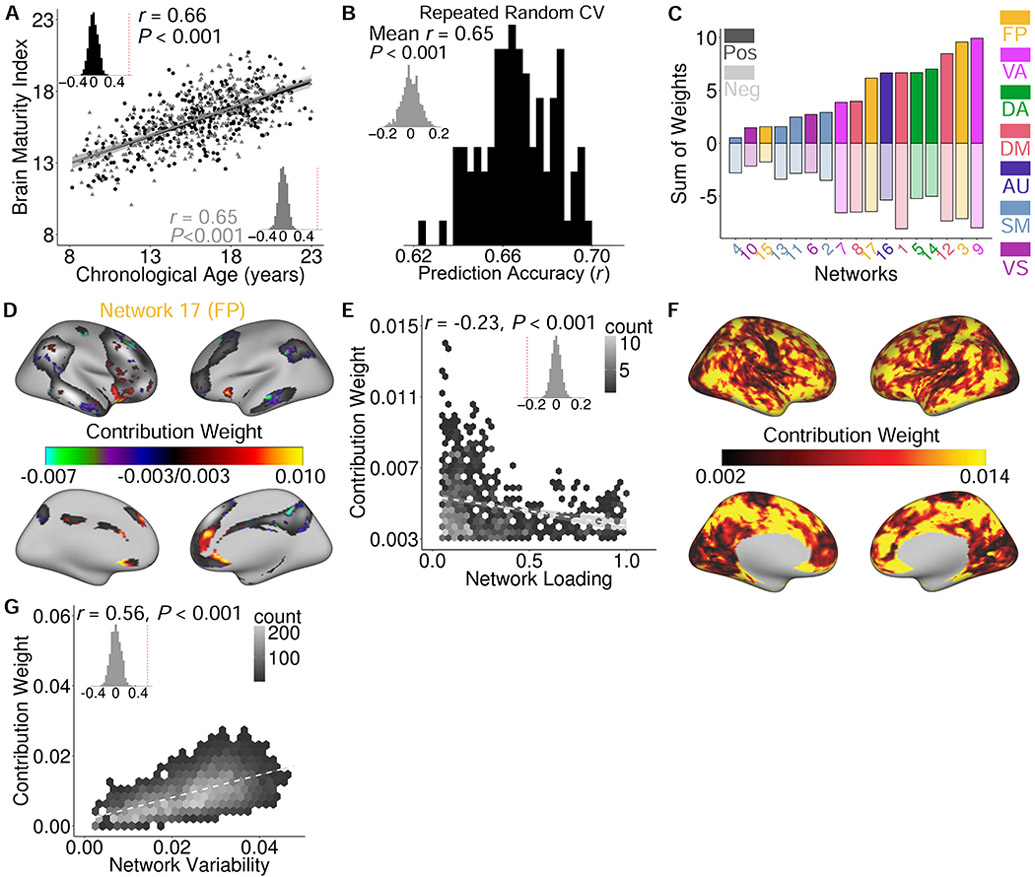
Functional topography evolves with age in youth and predicts unseen individuals’ brain maturity. (A) The complex pattern of functional topography could be used to predict brain maturity in unseen data. Data points represent predicted brain maturity of subjects in a model trained on independent data; inset histogram represents the null distribution of prediction accuracy from a permutation test. The 2-fold cross-validation was implemented by splitting all participants into two subsets that were matched on age. (B) Repeated random 2-fold cross-validation (100 runs) provided evidence of stable prediction accuracy, which was far better than a null distribution with permuted data (inset). (C) Examining the sum of the model weights of all positively-weighted and negatively-weighted vertices separately within each network revealed that association networks contributed the most in predicting brain maturity. Both positive and negative associations with age were present within each network. (D) Model feature weights driving prediction were highest at network edges for network 17; the top 25% of vertices in terms of feature importance are displayed. (E) Feature weight was negatively correlated with group network loadings across positively-weighted vertices (panel D) for network 17; inset displays spatial association compared to null distribution from permutation test. (F) At each location on the cortex, the absolute contribution weight of each network was summed, revealing that association cortex contributed the most to the multivariate model. (G) Functional network maturation is constrained by topographic variability. Vertices that contributed the most to the multivariate model predicting brain maturity were also those that varied the most across subjects. Inset histograms represent spatial association compared to a null distribution obtained from spatial permutation testing.

To understand the developmental effects underlying these results, we evaluated model feature weights. In the multivariate model, each vertex received a feature weight for each network. We averaged the feature weight maps from the repeated (i.e., 100 runs) random 2F-CV. Summing the positive and negative weights separately within each network, we found that association networks contributed the most to the multivariate model (Figure 5C). However, we also found that there was a complex pattern of both positive and negative relationships with age (Figure S3B), cohering with the initial finding that the total network representation did not change with age in most networks.

Examining the spatial distribution of these feature weights, we observed that the positively-weighted vertices that contributed the most to the prediction of brain maturity were systematically located at the border of networks, where there is a low average network loading (Figure S3B). For example, refinement of network boundaries with age was prominent in the lateral fronto-parietal networks (e.g., network 17; Figure 5D). To quantitatively evaluate this observation, for each network, we calculated the correlation between the contribution weight from the multivariate model predicting brain maturity and the group network loadings across the positively-weighted vertices that contributed the most to the multivariate model. Significance was evaluated using a permutation test, with multiple testing accounted for using Bonferroni correction. Of the 17 networks evaluated, 10 displayed a significant negative correlation between the group network loading and the feature importance (Figure S4); this set included the lateral fronto-parietal networks (e.g., network 17; Figure 5E). In contrast, no network showed the opposite effect to a significant degree. This result suggests that network loadings that strengthen with age tend to consistently be located at network boundaries.

Importantly, mass-univariate analyses provided convergent results. As in the multivariate analysis, we found that strong positive associations between age and network loadings were seen at network boundaries. For each network, we calculated the correlation between group network loading and the strength of the age effect across vertices that showed a significant positive association with age (FDR q < 0.05, Figure S3A). We found that 6 networks displayed a significant negative relationship between the strength of the age effect and the group network loading. As for multivariate analysis, no network showed the opposite effect to a significant degree. These analyses indicate that during development, network refinement primarily occurred at network borders.

To further visualize these effects, we compared the discrete network membership in the 100 youngest participants (Figure S5A) and 100 oldest participants (Figure S5B). Specifically, we averaged the network loadings for each group, and assigned each vertex to the network with the highest average loading. Notably, the discrete assignment primarily diverged between groups at borders of association networks (Figure S5C).

Next, we sought to understand whether variability of functional topography constrained patterns of network maturation. To concisely summarize the spatial contribution of locations in the multivariate model, we summed the absolute weights of each vertex across networks (Figure 5F), and related this to our non-parametric measure of network variability (see Figure 3A). We found that multivariate patterns of brain maturation were driven by vertices with high across-participant variability, and were present primarily in frontal, parietal, and temporal association cortex (Figure 5G; r = 0.56, P_spin < 0.001).

These results suggest that association networks contributed the most to the prediction of brain maturity (Figure 5C & F). To further verify this finding, we predicted brain maturity separately using features from either association or sensorimotor networks alone. We found that predictive performance was higher when using association networks (repeated random 2F-CV, mean partial r = 0.52) than sensorimotor networks (mean partial r = 0.28).

As a final step, we conducted several supplementary analyses to confirm that our results were robust to methodological choices. We repeated the brain maturity prediction using both the discrete network parcellation derived from NMF and also that from MS-HBM. While still highly significant (P_perm < 0.001), not considering network probability mildly degraded predictive accuracy (see Figure S6). To test if the number of networks impacted the results, we predicted brain maturity using a 7-network soft atlas created using NMF, which returned similar results (see Figure S6). Taken together, these results demonstrate that functional network topography encodes brain maturity, is driven by refinement of association networks, and is constrained by the variability of these systems.

Association network topography predicts individual differences in executive function

Having found that functional topography accurately encoded brain maturation, we next evaluated the implications of topographic variability for cognition. Specifically, we investigated whether variation in functional network topography predicted individual differences in executive function. Executive function was summarized using a previously-published factor analysis of the Penn Computerized Neurocognitive Battery (Moore et al., 2015). While controlling for age, sex, and in-scanner motion, general additive models revealed that the improved executive performance was associated with a greater total cortical representation of two fronto-parietal control networks, including one lateral fronto-parietal network (Figure 6A & B; network 17, Z = 5.58, P_Bonf = 5.78 × 10⁻⁷, partial r = 0.21, CI = [0.13, 0.28]) and the medial parietal network (Figure 6A & C, network 15, Z = 3.81, P_Bonf = 0.003, partial r = 0.14, CI = [0.07, 0.22]). In contrast, greater representation of the foot motor network (network 2, Z = −3.15, P_Bonf = 0.029, partial r = −0.12, CI = [−0.19, −0.04]) was associated with reduced executive performance.

Figure 6.

The total cortical representation of fronto-parietal networks is associated with executive function. (A) Executive function was positively correlated with the total cortical representation of two fronto-parietal networks, including one lateral fronto-parietal network (network 17) and the medial parietal network (network 15). In contrast, executive function was negatively correlated with the total cortical representation of the foot motor network (P_Bonf < 0.05; dashed lines indicate networks with non-significant age effects). Scatter plot of the relationship between executive function and the total cortical representation of both network 17 (B) and network 15 (C).

Notably, high resolution mass-univariate analysis returned broadly convergent results (Figure S7A), with significant positive associations mainly located in association networks. Moreover, we found that the number of significant vertices (FDR q < 0.05, Figure S7A) present in mass-univariate vertex-wise analyses was significantly related to the median network variability (from Figure 3B). Across the 17 networks, we found that networks with greater across-subject variability had more vertices associated with executive function in mass-univariate analyses (r = 0.73, P = 0.001).

As for our multivariate analyses of development, we also evaluated the degree to which an individual’s multivariate pattern of network topography could be used to predict executive performance using a model trained on independent data. We found that individualized functional topography accurately predicted executive function in matched split-half samples while controlling for age, sex, and motion (Figure 7A; split 1: partial r = 0.46, P_perm < 0.001; MAE = 0.59, P_perm < 0.001; split 2: partial r = 0.41, P_perm < 0.001; MAE = 0.60, P_perm < 0.001). Repeated random 2F-CV (100 runs) returned similar results (Figure 7B; mean partial r = 0.42, P_perm < 0.001; mean MAE = 0.60, P_perm < 0.001). Critically, topographic features within the cingulo-opercular/ventral attention and fronto-parietal networks were the most predictive of individual differences in executive function (Figure 7C & Figure S7B). Multivariate feature weights aligned with analyses of the total network representation, with a preponderance of positive relationships with executive performance being found within executive networks. As for patterns of brain maturation, we found that the topographic features that predicted executive function (Figure 7D) were also those that varied most across individuals (Figure 7E; r = 0.65, P_spin < 0.001).

Figure 7.

Functional topography of association networks predicts individual differences in executive function. (A) The complex pattern of functional network topography predicted executive function in unseen data (data points represent predicted executive function of subjects by a model trained on independent data; inset histogram represents the distribution of prediction accuracy from a permutation test). The 2-fold cross-validation was implemented by splitting all participants into two subsets that were matched on executive function. (B) Repeated random 2-fold cross-validation (100 runs) provided evidence of stable prediction accuracy, which was far better than a null distribution with permuted data (inset). (C) The most important topographic features in this model were found in association cortex critical for executive function, and were maximal in the cingulo-opercular/ventral attention and fronto-parietal control networks. (D) Functional topography within association cortex drives prediction of executive function. At each location on the cortex, the absolute contribution weight of each network was summed. (E) The vertices that contributed the most in this multivariate model were those that varied most across participants; inset histograms represent spatial association compared to a null distribution obtained from spatial permutation testing.

As for prediction of brain maturity, we found that the functional topography of association networks predicted executive function substantially better (repeated random 2F-CV, mean partial r = 0.38) than the topography of sensorimotor networks (mean partial r = 0.10). Furthermore, we repeated this procedure using a discrete network parcellation from either NMF or MS-HBM, which returned similar results (Figure S8). To test if the number of networks impacted the results, we predicted executive function using a 7-network soft atlas created using NMF, which returned the similar results (Figure S8). Finally, we found that the ability of functional topography to predict either memory (mean partial r = 0.22, P_perm < 0.001; mean MAE = 0.69, P_perm < 0.001) or social cognition (mean partial r = 0.12, P_perm = 0.010; mean MAE = 0.62, P_perm < 0.001) was substantially lower than the executive function. These results emphasize that patterns of functional topography within association networks predict individual differences in executive function.

Variability of functional topography is constrained by fundamental properties of brain organization

Having demonstrated that variability in functional topography predicts both brain maturity and individual differences in executive function in youth, we next sought to understand if topographic variability is constrained by evolutionary properties of brain structure. One prominent theory of cortical organization suggests that large-scale association networks arose in evolution by becoming untethered from rigid developmental programming present in lower-order sensorimotor systems (Buckner and Krienen, 2013). This theory is supported by the distribution of cortical myelin: association cortex that has undergone dramatic evolutionary expansion also has greatly reduced myelination compared to sensorimotor cortex. Notably, association cortex also has higher metabolic demands and receives a disproportionate amount of cerebral blood flow. Having demonstrated that functional topography is the highest in association cortex, and that this variation predicts both age and executive function, we sought to directly relate topographic variability to these fundamental properties of brain organization. Specifically, we hypothesized that higher variability in functional topography would be associated with greater evolutionary expansion, reduced myelin content, and higher cerebral blood flow.

Using spatial permutation testing, we found that the cortical regions that exhibit the most topographic variability are also those that have expanded the most in evolution (Figure 8A; r = 0.51, P_spin = 0.002). In contrast, variability in cortical topography was inversely related to cortical myelin content (Figure 8B; r = −0.59, P_spin < 0.001). Finally, higher network variability was significantly associated with higher cerebral blood flow (Figure 8C; r = 0.27, P_spin = 0.019). Thus, association cortex with the greatest variability in functional topography tends to have expanded disproportionately in evolution, is more lightly myelinated, and receives a disproportion degree of cerebral blood flow.

Figure 8.

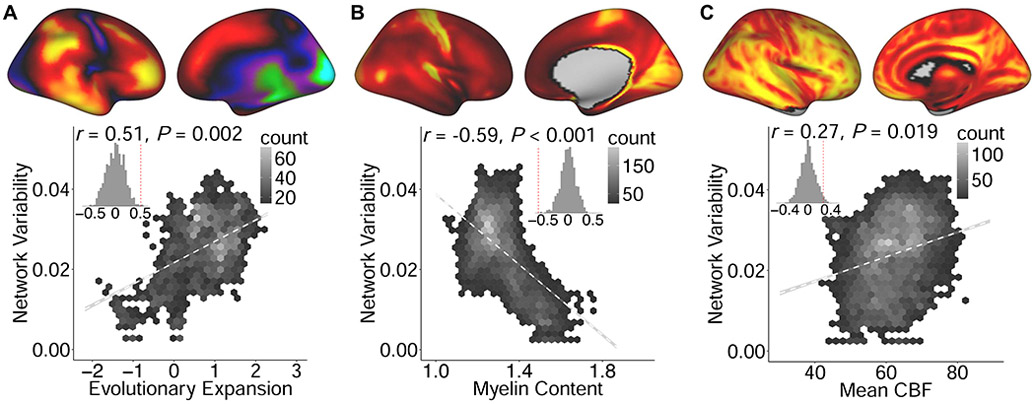
Variability in functional topography aligns with fundamental properties of brain organization. Higher variability in network topography was associated with greater evolutionary expansion (A), lower myelin content (B), and higher cerebral blood flow (CBF, C). Inset histograms represent spatial association compared to a null distribution obtained from spatial permutation testing.

DISCUSSION

In this study we leveraged advances in machine learning and a large sample to delineate how the functional topography of the cortex develops during youth and supports executive function. Building upon findings from studies of adults, we confirmed that association networks also show the most topographic variability in childhood and adolescence. Critically, we demonstrate that association networks are refined during development and predict individual differences in executive performance. Finally, we provide evidence that topographic variability is strongly linked to fundamental properties of brain organization. Taken together, these results offer a new account of both developmental plasticity and diversity, and highlight potential for progress in personalized diagnostics and therapeutics.

This work builds on a series of studies that have documented inter-individual variability in the spatial layout of canonical functional networks (Bijsterbosch et al., 2018; Braga and Buckner, 2017; Glasser et al., 2016; Gordon et al., 2017a; Gordon et al., 2017c; Kong et al., 2018; Laumann et al., 2015; Li et al., 2017; Li et al., 2019; Wang et al., 2015; Wang et al., 2018). Although previous efforts have used a variety of analysis techniques to define functional networks in individuals, they have yielded convergent results. Prior work in adults has emphasized that variability in functional topography is heterogeneously distributed across the cortex, with association networks displaying the greatest variance across individuals (Braga and Buckner, 2017; Gordon et al., 2017b; Gordon et al., 2017c; Kong et al., 2018; Li et al., 2019; Wang et al., 2015). Building upon these results from adults, we found that association networks are also the most variable in youth. Moreover, we demonstrated that this variability in functional topography constrains patterns of brain maturation and is associated with individual differences in executive capability during youth.

Our results demonstrate that individual variation in functional network topography of these networks is linked to both brain development and executive function. Specifically, we found that at any given age a greater cortical representation of control networks is associated with improved executive performance. In contrast, while the relative proportion of cortex allocated to association networks does not appear to undergo large shifts in youth, machine learning techniques were able to decode developmental processes from the complex pattern of functional topography. Dosenbach and colleagues (Dosenbach et al., 2010) were the first to use patterns of functional connectivity to predict brain maturity in unseen individuals using machine learning. However, the features used in this work and subsequent efforts (Nielsen et al., 2019) were patterns of inter-regional functional connectivity within a standardized group atlas. The current data provide evidence that the topography of personalized functional networks can be used to directly predict brain maturity. This is an important advance, as several independent efforts (Bijsterbosch et al., 2018; Li et al., 2019) have shown that topography and connectivity have distinct contributions to individual differences, and that ignoring topography aliases topographic signals into measurement of connectivity.

When integrated across levels of analysis, these developmental results are consistent with a process of network refinement (Baum et al., 2017; Fair et al., 2007a; Gu et al., 2015; Sherman et al., 2014; Wig, 2017). For example, while the fronto-parietal, cingulo-opercular/ventral attention, and default mode networks did not change in its total cortical representation with age, examination of multivariate feature weights revealed a complex pattern of reconfiguration with both positive and negative associations with age. Maturational changes were frequently concentrated at network boundaries, suggesting that the network borders are refined in development. Although further research is needed in parallel human and animal models, the observed developmental network refinement may be in part driven by focused myelination and ongoing pruning, which continues in association cortex through early adulthood (Hagmann et al., 2010). Furthermore, we found that youth with a greater cortical representation of two frontoparietal control networks had better executive function. Results of associations with executive function were generally convergent across multiple scales of analysis. Both vertex-wise mass-univariate and multivariate ridge regression analysis of the relationship between network loadings and executive function suggested that the topography of networks with higher across-subjects variability tended to be more predictive of executive function.

Nonetheless, these data suggest that the marked between-subject variability of association network topography has implications for behavior, and may be relevant for neuropsychiatric disorders. These results are consistent with recent work demonstrating that individual network variants often ‘switch’ from one association network to another and may reflect trait-like individual differences in functional brain organization (Seitzman et al., 2019). At present, the origins of such individual differences in association network topography remain unknown. However, the substantial heritability of both cognitive performance and functional connectivity suggests that topography is at least in part genetically encoded (Colclough et al., 2017; Mollink et al., 2019). Furthermore, accruing evidence from animal models and translational studies in humans emphasizes the likely importance of in-utero and early-life stressors, which could potentially impact developmental initialization of functional network topography (Graham et al., 2019). In the future, it will be possible to test this hypothesis using a combination of studies in animal models and human infants with varying levels of stress exposure.

The topographic variability, developmental plasticity, and potential vulnerability of association networks may be in part understood by evolutionary constraints. Leveraging independent data from multiple sources, we found that variability in topography is maximal in association networks that have undergone the most evolutionary expansion (Hill et al., 2010). These networks tend to have low myelin content (Glasser and Van Essen, 2011) and also receive the greater relative blood flow (Satterthwaite et al., 2014c). As noted in multiple prior accounts of cortical organization, higher-order association networks implicated in executive function are spatially embedded between sensorimotor and default mode regions (Margulies et al., 2016). One prominent theory suggests that these systems may have become untethered from the detailed developmental programing of highly conserved sensorimotor cortex as part of their rapid evolutionary expansion, thus allowing for non-canonical circuit properties and enhanced individual variability (Buckner and Krienen, 2013). Our results are consistent with such an account, as highly variable cortical networks that are under diminished anatomic constraints also evince the most marked developmental change and individual variability.

Several potential limitations and countervailing strengths of the present study should be noted. First, all data presented here were cross-sectional, which precludes inference regarding within-individual developmental effects. Ongoing follow-up studies will yield informative longitudinal data, as will large-scale studies such as the Adolescent Brain and Cognitive Development study (Casey et al., 2018). Second, we used data combined across three fMRI runs, including two where an fMRI task was regressed from the data. This choice was motivated by convergent results from several independent studies, which have shown that functional networks are primarily defined by individual-specific rather than task-specific factors (Gratton et al., 2018) and that intrinsic networks during task performance are similar to those present at rest (Fair et al., 2007b). By including task-regressed data, we were able to generate individualized networks using 27-minutes of high-quality data. Prior work suggests that parcellations created using a timeseries of this length show high concordance (r ~ 0.92) with those generated using 380 minutes of data (Laumann et al., 2015), and that longer timeseries allow for greatly improved prediction of individual differences (Elliott et al., 2019). Third, it should be acknowledged that our individualized parcellations are data driven, and at present there is no technique for ascertaining neurobiological ground truth in humans. Nonetheless, it is reassuring that our results were robust to substantial methodological variation, including the use of a completely independent method for defining individualized networks.

Fourth, because children tend to move more during the scanning session, in-scanner motion continues to be a concern for all functional imaging studies of brain development. However, in this study we rigorously followed the best practices for mitigating this confound, including use of an extensively-benchmarked, top-performing preprocessing pipeline, and covarying for motion in all hypothesis testing (Ciric et al., 2018; Satterthwaite et al., 2013a). Use of these conservative procedures bolsters confidence that our observed results are not driven by the confounding influence of in-scanner motion. Fifth, it should be noted that the correspondence between topographic variability and other properties such as myelin content were assessed at the group rather than individual level, and the relationship between these measures may in part be driven by shared properties of association cortex. Moving forward, individualized networks should be evaluated using complementary image types (including those sensitive to cortical myelin) on a within-subject basis. Finally, individualized delineation of subcortical and cerebellar networks requires specialized analysis procedures that are distinct from those applied to the cortex (Buckner et al., 2011; Choi et al., 2012; Greene et al., 2014; Marek et al., 2018), and were not evaluated in this study. Future work should evaluate the development of network topography in subcortical and cerebellar regions, which are critical for motor, emotional, and cognitive development (Pessoa and Adolphs, 2010; Sokolov et al., 2017).

These limitations notwithstanding, we provide novel evidence that individual-specific functional network topography is refined during development and predicts executive function. These findings also emphasize the relevance of functional network topography for translational clinical neuroscience. Notably, the association networks that undergo the most developmental change also are the same networks that have been linked to diverse neuropsychiatric illnesses including psychosis, mood disorders, and ADHD (Cole et al., 2014; Xia et al., 2018). As neuropsychiatric conditions are increasingly conceptualized as disorders of brain development (Insel, 2014), functional topography may be critically important for understanding the neurodevelopmental substrates of these debilitating disorders, and allow for early identification and intervention in youth at risk. Finally, these results suggest clear next steps for integration with clinical trials of personalized neuromodulatory interventions that are targeted using the specific functional neuroanatomy of an individual patient.

STAR★METHOD

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Theodore D. Satterthwaite (sattertt@pennmedicine.upenn.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Participants

Overall, 1,601 participants were studied as part of the PNC (Satterthwaite et al., 2014a). However, 340 subjects were excluded due to clinical factors, including medical disorders that could affect brain function, current use of psychoactive medications, prior inpatient psychiatric treatment, or an incidentally encountered structural brain abnormality. Among the 1,261 subjects eligible for inclusion, 54 subjects were excluded for a low quality T1-weighted image or low quality FreeSurfer reconstructions. Of the 1,207 subjects with a usable T1 image and adequate FreeSurfer reconstruction, 514 participants were excluded for missing functional data or poor functional image quality; all participants were required to have three functional runs that passed quality assurance (QA). Specifically, as in prior work (Ciric et al., 2018; Satterthwaite et al., 2013a), a functional run was excluded if mean relative root mean square (RMS) framewise displacement was higher than 0.2mm, or it had more than 20 frames with motion exceeding 0.25mm. This set of exclusion criteria resulted in a final sample of 693 participants (Figure S1), with mean age 15.93 years, standard deviation (SD) = 3.23 years; the sample included 301 males and 392 females. All subjects or their parent/guardian provided informed consent, and minors provided assent. All study procedures were approved by the Institutional Review Boards of both the University of Pennsylvania and the Children’s Hospital of Philadelphia.

METHOD DETAILS

Cognitive assessment

The Penn computerized neurocognitive battery (Penn CNB) was administered to all participants as part of a session separate from neuroimaging. The CNB consists of 14 tests adapted from tasks applied in functional neuroimaging to evaluate a broad range of cognitive domains (Gur et al., 2012). These domains include executive function (abstraction and mental flexibility, attention, working memory), episodic memory (verbal, facial, spatial), complex cognition (verbal reasoning, nonverbal reasoning, spatial processing), social cognition (emotion identification, emotion differentiation, age differentiation), and sensorimotor and motor speed. Accuracy for each test was z-transformed. As previously described in detail, factor analysis was used to summarize these accuracy scores into three factors (Moore et al., 2015), including executive and complex cognition, episodic memory, and social cognition. Here, we focused on the executive and complex cognition factor score. However, episodic memory and social cognition factor scores were evaluated in specificity analyses.

Image acquisition

As previously described (Satterthwaite et al., 2014a), all MRI scans were acquired using the same 3T Siemens Tim Trio whole-body scanner and 32-channel head coil at the Hospital of the University of Pennsylvania.

Structural MRI:

Prior to functional MRI acquisitions, a 5-min magnetization-prepared, rapid acquisition gradient-echo T1-weighted (MPRAGE) image (TR = 1810 ms; TE = 3.51 ms; TI = 1100 ms, FOV = 180 × 240 mm², matrix = 192 × 256, effective voxel resolution = 0.9 × 0.9 × 1 mm³) was acquired.

Functional MRI:

We used one resting-state and two task-based (i.e., n-back and emotion identification) fMRI scans as part of this study. All fMRI scans were acquired with the same single-shot, interleaved multi-slice, gradient-echo, echo planar imaging (GE-EPI) sequence sensitive to BOLD contrast with the following parameters: TR = 3000 ms; TE = 32 ms; flip angle = 90°; FOV = 192 × 192 mm²; matrix = 64 × 64; 46 slices; slice thickness/gap = 3/0 mm, effective voxel resolution = 3.0 × 3.0 × 3.0 mm³. Resting-state scans had 124 volumes, while the n-back and emotion recognition scans had 231 and 210 volumes, respectively. Further details regarding the n-back (Satterthwaite et al., 2013b) and emotion recognition (Wolf et al., 2015) tasks have been described in prior publications.

Field map:

In addition, a B0 field map was derived for application of distortion correction procedures, using a double-echo, gradient-recalled echo (GRE) sequence: TR = 1000ms; TE1 = 2.69ms; TE2 = 5.27ms; 44 slices; slice thickness/gap = 4/0 mm; FOV = 240 mm; effective voxel resolution = 3.8×3.8×4 mm.

Scanning procedure:

Before scanning, to acclimate subjects to the MRI environment, a mock scanning session where subjects practiced the task was conducted using a decommissioned MRI scanner and head coil. Mock scanning was accompanied by acoustic recordings of the noise produced by gradient coils for each scanning pulse sequence. During these sessions, feedback regarding head movement was provided using the MoTrack motion tracking system (Psychology Software Tools). Motion feedback was given only during the mock scanning session. To further minimize motion, before data acquisition, subjects’ heads were stabilized in the head coil using one foam pad over each ear and a third over the top of the head.

Image processing

The structural images were processed using FreeSurfer (version 5.3) to allow for the projection of functional timeseries to the cortical surface (Fischl, 2012). Functional images were processed using a top-performing preprocessing pipeline implemented using the extensible Connectivity Pipeline (XCP) Engine (Ciric et al., 2018), which includes tools from FSL (Jenkinson et al., 2012; Smith et al., 2004) and AFNI (Cox, 1996). This pipeline included (1) correction for distortions induced by magnetic field inhomogeneity using FSL’s FUGUE utility, (2) removal of the initial volumes of each acquisition (i.e., 4 volumes for resting-state fMRI and 6 volumes for emotion recognition task fMRI), (3) realignment of all volumes to a selected reference volume using FSL’s MCFLIRT, (4) interpolation of intensity outliers in each voxel’s time series using AFNI’s 3dDespike utility, (5) demeaning and removal of any linear or quadratic trends, and (6) co-registration of functional data to the high-resolution structural image using boundary-based registration. Images were de-noised using a 36-parameter confound regression model that has been shown to minimize associations with motion artifact while retaining signals of interest in distinct sub-networks. This model included the six framewise estimates of motion, the mean signal extracted from eroded white matter and cerebrospinal fluid compartments, the mean signal extracted from the entire brain, the derivatives of each of these nine parameters, and quadratic terms of each of the nine parameters and their derivatives. Both the BOLD-weighted time series and the artefactual model time series were temporally filtered using a fist-order Butterworth filter with a passband between 0.01 and 0.08 HZ to avoid mismatch in the temporal domain (Hallquist et al., 2013). Furthermore, to derive “pseudo-resting state” timeseries that were comparable across runs, the task activation model was regressed from n-back or emotion identification fMRI data (Fair et al., 2007b). The task activation model and nuisance matrix were regressed out using AFNI’s 3dTproject.

For each modality, the fMRI timeseries of each individual were projected to each subject’s FreeSurfer surface reconstruction and smoothed on the surface with a 6-mm full-width half-maximum (FWHM) kernel. The smoothed data was projected to the fsaverage5 template, which has 10,242 vertices on each hemisphere (18,715 vertices in total after removing the medial wall). Finally, we concatenated the three fMRI acquisitions, yielding timeseries of 27 minutes, 45 seconds (555 time points) in total.

As in prior work, we removed vertices with low signal noise ratio (SNR) (Gordon et al., 2016; Ojemann et al., 1997; Wig et al., 2014). To calculate a whole-brain SNR map, we extracted the first frame of acquisition (post-steady state magnetization) of each of the three runs for all participants. Next, we normalized each image to a mode of 1,000 and then averaged all of these images; this average image was further normalized to a mode of 1,000. A mean BOLD signal of 800 or less represents a substantial attenuation of signal (Wig et al., 2014), applying this threshold resulted in the exclusion of low SNR locations, which were primarily located in orbitofrontal cortex and ventral temporal cortex. Within this mask, 17,734 vertices were included in subsequent analyses.

Regularized non-negative matrix factorization

As previously described in detail (Li et al., 2017), we used non-negative matrix factorization (NMF) (Lee and Seung, 1999) to derive individualized functional networks. The NMF method factors the data by positively weighting cortical elements that covary, leading to a highly specific and reproducible parts-based representation (Lee and Seung, 1999; Sotiras et al., 2017). Our approach was enhanced by a group consensus regularization term that preserves the inter-individual correspondence, as well as a data locality regularization term that makes the decomposition robust to imaging noise, improves spatial smoothness, and enhances functional coherence of the subject-specific functional networks (see Li et al., 2017 for details of the method; see also: https://github.com/hmlicas/Collaborative_Brain_Decomposition). As NMF requires the input to be nonnegative values, we re-scaled the data by shifting time courses of each vertex linearly to ensure all values were positive (Li et al., 2017). To avoid features in greater numeric ranges dominating those in smaller numeric range, we further normalized the time course by its maximum value so that all the time points have values in the range of [0, 1].

Given a group of n subjects, each having fMRI data Xⁱ ∈ R^×, i = 1, … , n, consisting of S vertices and T time points, we aimed to find K non-negative functional networks $V^i=(V_{s,k}^i)\in R^{S\times K}$ and their corresponding time courses $U^i=(U_{t,k}^i)\in R^{T\times K}$ for each subject, such that

$$X^i\approx U^i(V^i{)}^{\prime }+E^i,s.t.U^i,V^i\ge 0,\forall 1\le i\le n,$$

where (Vⁱ)′ is the transpose of (Vⁱ), and Eⁱ is independently and identically distributed (i.i.d) residual noise following Gaussian distribution with a probability density function of $g(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}$. Both Uⁱ and Vⁱ were constrained to be non-negative so that each functional network does not contain any anti-correlated functional units (Lee and Seung, 1999). A group consensus regularization term was applied to ensure inter-individual correspondence, which was implemented as a scale-invariant group sparsity term on each column of Vⁱ and formulated as

$$R_c={\sum }_{k=1}^K\Vert V_{\cdot ,k}^{\widetilde{1,..,n}}{\Vert }_{2,1}={\sum }_{k=1}^K\frac{{\sum }_{s=1}^S({\sum }_{i=1}^n(V_{s,k}^i{)}^2{)}^{1∕2}}{({\sum }_{s=1}^S{\sum }_{i=1}^n(V_{s,k}^i{)}^2{)}^{1∕2}}.$$

The data locality regularization term was applied to encourage spatial smoothness and coherence of the functional networks using graph regularization techniques (Cai et al., 2011). The data locality regularization term was formulated as

$$R_M^i=Tr((V^i{)}^{\prime }{L}_M^i{V}^i),$$

where $L_M^i=D_M^i-W_M^i$ is a Laplacian matrix for subject I, $W_M^i$ is a pairwise affinity matrix to measure spatial closeness or functional similarity between different vertices, and $D_M^i$ is its corresponding degree matrix. The affinity between each pair of spatially connected vertices (i.e., vertices a and b) was calculated as $\left(1+corr(X_{.,a}^i,X_{.,b}^i)\right)∕2$, where $corr(X_{.,a}^i,X_{.,b}^i)$ is the Pearson correlation coefficient between time series $X_{.,a}^i$ and $X_{.,b}^i$, and others were set to zero so that $W_M^i$ has a sparse structure. We identified subject specific functional networks by optimizing a joint model with integrated data fitting and regularization terms formulated by

$$\begin{gathered} \begin{array}{c}\hfill min\hfill \\ \hfill (U^i,V^i)\hfill \end{array}{\sum }_{i=1}^n{\Vert X^i-U^i(V^i)\Vert }_F^2+{\lambda }_M{\sum }_{i=1}^n{R}_M^i+{\lambda }_c{R}_c, \\ s.t.U^i,V^i\ge 0,{\Vert V_{.,k}^i\Vert }_{\infty }=1,\forall 1\le k\le K,\forall 1\le i\le n \end{gathered}$$

where ${\lambda }_M=\beta \times \frac{T}{K\times n_M}$ and ${\lambda }_c=\alpha \cdot \frac{n\cdot T}{K}$ are used to balance the data fitting, data locality, and group consensus regularization terms, n_M is the number of neighboring vertices, α and β are free parameters. For this study, we used identical parameters settings as in prior validation studies (Li et al., 2017).

Defining individualized networks

Our approach for defining individualized networks included three steps (see Figure S2). In the first two steps, a consensus group atlas was created. In the third step, this group atlas was used to define individualized networks for each participant. We decomposed the whole-brain into 17 networks, which allowed for a direct comparison to other methods used in prior work (Kong et al., 2018; Wang et al., 2015; Yeo et al., 2011).

Step 1: Group network initialization.

Although individuals exhibit distinct network topography, they are also broadly consistent (Gordon et al., 2017c; Gratton et al., 2018). Therefore, we first generated a group atlas and used it as an initialization for individualized network definition. In this way, we also ensured spatial correspondence across all subjects. This strategy has also been applied in other methods for individualized network definition (Kong et al., 2018; Wang et al., 2015). To avoid the group atlas being driven by outliers and to reduce the computational memory cost, a bootstrap strategy was utilized to perform the group-level decomposition multiple times on a subset of randomly selected subjects. Subsequently, the resulting decomposition results were fused to obtain one robust initialization that is highly reproducible. As previously (Li et al., 2017), we randomly selected 100 subjects and temporally concatenated their timeseries, resulting in a timeseries matrix with 55,500 rows (time-points) and 17,734 columns (vertices). Notably, the choice of sub-sample size did not impact results (sub-samples of 200 and 300 were also evaluated). We applied the above-mentioned regularized non-negative matrix factorization method with a random non-negative initialization to decompose this matrix (Lee and Seung, 1999). A group-level network loading matrix V was acquired, which had 17 rows and 17,734 columns. Each row of this matrix represents a functional network, while each column represents the loadings of a given cortical vertex. As previously (Li et al., 2017), this procedure was repeated 50 times, each time with a different subset of subjects; this yielded 50 different group atlases.

Step 2: Group network consensus.

Next, we combined the 50 group network atlases to obtain one robust and highly reproducible group network atlas using spectral clustering (Li et al., 2017). Specifically, we concatenated the 50 group parcellations together across networks and acquired a matrix with 850 rows (i.e., functional networks, abbreviated as FN) and 17,734 columns (i.e., vertices). Inter-network similarity was calculated as

$$S_{ij}=exp\left(-\frac{d_{ij}^2}{{\sigma }^2}\right),$$

where d_ij = 1 − corr(FN_i, FN_j), corr(FN_i, FN_j) is Pearson correlation coefficient between FN_i and FN_j, and σ is the median of d_ij across all possible pairs of FNs. Then, we applied normalized-cuts (Cai et al., 2011) based spectral clustering method to group the 850 FNs into 17 clusters. For each cluster, the FN with the highest overall similarity with all other FNs within the same cluster was selected as the most representative. The final group network atlas was composed of the representatives of these 17 clusters.

Step 3: Individualized networks.

In this final step, we derived each individual’s specific network atlas using NMF based on the acquired group networks (17 × 17,734 loading matrix) as initialization and each individual’s specific fMRI times series (555 × 17,734 matrix). See Li et al. (2017) for optimization details. This procedure yielded a loading matrix V (17 × 17,734 matrix) for each participant, where each row is a FN, each column is a vertex, and the value quantifies the extent each vertex belongs to each network. This probabilistic (soft) definition can be converted into discrete (hard) network definitions for display and comparison with other methods (Kong et al., 2018; Wang et al., 2015; Yeo et al., 2011) by labeling each vertex according to its highest loading.

Multi-session Hierarchical Bayesian Model (MS-HBM)

To evaluate whether our results were robust to methodological variation, we also applied a recently introduced multi-session hierarchical Bayesian model (MS-HBM, https://github.com/ThomasYeoLab/CBIG/tree/master/stable_projects/brain_parcellation/Kong2019_MSHBM) that has been used for defining individualized networks. See Kong et al. (2018) for the details of the method. Using a group atlas, this method calculates inter-subject resting-state functional connectivity (RSFC) variability, intra-subject RSFC variability, and finally parcellates for each single subject based on this prior information. MS-HBM requires functional connectivity profiles of multiple sessions as input; here, the three fMRI runs were entered as three separate sessions. As in Kong et al. (2018), we used MS-HBM to define 17 discrete individualized networks for each participant. Specifically, we calculated all participants’ connectivity profiles, created the group parcellation using the average connectivity profile of all participants, estimated the inter-subject and intra-subject connectivity variability, and finally calculated each participant’s individualized parcellation. We used the pair of parameters (i.e., c = 30 and α = 200), which was optimized using Genomic Superstruct Project (GSP) dataset (Holmes et al., 2015) in Kong et al. (2018). Notably, GSP dataset was acquired using the identical fMRI sequences and scanning platform as the PNC. We used the adjusted Rand index (ARI) to calculate the similarity between the networks from MS-HBM and discretized networks from NMF. To evaluate if personalized network topography was consistently captured by both NMF and MS-HBM, we calculated the pairwise ARI between all participants’ discrete NMF and MS-HBM parcellations (i.e., both within participants and between participants).

Spatial permutation testing (spin test)

In order to evaluate the significance of the alignment between individualized networks derived using NMF and MS-HBM, we used a spatial permutation procedure called the spin test (Alexander-Bloch et al., 2018; Gordon et al., 2016; Sotiras et al., 2017; Vandekar et al., 2015) (https://github.com/spin-test/spin-test). The spin test is a spatial permutation method based on angular permutations of spherical projections at the cortical surface. Critically, the spin test preserves the spatial covariance structure of the data and as such is far more conservative than randomly shuffling locations, which destroys the spatial covariance structure of the data and produce an unrealistically weak null distribution. In contrast, the spin test generates a null distribution of randomly rotated brain maps that preserve spatial features of the original map.

To evaluate the significance of the alignment between NMF and MS-HBM based networks, we compared the ARI of two parcellations to the ARI of 1,000 random rotations, generating a null distribution that preserves the spatial covariance structure. The permutation-based p-value was calculated as the proportion of times that the observed ARI was higher than the null distribution of ARI values from rotated parcellations. As described below, we also used the spin test to evaluate the significance of the alignment between across-subject parcellation variability to informative maps of brain organization.

Homogeneity of functional networks

Network homogeneity is a commonly used method for evaluating the success of a functional parcellation (Gordon et al., 2016; Kong et al., 2018). As previously, network homogeneity was calculated as the average of the Pearson’s correlations between the time series of all pairs of vertices within each network (Kong et al., 2018). To summarize network homogeneity for comparisons across methods, we averaged the homogeneity value across networks.

Individualized networks improve functional homogeneity compared to group averaged networks

As in previous work (Gordon et al., 2016; Kong et al., 2018), we evaluated the quality of all individualized networks by calculating the homogeneity of the functional timeseries within each network. As expected, homogeneity within NMF-based individualized networks was higher than that in either the NMF-based group atlas or the canonical Yeo 17-network group atlas (Figure S2A). As an additional validation step, we compared our NMF-based method with a recently-introduced approach that uses a multi-session hierarchical Bayesian model (MS-HBM; Kong et al. (2018)) to identify individualized networks. The mean homogeneity of MS-HBM in our sample was very similar (if numerically lower) to our NMF based method, and nearly identical to a prior application of MS-HBM to adults (0.34 vs. approximately 0.32; Kong et al., 2018). Moreover, we found that the individual parcellations provided by NMF and MS-HBM were significantly aligned (P_spin < 0.001). Indeed, the within-subject similarity of discrete NMF and MS-HBM parcellations were always higher than the between-subject similarity (Figure S2B), suggesting that personalized networks can be reliably delineated across methods. These initial results suggest that single-subject parcellations provide an improved fit to each participant’s data compared to standard atlases that do not consider variation in functional neuroanatomy.

Across-subject variability of functional network topography

Prior studies of adults have consistently reported that across-subject variability of functional networks is high in association networks and lower in primary sensorimotor networks (Gordon et al., 2017b; Gordon et al., 2017c; Kong et al., 2018; Li et al., 2019; Mueller et al., 2013; Wang et al., 2015). Here we evaluated this observation in our sample of youth. For each of 17 networks, we calculated the median absolute deviation of loading values across all subjects for each vertex. We used this non-parametric measure of variance as loadings did not follow normal distribution. Next, we averaged the 17 median absolute deviation maps to generate the final across-network variability map that quantified the across-subject parcellation variance at each vertex.

Additionally, we also calculated the network variability of the discretized network atlas, allowing for further validation of our main results and better comparison to other methods (Kong et al., 2018). Specifically, we used entropy to define variability (Hoskisson et al., 1993):

$$V(x)=-{\sum }_{x_i}p(x_i)lo{g}_{2}p(x_i),$$

where x is a vertex; x_i is a value of the vertex x, which has 17 possible values; p(x_i) is the proportion of subjects have values x_i in the vertex x. If a vertex has same values for all subjects, V(x) will be 0, indicating there is no variance of this vertex.

Associations of network topography with development and executive function

We evaluated mass-univariate associations between network topography and both development and executive function at two scales: total relative network representation and at each vertex. As an initial step, for each network, we summed the loading of all vertices to quantify the relative presence of this network on the cortex. Notably, as this was conducted in normalized template space, this measure controls for individual differences in total surface area. To model both linear and nonlinear developmental effects, we used generalized additive models (GAMs) with penalized splines (Wood, 2004). Importantly, the GAM estimates nonlinearities using restricted maximum likelihood (REML), penalizing nonlinearity in order to avoid over-fitting the data. Within each GAM, age was modeled using a penalized spline, while including sex and in-scanner head motion during scanning as model covariates. As we considered three functional runs, in-scanner motion was summarized as the grand mean of the mean relative RMS displacement of each functional run. To evaluate associations with executive function, the executive function factor score was added as another model term with covariates as above (including a spline of age). Multiple comparisons were accounted for using the Bonferroni method.

To evaluate more complex topographic reconfiguration, we next evaluated each network at each vertex. For each network, we calculated associations between network loading and age for each vertex using GAMs while controlling for sex and in-scanner head motion. Similarly, we calculated associations between network loadings and executive function while controlling for sex, head motion, and a spline of age. Given the large number of multiple comparisons, for vertex-wise analyses we used the False Discovery Rate (q < 0.05).

Prediction of brain maturity and executive function performance from functional network topography

Having tested if network topography was related to development and executive function in mass-univariate fashion, we next evaluated whether the overall multivariate spatial pattern of network topography encodes brain maturity or executive function. To address this question, we used ridge regression with nested two-fold cross validation (2F-CV, see Figure S7) to test if multivariate network topography pattern could be used to identify an unseen individual participant’s brain maturity or executive function in an unbiased fashion. Accordingly, we combined the 17 network loading maps into a feature vector to represent the multivariate spatial pattern of network topography of each individual.

Ridge regression:

A linear regression model was adopted to predict the brain maturity and executive function performance using the pattern of whole-brain spatial topography of parcellations. The linear model can be formulized as follows:

$$y_i={\sum }_{j=1}^p{\beta }_j{x}_{i,j}+{\beta }_0,$$

where y_i is the age of the i^th individual, p is the number of features, x_i,j is the value of the j^th feature of the i^th subject, and β_j is the regression coefficient.

To avoid over-fitting and to improve the prediction accuracy, we used ridge regression. Ridge regression uses an L2 penalty during model fitting; we have previously shown often performs similarly to other machine learning methods for regression problems using highdimensional imaging data and computationally more efficient than other methods (Cui and Gong, 2018; Hoerl and Kennard, 1970). The objective function is:

$$\underset{\beta }{min}\sum _{i=1}^N(f(x_i)-y_i{)}^2+\lambda \sum _{j=1}^p{\mid \mid {\beta }_j\mid \mid }^2.$$

This technique shrinks the regression coefficients, resulting in better generalizability for predicting unseen samples. In this algorithm, a regularization parameter λ is used to control the trade-off between the prediction error of the training data and L2-norm regularization, i.e., a trade-off of penalties between the training error and model complexity. A large λ corresponds to a greater penalty on model complexity, and a small λ represents a greater penalty on training error.

Prediction framework:

We applied a nested 2-fold cross validation (2F-CV), with outer 2F-CV estimating the generalizability of the model and the inner 2F-CV determining the optimal parameter λ for the ridge regression model (see Figure S7 for schematic of the prediction framework).

Outer 2F-CV:

In the outer 2F-CV, the data was divided into 2 subsets. Specifically, we sorted the subjects according to the outcome (i.e., age or executive performance) and then assigned the individuals with an odd rank to subset 1 and the individuals with an even rank to subset 2 (Cui and Gong, 2018; Cui et al., 2018). We initially used subset 1 as the training set, with subset 2 used as the testing set. Each feature was linearly scaled between zero and one across the training dataset, and the scaling parameters were also applied to scale the testing dataset (Cui and Gong, 2018; Erus et al., 2015). We applied an inner 2-fold cross validation (2F-CV) within training set to select the optimal λ parameter. Based on the optimal λ, we trained a model using all subjects in the training set, and then used that model to predict the outcome of all subjects in the testing set. Analogously, we used subset 2 as the training set and subset 1 as the testing set, and repeated the above procedure. Across the testing subjects for each subset, the partial correlation and mean absolute error (MAE) between the predicted and actual outcome was used to quantify the prediction accuracy. In evaluation of the prediction of participant’s brain maturity, we controlled for sex and in-scanner head motion by calculating a partial correlation. Furthermore, we additionally controlled for participant’s age (in addition to sex and motion) when calculating the partial correlation between actual and predicted executive function. Here, we used the scikit-learn library to implement ridge regression (http://scikit-learn.org) (Pedregosa et al., 2011).

Inner 2F-CV:

Within each loop of the outer 2F-CV, we applied inner 2F-CVs to determine the optimal λ. Specially, the training set for each loop of the outer 2F-CV was further partitioned into 2 subsets according to their rank of the outcome (i.e., age or executive performance), as in the outer loop (i.e., subjects with odd rank in subset 1 and subjects with even rank in subset 2). One subset was selected to train the model under a given λ in the range [2⁻¹⁰, 2⁻⁹, …, 2⁴, 2⁵] (i.e., 16 values in total) (Cui and Gong, 2018; Hsu et al., 2003), and the remaining subset was used to test the model. This procedure was repeated 2 times such that each subset was used once as the testing dataset, resulting in two inner 2F-CV loops in total. For each λ value, the correlation r between the actual and predicted outcome as well as the mean absolute error (MAE) were calculated for each inner 2F-CV loop, and then averaged across the two inner loops. The sum of the mean correlation r and reciprocal of the mean MAE was defined as the inner prediction accuracy, and the λ with the highest inner prediction accuracy was chosen as the optimal λ (Cui and Gong, 2018; Cui et al., 2018). Of note, the mean correlation r and the reciprocal of the mean MAE cannot be summed directly, because the scales of the raw values of these two measures are quite different. Therefore, we normalized the mean correlation r and the reciprocal of the mean MAE across all values and then summed the resultant normalized values.

Randomly split 2F-CV:

In the above prediction analysis, we split subjects into two halves according to the rank of the outcome (i.e., age or executive performance). To validate that our split was representative, we tested the prediction accuracy using repeated random 2F-CV Specifically, we split the subjects randomly into two halves for both outer 2F-CV and inner 2F-CV, and calculated the mean partial correlation r and MAE across two folds. Because the split was random, we repeated outer 2F-CV 100 times and averaged the partial correlation (accounting for covariates) and MAE across the 100 times to determine the overall prediction accuracy. For computational efficiency, we executed the inner 2F-CV 20 times.

Significance of prediction performance.

To evaluate if prediction performance (i.e., the partial correlation r and MAE) were significantly better than expected by chance, we performed a permutation test (Mourao-Miranda et al., 2005). Specifically, prediction procedure was re-applied 1,000 times. In each run, we permuted the outcome (i.e., age or executive function) across the training samples without replacement. The significance was determined by ranking the actual prediction accuracy versus the permuted distribution; the p-value of the partial correlation r was the proportion of permutations that showed a higher value than the actual value for the real data. Similarly, the p-value of the MAE was the proportion of permutations that showed a lower value than the actual value for the real data.

For repeated random 2F-CV, we repeated the outer 2F-CV 1,000 times, but each time we permuted the outcome across the training data. Finally, we compared the empirical mean partial correlation r and mean MAE across 100 runs to the null distribution.

Interpreting model feature weights.

We acquired 200 regression coefficient/weight maps, as the random 2F-CV was repeated 100 times. Averaging these 200 weight maps, the features with a nonzero average weight can be understood as contributing features for the prediction model (Cui and Gong, 2018; Mourao-Miranda et al., 2005), with the absolute value of the weight quantifying the contribution of the features to the model (Mourao-Miranda et al., 2005). To understand which network contributed the most to the prediction, we summed the positive and negative weight separately across all vertices in each network. Then, we evaluated the features that had the highest (top 25%) absolute contribution weight. Based on these highly-weighted features, we further tested if the positive-weighted vertices with small network loadings, which were localized on the border of functional networks, contributed more to the age prediction in the multivariate model. Specifically, for each network, we calculated the Pearson correlation between the contribution weight and group network loading across all the positively- and highly-weighted vertices. Significance was evaluated using a permutation test, by permuting the contribution weight across vertices 10,000 times. Bonferroni correction was applied to correct for the 17 comparisons across networks. Finally, we tested if the spatial contribution of feature importance was constrained by the variability of functional topography. As each vertex had 17 loading values (one for each network), we summed the absolute weight across all 17 networks to summarize the prediction weight of each vertex. This sum represents the importance of a given vertex to the predictive model. Finally, we calculated the Pearson correlation between this total contribution weight and network variability across all vertices.

Validation of multivariate prediction analysis

Prediction using association versus sensorimotor networks.

Having demonstrated that association networks contributed the most to the prediction of both brain maturity and executive function when all networks were used as features, we next explored the relative predictive capability of association versus sensorimotor network features. Specifically, we re-calculated the prediction using repeated (i.e., 100 runs) random 2F-CV ridge regression when using only association or sensorimotor networks as features. Association networks included fronto-parietal (networks 3, 15, 17), default mode (networks 1, 8, 12), cingulo-opercular/ventral attention (networks 7, 9), and dorsal attention (networks 5, 14) networks. In contrast, sensorimotor networks included visual (networks 6, 10), somatomotor (networks 2, 4, 11, 13), and auditory (network 16) networks. Covariates were included as in the main analysis described above. To ensure specificity of results, we controlled for the brain maturity predicted from sensorimotor networks when evaluating the performance of the model using association network features. Similarly, we controlled for the brain maturity predicted from association networks when evaluating the performance of the model using sensorimotor network features. For this analysis, we only considered network loadings within association cortex defined by the discrete parcellation when extracting the association network features, and only considered network loadings within sensorimotor cortex defined by the discrete parcellation when extracting the sensorimotor network features. The same procedures were used when predicting executive function.

Prediction using a 7-network atlas:

To evaluate if the number of networks impacted the prediction of brain maturity or executive function, we additionally evaluated a 7-network atlas. Specifically, we generated a probabilistic (soft) parcellation with 7 networks using NMF. Using the network loadings of all 7 networks, we predicted both brain maturity and executive function using identical methods as those used for the 17-network atlas.

Prediction by discrete network parcellations:

We next tested if the pattern of discrete network labels could predict brain maturity and executive performance. We extracted the whole-brain discrete network labels into a feature vector to represent the multivariate spatial pattern of network topography of each individual. Based on these features, we applied the above 2F-CV framework to predict brain maturity and executive performance using multivariate ridge regression. As network labels are categorical features, we first encoded each vertex feature as a one-hot numeric array (https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html), which was further used as input of the prediction analysis. This framework was applied to discrete networks from both NMF and MS-HBM.

Prediction of other cognitive measurements by network loadings:

As a final step, we evaluated if the associations with network topography were specific to executive function. We used the same ridge regression framework and vertex-wise loading maps to try to predict factor scores summarizing memory accuracy and social cognition accuracy.

Visualization

Connectome Workbench (version: 1.3.2) provided by the human connectome project (https://www.humanconnectome.org/software/connectome-workbench; Marcus et al. (2013)) was used to visualize the brain surface.

Cortical organization maps

We downloaded the evolutionary expansion map (Hill et al., 2010) from http://brainvis.wustl.edu/wiki/index.php/Sums:About and downloaded the myelin map (Glasser and Van Essen, 2011) from https://balsa.wustl.edu/mpwM. We used the mean cerebral blood flow map from Satterthwaite et al. (2014b), and have posted this map online (https://github.com/PennBBL/MeanCBF).

Data & code availability

The PNC data is publicly available in the Database of Genotypes and Phenotypes: accession number: phs000607.v3.p2; https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2. All analysis code is available here: https://github.com/ZaixuCui/pncSingleFuncParcel, with detailed explanation in https://github.com/ZaixuCui/pncSingleFuncParcel/wiki.

KEY RESOURCES TABLE

REAGENT or	SOURCE	IDENTIFIER
Deposited Data
Philadelphia Neurodevelopmental Cohort	(Satterthwaite et al., 2014a)	https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2
Cognitive factor score	(Moore et al., 2015)	N/A
Software and Algorithms
MATLAB	Mathworks	RRID:SCR_001622 https://www.mathworks.com/
R	The R Foundation	RRID: SCR_001905 https://www.r-project.org
Penn CNB	(Gur et al., 2012)	https://penncnp.med.upenn.edu
Connectome Workbench	(Marcus et al., 2011)	RRID: SCR_008750 http://www.humanconnectome.org/software/connectome-workbench
FreeSurfer	(Fischl, 2012)	RRID: SCR_001847 https://surfer.nmr.mgh.harvard.edu/
FSL	(Smith et al., 2004)	RRID: SCR_002823 https://fsl.fmrib.ox.ac.uk/fsl/fslwiki
AFNI	(Cox, 1996)	RRID:SCR_005927 https://afni.nimh.nih.gov
XCP Engine	(Ciric et al., 2018)	https://xcpengine.readthedocs.io
FreeSurfer to fs_LR pipeline	(Van Essen et al., 2012)	http://brainvis.wustl.edu
Parcellation method	(Li et al., 2017)	https://github.com/hmlicas/Collaborative_Brain_Decomposition
Ridge regression prediction	(Cui and Gong, 2018)	https://github.com/ZaixuCui/pncSingleFuncParcel/tree/master/Functions
Scikit-learn	(Pedregosa et al., 2011)	RRID: SCR_002577 https://scikit-learn.org/stable/

Functional topography is most varibale in association cortex in youth.

Functional topography is refined during youth and encodes brain maturity.

Association network functional topography predicts executive function.

Cui et al. demonstrate that individual-specific functional networks are refined during youth in humans. Furthermore, the functional topography of association networks predicts individual differences in executive function.