Dynamics of an SEIR model with infectivity in incubation period and homestead-isolation on the susceptible

Abstract

In this paper, we present an SEIR epidemic model with infectivity in incubation period and homestead-isolation on the susceptible. We prove that the infection-free equilibrium point is locally and globally asymptotically stable with condition $R_0<1.$ We also prove that the positive equilibrium point is locally and globally asymptotically stable with condition $R_0>1.$ Numerical simulations are employed to illustrate our results. In the absence of vaccines or antiviral drugs for the virus, our results suggest that the governments should strictly implement the isolation system to make every effort to curb propagation of disease during the epidemic.

1. Introduction

The establishing and analyzing mathematical models play important roles in the control and prevention of disease transmission. Compartment model is the base and also a powerful mathematical framework for understanding the complex dynamics of epidemics. At present, Many researchers [1], [2], [3] are increasingly interested in the influence of these behavioral factors on the spread of infectious diseases. Cooke and Driessche [4] proposed and investigated a classical SEIR epidemic model, which has became the most important model in diseases control. Therefore, ODEs, PDEs and SDEs are employed to study SEIR epidemic models, and some results could be found in literatures [5], [6], [7], [8]. Zhao et al. [9] investigated an extended SEIR epidemic model with non-communicability in incubation period. National Health Commission of the People’s Republic of China declared that the incubation period of the COVID-19 is about ten days, the incubation period is infectious [10]. The COVID-19 outbreak in China presents that physical protection and social isolation are critical to controlling the epidemic in the absence of vaccines or antiviral drugs for the virus.

2. The model

Inspired by the above discussions, we consider an SEIR epidemic model with infectivity in incubation period and homestead-isolation on the susceptible.

$$\left\{\begin{array}{c}\frac{dS\left(t\right)}{dt}=\Lambda -\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]-\mu S\left(t\right),\hfill \\ \frac{dE\left(t\right)}{dt}=\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]-(\delta +\mu )E\left(t\right),\hfill \\ \frac{dI\left(t\right)}{dt}=\delta E\left(t\right)-(\gamma +\sigma +\mu )I\left(t\right),\hfill \\ \frac{dR\left(t\right)}{dt}=(\gamma +{\theta }_3\sigma )I\left(t\right)-\mu R\left(t\right),\hfill \end{array}\right)$$ (2.1)

where $S\left(t\right)$ represents the numbers of the susceptible population at time $t$. $E\left(t\right)$ represents the numbers of the exposed population at time $t$. $I\left(t\right)$ represents the numbers of the infected population at time $t$. $R\left(t\right)$ represents the numbers of the recovered population at time $t$. $\Lambda >0$ represents the enrolling rate. $\beta >0$ represents the infective rate from $S$ to $E$. $0<{\theta }_1<1$ represents the homestead-isolation rate of the susceptible. $0<{\theta }_2<1$ represents the infective effect of the exposed in incubation period. $\mu >0$ represents the natural death rate. $\delta >0$ represents the transition rate from $E$ to $I$. $\gamma >0$ represents the transition rate from $I$ to $R$. $\sigma >0$ represents hospitalized rate of $I$ for the disease. ${\theta }_3>0$ represents the recurring rate of $I$, and $\delta >{\theta }_2(\gamma +\sigma +\mu )$.

3. The dynamics

In this paper, We only consider the following system for $R\left(t\right)$ being not involved in the first, second and third equations of (2.1).

$$\left\{\begin{array}{c}\frac{dS\left(t\right)}{dt}=\Lambda -\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]-\mu S\left(t\right),\hfill \\ \frac{dE\left(t\right)}{dt}=\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]-(\delta +\mu )E\left(t\right),\hfill \\ \frac{dI\left(t\right)}{dt}=\delta E\left(t\right)-(\gamma +\sigma +\mu )I\left(t\right).\hfill \end{array}\right)$$ (3.1)

Then, one equilibrium point of system (3.1) can be easily obtained $P^0(S^0,0,0)$ with $S^0=\frac{\Lambda }{\mu }$, and another equilibrium $P^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ of system (3.1) is also obtained,where $S^{\ast }=\frac{(\gamma +\sigma +\mu )(\delta +\mu )}{\beta (1-{\theta }_{})[\delta +{\theta }_2(\gamma +\sigma +\mu )]}$, $E^{\ast }=\frac{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]-\mu (\gamma +\sigma +\mu )(\delta +\mu )}{\delta +\mu }$, $I^{\ast }=\frac{\delta \left\{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]\right\}}{(\gamma +\sigma +\mu )(\delta +\mu )}$ $-\frac{\mu (\gamma +\sigma +\mu )(\delta +\mu )}{(\gamma +\sigma +\mu )(\delta +\mu )}$ with $\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]>\mu (\gamma +\sigma +\mu )(\delta +\mu )$. Then, we define the basic reproduction number of system (3.1) as

$$R_0=\frac{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]}{\mu (\gamma +\sigma +\mu )(\delta +\mu )}.$$

Theorem 3.1

The equilibrium point $P^0(\frac{\Lambda }{\mu },0,0)$ system (3.1) is locally asymptotically stable if only if $R_0<1$ .

Proof

System (3.1) is linearized at equilibrium point $P^0(\frac{\Lambda }{\mu },0,0)$, and its Jacobian matrix $J^0$ is

$$\left(\begin{array}{c}{J}^0=\left(\begin{array}{ccc}\hfill -\mu \hfill & \hfill -\beta (1-{\theta }_1){\theta }_2{S}^0\hfill & \hfill -\beta (1-{\theta }_1)S^0\hfill \\ \hfill 0\hfill & \hfill \beta (1-{\theta }_1){\theta }_2{S}^0-(\delta +\mu )\hfill & \hfill \beta (1-{\theta }_1)S^0\hfill \\ \hfill 0\hfill & \hfill \delta \hfill & \hfill -(\gamma +\sigma +\mu )\hfill \end{array}\right).\hfill \end{array}\right)$$ (3.2)

We can easily have $f^0\left(\lambda \right)=det[\lambda I-J^0]$, where

$$\left(\begin{array}{c}{f}^0\left(\lambda \right)=(\lambda +\mu )\{[\lambda +(\delta +\mu )-\beta (1-{\theta }_1){\theta }_2{S}^0][\lambda +(\gamma +\sigma +\mu )]-\delta \beta (1-{\theta }_1)S^0\},\hfill \end{array}\right)$$ (3.3)

(3.3) is obviously a cubic polynomial, we can replace the coefficient with $a_3,a_2,a_1,a_0$. Therefore, (3.3) can be rewritten as

$$\left(\begin{array}{c}{f}^0\left(\lambda \right)=a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0,\hfill \end{array}\right)$$ (3.4)

where $a_0=\mu (AB-C)$, $a_1=[(AB-C)+\mu (A+B)]$, $a_2=\mu +A+B$, $a_3=1$ with $A=(\delta +\mu )-\beta (1-{\theta }_1){\theta }_2{S}^0$, $B=\gamma +\sigma +\mu$, $C=\delta \beta (1-{\theta }_1)S^0$.

According to Routh–Hurwitz criterion, equilibrium point $P^0(\frac{\Lambda }{\mu },0,0)$ of system (3.1) is locally asymptotically stable if only if $\left(i\right)a_0,a_1,a_2,a_3>0$, and $\left(ii\right)a_1{a}_2-a_0{a}_3>0$.

If $\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]<\mu (\gamma +\sigma +\mu )(\delta +\mu )$, then,

$$a_0=\mu (AB-C)=\mu (\gamma +\sigma +\mu )(\delta +\mu )-\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]>0,$$

$$a_1=[(AB-C)+\mu (A+B)]>(\delta +\mu )(\gamma +\sigma +\mu )$$

$$-\frac{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]}{\mu }+\frac{\mu (\delta +\mu )(\gamma +\sigma +\mu )-\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]}{\mu (\gamma +\sigma +\mu )}>0,$$

$$a_2=\mu +A+B=\mu +(\delta +\mu )-\beta (1-{\theta }_1){\theta }_2{S}^0+\gamma +\sigma +\mu$$

$$>\frac{\mu (\gamma +\sigma +\mu )(\delta +\mu )-\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]}{\mu (\delta +\mu )}>0,$$

and $a_3=1>0$. Therefore, $a_0,a_1,a_2,a_3$ satisfy the condition $\left(i\right)$ of Routh–Hurwitz criterion. While $a_0<\mu (\delta +\mu )(\gamma +\sigma +\mu )$, $a_1>\mu (\gamma +\sigma +\mu )$ and $a_2>(\delta +\mu )$, hence, $a_1{a}_2-a_0{a}_3>0$. Obviously, $a_0,a_1,a_2,a_3$ satisfy the condition $\left(ii\right)$ of Routh–Hurwitz criterion. Therefore, equilibrium point $P^0(\frac{\Lambda }{\mu },0,0)$ of system (3.1) is locally asymptotically stable if only if $R_0<1$.

Theorem 3.2

The equilibrium point $P^0(\frac{\Lambda }{\mu },0,0)$ system (3.1) is globally asymptotically stable if only if $R_0<1$ .

Proof

From system (3.1), we can obtain that

$$\left(\begin{array}{c}\frac{d}{dt}(S\left(t\right)+E\left(t\right)+I\left(t\right))\le \Lambda -\mu S\left(t\right).\hfill \end{array}\right)$$ (3.5)

This implies that

$$\left(\begin{array}{c}\underset{t\to \infty }{lim\; sup}(S\left(t\right)+E\left(t\right)+I\left(t\right))\le \frac{\Lambda }{\mu }.\hfill \end{array}\right)$$ (3.6)

For $t\ge 0$, (3.6) shows that

$$\left(\begin{array}{c}\Sigma =\{(S\left(t\right),E\left(t\right),I\left(t\right))\in R_{+}^3\mid S\left(t\right)+E\left(t\right)+I\left(t\right)\le \frac{\Lambda }{\mu }\},\hfill \end{array}\right)$$ (3.7)

is a positive invariant set of system (3.1).

Lyapunov functions are defined as

$$\left(\begin{array}{c}{V}_1\left(t\right)={\int }_{\frac{\Lambda }{\mu }}^{S\left(t\right)}(1-\frac{\Lambda }{\mu u})du,V_2\left(t\right)=E\left(t\right)+\frac{\delta +\mu }{\delta }I\left(t\right).\hfill \end{array}\right)$$ (3.8)

For all $t\ge 0$, the derivatives of $V_1\left(t\right)$ and $V_2\left(t\right)$ are

$$\left(\begin{array}{c}\frac{d{V}_1\left(t\right)}{dt}=(1-\frac{\Lambda }{\mu S\left(t\right)})\{\Lambda -\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]-\mu S\left(t\right)\}\hfill \\ =-\frac{{(\Lambda -\mu S\left(t\right))}^2}{\mu S\left(t\right)}-\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]+\frac{\Lambda (1-{\theta }_1)\beta [I\left(t\right)+{\theta }_{2}E\left(t\right)]}{\mu },\hfill \end{array}\right)$$ (3.9)

and

$$\left(\begin{array}{c}\frac{d{V}_2\left(t\right)}{dt}=\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]+\frac{(\delta +\mu )(\gamma +\sigma +\mu )}{\delta }I\left(t\right).\hfill \end{array}\right)$$ (3.10)

For $R_0<1$, we have

$$\left(\begin{array}{c}\frac{dV\left(t\right)}{dt}=\frac{d{V}_1\left(t\right)}{dt}+\frac{d{V}_2\left(t\right)}{dt}\hfill \\ =-\frac{{(\Lambda -\mu S\left(t\right))}^2}{\mu S\left(t\right)}-\frac{(\delta +\mu )(\gamma +\sigma +\mu )}{\delta }(1-R_0)I\left(t\right)\le 0.\hfill \end{array}\right)$$ (3.11)

As we know that $\frac{dV\left(t\right)}{dt}=0$ holds if and only if $S\left(t\right)=S^0,E\left(t\right)=0,I\left(t\right)=0$. From system (3.1), we know that $\left\{(\frac{\Lambda }{\mu },0,0)\right\}$ is the largest invariant set in the region ${\Sigma }_0=\{(S\left(t\right),E\left(t\right),I\left(t\right))\in R_{+}^3\mid \frac{dV\left(t\right)}{dt}=0\}$ for $t\ge 0$. Lyapunov–LaSallle asymptotic stability theorem in [11] implies that equilibrium $(\frac{\Lambda }{\mu },0,0)$ of system (3.1) is globally asymptotically stable.

Theorem 3.3

If $R_0>1$ , Equilibrium point $P^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ of system (3.1) is locally asymptotically stable.

Proof

System (3.1) is linearized at equilibrium point $P^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ and its Jacobian matrix $J^{\ast }$ is

$$\left(\begin{array}{c}{J}^{\ast }=\left(\begin{array}{ccc}\hfill -\mu -\beta (1-{\theta }_1)(I^{\ast }+{\theta }_2{E}^{\ast })\hfill & \hfill -\beta (1-{\theta }_1){\theta }_2{S}^{\ast }\hfill & \hfill -\beta (1-{\theta }_1)S^{\ast }\hfill \\ \hfill \beta (1-{\theta }_1)(I^{\ast }+{\theta }_2{E}^{\ast })\hfill & \hfill \beta (1-{\theta }_1){\theta }_2{S}^{\ast }-(\delta +\mu )\hfill & \hfill \beta (1-{\theta }_1)S^{\ast }\hfill \\ \hfill 0\hfill & \hfill \delta \hfill & \hfill -(\gamma +\sigma +\mu )\hfill \end{array}\right).\hfill \end{array}\right)$$ (3.12)

We can easily have $f^{\ast }\left(\lambda \right)=det[\lambda I-J^{\ast }]$, where

$$\left(\begin{array}{c}{f}^{\ast }\left(\lambda \right)=[\lambda +\mu +\beta (1-{\theta }_1)(I^{\ast }+{\theta }_2{E}^{\ast })]\hfill \\ \times \{[\lambda +(\delta +\mu )-\beta (1-{\theta }_1){\theta }_2{S}^{\ast }][\lambda +(\gamma +\sigma +\mu )]-\delta \beta (1-{\theta }_1)S^{\ast }\}\hfill \\ +\beta (1-{\theta }_1)(I^{\ast }+{\theta }_2{E}^{\ast })[\beta (1-{\theta }_1){\theta }_2{S}^{\ast }(\lambda +\gamma +\sigma +\mu )+\delta \beta (1-{\theta }_1)S^{\ast }].\hfill \end{array}\right)$$ (3.13)

(3.13) is obviously a cubic polynomial, we can replace the coefficient of (3.13) with $a_3,a_2,a_1,a_0$. Therefore, (3.13) can be rewritten as

$$\left(\begin{array}{c}{f}^{\ast }\left(\lambda \right)=a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0,\hfill \end{array}\right)$$ (3.14)

where $a_0=A(BC-D)+(A-\mu )\{[B-(\delta +\mu )]C+D\}$, $a_1=BC-D+AB+AC+(A-\mu )[B-(\delta +\mu )]$, $a_2=A+B+C$, $a_3=1$, where $A=\mu +\beta (1-{\theta }_1)[I^{\ast }+{\theta }_2{E}^{\ast }]>0$, $B=(\delta +\mu )-\beta (1-{\theta }_1){\theta }_2{S}^{\ast }>0$, $C=\gamma +\sigma +\mu >0$, $D=\delta \beta (1-{\theta }_1)S^{\ast }>0$.

According to Routh–Hurwitz criterion, equilibrium point $P^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ of system (3.1) is locally asymptotically stable if only if $\left(i\right)a_0,a_1,a_2,a_3>0$, and $\left(ii\right)a_1{a}_2-a_0{a}_3>0$. Obviously, $a_2>0$ and $a_3>0$. If $\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]>\mu (\gamma +\sigma +\mu )(\delta +\mu )$, then,

$$a_0=A(BC-D)+(A-\mu )\{[B-(\delta +\mu )]C+D\}$$

$$=\beta (1-{\theta }_1)[\delta -{\theta }_2(\gamma +\sigma +\mu )]\{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\delta +\mu )]-\mu (\gamma +\delta +\mu )(\delta +\mu )\}>0,$$

$$a_1=BC-D+AB+AC+(A-\mu )[B-(\delta +\mu )]$$

$$>\frac{[\delta +(\gamma +\sigma +\mu )][\delta +{\theta }_2(\gamma +\sigma +\mu )]}{(\gamma +\sigma +\mu )(\delta +\mu )}$$

$$\times \frac{\beta (1-{\theta }_1){\theta }_2(\gamma +\sigma +\mu )(\delta +\mu )\{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]-\mu (\gamma +\sigma +\mu )(\delta +\mu )\}}{\delta +{\theta }_2(\gamma +\sigma +\mu )}$$

$$-\frac{\beta (1-{\theta }_1){\theta }_2(\gamma +\sigma +\mu )(\delta +\mu )\{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]-\mu (\gamma +\sigma +\mu )(\delta +\mu )\}}{\delta +{\theta }_2(\gamma +\sigma +\mu )}$$

$$>0.$$

Then, $a_0,a_1$, $a_2,a_3$ satisfy the condition $\left(i\right)$ of Routh–Hurwitz criterion.

While $a_0<(A-\mu )D$, $a_1>AB+(A-\mu )[B-(\delta +\mu )]$ and $a_2>\gamma +\sigma +2\mu$, hence, $a_1{a}_2-a_0{a}_3>\frac{\mu \delta (\delta +\mu )(\gamma +\sigma +\mu )}{\delta +{\theta }_2(\gamma +\sigma +\mu )}+\mu \beta (1-{\theta }_1)(\delta +\mu )I^{\ast }>0$. Obviously, $a_0,a_1,a_2,a_3$ satisfy the condition $\left(ii\right)$ of Routh–Hurwitz criterion. Therefore, equilibrium point $E^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ of system (3.1) is locally asymptotically stable if only if $\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\delta +\mu )]>\mu (\gamma +\delta +\mu )(\delta +\mu )$.

Theorem 3.4

Equilibrium point $P^{\ast }(S^{\ast },E^{\ast },I^{\ast })$ of system (3.1) is globally asymptotically stable if and only if $R_0>1$ .

Proof

Lyapunov functions are defined as

$$\left(\begin{array}{c}{V}_3\left(t\right)={\int }_{S^{\ast }}^{S\left(t\right)}(1-\frac{S^{\ast }}{u})du,\hfill \end{array}\right)$$ (3.15)

and

$$\left(\begin{array}{c}{V}_4\left(t\right)=E\left(t\right)-E^{\ast }-E^{\ast }ln\frac{E\left(t\right)}{E^{\ast }}+\frac{\delta +\mu }{\delta }[I\left(t\right)-I^{\ast }-I^{\ast }ln\frac{I\left(t\right)}{I^{\ast }}].\hfill \end{array}\right)$$ (3.16)

For all $t\ge 0$, the derivatives of $V_3\left(t\right)$ and $V_4\left(t\right)$ are

$$\begin{array}{c}\frac{d{V}_3\left(t\right)}{dt}=(1-\frac{S^{\ast }}{S\left(t\right)})[\Lambda -\beta (1-{\theta }_1)S\left(t\right)(I\left(t\right)+{\theta }_{2}E\left(t\right))-\mu S\left(t\right)]\hfill \\ =\mu (S^{\ast }-S\left(t\right))(1-\frac{S^{\ast }}{S\left(t\right)})+(\delta +\mu )E^{\ast }(1-\frac{S^{\ast }}{S\left(t\right)})\text{[}1-\hfill \\ -\frac{S\left(t\right)(I\left(t\right)+{\theta }_{2}E\left(t\right))}{S^{\ast }(I^{\ast }+{\theta }_2{E}^{\ast })}\text{]},\hfill \end{array}$$ (3.17)

and

$$\left(\begin{array}{c}\frac{d{V}_4\left(t\right)}{dt}=(1-\frac{E^{\ast }}{E\left(t\right)})\frac{dE\left(t\right)}{dt}+\frac{\delta +\mu }{\delta }[1-\frac{I^{\ast }}{I\left(t\right)}]\frac{dI\left(t\right)}{dt}\hfill \\ -\frac{(\delta +\mu )E\left(t\right)I^{\ast }}{\delta }+\frac{(\delta +\mu )(\gamma +\sigma +\mu )I^{\ast }}{\delta }\hfill \\ =(\delta +\mu )E^{\ast }\text{{}\frac{S\left(t\right)[S\left(t\right)+{\theta }_{2}E\left(t\right)]}{S^{\ast }[I^{\ast }+{\theta }_2{E}^{\ast }]}\hfill \\ -\frac{\beta (1-{\theta }_1)S\left(t\right)[I\left(t\right)+{\theta }_{2}E\left(t\right)]}{(\delta +\mu )E\left(t\right)}+1-\frac{I\left(t\right)}{I^{\ast }}-\frac{E\left(t\right)I^{\ast }}{I\left(t\right)E^{\ast }}+1\text{}}.\hfill \end{array}\right)$$ (3.18)

Then,

$$\left(\begin{array}{c}\frac{dV\left(t\right)}{dt}=\frac{d{V}_3\left(t\right)}{dt}+\frac{d{V}_4\left(t\right)}{dt}\hfill \\ =-\frac{\mu {(S^{\ast }-S\left(t\right))}^2}{S\left(t\right)}+(\delta +\mu )E^{\ast }[3-\frac{S^{\ast }}{S\left(t\right)}-\frac{S\left(t\right)I\left(t\right)E^{\ast }}{S^{\ast }{I}^{\ast }E\left(t\right)}-\frac{E\left(t\right)I^{\ast }}{I\left(t\right)E^{\ast }}]\hfill \\ \le -\frac{\mu {(S^{\ast }-S\left(t\right))}^2}{S\left(t\right)}-(\delta +\mu )E^{\ast }\frac{{(S^{\ast }-S\left(t\right))}^2}{S^{\ast }S\left(t\right)}\le 0.\hfill \end{array}\right)$$ (3.19)

Therefore, $\frac{dV\left(t\right)}{dt}=0$ holds if only if $S\left(t\right)=S^{\ast },E\left(t\right)=E^{\ast },I\left(t\right)=I^{\ast }$. Applying Lyapunov–LaSalle asymptotic stable theorem in [11], $\left\{(S^{\ast },E^{\ast },I^{\ast })\right\}$ is the largest invariant set in ${\sum }_0$, and it is globally asymptotically stable. This completes the proof.

4. Conclusion and simulations

In this work, we consider an SEIR epidemic model with infectivity in incubation period and homestead-isolation on the susceptible. The basic reproduction number of system (2.1) is obtained as

$$R_0=\frac{\Lambda \beta (1-{\theta }_1)[\delta +{\theta }_2(\gamma +\sigma +\mu )]}{\mu (\gamma +\sigma +\mu )(\delta +\mu )}.$$

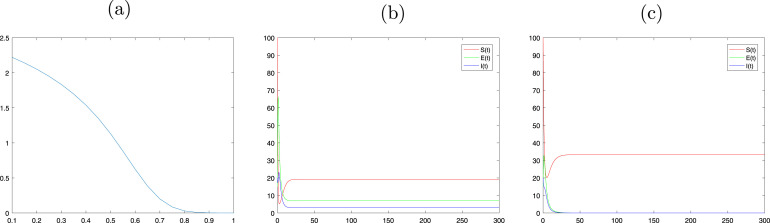
We have proved that the infection-free equilibrium point $P^o$ is locally and globally asymptotically stable if only if $R_0<1$. We also have proved that if $R_0>1$, equilibrium point $P^{\ast }$ is locally and globally asymptotically stable. If it is assumed that $S\left(0\right)=100,E\left(0\right)=15,I\left(0\right)=20,\Lambda =10,\beta =0.2,{\theta }_2=0.1,\mu =0.3,\delta =0.3,\gamma =0.2,\sigma =0.2$, we employ with computer aided techniques to obtain the threshold ${\theta }_1^{\ast }\approx 0.85$ of parameter ${\theta }_1$ (see $\left(a\right)$ in Fig. 1.). If we select ${\theta }_1=0.7$, the basic reproduction number of system $(2.1)R_0=1.7619>1$, it can be seen that the equilibrium point $P^{\ast }$ is globally asymptotically stable.(see $\left(b\right)$ in Fig. 1.). If we select $l=0.9$, the basic reproduction number of system $(2.1)R_0=0.5873<1$, it can be seen that the equilibrium point $P^0$ is globally asymptotically stable.(see $\left(c\right)$ in Fig. 1.). The proofs and the numerical simulations are employed to illustrate that the strategies of the homestead-isolation on the susceptible are very important in the epidemics of infectious diseases. Our results suggest that the governments should strictly implement the isolation system to make every effort to curb propagation of disease.

Fig. 1.

Threshold analysis of parameter ${\theta }_1$ and the basic reproduction number $R_0$ of system (2.1) with $S\left(0\right)=100,E\left(0\right)=15,I\left(0\right)=20,\Lambda =10,\beta =0.2,{\theta }_2=0.1,\mu =0.3,\delta =0.3,\gamma =0.2,\sigma =0.2$, (a) $I\left(t\right)$ changes with parameter ${\theta }_1$; (b) Time series of $S\left(t\right),E\left(t\right)$, and $I\left(t\right)$ change with parameter ${\theta }_1=0.7$; (c) Time series of $S\left(t\right),E\left(t\right)$, and $I\left(t\right)$ change with parameter ${\theta }_1=0.9$.

CRediT authorship contribution statement

Jianjun Jiao: Writing-orginal draft. Zuozhi Liu: Simulations. Shaohong Cai: Writing - review & editing.