Significance
We present a study to model the spread of ancestry in ancient genomes through time and space and a geostatistical framework for comparing human migrations and land-cover changes, while accounting for changes in climate. We show that the two major migrations during the European Holocene had different spatiotemporal structures and expansion rates. In addition, we find that the Yamnaya expansion had a stronger association with vegetational landscape changes than the earlier Neolithic farmer expansion. Our approach paves the way for future work linking paleogenomics with other archaeometric datasets in the study of the past.
Keywords: migrations, ancient DNA, Neolithic, Bronze Age, land cover
Abstract
The European continent was subject to two major migrations of peoples during the Holocene: the northwestward movement of Anatolian farmer populations during the Neolithic and the westward movement of Yamnaya steppe peoples during the Bronze Age. These movements changed the genetic composition of the continent’s inhabitants. The Holocene was also characterized by major changes in vegetation composition, which altered the environment occupied by the original hunter-gatherer populations. We aim to test to what extent vegetation change through time is associated with changes in population composition as a consequence of these migrations, or with changes in climate. Using ancient DNA in combination with geostatistical techniques, we produce detailed maps of ancient population movements, which allow us to visualize how these migrations unfolded through time and space. We find that the spread of Neolithic farmer ancestry had a two-pronged wavefront, in agreement with similar findings on the cultural spread of farming from radiocarbon-dated archaeological sites. This movement, however, did not have a strong association with changes in the vegetational landscape. In contrast, the Yamnaya migration speed was at least twice as fast and coincided with a reduction in the amount of broad-leaf forest and an increase in the amount of pasture and natural grasslands in the continent. We demonstrate the utility of integrating ancient genomes with archaeometric datasets in a spatiotemporal statistical framework, which we foresee will enable future studies of ancient populations’ movements, and their putative effects on local fauna and flora.
Up until about 8,500 y before present (BP), Europe was largely populated by groups of hunter-gatherers living at relatively low densities. This scenario changed when a wave of populations from the Middle East entered Europe via Anatolia, as evinced by recent ancient DNA studies (1–3). Studies based on radiocarbon-dated domestic plants, animals, and finds from associated contexts suggest that this migration wave spread farming practices into the region, initiating the Neolithic revolution in Europe (4–9). A second massive wave of movement occurred later, at the beginning of the Bronze Age, when populations associated with the Yamnaya culture in the Pontic steppe entered the continent from the east (10–12). These groups may have introduced horse herding and proto-Indo-European languages as they moved westward and are associated with the Corded Ware culture in central and northern Europe and, later on, the Bell Beaker phenomenon in northwestern Europe (13–16).
Over the last 10,000 y, the continent also underwent major changes in its land-cover composition, but it is unclear how much the Neolithic and Yamnaya migrations contributed to these changes. Recent pollen-based studies suggest that a dramatic reduction of broad-leaf forests occurred from about 6,000 BP until the present (17). This deforestation intensified from around 2,200 BP, resulting in a replacement of these forests by grassland and arable land throughout the continent (18, 19). These processes, however, did not occur at the same rate throughout all regions. For example, while considerable decreases in broad-leaf forests occurred in central Europe starting around 4,000 BP, the Atlantic seaboard was predominantly occupied by semiopen vegetation since well before this time, while southern Scandinavia experienced less significant reductions in forest cover, at least until the Middle Ages (19–21). Presumably, these phenomena were partly effected by new human land-use activities involving forest clearance and the establishment of farming and herding practices, as earlier hunter-gatherer groups likely had limited effects on their surrounding flora and fauna (although see refs. 22 and 23). Changes in climate patterns may have also played a role in vegetation changes. Additionally, changes in vegetation may have opened up new areas for populations to expand. Until now, however, few efforts have been carried out to explicitly link changes in paleovegetation to particular human population movements, or to distinguish between climatic and human-based factors, assuming these had causal roles in these changes (but see refs. 18 and 24).
In this study, we aim to trace how the major Holocene migrations unfolded across the European continent over time and to understand how they were associated with changes in the vegetational landscape. We do so by combining ancestry inference on ancient genomes with geostatistical methods, which explicitly account for space and time and are commonly used to model environmental processes. We use these methods to produce detailed spatiotemporal maps of ancestry movements and to uncover their relationship with the spread of farming practices and vegetation changes. Additionally, we estimate the front speed of these migrations and compare our results to reconstructions of cultural dispersal obtained from radiocarbon-dated archaeological sites.
Our modeling approach reveals important factors that may have affected land cover in the past 10,000 y. We find that a decline in broad-leaf forest and an increase in pasture/natural grassland vegetation was concurrent with a decline in hunter-gatherer ancestry and may have been associated with the fast movement of steppe peoples during the Bronze Age. We also find that natural variations in climate patterns during this period are associated with these land-cover changes. We believe that our approach paves the way for future geostatistical studies integrating paleogenomics with archaeometric datasets, which will yield new insights as information about our past continues to accumulate.
Results
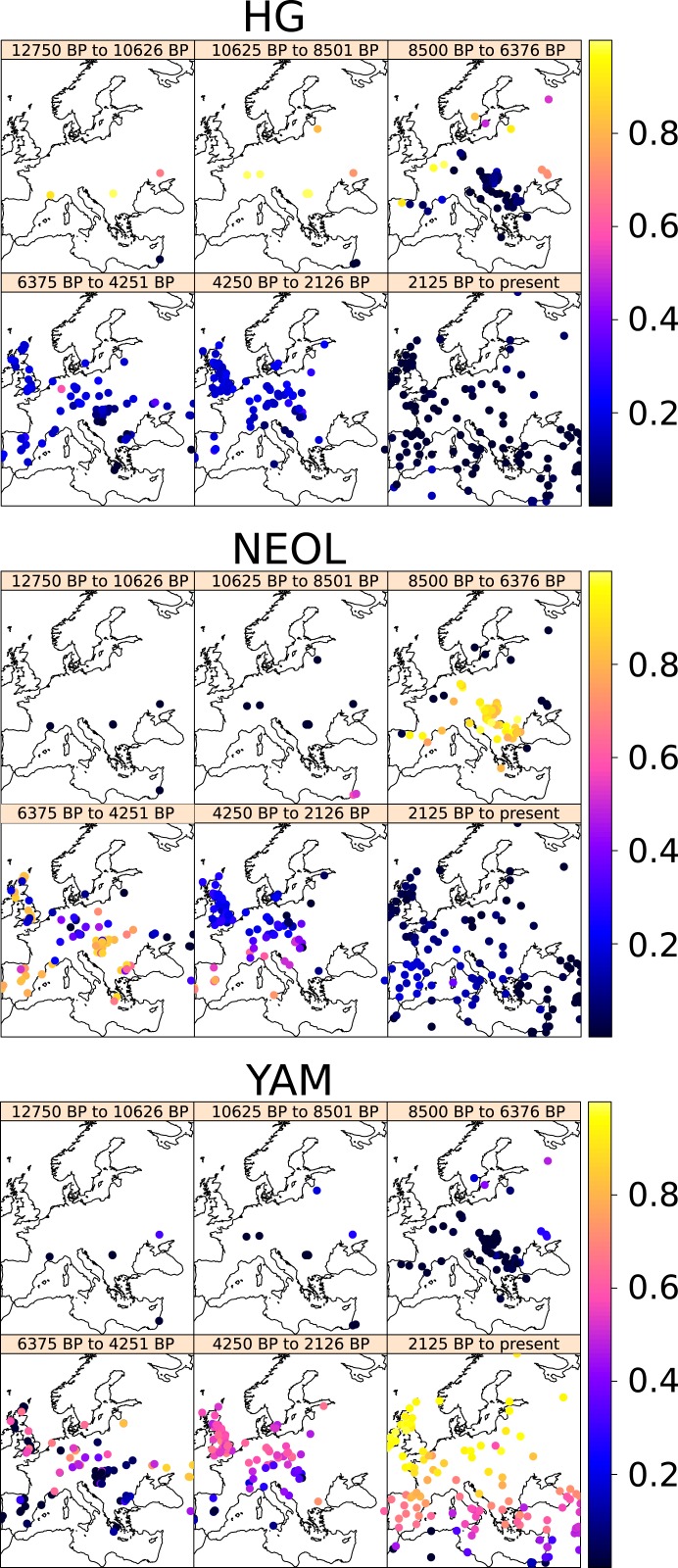
We downloaded publicly available ancient and present-day DNA sequences from human genomic studies (2, 3, 13–15, 25–32) (Dataset S1). We performed unsupervised latent ancestry estimation on these sequences using Ohana (33) with K = 4 hidden ancestry clusters. We chose this value of K because, under this scheme, three of the components correspond to the three major ancestral populations that have been previously shown to have resulted—via multiple migration and admixture events—into the present-day European gene pool: the original Mesolithic hunter-gatherers (HG), the Neolithic farmers who migrated from the Near East (NEOL), and the Yamnaya steppe peoples who entered Europe during the Bronze Age (YAM) (2, 13, 14) (Fig. 1). The fourth is an ancestry component that remains largely confined to Northern Africa and the Fertile Crescent throughout most of the Holocene (NAF) (SI Appendix, Fig. S1). We focus on the first three components and note that the specification of a larger number of ancestry components could provide further details into more subtle patterns of migration and population expansion, but may also be confounded by bottlenecks and ghost admixture events (34), so we do not pursue finer ancestry estimation here.
Fig. 1.
Spatiotemporal maps of ancestry proportions for ancient and present-day genomes in this study. Note that not all ancient samples in each map are strictly contemporaneous with each other.
As we demonstrate below, the YAM and NEOL ancestries closely parallel the Yamnaya and Neolithic farmer cultural horizons. However, ancestry and culture are distinct concepts that do not always overlap in time and space, so we choose to use the acronym nomenclature when referring to ancestries and the full name when referring to cultures, unless otherwise specified. Furthermore, there were various, quite differentiated hunter-gatherer populations (Eastern, Western, and Scandinavian hunter-gatherers) who migrated into Western Eurasia before the Holocene (3, 30, 32, 35, 36). The HG ancestry roughly corresponds to the ancestry referred to as “Western hunter-gatherer” in these publications. We note that under our K = 4 admixture scheme, Scandinavian hunter-gatherers are modeled as containing high amounts () of HG ancestry, while the rest of their ancestry is modeled as YAM (which works here as a stand-in for Eastern hunter-gatherer ancestry; for further details about hunter-gatherer ancestry movements, see refs. 25 and 32). The data for each of these populations is scarcer than for Bronze Age and Neolithic individuals, and, in this work, we chose only to focus on later Holocene ancestry movements.
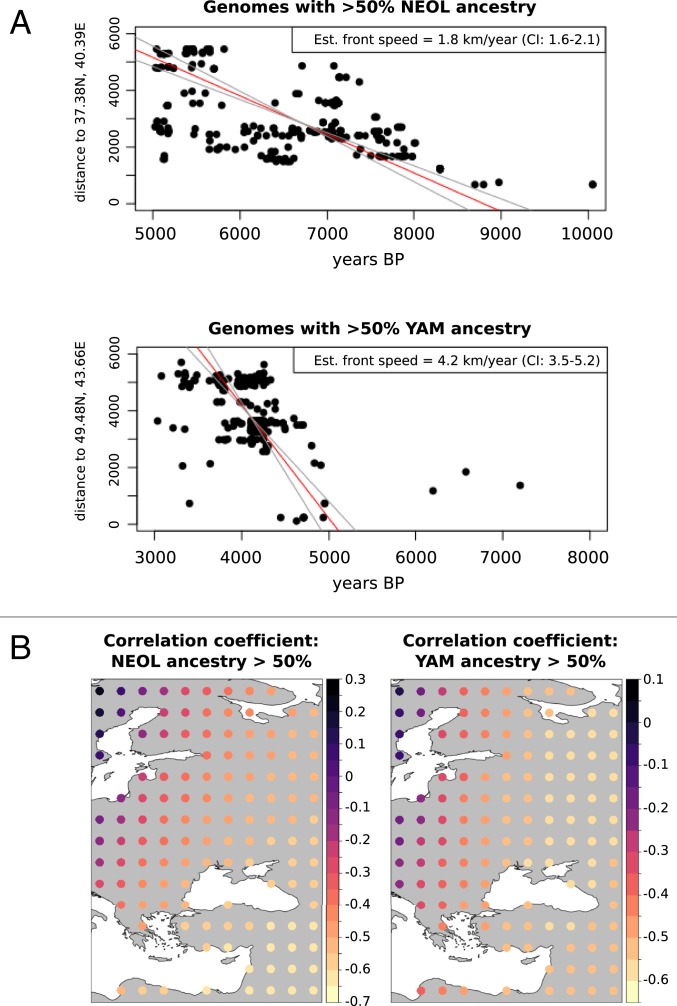
We first sought to compare the spread of dispersal of NEOL and YAM ancestries over time, using the calibrated C14 dates of each genome. We regressed time against distance from the presumed origin of the spread of each of these ancestries, using the ranged major axis (RMA) method (5, 8). This allowed us to obtain an estimate for the migration front speed. We first used samples that had at least of the corresponding ancestry we were studying, as a cutoff value is needed to be able to declare that a particular ancestry was high enough to consider the ancestry had “arrived” at that point in time and space. Using this cutoff, we found that the speed of the YAM migration (4.2 km/y; CI: 3.5 to 5.2) was at least twice as fast as the NEOL migration (1.8 km/y; CI: 1.6 to 2.1), assuming an origin of the YAM migration at the center of the Yamnaya historical range (Fig. 2A). A higher ancestry cutoff of to establish “first arrival” yielded the same estimate for the NEOL migration (1.8 km/y; CI: 1.6 to 2.2), but an even faster estimate for the YAM migration (9.3 km/y; CI: 6 to 20). YAM speed estimates were generally higher than NEOL speed estimates, for almost any choice of minimum ancestry cutoffs, unless these cutoffs were chosen to be very small () (SI Appendix, Table S1).
Fig. 2.
(A) Front speed estimation for the Neolithic farmer (Upper) and Yamnaya steppe peoples (Lower) population movements. We used an RMA regression on time against distance from the hypothesized origin of the spread to estimate average migration front speed. In this case, we used a ancestry cutoff to define genomes as belonging to a particular migration wave. Est., estimated. (B) Point-of-origin estimation. We computed the correlation coefficient between time of sampling and distance from a hypothesized origin, which should be negative for a range expansion. Each dot in the map represents a different hypothesized origin.
Given that the original Yamnaya range was quite large (10), we also aimed to see how our estimates varied as we altered the point of origin within this range. We obtained estimates of YAM ancestry speed, assuming a location of origin at the northernmost, easternmost, westernmost, and southernmost parts of the Yamnaya range, which yielded similar estimates of speed (SI Appendix, Table S2). The magnitude of the negative correlation coefficients between time and distance from origin can also be used to estimate the point of origin (8, 37), assuming a range expansion for the YAM and NEOL ancestries. Indeed, when we altered the point of origin, we found that the most negative correlation coefficients corresponded to Anatolia and the Middle East for the NEOL ancestry and to the Caspian steppe for the YAM ancestry (Fig. 2B).
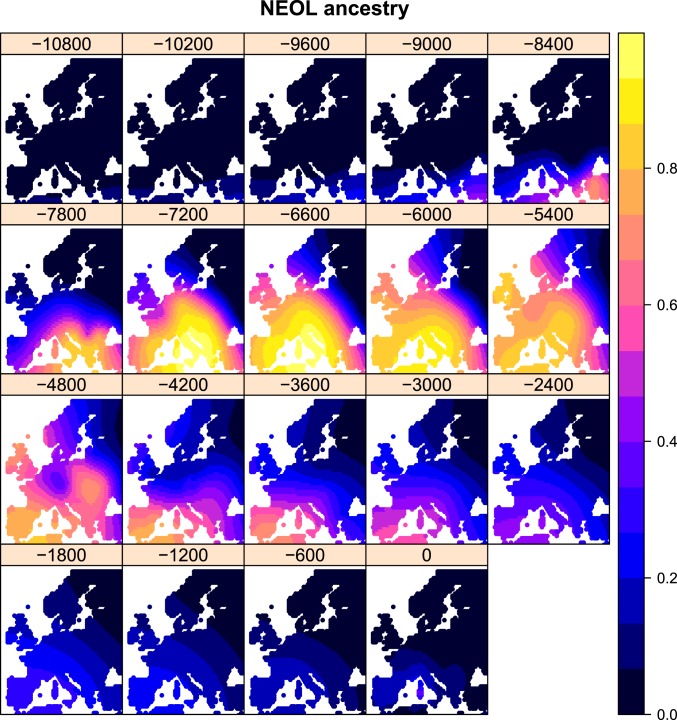
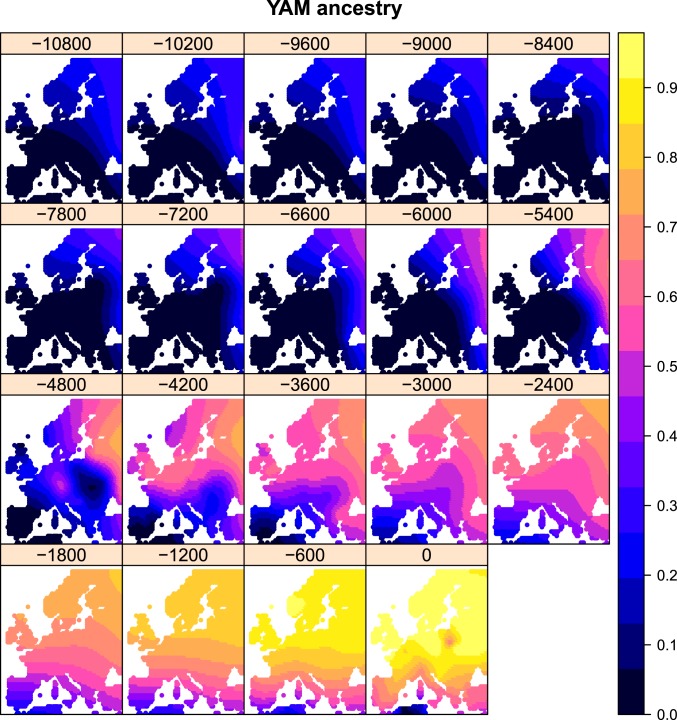
To be able to compare ancestry through time and space with other variables, we aimed to project our ancestry values to particular times and locations for which we do not necessarily have sampled genomes (Fig. 3). To do so, we computed a spatiotemporal variogram and fitted it to a metric covariance function (38, 39) (SI Appendix, Figs. S2–S5). We then performed spatiotemporal kriging of the inferred latent ancestry values on a dense grid of spatial points across Europe, over a 10,800-y span, with intervals of 600 y (Figs. 4 and 5, SI Appendix, Figs. S6 and S7, and Movies S1–S3). In practice, however, given the sparseness of the data in the distant past, we restrict our discussion to patterns seen more recently than 8,000 y BP.
Fig. 3.
Schematic of methodology for spatiotemporal kriging and vegetation modeling. (A) We first fitted a latent mixed-membership model to the ancient and present-day genomes. The ancestry proportions were then assigned the temporal and spatial metadata of their respective genomes, which allowed us to perform spatiotemporal kriging to any location and time in the European Holocene. (B) We used a spatiotemporally aware model to understand how patterns of human migration and climate relate to patterns of vegetation type changes during the European Holocene, while accounting for spatiotemporal autocorrelation. We used a bootstrapping method to account for biases due to uneven sampling of ancient genomes. Brighter colors represent higher values of each depicted variable.
Fig. 4.
Spatiotemporal kriging of NEOL ancestry during the Holocene, using 5,000 spatial grid points. The colors represent the predicted ancestry proportion at each point in the grid.
Fig. 5.
Spatiotemporal kriging of YAM steppe ancestry during the Holocene, using 5,000 spatial grid points. The colors represent the predicted ancestry proportion at each point in the grid.
We downloaded land-cover class (LCC) maps (19) and paleoclimatic variable maps (40) spanning the Holocene and projected them on the same spatiotemporal grid that we used for our kriged ancestry values (Materials and Methods). The paleovegetation types included needle-leaf forest (LCC1), broad-leaf forest (LCC2), heath/scrubland (LCC5), pasture/natural grassland (LCC6), and arable/disturbed land (LCC7). We computed correlations between each of the spatiotemporally projected ancestry proportions and vegetation types, and between the climate variables and vegetation types. This was done in three different ways. Firstly, we simply obtained the correlation of the raw values of any two variables (SI Appendix, Fig. S8 and Table S3). Secondly, we obtained the correlation of the differences in these variables between a particular time slice and the immediately previous time slice (SI Appendix, Fig. S9 and Table S3). Thirdly, we obtained the correlations of the variable anomalies, defined as the value of each ancient variable after subtracting the present-day value from the same location (SI Appendix, Fig. S10 and Table S3). We note, however, that this approach does not account for autocorrelation in time and space that may exist for all of the compared variables, not only because of real autocorrelation in the processes under study, but also as a result of enforced autocorrelation from the smoothing techniques that generated the maps.
The raw correlations reflect spatially static patterns of co-occurrence (SI Appendix, Fig. S8 and Table S3). For example, YAM ancestry was largely prevalent in northeast Europe throughout much of the Holocene, and this coincides with periods of abundant needle-leaf forests, which is why there is strong positive correlation between these variables. Conversely, NEOL ancestry was largely prevalent in southern Europe during this period, which is why there is a negative correlation with needle-leaf forest. In contrast, the correlations in differences and in anomalies reflect spatially dynamic patterns of co-occurrence (SI Appendix, Figs. S9 and S10 and Table S3). Here, temporal increases in one variable that coincide with temporal increases in a second variable at the same location will result in positive correlation. The same will result if there are co-occurring decreases. If, however, a variable decreases while another increases at the same location, this will result in negative correlation. For example, we see that YAM ancestry anomalies are positively correlated with pasture/natural grassland anomalies, but negatively correlated with broad-leaf forest anomalies. We also see that the correlations between ancestry differences and vegetation differences increase when looking at vegetation differences one or two time slices into the future (600 or 1,200 y later, respectively), perhaps suggesting that migrations could have had a role in these vegetational changes (SI Appendix, Fig. S11).
On a continental level, decreases in broad-leaf forest and increases in pasture/grassland occurred most notably after the arrival of YAM ancestry, not after the arrival of NEOL ancestry. However, vegetation changes behaved in different ways in different parts of the continent (Fig. 6 and SI Appendix, Fig. S12). In central France, increases in YAM ancestry coincided with decreases in broad-leaf forest cover. In contrast, in southeastern and southwestern Europe, forest cover remained stable (at low levels), even as YAM ancestry was increasing. If humans were responsible for this, it could perhaps be due to the development of tree cropping within the agropastoral system in the Mediterranean (24). Considerable increases in arable land cover occurred fairly late in the Holocene throughout the continent, and much later than the incursion of NEOL ancestry during the Neolithic (SI Appendix, Fig. S12). Interestingly, we observed a decrease in NEOL ancestry that continued even after the incursion of YAM ancestry into Europe, though our resolution for quantifying changes in this ancestry in the last 2,000 y is limited by the scarcity of ancient genomes from the very recent past.
Fig. 6.
(A) Timelines of kriged ancestry and vegetation type proportions at different points in Europe. (B) Change in pasture/natural grassland and broad-leaf forest cover composition after the arrival (first time there is ancestry) in each spatial grid point of YAM and NEOL ancestry. Each line corresponds to the postarrival progression of a different spatial grid point.
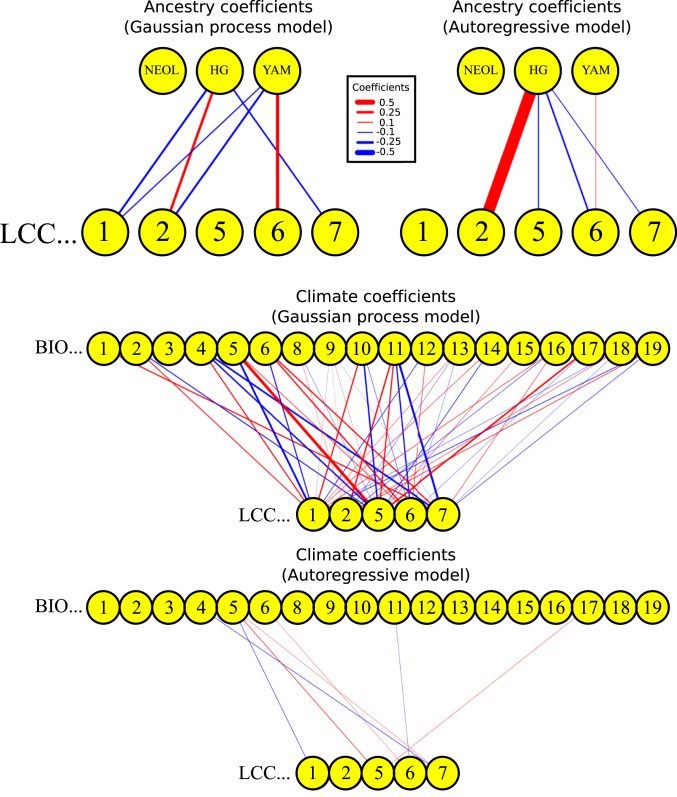
While correlations between vegetation and ancestry are interesting, they do not account for the fact that we are projecting the data to lie in a particular set of spatiotemporal grid points, which have complex autocorrelations in time and space, potentially affecting the correlations we observe between variables. To address this, we used a spatiotemporally explicit hierarchical Bayesian model to better understand the relationships between changes in climate, ancestry, and paleovegetation, while accounting for these autocorrelations (Fig. 3). We used two models, implemented in the R package spTimer (41). One is a Gaussian process (GP) model that incorporates a spatiotemporal nugget that is independent of time and has a distribution that depends on a spatial correlation matrix. The other is an extension of this method that incorporates a temporal autoregressive component (AR). We set the kriged ancestry and climate variables to be the explanatory variables, while each of the paleovegetation variables was set as a response variable. We fitted five separate models for each paleovegetation variable. SI Appendix, Table S4 lists the goodness-of-fit score for both models, along with the predictive model choice criteria (PMCC), which accounts for differences in model complexity (41, 42). In comparison to the GP model (Fig. 7 and Table 1), the AR model resulted in a more sparse set of posterior coefficients whose credible intervals do not overlap with 0 (Fig. 7 and Table 2). An evaluation of the root mean squared error (RMSE) of the predictions (Materials and Methods) suggested that the GP model with a uniform prior distribution for the decay parameter of the spatial correlation function generally had the lowest validation error (SI Appendix, Fig. S13).
Fig. 7.
Posterior mean coefficients of spatiotemporal model for paleovegetation anomalies, using kriged ancestry anomalies and anomalies from simulation-based paleoclimate reconstructions as explanatory variables. (Top Left and Middle) Posterior coefficients from GP model. (Top Right and Bottom) Coefficients from autoregressive model. Coefficients whose corresponding posterior distribution has a central probability mass interval that spans the value of 0 are not depicted. LCC1, needle-leaf forest; LCC2, broad-leaf forest; LCC5, heath/scrubland; LCC6, pasture/natural grassland; LCC7, arable/disturbed land. The climate variables follow the WorldClim nomenclature. BIO1, Annual Mean Temperature; BIO2, Mean Diurnal Range (Mean of monthly (max temp – min temp)); BIO3, Isothermality (BIO2/BIO7) (× 100); BIO4, Temperature Seasonality (SD × 100); BIO5, Max Temperature of Warmest Month; BIO6, Min Temperature of Coldest Month; BIO8, Mean Temperature of Wettest Quarter; BIO9, Mean Temperature of Driest Quarter; BIO10, Mean Temperature of Warmest Quarter; BIO11, Mean Temperature of Coldest Quarter; BIO12, Annual Precipitation; BIO13, Precipitation of Wettest Month; BIO14, Precipitation of Driest Month; BIO15, Precipitation Seasonality (Coefficient of Variation); BIO16, Precipitation of Wettest Quarter; BIO17, Precipitation of Driest Quarter; BIO18, Precipitation of Warmest Quarter; BIO19, Precipitation of Coldest Quarter.
Table 1.
Coefficients of the spatiotemporal GP model, using the PaleoClim (40) simulation-based paleoclimate variables as covariates
| Coefficient | Post. Med. | BCI | BCI |
| NEOL needle-leaf forest | −0.0567 | −0.149 | 0.035 |
| HG needle-leaf forest | −0.196 | −0.329 | −0.0654 |
| YAM needle-leaf forest | −0.114 | −0.183 | −0.0434 |
| NEOL broad-leaf forest | −0.0396 | −0.113 | 0.033 |
| HG broad-leaf forest | 0.245 | 0.138 | 0.344 |
| YAM broad-leaf forest | −0.191 | −0.244 | −0.139 |
| NEOL heath/scrubland | 0.0545 | −0.0584 | 0.167 |
| HG heath/scrubland | 0.0426 | −0.114 | 0.2 |
| YAM heath/scrubland | 0.0534 | −0.0262 | 0.132 |
| NEOL pasture/natural grassland | 0.0481 | −0.0026 | 0.0992 |
| HG pasture/natural grassland | 0.0196 | −0.0527 | 0.0947 |
| YAM pasture/natural grassland | 0.318 | 0.28 | 0.356 |
| NEOL arable/disturbed land | −0.0603 | −0.152 | 0.0275 |
| HG arable/disturbed land | −0.154 | −0.282 | −0.0285 |
| YAM arable/disturbed land | 0.0455 | −0.016 | 0.112 |
Post. med., posterior median. Coefficients whose 95% CIs do not overlap with 0 are in bold.
Table 2.
Coefficients of the spatiotemporal autoregressive model, using the PaleoClim x(40) simulation-based paleoclimate variables as covariates
| Coefficient | Post. Med. | BCI | BCI |
| NEOL needle-leaf forest | −0.0114 | −0.0712 | 0.0492 |
| HG needle-leaf forest | −0.00947 | −0.0938 | 0.0801 |
| YAM needle-leaf forest | −0.00891 | −0.0533 | 0.0343 |
| NEOL broad-leaf forest | 0.324 | −0.032 | 0.105 |
| HG broad-leaf forest | 0.225 | 0.121 | 0.331 |
| YAM broad-leaf forest | −0.00494 | −0.0462 | 0.0361 |
| NEOL heath/scrubland | −0.0289 | −0.0929 | 0.0361 |
| HG heath/scrubland | −0.105 | −0.199 | −0.0107 |
| YAM heath/scrubland | −0.00871 | −0.0556 | 0.0374 |
| NEOL pasture/natural grassland | −0.0271 | −0.0607 | 0.00651 |
| HG pasture/natural grassland | −0.153 | −0.207 | −0.0994 |
| YAM pasture/natural grassland | 0.0436 | 0.0219 | 0.0657 |
| NEOL arable/disturbed land | −0.0392 | −0.0827 | 0.0043 |
| HG arable/disturbed land | −0.0831 | −0.146 | −0.0208 |
| YAM arable/disturbed land | −0.0111 | −0.0415 | 0.0212 |
Post. med., posterior median. Coefficients whose 95% CIs do not overlap with 0 are in bold.
We also compared the predictive accuracy of models incorporating ancestry only, climate only, both sets of variables, or none of them. In general, adding both climate and ancestry resulted in a better PMCC score than adding either in isolation or adding none of them (Table 3). However, in all but one of the paleovegetation variables, there was no observable difference in the RMSE of the fitted model when adding climate only, ancestry only, or both climate and ancestry. The exception to this pattern was pasture/grassland (LCC6), which had both the lowest error and the lowest PMCC when including both climate and ancestry under the GP model (Table 3 and SI Appendix, Fig. S13).
Table 3.
PMCC for the hierarchical GP model of vegetation anomalies, including climate explanatory variables only, ancestry explanatory variables only, neither set of variables, or both of them
| Vegetation | None | Clim. only | Anc. only | Both |
| Needle-leaf forest | 2,579.09 | 2,514.75 | 2,574.54 | 2,508.52 |
| Broad-leaf forest | 1,671.87 | 1,651.12 | 1,641.98 | 1,623.55 |
| Heath/scrubland | 2,759.30 | 2,640.54 | 2,755.95 | 2,635.82 |
| Pasture/nat. grassland | 1,961.25 | 1,408.12 | 1,662.91 | 1,123.51 |
| Arable/disturbed land | 2,171.43 | 2,151.85 | 2,161.47 | 2,145.55 |
We used a Uniform(0.01,0.02) prior for the spatial decay parameter. Anc., ancestry; Clim., climate; nat., natural.
Because we are using kriged ancestry as an explanatory variable and our ancient genomes are unevenly sampled across space and time, we were mindful that the Bayesian credible intervals (BCIs) obtained from the hierarchical model would not accurately reflect uncertainty in particular regions of space–time. For that reason, we performed nonparametric bootstrapping of the parameter estimates. We randomly sampled ancient and present-day genomes with replacements from among the list of all genomes until we had as many genomes as were in the original dataset, then obtained their ancestry assignments, kriged them on the spatiotemporal grid, and inputted them into the Bayesian hierarchical model. We did this 100 times to obtain 100 pseudo-samples, which allowed us to obtain bootstrap-based CIs (BBCIs) around the mean posterior estimates (SI Appendix, Fig. S14 and Table S5). Below, we discuss results that are supported by one or both models and that are also supported by the bootstrapping approach.
Regardless of the model used, we found that HG ancestry is positively associated with broad-leaf forest anomalies, but negatively associated with arable land anomalies. YAM ancestry, in turn, is positively associated with pasture/natural grassland (Fig. 7 and SI Appendix, Fig. S14). In the fitted AR model and the bootstrapping approach, we also saw a negative association of HG ancestry to pasture/grassland and scrubland. In the fitted GP model and the bootstrapping approach, we observed a negative association of YAM ancestry with forest vegetation, which was strongest for broad-leaf forest. We saw weak or nonexistent associations of NEOL ancestry with any vegetation type. We cannot discard the possibility that we may lack the ability to detect some associations between ancestry movements and vegetation changes at our current scale of resolution.
We additionally observed associations of different climate variables with the different vegetation anomalies, which become sparser in the AR model (Fig. 7). For example, in both the AR and GP models, increases in temperature were related to increases in nonforest vegetation types (scrubland, pasture, and arable land). In addition, temperature seasonality may be interpreted as negatively associated with the proportion of arable land, while precipitation during the driest quarter may be interpreted as associated positively with heath/scrubland, under the fitted models.
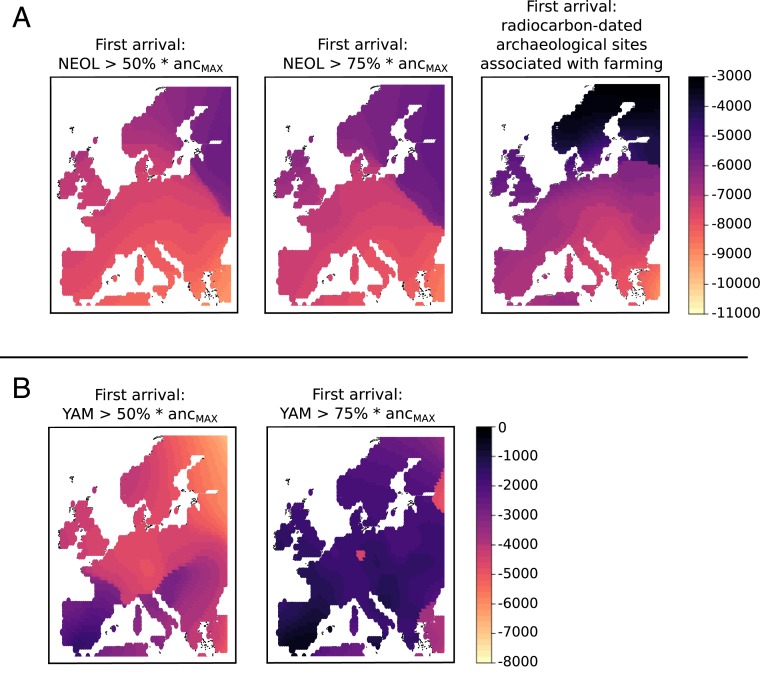
Finally, we built “first arrival” maps (7–9) for both NEOL and YAM, given that changes in these ancestries can be broadly interpreted as incursions of foreign populations into the European continent during the Neolithic and Bronze Age (13, 14). The first arrival map of NEOL ancestry shows that this ancestry spread closely paralleled the inferred cultural spread of farming, which has been inferred from archaeological sites (Fig. 8) (5–8). When performing the same type of reconstruction for the YAM ancestry, we observed that this spread occurred first via north and central Europe and only much later began to spread into southern Europe (Fig. 8), reflecting reconstructions from archaeological records for the spread of the Yamnaya, Corded Ware, and Bell Beaker phenomena (10–12).
Fig. 8.
Comparison of inferred spread of farming from archaeological sites and spread of NEOL (A) and YAM (B) ancestries. A and B, Left define first arrival as the first time slice in which a grid point has more than of the ancestry depicted, where is the maximum value that ancestry reaches at that point throughout the entire timeline. A, Center and B, Right are the result of using a more strict cutoff: ancestry. A, Right is a spatially kriged map of first arrivals of farming practices, based on radiocarbon-dated archaeological sites.
Discussion
An explicitly geostatistical approach allows us to visualize how movements of ancestry occurred during the Holocene in Europe. The NEOL ancestry expansion followed a two-pronged shape, paralleling the expansion of farming practices estimated from radiocarbon-dated archaeological sites. We observed two wave fronts, one northward across central Europe and one westward along the Mediterranean coast (Fig. 8). In the cultural map, these two wave fronts correspond to the Linear Pottery (LBK) culture (43) and the Impressa/Cardial Pottery culture (44–46). Given their close parallels in the ancestry map, this supports the view that these two cultural expansions were probably driven by migrations of people (13, 14).
We estimate that the expansion of YAM ancestry occurred faster than the expansion of NEOL ancestry. The reasons for this could be numerous, including the use of horses for long-distance travel (10). YAM ancestry predominates in individuals associated with the Yamnaya and Corded Ware cultures and is presumed to have moved into Europe from the Eurasian Steppes (12). Another possibility could be the opening of the landscape previous to the arrival of the Yamnaya people, perhaps due to Neolithic agricultural, grazing, and mining practices (47), which may have facilitated later movements of people. We did not observe a strong decrease in forest vegetation in Northern and Central Europe until the Bronze Age, however. On the other hand, there is limited evidence that Corded Ware people were horse herders, and evidence from settlements in central Europe suggests that they may have practiced mixed agriculture (48–50).
We can now begin to understand how these movements of people may have been associated with the European vegetational landscape, while accounting for autocorrelation in time and space (Fig. 7). We generally fit HG ancestry as positively associated with broad-leaf vegetation, while YAM ancestry was negatively associated with broad-leaf forest vegetation and positively associated with grassland and arable land. We also found associations between climate and changes in land-cover type. For example, increases in temperatures were related to increases in scrubland, pasture/grassland, and arable land.
We did not find that NEOL ancestry had a strong association to changes in vegetation. One possible explanation is that this association was too minor or localized for us to clearly detect an effect in our model. Earlier studies have shown that Neolithic communities did, in fact, alter their local environments (Mercuri et al. 2019 Holocene) and had a local effect on vegetation to a certain extent, at least in northwestern Europe (47, 51, 52). In particular areas, such as northern and northwestern Europe, there was a very minor decline in broad-leaf forest that coincided with the increase in NEOL ancestry, but this was not observed at a continental level (Fig. 6). A much more pronounced reduction in broad-leaf forest occurred later on throughout western and northwestern Europe and coincided with the increase in YAM ancestry. It is important to note that cultivated tree types (olive, chestnut, and walnut)—which are pervasive in the Mediterranean—also fall into the category of broad-leaf forest. Thus, our capacity to infer changes in forest types in regions with this type of cultivar (e.g., the Mediterranean; ref. 53) is limited.
The decrease in broad-leaf forest (starting around 6,000 y BP) was followed by a minor increase in grassland and disturbed land in some parts of the continent. These vegetation types were naturally present in the Mediterranean and the Black Sea region throughout the earlier part of the Holocene and remained fairly stable until the present (19). In contrast, in western Europe, these vegetation types only reached intermediate levels during the Bronze Age—as YAM ancestry began to increase—and they continued to increase after the end of this period. Furthermore, increases in YAM ancestry in southern and eastern Europe did not coincide with increases in grassland and disturbed land.
Pasture/natural grassland is the only land-cover type that considerably improves in fit as a result of adding ancestry and climate variables into our model. This might be because we currently lack the spatiotemporal resolution to provide much predictive power with the addition of climate or ancestry variables, or because these variables may not be strongly predictive of the other LCCs. Other factors that are not considered here may have had a stronger effect on the landscape. An obvious candidate is the dramatic increase in population density that occurred over the last 3,000 y (24, 54), which likely led to strong changes in land-use practices, consequently disturbing vegetation throughout the continent. Earlier population rises and collapses during the Neolithic and Bronze Age could have also influenced the vegetated landscape in significant ways, although on a smaller scale (51, 52, 55). Thus, a future study could aim to incorporate estimates of human population density or other measures of human activity into explanatory models for changes in vegetation, together with population movement. A recent approach using human land-use estimates, for example, showed that, on a continental scale, climate changes were the main driver of changes in vegetation when the Holocene is considered in its entirety, but the influence of human land use markedly increased from around 4000 BP onward (18).
There are a number of caveats and assumptions in our modeling procedure that are important to keep in mind. Firstly, we are assuming that changes in ancient ancestries can be used as a proxy for long-distance movement of people. This may be the case for particular periods of time—especially when peoples of highly divergent ancestries first met each other—but this assumption loses validity as we move closer to the present and the ancestry components tend to become more homogenized due to later migrations within the area of study (56). Tracing relatively high YAM ancestry in the present day is approximately equivalent to tracing people with high Northern European ancestry, who cannot be equated with ancient “steppe peoples.”
Second, our projection of inferred ancestry components to a spatiotemporal grid does not model processes that cause variation in ancestry proportions within a specific region of space–time. Indeed, local departures from the inferred kriged ancestry proportion in a given region are treated as noise in the kriging model. This fails to account for the fact that some regions (e.g., cosmopolitan centers of trade) may have harbored much more variation in proportions than other regions, in which the proportions may have been more homogeneous. These models also do not account for differences in population density, which could mean that certain migrations or population expansions may have involved much larger numbers of people than others, even if their consequent changes in ancestry proportions may be inferred to be relatively similar in size.
Third, we are relying on existing ancient DNA data, which has its own idiosyncrasies, due to environmental and historical biases in sampling. For example, North Africa and eastern Scandinavia were sparsely sampled in our dataset, so our ancestry estimates for those regions are much poorer than for the rest of the European continent. We attempted to account for these types of biases via a bootstrapping approach and various estimates of error due to temporal and spatial patchiness to assess how robust these were to accidents of sampling (Materials and Methods).
Additionally, we are relying on a particular choice of the number of ancestry clusters or components (K) under a latent mixed-membership model. We chose this model and parameter setting to be able to discretize patterns of ancestry into three major population clusters (HG, NEOL, and YAM), which have been documented via other, more involved, population genetic analyses (2, 13, 14). We also chose a low number of clusters to have enough data points across extended periods of time, in order to accurately estimate the space–time decay in covariance between ancestries (e.g., SI Appendix, Figs. S2 and S3). These clusters are, however, an approximation of a very complex genealogical process. Indeed, the clusters cannot be seen as discrete, originally isolated populations, as there may be both isolation-by-distance and hierarchical population structure within each of these groups (57–59), and it is unclear how incorporating these phenomena would affect the kriging or the RMA speed estimates. In our downstream analyses, we were also assuming that these clusters included groups of people with temporally and spatially self-consistent land-change practices. The clusters themselves were also the result of more complex admixture and migration events that occurred before the Holocene (30). Additionally, there is likely some differentiation in population structure over time and space, even when looking at the same admixture components (e.g., the NEOL component of a present-day Sardinian is differentiated relative to the NEOL component of a Bronze Age central European). These subtle patterns are hard to pick up by simple latent mixed-membership models (34), although there has recently been some progress in this regard (60, 61). Other types of population-genetic frameworks are able to better detect some of these more subtle signals by, for example, modeling patterns of haplotype sharing (62, 63), the full site-frequency spectrum (64, 65), or an approximation to the full ancestral recombination graph (66, 67). Nevertheless, these also have their own limitations and assumptions. For all these reasons, we advise the reader to consider that the ancestry components used in this study are approximations of the true historical admixture process.
Furthermore, in our model relating different ancestries to different land-cover types, we are making a unidirectional causality assumption, as we have a priori chosen ancestries and climate as the explanatory variables and land cover as the response variable. In other words, we are testing how migrations and climate may have affected vegetation. It is also possible that people moved to new environments as a consequence of vegetation or climate changes, or of other environmental factors that we are not studying here.
Finally, it is important to remember that the ancestry proportions exist in a simplex, so increases in one ancestry will proportionally lead to decreases in other ancestries. For this reason, a negative contribution to vegetation from one ancestry (e.g., YAM and broad-leaf forest) coupled with a positive contribution from another ancestry (e.g., HG and broad-leaf forest) may be two manifestations of the same process—change in land cover as a result of change in ancestry—rather than two independent processes.
An improvement to our current approach could involve developing a hierarchical dynamical model for explicitly modeling spatiotemporal movements on the genetic data directly, without relying on ancestry assignments estimated from a nonspatiotemporally aware model (68). This could also help to better deal with boundary constraints that are not accounted for by the kriging methodology. For example, we currently have to correct kriged estimates that are lower than 0 or higher than 1. A generative model of spatiotemporal ancestry would not allow for these types of parameters in the first place, for example, by placing Bayesian priors on ancestry with 0 probability outside of the 0 to 1 range. This could also be solved by extending compositional interpolation techniques to a spatiotemporal setting (69).
Keeping these considerations in mind, the approach developed here is an attempt at combining in an explicit, quantitative framework various categories of evidence, which have otherwise either not been considered together (e.g., ancestry and land-cover type) or have only been compared in a qualitative way. There is a lot of potential for new geostatistical approaches that could be designed to combine various types of datasets in an integrative approach for the study of the past, including at more local scales than considered here. This could encompass, for example, the combination of strontium and oxygen isotope analyses together with radiocarbon data and contextual archaeological information (70, 71), the joint analysis of genetic and linguistic changes over time (72), or the study of the interactions between population density and vegetation (73, 74).
In summary, although our methodology relies upon several assumptions and could benefit from a myriad of extensions, it provides a robust way to account jointly for space and time in the study of genetic and environmental variables. Our results demonstrate that the two major human migrations recorded in Holocene Europe differ markedly in their expansion rates and, possibly, had distinctive implications for the environment in which they unfolded. By explicitly modeling space and time, researchers can move beyond the mere identification of human migrations: We can begin to understand structural differences between and within human dispersal events and study local phenomena that may have unraveled in different ways across an area of study. Otherwise, we might run the risk of overlooking important historical processes by taking an overly global perspective. We should not ignore the forest for the trees, but, sometimes, the trees themselves might be hidden by the forest.
Materials and Methods
All R code used to perform the analyses in this manuscript has been deposited in: https://github.com/FerRacimo/STAdmix.
Kriged Ancestry Maps over Time and Space.
For our ancestry analyses, we used a combined dataset of 842 ancient and 955 present-day genomic sequences. The present-day sequences were obtained by using the Human Origins single nucleotide polymorphism (SNP) array, while the ancient sequences were either obtained via this array or via whole-genome sequencing, followed by filtering for SNPs that are in the array (2, 14, 25, 26). We restricted our analyses to modern human genomes obtained from human remains located within an area encompassing most of the European continent: north of N, south of N, east of W, and west of E. We inferred latent ancestry components on these genomes using Ohana (33).
We performed ordinary global spatiotemporal kriging using the R libraries gstat (38, 39) and spacetime (75) to obtain unbiased linear predictions of ancestry for unsampled locations and times. Suppose we have a set of noisy observations of a variable distributed unevenly across space and time. In our case, this will be the inferred proportion of a particular ancestry in each of our ancient genomes. Let be a vector representing the th site (out of ) in our grid, which is composed of two values: its longitude and latitude. Following the notation by Cressie and Wikle (68), suppose we have different temporal samples of a measured variable at site . A temporal sample obtained at the th time () from this site will be denoted as . Suppose these data are equal to the true spatiotemporal process plus some measurement error :
| [1] |
Let be the vector containing all values that were measured at different time points in location . Also, let , where is the number of locations sampled. We can obtain a linear predictor, , for a particular unsampled data point at time and location :
| [2] |
where and are parameters than can be optimized. In particular, for the case that the true process has a constant unknown mean , one can show that the linear unbiased predictor that minimizes the mean squared prediction error—also called the ordinary kriging predictor—is equal to:
| [3] |
where , , and . The latter can be obtained by fitting a spatiotemporal covariance function for the true process to the empirical spatiotemporal variogram of the observed measurements (SI Appendix, Fig. S2–S5). In our case, the variogram was computed over a range of 3,000 y, with 60-year windows, and we used the “metric” variogram model to fit it (76). For a more extensive explanation of spatiotemporal kriging, we refer the reader to Cressie and Wikle (68).
As our predicted grid, we used a set of spatial points distributed evenly across Europe. We used two types of spatial grids: one containing a dense set of 5,000 points and a sparser set, containing 200 points. We called this our “spatial grid.” The dense version of the spatial grid was used for plotting spatiotemporal maps (e.g., Fig. 5), while the sparse set was used to fit the Bayesian spatiotemporal model (e.g., Fig. 7), for ease of computation. We observed that the ancestry–vegetation and climate–vegetation correlations computed under both schemes were almost identical, suggesting that the use of the sparser grid should not affect inference under the Bayesian model. Potential biases arising from particular grid points possessing few nearby ancient genomes were accounted for in the bootstrapping method described below. Unless otherwise stated, our “temporal” grid had a 10,800-y span, with intervals of 600 y until the present, for a total of 19 time slices. Thus, if our spatial grid had spatial points, our “spatiotemporal grid” had spatiotemporal points. We bounded the kriged ancestry values between 0 and 1, and so kriged values that were negative were set to 0, and those that were larger than 1 were set to 1.
In all analyses below, we did not include a kriged ancestry component that is largely restricted to north Africa and the Fertile Crescent (NAF). The reasons for this were twofold: 1) This ancestry remained largely spatially static throughout the Holocene, at least with respect to the box we defined to bound our analyses; and 2) given that all latent ancestries must add up to 1 in each individual genome, this ancestry was equal to 1 minus the sum of the other three ancestries, and was therefore not linearly independent from them. This component was absent from Europe until the end of our temporal transect, where it surfaced in parts of central Europe, because of the presence of Ashkenazi Jewish genomes in our present-day dataset.
Assessment of Quality of Kriged Maps.
To assess the robustness of our kriged maps, we bootstrapped our data by sampling with replacement from the set of all genomes 100 times and recomputed the spatiotemporal kriging each time. This way, we obtained BBCIs for each predicted ancestry at all spatiotemporal grid points (SI Appendix, Figs. S15–S18).
To assess the effects of spatial patchiness in our data, we divided our map into 16 4 × 4 square sectors. We then computed, for each sector, the mean absolute error (MAE) of the kriged ancestry of the nearest spatiotemporal grid point of each ancient genome inside that sector, relative to the true (Ohana-inferred) ancestry of the genome. In SI Appendix, Fig. S19, Left, the kriged ancestry was obtained by kriging the complete dataset. Here, we observed that our kriging predictions were very accurate (MAE across all patches), regardless of the part of the map that we chose to focus on. In SI Appendix, Fig. S19, Right, the kriged ancestry was obtained by kriging a version of the dataset in which all genomes within that sector had been previously removed. Here, our MAE was considerably larger, especially for the YAM and NAF ancestries in northern Europe and Anatolia, suggesting that local genomes are especially important to include in order to derive accurate predictions in these regions.
To assess the effects of temporal patchiness in our data, we also divided our 10,800-y timeline into 10 periods of equal duration (1,080 y). Analogously to the previous analysis, we selected each of the periods in turn and computed, for each period, the MAE of the kriged ancestry of the nearest spatiotemporal grid point of each genome within that period, relative to the true ancestry of each ancient genome. In SI Appendix, Fig. S20, Left, the kriged ancestry was obtained by kriging using the entire dataset. As in the spatial patch analysis, our predictions were very accurate (MAE across all slices). In SI Appendix, Fig. S20, Right, the kriged ancestry was obtained by kriging a version of the dataset in which all genomes within that period had been previously removed. In this case, the predictions were less accurate, with particularly inaccurate predictions for NEOL and HG ancestries in the oldest time slices and for all ancestries in the most recent time slice, suggesting that there were ancestry changes during these periods that were poorly predicted by using ancestries from adjacent periods.
Paleovegetation Maps.
We downloaded inferred Holocene paleovegetation spatiotemporal maps (19). These paleovegetation reconstructions were built from 982 pollen records across Europe, using the pseudobiomization method (PBM) (77). They have a 10,800-y span, with intervals of 200 y until the present. To ease computation, we sampled every three time windows, resulting in intervals of 600 y until the present, and for each paleovegetation time slice, we rasterized the maps to have 6,540 points (down from 35,856). Then, for each time slice, we inferred the value of each point in our spatial grid by taking the median of the five nearest points in the rasterized maps.
Paleoclimate Maps.
We obtained a set of simulation-based Holocene paleoclimate reconstructions for Europe from PaleoClim (40), which includes surface temperature and precipitation estimates for the Early (11.7 to 8.326 thousand years ago [kya]), Middle (8.326 to 4.2 kya), and Late Holocene (4.2 to 0.3 kya), using snapshot-style climate model simulations. These simulations were accessed through PaleoView (78) and come from the TRaCE21ka experiment (79, 80), which used the Community Climate System Model (Version 3) (81–83), a general circulation model involving atmosphere, ocean, sea ice, and land. The PaleoClim authors refined the simulations from this model, incorporating small-scale topographic nuances of regional climatologies, thus creating high-resolution paleoclimate maps. We projected the three Holocene maps—together with the present-day WorldClim map (84)—onto the previously delineated temporal grid for each of the 19 climate variables that were present in the PaleoClim database. At each time slice, for each point in the spatial grid, we inferred the value of each climate variable, by taking a weighted average of the values of the two closest bounding paleoclimate time points (past and future) at that spatial point, weighted by their respective temporal distance to our time slice. These allowed us to obtain a spatiotemporal grid of the climate variables at the same locations and times for which we had kriged ancestry and paleovegetation data. In the Bayesian hierarchical model, we excluded one of these variables (temperature annual range) because it was a linear combination of two of the other climate variables.
Computation of Correlations.
We computed Pearson correlations between the kriged ancestry, climate, and vegetation variables in three ways. First, we simply took the vector containing the values of one variable across all points in our spatiotemporal grid and computed its correlation with the values of another variable at all of the same spatiotemporal points. We call these the “raw correlations” (SI Appendix, Fig. S8). Second, starting from the second oldest time slice, we took each of the values of a particular variable of a time slice and subtracted from them the values of the same variable at the same location, but from the immediately previous time slice. We did this for all variables and then computed their pairwise correlations, which we call the “correlations in differences” (SI Appendix, Fig. S9). Finally, we took each of the values of a particular variable of a time slice and subtracted from them the values of the same variable at the same location, but from the last (present-day) time slice. We then computed pairwise correlation between the resulting values for each of the variables, excluding the last time slice from the analysis (as it would just contain zeroes). We call these the “correlations in anomalies,” in the sense that the resulting values represent anomalies of a variable with respect to its present-day value at a given location (SI Appendix, Fig. S10).
We also computed the correlation between the difference in ancestry in a time window and the difference in vegetation one (or two) time window(s) later (SI Appendix, Fig. S11). In other words, for each time slice and spatial grid point , let be the difference in ancestry between time and time at spatial point , let be the difference in vegetation between time and time at spatial point , and let be the difference in vegetation between time and time . We computed the correlation between and , and also between and across all spatial grid points and all time slices , for each ancestry–vegetation pair.
Spatiotemporal Bayesian Modeling of Vegetation Anomalies.
We used two hierarchical spatiotemporal Bayesian models implemented in the R library spTimer (41) in order to jointly model climate and kriged ancestry anomalies as explanatory variables for vegetation-type anomalies. To simplify notation, we will now index time with the variable and assume that all sites have observations at the same time slices, i.e., for all sites . We will suppose we have sites, and so is the total number of spatiotemporal observations. The first of the spatiotemporal models treats the response variable —in our case, containing all vegetation-type values in our spatial map at time —as a noisy observation of a GP :
| [4] |
| [5] |
Here, is a vector of coefficients, is a matrix of covariates at time , is an error vector that only depends on an unknown pure error variance :
| [6] |
while is a spatiotemporal nugget vector that is independent of and whose distribution depends on a site-invariant spatial variance and the spatial correlation matrix :
| [7] |
The correlation matrix is obtained from the general Matérn correlation function (85), whose shape depends on two unknown parameters— and . These control the rate of decay of the correlation as the distance between sites increases and the smoothness of the random field, respectively (41).
The second model is a temporal autoregressive model that works by incorporating a term in Eq. 7 that depends on the previous instance of the process and a temporal correlation parameter :
| [8] |
spTimer can fit these models via Gibbs sampling and infer the posterior distribution of the unknown parameters , , and . We used spTimer’s default prior distributions for these parameters (described in ref. 41). Before inputting all explanatory and response variables into either model, we first centered and scaled them to have mean 0 and variance 1. We tried three different types of prior distributions for the spatial-decay parameter of the Matérn correlation function (SI Appendix, Fig. S13)—a fixed value, a Uniform distribution and a Gamma distribution, each with default hyperparameters—and compared their performance using the RMSE of the predictions (see below).
Assessment of Error of Hierarchical Model.
We randomly removed of the grid points in the map and fitted a spatiotemporal model to the remaining portion of the data. We computed the RMSE by comparing the predicted values across all temporal slices with the previously removed observed values. We then selected the spatiotemporal model (AR vs. GP) and the prior distribution for the spatial decay parameter of the Matérn correlation function (fixed value vs. Uniform vs. Gamma) based on visual comparison of the RMSE plots for each of these model choices (SI Appendix, Fig. S13) (41).
Predictive Model Choice Criterion.
We used the predictive model choice criterion (42) to compare different hierarchical Bayesian models. The criterion is implemented in spTimer (41) and is based on the concept of the posterior predictive distribution of a model, given a fitted dataset:
| [9] |
where is a vector containing all of the parameters of the model, is the dataset used for fitting, and is a replicated dataset. In our case, constitutes the land-cover scores at all fitted spatiotemporal grid points, while includes the ancestry and climate coefficients, as well as spatiotemporal decay parameters. The posterior predictive distribution can be estimated by:
| [10] |
where denotes the th Monte Carlo sample of . The PMCC is then defined as:
| [11] |
where and are the expectation and the variance of a replicate coming from the posterior predictive distribution. In practice, these are obtained from the aforementioned estimate of this distribution. The first term of the sum serves as a goodness-of-fit score, while the second term is a penalty score, which tends to be large for both underfitted and overfitted models.
Nonparametric Bootstrapping of Parameter Estimates.
The Gibbs sampler allows us to obtain posterior estimates and posterior credible intervals of the parameters relating the explanatory to the response variables. However, it relies on the kriged ancestry grid-point maps as input, so it does not account for the uncertainty in the estimation of these maps from the ancient genomes that we currently have. To address this, we derived CIs on the Bayesian posterior estimates using a nonparametric bootstrapping approach. We created 100 pseudo-samples, by randomly sampling ancient and present-day genomes 100 times—with replacement—from among the list of all ancient and present-day genomes, then obtaining their ancestry assignments and kriging them on the spatiotemporal grid. We then fitted the Bayesian spatiotemporal model to each pseudo-sample and, thus, obtained a distribution of bootstrapped parameter estimates, from which we obtained CIs.
Arrival Time Maps.
We first created ancestry arrival time maps by recording the time in each cell of the spatial grid at which the spatiotemporal surface map first reaches a value higher than a particular kriged ancestry proportion cutoff (SI Appendix, Fig. S21). In this case, we used a spatial grid of 5,000 points and 200-y time intervals. We found that these maps contain large proportions of missing data, in regions where an ancestry never reached the ancestry cutoff throughout the duration of the timeline. To correct for this, we instead recorded the times at which a particular ancestry first reached a value higher than , where is a chosen percentage cutoff for a particular ancestry and is the maximum value that ancestry reaches at a spatial point throughout the duration of the timeline (Fig. 8). Spatial points where is less than were kept blank.
To create the cultural arrival maps for the spread of farming, we overlaid a 50- × 50-km map covering Europe and selected, for each square, the oldest radiocarbon date directly associated with early farming. The dataset we used to obtain these dates came from the EUROFARM database, which contains 1,779 records of archaeological farming sites (downloadable at https://github.com/mavdlind/Geostat_Farmer). It was then spatially kriged by using the spatstat package (86) in R (87).
Front-Speed Estimation.
To estimate the front speed of the spread of NEOL and YAM ancestries, we regressed great-circle distances of sampled locations to a hypothesized migration origin against the time at which the migration reached those locations (5, 8). The negative inverse of the slope was then an estimate of the migration front speed. We restricted to genomes older than 5,000 y BP for the NEOL ancestry spread and to genomes older than 3,000 y BP for the YAM ancestry spread. We used Cayönü (37.38N, 40.39E) as the NEOL ancestry origin, based on estimates of the Neolithic farmer expansion origin (5, 8). We set various points at the center and extremes of the hypothesized original Yamnaya distribution in the Eurasian steppe as the YAM ancestry origin (SI Appendix, Table S2). We used an RMA regression approach implemented in the R package lmodel2 (88), which assumed a symmetrical distribution of measurement error in both distance and time.
Supplementary Material
Acknowledgments
We thank John Novembre, Rasmus Nielsen, Michael K. Borregaard, Mark G. Thomas, David Wesolowski, and Kurt H. Kjær for helpful advice and discussions. We also thank three anonymous reviewers for their helpful comments on the manuscript. F.R. was supported by Villum Fonden Young Investigator Award Project 00025300. The paleovegetation research was funded by Leverhulme Trust Grants RPG-2015-031 and F00568W. We gratefully acknowledge contributors to the European Pollen Database. We also thank the Lundbeck Fundation and the Novo Nordisk Foundation for their support of the GeoGenetics Centre.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. T.G. is a guest editor invited by the Editorial Board.
Data deposition: All R code used to perform the analyses in this manuscript has been deposited at GitHub (https://github.com/FerRacimo/STAdmix).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1920051117/-/DCSupplemental.
References
- 1.Sikora M., et al. , Population genomic analysis of ancient and modern genomes yields new insights into the genetic ancestry of the Tyrolean Iceman and the genetic structure of Europe. PLoS Genet. 10, e1004353 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lazaridis I., et al. , Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature 513, 409–413 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lazaridis I., et al. , Genomic insights into the origin of farming in the ancient Near East. Nature 536, 419–424 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ammerman A. J., Cavalli-Sforza L. L., Measuring the rate of spread of early farming in Europe. Man 6, 674–688 (1971). [Google Scholar]
- 5.Silva F., Steele J., New methods for reconstructing geographical effects on dispersal rates and routes from large-scale radiocarbon databases. J. Archaeol. Sci. 52, 609–620 (2014). [Google Scholar]
- 6.Fort J., “The neolithic transition: Diffusion of people or diffusion of culture?” in Diffusive Spreading in Nature, Technology and Society, Bunde A., Caro J., Kärger J., Vogl G., Eds. (Springer, Berlin, Germany, 2018), pp. 313–331. [Google Scholar]
- 7.Fort J., Demic and cultural diffusion propagated the neolithic transition across different regions of Europe. J. R. Soc. Interface 12, 20150166 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pinhasi R., Fort J., Ammerman A. J., Tracing the origin and spread of agriculture in Europe. PLoS Biol. 3, e410 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vander Linden M., Silva F., Comparing and modeling the spread of early farming across Europe. PAGES Mag. 26, 28–29 (2018). [Google Scholar]
- 10.Anthony D. W., The Horse, the Wheel, and Language: How Bronze-Age Riders from the Eurasian Steppes Shaped the Modern World (Princeton University Press, Princeton, NJ, 2010). [Google Scholar]
- 11.Shishlina N. I., Reconstruction of the Bronze Age of the Caspian Steppes: Life Styles and Life Ways of Pastoral Nomads (British Archaeological Reports Ltd., Oxford, UK, 2008). [Google Scholar]
- 12.Kristiansen K., Larsson T. B., The Rise of Bronze Age Society: Travels, Transmissions and Transformations (Cambridge University Press, Cambridge, UK, 2005). [Google Scholar]
- 13.Haak W., et al. , Massive migration from the steppe was a source for Indo-European languages in Europe. Nature 522, 207–211 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Allentoft M. E., et al. , Population genomics of Bronze Age Eurasia. Nature 522, 167–172 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Olalde I., et al. , The Beaker phenomenon and the genomic transformation of northwest Europe. Nature 555, 190–196 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vandkilde H., Culture and Change in Central European Prehistory (Aarhus University Press, Aarhus, Denmark, 2007). [Google Scholar]
- 17.Roberts N., et al. , Europe’s lost forests: A pollen-based synthesis for the last 11,000 years. Sci. Rep. 8, 716 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marquer L., et al. , Quantifying the effects of land use and climate on Holocene vegetation in Europe. Quat. Sci. Rev. 171, 20–37 (2017). [Google Scholar]
- 19.Fyfe R. M., Woodbridge J., Roberts N., From forest to farmland: Pollen-inferred land cover change across Europe using the pseudobiomization approach. Global Change Biol. 21, 1197–1212 (2015). [DOI] [PubMed] [Google Scholar]
- 20.Nielsen A. B., et al. , Quantitative reconstructions of changes in regional openness in north-central Europe reveal new insights into old questions. Quat. Sci. Rev. 47, 131–149 (2012). [Google Scholar]
- 21.Fyfe R. M., et al. , The Holocene vegetation cover of Britain and Ireland: Overcoming problems of scale and discerning patterns of openness. Quat. Sci. Rev. 73, 132–148 (2013). [Google Scholar]
- 22.Bishop R. R., Church M. J., Rowley-Conwy P. A., Firewood, food and human niche construction: The potential role of Mesolithic hunter–gatherers in actively structuring Scotland’s woodlands. Quat. Sci. Rev. 108, 51–75 (2015). [Google Scholar]
- 23.Warren G., Davis S., McClatchie M., Sands R., The potential role of humans in structuring the wooded landscapes of Mesolithic Ireland: A review of data and discussion of approaches. Veg. Hist. Archaeobot. 23, 629–646 (2014). [Google Scholar]
- 24.Roberts C. N., et al. , Mediterranean landscape change during the Holocene: Synthesis, comparison and regional trends in population, land cover and climate. Holocene 29, 923–937 (2019). [Google Scholar]
- 25.Mathieson I., et al. , Genome-wide patterns of selection in 230 ancient Eurasians. Nature 528, 499–503 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Patterson N., et al. , Ancient admixture in human history. Genetics 192, 1065–1093 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mathieson I., et al. , The genomic history of southeastern Europe. Nature 555, 197–203 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Olalde I., et al. , A common genetic origin for early farmers from Mediterranean Cardial and central European LBK cultures. Mol. Biol. Evol. 32, 3132–3142 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lipson M., et al. , Parallel palaeogenomic transects reveal complex genetic history of early European farmers. Nature 551, 368–372 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fu Q., et al. , The genetic history of Ice Age Europe. Nature 534, 200 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hofmanová Z., et al. , Early farmers from across Europe directly descended from Neolithic Aegeans. Proc. Natl. Acad. Sci. U.S.A. 113, 6886–6891 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Skoglund P., et al. , Genomic diversity and admixture differs for stone-age Scandinavian foragers and farmers. Science 344, 747–750 (2014). [DOI] [PubMed] [Google Scholar]
- 33.Cheng J. Y., Mailund T., Nielsen R., Fast admixture analysis and population tree estimation for SNP and NGS data. Bioinformatics 33, 2148–2155 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lawson D. J., Van Dorp L., Falush D., A tutorial on how not to over-interpret structure and admixture bar plots. Nat. Commun. 9, 3258 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Skoglund P., et al. , Origins and genetic legacy of Neolithic farmers and hunter-gatherers in Europe. Science 336, 466–469 (2012). [DOI] [PubMed] [Google Scholar]
- 36.Sánchez-Quinto F., et al. , Genomic affinities of two 7,000-year-old Iberian hunter-gatherers. Curr. Biol. 22, 1494–1499 (2012). [DOI] [PubMed] [Google Scholar]
- 37.Hunt H. V., et al. , Genetic evidence for a western Chinese origin of broomcorn millet (Panicum miliaceum). Holocene 28, 1968–1978 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pebesma E. J., Multivariable geostatistics in S: The gstat package. Comput. Geosci. 30:683–691 (2004). [Google Scholar]
- 39.Pebesma E., Heuvelink G., Spatio-temporal interpolation using gstat. RFID J. 8, 204–218 (2016). [Google Scholar]
- 40.Brown J. L., Hill D. J., Dolan A. M., Carnaval A. C., Haywood A. M., Paleoclim, high spatial resolution paleoclimate surfaces for global land areas. Sci. Data 5, 180254 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bakar K. S., Sahu S. K., sptimer: Spatio-temporal Bayesian modelling using R. J. Stat. Softw. 63, 1–32 (2015). [Google Scholar]
- 42.Gelfand A. E., Ghosh S. K., Model choice: A minimum posterior predictive loss approach. Biometrika 85, 1–11 (1998). [Google Scholar]
- 43.Bickle P., Whittle A., The First Farmers of Central Europe: Diversity in LBK Lifeways (Oxbow Books, Oxford, UK, 2013). [Google Scholar]
- 44.Barnett W. K., “Cardial pottery and the agricultural transition in Mediterranean Europe” in Europe’s First Farmers, Price T. D., Ed. (Cambridge University Press, Cambridge, UK, 2000), pp. 93–116. [Google Scholar]
- 45.Binder D., et al. , Modelling the earliest north-western dispersal of Mediterranean impressed wares: New dates and Bayesian chronological model. Doc. Praehist. 44, 54–77 (2018). [Google Scholar]
- 46.Manen C., et al. , The Neolithic transition in the western Mediterranean: A complex and non-linear diffusion process—the radiocarbon record revisited. Radiocarbon 61, 531–571 (2019). [Google Scholar]
- 47.Schauer P., et al. , Supply and demand in prehistory? Economics of Neolithic mining in northwest Europe. J. Anthropol. Archaeol. 54, 149–160 (2019). [Google Scholar]
- 48.Müller J., et al. , A revision of corded ware settlement pattern—new results from the central European low mountain range Proc. Prehistoric Soc. 75, 125–142 (2009). [Google Scholar]
- 49.Seregély T., Müller J., Endneolithische siedlungsstrukturen in oberfranken II. Wattendorf-Motzenstein: eine schnurkeramische siedlung auf der nördlichen frankenalb. Naturwissenschaftliche Ergebnisse und Rekonstruktion des schnurkeramischen Siedlungswesens in Mitteleuropa (Universitätsforschungen zur prähistorichen Archäologie 155), Bonn: Habelt (2008).
- 50.Jacomet S., “Subsistenz und Landnutzung während des 3. Jahrtausends v. Chr. aufgrund von archäobotanischen Daten aus dem südwestlichen Mitteleuropa” in Umwelt - Wirtschaft - Siedlungen in dritten vorchristlichen Jahrtausend Mitteleuropas und Südskandinaviens, W. Dörfler, J. Müller Eds. (Offa-Bücher 84. Neumünster, 2008) pp. 355–377.
- 51.Woodbridge J., et al. , The impact of the Neolithic agricultural transition in Britain: A comparison of pollen-based land-cover and archaeological 14C date-inferred population change. J. Archaeol. Sci. 51, 216–224 (2014). [Google Scholar]
- 52.Lechterbeck J., et al. , Is Neolithic land use correlated with demography? An evaluation of pollen-derived land cover and radiocarbon-inferred demographic change from central Europe. Holocene 24, 1297–1307 (2014). [Google Scholar]
- 53.Woodbridge J., Roberts N., Fyfe R., Pan-Mediterranean Holocene vegetation and land-cover dynamics from synthesized pollen data. J. Biogeogr. 45, 2159–2174 (2018). [Google Scholar]
- 54.Bevan A., et al. , Holocene fluctuations in human population demonstrate repeated links to food production and climate. Proc. Natl. Acad. Sci. U.S.A. 114, E10524–E10531 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Shennan S., et al. , Regional population collapse followed initial agriculture booms in mid-Holocene Europe. Nat. Commun. 4, 2486 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Margaryan A., et al. , Population genomics of the Viking world. bioRxiv:10.1101/703405 (17 July 2019).
- 57.Frantz A., Cellina S., Krier A., Schley L., Burke T., Using spatial Bayesian methods to determine the genetic structure of a continuously distributed population: Clusters or isolation by distance?. J. Appl. Ecol. 46, 493–505 (2009). [Google Scholar]
- 58.Janes J. K., et al. , The k = 2 conundrum. Mol. Ecol. 26, 3594–3602 (2017). [DOI] [PubMed] [Google Scholar]
- 59.Battey C., Ralph P. L., Kern A. D., Space is the place: Effects of continuous spatial structure on analysis of population genetic data. bioRxiv:10.1101/659235 (3 June 2019). [DOI] [PMC free article] [PubMed]
- 60.Joseph T. A., Pe’er I., “Inference of population structure from ancient DNA” in International Conference on Research in Computational Molecular Biology, Raphael B., Ed. (Lecture Notes in Computer Science, Springer, Cham, Switzerland, 2018), vol. 10812, pp. 90–104. [Google Scholar]
- 61.Bradburd G. S., Coop G. M., Ralph P. L., Inferring continuous and discrete population genetic structure across space. Genetics 210, 33–52 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hellenthal G., et al. , A genetic atlas of human admixture history. Science 343, 747–751 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Lawson D. J., Hellenthal G., Myers S., Falush D., Inference of population structure using dense haplotype data. PLoS Genet. 8, e1002453 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Excoffier L., Dupanloup I., Huerta-Sánchez E., Sousa V. C., Foll M., Robust demographic inference from genomic and SNP data. PLoS Genet. 9, e1003905 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kamm J., Terhorst J., Durbin R., Song Y. S., Efficiently inferring the demographic history of many populations with allele count data. J. Am. Stat. Assoc., 1–16 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kelleher J., Wong Y., Albers P., Wohns A. W., McVean G., Inferring the ancestry of everyone. bioRxiv:10.1101/458067 (1 November 2018).
- 67.Speidel L., Forest M., Shi S., Myers S., A method for genome-wide genealogy estimation for thousands of samples. bioRxiv:10.1101/550558 (14 February 2019). [DOI] [PMC free article] [PubMed]
- 68.Cressie N., Wikle C. K., Statistics for Spatio-Temporal Data (John Wiley & Sons, New York, NY, 2015). [Google Scholar]
- 69.Walvoort D. J., de Gruijter J. J., Compositional kriging: A spatial interpolation method for compositional data. Math. Geol. 33, 951–966 (2001). [Google Scholar]
- 70.Sjögren K. G., Price T. D., Kristiansen K., Diet and mobility in the corded ware of central Europe. PloS One 11, e0155083 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Mittnik A., et al. , Kinship-based social inequality in Bronze Age Europe. Science 366, 731–734 (2019). [DOI] [PubMed] [Google Scholar]
- 72.Kristiansen K., et al. , Re-theorising mobility and the formation of culture and language among the Corded Ware culture in Europe. Antiquity 91, 334–347 (2017). [Google Scholar]
- 73.Müller J., “Eight million Neolithic Europeans: Social demography and social archaeology on the scope of change—from the Near East to Scandinavia” in Paradigm Found: Archaeological Theory Present Past and Future: Essays in Honour of Evžen Neustupnỳ, Kristiansen K, Šmejda L., Turek J., Eds. (Oxbow, Oxford, UK, 2015), pp. 200–214. [Google Scholar]
- 74.Kolář J., et al. , Population and forest dynamics during the central European Eneolithic (4500–2000 BC). Archaeol. Anthropol. Sci. 10, 1153–1164 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Pebesma E., et al. , spacetime: Spatio-temporal data in R. J. Stat. Softw. 51, 1–30 (2012).23504300 [Google Scholar]
- 76.Gräler B., Pebesma E., Heuvelink G., Spatio-temporal geostatistics using gstat. R J. 8, 204–218 (2015). [Google Scholar]
- 77.Fyfe R., Roberts N., Woodbridge J., A pollen-based pseudobiomisation approach to anthropogenic land-cover change. Holocene 20, 1165–1171 (2010). [Google Scholar]
- 78.Fordham D. A., et al. , Paleoview: A tool for generating continuous climate projections spanning the last 21,000 years at regional and global scales. Ecography 40, 1348–1358 (2017). [Google Scholar]
- 79.Liu Z., et al. , Transient simulation of last deglaciation with a new mechanism for Bølling-Allerød warming. Science 325, 310–314 (2009). [DOI] [PubMed] [Google Scholar]
- 80.Liu Z., et al. , Evolution and forcing mechanisms of El Niño over the past 21,000 years. Nature 515, 550–553 (2014). [DOI] [PubMed] [Google Scholar]
- 81.Otto-Bliesner B. L., et al. , Climate sensitivity of moderate-and low-resolution versions of CCSM3 to preindustrial forcings. J. Clim. 19, 2567–2583 (2006). [Google Scholar]
- 82.Collins W. D., et al. , The community climate system model version 3 (CCSM3). J. Clim. 19, 2122–2143 (2006). [Google Scholar]
- 83.Yeager S. G., Shields C. A., Large W. G., Hack J. J., The low-resolution CCSM3. J. Clim. 19, 2545–2566 (2006). [Google Scholar]
- 84.Fick S. E., Hijmans R. J., Worldclim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315 (2017). [Google Scholar]
- 85.Matérn B., Spatial Variation (Lecture Notes in Statistics, Springer, Berlin, Germany, 1986), Vol. 36. [Google Scholar]
- 86.Baddeley A. J., Turner R., Spatstat: An R package for analyzing spatial point patterns. J. Statist. Software, 10.18637/jss.v012.i06 (2005). [DOI]
- 87.R Core Team , R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2019). [Google Scholar]
- 88.Borcard D., Gillet F., Legendre P., Numerical Ecology with R (Springer, Berlin, Germany, 2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.