Scaling up psychology via Scientific Regret Minimization

Significance

Behavioral scientists need a principled methodology for working with large datasets. We offer an exploratory approach that combines ideas from machine learning and psychology, and we conduct a case study in the domain of moral reasoning. We demonstrate that our approach allows us to both build a powerful and interpretable computational model, and identify subtle principles humans employ in moral dilemmas. The method we offer can be applied in any field with large datasets.

Abstract

Do large datasets provide value to psychologists? Without a systematic methodology for working with such datasets, there is a valid concern that analyses will produce noise artifacts rather than true effects. In this paper, we offer a way to enable researchers to systematically build models and identify novel phenomena in large datasets. One traditional approach is to analyze the residuals of models—the biggest errors they make in predicting the data—to discover what might be missing from those models. However, once a dataset is sufficiently large, machine learning algorithms approximate the true underlying function better than the data, suggesting, instead, that the predictions of these data-driven models should be used to guide model building. We call this approach “Scientific Regret Minimization” (SRM), as it focuses on minimizing errors for cases that we know should have been predictable. We apply this exploratory method on a subset of the Moral Machine dataset, a public collection of roughly 40 million moral decisions. Using SRM, we find that incorporating a set of deontological principles that capture dimensions along which groups of agents can vary (e.g., sex and age) improves a computational model of human moral judgment. Furthermore, we are able to identify and independently validate three interesting moral phenomena: criminal dehumanization, age of responsibility, and asymmetric notions of responsibility.

The standard methodology in psychological research is to identify a real-world behavior, create a laboratory paradigm that can induce that behavior, and then test a variety of hypotheses on a group of participants. This methodology was first pioneered over 100 y ago and remains the de facto approach today. While it enables researchers to dissociate individual variables of interest, it can also lead to overfixation on a specific paradigm and the small amount of variations it offers in contrast to more broadly sampling the space of experiments relevant to the behavior of interest. As a result, several researchers have started to call for a shift toward mining massive online datasets via crowdsourced experiments (1–8), because the scale offered by the Internet enables scientists to quickly evaluate thousands of hypotheses on millions of participants.

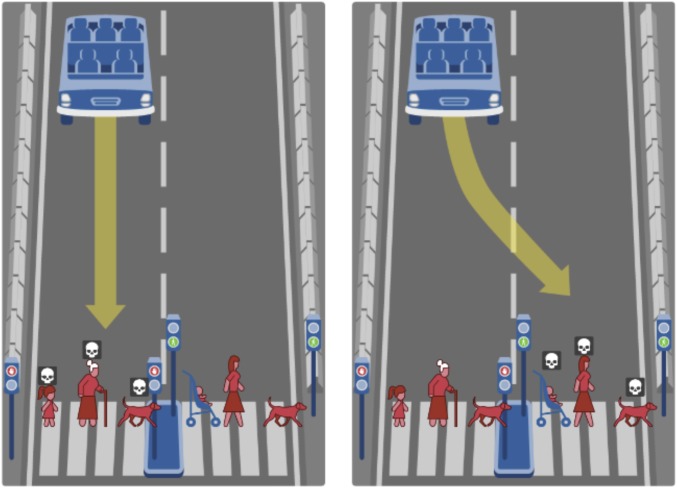
The Moral Machine experiment (7) is one recent example of a large-scale online study. Modeled after the trolley car dilemma (9–11), this paradigm asks participants to indicate how autonomous cars should act when forced to make life-and-death decisions. In particular, participants were presented with two types of dilemmas: pedestrians versus pedestrians, in which an empty car must choose between killing two sets of pedestrians (Fig. 1), and passengers versus pedestrians (not shown), in which a car must choose between saving its passengers or a group of pedestrians. The Moral Machine experiment collected roughly 40 million decisions from individuals in over 200 countries, making it the largest moral reasoning experiment ever conducted. In addition to the vast number of judgments collected, the experiment operated over a rich problem space: The many possible combinations of 20 different types of agents (e.g., man, girl, female doctor, dog) as well as contextual information (position of the car, crossing signal) resulted in millions of unique dilemmas being presented to participants. With all these variations, the question thus becomes: for any given dilemma, do participants prefer the car to stay or swerve? Furthermore, what factors influence each decision?

Fig. 1.

A sample moral dilemma using the Moral Machine paradigm (7). Here, the participant must choose whether an empty car should stay and kill a girl, old woman, and a dog, who are all illegally crossing, or whether the car should swerve and kill an infant, a woman, and a dog, who are all legally crossing.

Psychologists have developed a standard statistical approach for analyzing behavioral data to answer such questions: Identify all of the possible predictors for an individual’s decision and fit a model using these predictors. By analyzing the statistical significance of each predictor or an overall model metric that penalizes complexity [e.g., the Akaike information criterion (AIC) (12)], the researcher finds a model that best trades off model complexity with accuracy. Unfortunately, this approach does not scale well with large datasets. Statistical significance is achieved with lower effect sizes in large samples, and complexity penalties are dominated by measures of fit such as the log-likelihood. As a result, when the dataset is sufficiently large, this approach will always favor the more complex model even if the increase in predictive accuracy per data point is trivial, making it difficult to gain insights into the data.

An even stronger critique of this approach is that it assumes prior knowledge of the relevant predictors. In the Moral Machine dataset, the question is not just how important the different factors might be to making moral judgments but what these factors are to begin with. This suggests the need for exploratory data analysis, a ”detective-like” methodology of generating and evaluating hypotheses (13, 14). One may try to test all possible interactions, but there can easily be an exponential blowup in the number of parameters, reducing the interpretability and thus the explanatory power of the model. For example, a naive featurization of the Moral Machine dataset results in more than $\mathrm{11,000}$ three-way interactions. Given that the Moral Machine dataset allows 40-way interactions and the relevant predictors may be complex nonlinear functions of the lower-level features, this approach would be difficult to implement in practice. What is needed is an efficient and systematic way of conducting exploratory data analyses in large datasets to identify interesting behaviors and the features that give rise to them.

Understanding the Moral Machine dataset in this manner is simply a microcosm of the broader scientific enterprise. Consider a scientist interested in moral psychology. How does she contribute to the field? She reads papers and combines that knowledge with her own personal experiences, building an internal model that can predict behaviors in different settings. In parallel, she reads the scientific literature to find models that explain these effects. Then, by analyzing the differences between her own mental model and the literature, she either proposes an explanation for a known phenomenon or hypothesizes a novel effect. She conducts an experiment that evaluates her claim and continues this scientific process again.

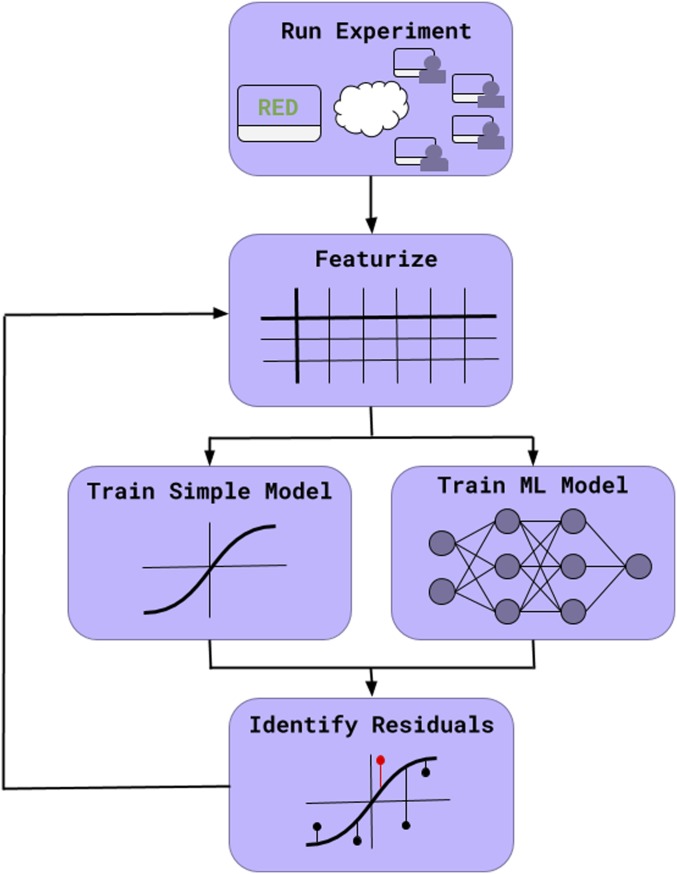
We believe large datasets should be tackled in the same way, and we formalize this intuition in a process we call “Scientific Regret Minimization” (SRM), by analogy to the notion of regret minimization in machine learning (15). First, we suggest that researchers should leverage the size of large datasets to train theoretically unconstrained machine learning models to identify the amount of variance in the dataset that can be explained (16–20). Next, because these models do not necessarily give insight to the underlying cognitive processes, a simple and interpretable psychological model should be fit on the same dataset. Researchers should then critique the psychological model with respect to the black box model rather than the data. The intuition here is that the psychological model should only be penalized for incorrectly predicting phenomena that are predictable (i.e., we should pay close attention to those errors that result in regret). This critiquing process should continue until the predictions of both models converge, thereby ending with a model that jointly maximizes predictive and explanatory power. The residuals from this process may correspond to novel effects, and one can run separate experiments that independently validate them. A summary of this approach is outlined in Fig. 2.

Fig. 2.

SRM. After collecting a large dataset, we use machine learning models to separate the signal from the noise. We then critique psychological models with respect to the signal identified by the machine learning model and continue doing so until both of the models converge.

The method of refining models by analyzing their errors (also known as “residuals”) is often employed in exploratory data analysis (21–23). In this paradigm, researchers begin by proposing a model and fitting it to the data. By looking at the inputs where the model’s predictions and the data diverge, they attempt to identify new relevant features that will hopefully increase the model’s accuracy. They then incorporate these new features into the model, fit it to the data, and continue repeating the process.

Our approach is different because we suggest that, once the dataset is sufficiently large, models should be critiqued with respect to a powerfully predictive model rather than the data. Critiquing with respect to the data in large datasets can be difficult because the largest residuals often reflect noise. Formally, let $f\left(x\right)$ be the true function we are trying to understand, and let the data be $y=f\left(x\right)+ϵ$, where $ϵ\sim \mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)$. Furthermore, let us assume we are trying to predict the data with a psychological model $g\left(x\right)$. The expected squared residual between the psychological model and the data is

$$\underset{p\left(x,y\right)}{\mathbb{E}}{[y-g\left(x\right)]}^2=\underset{p\left(x\right)}{\mathbb{E}}\left[{\left(f\left(x\right)-g\left(x\right)\right)}^2\right]+{\sigma }_{ϵ}^2.$$ [1]

That is, the expected residual between the model and the data, $y-g\left(x\right)$, will be the true residual, $f\left(x\right)-g\left(x\right)$, plus a term that captures the noise variance. (Derivations of all results appear in Materials and Methods.) Throughout this paper, we will refer to the residuals between the model and data as the raw residuals. Eq. 1 indicates that the correlation between the raw residuals and the true residuals will have an upper bound determined by the noise variance, thus highlighting an important problem with using them to guide model building. The manual process of critiquing models with respect to the raw residuals often focuses on using the largest $k$ residuals to formulate new predictors. However, as the number of unique inputs increases, these $k$ residuals will mostly reflect noise, because $\mathbb{E}\left[max\left|ϵ\right|\right]$ increases as well.

If we think back to our hypothetical scientist, she is analyzing the differences between her internal model and the psychological models in the literature. Once she has read enough of the literature and has enough real-world experience, her internal model will be more sophisticated than a simple table lookup of the data. Formally, let $\hat{f}\left(x\right)$ correspond to a data-driven machine learning algorithm, such as a neural network. The expected residual between this model and the psychological model is

$$\underset{p\left(x,y\right)}{\mathbb{E}}{\left[\hat{f}\left(x\right)-g\left(x\right)\right]}^2=\underset{p\left(x\right)}{\mathbb{E}}\left[{(f\left(x\right)-g\left(x\right))}^2+2(f\left(x\right)-g\left(x\right))\left(\widehat{f}\left(x\right)-f\left(x\right)\right)+{\left(\widehat{f}\left(x\right)-f\left(x\right)\right)}^2\right].$$ [2]

We will refer to these residuals as the smoothed residuals. The latter two terms in the right-hand expression correspond to the covariance of the predictive and psychological models’ errors, and the generalization error of the predictive model. When the expression in Eq. 2 is less than the expression in Eq. 1, i.e.,

$$\underset{p\left(x\right)}{\mathbb{E}}\left[2f\left(x\right)-g\left(x\right)\left(\widehat{f}\left(x\right)-f\left(x\right)\right)\hspace{0.17em}+\hspace{0.17em}{\left(\widehat{f}\left(x\right)-f\left(x\right)\right)}^2\right]<{\sigma }_{ϵ}^2,$$ [3]

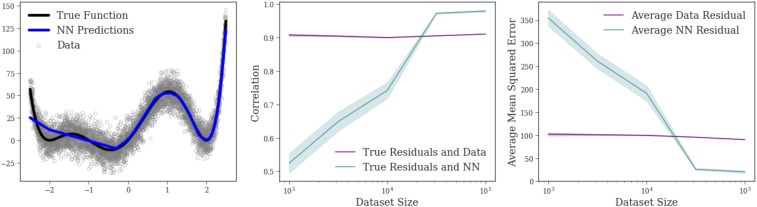
the smoothed residuals will be more highly correlated with the true residuals than will the raw residuals. Because the generalization error of sufficiently flexibile data-driven machine learning algorithms decreases with the amount of the data by which they are trained (24), the above inequality will hold when the dataset is sufficiently large. Once this condition is met, we should critique the psychological model with respect to the machine learning model rather than with respect to the dataset. Fig. 3 demonstrates an example of how smoothed residuals become more representative of the true residuals than do the raw residuals as the dataset becomes large. In practice, it is difficult to know when the dataset is large enough for this condition to be reached. For this paper, we approximated it as the point at which the machine learning model outperformed the psychological model.

Fig. 3.

SRM demonstration. (Left) A graph that outlines the true polynomial function, the data drawn from the polynomial function (with added noise), and a neural network’s (NN) prediction. (Middle) The correlation between the raw residuals and the true residuals versus the correlation between the smoothed residuals and the true residuals for a simple linear model fit to the data. (Right) The average squared residual between the data and the true function versus the average residual between the neural network and the true function. As predicted, smoothed residuals correlate better with the true residuals when the error of the neural network falls below the noise in the data. Ten simulations were run for each dataset size, and error shading in Middle and Right reflect $\pm 1$ SEM.

As a case study, we apply SRM to the Moral Machine dataset. We demonstrate that a multilayer feedforward neural network outperforms simple psychological models for predicting people’s decisions, and we then continuously critique a rational choice model until its predictive accuracy rivals that of the neural network. The result is an informative, interpretable psychological theory that identifies a set of moral principles that inform people’s judgments—exactly the kind of insight that is relevant to informing policy around new technologies such as autonomous vehicles. This process also allows us to identify three subtle and complex moral phenomena, which we validated by running preregistered experiments. Our end product is 1) a computational model of moral judgment that jointly maximizes explanatory and predictive power as well as 2) the identification and replication of several principles behind human moral reasoning.

Results

Computational Modeling.

Formalization.

SRM first calls for identifying a paradigm of interest and then critiquing a simple and interpretable psychological model with respect to a data-driven predictive model. We restricted ourselves to the subset of the Moral Machine dataset that contained pedestrians vs. pedestrians dilemmas (N = $\mathrm{15,226,477}$). We used a rational choice model (25, 26) as our psychological model to explain human moral judgment, assuming that, in the Moral Machine paradigm, humans constructed values for both sides of pedestrians (i.e., $v_{\text{left}}$ and $v_{\text{right}}$) and saved the side with the higher value. Each side’s value was determined by aggregating the utilities of its agents,

$$v_{\text{side}}=\sum _i{u}_i{l}_i,$$ [4]

in which $u_i$ is the utility given to every agent type $i$ (e.g., man, girl, female doctor, dog), and $l_i$ represents the number of those agents on that side. This formalization assumes that a participant’s choice $c$ obeys the softmax choice rule, which states that participants choose to save a side in the following way:

$$P\left(c=\text{left}|v_{\text{left}},v_{\text{right}}\right)=\frac{e^{v_{\text{left}}}}{e^{v_{\text{left}}}+e^{v_{\text{right}}}}.$$ [5]

We implemented this rule by fitting a logistic regression model to the data in order to infer the utility vector $\mathbf{u}$. We called this model the “Utilitarian” model.

This model, however, did not incorporate the main inspiration behind the trolley car dilemma: a resistance to intervening and thus killing bystanders, which is not justified by utilitarian calculus. In order to incorporate such principles, we created a “Deontological” model in which the value of a side is

$$v_{\text{side}}=\sum _m{\lambda }_m{f}_m.$$ [6]

Here, ${\lambda }_m$ refers to the strength of principle $m$, and $f_m$ is a binary variable indicating whether that principle was relevant to the given side. We proposed that two potential principles were relevant in the Moral Machine paradigm. The first was that a side was penalized if saving it required the participant to swerve. This penalty has been the primary focus of many moral psychology experiments based on the trolley car dilemma (11, 27, 28). Second, because the Moral Machine dataset had three different crossing signal statuses (crossing legally, crossing illegally, and the absence of a crossing signal), we added a penalty if a side’s pedestrians were crossing illegally. This side might have been penalized by participants because the participants were waiving their rights to protection by violating the law (29), and participants may have preferred to kill the pedestrians whose rights have been waived. We used logistic regression to infer the values $\mathit{\lambda }$.

Lastly, given research demonstrating that individuals have both utilitarian and deontological tendencies (30–34), we created a “Hybrid” model in which the value of a side is a combination of utilitarian and deontological features,

$$v_{\text{side}}=\sum _i{u}_i{l}_i+\sum _m{\lambda }_m{f}_m.$$ [7]

This model served as our baseline psychological model to iterate upon during SRM.

Central to SRM is that, in addition to training these three choice models, we need to train a data-driven machine learning model. We built a standard multilayer feedforward neural network with 42 inputs: 20 corresponding to the agents on the left, 20 for the agents on the right, one for the car side, and one for the crossing signal status, thus completely specifying the given dilemma. (It should be noted that one variable for the crossing signal status of the left-hand side is sufficient because the crossing signal status of the right-hand side is just the opposite). These inputs were the same as the Hybrid model, except that the Hybrid model had the added constraint that the value of an agent was constant across both sides (i.e., a girl on the left side was just as valuable as a girl on the right side), while the neural network had no restriction.

Finally, as a comparison to a standard data analysis method, we applied a Bayesian variable selection method to a model that started off with all features given to the Hybrid model as well as all two- and three-way interactions. Further details about this model are outlined in SI Appendix.

Initial results.

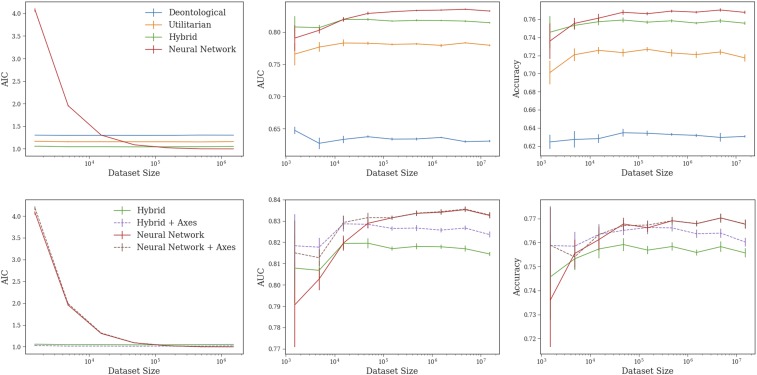
Fig. 4, Top reports the results of training all of the models on differently sized subsets of the data. Each model was trained on 80% of the subsets, and the metrics here reflect the results when tested on the held-out 20%. This procedure was completed for five different splits of the data. We report accuracy and area under the curve (AUC), two commonly used metrics in evaluating models of binary decisions. Furthermore, we also calculated the normalized AIC, a metric in which a smaller number suggests a better model (12).

Fig. 4.

Metrics for different models trained on subsets of the Moral Machine data. (Top) Performance of initial choice models and neural network as a function of dataset size. Five bootstrapped samples were taken for every dataset size. Error bars indicate $\pm$1 SEM. (Bottom) Comparison of a choice model and a neural network before incorporating axes of differences versus after incorporating axes of differences. The addition of these features resolves much of the gap between the choice model and the neural network. Error bars indicate $\pm$1 SEM.

In this training, the rational choice models performed extremely well at small sizes, and their performance stayed relatively consistent as the dataset size increased. On the other hand, the neural network performed poorly at small sizes, but became better with larger ones and eventually surpassed the choice models.* We also want to point out that the neural network had a better AIC than the Hybrid model despite the fact the former had over 3,000 parameters while the latter only had 22. This result affirms our earlier point that metrics like the AIC become uninformative, reducing to a measure of the log-likelihood, when the dataset is sufficiently large.

Most importantly, the neural network’s eventual performance suggested there were systematic effects that our choice models were predicting incorrectly. We leveraged these residuals via SRM to build a better choice model of human moral judgment.

Improving the Model.

Identifying axes of differences.

The standard methodology for critiquing models suggests prioritizing the raw residuals, the largest differences between the choice model and the data. Table 1 reports the five largest of these with a minimum sample size of 100 participants. We claim that the residuals for these dilemmas may often reflect noise and that the neural network’s predictions are more representative of the true function than the data are. For example, in the largest raw residual, a car is headed toward a group of four humans (a man, a woman, a girl, and a male executive). On the other side is a dog and three cats. According to the data, over $99\%$ of the 649 participants in this dilemma stayed in the lane and chose to kill the humans instead of the animals. The choice model predicted a strong effect in the opposite direction, and this prediction was reasonably close to the neural network’s prediction, suggesting that the choice model may not be mispredicting here. To confirm this, we looked at the dilemmas that followed these conditions: the car was headed toward agents that comprised men, women, girls, male executives, or any combination of them; the other side comprised dogs and/or cats; there was an absence of a crossing signal; the number of agents on each side were identical; and at least 50 participants responded to the dilemma. There were 45 such dilemmas. In 44 of these 45 dilemmas, only $11.3$ to $25.5\%$ of participants chose to kill the side with humans. The 45th dilemma was the one with the largest residual, and here, $99.4\%$ of participants chose to kill the human side. The results of the 44 other dilemmas suggest that the data for this dilemma are noisy, and thus we shouldn’t critique the choice model for disagreeing with the data here.

Table 1.

Biggest differences between choice model and data

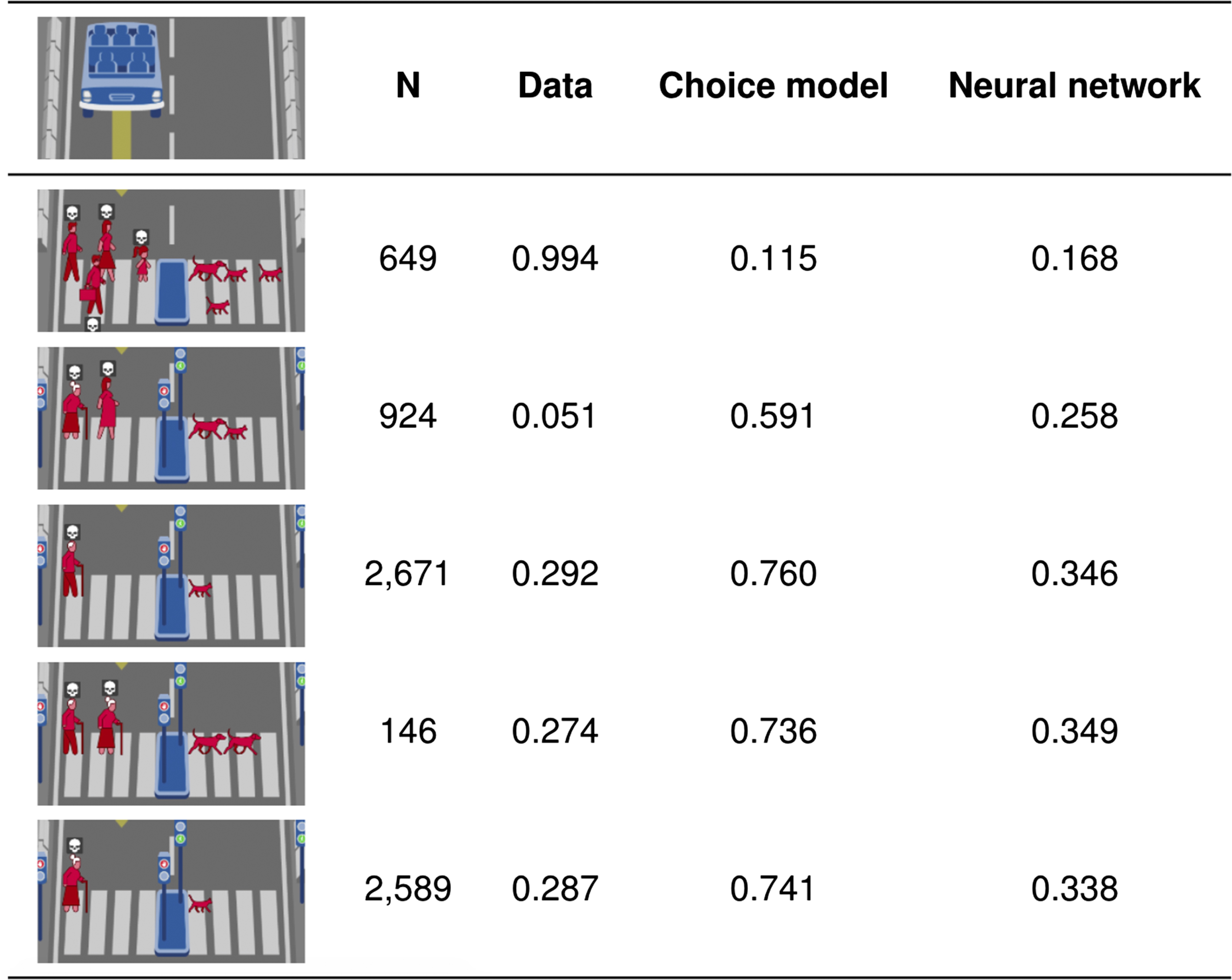Proportions show observed or predicted proportion killing left side.

Similarly, consider the second-largest raw residual. Here, a car is headed toward an old woman and a pregnant woman, who are crossing illegally. On the other side is a dog and cat crossing legally. Both the data and the neural network predicted participants would not kill the humans. However, the magnitudes were drastically different, and the correct magnitude is needed to understand the priority of this residual. In the data, only $5.1\%$ of the 924 participants killed the humans, while the neural network predicted $25.8\%$ of participants would. Like above, we conducted an analysis of the data in similar dilemmas. We looked at dilemmas in which the car was headed toward agents that were either pregnant women, old women, or both; the pedestrians in front of the car were crossing illegally; on the other side of the car were animals; the number of agents on the left and right side were equivalent; and at least 50 people responded to the dilemma. In 12 of the 13 dilemmas, $14.7$ to $35.8\%$ of participants chose to kill the side with humans. The 13th was the dilemma reflected here, and thus the data of similar dilemmas suggest the neural network’s prediction is more accurate than the data’s reported value. Therefore, while this dilemma exhibits a large residual for the choice model, the magnitude of the residual is overestimated when critiquing with respect to the data.

Table 2 reports the largest smoothed residuals, that is, the largest differences between the choice model and the neural network. We suggest that these residuals reflect the “true residuals” better than the data do. In these dilemmas, participants must decide whether the car should stay and kill the illegally crossing human or swerve and hit the legally crossing animal. Most participants chose to swerve, and the neural network correctly predicted this result. However, the Hybrid choice model often predicted the opposite. Looking at its coefficients, we can understand why: There was a penalty for both illegally crossing and swerving, and the sum of those penalties outweighed the utility differences between the human and the animal. We clustered those dilemmas as humans-versus-animal dilemmas, and it seemed that, in these instances, humans should be saved regardless of their crossing signal status and relationship to the side of the car. This represented a deontological principle, a moral rule independent of the consequences of the action (36). Thus, while our Hybrid choice model only used two deontological principles, we added a third for future iterations: If a given dilemma requires choosing between humans or animals, humans should be preferentially saved. This feature would have been difficult to justify when looking at the residuals from the data, because the largest residual there actually exhibited a strong effect in the opposite direction. Going down the list of smoothed residuals, we were able to cluster another group of dilemmas with high errors and conducted a similar analysis (SI Appendix, Table S1). Most salient to us in those dilemmas was an age gradient. Similar to above, future iterations of our model incorporated a deontological principle explicitly favoring the young in old-versus-young dilemmas.

Table 2.

Biggest differences between choice model and neural network

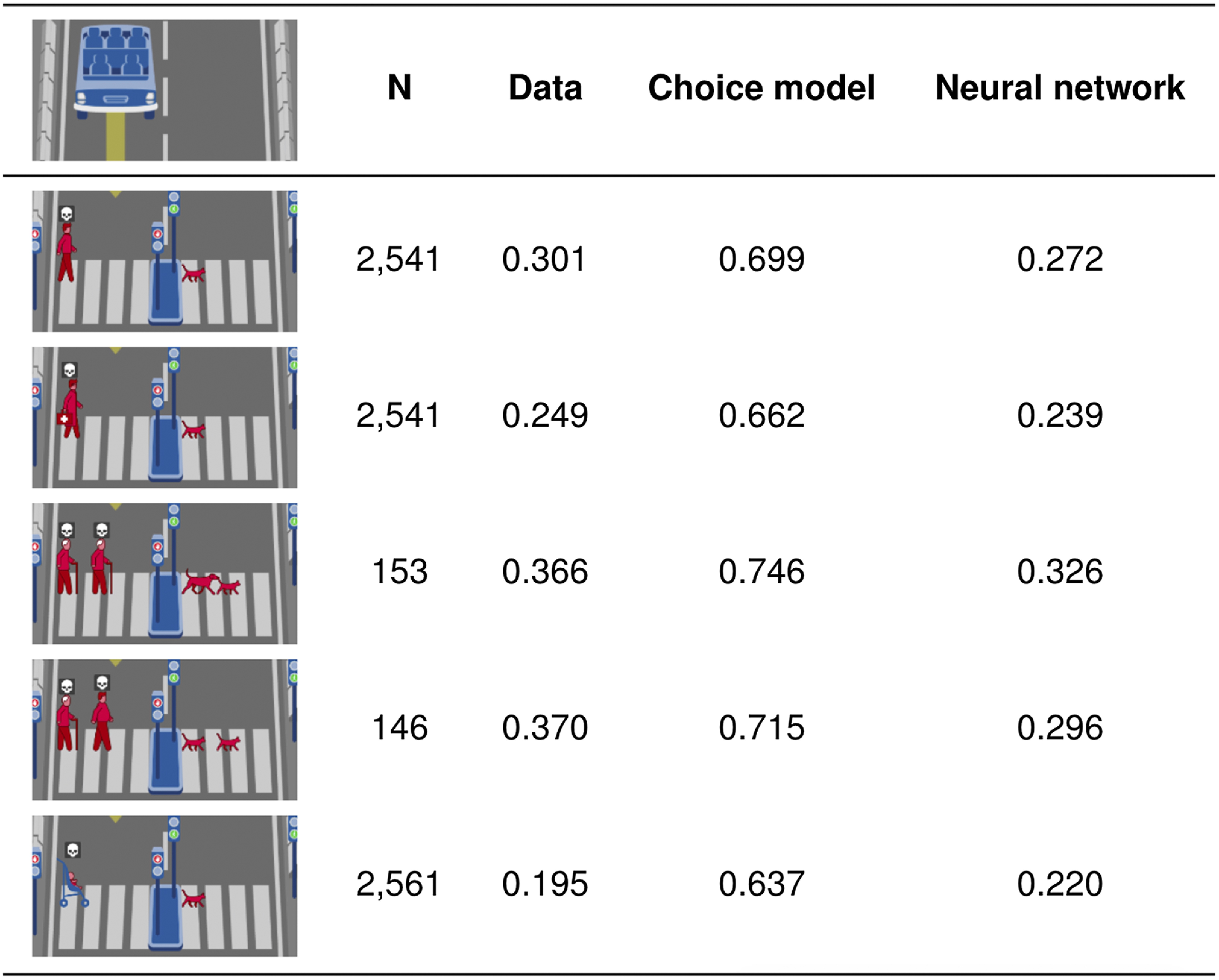Proportions show observed or predicted proportion killing left side.

Incorporating Axes of Differences.

Humans versus animals and old versus young were two of six “axes of difference” the Moral Machine researchers explicitly manipulated in their experiment, the other four being fat versus fit, more versus less, male versus female, and high status versus low status. While these axes were not explicitly revealed to the participant, the residuals we identified suggested participants were sensitive to them. We incorporated these six new features as additional deontological principles into our Hybrid choice model and plotted the results in Fig. 4, Bottom. The new choice model, Hybrid + Axes, had a significantly better accuracy than the Hybrid model, demonstrating that we were able to build a better predictive model of moral judgment while retaining interpretability and explanatory power. Furthermore, we added these axes as inputs into the neural network to create Neural Network + Axes. This model outperformed the original network at smaller dataset sizes but became seemingly identical to it at larger ones, suggesting that the original network could construct these axes once there were sufficient data. These axes were at least as complex as 20-way interactions.

This human part of identifying features from residuals is important in generating explanatory insights of human behavior. First, it allows the researcher to connect the new features with past research. For example, the “axes of difference” we found are reminiscent of work by Tversky regarding “features of similarity” (37). Second, this manual step helps ensure that the researcher is incorporating psychologically meaningful features rather than spurious information. For example, Zech et al. (38) found that machine learning models were overfitting to hospital-specific information in a training set of medical images, rather than validly approximating the true functional mapping between the images and diagnoses. A human-led featurization step as we propose would help ensure that the new features for the simple, interpretable model do not reflect this spurious information.

Despite the initial success in increasing accuracy after the first iteration, the model-building process still displayed a potential for improvement (as indicated by the AUC curve), and thus we conducted more iterations of our loop. Using the smoothed residuals from the second iteration, we identified axes not explicitly manipulated by the researchers, such as pregnant women and doctors versus other humans, and split previous axes into subaxes (e.g., young versus old was split into young versus adult, adult versus old, and young versus old). The third and fourth iterations modeled two-way and three-way conjunctive features between the axes of differences, the crossing signals, and the intervention status (e.g., a car headed toward illegally crossing humans in a humans-versus-animals dilemma).

Table 3 displays the final results of our model-building process. It is up to the modeler to decide when to stop the process, and, in this case study, we stopped when the metrics between the new choice model and the neural network were maximally close. SI Appendix, Tables S2–S7 reports the largest smoothed and raw residuals for the later iterations. The features we identified at these later iterations reflect more subtle and complicated principles. While there was conceptual overlap between the largest smoothed residuals and raw residuals for the first iteration, the gap seems to grow at the later iterations, in which the larger raw residuals seem to be very different from the largest smoothed residuals. Our resulting model predicted human decisions with an accuracy comparable to the neural network and was entirely interpretable (all features and their weights are outlined in SI Appendix, Table S8). Table 3 also shows the maximum possible accuracy when using the aggregate data to predict the choice for every given dilemma via a table lookup algorithm (i.e., if $90\%$ of participants in a given dilemma chose to swerve, the empirical prediction for that dilemma would be $90\%$; as a result, it should be noted that the performance of this “model” was not calculated out-of-sample, while all of the other models were).

Table 3.

Comparison of model fit under different metrics

Model type	Accuracy	AUC	AIC
Deontological	0.630	0.631	1.303
Utilitarian	0.719	0.779	1.161
Hybrid	0.756	0.814	1.052
Hybrid + Axes (iteration 1)	0.760	0.823	1.021
Additional Axes (iteration 2)	0.764	0.825	1.019
Two-way conjunctions (iteration 3)	0.764	0.829	1.003
Three-way conjunctions (iteration 4)	0.768	0.830	0.999
Neural network	0.768	0.833	0.999
Empirical upper bound	0.804	0.890	N/A

The AIC requires the number of model parameters, which is not applicable (N/A) for the empirical upper bound.

Empirical Results.

SRM is a form of exploratory data analysis. Such methods have the vulnerability of overfitting to data and thus need to be complemented with confirmatory data analysis techniques (39). We identified and empirically validated interesting effects from three iterations of SRM. First, regarding a new axis of difference, we found convincing evidence that participants excluded criminals from moral protections afforded to other human agents. We previously discussed the need to incorporate a deontological principle in humans-versus-animals dilemmas that prefers saving the human side. While doing this increased the model’s overall predictive power, our model started to err on a subclass of other dilemmas: criminals versus animals. In order to build a better model of human moral judgment, we had to introduce a separate criminals-versus-animals feature, thus dehumanizing criminals in the eyes of our model.

Second, we were able to identify an intuitive interaction between kids and an illegal crossing status. Consider two dilemmas (illustrated in SI Appendix, Fig. S2) where, in the first, the participant must choose between saving an old woman or a girl and, in the second, the participant must choose between saving either an old woman and a woman or a girl and a woman. Rational choice models are based on a linear utility function and would consider these dilemmas to be treated equivalently, but the Moral Machine data and the neural network revealed that participants did not always do so. Rather, participants treated the dilemmas as equivalent when the side with children was crossing legally or if there was an absence of a crossing signal, but not when the side with children was illegally crossing. In the latter cases, the side with children in the second dilemma (i.e., with an adult) was penalized more than the corresponding side in the first dilemma.

Lastly, there was an intriguing asymmetric interaction between car side and crossing signal status in both male-versus-female dilemmas and fat-versus-fit dilemmas. Here, when the car was headed toward the higher-valued individual (i.e., the female or the athlete) in the absence of a crossing signal, the probability of saving the individual was roughly halfway between the probability of saving them when they were legally crossing and the probability of saving them when they were illegally crossing. However, this relationship did not hold when the car was headed toward the lower-valued individual. Rather, in those cases, the probability of saving the individual was significantly lower than the halfway point and close to the probability of saving them when they were illegally crossing. Intuitively, lower-valued individuals aren’t given the “benefit of the doubt” when their crossing legality is ambiguous.

We ran three preregistered experiments on Amazon’s Mechanical Turk in order to replicate and confirm these effects revealed by SRM.

Experiment 1: Criminal Dehumanization.

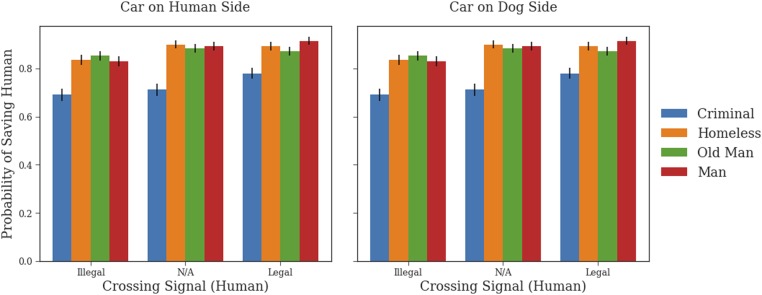
In this experiment, participants chose between saving a human and a dog. We varied the car side (dog, human), type of human (criminal, homeless man, old man, adult man), and crossing signal status (legally crossing, illegally crossing, N/A [not applicable]) for a total of 24 dilemmas. Each participant saw 4 of these 24 dilemmas. We calculated the percentage of participants that chose to save the human over the dog in every dilemma. For each car side and crossing signal combination, we conducted a ${\chi }^2$ test determining whether participants chose to save criminals less than each of the other three humans. This resulted in 18 separate ${\chi }^2$ analyses, and, for these 18 analyses, criminals were saved at a rate between $11\%$ and $28\%$ less than the other human agents. All analyses were significant at the $\alpha =0.05$ level, and 17 of the 18 were significant at the $\alpha =0.001$ level. Graphical results are displayed in Fig. 5. Tabular results and the original Moral Machine results are reported in SI Appendix, Tables S9 and S10.

Fig. 5.

Dehumanization of criminals. When pitted against dogs, participants save criminals at a significantly lower rate than other human agents. N/A refers to dilemmas in which there are no crossing signals.

Our results in experiment 1 suggest that criminals are excluded from certain protections most humans are given, namely, preferring to save them compared to dogs. These findings are consistent with a long line of work in sociology and psychology suggesting criminals are treated as a lower class of individuals than others in society when it comes to evaluating their status as a human being (40–43). Opotow (44) proposed that dehumanization is a form of moral exclusion in which a victim can lose their entitlement to compassion. Besides moral exclusion, other potential frameworks to understand participants’ behavior may be through retributive justice (45, 46) and standard consequentialist reasoning. We believe both of these factors were also present in this paradigm, but that they were already taken into account in our choice model as the inferred weight given to criminals. The moral exclusion argument is supported by the fact that incorporating a humans-versus-animals principle was an important predictor of Moral Machine behavior, but that we had to specifically remove this label from situations that pitted criminals versus animals. Since these axes of differences were derived from the features of the agents (47), our modeling suggests that participants did not honor the “human” feature for criminals.

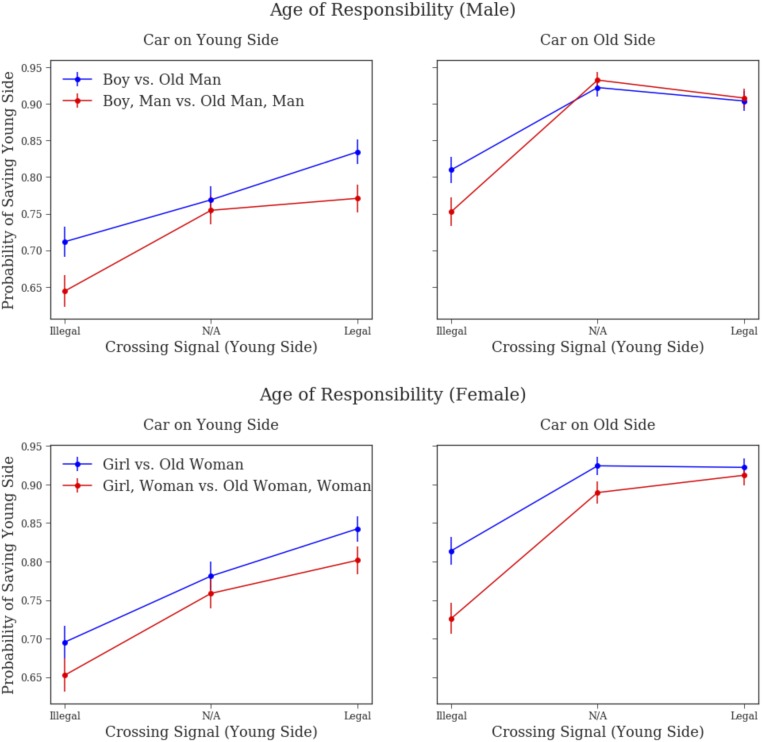
Experiment 2: Age of Responsibility.

In this experiment, participants either chose between saving a child or an old adult or they chose between saving a child and an adult versus an old adult and an adult. We varied car side (child, old adult), crossing signal condition (legally crossing, illegally crossing, N/A), and sex (male, female) for a total of 24 stimuli. Each participant saw 6 of the 24 dilemmas. We aggregated responses for all dilemmas in order to calculate the percentage of participants that chose to save the young side. For each car side, sex, and crossing signal combination, we conducted a ${\chi }^2$ analysis comparing the percentage that saved the young side in a child versus old adult dilemma to the percentage that saved the young side in a child and adult versus old adult and adult dilemma. Of these 12 analyses, we hypothesized 4 would be significant while the other 8 would not be. Specifically, we hypothesized that the analyses where the young side was crossing illegally would be significantly different but that the dilemmas in the other crossing signal conditions would not be. Three of the four hypothesized significant effects were significant at the $\alpha =0.05$ level, while seven of the eight hypothesized null effects were not significant at the $\alpha =0.05$ level. Results are graphically represented in Fig. 6. Tabular results and the original Moral Machine results are reported in SI Appendix, Tables S11 and S12.

Fig. 6.

Age of responsibility. Graphs demonstrate the differences in participants’ judgments when deciding between a child and an old adult versus when deciding between a child and an adult versus an adult and an old adult. The dilemmas are roughly equivalent when the side with children is either crossing legally or when there is absence of a crossing signal, but not when they are crossing illegally.

The results from experiment 2 suggest children are given a privileged status when assigning blame. The jurisprudential logic for the privileged status of children in the law is that children often lack the mens rea, that is, the knowledge of wrongdoing and a necessary condition for criminal conviction, when partaking in illegal activity (48–50). [An intuition for why mens rea is considered important is encapsulated by Justice Oliver Wendell Holmes Jr.’s famous quip: “Even a dog distinguishes between being stumbled over and kicked.” (51).] Earlier, we proposed that the negative penalty associated with crossing illegally is justified by a consensual theory of punishment (29), in which an individual waives their rights to being protected by the law when committing an illegal action. In our experiment, when the illegally crossing pedestrians solely comprised children, participants did not penalize them as much as when there was one adult. Formally, the jurisprudential logic behind participants’ decisions here would be that the children did not have the necessary mens rea when crossing illegally, and thus they did not willingly waive their rights to being protected by the law. As a result, they should not be penalized as much as adults, who presumably did have the mens rea and thus knowingly waived their rights. Furthermore, the empirical effect is stronger when the car is on the side of the old adult, which is intuitive under the consensual theory of punishment framework, as it seems more reasonable to excuse a child compared to an adult for not realizing they were crossing illegally when the car was on the opposite side.

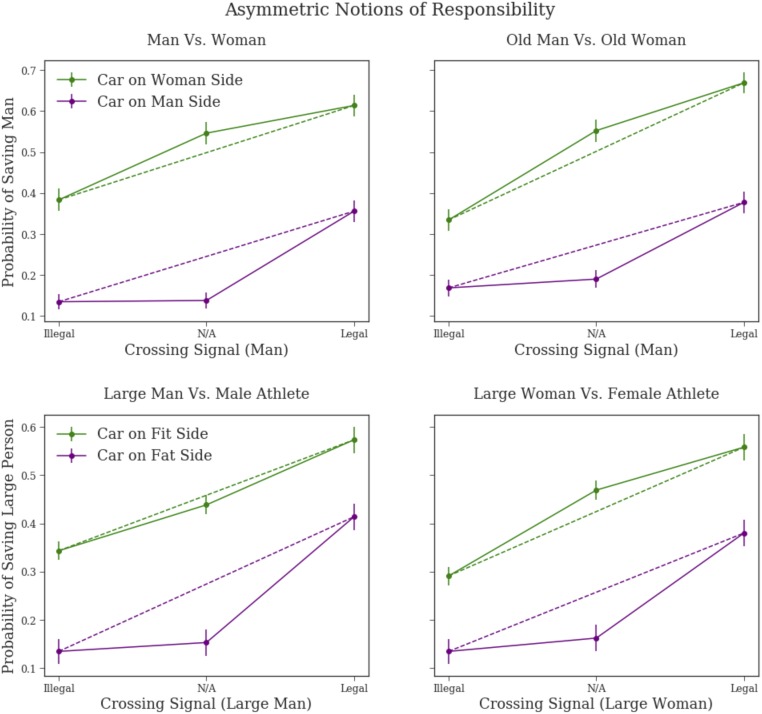
Experiment 3: Asymmetric Notions of Responsibility.

Each dilemma in this experiment was either a male versus female or an athlete versus a large person. We varied car side and crossing signal status, as well as age (adult, old) for the male–female dilemmas and sex for the fat–fit dilemmas, for a total of 24 dilemmas. Each participant only saw 4 of the 24 possible dilemmas. For each axis (i.e., male–female or fat–fit) and car side combination, we conducted a ${\chi }^2$ analysis comparing the percentage that saved the higher-valued individual in the absence of a crossing signal to the average of the percentages that saved the higher-valued individual in the legal and illegal crossing settings. We hypothesized that, when the car was headed toward the lower-valued individuals, the proportion saved in the absence of a crossing signal condition would be significantly less than the mean of the other two crossing signal settings, while we did not think there would be a significant difference when the car was headed toward the higher-valued individuals. All four of our hypothesized significant effects were significant at the $\alpha =0.05$ level, and all four of our hypothesized null effects were not significant at this level. Results are graphically represented in Fig. 7. Tabular results and the original Moral Machine results are reported in SI Appendix, Tables S13 and S14.

Fig. 7.

Asymmetric notions of responsibility. The dotted line indicates the average of the legal and illegal crossing conditions. When the car is headed toward the high-valued individual, participants’ judgments are close to that predicted by the dotted line. However, when the car is headed toward the lower-valued individual, their judgments are close to the ones in which the individual is crossing illegally.

The results in experiment 3 demonstrated that, when the car is headed toward the higher-valued individual and there is an absence of a crossing signal, the individual is treated half as if they are crossing legally and half as if they are crossing illegally. The same is not true when the car is headed toward the lower-valued individual. In those cases, the individual is treated in almost the same manner as when they are illegally crossing. One conjecture for this behavior is a form of motivated reasoning (52–54). Participants may have started off by assuming that the pedestrian in the same lane as the car is the one at fault. However, because the participant was motivated to save the higher-valued individual, they treated the absence of a crossing signal as an ambiguity that suggested equal probability of crossing legally or illegally. Conversely, when the car is headed toward the lower-valued individual, participants may have been motivated to infer that the individual was probably crossing illegally, and thus use the fact they are in front of the car to justify this belief.

Discussion

When there are so many data in front of us, where do we even start to look? This problem is not unique to large-scale experiments. Rather, it is the problem of the scientific enterprise in general. The scientific method has offered a solution: Identify the signal in the data and iteratively critique hypotheses until they are able to explain as much of the signal as possible. In this paper, we formalized this idea as an iterative loop in which we critique interpretable and theoretically constrained psychological models with respect to a data-driven machine learning algorithm. Standard forms of exploratory data analysis critique models with respect to the data, but, once the dataset is sufficiently large, a purely data-driven machine learning algorithm like a neural network can often provide a better estimate of the true underlying function than the data do.

We illustrated this methodology in the domain of moral decision-making. Psychological models of moral reasoning are often derived from consequentialist and deontological theories in moral philosophy (55, 56), and these theories have been extremely fruitful in motivating moral psychology research. However, it is inevitable that a highly theoretically driven scientific program will lead to incomplete models of human behavior. By contrasting these constrained models with data-driven models, we were able to identify shortcomings and use them to build a model that is both theoretically grounded and powerfully predictive. We found that incorporating axes of differences and their interactions with other deontological principles improved the accuracy of a rational choice model of moral decision-making. We then validated three of our findings by running independent preregistered experiments.

Our work is conceptually similar to model compression in which a “simple” model is trained on the predictions of a complex model (57). However, in that line of work, simplicity is defined with respect to a runtime processing, whereas, in ours, it is defined with respect to interpretability. Both our work and theirs leverage the fact that a neural network can serve as a universal function approximator (58, 59). They use it as their rationale to use a neural network to approximate the predictions of boosting trees, while we use it as our rationale to estimate the true underlying function. Because neural networks are the “simple” model in model compression, there is no residual analysis, and thus the majority of the work is dedicated to identifying ways to create a large dataset so that a neural network can be trained on, while the majority of our methodology is centered around residual analysis.

SRM is also similar to research by Rudin and colleagues (60, 61), in which the goal is to create interpretable machine learning models for high-stakes decisions. Our results in Table 3 demonstrate that there is not necessarily a tradeoff between accuracy and interpretability, as commonly thought by many machine learning researchers. Rather, if given structured features, interpretable models can perform similarly to (and perhaps even outperform) black box machine learning models. The methodology we propose in this paper is a systematic process for identifying and building structured features in the data.

The Moral Machine dataset proved to be a fruitful case study for SRM: Rational choice models performed well, but we were still able to use a neural network to identify shortcomings once the dataset became sufficiently large. We expect that this methodology can be used in different domains, especially in mature fields (which may have unwittingly missed important systematic effects), but also in newer fields wherein the gaps between theoretically inspired models and data-driven models remain large.

Future work can extend our method in at least three different ways. The first is automating the identification and clustering of residuals into human-interpretable features. The second is that, while we assumed a specific functional form (i.e., a rational choice model) for the final model, it is plausible that this theoretical model is incorrect, and thus we may need to develop a systematic way to identify the proper functional form itself. Third, the features identified in the resulting model are not necessarily unique—they depend on the sequence of models that have been compared. Following SRM with fitting a model with a set of features that includes and augments those that are discovered may provide a way to make principled inferences about feature uniqueness.

Lastly, on a broader note, we hope to further the development of a synergistic correspondence between psychology and data science approaches in scientific modeling (62–65). Cognitive science famously grew out of the intersection of six different fields (66), but some have suggested that this revolution did not create the emergence of a new discipline (67–69). Rather, research often proceeds independently in each contributing field. One potential reason for the lack of unification lies on a philosophical level: Different scientific traditions have different epistemic values and are methodologically incommensurable (70). For example, psychology prioritizes explanation, while machine learning is almost exclusively focused on prediction, and their methodologies reflect these differences (71–73). To live up to the promise of the cognitive revolution, we need to truly integrate the different values and methodologies implicit in these related fields. We hope the approach in this paper offers a step in that direction.

Materials and Methods

Mathematical Analysis and Simulations.

The proof for the result in Eq. 1 is below:

$$\begin{array}{ll}\hfill & \underset{p\left(x,y\right)}{\mathbb{E}}y-g\left(x\right){]}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x,y\right)}{\mathbb{E}}\left[\right(f\left(x\right)+ϵ-g\left(x\right){]}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x,y\right)}{\mathbb{E}}\left[\right(f\left(x\right)-g\left(x\right))+ϵ{]}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x,y\right)}{\mathbb{E}}\left[(f\left(x\right)-g\left(x\right){)}^2+2ϵ(f\left(x\right)-g\left(x\right))+{ϵ}^2\right]\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x\right)}{\mathbb{E}}\left[(f\left(x\right)-g\left(x\right){)}^2\right]+\underset{p\left(x\right)}{\mathbb{E}}\left[2ϵ\right(f\left(x\right)-g\left(x\right)\left)\right]+\underset{p\left(y\right)}{\mathbb{E}}\left[{ϵ}^2\right]\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x\right)}{\mathbb{E}}\left[(f\left(x\right)-g\left(x\right){)}^2\right]+\underset{p\left(x\right)}{\mathbb{E}}\left[2ϵ\right(f\left(x\right)-g\left(x\right)\left)\right]+{\sigma }_{ϵ}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x\right)}{\mathbb{E}}\left[(f\left(x\right)-g\left(x\right){)}^2\right]+{\sigma }_{ϵ}^2.\hfill \end{array}$$

The proof for the result in Eq. 2 is the following:

$$\begin{array}{cc}\hfill & \underset{p\left(x,y\right)}{\mathbb{E}}{\left[\widehat{f}\left(x\right)-g\left(x\right)\right]}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x\right)}{\mathbb{E}}{\left[\right(f\left(x\right)-g\left(x\right))+(\widehat{f}\left(x\right)-f\left(x\right)}^2\hfill \\ \hfill & \hspace{1em}=\underset{p\left(x\right)}{\mathbb{E}}\left[\right(f\left(x\right)-g\left(x\right){)}^2+\hfill \\ \hfill & \left.2(f\left(x\right)-g\left(x\right))\widehat{f}\left(x\right)-f\left(x\right)+{)\widehat{f}\left(x\right)-f\left(x\right)}^2\right].\hfill \end{array}$$

For Fig. 3, data were generated from the polynomial function $3x{\left(x-2\right)}^2{\left(x+2\right)}^2\left(x+1\right)$, and the input was uniformly sampled from the domain $\left[-2.5,2.5\right]$ and rounded to the nearest thousandth, thus allowing for multiple samples of the same data point. Each data point had noise independently drawn from a normal distribution $\mathcal{N}\left(\mathrm{0,10}\right)$. The neural network used a “ReLU” activation function and had two hidden layers, the first with 100 hidden neurons and the second with 50 hidden neurons. Ten different simulations were run for each different dataset size.

Computational Modeling.

The neural network was trained to minimize the binary cross-entropy between the model’s output and human binary decisions. We conducted a grid search on the space of hyperparameters to identify the optimal settings for the network. A neural network with three 32-unit hidden layers and a “ReLU” activation function was used for all of the analyses in this paper. Keras (74) was used for training the neural networks, and the networks were optimized through Adam (75). Logistic regression models were trained via sci-kit learn (76).

When calculating metrics for a given dataset size, five samples of that size were bootstrapped from the whole dataset. Each sample was split into training and testing sets. Train/test splits were based on unique dilemmas as opposed to individual judgments. There was a wide distribution of the number of participant judgments per unique dilemma, and we wanted both the training and test sets to have similar distributions. Thus, in order to approximate an 80/20 split, we sorted the dilemmas by the number of judgments and binned the dilemmas into groups of five. For every bin, four were randomly assigned to the training set, and the fifth was assigned to the testing set. As a result, all train/test splits were approximately, but not exactly, 80/20 splits.

Empirical Results.

The 2,086 participants across 12 conditions were recruited from Amazon Mechanical Turk and paid $\$0.50$ to participate in an experiment in which they indicated their preferences in 28 Moral Machine autonomous car dilemmas. The order of all 28 dilemmas was randomized for each participant. Five of the 28 dilemmas were attention checks. In the attention checks, participants had the option of either saving or killing everyone in the dilemma. If they chose to kill everyone more than once, they were excluded from further analysis. The experiment’s preregistration called for 163 participants per condition (12 conditions for a total $N=\mathrm{1,956}$) after the exclusion criteria were applied. This study was approved by the Institutional Review Board at Princeton University. All participants provided informed consent.

Nine of the remaining 23 dilemmas were passengers versus pedestrian dilemmas, while 14 were the stimuli for the hypotheses. The nine passengers versus pedestrian dilemmas were included to add variation because the 14 stimuli used for the hypotheses were all pedestrian versus pedestrian dilemmas. Answers for these dilemmas were not analyzed. Furthermore, both the nine passengers versus pedestrian dilemmas and five attention checks were kept constant across all 12 conditions.

Because there were a total of 24 possible stimuli for each hypothesis, hypothesis 1 and hypothesis 3 stimuli were split into six groups of four and allocated throughout the 12 conditions such that each group was assigned to 2 conditions. Hypothesis 2 stimuli were split into four groups of six and allocated such that each group was assigned to three conditions. Thus, of the 14 dilemmas participants saw for the hypotheses, 4 were for hypothesis 1, 6 were for hypothesis 2, and 4 were for hypothesis 3. The end result was that all hypothesis 1 and hypothesis 3 stimuli received 326 judgments, while all hypothesis 2 stimuli received 489 judgments. These sample sizes were chosen in order to achieve $95\%$ power at detecting a true effect using the ${\chi }^2$ proportion test at $\alpha =0.05$. Effect sizes were estimated using results from the Moral Machine dataset. It should be noted that our procedure was different from the original Moral Machine paradigm, which asked participants 13 dilemmas and operated over a wider range of experimental manipulations.

Experiments were coded using the jsPsych software package (77), and the interface with Amazon Mechanical Turk was provided with psiTurk (78). The dilemmas were created using the “Design” feature on the Moral Machine website.

Data from the experiments and the analysis script for the figures in this paper are uploaded at https://osf.io/25w3v/?view_only=b02f56f76f7648768ce3addd82f16abd (79). The preregistration can also be accessed from there.