Tubulin tails and their modifications regulate protein diffusion on microtubules

Significance

Diffusion is a common cellular transport mechanism, which often takes place in lower dimensionality such as of proteins along DNA or on microtubules that are crucial for various biological processes. Although traffic on microtubules is performed by motor proteins, these proteins and others also diffuse on microtubules spontaneously without adenosine triphosphate consumption while engaged in essential cellular transport processes, such as cell division and neuronal development. Here, we explored how the periodicity of the α and β tubulins and their electrostatic properties govern the speed and mechanism of protein diffusion along microtubules. Particularly, using various computational models, we quantified the effect of the negatively charged disordered tails and their diverse posttranslational modifications on protein–microtubule interactions and dynamics.

Abstract

Microtubules (MTs) are essential components of the eukaryotic cytoskeleton that serve as “highways” for intracellular trafficking. In addition to the well-known active transport of cargo by motor proteins, many MT-binding proteins seem to adopt diffusional motility as a transportation mechanism. However, because of the limited spatial resolution of current experimental techniques, the detailed mechanism of protein diffusion has not been elucidated. In particular, the precise role of tubulin tails and tail modifications in the diffusion process is unclear. Here, using coarse-grained molecular dynamics simulations validated against atomistic simulations, we explore the molecular mechanism of protein diffusion along MTs. We found that electrostatic interactions play a central role in protein diffusion; the disordered tubulin tails enhance affinity but slow down diffusion, and diffusion occurs in discrete steps. While diffusion along wild-type MT is performed in steps of dimeric tubulin, the removal of the tails results in a step of monomeric tubulin. We found that the energy barrier for diffusion is larger when diffusion on MTs is mediated primarily by the MT tails rather than the MT body. In addition, globular proteins (EB1 and PRC1) diffuse more slowly than an intrinsically disordered protein (Tau) on MTs. Finally, we found that polyglutamylation and polyglycylation of tubulin tails lead to slower protein diffusion along MTs, although polyglycylation leads to faster diffusion across MT protofilaments. Taken together, our results explain experimentally observed data and shed light on the roles played by disordered tubulin tails and tail modifications in the molecular mechanism of protein diffusion along MTs.

Microtubules (MTs) are essential components of the eukaryotic cytoskeleton, which among other functions, provide mechanical support to the cell and serve as “highways” for intracellular trafficking. The basic building block of MTs is the α/β tubulin heterodimer (Fig. 1), which self-associates longitudinally to form protofilaments. MTs are usually composed of 13 protofilaments connected laterally, although other compositions exist (1). The protofilaments form a stiff tube with a diameter that is about 250 Å (2). MTs can form a multitude of cellular structures ranging from neuronal arrays to disk-shaped marginal bands in platelets.

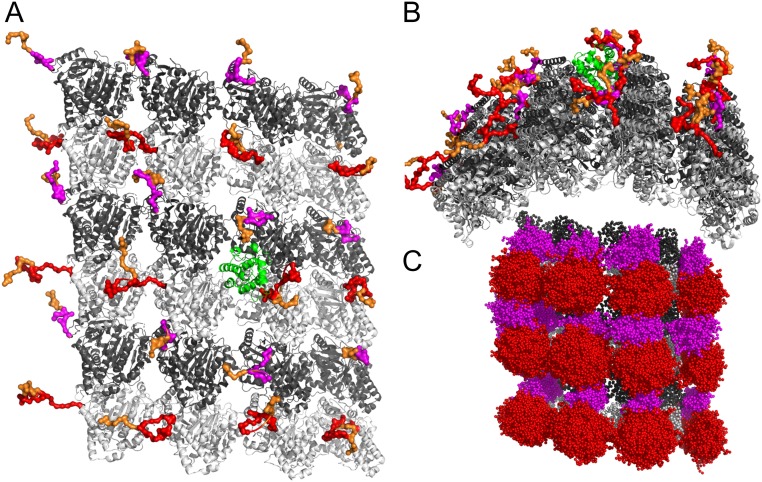
Fig. 1.

Structure of MT and MT binding proteins. (A) Vertical view of MT. A 4 × 6 MT lattice was generated based on PDB ID code 5JCO. The α and β tubulins are shown in dark gray and light gray, respectively, and their tails are shown in magenta and red, respectively. Polyglutamate branches on the tails are shown in orange. EB1 is shown in green cartoon. The conformations of the tails and tail modifications were taken from a single snapshot from our simulations. (B) Side view of the MT lattice. (C) Illustration of an ensemble of tail conformations taken from our CG MD simulations. Color code is the same as A.

Each tubulin monomer is composed of a globular folded domain (which defines the MT body) and an intrinsically disordered tubulin C-terminal tail (hereafter referred to as the “tail”), which is located on the exterior of the MT and has a net negative charge (3) (Fig. 1A). While the tubulin body is highly conserved across isoforms (80 to 95% sequence identity), the length and sequence of tails vary significantly, and the sequence identity between tails of different isoforms is ∼50%. In humans, eight tail isoforms of α tubulin and seven tail isoforms of β tubulin have been identified. These isoforms are composed of 9 to 12 and 18 to 26 residues, respectively, and correspond to 6 to 8 or 11 to 13 negative charges, respectively (4).

Tails are a key regulator of MT function and interactions. For example, the removal of tails lowers the processivity of cytoplasmic kinesin and dynein (5). In addition, the disordered MT-associated proteins, Tau and MAP2, bind tails (6–8). Furthermore, peptides derived from tails that were linked to bovine serum albumin were shown to inhibit the severing activity of the Katanin family of enzymes (9). Computational modeling suggests that glutamylases bind to the tails of both α and β tubulin (10). NMR (11) and computational (12–14) modeling of tails suggests that tails transiently bind the tubulin body and can form short-lived secondary structural elements.

The tails often undergo various posttranslational modifications (PTMs) (4) that may regulate their function. The chemical and genetic diversity of tubulin tails is commonly referred to as the “tubulin code” (15, 16). Tubulin tail modifications are common in many cell types, and deciphering the precise function of these PTMs is a very active research area (4, 15–17). One common PTM is polyglutamylation (polyE): that is, the attachment of glutamate residues to the γ carbon of a glutamate on the tubulin tail (in Fig. 1A, polyglutamate chains are shown in orange). It has been found that, among other PTMs, polyE leads to hyperstable MTs (4). The addition of glutamate residues to form branches of length up to 21 residues has been observed. Polyglycine chains can also be attached to the γ carbon of glutamate residues on the tubulin tails. Polyglycylation (polyG) occurs mostly in cilia and flagella and has been shown to be critical to the stability and maintenance of axonemes in some organisms (18). Polyglycine chains containing up to 34 glycine residues have been observed.

PTMs may affect MT function in various ways. There is evidence that polyE affects the processivity of motor proteins (being proteins from the kinesin and dynein superfamilies) (19), which utilize energy from adenosine triphosphate hydrolysis to move along MTs. In addition, it was shown that polyE acts as a rheostat to control the activity of spastin, an MT-severing enzyme important in neurogenesis and axon regeneration (20). An excess of polyE was also shown to perturb neuronal transport (21), and several links between various tubulin PTMs and human disease have been reported (17).

The existing evidence for the regulatory role that tubulin tails and their modifications play with respect to proteins that interact with MT gives rise to the possibility that the characteristics of tails may regulate the interactions of a broader class of proteins with MTs. One intriguing example is of proteins that use lattice diffusion (namely, a random walk driven by thermal energy only) to translocate along MTs and reach various target sites. The diffusing proteins exhibit a broad range of molecular properties, including with respect to dimension and degree of flexibility. For example, EB1 (22), the Dam1 (23) complex, XMAP215 (24), and kinesin 13 (25) (MCAK) use lattice diffusion to reach the plus end of MTs, where they are involved in tight regulation of MT length, which is crucial for cell division and neuronal development. By contrast, PRC1 (22), which cross-links two antiparallel MTs at way of forming spindle midzones at anaphase (26), and the intrinsically disordered protein Tau (27), which increases the stability of neuronal MTs, diffuse along the MT lattice, although they do not need to reach a specific end. Interestingly, some motor proteins combine diffusional and directed motility to diffuse in a biased manner along the MT lattice (28–31) or to side step across MT protofilaments (32, 33), a mechanism that may enable overcoming roadblocks on crowded MT lattice.

The diverse structures, sizes, and biological functions of the diffusing proteins suggest that lattice diffusion is a broadly applicable transportation mode for proteins that translocate along MTs. In order for proteins to diffuse along MTs, their affinity must be precisely tuned in that high affinity detracts from mobility on the lattice, whereas weak affinity detracts from binding the lattice. There is evidence that electrostatic interactions play a central role in this delicate balance (34). An increase in salt concentration leads to an increase in the diffusion coefficient of some proteins (22, 27) as does the enzymatic removal of the negatively charged tails (25, 27). These observations are somewhat expected since the surface of the MT lattice is negatively charged, and the surface of many MT-binding proteins includes both negatively and positively charged residues (SI Appendix, Fig. S1) (35). In this respect, diffusion of proteins along MTs is reminiscent of the one-dimensional diffusion of proteins along the negatively charged double-stranded DNA (36). However, in some cases, removal of tubulin tails has been found not to affect diffusion (37, 38), which gives rise to the possibility that electrostatic interactions alone cannot explain the diffusional motility of proteins along MTs (35).

Research thus far about protein diffusion along MTs, mostly using single-particle tracking by total internal reflection fluorescence (TIRF) spectroscopy, has shown that lattice diffusion is a transportation mode that proteins use broadly to translocate along MTs. However, because of the limited spatial resolution of TIRF spectroscopy (typically limited to the size of a fluorescently labeled protein, ∼1 to 2 nm) and challenges in purification of tubulin with well-determined isoforms and PTMs (39, 40), the molecular details of the mechanism of protein diffusion along MTs are still not fully understood. Most importantly, it is not known how the structural characteristics of the MT, including tubulin tails and their modifications, affect protein diffusion.

In this study, we use coarse-grained (CG) molecular dynamics (MD) simulations to study the molecular mechanism of the diffusion of three different proteins (EB1, PRC1, and Tau) along MTs. In particular, we study how the disordered tails and their modifications (i.e., polyE and polyG) affect the mechanism and the speed of diffusion. This is achieved by studying a variety of MT variants in which the electrostatic properties of the tubulin bodies and tails were manipulated. Our study not only reproduces the experimentally determined diffusion coefficients but also, provides a detailed biophysical understanding of the molecular mechanism of protein diffusion along MTs and predictions as to the effect that PTMs may have on protein diffusion on MTs.

Results

Electrostatic Interactions Control Protein Diffusion along MTs.

To study the dynamics of protein diffusion along MTs, we constructed a CG C_α-based model of a 4 × 6 MT lattice that includes the MT body with tubulin tails (Fig. 1 A and B; Methods has details). While the MT body remained rigid throughout the simulations, the tails were flexible (Fig. 1C). The degree of tail flexibility was validated against their flexibility in atomistic MD (Methods and SI Appendix, Fig. S2). The diffusing proteins (EB1, PRC1, and Tau) were modeled using a native topology-based potential, and the time evolution of the interaction between the proteins and MT was studied using the Langevin equation (Methods has details).

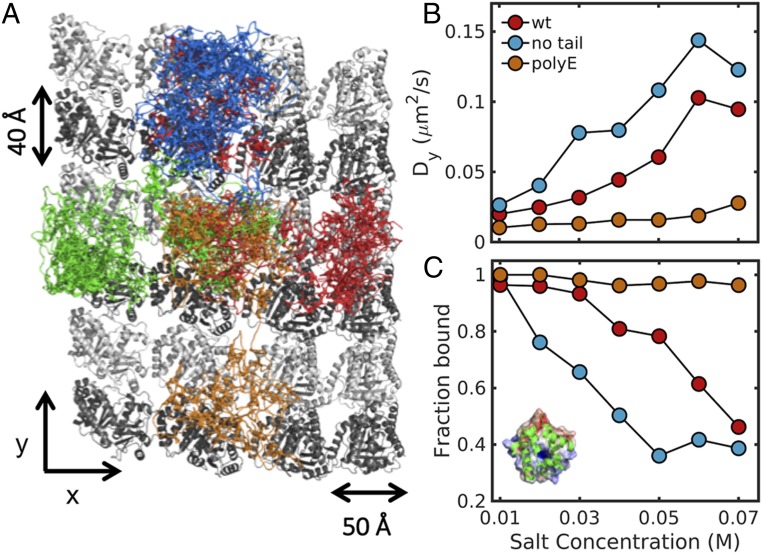
We studied the diffusion of each of the three different MT-binding proteins on three types of MT lattice: 1) MT with the wild-type (WT) tails of both α and β tubulin (Methods has the exact definition), 2) MT without α/β tails, and 3) MT tails modified by the addition of polyglutamate (polyE) chains that were 10 amino acids long (Fig. 2A and SI Appendix, Figs. S7 and S8 and Movies S1–S3). Each system was simulated at salt concentrations in the range from 0.01 to 0.07 M. For EB1, we found that increasing the salt concentration leads to a gradual increase in the diffusion coefficient along protofilaments (D_y, longitudinal diffusion) in systems with no tails (Fig. 2B, blue circles) or with WT tails (Fig. 2B, red circles). When the tails are polyglutamylated (Fig. 2B, orange circles), the increase in salt concentration does not lead to a significant increase in the D_y values. Similar results were observed for the lateral diffusion of EB1 on MTs (SI Appendix, Fig. S3). Increasing the salt concentration also leads to increased dissociation events for EB1 from the MT, and therefore, the fraction of EB1 bound to MT decreases. The effect of salt concentration on the nonspecific affinity of EB1 to MT is pronounced for MT with and without tails but is small for polyglutamylated MT (Fig. 2C).

Fig. 2.

Electrostatic interactions control protein diffusion on MTs. (A) Projected trajectories of EB1 on the lattice of WT MT. The figure highlights the diffusion of the center of mass of EB1 in four independent simulations that are represented by different colors (SI Appendix, Figs. S7 and S8). (B) The diffusion coefficient of EB1 is shown as a function of salt concentration as it translocates along a lattice of MT molecules with tails that have different properties: red circles, MT with α and β tails; blue circles, MT without tails; and orange circles, MT with polyglutamylated tails (10 glutamates). Errors of diffusion coefficients are ∼50% of the mean values from 50 independent MD runs (SI Appendix, Figs. S3, S6, and S9). (C) The fraction of time that EB1 is bound to the MT lattice as a function of salt concentration for MT molecules having different tail properties. (Inset) Cartoon representation of EB1 in which its electrostatic potential (50) is mapped on its surface, illustrating the large positive patch that is responsible for interaction with MT.

When comparing the dynamics of the three MT-binding proteins (EB1, PRC1, and Tau) with MTs, it seems that EB1 diffuses with a D_y of ∼0.03 μm²/s, which is similar to the experimental value. PRC1 diffuses with a D_y of ∼0.014 μm²/s, which is within a factor of three of the experimental result (22). The D_y value of the disordered protein Tau is ∼0.44 μm²/s, an order of magnitude larger than for the structured proteins (EB1 and PRC1), in accordance with the experimental results (SI Appendix, Figs. S3 and S4) (27). We note that similar D values are obtained when estimated by mean square displacement or by kinetic analysis (SI Appendix, Fig. S4). For the three proteins, the presence of tails slows down longitudinal and lateral diffusion (D_x, diffusion across protofilaments) and increases the nonspecific affinity (SI Appendix, Fig. S3). PolyE of the tails enhances these effects. Our results are also consistent with experimental studies that examined the effect of increasing salt concentration and the removal of tails on diffusion (25, 27). A plausible explanation of our results (35) is that increasing salt concentration leads to screening of electrostatic interactions and hence, to weaker interactions between the diffusing protein and MT and therefore, faster diffusion. Hence, we conclude that electrostatic interactions are a key molecular force that drives protein diffusion along MTs. Moreover, the observation that diffusion is slower in the presence of tails supports the possibility that interactions between tails and the diffusing protein are crucial.

Tubulin Tails Create Molecular “Lanes” for Protein Diffusion.

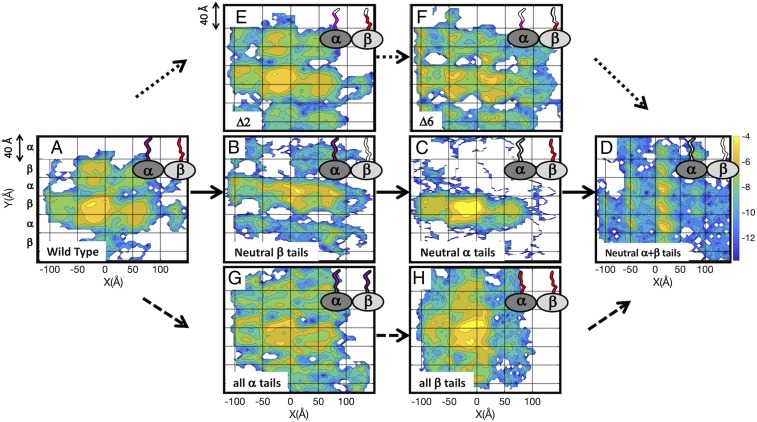
To better understand the effect of MT tails on protein diffusion, we focused on the diffusion of EB1 on MT lattices with tail components that have been manipulated. Four types of tails are considered: 1) WT tails, 2) electrostatically neutralized β tails and charged α tails, 3) electrostatically neutralized α tails and charged β tails, and 4) electrostatically neutralized α and β tails. In Fig. 3, we show two-dimensional heat maps of the probability of finding the center of mass of EB1 on MT lattices of the different systems. The heat maps are oriented such that the protofilaments are aligned along the y axis, and each row in the grid corresponds to either an α or β tubulin monomer.

Fig. 3.

Tubulin tails create molecular lanes for protein diffusion on MTs. Heat maps of the probability to find the EB1 protein at different locations on an MT lattice. Regions that are highly populated across the simulation time are yellow, and regions that are poorly populated are blue (color bar to the right of D). The probability intensities are on a log scale and calculated for the center of mass of the diffusing protein. Heat maps are shown for three series represented by three types of arrows, each of which begins with the WT MT (A) and ends with fully neutralized α and β tails (D). Solid arrows are from A to D. (A) The heat map of the WT MT is characterized by discrete areas with size that is about that of the α/β dimer such that a protein can progress only in a stepwise fashion along the protofilaments and across them (side stepping). (B) Removing the charge from the β tail leads to more significant side stepping along a lane having the width of a dimer. (C) Removing the charge from the α tail shifts the lane used for side stepping down one protofilament. (D) Removing the charge from α and β tubulin recovers the stepping along protofilaments, but in this system, the step is the size of one tubulin monomer, not a dimer. Dotted arrows are from A to E to F to D. Removing two (E) or six (F) charges from both α and β tails leads to a gradual shift from a heat map that resembles the WT (A) to one that resembles neutral α + β tails (D). Dashed arrows are from A to G to H to D. Replacing the tails of β tubulin with tails from α tubulin (G) and vice versa (H) diminishes the periodicity of the MT lattice compared with the WT (A). The grid lines reflect the lattice of α and β tubulins.

For the system with WT tails (Fig. 3A), we found that EB1 diffuses in discrete steps of size ∼8 nm (vertical grid square is 4 nm), which corresponds to the size of a tubulin dimer. In this system, EB1 diffuses both along protofilaments and across them (side stepping). In the system with neutral α + β tails (Fig. 3D), EB1 diffuses in discrete steps of size ∼4 nm, which corresponds to the size of a tubulin monomer. Diffusion occurs mostly along protofilaments, and side stepping is less frequent in this system. In the systems with neutral α tails (Fig. 3C) or neutral β tails (Fig. 3B), side stepping is the more populated diffusion mode. One interesting difference between the systems in which only one type of tail (the α or β tail) bears charges is the lane the protein uses for side stepping. In the neutral β tails system, protein diffusion takes place between two rows of α tubulin; however, in the system with neutral α tails, there is a clear 4-nm downshift, and protein diffusion takes place between two rows of β tubulin.

To obtain a deeper understanding of the importance of the precise composition of the tails, we constructed several intermediate systems. Fig. 3 A and D–F (visually linked by dotted arrows) shows the results of gradually shifting the MT system from one bearing WT-like tails (Fig. 3A) through intermediate systems in which two (Fig. 3E) or six (Fig. 3F) charged residues were neutralized from both the α and β tubulin tails of the WT MT lattice to a lattice bearing only neutralized tails (Fig. 3D).

Fig. 3 A, D, G, and H (visually linked by dashed arrows) represents contrasting systems comprising WT tails (Fig. 3A) compared with solely α (Fig. 3G) or solely β (Fig. 3H) tubulin tails compared with entirely neutralized tails (Fig. 3D). The heat maps for solely α or β tails (Fig. 3 G and H) are more uniform than those produced when only one type of tail is neutralized (Fig. 3 B and C) or when only some residues on both tails are neutralized (Fig. 3 E and F), and the discretization that is clear in Fig. 3 A–D seems to diminish. Hence, it is suggested that the periodicity of the alternating α/β tubulin heterodimer is important not only for MT polarity (3) but also, to shape the energy landscape of the MT tail-coated surface.

The main finding from the maps presented here is that diffusion both along and across protofilaments requires the protein to cross an energetic barrier with size that is highly dependent on the precise properties of the tubulin tails of the MT matrix on which the protein diffuses.

Energy Barrier for Protein Diffusion.

To quantitatively calculate the energy barrier for protein diffusion, we chose to break down the MT system into two components—body and tails—and to calculate the energy barrier for each component separately. We, therefore, constructed two types of systems: 1) systems in which diffusion is governed by the MT tails in that one or both of them remain charged, whereas the body residues are neutralized as schematized in the cartoon diagrams in Fig. 4 A, C, and D and 2) a system in which diffusion is governed by the MT body in that it remains charged, whereas charged tail residues are neutralized as schematized in the cartoon diagrams in Fig. 4B.

Fig. 4.

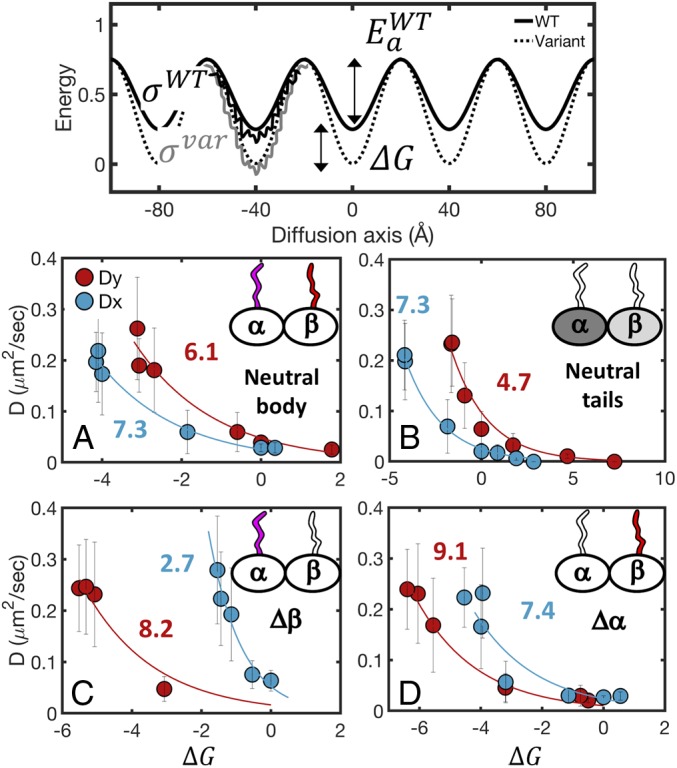
The energy barrier for protein diffusion on MTs. (Top) The energy landscape for protein diffusion on MTs can be modeled as a periodic potential with an energy barrier E_a and roughness σ. With the solid line, we show the landscape of the WT MT, and with the dashed line, we show the landscape of a modified system. The change in the height of the energy barrier between the WT and modified systems is represented as ΔG. The diffusion coefficients can be quantified based on Kramers' rate theory and Zwanzwig’s formalism for diffusion in a rough potential. Data for four systems, shown in A–D, were fit to Eq. 3 to extract values of E*_a. Details are in the text. Diffusion coefficient vs. ΔG for diffusion mediated by varying (A) the charge on both the α and β tubulin tails while maintaining a neutral MT body, (B) the charge on the MT body while maintaining neutral α/β tails, (C) the charge on the α tails while maintaining a neutral MT body and β tail, and (D) the charge on the β tails while maintaining a neutral MT body and α tail. Charged components are represented by a colored filling. Neutral components are represented by empty fillings. Each panel shows the diffusion both along and across the MT protofilament axis (D_y and D_x are red and blues circles, respectively). ΔG is estimated from the potential of mean force of the CG simulations (SI Appendix).

For each of the systems with charged tails (Fig. 4 A, C, and D), we created several subsystems (Methods has details) in which we successively neutralized the charges of the tail residues from 1) both the α and β tails (Fig. 4A), 2) only the α tails (Fig. 4C), or 3) only the β tails (Fig. 4D). For the charged body systems, we created subsystems in which we modified the charge of the MT body residues from 0.2 to 2.2 (where the default charge value is 1). For each subsystem, we calculated the diffusion coefficient and the free energy profile for diffusion both along and across the MT protofilament axis.

We developed a model to quantify the results presented in Fig. 4. Specifically, from the heat maps presented in Fig. 3, it seems plausible to suggest that the MT creates a periodic energy landscape with a defined energy barrier (G^#). We assume that the potential is one-dimensional (as can be appreciated from Fig. 3, neutral α + β tails) and further apply this model separately for diffusion along and across protofilaments. For each system, the energy barrier is defined as ΔG^# = E_a + ΔG, where E_a is the energy barrier for protein diffusion along a particular MT lattice model (Fig. 4, Top). To quantify the effect of the molecular features of the MT and the kinetics of diffusion, we quantified the energetic barriers of the three tail-governed MT system models and the body-governed MT system model. The barrier was estimated by modifying each MT model to perturb the charge on it, which leads to a corresponding change in the free energy barrier by a value of ΔG (Methods). Diffusion in a periodic potential can be written in terms of Kramers' escape rate theory, which at the high friction limit, can be written as

$$D=\frac{a^2{\omega }_0{\omega }_b}{4\pi \gamma }\cdot e^{-\frac{\mathrm{\Delta }{G}^{\ne }}{K_{B}T}},$$ [1]

where $a$ is the step size between the periodic wells, ω₀ is the curvature of the energy minima, ω_b is the curvature at the top of the energy barrier, γ is the friction, K_B is the Boltzmann constant, and T is the temperature (41). The preexponent will be referred to herein as D₀. Following Zwanzig’s derivation, γ is proportional to exp(ε/K_BT)², where ε is the ruggedness of the potential energy (Fig. 4, Top) (42). Accordingly,

$$D=D_0{e}^{-\left(\frac{E_a+\mathrm{\Delta }G}{K_{B}T}+{\left(\frac{\mathit{ϵ}}{K_{B}T}\right)}^2\right)}.$$ [2]

We assume that, in the systems studied here, ε < E_a + ΔG (SI Appendix, Fig. S5), and hence, the diffusion along MT is dominated by the periodic energetic barriers. Therefore,

$$D\sim \exp \left[-\left(\frac{E_a^{\ast }+\mathrm{\Delta }G}{K_B\hspace{0.17em}T}\right)\right].$$ [3]

E_a* is an effective change in free energy barrier that also includes possible changes in the value of D₀ such that E_a* = E_a − K_BTln(D₀).

We fit Eq. 3 to the eight datasets presented in Fig. 4, including diffusion along (D_y) (red circles in Fig. 4) and across (D_x) (blue circles in Fig. 4) the protofilament axis. From the fitted curves, we found that the effective energy barrier that a diffusing protein has to cross along the protofilament axis in a system with only charged tails is higher than the barrier in a system when only the body residues are charged (E_a,y^tail = 6.1 ± 0.4 K_BT in Fig. 4A, red and E_a,y^body = 4.7 ± 0.3 K_BT in Fig. 4B, red). In addition, the energy barrier for the system with neutral α tails (E_a,y^tail,β = 9.1 ± 0.2 K_BT in Fig. 4D, red) is higher than the barrier in the system with neutral β tails (E_a,y^tail,α = 8.2 ± 0.6 K_BT in Fig. 4C, red). Moreover, the systems in which only one type of tail is charged are dominated by side stepping (Fig. 3 B and C). Indeed, the energy barriers for lateral diffusion (D_x) for systems with neutral α or β tails are lower than the barrier for longitudinal diffusion. Still, the energy barrier for side stepping in the system with neutral α tails (E_a,x^tail = 7.4 ± 0.7 K_BT in Fig. 4D, blue) is significantly higher than the barrier in the system with neutral β tails (E_a,x^tail = 2.7 ± 0.9 K_BT in Fig. 4C, blue). Noticeably, the barrier for lateral diffusion in the system with neutral tails (E_a,x^body = 7.3 ± 0.1 K_BT in Fig. 4B, blue) is almost twofold higher than the barrier for longitudinal diffusion.

From the analytical model presented here, we conclude that the tubulin tails are the rate-limiting component in protein diffusion on MTs and that the β tails constitute a larger effective energy barrier to protein diffusion than do the α tails. It is possible that the reason for the domination of the β tails is that they are longer and more charged than the α tails (β tails are 24 amino acids long with 13 charged residues, and α tails are 14 amino acids long with eight charged residues) (19).

Protein Diffusion Relies Principally on the Tubulin Tails.

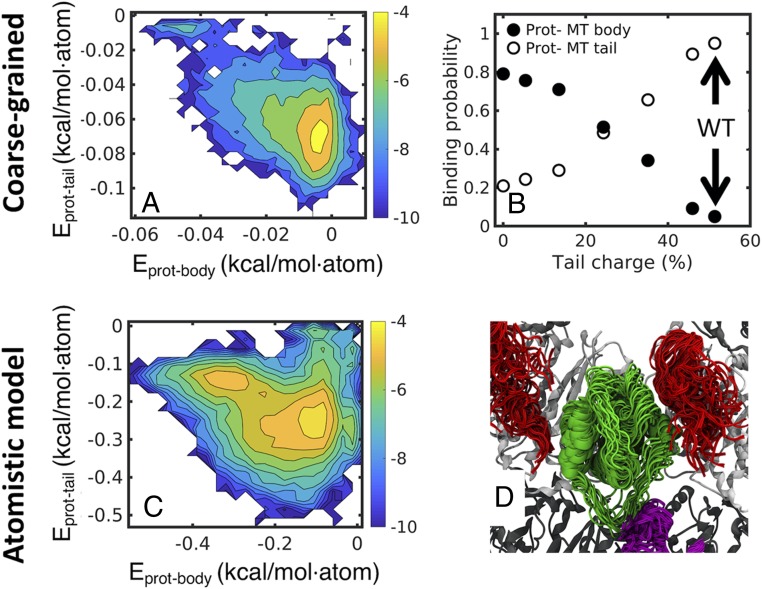
In the previous section, we investigated mutated MT components (body vs. tail). To answer the question of whether protein diffusion along MTs is tail or body mediated in a WT MT, we studied protein diffusion on MT systems in which the tail charge was modified but the MT body remained charged (dotted arrows in Fig. 3 A–G). In this system, we calculated the heat maps of the interaction energy between the protein and either the MT body (E_prot-body) or the tubulin tails (E_prot-tail) (Fig. 5 A and B). It is clear from the heat map (Fig. 5A) that the tail-bound fraction (bottom right side of Fig. 5A) is more populated than the body-bound fraction (top left side of Fig. 5A). Based on the heat maps, we calculated the fraction of time in which the protein was bound to the MT body or to the tails (Methods has details) as a function of charge density for each system. When increasing the charge density of the tails, the protein shifted gradually from the body-bound mode (Fig. 5C, black) to the tail-bound mode (Fig. 5C, white). In the WT system in which the tails have their native charge, the protein is almost solely in the tail-bound mode. Hence, we can conclude that protein diffusion along WT MT is mediated mostly by the MT tails.

Fig. 5.

Protein diffusion relies mostly on the tubulin tails. Heat maps of the interaction energy between the EB1 protein and WT MT tails (y axis) and between EB1 and the WT MT body (x axis). (A) Heat maps based on energies derived from CG simulations indicating two major states. The higher-populated state is characterized by low-protein tail and high-protein body energy (bottom right corner), indicative of a higher preference of interaction of EB1 with the tubulin tails. (B) The probability of EB1 to bind MT tail or body (y axis) as a function of the total charge of the α and β tails relative to the WT tails (percentage). (C) Heat maps are based on energies calculated from five independent atomistic simulations of EB1 diffusing on an MT lattice, with accumulated time of 2.5 μs. Note that, despite their different simulation resolutions, A and B show similar energy landscapes. (D) Selective snapshots from the atomistic simulations demonstrating the interactions between EB1 (green cartoon) and α (magenta) or β (red) tubulin tails. In all of the snapshots shown, three tails interact simultaneously with the EB1 protein.

To further validate our observations from the CG simulations, we preformed five repeats of all-atom simulations lasting 500 ns. In each simulation, we varied the initial position of the diffusing protein relative to the MT. In the all-atom simulations, we also found that the protein was mostly bound to the tails as can be seen from the heat map in Fig. 5B and in the selected conformations from the all-atom simulations (Fig. 5D and Movie S5).

Effect of Posttranslational Modifications on Protein Diffusion.

Having found that tubulin tails are the main effector of protein diffusion along MTs, we sought to investigate the effect that PTMs have on protein diffusion. Two common PTMs are polyE and polyG, which arise from the addition of polyglutamate or polyglycine chains, respectively, to the C_γ carbon of one of the glutamate residues on either one of the tubulin tails. Based on the different molecular properties of polyG and polyE chains, it is expected that they will exert different effects on protein diffusion along MTs. The results that we obtained thus far suggest that increasing tail charge may slow down protein diffusion. Therefore, we would expect that the addition of highly charged polyE chains to the MT tails will slow protein diffusion on MTs, while the addition of neutral polyG may not affect diffusion.

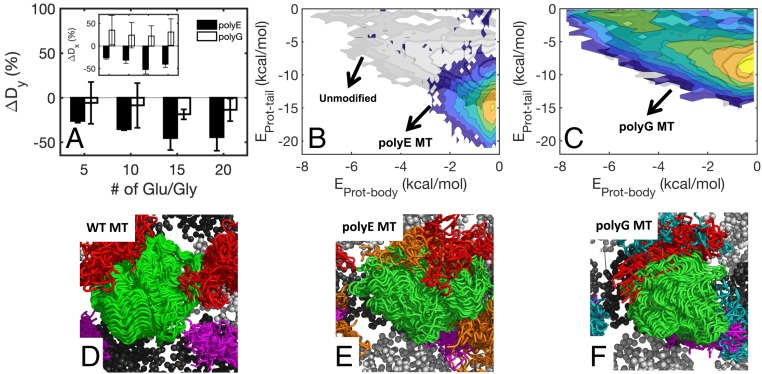
To examine the effect that PTMs have on protein diffusion, we constructed systems with polyE/G chains of various lengths branching off both α and β tubulin tails. The size of the polyE/G branches ranged from 5 to 20 additional E/G residues per tubulin tail (Methods has details; see Movies S2 and S4 for representative simulations). We found that the addition of polyE or polyG decreases the longitudinal diffusion coefficient D_y (Fig. 6A, black and white bars, respectively) and that the effect is significantly higher on addition of polyE. The origin of this effect may be that the addition of polyE but not polyG also leads to an increase in the interaction energy between the diffusing protein and the tubulin tails (Fig. 6 B and C; illustrations of protein–tail interactions are shown in Fig. 6 D–F). Interestingly, although addition of polyG leads to decrease in D_y, it leads to increase in the lateral diffusion coefficient D_x (Fig. 6 A, Inset, white bars). A plausible explanation for this dual effect exerted by additional glycine chains on diffusion is that, on one hand, polyG acts to screen electrostatic interactions between the protein and charged tail residues and that, on the other hand, the chain has a crowding effect. The former is expected to facilitate diffusion, but the latter is expected to slow it down. Accordingly, the increase in lateral diffusion coefficients due to addition of polyG is in concert with our observation that systems with neutral α or β tails have low-energy barriers for side stepping (Figs. 3 B and C and 4 C and D), which supports the possibility that polyG screens electrostatic interactions.

Fig. 6.

Effect of PTMs on protein diffusion on MTs. (A) Change in the longitudinal diffusion coefficient (ΔD_y%) for MT with polyE or polyG tubulin tails (black and white bars, respectively). Degree of polyE/G is indicated on the x axis. (Inset) Change in lateral diffusion coefficient (ΔD_x%). (B and C) Same as Fig. 5A but for polyE and polyG MT, respectively. The landscape of EB1 interacting with WT MT is shown in partially transparent grayscale background for reference. (D–F) Illustration of EB1–tail interactions derived from CG simulations of EB1 diffusion on WT MT (D), polyE MT (E), and polyG MT (F). In B–F, the polyE and polyG comprise 10 residues. The polyE and polyG chains are shown in orange and cyan, respectively. D–F show 50 frames each.

Conclusions

Tubulin tails are known to regulate MT function and interactions (5–10). Computational and experimental studies have revealed molecular properties of tubulin tails (11–13), and there is accumulating evidence that PTMs of tubulin tails are abundant and crucial for proper MT function (17, 18). However, due to their intrinsic disorder, the molecular details of the regulatory role that tubulin tails and their modifications have on MT interactions with other proteins remain poorly understood (19, 20).

In this study, we used CG and atomistic MD simulations to unravel the molecular details of the role that tubulin tails and their modifications have on the protein diffusion on MT—a transportation mode used by many proteins (35). We found that increasing salt concentration and removal of tubulin tails lead to faster diffusion of EB1, PRC1, and Tau on MTs. These results are in line with experimental observations (22, 27) and indicate that electrostatic interactions play a central role in diffusion of proteins on MTs. Notably, electrostatic interactions are also important in the diffusion of proteins along DNA (36, 43). Still, the effect that removal of tubulin tails has on the diffusion of two members of the kinesin family is ambiguous (25, 37), suggesting that the effect that tubulin tails have on diffusing protein may depend on the interacting protein.

Protein diffusion on MTs occurs in discrete steps in the size of a tubulin dimer (∼8 nm) in accordance with the step size of 8 nm reported experimentally for EB1 (22), PRC1 (22), and human (44) and yeast kinesin 8 (37). The precise properties of the tails are directly linked to step size, directionality, and energy barriers of proteins diffusing on MTs. Specifically, removal of tubulin tails changes step size to ∼4 nm (tubulin monomer) in contrast to what was suggested experimentally for various proteins diffusing on WT MT. A step size of 4 nm for nonmotor MAPs was not previously reported and is expected for tails with fewer charges, but it may also be protein dependent.

We also found that diffusion occurs both along and across (side stepping) protofilaments. Interestingly, it was shown recently that kinesin 8 uses side stepping in order to bypass obstacles (32, 33), such as other motor or nonmotor proteins. Hence, it is possible that side stepping is a general mechanism that proteins can use in order to bypass obstacles on MTs. The spontaneous diffusion of the three studied proteins on MT is bidirectional; however, on force application, they may have directional preference due to an asymmetric friction (22).

The energy barrier for protein diffusion on MTs was previously reported to be in the range of ∼2 to 13 K_BT (37, 45). However, the contributions of tubulin tails to the energy barrier and the energy barrier for side stepping were not yet determined. Here, we report that the energy barrier for tubulin tail-mediated diffusion is higher than the barrier of MT body-mediated diffusion and that the tails of β tubulin are the main contributor for this barrier. Finally, our findings provide biophysical insight to the still unresolved tubulin code. We found that PTMs can regulate the delicate balance between the affinity of proteins to MTs and the speed of diffusion, with polyE leading to a slowdown in diffusion of proteins on MTs and polyglycilation increasing the diffusion rate across MT protofilaments. This molecular perspective may have further implications on additional roles played by the tails modifications, including effect on MT mechanical stability and interactions of MTs with severing enzymes and motor proteins.

Methods

To study the diffusion of proteins along MTs, we constructed an MT lattice consisting of four protofilaments each consisting of six tubulin monomers. The coordinates of the MT lattice were based on the structure of a single isoform neuronal human MT (Protein Data Bank [PDB] ID code 5JCO) (46). The sequences of disordered tails follow the tails of isoform α1A and β3, which comprise 13 and 24 residues, respectively, and they were added as linear chains to the C terminus of each tubulin monomer. The diffusing proteins used in this study are MT-binding domains of EB1, PRC1, and Tau.

The dynamics of protein diffusion along MTs was studied using CG MD simulations, and the interactions between the diffusing proteins and the MT are modeled by electrostatic interactions. The beads of the structured part of the MT (referred to herein as “MT body”) were kept fixed in our simulations, but the tails were flexible.

To study the contributions to protein diffusion along MT that arise from the electrostatic potential of the tubulin folded domains, the tails, and cross-talks between them, we constructed several variants of MT where the charges of the body or of the tail residues were modified (SI Appendix). The effect of polyE or polyG on protein diffusion along MT was studied by modifying the tail through the addition of polyE or polyG chains, respectively. The polyE/G chains were added by creating a peptide bond between the amino terminal of the chains and the C_γ atom of glutamate 445 in α tubulin or glutamate 435 in β tubulin. These sites were previously identified as common positions for polyE (47–49). We constructed CG systems with 5-, 10-, 15-, and 20-residue polyE/G chains branched off the α and β tails.

To complement the CG model, we also preformed all-atom simulations, which were performed on a smaller “slice” of MT consisting of three protofilaments, each consisting of four tubulin monomers. The atomistic simulations were performed for the MT lattice in order to quantify the conformational dynamics of the tails. In addition, simulations were performed on MT with EB1 to examine the interactions between EB1 and the MT body and disordered tails. Additional details can be found in SI Appendix, SI Methods.

Data Availability Statement.

All data discussed in the paper have been deposited in Open Science Framework (https://osf.io/nz8yj/).

ACKNOWLEDGEMENTS.

This work was supported by the Kimmelman Center for Macromolecular Assemblies and the Minerva Foundation. Y.L. holds The Morton and Gladys Pickman professional chair in Structural Biology. This work was supported by a grant from the Swiss National Supercomputing Centre (CSCS) under project ID s918.