The carbon content of Earth and its core

Significance

Carbon is critical to life on Earth, climate regulation, and many geological processes. Despite its importance, the amount of carbon in the planet has been poorly understood due to uncertainty in the composition of Earth’s core, likely the largest reservoir of carbon. Here, we demonstrate that carbon becomes increasingly compatible in silicate compared to metal at the high pressures and temperatures at which Earth’s core formed. Therefore, carbon can only be present in the core in low abundances, although the core still likely holds the vast majority of the planet’s carbon.

Abstract

Earth’s core is likely the largest reservoir of carbon (C) in the planet, but its C abundance has been poorly constrained because measurements of carbon’s preference for core versus mantle materials at the pressures and temperatures of core formation are lacking. Using metal–silicate partitioning experiments in a laser-heated diamond anvil cell, we show that carbon becomes significantly less siderophile as pressures and temperatures increase to those expected in a deep magma ocean during formation of Earth’s core. Based on a multistage model of core formation, the core likely contains a maximum of 0.09(4) to 0.20(10) wt% C, making carbon a negligible contributor to the core’s composition and density. However, this accounts for ∼80 to 90% of Earth’s overall carbon inventory, which totals 370(150) to 740(370) ppm. The bulk Earth’s carbon/sulfur ratio is best explained by the delivery of most of Earth’s volatiles from carbonaceous chondrite-like precursors.

Carbon plays a key role in living organisms, climate regulation, plate tectonics, and possibly the geodynamo (e.g., ref. 1). Deep carbon influences mantle dynamics, fluxing melting, and mobilizing structurally bound water (e.g., refs. 2 and 3). If abundant in Earth’s iron-rich metallic core (e.g., ref. 4), carbon would play an important role in core dynamics, thermal structure, and physical properties (e.g., ref. 5). Earth’s bulk carbon content informs our understanding of the planet’s building blocks, its bulk composition, and the processes of volatile delivery and loss (6). However, the bulk carbon content of Earth is poorly constrained, because a large and uncertain amount of carbon is “hidden” in Earth’s core.

Earth’s core is ∼10% less dense than pure iron–nickel under the same pressures and temperatures, due primarily to the presence of “light elements” such as Si, O, S, C, and/or H (e.g., refs. 4 and 7). It is important to understand both the identities and abundances of these elements due to the roles they play in depressing the melting point of pure iron and driving compositional convection in the outer core that contributes to magnetic field generation. Knowledge of the core’s composition would greatly enhance our understanding of the thermal structure in the core, whose temperature is equal to the liquidus temperature of the core alloy at the inner core boundary, and would also constrain Earth’s bulk composition, and hence the identities of Earth’s precursory building blocks. Carbon is a good candidate light element due to its siderophile nature (e.g., ref. 8), abundance in primitive chondritic meteorites (e.g., ref. 9), and ability to match inner core seismic properties when alloyed with iron (10, 11).

Due to its volatility, carbon is expected to be depleted in Earth relative to primitive meteorites. However, estimating the bulk Earth carbon content from volatile depletion trends is challenging because the condensation temperature of C (a common measure of volatility) is difficult to define (5). While there is considerable uncertainty in the carbon abundance of Earth’s mantle, the uncertainty in the bulk Earth C content is dominated by the uncertainty in the core carbon content, as the core likely contains most of Earth’s carbon (e.g., ref. 7) and its composition is the subject of much debate. Previous estimates of Earth’s core carbon content include ∼0.2 wt% based on volatility trends (7); 0.25(15) wt% based on mass balance, assuming a bulk Earth carbon content of 1,000 ppm (12); 0.6 wt% based on Mo and W metal–silicate partitioning (5); 0.5 to 2 wt% based on carbon isotopic fractionation during core formation (5); <1.1 wt% based on an estimated S content of the core and a CI chondritic C/S ratio (5); and ∼2 to 4 wt% based on volatility and solubility arguments (8, 13). It has been suggested, based on the core’s shear wave velocity structure, that the core may contain enough carbon to precipitate a carbide inner core (e.g., ref. 10).

A different approach to quantifying core carbon, and thus bulk planetary carbon, is to determine how much C should have entered the core during its formation, by assessing carbon’s preference for metallic versus silicate melts under core formation conditions. This preference is quantified by a partition coefficient $D_{\text{C}}=C_{\text{C}}^{\text{metal}}/C_{\text{C}}^{\text{silicate}}$, where $C_{\text{C}}^{\text{metal}}$ and $C_{\text{C}}^{\text{silicate}}$ are the concentrations (in wt%) of carbon in the equilibrating metallic and silicate melts, respectively. A number of previous studies have measured the metal–silicate partitioning behavior of carbon at moderate pressures and temperatures (8, 14–22), finding a dependence on variables including pressure (P), temperature (T), oxygen fugacity (fO₂), metallic melt composition, and nonbridging oxygen atoms per tetrahedrally coordinated cation (NBO/T, a measure of the degree of silicate melt polymerization). However, these data only extend to a maximum pressure of 15 GPa and temperature of 2573 K (19), significantly lower than the average conditions of core formation in the Earth of 45 to 55 GPa and the mantle liquidus temperature at that pressure (e.g., refs. 23 and 24). Extrapolations of these data to higher P–T suggest D_C for terrestrial core formation ranging from ∼10³ (14) to ∼6 × 10⁴ (15). Such siderophile behavior for carbon during core formation would require an additional mechanism for increasing the carbon content of the mantle after core formation to match the observed value (e.g., refs. 8 and 18), such as delivery of carbon in the late veneer (Discussion).

Results

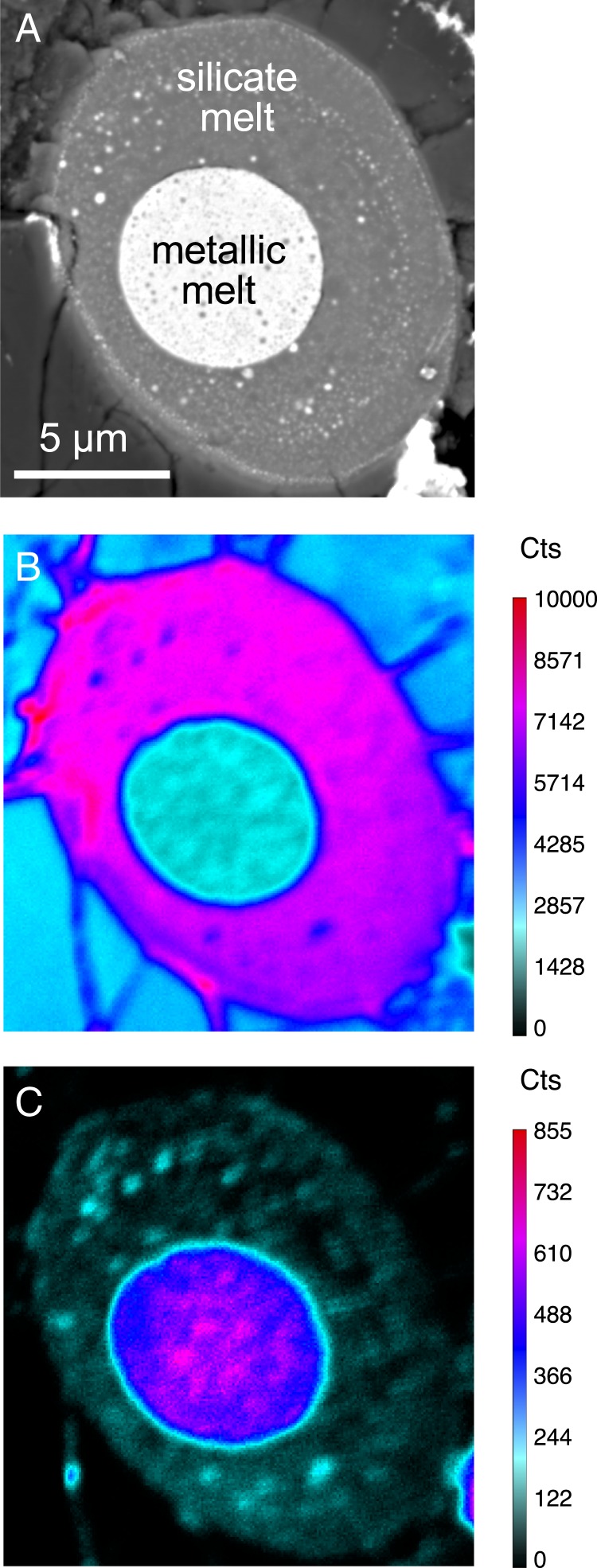
To investigate the metal–silicate partitioning behavior of carbon at conditions more directly applicable to Earth’s core formation, we performed experiments on mixtures of olivine, iron, nickel, and graphite (undersaturated with respect to carbon), using a laser-heated diamond anvil cell to achieve pressures of 37 to 59 GPa and temperatures above the silicate liquidus, 4200 to 5200 K (SI Appendix, Table S1). Multiwavelength imaging radiometry was used to map temperatures in two dimensions during the experiments (25). Following the experiments, we recovered the samples to ambient conditions and hand polished them. We measured carbon in the silicate glass using nano-secondary ionization mass spectrometry (nanoSIMS), and we measured all major and minor elements in the silicate and metal, including carbon, using a field emission electron probe microanalyzer (EPMA) (Fig. 1 and SI Appendix, Tables S1 and S2). Silicate carbon analyses using the two methods were used to bracket the partitioning behavior of carbon (Materials and Methods and SI Appendix).

Fig. 1.

Backscattered electron image (A) and nanoSIMS compositional maps of ¹⁶O (B) and ¹²C (C) of sample R187 recovered from 50(9) GPa and 5,150(500) K. All images have the same spatial scale.

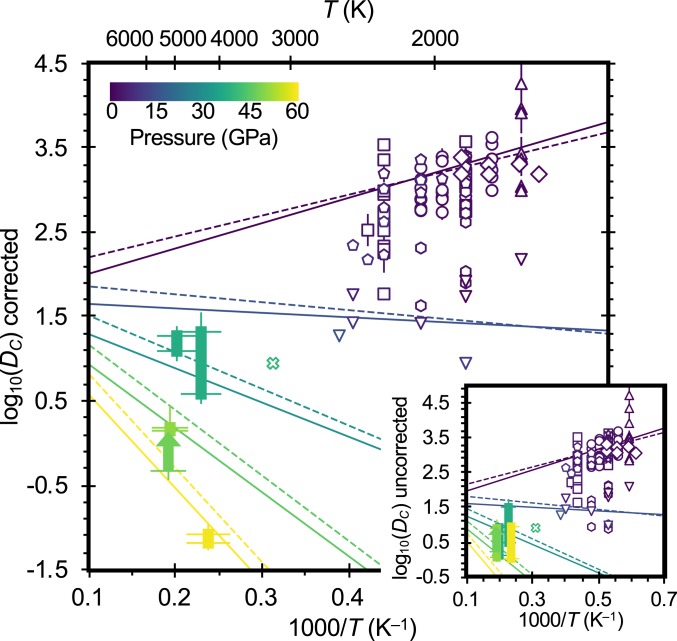
We find that carbon is approximately two orders of magnitude less siderophile at the deep magma ocean conditions of this study compared to results of previous studies at more modest pressures and temperatures (8, 14–22) (D_C = 1 to 100 vs. ∼100 to 10,000; Fig. 2), consistent with a previous ab initio calculation of D_C = 9(3) at 40 GPa and 3200 K (26). We performed a stepwise, unweighted linear regression to the data of this study and 100 measurements of C metal–silicate partitioning in the literature (8, 14–20) (Materials and Methods, Dataset S1, and SI Appendix, Fig. S1), with C partitioning exhibiting a statistically significant (P values < 0.05) dependence on T, P, mole fractions of sulfur and oxygen in the metal (X_S and X_O), NBO/T, and fO₂ in the combined dataset. Using either the nanoSIMS (Eq. 1) or microprobe (Eq. 2) analyses of carbon in the silicate from this study, the resulting fits are, respectively:

$${\text{log}}_{10}\left(D_{\text{C}}\right)=1.49\left(70\right)+\frac{\mathrm{3,000}\left(\mathrm{1,110}\right)}{T}-\frac{235\left(60\right)\text{*}P}{T}+9.6\left(14\right){\text{*log}}_{10}\left(1-X_{\text{S}}\right)-19.5\left(89\right){\text{*log}}_{10}\left(1-X_{\text{O}}\right)-0.118\left(42\right)\text{*NBO}/\text{T}-0.238\left(92\right)\text{*}\mathrm{\Delta }\text{IW},$$ [1]

$${\text{log}}_{10}\left(D_{\text{C}}\right)=1.81\left(74\right)+\frac{\mathrm{2,470}\left(\mathrm{1,170}\right)}{T}-\frac{227\left(63\right)\text{*}P}{T}+9.7\left(14\right){\text{*log}}_{10}\left(1-X_{\text{S}}\right)-30.6\left(99\right){\text{*log}}_{10}\left(1-X_{\text{O}}\right)-0.123\left(46\right)\text{*NBO}/\text{T}-0.211\left(94\right)\text{*}\mathrm{\Delta }\text{IW},$$ [2]

with T in kelvin, P in gigapascals, and fO₂ in log₁₀ units relative to the iron–wüstite (IW) buffer (numbers in parentheses are uncertainties on the last digit[s]; covariance matrices of these fits are shown in SI Appendix, Tables S3 and S4). Measured versus predicted partition coefficients from Eq. 1 are shown in SI Appendix, Fig. S2. The magnitudes of the terms in the two equations are in agreement within their mutual uncertainties. Eqs. 1 and 2 indicate that carbon becomes less siderophile with increasing pressure, the opposite dependence than previously determined in low pressure studies from 1 to 5 GPa (8, 15, 16), but in agreement with the three previous highest-pressure studies of carbon partitioning, which spanned pressures up to 12 to 15 GPa (19, 21, 22). C also becomes less siderophile with increasing NBO/T (in agreement with many previous studies, e.g., refs. 8, 15, 17–19, and 21), increasing sulfur in the metal (in agreement with refs. 16 and 22), decreasing oxygen in the metal (not previously investigated, since oxygen only dissolves into metallic melts at high P–T; e.g., ref. 23), and increasing oxygen fugacity (in agreement with many previous studies, e.g., refs. 14, 15 and 19–21; although this behavior seems to reverse at sufficiently low fO₂; refs. 17 and 18). At low pressures, carbon becomes less siderophile with increasing temperature (Fig. 2), in agreement with most previous studies (8, 16, 18, 19, 22). At pressures above ∼15 GPa, Eqs. 1 and 2 predict that carbon becomes more siderophile with increasing temperature (Fig. 2), although we caution that it is difficult to deconvolve pressure and temperature effects as these correlate in experimental datasets. Eqs. 1 and 2 should be regarded as empirical fits that adequately describe the behavior of carbon over the conditions of the experimental data (Fig. 2).

Fig. 2.

Metal–silicate partition coefficients of carbon from this study (solid rectangles) and previous studies (open symbols; Dataset S1). Data are color-coded by pressure and are corrected to a common NBO/T = 2.6, X_O = X_S = 0, and fO₂ = IW–2.2 using Eq. 2 (or Eq. 1 for the nanoSIMS data from this study). Triangles: 14. Circles: 15. Squares: 8. Hexagons: 16. Stars: 17. Pentagons: 18. Inverted triangles: 19. Diamonds: 20. × symbol: ab initio calculation (26, uncorrected). Data from this study are shown as ranges encompassing microprobe and nanoSIMS analyses of carbon in the silicate glass (one datum only has a lower bound, shown as an arrow). Solid lines: fit to complete dataset, using nanoSIMS analyses for silicate C from the present study (Eq. 1). Dashed lines: fit to complete dataset, using microprobe analyses for silicate C from the present study (Eq. 2). Curves are shown for NBO/T = 2.6, X_O = X_S = 0, fO₂ = IW–2.2, and pressures of 0, 15, 30, 45, and 60 GPa. (Inset) Uncorrected metal–silicate partition coefficients.

We collected Raman spectra on the quenched silicate glass to determine the speciation of dissolved carbon (Materials and Methods). The spectra are dominated by bands assigned to carbon/graphite, CH₄, and alkyne C–H (SI Appendix, Fig. S3); no other volatile species were present in detectable quantities. Glass spectra cannot be unambiguously related to carbon speciation in the melt, and several interpretations are possible. However, the details of carbon speciation do not affect our major findings or conclusions. The carbon bands resemble those reported by Armstrong et al. (14) in silicate glass from similar fO₂. The strong carbon signal supports the microprobe and nanoSIMS analyses of high carbon abundances in the glass, and the absence of OH or H₂O species is consistent with a low water abundance in these nominally anhydrous experiments.

Discussion

The metal–silicate partition coefficients determined in this study are smaller than those previously reported at lower P–T (8, 14–20), although there is some overlap, especially with the previous studies that extended to the highest pressures (e.g., ref. 19) (SI Appendix). A change in partition coefficient of similar magnitude is seen in silicon over the same P–T range, for example (e.g., refs. 23 and 24). This partitioning behavior for carbon is consistent with a positive 1/T dependence found by most previous studies (e.g., refs. 8, 16, 18, 19, and 22). It is also consistent with a negative pressure dependence found by the previous studies that spanned the largest pressure ranges (19, 21, 22), a factor of >2 greater P range than other studies (8, 14–18, 20). Additionally, the experiments presented here were undersaturated with respect to carbon, while the experiments in most lower P–T studies (8, 14–20, 22) were performed at carbon-saturated conditions. A recent study (21) suggested that lower partition coefficients result from carbon-undersaturated conditions, which are more applicable to conditions in the Earth.

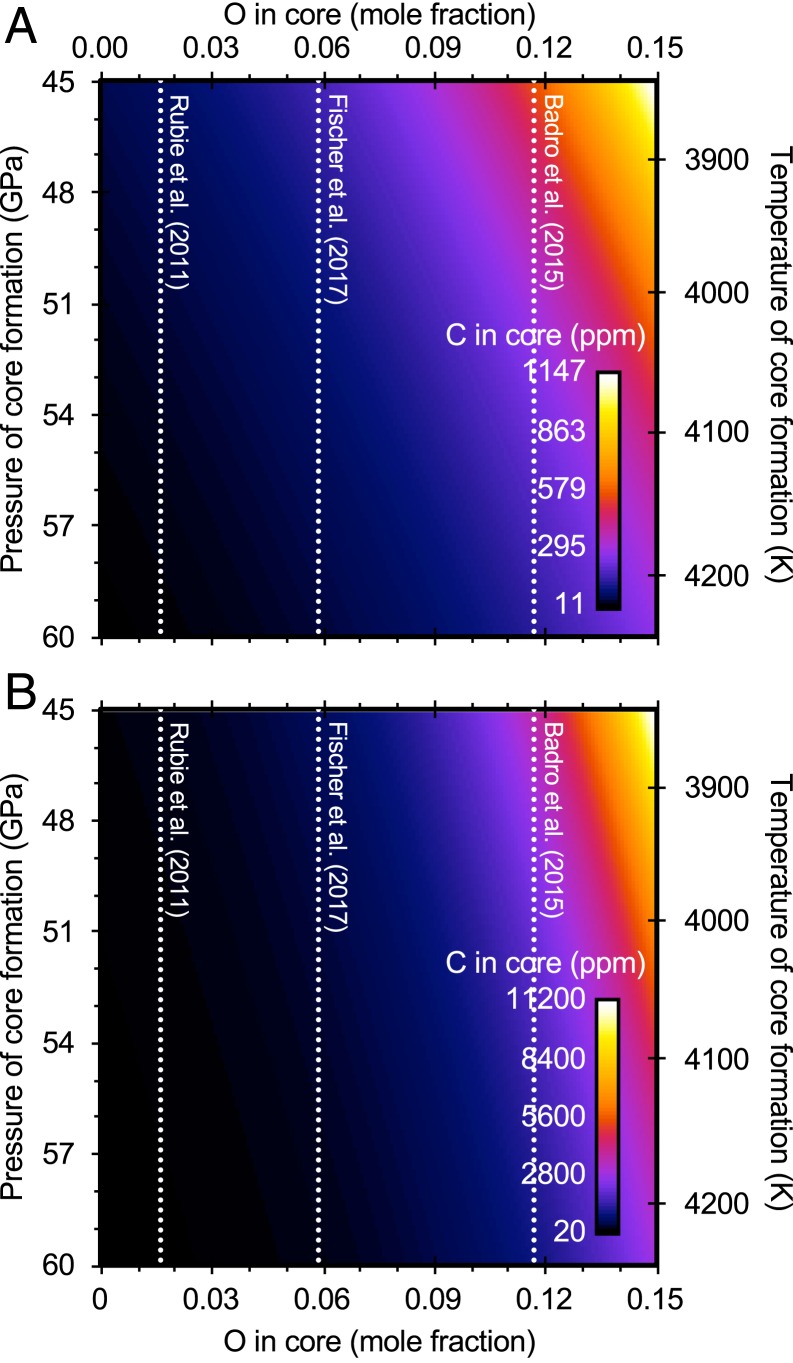
For single-stage core formation at 54 GPa (23), the peridotite liquidus temperature, 4100 K (27), NBO/T = 2.6, IW–2.2, X_O = 0.06 (e.g., ref. 28), and X_S = 0.03 (e.g., ref. 7), Eqs. 1 and 2 yield a partition coefficient for carbon of 0.5 to 1.8. At these conditions, extrapolations of the parameterizations of previous studies give partition coefficients ranging from 0.5 (19), in good agreement with our results, to 2 × 10⁶ (16). For a mantle carbon content of 120(60) ppm (29), a partition coefficient of 0.5 to 1.8 implies a core carbon content of 66(55) to 220(190) ppm. More oxygen in the core would result in higher core carbon contents; for example, using X_O = 0.12 (e.g., ref. 30) results in a core with 0.024(15) to 0.16(11) wt% C. Fig. 3 illustrates the trade-offs between core formation depth (pressure and temperature), core oxygen content, and core carbon content in this single-stage core formation model.

Fig. 3.

Core carbon content as a function of the pressure of core formation (with temperature along the peridotite liquidus of 27) and oxygen content of the core. Calculation is for single-stage core formation, assuming a mantle carbon content of 120 ppm (29), a peridotitic NBO/T of 2.6, oxygen fugacity of IW–2.2, and a core sulfur content of X_S = 0.03 (e.g., ref. 7). Dotted lines: approximate core oxygen contents from previous studies (28, 30, 34). (A) Based on fit using nanoSIMS analyses for silicate C from the present study (Eq. 1). (B) Based on fit using microprobe analyses for silicate C from the present study (Eq. 2).

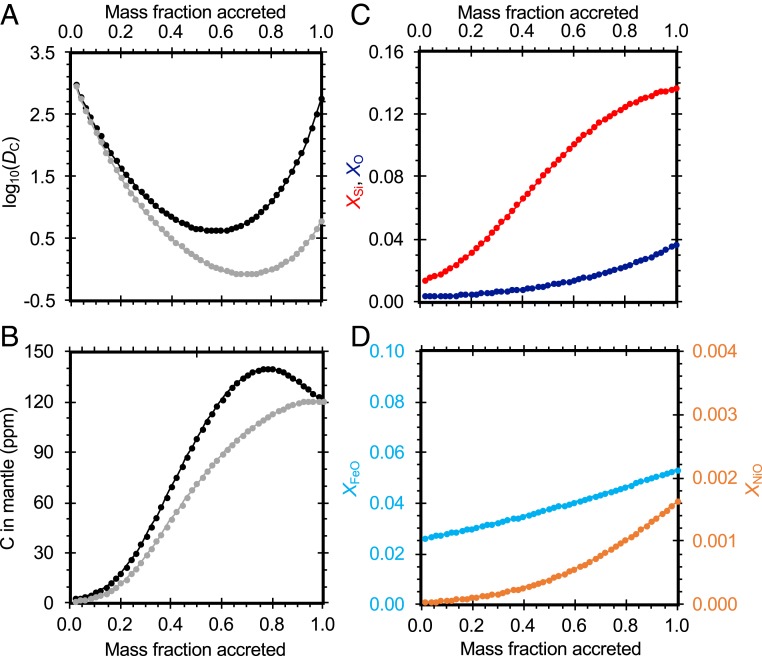
Abundances of most major, minor, and trace elements in the Earth’s mantle and core are most consistent with a series of metal–silicate equilibration events at increasing P–T, although there are exceptions (31), and limitations in the experimental data make it difficult to distinguish among P–T–fO₂ paths (32). Despite these uncertainties, core formation on Earth was likely a protracted process occurring over a range of pressures and temperatures as the Earth accreted (e.g., ref. 33), and this informs our approach to estimating the carbon content of the Earth’s core, as it has previous models (e.g., refs. 24, 28, 34, and 35). Here we formed the Earth from the accretion of 50 smaller bodies, each 2% of an Earth mass. Each body had the same initial bulk composition, that of a refractory element-enriched CI chondrite (ref. 34; sulfur from ref. 7). The model tracks the partitioning of iron, silicon, oxygen, nickel (23), sulfur (36), and carbon. At each step, metal–silicate equilibration occurred at 65% of the core–mantle boundary pressure (consistent with values of 40 to 65% used in similar previous studies, e.g., refs. 24, 34, and 35), the peridotite liquidus temperature at that pressure (27), a peridotitic NBO/T = 2.6, and an oxygen fugacity [approximated as ∆IW ∼ 2*log₁₀(X_FeO/X_Fe)] that increased linearly from IW–3 to IW–1.5. This type of increase in oxygen fugacity as accretion proceeds has been previously shown to be necessary to reproduce the mantle’s trace element abundances (e.g., ref. 35), and it is a natural consequence of both the accretion of more oxidized material from the outer disk toward the end of planetary accretion (e.g., ref. 37) and the redox reaction SiO₂ + 2Fe → 2FeO + Si, which proceeds to the right as pressures and temperatures increase (e.g., refs. 23, 34, and 38). The degree of metal equilibration was k = 0.4, consistent with the Earth’s Hf–W isotopic composition for the case of whole-mantle equilibration (e.g., ref. 39). These model conditions were chosen to approximately reproduce the FeO, NiO, and SiO₂ contents of the mantle (29) (Fig. 4). The resulting core contains 7.8 wt% Si, 1.2 wt% O, 0.9 wt% S, and 5.2 wt% Ni. For a mantle carbon content of 120(60) ppm (29), the core contains 0.09(4) to 0.20(10) wt% C (range corresponding to the use of Eqs. 1 and 2, respectively).

Fig. 4.

Results of a multistage model of core formation. (A) Evolution of the carbon metal–silicate partition coefficient D_C as Earth grows, using either Eq. 1 (fit based on nanoSIMS measurements; gray symbols and curve) or Eq. 2 (fit based on microprobe measurements; black symbols and curve). (B) Mantle carbon content. Colors are as in part A. (C) Core silicon (red symbols and curve) and oxygen (dark blue symbols and curve) contents. (D) Mantle FeO (light blue symbols and curve, left axis) and NiO (orange symbols and curve, right axis) contents.

These core carbon abundances indicate that carbon is unlikely to be a major contributor to Earth’s core density deficit with respect to pure iron. To explain the seismologically observed density, Earth’s core must contain significant amounts of other light elements such as silicon and oxygen (e.g., refs. 24, 28, and 34), both of which become more siderophile at the high temperatures of Earth’s core formation (e.g., refs. 23 and 24), and/or sulfur and hydrogen. Despite carbon comprising a small fraction of the core, the core remains the largest reservoir of carbon in the Earth, containing 78(12) to 89(7)% of the planet’s carbon budget. Therefore, any analysis of the Earth’s carbon content must account for this dominant reservoir, which has implications for understanding of the planet’s bulk composition and volatile inventory and delivery. This core composition corresponds to a bulk Earth carbon content of 2.2(9) to 4.4(22) × 10²¹ kg, or 370(150) to 740(370) ppm.

This analysis assumes that carbon was delivered throughout Earth’s accretion history, such that the depth of metal–silicate equilibration that reproduces the mantle’s major and trace element composition also applies to carbon. N-body simulations of terrestrial planet accretion show that Earth-like planets preferentially accrete material from the outer disk, which is likely more volatile-rich, later in their growth histories (e.g., ref. 37). If more of Earth’s carbon were accreted later in its history, when the Earth was larger, the average P–T conditions of metal–silicate equilibration relevant for carbon may have been significantly higher. With increasing depth along the peridotite liquidus (27), carbon generally becomes even less siderophile (Eqs. 1 and 2). Therefore, the actual core carbon abundance, and thus the bulk Earth carbon abundance, may be even lower than that determined here. For example, if carbon equilibration occurred at 50% higher pressures (representing conditions in a deeper magma ocean), the core carbon content would be ∼20 to 30% lower. If graphite floatation on a magma ocean was an important process (40), this may have further reduced the core carbon content. Carbon delivery to Earth’s mantle via a late veneer would also reduce the core carbon content; in the limit of all mantle carbon being delivered in the late veneer, there would be none in the core. A late veneer with a mass of 0.7 to 2.7 × 10²² kg (41) and chondritic 0.09 to 3.2 wt% C (9) would account for 1 to 181% of the mantle’s carbon inventory (29), assuming no volatile loss.

This bulk Earth carbon content can be compared to that of known meteorites to estimate their relative contributions to Earth’s mass. CI carbonaceous chondrites contain ∼3.2 wt% carbon (9), so a bulk carbon content of 370(150) to 740(370) ppm corresponds to the addition of only 1.2(5) to 2.3(10)% CI material to an otherwise C-free Earth, assuming no carbon loss during accretion. Dauphas (42) used the isotopic composition of the Earth to constrain the nature of accreting material through time, finding a best-fit model Earth composed of ∼71.6% enstatite, 5.4% carbonaceous (CO/CV), and 24% ordinary chondrites. For carbon abundances of EH, CV, and L chondrites (9), this combination corresponds to 3,300 ppm C, requiring significant volatile loss to explain the bulk Earth carbon contents determined here.

Ratios of volatile element abundances are often used as a fingerprinting technique to assess the source material of Earth’s volatiles (e.g., ref. 43), but the abundances of volatiles in the core (and thus in the bulk Earth, since the core is likely the largest reservoir for some of these elements) are poorly constrained because metal–silicate partitioning behaviors of these elements have largely not been studied at P–T conditions relevant to Earth’s core formation, except for sulfur (36). Combining our constraint on Earth’s carbon content with a bulk Earth S abundance of ∼3,000 ppm (36), we find a bulk Earth C/S ratio of 0.12(5) to 0.25(11). This ratio is lower than the bulk silicate Earth C/S ratio of 0.49(14) (ref. 43, which used a sulfur content derived from peridotites and a carbon content derived from C/Nb and C/Ba ratios of undegassed basalts), indicating that core formation fractionates S from C (18). Of known meteorite groups, a bulk C/S ratio of 0.12 to 0.25 is closest to those of EL, CO, and CV chondrites (9) and is slightly higher than the meteorite mixture proposed by Dauphas (42), which has a C/S ratio of 0.07 (9). However, our result for this ratio is likely most consistent with the carbonaceous chondrites, which have similar to higher C/S (0.23 to 0.67; ref. 9), considering that atmospheric/volatile loss is expected to decrease this ratio (e.g., ref. 43). Thus, our study supports models in which carbonaceous chondrite-like precursors contributed a substantial proportion of Earth’s volatiles.

Materials and Methods

Starting Materials and Samples.

Powdered iron (Alfa Aesar; 99.9+%), nickel (Alfa Aesar; 99.9%), graphite (from a spectroscopic graphite electrode; United Carbon Products Company), and San Carlos olivine were mixed in a ratio of 41.9:2.2:1.4:54.5 by weight. This mixture was pressed into a flake ∼10 to 15 µm thick and loaded between two plates of single crystal MgO, polished to a thickness of ∼10 µm, into preindented steel or rhenium gaskets. The MgO acted as the pressure medium and thermal insulator. A symmetric diamond anvil cell was used to generate high pressures. Reported pressures were measured at the laser-heated spot before and after heating using diamond Raman (44), and were corrected for an estimated thermal pressure contribution based on previous experiments with similar geometry performed with in situ X-ray diffraction (23). Reported pressure uncertainties include contributions from the measurement at room temperature and the estimated thermal pressure correction (SI Appendix, Table S1).

Laser-Heating Experiments.

Double-sided laser-heating experiments were performed at Yale University (25) using an infrared fiber laser. Laser power was held at a low power for 2 s, increased over a period of 1 s, held at the target high power for 3 s, then shut off to rapidly quench the samples (45), producing a noncrystalline silicate glass. This should have been sufficient time to allow for metal–silicate equilibration (SI Appendix). While at the target laser power, we monitored temperature fluctuations by measuring the thermal emission with a photodiode to ensure that the sample was quenched at the peak temperature (SI Appendix, Fig. S4A). Temperatures were measured using four-color multiwavelength imaging radiometry (25, 46), which allows for mapping of the temperature in the laser-heated spot in two dimensions, immediately before quenching the experiment. Successful experiments were performed at 37 to 59 GPa; attempts to perform experiments at significantly lower pressures failed due to temperature instabilities during laser heating (SI Appendix, Fig. S4B).

Reported temperatures were taken from the central, hottest portion of the laser-heated spot and corrected for wavelength-dependent absorption (47), assuming that the MgO insulation layer remained transparent, so it exhibited no wavelength-dependent absorption and emission, and that the unreacted silicate starting material remained olivine (Fo90) and retained low absorption coefficients (<100 cm^–1) (48). Taking into account these assumptions and the difference in temperatures between the two sides of the experiment, estimated temperature uncertainties are ±10%. Experimental pressures, temperatures, and accompanying uncertainties are summarized in SI Appendix, Table S1.

Sample Recovery and Analysis.

Following decompression, we mounted the entire assembly in epoxy under vacuum. We polished either parallel or perpendicular to the compression axis to expose the laser-heated spot for analysis. We cut away the epoxy medium and embedded the sample in indium, then coated all samples and standards with Ir for analysis of light elements first by nanoSIMS, followed by EPMA. After obtaining surprisingly high carbon contents in the quenched silicate melt (glass) by nanoSIMS, we analyzed all elements by EPMA, including direct analysis of carbon and oxygen. Silicate carbon contents measured by nanoSIMS were higher than the carbon contents measured by EPMA, and therefore the nanoSIMS measurements constrain the minimum partition coefficients of carbon. In light of this surprising result, we take the conservative approach of bracketing the carbon contents of the experiments with results from nanoSIMS and EPMA (SI Appendix).

We carried out nanoSIMS analyses on the quenched silicate using the Cameca NanoSIMS 50L at the Carnegie Institution of Washington (e.g., ref. 49). We measured isotopes ¹²C, ¹³C, ¹⁶O, ²⁸Si, ⁵⁶Fe, and ⁶⁰Ni simultaneously using the scanning ion imaging mode of operation on both standards and unknowns, with a Cs⁺ primary beam. We applied a beam current of 4 to 14 pA, with a raster size ranging from 10 × 10 µm² to 25 × 25 µm² after a 160-s presputter over an area 5 µm larger (to remove surface contamination before the analyses). We collected 15 frames per image with a 16-s count time, at 256 × 256 pixels. We used ¹²C/¹⁶O to quantify carbon abundances based on a calibration (linear regression with R² > 0.98) built from five silicate glasses with known carbon contents in the range 45 to 1,500 ppm C. SIMS carbon calibrations are linear up to at least >2.4 wt% C when normalizing against ³⁰Si (50); we expect similar linear behavior when normalizing against ¹⁶O (e.g., refs. 50–52) (SI Appendix). We processed the data using the L’Image software package for IDL (L. R. Nittler, Carnegie Institution) and corrected all data for spatial drift and deadtime. We averaged over 15 to 30 nonoverlapping regions of interest (ROIs), with ROIs chosen to avoid the edges of the silicate glass and any decompression fractures. Results are insensitive to the number/size of ROIs used. Quoted uncertainties include contributions from the spatial variability of the silicate glasses (the SD of multiple ROIs) and the uncertainty on the calibration fit and extrapolation. Analytical uncertainties (typically 1 to 3% relative) are negligible in comparison to these other sources. Carbon abundances measured by nanoSIMS can be found in SI Appendix, Table S1.

We quantified all major and minor elements in the quenched metal and silicate at the Smithsonian National Museum of Natural History using a JEOL JXA-8530F field emission electron probe microanalyzer. We Ir-coated all standards and unknowns simultaneously. We employed a liquid-nitrogen cold-finger to minimize the carbon background. The accelerating voltage was 10 keV, beam current was 10 nA, and beam diameter ranged from 3 µm when the available area was sufficiently large, down to a point analysis when it was not. The beam size (including activation volume) was large enough to average over quench features, and measured composition was insensitive to beam size. We used the following crystals for quantification: LIFL for Fe kα and Ni kα; TAPL for Si kα and Mg kα; LDE1L for O kα; and LDE5L for C kα. We counted for 10 s on-peak and for 5 s at high and low background off-peak positions. We employed the following primary standards (Ir-coated) for analysis of the metal phase: stoichiometric Fe₃C for carbon, Ni₁₀Fe₉₀ for nickel and iron, Mg metal for magnesium, Harvard hematite 92649 for oxygen, and Si metal for silicon. We employed the following primary standards (Ir-coated) for analysis of the silicate phase: stoichiometric Fe₃C for carbon, Ni₁₀Fe₉₀ for nickel, and San Carlos olivine for magnesium, iron, and silicon (oxygen assigned stoichiometrically). We monitored Ir-coated San Carlos and Springwater olivines, iron metal, Ni₂₅Fe₇₅ (all with 0% carbon), SRM479 (0.3 wt% carbon), and Fe₇C₃ (8.44 wt% C) throughout the runs as secondary standards. Off-peak corrections were linear for all elements except carbon, which was exponential. The matrix correction method was Phi-Rho-Z. Carbon analyses were corrected for a background based on analysis of multiple carbon-free standards and ferropericlase [(Mg,Fe)O] exposed proximal to the quenched metal and glass of our laser-heated spots (0.3 wt% C in silicates and 0.3 to 0.6 wt% C in metals, depending on the probe session). Consistent with previous studies on metal–silicate partitioning in the diamond anvil cell (e.g., ref. 53), we observed low totals in the metals of some samples, possibly due to quench textures (53). Reported compositions and uncertainties are averages and SDs, respectively, of four to seven analyses, and can be found in SI Appendix, Tables S1 and S2. Intersample variability in, for example, total Ni and C contents was likely produced by heterogeneity in the starting material on the scale of the laser-heated spots and possible carbon contamination from the diamond anvils (e.g., refs 23 and 54).

We performed confocal Raman spectroscopy on the quenched silicate glass of sample R193 (SI Appendix, Fig. S3). This sample exhibited areas with few to no exsolved metallic blebs in the silicate glass, and therefore was most likely to have preserved the high-temperature carbon speciation. The sample was repolished before Raman analysis. Analyses were performed using the Horiba LabRAM HR Evolution confocal Raman microscope at the Smithsonian National Museum of Natural History. Spatial resolution for the configuration used was ∼1 µm. We experimented with several laser and grating combinations. We found that a 532-nm laser operating at 25% output power (10.9 mW on the sample surface) resulted in significant visible damage to the sample and permanent changes to the Raman spectra, despite the fact that this power density was significantly less than was used in previous studies (e.g., refs. 8, 14, 17–20, and 55). We obtained high-quality spectra using a 405-nm laser operating at 100% power (4.3 mW on the sample surface) with a 600 gr/mm grating (30 accumulations, 15-s acquisitions). Strong peaks were observed at ∼1,340, 1,600, 2,720, 2,930, and 3,200 cm^–1, likely corresponding to elemental carbon (1,340, 1,600, and 2,720 cm^–1) (e.g., refs. 14 and 56), which may have precipitated upon P–T quench; CH₄ (2,930 cm^–1) (e.g., refs. 8, 14–16, 18, 19, and 55); and possibly alkyne C–H (3,200 cm^–1) (e.g., ref. 19).

Data Availability.

All relevant data supporting this study are available in the paper and SI Appendix.