Current status of genomic evaluation

Abstract

Early application of genomic selection relied on SNP estimation with phenotypes or de-regressed proofs (DRP). Chips of 50k SNP seemed sufficient for an accurate estimation of SNP effects. Genomic estimated breeding values (GEBV) were composed of an index with parent average, direct genomic value, and deduction of a parental index to eliminate double counting. Use of SNP selection or weighting increased accuracy with small data sets but had minimal to no impact with large data sets. Efforts to include potentially causative SNP derived from sequence data or high-density chips showed limited or no gain in accuracy. After the implementation of genomic selection, EBV by BLUP became biased because of genomic preselection and DRP computed based on EBV required adjustments, and the creation of DRP for females is hard and subject to double counting. Genomic selection was greatly simplified by single-step genomic BLUP (ssGBLUP). This method based on combining genomic and pedigree relationships automatically creates an index with all sources of information, can use any combination of male and female genotypes, and accounts for preselection. To avoid biases, especially under strong selection, ssGBLUP requires that pedigree and genomic relationships are compatible. Because the inversion of the genomic relationship matrix (G) becomes costly with more than 100k genotyped animals, large data computations in ssGBLUP were solved by exploiting limited dimensionality of genomic data due to limited effective population size. With such dimensionality ranging from 4k in chickens to about 15k in cattle, the inverse of G can be created directly (e.g., by the algorithm for proven and young) at a linear cost. Due to its simplicity and accuracy, ssGBLUP is routinely used for genomic selection by the major chicken, pig, and beef industries. Single step can be used to derive SNP effects for indirect prediction and for genome-wide association studies, including computations of the P-values. Alternative single-step formulations exist that use SNP effects for genotyped or for all animals. Although genomics is the new standard in breeding and genetics, there are still some problems that need to be solved. This involves new validation procedures that are unaffected by selection, parameter estimation that accounts for all the genomic data used in selection, and strategies to address reduction in genetic variances after genomic selection was implemented.

Introduction

Genomic selection is now widely practiced across the breeding and genetics industry. This is evident by large-scale genotyping using inexpensive SNP chips. As of November of 2019, genotypes were available for over 3 million U.S. Holsteins (https://queries.uscdcb.com/Genotype/cur_freq.html), over 700,000 for American Angus (S. P. Miller, American Angus Association, Saint Joseph, MO, personal communication), and over 100,000 animals per line for some pig and broiler breeding companies.

Generally, the beginning of genomic selection is attributed to a study by Meuwissen et al. (2001). They used simulated data to conduct analyses with a large number of equally spaced markers; no attempt was made to identify QTLs but some markers were by chance to be closely linked to QTLs. Computations included haplotypes, and analyses were done by methods called BayesA and BayesB that assumed different distribution of haplotype effects. With 2,200 genotyped animals, they obtained prediction accuracies of 0.85. The accuracies were >0.7 after five generations without phenotyping or with only 500 genotyped animals. Such high accuracies with small data created high hopes in the animal breeding community.

The first large-scale genotyping was possible after the introduction of the SNP 50k bovine chip (Matukumalli et al., 2009), which provided an affordable and accurate technology for genotyping. Much subsequent work on the methodology of genomic selection focused on SNP effects and on the creation of a genomic relationship matrix (G) (VanRaden, 2008), a concept that allowed conceptual comparisons between pedigree-based and genome-based predictions. Methods using either SNP effects or genomic relationships led initially to field data analyses using a multistep methodology (VanRaden, 2008; VanRaden et al., 2009), where a regular genetic evaluation by pedigree BLUP (meant as non-genomic method throughout the paper) is followed by the extraction of pseudo-phenotypes of genotyped animals, a genomic analysis for genotyped animals, and the creation of an index combining results from BLUP and the genomic analysis (VanRaden et al., 2009). The multistep methodology is the natural choice when the genomic and pedigree/phenotypic data are owned by separate organizations.

When the genomic selection was introduced, the main focus was on testing models to increase accuracy, in particular increasing the accuracy of prediction by SNP selection (or differential weighting), assuming that it was possible to identify most pairs QTL-closest SNP from data. However, as the data grows bigger, gains with SNP selection become smaller or nonexistent (Karaman et al., 2016). Subsequently, most commercial evaluations do not use SNP selection.

The multistep method is relatively complicated and in its initial form relies on the existence of animals (bulls) with high accurate EBVs from pedigree information. It is also subject to double counting of the genomic information when both parents and progenies are genotyped. Because the genomic information can be expressed as genomic relationships (VanRaden, 2008), Misztal et al. (2009) proposed a single-step evaluation that enhanced the BLUP machinery with a relationship matrix that combines pedigree and genomic relationships. Subsequently, a pedigree-based BLUP with any model of analysis could support genomic models just by replacing the relationship matrix. A combined matrix was first shown by Legarra et al. (2009) and complete analysis using the so-called single-step genomic BLUP (ssGBLUP) was presented by Aguilar et al. (2010) and Christensen and Lund (2010). In the following studies, ssGBLUP was shown to be as accurate, or more, than multistep analyses.

Initially, the main focus of the single-step research was ensuring compatibility of genomic and pedigree information (Vitezica et al., 2011) because incompatibility creates biases, especially under strong selection. A later focus was extending ssGBLUP to larger numbers of genotyped animals (Legarra and Ducrocq, 2012; Fernando et al., 2014, Liu et al., 2014;Misztal et al., 2014a). Currently, ssGBLUP is the main tool for genomic evaluation in species other than dairy. If a population includes non-genotyped animals with phenotypes, the transition to some form of single step is unavoidable because BLUP, which is used to created pseudo-observations adopted in multistep, becomes biased by genomic preselection (Patry and Ducrocq, 2011b). The only alternative to ssGBLUP that has been explored is the use of segregation analysis to partially “infer” genotypes of the ancestors of genotyped animals, to later introduce this information in a refined ssGBLUP (Meuwissen et al., 2015). This strategy gave promising results but it is computationally complex and has not been pursued.

Advances in genotyping techniques are allowing sequence data to be generated at a lower cost; therefore, there is an interest to exploit these data (Georges et al., 2019). Sequence data can be used to identify recessive genes, targets for gene editing, and also potential causative SNP that can aid a genetic prediction across breeds or lines (Hayes and Daetwyler, 2019). However, gains with using the potential causative variants for genetic prediction appear to be limited (VanRaden et al., 2017; Fragomeni et al., 2019), with perhaps the exception of across-breed prediction (Moghaddar et al., 2019).

Although the rate of increase in genetic gain delivered by genomic selection can be over 100 % in some cases (García-Ruiz et al., 2016), issues have recently emerged. One important issue is the fast reduction in additive genetic variance and more undesirable genetic correlations between important traits (Hidalgo et al., 2020). This reduction is even more noticeable when genomic information is not used for variance components estimation. The same phenomenon may be responsible for the reported reduction of 33% in heritability in computations of genomic predictions for production yield traits to avoid bias in genomic estimated breeding values (GEBV; VanRaden et al., 2014).

From the onset of genomic selection, many ideas were proposed and usually tested by simulation, and many of these ideas were later applied to real data sets, first small then large. Many of these studies led to questions about various aspects of genomic selection, for example: Is it better to use haplotypes instead of SNP? What is the optimal number of SNP? Why there are discrepancies between simulation and field studies? Why is SNP selection less useful with large data? How can we use unknown parent groups (UPG) in genomic models? Is there any limit to genomic selection?. The purpose of this paper is to present and evaluate proposed ideas on genomic selection considering most up-to-date experiences with field data.

Exploring Genomic Selection Developments

Initial developments

Genomic selection is generally attributed to a study by Meuwissen et al. (2001) where simulated data for up to 2,200 phenotyped animals with genomic information expressed as 50k haplotypes. For prediction, haplotype effects were estimated by several methods including treating them as fixed effects, by haplotype-BLUP assuming haplotypes as normal random effects, by BayesA assuming a t-distribution of effects (allowing for large effects), and by BayesB assuming a mixture distribution where most haplotypes had null effects. The accuracy of predicting breeding values for the next generation was the highest using BayesB and reached 0.85. The persistence of accuracies over generations (without additional phenotypes) was excellent, decaying only to 0.72 after an additional five generations of data. Reducing the number of animals with phenotypes to 1,000 only slightly reduced the accuracy to 0.79. The study by Meuwissen et al. (2001) generated great excitement in the animal breeding community, showing the possibility of very high accuracy with small data. However, this turned out to be true because the simulation was unrealistic with a small genome and QTLs of large effect, and no selection. Muir (2007) showed low persistence of genomic predictions under selection and dependence of accuracy on population parameters.

Much of the work involving the methodology of genomic selection on a practical side was accomplished by VanRaden (2008) using SNP markers instead of haplotypes. Also, he showed the equivalence of BLUP with SNP effects to genomic BLUP (GBLUP) using G; where G = ZZ/k, with Z being the matrix of gene content, ${\displaystyle k=2^n{\displaystyle \sum _{i=1}^{SNP}}{p}_i(1-p_i)}$, and $p_i$ the frequency of the ith SNP. While genomic and pedigree inbreeding were highly correlated (r = 0.68) using base allele frequencies (AF) but lowly using current AF (r = 0.12), any AF resulted in similar prediction accuracy. The SE for elements of G was inversely proportional to the square root of the number of markers. He stated that genomic relationships are due to shared alleles, and he related the distribution of such alleles to a study by Stam (1980). VanRaden (2008) findings on gene frequencies were validated by Strandén and Christensen (2011) who showed that in SNP, BLUP and GBLUP AF only affect the mean of predictions. The number of shared alleles, also known as independent chromosome segments (ICS), was used for approximating the accuracy of genomic selection based on the number of genotyped animals and heritability (Goddard, 2009); lower Ne means fewer segments to estimate and higher accuracy of genomic selection for the same population size.

Limited dimensionality of genomic information

Genomic prediction in farm animals is possible because of the small effective population size (Ne). Stretches of DNA from overrepresented ancestors (i.e., popular bulls) form relatively few segments called LD blocks (Muir, 2007), shared segments (VanRaden, 2008), or ICS (Goddard, 2009). While the segments are not easily identified and have fuzzy limits (i.e., they are broken at slightly different places across two sibs), they appear indirectly, for example, as singular G that needs to be blended to become full rank. The number of chromosome segments is usually quantified by the formula presented by Stam (1980) as 4 NeL, where L is genome length. In a simulated population, Pocrnic et al. (2016a) found that the accuracy of prediction using a recursion was maximized assuming 4 NeL segments. They also showed that for a large population the number of segments can be estimated as the number of the largest eigenvalues explaining 98% of the variation in G, with the remaining 2% interpreted as noise. Extension of their studies to farm animals (Pocrnic et al., 2016b) allowed to determine the number of segments, and indirectly Ne, and the optimal size of the SNP chip for several species (see Table 1).

Table 1.

Estimated number of chromosome segments, effective population size, and the optimal size of SNP chip following Pocrnic et al. (2016)

Species	Estimated number of segments	Estimated optimal size of SNP chip	Estimated effective population size
Broiler chicken	4.2k	50k	44
Pig	4.1k	49k	48
Angus cattle	10.6k	127k	113
Jersey cattle	11.5k	138k	101
Holstein cattle	14.0k	168k	149

The genomic prediction does not act on individual segments but on their clusters, where the four largest clusters could account for 10% of the genetic variation (Pocrnic et al., 2019a). Small data only allow to estimate only the largest eigenvalues (or clusters), but they explain a large portion of the genomic variation in G. Subsequently, moderate accuracy of genomic selection can be achieved with small data sets, and large data sets are needed for additional improvements. The same study explains why SNP selection improves accuracy in small but not in large data sets. Genomic selection works by estimating the effects of chromosome segments, and once nearly all are well estimated, the accuracy is high without SNP selection (Karaman et al., 2016) or weighting (Lourenco et al., 2017).

Estimation of haplotypes or SNP effects

If the DNA information is inherited as chromosome segments, it would be natural to base the estimation on haplotypes rather than on SNP effects. Using haplotypes would potentially account for epistasis within each block, as for instance, a segment of 5 SNP can be estimated as having 25 different SNP combinations, as opposed to only 5 SNP effects. In practice, the difference in accuracy in models with haplotypes and SNP effects is negligible (Cuyabano et al., 2015; Jónás et al., 2016). Problems using haplotypes are the need for a complex data preparation and arbitrary choices in their definition, poor estimates for rare haplotypes and the existence of spurious haplotypes due to genotyping errors.

Multistep genomic evaluation

A study by VanRaden et al. (2009) using field data sets established a mature multistep methodology for genomic selection in dairy cattle. The steps included running pedigree-based BLUP with the national database, creating pseudo-observations for genotyped animals (bulls) such as daughter yield deviation (DYD). These pseudo-observations are fit into a model estimating on SNP effects assuming normal (linear) or non-normal (nonlinear) distributions. Finally, genomic predictions for a genotyped animal or candidate to selection are obtained combining pedigree and genomic-based predictions into an index:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{G}\mathrm{E}\mathrm{B}\mathrm{V}={\mathrm{w}}_1\mathrm{P}\mathrm{A}+{\mathrm{w}}_2\mathrm{D}\mathrm{G}\mathrm{V}-{\mathrm{w}}_3\mathrm{P}\mathrm{I},}\end{array}}$$

where GEBV is the genomic estimated breeding value, PA is parent average, DGV is direct genomic value, and PI is parental index created based on pedigree relationships for genotyped animals. Essentially, PI removes double counting of relationship information because part of PA is included in DGV, and weights w1 to w3 could be approximated from reliabilities of each component. Genomic prediction in the aforementioned paper was validated by forward prediction, where prediction for young bulls using truncated data were compared with pseudo-phenotypes of those bulls obtained by BLUP with complete data. That study also showed that increasing the reference size of the genotyped population has a higher impact on prediction accuracy than the number of SNP markers and that assuming non-normal SNP distribution has a positive effect only on traits with large effect QTL. Instead of creating DYD, which is time-consuming, pseudo-observation could be calculated as deregressed proofs (DRP) (VanRaden and Wiggans, 1991; Garrick et al., 2009; Wiggans et al., 2011).

Another version of a multistep method depended on using genomic predictions called molecular breeding value as a correlated trait (Kachman, 2008; MacNeil et al., 2010). In this version, GEBVs for genotyped animals based on previously estimated SNP effects were added as an extra trait with genetic correlation computed separately. Because genomic predictions indirectly include parent average, it was hard to account for double counting, and genetic trend was abnormally high even for early time periods when the genomic selection was not practiced (Lourenco et al., 2018).

Single-step genomic evaluations

The multistep methodology was well suited for scenarios where the phenotype and genomic data belong to separate organizations, and especially when most information can be condensed in a small number of animals to genotype. This includes dairy populations with a large number of average information bulls with many daughters. When a population includes both males and females, creating DRP free of double counting is hard, especially when genotyping includes parents and their progeny (Legarra et al., 2014). As the genomic information can be used to capture relationships, Misztal et al. (2009) proposed combining pedigree and genomic relationships into a combined relationship matrix. Subsequently, pedigree-only analyses could be converted to genomic analyses only by replacing the pedigree relationship matrix by the combined matrix, and the steps of construction pseudo-phenotypes and the index would no longer be needed. This combined matrix (H) was first presented by Legarra et al. (2009) who proposed to extend the genomic information to non-genotyped animals based on the joint distribution of breeding values of non-genotyped (u₁) and genotyped (u₂) animals:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{H}=\left[\begin{array}{ll}var\left(u_1\right)& {\displaystyle cov(u_1,u_2)}\\ cov(u_2,u_1)& {\displaystyle var\left(u_2\right)}\end{array}\right]=\left[\begin{array}{ll}{\mathbf{A}}_{11}+{\mathbf{A}}_{12}{\mathbf{A}}_{22}^{-1}(\mathbf{G}-{\mathbf{A}}_{22}){\mathbf{A}}_{22}^{-1}{\mathbf{A}}_{21}& {\displaystyle {\mathbf{A}}_{12}{\mathbf{A}}_{22}^{-1}\mathbf{G}}\\ {\mathbf{G}\mathbf{A}}_{22}^{-1}{\mathbf{A}}_{21}& {\displaystyle \mathbf{G}}\end{array}\right]}\end{array}}$$

where subscripts 1 and 2 refer to non-genotyped and genotyped animals, respectively; A is the pedigree relationship matrix and G is the genomic relationship matrix or G. Christensen and Lund (2010) arrived to the same results, using the notion of predicting the genotype at non-genotyped individuals using pedigree information.

The inverse of H was presented by Aguilar et al. (2010) and Christensen and Lund (2010) as:

$${\displaystyle \begin{array}{l}{\displaystyle H^{-1}=A^{-1}+\left[\begin{array}{cc}0& {\displaystyle 0}\\ 0& {\displaystyle G^{-1}{}^{-}{A}_{22}^{-1}}\end{array}\right]}\end{array}}$$

In the analyses done by Aguilar et al. (2010), the reliability of the new method called ssGBLUP was as high or higher than in multistep.

Further research involving ssGBLUP was split into several directions. The first was compatibility between pedigree and genomic relationships, as incompatibility can generate biases or losses of accuracy under selection (Vitezica et al., 2011). The second was an extension to a very large number of genotyped animals as initial implementation was based on dense matrices (Aguilar et al., 2011), which restricted the number of genotyped animals to about 100k animals. Finally, there was an interest in accommodating SNP weighting via a weighted G, especially with potential causative SNP obtained from sequence data. The interest in single-step methods increased as the genomic selection was underway, because pedigree BLUP and, therefore, multistep methods were becoming biased due to genomic preselection (Patry and Ducrocq, 2011b), whereas ssGBLUP accounts for preselection.

Different single-step formulations

Several alternative single-step formulas were proposed. These included equations where G is not inverted (Legarra and Ducrocq, 2012), where SNP effects are estimated for the genotyped animals and a polygenic effect is fit for non-genotyped animals (Legarra and Ducrocq, 2012; Liu et al., 2014), and where SNP effects were fit for all animals using imputed genotypes (Fernando et al., 2014; Taskinen et al., 2017). The purpose of these formulas was to reduce computations with many genotyped animals. As opposed to a regular ssGBLUP, which can be applied to an existing BLUP software just by replacing the relationship matrix, SNP-based models require new programming. Meuwissen et al. (2014) proposed an alternative single-step approach by combining identical by descent and identical by state approaches.

Compatibility between genomic and pedigree relationships

An important issue in single-step methodology is the compatibility of genomic and pedigree relationships. While the genomic relationships indirectly account for all the ancestors but have an arbitrary scale depending on gene frequencies, the pedigree relationships have a well-defined scale but are limited by the depth and completeness of the pedigree. When pedigrees were complete up to a base population, scaling G for compatibility (same means for diagonals and off-diagonals) with the pedigree relationship matrix for genotyped animals (A₂₂) improved accuracy and eliminated bias for a population under strong selection (Chen et al., 2011a; Vitezica et al., 2011). With no selection, the impact of scaling was minimal. Similar scaling could be accomplished automatically by using base population gene frequencies (Strandén and Christensen, 2011; Christensen, 2012), although finding those frequencies when the base population is not genotyped, for example, using the method of Gengler et al. (2008), can be time-consuming, and it suffers sometimes from a clear definition of base population as described below.

When the base populations are heterogeneous with missing pedigrees across generations, as is typical in ruminants, ssGBLUP may diverge or become biased, and the standard way to ensure convergence was by including a parameter ω as in Tsuruta et al. (2011):

$${\displaystyle \begin{array}{l}{\displaystyle H^{-1}=A^{-1}+\left[\begin{array}{cc}0& {\displaystyle 0}\\ 0& {\displaystyle G^{-1}-\mathrm{\omega }{A}_{22}^{-1}}\end{array}\right]}\end{array}}$$

The parameter ω compensates for incomplete pedigree and incomplete accounting of inbreeding (Misztal et al., 2017). Incompleteness of pedigree in A₂₂ can be minimized by truncating old data and pedigree (Misztal et al., 2013b) or by assigning nonzero inbreeding to unknown parents (VanRaden, 1992); old missing pedigree becomes irrelevant with truncation of data. Truncation to two generations of phenotypes and three generations of pedigree reduced bias without lowering accuracy (Lourenco et al., 2014; Howard et al., 2018).

In a single-step SNP-based model known as single-step Bayesian Regression (ssBR) developed by Fernando et al. (2014), the compatibility between genomic and pedigree information is provided partially by the use of fixed effects in a model for genotyped animals (Hsu et al., 2017), similar to Vitezica et al. (2011) where this effect is implicitly fit as random. This arises from the findings of Strandén and Christensen (2011) that solutions from SNP BLUP and GBLUP are independent of gene frequencies if the model includes a mean. However, the missing pedigree problem is present in all single-step formulations and it becomes more complex with several base populations as described below.

Missing pedigree and UPG

In several species, there is a need to define several populations. This is the case in ruminants with missing parents (whereas unknown parents of animals born in 2000 are better than unknown parents of animals born in 2016), and the case in pigs and birds (with several lines collapsing into one, and with 2-, 3-, and 4-way crosses). These base populations have different means due to selection and not considering them leads to strong biases.

In BLUP, the genetic merit of these different base populations is often modeled by genetic or UPG (Quaas and Pollak, 1981; Quaas, 1988; Westell et al., 1988). In ssGBLUP, when UPG are applied only to pedigree relationships (A) as follows:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}^{\ast }={\mathbf{A}}^{\ast }+\left[\begin{array}{lll}0& {\displaystyle 0}& {\displaystyle 0}\\ 0& {\displaystyle {\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}}& {\displaystyle 0}\\ 0& {\displaystyle 0}& {\displaystyle 0}\end{array}\right]}\end{array}}$$

The convergence rate can be slow or no convergence may be reached (Tsuruta et al., 2014; Matilainen et al., 2016), partly because UPG were ignored in pedigree relationships for genotyped animals (A₂₂). Indeed, construction of A₂₂ implicitly assumes complete pedigrees. Misztal et al. (2013b) revised UPG equations to include groups also in the genomic portion of H based on Quaas–Pollak (QP) transformation:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{H}}^{\ast }={\mathbf{A}}^{\ast }+\left[\begin{array}{lll}0& {\displaystyle 0}& {\displaystyle 0}\\ 0& {\displaystyle {\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}}& {\displaystyle -({\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}){\mathbf{Q}}_2}\\ 0& {\displaystyle -{\mathbf{Q}}_2^{\prime }({\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1})}& {\displaystyle {\mathbf{Q}}_2^{\prime }({\mathbf{G}}^{-1}-{\mathbf{A}}_{22}^{-1}){\mathbf{Q}}_2}\end{array}\right]}\end{array}}$$

When UPGs were applied to all components of H as above, convergence dramatically improved for a multitrait model in the Nordic dairy cattle population (Matilainen et al., 2016). Revised UPGs also worked well for the U.S. Holstein data up to 2014 (Misztal et al., 2017). However, using data updated to 2015, Masuda et al. (2018a), based on cross-validation, reported lower reliabilities using revised UPG than not using UPG at all. While most animals genotyped earlier were potentially elite, with complete pedigree, most genotyped animals after 2014 were commercial cows, often with incomplete pedigree and high pedigree error rate (Bradford et al., 2019a).

It is not clear whether the equations for UPG in ssGBLUP should be considered for G for a single breed as genomic relationships are not affected by missing pedigree, and, therefore, UPG are automatically accounted for. In other words, if all animals were genotyped, terms involving UPG should disappear from H* above. Tsuruta et al. (2019a) found that removing G from the equation above improved accuracy and reduced bias. In GBLUP, using UPG for G did not increase accuracy for multi-breed populations (Plieschke et al., 2015).

Missing relationships also cause underestimation of inbreeding as animals with missing parents are automatically treated as not inbred. One solution is assigning nonzero inbreeding to missing parents (VanRaden, 1992; Lutaaya et al., 1999; Aguilar and Misztal, 2008). Such assignment improved convergence rate and bias in ssGBLUP in Holsteins (Misztal et al., 2017; Tsuruta et al., 2019a) although it only slightly affected the accuracy.

The concept of metafounders

Legarra et al. (2015) proposed to account for UPG while providing proper scaling by generalizing UPG to metafounders. In their approach, G would be derived using 0.5 AF as an “absolute reference” (Christensen, 2012), and A would be scaled for compatibility with G using relationships among and within metafounders, which are seen as pseudo-individuals. These relationships represent sizes and overlaps of the different base populations (Legarra et al., 2014). They can be estimated in such a way so that they account for scaling, unaccounted inbreeding, different genetic level (e.g., when using multi-breed animals or selected populations), and multiple breeds and crosses. Several methods were proposed to estimate the relationships, and, in practice, they imply estimating gene frequencies in the different base populations (Garcia-Baccino et al., 2017). In simulations and real data, the concept of metafounders delivered the least biased predictions (Garcia-Baccino et al., 2017; Meyer et al., 2018; Bradford et al., 2019b). When applied to dairy cattle, the relationships across metafounders could be well estimated only for metafounders associated with sufficient number of genotypes (S. Tsuruta, University of Georgia, Athens GA, personal communication). In dairy sheep, the use of metafounders reduces biases in predictions and instability of UPG estimates for small data sizes (F Macedo, INRAE, Toulouse, France, personal communication).

Evaluations of crossbred populations

Genomic evaluation of crossbred populations may be separated into two types, for specific crosses or for complex crosses. In pigs and chicken, there is an interest in using F1 and possibly three- to four-way crosses for the evaluation of purebreds on the commercial scale. In beef and dairy, the interest is to have a joint analysis of many breeds with complex crosses (e.g., “Kiwi” Jersey–Holstein crosses in New Zealand, 10+ breed crosses by International Genetic Solutions, and 50+ beef crosses by The Irish Cattle Breeding Federation). More recently, across-breed prediction with genomic data is not successful (Erbe et al., 2012; Kachman et al., 2013) because the breeds do not share the same chromosome segments. Also, the crossbreeds generate limited information if the amount of crossbred data is small and if they are progeny of very few parents (Pocrnic et al., 2019b). Genetic by environment interaction and purebred-crossbred correlations can be considered using multiple-trait models (Xiang et al., 2016; Vandenplas et al., 2017). With purebreds and defined crosses (F1), the genomic relationships can be adjusted separately for each breed combination using gene frequencies or other methods (Makgahlela et al., 2014; Lourenco et al., 2016) although the impact of such adjustment is small if the selection pressure is low. With many crosses, a simple approach is to ignore gene frequencies and have one set of SNP effects (Golden et al., 2018) or one G (Mäntysaari et al., 2017) for all breeds and breed combinations. Steyn et al. (2019) simulated five breeds using either shared or separate relationships. In the second case, the accuracy was compromised if the number of SNPs was reduced from 45k to 9k, and despite all breeds having identical QTLs, interbreed predictions had low accuracy. In U.S. dairy, SNP effects are estimated separately for each breed as otherwise the predictions would be based on the dominating breed—Holsteins (VanRaden et al., 2020); phenotypes of crossbreds are not used in the regular genetic evaluation of purebreds because of concerns of compromising the evaluation of purebreds. The most refined method for the F1 crossbreds is by phasing haplotypes in crossbreds originating from two parental lines and building a model with two H matrices, one per breed (sometimes called the breed of origin [BOO] model) (Christensen et al., 2014). Xiang et al. (2016) observed an increase in accuracy compared with fitting a single H matrix in an analysis of Landrace, Yorkshire, and crosses. The method becomes complex for more complex crosses as the origin of alleles in each crossbred is more difficult to establish.

The concept of metafounders provides a convenient solution to ssGBLUP applied to purebreds and crossbreds (Christensen et al., 2015; Xiang et al., 2017). In such a case, the relationship across breeds represent a distance from a common genetic origin (usually a small relationship, but potentially different across pairs of breeds), and the variances within breed reflect correct scaling separately for each breed and for all breeds simultaneously (Legarra et al., 2015). Xiang et al. (2017) fit this model treating each breed combination as a different trait to account for G × E and observed the same accuracy as in the BOO model of Xiang et al. (2016).

Modifying single step for large data sets

Single-step GBLUP requires explicit or implicit computations of G^-1 and ${\mathbf{A}}_{22}^{-1}$. When created using dense matrix techniques (Aguilar et al., 2011), the practical limit is about 100k animals. This is because computations increase cubically and storage quadratically with the number of genotyped animals. Several strategies were proposed to overcome size limitations.

Indirect computations of A₂₂⁻¹

Matrix ${\mathbf{A}}_{22}^{-1}$ is dense and, therefore, cannot be created efficiently for a large number of genotyped animals. Henderson (1976) showed that the inverse of a submatrix of A could be obtained based on the rules for inversion of a partitioned matrix:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{A}}_{22}^{-1}={\mathbf{A}}^{22}-({\mathbf{A}}^{12}{)}^{\prime }{\left({\mathbf{A}}^{11}\right)}^{-1}{\mathbf{A}}^{12}}\end{array}}$$

When only a product of ${\mathbf{A}}_{22}^{-1}$ and a vector is required in the iteration process as in the preconditioned conjugate gradient (PCG) algorithm, that product can be calculated sequentially every round as follows (Masuda et al., 2017; Strandén et al., 2017):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{A}}_{22}^{-1}\mathbf{q}=[{\mathbf{A}}^{22}-({\mathbf{A}}^{12}{)}^{\prime }{\left({\mathbf{A}}^{11}\right)}^{-1}{\mathbf{A}}^{12}]\mathbf{q}}\end{array}}$$

where the product:

$${\displaystyle \begin{array}{l}{\displaystyle s={\left({\mathbf{A}}^{11}\right)}^{-1}{\mathbf{A}}^{12}\mathbf{q}}\end{array}}$$

is computed as a solution to:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{A}}^{11}s={\mathbf{A}}^{12}\mathbf{q}}\end{array}}$$

using sparse matrix techniques, in particular, because A¹¹ is sparse and small. Masuda et al. (2017) found that, for a U.S. Holstein population, this algorithm required 2 min to set up and less than 1 s per round of multiplication.

Algorithm for proven and young

Because of small effective population size in farm animals, G has a rank of about 5k for pigs and chicken to about 15k for beef and dairy (Pocrnic et al., 2016b), indicating the existence of that many LD blocks or chromosome segments. Subsequently, the inverse of G can be obtained by recursion on a number of “core” animals equal to the rank of G, indirectly assuming that breeding values of N animals contain the same information as the effects of N chromosome segments. When animals are designated as core (c) or noncore (n), the inverse of G can be directly obtained as (Misztal, 2016):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{G}}_{\mathrm{A}\mathrm{P}\mathrm{Y}}^{-1}=\left[\begin{array}{ll}{\mathbf{G}}_{\mathbf{c}\mathbf{c}}^{-1}& {\displaystyle 0}\\ 0& {\displaystyle 0}\end{array}\right]+\left[\begin{array}{l}-{\mathbf{G}}_{\mathbf{c}\mathbf{c}}^{-1}{\mathbf{G}}_{\mathbf{c}\mathbf{n}}\\ \mathbf{I}\end{array}\right]{\mathbf{M}}^{-1}\left[\begin{array}{ll}-{\mathbf{G}}_{\mathbf{n}\mathbf{c}}{\mathbf{G}}_{\mathbf{c}\mathbf{c}}^{-1}& {\displaystyle \mathbf{I}}\end{array}\right]}\end{array}}$$

where M is a diagonal matrix with elements:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{m}}_{\mathrm{i}}={\mathrm{g}}_{\mathrm{i}\mathrm{i}-}{\mathbf{g}}_{\mathrm{i}\mathrm{c}}{\mathbf{G}}_{\mathrm{c}\mathrm{c}}^{-1}{\mathbf{g}}_{\mathrm{c}\mathrm{i}}}\end{array}}$$

where i refers to the ith genotyped, noncore animal. This method has almost a linear cost (computations and memory) with the number of animals (Fragomeni et al., 2015) and has been successfully applied to 2.3 M genotyped animals (Tsuruta et al., 2019b). The choice of core animals for recursion is not critical for accuracy when the number of core animals is sufficient but influences the convergence rate; the random choice is preferable (Bradford et al., 2017). Lately, Pocrnic et al. (2019a) found that accuracies obtained with N core animals are like those obtained with G ignoring all but the largest N eigenvalues. This explains why the accuracy with the algorithm for proven and young (APY) using 25% of the optimal number of core animals is almost the same, as 25% of important eigenvalues explain 90% of the genetic variation in G. In fact, the recursion acts not on individual chromosome segments but on their clusters.

Inverse by singular value decomposition

The inverse of G can be derived from the eigenvalue decomposition:

$${\displaystyle \begin{array}{l}\mathbf{G}={\mathbf{U}\mathbf{D}\mathbf{U}}^{\prime }\end{array}}$$

where U is a matrix of eigenvectors and D is a matrix of eigenvalues. If all eigenvalues are positive, the inverse of G is:

$${\displaystyle \begin{array}{l}{\mathbf{G}}^{-1}=\mathbf{U}{}^{\prime }{\mathbf{D}}^{-1}\mathbf{U}\end{array}}$$

If G has small rank, only a small fraction of eigenvalues will be meaningful. Let D_t indicate a fraction of D with non-negligible eigenvalues, and let U_t be the corresponding eigenvectors. Then:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{G}}_t^{-1}={\mathbf{U}}_t^{{}^{\prime }}{\mathbf{D}}_t^{-1}{\mathbf{U}}_t}\end{array}}$$

While eigenvalue decomposition of G requires creating G explicitly and can be very expensive, a less expensive alternative, when there are more genotyped animals than SNP, is the singular value decomposition (SVD) of the matrix of SNP content (Z), where $\mathbf{Z}=\mathbf{U}{\mathbf{D}}^{0.5}\mathbf{V}$. The SVD for a matrix of 720k animals by 60k SNP takes less than a day (Y. Masuda, University of Georgia, Athens, GA, personal communication). The SVD concept can be applied separately for each chromosome (Ødegård et al., 2018)

Inverse by the Woodbury formula

Mäntysaari et al. (2017) proposed an inverse of $\mathbf{G}={\mathbf{Z}\mathbf{Z}}^{\prime }+\mathbf{I}\epsilon$ based on the Woodbury formula to overcome computing challenges when the number of genotyped animals is greater than the number of SNP:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{G}}^{-1}=\frac{1}{\epsilon }\mathbf{I}-\frac{1}{\epsilon }\mathbf{Z}{(\frac{1}{\epsilon }\mathbf{Z}{}^{\prime }\mathbf{Z}+\mathbf{I})}^{-1}\mathbf{Z}{}^{\prime }\frac{1}{\epsilon }}\end{array}}$$

where ${\mathbf{Z}}^{\prime }\mathbf{Z}$ is the design matrix of SNP BLUP and I is an identity matrix with the same dimension. The formula is an exact inversion but is based on an arbitrary value of ε (i.e., 0.05I, 0.05A₂₂), without which G could not be full rank. The “Woodbury” G^-1 is dense and is not used explicitly. Its use is only for PCG systems in which only a product of this matrix by a vector is desired, being reformulated as:

$${\displaystyle \begin{array}{ll}& {\mathbf{G}}^{-1}\mathbf{q}=\frac{1}{\epsilon }\{\mathbf{I}-\mathbf{Z}{(\mathbf{Z}{}^{\prime }\mathbf{Z}+\mathbf{I}\epsilon )}^{-1}\mathbf{Z}{}^{\prime }\}\\ & q=\frac{1}{\epsilon }\{\mathbf{I}-\mathbf{Z}{(\mathbf{U}\mathbf{D}\mathbf{U}{}^{\prime })}^{-1}\mathbf{Z}{}^{\prime }\}\\ & xq=\frac{1}{\epsilon }\{\mathbf{I}-\mathbf{S}\mathbf{S}{}^{\prime }\}q,\end{array}}$$

with

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{S}=\mathbf{Z}\mathbf{U}{}^{\prime }{\mathbf{D}}^{-1/2}}\end{array}}$$

Matrix S has dimensions equal to the number of animals by the number of SNP. In practice, the SNP BLUP design-matrix ${\mathbf{Z}}^{\prime }\mathbf{Z}$ is not full rank, and one dimension can be reduced to the actual rank (5k to 15k for one breed) by truncating U and D to eliminate small eigenvalues.

Single-step Bayesian Regression

If 50k SNP are enough for predictions, an alternative idea was to impute genotypes of non-genotyped animals, resulting in the same 50k SNP effects to estimate regardless of the number of genotyped animals. Let u₂, the vector of breeding values for genotyped animals be equal to Za, where a is a vector of SNP effects. Legarra et al. (2009) showed that the conditional distribution of breeding values for non-genotyped and genotyped animals has an expectation equal to ${\mathbf{A}}_{12}{\mathbf{A}}_{22}^{-1}{\mathbf{u}}_2$. Replacing u₂ by Za:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathbf{u}}_1=E\left({\mathbf{u}}_1|{\mathbf{u}}_2\right)+\epsilon ={\mathbf{A}}_{12}{\left({\mathbf{A}}_{22}\right)}^{-1}\mathbf{Z}\mathbf{a}+\epsilon =\mathbf{T}\mathbf{a}+\epsilon }\end{array}}$$

where T can be called an imputation matrix for non-genotyped animals and ε can be called an imputation error. Then, the breeding values in an animal model can be replaced by:

$${\displaystyle \begin{array}{l}{\displaystyle u=\left[\begin{array}{l}{u}_1\\ u_2\end{array}\right]=\left[\begin{array}{l}T\\ Z\end{array}\right]\mathbf{a}+\left[\begin{array}{l}\mathit{\epsilon }\\ 0\end{array}\right]}\end{array}}$$

Regardless of the number of animals, the number of “genomic” unknowns is equal to the number of SNP, although there is an additional uncorrelated effect ε with a simple relationship structure (Fernando et al., 2014). The model was reformulated for economy of memory by Fernando et al. (2016) who called it “hybrid model,” although the same model had already been proposed by Legarra and Ducrocq (2012). As the imputation was expensive, and the model is conceived to use Gibbs sampling methods, the implementation of ssBR in the BOLT software used graphical processing units, that is, GPU (Garrick et al., 2018). Compared with ssGBLUP, ssBR allows the user to estimate SNP effects directly but the implementation of complex models (e.g., correlated maternal effects with multiple traits) is quite complex. The method of ssBR was used for a multi-breed evaluation done by the Simmental association for more than 10 breeds (Golden et al., 2018) but they decreased the number of SNPs from 50k to about 2.5k preselected SNP, contrary to all other species who abandoned the idea of preselecting markers because an optimal subset of markers may not be optimal a few generations later. A more general (and simple) formulation of the ssBR model was given by Taskinen et al. (2017).

Other approaches

Legarra and Ducrocq (2012) developed an assymetric method where G was not inverted, but the method did not scale up well. Also, both Legarra and Ducrocq (2012) and Liu et al. (2014) proposed methods that used SNP effects estimated for genotyped animals. Vandenplas et al (2019) showed that such models when solved by the PCG algorithm require a special preconditioner for convergence.

Preselection bias

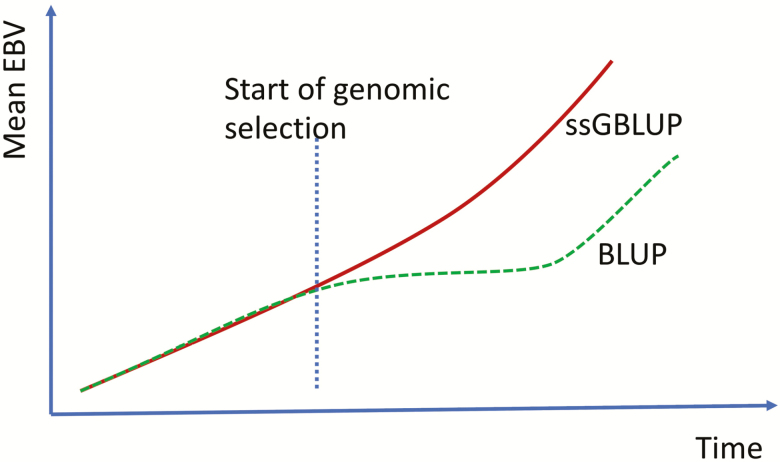
Under genomic selection, BLUP becomes biased (Patry and Ducrocq, 2011a, 2011b) due to preselection on Mendelian sampling; for instance, only offspring that has received the “good” alleles from a sire gets to be recorded. This has an impact on multistep methods which use BLUP as a first step, because they will tend to penalize genomically selected animals and, therefore, to underestimate the genetic trend. The bias can be corrected for (Wiggans et al., 2011, 2012), but the corrections need to be reevaluated as genotyping increases. Single-step GBLUP is expected to be resistant to selection bias (VanRaden et al., 2012; Legarra et al., 2014) as it considers all available information jointly. Masuda et al. (2018b) ran evaluations with BLUP and ssGBLUP for production traits in U.S. Holsteins. They found that the trends for BLUP level off, when they should actually increase, whereas trends for ssGBLUP were consistent. Based on the work at UGA in dairy and in pigs (unpublished), typical trends for genotyped animals by BLUP and ssGBLUP indicating preselection in BLUP are shown in Figure 1. The preselection bias can intensify when more animals are genotyped.

Figure 1.

Trend of (G)EBV with ssGBLUP (solid) and BLUP (dashed) indicating preselection bias in BLUP.

Differences between trends from BLUP and ssGBLUP can be used indirectly as a measure of the effectiveness of the genomic section. If the trend by ssGBLUP is increasing and the trend by BLUP is lower, genomic selection is successful. If the trends by both methods are identical, genomic selection does not have an impact over the regular selection. If in an extreme case, the trends by ssGBLUP decrease, it means either poor implementation of genomic selection or a change in the selection objectives.

Validation of genomic predictions

Genomic evaluations are validated by realized accuracies or reliabilities computed from predictions based on incomplete data to predictions/phenotypes based on complete data —see review by Daetwyler et al. (2013) and Legarra and Reverter (2018). Several types of validations are currently applied, and each one is suitable for a different data structure. The k-fold cross-validation depends on splitting the population into n samples and predicting phenotypes of one sample from the remaining samples (Saatchi et al., 2011). It is primarily used for small data sets when only one generation is genotyped or when other methods cannot be applied. As it follows from the decomposition of GEBV (VanRaden and Wright, 2013; Lourenco et al., 2015a), accuracies by clustering methods, such as the k-fold, depend on the algorithm for creating the clusters. In particular, BLUP may emerge as the best method if most animals in each cluster are progeny of the same ancestors.

The validation needs to consider that the breeder wants to predict the next generation from former ones, in other words, forward and not backward or “sideways.” Thus, another validation method is based on a comparison of pseudo-observations of sires (DYD or DRP) with their (G)EBV obtained without their daughter’s information (VanRaden et al., 2009). This validation type is only realistic for populations with sires that have large progeny sizes and phenotype recording is mainly on progeny, such as in dairy cattle. If pseudo-observations are computed by BLUP under genomic selection, this validation may be biased by preselection (Masuda et al., 2018b). If pseudo-observations are computed by ssGBLUP, the bias can be avoided but there is a danger of double counting of the genomic information, especially if progeny sizes are small. Yet another validation method that is called predictive ability or predictivity can be used when the validation animals have only their own records but not progeny (Legarra et al., 2008). It is based on correlations between GEBV obtained without a phenotype and the phenotype adjusted for fixed effects. However, it can only be computed for simple models and depends on the quality of adjustments (Legarra and Reverter, 2018). Accuracies based on validation are depressed by selection and, therefore, are lower than individual theoretical accuracies based on prediction error variance (PEV; Bijma, 2012; Lourenco et al., 2015a).

A completely different approach to validation was taken by Legarra and Reverter (2018) in a method called LR, which stands for linear regression. The method LR examines regressions and correlations of (G)EBV using complete and partial data sets while accounting for the relatedness of animals in the validation and additive variances under selection. The advantage of method LR is the ability to support any model and any data structure. For example, Bermann et al. (2020) were able to calculate the accuracy of evaluations for a threshold model. However, the method requires the additive variance for the validation population, which may be hard to estimate as typically these are a subset of selected animals. Without such a variance, only relative comparisons among methods are possible, although they are useful to rank methods.

Individual theoretical accuracies

Individual accuracies are published with (G)EBV as a measure of precision and they are based on true or approximated PEV derived from mixed model equations (Henderson, 1984). The PEV can be obtained either via efficient matrix inversion, for example, by REML with sparse matrix package YAMS (Masuda et al., 2015) or via Gibbs sampling (Tsuruta et al., 2017; Garrick et al., 2018). This is affordable for up to ~100K individuals genotyped. The last option can support larger data sets if the computation is by GPU (Garrick et al., 2018). For complex models and large populations, the computation of PEV is usually too expensive and approximations are used instead. With genomic information, the PEV for the ith animal can be approximated as (Misztal et al., 2013a):

$${\displaystyle \begin{array}{l}{\displaystyle PE{V}_i{\sigma }_e^2\approx \frac{1}{\frac{{\sigma }_e^2}{{\sigma }_a^2}+d_i^r+d_i^p+d_i^g}}\end{array}}$$

where $d$ are contributions (in terms of effective daughters or observations) due to pedigrees (r), phenotypes (p), and genomic information (g), and ${\sigma }_a^2$ and ${\sigma }_e^2$ are additive and residual variances, respectively. Approximate contributions due to pedigree and phenotypic information were determined by earlier studies (Misztal and Wiggans, 1988; Meyer, 1989; VanRaden and Wiggans, 1991).

With the multistep SNP model, the contribution due to genomic information could be calculated by inversion for any number of genotyped animals (VanRaden et al., 2011; Liu et al., 2017b). To avoid double counting, the calculations exclude the genomic information that is already included in the pedigree information. In ssGBLUP, the genomic contribution can be calculated by combined differences between genomic and pedigree relationships (Misztal et al., 2013a). Edel et al. (2019) provided formulas for avoiding double counting in ssBR. Efficient computation of genomic accuracies for any model and data set is still a research topic but not a hot one because when the models are too large for direct inversion, genomic predictions are accurate enough for selection.

Genetic parameters under genomic selection

Plant breeders estimate variance components at each genetic evaluation, partly because they have several random effects (e.g., blocks) and partly because their data sets are small. In contrast, animal breeders tend to use either once-in-a-while estimates or to use pedigree-based estimates for genomic evaluation purposes, for example, as in VanRaden (2008). Genetic parameters can be estimated with genomic information using ssGBLUP and normal tools such as REML or Monte Carlo Markov Chain via Gibbs sampling. The use of the genomic information increases the costs of computations because the inverse of G is usually dense, whereas non-genomic mixed model equations are sparse. Masuda et al. (2014) developed a sparse matrix package that recognizes and processes dense blocks rapidly. A four-trait single-step AIREML model with 15k genotyped animals took less than 1 h with the new package (Masuda et al., 2015); the computations increase cubically with the number of genotyped animals and of traits.

Comparing genomic and pedigree-based estimates of variance components relies on the compatibility of genomic and pedigree information (Legarra, 2016). Without selection and with a complete pedigree, the estimates of variance components ignoring or using the genomic information are usually similar, although with the genomic information they have lower standard errors (Forni et al., 2011). Under strong selection, the estimates ignoring the genomic information are biased (Gao et al., 2019; Hidalgo et al., 2020). The computed bias due to preselection depends on the accuracy of modeling and intensity of selection. For example, the popular QMSim program for simulation of genomic data (Sargolzaei and Schenkel, 2009) only performs BLUP selection. If various types of single-step methods show different results despite being equivalent models, the actual variances are affected by small details in the models (e.g., Gao et al., 2019)

Before genomic selection, the genetic parameters were thought to be generally stable, but this was not studied in depth. Under genomic selection, there are indications of rapidly changing parameters, perhaps due to the Bulmer effect (Van Grevenhof et al., 2012; Hidalgo et al., 2020). For instance, bias for U.S. dairy genomic evaluations decreased when heritability was reduced to about 70%—50% of the original value (Wiggans et al., 2012; Misztal et al., 2017), which is an indicator of overestimated heritability. Hidalgo et al. (2020) used a Gibbs sampling approach to analyze the changes in genetic parameters for growth and fitness traits in pigs. To make the computations possible, analyses were done in time slices of 3 yr, and genotypes were restricted to parents and animals with records. Over time, heritabilities for growth were reduced by one half and the antagonistic genetic correlations between growth and fitness traits became almost twice as strong. Estimates without genomic information were quite different. The aforementioned study illustrated the tradeoffs in parameter estimation under genomic selection. Without genomic information, the estimates may be biased, and with all the genomic information available the computation are expensive. Cesarani et al. (2019) reported biased variance components estimates under genomic selection when the genomic information was truncated or too few generations were used. A modest compromise is to restrict genotypes only to those animals on which selection was more intense and to remove genotypes of all young animals and possibly of nonparents. Genetic parameter estimation with a large number of genotypes can be possible in GBLUP when the APY algorithm is applied. However, in ssGBLUP, ${\mathbf{A}}_{22}^{-1}$is relatively dense and using it in computations eliminates most of the gains due to using a sparse ${\mathbf{G}}_{\mathrm{A}\mathrm{P}\mathrm{Y}}^{-1}$.

Stability of GEBV

Under BLUP, the evaluation of an animal depends nearly only on its phenotype, parents, and progeny. Therefore, EBV for animals with no new information are stable even if the accuracy is low (and PEV high). In genomic evaluations, all genotyped animals are connected through G. It means that information on new genotyped animals affects all the other genotyped animals, causing fluctuations. Changing core animals in the APY algorithm also causes fluctuations in GEBV even though the accuracy is not affected (Misztal et al., 2019). When short-term fluctuations are undesirable, for example, for merchandising, one solution is to use full model genomic prediction (by SSGBLUP or multistep methods) periodically (say once a month), compute SNP effects, and run interim (e.g., weekly) indirect predictions based on backsolved SNP effects. While with small data the indirect predictions can be inaccurate due to ignoring parent average, in large populations, the fraction of parent average in GEBV is small and indirect predictions have similar accuracy to complete predictions (Lourenco et al., 2015b; Garcia et al, 2020). To mitigate risk associated with potential rank changes of young bulls, semen from a team of bulls may be marketed instead of semen from individual bulls (e.g., https://www.dairynz.co.nz/animal/animal-evaluation/bull-team/).

Using sequence data for genomic predictions

As sequencing is becoming less expensive, there is an interest in exploiting sequence information in animal genetics. If all causative variants and their substitution effects could be identified, genomic prediction would be perfect (i.e., selection accuracy = 1.0). If those effects were conserved across breeds, accurate multi-breed evaluation would be possible (Goddard, 2017). But substitution effects may vary from breed to breed, even at the QTL level, due to gene–environment interaction and to nonadditive gene action (Duenk et al., 2020). Sequence data are available through selective sequencing of key animals across species (e.g., 1000 Bull Genomes Project; http://www.1000bullgenomes.com/; Hayes and Daetwyler, 2019) and imputation for the remaining animals (Ros-Freixedes et al., 2020). For a successful incorporation of potential causative SNP, they need to be very close to the actual causative SNP, and their a priori variance in a model need to be large as otherwise their value is strongly regressed toward 0 (Brøndum et al., 2015).

Practical results using sequence data from large data sets yielded mixed results. Some studies have found no improvement (Erbe et al., 2012) and some showed a small improvement, in particular Moghaddar et al. (2019) who found an increase in the accuracy of “distant” animals of ~0.10 using selected sequence variants. In a study that yielded up to 5% improvement in reliability across traits, VanRaden et al. (2017) partly used a bin concept, where they eliminated most of the SNP close to SNP with the largest effects. The bin concept, popular in plants, recognizes that QTLs are nested in chromosome segments and attempts to locate at most a few SNP per segment (Xu, 2013); fewer SNP reduce the impact of priors and reduce shrinkage of causative SNP. Fragomeni et al. (2017) showed that ssGBLUP can account for causative SNP if they have a large weight in a weighted G. In a study on stature in U.S. Holstein using the potential causative SNP identified by VanRaden et al. (2017), Fragomeni et al. (2019) found that the addition of potential causative SNP to the current SNP panel increased reliabilities in GBLUP but not in ssGBLUP, and reliabilities from ssGBLUP were the highest. Similar results were found in Belgian Blue cattle (J.L. Gualdrón-Duarte, University of Liege, Belgium, personal communication) and for health traits in dairy cattle (S. DeNise, Zoetis, Kalamazoo MO, personal communication). A few real, validated major genes (as identified by molecular genetics) explaining up to 10% of the genetic variance have been found and included in ssGBLUP evaluations, either as correlated traits (Legarra and Vitezica, 2015) or as weighting the G matrix appropriately. In general, any of these two strategies work and result in small, but less than expected, improvements on accuracy (Carillier-Jacquin et al., 2016; Teissier et al., 2018; Oget et al., 2019). Possibly, the causative SNP are already accounted for by the values of chromosome segments with large data. Some improvement with the causative SNP could be due to imperfect modeling by GBLUP with pseudo-data such as DRP or DYD instead of records.

There is a dilemma whether causative SNP with large effect, if found, should be used in selection programs for strongly selected traits. With long-term selection, most likely genes with positive effect for most traits are fixed or close to fixation, and genes that still have a large effect but are not fixed are likely to show undesirable pleiotropy. A chromosomal deletion in pigs increased growth but decreased fertility (Derks et al., 2018). Manhattan plots for mortality and milk yield, using a two-trait analysis, in U.S. Holstein showed the same peaks on chromosome 14 (Tsuruta et al., 2017). Georges et al. (2019) cite many studies indicating pleiotropy as a result of balancing selection, for example, where disruptive variants in genes increase muscularity but affect the viability of fitness. Negative effects of pleiotropy on low heritability traits may be hard to identify but can be important in the long run.

Balancing selection resulting in intermediate gene frequencies may be unlikely in cases where selection indices are utilized even with pleiotropy. While causative SNPs with large effects are not likely to be fixed after years of pedigree BLUP, the trend toward fixation will be faster with genomic selection. In the extreme, the fixation will negatively affect low heritability or sparsely recorded traits.

Genome-wide association studies

A standard tool for traditional genome-wide association studies (GWAS) is a model where one marker is analyzed at a time as fixed effect (Kennedy et al., 1992), for example, an efficient mixed-model association expedited—EMMAX (Kang et al., 2010). To reduce spurious signals due to a population structure, an animal effect using a pedigree or G is added to the model (Kennedy et al., 1992). Alternatively, many studies use Bayesian methods such as BayesB or BayesR with all SNP considered jointly, interpreting large signals as markers to nearby QTLs. While the former studies determine SNP significance using P-values, the latter usually estimate fractions of explained variance per segment of the genome, for example, 1 Mb.

Many studies, especially using small data, detect a large number of “large” markers, interpreting those as close to a QTL; however, the overlap of those markers across multiple populations or generations in a population under selection is minimal. This suggests that many detected associations are spurious (Fragomeni et al., 2014; Liu et al., 2017a). Studies using BayesB often show very high peaks, sometimes explaining >10% of the additive variance, especially with small data sets. As genomic selection with small data works on large clusters of chromosome segments (Pocrnic et al., 2019a), it is possible that some peaks may be tags to those clusters.

Many of these signals in GWAS are, therefore, probably false positives and can probably be explained by small data sets. If pedigree relationships are incomplete (e.g., ancestors not included), they would not account for population structure. In addition, P-values or False Discovery Rate are rarely reported.

Classical GWAS in EMMAX is conceived for a set of individuals that are genotyped and phenotyped. When genotyped animals have only records from progeny or other relatives, this method is only applicable in a multiple-step manner, that is, creating pseudo-phenotypes such as DRP or DYD as it was typically the case in dairy cattle (Boichard et al., 2003), but this is difficult to generalize to other species, where progeny sizes are smaller and many genotyped have phenotypes (e.g., weights) but not genotypes. However, Gualdrón-Duarte et al. (2014) and Bernal Rubio et al. (2016) showed the equivalence of P-values in GBLUP-based models with P-values in single-marker fixed regressions with a polygenic effect. Lu et al. (2018) extended the theory to ssGBLUP, and Aguilar et al. (2019) added this concept to the BLUPF90 package (Misztal et al., 2014b), with a successful implementation using 1 million birth weight phenotypes for American Angus, almost 2 million animals in the pedigrees, and 1,424 genotyped sires. The GWAS with P-values from ssGBLUP accounts for population structure, considers phenotypes from both genotyped and non-genotyped animals without additional steps, and allows for arbitrarily complex models. At this time, the method is limited to models where the left-hand side of the mixed model equations can be inverted, which sets a soft limit of perhaps ~100K genotyped animals.

Conclusions

Genomic selection methodology has been widely embraced by the animal breeding industry as evidenced by the scale of genotyping. The evaluation in most species except dairy cattle is by single-step methods, which consider all sources of information jointly, with methodology refined sufficiently to provide relatively unbiased evaluation for any data size, and easily accommodating causal genes. The dairy industry plans to move to single step are hampered by distributed ownership of phenotypic and genomic data. Most evaluations use <100K SNP chips without SNP selection or weighting, indirectly acknowledging that the prediction acts mostly on chromosome segments and less on markers of QTLs. Whether accurate determination of causative SNPs will lead to substantially increased accuracy of selection also across breeds is unclear. While the validations methods are less than perfect, they illustrate higher accuracy of evaluation with the genomic information. An important concern in long-term genomic selection may be a serious reduction of the additive variance that may limit future gains, especially given that the parameter estimation with the genomic information is difficult.

Glossary

Abbreviations

AF

allele frequencies

APY

algorithm for proven and young

BOO

breed of origin

DGV

direct genomic value

DRP

deregressed proofs

DYD

daughter yield deviation

G

genomic relationship matrix

GBLUP

genomic BLUP

GEBV

genomic estimated breeding values

GPU

graphical processing units

GWAS

genome-wide association studies

ICS

independent chromosome segments

LR

linear regression

PCG

preconditioned conjugate gradient

PEV

prediction error variance

ssBR

single-step Bayesian regression

ssGBLUP

single-step genomic BLUP

SVD

singular value decomposition

UPG

unknown parent groups

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.