Experimental measurements of ultrasound attenuation in human chest wall and assessment of the mechanical index for lung ultrasound

Abstract

Knowledge of the acoustic attenuation characteristics of the chest wall is necessary to estimate the acoustic exposure at the pleural surface during lung ultrasound and is useful in the prediction of bioeffects (e.g., pulmonary capillary hemorrhage) and the development of safe, effective lung imaging. Currently, this property is not well characterized in humans. The aim of this work was to characterize ultrasonic attenuation in human chest wall such that the ultrasound exposures of the lung can be estimated for clinically relevant conditions. In this study, we experimentally measured ultrasound transmitted through the intercostal tissue of 15 human cadaver chest wall samples relative to ultrasound transmitted through saline to determine attenuation coefficients for each sample. A GE Vivid 7 diagnostic ultrasound machine (GE Vingmed, Horten, Norway) and 3S and 5S phased array probes were used at center frequencies from 1.6 to 5 MHz. The chest wall samples varied in thickness from 2.3 to 5.5 cm with a median thickness of 3.8 cm. The frequency normalized attenuation coefficient was approximately 1.44 dB/cm/MHz based on a linear best fit through all attenuation measurements. The attenuation characteristics varied appreciably between samples and the sample-averaged linear attenuation coefficient was 1.43±0.32 (mean±std) dB/cm/MHz. This attenuation is higher than that previously measured in mammalian chest wall samples (1.1–1.3 dB/cm/MHz for mice and rats) and is much greater than that used by the mechanical index (0.3 dB/cm/MHz). Mechanical index values calculated using saline values derated by 0.3 dB/cm/MHz were up to 1.2 MPa/MHz^1/2 greater than those calculated using the measured through-tissue ultrasound waves. We conclude that the mechanical index overestimates exposures for lung ultrasound and thus may not be an appropriate dosimetry metric for pulmonary ultrasound.

Introduction

Diagnostic cardiac and lung ultrasound are regularly performed by transmitting ultrasound through the chest wall via the soft intercostal tissue between the ribs. Knowledge of the acoustic attenuation characteristics of the chest wall is necessary to estimate the ultrasonic exposure at the lung and is useful for the development of safe, effective ultrasound and the study of bioeffects such as pulmonary capillary hemorrhage (Miller et al. 2002; Teotico et al. 2001). Thus far there has been little research characterizing the acoustic properties of human chest wall and there is a need for data relevant to clinical diagnostic ultrasound. This study aimed to acquire clinically relevant measurements of ultrasound exposure for the human lung surface. We used a clinical diagnostic ultrasound machine to measure the bulk acoustic attenuation properties in human chest wall samples. Based on these measurements, we assessed the appropriateness of the mechanical index (MI) as a metric for lung ultrasound dosimetry.

Past studies have sought to characterize various acoustic properties of mammalian chest wall tissue. Miller et al. (2015) reported approximate chest wall attenuation coefficients of 1.1–1.3 dB/cm/MHz in rats and Teotico et al. (2001) similarly reported coefficients of 1.1 dB/cm/MHz in both mice and rats. Miller et al. (2002) measured the frequency-normalized acoustic attenuation coefficient α (dB/cm) of intercostal tissue in neonate pigs and found that, for 3.1–9.2 MHz ultrasound, it did not vary with age and was described by the best fit power-law α = 1.94 f^0.9 (dB/cm). Hinkelman et al. (1997) used a half-inch-diameter piston transducer to transmit 2.3 MHz ultrasound through human chest wall samples and reported energy level fluctuations with an average rms value of 1.57 dB. Later, Mast et al. (1999) computationally investigated ultrasound waveform deformation by simulating acoustic wave propagation through simulated ribs with geometries and material properties based on histological cross-sections of human rib samples. The results of this study were qualitatively consistent with Hinkelman et al. (1997) but underestimated waveform distortion. To accurately access the ultrasound exposure at the lung surface, experimental measurements of ultrasonic properties of intercostal tissues are necessary (Teotico et al. 2001), however, there appear to be no previous works reporting bulk attenuation coefficients in human chest wall intercostal tissue.

The FDA regulatory metric used for mechanical bioeffects of diagnostic ultrasound is the mechanical index (MI). This metric was designed as a means of assessing the potential for cavitation bioeffects. Subsequent evidence suggests that ultrasound-induced pulmonary capillary hemorrhage (PCH) is not driven by cavitation (O’Brien et al. 2000; Raeman et al. 1997). Furthermore, several previous studies have suggested that the MI is not an adequate safety metric for lung ultrasound or pulmonary capillary hemorrhage (Church and O’Brien 2007; Miller 2016; O’Brien et al. 2006). Despite this, safety regulations require the MI to be less than 1.9 for rapid vendor pre-market clearance and this serves as the primary limitation on the strength of lung ultrasound. It has been repeatedly shown that diagnostic ultrasound at MI less than 1.9 MPa/MHz^1/2 can directly cause PCH in mammals. Additionally, the MI is the only mechanical safety metric displayed on-screen to clinicians during diagnostic ultrasound procedures. Hence, there is a need to assess the applicability of the mechanical index to lung ultrasound.

In this study, we characterized the morphology of several unembalmed, never-frozen human chest wall samples and determined acoustic attenuation coefficients for each. To obtain clinically relevant data, a commercial diagnostic ultrasound machine was used and parameters relevant to lung ultrasound were considered. Additionally, we assessed the applicability of the MI to lung ultrasound. This work aimed to advance our ability to estimate the acoustic dose received by the lungs during diagnostic ultrasound in humans and thus may be useful for assessing the risk of pulmonary capillary hemorrhage.

Materials and methods

In this study, we ultrasonically imaged human cadaver chest wall samples in situ to characterize their morphology. Then, to determine the acoustic attenuation coefficient for each sample, we measured ultrasound transmitted through both saline and the ex vivo chest wall samples and compared these measurements.

Tissue sample preparation

15 axillary chest wall tissue samples were obtained from the University of Michigan Anatomical Donations program. Each sample was taken from a different never-frozen, unembalmed human cadaver donor. There were 6 male and 9 female donors. Donors’ ages at death ranged from 58 to 91 years with a median age of 77 years. At the time of measurement, donors were between 2 and 24 days after death, with an average death-to-measurement time of 8.7 days. For each donor, the cause of death was known. Of the available potential donors, only those with apparent damage to the chest wall or infectious diseases were excluded from this study.

The axillary chest wall of each potential tissue donor was ultrasonically imaged in situ using a Zonare ZS3 or Z.One ultrasound system (Zonare Medical Systems, Mountainview, CA) with an L14–5W probe at 12 MHz. The thorax can be scanned in several positions depending on the required exam, but the axillary region is relatively thin and useful for lung surface examination (Gargani and Volpicelli, 2014). A region appropriate to lung ultrasound was located, and the probe location was marked on the skin with a permanent marker. The probe was oriented such that the visible space between the ribs appeared minimized and the B-mode image was saved. The area around the probe location was marked using a permanent marker and a trained anatomical preparator removed the chest wall sample from the body. Each sample area was chosen indiscriminately from either the left or right side because the chest wall is morphologically symmetric (Mast et al. 1999). A typical sample area was approximately 14 cm × 14 cm though the exact size varied between donors due to variations in chest morphology. These size variations did not affect results as only a small portion of the sample was used for ultrasound measurements. When appropriate, the corners of the rectangular tissue sample were sutured immediately after removal from the body, to preserve the sample conformation. Upon removal, samples were immediately wrapped in Spilfyter Sorbent pads (NPS Corp, Green Bay, WI), sealed in a Ziploc 1 Gallon freezer bag (S. C. Johnson & Son, Inc., Racine, WI), and stored in a refrigerator at 4° C. Experiments were performed within one week of obtaining the tissue samples, though past research in pigs, rats, and mice suggests that intercostal attenuation coefficients are independent of postmortem storage time (Miller et al. 2002; Teotico et al. 2001).

Tissue sample morphology measurements

The in-situ chest wall ultrasound images were analyzed using the FIJI distribution of ImageJ (Rueden et al. 2017; Schindelin et al. 2012). Figure 1 shows an example image illustrating the relevant measurements. The approximate rib-to-rib distance (i.e., rib spacing) and depth were measured for each image. Efforts were made during imaging to orient the probe such that the on-screen image showed the shortest possible rib spacing for these measurements. A sample’s rib depth was taken as the average depth at the horizontal center of the visible ribs. For images in which the pleural line was visible between the ribs, the pleural depth was also measured at the center location between the ribs.

Figure 1:

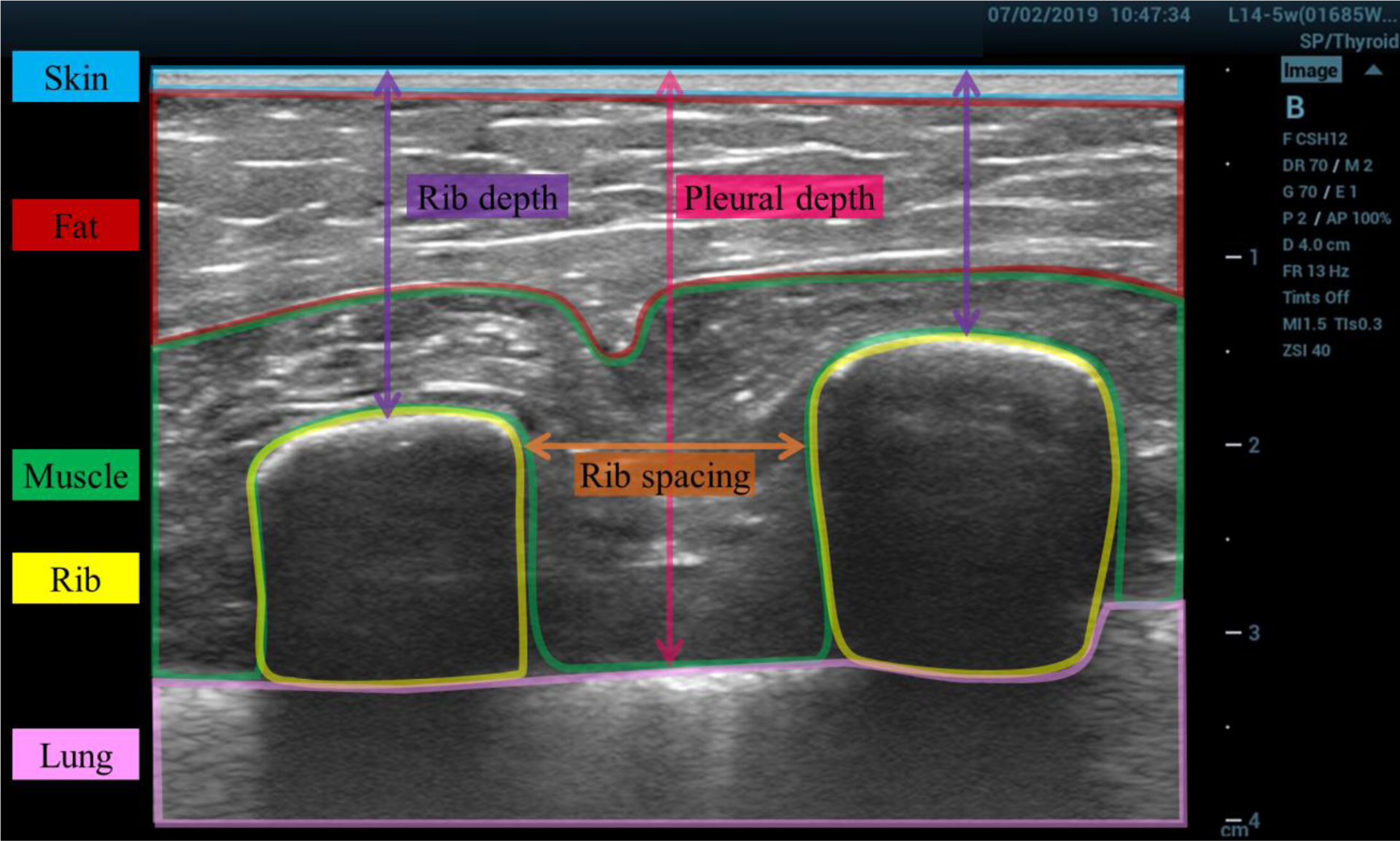
Example ultrasound image of the chest wall, with labeled tissue layers. The image was taken in situ prior to excision. The approximate borders of different tissue layers are highlighted and labeled: skin (blue), fat (red), muscle (green), rib (yellow), lung (pink). The rib spacing (orange), rib depth (purple), and pleural depth (magenta) measurements are illustrated.

Experimental setup for ultrasound measurements

Ultrasound measurements were performed in a large bath of degassed saline. Tap water was degassed under vacuum pressure for at least one hour and 9 mg/L NaCL was added to produce 0.9% normal saline. The water was heated to 37 °C in the bath and temperature was held approximately constant.

Figure 2 illustrates the experimental setup within the water bath for the through-tissue case, showing the hydrophone, ultrasound transducer, tissue sample in its holder, and their relative orientations. The hydrophone was rigidly mounted such that it remained in a fixed position within the bath throughout each experiment. The ultrasound probe and tissue sample holders were attached to separate 3D micropositioning systems. The ultrasound probe was placed against the skin side of the tissue sample, with the hydrophone behind the rib side, consistent with diagnostic lung ultrasound. The hydrophone was an HGL-0200 (Onda Corp., Sunnyvale, CA, USA), with a 0.2 mm sensitive spot, which was connected to a Tektronix MDO3052 Mixed Domain Oscilloscope (Tektronix, Beaverton, OR, USA) to record data.

Figure 2:

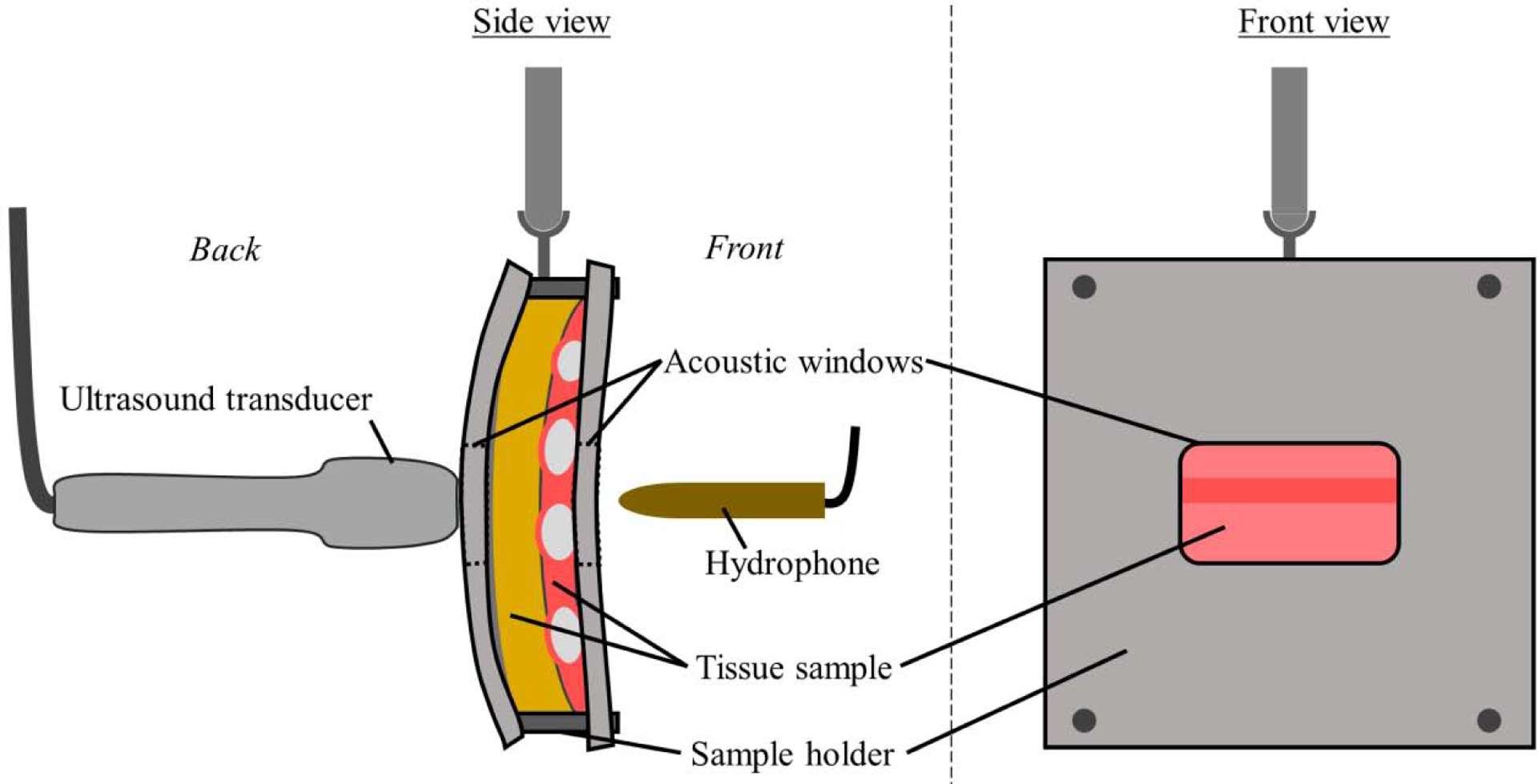
The experimental setup within the water bath. The ultrasound probe, hydrophone and tissue sample in its holder are shown. The hydrophone is rigidly mounted, while the probe and tissue sample are attached to 3D micropositioning systems (not shown). Within the tissue sample, the fat, muscle, and ribs are shown in yellow, pink, and light gray respectively.

Ultrasound equipment and parameters

For the attenuation measurements, a GE Vivid 7 ultrasound machine (GE Vingmed, Horten, Norway) was used to transmit ultrasound through chest wall samples and saline. A 3S phased array probe was used in cardiac mode at 1.6, 2.0, 2.5, 3.3, and 3.6 MHz frequency settings and a 5S phased array probe was used, also in cardiac mode, at 2.2, 2.8, 3.1, 4.0, and 5.0 MHz frequency settings. Clinical lung ultrasound frequencies vary from 3 to 13 MHz (Bouhemad et al. 2007; Saraogi 2015), though relevant bioeffects research has been performed at frequencies as low as 1.0 MHz (O’Brien 2007). The frequencies used in this study are within this range and were chosen from those possible based on the clinical ultrasound machine and probes used. The on-screen ultrasound focus was set at the tip of the hydrophone, at a focal depth of 5 or 6 cm depending on the specific sample being measured. Ultrasound measurements using higher frequency linear array probes were also attempted during the experimental design process, but successful measurements could not be consistently obtained for the thicker tissue samples due to strong acoustic attenuation.

Tissue holder

To hold the tissue during the experiments, each sample was placed in a low-density polyethylene plastic zipper bag filled with 0.9% normal saline such that no air remained in the bag. The sample was then clamped between two high-density polyethylene plastic sheets. Each sheet had an approximately 9 × 6 cm hole which served as an acoustic window. The 1.5 mm thick sheets were flexible enough to conform to the shape of each sample when clamped but rigid enough to maintain their shape throughout each experiment.

Measurement procedure

With the hydrophone, probe, and tissue sample placed in the bath, the tissue sample was moved aside (out of the page in Figure 2 - side view) and the probe position was adjusted according to the following procedure to perform the measurements. Using the B-mode image, the probe was initially positioned such that the axis of the hydrophone was aligned with the on-screen ultrasound axis and the tip of the hydrophone (i.e., the sensitive spot) was placed at a nominal depth of 5 or 6 cm such that the sample could be easily moved between the hydrophone and probe. The ultrasound was set to the minimum frequency setting of the probe (3S – 1.6 MHz; 5S – 2.2 MHz) and maximum power (−0 dB) setting. The probe was then moved within the scan plane, to find the position where the maximum peak-to-peak acoustic amplitude could be detected. At this location, two redundant acoustic measurements were taken at each power setting: −0, −2, −4, and −6 dB. These through-saline measurements will sometimes be referred to as reference signals and measurements hereafter.

Keeping the probe and hydrophone in place, the tissue sample and holder were placed between the probe and hydrophone. The sample was oriented such that the ultrasound scan plane was parallel to and between the ribs with the aim of transmitting as much ultrasound as possible through purely intercostal tissue. Keeping the skin-side of the sample against the ultrasound probe, the tissue sample was moved within the plane (up and down and in- and out-of-the-page on Figure 2) via the 3D positioning system, to search for an appropriate location for the through-tissue measurements. Each sample was positioned such that peak pressures observed were at a maximum for that sample, though transmission through the near-edge areas of the samples was avoided as some of this tissue may have been damaged or altered by the excision process. The tissue thickness along the ultrasound axis was measured to the nearest millimeter using the ultrasound machine’s on-screen caliper tool. The coordinates of the 3D positioning system were recorded to be used as a reference location for the tissue placement for experiments at subsequently higher frequencies. With the tissue in place between the probe and hydrophone, two redundant through-tissue acoustic measurements were taken at −0, −2, −4, and −6 dB power settings. It should be noted that for a few of the thickest samples, low power through-tissue signals could not be measured at the highest frequency settings (4.0, 5.0 MHz) due to attenuation.

To summarize, for each ultrasound probe, the aforementioned process was repeated at every frequency setting, going from lower to higher frequencies. At each frequency setting, the probe position was scanned to find the maximum peak-to-peak amplitude in saline and reference measurements were performed. Then the tissue sample was moved back into the position at which the previous through-tissue measurements were taken, and small adjustments were made to find the tissue position which produced the local maximum peak-to-peak acoustic amplitude, and through-tissue measurements were recorded. Hence for a given tissue sample, 80 measurements were attempted with each probe, for a total of 160 measurements per sample.

Data selection

Two measurements were taken for every probe-power-frequency-sample combination. The purpose of the redundant measurements was to serve as a safeguard against data corruption. As such, redundant measurements were not used in the final analysis. This did not appear to appreciably change the results. Additionally, at each frequency setting, attenuation coefficient values that were more than three standard deviations from the mean at that frequency were marked as outliers and were not used in the analysis and/or included in the reported results, except where otherwise indicated. Only a single outlier was detected.

Analysis: obtaining the pressure signal

Acoustic signals were obtained by converting the recorded hydrophone voltage signals into the frequency domain and calibrating the various frequency components with frequency-dependent hydrophone sensitivity data (e.g., pressure per unit voltage) before converting back to the time domain. Sensitivity data was provided by the hydrophone manufacturer (Onda Corp) from 1 to 20 MHz at a 0.05 MHz resolution and linear interpolation was used to fill in the gaps. Signal energy outside this range (e.g. from higher harmonics in water) was discarded, though this did not affect the attenuation results which were calculated at center frequencies (as defined by FDA 2008) from 1.6 to 5.0 MHz. All calculations and analyses were performed using MATLAB (Mathworks, Natick, MA).

Analysis: tissue attenuation calculations

To calculate the attenuation of a through-tissue signal, its complex amplitude was compared to that of a reference (i.e., through-saline) signal in the frequency domain. Both pressure signals were transformed into the frequency domain using Matlab’s FFT function. The portion of the pressure signal within the −3 dB bandwidth was extracted (FDA 2008). Approximating the ultrasound wave at the hydrophone as a plane wave, at a given frequency f the acoustic attenuation coefficient α(f) can be calculated as

$$\alpha (f)=\frac{1}{d}\left[20{\text{log}}_{10}\left(\frac{4z_t{z}_s}{{\left(z_t+z_s\right)}^2}\right)-20{\text{log}}_{10}\left(\frac{|P_t(f)|}{|P_s(f)|}\right)\right]\text{dB}/\text{cm}.$$ #(1)

Here the t and s subscripts indicate tissue and saline. d is the tissue sample thickness in cm. z is the acoustic impedance (density × sound speed) of a medium in Rayl (i.e. kg/s∙m²). P(f) is the complex pressure.

The first term of Equation (1) represents the portion of the acoustic wave reflected by the saline-tissue interface. The second term represents the portion of the acoustic wave attenuated by the tissue sample, relative to saline. If we assume constant densities and sound speeds of ρ_s = 1004.6 kg/m³, c_s = 1534 m/s, ρ_t = 1000 kg/m³, and c_t = 1540 m/s then the acoustic impedance values for soft tissue and saline are such that the reflective term is of order O(10⁻²). From tissue measurements, we know that the absorptive term is of order O(1), so the attenuation coefficient can be reasonably approximated as

$$\alpha (f)=\frac{20}{d}{\text{log}}_{10}\left(\frac{|P_t(f)|}{|P_s(f)|}\right)\text{dB}/\text{cm}.$$ #(2)

For each through-saline/tissue measurement pair, the attenuation coefficient was calculated at the reference center frequency f_c,s using this expression. This analysis neglects losses due to the plastic zipper bag used to hold the tissue samples, which did not appear to introduce significant attenuation. Specifically, when separately tested for the most nonlinear case (f_c = 5 MHz, 0 dB) the plastic zipper bag produced less than 1% change in the peak positive hydrophone voltage relative to saline.

As part of our effort to describe the measured attenuation data and its dependence on frequency, linear and power-law fits of the forms α(f_c,s) = mf dB/cm and α(f_c,s) = kf_c,s^b dB/cm, respectively, are used, where m, k, and b are constants. This was done using MATLAB’s built-in curve fitting tools. The linear fit is performed using a linear least squares method and the power-law fit is performed using a nonlinear least-squares method and a trust-region algorithm.

Analysis: mechanical index calculations

The mechanical index is defined as

$$\text{MI}=\frac{{\text{PRPA}}_s}{\sqrt{f_{c,s}}},$$ #(3)

where f_c,s is the center frequency of the measured signal in saline and PRPA_s is the measured peak rarefactional pressure amplitude, linearly derated by 0.3 dB/cm/MHz. The MI has units of MPa/MHz^1/2. The traditional derating of the PRPA by 0.3 dB/cm/MHz is performed to account for the difference in attenuation between water and tissue. The attenuation coefficient of 0.3 dB/cm/MHz is assumed for any path in the body and is less than what has been typically measured in soft tissue (AIUM/NEMA 1992, Nyborg, 2001). To assess the applicability of the MI to lung ultrasound, we will also define an adjusted mechanical index MI* that does not assume an attenuation coefficient, but rather uses the through-tissue measured peak rarefactional pressure amplitudes PRPA_t such that

$${\text{MI}}^{*}=\frac{{\text{PRPA}}_t}{\sqrt{f_{c,s}}},$$ #(4)

such that MI* also has units of MPa/MHz^1/2.

Note that in calculating MI*, the reference center frequency f_c,s from the through-saline measurement is used, even though the through-tissue measured PRPA_t is used. Frequency-dependent attenuation in the intercostal tissue inherently shifts the center frequency of the through-tissue signal by preferentially attenuating the higher frequency components of the signal bandwidth. However, it is most meaningful to compare the through-saline and through-tissue PRPAs at the same frequency and f_c,s is chosen for this because it reflects the center frequency of both the through-saline and pre-attenuated through-tissue signal.

To evaluate the MI for lung ultrasound, we define the difference between the original and adjusted mechanical indices as ε_MI = MI − MI* MPa/MHz^1/2. ε_MI can be thought of as an error measure of how much the on-screen mechanical index over or underestimates the acoustic exposure, due to the difference between the true attenuation and the 0.3 dB/cm/MHz assumption.

To understand how this error depends on relevant ultrasound parameters (e.g., frequency, amplitude, focal depth), we developed a theoretical expression to approximate ε_MI. Let the ultrasound be treated as a plane wave and assume there exists some attenuation coefficient α(f_c,s) (dB/cm) such that PRPA_t may be obtained by derating PRPA_s. This assumption is justified if the energy driving the strongest rarefaction, and hence PRPA_s is predominately at the center frequency f_c,s. Hence, we write a theoretical expression for ε_MI as,

$$\widetilde{\epsilon MI}=\frac{{\text{PRPA}}_s}{\sqrt{f_{c,s}}}\left[\text{exp}\left(-0.3f_{c,s}\mathit{\text{d K}}\right)-\text{exp}\left(-\alpha \left(f_{c,s}\right)\mathit{\text{d K}}\right)\right],$$ #(5)

where d is the sample thickness (i.e., the length of the acoustic path through the attenuative media), and K = ln(10) / 20 Np/dB is a constant to convert α from dB/cm to Np/cm.

The above expression for $\widetilde{\epsilon MI}$. (Equation 5) is useful for understanding the dependence of the mechanical index error on tissue and ultrasound properties, given a specified attenuation function α(f_c,s). In contrast, ε_MI = MI - MI* calculated using (Equations 3) and (4) and experimentally measured values of PRPA, is perhaps more useful for assessing the mechanical index error for the through-tissue ultrasound measurements because it makes no assumptions about the attenuation or wave.

Results

Variations in chest wall samples morphology and composition

Chest wall morphology and composition varied appreciably between individuals. Figure 1 shows an example ultrasound image of sample J with tissue layers labeled as skin, fat, muscle, rib, or lung. The layers are labeled based on what appeared to be the predominant type of tissue in the indicated layer. Figure 3 shows ultrasound images of each tissue sample, obtained in situ, prior to excision. Each image is 4 cm deep and shows the skin layer at the top and deeper layers of fat, muscle, and connective tissue as well as two ribs (three for sample N) and the intercostal space between. Attempts to quantify the dimensions of individual tissue layers were not feasible for all samples because the layers did not always have clear boundaries. There is substantial variation in the thickness of the striated fat layer, which can be seen immediately beneath the skin (See Figure 2 for example). In some images, the pleural line is visible as a bright line that is deeper than but between and adjacent to the ribs. To quantify the morphological variation between samples in situ, the rib depth, rib spacing, and pleural depth measurements (as illustrated in Figure 1) are reported in Table 1 for each sample along with the range and median values.

Figure 3:

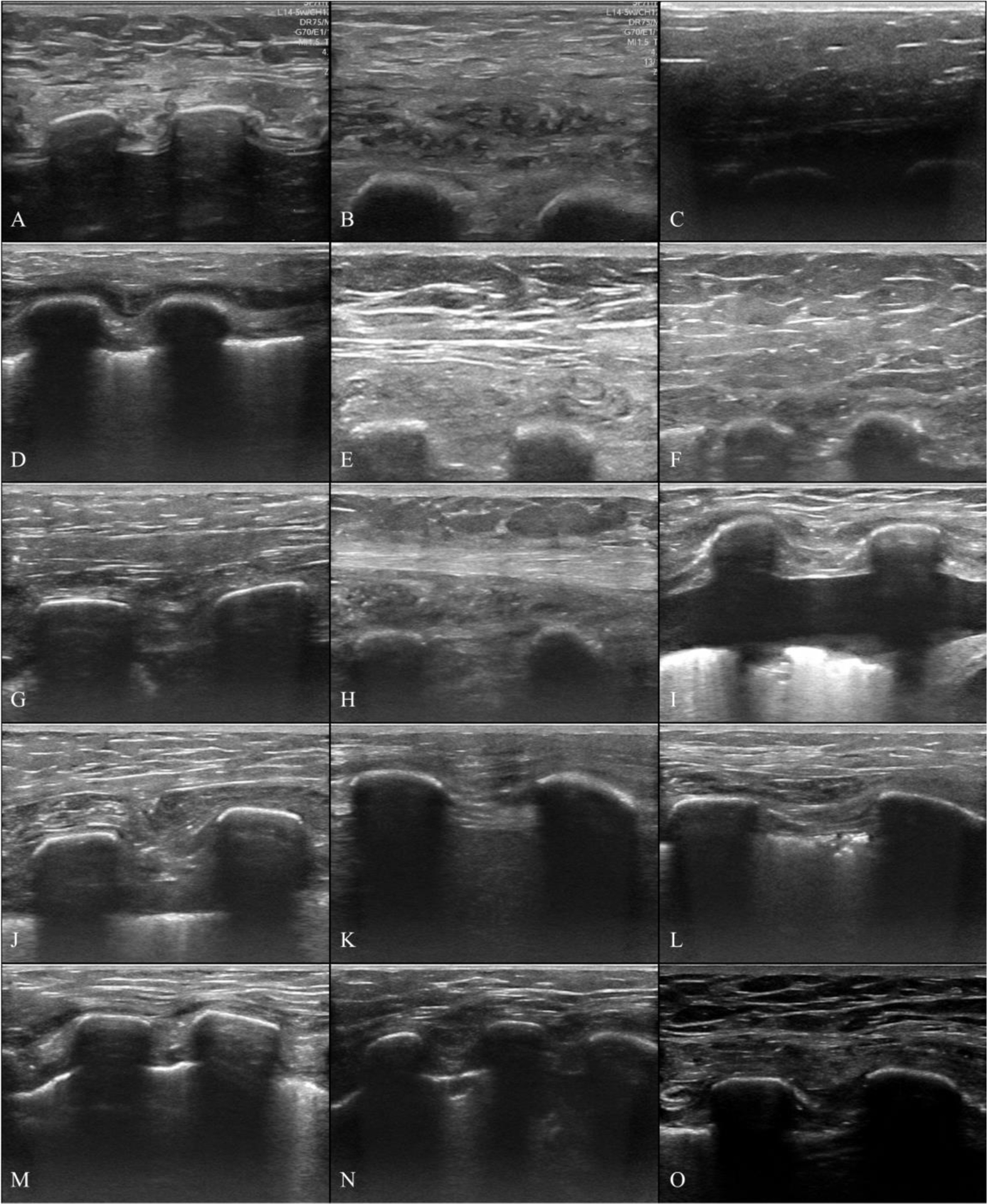
In situ ultrasound images of human chest wall samples. Images were taken immediately before the samples were excised. Images are 4 cm deep and highlight differences in tissue sample morphology between donors. Each image shows a thin layer of skin at the top, subdermal soft tissue (e.g. adipose, muscle, connective tissue, etc…), and two (three for Sample N) ribs.

Table 1:

Donor and tissue sample properties. The sex, age, height, and mass of each tissue donor are shown. The Rib depth, rib spacing, and pleural depth reported here were measured in situ before the samples were excised. The chest wall sample thickness reported was determined from the ultrasound imaging of excised samples, during the attenuation measurements.

Donor	Sex (M/F)	Age (yrs)	Height (cm)	Mass (kg)	BMI (kg/m2)	Rib Depth (cm)	Rib Spacing (cm)	Pleural Depth (cm)	Sample thickness (cm)
A	F	82	142	64	31.4	2.0	0.9	2.6	3.7
B	M	82	175	82	26.6	3.2	1.4	N/A	3.6
C	M	83	178	92	29.0	2.8	1.2	N/A	5.5
D	F	75	165	48	17.5	1.0	0.9	1.8	2.3
E	F	77	173	77	25.8	3.1	1.4	N/A	4.0
F	F	58	137	73	38.6	2.9	0.8	N/A	5.2
G	M	69	173	76	25.4	1.9	1.3	2.7	3.9
H	F	71	155	94	39.3	2.6	1.7	N/A	3.9
I	F	68	157	51	20.7	0.7	1.4	2.8	2.6
J	M	68	170	83	28.5	1.7	1.5	3.2	4.0
K	F	84	157	74	30.0	0.9	1.5	1.8	3.8
L	F	91	152	70	30.1	1.3	1.9	1.9	3.4
M	M	89	178	75	23.7	0.9	0.6	1.7	3.7
N	F	58	165	55	20.1	1.1	1.0	1.9	3.2
O	M	86	175	86	28.1	1.8	1.1	2.8	3.8
Median [Min, Max]	-	77 [58, 91]	165 [137, 178]	75 [48, 94]	28.1 [17.5, 39.3]	1.8 [0.7, 3.1]	1.3 [0.6, 1.9]	N/A	3.8 [2.3, 5.5]

Chest wall attenuation coefficient

Figure 4a shows the attenuation coefficient α(f_c) (dB/cm) calculated for each through-saline/tissue measurement pair at the reference center frequency (blue, circular markers). Power law (red) and linear (black) best-fit curves are also shown. Values describing the best fit lines are reported with the 95% confidence intervals (95% CI) shown in parenthesis. For the linear best fit through zero of the form α = mf dB/cm, m = 1.44 (1.40, 1.47), and the coefficient of determination is R² = 0.57. For the best-fit power law of the form $\alpha \left(f_{c,s}\right)=k{f}_{c,s}^b$ dB/cm, k = 0.83 (0.76, 0.89), b = 1.45 (1.40, 1.51), and R² = 0.78.

Figure 4:

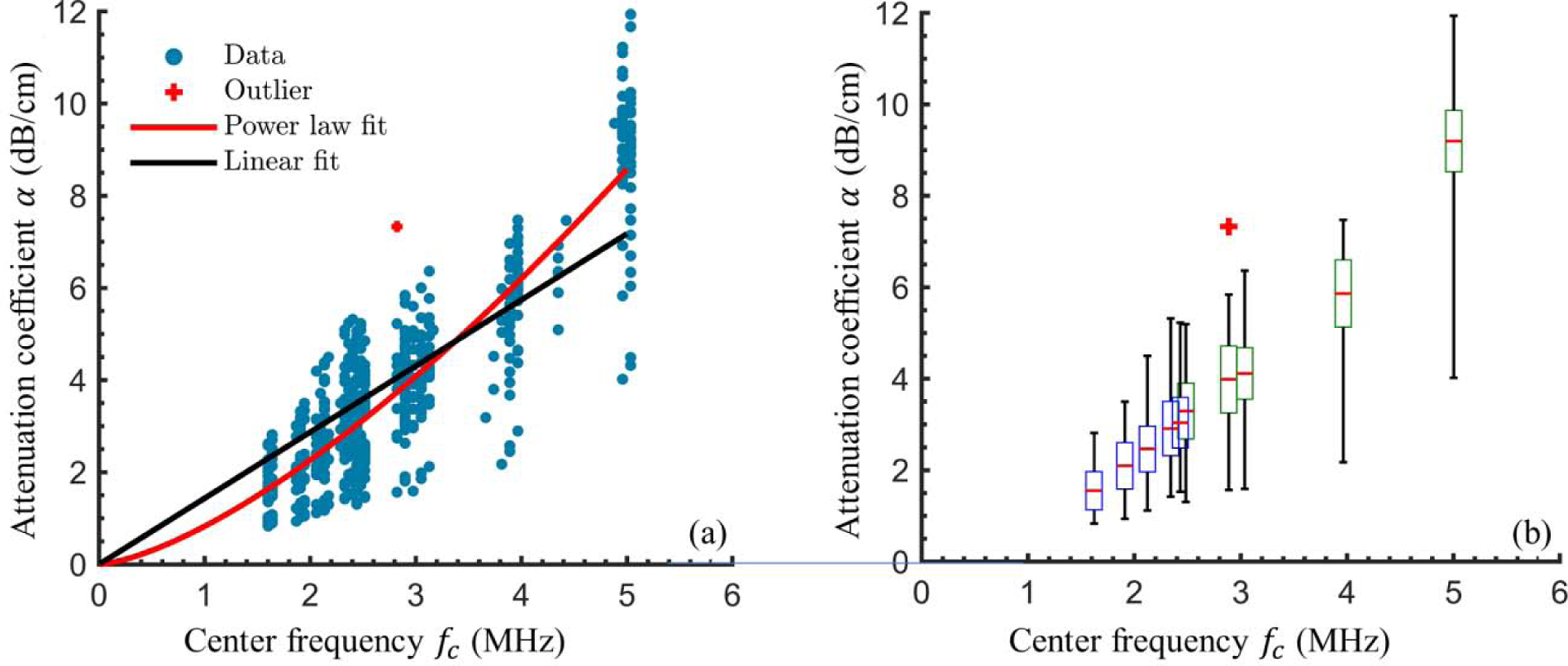
Chest wall attenuation coefficients and best-fit curves. (a) Attenuation coefficient calculated from through-tissue and through-saline ultrasound measurements (blue circles) and best fit linear (black line) and power-law (red line) curves. (b)A box and whisker plot illustrates statistics relevant to the experimentally-determined chest wall attenuation coefficients at the mean reference center frequency for each ultrasound frequency setting. The median (red line), twenty-fifth and seventy-fifth percentiles (bottom and top box boundaries), and range (lines above and below each box) are indicated. The box color indicates the relevant probe (3S – blue, 5S – green). In both (a) and (b) the red plus-symbol indicates an outlier that was not used in the statistical analysis or curve fitting.

Figure 4b contains a box and whisker plot, which illustrates several statistics describing the calculated α values (vertical axis). To perform the statistics, α was grouped according to the frequency setting on the ultrasound machine. The x-axis locations of each group are determined from the mean center frequency of the reference signals recorded at each frequency setting. We make this distinction because the calculated center frequency of the reference signals differed from the on-screen frequency settings by up to 1.2 MHz. The red line indicates the median value of α(f_c,s) measured. The upper and lower bounds of the boxes show the twenty-fifth and seventy-fifth quartiles, with the color indicating which ultrasound probe corresponded to that frequency setting, either 3S (blue) or 5S (green). The black lines above and below the boxes show the range of the data, ignoring outliers, which are denoted by red plus symbols. The range of calculated attenuation coefficients tended to increase with frequency, which was expected since attenuation is known to increase with frequency in soft tissue.

Variation of the attenuation coefficient between donors

To illustrate the variation in the attenuation coefficient α(f_c) from sample to sample, Figure 5 shows the calculated attenuation coefficients and the corresponding best-fit power laws, using a different color for each sample. The best-fit power laws had an average coefficient of determination of R² = 0.94. Sample-specific frequency-normalized linear attenuation coefficients (not shown in Figure) ranged from 0.71 (sample C) to 1.84 (Sample O) dB/cm/MHz and the sample-averaged linear attenuation coefficient was 1.43 dB/cm/MHz with a standard deviation of 0.32 dB/cm/MHz. Though some of the best-fit power-law curves overlap and intersect, the relative attenuation of different samples appeared fairly consistent across the tested frequency range. Simply put, samples which had relatively high (or low) attenuation at low frequencies, typically also had relatively high (or low) attenuation at higher frequencies. The correlation coefficient between the sample-specific average linear attenuation coefficient and the corresponding donor’s body mass index (BMI) was −0.50 (P = 0.06), suggesting that more data is needed to determine a clear relationship between BMI and acoustic attenuation coefficient.

Figure 5:

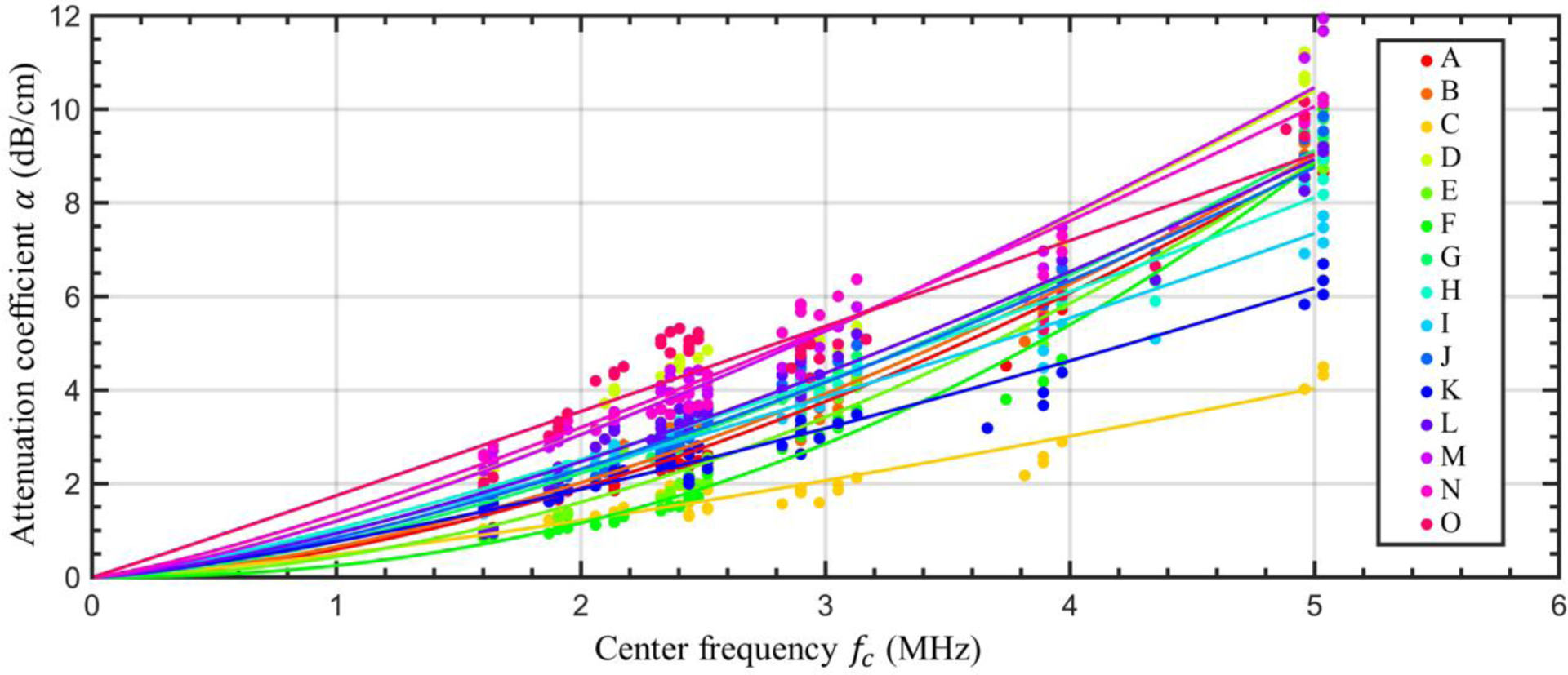
Sample-specific attenuation coefficients. The experimentally determined attenuation coefficients for each through-saline/tissue measurement pair (circular markers) and sample-specific best-fit power laws (lines) are shown. A different color is used for each tissue sample.

Mechanical index measurements and calculations

To assess the efficacy of the mechanical index for diagnostic lung ultrasound, the MI (Equation 3) and MI* (Equation 4) were calculated using the derated through-saline measured PRPA and the through-tissue measured PRPA respectively. Figure 6a shows the mean MI (blue circle) and MI* (red square) for each frequency setting at maximum power (0 dB). The x-location is again determined by the mean reference center frequency. The mechanical index error ε_MI = MI - MI* is equal to the length of each black line segment. The minimum ε_MI was 0.5 at the 1.6 MHz setting. The maximum ε_MI was 1.0 at the 3.1 MHz setting. Both MI and ε_MI scale linearly with PRPA, and the increases in both quantities near 3 MHz appears to be due to an increase in ultrasound amplitude, which could not be precisely controlled on our clinical diagnostic ultrasound machine.

Figure 6:

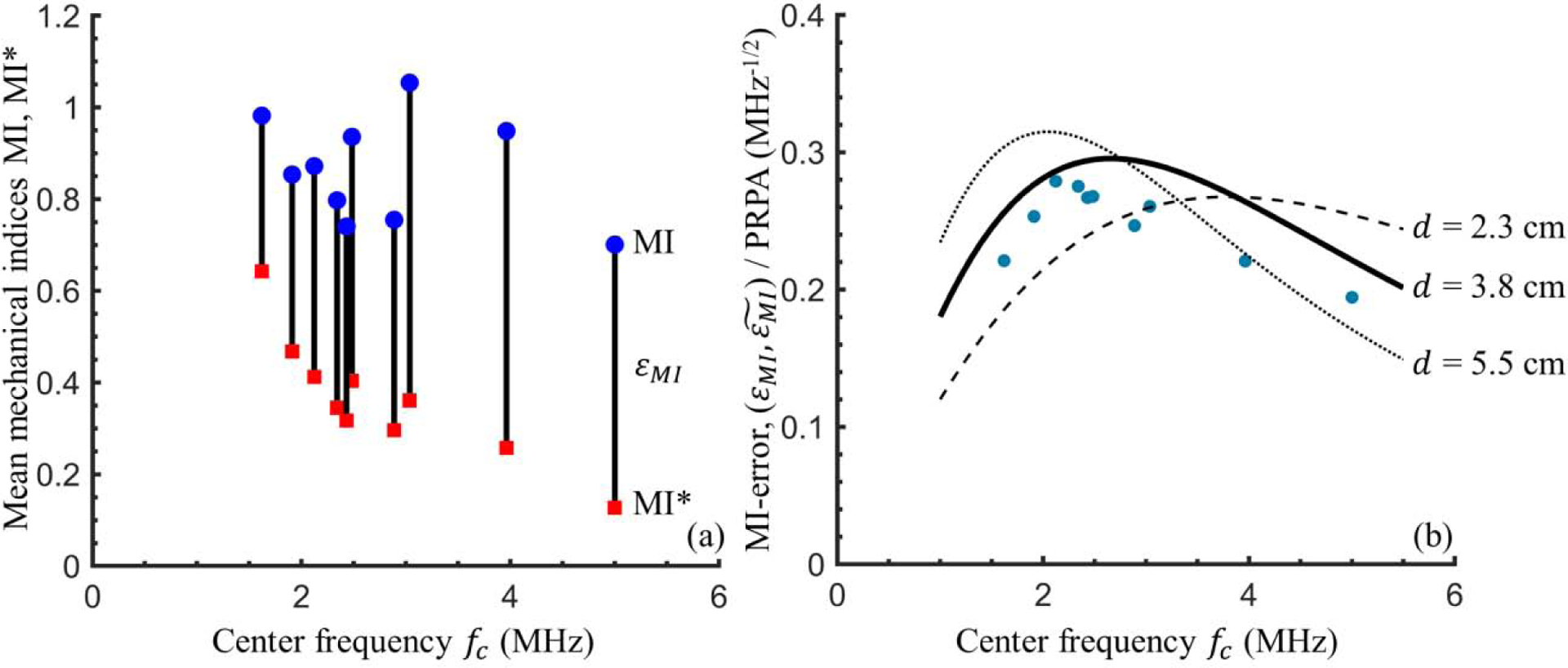
Mechanical index errors calculations. (a) For the maximum power (0 dB) case at each frequency setting, the mean Mechanical Index MI (blue circular markers) and mean adjusted mechanical index MI* (red square markers) are calculated using the through-saline measured PRPA derated by 0.3 dB/cm/MHz and through-tissue measured PRPA, respectively. The black vertical lines of length ε_MI highlight the difference between the two. (b) The PRPA-scaled mechanical index error illustrated. Blue dots show the mean ε_MI/PRPA at each frequency setting. To illustrate the expected dependence of the mechanical index error on frequency and depth, black lines show $\widetilde{{\epsilon }_{MI}}$. (see Equation 5) for tissue thicknesses of d = 2.3 cm (dashed), 3.8 cm (solid), and 5.5 cm (dotted), using the calculated best fit power law for attenuation, $\alpha \left(f_c\right)=0.83f_c^{1.45}$.

The error in the mechanical index increased with increasing frequency, up to some critical frequency, then decreased for frequencies beyond this. The critical frequency depends on the tissue thickness and attenuation. To illustrate the dependence of the mechanical index error on frequency and tissue thickness we take advantage of the aforementioned linear scaling and divide both ε_MI and $\widetilde{\epsilon MI}$. by PRPA and plot the results in Figure 6b. Experimental values (blue circular markers) were averaged across all tissue samples and power settings and the x-location again indicates the mean reference center frequency, at each frequency setting. $\widetilde{{\epsilon }_{MI}}/\text{PRPA}$ was calculated from Equation (5) and is plotted as black lines for the minimum (2.3 cm, dashed), median (3.8 cm, solid), and maximum (5.5 cm, dotted) tissue sample thicknesses with α(f_c) evaluated via the best-fit power law reported earlier in this section. The experimentally determined average values of ε_MI/PRPA showed some variation with frequency, ranging from 0.19 to 0.28 per MPa. As expected, there was considerably more variation across the individual measurements (not shown) — individual values of ε_MI/PRPA ranged from 0.08 to 0.41 per MPa. This again highlights the large difference between tissue samples and donors.

Discussion

Human chest wall attenuation

We measured the bulk attenuation coefficient of human chest wall samples. The chest wall is highly inhomogeneous, with multiple tissue layers (e.g., skin, muscle, fat, connective tissue, etc…), and scattering at tissue interfaces may be an important contribution to the overall attenuation. So, it is not particularly meaningful to compare chest wall attenuation to that of any single tissue, such as fat or muscle. The attenuation reported here should not be taken as an intrinsic tissue property, as one might think of for water or oil, but rather as a useful characterization of acoustic attenuation in humans, as it pertains to lung ultrasound.

The attenuation coefficients found here for human chest wall are higher than those previously measured for chest wall in other mammals but agree well with previously simulated results for humans. The average frequency dependence of the best fit power-law from this study, $\alpha \left(f_c\right)=0.83f_c^{1.45}$. dB/cm, is greater than that previously reported for neonate pigs, α(f) = 1.94f^0.9 dB/cm (Miller et al. 2002). The frequency-normalized attenuation coefficient found here from the linear best fit was α = 1.44 dB/cm/MHz is slightly higher than the α = 1.1–1.3 dB/cm/MHz reported for mice and rats (Miller et al. 2015; Teotico et al. 2001). However, this result is in good agreement with Mast et al. (1999, Table II), which simulated 2.3 MHz plane wave ultrasound passing through geometries based human rib samples and found an average attenuation of 5.8 dB across 13 through-chest wall paths of average length 1.75 cm; this corresponds to a mean frequency-normalized attenuation coefficient of 1.44 dB/cm/MHz.

There are a few possible explanations for the high values of the acoustic attenuation coefficient, relative to rodents and pigs. Variations in the distributions of tissues (e.g., fat, muscle, skin) between human samples are evident, and it is reasonable to expect even greater differences relative to other species. Additionally, it is important to keep in mind here that we measured a bulk attenuation coefficient, which incorporates both absorption and scattering for a multi-layered tissue structure. In this study, effort was made to aim the ultrasound between the ribs, however, it is possible that a portion of the incident field encountered the ribs. Strong scattering is expected of any waves that encounter the ribs because of the relatively large impedance mismatch between bone and soft tissue. It should also be noted that the median age of the tissue donors in this study is 77 years, much greater than the lifespan of any of the previously studied animal models, and the effects of such an age difference on attenuation are not well understood. Also, it is possible for the heating of gas-saturated tissue from 4 to 37 C to result in gas supersaturated tissue and subsequent bubble creation and corresponding increased attenuation, however, there were no obvious signs of this in the ultrasound images or surrounding degassed saline.

Measured attenuation coefficients varied widely between chest wall samples, which is unsurprising given the variation in morphology and composition (see Figure 3). This variation is important to acknowledge when we consider the utility of mathematical approximations of attenuation. The power-law and linear fit curves for the attenuation coefficient have limited ability to capture the range of measured properties. These best-fit curves are useful for understanding the general behavior of ultrasound attenuation in human chest wall but are not recommended for estimating attenuation in any specific individual or chest wall sample.

While person-to-person variation makes it impractical to provide a general expression for human chest wall attenuation, it may be possible to describe or predict local, bulk attenuation properties for individuals. This is suggested by the ability of sample-specific power-laws to accurately capture the measured attenuation behavior (sample-average R² = 0.94). Patient-specific descriptions of ultrasound attenuation characteristics, based on morphological and tissue composition data from ultrasound or other sources, could be a useful area of future research as it may help in optimizing lung ultrasound for both greater image quality and decreased risk of bioeffects. However, the specific dependencies of the attenuation on the donor and ultrasound properties were not obvious in this work and may not be simple to determine.

Assessment of the mechanical index for lung ultrasound

The results of this study suggest that the mechanical index is likely to overestimate the acoustic exposure at the surface of the lung. The mechanical index assumes a constant attenuation coefficient of 0.3 dB/cm/MHz, which is much lower than the human chest wall attenuation coefficients found here. Consequently, the PRPA used in calculating the MI and other clinical metrics (e.g., average intensities) will be greater than what we would physically expect at the lung’s surface. Hence the on-screen MI and other exposure metrics with similar attenuation assumptions (e.g., pulse average intensity) may be improved for diagnostic lung ultrasound by incorporating more realistic attenuation.

The error in the mechanical index due to its assumed attenuation coefficient of 0.3 dB/cm/MHz, defined here as ε_MI = MI − MI* depends on the ultrasound frequency and amplitude and the chest wall attenuation properties. The MI and ε_MI increase linearly with PRPA based on our simple analysis (see Equation 5), such that the greater the PRPA (or the MI), the more the MI will overestimate the lung surface exposure.

As the chest wall thickness or ultrasound frequency increases, the attenuation increases and the PRPA at the focus and MI both decrease. The dependencies of the mechanical index error, ε_MI, on the chest wall thickness, frequency, and attenuation are coupled in a nonlinear way that can be seen in Equation 5 and is not easily explained. While increases in PRPA are always expected to increase the mechanical index error, increases (or decreases) in chest wall thickness or ultrasound frequency may result in an increase or decrease in ε_MI, depending on the specific conditions, as can be seen in Figure 6b. Assessments of the mechanical index errors for practical, clinical scenarios are expected to be further complicated by patient-to-patient variation, along with limited control of and information about the acoustic waveform from typical clinical ultrasound machines.

To summarize, the mechanical index is likely to overestimate the acoustic exposure at the lung surface. The degree to which the MI overestimates is complicated and depends on many factors (e.g., patient-specific attenuation, chest wall thickness, ultrasound frequency), but the error can be reduced by using the lowest power ultrasound which is suited to the task, in accordance with the “As Low as Reasonably Achievable” or ALARA principles. In the past, it has been suggested that a lung-specific ultrasound safety metric is needed and Church and O’Brien (2007) proposed a modified mechanical index specifically for lung bioeffects based on early experimental findings. While the specific form of the proposed index has since proven not to capture the frequency-dependence of the lung hemorrhage bioeffect (Miller 2012), the present work aims to be useful in the future development of such safety metrics. Specifically, this work illustrates some of the differences in ultrasonic pressure amplitudes that are likely to reach human versus animal lungs. Hence, these findings may be important for accurate assessment of the risk of pulmonary capillary hemorrhage in humans. Greater attenuation in humans relative to other animals implies that, on average, greater power ultrasound may be used in humans without breaching pulmonary capillary hemorrhage thresholds. However, the MI is an imperfect metric for lung ultrasound and safety limits should be considered carefully, with acknowledgment of the wide person-to-person variations in chest wall attenuation properties.

Limitations of this work

This study aimed to characterize the acoustic attenuation properties of human chest wall, however, there are several limitations of this work that should be considered when interpreting the results of this study. The first limitation is the small number of chest wall samples and donors used in this study. The nature of the work restricts the sample donors to individuals that donate their bodies to a university anatomical donations program. Additionally, this study included no tissue samples from children or young adults — the youngest sample donor was 57 years old at death. While previous work has not found significant age-dependence in acoustic attenuation coefficients for pigs ages 2 to 71 days (Miller et al. 2002), there has been little work investigating this dependence amongst adults mammal of increasing age. It is worth noting that past research has shown that the chest walls of children ages zero and five years can be less than 1 cm thick. It is plausible that children would have the thinnest, and thus least attenuative, chest walls, and as such could be especially vulnerable to ultrasound-induced pulmonary capillary hemorrhage. Future research investigating ultrasonic attenuation from youth to old age would be valuable.

Additionally, this study only considered a limited range of medical ultrasound frequencies, transducers, and parameters. Here we considered phased array probes with center frequencies from 1.6–5.0 MHz. Clinical lung ultrasound is also performed using curvilinear probes in this range and linear probes up to 13 MHz. In this study, attenuation in some chest wall samples made higher frequency probes impractical for the current research setup. Furthermore, while this study only considered focal depths of 5–6 cm, focal depth may be important in vivo, as it changes the ultrasound incidence angles, and hence path lengths and attenuation. For this study, the source and receiver were chosen to measure an effective chest wall attenuation coefficient relevant to clinical diagnostic ultrasound. These results may vary some from those obtainable via traditional measurement setups using single element unfocused sources and receivers, which typically have narrower band pulses and would not include multiple source array or multipath effects.

Finally, in performing this study it was not possible to perfectly preserve the in vivo morphology of the chest wall. Under typical healthy conditions, the chest wall receives support from the intercostal muscles and connective tissue, which join the ribs to each other and to respiratory muscles. Following death and excision, much of this support is lost. The tissue sample holder used here was designed to hold the sample in as close to its natural conformation as possible, however, without the lung and other support structures of the thoracic cavity, the tissue samples sometimes bulged at the acoustic windows. The thickness of the sample at the measurement windows was sometimes greater than the in situ pleural depth, though the overall thicknesses during measurement align reasonably well with previous axillary chest wall thickness measurements (Schroeder et al. 2013). Though it is not feasible with the current setup, future studies could benefit from an experimental apparatus that allows for the entire chest wall to remain whole.

Summary and conclusions

In this work, we experimentally characterize the acoustic attenuation properties of human chest wall and evaluate the mechanical index as an exposure metric for diagnostic lung ultrasound. A GE Vivid 7 clinical diagnostic ultrasound machine was used to transmit 1.6–5.0 MHz ultrasound through saline and 15 human chest wall samples, and the acoustic pressure was experimentally measured. Through-saline/tissue measurement pairs were compared to calculate acoustic attenuation coefficients. These measurements were used to evaluate the efficacy of the mechanical index for lung ultrasound.

Based on the results of this study, we offer three conclusions. First, ultrasonic attenuation in the human chest wall is greater than that previously measured for other mammals (i.e., mice, rats, and pigs). For the 1.6–5.0 MHz frequency range considered here, the frequency normalized bulk attenuation coefficient of human chest wall intercostal tissue was 1.44 dB/cm/MHz, based on a linear best-fit curve of the attenuation coefficient from all samples. The best fit power-law for the attenuation coefficient was $\alpha \left(f_c\right)=0.83f_c^{1.45}$ dB/cm. Second, ultrasonic attenuation is likely to be patient specific. Bulk attenuation properties in the chest wall varied appreciably between individual chest wall samples, with patient-specific linear attenuation coefficients from 0.71 to 1.84 dB/cm/MHz and power-law frequency dependencies from f^1.0 to f^2.2. Sample-specific attenuation coefficients could typically be well described by a power law. Finally, the mechanical index is likely to overestimate the acoustic exposure at the pleural surface. MI values calculated using PRPA measurements in water derated by 0.3 dB/cm/MHz were up to 1.2 MPa/MHz^1/2 greater than MI* values calculated using through-tissue measured PRPA. This is because the chest wall attenuation found here was consistently much greater than 0.3 dB/cm/MHz. Hence the MI and MI-based limitations (i.e., MI<1.9) may not be appropriate for assessing lung ultrasound and ensuring its safety.